układu otwartego na płaszczyźnie zmiennej zespolonej. Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:
|
|
|
- Marek Kujawa
- 6 lat temu
- Przeglądów:
Transkrypt
1 Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej. Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco: 1. Układ zamknięty jest stabilny asymptotycznie, przy załoŝeniu, Ŝe równanie charakterystyczne układu otwartego ma k pierwiastków w prawej półpłaszczyźnie i n-k pierwiastków w lewej półpłaszczyźnie, wtedy i tylko wtedy, gdy charakterystyka amplitudowo-fazowa układu otwartego przy zmianie pulsacji ω od - do obejmuje w kierunku dodatnim k razy punkt (-1,j). Układ zamknięty jest stabilny asymptotycznie, przy załoŝeniu, Ŝe równanie charakterystyczne układu otwartego nie ma pierwiastków w prawej półpłaszczyźnie zmiennej zespolonej, wtedy i tylko wtedy, gdy charakterystyka amplitudowofazowa układu otwartego przy zmianie pulsacji ω od - do nie obejmuje punktu (-1,j).. Na płaszczyźnie zmiennej zespolonej punkt (-1,j) nazywamy punktem Nyquista. W pewnych przypadkach wygodniej jest posługiwać tzw. regułą lewej strony, która mówi, Ŝe układ zamknięty jest stabilny, jeŝeli przy wzroście ω od do, punkt (-1,j) znajduje się w obszarze po lewej stronie wykresu G o (jw). W praktycznych zastosowaniach kryterium Nyquista jest szczególnie przydatne w przypadku, gdy układ otwarty jest stabilny. MoŜna wtedy korzystać z przebiegu charakterystyki G o ( jω) układu otwartego zdjętej doświadczalnie, co pozwala na badanie stabilności takŝe układu, którego opis matematyczny nie jest znany. Przykład 1 PokaŜemy obszar płaszczyzny zmiennej zespolonej zakreślany przez charakterystykę amplitudowo fazową stabilnego modelu. 1 T ( s), zmiana pulsacji ω od - do s + 1 Punkt Nyquista nie naleŝy do obszaru zakreślonego przez charakterystykę czyli nie jest przez nią obejmowany. W związku z tym po zamknięciu pętlą sprzęŝenia zwrotnego powstały układ nadal będzie stabilny, co wynika z tw. Nyquista. Transmitancja układu zamkniętego : T ( s) 1 Tz ( s) <- układ jest nadal stabilny, s- 1 + T ( s) s +
2 .5 Nyquist Diagram.4.. Imaginary Axis Real Axis Komendy w Matlabie: Tstf([1],[1 1]); nyquist(ts); Przykład RozwaŜmy układ niestabilny. Zbadamy moŝliwość ustabilizowania modelu układu o transmitancji :.1s + 1 T ( s) Pierwiastki równania charakterystycznego tego modelu to : s +.5s.5 s 1-1, s.5 Wynika stąd, Ŝe model jest niestabilny. W celu ustabilizowania układu opisanego transmitancją T(s) zastosujemy sprzęŝenie zwrotne. Przed zamknięciem pętli sprzęŝenia zwrotnego naleŝy sprawdzić, wykorzystując twierdzenie Nyquista, czy ten zabieg moŝe spowodować ustabilizowanie układu. Z wykonanej charakterystyki widać, Ŝe punkt Nyquista jest nią obejmowany jednokrotnie podczas zmiany pulsacji od - do. PoniewaŜ badany układ ma jeden pierwiastek w prawej półpłaszczyźnie zmiennej zespolonej, wiec na mocy tw. Nyquista wiadomo, Ŝe po zamknięciu pętli sprzęŝenia zwrotnego układ ten stanie się stabilny. Po zamknięciu pętli sprzęŝenia zwrotnego uzyskujemy układ o transmitancji :
3 .1s + 1 Tz ( s), którego pierwiastki leŝą w lewej półpłaszczyźnie zmiennej s +.6s +.5 zespolonej s 1 -.+j,64 oraz s -.-j,64 oraz.5 Nyquist Diagram.4.. Imaginary Axis Komendy w Matlabie: Tstf([.1 1],[ ]); nyquist(ts); Tszfeedback(Ts); Proots([1.6.5]); Przykład Obiekt o transmitancji G( s) s + s k + s + 1 Real Axis pracuje w układzie zamkniętym z regulatorem proporcjonalno-całkującym o transmitancji G r 1 k p 1 + Ti s
4 G r 1 k p 1 + Ti s G( s) s + s k + s + 1 Rys. Błąd! Nie zdefiniowano zakładki. Schemat układu zamkniętego z obiektem statycznym trzeciego rzędu i regulatorem PJ Transmitancja układu otwartego G ( s) G ( s) G( s) o r Rozpatrzymy dwa przypadki regulacji: z regulatorem nastawionym na działanie wyłącznie proporcjonalne i drugi z regulatorem proporcjonalno-całkującym. a) Przyjmiemy wzmocnienie obiektu k 1 oraz wyłączamy działanie całkujące regulatora przez nastawienie czasu izodromu T i. Stąd mamy G o ( s) s k + s p + s + 1 Za pomocą polecenia nyquist z pakietu MATLAB-a, wykonamy wykresy charakterystyk amplitudowo-fazowych układu otwartego Go(jw) dla trzech wartości wzmocnienia regulatora k p, i 4. 1 W ykres Nyquista Go(jw) Q(w) kp w kp kp Rys. Błąd! Nie zdefiniowano zakładki. Charakterystyki amplitudowo-fazowe układu otwartego Go(jw) dla k p,, 4 P(w)
5 Wykresy Nyquista układu otwartego Go(jw) obejmują trzy charakterystyczne przypadki regulacji. W pierwszym z nich dla k p charakterystyka Go(jw) przy zwiększaniu częstotliwości ω od do nie obejmuje punktu (-1,j) układ zamknięty jest wtedy stabilny. W drugim przypadku dla k p charakterystyka G(jw) przechodzi przez punkt (- 1,j) układ jest na granicy stabilności. Wreszcie dla k p 4 charakterystyka Go(jw) przy wzroście ω od do obejmuje punkt (-1,j) układ po zamknięciu sprzęŝenia zwrotnego będzie niestabilny. Potwierdzenie tego znajdujemy przez stwierdzenie połoŝenia biegunów transmitancji układu zamkniętego na płaszczyźnie zmiennej zespolonej. Wyznaczamy transmitancję układu zamkniętego Go ( s) Gz ( s) 1+ G ( s) s o + s k p + s + k A stąd równanie charakterystyczne układu M z ( s) s + s + s + k p + 1 p + 1 Wyznaczamy pierwiastki równania charakterystycznego za pomocą polecenia roots z pakietu MATLAB-a, dla k p mamy s s j s j Jak widać wszystkie pierwiastki mają części rzeczywiste ujemne, czyli istotnie układ zamknięty spełnia warunek konieczny i dostateczny stabilności. Obliczamy z kolei pierwiastki dla k p s 1 -. s j s j W tym przypadku występują pierwiastki urojone sprzęŝone, zatem układ zamknięty jest na granicy stabilności. W końcu dla k p 4, mamy pierwiastki s s j s j Tym razem występują pierwiastki zespolone sprzęŝone, których części rzeczywiste są dodatnie, wobec tego układ zamknięty jest dla tego przypadku niestabilny. Innym sposobem jak najbardziej wizualnym, zaprezentowania reakcji układu zamkniętego na zakłócenie w postaci skoku jednostkowego przyłoŝonego do jego wejścia, jest przedstawienie przebiegów charakterystyk skokowych.
6 6 4 Reakcja układu zamkniętego na skok jednostkowy dla kp dla kp4 dla kp W yjscie Czas [sek] Rys. Błąd! Nie zdefiniowano zakładki. Odpowiedzi układu zamkniętego z regulatorem proporcjonalnym na zakłócenie na wejściu w postaci skoku jednostkowego b) Zbadamy teraz stabilność układu zamkniętego z regulatorem proporcjonalnocałkującym dla stałego wzmocnienia regulatora kp 1 i róŝnych wartości czasu izodromu. Wykonujemy charakterystyki amplitudowo-fazowe układu otwartego G o kk p ( Ti s + 1) ( s) T s( s + s + s + 1) i
7 .5 W ykres Nyquista Go(jw) Ti -1.5 Ti 1 Q(w) Ti, w Rys. 4 Charakterystyki amplitudowo-fazowe układu otwartego Go(jw) z regulatorem proporcjonalno-całkującym przy k p 1 dla czasu izodromu T i,8, 1 i Układ otwarty jest w tym przypadku astatyczny ze względu na akcję całkującą regulatora. Charakterystyka Nyquista biegnie po ujemnych wartościach od minus nieskończoności do zera przy zwiększaniu częstotliwości od zera do nieskończoności. P(w) JeŜeli wykres G o (jw) przechodzi przez punkt (-1,j), to układ zamknięty jest na granicy stabilności, a na jego wyjściu występują drgania o ustalonej amplitudzie, jak na wykresie dla T i 1 na rys. 5. Transmitancja układu zamkniętego z regulatorem PI przyjmuje postać: Gz ( s) T s i 4 + T s i kk p i i + T s ( T s + 1) + T s(1 + kk i p ) + kk p
8 Stąd dla przyjętych wartości parametrów układu otrzymujemy przebiegi charakterystyk skokowych jak na rys Charakterystyka skokowa 4 Ti 1 Ti Ti,8 Odpowiedz Czas [sek] Rys. 5 Reakcja układu zamkniętego z regulatorem proporcjonalno-całkującym na zakłócenie na jego wejściu w postaci skoku jednostkowego Zbadamy teraz połoŝenie biegunów transmitancji układu zamkniętego z regulatorem proporcjonalno-całkującym. PosłuŜymy się tym razem poleceniem pzmap MATLAB-a, które tworzy wykres na płaszczyźnie zmiennej zespolonej z zaznaczonymi biegunami i zerami transmitancji układu zamkniętego. Jak widać na rys. 6 dla Ti,8 dwa bieguny transmitancji mają części rzeczywiste dodatnie, więc układ zamknięty jest dla tej wartości czasu izodromu niestabilny. Dla Ti 1 układ ma dwa bieguny połoŝone na osi urojonej, zatem jest na granicy stabilności. I wreszcie dla Ti wszystkie bieguny leŝą w lewej półpłaszczyźnie, czyli układ jest w tym przypadku stabilny.
9 Bieguny dla Ti,8 Zero dla Ti,8 Ti 1 Ti 1 Ti Ti Mapa zer i biegunów Imaginary Axis Real Axis Rys. Błąd! Nie zdefiniowano zakładki. Rozkład biegunów i zer transmitancji układu zamkniętego Zapas stabilności Nyguist Zapas wzmocnienia Gm odwrotność długości odcinka wyznaczonego przez początek układu współrzędnych oraz punkt przecięcia wykresu Nyquista z ujemną półosią Re(G(jω)). Zapas fazy Pm kąt między półprostą wychodzącą z początku układu współrzędnych i przechodzącą przez punkt przecięcia wykresu Nyquista z kołem jednostkowym.
10 Wyznaczenie zapasu wzmocnienia i zapasu fazy na podstawie wykresów Bodego Zapas wzmocnienia Gm (ang. gain margin) wartość wzmocnienia, dla którego faza osiąga Jego wartość oznacza o ile moŝna zwiększyć wzmocnienie zanim stracimy stabilność. Zapas fazy Pm (ang. phase margin) wartość fazy dla częstotliwości, przy której zmocnienie wynosi 1 ( db). Jego wartość oznacza o ile moŝna zmniejszyć przesunięcie fazowe zanim stracimy stabilność. W celu wyznaczenia zapasu fazy naleŝy wyznaczyć tzw. pulsację odcięcia, tj. pulsacje,która spełnia warunek lg M(ωo) a następnie określić fazę Φ(ωo). Zapasem fazy określa się sumę f 18 - Φ(ωo) [deg] Jeśli jest ona dodatnia układ jest stabilny z zapasem fazy f, który mówi o tym, o ile moŝna zwiększyć fazę układu otwartego bez zmiany jego wzmocnienia, aby układ pozozstawał jeszcze stabilnym. Zapas modułu moŝna wyznaczyć określając ω dla której Φ(ω -Π) -18 deg a następnie pomierzyć dla tej samej pulsacji moduł Lm(ω -Π). Jest on równy zapasowi modułu, gdyŝ właśnie o tyle moŝna zwiększyć moduł w układzie, aby przy niezmiennej fazie pozostawał on stabilny. Aby wyznaczyć, o ile moŝna zwiększyć wzmocnienie układu otwartego, naleŝy skorzystać z zaleŝności: LmlgK.
11 Przykład 4 Model o transmitancji : s +.5 K ( s) s(.1s +.7s +.) Wyznaczyć zapas amplitudy i fazy na charakterystyce Bodego. K s) s(.1s s s +.).1s s +.5 ( 4 Komendy w Matlabie: Kstf([1.5],[.1.7. ]) Figure(1),margin(Ks); kroots([.1.7. ]) figure(),nyquist(ks); +.7s +.s
12 5 Bode Diagram Gm Inf, Pm -4. deg (at 1.8 rad/sec) Magnitude (db) Phase (deg) Frequency (rad/sec) Biegunami modelu są liczby s 1, s -7.6, s.1+j.651, s 4.1-j.651 Model ten jest niestabilny, co rozpoznajemy po wartościach biegunów modelu. Dwa z nich (s,s4) znajdują się w prawej półpłaszczyźnie zmiennej zespolonej. Według tw. Nyquista zamknięcie pętli sprzęŝenia zwrotnego ustabilizuje model tylko wtedy, gdy charakterystyka modelu dwukrotnie obejmuje punkt Nyquista przy zmianie pulsacji od - do. PoniewaŜ charakterystyka fazowa znajduje się poniŝej linii odpowiadającej przesunięciu fazowemu π to punkt Nyquista nie jest obejmowany przez nią ani razu. Objęcie danego modelu pętlą sprzęŝenia zwrotnego nie ustabilizuje go. Charakterystykę pokazano poniŝej.
13 6 Nyquist Diagram 4 Imaginary Axis Real Axis Kryterium stabilności Michałowa Układ jest stabilny asymptotycznie, jeŝeli charakterystyka amplitudowo-fazowa mianownika transmitancji przebiega kolejno, w lewo przez tyle ćwiartek płaszczyzny zespolonej s ile wynosi stopień tego mianownika., tzn charakterystyki układów stabilnych przebiegają kolejno, w lewo przez tyle ćwiartek płaszczyzny ile wynosi ich rząd, gdy pulsacja dąŝy do nieskończoności.
Badanie stabilności liniowych układów sterowania
 Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 6. Badanie
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 6. Badanie
Stabilność. Krzysztof Patan
 Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
( 1+ s 1)( 1+ s 2)( 1+ s 3)
 Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki Stabilność systemów sterowania kryterium Nyquist a Materiały pomocnicze do ćwiczeń termin
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki Stabilność systemów sterowania kryterium Nyquist a Materiały pomocnicze do ćwiczeń termin
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
analogowego regulatora PID doboru jego nastaw i przetransformowanie go na cyfrowy regulator PID, postępując według następujących podpunktów:
 Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Projektowanie układów regulacji w dziedzinie częstotliwości. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
Automatyka i robotyka
 Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
Automatyka i robotyka
 Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
Kompensacja wyprzedzająca i opóźniająca fazę. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Podstawowe człony dynamiczne
 . Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
. Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
Języki Modelowania i Symulacji
 Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
Ćwiczenie nr 6 Charakterystyki częstotliwościowe
 Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Laboratorium nr 3. Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka
 Laboratorium nr 3. Cele ćwiczenia Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka poznanie sposobów tworzenia liniowych modeli układów automatyki, zmiana postaci modeli, tworzenie
Laboratorium nr 3. Cele ćwiczenia Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka poznanie sposobów tworzenia liniowych modeli układów automatyki, zmiana postaci modeli, tworzenie
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
Automatyka i sterowanie w gazownictwie. Regulatory w układach regulacji
 Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Transmitancje i charakterystyki częstotliwościowe. Krzysztof Patan
 Transmitancje i charakterystyki częstotliwościowe Krzysztof Patan Transmitancja systemu czasu ciągłego Przekształcenie Laplace a systemu czasu ciągłego jest superpozycją składowych pochodzących od wymuszenia
Transmitancje i charakterystyki częstotliwościowe Krzysztof Patan Transmitancja systemu czasu ciągłego Przekształcenie Laplace a systemu czasu ciągłego jest superpozycją składowych pochodzących od wymuszenia
PAiTM. materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż.
 PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Podstawowe człony dynamiczne. dr hab. inż. Krzysztof Patan
 Podstawowe człony dynamiczne dr hab. inż. Krzysztof Patan Człon proporcjonalny Równanie w dziedzinie czasu Transmitancja y(t) = Ku(t) Y (s) = KU(s) G(s) = Y (s) U(S) = K Transmiancja widmowa G(s) = K G(jω)
Podstawowe człony dynamiczne dr hab. inż. Krzysztof Patan Człon proporcjonalny Równanie w dziedzinie czasu Transmitancja y(t) = Ku(t) Y (s) = KU(s) G(s) = Y (s) U(S) = K Transmiancja widmowa G(s) = K G(jω)
UKŁADY JEDNOWYMIAROWE. Część II UKŁADY LINIOWE Z OPÓŹNIENIEM
 UKŁADY JEDNOWYMIAROWE Część II UKŁADY LINIOWE Z OPÓŹNIENIEM 1 8. Wprowadzenie do części II W praktyce występują układy regulacji, których człony mogą przejawiać opóźnioną reakcję na sygnał wejściowy. Rozróżniamy
UKŁADY JEDNOWYMIAROWE Część II UKŁADY LINIOWE Z OPÓŹNIENIEM 1 8. Wprowadzenie do części II W praktyce występują układy regulacji, których człony mogą przejawiać opóźnioną reakcję na sygnał wejściowy. Rozróżniamy
Ćw. S-III.3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR
 Dr inż Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw S-III3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem
Dr inż Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw S-III3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem
PRZEMYSŁOWE UKŁADY STEROWANIA PID. Wykład 5 i 6. Michał Grochowski, dr inż. Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki PRZEMYSŁOWE UKŁADY STEROWANIA PID Wykład 5 i 6 Michał Grochowski, dr inż. Studia I stopnia inżynierskie, Semestr IV Charakterystyki częstotliwościowe
Politechnika Gdańska Wydział Elektrotechniki i Automatyki PRZEMYSŁOWE UKŁADY STEROWANIA PID Wykład 5 i 6 Michał Grochowski, dr inż. Studia I stopnia inżynierskie, Semestr IV Charakterystyki częstotliwościowe
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
A-4. Filtry aktywne RC
 A-4. A-4. wersja 4 4. Wstęp Filtry aktywne II rzędu RC to układy liniowe, stacjonarne realizowane za pomocą elementu aktywnego jakim jest wzmacniacz, na który załoŝono sprzęŝenie zwrotne zbudowane z elementów
A-4. A-4. wersja 4 4. Wstęp Filtry aktywne II rzędu RC to układy liniowe, stacjonarne realizowane za pomocą elementu aktywnego jakim jest wzmacniacz, na który załoŝono sprzęŝenie zwrotne zbudowane z elementów
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
Techniki regulacji automatycznej
 Techniki regulacji automatycznej Metoda linii pierwiastkowych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 25 Plan wykładu Podstawy metody linii pierwiastkowych
Techniki regulacji automatycznej Metoda linii pierwiastkowych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 25 Plan wykładu Podstawy metody linii pierwiastkowych
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Transmitancja operatorowa członu automatyki (jakiego??) jest dana wzorem:
 PoniŜej przedstawiono standardowy tok otrzymywania charakterystyk częstotliwościowych: 1. Wyznaczenie transmitancji operatorowej. Wykonanie podstawienia s ωj. Wyznaczenie Re(G(jω )) oraz Im(G(jω ))-najczęściej
PoniŜej przedstawiono standardowy tok otrzymywania charakterystyk częstotliwościowych: 1. Wyznaczenie transmitancji operatorowej. Wykonanie podstawienia s ωj. Wyznaczenie Re(G(jω )) oraz Im(G(jω ))-najczęściej
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Interpolacja, aproksymacja całkowanie. Interpolacja Krzywa przechodzi przez punkty kontrolne
 Interpolacja, aproksymacja całkowanie Interpolacja Krzywa przechodzi przez punkty kontrolne Aproksymacja Punkty kontrolne jedynie sterują kształtem krzywej INTERPOLACJA Zagadnienie interpolacji można sformułować
Interpolacja, aproksymacja całkowanie Interpolacja Krzywa przechodzi przez punkty kontrolne Aproksymacja Punkty kontrolne jedynie sterują kształtem krzywej INTERPOLACJA Zagadnienie interpolacji można sformułować
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ. T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
 REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
Korekcja układów regulacji
 Korekcja układów regulacji Powszechnym sposobem wpływania na jakość procesów regulacji jest wprowadzenie urządzeń (członów) korekcyjnych. W przeważającej większości przypadków niezbędne jest umieszczenie
Korekcja układów regulacji Powszechnym sposobem wpływania na jakość procesów regulacji jest wprowadzenie urządzeń (członów) korekcyjnych. W przeważającej większości przypadków niezbędne jest umieszczenie
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
7.2.2 Zadania rozwiązane
 7.2.2 Zadania rozwiązane PRZYKŁAD 1 (DOBÓR REGULATORA) Do poniŝszego układu (rys.1) dobrać odpowiedni regulator tak, aby realizował poniŝsze załoŝenia: -likwidacja błędu statycznego, -zmniejszenie przeregulowania
7.2.2 Zadania rozwiązane PRZYKŁAD 1 (DOBÓR REGULATORA) Do poniŝszego układu (rys.1) dobrać odpowiedni regulator tak, aby realizował poniŝsze załoŝenia: -likwidacja błędu statycznego, -zmniejszenie przeregulowania
Regulator P (proporcjonalny)
 Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne.
 Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM
 ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
Laboratorium z automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z automatyki Algebra schematów blokowych, wyznaczanie odpowiedzi obiektu na sygnał zadany, charakterystyki częstotliwościowe Kierunek studiów:
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z automatyki Algebra schematów blokowych, wyznaczanie odpowiedzi obiektu na sygnał zadany, charakterystyki częstotliwościowe Kierunek studiów:
1. Podstawowe pojęcia
 1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
cos(w o. t) + jsin(w Q. 3S(u t) - jsinfw t). Obydwa rozwiązania (6.39) są zespolone. Jeżeli teraz przyjmie
 - 156 - Podstawiając (6.38) do (6.37), znaleziono j
- 156 - Podstawiając (6.38) do (6.37), znaleziono j
TEORIA STEROWANIA I, w 5. dr inż. Adam Woźniak ZTMiR MEiL PW
 TEORIA STEROWANIA I, w 5 dr inż. Adam Woźniak ZTMiR MEiL PW Układy LTI- SISO Stacjonarne, przyczynowe liniowe układy z jednym wyjściem i jednym wejściem najczęściej modeluje się przy pomocy właściwej transmitancji
TEORIA STEROWANIA I, w 5 dr inż. Adam Woźniak ZTMiR MEiL PW Układy LTI- SISO Stacjonarne, przyczynowe liniowe układy z jednym wyjściem i jednym wejściem najczęściej modeluje się przy pomocy właściwej transmitancji
Ćwiczenie 3 BADANIE OBWODÓW PRĄDU SINUSOIDALNEGO Z ELEMENTAMI RLC
 Ćwiczenie 3 3.1. Cel ćwiczenia BADANE OBWODÓW PRĄD SNSODANEGO Z EEMENTAM RC Zapoznanie się z własnościami prostych obwodów prądu sinusoidalnego utworzonych z elementów RC. Poznanie zasad rysowania wykresów
Ćwiczenie 3 3.1. Cel ćwiczenia BADANE OBWODÓW PRĄD SNSODANEGO Z EEMENTAM RC Zapoznanie się z własnościami prostych obwodów prądu sinusoidalnego utworzonych z elementów RC. Poznanie zasad rysowania wykresów
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Podstawy środowiska Matlab
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
WZMACNIACZ OPERACYJNY. Podstawowe właściwości wzmacniaczy operacyjnych. Rodzaj wzmacniacza Rezystancja wejściowa Rezystancja wyjściowa
 WZMACNIACZ OPEACYJNY kłady aktywne ze wzmacniaczami operacyjnymi... Podstawowe właściwości wzmacniaczy operacyjnych odzaj wzmacniacza ezystancja wejściowa ezystancja wyjściowa Bipolarny FET MOS-FET Idealny
WZMACNIACZ OPEACYJNY kłady aktywne ze wzmacniaczami operacyjnymi... Podstawowe właściwości wzmacniaczy operacyjnych odzaj wzmacniacza ezystancja wejściowa ezystancja wyjściowa Bipolarny FET MOS-FET Idealny
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Drgania. W Y K Ł A D X Ruch harmoniczny prosty. k m
 Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
PODSTAWY AUTOMATYKI. MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
Matura z matematyki?- MATURALNIE, Ŝe ZDAM! Zadania treningowe klasa I III ETAP
 Matura z matematyki?- MATURALNIE, Ŝe ZDAM! Zadania treningowe klasa I III ETAP I Zadania zamknięte (pkt) Zadanie Liczba - jest miejscem zerowym funkcji liniowej = x + B. f ( x) = x C. f ( x) = x + D. f
Matura z matematyki?- MATURALNIE, Ŝe ZDAM! Zadania treningowe klasa I III ETAP I Zadania zamknięte (pkt) Zadanie Liczba - jest miejscem zerowym funkcji liniowej = x + B. f ( x) = x C. f ( x) = x + D. f
1 Dana jest funkcja logiczna f(x 3, x 2, x 1, x 0 )= (1, 3, 5, 7, 12, 13, 15 (4, 6, 9))*.
 EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 0/0 Odpowiedzi do zadań dla grupy elektronicznej na zawody II stopnia (okręgowe) Dana jest funkcja logiczna f(x 3, x,
EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 0/0 Odpowiedzi do zadań dla grupy elektronicznej na zawody II stopnia (okręgowe) Dana jest funkcja logiczna f(x 3, x,
A-2. Filtry bierne. wersja
 wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy automatyki MATLAB przykłady Materiały pomocnicze do ćwiczeń laboratoryjnych Część III termin T
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy automatyki MATLAB przykłady Materiały pomocnicze do ćwiczeń laboratoryjnych Część III termin T
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów
 ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
jest rozwiązaniem równania jednorodnego oraz dla pewnego to jest toŝsamościowo równe zeru.
 Układy liniowe Układ liniowy pierwszego rzędu, niejednorodny. gdzie Jeśli to układ nazywamy jednorodnym Pamiętamy, Ŝe kaŝde równanie liniowe rzędu m moŝe zostać sprowadzone do układu n równań liniowych
Układy liniowe Układ liniowy pierwszego rzędu, niejednorodny. gdzie Jeśli to układ nazywamy jednorodnym Pamiętamy, Ŝe kaŝde równanie liniowe rzędu m moŝe zostać sprowadzone do układu n równań liniowych
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
Stabilność II Metody Lapunowa badania stabilności
 Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Model dopasowywania się cen na rynku
 Model dopasowywania się cen na rynku autor: Milena Ścisłowska Uniwersytet Kardynała Stefana Wyszyńskiego, wydział Matematyczno Przyrodniczy Warszawa 2013 Prosty model rynku - kupujący i sprzedający na
Model dopasowywania się cen na rynku autor: Milena Ścisłowska Uniwersytet Kardynała Stefana Wyszyńskiego, wydział Matematyczno Przyrodniczy Warszawa 2013 Prosty model rynku - kupujący i sprzedający na
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Kompensator PID. 1 sω z 1 ω. G cm. aby nie zmienić częstotliwości odcięcia f L. =G c0. s =G cm. G c. f c. /10=500 Hz aby nie zmniejszyć zapasu fazy
 Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
6. FUNKCJE. f: X Y, y = f(x).
 6. FUNKCJE Niech dane będą dwa niepuste zbiory X i Y. Funkcją f odwzorowującą zbiór X w zbiór Y nazywamy przyporządkowanie każdemu elementowi X dokładnie jednego elementu y Y. Zapisujemy to następująco
6. FUNKCJE Niech dane będą dwa niepuste zbiory X i Y. Funkcją f odwzorowującą zbiór X w zbiór Y nazywamy przyporządkowanie każdemu elementowi X dokładnie jednego elementu y Y. Zapisujemy to następująco
Analiza ustalonego punktu pracy dla układu zamkniętego
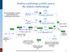 Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II
 ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
KRYTERIA ALGEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH
 KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
3 Podstawy teorii drgań układów o skupionych masach
 3 Podstawy teorii drgań układów o skupionych masach 3.1 Drgania układu o jednym stopniu swobody Rozpatrzmy elementarny układ drgający, nazywany też oscylatorem harmonicznym, składający się ze sprężyny
3 Podstawy teorii drgań układów o skupionych masach 3.1 Drgania układu o jednym stopniu swobody Rozpatrzmy elementarny układ drgający, nazywany też oscylatorem harmonicznym, składający się ze sprężyny
Własności dynamiczne przetworników pierwszego rzędu
 1 ĆWICZENIE 7. CEL ĆWICZENIA. Własności dynamiczne przetworników pierwszego rzędu Celem ćwiczenia jest poznanie własności dynamicznych przetworników pierwszego rzędu w dziedzinie czasu i częstotliwości
1 ĆWICZENIE 7. CEL ĆWICZENIA. Własności dynamiczne przetworników pierwszego rzędu Celem ćwiczenia jest poznanie własności dynamicznych przetworników pierwszego rzędu w dziedzinie czasu i częstotliwości
Temat ćwiczenia. Pomiary przemieszczeń metodami elektrycznymi
 POLITECHNIKA ŚLĄSKA W YDZIAŁ TRANSPORTU Temat ćwiczenia Pomiary przemieszczeń metodami elektrycznymi Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z elektrycznymi metodami pomiarowymi wykorzystywanymi
POLITECHNIKA ŚLĄSKA W YDZIAŁ TRANSPORTU Temat ćwiczenia Pomiary przemieszczeń metodami elektrycznymi Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z elektrycznymi metodami pomiarowymi wykorzystywanymi
Ćwiczenie 14. Maria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYMATYCZNYCH
 Ćwiczenie 14 aria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYATYCZNYCH Zagadnienia: Podstawowe pojęcia kinetyki chemicznej (szybkość reakcji, reakcje elementarne, rząd reakcji). Równania kinetyczne prostych
Ćwiczenie 14 aria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYATYCZNYCH Zagadnienia: Podstawowe pojęcia kinetyki chemicznej (szybkość reakcji, reakcje elementarne, rząd reakcji). Równania kinetyczne prostych
Badanie funkcji. Zad. 1: 2 3 Funkcja f jest określona wzorem f( x) = +
 Badanie funkcji Zad : Funkcja f jest określona wzorem f( ) = + a) RozwiąŜ równanie f() = 5 b) Znajdź przedziały monotoniczności funkcji f c) Oblicz największą i najmniejszą wartość funkcji f w przedziale
Badanie funkcji Zad : Funkcja f jest określona wzorem f( ) = + a) RozwiąŜ równanie f() = 5 b) Znajdź przedziały monotoniczności funkcji f c) Oblicz największą i najmniejszą wartość funkcji f w przedziale
CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera)
 I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa.
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
Z-ZIP-103z Podstawy automatyzacji Basics of automation
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 01/013 Z-ZIP-103z Podstawy automatyzacji Basics of automation A. USYTUOWANIE MODUŁU
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 01/013 Z-ZIP-103z Podstawy automatyzacji Basics of automation A. USYTUOWANIE MODUŁU
ROZWIĄZANIA DO ZADAŃ
 TURNIRJ MATEMATYCZNY ELIPSA dla klas LO ROZWIĄZANIA DO ZADAŃ Zadanie. (2 pkt.) Dla jakich wartości parametru m (m R), część wspólna przedziałów A = (, m m i B = 2m 2, + ) jest zbiorem pustym? / Jeśli A
TURNIRJ MATEMATYCZNY ELIPSA dla klas LO ROZWIĄZANIA DO ZADAŃ Zadanie. (2 pkt.) Dla jakich wartości parametru m (m R), część wspólna przedziałów A = (, m m i B = 2m 2, + ) jest zbiorem pustym? / Jeśli A
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 4 WYZNACZANIE CHARAKTERYSTYK CZĘSTOTLIWOŚCIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia jest doświadczalne
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 4 WYZNACZANIE CHARAKTERYSTYK CZĘSTOTLIWOŚCIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia jest doświadczalne
