Dane modelu - parametry
|
|
|
- Ksawery Stefaniak
- 5 lat temu
- Przeglądów:
Transkrypt
1 Dae modelu - paramer ˆ Ozaczea zmech a0 ax ax - osz w s. zł Budowa modelu: x - welość producj w seach o x - welość zarudea w osobach Meoda MNK Dae: x x X T fucja: raspouj X 0 Crl+Shf+Eer WZÓR a T T X X X fucja: REGLINP X T X T X fuccja: macerz.locz , , ,0044 5, , , , ,495 #N/D! 77, #N/D! 30600,0044 5, , , , ,4 #N/D! 60, , , , a (X T X) - fucja: macerz.odw 6, , , , REGLINP a a a 0 a 0 a a a 0 a S(a ) S(a ) S(a 0) a e a R S F -- S(^- śr) Se Dopasowae x x e e (^- śr) ( - śr) ^ , ,343 75, , , ,087-48,09 658, , , , ,09 905, , , ,6755 ` -88, , , , , ,74 637, , , , , , , , , ,80 346, , , , , , , , ,536 4, ,00 409, , ,097 56, , , , , , , , , ,67-6,6 4690, , ,3403 suma średa e e T e Se R e ˆ ~ R R R R F R -- 9 S e 78075,683 waracja słada reszowego S e 79,49503 odchlee sadardowe resz f 0, ,5% współcz zbeżośc R 0, ,5% współcz deermacj R ~ 0, ,3% sorgowa R F 77, warość sas F -> parz es dopasowaa D T a S X X e 44,3-4570,353 6,49 S (a 0) 44 S(a 0) 643, ,35 754, ,357 S (a ) 754,84 S(a ) 84, D (a) 6, , ,408 S (a ) 3,408 S(a ) 5, cov(a 0,a 0) cov(a 0,a ) cov(a 0,a ) S (a 0) cov(a 0,a ) cov(a 0,a ) D (a) cov(a,a 0) cov(a,a ) cov(a,a ) = cov(a,a 0) S (a ) cov(a,a ) cov(a,a 0) cov(a,a ) cov(a,a ) cov(a,a 0) cov(a,a ) S (a ) Koec eapu esmacj paramerów.. Model wdaje sę bć bardzo dobrze dopasowa R - 94,5% - w lu % model wjaśa zmaę oszów... Ierpreacja paramerów a ,00 [s. zł] osz sałe (a0 - przeważe e posada możlwośc erpreacj) a 60,76 [s. zł/se o] producj wzrośe o jedą jedosę (00 o) wówczas jeśl welość osz wzrośe o 60,8 s. zł, prz założeu, że zarudee e ulege zmae a 6,55 [s. zł/osoba] jeśl welość zarudea wzrośe o jedą jedosę ( osoba) wówczas osz wzrośe o 6,6 s. zł, prz założeu, że welość producj e ulege zmae Ierpreacja błędów szacuów paramerów. S(a 0) 643,6 warość rzeczwsa parameru róż sę od oszacowaej o ± 643,6 [s. zł] S(a ) 84,6 warość rzeczwsa parameru róż sę od oszacowaej o ± 84,6 [s. zł/se o] S(a ) 5,7 warość rzeczwsa parameru róż sę od oszacowaej o ± 5,7 [s. zł/osoba] 3. Odchlee sadardowe resz S e 79,4 [s. zł] warośc eorecze orzmae z modelu różą sę od rzeczwsch średo o 79,4 [s. zł]
2 Tesowae dopasowaa. Badae soośc współcza deermacj. Hpoez: H 0 : R=0 a = a = = a =0 H : R 0 a + a + + a 0 Sasa/procedura R F R Warośd rcza F - odczaa z ablc rozładu F Sedecora dla pozomu soośc a oraz sop swobod: m = m = -- Deczja: jeśl F F, o bra podsaw do odrzucea hpoez H 0 jeśl F > F, o hpoezę H 0 odrzucam Dae: x x REGLINP , , , , , , ,495 #N/D! , #N/D! ,4 #N/D! F= 77, a 0, F 4,56495 Deczja: Wose Iseją paramer sruurale, óre są sascze soe Współcz deermacj jes sascze so Współcz orelacj weloraej jes sascze so. Badae soośc poszczególch paramerów. Hpoez: H 0 : a =0 H : a 0 Sasa/procedura a I S a Warośd rcza I - odczaa z ablc esu Sudea dla pozomu soośc a oraz sop swobod: -- Deczja: jeśl I I, o bra podsaw do odrzucea hpoez H 0 jeśl I > I, o hpoezę H 0 odrzucam pozom soośc a 0,05 Badae soośc a H 0 : a =0 H : a 0 I a S a I 3,08755 a 60,7588 S(a ) 84,5867 I,657 Deczja Wos paramer jes sascze so, zmea X w sposób so wpłwa a zmeą Y Badae soośc a H 0 : a =0 H : a 0 I a S a I 4,66377 a 6,5508 S(a ) 5, I,657 Deczja Wos paramer jes sascze so, zmea X w sposób so wpłwa a zmeą Y Wos oba paramer są sascze soe, obe zmee oddzałwują w sposób so a zmea Y
3 własośc resz - es ser Badae losowośc Hpoez: H 0 : Y model = f(x,x,,x ) H : Y model f(x,x,,x ) Sasa/procedura oraz warośd rcza Dla cągu resz oblczam lczbę ser r pojawaa sę resz dodach ujemch. Dla warośc oraz ozaczającch lczbę resz dodach albo ujemch (bądź odwroe) odczujem z ablc esu ser lewosroego oraz prawosroego warośc: rm oraz rmax. Jeśl: Oblczea rm < r < rmax, e ma podsaw do odrzucea hpoez Ho. w przecwm przpadu hpoezę H 0 ależ odrzucd przjmując e 0, A sera Lczba ser r 6-48,08705 B sera 3-30,0906 B sera ,67554 B sera ,74967 A sera ,43885 A sera ,7968 B sera 4 rm , A sera 5 9 4, A sera 5 rmax , A sera 5-94,57764 B sera 6-6,675 B sera 6 Suma deczja 7,7596E- a Warośc rcze dla esu ser lczb (es lewosro) 0,05 Wose Posać aalcza jes dobrze dobraa Rozład resz jes losow a Warośc rcze dla esu ser lczb (es lewosro) 0,
4 własośc resz - es Hellwga Normalośd rozładu es Hellwga Hpoez: H 0 : F() = F N () u e e s e s e e 0 H : F() F N () Sasa/procedura. Sadarzujem resz zgode ze wzorem:. Wzacza sę warośc dsrbua rozładu N(0,) - F(u ) 3. Wzacza sę zw. cele, órm są przedzał lczbowe powsałe z podzału odca 0,+ a rówch częśc o długośc / ażda. 4. Warośc dsrbua F(u ) przporządowuje sę odpowedm celom, asępe zlcza sę lczbę cel pusch K. 5. Z ablc esu Hellwga odczuje sę warośc rcze K oraz K dla zadaego pozomu soośc Jeśl K K K, o e ma podsaw do odrzuceu H 0 w przecwm przpadu H 0 odrzucam a orzśd H s e e e e e u F(u ) cele le w cel 0, ,5877 0,46 0,6758 0,0000 0, , ,385 -,0 0,57 0,0833 0, , , , 0,4505 0,667 0, , ,3564-0,78 0,78 0,500 0, , ,0509,03 0,8490 0,3333 0, , ,07,4 0,97 0,467 0, , ,5679 -,50 0,067 0,5000 0, , ,074,80 0,9643 0,5833 0, , , ,8 0,5697 0,6667 0, , ,959 0,4 0,5930 0,7500 0, , , ,80 0,07 0,8333 0,967-6, , ,90 0,854 0,967,0000 Suma 0, ,4 Cel pusch 3 s 4, Tablce esu Hellwga Deczja a = 0,05 K K Wos:
5 własośc resz - sałość wara Badae sałośc waracj soośd współcza orelacj pomędz reszam a zmeą czasową Hpoez: H 0 : r = 0 H : r 0 Sasa/Procedura Wzacza współcz orelacj Pearsoa pomędz modułam resz a zmeą czasową oraz wzacza sę warośd sas I r e e e e I r r Odczwaa jes warośd I z ablc esu Sudea dla pozomu soośc a oraz sop swobod m = -. Deczja: jeśl I I, o bra podsaw do odrzucea hpoez H 0 jeśl I > I, o hpoezę H 0 odrzucam pozom soośc a 0,05 e e 0, ,343 współcz orelacj Pearsoa -48,087 48, , ,09 0, , , , ,74 I 0, , , ,797 36,80 I, , , , , , ,903-94, ,578-6,6 6,6 Suma 0, ,56 Deczja Wos waracja e zależ od czasu - sałość waracj
6 własośc resz - auoorelacja Badae auoorelacj rzędu es Durba-Wasoa Hpoez: H 0 : r = 0 H : r > 0 albo H : r < 0 dla dodaej albo ujemej auoorelacj Sasa/Procedura Wzacza współcz d pomędz reszam z oresu a oresu -. Jeśl d (0,) auoorelacja może bd dodaa Jeśl d (,4) auoorelacja może bd ujema wed podsawam d =4-d d e e e Z ablc esu Durba-Wasoa odczujem warośc d u d l. Deczja: jeśl d < d l (bądź dla ujemej d < d l), hpoezę H 0 odrzucam seje auoorelacja rzędu perwszego jeśl d > du, e ma podsaw do odrzucea Ho e wsępuje zjawso auoorelacj jeśl d l d d u e moża podjąd żadej deczj Wzaczee e e - (e -e -) e 0,343-75,6-48,09 0, ,3 658, 3-30,09-48, ,0 905,4 4-88,675-30,09 549, ,4 5 49,74-88, ,66 637, 6 344,439 49, , , 7-36,80 344, ,04 346, ,349-36, , , d,50676 > 9 4, , ,43 805, 0 56,903 4,488 07,80 338,0 d:=4-d, ,578 56, , ,4-6,6-94, , ,4 Suma 0,000 6, , ,4 H 0 : r =0 pozom soośc a 0,05 H : r < 0 K = d l d u d =,50 7 0,467,897 d =,50 8 0,559, ,69, ,697,64 d l 0,8 0,758,604 d u,579 0,8, ,86,56 4 0,905,55 Deczja Wose Należ zasosować es p.. Zbadać soość współcza orelacj lowej Pearsoa pomędz odpowedm reszam Badae auoorelacj rzędu Hpoez: H 0 : r = 0 H : r 0 Sasa/Procedura Wzacza współcz orelacj Pearsoa pomędz reszam z oresu a oresu -. r e e e e e e e e Wzaczaa jes warośd I r I r Odczwaa jes warośd I z ablc esu Sudea dla pozomu soośc a oraz sop swobod m = --. Deczja: jeśl I I, o bra podsaw do odrzucea hpoez H 0 jeśl I > I, o hpoezę H 0 odrzucam pozom soośc a 0,05 Wzaczee warośc współcza Pearsoa r -0, I 0, I,657 Deczja Wose Bra auoorelacj rzędu Wos ogóle model speła założea KMNK
7 prog x pozom bez zma x x x^ (x -x^ ) S 3,888 średa, RMSE^ x x x^ Meoda awa: POZIOM BEZ ZMIAN Progozę a oresów w przód wzacza sę a pozome osaej realzacj zmeej progozowaej: Warośd dla modelu wzaczaa jes jao: ˆ
8 prog x przros bez zma x x x^ (x -x^ ) S 0,9 średa 3,3055 RMSE^ x x x^ Meoda awa: PRZYROST BEZ ZMIAN Progozę a oresów w przód wzacza sę a pozome osaej realzacj zmeej progozowaej oraz osaego przrosu: Warośd dla modelu wzaczaa jes jao: ˆ
9 prog x średa ruch 3 prosa x x x^ (x -x^ ) ,66667, ,33333, , , 7 0,66667, ,66667, , , , , , , ,66667 S, średa,44065 RMSE^ Wzaczam progozę dla średej 3 oresowej x x x^ Model średej ruchomej prosej: ˆ... Progoza za pomocą średej ruchomej prosej wzaczaa jes jao: ~ ~ ~... ~ ozacza warośd rzeczwsą zmeej progozowaej jeśl dam orese lub momece czasu jes zaa bądź ozacza warośd progoz w azwaa jes sałą wgładzaa
10 prog x średa ruch 3 ważoa x x x^ (x -x^ ) ,6963 0, , 3, ,6963 3,6963 0, , , ,4364 8,5959 S, średa, RMSE^ w 0,37037 Należ meć zasalowa dodae SOLVER , ,8585 3, 3,03078,3844, ,596, ,03078, w 0,37037 Wzaczam progozę dla średej 3 oresowej w 3 0,5959 S x x x^ Wag doberam mmalzując błąd modelu RMSE^ Meoda średej ruchomej ważoej: ˆ w w... w w w ~ w ~ w ~ w ~... w w... w 0 w
11 prog x me. BROWNA wgł wł x x x^ (x -x^ ) ,4777 0, ,7675, ,9063 4, , , ,94963, ,45093, ,905 3, ,05398,0878 5, , ,798 3,798 0, , , ,3766 3,06807 S,9339 średa, RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej a 0,47766 alfa Paramer a doberam mmalzując błąd modelu RMSE^ Prose wgładzae władcze (meoda Browa) ˆ ˆ a a ˆ Paramer a zwa jes paramerem wgładzaa, gd ma warośd blsą progoza będze w dużm sopu uwzględała warośc błędów ex pos progoz poprzedch. Jeśl a będze bls 0 progoza będze w małm sopu uwzględała błęd z poprzedch progoz. Dla a= meoda sprowadza sę do progoz awej. Paramer α jes wzacza poprzez mmalzację błędu progoz ex pos (p. RMSE).
12 prog x me. HOLTA I x x x^ (x -x^ ) F S ,3950 0, ,7904 0, , , ,6974, , , ,40787, , , ,8666 0, , , ,3984 0,739879, , ,63477,863846, , ,39065,590004, , ,4053, , , ,8098, , , , ,73089, , , , , , ,9303 S, średa,89575 RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej Paramer a doberam mmalzując błąd modelu RMSE^ a 0,395 b Model low HOLTA Sosowa jes do szeregu czasowego, w órm wsępuje: edecja rozwojowa, wahaa przpadowe. Model e jes dwurówaow: F S a b a F S F F b S F - - wgładzoa warośd zmeej progozowaej a mome lub ores - S - wgładzoa warośd przrosu redu a mome lub ores - a, b - paramer modelu o waroścach z przedzału 0,+ Model low HOLTA Progoza a mome lub ores czasu + : Warośc dla modelu F S ˆ F S Warośc począowe F oraz S mogą bć asępujące: Propozcja F S 3 Wraz wol lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj) 0 Współcz eruow lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj)
13 prog x me. HOLTA II x x x^ (x -x^ ) F S , , ,5487,59337, , ,859 0,035499, , ,7963,637457, , ,07 0,06, , ,9576 0,495955, , ,83356, ,0745 0, ,67547, , , ,39307,58 3, , ,3647 4,3647, , , , , ,779 4,38699 S,6999 średa, RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej Paramer a doberam mmalzując błąd modelu RMSE^ a 0,35647 b 0,4978 Model low HOLTA Sosowa jes do szeregu czasowego, w órm wsępuje: edecja rozwojowa, wahaa przpadowe. Model e jes dwurówaow: F S a b a F S F F b S F - - wgładzoa warośd zmeej progozowaej a mome lub ores - S - wgładzoa warośd przrosu redu a mome lub ores - a, b - paramer modelu o waroścach z przedzału 0,+ Model low HOLTA Progoza a mome lub ores czasu + : Warośc dla modelu F S ˆ F S Warośc począowe F oraz S mogą bć asępujące: Propozcja F S 0 3 Wraz wol lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj) Współcz eruow lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj)
14 prog x me. HOLTA III x x x^ (x -x^ ) F S 0 0 0, 6 0, 0,64 0, , , ,0304 0, , ,876 3, , , ,87045, , , ,0565 0,049, ,6836 7,4504 0,3478, , ,73674,5958, , ,697 3,793, ,5668 0,885 0,78359,8939 0, ,633 3, , , ,9973 3,9973 0, , , , , ,4484 5,59655 S,47868 średa,90743 RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej Paramer a doberam mmalzując błąd modelu RMSE^ a 0,08647 b REGLINP 0, 0 0,4, ,07693, ,5 3 0,4 4,8 Model low HOLTA Sosowa jes do szeregu czasowego, w órm wsępuje: edecja rozwojowa, wahaa przpadowe. Model e jes dwurówaow: F S a b a F S F F b S F - - wgładzoa warośd zmeej progozowaej a mome lub ores - S - wgładzoa warośd przrosu redu a mome lub ores - a, b - paramer modelu o waroścach z przedzału 0,+ Model low HOLTA Progoza a mome lub ores czasu + : Warośc dla modelu F S ˆ F S Warośc począowe F oraz S mogą bć asępujące: Propozcja F S 0 3 Wraz wol lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj) Współcz eruow lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj)
15 prog x red low x x x^ (x -x^ ) (- średe ) S PT V PT 0 9,8974 0,005 30,5 0,646 0,5409 0,5 3 0,637 0,356, ,9988 3,9953 6,5 5,3660 0,400,5 6,733 0,5374 0,5 7,00 0,000 0,5 8 3,4674 0,837,5 9 4,8345,3584 6,5 0 3,06,4439,5 5 3,5688,0484 0,5 3 3,9359 3,9359 0, ,5 3 4,3030,6697 8,86% 4 4,670,38 8,94% 5 5,0373, ,04%, S 0,97083 średa 0, RMSE^ fucja REGLINP 0,367 9,5303 S u ,090 0,664 0,634,0790 średe 6,5 6,5557 0,0000 S 43 9,745,64 S PT S u ( T ) ( ) = 0,367x + 9,5303 R² = 0,634 x x x^ Low (x) MODEL redu lowego ˆ a b b a V PT S PT T 00% a
16 prog x red + ws sez r x x x^ (x -x^ ) c x^ 0 0,4977 0,477 0,600 9,8974 0,06 9,6643,7840-0,600 0,646 0,7354 3,39 0,0538 0,600 0,637 0, ,3986,956-0,600 0,9988 -,9988 5,966 0,00 0,600,3660 0,6340 6,39 0,077-0,600,733-0,733 7,7005 0,4907 0,600,00-0,00 8 3,867,834-0,600,4674 0, ,4347 0,395 0,600,8345,655 0,604 0,367-0,600 3,06 -,06 5 4,690 0,6906 0,600 3,5688,43 3 3,3357 3,3357 0,7-0,600 3,9359-0, ,9033 0,600 z c 4 4,0699-0,600 0,600 0,600 0,600 S 5 5,6375 0,600-0,600-0,600-0,600 S 7,38834 średa 0,6099 RMSE^ 0, ,0000 z fucja REGLINP 0,367 9,5303 0,090 0,664 0,634,0790 6,5557 0,0000 9,745,64 MODEL redu lowego ˆ b a b a = 0,367x + 9,5303 R² = 0,634 x x x^ Low (x) a c z ˆ z z jr, j0 c r c z 0 q q r r z
17 prog x red + ws sez r3 x x x^ (x -x^ ) c x^ 0 9,0979 0,838-0,7995 9,8974 0,06,0979 0,0096 0,8333 0,646 0, ,5979 0,67-0,0338 0,637 0, ,993,4383-0,7995 0,9988 -,9988 5,993 0,0397 0,8333,3660 0,6340 6,6993 0,4890-0,0338,733-0,733 7,3007 0,4890-0,7995,00-0, ,3007 0,0904 0,8333,4674 0, ,8007,4383-0,0338,8345,655 0,40 0,67-0,7995 3,06 -,06 5 4,40 0,3575 0,8333 3,5688,43 3 3,90 3,90 0,838-0,0338 3,9359-0, ,5035-0,7995 z c 4 5,5035 0,8333-0,7995-0,7995-0,7995 S 5 5,0035-0,0338 0,8333 0,8333 0,8333 S 6,3087-0,0338-0,0338-0,0338 średa 0,55 RMSE^ 0,7473 0,0000 z fucja REGLINP 0,367 9,5303 0,090 0,664 0,634,0790 6,5557 0,0000 9,745,64 MODEL redu lowego ˆ b a b a = 0,367x + 9,5303 R² = 0,634 x x x^ Low (x) a c z ˆ z z jr, j0 c r c z 0 q q r r z
18 prog x red oresjedom r faza faza x x x^ (x -x^ ) x x^ x 0 9,9048 0, , ,0000,0000 0, ,6 3 0,876 0,053 3,8476, 4 9 0,6000,5600 4,8905 3,8 5,8476 0, ,79048,4 6,000 0, , ,890 0, , ,6 8 3,8000, , , 9 4 3,7905 0, ,6769 4,8 0,4000 0, ,769 0,0567 Faza Faza 3 3,0000 3,0000 0,0000 0, , ,6 9,4 3 5,7333 0, ,3% 0, ,4% 4 3,6000 0, ,455 0,54786,40 5 6, , ,00% 4, ,00% S 6,090 6, , ,3 5, średa 0,506 RMSE^ 0,7088 fucja REGLINP 0,367 9,5303 0,090 0,664 0,634,0790 6,5557 0,0000 9,745,64 MODEL redu lowego ˆ b a b a x x x^ a
19 prog x red oresjedom r3 faza faza faza x x x^ (x -x^ ) x x^ x x 0 9,4 0, ,4 0,8 0,9 0,8 0, ,3,,8 3 0,9 0,000 3, 3 3,4 4, ,3,6900 4, 5 4,7 3 3,6 5, 0, ,5 6,8 0, ,9 7,3 5,4 7, 0, ,8 8,6 6, ,4 0, ,7 9,9 7, 9 4,7, ,6, 8, 0, 0, ,7 0,0900 Faza Faza Faza 3 3 3,6 3,6 0,3600 0,9000 8,5000,3 9,5 0, ,0000 0,596,430 0, ,43% 0,5965, ,0000 0,6000,69 0, ,3873 0,6000, ,5000 3,0000, , ,00% 3,0000 S 5,7000 4,0500,7000 8,45 0,3 4,05,7 średa 0,4750 RMSE^ 0,68904 fucja REGLINP 0,367 9,5303 0,090 0,664 0,634,0790 6,5557 0,0000 9,745,64 MODEL redu lowego ˆ a b b a x x x^ a
20 prog x pozom bez zma x x x^ (x -x^ ) S 6,45455 średa 7,83995 RMSE^ x x x^ Meoda awa: POZIOM BEZ ZMIAN Progozę a oresów w przód wzacza sę a pozome osaej realzacj zmeej progozowaej: Warośd dla modelu wzaczaa jes jao: ˆ
21 prog x przros bez zma x x x^ (x -x^ ) S 4,9 średa 4,98999 RMSE^ x x x^ Meoda awa: PRZYROST BEZ ZMIAN Progozę a oresów w przód wzacza sę a pozome osaej realzacj zmeej progozowaej oraz osaego przrosu: Warośd dla modelu wzaczaa jes jao: ˆ
22 prog x średa ruch 3 pros x x x^ (x -x^ ) , , , , , , 8 3 0, , , , ,6667 7,6667 8, ,333 S 80,848 średa 3,44674 RMSE^ Wzaczam progozę dla średej 3 oresowej x x x^ Model średej ruchomej prosej: ˆ... Progoza za pomocą średej ruchomej prosej wzaczaa jes jao: ~ ~ ~... ~ ozacza warośd rzeczwsą zmeej progozowaej jeśl dam orese lub momece czasu jes zaa bądź ozacza warośd progoz w azwaa jes sałą wgładzaa
23 prog x średa ruch 3 ważo x x x^ (x -x^ ) S 45,66667 średa 6,7577 RMSE^ w Należ meć zasalowa dodae SOLVER w 0 Wzaczam progozę dla średej 3 oresowej w 3 0 S x x x^ Wag doberam mmalzując błąd modelu RMSE^ Meoda średej ruchomej ważoej: ˆ w w... w w w ~ w ~ w ~ w ~... w w... w 0 w
24 prog x me. BROWNA wgł w x x x^ (x -x^ ) S 56,33333 średa 7, RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej a alfa Paramer a doberam mmalzując błąd modelu RMSE^ Prose wgładzae władcze (meoda Browa) ˆ ˆ a a ˆ Paramer a zwa jes paramerem wgładzaa, gd ma warośd blsą progoza będze w dużm sopu uwzględała warośc błędów ex pos progoz poprzedch. Jeśl a będze bls 0 progoza będze w małm sopu uwzględała błęd z poprzedch progoz. Dla a= meoda sprowadza sę do progoz awej. Paramer α jes wzacza poprzez mmalzację błędu progoz ex pos (p. RMSE).
25 prog x me. HOLTA I x x x^ (x -x^ ) F S , ,9538 5, , ,483 4, , ,56 0, , ,686 8, , ,735 0,5779 8, ,636, , ,9 68, , ,045 7, , ,39 0, , , ,0669 9, , , , , ,933 S 3,6630 średa 5,6699 RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej Paramer a doberam mmalzując błąd modelu RMSE^ a b 0,49948 Model low HOLTA Sosowa jes do szeregu czasowego, w órm wsępuje: edecja rozwojowa, wahaa przpadowe. Model e jes dwurówaow: F S a b a F S F F b S F - - wgładzoa warośd zmeej progozowaej a mome lub ores - S - wgładzoa warośd przrosu redu a mome lub ores - a, b - paramer modelu o waroścach z przedzału 0,+ Model low HOLTA Progoza a mome lub ores czasu + : Warośc dla modelu F S ˆ F S Warośc począowe F oraz S mogą bć asępujące: Propozcja F S 0 3 Wraz wol lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj) Współcz eruow lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj)
26 prog x me. HOLTA II x x x^ (x -x^ ) F S , ,486 89, , , , , ,775, , ,734 0, , ,8668 9, , ,49 7, , ,0893 6,76 7 3, ,9694 0, , , ,9853 8,9803 3, , , ,33,947 S 0,086 średa 4,4846 RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej Paramer a doberam mmalzując błąd modelu RMSE^ a b 0,58399 Model low HOLTA Sosowa jes do szeregu czasowego, w órm wsępuje: edecja rozwojowa, wahaa przpadowe. Model e jes dwurówaow: F S a b a F S F F b S F - - wgładzoa warośd zmeej progozowaej a mome lub ores - S - wgładzoa warośd przrosu redu a mome lub ores - a, b - paramer modelu o waroścach z przedzału 0,+ Model low HOLTA Progoza a mome lub ores czasu + : Warośc dla modelu F S ˆ F S Warośc począowe F oraz S mogą bć asępujące: Propozcja F S 0 3 Wraz wol lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj) Współcz eruow lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj)
27 prog x me. HOLTA III x x x^ (x -x^ ) F S 60 55,7 7, , 77,44 7 7, ,5,5 83 7, ,5 30,5 85 7, ,5,5 9 7, ,5,5 0 7, ,5,5 7, ,5 0,5 3 7, ,5 30,5 5 7, ,5 30,5 7 7, ,5,5 3 7, ,5 38,5 4,5 3 7,5 3 39, ,5 7,94 S 4,78 średa 4,9704 RMSE^ Należ meć zasalowa dodae SOLVER x x x^ Wzaczam progozę dla średej 3 oresowej Paramer a doberam mmalzując błąd modelu RMSE^ a b 0 REGLINP 7,5 55,7,5903 3, , , , ,5 40,3 Model low HOLTA Sosowa jes do szeregu czasowego, w órm wsępuje: edecja rozwojowa, wahaa przpadowe. Model e jes dwurówaow: F S a b a F S F F b S F - - wgładzoa warośd zmeej progozowaej a mome lub ores - S - wgładzoa warośd przrosu redu a mome lub ores - a, b - paramer modelu o waroścach z przedzału 0,+ Model low HOLTA Progoza a mome lub ores czasu + : Warośc dla modelu F S ˆ F S Warośc począowe F oraz S mogą bć asępujące: Propozcja F S 0 3 Wraz wol lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj) Współcz eruow lowej fucj redu oszacowaej dla prób wsępej (p. lu perwszch obserwacj)
28 prog x red low x x x^ (x -x^ ) (- średe ) S PT V PT 60 66,69 39, ,5 7 73,0385,0784 0, ,8077 0,908, ,5769,4867 6, ,346 5,5044, ,54 3,558 0,5 7 06,8846 6,9364 0, , ,3506, ,43 0,948 6, ,93 0,0370,5 3 33,965 8,7707 0,5 3 40, , ,63 30,5 3 47,5000 6,830 4,5% 4 54,69 6,344 4,% 5 6,0385 6, ,08% 7, S,6987 średa 4,76437 RMSE^ fucja REGLINP 6,769 59,5000 S u ,4364 3, 0,960 5,90 średe 6,5 40,5648 0,0000 S ,654 7,3846 S PT S u ( T ) ( ) = 6,769x + 59,5 R² = 0,960 x x x^ Low (x) MODEL redu lowego ˆ a b b a V PT S PT T 00% a
29 prog x red + ws sez r x x x^ (x -x^ ) c x^ z 60 66,305 39,9489 0,053 66,69-6,69 7 7,987 0,9745-0,053 73,0385 -, ,8590 9,8660 0,053 79,8077 3, ,556,376-0,053 86,5769 -, ,3974 5,7477 0,053 93,346 -, ,064 3,7477-0,053 00,54, ,9359 6,569 0,053 06,8846 4, ,606 88,38-0,053 3,6538 9, ,4744 0,484 0,053 0,43 4, ,40 0,099-0,053 7,93-0, ,08 9,077 0,053 33,965 -, , , ,3335-0,053 40,7308-8, ,553 0,053 z c 4 54,79-0,053 0,053 0,053 0,053 S 5 6,0897 0,053-0,053-0,053-0,053 S 7,353 średa,696 RMSE^ 4, ,0000 fucja REGLINP 6,769 59,5000 0,4364 3, 0,960 5,90 40,5648 0, ,654 7,3846 MODEL redu lowego ˆ b a b a = 6,769x + 59,5 R² = 0,960 x x x^ Low (x) a c z ˆ z z jr, j0 c r c z 0 q q r r z
30 prog x red + ws sez r3 x x x^ (x -x^ ) c x^ z 60 65,885 7,9678-0, ,69-6, ,7885 3,986 0, ,0385 -, ,0385 8,7707 0,308 79,8077 3, ,596 0,3554-0, ,5769 -, ,096 9,586 0, ,346 -, ,346,735 0,308 00,54, ,9038 5,9708-0, ,8846 4, , ,8939 0,7500 3,6538 9, ,6538 8,889 0,308 0,43 4, ,5 0,67-0,9808 7,93-0, ,75 3,7755 0, ,965 -, ,965 40,965 80,309 0,308 40,7308-8, ,59-0,9808 z c 4 55,09 0,7500-0,9808-0,9808-0,9808 S 5 6,69 0,308 0,7500 0,7500 0,7500 S 66,074 0, , ,308 średa,78 RMSE^ 4, ,0000 fucja REGLINP 6,769 59,5000 0,4364 3, 0,960 5,90 40,5648 0, ,654 7,3846 MODEL redu lowego ˆ b a b a = 6,769x + 59,5 R² = 0,960 x x x^ Low (x) a c z ˆ z z jr, j0 c r c z 0 q q r r z
31 prog x red oresjedom r faza faza x x x^ (x -x^ ) x x^ x 60 64,380 9, , , ,9048 8, , , ,695 8, , , ,676 7, , , ,0095 4, , , ,4476, , , ,338 3, ,667 5, ,90 95, ,58 64, ,638, ,895 77, ,9905, ,954 4,56 Faza Faza 3 38,769 38,769 45,734 4, ,066667,7749 6, ,667, ,9%, ,55% 4 5,5333 0, ,774 0, , ,580 57, ,00% 7, ,00% S 5, ,7857 9, ,443 60,4905 średa 0,9603 RMSE^ 4,57844 fucja REGLINP 6,769 59,5000 0,4364 3, 0,960 5,90 40,5648 0, ,654 7,3846 MODEL redu lowego ˆ b a b a x x x^ a
32 prog x red oresjedom r3 faza faza faza x x x^ (x -x^ ) x x^ x x 60 6,7, ,7 7 7, ,9 0, ,4 9 93, , , 3 4, ,4 0, ,8 3 35, ,8 7, ,5 56, , , 77, , 5, ,9 98, ,7 68, ,6 9, , ,3 40, 0 7 9,8 7, ,6,600 Faza Faza Faza ,0000, ,0000 0, ,5000,67 4,443 3, ,38%, , ,5000 0,9899 3,663 0, ,050 0,967 5, , ,978, , ,00% 5,607 S 8, ,4500 6, ,05 98, średa 5,0833 RMSE^ 3, fucja REGLINP 6,769 59,5000 0,4364 3, 0,960 5,90 40,5648 0, ,654 7,3846 MODEL redu lowego ˆ a b b a x x x^ a
33 pozom bez zma przros bez zma średa prosa średa ważoa Brow Hol I Hol II Hol III red low red low + wsaź sezoowośc ores red low + wsaź sezoowośc ores 3 red ores jedomee red ores jedomee 3 Zesawee x Meoda RMSE^, ,3055,44065,437304,386484,89575,488959, , , ,7473 0,7088 0,6890 Progoza 3 3, ,4848 3,3766 5,0088 4,37 4,4663 4, ,9036 3,5035 5, , , ,3766 5,58 4,4958 4, ,6706 4, ,5035 3, , ,4364 3,3766 6, ,779 5,4484 5,0373 5, ,0035 6, ,5 zmea x
34 pozom bez zma przros bez zma średa prosa średa ważoa Brow Hol I Hol II Hol III red low red low + wsaź sezoowośc ores red low + wsaź sezoowośc ores 3 red ores jedomee red ores jedomee 3 Zesawee x Meoda RMSE^ 7, , , ,7577 7, ,6699 4,4846 4,9704 4, , , , ,88377 Progoza ,555 34, ,5 47,5 47,553 46,59 50,667 5, ,0 36, ,69 54,79 55,09 5, , ,665 39,33 54,5 6,0385 6,0897 6,69 64,58 53 Zmea x
35 progoza zmea ^ x x x^ x x x^ , , , , , , , , , , , , ,9 3 5, , , ,3 4,5 53 ` ,7588 6,5508 a 0 a a S pt T T x D ax S x, x, x,, x T T e T T T T 44, ,35 6,488 S e 78075,7 D (a) -4570,35 754, ,357 6, ,357 3,408 T = 3 44,3-4570,4 6, ,5-4570,4 754, , ,7 = 967,5 6, ,357 3, ,5 S PT 360,006 T = 4 44,3-4570,4 6, ,5-4570,4 754, , ,7 = 759,4 6, ,357 3, ,5 S PT 356,7343 T = 5 44,3-4570,4 6,4879 4, ,4 754, ,3576 4, ,7 = 678, 6, ,357 3, S PT 335,6756 Progoza przedzałowa wargodość 90% -- 9 T T S PT V pt u b dola graca góra graca b 90% ,9 360,006 0,95%, , ,03,833 N< ,39 356,7343 0,9%, , ,33 u b,6449 N> ,3 335,6756 0,87%, , ,653 3,63 Model speła założea KMNK TAK TAK NIE Graca dola graca góra
36 rafość progoz ^ , , , , , , , , , , , , , , ,305 Współcz Thela ( - ) , , , , , ,90 Współcz Thela , ,09 suma 37566, , ,343 średa 69, ,065 odchlee sadardowe 0, Pearso I ep I I ep I 0, I,50% Błąd względ progoz o,50% I 0, ,35% Neodgadęce warośc średej a cał błąd wpłwa w 9,35% I 0, ,3% Neodgadęce odchlea a cał błąd wpłwa w 4,3% I 3 0, ,4% Neodgadęca eruu zma wpłwa a cał błąd w 3,4% SUMA 0, ,00% współcz Jausow 5, Model jes dalej aual J m I ep ˆ I I ep m I ep I ep I ep s I s ep I m s I 3 I ep s m I ep I ep I ep r I ep
Wnioskowanie statystyczne dla korelacji i regresji.
 STATYSTYKA MATEMATYCZNA WYKŁAD 6 Woskowae statstcze dla korelacj regresj. Aalza korelacj Założee: zmea losowa dwuwmarowa X, Y) ma rozkład ormal o współczku korelacj ρ. X, Y cech adae rówocześe. X X X...
STATYSTYKA MATEMATYCZNA WYKŁAD 6 Woskowae statstcze dla korelacj regresj. Aalza korelacj Założee: zmea losowa dwuwmarowa X, Y) ma rozkład ormal o współczku korelacj ρ. X, Y cech adae rówocześe. X X X...
PROGNOZY I SYMULACJE
 orecasig is he ar of saig wha will happe, ad he explaiig wh i did. Ch. Chafield (986 PROGNOZY I YMULACJE Kaarza Chud Laskowska kosulacje: p. 400A środa -4 czwarek -4 sroa iereowa: hp://kc.sd.prz.edu.pl/
orecasig is he ar of saig wha will happe, ad he explaiig wh i did. Ch. Chafield (986 PROGNOZY I YMULACJE Kaarza Chud Laskowska kosulacje: p. 400A środa -4 czwarek -4 sroa iereowa: hp://kc.sd.prz.edu.pl/
t t t t T 2 Interpretacja: Przeciętna wartość zmiennej objaśnianej różni się od wartości teoretycznej średnio o
 Cele werfacj odelu Werfacja sasczna odelu polega na oblczenu szeregu ernów jaośc odelu oraz werfacj pewnch hpoez sascznch w celu sprawdzena cz na podsawe ego odelu ożna wcągać wnos doczące badanego zjawsa
Cele werfacj odelu Werfacja sasczna odelu polega na oblczenu szeregu ernów jaośc odelu oraz werfacj pewnch hpoez sascznch w celu sprawdzena cz na podsawe ego odelu ożna wcągać wnos doczące badanego zjawsa
t t t t T 2 Interpretacja: Przeciętna wartość zmiennej objaśnianej różni się od wartości teoretycznej średnio o ˆ
 Eonoera Ćwczena Werfacja odelu eonoercznego Maerał poocncze Cele werfacj odelu Werfacja sasczna odelu polega na oblczenu szeregu ernów jaośc odelu oraz werfacj pewnch hpoez sascznch w celu sprawdzena cz
Eonoera Ćwczena Werfacja odelu eonoercznego Maerał poocncze Cele werfacj odelu Werfacja sasczna odelu polega na oblczenu szeregu ernów jaośc odelu oraz werfacj pewnch hpoez sascznch w celu sprawdzena cz
PROGNOZOWANIE. Ćwiczenia 3. tel.: (061)
 Ćwiczeia 3 mgr iż.. Mara Krueger mara.krueger@edu.wsl.com.pl mara.krueger@ilim.poza.pl el.: (06 850 49 57 Meod progozowaia krókoermiowego sał poziom red sezoowość Y Y Y Czas Czas Czas Model aiw Modele
Ćwiczeia 3 mgr iż.. Mara Krueger mara.krueger@edu.wsl.com.pl mara.krueger@ilim.poza.pl el.: (06 850 49 57 Meod progozowaia krókoermiowego sał poziom red sezoowość Y Y Y Czas Czas Czas Model aiw Modele
(liniowy model popytu), a > 0; b < 0
 MODELE EKONOMERYCZNE Model eoomercz o ops sochasczej zależośc adaego zjawsa eoomczego od czów szałującch go, wrażo w posac rówośc lu uładu rówośc. Jeśl p. rozparujem zjawso popu a oreślo owar lu grupę
MODELE EKONOMERYCZNE Model eoomercz o ops sochasczej zależośc adaego zjawsa eoomczego od czów szałującch go, wrażo w posac rówośc lu uładu rówośc. Jeśl p. rozparujem zjawso popu a oreślo owar lu grupę
Rachunek różniczkowy funkcji wielu zmiennych
 Iormaa - Wład 9 - dr Bogda Ćmel cmelbog@ma.ag.edu.pl Racue różczow ucj welu zmec Z uwag a prosoę zapsu ławe erpreacje gracze ograczm sę jede do ucj lub zmec. Naurale uogólea wprowadzac pojęć a ucje zmec
Iormaa - Wład 9 - dr Bogda Ćmel cmelbog@ma.ag.edu.pl Racue różczow ucj welu zmec Z uwag a prosoę zapsu ławe erpreacje gracze ograczm sę jede do ucj lub zmec. Naurale uogólea wprowadzac pojęć a ucje zmec
PROGNOZOWANIE. mgr Żaneta Pruska. Katedra Systemów Logistycznych.
 PROGNOZOWANIE Kaedra Ssemów Logisczch mgr Żaea Pruska zaea_pruska@wp.pl zaea.pruska@wsl.com.pl PROJEKT 0 pk. (grup 4-osobowe) Projek: Wersja w Wordzie Powia zawierać opis projeku z zasosowaiem eapów progozowaia.
PROGNOZOWANIE Kaedra Ssemów Logisczch mgr Żaea Pruska zaea_pruska@wp.pl zaea.pruska@wsl.com.pl PROJEKT 0 pk. (grup 4-osobowe) Projek: Wersja w Wordzie Powia zawierać opis projeku z zasosowaiem eapów progozowaia.
Rachunek różniczkowy funkcji wielu zmiennych
 EAIB-Iormaa-Wład 9- dr Adam Ćmel cmel@.ag.edu.pl Racue różczow ucj welu zmec Z uwag a prosoę zapsu ławe erpreacje gracze ograczm sę jede do ucj lub zmec. Naurale uogólea wprowadzac pojęć a ucje zmec zosawam
EAIB-Iormaa-Wład 9- dr Adam Ćmel cmel@.ag.edu.pl Racue różczow ucj welu zmec Z uwag a prosoę zapsu ławe erpreacje gracze ograczm sę jede do ucj lub zmec. Naurale uogólea wprowadzac pojęć a ucje zmec zosawam
KORELACJA KORELACJA I REGRESJA. X, Y - cechy badane równocześnie. Dane statystyczne zapisujemy w szeregu statystycznym dwóch cech
 KORELACJA I REGRESJA. KORELACJA X, Y - cech badae rówocześe. Dae statstcze zapsujem w szeregu statstczm dwóch cech...... lub w tablc korelacjej. X Y... l.... l.... l................... k k k... kl k..j......l
KORELACJA I REGRESJA. KORELACJA X, Y - cech badae rówocześe. Dae statstcze zapsujem w szeregu statstczm dwóch cech...... lub w tablc korelacjej. X Y... l.... l.... l................... k k k... kl k..j......l
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
Miary położenia wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości danej zmiennej. Mówią o przeciętnym poziomie analizowanej
 Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Prognozowanie na podstawie szeregów czasowych.
 Progozowaie a podsawie szeregów czasowch. Sładowe szeregów czasowch. Szereg czasow sładowa ssemacza sładowa przpadowa red sał poziom sładowa oresowa wahaia clicze wahaia sezoowe Tred (edecja rozwojowa
Progozowaie a podsawie szeregów czasowch. Sładowe szeregów czasowch. Szereg czasow sładowa ssemacza sładowa przpadowa red sał poziom sładowa oresowa wahaia clicze wahaia sezoowe Tred (edecja rozwojowa
Prognozowanie i symulacje
 Prognozowanie i smulacje Lepiej znać prawdę niedokładnie, niż dokładnie się mlić. J. M. Kenes dr Iwona Kowalska ikowalska@wz.uw.edu.pl Prognozowanie meod naiwne i średnie ruchome Meod naiwne poziom bez
Prognozowanie i smulacje Lepiej znać prawdę niedokładnie, niż dokładnie się mlić. J. M. Kenes dr Iwona Kowalska ikowalska@wz.uw.edu.pl Prognozowanie meod naiwne i średnie ruchome Meod naiwne poziom bez
JEDNOWYMIAROWA ZMIENNA LOSOWA
 JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
TESTY NORMALNOŚCI. ( Cecha X populacji ma rozkład normalny). Hipoteza alternatywna H1( Cecha X populacji nie ma rozkładu normalnego).
 TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
MODELOWANIE I PROGNOZOWANIE
 L.Kowalsk-Modelowae progozowae MODELOWANIE I PROGNOZOWANIE MATERIAŁY DYDAKTYCZNE o Podsawowe charakersk dach sasczch, o Ideks, o Progozowae- wadomośc wsępe, o Modele ekoomercze, o Jedorówaow model low,
L.Kowalsk-Modelowae progozowae MODELOWANIE I PROGNOZOWANIE MATERIAŁY DYDAKTYCZNE o Podsawowe charakersk dach sasczch, o Ideks, o Progozowae- wadomośc wsępe, o Modele ekoomercze, o Jedorówaow model low,
Statystyka. Katarzyna Chudy Laskowska
 Statstka Katarza Chud Laskowska http://kc.sd.prz.edu.pl/ Aalza korelacj umożlwa stwerdzee wstępowaa zależośc oraz oceę jej atężea ZALEŻNOŚCI pomędz CECHAMI: CECHY: ILOŚCIOWA ILOŚCIOWA CECHY: JAKOŚCIOWA
Statstka Katarza Chud Laskowska http://kc.sd.prz.edu.pl/ Aalza korelacj umożlwa stwerdzee wstępowaa zależośc oraz oceę jej atężea ZALEŻNOŚCI pomędz CECHAMI: CECHY: ILOŚCIOWA ILOŚCIOWA CECHY: JAKOŚCIOWA
W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:
 Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
opisać wielowymiarową funkcją rozkładu gęstości prawdopodobieństwa f(x 1 , x xn
 ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
Zajęcia 2. Estymacja i weryfikacja modelu ekonometrycznego
 Zajęcia. Esmacja i werfikacja modelu ekonomercznego Celem zadania jes oszacowanie liniowego modelu opisującego wpłw z urski zagranicznej w danm kraju w zależności od wdaków na urskę zagraniczną i liczb
Zajęcia. Esmacja i werfikacja modelu ekonomercznego Celem zadania jes oszacowanie liniowego modelu opisującego wpłw z urski zagranicznej w danm kraju w zależności od wdaków na urskę zagraniczną i liczb
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 7-8
 Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
PROGNOZOWANIE. mgr Żaneta Pruska. Katedra Systemów Logistycznych.
 PROGNOZOWANIE Kaedra Ssemów Logisczch mgr Żaea Pruska zaea_pruska@wp.pl zaea.pruska@wsl.com.pl PROJEKT 5 pk. (grup 4-osobowe) Projek: Wersja w Wordzie Powia zawierać opis projeku z zasosowaiem eapów progozowaia.
PROGNOZOWANIE Kaedra Ssemów Logisczch mgr Żaea Pruska zaea_pruska@wp.pl zaea.pruska@wsl.com.pl PROJEKT 5 pk. (grup 4-osobowe) Projek: Wersja w Wordzie Powia zawierać opis projeku z zasosowaiem eapów progozowaia.
Statystyka Opisowa Wzory
 tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
Materiały do wykładu 7 ze Statystyki
 Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
ANALIZA DYNAMIKI ZJAWISK (dok.) WYGŁADZANIE szeregu czasowego
 D. Miszczńska,M.Miszczński, Maeriał do wkładu 6 ze Saski, 009/0 [] ANALIZA DYNAMIKI ZJAWISK (dok.). szereg czasow, chroologicz (momeów, okresów). średi poziom zjawiska w czasie (średia armecza, średia
D. Miszczńska,M.Miszczński, Maeriał do wkładu 6 ze Saski, 009/0 [] ANALIZA DYNAMIKI ZJAWISK (dok.). szereg czasow, chroologicz (momeów, okresów). średi poziom zjawiska w czasie (średia armecza, średia
BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ
 Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB WYKŁAD 2 BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB Przkład.
Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB WYKŁAD 2 BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB Przkład.
k k M. Przybycień Rachunek Prawdopodobieństwa i Statystyka Wykład 13-2
 Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
PROGNOZOWANIE I SYMULACJE. mgr Żaneta Pruska. Ćwiczenia 2 Zadanie 1
 PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
Zadanie 1. ), gdzie 1. Zmienna losowa X ma rozkład logarytmiczno-normalny LN (, . EX (A) 0,91 (B) 0,86 (C) 1,82 (D) 1,95 (E) 0,84
 Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
FUNKCJE ZMIENNYCH LOSOWYCH. Uwagi o rozkładzie funkcji zmiennej losowej jednowymiarowej.
 L.Kowals Fucje zmeych losowych FUNKCJE ZMIENNYCH LOSOWYCH Uwag o rozładze fucj zmeej losowej jedowymarowej. Jeśl - soowa, o fucj prawdopodobeńswa P( x ) p, g - dowola o fucja prawdopodobeńswa zmeej losowej
L.Kowals Fucje zmeych losowych FUNKCJE ZMIENNYCH LOSOWYCH Uwag o rozładze fucj zmeej losowej jedowymarowej. Jeśl - soowa, o fucj prawdopodobeńswa P( x ) p, g - dowola o fucja prawdopodobeńswa zmeej losowej
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
Statystyczna analiza miesięcznych zmian współczynnika szkodowości kredytów hipotecznych
 dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
( ) ( ) ( ) ( ) ( ) ( )
 ,,, ~ B, β ( β β ( ( Γ( β Γ + f ( Γ ( + ( + β + ( + β Γ + β Γ + Γ + β Γ + + β E Γ Γ β Γ Γ + + β Γ + Γ β + β β β Γ + β Γ + Γ + β Γ + + β E ( Γ Γ β Γ Γ + + β Γ + Γ β β + β Metoda mometów polega a przyrówau
,,, ~ B, β ( β β ( ( Γ( β Γ + f ( Γ ( + ( + β + ( + β Γ + β Γ + Γ + β Γ + + β E Γ Γ β Γ Γ + + β Γ + Γ β + β β β Γ + β Γ + Γ + β Γ + + β E ( Γ Γ β Γ Γ + + β Γ + Γ β β + β Metoda mometów polega a przyrówau
Prawdopodobieństwo i statystyka r.
 Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
INSTRUKCJA LABORATORIUM Metrologia techniczna i systemy pomiarowe.
 INSTRUKCJA LABORATORIUM Metrologa techcza sstem pomarowe. MTSP pomar MTSP 00 Autor: dr ż. Potr Wcślok Stroa / 5 Cel Celem ćwczea jest wkorzstae w praktce pojęć: mezurad, estmata, błąd pomaru, wk pomaru,
INSTRUKCJA LABORATORIUM Metrologa techcza sstem pomarowe. MTSP pomar MTSP 00 Autor: dr ż. Potr Wcślok Stroa / 5 Cel Celem ćwczea jest wkorzstae w praktce pojęć: mezurad, estmata, błąd pomaru, wk pomaru,
licencjat Pytania teoretyczne:
 Plan wykładu: 1. Wiadomości ogólne. 2. Model ekonomeryczny i jego elemeny 3. Meody doboru zmiennych do modelu ekonomerycznego. 4. Szacownie paramerów srukuralnych MNK. Weryfikacja modelu KMNK 6. Prognozowanie
Plan wykładu: 1. Wiadomości ogólne. 2. Model ekonomeryczny i jego elemeny 3. Meody doboru zmiennych do modelu ekonomerycznego. 4. Szacownie paramerów srukuralnych MNK. Weryfikacja modelu KMNK 6. Prognozowanie
Hipotezy o istotności oszacowao parametrów zmiennych objaśniających ˆ ) ˆ
 WERYFIKACJA HIPOTEZY O ISTOTNOŚCI OCEN PARAMETRÓW STRUKTURALNYCH MODELU Hpoezy o sonośc oszacowao paramerów zmennych objaśnających Tesowane sonośc paramerów zmennych objaśnających sprowadza sę do nasępującego
WERYFIKACJA HIPOTEZY O ISTOTNOŚCI OCEN PARAMETRÓW STRUKTURALNYCH MODELU Hpoezy o sonośc oszacowao paramerów zmennych objaśnających Tesowane sonośc paramerów zmennych objaśnających sprowadza sę do nasępującego
FUNKCJE DWÓCH ZMIENNYCH
 FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
Średnia arytmetyczna Klasyczne Średnia harmoniczna Średnia geometryczna Miary położenia inne
 Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
EKONOMETRIA. Liniowy model ekonometryczny (regresji) z jedną zmienną objaśniającą
 EKONOMETRIA Tema wykładu: Liiowy model ekoomeryczy (regresji z jedą zmieą objaśiającą Prowadzący: dr iż. Zbigiew TARAPATA e-mail: Zbigiew.Tarapaa Tarapaa@isi.wa..wa.edu.pl hp:// zbigiew.arapaa.akcja.pl/p_ekoomeria/
EKONOMETRIA Tema wykładu: Liiowy model ekoomeryczy (regresji z jedą zmieą objaśiającą Prowadzący: dr iż. Zbigiew TARAPATA e-mail: Zbigiew.Tarapaa Tarapaa@isi.wa..wa.edu.pl hp:// zbigiew.arapaa.akcja.pl/p_ekoomeria/
Stanisław Cichocki. Natalia Nehrebecka. Zajęcia 5
 Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH
 STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH 1 Test zgodnośc χ 2 Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład o dystrybuance F). Hpoteza alternatywna H1( Cecha X populacj
STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH 1 Test zgodnośc χ 2 Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład o dystrybuance F). Hpoteza alternatywna H1( Cecha X populacj
Prawdopodobieństwo i statystyka r.
 Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadanie 1. Rzucamy symetryczną monetą tak długo, aż w dwóch kolejnych rzutach pojawią się,,reszki. Oblicz wartość oczekiwaną liczby wykonanych rzutów.
 Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1
 ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
dev = y y Miary położenia rozkładu Wykład 9 Przykład: Przyrost wagi owiec Odchylenia Mediana próbkowa: Przykłady Statystyki opisowe Σ dev i =?
 Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Podstawy opracowania wyników pomiarowych, analiza błędów
 Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
. Wtedy E V U jest równa
 Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
SZEREGI CZASOWE W PLANOWANIU PRODUKCJI W PRZETWÓRSTWIE SPOŻYWCZYM
 SZEREGI CZASOWE W PLANOWANIU PRODUKCJI W PRZETWÓRSTWIE SPOŻYWCZYM Arur MACIĄG Sreszczee: W pracy przedsawoo echk aalzy szeregów czasowych w zasosowau do plaowaa progozowaa produkcj w przewórswe spożywczym.
SZEREGI CZASOWE W PLANOWANIU PRODUKCJI W PRZETWÓRSTWIE SPOŻYWCZYM Arur MACIĄG Sreszczee: W pracy przedsawoo echk aalzy szeregów czasowych w zasosowau do plaowaa progozowaa produkcj w przewórswe spożywczym.
ma rozkład normalny z nieznaną wartością oczekiwaną m
 Zadae Każda ze zmeych losowych,, 9 ma rozkład ormaly z ezaą wartoścą oczekwaą m waracją, a każda ze zmeych losowych Y, Y,, Y9 rozkład ormaly z ezaą wartoścą oczekwaą m waracją 4 Założoo, że wszystke zmee
Zadae Każda ze zmeych losowych,, 9 ma rozkład ormaly z ezaą wartoścą oczekwaą m waracją, a każda ze zmeych losowych Y, Y,, Y9 rozkład ormaly z ezaą wartoścą oczekwaą m waracją 4 Założoo, że wszystke zmee
KURS STATYSTYKA. Lekcja 7 Analiza dynamiki zjawisk (zjawiska w czasie) ZADANIE DOMOWE. Strona 1
 KURS STATYSTYKA Lekcja 7 Aaliza damiki zjawisk (zjawiska w czasie) ZADANIE DOMOWE www.erapez.pl Sroa Część : TEST Zazacz poprawą odpowiedź (lko jeda jes prawdziwa). Paie Szereg damicz o: a) ciąg prędkości
KURS STATYSTYKA Lekcja 7 Aaliza damiki zjawisk (zjawiska w czasie) ZADANIE DOMOWE www.erapez.pl Sroa Część : TEST Zazacz poprawą odpowiedź (lko jeda jes prawdziwa). Paie Szereg damicz o: a) ciąg prędkości
Józef Beluch Akademia Górniczo-Hutnicza w Krakowie. Wpływ wag współrzędnych na wyniki transformacji Helmerta
 Józef Beluch Akadema Górczo-Hutcza w Krakowe płw wag współrzędch a wk trasformacj Helmerta . zór a trasformację współrzędch sposobem Helmerta: = c + b = d + a + a b () 2 2. Dwa modele wzaczea parametrów
Józef Beluch Akadema Górczo-Hutcza w Krakowe płw wag współrzędch a wk trasformacj Helmerta . zór a trasformację współrzędch sposobem Helmerta: = c + b = d + a + a b () 2 2. Dwa modele wzaczea parametrów
Tablica Galtona. Mechaniczny model rozkładu normalnego (M10)
 Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ
 ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ Podstawowe pojęca rachuu prawdopodobeństwa: zdarzee losowe, zdarzee elemetare, prawdopodobeństwo, zbór zdarzeń elemetarych. Def. Nech E będze zborem
ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ Podstawowe pojęca rachuu prawdopodobeństwa: zdarzee losowe, zdarzee elemetare, prawdopodobeństwo, zbór zdarzeń elemetarych. Def. Nech E będze zborem
Planowanie eksperymentu pomiarowego I
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
Statystyka Matematyczna Anna Janicka
 Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
Teoria i praktyka. Wyższa Szkoła Turystyki i Ekologii. Fizyka. WSTiE Sucha Beskidzka Fizyka
 Nepewośc pomarowe. Teora praktka. Prowadząc: Dr ż. Adrzej Skoczeń Wższa Szkoła Turstk Ekolog Wdzał Iformatk, rok I Fzka 014 03 30 WSTE Sucha Beskdzka Fzka 1 Iformacje teoretcze zameszczoe a slajdach tej
Nepewośc pomarowe. Teora praktka. Prowadząc: Dr ż. Adrzej Skoczeń Wższa Szkoła Turstk Ekolog Wdzał Iformatk, rok I Fzka 014 03 30 WSTE Sucha Beskdzka Fzka 1 Iformacje teoretcze zameszczoe a slajdach tej
Statystyczne charakterystyki liczbowe szeregu
 Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZA. Wkład węp. Teora prawdopodobeńwa elemet kombatork 3. Zmee losowe 4. Populace prób dach 5. Teowae hpotez emaca parametrów 6. Te t 7. Te 8. Te F 9. Te eparametrcze 0. Podsumowae dotchczasowego
STATYSTYKA MATEMATYCZA. Wkład węp. Teora prawdopodobeńwa elemet kombatork 3. Zmee losowe 4. Populace prób dach 5. Teowae hpotez emaca parametrów 6. Te t 7. Te 8. Te F 9. Te eparametrcze 0. Podsumowae dotchczasowego
Statystyka Opisowa 2014 część 3. Katarzyna Lubnauer
 Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
Ćwiczenia 10 KORELACJA
 Ćwczea 0 KORELACJA Zadae W odażu przeprowadzom przed wboram prezdecm aazowao poparce da addatów A B W zaprezetowao w tabe: Y addat X płeć A B M 0 40 K 0 30 00 a Naeż prawdzć cz wbór addata a prezdeta zaeż
Ćwczea 0 KORELACJA Zadae W odażu przeprowadzom przed wboram prezdecm aazowao poparce da addatów A B W zaprezetowao w tabe: Y addat X płeć A B M 0 40 K 0 30 00 a Naeż prawdzć cz wbór addata a prezdeta zaeż
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Natalia Nehrebecka. Dariusz Szymański
 atala ehreecka Darusz Szmańsk Wkład . MK przpadek welu zmech. Własośc hperpłaszczz regresj 3. Doroć ć dopasowaa rówaa regresj. Współczk determacj R Dekompozcjawaracj zmeejzależejzależej Współczk determacj
atala ehreecka Darusz Szmańsk Wkład . MK przpadek welu zmech. Własośc hperpłaszczz regresj 3. Doroć ć dopasowaa rówaa regresj. Współczk determacj R Dekompozcjawaracj zmeejzależejzależej Współczk determacj
Analiza współzależności
 Aalza wsółzależośc Pozawae zwązków mędz cecham jes aalzą ze względów ozawczch. W rzeczwsośc rzadko jes ak ab jakaś cecha obeków lub zjawsko ewego rodzaju kszałowało sę zuełe ezależe od ch cech lub zjawsk.
Aalza wsółzależośc Pozawae zwązków mędz cecham jes aalzą ze względów ozawczch. W rzeczwsośc rzadko jes ak ab jakaś cecha obeków lub zjawsko ewego rodzaju kszałowało sę zuełe ezależe od ch cech lub zjawsk.
MODEL SHARP A - MIARY WRAŻLIWOŚCI
 MODEL SHARP A - MIARY WRAŻLIWOŚCI Współzależość cech Rozważam jedostk zborowośc badae ze względu a dwe, lub węcej zmech W przpadku obserwacj opartch a dwóch zmech możem wkreślć dagram korelacj. Każda obserwacja
MODEL SHARP A - MIARY WRAŻLIWOŚCI Współzależość cech Rozważam jedostk zborowośc badae ze względu a dwe, lub węcej zmech W przpadku obserwacj opartch a dwóch zmech możem wkreślć dagram korelacj. Każda obserwacja
Pojęcie modelu. Model ekonometryczny. Przykład modelu ekonometrycznego. Klasyfikacja modeli ekonometrycznych. Etapy analizy ekonometrycznej
 Poęc modlu Modl s o uproszczo przdsw rzczwsośc Lwrc R Kl: Modl s o schmcz uproszcz pomąc so sp w clu wś wwęrzgo dzł form lub osruc brdz somplowgo mchzmu Główą zlą modlu s możlwość go bzpczgo przprowdz
Poęc modlu Modl s o uproszczo przdsw rzczwsośc Lwrc R Kl: Modl s o schmcz uproszcz pomąc so sp w clu wś wwęrzgo dzł form lub osruc brdz somplowgo mchzmu Główą zlą modlu s możlwość go bzpczgo przprowdz
$y = XB KLASYCZNY MODEL REGRESJI LINIOWEJ Z WIELOMA ZMIENNYMI NIEZALEŻNYMI
 KASYCZNY ODE REGRESJI INIOWEJ Z WIEOA ZIENNYI NIEZAEŻNYI. gdz: wtor obsrwacj a zmj Y, o wmarach ( macrz obsrwacj a zmch zalżch, o wmarach ( ( wtor paramtrów struturalch (wtor współczów, o wmarach (( wtor
KASYCZNY ODE REGRESJI INIOWEJ Z WIEOA ZIENNYI NIEZAEŻNYI. gdz: wtor obsrwacj a zmj Y, o wmarach ( macrz obsrwacj a zmch zalżch, o wmarach ( ( wtor paramtrów struturalch (wtor współczów, o wmarach (( wtor
Statystyka powtórzenie (II semestr) Rafał M. Frąk
 Statstka powtórzee (II semestr) Rafał M. Frąk TEORIA, OZNACZENIA, WZORY Rodzaje mar statstczch mar położea - wzaczają przecęta wartość cech statstczej mar zróżcowaa (lub zmeośc, rozproszea, dspersj) -
Statstka powtórzee (II semestr) Rafał M. Frąk TEORIA, OZNACZENIA, WZORY Rodzaje mar statstczch mar położea - wzaczają przecęta wartość cech statstczej mar zróżcowaa (lub zmeośc, rozproszea, dspersj) -
Analiza Matematyczna Ćwiczenia. J. de Lucas
 Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Szeregi czasowe, modele DL i ADL, przyczynowość, integracja
 Szereg czasowe, modele DL ADL, rzyczyowość, egracja Szereg czasowy, o cąg realzacj zmeej losowej, owedzmy y, w kolejych okresach czasu: { y } T, co rówoważe możemy zasać: = 1 y = { y1, y,..., y T }. Najogólej
Szereg czasowe, modele DL ADL, rzyczyowość, egracja Szereg czasowy, o cąg realzacj zmeej losowej, owedzmy y, w kolejych okresach czasu: { y } T, co rówoważe możemy zasać: = 1 y = { y1, y,..., y T }. Najogólej
Pojęcie statystyki. Definicja. Wektorową funkcję mierzalną T: X T(X)=(T 1 (X),...,T k (X)) R k wymiarową statystyką. próby X nazywamy k
 Statystya Wyład Adam Ćmel A4 5 cmel@agh.edu.pl Pojęce statysty Pojęce statysty w statystyce matematyczej jest odpowedem pojęca zmeej losowej w rachuu prawdopodobeństwa. Nech X(X,...,X ) będze próbą z pewej
Statystya Wyład Adam Ćmel A4 5 cmel@agh.edu.pl Pojęce statysty Pojęce statysty w statystyce matematyczej jest odpowedem pojęca zmeej losowej w rachuu prawdopodobeństwa. Nech X(X,...,X ) będze próbą z pewej
Statystyka. Analiza zależności. Rodzaje zależności między zmiennymi występujące w praktyce: Funkcyjna
 Aalza zależośc Rodzaje zależośc mędzy zmeym występujące w praktyce: Fukcyja wraz ze zmaą wartośc jedej zmeej astępuje ścśle określoa zmaa wartośc drugej zmeej (p. w fzyce: spadek swobody gt s ) tochastycza
Aalza zależośc Rodzaje zależośc mędzy zmeym występujące w praktyce: Fukcyja wraz ze zmaą wartośc jedej zmeej astępuje ścśle określoa zmaa wartośc drugej zmeej (p. w fzyce: spadek swobody gt s ) tochastycza
Sprzedaż finalna - sprzedaż dóbr i usług konsumentowi lub firmie, którzy ostatecznie je zużytkują, nie poddając dalszemu przetworzeniu.
 W 1 Rachu maroeoomcze 1. Produ rajowy bruo Sprzedaż fala - sprzedaż dóbr usług osumeow lub frme, órzy osaecze je zużyują, e poddając dalszemu przeworzeu. Sprzedaż pośreda - sprzedaż dóbr usług zaupoych
W 1 Rachu maroeoomcze 1. Produ rajowy bruo Sprzedaż fala - sprzedaż dóbr usług osumeow lub frme, órzy osaecze je zużyują, e poddając dalszemu przeworzeu. Sprzedaż pośreda - sprzedaż dóbr usług zaupoych
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
AKADEMIA MORSKA W SZCZECINIE
 AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
Rachunek prawdopodobieństwa i statystyka matematyczna. Estymacja przedziałowa parametrów strukturalnych zbiorowości generalnej
 Rachek prawdopodobeńswa saysyka maemaycza Esymacja przedzałowa paramerów srkralych zborowośc geeralej Częso zachodz syacja, że koecze jes zbadae ogół poplacj pod pewym kąem p. średa oce z pewego przedmo.
Rachek prawdopodobeńswa saysyka maemaycza Esymacja przedzałowa paramerów srkralych zborowośc geeralej Częso zachodz syacja, że koecze jes zbadae ogół poplacj pod pewym kąem p. średa oce z pewego przedmo.
L.Kowalski PODSTAWOWE TESTY STATYSTYCZNE WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH
 L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
Testy oparte na ilorazie wiarygodności
 Ts opar a loraz wargodośc Probl sowaa hpoz Nch B P=P będz przsrzą sasczą prz cz = =. Probl. Na podsaw prób wu spru zwrfować hpozę wobc alraw. Rozwąza powższgo problu s fuca [] zwaa s sascz zradozowa lub
Ts opar a loraz wargodośc Probl sowaa hpoz Nch B P=P będz przsrzą sasczą prz cz = =. Probl. Na podsaw prób wu spru zwrfować hpozę wobc alraw. Rozwąza powższgo problu s fuca [] zwaa s sascz zradozowa lub
Prognozowanie i symulacje
 Progozowaie i smulacje Ramow pla wkładu. Wprowadzeie w przedmio. rafość dopuszczalość i błąd progoz 3. Progozowaie a podsawie szeregów czasowch 4. Progozowaie a podsawie modelu ekoomerczego 5. Heurscze
Progozowaie i smulacje Ramow pla wkładu. Wprowadzeie w przedmio. rafość dopuszczalość i błąd progoz 3. Progozowaie a podsawie szeregów czasowch 4. Progozowaie a podsawie modelu ekoomerczego 5. Heurscze
Reprezentacja krzywych...
 Reprezeacja rzywych... Reprezeacja przy pomocy fcj dwóch zmeych rzywe płase płase - jedej: albo z z f x y x [ x x2] y [ y y2] f x y g x x [ x x2] Wady: rzywe óre dla pewych x y mogą przyjmować wele warośc
Reprezeacja rzywych... Reprezeacja przy pomocy fcj dwóch zmeych rzywe płase płase - jedej: albo z z f x y x [ x x2] y [ y y2] f x y g x x [ x x2] Wady: rzywe óre dla pewych x y mogą przyjmować wele warośc
STATYSTYKA MATEMATYCZNA WYKŁAD 2 ESTYMACJA PUNKTOWA
 STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
Pomiary bezpośrednie i pośrednie obarczone błędem przypadkowym
 Pomary bezpośrede pośrede obarczoe błędem przypadkowym I. Szacowae wartośc przyblŝoej graczego błędu przypadkowego a przykładze bezpośredego pomaru apęca elem ćwczea jest oszacowae wartośc przyblŝoej graczego
Pomary bezpośrede pośrede obarczoe błędem przypadkowym I. Szacowae wartośc przyblŝoej graczego błędu przypadkowego a przykładze bezpośredego pomaru apęca elem ćwczea jest oszacowae wartośc przyblŝoej graczego
ANALIZA SZEREGÓW CZASOWYCH
 ANALIZA SZEREGÓW CZASWYCH Szereg czasow zbór warośc baanej cech lub warośc baanego zjawska zaobserwowanch w różnch momenach czasu uporząkowan chronologczne. Skłank szeregu czasowego:. enencja rozwojowa
ANALIZA SZEREGÓW CZASWYCH Szereg czasow zbór warośc baanej cech lub warośc baanego zjawska zaobserwowanch w różnch momenach czasu uporząkowan chronologczne. Skłank szeregu czasowego:. enencja rozwojowa
L.Kowalski zadania ze statystyki opisowej-zestaw 5. ZADANIA Zestaw 5
 L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
ANALIZA ZALEŻNOŚCI DWÓCH ZMIENNYCH ILOŚCIOWYCH
 ANALIZA ZALEŻNOŚCI DWÓCH ZMIENNYCH ILOŚCIOWYCH Na ogół oprócz obserwacj jedej zmeej zberam róweż formacje towarzszące, które mogą meć zaczee w aalze teresującej as welkośc. Iformacje te mogą bć p. wkorzstae
ANALIZA ZALEŻNOŚCI DWÓCH ZMIENNYCH ILOŚCIOWYCH Na ogół oprócz obserwacj jedej zmeej zberam róweż formacje towarzszące, które mogą meć zaczee w aalze teresującej as welkośc. Iformacje te mogą bć p. wkorzstae
Ekonometria I materiały do ćwiczeń
 lp daa wkładu ema Wkład dr Doroa Ciołek Ćwiczenia mgr inż. - Rodzaje danch sascznch - Zmienne ekonomiczne jako zmienne losowe 1a) Przkład problemów badawczch hipoeza, propozcja modelu ekonomercznego, zmienne
lp daa wkładu ema Wkład dr Doroa Ciołek Ćwiczenia mgr inż. - Rodzaje danch sascznch - Zmienne ekonomiczne jako zmienne losowe 1a) Przkład problemów badawczch hipoeza, propozcja modelu ekonomercznego, zmienne
MATERIAŁY POMOCNICZE DLA STUDENTÓW DO NAUKI STATYSTYKI
 STATYSTYKA MATERIAŁY POMOCNICZE DLA STUDENTÓW DO NAUKI STATYSTYKI Mara Borowsa STATYSTYKA MATERIAŁY POMOCNICZE DLA STUDENTÓW DO NAUKI STATYSTYKI "Ale t, Pae wszsto pod marą lczbą, wagą urządzłeś" (Ks.
STATYSTYKA MATERIAŁY POMOCNICZE DLA STUDENTÓW DO NAUKI STATYSTYKI Mara Borowsa STATYSTYKA MATERIAŁY POMOCNICZE DLA STUDENTÓW DO NAUKI STATYSTYKI "Ale t, Pae wszsto pod marą lczbą, wagą urządzłeś" (Ks.
STATYSTYKA OPISOWA WYKŁAD 3,4
 STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
Linie regresji II-go rodzaju
 Lam regresj II-go rodzaju zmeej () względem () azwam zadae krzwe g(;,, ) oraz h(;,, ) gd spełają oe odpowedo waruk: E E Le regresj II-go rodzaju ( ( )) ( ) ( ) ( ) ( ) g ;,,... g ;,,... f, dd m,,... (
Lam regresj II-go rodzaju zmeej () względem () azwam zadae krzwe g(;,, ) oraz h(;,, ) gd spełają oe odpowedo waruk: E E Le regresj II-go rodzaju ( ( )) ( ) ( ) ( ) ( ) g ;,,... g ;,,... f, dd m,,... (
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
x, y środek ciężkości zbioru
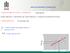 Y ANALIZA REGRESJI I KORELACJI zwązek stochastyczy (losowy), probablstyczy Y X KAŻDEJ WARTOŚCI x ODPOWIADA CAŁY ZBIÓR WARTOŚCI y TWORZĄCYCH OKREŚLONY ROZKŁAD zwązek statystyczy ŷ a a x ŷ średa rozkładu
Y ANALIZA REGRESJI I KORELACJI zwązek stochastyczy (losowy), probablstyczy Y X KAŻDEJ WARTOŚCI x ODPOWIADA CAŁY ZBIÓR WARTOŚCI y TWORZĄCYCH OKREŚLONY ROZKŁAD zwązek statystyczy ŷ a a x ŷ średa rozkładu
Wybór projektu inwestycyjnego ze zbioru wielu propozycji wymaga analizy następujących czynników:
 Wybór projeu wesycyjego ze zboru welu propozycj wymaga aalzy asępujących czyów:. Korzyśc z przyjęca do realzacj daego projeu. 2. Ryzya z m zwązaego. 3. Czasu, óry powoduje zmaę warośc peądza. Czy czasu
Wybór projeu wesycyjego ze zboru welu propozycj wymaga aalzy asępujących czyów:. Korzyśc z przyjęca do realzacj daego projeu. 2. Ryzya z m zwązaego. 3. Czasu, óry powoduje zmaę warośc peądza. Czy czasu
Wyrażanie niepewności pomiaru
 Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
STATYSTYKA MATEMATYCZNA WYKŁAD 1. Wiadomości wstępne
 TATYTYKA MATEMATYCZNA WYKŁAD Wadomośc wstępe tatystyka to dyscypla aukowa, której zadaem jest wykrywae, aalza ops prawdłowośc występujących w procesach masowych. Populacja to zborowość podlegająca badau
TATYTYKA MATEMATYCZNA WYKŁAD Wadomośc wstępe tatystyka to dyscypla aukowa, której zadaem jest wykrywae, aalza ops prawdłowośc występujących w procesach masowych. Populacja to zborowość podlegająca badau
 ń Ę Ę Ę Ę ń ń Ś ź Ę ś ś Ę Ś Ą Ę Ę Ę Ę Ż Ę Ę ść Ą Ł Ę Ć ć Ś Ę Ę ś Ę Ż Ś Ę Ę ń Ż Ę Ć ź ć Ł ś Ę ś Ż ś Ś ś Ę ć Ł ś Ż ŚĆ Ę ń ŚĆ ść ś ś ń ś Ś ś ś Ęś Ę ć ś ść ń ń Ć ś Ą ń ć Ą Ś ń ś ś ć ć ś źć ć ź ś ń Ę ś Ę ć
ń Ę Ę Ę Ę ń ń Ś ź Ę ś ś Ę Ś Ą Ę Ę Ę Ę Ż Ę Ę ść Ą Ł Ę Ć ć Ś Ę Ę ś Ę Ż Ś Ę Ę ń Ż Ę Ć ź ć Ł ś Ę ś Ż ś Ś ś Ę ć Ł ś Ż ŚĆ Ę ń ŚĆ ść ś ś ń ś Ś ś ś Ęś Ę ć ś ść ń ń Ć ś Ą ń ć Ą Ś ń ś ś ć ć ś źć ć ź ś ń Ę ś Ę ć
PROGNOZOWANIE STOPY ZYSKU PORTFELA AKCJI. 1. Wstęp
 B A D A N I A O P A C Y J N I D C Y Z J Nr 004 Ja MIKUŚ POGNOZOWANI SOPY ZYSKU POFLA AKCJI Oreśoo sopę zysu porfea acj zarówo w orese rerospeywym ja progozowaym. Wyorzysując aprosymację erpoacyją wyzaczoo
B A D A N I A O P A C Y J N I D C Y Z J Nr 004 Ja MIKUŚ POGNOZOWANI SOPY ZYSKU POFLA AKCJI Oreśoo sopę zysu porfea acj zarówo w orese rerospeywym ja progozowaym. Wyorzysując aprosymację erpoacyją wyzaczoo
Estymacja to wnioskowanie statystyczne koncentrujące się wokół oszacowania wartości parametrów rozkładu populacji.
 Botatytyka, 018/019 dla Fzyk Medyczej, tuda magterke etymacja etymacja średej puktowa przedzał ufośc średej rozkładu ormalego etymacja puktowa przedzałowa waracj rozkładu ormalego etymacja parametrów rozkładu
Botatytyka, 018/019 dla Fzyk Medyczej, tuda magterke etymacja etymacja średej puktowa przedzał ufośc średej rozkładu ormalego etymacja puktowa przedzałowa waracj rozkładu ormalego etymacja parametrów rozkładu
