Sterowanie obiektu wysokiego rzędu z wykorzystaniem regulatora redukcyjnego
|
|
|
- Gabriela Kozłowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Pomiay Automatya Robotya 7-8/00 Steoanie obietu ysoiego zędu z yozystaniem egulatoa eduyjnego Kzysztof Opzędieiz W pay pzedstaiono popozyję syntezy egulatoa eduyjnego obietu ysoiego zędu, opisanego tansmitanją opeatooą. Zasadnizą ideą onstuji egulatoa jest eduja słabo tłumionej zęśi tansmitanji obietu. Pełna eduja tej zęśi tansmitanji jest możlia yłąznie pzy doładnej znajomośi jej paametó, natomiast ynii badań symulayjnyh sazują, że naet pzypadu niepenośi paametó egulato eduyjny zapenia dobą jaość egulaji. ielu sytuajah patyznyh stosoanie typoyh algoytmó egulayjnyh nie zapenia dobej jaośi egulaji zy odponośi uładu steoania na niepeność paametó obietu. W taih sytuajah uzasadnione jest stosoanie algoytmó spejalnyh, bazująyh na znajomośi modelu obietu postai ónania stanu lub tansmitanji opeatooej. Dodatoym atutem uzasadniająym stosoanie taih algoytmó jest ih zględnie posta implementaja typoyh pzemysłoyh uządzeniah steująyh, m.in. steoniah PLC (np. [8]). W pay pzedstaiono popozyję onstuji postego egulatoa eduyjnego dla obietu opisanego tansmitanją opeatooą, pzy założeniu, że tansmitanji tej można yóżnić zęść osylayjną lub słabo tłumioną. Oazuje się, że eduja za pomoą egulatoa tylo tej słabo tłumionej zęśi zapenia dobą jaość egulaji uładzie. Dodatoo ynii badań symulayjnyh sazują, że poponoany uład zapenia taże dobą odponość uładu egulaji na niepeność paametó obietu egulaji. Opis ozażanyh obietó egulaji Jao obiet egulaji ozażmy obiet ysoiego zędu bez ze, tóego tansmitanji opeatooej można yóżnić die zęśi, z tóyh piesza ma nieozystny pły na dynamię obietu (np. jest słabo tłumiona lub osylayjna), a duga tego nieozystnego płyu nie ma. Tansmitanja obietu może być zapisana następująo: G = M M p () W () oznaza zmonienie statyzne obietu, zynni M p opisuje słabo tłumioną lub osylayjną zęść tansmitanji obietu, tóa może być yażona następująo: p Mp = aps as + a () 0 Czynni M opisuje pozostałą zęść tansmitanji obietu, tóą można zapisać następująo: M = b s b s + b o (3) Załóżmy, że stopień mianonia tansmitanji obietu jest óny n: n = p + (4) Model () (4) opisuje badzo dużą lasę zezyistyh obietó dynamiznyh. Regulato eduyjny dla ozażanej lasy obietó Dla obietu opisanego pzez () ozażmy zamnięty uład steoania (ys. ). Załóżmy, że dynamia egulatoa uładzie ma zastąpić dynamię słabo tłumionej zęśi obietu egulaji, opisanej ielomianem M p. To założenie może być spełnione, jeżeli egulato będzie egulatoem eduyjnym, zbudoanym opaiu o znajomość dynamii obietu. Zagadnienia syntezy egulatoó eduyjnyh (ang. anellation ontolles) bazująej na znajomośi tansmitanji obietu egulaji były omaiane liznyh paah: [4, 5, 8]. Poblemy syntezy egulatoa ompensująego najsłabiej tłumioną zęść dynamii obietu opisanego ónaniem stanu są omóione paah: [6, 7]. Załóżmy, że ozażany egulato eduyjny ma postać uogólnionego egulatoa linioego z ałoaniem o tansmitanji: L G = (5) M d hab. inż. Kzysztof Opzędieiz Kateda Automatyi, AGH Kaoie Rys.. Zamnięty uład egulaji 66
2 Pomiay Automatya Robotya 7-8/00 L oaz M są ielomianami zmiennej zespolonej s następująej postai: l L = vls vs + v0 (6) M = s s (7) m m Całoanie egulatoze (5) jest niezbędne do yeliminoania uhybu ustalonego uładzie egulaji. Załóżmy, że modelu obietu egulaji postai () znamy doładnie paamety jego słabo tłumionej lub osylayjnej zęśi, opisanej pzez (). W taiej sytuaji można założyć, że lizni tansmitanji egulatoa L jest óny post zęśi tansmitanji obietu, opisanej pzez ielomian (): L = M (8) Po uzględnieniu (8) tansmitanja egulatoa linioego (5) pzyjmie postać: p Mp G = (9) M W pzypadu, gdy egulato ma postać (9), stopień mianonia tansmitanji egulatoa m musi spełniać założenie yniająe z fizyznej ealizoalnośi egulatoa: m p (0) Jeżeli tansmitanja egulatoa ma postać (9), a tansmitanja obietu egulaji ma postać (), to tansmitanja uładu otatego, zaieająego i obiet, i egulato, ma postać następująą: Go = G G = () M M Tansmitanja ymuszenioa zamniętego uładu egulaji (ys. ) ma postać: G Y R M M + () Na podstaie () można stiedzić, że pzypadu doładnej znajomośi ielomianu M p, zęść dynamii obietu epezentoana pzez M p została uładzie zamniętym zastąpiona pzez dynamię egulatoa, a ozład biegunó tansmitanji () jest zdeteminoany pzez atość zmonienia obietu oaz paamety egulatoa opisane spółzynniami m.... Pzy odpoiednim doboze tyh spółzynnió możlie jest otzymanie założonego ozładu i typu biegunó uładu zamniętego, pzy zym założeniem fundamentalnym jest asymptotyzna stabilność zamniętego uładu egulaji. Dobó spółzynnió m... egulatoa może być szzególnyh pzypadah yonany analityznie, a pzypadu ogólnym metodami symulayjnymi, np. z yozystaniem śodoisa MATLAB. Zagadnienie symulayjnego dostajania spejalnyh algoytmó steoania yfoego jest omóione np. pay [9]. W tym momenie pojaia się pytanie, jaie są łaśiośi pzedstaionego uładu steoania sytuaji, gdy paamety zęśi tansmitanji obietu, opisane ielomianem M p, nie są doładnie znane? Taa sytuaja najzęśiej ystępuje patye. Ogólna analiza łaśiośi uładu egulaji dla taih pzypadó jest znaznie badziej złożona, natomiast omóione dalszej zęśi pay ynii badań symulayjnyh yazują, że jaość egulaji jest tedy ónież ysoa. Z olei tansmitanja załóenioa może być yznazona pzy założeniu, że atość zadana na ejśiu uładu (t) = 0. Ma ona postać: Y M Gz Z M M M + ( ) p (3) Tansmitanja (3) może być użyta do analizy zahoania się ozażanego uładu egulaji podzas ealizaji zadania stabilizaji. Pzedstaiona poyżej metoda syntezy egulatoa eduyjnego zostanie zilustoana pzyładami. Pzyład Jao pieszy pzyład ozażmy obiet osylayjny II zędu, tóego tansmitanja opeatooa zaiea jedną paę biegunó zespolonyh spzężonyh i może być zapisana następująo: G = s + zs + (4) Na atośi spółzynnió z oaz tansmitanji (4) nałożony jest następująy aune, yniająy z założenia o osylayjnośi obietu: z < (5) Tansmitanja (4) opisuje dużą lasę zezyistyh obietó dynamiznyh, na pzyład są to elementy dgająe typu mehaniznego lub eletyzne obody RLC. Jest ona pzypadiem szzególnym tansmitanjj (), dla tóej: Mp = s + zs + M = (6) Po uzględnieniu (6) egulato eduyjny (9) dla obietu (4) pzyjmie następująą postać: v s v s v G ( s ) = + + s + s 0 (7) Jeżeli założymy, że spółzynnii tansmitanji obietu z oaz są doładnie znane, to spółzynnii liznia tansmitanji egulatoa (7) można pzyjąć następująo: v = v = z (8) v0 = 67
3 Pomiay Automatya Robotya 7-8/00 = () Rys.. Model do badań symulayjnyh dla pzyładu Tab.. Lizboe atośi paametó obietu i egulatoa do testó symulayjnyh dla pzyładu N testu Paamety obietu Po uzględnieniu (8) tansmitanja egulatoa G (7) pzyjmie następująą postać: s + zs + G = s + s Paamety egulatoa L (9) Jeżeli obiet egulaji jest opisany tansmitanją (4) a egulato tansmitanją (9), tansmitanja ymuszenioa zamniętego uładu egulaji () jest óna: Y G (0) R s + s + M Komentaz z v v v 0 0,05,0 0,05 Regulato dostojony pzy założeniu doładnej znajomośi paametó obietu 0,09,0 0,05 Paamety egulatoa 3 0,05, z testu (), zmienione paamety obietu 4 0,03, Dla spółzynnió () i pzy założeniu, że paamety tansmitanji obietu egulaji są doładnie znane, tansmitanja uładu zamniętego (0) na jeden podójny biegun óny. Dla lepszej ilustaji poyższyh ozażań yonano ónież badania symulayjne z użyiem śodoisa MATLAB/SIMULINK. Model SIMULINK-oy do testó jest poazany na ys.. Wyozystują uład z ys. yonano badania symulayjne egulatoa eduyjnego zbudoanego zgodnie z zoami (7) (0). Zbadano pzypadi: gdy paamety obietu egulaji (4) są doładnie znane (dla tego pzypadu został zbudoany egulato) oaz gdy paamety obietu egulaji z oaz są znane pzybliżeniu, a doładnie znane jest tylo zmonienie statyzne obietu. Watośi lizboe paametó obietu i egulatoa są podane tab.. Podzas szystih testó atość zmonienia statyznego obietu była óna. Pzebiegi ielośi eguloanej y(t) funji zasu pzy sooej zmianie atośi zadanej z atośi = 0 na atość = są poazane na ys. 3. Tansmitanja (0) opisuje zahoanie się uładu egulaji odpoiedzi na zmiany atośi zadanej na ejśiu (zadanie pzestaienia, ang. sevo poblem). Na podstaie (0) można stiedzić, że dla ozażanego pzypadu dynamia obietu egulaji została ałoiie zastąpiona pzez dynamię egulatoa opisaną spółzynniami oaz. Odpoiedni dobó tyh spółzynnió pozala na otzymanie założonyh łaśiośi dynamiznyh uładu egulaji. Zauażmy, że zamnięty uład egulaji opisany tansmitanją (0) jest asymptotyznie stabilny dla ażdej dodatniej atośi spółzynnió oaz. Załóżmy, że ozażany uład egulaji z obietem (4) i egulatoem eduyjnym (7) ma ealizoać zadanie pzestaienia. Z puntu idzenia ealizaji tego zadania steoania najbadziej ozystna jest sytuaja, gdy tansmitanja uładu zamniętego (0) ma jeden podójny biegun zezyisty ujemny, gdyż gaantuje to óti zas egulaji pzy bau pzeeguloań. W ozażanym ypadu spełnienie tego aunu impliuje natyhmiast następująy aune na spółzynnii oaz egulatoa: Rys. 3. Pzebiegi ielośi eguloanej y(t) uładzie egulaji dla pzyładu Dla pzebiegó z ys. 3 można oblizyć atośi bezpośednih saźnió jaośi egulaji: pzeeguloanie poentah atośi ustalonej i zas egulaji lizony jao zas, po tóym atość uhybu egulaji jest sposób tały mniejsza od 5 %. 68
4 Pomiay Automatya Robotya 7-8/00 Tab.. Watośi bezpośednih saźnió jaośi egulaji dla pzebiegó z ys. 3 N testu Pzeeguloanie [% atośi ustalonej] Watośi tyh saźnió dla szystih testó są podane tab.. Na podstaie analizy pzebiegó z ys. 3 oaz atośi saźnió jaośi egulaji pzedstaionyh tab. można stiedzić, że pzypadu ozażanego pzyładoego obietu egulaji poponoany egulato eduyjny zapenia badzo dobą jaość egulaji oaz odponość na niepeność paametó obietu. Pzyład Jao dugi pzyład ozażmy syntezę egulatoa eduyjnego dla obietu III zędu, tóego tansmitanja zaiea jedną paę biegunó zespolonyh spzężonyh oaz jeden stabilny biegun zezyisty: G = s + zs + s l ( ) + ( ) Czas egulaji [s] 0,0000 5,933,4009 5, ,6333,75 4 4,493,3479 () Odpoiedź sooa samego obietu egulaji opisanego tansmitanją () dla atośi paametó: =, z = 0,05, =, l = poazana jest na ys. 4. Tansmitanja () ónież opisuje dużą lasę zezyistyh obietó dynamiznyh. Załóżmy, że egulato eduyjny dla ozażanego obietu jest budoany elu eliminaji płyu zęśi osylayjnej na uład egulaji. W tej sytuaji można pzyjąć, że: Wauniem onieznym stabilnośi asymptotyznej uładu opisanego pzez (4) jest, aby obyda paamety egulatoa eduyjnego oaz były dodatnie. Wynia to bezpośednio z aunu onieznego stabilnośi uładu linioego iągłego opisanego tansmitanją opeatooą (zob. np. [7]). > 0 > 0 (5) Dla paametó spełniająyh (5) należy następnie yznazyć obszay stabilnośi. Do oziązania tego poblemu można zastosoać np. yteium Huitza. Po jego zastosoaniu otzymujemy następująy aune na spółzynnii egulatoa oaz. l < l (6) W nieónośi (6) można zauażyć natyhmiast, że funja ozganizająa obszay stabilnośi ma asymptotę pionoą dla ganiznej atośi paametu g ónej: g = (7) l Obsza stabilnośi na płaszzyźnie paametó oaz musi jednoześnie spełniać auni (5) oaz Mp = s + zs + M = s + l (3) Regulato eduyjny ozażanym pzypadu może mieć identyzną postać, ja pzyładzie i jest on opisany pzez (7) (9). Pzy założeniu, że spółzynnii ielomianu M p opisująego osylayjną zęść dynamii obietu są doładnie znane, tansmitanja ymuszenioa ałego uładu egulaji ma ozażanym pzypadu następująą postać: Rys. 4. Odpoiedź sooa obietu egulaji z pzyładu Y s G ( s ) ( ) 3 R s + ( l + ) s + ls + (4) W ozażanym ypadu syntezę egulatoa eduyjnego ozpozynamy od yznazenia obszaó stabilnośi na płaszzyźnie paametó egulatoa oaz. Zagadnienie yznazania obszaó stabilnośi uładu egulaji na płaszzyźnie paametó egulatoa ma fundamentalne znazenie dla popanośi działania uładu egulaji i jest pzedstaione między innymi pay []. Rys. 5. Pzyładoy obsza stabilnośi na płaszzyźnie paametó egulatoa dla pzyładu i atośi paametó: l =, = 69
5 Pomiay Automatya Robotya 7-8/00 Rys. 6. Model do badań symulayjnyh dla pzyładu Tab. 3. Lizboe atośi paametó obietu i egulatoa do testó symulayjnyh dla pzyładu N testu Paamety obietu Paamety egulatoa L M z l v v v 0 Komentaz 0,05,0 0,05 0,9 Regulato dostojony pzy założeniu doładnej znajomośi paametó obietu 0,09,0,0 0,05,0 0,9 Paamety egulatoa 3 0,05,,0 z testu (), zmienione paamety obietu 4 0,03,,0 5 0,05,0, 6 0,05,0 0,9 (6). Pzyładoy obsza stabilnośi dla zmonienia statyznego obietu = oaz bieguna zezyistego ónego l = jest pzedstaiony na ys. 5. Obsza stabilnośi znajduje się pod zyą ozganizająą. Dla ozażanego uładu egulaji pzepoadzono testy symulayjne analogiznie, ja popzednim pzyładzie, z użyiem modelu pzedstaionego na ys. 6, pzy założeniu, że egulato eduyjny jest opisany tansmitanją (7) (9), a obiet egulaji jest opisany tansmitanją (). Dodatoym oganizeniem jest ozażanym ypadu oniezność spełnienia aunó stabilnośi (5) i (6) pzez paamety egulatoa. Podobnie, ja pzyładzie, testy symulayjne yonano dla sytuaji, gdy znane są doładne atośi paametó tansmitanji obietu oaz dla sytuaji, gdy te paamety znane są jedynie pzybliżeniu. Zbadano następująe sytuaje: gdy pzybliżeniu znane są paamety zęśi osylayjnej obietu: z i, oaz gdy pzybliżeniu znany jest paamet l zęśi apeiodyznej tansmitanji obietu. Podzas szystih testó atość zmonienia statyznego obietu była óna. Watośi lizboe paametó obietu i egulatoa są podane tab. 3, pzebiegi ielośi eguloanej y(t) dla szystih testó są podane na ys. 7. Analogiznie ja pzyładzie, dla pzebiegó z ys. 6. można oblizyć bezpośednie saźnii jaośi egulaji: pzeeguloanie poentah atośi ustalonej i zas egulaji lizony jao zas, po tóym atość uhybu egulaji jest sposób tały mniejsza od 5 %. Watośi tyh saźnió dla szystih testó są podane tab. 4. Na podstaie analizy pzebiegó poazanyh na ys. 7 oaz bezpośednih saźnió jaośi egulaji podanyh tab. 4 można stiedzić, że popo- Rys. 7. Pzebiegi ielośi eguloanej y(t) uładzie egulaji z egulatoem eduyjnym dla pzyładu Tab. 4. Watośi bezpośednih saźnió jaośi egulaji dla pzebiegó z ys. 7 N testu noany egulato eduyjny zapenia dobą jaość egulaji uładzie i dodatoo zapenia zadoalająą odponość uładu na niepeność paametó obietu egulaji. W elu poónania jaośi egulaji ozażanym uładzie z poponoanym egulatoem eduyjnym, dla ozażanego obietu egulaji pzepoadzono taże testy z yozystaniem typoego egulatoa PID dostojonego na podstaie zmonienia ytyznego z użyiem eguł Zieglea Niholsa. Model zastosoany do testó poazany jest na ys. 8, zmonienie ytyzne i oes osylaji nietłumionyh obietu oaz yznazona na ih podstaie nastay egulatoa są podane tab. 5. Wszystie testy zostały yonane dla paametó obietu opisanyh tab. 3, pzebiegi odpoiedzi sooyh uładu egulaji podzas testó są podane na ys. 9, a atośi bezpośednih saźnió jaośi egulaji dla szystih testó z ys. 9 są podane tab. 6. Pzeeguloanie [% atośi ustalonej] Czas egulaji [s] 0,56 6,3940 9,74 3,47 3 6,46 7, ,87 9,576 5,37 6, ,06 8,986 70
6 Pomiay Automatya Robotya 7-8/00 Uagi ońoe Rys. 8. Model do badań symulayjnyh z egulatoem PID dla pzyładu Tab. 5. Nastay egulatoa PID do pzyładu Wzmonienie ytyzne obietu 0,888 Oes osylaji nietłumionyh T os [s] 5,9908 Wzmonienie egulatoa 0,8 Czas ałoania T i [s],9954 Czas óżnizoania T d [s] 0,7488 Na podstaie poónania pzebiegó z ys. 7 i ys. 9 oaz tab. 4 i tab. 6 można stiedzić natyhmiast, że poponoany pay egulato eduyjny zapenia znaznie lepszą jaość egulaji sensie ozażanyh bezpośednih saźnió, niż egulato PID dostojony g eguł Zieglea Niholsa. Dodatoo uład z egulatoem eduyjnym jest znaznie mniej ażliy na niepeność paametó obietu egulaji, niż uład z egulatoem PID, gdzie pzy zabuzeniu atośi paametó obietu dóh pzypadah nastąpiła utata stabilnośi uładu. Rys. 9. Pzebiegi ielośi eguloanej y(t) uładzie egulaji z egulatoem PID dla pzyładu Tab. 6. Watośi bezpośednih saźnió jaośi egulaji dla pzebiegó z ys. 9 N testu Pzeeguloanie [% atośi ustalonej] Czas egulaji [s] 5,0 >00 (gania stabilnośi) 0,0 9, ,0 45,855 4 Utata stabilnośi 5,5 34,796 6 Utata stabilnośi Uagi ońoe mogą być sfomułoane następująo: Wynii badań symulayjnyh pozalają niosoać, że poponoany egulato eduyjny zbudoany opaiu o znajomość modelu obietu postai tansmitanji opeatooej, może zapenić dobą jaość egulaji uładzie oaz zapenia zadoalająą odponość uładu na niepeność paametó obietu egulaji. Stutua poponoanego egulatoa jest łata do ealizaji na typoyh pzemysłoyh yfoyh uządzeniah steująyh, np. na steoniah PLC. Pzedmiotem dalszyh pa będzie uzasadnienie teoetyzne otzymanyh ynió symulayjnyh z yozystaniem metod analizy systemó o niepenyh paametah, omaianyh pzyładoo paah [], [3] lub [] oaz patyzna implementaja omaianego algoytmu na steoniah PLC z yozystaniem podejśia zapezentoanego pay [0]. Bibliogafia. Bysi W.: Obseaja i steoanie systemah dynamiznyh Wyd. AGH Busłoiz M.: Stabilność uładó linioyh stajonanyh o niepenyh paametah. Wydanito Politehnii Białostoiej Busłoiz M.: Robust Stability analysis of linea eletial iuits ith unetain paametes. Pzegląd Eletotehnizny n 8 (), 006, s Góei R.: Regulato eduyjny. Zeszyty Nauoe AGH Eletotehnia Tom 5 (996) Zeszyt 3, s Isemann R.: Digital Contol Systems vol. Spinge, Mitosi W.: Stabilizaja linioego systemu paaboliznego za pomoą dysetnego ompensatoa dynamiznego. Kat. AGH Eletotehnia T. 4, (985) Z., s Mitosi W.: Stabilizaja systemó dynamiznyh, WNT, Waszaa Opzędieiz K.: Dysetny egulato eduyjny i jego patyzna implementaja Pomiay, Automatya, Robotya (PAR) n /00, s Opzędieiz K.: Symulayjne dostajanie spejalnyh egulatoó yfoyh. Automatya 003 t. 7, z. s Opzędieiz K.: Poblemy implementaji spejalnyh algoytmó egulaji iągłej na platfomah spzętoo pogamoyh PLC. W: Steoanie i Automatyzaja: atualne poblemy i ih oziązania, pod edają K. Malinosiego i L. Rutosiego, 008, s Palmo Z. J.: Time delay Compensation. Int. Jounal of Contol, vol. 36, 980, pp
( ) ( ) s = 5. s 2s. Krzysztof Oprzędkiewicz Kraków r. Podstawy Automatyki Zadania do części rachunkowej
 Kzyztof Opzędiewicz Kaów 09 0 0. Zajęcia : (ba zadań-wpowadzenie) Zajęcia : (ba zadań wyłącznie część laboatoyjna) Podtawy Automatyi Zadania do części achunowej Zajęcia : Chaateytyi czaowe podtawowych
Kzyztof Opzędiewicz Kaów 09 0 0. Zajęcia : (ba zadań-wpowadzenie) Zajęcia : (ba zadań wyłącznie część laboatoyjna) Podtawy Automatyi Zadania do części achunowej Zajęcia : Chaateytyi czaowe podtawowych
POLITECHNIKA WARSZAWSKA WYDZIAŁ ELEKTRYCZNY LABORATORIUM TERMOKINETYKI WYZNACZANIE WSPÓŁCZYNNIKÓW PRZEJMOWANIA CIEPŁA. W m
 POLITECHNIKA WARSZAWSKA WYDZIAŁ ELEKTRYCZNY LABORATORIUM TERMOKINETYKI WYZNACZANIE WSPÓŁCZYNNIKÓW PRZEJMOWANIA CIEPŁA. Wstęp Tempeatua uładó temoinetyznyh zależna jest nie tylo od źódeł iepła postająyh
POLITECHNIKA WARSZAWSKA WYDZIAŁ ELEKTRYCZNY LABORATORIUM TERMOKINETYKI WYZNACZANIE WSPÓŁCZYNNIKÓW PRZEJMOWANIA CIEPŁA. Wstęp Tempeatua uładó temoinetyznyh zależna jest nie tylo od źódeł iepła postająyh
1. Wstęp Temperatura układów termokinetycznych zależna jest nie tylko od źródeł ciepła powstających na przykład wskutek przepływy prądu elektrycznego,
 . Wstęp Tempeatua uładó temoinetyznyh zależna jest nie tylo od źódeł iepła postająyh na pzyład sute pzepłyy pądu eletyznego, eaji hemiznyh, itp. Badzo ażnym zynniiem, deydująym o tempeatuze uładó są auni
. Wstęp Tempeatua uładó temoinetyznyh zależna jest nie tylo od źódeł iepła postająyh na pzyład sute pzepłyy pądu eletyznego, eaji hemiznyh, itp. Badzo ażnym zynniiem, deydująym o tempeatuze uładó są auni
POLITECHNIKA WARSZAWSKA WYDZIAŁ ELEKTRYCZNY LABORATORIUM ELEKTROTERMII WYZNACZANIE WSPÓŁCZYNNIKÓW PRZEJMOWANIA CIEPŁA. Wykaz ważniejszych oznaczeń:
 POLITECHNIKA WARSZAWSKA WYDZIAŁ ELEKTRYCZNY LABORATORIUM ELEKTROTERMII WYZNACZANIE WSPÓŁCZYNNIKÓW PRZEJMOWANIA CIEPŁA 1. Wstęp... 1.1. Loalny i śedni spółzynni pzejmoania iepła... 3 1.3. Koneja... 4 1.5.
POLITECHNIKA WARSZAWSKA WYDZIAŁ ELEKTRYCZNY LABORATORIUM ELEKTROTERMII WYZNACZANIE WSPÓŁCZYNNIKÓW PRZEJMOWANIA CIEPŁA 1. Wstęp... 1.1. Loalny i śedni spółzynni pzejmoania iepła... 3 1.3. Koneja... 4 1.5.
Relaksacja. Chem. Fiz. TCH II/19 1
 Relasaja Relasaja oznaza powrót uładu do stanu równowagi po zaburzeniu równowagi pierwotnej jaimś bodźem (wielośią zewnętrzną zmieniająą swoją wartość soowo, np. stężenie jednego z reagentów, iśnienie
Relasaja Relasaja oznaza powrót uładu do stanu równowagi po zaburzeniu równowagi pierwotnej jaimś bodźem (wielośią zewnętrzną zmieniająą swoją wartość soowo, np. stężenie jednego z reagentów, iśnienie
UKŁADY REGULACJI PID DOBÓR NASTAW
 UŁADY REGULACJI PID DOBÓR NASAW. CEL ĆWICZENIA Celem ćwicenia jest ponanie właściwości i funcji egulatoów PID w uładie e spężeniem wotnym. W aes ćwicenia wchodi: - badanie odpowiedi casowych na so jednostowy
UŁADY REGULACJI PID DOBÓR NASAW. CEL ĆWICZENIA Celem ćwicenia jest ponanie właściwości i funcji egulatoów PID w uładie e spężeniem wotnym. W aes ćwicenia wchodi: - badanie odpowiedi casowych na so jednostowy
LINIA PRZESYŁOWA PRĄDU STAŁEGO
 oitechnia Białostoca Wydział Eetyczny Kateda Eetotechnii Teoetycznej i Metoogii nstucja do zajęć aboatoyjnych Tytuł ćwiczenia LNA RZEYŁOWA RĄD TAŁEGO Nume ćwiczenia E Auto: mg inŝ. Łuasz Zaniewsi Białysto
oitechnia Białostoca Wydział Eetyczny Kateda Eetotechnii Teoetycznej i Metoogii nstucja do zajęć aboatoyjnych Tytuł ćwiczenia LNA RZEYŁOWA RĄD TAŁEGO Nume ćwiczenia E Auto: mg inŝ. Łuasz Zaniewsi Białysto
Powtórzenie na kolokwium nr 4. Dynamika punktu materialnego
 Powtórzenie na olowiu nr 4 Dynaia puntu aterialnego 1 zadanie dynaii: znany jest ruh, szuay siły go wywołująej. Znane funje opisująe trajetorię ruhu różnizujey i podstawiay do równań ruhu. 2 zadanie dynaii:
Powtórzenie na olowiu nr 4 Dynaia puntu aterialnego 1 zadanie dynaii: znany jest ruh, szuay siły go wywołująej. Znane funje opisująe trajetorię ruhu różnizujey i podstawiay do równań ruhu. 2 zadanie dynaii:
ZESZYTY NAUKOWE NR 5(77) AKADEMII MORSKIEJ W SZCZECINIE. Stabilizacja kursu statku w oparciu o uproszczony komputerowy model dynamiki
 ISSN 17-867 ZESZYTY NAUKOWE NR 5(77) AKADEMII MORSKIEJ W SZCZECINIE OBSŁUGIWANIE MASZYN I URZĄDZEŃ OKRĘTOWYCH O M i U O 2 5 Piot Boowsi, Zenon Zwiezewicz Stabilizacja usu statu w opaciu o uposzczony omputeowy
ISSN 17-867 ZESZYTY NAUKOWE NR 5(77) AKADEMII MORSKIEJ W SZCZECINIE OBSŁUGIWANIE MASZYN I URZĄDZEŃ OKRĘTOWYCH O M i U O 2 5 Piot Boowsi, Zenon Zwiezewicz Stabilizacja usu statu w opaciu o uposzczony omputeowy
Temat ćwiczenia: OBWODY PRĄDU SINUSOIDALNEGO Pomiary w obwodzie z obciążeniem rezystancyjnym, indukcyjnym i pojemnościowym.
 aboatoium eoii Obwodów emat ćwiczenia: OBODY ĄD SNSODNEGO BOOM MD omiay w obwodzie z obciążeniem ezystancyjnym, inducyjnym i pojemnościowym.. estawiamy uład połączeń obwodu ja na schemacie.. yonujemy pomiay
aboatoium eoii Obwodów emat ćwiczenia: OBODY ĄD SNSODNEGO BOOM MD omiay w obwodzie z obciążeniem ezystancyjnym, inducyjnym i pojemnościowym.. estawiamy uład połączeń obwodu ja na schemacie.. yonujemy pomiay
Rama płaska metoda elementów skończonych.
 Pzyład. Rama płasa metoda elementów sończonych. M p l A, EJ P p l A, EJ l A, EJ l l,5 l. Dysetyzacja Podział na elementy i węzły x st. sw. M 5 P Z X, M, V, H 7, M, H Y, V Element amy płasiej węzły, x stopni
Pzyład. Rama płasa metoda elementów sończonych. M p l A, EJ P p l A, EJ l A, EJ l l,5 l. Dysetyzacja Podział na elementy i węzły x st. sw. M 5 P Z X, M, V, H 7, M, H Y, V Element amy płasiej węzły, x stopni
LABORATORIUM: Sterowanie rzeczywistym serwomechanizmem z modułem przemieszczenia liniowego Wprowadzenie
 Utwozenie: PRz, 1, Żabińsi Tomasz Modyfiacja: PRz, 15, Michał Maiewicz LABORATORIUM: Steowanie zeczywistym sewomechanizmem z modułem zemieszczenia liniowego Wowadzenie Celem ćwiczenia jest identyfiacja
Utwozenie: PRz, 1, Żabińsi Tomasz Modyfiacja: PRz, 15, Michał Maiewicz LABORATORIUM: Steowanie zeczywistym sewomechanizmem z modułem zemieszczenia liniowego Wowadzenie Celem ćwiczenia jest identyfiacja
Określanie rzędu reakcji
 Oreślanie rzędu reaji Ponieważ rząd reaji jest wielośią zysto formalną, jego oreślenie jest możliwe tylo esperymentalnie. Jedynie dla reaji elementarnyh rząd reaji jest równy ih ząstezowośi (o zym dalej).
Oreślanie rzędu reaji Ponieważ rząd reaji jest wielośią zysto formalną, jego oreślenie jest możliwe tylo esperymentalnie. Jedynie dla reaji elementarnyh rząd reaji jest równy ih ząstezowośi (o zym dalej).
WŁAŚCIWOŚCI DYNAMICZNE POLOWO ZORIENTOWANEGO UKŁADU STEROWANIA SILNIKA INDUKCYJNEGO Z OBSERWATOREM STRUMIENIA I ESTYMATOREM PRĘDKOŚCI WIRNIKA
 Pace Naukoe Instytutu Maszyn, Napędó i Pomiaó Elektycznych N 56 Politechniki Wocłaskiej N 56 Studia i Mateiały N 24 24 Teesa ORŁOWSKA-KOWALSKA *, Mateusz DYBKOWSKI * Silnik indukcyjny, obseato stumienia
Pace Naukoe Instytutu Maszyn, Napędó i Pomiaó Elektycznych N 56 Politechniki Wocłaskiej N 56 Studia i Mateiały N 24 24 Teesa ORŁOWSKA-KOWALSKA *, Mateusz DYBKOWSKI * Silnik indukcyjny, obseato stumienia
POMIAR PĘTLI HISTEREZY MAGNETYCZNEJ
 POMIAR PĘTLI ITEREZY MAGNETYZNEJ 1. Opis teoetyczny do ćiczenia zamieszczony jest na stonie.tc.at.edu.pl dziale DYDAKTYKA FIZYKA ĆWIZENIA LAORATORYJNE.. Opis układu pomiaoego Mateiały feomagnetyczne (feyt,
POMIAR PĘTLI ITEREZY MAGNETYZNEJ 1. Opis teoetyczny do ćiczenia zamieszczony jest na stonie.tc.at.edu.pl dziale DYDAKTYKA FIZYKA ĆWIZENIA LAORATORYJNE.. Opis układu pomiaoego Mateiały feomagnetyczne (feyt,
XXX OLIMPIADA FIZYCZNA (1980/1981). Stopień I, zadanie teoretyczne T4 1
 XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
Rozciąganie i ściskanie prętów projektowanie 3
 Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
Wyznaczanie temperatury i ciśnienia gazu z oddziaływaniem Lennarda Jonesa metodami dynamiki molekularnej
 Pojekt n C.4. Wyznazanie tempeatuy i iśnienia gazu z oddziaływaniem Lennada Jonesa metodami dynamiki molekulanej Wpowadzenie Fizyka Rozważamy model gazu zezywistego zyli zbió atomów oddziaływująyh z sobą
Pojekt n C.4. Wyznazanie tempeatuy i iśnienia gazu z oddziaływaniem Lennada Jonesa metodami dynamiki molekulanej Wpowadzenie Fizyka Rozważamy model gazu zezywistego zyli zbió atomów oddziaływująyh z sobą
Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na okres drgań
 KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
Wyznaczenie współczynnika dyfuzji cieplnej κ z rozkładu amplitudy fali cieplnej
 ace Instytutu Mechanii Góotwou AN Tom 15, n 3-, gudzień 13, s. 69-75 Instytut Mechanii Góotwou AN Wyznaczenie współczynnia dyfuzji cieplnej κ z ozładu amplitudy fali cieplnej JAN KIEŁBASA Instytut Mechanii
ace Instytutu Mechanii Góotwou AN Tom 15, n 3-, gudzień 13, s. 69-75 Instytut Mechanii Góotwou AN Wyznaczenie współczynnia dyfuzji cieplnej κ z ozładu amplitudy fali cieplnej JAN KIEŁBASA Instytut Mechanii
Krzywe stożkowe. 1 Powinowactwo prostokątne. 2 Elipsa. Niech l będzie ustaloną prostą i k ustaloną liczbą dodatnią.
 Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
Blok 8: Moment bezwładności. Moment siły Zasada zachowania momentu pędu
 Blo 8: Moent bezwładności Moent siły Zasada zachowania oentu pędu Moent bezwładności awiając uch postępowy ciała, posługujey się pojęciai pzeieszczenia, szybości, pzyspieszenia tego ciała oaz wypadowej
Blo 8: Moent bezwładności Moent siły Zasada zachowania oentu pędu Moent bezwładności awiając uch postępowy ciała, posługujey się pojęciai pzeieszczenia, szybości, pzyspieszenia tego ciała oaz wypadowej
Informacje. Danuta Kruk. Pokój: D2/20. Telefon:
 Infomacje Danuta Ku danuta.u@matman.uwm.edu.pl Poój: D/0 Telefon: 89 54 6011 Konsultacje: poniedziałe: 11-14, wtoe: 1-15, śoda: 1-15, czwate 13.30-15.30 inne teminy jeśli Państwu badziej odpowiadają -
Infomacje Danuta Ku danuta.u@matman.uwm.edu.pl Poój: D/0 Telefon: 89 54 6011 Konsultacje: poniedziałe: 11-14, wtoe: 1-15, śoda: 1-15, czwate 13.30-15.30 inne teminy jeśli Państwu badziej odpowiadają -
POLITECHNIKA WARSZAWSKA Instytut Podstaw Budowy Maszyn XIX Konferencja nt METODY I ŚRODKI PROJEKTOWANIA WSPOMAGANEGO KOMPUTEROWO
 MECHANIK NR /03 43 POLITECHNIKA WARSZAWSKA Instytut Podstaw Budowy Maszyn XIX Konfeenja nt METODY I ŚRODKI PROJEKTOWANIA WSPOMAGANEGO KOMPUTEROWO Łańut, paździeni 03 Elżbieta Ziąbsa Uniwesytet Tehnologizno
MECHANIK NR /03 43 POLITECHNIKA WARSZAWSKA Instytut Podstaw Budowy Maszyn XIX Konfeenja nt METODY I ŚRODKI PROJEKTOWANIA WSPOMAGANEGO KOMPUTEROWO Łańut, paździeni 03 Elżbieta Ziąbsa Uniwesytet Tehnologizno
THE FUZZY-PROBABILISTIC SEQUENT SYSTEM FOR CONTROL- LING THE SPARK IGNITION IN FUEL ENGINE
 Joual of KONES Iteal Combustio Egies 2005, vol. 2, 3-4 THE FUZZY-PROBABILISTIC SEQUENT SYSTEM FOR CONTROL- LING THE SPARK IGNITION IN FUEL ENGINE Maiusz Topolsi Politechia Wocławsa, Wydział Eletoii Kateda
Joual of KONES Iteal Combustio Egies 2005, vol. 2, 3-4 THE FUZZY-PROBABILISTIC SEQUENT SYSTEM FOR CONTROL- LING THE SPARK IGNITION IN FUEL ENGINE Maiusz Topolsi Politechia Wocławsa, Wydział Eletoii Kateda
LABORATORIUM PODSTAW AUTOMATYKI
 POLITECHNIKA WROCŁAWSKA WYDZIAŁ TECHNICZNO-INŻYNIERYJNY WAŁBRZYCH KIERUNEK STUDIÓW: MECHATRONIKA POJAZDÓW Specjalność: Konstrucja Uładów Mechatronicznych w Pojazdach Studia stacjonarne inżyniersie LABORATORIUM
POLITECHNIKA WROCŁAWSKA WYDZIAŁ TECHNICZNO-INŻYNIERYJNY WAŁBRZYCH KIERUNEK STUDIÓW: MECHATRONIKA POJAZDÓW Specjalność: Konstrucja Uładów Mechatronicznych w Pojazdach Studia stacjonarne inżyniersie LABORATORIUM
POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN ZAKŁAD MECHATRONIKI LABORATORIUM PODSTAW AUTOMATYKI INSTRUKCJA
 POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN ZAKŁAD MECHATRONIKI LABORATORIUM PODSTAW AUTOMATYKI INSTRUKCJA ĆWICZENIE LABORATORYJNE NR 4 Temat: Identyfiacja obietu regulacji
POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN ZAKŁAD MECHATRONIKI LABORATORIUM PODSTAW AUTOMATYKI INSTRUKCJA ĆWICZENIE LABORATORYJNE NR 4 Temat: Identyfiacja obietu regulacji
Obserwator typu M prędkości kątowej wirnika maszyny asynchronicznej z estymacją rezystancji stojana i wirnika
 Macin MORAWIEC Politechnika Gdańska Kateda Automatyki Napędu Elektycznego Obseato typu M pędkości kątoej inika maszyny asynchonicznej z estymacją ezystancji stojana i inika Steszczenie W efeacie pzedstaiono
Macin MORAWIEC Politechnika Gdańska Kateda Automatyki Napędu Elektycznego Obseato typu M pędkości kątoej inika maszyny asynchonicznej z estymacją ezystancji stojana i inika Steszczenie W efeacie pzedstaiono
X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH
 X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH 1.1 Definice; metoda wsteczne poeci w tomogafii tansmisyne Rys. 1.1 Pzyład dwóch zutów pzedmiotu złożonego z dwóch cylindycznych obietów Z czysto
X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH 1.1 Definice; metoda wsteczne poeci w tomogafii tansmisyne Rys. 1.1 Pzyład dwóch zutów pzedmiotu złożonego z dwóch cylindycznych obietów Z czysto
ZASTOSOWANIE SIECI NEURONOWEJ RBF W REGULATORZE KURSU STATKU
 Mirosław Tomera Aademia Morsa w Gdyni Wydział Eletryczny Katedra Automatyi Orętowej ZASTOSOWANIE SIECI NEURONOWEJ RBF W REGULATORZE KURSU STATKU W pracy przedstawiona została implementacja sieci neuronowej
Mirosław Tomera Aademia Morsa w Gdyni Wydział Eletryczny Katedra Automatyi Orętowej ZASTOSOWANIE SIECI NEURONOWEJ RBF W REGULATORZE KURSU STATKU W pracy przedstawiona została implementacja sieci neuronowej
14. Regulatory w układach z opóźnieniem Wprowadzenie. Hs () Ws () Es () Ys () Us () Vs ()
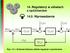 4. Regulatoy układach opóźnieniem 4.0. Wpoadenie Z s u( ) Z s y( ) Ws () Es () G s ( ) Us () G s o( ) Ys () Vs () Hs () Rys. 4.. Schemat blokoy układu egulacji opóźnieniem Ped omóieniem egulatoó stosoanych
4. Regulatoy układach opóźnieniem 4.0. Wpoadenie Z s u( ) Z s y( ) Ws () Es () G s ( ) Us () G s o( ) Ys () Vs () Hs () Rys. 4.. Schemat blokoy układu egulacji opóźnieniem Ped omóieniem egulatoó stosoanych
DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH
 Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
STRUKTURA STEROWANIA UKŁADEM TRÓJMASOWYM Z REGULATOREM STANU
 Pace Naukowe Instytutu Maszyn, Napędów i Pomiaów Elektycznych N 69 Politechniki Wocławskiej N 69 Studia i Mateiały N 0 Kaol WRÓBEL* egulato stanu, układy tójmasowe, układy z połączeniem spężystym STRUKTURA
Pace Naukowe Instytutu Maszyn, Napędów i Pomiaów Elektycznych N 69 Politechniki Wocławskiej N 69 Studia i Mateiały N 0 Kaol WRÓBEL* egulato stanu, układy tójmasowe, układy z połączeniem spężystym STRUKTURA
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
Mechanika relatywistyczna
 Mehanika relatywistyzna Konepja eteru Eter kosmizny miał być speyfiznym ośrodkiem, wypełniająym ałą przestrzeń, który miał być nośnikiem fal świetlnyh (później w ogóle pola elektromagnetyznego). W XIX
Mehanika relatywistyzna Konepja eteru Eter kosmizny miał być speyfiznym ośrodkiem, wypełniająym ałą przestrzeń, który miał być nośnikiem fal świetlnyh (później w ogóle pola elektromagnetyznego). W XIX
Nr 2. Laboratorium Maszyny CNC. Politechnika Poznańska Instytut Technologii Mechanicznej
 Politechnia Poznańsa Instytut Technologii Mechanicznej Laboratorium Maszyny CNC Nr 2 Badania symulacyjne napędów obrabiare sterowanych numerycznie Opracował: Dr inż. Wojciech Ptaszyńsi Poznań, 3 stycznia
Politechnia Poznańsa Instytut Technologii Mechanicznej Laboratorium Maszyny CNC Nr 2 Badania symulacyjne napędów obrabiare sterowanych numerycznie Opracował: Dr inż. Wojciech Ptaszyńsi Poznań, 3 stycznia
L.Kowalski zadania z rachunku prawdopodobieństwa-zestaw 1 ZADANIA - ZESTAW 1. . (odp. a)
 ZADANIA - ZESTAW 1 Zadanie 11 Rzucamy trzy razy monetą A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie Oreślić zbiór zdarzeń elementarnych Wypisać zdarzenia elementarne sprzyjające
ZADANIA - ZESTAW 1 Zadanie 11 Rzucamy trzy razy monetą A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie Oreślić zbiór zdarzeń elementarnych Wypisać zdarzenia elementarne sprzyjające
Problem syntezy sterowania w systemach automatycznego prowadzenia statku wzdłuż zadanej trajektorii. Zenon Zwierzewicz
 Poblem syntezy steowania w systemach automatycznego powadzenia statku wzdłuż zadanej tajektoii Zenon Zwiezewicz Szczecin, Poblem syntezy steowania w systemach automatycznego powadzenia statku wzdłuż zadanej
Poblem syntezy steowania w systemach automatycznego powadzenia statku wzdłuż zadanej tajektoii Zenon Zwiezewicz Szczecin, Poblem syntezy steowania w systemach automatycznego powadzenia statku wzdłuż zadanej
ROZDZIAŁ 7. Elektrotechnika podstawowa 131
 lektotechnika podstaoa ODŁ 7 oziązyanie obodó pądu s inusoidalnego - - N N N ϕ N N N b a Podobnie jak pzy pądzie stałym istotnych infomacji dostacza analiza postych układó utozonych z idealnych elementó
lektotechnika podstaoa ODŁ 7 oziązyanie obodó pądu s inusoidalnego - - N N N ϕ N N N b a Podobnie jak pzy pądzie stałym istotnych infomacji dostacza analiza postych układó utozonych z idealnych elementó
Graf skierowany. Graf zależności dla struktur drzewiastych rozgrywających parametrycznie
 Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII.
 ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
MODYFIKACJA KOSZTOWA ALGORYTMU JOHNSONA DO SZEREGOWANIA ZADAŃ BUDOWLANYCH
 MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
I. Konstrukcja modeli dynamiki i podstawowe badania symulacyjne 1 Charakterystyki czasowe 1.1 Modele w trybie graficznym
 I. Konsruja modeli dynamii i odsaoe badania symulayjne haraerysyi zasoe. Modele rybie graiznym.. Proedura onsruji i eryiaji modelu el: Badanie reaji obieu na sooe załóenia na ybranyh ejśiah, róŝnyh unah
I. Konsruja modeli dynamii i odsaoe badania symulayjne haraerysyi zasoe. Modele rybie graiznym.. Proedura onsruji i eryiaji modelu el: Badanie reaji obieu na sooe załóenia na ybranyh ejśiah, róŝnyh unah
9.1 POMIAR PRĘDKOŚCI NEUTRINA W CERN
 91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
MODELOWANIE I STEROWANIE REAKTORA ZBIORNIKOWEGO PRZEPŁYWOWEGO Z UŻYCIEM REGULATORA PID
 Inżynieia Ekologizna Eologial Engineeing Vol. 49, Sept. 206, p. 95 20 DOI: 0.292/23920629/64528 MODELOWANIE I STEROWANIE REAKTORA ZBIORNIKOWEGO PRZEPŁYWOWEGO Z UŻYCIEM REGULATORA PID Atu Wodołażski Zakład
Inżynieia Ekologizna Eologial Engineeing Vol. 49, Sept. 206, p. 95 20 DOI: 0.292/23920629/64528 MODELOWANIE I STEROWANIE REAKTORA ZBIORNIKOWEGO PRZEPŁYWOWEGO Z UŻYCIEM REGULATORA PID Atu Wodołażski Zakład
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
Zadanie 1. Podaj model matematyczny układu jak na rysunku: a) w postaci transmitancji, b) w postaci równań stanu (równań różniczkowych).
 Zadanie Podaj model matematyczny uładu ja na ryunu: a w potaci tranmitancji, b w potaci równań tanu równań różniczowych. a ranmitancja operatorowa LC C b ównania tanu uładu di dt i A B du c u c dt i u
Zadanie Podaj model matematyczny uładu ja na ryunu: a w potaci tranmitancji, b w potaci równań tanu równań różniczowych. a ranmitancja operatorowa LC C b ównania tanu uładu di dt i A B du c u c dt i u
WYKORZYSTANIE METOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU
 M.Miszzyńsi KBO UŁ, Badania perayjne I (wyład 7A 7) [] WYKORZYSANIE MEOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU Omówimy tutaj dwa prste warianty nieliniwyh mdeli deyzyjnyh,
M.Miszzyńsi KBO UŁ, Badania perayjne I (wyład 7A 7) [] WYKORZYSANIE MEOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU Omówimy tutaj dwa prste warianty nieliniwyh mdeli deyzyjnyh,
Wykład 9. Fizyka 1 (Informatyka - EEIiA 2006/07)
 Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI
 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
REFERAT PRACY MAGISTERSKIEJ Symulacja estymacji stanu zanieczyszczeń rzeki z wykorzystaniem sztucznych sieci neuronowych.
 REFERAT PRACY MAGISTERSKIEJ Symulacja estymacji stanu zanieczyszczeń rzei z wyorzystaniem sztucznych sieci neuronowych. Godło autora pracy: EwGron. Wprowadzenie. O poziomie cywilizacyjnym raju, obo wielu
REFERAT PRACY MAGISTERSKIEJ Symulacja estymacji stanu zanieczyszczeń rzei z wyorzystaniem sztucznych sieci neuronowych. Godło autora pracy: EwGron. Wprowadzenie. O poziomie cywilizacyjnym raju, obo wielu
Zbigniew Otremba, Fizyka cz.1: Mechanika 5
 Zbigniew Otemba, Fizya cz.: Mechania 5. MECHANIKA Mechania - to idee odnoszące się do zozumienia i opisu wszeliego uchu. Wpowadzone tu pojęcia i wielości dają postawy innym działom fizyi oaz mechanice
Zbigniew Otemba, Fizya cz.: Mechania 5. MECHANIKA Mechania - to idee odnoszące się do zozumienia i opisu wszeliego uchu. Wpowadzone tu pojęcia i wielości dają postawy innym działom fizyi oaz mechanice
Implementacja rozmytych systemów wnioskujących w zdaniach regulacji
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 5 Implementacja rozmytych systemów wnioskujących w zdaniach regulacji Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 5 Implementacja rozmytych systemów wnioskujących w zdaniach regulacji Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Pytanie 2 Belkę przedstawioną na rysunku, obciążono momentem skupionym M = 3 [knm] w punkcie C. Odległości wynoszą a=2 [m], b=1 [m].
![Pytanie 2 Belkę przedstawioną na rysunku, obciążono momentem skupionym M = 3 [knm] w punkcie C. Odległości wynoszą a=2 [m], b=1 [m]. Pytanie 2 Belkę przedstawioną na rysunku, obciążono momentem skupionym M = 3 [knm] w punkcie C. Odległości wynoszą a=2 [m], b=1 [m].](/thumbs/30/14265959.jpg) Pytanie 1 Belkę przedstawioną na rysunku, obiążono siłą P = 3 [kn]. Odległośi wynoszą a= [m], b=1 [m]. A a Reakje podpór dla belki wynoszą: A) R A = [kn], R B =1 [kn] B) R A =1 [kn], R B = [kn] C) RA=
Pytanie 1 Belkę przedstawioną na rysunku, obiążono siłą P = 3 [kn]. Odległośi wynoszą a= [m], b=1 [m]. A a Reakje podpór dla belki wynoszą: A) R A = [kn], R B =1 [kn] B) R A =1 [kn], R B = [kn] C) RA=
LABORATORIUM. Sterowanie rzeczywistym serwomechanizmem z modułem przemieszczenia liniowego
 PRz, 1, Żabińi Tomaz LABORATORIUM Steowanie zeczywitym ewomechanizmem z modułem zemiezczenia liniowego 1. Na odtawie ztałtu odowiedzi oowych uładu, oeśl ty teowania (ądowy, naięciowy) ewomechanizmu oaz
PRz, 1, Żabińi Tomaz LABORATORIUM Steowanie zeczywitym ewomechanizmem z modułem zemiezczenia liniowego 1. Na odtawie ztałtu odowiedzi oowych uładu, oeśl ty teowania (ądowy, naięciowy) ewomechanizmu oaz
Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci
 Ćwiczenie 4 - Badanie wpływu asymetrii obciążenia na pracę sieci Strona 1/13 Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci Spis treści 1.Cel ćwiczenia...2 2.Wstęp...2 2.1.Wprowadzenie
Ćwiczenie 4 - Badanie wpływu asymetrii obciążenia na pracę sieci Strona 1/13 Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci Spis treści 1.Cel ćwiczenia...2 2.Wstęp...2 2.1.Wprowadzenie
IDENTIFICATION OF PARAMETERS OF THE SET THE VEHICLE-THE LIGHTWEIGHT SEMITRAILER GN2000 BY MEANS OF THE EXPERIMENTAL MODAL ANALYSIS METHOD
 Tadeusz PAWŁOWSKI Pzemysłowy Instytut Maszyn Rolniczych ul. Staołęca 31, 60-963 Poznań e-mail: office@pim.poznan.pl IDENTIFICATION OF PARAMETERS OF THE SET THE VEHICLE-THE LIHTWEIHT SEMITRAILER N000 BY
Tadeusz PAWŁOWSKI Pzemysłowy Instytut Maszyn Rolniczych ul. Staołęca 31, 60-963 Poznań e-mail: office@pim.poznan.pl IDENTIFICATION OF PARAMETERS OF THE SET THE VEHICLE-THE LIHTWEIHT SEMITRAILER N000 BY
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ.
 ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
Grupowanie sekwencji czasowych
 BIULETYN INSTYTUTU AUTOMATYKI I ROBOTYKI NR 3, 006 Grupowanie sewencji czasowych Tomasz PAŁYS Załad Automatyi, Instytut Teleinformatyi i Automatyi WAT, ul. Kalisiego, 00-908 Warszawa STRESZCZENIE: W artyule
BIULETYN INSTYTUTU AUTOMATYKI I ROBOTYKI NR 3, 006 Grupowanie sewencji czasowych Tomasz PAŁYS Załad Automatyi, Instytut Teleinformatyi i Automatyi WAT, ul. Kalisiego, 00-908 Warszawa STRESZCZENIE: W artyule
OPTYMALIZACJA KSZTAŁTU WIELOKĄTNYCH OBSZARÓW
 MODELOWANIE INśYNIERSKIE ISSN 896-77X 35, s. 63-68, Gliwice 008 OPTYMALIZACJA KSZTAŁTU WIELOKĄTNYCH OBSZARÓW MODELOWANYCH RÓWNANIAMI NAVIERA-LAMEGO NA PODSTAWIE PURC I ALGORYTMÓW GENETYCZNYCH EUGENIUSZ
MODELOWANIE INśYNIERSKIE ISSN 896-77X 35, s. 63-68, Gliwice 008 OPTYMALIZACJA KSZTAŁTU WIELOKĄTNYCH OBSZARÓW MODELOWANYCH RÓWNANIAMI NAVIERA-LAMEGO NA PODSTAWIE PURC I ALGORYTMÓW GENETYCZNYCH EUGENIUSZ
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
m q κ (11.1) q ω (11.2) ω =,
 OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
TERMODYNAMIKA PROCESOWA. Wykład V
 ERMODYNAMIKA PROCESOWA Wykład V Równania stanu substancji czystych Równanie stanu gazu doskonałego eoia stanów odpowiadających sobie Równania wiialne Pof. Antoni Kozioł, Wydział Chemiczny Politechniki
ERMODYNAMIKA PROCESOWA Wykład V Równania stanu substancji czystych Równanie stanu gazu doskonałego eoia stanów odpowiadających sobie Równania wiialne Pof. Antoni Kozioł, Wydział Chemiczny Politechniki
A4: Filtry aktywne rzędu II i IV
 A4: Filtry atywne rzędu II i IV Jace Grela, Radosław Strzała 3 maja 29 1 Wstęp 1.1 Wzory Poniżej zamieszczamy podstawowe wzory i definicje, tórych używaliśmy w obliczeniach: 1. Związe między stałą czasową
A4: Filtry atywne rzędu II i IV Jace Grela, Radosław Strzała 3 maja 29 1 Wstęp 1.1 Wzory Poniżej zamieszczamy podstawowe wzory i definicje, tórych używaliśmy w obliczeniach: 1. Związe między stałą czasową
 ź Ś ś ś Ś Ś ś ś ś ś ś ś ź ś ś Ś Ś Ś źś Ń Ś ś Ą Ź ś ś ś ś Ś ś ś Ą Ś Ą Ą ś ś Ś Ś ść ś Ś ś ś Ś ś ś ś ź ś Ś Ś Ś Ś ś Ś Ź ś ś ś ś ś Ś ś Ś ć ć Ś Ś Ą ć ć Ś Ś Ś ś Ś ś Ę Ś Ę ś Ś Ś Ś Ś ś ś ś Ś Ś Ś Ś ś ś ć Ć Ę Ś Ś
ź Ś ś ś Ś Ś ś ś ś ś ś ś ź ś ś Ś Ś Ś źś Ń Ś ś Ą Ź ś ś ś ś Ś ś ś Ą Ś Ą Ą ś ś Ś Ś ść ś Ś ś ś Ś ś ś ś ź ś Ś Ś Ś Ś ś Ś Ź ś ś ś ś ś Ś ś Ś ć ć Ś Ś Ą ć ć Ś Ś Ś ś Ś ś Ę Ś Ę ś Ś Ś Ś Ś ś ś ś Ś Ś Ś Ś ś ś ć Ć Ę Ś Ś
DSP-MATLAB, Ćwiczenie 5, P.Korohoda, KE AGH. Ćwiczenie 5. Przemysław Korohoda, KE, AGH
 DSP-MATLAB, Ćwiczenie 5, P.Korohoda, KE AGH Instrucja do laboratorium z cyfrowego przetwarzania sygnałów Ćwiczenie 5 Wybrane właściwości Dysretnej Transformacji Fouriera Przemysław Korohoda, KE, AGH Zawartość
DSP-MATLAB, Ćwiczenie 5, P.Korohoda, KE AGH Instrucja do laboratorium z cyfrowego przetwarzania sygnałów Ćwiczenie 5 Wybrane właściwości Dysretnej Transformacji Fouriera Przemysław Korohoda, KE, AGH Zawartość
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
A i A j lub A j A i. Operator γ : 2 X 2 X jest ciągły gdy
 3. Wyład 7: Inducja i reursja struturalna. Termy i podstawianie termów. Dla uninięcia nieporozumień notacyjnych wprowadzimy rozróżnienie między funcjami i operatorami. Operatorem γ w zbiorze X jest funcja
3. Wyład 7: Inducja i reursja struturalna. Termy i podstawianie termów. Dla uninięcia nieporozumień notacyjnych wprowadzimy rozróżnienie między funcjami i operatorami. Operatorem γ w zbiorze X jest funcja
WYKŁAD 15. Rozdział 8: Drgania samowzbudne
 WYKŁAD 5 Rozdział 8: Drgania samowzbudne 8.. Istota uładów i drgań samowzbudnych W tym wyładzie omówimy właściwości drgań samowzbudnych [,4], odróżniając je od poznanych wcześniej drgań swobodnych, wymuszonych
WYKŁAD 5 Rozdział 8: Drgania samowzbudne 8.. Istota uładów i drgań samowzbudnych W tym wyładzie omówimy właściwości drgań samowzbudnych [,4], odróżniając je od poznanych wcześniej drgań swobodnych, wymuszonych
A-4. Filtry aktywne rzędu II i IV
 A-4. Filtry atywne rzędu II i IV Filtry atywne to ułady liniowe i stacjonarne realizowane za pomocą elementu atywnego, na tóry założono sprzężenie zwrotne zbudowane z elementów biernych i. Elementem atywnym
A-4. Filtry atywne rzędu II i IV Filtry atywne to ułady liniowe i stacjonarne realizowane za pomocą elementu atywnego, na tóry założono sprzężenie zwrotne zbudowane z elementów biernych i. Elementem atywnym
f s moŝna traktować jako pracę wykonaną przez siłę tarcia nad ślizgającym się klockiem. Porównując
 Wykład z fizyki. Piotr Posmykiewiz 63 s = ma s = m v f vi = mvi 7- f W równaniu powyŝszym zastosowano równanie Porównują równania 7-0 i 7- otrzymamy: i a s = v f v i v f = 0 ( Patrz równanie -). f s =
Wykład z fizyki. Piotr Posmykiewiz 63 s = ma s = m v f vi = mvi 7- f W równaniu powyŝszym zastosowano równanie Porównują równania 7-0 i 7- otrzymamy: i a s = v f v i v f = 0 ( Patrz równanie -). f s =
Analiza rozkładu sił reakcji podłoża podczas dynamicznie stabilnego chodu robota dwunożnego
 Pomiary Automatya obotya 7-8/2009 Analiza rozładu sił reacji podłoża podczas dynamicznie stabilnego chodu robota dwunożnego Teresa Zielińsa Maciej T. Trojnaci Praca stanowi ontynuację badań opisanych w
Pomiary Automatya obotya 7-8/2009 Analiza rozładu sił reacji podłoża podczas dynamicznie stabilnego chodu robota dwunożnego Teresa Zielińsa Maciej T. Trojnaci Praca stanowi ontynuację badań opisanych w
Laboratorium Inżynierii bioreaktorów Ćwiczenie 2: Rozkład czasu przybywania w reaktorach przepływowych
 EL Laboratorium Inżynierii bioreaktorów Ćwizenie 2: Rozkład zasu przybywania w reaktorah przepływowyh Wyznazenie rzezywistego rozkładu zasu przebywania w reaktorze mieszalnikowym metodą skokową oraz w
EL Laboratorium Inżynierii bioreaktorów Ćwizenie 2: Rozkład zasu przybywania w reaktorah przepływowyh Wyznazenie rzezywistego rozkładu zasu przebywania w reaktorze mieszalnikowym metodą skokową oraz w
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
13. 13. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE
 Część 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3. 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3.. Metoda trzech momentów Rozwiązanie wieloprzęsłowych bele statycznie niewyznaczalnych można ułatwić w znaczącym
Część 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3. 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3.. Metoda trzech momentów Rozwiązanie wieloprzęsłowych bele statycznie niewyznaczalnych można ułatwić w znaczącym
DRGANIA WŁASNE STOJANA SILNIKA INDUKCYJNEGO KLATKOWEGO MAŁEJ MOCY - POMIARY
 Zeszyty Poblemowe Maszyny Eletyczne N 3/01 (96) 5 Sławomi Szymaniec Politechnia Opolsa, Opole DRGANIA WŁASNE STOJANA SILNIKA INDUKCYJNEGO KLATKOWEGO MAŁEJ MOCY - POMIARY NATURAL VIBRATIONS OF SQUIRREL-CAGE
Zeszyty Poblemowe Maszyny Eletyczne N 3/01 (96) 5 Sławomi Szymaniec Politechnia Opolsa, Opole DRGANIA WŁASNE STOJANA SILNIKA INDUKCYJNEGO KLATKOWEGO MAŁEJ MOCY - POMIARY NATURAL VIBRATIONS OF SQUIRREL-CAGE
Koła rowerowe malują fraktale
 Koła rowerowe malują fratale Mare Berezowsi Politechnia Śląsa Rozważmy urządzenie sładającego się z n ół o różnych rozmiarach, obracających się z różnymi prędościami. Na obręczy danego oła, obracającego
Koła rowerowe malują fratale Mare Berezowsi Politechnia Śląsa Rozważmy urządzenie sładającego się z n ół o różnych rozmiarach, obracających się z różnymi prędościami. Na obręczy danego oła, obracającego
 Ł ź ź Ź ż Ż ż ż ć ć ć Ę Ż ć Ź Ż ż ż Ż Ż Ż ć ż Ż ż ż ć ż ć ż ż ż ż Ż Ó ż Ż ć ż ż Ż ć Ż Ź ż Ż Ż ź Ż ż Ź ż Ż ź ż Ż Ź Ą Ę ć ć Ź Ż Ż ć Ż Ź ż Ź Ż ć ć ż ż Ż Ż Ż Ż ż Ź Ż Ż ć Ź Ż Ż Ż ż ć Ż ć Ż ć Ź Ż ż Ż Ż ż ż Ż
Ł ź ź Ź ż Ż ż ż ć ć ć Ę Ż ć Ź Ż ż ż Ż Ż Ż ć ż Ż ż ż ć ż ć ż ż ż ż Ż Ó ż Ż ć ż ż Ż ć Ż Ź ż Ż Ż ź Ż ż Ź ż Ż ź ż Ż Ź Ą Ę ć ć Ź Ż Ż ć Ż Ź ż Ź Ż ć ć ż ż Ż Ż Ż Ż ż Ź Ż Ż ć Ź Ż Ż Ż ż ć Ż ć Ż ć Ź Ż ż Ż Ż ż ż Ż
5 k. EKSTRAKCJA. faza dolna CH3COOH np. woda
 5 k. ESTRACJA Zagadnienia teoretyzne Prao podziału Nernsta. Stała podziału i stężenioy stosunek podziału. Czynniki płyająe na stałą podziału (rodzaj układu, temperatura, substanja). Zależność spółzynnika
5 k. ESTRACJA Zagadnienia teoretyzne Prao podziału Nernsta. Stała podziału i stężenioy stosunek podziału. Czynniki płyająe na stałą podziału (rodzaj układu, temperatura, substanja). Zależność spółzynnika
W pełni optyczny przełącznik wykorzystujący jednorodne światłowodowe siatki Bragga
 doi:.599/48.5..6 Piot KISAŁA Jace KLIEK Kzysztof SKORUPSKI Politechnia Lubelsa Instytut Eletonii i Techni Infomacyjnych () Politechnia Lubelsa Instytut Infomatyi () W pełni optyczny pzełączni wyozystujący
doi:.599/48.5..6 Piot KISAŁA Jace KLIEK Kzysztof SKORUPSKI Politechnia Lubelsa Instytut Eletonii i Techni Infomacyjnych () Politechnia Lubelsa Instytut Infomatyi () W pełni optyczny pzełączni wyozystujący
L(x, 0, y, 0) = x 2 + y 2 (3)
 0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
4. Elementy teorii powierzchni. Odwzorowanie powierzchni na powierzchnię.
 Katogafia matematyczna. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4.. Powiezchnie Powiezchnią w geometii óŝniczowej
Katogafia matematyczna. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4.. Powiezchnie Powiezchnią w geometii óŝniczowej
Materiały do wykładów na temat Obliczanie sił przekrojowych i momentów przekrojowych. dla prętów zginanych.
 ateriały do wyładów na temat Obliczanie sił przerojowych i momentów przerojowych dla prętów zginanych Wydr eletroniczny. slajdów na. stronach przeznaczony do celów dydatycznych dla stdentów II ro stdiów
ateriały do wyładów na temat Obliczanie sił przerojowych i momentów przerojowych dla prętów zginanych Wydr eletroniczny. slajdów na. stronach przeznaczony do celów dydatycznych dla stdentów II ro stdiów
MODELE OBIEKTÓW STEROWANIA
 Pz ODELE OBIEKÓW SEOWAIA Bilan may. Zbiorni z wpłym pod iśnieniem ydrotatyznym. Bilan energii podgrzewaz. Opóźnienie. apięio terowanie ilniiem DC. Sterowanie prądo.. etodologia axlla 868 BILAS ASY o potępowania
Pz ODELE OBIEKÓW SEOWAIA Bilan may. Zbiorni z wpłym pod iśnieniem ydrotatyznym. Bilan energii podgrzewaz. Opóźnienie. apięio terowanie ilniiem DC. Sterowanie prądo.. etodologia axlla 868 BILAS ASY o potępowania
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne.
 Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
KOMPENSACJA UOGÓLNIONEJ MOCY BIERNEJ
 Prace Nauowe Instytutu Maszyn, Napędów i Pomiarów Eletrycznych Nr 66 Politechnii Wrocławsiej Nr 66 Studia i Materiały Nr 3 Józef NOWAK*, Jerzy BAJOREK*, Dominia GAWORSKA-KONIAREK**, omasz JANA* moc bierna,
Prace Nauowe Instytutu Maszyn, Napędów i Pomiarów Eletrycznych Nr 66 Politechnii Wrocławsiej Nr 66 Studia i Materiały Nr 3 Józef NOWAK*, Jerzy BAJOREK*, Dominia GAWORSKA-KONIAREK**, omasz JANA* moc bierna,
LXIV Olimpiada Matematyczna
 LXIV Olimpiada Matematyzna Rozwiązania zadań konkursowyh zawodów stopnia drugiego 22 lutego 203 r. (pierwszy dzień zawodów) Zadanie. Dane są lizby ałkowite b i oraz trójmian f(x) = x 2 +bx+. Udowodnić,
LXIV Olimpiada Matematyzna Rozwiązania zadań konkursowyh zawodów stopnia drugiego 22 lutego 203 r. (pierwszy dzień zawodów) Zadanie. Dane są lizby ałkowite b i oraz trójmian f(x) = x 2 +bx+. Udowodnić,
MIERNICTWO WIELKOŚCI ELEKTRYCZNYCH I NIEELEKTRYCZNYCH
 Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Skojarzone wytwarzanie energii elektrycznej i ciepła na bazie elektrowni jądrowej w Polsce
 onfeencja nauowo-techniczna 13 15 lutego 2013. NAUA I TECHNIA WOBEC WYZWANIA BUDOWY ELETROWNI JĄDROWEJ MĄDRALIN 2013 Wazawa, Intytut Technii Cieplnej Politechnii Wazawiej D hab. inż. azimiez Duziniewicz
onfeencja nauowo-techniczna 13 15 lutego 2013. NAUA I TECHNIA WOBEC WYZWANIA BUDOWY ELETROWNI JĄDROWEJ MĄDRALIN 2013 Wazawa, Intytut Technii Cieplnej Politechnii Wazawiej D hab. inż. azimiez Duziniewicz
Rolainformatykiwnaukach ekonomicznychispoųecznych Innowacjeiimplikacjeinterdyscyplinarne
 Rolainfomatykiwnauka ekonomiznyispoųezny Innowaeiimplikaeintedysyplinane Te Role of Infomatis in Eonomi and Soial Sienes Innovations and Intedisiplinay Impliations edaka ZBIGNIEWE.ZIELIFSKI TOM Wydawnitwo
Rolainfomatykiwnauka ekonomiznyispoųezny Innowaeiimplikaeintedysyplinane Te Role of Infomatis in Eonomi and Soial Sienes Innovations and Intedisiplinay Impliations edaka ZBIGNIEWE.ZIELIFSKI TOM Wydawnitwo
Ćwiczenie nr 1: Wahadło fizyczne
 Wydział PRACOWNA FZYCZNA WFi AGH mię i nazwiso 1.. Temat: Ro Grupa Zespół Nr ćwiczenia Data wyonania Data oddania Zwrot do popr. Data oddania Data zaliczenia OCENA Ćwiczenie nr 1: Wahadło fizyczne Cel
Wydział PRACOWNA FZYCZNA WFi AGH mię i nazwiso 1.. Temat: Ro Grupa Zespół Nr ćwiczenia Data wyonania Data oddania Zwrot do popr. Data oddania Data zaliczenia OCENA Ćwiczenie nr 1: Wahadło fizyczne Cel
CHARAKTERYSTYKI UŻYTKOWE I WZORCOWANIE SZEROKOPASMOWYCH MIERNIKÓW NADFIOLETU
 Jezy PIETRZYKOWSKI CHARAKTERYSTYKI UŻYTKOWE I WZORCOWANIE SZEROKOPASMOWYCH MIERNIKÓW NADFIOLETU STRESZCZENIE Okeślono haakteystyki użytkowe szeokopasmowyh mieników nadfioletu oaz ih klasyfikaję. Podano
Jezy PIETRZYKOWSKI CHARAKTERYSTYKI UŻYTKOWE I WZORCOWANIE SZEROKOPASMOWYCH MIERNIKÓW NADFIOLETU STRESZCZENIE Okeślono haakteystyki użytkowe szeokopasmowyh mieników nadfioletu oaz ih klasyfikaję. Podano
9. Sprzężenie zwrotne własności
 9. Sprzężenie zwrotne własności 9.. Wprowadzenie Sprzężenie zwrotne w uładzie eletronicznym realizuje się przez sumowanie części sygnału wyjściowego z sygnałem wejściowym i użycie zmodyiowanego w ten sposób
9. Sprzężenie zwrotne własności 9.. Wprowadzenie Sprzężenie zwrotne w uładzie eletronicznym realizuje się przez sumowanie części sygnału wyjściowego z sygnałem wejściowym i użycie zmodyiowanego w ten sposób
OPRACOWANIE PROGRAMU DO SYMULOWANIA LOTU RAKIET BALISTYCZNYCH DALEKIEGO ZASIĘGU
 Dr inż. Marin WACHULSKI Dr inż. Jaek WACHULSKI Wojskowa Akademia Tehnizna DOI: 10.17814/mehanik.015.7.315 OPACOWANI POGAMU DO SYMULOWANIA LOTU AKIT BALISTYCZNYCH DALKIGO ZASIĘGU Streszzenie: W referaie
Dr inż. Marin WACHULSKI Dr inż. Jaek WACHULSKI Wojskowa Akademia Tehnizna DOI: 10.17814/mehanik.015.7.315 OPACOWANI POGAMU DO SYMULOWANIA LOTU AKIT BALISTYCZNYCH DALKIGO ZASIĘGU Streszzenie: W referaie
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
Sterowanie Ciągłe. Używając Simulink a w pakiecie MATLAB, zasymulować układ z rysunku 7.1. Rys.7.1. Schemat blokowy układu regulacji.
 emat ćwiczenia nr 7: Synteza parametryczna uładów regulacji. Sterowanie Ciągłe Celem ćwiczenia jest orecja zadanego uładu regulacji wyorzystując następujące metody: ryterium amplitudy rezonansowej i metodę
emat ćwiczenia nr 7: Synteza parametryczna uładów regulacji. Sterowanie Ciągłe Celem ćwiczenia jest orecja zadanego uładu regulacji wyorzystując następujące metody: ryterium amplitudy rezonansowej i metodę
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Arytmetyka finansowa Wykład 6 Dr Wioletta Nowak
 Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
