TABELA PRZELICZENIOWA
|
|
|
- Dominik Leśniak
- 7 lat temu
- Przeglądów:
Transkrypt
1 Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Nr 7 Korzystanie z przyrządów (). Sztuka trasowania - z.6. Ruch równoleżnikowy. (Patrz na MPĘ). THNIK Koszalin dnia r 24h;0h TL PRZLIZNIW wg () Przyrząd w () 23h 1h bwodu koła: 24[mm/h]*24[h]=576mm (liczba całkowita) "Słońce Majów" Promień r= bwód/(2*π) = 91, h 2h [mm] [ /mm]; [h/mm]; [mm/h]; [ /h]; [h/ ]. o zamienić, na co? [ ] [mm] 576[mm]*(1/360[ ])= 1,6000 [mm/ ] 21h 3h Przykł.1: L=4,321[ ] tj. L[ ]*1,6[mm/ ]= 6, [mm] [mm] [ ] Przykł.2: L=90,0[mm] tj. L[mm]*0,625[ /mm]= 56,2500 [ ] [h] [mm] 576[mm]*(1/24[h])= 24,000 [mm/h] 20h 4h Przykł.3: L=7,04[h] tj. L[h]*24,0[mm/h]= 168,960 [mm] [mm] [h] Przykł.4: L=17,07[mm] tj. L[mm]*0,041667[h/mm]= 0,71125 [h] [ ] [h] 24[h]*(1/360[ ])= 0,06667 [h/ ] 19h 5h Przykł.5: L=139,3[ ] tj. L[h]*0,06667[h/ ]= 9,28667 [h] X(r) [h] [ ] 360[ ]*(1/24[h])= 15,000 [ /h] 16h &=75[ ] r 8h 6h L - liczba z określonym mianem np. [ ]; [mm]; [h]; [mm/ ]; 360[ ]*(1/576[mm])= 0,6250 [ /mm] 24[h]*(1/576[mm])= 0, [h/mm] Radiany są obliczne z [ ], a stopnie z radianów [rad]. Przykład 6: L=71,95[ ] tj. formuła fx : ((=)radiany(l)) Przykład 6: 1, [rad] Przykład 7: L=1,965[rad] tj. formuła fx : ((=)stopnie(l)) Przykład 7: 112, [ ] o się stanie, gdy promień r= 120,000 [mm]? dpowiedź: nic. Wtedy trzeba używać mnożnik U: U=r(120)/r= 1, Stąd obwód: 17h 7h b = 576[mm]*U= 753, Y(r) [mm] W ten sposób należy postępować ze wszystkimi wym. Kiedy potrzebuję przeliczyć wymiar na innę jednostkę, wtedy szukam w mianowniku tę jednostkę, a potem sprawdzam jaką jednostką dysponuję która jest w liczniku. Jeśli jest tą, którą mam przeliczyć - jest K! Proszę zwrócić uwagę na liczbę U(udział). Jest bez miana. Gdybym tej liczbie nadał status miana np. w [rad], 15h 9h wówczas byłby TN kąta: 75,000 [ ] tj. Kierunkowa. Wtedy: r(120)=r*u= 120,000 [mm] X(r(120))=X(r)*U = (r*sin&)*u= 115, [mm] 14h 10h Y(r(120))=Y(r)*U = (r*cos&)*u= 31, [mm] Sprawdzenie oblicz.promienia: r*u=(x(r)^2+y(r)^2)^0,5 13h 12h 11h r*u = 120,000 [mm] K! Zachowana proporcjonalność. Na str.2 pokazuję dwa rys.1 i 2. Na rys.2 walca, zawierającego piłkę, zaznaczyłem ważne pkty:; ; ; ; ;. ez rys.1 nie byłbym w stanie stwierdzić, który z tych punktów jest najwyżej, względem osi: (-Z+Z). Można się dowiedzieć dzięki płaszczyźnie (YZ), gdzie jest ta oś. entralny pkt. jest w centrum piłki, który jest początkiem układu przestrzennego (XYZ). Tym razem przedstawiłem ruch w (). Jeśli odniosę się do mapy to będzie ruch równoleżnikowy. Jeżeli odniosę się do płaszczyzny (XZ) będzie to ruch równoleżnikowy. brót wokół osi (-X+X).
2 Y (-)X (+)X Y (+)Z (+)Z (+)Z str.2 Rys.2a.(21h) Rys.4a.(22h) Z(21h) Zg(22h) ; ; (-)X Zd (+)X Zd Z(21h) (-)Z (-)Z (-)Z Y (-)X Płaszczyzna pionowa w pozycji leżącej (XZ) (+)X Y Zg(22h) Strzałki informują o odległościach elips od osi (-X+X) wym.wzieto ze Skryptu 006. wym.lips 2*b=Zg(22h)+Zd(22h) Z (-)X (+)X Z (+)Y (-)Y (+)Y Rys.2.(21h) Rys.4.(22h) ; ; (+)Y (-)Y (-)Y MP Z (-)X Płaszczyzna pozioma (+)X Z MP
3 str.3 Zg(23h) Rys.6a.(23h) r = Zg(24h) Rys.8a.(24h;0h) Zd(23h) (-)X (+)X (-)X (+)X Zd(23h) Zg(23h) wym.lips 2*b=Zg(23h)+Zd(23h) r = Zd(24h) Koło Zg(24h) = Zd(24h) = r Rys.6.(23h) Rys.8.(24h;0h) (-)X (+)X (-)X (+)X MP MP
4 str.4 Rys.10a.(1h) Rys.12a.(2h) Zg(1h) Zg(2h) (-)X Zd(1h) Zd(1h) (+)X Zg(1h) (-)X Zd(2h) (+)X Zd(2h) Zg(2h) wym.lips 2*b=Zg(1h)+Zd(1h) wym.lips 2*b=Zg(2h)+Zd(2h) Rys.10.(1h) Rys.12.(2h) MP MP
5 str.5 Rys.14a.(3h) Rys.16a.(4h) Zg(3h) Zg(4h) (-)X (+)X (-)X Zd(4h) (+)X Zd(4h) Zg(3h) Zg(4h) wym.lips 2*b=Zg(3h) wym.lips 2*b=Zg(4h)-Zd(4h) Rys.14.(3h) Rys.16.(4h) MP MP
6 str.6 Zd(5h) Zg(5h) Zg(6h) Rys.20a.(6h) Zd(5h) Zg(5h) Rys.18a.(5h) Zg(6h) wym.lips 2*b=Zg(5h)-Zd(5h) wym.koła r=zg(6h) Rys.18.(5h) Rys.20.(6h) MP MP
7 str.7 Rys.22a.(7h) Rys.24a.(8h) Zg(7h) Zg(8h) Zd(7h) (-)X (+)X (-)X Zd(8h) (+)X Zd(8h) Zd(7h) Zg(7h) wym.lips 2*b=Zg(7h)-Zd(7h) wym.lips 2*b=Zg(8h)-Zd(8h) Rys.22.(7h) Rys.24.(8h) MP MP
8 str.8 Rys.26a.(9h) Rys.28a.(10h) Zg(9h) Zg(10h) (-)X (+)X (-)X Zd(10h) (+)X Zd(10h) Zd(9h) Zg(10h) wym.lips 2*b=Zg(9h) wym.lips 2*b=Zg(10h)+Zd(10h) Rys.26.(9h) Rys.28.(10h) MP MP
9 str.9 Zg(11h) Rys.30a.(11h) Rys.32a.(12h) Zg(12h) Zd(11h) Zd(11h) Zg(11h) Zg(12h) wym.lips 2*b=Zg(11h)+Zd(11h) wym.koła r=zg(12h) Rys.30.(11h) Rys.32.(12h) MP MP
10 Zd(13h) Zg(13h) Rys.34a.(13h) (-)X (+)X (-)X Zd(14h) (+)X Zd(14h) Zd(13h) Rys.36a.(14h) Zg(14h) str.10 Zg(13h) Zg(14h) wym.lips 2*b=Zg(13h)+Zd(13h) wym.lips 2*b=Zg(14h)+Zd(14h) Rys.34.(13h) Rys.36.(14h) MP MP
11 str.11 Rys.38a.(15h) Rys.40a.(16h) Zd(15h) Zg(16h) (-)X (+)X (-)X Zd(16h) (+)X Zd(16h) Zd(15h) Zg(16h) wym.lips 2*b=Zg(15h) wym.lips 2*b=Zg(16h)-Zd(16h) Rys.38.(15h) Rys.40.(16h) MP MP
12 str.12 Zg(17h) Rys.42a.(17h) Zg(6h) Rys.44a.(18h) Zd(17h) Zd(17h) Zg(6h) wym.lips 2*b=Zg(17h)-Zd(17h) wym.koła r=zg(6h) Rys.42.(17h) Rys.44.(18h) MP MP
13 Rys.46a.(19h) Rys.48a.(20h) str.13 Zg(19h) Zg(20h) Zd(19h) (-)X (+)X (-)X Zd(20h) (+)X Zd(19h) Zg(19h) Zg(20h) wym.lips 2*b=Zg(19h)-Zd(19h) wym.lips 2*b=Zg(20h)-Zd(20h) Rys.46a.(19h) Rys.48.(20h) MP MP
14 ZS: Nr 7 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Przyrządy analityczne w (). Jeśli ciągle korzystasz z tego samego sposobu obliczenia w matematyce, to sposób ten, staje się twoim narzędziem pracy. Korzystanie z przyrządów (). Sztuka trasowania - z.6. Ruch równoleżnikowy. (Patrz na MPĘ). str.14 KPI PRZYKŁU LIZNIWG RZWIĄZUJĄ TRÓJKĄT: PLIK.ZSZYT.003. PRZYRZĄ NLIT. ane a = 124, b = 110, &= 41,333 [ ] Szukane: ; c; r; h ; µ[ ]; β[ ] Ł1; Ł2; Ł3; Trójkąt: () jak poprzednie dwa trójkąty h = 2*/a = 72, twierdzenie rzutów: a = c*cosµ+b*cos& tj. () = 0,5*a*b*sin& = 4 526, tj. c = (a-b*cos&)/cosµ c*cosµ = (a-b*cos&)= 41, β[ ]= 180 -(&+µ) = 78, Ł3 c=h/sinµ cosµ*h/sinµ = h/tanµ = 41,5553 µ [ ]= 60, s=0,5*(a+b+c) β c = h/sinµ = 83, [mm] Twierdzenie sinusów: s= 159, Ł1 c r= (a/sinβ)/2 = 63, *r=a/sinβ=b/sinµ=c/sin& Kąty środkowe: h b Ł1(&1)= 91, Ł2(β1)= 173, Ł3(µ1)= 133, &[ ] &1[ ] = 82, µ a & Łz= Ł1(&1)+Ł2(β1)+Ł1(µ1)= 398, Łuk zamknięty 360 β[ ] β1[ ] = 156, r bwód okręgu: 2*π*r = 398, µ[ ] µ1[ ] = 120, Ł1(&1)/r= 1, [rad] Sprawdzenie poprawności Suma kątów środk. 360, Ł2(β1)/r= 2, [rad] wyliczeń matematycznych: Na rysunku nie ma oznaczonych Ł2 Ł3(µ1)/r= 2, [rad] =(s*(s-a)*(s-b)*(s-c))^0,5= 4 526,49816 kątów środkowych. Łz/r = 6, [rad] =a*b*c/(4*r)= 4 526, KPI PRZYKŁU LIZNIWG RZWIĄZUJĄ TRÓJKĄT: PLIK.ZSZYT.003. PRZYRZĄ ane: (:)=c= 451,23 &[ ] = 34,123 β[ ] = 54,321 Jak na rysunku. Rozwiąż powstały trójkąt. NLITYZNY Warunek: &[rad] = 0, Szukam: ; (:); (:); µ ; α ; ε ; η ; r; strzałki: h1; h2;h3 β (& +90 ) PRW Rys.2 Powstały trójkąt Rys.3 Ł1 ; ; łuki: Ł1; Ł2; Ł3; Łz Ramiona w trójk.nie mogą być równoległe!!! µ Ł2 µ h1 Wyliczenia: β h2 c r c 90 -β = 35, [ ] c & 90 -β c & a b 90 -ß c & 90 -β = 0, [rad] r ε η r cięciwy::=c; :=c; :=c β β µ = 180 -((90-β)+&) S Twierdzenie sinusów: µ = 110,198 µ= 1,92332 [rad] α 2*r=c/sin(90-β)=c/sinµ=c/sin& Na rys.3 są środkowe boków powstałego trójkąta. Wszystkie trzy środkowe h3 r=0,5*c/sinµ= 240, krzyżują się w punkcie centralnym S. Jest nim środek koła opisanego na tym. c= 2*r*sin& = 269, Wzór Pitagorasa: c^2=a^2+b^2 a = (r^2-(0,5*c)^2)^0,5 = 199, Ł3 c=2*r*sin(90 -β )= 280, h2=r-a = 41, b = (r^2-(0,5*c)^2)^0,5 = 195,276 bwód: 1510,48 = π*r^2 = ,31 =c*c*c/(4*r)= , h1=r-b = 45, ε = 2*asin(0,5*c/r)= 68,246 ε= 1, [rad] Ł1=r*η[rad]= 299, Ł2=r*ε[rad]= 286, η = 2*asin(0,5*c/r)= 71,358 η= 1,24543 [rad] α = 360 -(ε +η )= 220,396 α= 3,8466 [rad] Ł3=r*α[rad]= 924, Łz= 1510,47728 Wzór na strzałkę: h1=r*(1-cos(0,5*α[rad])) = 323, Z wyliczeń wynika, że strzałka "h1" jest większa od prom. koła "r" o: 83, Modyfikację wykonałem dnia r uzupełniając geometrię kulową (). T THNIK Ruch w przestrzeni i przyrządy analityczne w (). opracował: inż. Kazimierz arski Koszalin dnia r
TABELA PRZELICZENIOWA
 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
1/4(koła; okrągu) A A' P'(x)
 skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
Koszalin dnia r Rys.1 o promieniu: r = 91, h;0h TABELA PRZELICZENIOWA wg (gk)
 skrypt Romany (R) gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Lekcja korzystania z przyrządu (rozw.trójkąt)
skrypt Romany (R) gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Lekcja korzystania z przyrządu (rozw.trójkąt)
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
OBLICZENIE PRZEKROJU WALCA PO CIĘCIU SKOŚNYM. Rysunki i obliczenia dotyczą walca
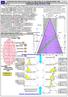 Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
gk T Rozwiązanie Zadania nr1 - uzupełnienie
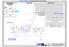 TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
gk T Zadania nr 2. opracował: inż. Kazimierz Barski dla wszystkich ludzi świata TECHNIKA Koszalin dnia r
 ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
V Konkurs Matematyczny Politechniki Białostockiej
 V Konkurs Matematyczny Politechniki Białostockiej Rozwiązania - klasy drugie 1. Znaleźć wszystkie pary liczb całkowitych (x, y) spełniające nierówności x + 1 + y 4 x + y 4 5 x 4 + y 1 > 4. Ważne jest zauważenie,
V Konkurs Matematyczny Politechniki Białostockiej Rozwiązania - klasy drugie 1. Znaleźć wszystkie pary liczb całkowitych (x, y) spełniające nierówności x + 1 + y 4 x + y 4 5 x 4 + y 1 > 4. Ważne jest zauważenie,
PRÓBNA MATURA ZADANIA PRZYKŁADOWE
 ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0, C. 0. D. 0 5% 6 II sposób: x nieznana liczba
ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0, C. 0. D. 0 5% 6 II sposób: x nieznana liczba
G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm
![G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm](/thumbs/71/64805542.jpg) Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
PRÓBNA MATURA ZADANIA PRZYKŁADOWE
 ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA 3, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0,3 C. 30. D. 0 5% 6 II sposób: x nieznana liczba
ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA 3, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0,3 C. 30. D. 0 5% 6 II sposób: x nieznana liczba
MAGAZYN WIEDZY NR 1 O GEOMETRII KULOWEJ. PROJEKT TWÓRCY (gk). PRZYPOMINA POMNIK. WALEC TRAPEZOWY Z KORYTEM KOŁO. Nr2 6h(48h) ELIPSA pionowa O
 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
gk T Okrąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 Rys.2
 krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
Geometria. Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7
 Geometria Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7 W tym przypadku możemy wykonać szkic pięciokąta i policzyć przekątne: Zadanie. Promień okręgu opisanego na kwadracie
Geometria Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7 W tym przypadku możemy wykonać szkic pięciokąta i policzyć przekątne: Zadanie. Promień okręgu opisanego na kwadracie
ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna
 Arkusz A06 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Wartość wyrażenia 1 3 + 1 + 3
Arkusz A06 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Wartość wyrażenia 1 3 + 1 + 3
MATEMATYKA ZBIÓR ZADAŃ MATURALNYCH. Lata Poziom podstawowy. Uzupełnienie Zadania z sesji poprawkowej z sierpnia 2019 r.
 MATEMATYKA ZBIÓR ZADAŃ MATURALNYH Lata 010 019 Poziom podstawowy Uzupełnienie 019 Zadania z sesji poprawkowej z sierpnia 019 r. Opracował Ryszard Pagacz Spis treści Zadania maturalne.........................................................
MATEMATYKA ZBIÓR ZADAŃ MATURALNYH Lata 010 019 Poziom podstawowy Uzupełnienie 019 Zadania z sesji poprawkowej z sierpnia 019 r. Opracował Ryszard Pagacz Spis treści Zadania maturalne.........................................................
Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną)
 Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną) Zadania zamknięte (jedna poprawna odpowiedź) 1 punkt Wyrażenia algebraiczne Zadanie 1. Wartość wyrażenia 3 x 3x
Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną) Zadania zamknięte (jedna poprawna odpowiedź) 1 punkt Wyrażenia algebraiczne Zadanie 1. Wartość wyrażenia 3 x 3x
Rys.1 pomocniczy. Okrąg z którego powstały łuki na rys.1b.
 OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
I. Funkcja kwadratowa
 Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy w roku szkolnym 2018/2019 w CKZiU nr 3 Ekonomik w Zielonej Górze KLASA III fl POZIOM PODSTAWOWY I. Funkcja kwadratowa narysować wykres funkcji
Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy w roku szkolnym 2018/2019 w CKZiU nr 3 Ekonomik w Zielonej Górze KLASA III fl POZIOM PODSTAWOWY I. Funkcja kwadratowa narysować wykres funkcji
gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii
![gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii](/thumbs/103/159774468.jpg) Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Geometria. Rodzaje i własności figur geometrycznych:
 Geometria Jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Figury geometryczne na płaszczyźnie noszą nazwę figur płaskich, w przestrzeni
Geometria Jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Figury geometryczne na płaszczyźnie noszą nazwę figur płaskich, w przestrzeni
KORZYSTANIE Z SZABLONÓW LISTWOWYCH I TARCZY ZEGARÓW: 12h i 24h
 Rys.nr 46. dokończenie Rys.nr 44. HIZY KRZYAI Z ZABLÓ LIYH I ARZY ZGARÓ: 1 i 24h str.12 KPIA Z ZZYU R 001: ciąg dalszy LKJI r 10 i efekty pracy LKJA r 10 - posługiwanie się szablonami listwowymi (rysunki
Rys.nr 46. dokończenie Rys.nr 44. HIZY KRZYAI Z ZABLÓ LIYH I ARZY ZGARÓ: 1 i 24h str.12 KPIA Z ZZYU R 001: ciąg dalszy LKJI r 10 i efekty pracy LKJA r 10 - posługiwanie się szablonami listwowymi (rysunki
Kurs ZDAJ MATURĘ Z MATEMATYKI - MODUŁ 11 Teoria planimetria
 1 Pomimo, że ten dział, to typowa geometria wydawałoby się trudny dział to paradoksalnie troszkę tu odpoczniemy, jeśli chodzi o teorię. Dlaczego? Otóż jak zapewne doskonale wiesz, na maturze otrzymasz
1 Pomimo, że ten dział, to typowa geometria wydawałoby się trudny dział to paradoksalnie troszkę tu odpoczniemy, jeśli chodzi o teorię. Dlaczego? Otóż jak zapewne doskonale wiesz, na maturze otrzymasz
gk T Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (gk), w sposób praktyczny. Rys.2a
 Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Rachunek wektorowy - wprowadzenie. dr inż. Romuald Kędzierski
 Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rys.1. str.1. 48h;0h 18h 19h 20h 21h 22h 46h. 44h r1 4h. 10h. 38h. 34h 14h. 32h 16h. 24h jest linią do przenoszenia szablonów
 Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Skrypt 20. Planimetria: Opracowanie L6
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Planimetria: 1. Kąty w
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Planimetria: 1. Kąty w
LUBELSKA PRÓBA PRZED MATURA
 NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI LUBELSKA PRÓBA PRZED MATURA DLA KLAS TRZECICH POZIOM PODSTAWOWY GRUPA I 1 STYCZNIA 011 CZAS PRACY: 170 MINUT Zadania zamknięte ZADANIE 1 (1 PKT.) Liczba
NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI LUBELSKA PRÓBA PRZED MATURA DLA KLAS TRZECICH POZIOM PODSTAWOWY GRUPA I 1 STYCZNIA 011 CZAS PRACY: 170 MINUT Zadania zamknięte ZADANIE 1 (1 PKT.) Liczba
FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE
 Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
GEOMETRIA ELEMENTARNA
 Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
KONKURS ZOSTAŃ PITAGORASEM MUM. Podstawowe własności figur geometrycznych na płaszczyźnie
 KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1
 PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
A. fałszywa dla każdej liczby x.b. prawdziwa dla C. prawdziwa dla D. prawdziwa dla
 Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
KLASA I LO Poziom podstawowy (styczeń) Treści nauczania wymagania szczegółowe:
 KLASA I LO Poziom podstawowy (styczeń) Treści nauczania wymagania szczegółowe: ZAKRES PODSTAWOWY 7. Planimetria. Uczeń: 1) rozpoznaje trójkąty podobne i wykorzystuje (także w kontekstach praktycznych)
KLASA I LO Poziom podstawowy (styczeń) Treści nauczania wymagania szczegółowe: ZAKRES PODSTAWOWY 7. Planimetria. Uczeń: 1) rozpoznaje trójkąty podobne i wykorzystuje (także w kontekstach praktycznych)
Skrypt 24. Geometria analityczna: Opracowanie L5
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 24 Geometria analityczna:
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 24 Geometria analityczna:
Zad.3. Jakub Trojgo i Jakub Wieczorek. 14 grudnia 2013
 Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI poziom rozszerzony
 Próbny egzamin maturalny z matematyki. Poziom rozszerzony 1 PRÓNY EGZMIN MTURLNY Z MTEMTYKI poziom rozszerzony ZNI ZMKNIĘTE W każdym z zadań 1.. wybierz i zaznacz jedną poprawną odpowiedź. Zadanie 1. (0
Próbny egzamin maturalny z matematyki. Poziom rozszerzony 1 PRÓNY EGZMIN MTURLNY Z MTEMTYKI poziom rozszerzony ZNI ZMKNIĘTE W każdym z zadań 1.. wybierz i zaznacz jedną poprawną odpowiedź. Zadanie 1. (0
(a 1 2 + b 1 2); : ( b a + b ab 2 + c ). : a2 2ab+b 2. Politechnika Białostocka KATEDRA MATEMATYKI. Zajęcia fakultatywne z matematyki 2008
 Zajęcia fakultatywne z matematyki 008 WYRAŻENIA ARYTMETYCZNE I ALGEBRAICZNE. Wylicz b z równania a) ba + a = + b; b) a = b ; b+a c) a b = b ; d) a +ab =. a b. Oblicz a) [ 4 (0, 5) ] + ; b) 5 5 5 5+ 5 5
Zajęcia fakultatywne z matematyki 008 WYRAŻENIA ARYTMETYCZNE I ALGEBRAICZNE. Wylicz b z równania a) ba + a = + b; b) a = b ; b+a c) a b = b ; d) a +ab =. a b. Oblicz a) [ 4 (0, 5) ] + ; b) 5 5 5 5+ 5 5
METODA RZUTÓW MONGE A (II CZ.)
 RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 1 KWIETNIA 017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Suma sześciu kolejnych
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 1 KWIETNIA 017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Suma sześciu kolejnych
ARKUSZ ĆWICZENIOWY Z MATEMATYKI MARZEC 2012 POZIOM PODSTAWOWY
 Centralna Komisja Egzaminacyjna ARKUSZ ĆWICZENIOWY Z MATEMATYKI POZIOM PODSTAWOWY MARZEC 2012 Instrukcja dla zdającego 1. Sprawdź, czy arkusz ćwiczeniowy zawiera 28 stron (zadania 1 32). 2. Odpowiedzi
Centralna Komisja Egzaminacyjna ARKUSZ ĆWICZENIOWY Z MATEMATYKI POZIOM PODSTAWOWY MARZEC 2012 Instrukcja dla zdającego 1. Sprawdź, czy arkusz ćwiczeniowy zawiera 28 stron (zadania 1 32). 2. Odpowiedzi
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 11 Zadania planimetria
 1 TEST WSTĘPNY 1. (1p) Wysokość rombu o boku długości 6 i kącie ostrym 60 o jest równa: A. 6 3 B. 6 C. 3 3 D. 3 2. (1p) W trójkącie równoramiennym długość ramienia wynosi 10 a podstawa 16. Wysokość opuszczona
1 TEST WSTĘPNY 1. (1p) Wysokość rombu o boku długości 6 i kącie ostrym 60 o jest równa: A. 6 3 B. 6 C. 3 3 D. 3 2. (1p) W trójkącie równoramiennym długość ramienia wynosi 10 a podstawa 16. Wysokość opuszczona
ROZWIĄZANIA DO ZADAŃ
 TURNIRJ MATEMATYCZNY ELIPSA dla klas LO ROZWIĄZANIA DO ZADAŃ Zadanie. (2 pkt.) Dla jakich wartości parametru m (m R), część wspólna przedziałów A = (, m m i B = 2m 2, + ) jest zbiorem pustym? / Jeśli A
TURNIRJ MATEMATYCZNY ELIPSA dla klas LO ROZWIĄZANIA DO ZADAŃ Zadanie. (2 pkt.) Dla jakich wartości parametru m (m R), część wspólna przedziałów A = (, m m i B = 2m 2, + ) jest zbiorem pustym? / Jeśli A
400% Rys.2a Negatyw *** ZASADA *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na OPIS WYKONYWANYCH CZYNNOŚCI.
 Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
3.3. dwie płaszczyzny równoległe do siebie α β Dwie płaszczyzny równoległe do siebie mają ślady równoległe do siebie
 Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZMIN MTURLNY Z MTEMTYKI ZESTW PRZYGOTOWNY PRZEZ SERWIS WWW.ZDNI.INFO POZIOM PODSTWOWY 7 KWIETNI 2018 ZS PRY: 170 MINUT 1 Zadania zamknięte ZDNIE 1 (1 PKT) Wyrażenie x+3 1 x dla x < 1 ma wartość
PRÓBNY EGZMIN MTURLNY Z MTEMTYKI ZESTW PRZYGOTOWNY PRZEZ SERWIS WWW.ZDNI.INFO POZIOM PODSTWOWY 7 KWIETNI 2018 ZS PRY: 170 MINUT 1 Zadania zamknięte ZDNIE 1 (1 PKT) Wyrażenie x+3 1 x dla x < 1 ma wartość
Skrypt 33. Powtórzenie do matury:
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 33 Powtórzenie do matury:
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 33 Powtórzenie do matury:
Funkcje trygonometryczne
 Funkcje trygonometryczne Sinus kąta ostrego α stosunek długości przyprostokątnej leżącej naprzeciw kąta α do długości przeciwprostokątnej: sin α = a : c = a/c Cosinus kąta ostrego α stosunek długości przyprostokątnej
Funkcje trygonometryczne Sinus kąta ostrego α stosunek długości przyprostokątnej leżącej naprzeciw kąta α do długości przeciwprostokątnej: sin α = a : c = a/c Cosinus kąta ostrego α stosunek długości przyprostokątnej
Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość:
 Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość: A. r 2 + q 2 = p 2 B. p 2 + r 2 = q 2 C. p 2 + q 2 = r 2 D. p + q
Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość: A. r 2 + q 2 = p 2 B. p 2 + r 2 = q 2 C. p 2 + q 2 = r 2 D. p + q
ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna
 Arkusz A05 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Ułamek 5+2 5 2 ma wartość: A.
Arkusz A05 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Ułamek 5+2 5 2 ma wartość: A.
8. TRYGONOMETRIA FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO.
 WYKŁAD 6 1 8. TRYGONOMETRIA. 8.1. FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO. SINUSEM kąta nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej w trójkącie prostokątnym : =. COSINUSEM
WYKŁAD 6 1 8. TRYGONOMETRIA. 8.1. FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO. SINUSEM kąta nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej w trójkącie prostokątnym : =. COSINUSEM
I. Funkcja kwadratowa
 Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy dla klas III w roku szkolnym 2017/2018 w Zespole Szkół Ekonomicznych w Zielonej Górze Dla każdej klasy 3 obowiązuje taka ilość poniższego
Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy dla klas III w roku szkolnym 2017/2018 w Zespole Szkół Ekonomicznych w Zielonej Górze Dla każdej klasy 3 obowiązuje taka ilość poniższego
Stożkiem nazywamy bryłę obrotową, która powstała przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych.
 1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
KURS MATURA PODSTAWOWA Część 2
 KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
Matematyczne słowa Autorki innowacji: Jolanta Wójcik Magda Kusyk
 Szkoła Podstawowa im Kornela Makuszyńskiego w Łańcuchowie Krzyżówki matematyczne klasy V, które powstały jako efekt realizacji innowacji pedagogicznej Matematyczne słowa Autorki innowacji: Jolanta Wójcik
Szkoła Podstawowa im Kornela Makuszyńskiego w Łańcuchowie Krzyżówki matematyczne klasy V, które powstały jako efekt realizacji innowacji pedagogicznej Matematyczne słowa Autorki innowacji: Jolanta Wójcik
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 b BS
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 b BS Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 b BS Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
NOWA FORMUŁA EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MMA 2019 UZUPEŁNIA ZDAJĄCY. miejsce na naklejkę UZUPEŁNIA ZESPÓŁ NADZORUJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 4 czerwca 2019
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 4 czerwca 2019
gk T MAŁA C 18h O 6h F
 ROZWIĄZANIE ZADANIA TPO.Nr 1. (TYLKO PRZEZ ORŁÓW) Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). TO JEST MÓJ I TWÓJ EGZAMIN Z MYŚLENIA (). str.25 1 Plik cz.i. rozwiązania zadania jest przeciążony ilością
ROZWIĄZANIE ZADANIA TPO.Nr 1. (TYLKO PRZEZ ORŁÓW) Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). TO JEST MÓJ I TWÓJ EGZAMIN Z MYŚLENIA (). str.25 1 Plik cz.i. rozwiązania zadania jest przeciążony ilością
Za czym odrzucisz, co mam do pokazania, zobacz kolejne strony pliku! TABELA ANALITYCZNA TRÓJKĄTA MK - TURBO Nr wzoru WZÓR: WYNIK: JM:
 MK JES RÓJKĄEM RÓWNORAMIENNYM, KÓREGO WIELKOŚĆ KĄA ŚRODKOWEGO WYZNACZAJĄ str.1 DZIESIĘNE KĄA PEŁNEGO W OKRĘGU. JEGO KĄ ŚRODKOWY WYNIKA Z WZORU: 2*π-6[rad]= 0,283185307 SĄD: MK kąt środkowy ma = 16,225322921506100
MK JES RÓJKĄEM RÓWNORAMIENNYM, KÓREGO WIELKOŚĆ KĄA ŚRODKOWEGO WYZNACZAJĄ str.1 DZIESIĘNE KĄA PEŁNEGO W OKRĘGU. JEGO KĄ ŚRODKOWY WYNIKA Z WZORU: 2*π-6[rad]= 0,283185307 SĄD: MK kąt środkowy ma = 16,225322921506100
gk T GEOMETRIA WYKREŚLNA PRZESTRZENNA T (GK) W PRAKTYCE. SZTUKA TRASOWANIA CZ.1. Rys.3. Rys.4. Rysunek jest zbyt duży, zmniejszę go na str.2.
 GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
V Międzyszkolny Konkurs Matematyczny
 V Międzyszkolny Konkurs Matematyczny im. Stefana Banacha dla uczniów szkół średnich Zespół Szkół Nr 1 im. Adama Mickiewicza w Lublińcu 42-700 Lubliniec, ul. Sobieskiego 22 18. kwiecień 2011 rok 1. W trapezie
V Międzyszkolny Konkurs Matematyczny im. Stefana Banacha dla uczniów szkół średnich Zespół Szkół Nr 1 im. Adama Mickiewicza w Lublińcu 42-700 Lubliniec, ul. Sobieskiego 22 18. kwiecień 2011 rok 1. W trapezie
Mini tablice matematyczne. Figury geometryczne
 Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Matematyka kompendium 2
 Matematyka kompendium 2 Spis treści Trygonometria Funkcje trygonometryczne Kąt skierowany Kąt skierowany umieszczony w układzie współrzędnych Wartości funkcji trygonometrycznych kątów 30 o, 45 o, 60 o
Matematyka kompendium 2 Spis treści Trygonometria Funkcje trygonometryczne Kąt skierowany Kąt skierowany umieszczony w układzie współrzędnych Wartości funkcji trygonometrycznych kątów 30 o, 45 o, 60 o
WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 2017/2018
 WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 017/018 etap wojewódzki Kryteria oceniania Zad.1.(0 3) Michał, Romek, Staszek, Tomek
WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 017/018 etap wojewódzki Kryteria oceniania Zad.1.(0 3) Michał, Romek, Staszek, Tomek
ARKUSZ ĆWICZENIOWY Z MATEMATYKI MARZEC 2012 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Centralna Komisja Egzaminacyjna ARKUSZ ĆWICZENIOWY Z MATEMATYKI POZIOM PODSTAWOWY 1. Sprawdź, czy arkusz ćwiczeniowy zawiera strony (zadania 1 3).. Rozwiązania zadań i odpowiedzi wpisuj w miejscu na to
Centralna Komisja Egzaminacyjna ARKUSZ ĆWICZENIOWY Z MATEMATYKI POZIOM PODSTAWOWY 1. Sprawdź, czy arkusz ćwiczeniowy zawiera strony (zadania 1 3).. Rozwiązania zadań i odpowiedzi wpisuj w miejscu na to
EGZAMIN MATURALNY Z MATEMATYKI CZERWIEC 2011 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50 WPISUJE ZDAJĄCY
 entralna Komisja Egzaminacyjna rkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny KE 00 KO WPISUJE ZJĄY PESEL Miejsce na naklejkę z kodem EGZMIN MTURLNY Z MTEMTYKI
entralna Komisja Egzaminacyjna rkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny KE 00 KO WPISUJE ZJĄY PESEL Miejsce na naklejkę z kodem EGZMIN MTURLNY Z MTEMTYKI
Repetytorium z matematyki ćwiczenia
 Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów
 Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów stycznych, c) rozpoznaje trójkąty podobne i wykorzystuje
Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów stycznych, c) rozpoznaje trójkąty podobne i wykorzystuje
STEREOMETRIA. Poziom podstawowy
 STEREOMETRIA Poziom podstawowy Zadanie ( 8 pkt ) W stożku tworząca o długości jest nachylona do powierzchni podstawy pod kątem, którego tangens jest równy Oblicz stosunek pola powierzchni bocznej do pola
STEREOMETRIA Poziom podstawowy Zadanie ( 8 pkt ) W stożku tworząca o długości jest nachylona do powierzchni podstawy pod kątem, którego tangens jest równy Oblicz stosunek pola powierzchni bocznej do pola
POWIERZCHNIA CAŁK. I KONSTRUKCJA 1 ELEM. DENNICY ELIPSOIDALNEJ WYPUKŁEJ W WYK. "TURBO"
 POWIERZCHNIA CAŁK. I KONSRUKCJA 1 ELEM. DENNICY ELIPSOIDALNEJ WYPUKŁEJ W WYK. "URBO" str.1. woje dane wpisz w zielone pola: Dz = 1224 h = 360 G= 50 L= 3280 Zz= 17 zakład Zm= 3 Zd= 5 Pas = 120 A= 662 B=
POWIERZCHNIA CAŁK. I KONSRUKCJA 1 ELEM. DENNICY ELIPSOIDALNEJ WYPUKŁEJ W WYK. "URBO" str.1. woje dane wpisz w zielone pola: Dz = 1224 h = 360 G= 50 L= 3280 Zz= 17 zakład Zm= 3 Zd= 5 Pas = 120 A= 662 B=
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasy 2 a BS i 2 b BS
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasy 2 a BS i 2 b BS Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasy 2 a BS i 2 b BS Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność
UZUPEŁNIA ZDAJĄCY miejsce na naklejkę
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 maja 017 r.
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 maja 017 r.
23h 24h;0h(koła) 24[h]*15[ /h]=360[ ]
![23h 24h;0h(koła) 24[h]*15[ /h]=360[ ] 23h 24h;0h(koła) 24[h]*15[ /h]=360[ ]](/thumbs/53/31835593.jpg) Dla młodzieży. brót w kole dużych kropek w prawo, po jego obwodzie. Koło jest odchylone od pionu. W tym opracowaniu będę posługiwał się swoimi przyrządami stosowanymi w geometrii kulowej (). Nabyłem na
Dla młodzieży. brót w kole dużych kropek w prawo, po jego obwodzie. Koło jest odchylone od pionu. W tym opracowaniu będę posługiwał się swoimi przyrządami stosowanymi w geometrii kulowej (). Nabyłem na
Rok akademicki 2005/2006
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
24h MAPA MAPA MAPA MAPA
 24h 1h str.1 2h 3h 4h 5h str.2 6h 7h 8h 9h str.3 10h 11h 12h 13h str.4 14h 15h 16h 17h str.5 18h 19h 20h 21h str.6 22h 23h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.7 gk
24h 1h str.1 2h 3h 4h 5h str.2 6h 7h 8h 9h str.3 10h 11h 12h 13h str.4 14h 15h 16h 17h str.5 18h 19h 20h 21h str.6 22h 23h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.7 gk
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom podstawowy
 KRYTERIA OCENIANIA ODPOWIEDZI Matematyka Poziom podstawowy Marzec 09 Zadania zamknięte Za każdą poprawną odpowiedź zdający otrzymuje punkt. Poprawna odpowiedź. D 8 9 8 7. D. C 9 8 9 8 8 9 8 9 8 ( 89 )
KRYTERIA OCENIANIA ODPOWIEDZI Matematyka Poziom podstawowy Marzec 09 Zadania zamknięte Za każdą poprawną odpowiedź zdający otrzymuje punkt. Poprawna odpowiedź. D 8 9 8 7. D. C 9 8 9 8 8 9 8 9 8 ( 89 )
O kula. w (gks). Rzutnie: (XZ); (YZ); (XY). A B (YZ) (XY) D sześciana
 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
KORESPONDENCYJNY KURS PRZYGOTOWAWCZY Z MATEMATYKI
 KORESPONDENCYJNY KURS PRZYGOTOWAWCZY Z MATEMATYKI PRACA KONTROLNA nr 1 październik 1999 r 1. Stop składa się z 40% srebra próby 0,6, 30% srebra próby 0,7 oraz 1 kg srebra próby 0,8. Jaka jest waga i jaka
KORESPONDENCYJNY KURS PRZYGOTOWAWCZY Z MATEMATYKI PRACA KONTROLNA nr 1 październik 1999 r 1. Stop składa się z 40% srebra próby 0,6, 30% srebra próby 0,7 oraz 1 kg srebra próby 0,8. Jaka jest waga i jaka
I Liceum Ogólnokształcące w Warszawie
 I Liceum Ogólnokształcące w Warszawie Imię i Nazwisko Klasa Nauczyciel PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Liczba punktów Wynik procentowy Informacje dla ucznia 1 Sprawdź, czy zestaw
I Liceum Ogólnokształcące w Warszawie Imię i Nazwisko Klasa Nauczyciel PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Liczba punktów Wynik procentowy Informacje dla ucznia 1 Sprawdź, czy zestaw
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 4 CZERWCA Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 MARCA 2019 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Cena towaru bez podatku
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 MARCA 2019 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Cena towaru bez podatku
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN
 ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
Nauka, poprzez zabawę w swoim domu. Rodzice z dziećmi. Rzutowanie bryły geometrycznej. Format ark.a4 12,75*1,75 str.1. "TABLICZKA MNOśENIA AWERS * A
 dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
Geometria analityczna
 Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
LUBELSKA PRÓBA PRZED MATURĄ POZIOM PODSTAWOWY Klasa 1 Klasa 1
 Klasa 1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 18 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3. W zadaniach
Klasa 1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 18 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3. W zadaniach
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 25 MARCA 2017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Najmniejsza liczba całkowita
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 25 MARCA 2017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Najmniejsza liczba całkowita
Wskazówki do zadań testowych. Matura 2016
 Wskazówki do zadań testowych. Matura 2016 Zadanie 1 la każdej dodatniej liczby a iloraz jest równy.. C.. Korzystamy ze wzoru Zadanie 2 Liczba jest równa.. 2 C.. 3 Zadanie 3 Liczby a i c są dodatnie. Liczba
Wskazówki do zadań testowych. Matura 2016 Zadanie 1 la każdej dodatniej liczby a iloraz jest równy.. C.. Korzystamy ze wzoru Zadanie 2 Liczba jest równa.. 2 C.. 3 Zadanie 3 Liczby a i c są dodatnie. Liczba
LUBELSKA PRÓBA PRZED MATURĄ MATEMATYKA - poziom podstawowy klasa 1
 1 MATEMATYKA - poziom podstawowy klasa 1 MAJ 2016 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 17 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.
1 MATEMATYKA - poziom podstawowy klasa 1 MAJ 2016 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 17 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 5 MAJA Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Kryteria oceniania osiągnięć uczniów z matematyki w kl. III gimnazjum. (Program Matematyka z plusem dla III etapu edukacyjnego)
 Kryteria oceniania osiągnięć uczniów z matematyki w kl. III gimnazjum. (Program Matematyka z plusem dla III etapu edukacyjnego) Ocena DOPUSZCZAJĄCY DOSTATECZNY DOBRY BARDZO DOBRY CELUJĄCY Uczeń: Uczeń:
Kryteria oceniania osiągnięć uczniów z matematyki w kl. III gimnazjum. (Program Matematyka z plusem dla III etapu edukacyjnego) Ocena DOPUSZCZAJĄCY DOSTATECZNY DOBRY BARDZO DOBRY CELUJĄCY Uczeń: Uczeń:
PODSTAWY > Figury płaskie (1) KĄTY. Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach:
 PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
Planimetria VII. Wymagania egzaminacyjne:
 Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
MATURA Powtórka do matury z matematyki. Część VII: Planimetria ODPOWIEDZI. Organizatorzy: MatmaNa6.pl, naszemiasto.pl
 MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ODPOWIEDZI Organizatorzy: MatmaNa6.pl, naszemiasto.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ODPOWIEDZI Organizatorzy: MatmaNa6.pl, naszemiasto.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
