KORZYSTANIE Z SZABLONÓW LISTWOWYCH I TARCZY ZEGARÓW: 12h i 24h
|
|
|
- Robert Kot
- 7 lat temu
- Przeglądów:
Transkrypt
1 Rys.nr 46. dokończenie Rys.nr 44. HIZY KRZYAI Z ZABLÓ LIYH I ARZY ZGARÓ: 1 i 24h str.12 KPIA Z ZZYU R 001: ciąg dalszy LKJI r 10 i efekty pracy LKJA r 10 - posługiwanie się szablonami listwowymi (rysunki pomocnicze) str.13 zablon listwowego "B"(str.L) nr 15 Jak wypełnić kolumnę (i:j)? d początku współrzędnych odmierzam linijką długość promienia R i odczytuję: 113mm na ekranie monitora. o samo robię z pkt.1. dczyt: 70mm. Promień koła ro- boczego r =400 j.m. tąd: R = (70mm/113mm)*400=247,79 23h 1h Podobnie pkt.2. Długość: (76/113)*400=269,03 2 ak samo jest z pkt.3. bliczenie długości (97/113)*400= 343,36 mm 27 3h h h h h h 6h Rys.nr 47. pomocniczy (kopia) 17h h 18 8h (+)Z 15h h 7h 2 y2 β L 14h 10h 11 (-)X x2 (+)X 13h 1 11h Geometryczne centrum Polski * RZZPPLIA PLKA * LKJA r 12 - teoria: przykład powtarzalny w trzech wersjach, oparty na tych samych danych. ersja nr 1. PRZYKŁAD r 1 Dwa odcinki (A:B) i (B:) mają wspólny punkt B i tworzą kąt β =42. Połącz odcinkiem pkt Lekcje: nr 12 - nr 16 A i, tworząc trójkąt. RozwiąŜ ten trójkąt: (A:B:). Dane: c = 120 c = 85 odrobiłem wcześniej. ięc, ε µ h A:B= c B:D= c*cosβ = 63, (c/2)/r=sinβ r = 0,5*c/sinβ= 60, przyszedł czas, by je pokazać. ζ h c c B:= c H = c*sinβ = 56, cięciwy: c;c;c strzałki:h;h;h łuki: ; ; & H η A:= c = (H^2+(A:D)^2)^0,5= 80,404 & =2*β = 84,000 [ ] =π*r*& /180 88,0836 α c β A:D= c-(b:d)= 56, AA(α)= H/(A:D)= 0,78578 [rad] =π*r*ω /180 = 194,996 A D B α = 45,0219 [ ] ε = 90 -α = 44,9781 [ ] =π*r*η /180 = 94, ω r β = 42 [ ] = 0,5*c*H= 3412,57 mm2 ω =2*ζ = 185,956 [ ] η =360 -(& +ω ) h β= 0,73304 [rad] µ = 90 -β = 48 [ ] ζ =ε +µ = 92,978 [ ] η = 90, [ ] PRADA PRADA /ω = /η = /& = 60, Łd= 2*π*r = 377, k= π*r^2 = 11340, PRADA PRADA pracowanie to powstało znacznie wcześniej. Dzisiej znalazło swoje miejsce. KaŜde rozwiązanie z trzech wersji przykładu opiera się na zastosowaniu trzech róŝnych wzorów. miejscowość: PIĄK woj. łódzkie Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
2 r 1 24h r 2 r 3 r 4 r 5 r 6 r 7 r 8 r 9 r 10 r 11 r 12 r 13 r 14 r 15 r 16 r 17 r 18 r 19 r 20 r 21 r 22 r 23 r 24 r 25 r 26 r 27 r 28 r 29 r 30 r 31 r 32 r 33 r 34 r 35 r 36 r 37 r 38 r 39 r 40 r 41 r 42 r 43 r 44 HIZY LKJA r 13 - szablony listwowe "A" i "B" 24h i 1 (w innym rozstawieniu) str.14 r 45 24h 24h r46 r47 r48 r49 r50 r51 r52 r53 r r55 YKAŁM U GRM PRAY! PMYLIŁY MI IĘ UMRAJ RYUKÓ. I ZMIIAM PIśJ Przy silnym wietrze, na bramie od stodoły, teŝ moŝna latać! Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
3 str.15 LKJA r 14 - teoria: przykład powtarzalny w trzech wersjach, oparty na tych samych danych. ersja nr 2. PRZYKŁAD r 2 Dane a = 120,00 b = 85,00 &= 42 [ ] zukane: ; c; r; h ; µ [ ]; ß [ ] Ł1; Ł2; Ł3; rójkąt: (AB) jak poprzednie dwa trójkąty h = 2*/a = 56, twierdzenie rzutów: a = c*cosµ +b*cos& tj. (A:B:) = 0,5*a*b*sin& = 3412, tj. c= (a-b*cos&)/cosµ c*cosµ = (a-b*cos&)= 56, ß [ ]= 180 -(&+µ ) = 92, Ł3 c=h/sinµ cosµ *h/sinµ = h/tanµ = 56,8327 µ [ ]= 45, s=0,5*(a+b+c) ß c= h/sinµ = 80, wierdzenie sinusów: s= 142, Ł1 c r= (a/sinß )/2 = 60, Kąty środkowe: h b Ł1(&1)= 88, Ł2(β 1)= 194, Ł1(µ 1)= 94, &[ ] &1[ ] = 84, µ a & Łz= Ł1(&1)+Ł2(β1)+Ł1(µ1)= 377, Łuk zamknięty 360 ß [ ] ß 1[ ] = 185, A r B bwód okręgu: 2*π*r = 377, µ [ ] µ 1[ ] = 90, Ł1(&1)/r= 1, [rad] prawdzenie poprawności uma kątów środk. 360, Ł2(β 1)/r= 3, [rad] wyliczeń matematycznych: a rysunku nie ma oznaczonych Ł2 Ł1(µ 1)/r= 1, [rad] =(s*(s-a)*(s-b)*(s-c))^0,5= kątów środkowych. Łz/r = 6, [rad] =a*b*c/(4*r)= LKJA r 15 - teoria: przykład powtarzalny w trzech wersjach, oparty na tych samych danych. ersja nr 3. PRÓĘ U! PRZYKŁAD r 3. J RJA r 3 tego samego przykładu A:B= 120 B:= 85 µ = Ł Identyczne dane jakie występowały w przykładzie nr 2: 42 środkowa odcinka (A:B) ε = 48 ε[rad]= c D BLIZIA: 90 -µ = 0,83776 π A η η B φ r środkowa odcinka (B:) Z podobieństwa trójkątów wynikają wielkości η r η β trójkąty: kątów: & = 180 -ε = 132&[rad]= 2,30383 ζ & Ł1 B B B:J= (B:)/sin(ε[rad]) [ ] c r r B B:J= 57, Ł c η η α Ł A G B mały 60 :J= 0,5*(A:B)-(B:J) J µ ε α µ µ µ c r ε 42,5 :J= 2, Ł3 H ε J ε 90 ε := (:J)*tan(ε[rad]) Ł2 ω H J := 3, α = stopnie(asin((:)/r))= 2, [ ] (A:B:) φ = *α = 185, [ ] r = Ł1= 3, *r = 194, pow.trójkąta φ[rad]= 3, [rad] Łd= 377, zy spełniony jest warunek: /r=β[rad] k pow.koła ω = 2*(90 -(α +µ )) = 90,0437 [ ] Ł2= 1, *r = 94,42111 Łd/r = 6,28319 Ł1/r = 3,24555 Ł2/r = 1,57156 Ł3/r = 1,46608 Ł3= 88, ω = 1,57156 [rad] Ł3/r = 1,46608 Łd= Ł1+Ł2+Ł3 = 377, h= 15, A:=c= 2*(h*(2*r-h))^0,5= 80, k= 11340, = 3412, LKJA r 16 - teoria: przykład inny, oparty na odcinku i dwóch kątach (patrz rysunek) PRZYKŁAD r 4 Dane: (A:B)=c= 120,00 &[ ] = 34,123 ß [ ] = 54,321 Jak na rysunku. RozwiąŜ powstały trójkąt. &[rad] = 0,59556 Rysunek 1 - do wykonania trójkąta: Rys.2 Powstały trójkąt Rys.3 Ł1 ; ; łuki: Ł1; Ł2; Ł3; Łz µ Ł2 µ h1 yliczenia: ß h2 c r c 90 -ß = 35,679 [ ] a b A c & B A 90 -ß c & B A 90 - ß c & B 90 - ß = 0,62272 [rad] r ε η r cięciwy:a:b=c;a:=c;b:=c ß ß µ = 180 -((90-β)+&) wierdzenie sinusów: µ = 110,198 µ= 1,92332 [rad] α 2*r=c/sin(90-ß )=c/sinµ =c/sin& a rys.3 są środkowe boków powstałego trójkąta. szystkie trzy środkowe h3 r=0,5*c/sinµ = 63, zór Pitagorasa: c^2=a^2+b^2 a = (r^2-(0,5*c)^2)^0,5 = 52, Ł3 c=2*r*sin(90 -β )= 74, h2=r-a = 11, b = (r^2-(0,5*c)^2)^0,5 = 51,9314 bwód: 401,693 = π*r^2 = ,4168 2*r=a/sinß =b/sinµ =c/sin& ((:B)^2+(:)^2)^0,5= 3412,57 bwód jedn.miar 3412,57 60, zukam: ; (A:); (B:); µ ; α ; ε ; η ; r; strzałki: h1; h2;h3 krzyŝują się w punkcie centralnym. Jest nim środek koła opisanego na tym. c= 2*r*sin& = 71, =c*c*c/(4*r)= 2 510,07376 h1=r-b = 12, ε = 2*asin(0,5*c/r)= 68,2460 ε= 1,19112 [rad] Ł1=r*η[rad]= 79, Ł2=r*ε[rad]= 76, η = 2*asin(0,5*c/r)= 71,3580 η= 1,24543 [rad] α = 360 -(ε +η )= 220,396 α= 3,84664 [rad] Ł3=r*α[rad]= 245, Łz= 401,693 zór na strzałkę: h1=r*(1-cos(0,5*α[rad])) = 86, Z wyliczeń wynika, Ŝe strzałka "h1" jest większa od prom. koła "r" o: LKJA r 17 - AIAA AMRYKAŃKIG o przypadnie spadkobiercy gen.kazimierza Pułaskiego: koło; wycinek koła; trójkąt w kole, czy jego odcinek koła n/w? Z informacji na blogach wynika, Ŝe renomowana firma prawnicza Johnson and ox z owego Yorku zajmuje się tą sprawą. Polski rząd takŝe współpracuje ze spadkobiercą Panem Albinem, ubogim Polakiem z nadbuŝańskiej wsi. śyczę mu pomyślności, zdrowia, dumy z przodka i oby pamiętał, Ŝe Ŝyje do tej pory wśród takich samych ludzi jak on sam. r = 3, * ZÓR KRZYA Z PRPRJALŚI KŁA ΣŁ=Ł+Ł+Ł= 3*(2*r)= 6*r ΣŁ/(360 -β )= 17, Pytania: Łuk koła ma wymiar: = 1 016, m β = constans = 16, [ ] 22,073 Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
4 ciąg dalszy: LKJA r 17 - AIAA AMRYKAŃKIG str.16 Podaj:1).Ile wynosi długość jego promienia r? dp.1: 3 589, ).bwód koła, wyliczonego promienia r? dp.2: , m c przy r = 1000 m π 3).Pole powierzchni koła o promieniu r? dp.3: ,00 m2 A η η B constans Pow akrów jest własnością spadko- w przeliczeniu na: akrów η r η β = 16, [ ] biercy po gen. Kazimierzu Pułaskim. Jest nim 1 akr = 4 046,8564 m2 β = 0, [rad] potomek jego brata, bo generał był kawalerem. Powierzchnia wycinka koła β : [ ] c /β = 17, a tej pow.stoi znaczna część aszyngtonu. stanowi to: (4)/3))*100%= 4,5070 % Ł c η η Ł /β[rad] = r 4).Gdyby miała być wycinkiem koła o łuku? dp.4: ,9974 m2 /r= β[rad] 5).Pole odcinka koła opartego na tym łuku? stanowi to: (5)/3))*100%= 0,0600 % D = 283, ).Pole powierzchni trójkąta równobocznego dp.5: ,48 m2 = 6*r*(β /(360 -β ))= 0,28319 *r (blada czerwień) opartego na łuku, stano- stanowi to: 5,99984 akrów = 6*r*(β /(360 -β ))= 0, *r wiąca róŝnicę powierzchni między polem wy- stanowi to: (6)/3))*100%= 4,447 % /r = 0, cinka a polem odcinka, tego samego łuku? dp.6: ,52 m2 tj $/m2 r/ = 3, BUDś państwa na 2010r tys.zł. Ile wart 1m2 terenu? dp.: 7 439,92 zł r = 3, * Przyjąłem UD/PL=3,0000. Gdyby decyzja ode mnie zaleŝała, wolałbym spadek otrzymać w złocie, poniewaŝ minione rządy UA i D cięŝko zapracowały, by $ nadać wyjątkowo wirtualny charakter i wzmóc jego kreatywność. Kreatywność z kolei jest niestety uznaniowa. atomiast doskonale przekształca się w gwoździa do trumny. aktem jest, Ŝe to roczny budŝet RP. PRA RAAĆ A ZIMIĘ! LKJA r 18 - posługiwanie się szablonami listwowymi (rysunki porównawcze) Rys.nr 50. LIPA PRA r 1 (1386) Rys.nr 51. LIPA PRA r 2 (1665) m 18h ;1 3h 6h h Konstrukcja elipsy stosowana obecnie w szkolnictwie. Jest to całkowicie moja konstrukcja, na moim kole. LPA A PAŁA P AŁśIU A IBI Rys.nr 52. RZH LIP: r 1; 2; 3. PRGRAM DZYAŁ, LIPA PRA r 3 (1687) Rys.nr 53. ś J LIPA PRA r 4 (1695) HIZY Ł ;1 18h lipsę wstawiłem w błękitny prostokąt z tego programu 90 b' 3h β1 b 4,78h r 18h 6h (-)X β (+)X b β1 b' 15h 9h β1 = 360,00 [ ] (-)Y 1 Rys.nr 54. dowolny kształt I PRAIĘ UAIĆ IDALI LIPĘ UKŚĄ Rys.nr 56. Powiększ! ie widzę róŝnicy między tymi trzema elipsami. Jest dzień: lipsy: nr 1(1974); nr 2(1973); nr 3(2117); nr 4(2124) zmieniły swoje numery. ie wiem o co tu chodzi? 22,78h Rys.nr 55. HIZY LIPA r 5 (2275) kopia dowolnego kształtu rys. nr 54. a rysunku nr 56 nałoŝyłem na "dowolny kształt" (kopia rys.nr 54), elipsę (kopię rys.nr 55). a tym rysunku nr 56 elipsa ma (2282). HIZY Zobacz! Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
5 LKJA r 19 - posługiwanie się szablonami listwowymi (rysunki pomocnicze) str.17 Rys.nr 57. Rysunek kuli i płaszczyzny poziomej pkt.a; ; B. Rys.nr 59. Przedstawia cięcie kuli przez środek tj.pkt.. Rys.nr 58. Rys.kuli ciętej płaszczyzną pod kątem β(elipsa prosta) Ukazuje kąt β pochyłu elipsy prostej nr 1 18h 20h 2 4h 6h 18h 20h 2 4h 6h 19h 23h (+) Z 1h 3h 5h 19h 23h (+) Z 1h 3h 5h A lipsa prosta nr 1 odczyt wg programu (2433) B D D G β 90 H Rys.nr 60. lipsa ukośna nr 3 odczyt wg programu (3140) Rys.nr 61. Rzut pionowy lekko pochylonego koła o kąt β. 18h 20h 2 4h 6h 18h 20h 2 4h 6h 19h 23h (+) Z 1h 3h 5h 19h 23h 1h 3h 5h 5h;6h 4h 3h b1 1h A B 24h;0 G' H' Kopia elipsy ukośnej nr 3 odczyt wg programu (3140) µ 90 D 23h lipsa prosta nr 2 odczyt wg programu (2727) 2 Rys.nr h 19h;18h Konstrukcja elipsy ukośnej 18h 20h 2 4h 6h 20h 2 4h 6h 8h 23h 1h 3h 5h 23h 1h 3h 5h 7h lipsa ukośna nr 3 odczyt wg programu (3139) GRĄ PLAM AALIZĘ IĘG śka (Zeszyt nr 001). MoŜna tam znaleźć w jaki sposób rozwiązuję róŝne problemy. Lekcja ta nie wymaga więcej komentarzy, bo poziom tematyki jest stosunkowo łatwy do zrozumienia, po obserwacji rysunków. a rysunku nr 62 wykonałem elipsę ukośną (3139), która powstała w wyniku obrotu kuli o dwie godziny, tj. *15 /h=30. tąd wniosek, iŝ z elipsą ukośną mamy doczynienie w przypadku obrotu kuli. Jeszcze raz powtarzam. KaŜda elipsa ma rodowód z kuli w przypadku przestrzeni, lub z koła w przypadku figury płask. HIZY Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
6 LKJA r 20 - posługiwanie się szablonami listwowymi (rysunki pomocnicze) str.18 a tej lekcji pokazuję, jak moŝna doskonale posługiwać się moim kołem, kulą, tarczą zegarową. ego typu ćwiczenia udoskonalają przede wszystkim wyobraźnię, bo to ona jest najwaŝniejsza oraz umysł. Bardzo waŝne jest upór i wytrwanie. Dzięki nim moŝna wszystko osiągnąć. e rysunki sam wymyśliłem i sam rozwiązałem. Bystremu obserwatorowi wystarczą te cztery rysunki, by samodzielnie pracować nad własnymi pomysłami. Potrzeba mu tylko: moje koło, moja kula i moje tarcze zegarowe i moje zacięcie. 18h 20h 2 4h 6h 18h 20h 2 4h 6h 19h 23h (+) Z 1h 3h 5h 19h 23h (+) Z 1h 3h 5h Rys.nr 63. Rys.nr h 20h 2 4h 6h 18h 20h 2 4h 6h 19h 23h 1h 3h 5h 19h 23h 1h 3h 5h A Rys.nr 65. Rys.nr 66. HIZY Rozpocząłem swoje rysunki od skopiowania kul z lekcji nr 19 i usunięcia zbędnych linii. Potem wybrałem kulę rys.nr 64. stawiłem na tym rysunku walec w kolorze zielonym. stawiłem w taki sposób, by oba wycięcia przestrzenne kuli miały po środku wspólny punkt. tosując orientacje kierunkową stron kuli wskazałem usytuowanie walca (rys.nr.66). a prędce wykonałem rysunek pomocniczy koła. Dla mnie nie było istotne, na ilę łuków podzielą półkole. Podzieliłem dwusieczną na pół i po ponowieniu dwusiecznych na dwie ćwiartki. trzymałem podział ćwiartki koła na cztery części tj. 90 /4=22,5. Patrz zielone koło z ciemnymi zielonymi kropkami. d punktu centralnego kuli, (koła) narysowałem koła (białe na ciemnym tle). elem ich było przejść przez oba punkty na linii pionowej koła. Białe koła przecinając średnicę poziomą zielonego koła wskazywały kierunki miejsc krzywizny kuli. ystarczyło teraz wykorzystać linie kropkowane (czarne i niebieskie). Miejsca przecięć linii wyznaczyły punkty krzywizn na rys.nr 64. ajwiększym problemem jest przedstawienie wycięć krzywizn jak równieŝ kompozycja malarska. o ona ma wpływ na wizerunek opracowania. rys.nr 66 wykorzystałem równoleŝniki (koła). Podobnie postąpiłem z rys.nr 63, lecz teraz są to linie poziome. Zielone koło skopiowałem z rys.nr 66 i wstawiłem do rys.nr 65. Białe linie pionowe z zielonego koła składającego się z 16 łuków, czyli 8 linii pionowych, białych skierowałem na rys.nr 63. Po przecięciu z równoleŝnikami wyznaczyły pkty krzywizn. Z rys.nr 64 przeniosłem wymiar wysok.na rys.nr 63. Mam juŝ zamkniętą krzywiznę na rys.nr 63. a rys.nr 65 powstała krzywa która powstała ze skopiow.konstrukcji zielonego koła i dwóch białych równoleŝnik., poniŝej średnicy tego koła. Krzywą kopiuję i wstawiam do rys.nr 66. Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
7 ciąg dalszy: LKJI r 19 - posługiwanie się szablonami listwowymi (rysunki pomocnicze) str.19 zęsto przeskakuję z tematu na inny temat, bo potrzebuję urozmaicenia. Mam tysiące pomysłów. Moje własne oprzyrządowanie do geometrii jest tak wspaniałe, Ŝe kojarzy mi się z manufakturę do produkcji wzorów uŝytkowych, patentów. listopadzie kończę 65 lat. A przede mną jeszcze jest wiele pracy. Muszę wykonać taką ilość róŝnorodnych opracowań, by uwierzono mi, Ŝe wnoszą nowość, ułatwiającą pracę i naukę uczniom. Będąc emerytem, mam poczucie wartości swoich dokonań, wniesionej wiedzy i bogatej wyobraźni. Świadomość ta, jest moją najlepszą nagrodą. kopia: Po wklejeniu kopii elipsa ukośna nr 3 ma odczyt wg programu (3971) Rys.nr 60. lipsa ukośna nr 3 odczyt wg programu (3971) PI PRAAIA 18h 20h 2 4h 6h Moim zamiarem jest wykonanie elipsy ukośnej nr 4 19h 23h (+) Z 1h 3h 5h leŝącej na płaszczyźnie pionowej, po obrocie z 0h na 5h;6h 4h. ak jak to było z elipsą ukośną nr 3 poziomą (rys. nr 60). śeby była to elipsa ukośna wykorzystałem program obracając elipsę prostą. Punktami granicznymi 3h elipsy to pkt. na kole kuli z pionowego opuszczenia linii pomocniczej. Przy pomocy kombinacji szablonami listwowymi, jak widzicie (linie pomocn.równoległe), wyznaczyłem linie skośne ograniczające szer.elipsę b1 1h w punktach 2 i. kośny kwadrat w kolorze złotym HIZY A Kopia elipsy ukośnej nr 3 odczyt wg programu (3971) µ 90 (-) Z D B 23h 2 20h Rys.nr h;18h nadaje kierunki liniom pomocniczym tarczy zegara 24h. Bardzo waŝnym punktem jest centrum kuli. o dzięki niemu wyznaczyłem połoŝenie kierunków:,,. Dzięki wyznaczeniu tych punktów, obie linie: (:) i (H:J) przecinają się w centralnym punkcie pod kątem 90 (rys.nr 67). atomiast odcinek zawarty między punktami (K:L) wyznaczają linię przecięcia obu płaszczyzn elips ukośnych. Punkty M i P są osią elipsy pionowej, nadając jej ukos. lipsa ukośna nr 3 odczyt wg programu (4175) i dorysowanie elipsy ukośnej nr 4 (4199) 18h 20h 2 4h 6h 19h 23h (+)Z 2 1h 3h 5h M (+)Z 5h;6h 4h 3h b1 A (-)X K H (-)Y (+)Y µ 90 P (-) Z J L (+)X D B 1h 23h 2 20h 19h;18h Kwadrat konstrukcji szablonu listwowego "A"; 24h Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
8 ciąg dalszy: LKJI r 19 - posługiwanie się szablonami listwowymi (rysunki pomocnicze) str.20 Kopia Po wklejeniu kopii elipsa ukośna nr 3 ma odczyt wg programu (3971) nioski i tezy wyciągnięte z lekcji nr 19 Rys.nr 60. lipsa ukośna nr 3 odczyt wg programu (3971) a stronie 17 rys.57 pokazałem kulę i elipsę prostą. lipsa prosta 18h 20h 2 4h 6h b1 19h 23h (+) Z 1h 3h 5h A (-) Z 5h;6h 4h 3h 1h Kopia elipsy ukośnej nr 3 odczyt wg programu (3971) D 23h 18h 9h 2 20h 19h;18h gają linie przenikania (przecięcia) się obu elips. Jedna z nich jest elipsą powtarzalną, którą pokazałem na rys.nr 60; 61; 62 oraz elipsy pionowe dla godzin: rys.nr 67 i 9h rys.nr 68. ysokości: (+)Z i są wielkościami pionowymi mierzonymi od punktu. ie naleŝy się sugerować, Ŝe jest inaczej, patrząc na rysunek. RY.PMIJZ.PRZD.LIPY PR P IH BRI KÓŁ I"Z" Rys.nr 67. elipsa prosta Rys.nr 57. elipsa prosta HIZY Rys.nr 68. (+)Z µ 90 Rys.nr 58. elipsa prosta B ukośnie połoŝoną elipsę. Proszę się przyjrzeć pkt. A i B elips. ie są na skraju linii okręgu kuli. Z kolei na rysunkach nr 67 i 68 pokazuję jak przebieszablon listwowy "A" 24h Rys.nr 60. elipsa prosta wyznaczają punkty A:B pochylona pod kątem β obrócona z godz. 0h na obrócona z godz. 0h na i elipsa pionowa obróc.na (+) Z (+) Z (+) Z (+) Z (+) Z pokazana jest jako (turkusowy odcinek) leŝący na płaszczyźnie poziomej. a tym samym rys.57 pokazałem takŝe elipsę prostą rys.58, lecz połoŝoną pod kątem β, potwierdzoną rys.59 (nie- bieski odcinek) w stosunku do poziomu. a rys.60 elipsę prostą obróciłem z () na, nadając jej ukos. tym momencie dostrzegłem coś, co duŝo wcześniej podejrzewałem. tóŝ wydawało mi się, Ŝe owy ukoś jest sztucznie wywołany. a uczelni I w Koszalinie uczyłem się rysowania konstr. elipsy ukośnej. zn. Pytanie: czy istnieje w rzeczywistości elipsa ukośna? a to pytanie chcę znaleźć odpowiedź, poniewaŝ zaczynam podwaŝać sens istnienia takiej elipsy. koło nas widzimy całe 6h Rys.nr 61. elipsa prosta mnóstwo naczyń stołowych okrągłych. iezleŝnie z jakiego punktu patrzymy na nie, zawsze widzimy elipsy proste. Jeszcze nie spotkałem w sensie rzeczywistym elipsy ukośnej. MoŜna co najwyŝej "umownie", dopuścić taką nazwę. racając do rys.nr 60 pokazałem w jaki sposób działa moje oprzyrządowanie do wykonywania konstrukcji elementów przestrzennych w geometrii wykreślnej. Powtarzam zmiana połoŝenia godziny na powoduje, Ŝe szablon listwowy ulega obrotowi względem pkt.centralnego. koro nastąpił obrót szablonu, rzuty łuków na średnicę nie zmieniają się. Zachowu- ją te same odległości linii pomocniczych. Aś: AJAśIJZA J PZYJA PDAA ARZY ZGARJ J. PIA () a rys.nr 61pokazuje rzut pionowy lekko obrócona z godz. 0h na A B A B A B A B 14h (-) Z (-) Z (-) Z (-) Z (-) Z Rys.nr 67. elipsa prosta związku z powyŝszym stawiam tezę, iŝ nie istnieją epipsy ukośne. Istnieją za to punkty konstrukcyjne, decydujące o ich kształcie i wymiarach. ie wiem, czy udało mi się przekonać Państwa obrócona z godz. 0h na i elipsa pionowa obróc.na 9h HIZY do mojej teorii. aktem jest, Ŝe ten temat naleŝy bardziej rozwinąć, co pozostawiam Państwu do (+) Z dalszej analizy i opracowania. e małe rysunki są szkicami, bez linii pomocniczych.o wszystko. A B 14h (-) Z 9h Komputer LAR 710BH; ystem Microft indows 98; program Microft xcel 99 pracował inŝ. Kazimierz Barski
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Rok akademicki 2005/2006
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm
![G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm](/thumbs/71/64805542.jpg) Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Zadanie I. 2. Gdzie w przestrzeni usytuowane są punkty (w której ćwiartce leży dany punkt): F x E' E''
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
MAGAZYN WIEDZY NR 1 O GEOMETRII KULOWEJ. PROJEKT TWÓRCY (gk). PRZYPOMINA POMNIK. WALEC TRAPEZOWY Z KORYTEM KOŁO. Nr2 6h(48h) ELIPSA pionowa O
 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
gk T GEOMETRIA WYKREŚLNA PRZESTRZENNA T (GK) W PRAKTYCE. SZTUKA TRASOWANIA CZ.1. Rys.3. Rys.4. Rysunek jest zbyt duży, zmniejszę go na str.2.
 GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
Rys 3-1. Rysunek wałka
 Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
Geometria wykreślna. 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław. Politechnika Gdańska, Wydział Architektury
 Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
Stożkiem nazywamy bryłę obrotową, która powstała przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych.
 1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
Praktyczne przykłady wykorzystania GeoGebry podczas lekcji na II etapie edukacyjnym.
 Praktyczne przykłady wykorzystania GeoGebry podczas lekcji na II etapie edukacyjnym. Po uruchomieniu Geogebry (wersja 5.0) Pasek narzędzi Cofnij/przywróć Problem 1: Sprawdź co się stanie, jeśli połączysz
Praktyczne przykłady wykorzystania GeoGebry podczas lekcji na II etapie edukacyjnym. Po uruchomieniu Geogebry (wersja 5.0) Pasek narzędzi Cofnij/przywróć Problem 1: Sprawdź co się stanie, jeśli połączysz
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7
 Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7 Lang: Pole powierzchni kuli Nierówność dla objętości skorupki: (pow. małej kuli) h objętość skorupki
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7 Lang: Pole powierzchni kuli Nierówność dla objętości skorupki: (pow. małej kuli) h objętość skorupki
Rys.1. str.1. 48h;0h 18h 19h 20h 21h 22h 46h. 44h r1 4h. 10h. 38h. 34h 14h. 32h 16h. 24h jest linią do przenoszenia szablonów
 Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
OBLICZENIE PRZEKROJU WALCA PO CIĘCIU SKOŚNYM. Rysunki i obliczenia dotyczą walca
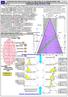 Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Klasa 3.Graniastosłupy.
 Klasa 3.Graniastosłupy. 1. Uzupełnij nazwy odcinków oznaczonych literami: a........................................................... b........................................................... c...........................................................
Klasa 3.Graniastosłupy. 1. Uzupełnij nazwy odcinków oznaczonych literami: a........................................................... b........................................................... c...........................................................
Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów
 Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów stycznych, c) rozpoznaje trójkąty podobne i wykorzystuje
Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów stycznych, c) rozpoznaje trójkąty podobne i wykorzystuje
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1
 PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
Grafika inżynierska geometria wykreślna. 5a. Obroty i kłady. Rozwinięcie wielościanu.
 Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
GEOMETRIA ELEMENTARNA
 Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość:
 Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość: A. r 2 + q 2 = p 2 B. p 2 + r 2 = q 2 C. p 2 + q 2 = r 2 D. p + q
Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość: A. r 2 + q 2 = p 2 B. p 2 + r 2 = q 2 C. p 2 + q 2 = r 2 D. p + q
A. fałszywa dla każdej liczby x.b. prawdziwa dla C. prawdziwa dla D. prawdziwa dla
 Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
gk T Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (gk), w sposób praktyczny. Rys.2a
 Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
ROZWINIĘCIA POWIERZCHNI STOPNIA DRUGIEGO W OPARCIU O MIEJSCA GEOMETRYCZNE Z ZA- STOSOWANIEM PROGRAMU CABRI II PLUS.
 Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
Rysunek 1. Udowodnij, że AB CD = BC DA. Rysunek 2. Po inwersji o środku w punkcie E. Rysunek 3. Po inwersji o środku w punkcie A
 g H e D c H' E g' h e' O d A C' d' C A' F' f' I' G' B' G I F f INWERSJA Inwersją o środku O i promieniu r nazywamy takie przekształcenie płaszczyzny (bez punktu O), które każdemu punktowi X O przyporządkowuje
g H e D c H' E g' h e' O d A C' d' C A' F' f' I' G' B' G I F f INWERSJA Inwersją o środku O i promieniu r nazywamy takie przekształcenie płaszczyzny (bez punktu O), które każdemu punktowi X O przyporządkowuje
V Konkurs Matematyczny Politechniki Białostockiej
 V Konkurs Matematyczny Politechniki Białostockiej Rozwiązania - klasy drugie 1. Znaleźć wszystkie pary liczb całkowitych (x, y) spełniające nierówności x + 1 + y 4 x + y 4 5 x 4 + y 1 > 4. Ważne jest zauważenie,
V Konkurs Matematyczny Politechniki Białostockiej Rozwiązania - klasy drugie 1. Znaleźć wszystkie pary liczb całkowitych (x, y) spełniające nierówności x + 1 + y 4 x + y 4 5 x 4 + y 1 > 4. Ważne jest zauważenie,
Planimetria poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie
 Planimetria poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/) 1. W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu
Planimetria poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/) 1. W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu
Nauka, poprzez zabawę w swoim domu. Rodzice z dziećmi. Rzutowanie bryły geometrycznej. Format ark.a4 12,75*1,75 str.1. "TABLICZKA MNOśENIA AWERS * A
 dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 11 Zadania planimetria
 1 TEST WSTĘPNY 1. (1p) Wysokość rombu o boku długości 6 i kącie ostrym 60 o jest równa: A. 6 3 B. 6 C. 3 3 D. 3 2. (1p) W trójkącie równoramiennym długość ramienia wynosi 10 a podstawa 16. Wysokość opuszczona
1 TEST WSTĘPNY 1. (1p) Wysokość rombu o boku długości 6 i kącie ostrym 60 o jest równa: A. 6 3 B. 6 C. 3 3 D. 3 2. (1p) W trójkącie równoramiennym długość ramienia wynosi 10 a podstawa 16. Wysokość opuszczona
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
w jednym kwadrat ziemia powietrze równoboczny pięciobok
 Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
MATEMATYKA ZBIÓR ZADAŃ MATURALNYCH. Lata Poziom podstawowy. Uzupełnienie Zadania z sesji poprawkowej z sierpnia 2019 r.
 MATEMATYKA ZBIÓR ZADAŃ MATURALNYH Lata 010 019 Poziom podstawowy Uzupełnienie 019 Zadania z sesji poprawkowej z sierpnia 019 r. Opracował Ryszard Pagacz Spis treści Zadania maturalne.........................................................
MATEMATYKA ZBIÓR ZADAŃ MATURALNYH Lata 010 019 Poziom podstawowy Uzupełnienie 019 Zadania z sesji poprawkowej z sierpnia 019 r. Opracował Ryszard Pagacz Spis treści Zadania maturalne.........................................................
gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii
![gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii](/thumbs/103/159774468.jpg) Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
TABELA PRZELICZENIOWA
 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Koszalin dnia r Rys.1 o promieniu: r = 91, h;0h TABELA PRZELICZENIOWA wg (gk)
 skrypt Romany (R) gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Lekcja korzystania z przyrządu (rozw.trójkąt)
skrypt Romany (R) gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Lekcja korzystania z przyrządu (rozw.trójkąt)
METODA RZUTÓW MONGE A (II CZ.)
 RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
Matematyka podstawowa VII Planimetria Teoria
 Matematyka podstawowa VII Planimetria Teoria 1. Rodzaje kątów: a) Kąty wierzchołkowe; tworzą je dwie przecinające się proste, mają takie same miary. b) Kąty przyległe; mają wspólne jedno ramię, ich suma
Matematyka podstawowa VII Planimetria Teoria 1. Rodzaje kątów: a) Kąty wierzchołkowe; tworzą je dwie przecinające się proste, mają takie same miary. b) Kąty przyległe; mają wspólne jedno ramię, ich suma
Treści zadań Obozu Naukowego OMG
 STOWARZYSZENIE NA RZECZ EDUKACJI MATEMATYCZNEJ KOMITET GŁÓWNY OLIMPIADY MATEMATYCZNEJ GIMNAZJALISTÓW Treści zadań Obozu Naukowego OMG Poziom OM 2015 rok SZCZYRK 2015 Pierwsze zawody indywidualne Treści
STOWARZYSZENIE NA RZECZ EDUKACJI MATEMATYCZNEJ KOMITET GŁÓWNY OLIMPIADY MATEMATYCZNEJ GIMNAZJALISTÓW Treści zadań Obozu Naukowego OMG Poziom OM 2015 rok SZCZYRK 2015 Pierwsze zawody indywidualne Treści
(a) (b) (c) o1" o2" o3" o1'=o2'=o3'
 Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
w najprostszych przypadkach, np. dla trójkątów równobocznych
 MATEMATYKA - klasa 3 gimnazjum kryteria ocen według treści nauczania (Przyjmuje się, że jednym z warunków koniecznych uzyskania danej oceny jest spełnienie wszystkich wymagań na oceny niższe.) Dział programu
MATEMATYKA - klasa 3 gimnazjum kryteria ocen według treści nauczania (Przyjmuje się, że jednym z warunków koniecznych uzyskania danej oceny jest spełnienie wszystkich wymagań na oceny niższe.) Dział programu
gk T Okrąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 Rys.2
 krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
Pytania do spr / Własności figur (płaskich i przestrzennych) (waga: 0,5 lub 0,3)
 Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
KURS MATURA PODSTAWOWA Część 2
 KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
Definicja obrotu: Definicja elementów obrotu:
 5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3
 DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
MATURA Przygotowanie do matury z matematyki
 MATURA 2012 Przygotowanie do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej. Witaj,
MATURA 2012 Przygotowanie do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej. Witaj,
KRYTERIA WYMAGAŃ Z MATEMATYKI NA POSZCZEGÓLNE OCENY
 KRYTERIA WYMAGAŃ Z MATEMATYKI NA POSZCZEGÓLNE OCENY KLASA III FUNKCJE rozumie wykres jako sposób prezentacji informacji umie odczytać informacje z wykresu umie odczytać i porówna ć informacje z kilku wykresów
KRYTERIA WYMAGAŃ Z MATEMATYKI NA POSZCZEGÓLNE OCENY KLASA III FUNKCJE rozumie wykres jako sposób prezentacji informacji umie odczytać informacje z wykresu umie odczytać i porówna ć informacje z kilku wykresów
Zad.3. Jakub Trojgo i Jakub Wieczorek. 14 grudnia 2013
 Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
COMENIUS PROJEKT ROZWOJU SZKOŁY. Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów.
 COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2007 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STOLIKÓW
COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2007 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STOLIKÓW
Skrypt 20. Bryły: 24. Obliczanie pól powierzchni walców w sytuacjach praktycznych. 26. Zastosowanie tw. Pitagorasa do obliczania objętości walców
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Bryły: 21. Przykłady brył obrotowych 22.
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Bryły: 21. Przykłady brył obrotowych 22.
Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną)
 Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną) Zadania zamknięte (jedna poprawna odpowiedź) 1 punkt Wyrażenia algebraiczne Zadanie 1. Wartość wyrażenia 3 x 3x
Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną) Zadania zamknięte (jedna poprawna odpowiedź) 1 punkt Wyrażenia algebraiczne Zadanie 1. Wartość wyrażenia 3 x 3x
Geometria. Rodzaje i własności figur geometrycznych:
 Geometria Jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Figury geometryczne na płaszczyźnie noszą nazwę figur płaskich, w przestrzeni
Geometria Jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Figury geometryczne na płaszczyźnie noszą nazwę figur płaskich, w przestrzeni
Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 2017/2018.
 Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 017/018 19 grudnia 017 1 1 Klasy pierwsze - poziom podstawowy 1. Dane są zbiory
Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 017/018 19 grudnia 017 1 1 Klasy pierwsze - poziom podstawowy 1. Dane są zbiory
Plan wynikowy, klasa 3 ZSZ
 Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Pole powierzchni całkowitej prostopadłościanu o wymiarach 5 x 3 x 4 jest równe A. 94 B. 60 C. 47 D. 20
 STEREOMETRIA - ZADANIA MATURALNE lata 2010-2017 Zadanie 1. (0-1) Maj 2010 [I. Wykorzystanie i tworzenie informacji] Pole powierzchni całkowitej prostopadłościanu o wymiarach 5 x x 4 jest równe A. 94 B.
STEREOMETRIA - ZADANIA MATURALNE lata 2010-2017 Zadanie 1. (0-1) Maj 2010 [I. Wykorzystanie i tworzenie informacji] Pole powierzchni całkowitej prostopadłościanu o wymiarach 5 x x 4 jest równe A. 94 B.
Wykorzystanie programu C.a.R na lekcjach matematyki
 Ireneusz Trębacz Wykorzystanie programu C.a.R na lekcjach matematyki Jakiś czas temu zetknąłem się programem umożliwiającym tworzenie dynamicznych konstrukcji geometrycznych (dynamic geometry software,
Ireneusz Trębacz Wykorzystanie programu C.a.R na lekcjach matematyki Jakiś czas temu zetknąłem się programem umożliwiającym tworzenie dynamicznych konstrukcji geometrycznych (dynamic geometry software,
Zadanie PP-GP-1 Punkty A, B, C, D i E leżą na okręgu (zob. rysunek). Wiadomo, że DBE = 10
 Zadanie PP-GP-1 Punkty A, B, C, D i E leżą na okręgu (zob. rysunek). Wiadomo, że DBE = 10, ACE = 60, ADB = 40 i BEC = 20. Oblicz miarę kąta CAD. B C A D E Typ szkoły: LO LP T Czy jesteś w klasie z rozszerzonym
Zadanie PP-GP-1 Punkty A, B, C, D i E leżą na okręgu (zob. rysunek). Wiadomo, że DBE = 10, ACE = 60, ADB = 40 i BEC = 20. Oblicz miarę kąta CAD. B C A D E Typ szkoły: LO LP T Czy jesteś w klasie z rozszerzonym
Matematyka rozszerzona matura 2017
 Matematyka rozszerzona matura 017 Zadanie 1 Liczba ( 3 + 3) jest równa A. B. 4 C. 3 D. 3 ( 3 + 3) = 3 ( 3)( + 3) + + 3 = A. 3 4 3 + + 3 = 4 1 = 4 = Zadanie. Nieskończony ciąg liczbowy jest określony wzorem
Matematyka rozszerzona matura 017 Zadanie 1 Liczba ( 3 + 3) jest równa A. B. 4 C. 3 D. 3 ( 3 + 3) = 3 ( 3)( + 3) + + 3 = A. 3 4 3 + + 3 = 4 1 = 4 = Zadanie. Nieskończony ciąg liczbowy jest określony wzorem
Skrypt 33. Powtórzenie do matury:
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 33 Powtórzenie do matury:
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 33 Powtórzenie do matury:
NOWA FORMUŁA EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MMA 2019 UZUPEŁNIA ZDAJĄCY. miejsce na naklejkę UZUPEŁNIA ZESPÓŁ NADZORUJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 20 sierpnia
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 20 sierpnia
Własności walca, stożka i kuli.
 Własności walca, stożka i kuli. 1. Cele lekcji a) Wiadomości Uczeń: - zna pojęcie bryły obrotowej, - zna definicje: walca, stożka, kuli, - zna budowę brył obrotowych, - zna pojęcia związane z symetrią
Własności walca, stożka i kuli. 1. Cele lekcji a) Wiadomości Uczeń: - zna pojęcie bryły obrotowej, - zna definicje: walca, stożka, kuli, - zna budowę brył obrotowych, - zna pojęcia związane z symetrią
Mini tablice matematyczne. Figury geometryczne
 Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
gk T Zadania nr 2. opracował: inż. Kazimierz Barski dla wszystkich ludzi świata TECHNIKA Koszalin dnia r
 ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii
 Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Obliczenia geometryczne z zastosowaniem własności funkcji trygonometrycznych w wielokątach wypukłych Wielokąt - figura płaską będąca sumą
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Obliczenia geometryczne z zastosowaniem własności funkcji trygonometrycznych w wielokątach wypukłych Wielokąt - figura płaską będąca sumą
Planimetria VII. Wymagania egzaminacyjne:
 Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
Matematyczne słowa Autorki innowacji: Jolanta Wójcik Magda Kusyk
 Szkoła Podstawowa im Kornela Makuszyńskiego w Łańcuchowie Krzyżówki matematyczne klasy V, które powstały jako efekt realizacji innowacji pedagogicznej Matematyczne słowa Autorki innowacji: Jolanta Wójcik
Szkoła Podstawowa im Kornela Makuszyńskiego w Łańcuchowie Krzyżówki matematyczne klasy V, które powstały jako efekt realizacji innowacji pedagogicznej Matematyczne słowa Autorki innowacji: Jolanta Wójcik
( 2) 6 III EDYCJA MIĘDZYSZKOLNEGO KONKURSU MATEMATYCZNEGO DLA UCZNIÓW SZKÓŁ PONADGIMNAZJALNYCH O PROFILU ZAWODOWYM I TECHNICZNYM.
 GRUPA WIEKOWA I część pierwsza Na rozwiązanie zadań masz godzinę lekcyjną Za kaŝde zadanie moŝesz zdobyć 1 punkt Wyznacz iloraz NWW (35,14) NWD(16,38) Zamień ułamek 0,(27) na ułamek zwykły Płaszcz z ceny
GRUPA WIEKOWA I część pierwsza Na rozwiązanie zadań masz godzinę lekcyjną Za kaŝde zadanie moŝesz zdobyć 1 punkt Wyznacz iloraz NWW (35,14) NWD(16,38) Zamień ułamek 0,(27) na ułamek zwykły Płaszcz z ceny
MATEMATYKA KLASY III gimnazjum LICZBY I WYRAŻENIA ALGEBRAICZNE
 MATEMATYKA KLASY III gimnazjum LICZBY I WYRAŻENIA ALGEBRAICZNE - pojęcie liczby naturalnej, całkowitej, wymiernej, niewymiernej, - sposób i potrzebę zaokrąglania liczb, - pojęcie wartości bezwzględnej,
MATEMATYKA KLASY III gimnazjum LICZBY I WYRAŻENIA ALGEBRAICZNE - pojęcie liczby naturalnej, całkowitej, wymiernej, niewymiernej, - sposób i potrzebę zaokrąglania liczb, - pojęcie wartości bezwzględnej,
Co należy zauważyć Rzuty punktu leżą na jednej prostej do osi rzutów x 12, którą nazywamy prostą odnoszącą Wysokość punktu jest odległością rzutu
 Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Ćwiczenia z Geometrii I, czerwiec 2006 r.
 Waldemar ompe echy przystawania trójkątów 1. unkt leży na przekątnej kwadratu (rys. 1). unkty i R są rzutami prostokątnymi punktu odpowiednio na proste i. Wykazać, że = R. R 2. any jest trójkąt ostrokątny,
Waldemar ompe echy przystawania trójkątów 1. unkt leży na przekątnej kwadratu (rys. 1). unkty i R są rzutami prostokątnymi punktu odpowiednio na proste i. Wykazać, że = R. R 2. any jest trójkąt ostrokątny,
FUNKCJA LINIOWA, OKRĘGI
 FUNKCJA LINIOWA, OKRĘGI. Napisz równanie prostej przechodzącej przez początek układu i prostopadłej do prostej 3x-y+=0.. Oblicz pole trójkąta ograniczonego osiami układy i prostą x+y-6=0. 3. Odcinek o
FUNKCJA LINIOWA, OKRĘGI. Napisz równanie prostej przechodzącej przez początek układu i prostopadłej do prostej 3x-y+=0.. Oblicz pole trójkąta ograniczonego osiami układy i prostą x+y-6=0. 3. Odcinek o
gk T Rozwiązanie Zadania nr1 - uzupełnienie
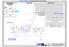 TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
Trójkąty Zad. 0 W trójkącie ABC, AB=40, BC=23, wyznacz AC wiedząc że jest ono sześcianem liczby naturalnej.
 C Trójkąty Zad. 0 W trójkącie ABC, AB=40, BC=23, wyznacz AC wiedząc że jest ono sześcianem liczby naturalnej. Zad. 1 Oblicz pole trójkąta o bokach 13 cm, 14 cm, 15cm. Zad. 2 W trójkącie ABC rys. 1 kąty
C Trójkąty Zad. 0 W trójkącie ABC, AB=40, BC=23, wyznacz AC wiedząc że jest ono sześcianem liczby naturalnej. Zad. 1 Oblicz pole trójkąta o bokach 13 cm, 14 cm, 15cm. Zad. 2 W trójkącie ABC rys. 1 kąty
O kula. w (gks). Rzutnie: (XZ); (YZ); (XY). A B (YZ) (XY) D sześciana
 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
KONKURS ZOSTAŃ PITAGORASEM MUM. Podstawowe własności figur geometrycznych na płaszczyźnie
 KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
Zadania do samodzielnego rozwiązania zestaw 11
 Zadania do samodzielnego rozwiązania zestaw 11 1 Podać definicję pochodnej funkcji w punkcie, a następnie korzystając z tej definicji obliczyć ( ) π (a) f, jeśli f(x) = cos x, (e) f (0), jeśli f(x) = 4
Zadania do samodzielnego rozwiązania zestaw 11 1 Podać definicję pochodnej funkcji w punkcie, a następnie korzystając z tej definicji obliczyć ( ) π (a) f, jeśli f(x) = cos x, (e) f (0), jeśli f(x) = 4
VIII Olimpiada Matematyczna Gimnazjalistów
 VIII Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa www.omg.edu.pl (18 października 01 r.) Rozwiązania zadań testowych 1. Miary α, β, γ kątów pewnego trójkąta spełniają warunek
VIII Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa www.omg.edu.pl (18 października 01 r.) Rozwiązania zadań testowych 1. Miary α, β, γ kątów pewnego trójkąta spełniają warunek
Kurs ZDAJ MATURĘ Z MATEMATYKI - MODUŁ 13 Teoria stereometria
 1 GRANIASTOSŁUPY i OSTROSŁUPY wiadomości ogólne Aby tworzyć wzory na OBJĘTOŚĆ i POLE CAŁKOWITE graniastosłupów musimy znać pola figur płaskich a następnie na ich bazie stosować się do zasady: Objętość
1 GRANIASTOSŁUPY i OSTROSŁUPY wiadomości ogólne Aby tworzyć wzory na OBJĘTOŚĆ i POLE CAŁKOWITE graniastosłupów musimy znać pola figur płaskich a następnie na ich bazie stosować się do zasady: Objętość
MATURA Powtórka do matury z matematyki. Część VII: Planimetria ROZWIĄZANIA. Organizatorzy: MatmaNa6.p l i Dziennik.pl
 MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Organizatorzy: MatmaNa6.p l i Dziennik.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Organizatorzy: MatmaNa6.p l i Dziennik.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
Klasa III technikum Egzamin poprawkowy z matematyki sierpień I. CIĄGI LICZBOWE 1. Pojęcie ciągu liczbowego. b) a n =
 /9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
/9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
Wymagania na egzamin poprawkowy z matematyki z zakresu klasy drugiej TECHNIKUM
 Zespól Szkół Ogólnokształcących i Zawodowych w Ciechanowcu 23 czerwca 2017r. Wymagania na egzamin poprawkowy z matematyki z zakresu klasy drugiej TECHNIKUM Strona 1 z 9 1. Geometria płaska trójkąty zna
Zespól Szkół Ogólnokształcących i Zawodowych w Ciechanowcu 23 czerwca 2017r. Wymagania na egzamin poprawkowy z matematyki z zakresu klasy drugiej TECHNIKUM Strona 1 z 9 1. Geometria płaska trójkąty zna
Plan wykładu. Wykład 3. Rzutowanie prostokątne, widoki, przekroje, kłady. Rzutowanie prostokątne - geneza. Rzutowanie prostokątne - geneza
 Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie
 9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (c.d).
9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (c.d).
Stereometria bryły. Wielościany. Wielościany foremne
 Stereometria bryły Stereometria - geometria przestrzeni trójwymiarowej. Przedmiotem jej badań są własności brył oraz przekształcenia izometryczne i afiniczne przestrzeni. Przyjęte oznaczenia: - Pole powierzchni
Stereometria bryły Stereometria - geometria przestrzeni trójwymiarowej. Przedmiotem jej badań są własności brył oraz przekształcenia izometryczne i afiniczne przestrzeni. Przyjęte oznaczenia: - Pole powierzchni
PODSTAWY > Figury płaskie (1) KĄTY. Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach:
 PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
Zadanie 1. W trapezie ABCD poprowadzono przekątne, które podzieliły go na cztery trójkąty. Mając dane pole S 1
 Zadanie. W trapezie ABCD poprowadzono przekątne, które podzieliły go na cztery trójkąty. Mając dane pole S i S 2 obliczyć pole trapezu ABCD. Zadanie 2. Mamy trapez, w którym suma kątów przy dłuższej podstawie
Zadanie. W trapezie ABCD poprowadzono przekątne, które podzieliły go na cztery trójkąty. Mając dane pole S i S 2 obliczyć pole trapezu ABCD. Zadanie 2. Mamy trapez, w którym suma kątów przy dłuższej podstawie
Zestaw Obliczyć objętość równoległościanu zbudowanego na wektorach m, n, p jeśli wiadomo, że objętość równoległościanu zbudowanego na wektorach:
 Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
- umie obliczyć potęgę o wykładniku: naturalnym(k), całkowitym ujemnym - umie oszacować wartość wyrażenia zawierającego pierwiastki
 KLASA III LICZBY I WYRAŻENIA ALGEBRAICZNE - zna pojęcie liczby naturalnej, całkowitej, wymiernej - zna pojęcie liczby niewymiernej, rzeczywistej - zna sposób zaokrąglania liczb - zna pojęcie potęgi o wykładniku:
KLASA III LICZBY I WYRAŻENIA ALGEBRAICZNE - zna pojęcie liczby naturalnej, całkowitej, wymiernej - zna pojęcie liczby niewymiernej, rzeczywistej - zna sposób zaokrąglania liczb - zna pojęcie potęgi o wykładniku:
ZADANIE 1 (5 PKT) ZADANIE 2 (5 PKT) Oblicz objętość czworościanu foremnego o krawędzi a.
 ZADANIE 1 (5 PKT) Czworościan foremny o krawędzi a rozcięto płaszczyzna prostopadła do jednej z krawędzi, przechodzac a w odległości 0, 25a od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
ZADANIE 1 (5 PKT) Czworościan foremny o krawędzi a rozcięto płaszczyzna prostopadła do jednej z krawędzi, przechodzac a w odległości 0, 25a od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii. Trójkąty. Trójkąt dowolny. Wielokąty trygonometria 1.
 Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Wielokąt wypukły miara każdego kąt wewnętrznego jest mniejsza od 180 o. Liczba przekątnych: n*(n-2) Suma kątów wewnętrznych wielokąta
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Wielokąt wypukły miara każdego kąt wewnętrznego jest mniejsza od 180 o. Liczba przekątnych: n*(n-2) Suma kątów wewnętrznych wielokąta
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5
 Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Wyciągnięcie po ścieŝce, dodawanie Płaszczyzn
 Wyciągnięcie po ścieŝce, dodawanie Płaszczyzn Przykład wg pomysłu dr inŝ. Grzegorza Linkiewicza. Zagadnienia. Tworzenie brył przez Dodanie/baza przez wyciągnięcie po ścieŝce, Geometria odniesienia, Płaszczyzna,
Wyciągnięcie po ścieŝce, dodawanie Płaszczyzn Przykład wg pomysłu dr inŝ. Grzegorza Linkiewicza. Zagadnienia. Tworzenie brył przez Dodanie/baza przez wyciągnięcie po ścieŝce, Geometria odniesienia, Płaszczyzna,
Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON.
 Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON. Zadanie 6. Dane są punkty A=(5; 2); B=(1; -3); C=(-2; -8). Oblicz odległość punktu A od prostej l przechodzącej
Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON. Zadanie 6. Dane są punkty A=(5; 2); B=(1; -3); C=(-2; -8). Oblicz odległość punktu A od prostej l przechodzącej
Łożysko z pochyleniami
 Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
Dopuszczający Dostateczny Dobry Bardzo dobry Celujący
 Liczby i wyrażenia zna pojęcie liczby naturalnej, całkowitej, wymiernej zna pojęcie liczby niewymiernej, rzeczywistej zna sposób zaokrąglania liczb umie zapisać i odczytać liczby naturalne dodatnie w systemie
Liczby i wyrażenia zna pojęcie liczby naturalnej, całkowitej, wymiernej zna pojęcie liczby niewymiernej, rzeczywistej zna sposób zaokrąglania liczb umie zapisać i odczytać liczby naturalne dodatnie w systemie
Skrypt 24. Geometria analityczna: Opracowanie L5
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 24 Geometria analityczna:
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 24 Geometria analityczna:
Geometria. Planimetria. Podstawowe figury geometryczne
 Geometria Geometria (słowo to pochodzi z języka greckiego i oznacza mierzenie ziemi) jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Aksjomaty
Geometria Geometria (słowo to pochodzi z języka greckiego i oznacza mierzenie ziemi) jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Aksjomaty
Kolektor. Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk. Wykonajmy model kolektora jak na rys. 1.
 Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
Podstawowe pojęcia geometryczne
 PLANIMETRIA Podstawowe pojęcia geometryczne Geometria (słowo to pochodzi z języka greckiego i oznacza mierzenie ziemi) jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych
PLANIMETRIA Podstawowe pojęcia geometryczne Geometria (słowo to pochodzi z języka greckiego i oznacza mierzenie ziemi) jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych
