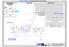
Koszalin dnia r Rys.1 o promieniu: r = 91, h;0h TABELA PRZELICZENIOWA wg (gk)

Transkrypt

1 skrypt Romany (R) gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Lekcja korzystania z przyrządu (rozw.trójkąt) Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski 12 W ćw.iii. umieściłem dwa odcinki: () i (). Należy końcówki odc.połączyć, zamkąć trójkąt i go rozwiązać. TECHNIK Koszalin dnia r Rys.1 o promieniu: r = 91, h;0h TEL PRZELICZENIW wg (gk) Przyrząd w (gk) 23h 1h bwodu koła: 24[mm/h]*24[h]=576mm (liczba całkowita) "Słońce Majów" Promień r= bwód/(2*π) = 91, Ł2= 22,5[h]*24[mm/h]=540 L=540*0,625[ /mm] 22h 2h [ /mm]; [h/mm]; [mm/h]; [ /h]; [h/ ]. Co zamienić, na co? [ ] 576*(1/360[ ])= 1,6000 [mm/ ] &2= 337,50 [ ] 21h 3h Ł1=3h*24[mm/h]+9 Przykł.1: L=4,321[ ] tj. L[ ]*1,6[mm/ ]= 6, Ł2= 19,5h*24[mm/h]+4,3mm Ł1= 81,000 [ ] Ł2= 472,3 L=81*0,625[ /mm] Przykł.2: L=90,0 tj. L*0,625[ /mm]= 56,2500 [ ] &'2= 472,3mm*0,625[ /mm] ĆW.II. ĆW.I. &1= 50,625 [ ] [h] 576*(1/24[h])= 24,000 [mm/h] 20h 4h Przykł.3: L=7,04[h] tj. L[h]*24,0[mm/h]= 168,960 r &'2= 295,18750 [ ] Ł1a=4,5h+1,7 [h] 24[h]*(1/576)= 0, [h/mm] X2 Ł1a= 109,7 r Przykł.4: L=17,07 tj. L*0,041667[h/mm]= 0,71125 [h] &'1= 68,56 [ ] [ ] [h] 24[h]*(1/360[ ])= 0,06667 [h/ ] 19h 90 5h Przykł.5: L=139,3[ ] tj. L[h]*0,06667[h/ ]= 9,28667 [h] &'2 [h] [ ] 360[ ]*(1/24[h])= 15,000 [ /h] &1 r &'1 r 2(r) c - cięciwa (X) Wzór: c/2= r*sin(&) 1(r) wysokość: () Wzór: = r*cos(&) &1 Radiany są obliczne z [ ], a stopnie z radianów [rad]. 18h 90 6h Przykład 6: L=71,95[ ] tj. formuła fx : ((=)radiany(l)) X2(r) Przykład 6: 1, [rad] Przykład 7: L=1,965[rad] tj. formuła fx : ((=)stopnie(l)) &2 Przykład 7: 112, [ ] X1 Co się stanie, gdy promień r = 120,000? 17h X1(r) 7h dpowiedź: nic. Wtedy trzeba używać mnożnik U: U=r(120)/r= 1, Stąd obwód: b = 576*U= 753, h 15h 14h ĆW.III 13h 12h 11h ĆW.IV. 10h 9h 8h L - liczba z określonym mianem np. [ ]; ; [h]; [mm/ ]; 360[ ]*(1/576)= 0,6250 [ /mm] W ten sposób należy postęp.ze wszystkimi wymiarami Kiedy potrzebuję przeliczyć wymiar na innę jednostkę, szukam w mianowniku tę jednostkę. Sprawdzam czy ta jednostka przelicz.jest w liczniku. Jeśli to ona - jest K.! Przyrząd "Słońce Majów" jest przyrządem wirtualnym, za sprawą jednostki miary. W tej chwili operuję jm., lecz mogą to być jednostki miary stosowane obecnie, na całym świecie. Zadanie to rozwiąże, jako przykład, w jaki sposób można korzystać z (gk). Poza kątem odchylenia od pionu, czyli (0h) (patrz: strzałki łukowe prawe), przedstawione odcinki żadnych danych nie mają. Ma tą da- ną przyrząd tj. PRMIEŃ r. W tym tkwi tajemnica geniuszu "koła".

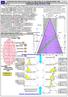
2 Lp. Słońce Majów r Przel. x x [h] [ /mm] a Promień Przyrządu Nazwa rozpatry- wanego odcinka 0,625 L ± Ł (b:d) (e:f) (g:h) (i:j) (k:l) m (n;o) (p:q) (r:s) (t;u) (v;w) (x:y) (z:aa) (ab:ac) (ad:ah) (af:ag) (ak:am) (an:aq) 91, () 22,500 0, ,00 337,50 19,500 4, ,30 295,19-82, ,014-16,160 42, , () 3,000 9,000 81,00 50,625 4,500 1, ,70 68,56 85,331 33,505 40,826 52, ,125 57, , , (C) 19,000-2, ,30 283,313 19,500 4, ,30 295,19-82, , ,88 169, , (D) 6,500 3, ,00 99,375 4,500 1, ,70 68,56 85,331 33, ,94 205, , , , , , , ,625 DNSZĘ WRŻENIE, ŻE T PRCWNIE MŻE Ć NIE DL WSZSTKICH ZRZUMIŁE. STĄD MÓWIĘ KNSTRUCJĘ TELI I FRMUŁ M. WSZSTK T, C SŁUŻ MI D LICZEŃ "TUR" NZWM PRZRZĄDEM. TEN PRZKŁD JEST TEG DWDEM. KPI PRZKŁDU LICZENIWEG RZWIĄZUJĄC TRÓJKĄT: PLIK.ZESZT.003. str.15 LEKCJ Nr 14 - teoria: przykład powtarzalny w trzech wersjach, oparty na tych samych danych. Wersja nr 2. PRZKŁD Nr 2 Dane a = 42, b = 52, &= 73,125 [ ] Szukane: F ; c; r; h ; µ [ ]; ß [ ] Ł1; Ł2; Ł3; Trójkąt: (C) jak poprzednie dwa trójkąty h = 2*F/a = 50, twierdzenie rzutów: a = c*cosµ +b*cos& tj. F (::C) = 0,5*a*b*sin& = 1 067, tj. c = (a-b*cos&)/cosµ c*cosµ = (a-b*cos&)= 26, ß [ ]= 180 -( &+µ ) = 44, C Ł3 c=h/sinµ cosµ *h/sinµ = h/tanµ = 26,8977 µ [ ] = 61, s=0,5*(a+b+c) ß c = h/sinµ = 57, Twierdzenie sinusów: s= 76, Ł1 c r= Kąty środkowe: h b Ł1(&1)= 76, Ł2(β 1)= &[ ] &1[ ] = 146, µ a & Łz= Ł1(&1)+Ł2(β 1)+Ł1(µ 1)= 187, Łuk zamknięty 360 ß [ ] ß 1[ ] = 89, r bwód okręgu: 2*π*r = 187, µ [ ] µ 1[ ] = 123, Ł1(&1)/r= 2, [rad] Sprawdzenie poprawności Suma kątów środk. 360, Ł2(β 1)/r= 1, [rad] wyliczeń matematycznych: Na rysunku nie ma oznaczonych Ł2 Ł1(µ 1)/r= 2, [rad] kątów środkowych. Łz/r = 6, [rad] F=a*b*c/(4*r)= a = () [j] b = () [j] &= 73,125 [ ] odcinki nie posiadają żadnych danych. I tutaj użyję znane przysłowie cyt. "Jak wchodzisz między wrony, kraczesz jak ony" Mam tu na myśli promień koła przyrządu SM, zapisany w kol.(b:d) tabeli obliczeniowej "TUR". Przyrząd ten ma charakter wirtualny, pozwalający dostosować wymiar promienia przyrządu, do wielkości jaką chcemy, lub jaką jednostką miary chcemy stosować. Tabela ta ma w kol.(g:h) L=22,00[h] i kol.(i:j)= 0,0 a wynik w kol.(k:l): Ł=540,00. bliczenie: 22,00[h]*0,625[ /mm]kol.(m)+(0,0)= 540,00 łuku (Ł). Kiedy mam łuk mierzony w prawo od 0[h] na tarczy zegara(24h), wtedy obliczam kąt &2= Ł/r= 5, [rad] &2= 337,50 [ ]. Teraz znam już kąt &2. Żeby obliczyć wielkość 2(r) muszę obliczyć kąt &2, w taki sam sposób tj.w prawo od 0[h]. Najpierw odczytuję i zapisuję w kol.(p:g) L=19,50[h] i kol.(r:s)= 4,30 a wynik w kol.(t:u): Ł= 472,30. bliczenie: 19,5[h]*0,625[ /mm]kol.(m)+(4,3)=472,3 Ł &2= Ł/r = 5, [rad] &2= 295,19 [ ]. W kol.(x:y) podaję rzuty prostokątne odcinków z udziałem promienia r na oś X2(r), stąd formuła: X2(r) = r*sin(rdin(&2) X2(r) = -82, bliczyłem drugą wielkość X2(r). Teraz w kol.(z:aa) obliczę trzecią wielkość tj. rzut tego samego odcinka na oś 2(r) także z udziałem promienia r z kol.(b:d). 2(r) = r*cs(rdin(&2) 2(r) = 39, W kol.(ab:ac) obliczę wymiar rzutu X2 (Xn) tj. rzut na oś X stosując formułę: X2= 2(r)*TN(RDIN(&2)). X2=. I. PRZKŁD KRZSTNI Z PRZRZĄDU: SŁŃCE MJÓW TEL LICZENIW "TUR" D RZWIĄZWNI TRÓJKĄTÓW DWLNCH Zapis pochylenia odcinka mierzony w prawo od (0h) liczba L dodatk. pis danych w nawiązaniu do przykładu ze str.1: ± Wynik odczytu w postaci łuku Ł Kąty & pochylen. przeliczane 0,625[ /mm] [ ] Zapis pochylenia odcinka mierzony w prawo od (0h) dodatk. w postaci przeliczane -16, Znak minus przed obliczeniem oznacza, że odcinek () znajduje się II ćwiartce koła przyrządu SM. liczba [h] Wynik odczytu łuku Na (Rys.1) widać, że wielkości: X2 i 2(r) są przyprostokątnymi trójkąta prostego, a odcinek () jest jego przeciwprostokątną. Wobec tego obliczę jego wymiar rzeczywisty oparty na dwóch odczytach:. gk T Lekcja korzystania z przyrządu (rozw.trójkąt) Kąty &'n pochylen. 0,625[ /mm] Xn(r) () = (X2^2+(2(r))^2)^0,5= 42, [ ] Wymiary rzutów prostok.odcinków z udziałem prom.r i kąta &'n n(r) Wymiar rzutu prost. odcinka na oś(+x-x) Xn (a/sinß )/2 = 29, *r=a/sinß =b/sinµ =c/sin& Podobnie postępuję z odcinkiem () wypełniając tabelę obliczeniową w pozycji lp.2 obliczając jego wymiar rzeczywisty. 46, Ł1(µ 1)= F=(s*(s-a)*(s-b)*(s-c))^0,5= Wymiary rzeczywiste rozpatrywanych odcinków 64, , , Kąt β zawarty między odcinkami [ ] Wymiar rzeczywisty odcinka zamykającego trójkąt opracował: inż. Kazimierz arski Koszalin dnia r [mm^2] str.2 Powierzchnia trójkąta dowolnego Gdyby ktoś zadał pytanie. Czy da się wykorzystać powyższą tabelę TUR, w przy- padku długości odcinków od kilku, do kilkudzie- sięciu mertów? Tak. Proszę spojrzeć na lp.3. i 4/ kol.(ad:ah); (ak:am); ()*10^3; (an:aq) na tle błękitu odnoszą się do wielkości obli- po przecinku). Gdy liczba miejsc przed przeczeniowych z przyrządu: PRZKŁD NR 2. Wszystkie podane kąty w tabeli nie ulegają żadnym zmianom. W tym przypadku wykorzystałem dokładność obliczeń programu komputerowego (13 miejsc cinkiem się zwiększa, to wtedy liczba miejsc po przecinku maleje. Jak widać. Po przesunięciu odcinków do pktu (centralnego) stały się odcinkami: () i (). ba te TECHNIK blicz.na podst.: Lekcja Nr 14. ()*10^6. Tabela TUR funkcjon.w zakresie: <a (af:ag)>.natomiast kol.(ak:am); (an:aq),

3 Ciąg dalszy opisu moich obliczeń: str.3 Teraz przejdę do obliczenia kąta mniejszego β zawartego między tymi odcinkami (); (). Jest to łatwe zadanie. Wystarczy spojrzeć na (Rys.1). β = (360 -&2)+&1 = ( ,50 )+50,625 β = 73,125 [ ] Jest to kol.(af:ag). Kolejną kolumnę obliczam korzystając z przyrzadu na str.2 w obwódce szarej. Maja praca polega na wpisaniu do komórek zielonych trzech obliczonych wielkości. Reszta jest już zaprogramowana, rozwiązująca powstały trójkąt. bliczenie boku zamykającego trójkąt kopiuję i wklejam do kol.(ak:am), a powierzchnię trójkąta do kol.(an:aq). W tym to wszystko polega. Ten przykład występuje w tej samej tabeli w poz.lp. 3 i 4. Nie narysowałem dla niego żadnego rysunku, ponieważ zostały zmienione wielkości: odc. (C) i (D) mają inne wymiary, zapisane w tabeli. Z wymiarów jasno wynika, że dane KPI PRZKŁDU LICZENIWEG RZWIĄZUJĄC TRÓJKĄT: PLIK.ZESZT.003. str.15 wprowadzone do tabeli nie mieszczą LEKCJ Nr 14 - teoria: przykład powtarzalny w trzech wersjach, oparty na tych samych danych. Wersja nr 2. się w przyrządzie SM. To nie ma już PRZKŁD Nr 2 Dane a = 169, b = 205, &= 176,063 [ ] Szukane: F ; c; r; h ; µ [ ]; ß [ ] Ł1; Ł2; Ł3; znaczenia. Ważne są formuły matema- Trójkąt: (C) jak poprzednie dwa trójkąty h = 2*F/a = 14, twierdzenie rzutów: a = c*cosµ +b*cos& tj. tyczne zapisane w tabeli obliczeniowej. F (::C) = 0,5*a*b*sin& = 1 196, tj. c = (a-b*cos&)/cosµ c*cosµ = (a-b*cos&)= 374, Na przykładzie II zakończę geometrię ß [ ]= 180 -( &+µ ) = 1, C Ł3 c=h/sinµ cosµ *h/sinµ = h/tanµ = 374,635 µ [ ] = 2, płaską związaną z płaszczyzną (X). s=0,5*(a+b+c) ß c = h/sinµ = 374, Twierdzenie sinusów: Pora przejść na geometrię przestrzenną. s= 375, Ł1 c r= (a/sinß )/2 = 2729, *r=a/sinß =b/sinµ =c/sin& Chcę pokazać płaszczyznę w przestrzeni. Kąty środkowe: h II. PRZKŁD KRZSTNI Z PRZRZĄDU: SŁŃCE MJÓW b Ł1(&1)= 16776,65954 Ł2(β 1)= 169, Ł1(µ 1)= 205, &[ ] &1[ ] = 352, µ a & Łz= Ł1(&1)+Ł2(β 1)+Ł1(µ 1)= 17151,8564 Łuk zamknięty 360 ß [ ] ß 1[ ] = 3, r bwód okręgu: 2*π*r = 17151, µ [ ] µ 1[ ] = 4, Ł1(&1)/r= 6, [rad] Sprawdzenie poprawności Suma kątów środk. 360, Ł2(β 1)/r= 0, [rad] wyliczeń matematycznych: Na rysunku nie ma oznaczonych Ł2 Ł1(µ 1)/r= 0, [rad] F=(s*(s-a)*(s-b)*(s-c))^0,5= 1 196,55830 kątów środkowych. Łz/r = 6, [rad] F=a*b*c/(4*r)= 1 196, REWERS WERS gk T TECHNIK ędą to dwa odcinki i jeden łuk. Łuk w tym przypadku pochodzi od odchylonego koła, czyli elipsy., jak wiemy każda elipsa ma półosie: a i b. Wystarczy wtedy wprowadzić te wymiary do dwóch pktów końcowych odcinków, by zamknąć tę figurę płaską i tym chcę się teraz zająć. Muszę skopiować i wprowadzić przestrzeń. PRZKŁD oderwany od tematu, lecz związany z opisem Proszę Państwa. Po stwierdzeniu, że już nie nadaję się do wykonywania obliczeń matemarycznych z powodu błędów ze str.4. tóż przy występowaniu śladu na pł.(xz), czy w postanowiłem ograniczyć swoje możliwości do trasowania. łędy popełniłem w tworzeniu formuł, bo rozumowanie poziomie, czy skośnie zawsze zachodzi symetria między było poprawne. Chodzi o zakwestionowanie teorii krzywych stożkowych dot.elips. W elipsie osie: 2*a i 2*b są płaszczyznami: (X) i (Z). Ten przykład dotyczy trasowania symetryczne. Natomiast z moich obliczeń, gdzie były błędne formuły, wynikało, iż nała oś 2*b nie zachowuje symetrii. tj. rzutowania prostokąt- (+)Z (+)Z To chciałem przede wszystkim przekazać Państwu. Teraz chcę powiedzieć o trasowaniu, czyli geometrii wykreślnej, nego na powierzchnię rzutni. a konkretnie o sztuce trasowania. Mój sposób trasowania opiera się na rzutach prostokątnych odcinka; łuku; figury Potwierdzenie: ŚLD płaskiej i bryły na podstawę, którą nazywam MP. Traktuję tę płaszczyznę jako podstawową (X). Jest wyposażona.skrypt (R).016 X X w tarczę zegara (24h). X Ten kolor jest związany z osią (-X+X) tzn.po lewej stronie są wartości (-), z prawej (+). Ten kolor jest związany z osią (góra, dół) (+-). Nad osią są wartości (+), a pod osią (-). ile na osi (X) rozkład godzin zaczyna się po środku u góry (prawa strona: 0h do 6h), to (lewa str.: 18h do 24h). Potem na dole (-)Z (-)Z (z prawej strony: 12h do 6h), a (z lewej strony: 12h do 18h). Godziny skrajne obu osi zazębiaję się, lecz oto chodziło. (+) (+) (+) (+) Poza tym na pł.(z) występuje także oś (góra, dół) (+-). Ten kolor przypisany jest pł.(xz) i (Z).Pł.ma podwójne znaczenie. Występuje na osi pł.(xz) (góra, dół) (+Z-Z). Po drugie występuje na osi pł.(z) (lewa, prawa) (+Z-Z). znaczenia godzinowe pł.(xz) (góra, dół) (od 12h do 24h prawa strona) i (dół, góra) (od 0h do 12h lewa strona). X X znaczenia godz.pł.(z) nad osią(+z-z) (s.lewa, s.prawa) (od 0h do 6h prawa strona) i (od 18h do 24h lewa strona). znaczenia godz.pł.(z) pod osią(+z-z) (s.lewa, s.prawa) (od 6h do 12h prawa strona) i (od 12h do 18h lewa strona). f' e' c' b' a' a b c e f To wszystko co opisałem sam tworzyłem, ucząc się jednocześnie. Innymi słowy doskonaliłem swoją wiedzę. ywa, że (-) d' (-) (-) d (-) późniejsze opracowania różnią się od wcześniej opracowanych. Zastosowane zawiasy pełnią b.ważną rolę. Proszę Płytki widziane od spodu Płytki łazienk. z niebieskimi fugami obrócić pł.(z) z pozycji leżącej do pionu tj.90[ ], a potem do 180[ ]. Podobnie proszę obrócić na zawiasie pł.(xz) względem pł.(x). trzymacie efekty podobne. Warto teraz popatrzyć na rysunek obok. (REWERS-WERS). To wszystko co mogę przedstawić na dzień dzisiejszy. lekcja korzystania z przyrządu Słońce Majów opracował: inż. Kazimierz arski Koszalin dnia r

4 1). 2). 3). 4). III. PRZKŁD KRZSTNI Z PRZRZĄDU: SŁŃCE MJÓW Rysowanie, czy jak kto woli nazywać trasowanie lub geometrię wykreślną zacząłem od (Rys.1). Potem od wyznaczonych punktów: ; ; narysowałem linie przerywane pionowe 0,25. Najważniejszy pkt musiał być w punkcie centralnym koła. Punkty i wyznaczyłem w sposób dowolny, lecz w wyznaczonym kole, by całość figury była w tym kole. Z programu M.Excel wykorzystałem funkcję łuk i od pktu narysowałem łuk do pktu. Pkt C wyznacza punkt centralny łuku ELIPS. Teraz strzałkami wyznaczam na (Rys.2) wymiary. Przypomnę Państwu, że jakie są w (gk) reguły trasowania: Co łączy MPĘ pł.(x) z pł.(xz)? dp. ś (+X::-X). To oznacza, że wymiary mierzone są od pktu na tej osi i przenoszone na pł.(xz). Linie przer. Co łączy MPĘ pł.(x) z pł.(z)? dp. ś (+::-). To oznacza, że wymiary mierzone są od pktu na tej osi. W górę mają wielkości dodatnie, a w dół mają wielkości ujemne. Dokładnie tak, jak na MPIE. Ciekawostka. Proszę zwrócić uwagę, co łączy poszczególne płaszczyzny parami. Czy nie te? (X) (XZ); (X) (Z); (XZ) (Z) oś X oś oś Z Tylko dwie pierwsze pary mają te osie równoległe i wystarczy przenieść liniami z jednej płaszczyzny na drugą. W przypadku trzeciej pary osie Z są do siebie prostopadłe. Wtedy wymiar przenoszę i obracam o kąt 90[ ]. W przypadku występowania ŚLDu na na pł.(xz) poziomego lub skośnego, wtedy zachodzi symetria tej figury geometr. na płaszczyznach: (X) i (Z). (-)X (+)X (+)Z Rys.2 Z (+)Z X X C (-)Z Z (-)Z (-)X (+)X Zg Zd str.4 X (+)Z (-)Z X Z (-)X 24h;0h (+) Rys.3 (+) (+) Rys.1 (+) b1 Z Z 18h X X 6h Zg Zd a1 C (-) (-) (-) (-) X (+)Z Płaszczyzna pionowa w pozycji leżącej (-)Z X Z (-)X Płaszczyzna pozioma 12h MP

5 Z (-)X Z (-)X (+) Rys.4 (+) (+) Rys.5 (+) str.5 Rzeczywisty obraz figury płaskiej ' ' b1 b1 2 1 ' ' C' a1 C C (-) (-) (-) (-) Z (-)X Płaszczyzna pozioma MP Z (-)X Płaszczyzna pozioma MP Z (-)X 24h;0h (+) Rys.6 (+) ' h 6h ' C' Ta strona jest poświęcona płaszczyźnie (X) tj. MPIE. Mam zamiar pokazać rzeczywisty obraz figury płaskiej, która jest zawieszona w przestrzeni i tylko dysponuję rzutami prostopadłymi tej figury na płaszczyzny. Żeby zobaczyć rzeczywisty obraz tej figury muszą doprowadzić ją do takiej pozycji w przestrze- ni, by zobaczyć jej ślad. Ślad tej figury jest linia prosta, wraz z punktami: ; ; na tej linii. Przy rysowaniu korzystałem z kopiowania. Rys.4 po skopiowaniu i wklejeniu obróciłem w prawo. Przedtem wykonałem okrąg z centralnym pkt, po to by po przecięciu się z osią X wyznaczyć pkt '. Punkt ' wyznacza początek łuku (elipsy). Po obrocie w prawo przesunąłem łuk do pktu '. Następnie wyznaczyłem pkt ' na tym rysunku. Po skopiowaniu (Rys.4) i wklejeniu obok, skorygowałem odcinki:(') i ('). Usunąłem także zbędną powierzchnię elipsy trójkątami prostokątnymi. Punkt ' zrzutowałem na oś X wyznaczając pkt C'. Rys.6 powstał także po skopiowaniu i wklejeniu obok. Teraz linią fioletową 2,25 wyznaczyłem ślad figury płaskiej. Na tych trzech rysunkach zapisałem symbolicznie wymiary wraz z numerami ( ) odcinków. Teraz już mogę narysować wszystkie trzy rzuty. Z tym, że płaszczyzna (Z) także będzie pokazywać tylko ślad. Natomiast płaszczyzna pionowa (XZ) ukaże w pełni powierzchnię figury. C (-) (-) Z (-)X 12h gk T lekcja korzystania z przyrządu Słońce Majów opracował: inż. Kazimierz arski Płaszczyzna pozioma TECHNIK Koszalin dnia r MP Płaszczyzna

6 III. PRZKŁD KRZSTNI Z PRZRZĄDU: SŁŃCE MJÓW Na (Rys.8) występuje łuk pochodzący od ELIPS. To oznacza, że nie pochodzi od koła, ponieważ dla tej krzywej pkt C' nie jest punktem centralnym tego koła narysowanego kropkami. W przypadku ELIPS istnieje: a1 b1. Natomiast w przypadku KŁ: a1=b1, To jest tak, jak pokazałem na tym rysunku, którego koło, okrąg, nachodzi na (Rys.6). Narysowałem ELIPSĘ, wykorzystując narysowany kropkowany okrąg. Ta czynność wcale nie należy do prostych czynności, stąd małe uchybienia przy rysowaniu. Przykro mi, że (Rys.8) jest taki zamazany. nalitykom taki rysunek - odpowieda. Z takiego rysunku czerpią wiedzę. Widać na nim jaka część powierzchni ELIPS i jej łuku bierze udział w figurze płaskiej ograniczonej dwoma odcinkami prostymi. To był jeden z moich celów. Powiem Państwu, że rysuję, coś takiego, pierwszy raz w życiu. Rys.8. Nałożenie na siebie krzywych w pkt.;w; [xls] jest kłopotliwe. Natomiast druko- wanie w [pdf] krzywej elipsy; elipsy i okręgu jest złe, bo figury nie trzymają się tych pkt. Na str.5 miałem powrócić do obliczeń matematycznych związanych z tabelą obliczeniową, lecz coraz częściej wyłapuję swoje błędy. W związku z tym ograniczę swoją pasję do sztuki trasowania (przekazu). inż. Kazimierz arski z Koszalina (+)Z str.6 Rys.8 (+)Z liniał do wyznaczania pkt.(równoległe do osi koła) Zg 2 ' 1 1 Zd 0 0 centrum ELIPS gk T TECHNIK lekcja korzystania z przyrządu Słońce Majów opracował: inż. Kazimierz arski Koszalin dnia r dwa centra: wycinka łuku ELIPS i KŁ (-)Z C' (-)Z X (+)Z 24h;0h (-)Z X Z (-)X 24h;0h (+) Rys.7 (+) (+) Rys.6 (+) liniał 5 3 ' 2 ŚLD 1 FIGUR Z Z 18h h ' ' ' ' ŚLD FIGUR C Zg Zd 4 liniał do przenoszenia pkt.(od 0 do 6) (-) (-) (-) (-) X (+)Z Płaszczyzna pionowa 12h w pozycji leżącej (-)Z X Z (-)X Płaszczyzna pozioma 12h MP