O kula. w (gks). Rzutnie: (XZ); (YZ); (XY). A B (YZ) (XY) D sześciana

Transkrypt

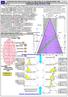
1 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych do Podgląd układu (XYZ) rozwiązania zadania nr 14 Rzutnie: (XZ); (YZ); (XY). E (XZ) F A B C O kula (YZ) G Hściany (XY) D sześciana Kto nie poznał wiedzy zawartej w (gk) lub (), moŝe mieć trudności z rozwiązaniem tego zadania, poniewaŝ rzutami na poziom, są dwie EK. EK - Elipsa Koła Rys.2 pł.( X Y )pm. w (). 1 2 Pkt. Jest pkt.skrzyŝowania osi stoŝków n G T Dobry człowiek K TECHNIKA Koszalin dnia: 25 kwietnia 2017r

2 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W UP RP. Format.Ark.A4 12,75*1,75 str.2 Rys.3 pł.( X Z )pn.w () Rys.5 pł.( Y Z )pn.w () Chcielibyśmy zwrócić Państwa uwagę, na brak promieni od wierzchołka stoŝka. ą zbyteczne. klamerka Dla : 2h;10h 6,36 cm 7,83165 cm 7,37527 cm Wymiary rzeczywiste prom.stoŝka nr1: 2h; 10h Linia prostopadła do osi stoŝka 1,13371 cm ,1360 cm 14h 60 Gdyby był sam stoŝek, to promienie od wierzchołka (linie ciągłe) do podstawy byłyby po stronie widocznej, czyli wypukłej. Natomiast, stoŝek, ma promienie od wierzchołka (linie przerywane), bo na tym rzucie, jego aktywna strona przenikania jest z tyłu, niewidoczna. Jednak tego nie zrobiliśmy,umieściliśmy stoŝek nr 2 z tyłu, bo bohaterami nie są czubate stoŝki, lecz ich ODPADY h Gdyby były i nie miały pkt. wspólnych z promieniami stoŝka, to niebyłoby z nich Ŝadnego poŝytku. Mamy za to poziomy poło- Ŝenia pkt.wspólnych przeniesionych z rys.3. 18h > 11h 10h ϕ 3,96913 cm > 9h 18h 8h 7h 4,08 cm Na obecnym etapie ϕ/2= 2,35262 cm trudno jest odwaŝyć 24h;0h się, co to za owal Rys.4 24h;0h 4,07722 cm INTERPRETACJA Z OBLICZENIAMI na tle jasnego koloru purpury. pł.( X Y )pm. taramy się nie ukrywać swoją wiedzę, by na rzutni ( X Y )pm.były poprawne w (). 3,48 cm 18h 1 2 (7, cm + 1, cm)=8, cm. Przyjrzyjmy się płaszczyźnie trójkąta równoramiennego, którego na nieszczęście wodzimy jego ślad. Więc, chcemy przemówić do wyobraźni Państwa. Wg Tallesa jest taka proporcja w podobieństwie trójkątów. Obliczenie: x =( b * y )/( a + b )= 1, cm y = ϕ 3,96913 cm Pkt. Jest pkt.skrzyŝowania osi stoŝków Rys.6 Przyrząd "parawanik kołowy" na EK podstawy stoŝka ciętego. Rozkład promieni czarnych 1 i niebieskich podstawy ciętej. W obu przypadkach na rys.3 i rys.4 mamy do czynienie z przesunięciem pół(ek) nr 1 zkic bez skali, wymiary w [cm]: b = pół(ek) rozłoŝonych promieni pionowych. Jest x to związane z wydłuŝaniem się promieni stoŝkowych, od jego wierzchołka do y/2 = 1,98457 podstawy. To zjawisko będzie doskonale widoczne na rozwinięciu stoŝków. Obliczenie: x =( b * y )/( a + b )= pół(ek) nr 2 Rys.7 Jak w. Przyrząd: "parawanik prostokątny" szablonu listw."a", przy promieniach b = 7, pionowych. Na obu rys.3 i 4 są pokazane czerwo- ne pkt.centrum EK. wymiary EK podstawy stoŝka ściętego. Potrzebni są nam dwaj staroŝytni uczeni. Talles i Pitagoras. Z odczytu oblicz.dwa odcinki wysok.stoŝka nr 1. a = 17h 1 15h 2, cm zkic bez skali, wymiary w [cm]: pół(ek) 1,13371 x a = y = 1,1360 7, ,35262 NaleŜy pamiętać, Ŝe na rys.1 i rys.2 są krzywe zamknięte, dlatego przypominamy o tylnej stronie, która jest zasłonięta przez drugą połowę tej krzywej. Po dokonaniu analizy skrzyŝowań promieni oby stoŝków, od ich wierzchołków do ich podstaw, nie widzimy więcej krzywych. A, zatem naleŝy przejść do rozwinięć obu stoŝków.obliczenie obwodu Koła ϕ 3,9691 cm Ob.= 12,46939 cm łuk. Najmniejszy łuk: 0,5196 cm Najmniejszy kąt: 15,00 [ /kąt] Oblicz.kąta α = Ł*180/(R*π)= 77,82610 [ ] r = 1, cm Oblicz.strzałki= h= R*(1-cos(radiany( α /2 ))) = 2,037 cm Dług.cięciwy= c= 2*(h*(2*R-h)^0,5= 11,53266 cm Dobry człowiek K TECHNIKA Koszalin dnia: 25 kwietnia 2017r

3 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W UP RP. Format.Ark.A4 12,75*1,75 Rys.8 Rozwinięcie stoŝka nr 1 z naniesieniem krzywej do odcięcia. Tabl. 2. Tylko do wyznaczania kątów [h] Dług.prom.[cm] Kilka przykł.oblicz.z odczytów Tabl. 1. na rozwinięciu stoŝka nr , , [h] (±)kąty narast.[ ] , (6,74^2+6,17^2)^0,5 38,91305 [ ]=α/2 α /2= 38,91305 [ ] , (6,62^2+6,05^2)^0,5 α /24= 3, [ ] , , (6,48^2+5,92^2)^0, , , (6,29^2+5,78^2)^0,5 Rozwinięty stoŝek nr , , (6,13^2+5,56^2)^0, , ; , (5,9^2+5,41^2)^0,5 ELEMENT NR II , , (5,72^2+5,25^2)^0,5 ELEMENT NR I 6 24 ; , , (5,55^2+5,07^2)^0,5 MUZLA CZ. NR , , Krzywa zamknięta , , Linia pozioma do przenoszenia pkt , , , , , , str.3 5h 4h 8h 7h h= 2,037 cm 3h 2h 0h 10h strzałka odcinka Koła 1h 24h 23h 13h 11h 22h 21h 20h 19h 18h 17h 1 15h 14h Długość cięciwy 11,53266 cm 9h Rozwinięcie stoŝka prostego o podst.koła. linia przerywana krótka do pkt.. toŝek nr 2 ma podstawę EK w połoŝeniu ciętym. Natomiast, w pozycji pochyłej (odchylonej) na pł.pionowej rzutni ( X Z ) ma podstawę Koła. Promień Koła wynosi: R= 2, cm. NajdłuŜszy promień stoŝka nr 2 jest od wierzchołka do pkt.. kłada się z dwóch odcinków H= 8, cm Obwód podstawy Koła wynosi Ob.;Ł2= 2*π*R = 14, cm. Jest to Ł2 (łuk). ϕ Koła w celu rozwinięcia stoŝka wynosi: 2*R= 17, cm Tę pracę proponujęmy wykonać przez Państwo, dla utrwalenia wiedzy. Lepiej jest ćwiczyć swój umysł, niŝ grać w gry, aŝ do znudzenia. Ciąg dalszy obliczeń. Wycinka otworu krzywej zamkniętej. Po wykonaniu rozwinięć z uwzględnieniem dodatków na zakłady, zwijamy stoŝek ,56 A. B ; , [h] Dług.prom.[cm] Tabl ,34 6,36 4,87 3,95 3,64 3,46 3,36 3,29 Rys.9 1 Odczyty z klamerek. Taka jest nasza propozycja. Wykonano szablon nieznanej EK, bo tak było najłatwiej, do tego zadania. Czarne EK mają własne punkty, ale potrzeba nowe pkt. EK np. A ma trzy rodzaje punktów na obwodzie. Natomiast EK B ma tylko dwa rodzaje punktów. Rys.10 Wykonano szablon nieznanej EK. Podobnie jak rys.9 mają dwa róŝne punkty na obwodzie do tego naleŝy uwzględnić "parawanik EK prostej, przesuwny". Najlepiej uŝywać klamerek do odczytywania odcinków lub nanoszenia punktów w tym programie. Chodzi o to, Ŝe kiedy ustawimy pod kątem odcinek, z funkcji to górna liczba podaje wymiar jego długości. Druga dolna liczba podaje wymiar wysokości klamerki, która nie ma wpływu na długość odcinka. Zatem zaleca się stosowanie tabl. II i tabl. III, które przyspieszą prace i są dokładniejsze z racji jednego odczytu wymiaru. Rys.11 pł.( X Z )pm.w (). Rzuty obu podstaw stoŝków, jako EK. Rys.12 Wspólna posadzka apartamentowca bisnessmena z Kataru. ugestia. Koncepcja. Dobry człowiek K TECHNIKA Koszalin dnia: (26-28) kwietnia 2017r

4 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W UP RP. Format.Ark.A4 12,75*1,75 str.4 Rys.13 pł.( X Z )pn.w () Efekt końcowy przenikania dwóch stoŝków. Rys.15 pł.( Y Z )pn.w () Efekt końcowy przenikania dwóch stoŝków. toŝek nr1 byłby zasłaniał stoŝka nr2, który jest element.nr II rozwinięcia. ELEMENT NR II 1 2 Rys.12 zmienił nas cel. Chodzi o to, Ŝe przez przypadek poznajemy coś, co decyduje o naszej pracy. Mówiąc inaczej na rys.12 spotkały się jednocześnie: wyobraźnia, skojarzenie i fantazja. Dlatego rys.13 przedstawia dwa stoŝki jako pamiątkę turystyczną, reklamujące hotel zejka z Dubaju. Na stałej płytce gr.0,45 cm o kształcie EK z wygrawerowanymi słowami mądrości. Rys.14 pł.( X Y )pn.w () Rys.16 pł.( X Y )pn.w () Pamiątka nr 2 z hotelu: "PERŁA DUBAJU". 5, cm 7,81 cm Część oblicz.rozwinięcia stoŝka nr2 UWAGA wszystkie odczyty wykonujemy przy pomocy klamerki. Oblicz.kąta β = Ł2*180/(R*π)= 95,91638 [ ] Oblicz.kątaβ/2 = 47,95819 [ ] Oblicz.strzałki= h= R*(1-cos(radiany( β /2 ))) = 2,917 cm Oblicz.najmniejszego kąta β/24h = 3, [ /h] Dług.cięciwy= c= 2*(h*(2*R-h)^0,5= 13,11531 cm Z odczytu R= 8,83 cm Z przeniesienia Ł2= 14,78192 cm Rys.17 pł.( Y Z )pn.w () Efekt połączenia dwóch cz. MUZLI NR 1 i NR 2. Rys.18 pł.( Y Z )pn.w () Efekt połączenia dwóch cz. MUZLI. ELEMENT NR I Eksponaty miniatury hotelu "PERŁA DUBAJU" jako reklamy, pamiątki z wakacji. Pamiątka moŝe być wykonana z jednolitego materiału z wygrawerowanymi słowami. Postanowiliśmy poszerzyć dzieło o rozwinięcie stoŝka nr 2, uŝywając klamerki do wymiarowania. Niniejsze dzieło jest tworem intelektualnym wyobraźni, skojarzenia i fantazji. W myśl prawa twórczego autorów, dzieło podlega ochronie prawnej zgodnie z ustawą.autorzy dzieła w obecnym stanie, jako koncepcji, wyceniają je w (?) tys.. Taka jest nasza oferta. Mamy nadzieję,ŝe nikt nie pokusi się do zawłaszczenia naszego współnego dzieła. G T Dobry człowiek K TECHNIKA Koszalin dnia: 29 kwietnia 2017r

5 Rys.19 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W UP RP. Format.Ark.A4 12,75*1,75 Rozwinięcie stoŝka nr 1 z naniesieniem krzywej do odcięcia. [h] Dług.prom.[cm] Tabl , ,80 47,95819 [ ] ` =β/2 β /2= 47,95819 [ ] , ,45 rozwinięcia stoŝka nr , , ;0 12 7, , ; , , , , , ,66 MUZLA NR , Krzywa zamknięta , Tabl. 5. str.5 Tylko do wyznaczania kątów na rozwinięciu stoŝka nr 2 [h] (±)kąty narast.[ ] 18 0, , , , , , , , , , h 18h 17h Długość cięciwy 13,12 cm 19h 1 20h [h] Dług.prom.[cm] Tab h 22h 21h 2,92 cm 14h 13h 23h ,97 11h 1h ,03 10h 9h 8h 7h 5h 4h 3h 2h , ; 0 4, , , , , , ,05 Rys.17 pł.( Y Z )pn.w () Rys.19 pł.( Y Z )pn.w () 0h ; 24h strzałka odcinka Koła Rys.18 pł.( Y Z )pn.w () Rys.20 pł.( Y Z ) pn. w () Głównymi bohaterami konstrukcji kształtu hotelu " PERŁY DUBAJU " są boczne elementy ścian obu stoŝków skośnie ciętych, zapewniając stabilność budowli. Dobry człowiek K TECHNIKA Koszalin dnia: 02 maja 2017r