Za czym odrzucisz, co mam do pokazania, zobacz kolejne strony pliku! TABELA ANALITYCZNA TRÓJKĄTA MK - TURBO Nr wzoru WZÓR: WYNIK: JM:
|
|
|
- Bartosz Kowalski
- 6 lat temu
- Przeglądów:
Transkrypt
1 MK JES RÓJKĄEM RÓWNORAMIENNYM, KÓREGO WIELKOŚĆ KĄA ŚRODKOWEGO WYZNACZAJĄ str.1 DZIESIĘNE KĄA PEŁNEGO W OKRĘGU. JEGO KĄ ŚRODKOWY WYNIKA Z WZORU: 2*π-6[rad]= 0, SĄD: MK kąt środkowy ma = 16, [ ] OGÓLNIE O RÓJKĄCIE: MK I. Ł F Ł/2 II. Ł' F Ł'/2 Dla analizy przyjąłem promień "r" równy 1j. c' c'' r = 1, j Promień okręgu; koła. πc E πc' A B A' E η η η' η' B' Oznaczenia: η r η µ η' r η' µ µ Jest kątem środkowym trójkąta MK S ζ' S ζ Ł Jest łukiem trójkąta MK c c c' c' c Jest cięciwą i podstawą trójkąta MK r r r r Ł η η Ł Ł' η' η' Ł' s Jest strzałką łuku przy trójkącie MK Ł Ł h (Jest zbyt mała, by ją pokazać na rys.) C;c; D MK kąty: 2*η' = C;c; D 2*30 = 60 h Jest wysokością w trójkącie MK G tj. 1, [rad] Rys.I. RAPEZ: (ABCD) Rys.III. MAŁY RÓJKĄ (B'FS) Rys.IV. DUŻY RÓJKĄ(A'B'G) [rad] Za czym odrzucisz, co mam do pokazania, zobacz kolejne strony pliku! ABELA ANALIYCZNA RÓJKĄA MK - URBO Nr wzoru WZÓR: WYNIK: JM: x Kąt środkowy wg miary łukowej [rad] MK 1 µ = (2*π-6) [rad] 0, [rad] 2 µ = (2*π-6) [rad] [ ] 16, [ ] x Obwód koła: OB( ), przy r = 1j x x 3 OB(o)= 2*π*r 6, [j^2] x Powierzchnia koła: F( ), przy r = 1j x x 4 F(o)= π*r^2 3, [j^2] x Długość łuków Ł w [j], przy r = 1j x x 5 Ł = r*µ 0, [j] x Długość strzałki "s" w [j], przy r = 1j x x 6 s=r*(1-cos(µ/2)) 0, [j] x I.(sposób).Dług.cięciwy: "c", przy r=1j x x 7 c=2*(s*(2*r-s))^0,5 0, [j] x Pow.wycinka pola w [j]^2, przy r = 1j x x 8 F(wycinka koła) = 0,5 * r * Ł 0, [j^2] x Wysokość h w MK w [j], przy r = 1j x x 9 h=(r^2-(c/2)^2)^0,5 0, [j] x Powierzchnia pola w [j^2], przy r = 1j MK 10 F MK=0,5*h*c 0, [j^2] Łuk rozpatrywany x Pow.odcinka pola w [j^2], przy r = 1j x x 11 F(odc.pola) = F(wycink koła) - F MK 0, [j^2] x II.(sposób).Dług.cięciwy: "c", przy r=1j MK c=2*(r*(1-cos(µ/2))*(2*r-r*(1-cos(µ/2))))^0,5 12 c=2*(r^2*(sin(µ/2))^2)^0,5 0, [j] c=2*(r^2*(sin(µ/2))^2)^0,5 x Długość strzałki "s" w [j], przy r = 1j x x Strzałka "s" ma zwrot przeciwny do łuku rozpatrywanego. 13 s = r + h 1, [j] strzałka x Długość łuków Ł w [j], przy r = 1j x x Suma długości strzałek s obu łuków: czerwonego i czarnego 14 Ł = F(o) - Ł 6, [j] powinna wynosić: 2*r tj. długość średnicy koła Ø. 14 Zależność: "c/s"= 28, x 15 Zależność: "s/c"= 0, x 16 Zależność: "h/s"= 98, x 17 Poprawność obliczeń: r=h+s 1, [mm] GEOMERIA KULOWA. WZORY DOYCZĄCE ZALEŻNOŚCI: x Pochyłość trójkąta MK: x x 1(gk) P( MK) = l/p 1, brak x Smukłość trójkąta MK: x x 2(gk) S( MK) = (l+p)/c 7, brak x Charakterystyka trójkąta MK: x x 3(gk) CH( MK) = l*(l+p)/(c*p) 7, brak OD NIKI DO KŁĘBKA rójkąt MK z obliczeniami wielkości elementów ECHNIKA Koszalin dnia 15 października 2011.
2 MK JES RÓJKĄEM RÓWNORAMIENNYM, KÓREGO WIELKOŚĆ KĄA ŚRODKOWEGO WYZNACZAJĄ str.2 DZIESIĘNE KĄA PEŁNEGO W OKRĘGU. JEGO KĄ ŚRODKOWY WYNIKA Z WZORU: 2*π-6[rad]= 0, SĄD: MK kąt środkowy ma = 16, [ ] "Słońce Majów" JES PRZYRZĄDEM, KÓRY PEŁNI Ą SAMĄ FUNKCJĘ, CO ZWYKŁA LINIJKA Z PODZIAŁEM [ mm ]. RÓŻNI SIĘ YM, ŻE WYZNACZA ŁUKI KOŁOWE. "Słońce Majów" r = 91, [mm] Promień przyrządu ABELA ANALIYCZNA RÓJK. MK DO PRZYRZĄDU "SŁOŃCE MAJÓW". Oznaczenia: Nr wzoru WZÓR: WYNIK: JM: µ Jest kątem środkowym trójkąta MK x Kąt środkowy wg miary łukowej [rad] MK Ł Jest łukiem trójkąta MK 1 µ = (2*π-6) [rad] 0, [rad] c Jest cięciwą i podstawą trójkąta MK 2 µ = (2*π-6) [rad] [ ] 16, [ ] s Jest strzałką łuku przy trójkącie MK x Obwód koła: OB( ) x x 3 OB(o)= 2*π*r 576, [mm] h Jest wysokością w trójkącie MK x Powierzchnia koła: F( ) x x 4 F= π*r^ , [mm^2] x Długość łuków: Ł x x 5 Ł = r*µ 25, [mm] x Długość strzałki: "s" x x 6 s=r*(1-cos(µ/2)) 0, [mm] x I.(sposób). Długość cięciwy: "c" x x 7 c=2*(s*(2*r-s))^0,5 25, [mm] x Pow.wycinka pola: F(w.k.) x x 8 F(wycinka koła) = 0,5 * r * Ł 1189, [mm^2] x Wysokość h w MK x x 9 h=(r^2-(c/2)^2)^0,5 90, [mm] x Powierzchnia pola: F MK MK 10 F MK=0,5*h*c 1174, [mm^2] Łuk rozpatrywany (Jest zbyt mała, by ją pokazać na rys.) x Pow.odcinka pola: F(o.k.) x x 11 F(odc.koła) = F(wycink koła) - F MK 15, [mm^2] x II.(sposób). Długość cięciwy: "c" MK c=2*(r*(1-cos(µ/2))*(2*r-r*(1-cos(µ/2))))^0,5 12 c=2*(r^2*(sin(µ/2))^2)^0,5 25, [mm] c=2*(r^2*(sin(µ/2))^2)^0,5 x Długość strzałki "s" w [j], przy r = 1j x x Strzałka "s" ma zwrot przeciwny do łuku rozpatrywanego. 13 s = r + h 182, [mm] strzałka 14 Zależność: "c/s"= 28, x Suma długości strzałek s obu łuków: czerwonego i czarnego 15 Zależność: "s/c"= 0, x powinna wynosić: 2*r tj. długość średnicy koła Ø. 16 Zależność: "h/s"= 98, x 17 Poprawność obliczeń: r=h+s 91, [mm] [rad] GEOMERIA KULOWA. WZORY DOYCZĄCE ZALEŻNOŚCI: x Pochyłość trójkąta MK: x x 1(gk) P( MK) = l/p 1, brak x Smukłość trójkąta MK: x x 2(gk) S( MK) = (l+p)/c 7, brak x Charakterystyka trójkąta MK: x x 3(gk) CH( MK) = l*(l+p)/(c*p) 7, brak KRÓKI OPIS SRON ZWIĄZANY Z INFORMACJĄ DOYCZĄCĄ ZWIĄZKU MK i PRZYRZĄDU "SŁOŃCE MAJÓW". Str.1 Zaczyna się od definicji trójkąta MK. Zawiera obliczenia wielkości związane kątem środkowym koła µ, przy promieniu r=1 Str.2 Podaje to samo, lecz odnosi się już do promienia r z przyrządu "SŁOŃCE MAJÓW". Dodatkowo są obliczone wielkości (gk). Obie powyższe strony mają charakter stały (constans). Rzecz w tym, by wykorzystać to, do celów praktycznych. Stąd są str Str.3 Zawiera przykład nr1,w którym kąt środkowy zajmuje ćw.i.zatem mieści się w kącie 90[ ].Występują tu po dwa(łuki+strzałki). Str.4 Zawiera rysunek do przykładu nr 1. Dopiero tu można znaleźć pewne ciekawostki, dzięki którym można opisać wzory oblicz. Str.:5; 6; 7; 8; 9 i 10. Powielają strony 3 i 4, lecz dotyczą kątów większych: od 90[ ]; od 180[ ]; od 270[ ], co wpływa na wzory oblicz. Wszystko to jest po to, by odróżnić "wiedzę nabytą" np. w szkołach, od "wiedzy wypracowanej" w praktyce. o jest taki przykład. Str.11 i 12 Pokazują wykorzystanie "wiedzy wypracowanej" do celów nawigacyjnych i w zabawę w różne gry, wg fantazji użytk. en plik jest zbiorem wiedzy wypracowanej w geometrii kulowej (gk). Nic tu nie ma odkrywczego. Na pewno przypomina program komputerowy - w stanie pierwotnym, który w postaci raczkującej odkrywa swoje tajemnice, dzięki przedstawionym obliczeniom i rysunkom. Na stronie 11 i 12 są dwie tabele, które były moim celem w tym opracowaniu. o dzięki tabeli na str.12 można poznać położenie współrzędnych punktów; ich odległości od centrum i ich długości, jako linii łamanej. Wystarczy wpisać odczyty łuków: poziomego i pionowego związanego z określonym punktem. rójkąt: MK ECHNIKA Koszalin dnia 15 października 2011.
3 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW W NW ZAKRESIE KĄA ŚRODKOWEGO str.3 OD β >0[ ] DO β =<360[ ]. DANĄ JES YLKO KĄ: β 1= 77, [ ] β 1= 1, [rad] DOWOLNY RÓJKĄ RÓWNORAMIENNY Z KĄEM ŚRODKOWYM "β " W OKRĘGU PRZYRZĄDU "SŁOŃCE MAJÓW" W ZAKRESIE: OD β >0[ ] DO β =<360[ ] Promień przyrządu PRZYKŁAD NR 1 "Słońce Majów" r = 91, [mm] 1.ABELA OBLICZENIOWA DOWOLNEGO RÓJKĄA - URBO Nr wzoru WZÓR: WYNIK: JM: Ogólnie: x Kąt środkowy wg miary łukowej [rad] rójkąt: β 1 1 β 1= 1, [rad] 2 β 1= 77, [ ] x Obwód koła: OB( ) x x 3 OB(o)= 2*π*r 576, [mm] x Powierzchnia koła: F( ) x x 4 F= π*r^ , [mm^2] x Długość łuku rozpatrywanego: Ł(łuk) x x 5 Ł = r* β 1 123, [mm] x Długość strzałki łuku rozpatryw.: "s" x x 6 s=r*(1-cos(β 1/2)) 20, [mm] x I.(sposób). Długość cięciwy: "c" x x 7 c=2*(s*(2*r-s))^0,5 114, [mm] x Powierzchnia wycinka koła: F(w.k.) x x 8 F(w.k.) = 0,5*r*Ł 5 680, [mm^2] x Wysokość w trójkącie: "h" x x 9 h=(r^2-(c/2)^2)^0,5 71, [mm] x Powierzchnia trójkąta: F( ) x x 10 F( )=0,5*h*c 4 101, [mm^2] Warunek: β > 0 Warunek: β <=360 PRAWDA PRAWDA Łuk rozpatrywany x Powierzchnia odcinka koła: F(o.k.) x x 11 F(o.k.) = F(w.k.) - F( ) 1 579, [mm^2] Wzór ogólny x II.(sposób). Długość cięciwy: "c" x x c=2*(r*(1-cos(β /2))*(2*r-r*(1-cos(β /2))))^0,5 12 c=2*(r^2*(sin(β 1/2))^2)^0,5 114, [mm] c=2*(r^2*(sin(β /2))^2)^0,5 x Długość strzałki:"s"(łuku przeciwnego ) x x Strzałka "s" ma zwrot przeciwny do łuku rozpatrywanego. 13 dla β1<180[ ]: s = r + h 163, [mm] strzałka 14 Zależność: "c/s"= 5, x Suma długości strzałek s obu łuków: czerwonego i czarnego 15 Zależność: "s/c"= 0, x powinna wynosić: 2*r tj. długość średnicy koła Ø. 16 Zależność: "h/s"= 3, x 17 Poprawność obliczeń: r=h+s 91, [mm] GEOMERIA KULOWA. WZORY DOYCZĄCE ZALEŻNOŚCI: x Pochyłość trójkąta : x x 1(gk) P( ) = l/p 1, brak x Smukłość trójkąta : x x 2(gk) S( ) = (l+p)/c 1, brak x Charakterystyka trójkąta : x x 3(gk) CH( ) = l*(l+p)/(c*p) 1, brak Związek Ćw.I z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
4 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW W NW ZAKRESIE KĄA ŚRODKOWEGO. RÓJKĄ (AOB) WYSĘPUJE W ĆW. I. KĄ ŚRODKOWY. ODMIERZAM OD: 0h (w prawo). str.4 23h r = 91, [mm] PRZYKŁAD NR 1 24h;0h 1h 22h 2h β 1= 77, [ ] Łłuk = 5h+3,94[mm] [mm] Łłuk = 5h*24[mm/h]+3,94[mm] 21h η 1 3h Ł(łuk) = 123,94 [mm] ĆW.II A ĆW.I Ł(łuk) c=(ab) (jest także podstawą ) 20h 90[ ] s(strzałka) 4h 19h r( MK) p 5h h(wysokość ) η 1 B 18h O β 1 l 6h Ł(łuk przeciwny ) 17h s(strzałka łuku przeciwnego ) 7h 16h 8h ĆW.III ĆW.IV 15h 9h η 1= (180[ ]-β 1)/2 = 14h 10h η 1= 51, [ ] η 1= 0, [rad] 13h 11h 12h Związek Ćw.I z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
5 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW W NW ZAKRESIE KĄA ŚRODKOWEGO str.5 OD β >0[ ] DO β =<360[ ]. DANĄ JES YLKO KĄ: β 2= 129, [ ] β 2= 2, [rad] DOWOLNY RÓJKĄ RÓWNORAMIENNY Z KĄEM ŚRODKOWYM "β " W OKRĘGU PRZYRZĄDU "SŁOŃCE MAJÓW" W ZAKRESIE: OD β >0[ ] DO β =<360[ ] Promień przyrządu PRZYKŁAD NR 2 "Słońce Majów" r = 91, [mm] 2.ABELA OBLICZENIOWA DOWOLNEGO RÓJKĄA - URBO Nr wzoru WZÓR: WYNIK: JM: Ogólnie: x Kąt środkowy wg miary łukowej [rad] rójkąt: β 2 1 β 2= 2, [rad] 2 β 2= 129, [ ] x Obwód koła: OB( ) x x 3 OB(o)= 2*π*r 576, [mm] x Powierzchnia koła: F( ) x x 4 F= π*r^ , [mm^2] x Długość łuku: "Łłuk" x x 5 Ł = r* β 2 207, [mm] x Długość strzałki łuku rozpatryw.: "s" x x 6 s=r*(1-cos(β 2/2)) 52, [mm] x Długość cięciwy: "c" x x 7 c=2*(s*(2*r-s))^0,5 165, [mm] x Powierzchnia wycinka koła: F(w.k.) x x 8 F(w.k.) = 0,5*r*Ł 9 514, [mm^2] x Wysokość w trójkącie: "h" x x 9 h=(r^2-(c/2)^2)^0,5 38, [mm] x Powierzchnia trójkąta: F( ) x x 10 F( )=0,5*h*c 3 231, [mm^2] Warunek: β > 0 Warunek: β <=360 PRAWDA PRAWDA Łuk rozpatrywany x Powierzchnia odcinka koła: F(o.k.) x x 11 F(o.k.) = F(w.k.) - F( ) 6 283, [mm^2] Wzór ogólny x II.(sposób). Długość cięciwy: "c" x x c=2*(r*(1-cos(β /2))*(2*r-r*(1-cos(β /2))))^0,5 12 c=2*(r^2*(sin(β 2/2))^2)^0,5 165, [mm] c=2*(r^2*(sin(β /2))^2)^0,5 x Długość strzałki:"s"(łuku przeciwnego ) x x a strzałka "s" ma zwrot przeciwny do łuku rozpatrywanego. 13 dla β2<180[ ]: s = r + h 130, [mm] strzałka 14 Zależność: "c/s"= 3, x Suma długości strzałek s obu łuków: czerwonego i czarnego 15 Zależność: "s/c"= 0, x powinna wynosić: 2*r tj. długość średnicy koła Ø. 16 Zależność: "h/s"= 0, x 17 Poprawność obliczeń: r=h+s 91, [mm] GEOMERIA KULOWA. WZORY DOYCZĄCE ZALEŻNOŚCI: x Pochyłość trójkąta : x x 1(gk) P( ) = l/p 1, brak x Smukłość trójkąta : x x 2(gk) S( ) = (l+p)/c 1, brak x Charakterystyka trójkąta : x x 3(gk) CH( ) = l*(l+p)/(c*p) 1, brak Związek Ćw.I; IV z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
6 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW Z KĄEM ŚRODKOWYM. RÓJKĄ (AOB) WYSĘPUJE W ĆW. I i ĆW. IV. KĄ ŚRODKOWY. ODMIERZAM OD: 0h (w prawo). str.6 23h r = 91, [mm] PRZYKŁAD NR 2 24h;0h 1h 22h 2h 21h A 3h ĆW.II η 2 ĆW.I 20h 4h p Ł(łuk) 19h r= MK c=(ab)(jest także podstawą ) 5h 90[ ] s(strzałka ) 18h β2 O h 6h Ł(łuk przeciwny ) 17h s(strzałka łuku przeciwnego ) l 7h η 2 16h 15h ĆW.III ĆW.IV B 9h Ł=8h+15,58mm 8h Ł=8h*24[mm/h]+15,48mm Ł(łuk)= 207,58 [mm] β 2= 129, [ ] 14h 10h η 2= (180[ ]-β 2)/2 = 13h 11h η 2= 25, [ ] 12h η 2= 0, [rad] Związek Ćw.: I; IV z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
7 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW W NW ZAKRESIE KĄA ŚRODKOWEGO str.7 OD β >0[ ] DO β =<360[ ]. DANĄ JES YLKO KĄ: β 3= 212, [ ] β 3= 3, [rad] DOWOLNY RÓJKĄ RÓWNORAMIENNY Z KĄEM ŚRODKOWYM "β " W OKRĘGU PRZYRZĄDU "SŁOŃCE MAJÓW" W ZAKRESIE: OD β >0[ ] DO β =<360[ ] Promień przyrządu PRZYKŁAD NR 3 "Słońce Majów" r = 91, [mm] 3.ABELA OBLICZENIOWA DOWOLNEGO RÓJKĄA - URBO Nr wzoru WZÓR: WYNIK: JM: Ogólnie: x Kąt środkowy wg miary łukowej [rad] rójkąt: β 3 1 β 3= 3, [rad] 2 β 3= 212, [ ] x Obwód koła: OB( ) x x 3 OB(o)= 2*π*r 576, [mm] x Powierzchnia koła: F( ) x x 4 F= π*r^ , [mm^2] x Długość łuku: "Łłuk" x x 5 Ł = r* β 3 339, [mm] x Długość strzałki łuku rozpatryw.: "s" x x 6 s=r*(1-cos(β 3/2)) 116, [mm] x I.(sposób). Długość cięciwy: "c" x x 7 c=2*(s*(2*r-s))^0,5 176, [mm] x Powierzchnia wycinka koła: F(w.k.) x x 8 F(w.k.) = 0,5*r*Ł , [mm^2] x Wysokość w trójkącie: "h" x x 9 h=(r^2-(c/2)^2)^0,5 25, [mm] x Powierzchnia trójkąta: F( ) x x 10 F( )=0,5*h*c 2 228, [mm^2] Warunek: β > 0 Warunek: β <=360 PRAWDA PRAWDA Łuk rozpatrywany x Powierzchnia odcinka koła: F(o.k.) x x 11 F(o.k.) = F(w.k.) - F( ) , [mm^2] Wzór ogólny x II.(sposób). Długość cięciwy: "c" x x c=2*(r*(1-cos(β /2))*(2*r-r*(1-cos(β /2))))^0,5 12 c=2*(r^2*(sin(β 3/2))^2)^0,5 176, [mm] c=2*(r^2*(sin(β /2))^2)^0,5 x Długość strzałki:"s"(łuku przeciwnego ) x x a strzałka "s" ma zwrot przeciwny do łuku rozpatrywanego. 13 dla β3>180[ ]: s = r - h 66, [mm] strzałka 14 Zależność: "c/s"= 1, x Suma długości strzałek s obu łuków: czerwonego i czarnego 15 Zależność: "s/c"= 0, x powinna wynosić: 2*r tj. długość średnicy koła Ø. 16 Zależność: "h/s"= 0, x 17 Poprawność obliczeń: r=h+s 142, [mm] GEOMERIA KULOWA. WZORY DOYCZĄCE ZALEŻNOŚCI: x Pochyłość trójkąta : x x 1(gk) P( ) = l/p 1, brak x Smukłość trójkąta : x x 2(gk) S( ) = (l+p)/c 1, brak x Charakterystyka trójkąta : x x 3(gk) CH( ) = l*(l+p)/(c*p) 1, brak Związek Ćw.: I; IV; III z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
8 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW Z KĄEM ŚRODKOWYM. RÓJKĄ (AOB) WYSĘPUJE W ĆW.I; ĆW. IV i ĆW.III. KĄ ŚRODKOWY. ODMIERZAM OD: 0h (w prawo). str.8 23h r = 91, [mm] PRZYKŁAD NR 3 24h;0h 1h 22h 2h 21h A 3h ĆW.II ĆW.I 20h η 3 4h I 19h c=(ab)(jest także podstawą ) 5h 18h h(wysok.trój. ) 90[ ] O Ł(łuk) 6h r= MK β 3 s(strzałka)=r+h( ) 17h 7h p η 3 16h Ł=14h+3,25mm B ĆW.III ĆW.IV 8h 15h 9h Ł=14h*24[mm/h]+3,25mm Łłuk= 339,25 [mm] β 3= 212, [ ] 14h 10h η 3= (180[ ]-(360[ ]-β 3))/2= η 3= 16, [ ] 13h 11h η 3= 0, [rad] 12h Związek Ćw.: I; IV; III z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
9 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW W NW ZAKRESIE KĄA ŚRODKOWEGO str.9 OD β >0[ ] DO β =<360[ ]. DANĄ JES YLKO KĄ: β 1= 297, [ ] β = 5, [rad] DOWOLNY RÓJKĄ RÓWNORAMIENNY Z KĄEM ŚRODKOWYM "β " W OKRĘGU PRZYRZĄDU "SŁOŃCE MAJÓW" W ZAKRESIE: OD β >0[ ] DO β =<360[ ] Promień przyrządu PRZYKŁAD NR 1 "Słońce Majów" r = 91, [mm] 1.ABELA OBLICZENIOWA DOWOLNEGO RÓJKĄA - URBO Nr wzoru WZÓR: WYNIK: JM: Ogólnie: x Kąt środkowy wg miary łukowej [rad] rójkąt: β 4 1 β 4= 5, [rad] 2 β 4= 297, [ ] x Obwód koła: OB( ) x x 3 OB(o)= 2*π*r 576, [mm] x Powierzchnia koła: F( ) x x 4 F= π*r^ , [mm^2] x Długość łuku rozpatrywanego: Ł(łuk) x x 5 Ł = r* β 4 476, [mm] x Długość strzałki łuku rozpatryw.: "s" x x 6 s=r*(1-cos(β 4/2)) 170, [mm] x I.(sposób). Długość cięciwy: "c" x x 7 c=2*(s*(2*r-s))^0,5 95, [mm] x Powierzchnia wycinka koła: F(w.k.) x x 8 F(w.k.) = 0,5*r*Ł , [mm^2] x Wysokość w trójkącie: "h" x x 9 h=(r^2-(c/2)^2)^0,5 78, [mm] x Powierzchnia trójkąta: F( ) x x 10 F( )=0,5*h*c 3 726, [mm^2] Warunek: β > 0 Warunek: β <=360 PRAWDA PRAWDA Łuk rozpatrywany x Powierzchnia odcinka koła: F(o.k.) x x 11 F(o.k.) = F(w.k.) - F( ) , [mm^2] Wzór ogólny x II.(sposób). Długość cięciwy: "c" x x c=2*(r*(1-cos(β /2))*(2*r-r*(1-cos(β /2))))^0,5 12 c=2*(r^2*(sin(β 4/2))^2)^0,5 95, [mm] c=2*(r^2*(sin(β /2))^2)^0,5 x Długość strzałki:"s"(łuku przeciwnego ) x x Strzałka "s" ma zwrot przeciwny do łuku rozpatrywanego. 13 dla β4>180[ ]: s = r - h 13, [mm] strzałka 14 Zależność: "c/s"= 0, x Suma długości strzałek s obu łuków: czerwonego i czarnego 15 Zależność: "s/c"= 1, x powinna wynosić: 2*r tj. długość średnicy koła Ø. 16 Zależność: "h/s"= 0, x 17 Poprawność obliczeń: r=h+s 248, [mm] GEOMERIA KULOWA. WZORY DOYCZĄCE ZALEŻNOŚCI: x Pochyłość trójkąta : x x 1(gk) P( ) = l/p 1, brak x Smukłość trójkąta : x x 2(gk) S( ) = (l+p)/c 1, brak x Charakterystyka trójkąta : x x 3(gk) CH( ) = l*(l+p)/(c*p) 1, brak Związek Ćw.I;IV;III;II z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
10 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ DOWOLNYCH RÓJKĄÓW W NW ZAKRESIE KĄA ŚRODKOWEGO. RÓJKĄ (AOB) WYSĘPUJE W ĆW. IV. KĄ ŚRODKOWY. ODMIERZAM OD: 0h (w prawo). str.10 r = 91, [mm] PRZYKŁAD NR 4 β 4= 297, [ ] 24h;0h Łłuk = 19h+20,03[mm] [mm] 23h 1h Łłuk = 19h*24[mm/h]+20,03[mm] Ł(łuk) = 476,03 [mm] 22h 2h 21h ĆW.II 90[ ] η 4 A c=(ab) (jest także podstawą ) s(strzałka łuku przeciwnego ) ĆW.I 3h 20h Ł(łuk przeciwny ) 4h 19h B η 4 h(wysokość ) r( MK) 5h 18h O β 4 6h 17h s(strzałka) 7h 16h Ł(łuk) 8h ĆW.III ĆW.IV 15h 9h η 4= (180[ ]-(360[ ]-β 4))/2= 14h 10h η 4= 58, [ ] η 4= 1, [rad] 13h 11h 12h Związek Ćw.I;IV;III;II z przyrządem "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
11 PRZYRZĄD "SŁOŃCE MAJÓW" DO OBLICZEŃ LOKALIZACJI CELÓW "B" W NW ZAKRESIE KĄA ŚRODKOWEGO. str.11 PRZYSOSOWUJĘ POZNANY WYŻEJ MAERIAŁ DO WYKORZYSANIA GO W PRAKYCE. PRZYKŁADEM JES SAMOLO. Wzór Długość strzałki łuku rozpatryw.: "s" r = 91, [mm] PRZYKŁAD NR 5 6 s=r*(1-cos(ψ/2)) Skala: 1: *β 1= 2, [rad] wtedy: r = ,25 [m] 2*β 1= 162, [ ] 24h;0h liniał roboczy pion. Ł(AC)1 = 2*(5h*24mm/h+9,8mm) 23h 1h do odczytu łuku [mm] Ł(AC)1 = 259,6000 [mm] 20h 22h 2h 2*(η 1) = 85, [ ] 2*(η 1) = 1, [rad] Ł(FD)1= 2*(2h*24mm/h+20,1mm) A 21h 3h Ł(FD)1= 136,300 [mm] ĆW.II ĆW.I s(n)strzałka płn. B5 G liniał roboczy poziomy do odczytu łuku [mm] Ł(GH)1 4h B4 19h B3 5h 18h C strzałki łuków przeciwnych η 1 η 1 β 1 β 1 O B6 X(OE)=h(E)=r-s(E) B2 B1 D Y(B1E)= E h(n)=r-s(n) s(e)strzałka wsch. 6h Ł(CD)1 17h 7h 16h ĆW.III ĆW.IV H 8h 15h 9h 14h 10h 13h 12h 11h Lp. Odczyt łuku Dług.Ł(lp) r Kąt s.β (lp) Cięciwa c1/2 Odczyt łuku Dług.Ł(lp) Kąt s.η (lp) Cięciwa c1/2 Współrzędne punktów docelowych "B": Odl.odc.od bazy U= nr pkt [h] [mm] [mm] [mm] [rad] [ ] [mm] [h] [mm] [mm] [rad] [ ] [mm] X(OE)=r-s(E) Y(BE)=r-s(N) Z L(OB) [mm] L(OB)/r a b c (d:e) f g h (i:j) k l (m:n) p q (q:r) (s:u) (v:x) (y:aa) (ab:ad) (ae) 1 5 9,8 259,600 91,7 2, ,3 90, ,1 151,800 1,656 94,88 67, , , x 63, , ,0 238,000 91,7 2, ,8 88, ,7 132,600 1,446 82,88 60, , , x 73, , ,1 220,200 91,7 2, ,6 85, ,4 185,300 2, ,81 77, , , x 58, , ,1 189,800 91,7 2, ,6 78, ,5 209,000 2, ,63 83, , , x 60, , ,2 122,400 91,7 1,335 76,5 56, ,7 216,600 2, ,38 84, , , x 79, , ,0 288,000 91,7 3, ,0 91, ,7 252,600 2, ,88 89, , , x 17, ,192 Σ(1:6) 3, GEOMERIA KULOWA (gk) POKAZANA NA PŁASZCZYŹNIE (XY) Z UŻYCIEM PRZYRZĄDU: "SŁOŃCE MAJÓW" PRZYKŁAD NR 5. SKŁADA SIĘ Z SIEDMIU PUNKÓW "B" Z NUMERAMI (Lp.) OD 1 DO 6. LO SAMOLOU Spełnienie warunku: Samolot wystartował z pktu "B1". Przeleciał najkrótszą trasę zaliczając cele ("B2"; "B3"; "B4"). Podczas zaliczania ce- r>=l1(ob) PRAWDA lu "B5" wykonał większy skręt w lewo, by zaliczyć najkrótszą trasę. en manewr zapewnił pilotowi świetny wynik. r>=l2(ob) PRAWDA Był manewrem nieco trudniejszym niż z celu "B1" do celu "B2", lecz także udanym. Lot był rejestowany w bazie centr. r>=l3(ob) PRAWDA z zapisem poszczególnych celów, przesyłanym przez pilota sygnał elektroniczny. Niebieska linia pokazuje tor lotu. r>=l4(ob) PRAWDA Lokalizacja celu na przyrządzie "Słońce Majów" r>=l5(ob) PRAWDA r>=l6(ob) PRAWDA ECHNIKA Koszalin dnia 15 października 2011.
12 PRZYRZĄD "SŁOŃCE MAJÓW" DO LOKALIZACJI PUNKÓW "B(lp.)" NA MAPIE - PŁASZCZYZNA (XY). str.12 Cel Ćw. Odczyt łuku poziom."ł" Cel Ćw. Odczyt łuku pion."ł" B1 IV B1 IV 6h*24mm/h + 0,8mm PRZYKŁAD NR 6 12h*24mm/h-5,3mm B2 III 6h*24mm/h + 11,7mm B2 III 12h*24mm/h+0,0mm B3 III 16h*24mm/h - 6,3mm r = 91, [m] B3 III 15h*24mm/h-0,5mm B4 III 18h*24mm/h + 0,00mm 24h;0h B4 III 15h*24mm/h+0,3mm B5 II 20h*24mm/h + 10,3mm 23h 1h B5 II 23h*24mm/h+4,2mm B6 II 19h*24mm/h + 4,6mm B6 II 24h*24mm/h+0,0mm B7 I 5h*24mm/h + 9,3mm 22h 2h B7 I 2h*24mm/h+6,0mm O x 0h*24mm/h + 0,0mm O x 0h*24mm/h+0,0mm 21h 3h ĆW.II ĆW.I 20h B5 4h 19h B6 5h B7 18h B4 O B1 6h B2 17h 7h B3 16h ĆW.III ĆW.IV 8h 15h 9h 14h 10h Lp. Odczyt łuku Dług.Ł(lp) r Kąt środk.β(lp) Odczyt łuku Dług.Ł(lp) Kąt środk.η(lp) Współrzędne celów "B": Odc.proste lotu Odc.od bazy do U= nr pkt [h] [mm] [mm] [mm] [rad] [ ] [h] [mm] [mm] [rad] [ ] X(OE)=r-s(E) Y(BE)=r-s(N) Σ(OB BO) pktu L(OB)[mm] L(OB)/r a b (c:d) (e:f) g h (i:j) k (l:m) (m:n) p (q:r) (s:u) (v:x) (y:aa) (ab:ad) (ae) 1 6 0,8 289,60 91,7 3,16 181, ,3-277,40-3,0-173,38 5, , , , , ,7 311,40 91,7 3,40 194, ,0-288,00-3,1-180,00 0, , , , , ,3 755,40 91,7 8,24 472, ,5-431,00-4,7-269,38-64, , , , , ,0 864,00 91,7 9,42 540, ,3-432,60-4,7-270,38-65, , , , , ,3 980,60 91,7 10,70 612, ,2-824,40-9,0-515,25-19, , , , , ,6 921,20 91,7 10,05 575, ,0-864,00-9,4-540,00 0, , , , , ,3 258,60 91,7 2,82 161, ,0 180,00 2,0 112,50 50, , , , ,578 O 0 0,0 0,00 91,7 0,00 0, ,0 288,00 3,1 180,00 0, , , , ,000 RAZEM: x x x x x x x x x x x 353, , , h 11h Odczyty z okrągłej linijki odczytuję z dokład- 12h nością do 0,1 [mm]. Mierząc od 0h w prawo. GEOMERIA KULOWA (gk) POKAZANA NA PŁASZCZYŹNIE (XY) Z UŻYCIEM PRZYRZĄDU: "SŁOŃCE MAJÓW" PRZYKŁAD NR 6. SKŁADA SIĘ Z SIEDMIU PUNKÓW "B" Z NUMERAMI (Lp.) OD 1 DO 6. LO SAMOLOU Odczytane łuki z lewej str.[h; mm] wpisać niżej w kol. b; c. Odczytane łuki z prawej str.[h; mm] wpisać niżej w kol. k; l. r>=l1(ob) PRAWDA r>=l2(ob) PRAWDA r>=l3(ob) PRAWDA r>=l4(ob) PRAWDA Wszystkie pkty występują w różnych ćwiartkach. Nie są potrzebne obliczenia cięciw. Z obliczeń wynika, że łuki się nakła- dają. Nie ma to żadnego znaczenia. Ważne są obliczenia strzałek: s(e); s(w) poziome; s(n); s(s) pionowe. o one, po ich odjęciu od wielkości promienia r dają rzeczywiste wartości (±) współrzędnych punktów (kolor żółty w tabeli). Ważne jest ustalenie ćwiartki koła, bo od tego zależy poprawny wynik! 5 r>=l5(ob) PRAWDA Spełnienie warunku: Spełnienie warunku: 6 r>=l6(ob) PRAWDA 7 r>=l7(ob) PRAWDA O r>=l(o) PRAWDA Lokalizacja celu na przyrządzie "Słońce Majów" ECHNIKA Koszalin dnia 15 października 2011.
gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii
![gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii](/thumbs/103/159774468.jpg) Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
1/4(koła; okrągu) A A' P'(x)
 skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm
![G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm](/thumbs/71/64805542.jpg) Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
gk T GEOMETRIA WYKREŚLNA PRZESTRZENNA T (GK) W PRAKTYCE. SZTUKA TRASOWANIA CZ.1. Rys.3. Rys.4. Rysunek jest zbyt duży, zmniejszę go na str.2.
 GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
TABELA PRZELICZENIOWA
 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
gk T Zadania nr 2. opracował: inż. Kazimierz Barski dla wszystkich ludzi świata TECHNIKA Koszalin dnia r
 ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną)
 Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną) Zadania zamknięte (jedna poprawna odpowiedź) 1 punkt Wyrażenia algebraiczne Zadanie 1. Wartość wyrażenia 3 x 3x
Bank zadań na egzamin pisemny (wymagania podstawowe; na ocenę dopuszczającą i dostateczną) Zadania zamknięte (jedna poprawna odpowiedź) 1 punkt Wyrażenia algebraiczne Zadanie 1. Wartość wyrażenia 3 x 3x
Planimetria VII. Wymagania egzaminacyjne:
 Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość:
 Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość: A. r 2 + q 2 = p 2 B. p 2 + r 2 = q 2 C. p 2 + q 2 = r 2 D. p + q
Klasa 3. Trójkąty. 1. Trójkąt prostokątny ma przyprostokątne p i q oraz przeciwprostokątną r. Z twierdzenia Pitagorasa wynika równość: A. r 2 + q 2 = p 2 B. p 2 + r 2 = q 2 C. p 2 + q 2 = r 2 D. p + q
Rys.1 pomocniczy. Okrąg z którego powstały łuki na rys.1b.
 OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
9. PLANIMETRIA zadania
 Zad.9.1. Czy boki trójkąta mogą mieć długości: a),6, 10 b) 5,8, 10 9. PLANIMETRIA zadania Zad.9.. Dwa kąty trójkąta mają miary: 5, 40. Jaki to trójkąt: ostrokątny, prostokątny, czy rozwartokątny? Zad.9..
Zad.9.1. Czy boki trójkąta mogą mieć długości: a),6, 10 b) 5,8, 10 9. PLANIMETRIA zadania Zad.9.. Dwa kąty trójkąta mają miary: 5, 40. Jaki to trójkąt: ostrokątny, prostokątny, czy rozwartokątny? Zad.9..
Odcinki, proste, kąty, okręgi i skala
 Odcinki, proste, kąty, okręgi i skala str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Na którym rysunku przedstawiono odcinek? 2. Połącz figurę z jej nazwą. odcinek łamana prosta półprosta
Odcinki, proste, kąty, okręgi i skala str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Na którym rysunku przedstawiono odcinek? 2. Połącz figurę z jej nazwą. odcinek łamana prosta półprosta
KURS MATURA PODSTAWOWA Część 2
 KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
Skrypt 20. Planimetria: Opracowanie L6
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Planimetria: 1. Kąty w
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Planimetria: 1. Kąty w
Radomski Ośrodek Doskonalenia Nauczycieli, Radomski Oddział SNM Test diagnostyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych Wersja A
 Radomski Ośrodek Doskonalenia Nauczycieli, Radomski Oddział SNM Test diagnostyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych Wersja A Imię i nazwisko. Klasa. Drogi uczniu! Masz przed sobą test
Radomski Ośrodek Doskonalenia Nauczycieli, Radomski Oddział SNM Test diagnostyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych Wersja A Imię i nazwisko. Klasa. Drogi uczniu! Masz przed sobą test
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap szkolny 5 listopada 2013 Czas 90 minut
 Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
11. Znajdż równanie prostej prostopadłej do prostej k i przechodzącej przez punkt A = (2;2).
 1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 11 Zadania planimetria
 1 TEST WSTĘPNY 1. (1p) Wysokość rombu o boku długości 6 i kącie ostrym 60 o jest równa: A. 6 3 B. 6 C. 3 3 D. 3 2. (1p) W trójkącie równoramiennym długość ramienia wynosi 10 a podstawa 16. Wysokość opuszczona
1 TEST WSTĘPNY 1. (1p) Wysokość rombu o boku długości 6 i kącie ostrym 60 o jest równa: A. 6 3 B. 6 C. 3 3 D. 3 2. (1p) W trójkącie równoramiennym długość ramienia wynosi 10 a podstawa 16. Wysokość opuszczona
OGÓLNE KRYTERIA OCENIANIA DLA KLASY IV
 OGÓLNE KRYTERIA OCENIANIA DLA KLASY IV LICZBY NATURALNE - umie dodawać i odejmować pamięciowo w zakresie 100 bez przekraczania progu dziesiątkowego, - zna tabliczkę mnożenia i dzielenia w zakresie 100,
OGÓLNE KRYTERIA OCENIANIA DLA KLASY IV LICZBY NATURALNE - umie dodawać i odejmować pamięciowo w zakresie 100 bez przekraczania progu dziesiątkowego, - zna tabliczkę mnożenia i dzielenia w zakresie 100,
KONKURS ZOSTAŃ PITAGORASEM MUM. Podstawowe własności figur geometrycznych na płaszczyźnie
 KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
PLANIMETRIA - TRÓJKATY (2) ZDANIA ŁATWE
 PLANIMETRIA - TRÓJKATY (2) ZDANIA ŁATWE ZADANIE 1 Jeżeli wysokość trójkata równobocznego wynosi 2, to długość jego boku jest równa A) 6 B) 4 3 3 C) 2 3 D) 4 3 ZADANIE 2 Pole trójkata o bokach a = 4 cm
PLANIMETRIA - TRÓJKATY (2) ZDANIA ŁATWE ZADANIE 1 Jeżeli wysokość trójkata równobocznego wynosi 2, to długość jego boku jest równa A) 6 B) 4 3 3 C) 2 3 D) 4 3 ZADANIE 2 Pole trójkata o bokach a = 4 cm
VII Olimpiada Matematyczna Gimnazjalistów
 VII Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa, test próbny www.omg.edu.pl (wrzesień 2011 r.) Rozwiązania zadań testowych 1. Liczba krawędzi pewnego ostrosłupa jest o
VII Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa, test próbny www.omg.edu.pl (wrzesień 2011 r.) Rozwiązania zadań testowych 1. Liczba krawędzi pewnego ostrosłupa jest o
DŁUGOŚĆ OKRĘGU. POLE KOŁA
 Zadania za 1 punkt Zadanie 1.1 Zadanie 1.2 Pole koła o promieniu długości 9 m A. 81π m 2 C. 18π m 2 B. 81 m 2 D. 9π m 2 Długość okręgu o średnicy 4 cm A. 4 cm C. 8π cm B. 4π cm D. 16π cm Zadanie 1.3 Zadanie
Zadania za 1 punkt Zadanie 1.1 Zadanie 1.2 Pole koła o promieniu długości 9 m A. 81π m 2 C. 18π m 2 B. 81 m 2 D. 9π m 2 Długość okręgu o średnicy 4 cm A. 4 cm C. 8π cm B. 4π cm D. 16π cm Zadanie 1.3 Zadanie
Skrypt 24. Geometria analityczna: Opracowanie L5
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 24 Geometria analityczna:
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 24 Geometria analityczna:
ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna
 Arkusz A06 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Wartość wyrażenia 1 3 + 1 + 3
Arkusz A06 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Wartość wyrażenia 1 3 + 1 + 3
Kurs ZDAJ MATURĘ Z MATEMATYKI - MODUŁ 11 Teoria planimetria
 1 Pomimo, że ten dział, to typowa geometria wydawałoby się trudny dział to paradoksalnie troszkę tu odpoczniemy, jeśli chodzi o teorię. Dlaczego? Otóż jak zapewne doskonale wiesz, na maturze otrzymasz
1 Pomimo, że ten dział, to typowa geometria wydawałoby się trudny dział to paradoksalnie troszkę tu odpoczniemy, jeśli chodzi o teorię. Dlaczego? Otóż jak zapewne doskonale wiesz, na maturze otrzymasz
Klasa III technikum Egzamin poprawkowy z matematyki sierpień I. CIĄGI LICZBOWE 1. Pojęcie ciągu liczbowego. b) a n =
 /9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
/9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
Skrypt 13. Koło i okrąg. Opracowanie: GIM3. 1. Okrąg i koło - podstawowe pojęcia (promień, średnica, cięciwa) 2. Wzajemne położenie dwóch okręgów
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 13 Koło i okrąg 1. Okrąg i koło - podstawowe
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 13 Koło i okrąg 1. Okrąg i koło - podstawowe
Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów
 Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów stycznych, c) rozpoznaje trójkąty podobne i wykorzystuje
Planimetria Uczeń: a) stosuje zależności między kątem środkowym i kątem wpisanym, b) korzysta z własności stycznej do okręgu i własności okręgów stycznych, c) rozpoznaje trójkąty podobne i wykorzystuje
Wskazówki do zadań testowych. Matura 2016
 Wskazówki do zadań testowych. Matura 2016 Zadanie 1 la każdej dodatniej liczby a iloraz jest równy.. C.. Korzystamy ze wzoru Zadanie 2 Liczba jest równa.. 2 C.. 3 Zadanie 3 Liczby a i c są dodatnie. Liczba
Wskazówki do zadań testowych. Matura 2016 Zadanie 1 la każdej dodatniej liczby a iloraz jest równy.. C.. Korzystamy ze wzoru Zadanie 2 Liczba jest równa.. 2 C.. 3 Zadanie 3 Liczby a i c są dodatnie. Liczba
Wymagania na egzamin poprawkowy z matematyki dla klasy I A LO (Rok szkolny 2015/16)
 Wymagania na egzamin poprawkowy z matematyki dla klasy I A LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
Wymagania na egzamin poprawkowy z matematyki dla klasy I A LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM PODSTAWOWY. Etapy rozwiązania zadania
 Przykładowy zestaw zadań nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Nr zadania Nr czynności Etapy rozwiązania zadania Liczba punktów Uwagi. Podanie dziedziny funkcji f:
Przykładowy zestaw zadań nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Nr zadania Nr czynności Etapy rozwiązania zadania Liczba punktów Uwagi. Podanie dziedziny funkcji f:
Rys.1. str.1. 48h;0h 18h 19h 20h 21h 22h 46h. 44h r1 4h. 10h. 38h. 34h 14h. 32h 16h. 24h jest linią do przenoszenia szablonów
 Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie
 9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (c.d).
9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (c.d).
Zadanie PP-GP-1 Punkty A, B, C, D i E leżą na okręgu (zob. rysunek). Wiadomo, że DBE = 10
 Zadanie PP-GP-1 Punkty A, B, C, D i E leżą na okręgu (zob. rysunek). Wiadomo, że DBE = 10, ACE = 60, ADB = 40 i BEC = 20. Oblicz miarę kąta CAD. B C A D E Typ szkoły: LO LP T Czy jesteś w klasie z rozszerzonym
Zadanie PP-GP-1 Punkty A, B, C, D i E leżą na okręgu (zob. rysunek). Wiadomo, że DBE = 10, ACE = 60, ADB = 40 i BEC = 20. Oblicz miarę kąta CAD. B C A D E Typ szkoły: LO LP T Czy jesteś w klasie z rozszerzonym
O D P O W I E D Z I D O Z A D A Ń T E S T O W Y C H
 O D P O W I E D Z I D O Z A D A Ń T E S T O W Y C H 1. Niech A = {(x, y) R R : 3 x +4 x = 5 y } będzie zbiorem rozwiązań równania 3 x +4 x = 5 y w liczbach rzeczywistych. Wówczas zbiór A i zbiór N N mają
O D P O W I E D Z I D O Z A D A Ń T E S T O W Y C H 1. Niech A = {(x, y) R R : 3 x +4 x = 5 y } będzie zbiorem rozwiązań równania 3 x +4 x = 5 y w liczbach rzeczywistych. Wówczas zbiór A i zbiór N N mają
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 4 CZERWCA Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
NOWA FORMUŁA EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MMA 2019 UZUPEŁNIA ZDAJĄCY. miejsce na naklejkę UZUPEŁNIA ZESPÓŁ NADZORUJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 4 czerwca 2019
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 4 czerwca 2019
Kąty, trójkąty i czworokąty.
 Kąty, trójkąty i czworokąty. str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Do kartonu wstawiono 3 garnki (zobacz rysunek), których dna mają promienie:13 cm, 15 cm i 11 cm. Podaj długość
Kąty, trójkąty i czworokąty. str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Do kartonu wstawiono 3 garnki (zobacz rysunek), których dna mają promienie:13 cm, 15 cm i 11 cm. Podaj długość
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 MARCA 2019 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Cena towaru bez podatku
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 MARCA 2019 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Cena towaru bez podatku
Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 2015/16) Wykaz zakładanych osiągnięć ucznia klasy I liceum
 Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
MATURA Powtórka do matury z matematyki. Część VII: Planimetria ROZWIĄZANIA. Organizatorzy: MatmaNa6.p l i Dziennik.pl
 MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Organizatorzy: MatmaNa6.p l i Dziennik.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Organizatorzy: MatmaNa6.p l i Dziennik.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
WOJEWÓDZKI KONKURS MATEMATYCZNY
 WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM W ROKU SZKOLNYM 08/09 Schemat punktowania zadania zamknięte Za każdą poprawną odpowiedź uczeń otrzymuje punkt. Numer zadania Poprawna odpowiedź...
WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM W ROKU SZKOLNYM 08/09 Schemat punktowania zadania zamknięte Za każdą poprawną odpowiedź uczeń otrzymuje punkt. Numer zadania Poprawna odpowiedź...
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 8 KWIETNIA 2017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Dla każdej dodatniej
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 8 KWIETNIA 2017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Dla każdej dodatniej
Trójkąty Zad. 0 W trójkącie ABC, AB=40, BC=23, wyznacz AC wiedząc że jest ono sześcianem liczby naturalnej.
 C Trójkąty Zad. 0 W trójkącie ABC, AB=40, BC=23, wyznacz AC wiedząc że jest ono sześcianem liczby naturalnej. Zad. 1 Oblicz pole trójkąta o bokach 13 cm, 14 cm, 15cm. Zad. 2 W trójkącie ABC rys. 1 kąty
C Trójkąty Zad. 0 W trójkącie ABC, AB=40, BC=23, wyznacz AC wiedząc że jest ono sześcianem liczby naturalnej. Zad. 1 Oblicz pole trójkąta o bokach 13 cm, 14 cm, 15cm. Zad. 2 W trójkącie ABC rys. 1 kąty
MATURA Przygotowanie do matury z matematyki
 MATURA 2012 Przygotowanie do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej. Witaj,
MATURA 2012 Przygotowanie do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej. Witaj,
Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 2017/2018.
 Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 017/018 19 grudnia 017 1 1 Klasy pierwsze - poziom podstawowy 1. Dane są zbiory
Zadania przygotowawcze do konkursu o tytuł NAJLEPSZEGO MATEMATYKA KLAS PIERWSZYCH I DRUGICH POWIATU BOCHEŃSKIEGO rok szk. 017/018 19 grudnia 017 1 1 Klasy pierwsze - poziom podstawowy 1. Dane są zbiory
PLANIMETRIA pp 2015/16. WŁASNOŚCI TRÓJKĄTÓW (nierówność trójkąta, odcinek łączący środki boków, środkowe, wysokość z kąta prostego)
 PLNIMETRI pp 2015/16 WŁSNOŚI TRÓJKĄTÓW (nierówność trójkąta, odcinek łączący środki boków, środkowe, wysokość z kąta prostego) Zad.1 Wyznacz kąty trójkąta jeżeli stosunek ich miar wynosi 5:3:1. Zad.2 Znajdź
PLNIMETRI pp 2015/16 WŁSNOŚI TRÓJKĄTÓW (nierówność trójkąta, odcinek łączący środki boków, środkowe, wysokość z kąta prostego) Zad.1 Wyznacz kąty trójkąta jeżeli stosunek ich miar wynosi 5:3:1. Zad.2 Znajdź
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 1 KWIETNIA 017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Suma sześciu kolejnych
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 1 KWIETNIA 017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Suma sześciu kolejnych
UZUPEŁNIA ZDAJĄCY miejsce na naklejkę
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 2 czerwca 2017
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 2 czerwca 2017
LUBELSKA PRÓBA PRZED MATURĄ 2013
 LUBELSKA PRÓBA PRZED MATURĄ 03 MATEMATYKA - poziom podstawowy STYCZEŃ 03 Instrukcja dla zdającego Czas pracy: 70 minut. Sprawdź, czy arkusz zawiera 4 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu
LUBELSKA PRÓBA PRZED MATURĄ 03 MATEMATYKA - poziom podstawowy STYCZEŃ 03 Instrukcja dla zdającego Czas pracy: 70 minut. Sprawdź, czy arkusz zawiera 4 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1
 PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
gk T MAŁA C 18h O 6h F
 ROZWIĄZANIE ZADANIA TPO.Nr 1. (TYLKO PRZEZ ORŁÓW) Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). TO JEST MÓJ I TWÓJ EGZAMIN Z MYŚLENIA (). str.25 1 Plik cz.i. rozwiązania zadania jest przeciążony ilością
ROZWIĄZANIE ZADANIA TPO.Nr 1. (TYLKO PRZEZ ORŁÓW) Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). TO JEST MÓJ I TWÓJ EGZAMIN Z MYŚLENIA (). str.25 1 Plik cz.i. rozwiązania zadania jest przeciążony ilością
Ćwiczenia z Geometrii I, czerwiec 2006 r.
 Waldemar ompe echy przystawania trójkątów 1. unkt leży na przekątnej kwadratu (rys. 1). unkty i R są rzutami prostokątnymi punktu odpowiednio na proste i. Wykazać, że = R. R 2. any jest trójkąt ostrokątny,
Waldemar ompe echy przystawania trójkątów 1. unkt leży na przekątnej kwadratu (rys. 1). unkty i R są rzutami prostokątnymi punktu odpowiednio na proste i. Wykazać, że = R. R 2. any jest trójkąt ostrokątny,
IX Olimpiada Matematyczna Gimnazjalistów
 IX Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa www.omg.edu.pl (3 października 2013 r.) Rozwiązania zadań testowych 1. Liczba 3 9 3 27 jest a) niewymierna; b) równa 3 27;
IX Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa www.omg.edu.pl (3 października 2013 r.) Rozwiązania zadań testowych 1. Liczba 3 9 3 27 jest a) niewymierna; b) równa 3 27;
Skrypt 29. Przygotowanie do egzaminu Koło i okrąg. Opracowanie: GIM3. 1. Obliczanie obwodów i pól kół - powtórzenie
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 29 Przygotowanie do egzaminu Koło i okrąg
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 29 Przygotowanie do egzaminu Koło i okrąg
EGZAMIN MATURALNY Z MATEMATYKI
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
OCENIANIE ARKUSZA POZIOM ROZSZERZONY
 Numer zadania... Etapy rozwiązania zadania Przekształcenie wzoru funkcji do żądanej postaci f( x) = + lub f( x) x = x. I sposób rozwiązania podpunktu b). Zapisanie wzoru funkcji w postaci sumy OCENIANIE
Numer zadania... Etapy rozwiązania zadania Przekształcenie wzoru funkcji do żądanej postaci f( x) = + lub f( x) x = x. I sposób rozwiązania podpunktu b). Zapisanie wzoru funkcji w postaci sumy OCENIANIE
V Konkurs Matematyczny Politechniki Białostockiej
 V Konkurs Matematyczny Politechniki Białostockiej Rozwiązania - klasy drugie 1. Znaleźć wszystkie pary liczb całkowitych (x, y) spełniające nierówności x + 1 + y 4 x + y 4 5 x 4 + y 1 > 4. Ważne jest zauważenie,
V Konkurs Matematyczny Politechniki Białostockiej Rozwiązania - klasy drugie 1. Znaleźć wszystkie pary liczb całkowitych (x, y) spełniające nierówności x + 1 + y 4 x + y 4 5 x 4 + y 1 > 4. Ważne jest zauważenie,
Zadania otwarte krótkiej odpowiedzi na dowodzenie
 Zadania otwarte krótkiej odpowiedzi na dowodzenie Zadanie 1. Na bokach trójkąta równobocznego ABC tak wybrano punkty E, F oraz D, że AE = BF = CD = 1 AB (rysunek obok). a) Udowodnij, że trójkąt EFD jest
Zadania otwarte krótkiej odpowiedzi na dowodzenie Zadanie 1. Na bokach trójkąta równobocznego ABC tak wybrano punkty E, F oraz D, że AE = BF = CD = 1 AB (rysunek obok). a) Udowodnij, że trójkąt EFD jest
gk T Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (gk), w sposób praktyczny. Rys.2a
 Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Matematyka podstawowa VII Planimetria Teoria
 Matematyka podstawowa VII Planimetria Teoria 1. Rodzaje kątów: a) Kąty wierzchołkowe; tworzą je dwie przecinające się proste, mają takie same miary. b) Kąty przyległe; mają wspólne jedno ramię, ich suma
Matematyka podstawowa VII Planimetria Teoria 1. Rodzaje kątów: a) Kąty wierzchołkowe; tworzą je dwie przecinające się proste, mają takie same miary. b) Kąty przyległe; mają wspólne jedno ramię, ich suma
ZADANIE 2 Czy istnieje taki wielokat, który ma 2 razy więcej przekatnych niż boków?
 PLANIMETRIA 2 ZADANIE 1 W rombie jedna z przekatnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekatnych pole rombu jest większe od 5cm 2? 1 ZADANIE 2 Czy istnieje taki wielokat, który ma 2
PLANIMETRIA 2 ZADANIE 1 W rombie jedna z przekatnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekatnych pole rombu jest większe od 5cm 2? 1 ZADANIE 2 Czy istnieje taki wielokat, który ma 2
Matematyka rozszerzona matura 2017
 Matematyka rozszerzona matura 017 Zadanie 1 Liczba ( 3 + 3) jest równa A. B. 4 C. 3 D. 3 ( 3 + 3) = 3 ( 3)( + 3) + + 3 = A. 3 4 3 + + 3 = 4 1 = 4 = Zadanie. Nieskończony ciąg liczbowy jest określony wzorem
Matematyka rozszerzona matura 017 Zadanie 1 Liczba ( 3 + 3) jest równa A. B. 4 C. 3 D. 3 ( 3 + 3) = 3 ( 3)( + 3) + + 3 = A. 3 4 3 + + 3 = 4 1 = 4 = Zadanie. Nieskończony ciąg liczbowy jest określony wzorem
Praca klasowa nr 2 - figury geometryczne (klasa 6)
 Praca klasowa nr 2 - figury geometryczne (klasa 6) MARIUSZ WRÓBLEWSKI IMIĘ I NAZWISKO: KLASA: GRUPA A 1. Dany jest równoległobok ABCD. Narysuj za pomocą linijki i ekierki odcinek BF prostopadły do odcinka
Praca klasowa nr 2 - figury geometryczne (klasa 6) MARIUSZ WRÓBLEWSKI IMIĘ I NAZWISKO: KLASA: GRUPA A 1. Dany jest równoległobok ABCD. Narysuj za pomocą linijki i ekierki odcinek BF prostopadły do odcinka
LUBELSKA PRÓBA PRZED MATURĄ klasa 2 poziom podstawowy
 Kod ucznia.. M A T E M A T Y K A klasa 2 - pp MAJ 2019 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 16 stron. Ewentualny brak zgłoś przewodniczącemu zespołu nadzorującego
Kod ucznia.. M A T E M A T Y K A klasa 2 - pp MAJ 2019 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz zawiera 16 stron. Ewentualny brak zgłoś przewodniczącemu zespołu nadzorującego
OCENIANIE ARKUSZA POZIOM ROZSZERZONY
 OCENIANIE ARKUSZA POZIOM ROZSZERZONY Numer zadania... Etapy rozwiązania zadania Przekształcenie wzoru funkcji do żądanej postaci f( x) = + lub f( x) =. x x I sposób rozwiązania podpunktu b). Zapisanie
OCENIANIE ARKUSZA POZIOM ROZSZERZONY Numer zadania... Etapy rozwiązania zadania Przekształcenie wzoru funkcji do żądanej postaci f( x) = + lub f( x) =. x x I sposób rozwiązania podpunktu b). Zapisanie
XV WOJEWÓDZKI KONKURS Z MATEMATYKI
 XV WOJEWÓDZKI KONKURS Z MATEMATYKI DLA UCZNIÓW DOTYCHCZASOWYCH GIMNAZJÓW ORAZ KLAS DOTYCHCZASOWYCH GIMNAZJÓW PROWADZONYCH W SZKOŁACH INNEGO TYPU WOJEWÓDZTWA ŚWIĘTOKRZYSKIEGO W ROKU SZKOLNYM 2017/2018 ETAP
XV WOJEWÓDZKI KONKURS Z MATEMATYKI DLA UCZNIÓW DOTYCHCZASOWYCH GIMNAZJÓW ORAZ KLAS DOTYCHCZASOWYCH GIMNAZJÓW PROWADZONYCH W SZKOŁACH INNEGO TYPU WOJEWÓDZTWA ŚWIĘTOKRZYSKIEGO W ROKU SZKOLNYM 2017/2018 ETAP
Równania prostych i krzywych; współrzędne punktu
 Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
PRÓBNY EGZAMIN MATURALNY Z NOWĄ ERĄ
 KOD ZDAJĄCEGO WPISUJE ZDAJĄCY symbol klasy symbol zdającego PRÓBNY EGZAMIN MATURALNY Z NOWĄ ERĄ MATEMATYKA-POZIOM PODSTAWOWY dysleksja Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera
KOD ZDAJĄCEGO WPISUJE ZDAJĄCY symbol klasy symbol zdającego PRÓBNY EGZAMIN MATURALNY Z NOWĄ ERĄ MATEMATYKA-POZIOM PODSTAWOWY dysleksja Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera
MATERIAŁ ĆWICZENIOWY Z MATEMATYKI
 Materiał ćwiczeniowy zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Materiał ćwiczeniowy chroniony jest prawem autorskim. Materiału nie naleŝy powielać ani udostępniać w Ŝadnej formie
Materiał ćwiczeniowy zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Materiał ćwiczeniowy chroniony jest prawem autorskim. Materiału nie naleŝy powielać ani udostępniać w Ŝadnej formie
UZUPEŁNIA ZDAJĄCY miejsce na naklejkę
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 22 sierpnia
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 22 sierpnia
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI PRZED MATURĄ MAJ 2017 POZIOM PODSTAWOWY Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 15 stron (zadania 1 33). 2. Rozwiązania zadań wpisuj
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI PRZED MATURĄ MAJ 2017 POZIOM PODSTAWOWY Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 15 stron (zadania 1 33). 2. Rozwiązania zadań wpisuj
VIII. ZBIÓR PRZYKŁADOWYCH ZADAŃ MATURALNYCH
 VIII. ZIÓR PRZYKŁDOWYCH ZDŃ MTURLNYCH ZDNI ZMKNIĘTE Zadanie. ( pkt) 0 90 Liczba 9 jest równa 0.. 00 C. 0 9 D. 700 7 Zadanie. 8 ( pkt) Liczba 9 jest równa.. 9 C. D. 5 Zadanie. ( pkt) Liczba log jest równa.
VIII. ZIÓR PRZYKŁDOWYCH ZDŃ MTURLNYCH ZDNI ZMKNIĘTE Zadanie. ( pkt) 0 90 Liczba 9 jest równa 0.. 00 C. 0 9 D. 700 7 Zadanie. 8 ( pkt) Liczba 9 jest równa.. 9 C. D. 5 Zadanie. ( pkt) Liczba log jest równa.
MATURA Powtórka do matury z matematyki. Część VII: Planimetria ODPOWIEDZI. Organizatorzy: MatmaNa6.pl, naszemiasto.pl
 MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ODPOWIEDZI Organizatorzy: MatmaNa6.pl, naszemiasto.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
MATURA 2012 Powtórka do matury z matematyki Część VII: Planimetria ODPOWIEDZI Organizatorzy: MatmaNa6.pl, naszemiasto.pl Witaj, otrzymałeś już siódmą z dziesięciu części materiałów powtórkowych do matury
Rysunek 1. Udowodnij, że AB CD = BC DA. Rysunek 2. Po inwersji o środku w punkcie E. Rysunek 3. Po inwersji o środku w punkcie A
 g H e D c H' E g' h e' O d A C' d' C A' F' f' I' G' B' G I F f INWERSJA Inwersją o środku O i promieniu r nazywamy takie przekształcenie płaszczyzny (bez punktu O), które każdemu punktowi X O przyporządkowuje
g H e D c H' E g' h e' O d A C' d' C A' F' f' I' G' B' G I F f INWERSJA Inwersją o środku O i promieniu r nazywamy takie przekształcenie płaszczyzny (bez punktu O), które każdemu punktowi X O przyporządkowuje
ROZWIĄZANIA DO ZADAŃ
 TURNIRJ MATEMATYCZNY ELIPSA dla klas LO ROZWIĄZANIA DO ZADAŃ Zadanie. (2 pkt.) Dla jakich wartości parametru m (m R), część wspólna przedziałów A = (, m m i B = 2m 2, + ) jest zbiorem pustym? / Jeśli A
TURNIRJ MATEMATYCZNY ELIPSA dla klas LO ROZWIĄZANIA DO ZADAŃ Zadanie. (2 pkt.) Dla jakich wartości parametru m (m R), część wspólna przedziałów A = (, m m i B = 2m 2, + ) jest zbiorem pustym? / Jeśli A
NOWA FORMUŁA EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY MMA 2019 UZUPEŁNIA ZDAJĄCY. miejsce na naklejkę
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 4 czerwca 2019
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2019 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 4 czerwca 2019
OBLICZENIE PRZEKROJU WALCA PO CIĘCIU SKOŚNYM. Rysunki i obliczenia dotyczą walca
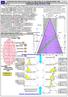 Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Test diagnostyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych Wersja A
 Test diagnostyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych Wersja A Imię i nazwisko. Klasa. Drogi uczniu! Masz przed sobą test sprawdzający Twoją wiedzę i umiejętności, które nabyłeś na wcześniejszych
Test diagnostyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych Wersja A Imię i nazwisko. Klasa. Drogi uczniu! Masz przed sobą test sprawdzający Twoją wiedzę i umiejętności, które nabyłeś na wcześniejszych
Ostrosłupy ( ) Zad. 4: Jedna z krawędzi ostrosłupa trójkątnego ma długość 2, a pozostałe 4. Znajdź objętość tego ostrosłupa. Odp.: V =
 Ostrosłupy Zad 1: W ostrosłupie prawidłowym trójkątnym kwadrat długości krawędzi podstawy, kwadrat długości wysokości ostrosłupa i kwadrat długości krawędzi bocznej są kolejnymi wyrazami ciągu arytmetycznego
Ostrosłupy Zad 1: W ostrosłupie prawidłowym trójkątnym kwadrat długości krawędzi podstawy, kwadrat długości wysokości ostrosłupa i kwadrat długości krawędzi bocznej są kolejnymi wyrazami ciągu arytmetycznego
Geometria. Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7
 Geometria Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7 W tym przypadku możemy wykonać szkic pięciokąta i policzyć przekątne: Zadanie. Promień okręgu opisanego na kwadracie
Geometria Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7 W tym przypadku możemy wykonać szkic pięciokąta i policzyć przekątne: Zadanie. Promień okręgu opisanego na kwadracie
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami, łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej ł
 1. Dane Droga klasy technicznej G 1/2, Vp = 60 km/h poza terenem zabudowanym Prędkość miarodajna: Vm = 90 km/h (Vm = 100 km/h dla krętości trasy = 53,40 /km i dla drogi o szerokości jezdni 7,0 m bez utwardzonych
1. Dane Droga klasy technicznej G 1/2, Vp = 60 km/h poza terenem zabudowanym Prędkość miarodajna: Vm = 90 km/h (Vm = 100 km/h dla krętości trasy = 53,40 /km i dla drogi o szerokości jezdni 7,0 m bez utwardzonych
METODA RZUTÓW MONGE A (II CZ.)
 RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
EGZAMIN MATURALNY Z MATEMATYKI
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 2016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
Geometria analityczna
 Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna
 Arkusz A05 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Ułamek 5+2 5 2 ma wartość: A.
Arkusz A05 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Ułamek 5+2 5 2 ma wartość: A.
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii. Trójkąty. Trójkąt dowolny. Wielokąty trygonometria 1.
 Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Wielokąt wypukły miara każdego kąt wewnętrznego jest mniejsza od 180 o. Liczba przekątnych: n*(n-2) Suma kątów wewnętrznych wielokąta
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Wielokąt wypukły miara każdego kąt wewnętrznego jest mniejsza od 180 o. Liczba przekątnych: n*(n-2) Suma kątów wewnętrznych wielokąta
O kula. w (gks). Rzutnie: (XZ); (YZ); (XY). A B (YZ) (XY) D sześciana
 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
Czas pracy 170 minut
 ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 01 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 01 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
POWIERZCHNIA CAŁK. I KONSTRUKCJA 1 ELEM. DENNICY ELIPSOIDALNEJ WYPUKŁEJ W WYK. "TURBO"
 POWIERZCHNIA CAŁK. I KONSRUKCJA 1 ELEM. DENNICY ELIPSOIDALNEJ WYPUKŁEJ W WYK. "URBO" str.1. woje dane wpisz w zielone pola: Dz = 1224 h = 360 G= 50 L= 3280 Zz= 17 zakład Zm= 3 Zd= 5 Pas = 120 A= 662 B=
POWIERZCHNIA CAŁK. I KONSRUKCJA 1 ELEM. DENNICY ELIPSOIDALNEJ WYPUKŁEJ W WYK. "URBO" str.1. woje dane wpisz w zielone pola: Dz = 1224 h = 360 G= 50 L= 3280 Zz= 17 zakład Zm= 3 Zd= 5 Pas = 120 A= 662 B=
LUBELSKA PRÓBA PRZED MATURĄ klasa 2 poziom podstawowy
 Kod ucznia lub Nazwisko i imię M A T E M A T Y K A klasa - pp MAJA 018 Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera 16 stron (zadania 1-4). Ewentualny brak zgłoś przewodniczącemu zespołu nadzorującego
Kod ucznia lub Nazwisko i imię M A T E M A T Y K A klasa - pp MAJA 018 Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera 16 stron (zadania 1-4). Ewentualny brak zgłoś przewodniczącemu zespołu nadzorującego
Planimetria poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie
 Planimetria poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/) 1. W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu
Planimetria poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/) 1. W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 WPISUJE ZDAJĄCY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY PRZED MATURĄ MAJ 2015 1. Sprawdź, czy arkusz egzaminacyjny zawiera 22 strony ( zadania 1 19). Ewentualny brak zgłoś przewodniczącemu
WPISUJE ZDAJĄCY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY PRZED MATURĄ MAJ 2015 1. Sprawdź, czy arkusz egzaminacyjny zawiera 22 strony ( zadania 1 19). Ewentualny brak zgłoś przewodniczącemu
Mini tablice matematyczne. Figury geometryczne
 Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
GEOMETRIA ELEMENTARNA
 Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
