gk T Rozwiązanie Zadania nr1 - uzupełnienie

Transkrypt

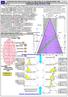
1 TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R) str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka prostego, na ***KULA*** położenie równoległe tego stożka względem płaszczyzny rzutu prostopadłego (XZ). Rys.10 odiega od pozostałyc rysunków tego pliku. Gdyym próował zacować wymiary, to duże koło, nie pł.(xz) zmieściłoy się tej stronie. Stąd, największą wartością tej strony pliku, jest zawarta w niej wiedza. aktywna (+)Z Na odcylonej, czarnej osi ędącej na pł.poziomie znajdują się czarne nieoznaczone punkty. Każdy (+)X z tyc punktów znalazł się nieprzypadkowo na tej osi, ponieważ znajduje się na linii pionowej pkt.: Patrzymy I; II; III; IV; V; VI i VII. Strzałki czarne (wskazujące) pokazują te punkty na rzutni. Natomiast liniały (-)Y (+)Y różowe 0,25 wskazują kierunek przywracania rzeczywistego wymiaru wysokości tego stożka. Ccę Państwu przypomnieć, iż ten temat przeraialiśmy w poprzednic plikac. Dla przypomnienia Trzy okręgi, ukazujące cciałym podać słowa: CHINKA w geometrii kulowej. (-)X różowe cięciwy na osi Natomiast, nie pokazałem w całości przejścia ze stożka z otaczającymi (-)Z odcylonego stożka. go punktami (też odcylonymi) do wymiarów rze- czywistyc. Stąd, powstał ten rysunek. Temu rysunkowi ędzie towarzyszyła orientacja przestrzenna (np.lewym rogu). Z prawej strony narysowałem strzałki z dwoma grotami każda. Są to rzeczywiste wymiary odległości poszczególnyc punktów od osi poziomej stożka, ponieważ oś stożka leży na płaszczyźnie poziomej. Stożek odcylony Bardzo ważną funkcję pełni pozioma czarna linia osi stożka w sensie geometrycznym symatrii. Codzi tutaj o zmianę położenia tyc punktów, gdy ędę cciał pokazać rzut prostokątny 2 4 na pł.(xy)mapę widzianą od spodu. Mam taki za miar pokazać na str.11 tego pliku. I' II' III' IV' V' VI' I IV (II) (IV) (V) V (I) (VII) II VII (III) (VI) III TRÓJKĄT LGICZNY z osią symetrii od pkt. VI T Rozwiązanie Zadania nr1 - uzupełnienie Romana - imię mojej małżonki Koszalin dnia r

2 TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R) str.2 RIENTACJA Część górna Rys.11 pł.(xy) c.dalszy PRZYKŁAD Nr1 PRZESTRZENNA Rys.11 podzieliłem na dwie części: górną i dolną. Codzi o punkty. Poszczególnym punktom nadałem kolory, y się różniły od sieie. Punkty: I; II; III; ***KULA*** IV; V; VI; VII (czarne kropki) są punktami zacowyjące odcylenie w rzucie prostokątnym na pł.(xz). Punkty (nieieskie kropki) są punktami na osi poziomej (X) pł.(xz): I'; II'; III'; IV'; V'; VI'; VII'. Punkty (czarne kropki) są wyznaczane prostopadle od punktów nieieskic osi stożka: I"; II"; III": IV"; V"; pł.(xy) VI"; VII". To te punkty ędą decydowały o orocie stożka o kąt 180[ ], y pokazać stronę odwrotną stożka, już na MAPIE tj. pł.(xy). Punkty aktywna (+)Z (czarne kropki) są identycznie oddalone od osi: I"; II"; III"; IV"; V; VI"; VII", jak punkty oznaczone kolorem zielonym. Położenie tyc punktów jest (+)X pokazane ez ic odcylenia. Gdy spojrzymy na pł.(xy) od dołu, ędziemy widzieli punkty o kolorze zielonym. Natomiast, gdy spojrzymy na tę Rys.2 samą pł.(xy) z góry, wtedy zoaczymy punkty oznaczone (-)Y (+)Y kolorem jasnonieieskim. Nie potrafię lepiej opisać, to co ędę roić. Trzea to zoaczyć VI" Mam wrażenie, jakym kiedyś tego rodzaju zadanie roił. Być (-)X może, granica między podświadomością a świadomością (-)Z Patrzymy staje się powoli niedostrzegalna. Faktem jest, że w żadne cuda nie wierzę, jak większość z Państwa. III" Różowe liniały, na rysunku, przesuwają punkty na właściwe miejsce na osi stożka, gdzie wyzywają się odcyleń. (III) (VI) Trocę niezręcznie rzmią słowa: właściwe miejsce. To nie I'" oznacza, że punkt znajdował się nie tam gdzie trzea. Był we II"' właściwym miejscu, lecz zmienia swoje położenie. V" VII" IV" (I) (VII) (II) (IV) (V) I' II' III' IV' V' VI' pł.(xy) aktywna IV (II) (IV) (V) IV" V (I) (VII) II V" VII I" I II" VII" (III) RIENTACJA PRZESTRZENNA ***KULA*** III (+)Z Patrzymy (+)X III" VI VI" (-)Y (+)Y Dzisiaj jest już 02.stycznia 2015r. Erupcja wulkanu mojej wyoraźni po pliku: Skrypt (R) yła tak ogromna, że wywołała lawinę plików. Nawet Część dolna Rys.11 pł.(xz) teraz przejdę do pliku:" Magazynu Wiedzy Cz.I. geometrii kulowej () ". (-)X Ma zawierać coś, co jest ermetycznie zamknięte i ściśle powiązane ze soą. (-)Z (VI) T Rozwiązanie Zadania nr1 - uzupełnienie Koszalin dnia r

3 ELIPSA PMARAŃCZWA DCHYLNA WZGLĘDEM LINII PZIMEJ I PINWEJ. JEST PDSTAWĄ STŻKA DCHYLNEG. NIE MA WYZNACZNEG WIERZCHŁKA. str.3 ELIPSA jest w tym przypadku kołem odcylonym względem płaszczyzny poziomej i płaszczyzny pionowej. Nie wyznaczyłem jej wierzcołka. Będzie stożkiem prostym, orotowym. Na kole w którym wpisałem tę ELIPSĘ znajdują się ograniczniki kończące się czerwonymi krzyżykami. Sama ELIPSA ma dwie osie, które postanowiłem pokazać Państwu. PRZYKŁAD NR I Rys.3 Mam zamiar rozłożyć, na podstawie tej ELIPSY, dwie składowe układy ELIPS, oparte na średnicy koła. Wymiary wysokości TRÓJKĄTÓW LGICZNYCH, są związane z promieniami "r" koła. Czyli, mierzone od punktu. T Rozwiązanie Zadania nr1 - Tylko Przez rłów. Koszalin dnia 22 stycznia 2015r

4 RZKŁAD ELIPSY NA DWIE SKŁADWE, KTÓRE SĄ ŚCIŚLE ZWIĄZANE Z RYS.3, GDZIE SĄ GRANICZNIKI. str.4 Rys.4 E W2 Pomarańczową ELIPSĘ zamieniłem na dwie składowe ELIPSY. ELIPSY na rys.4 pomarańczowa ma owódkę czarną, a E2 fioletową. Prawie nacodzą na sieie. Do tyc ELIPS E1 i E2 narysowałem osie duże. Postanowiłem ten sam wymiar przenieść na ic wysokości od punktu, pod kątem prostym. W ten sposó uzyskałem wymiary 1 i 2, które są soie równe. Na rys.5 już ez ELIPS żółtyc pokazuję rozkład składowyc TRÓJKĄTA LGICZ- NEG. Teraz przejdę do wyznaczenia TRÓJKĄTA LGICZNEG, na podstawie jego składowyc - Rys.6. W1 E2 Rys.5 W W1 5 W2 2 Składowa pionowa TRÓJKĄTA LGICZNEG W2 T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 23 stycznia 2015r

5 RZKŁAD ELIPSY NA DWIE SKŁADWE, KTÓRE SĄ ŚCIŚLE ZWIĄZANE Z RYS.3, GDZIE SĄ GRANICZNIKI. str.5 Rys.6 W W1 5 W2 2 Składowa pionowa TRÓJKĄTA LGICZNEG W W2 T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 23 stycznia 2015r

6 ZBUDWANIE TRÓJKĄTA LGICZNEG Z DWÓCH SKŁADWYCH TRÓJKĄTÓW LGICZNYCH. str.6 Składowa pozioma TRÓJKĄTA LGICZNEG Rys.7 7 W TRÓJKĄT LGICZNY tworzące stożka. W1 5 W2 2 Składowa pionowa TRÓJKĄTA LGICZNEG W W2 Proszę zwrócić uwagę na położenie czterec punktów:, W1, W, W2. Rozkład tyc punktów wskazuje o istnieniu kwadratu. Natomiast punkty i W wyznaczają przekątną "" tego kwadratu. Zastosuję wzór Pitagorasa: ((2*r)^2+(2*r)^2)^0,5 j. (8*r^2)^0,5 j. Dla r 10 j. 28, j. T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 23 stycznia 2015r

7 TRÓJKĄT LGICZNY WRAZ Z PRPRCJĄ DSKNAŁĄ, WYRAŻNA "r/". str.7 Rys.8 W Rys.9 r/ 0, F2 *r 282, j^2 β /2 β /2 Dla: r 10 j. F2/r 28, j. r/ atan(β/2) β /2 atan(r/) W φ r r φ φ (180 -β)/2 β/2 0, [rad] φ 70, [ ] β/2 19, [ ] β 38, [ ] Rys.10 &45 2*r/sin& 28, j. 2*r/cos& 28, j. Stąd: atan& 1 & 0, [rad] 2*r & 45, [ ] F1 F1 (2*r)^2/2 2*r^2 Dla: r 10 j. F1 338,00 [j^2] &45 2*r 90 T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 24 stycznia 2015r

8 TRÓJKĄT LGICZNY WRAZ ZE STAŁĄ PRPRCJĄ, WYRAŻNĄ "r/". str.8 Rys.11 Rys.12 DANE: r 10 j. 28, j. a 2*r 20 j. - a 8, j. W a + 28, j. r W a a + 2^0,5 a + 1, a a ζ a - 2^0,5 a - 1, β /2 β /2 β /2 β /2 a STAŁA PRPRCJNALNA: rosnący Fraktal malejący a + a - Poszukaj a na str.12. wg walca STAŁA PRPRCJNALNA: Fraktal rosnący a ζ a r 0 0, , wg stożka a - a - r 0 0, , Dla n 1; 2; 3 lu dowolne liczy dziesiętne. ζ (a - 2*) φ φ φ φ Występowanie FRAKTALI jest przy- 2*r Ø (a - 2*)*2^0,5) padkowe, nie mające nic wspólnego 2*r Ø a z celem mojego opracowania. Na rys.10 pokazuję przede wszystkim TRÓJKĄT Rys.11 ofituje w różnego rodzaju kominacje. Z pewnością nie ma nic wspólnego ze ZŁTYM DCINKIEM, LGICZNY na tle walca, którego parametry są takie same. czy ŚWIĘTĄ GEMETRIĄ. Wystarczy stała proporcjonalna: wysokości (a + ), do średnicy walca Ø. Przy Codzi o postawę 2*r Ø i o wysokość "". tym dodatkowo otrzymuję w prezencie "mniejszy walec" o podonyc parametrac, związany ze stałą pro- Ten układ relacji między promieniem podstawy "r" i wyso- porcjonalną: (a-)/. kością walca, czy stożka nigdy się nie zmienia. Zawsze ędzie taka sama: r/ 0, , to Reasumując powyższą pracę, ccę żey yło wiadomo, że jakiekolwiek położenie ELIPSY wpisanej ATAN(r/) 0, [rad] Wówczas kąt tworzą- w koło, należy rozłożyć na dwa składowe TRÓJKĄTY LGICZNE związane z linią pionową i poziomą danej cy stożek wyosi: β /2 19, [ ] płaszczyzny, na której występują. W przyszłości te rysunki, czy oliczenia ędą uproszczone. T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 28 stycznia 2015r

9 ELIPSA PMARAŃCZWA DCHYLNA WZGLĘDEM LINII PZIMEJ I PINWEJ. JEST PDSTAWĄ STŻKA DCHYLNEG. NIE MA WYZNACZNEG WIERZCHŁKA. str.9 PRZYKŁAD NR II Rys.13 Rys.14 ELIPSA wpisana w koło jest inna niż ELIPSA na rys.3. Jej osie także nie są równoległe ani do poziomu, ani do pionu. ELIPSY różnią się wielkościami dużej osi od małej. W przypadku ELIPSY rys.3 jest znaczna,a na rys.13 jest nieco mniejsza. Nie podaję położenie osi dużyc w [], o nie ma to większego znaczenia. Ccę uzyskać potwierdzenie o istnieniu: stałej proporcji, gdzie r/ ma wartość stałą i że takie wymiary jak: 2*r, czyli Ø i - wysokość stożka prostego, czy też walca, mają wartość stałej proporcji. Zatem, to składowe pionowe i poziome TRÓJKĄTÓW LGICZNYCH wyznaczają wymiary *** STAŁEJ PRPRCJI *** Swoją działalność dot.geometrii kulowej () kończę. Już w tym roku 2015 nie wykupię domeny. Nikomu nie ędę podpowiadać, co należy uczynić. Co cciałem dodać, zapisałem w ostatniej linijce. T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 26 stycznia 2015r

10 ELIPSA PMARAŃCZWA DCHYLNA WZGLĘDEM LINII PZIMEJ I PINWEJ. JEST PDSTAWĄ STŻKA DCHYLNEG. NIE MA WYZNACZNEG WIERZCHŁKA. Rys.15 Rys.16 str.10 T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 29 stycznia 2015r

11 ELIPSA PMARAŃCZWA DCHYLNA WZGLĘDEM LINII PZIMEJ I PINWEJ. JEST PDSTAWĄ STŻKA DCHYLNEG. NIE MA WYZNACZNEG WIERZCHŁKA. str.11 Rys.18 Rys.17 W β /2 β /2 W1 r r W W2 T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 29 stycznia 2015r

12 EFEKTY P: PMARAŃCZWYCH ELIPSACH, TRÓJKĄTACH LGICZNYCH, PRPRCJACH STAŁYCH. WSZYSTK T, NA MJE SZCZĘŚCIE, TARŁ SIĘ "ŚWIĘTĄ GEMERTIĘ" I "ZŁTY DCINEK". GEMETRIA KULWA NIE BYŁA I DLA MNIE NIE BĘDZIE NIGDY - "ŚWIĘTĄ" str.12 Rys.19 Rys.20 DANE: r 10 j. 28, j. Stożki proste, orotowe a 2*r 20 j. - a 8, j. W β /2 β /2 (a+) a *0,5 (a - ) *0,25 (a - 2*) r*0,25 r a*0,5 r*0,5 *0,5 *(a-2*) r r (a-) *(a - 2*) r 0 0,35355 *1 0,35355, 0,35355 *0,5 0,17678, (a - )*(a - 2*) 0 1 *1 1, 1 *0,5 0,5, a*0,5 a*0,5 r 0 0,35355 *0,25 0,08839 STAŁA PRPRCJNALNA: 2^0,5 Ciąg dalszy stałej proporcji, czyli stałej: 0 1 *0,25 0,25 rosnący Fraktal malejący "2^0,5" pozostawiam matematykom, którzy z a + a - łatwością ułożą ciąg matematyczny, posługując rosnący a a - się wielkościami: "a" i "" dla "r" promienia 2*a Nr.1 Nr.2 Nr.3 o dowolonej wielkości, lecz o stałym wymiarze. a + Nr.4 Część ciągu licz.wykonałem,o jaki mi codziło,który również zawiera cecy wizualne fraktala. T SKŁADWE TRÓJKĄTA LGICZNEG Koszalin dnia 02 luty 2015r