MAGAZYN WIEDZY NR 1 O GEOMETRII KULOWEJ. PROJEKT TWÓRCY (gk). PRZYPOMINA POMNIK. WALEC TRAPEZOWY Z KORYTEM KOŁO. Nr2 6h(48h) ELIPSA pionowa O
|
|
|
- Beata Pawlak
- 9 lat temu
- Przeglądów:
Transkrypt
1 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM () Nr1 Widziane KŁ przy kierunku poziomym patrzenia na ELIPSĘ. Wydrążone koryto w walcu przez walec. Moja wyobraźnia podpowiada mi, że rzut prostokątny od tej strony patrząc, wykaże ELIPSĘ. 3 A Warto też pod takim kątem zobaczyć poziomą ELIPSĘ. A przekrój () 18h() KŁ. Nr1 ELIPSA Nr2 Nr3 () KŁ. () Linia przerywana 0,75 - przewidywany zarys "poszkodowanego", przyciętego z symetrycznością, grubego walca, po obróceniu o kąt 90 w prawo. Gdy będziesz obchodził w koło tę bryłę geometryczną, wszędzie napotkasz pionowe linie czarno-niebieskie (parzyste i nieparzyste) równo rozstawione, lecz gdy patrzysz stojąc nieruchomo, masz wrażenie, że są różne odstępy. Romana - imię mojej małżonki T Projekt: Magazyn Wiedzy z (). Pomnik. Koszalin dnia 02 stycznia 2015r
2 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). Rys.2 pł.(xy) MAPA PRZEKRÓJ: A - A str.2 strzałka 3 łuk 5 symbol - obliczanie wymiarów z odczytów, na podstawie okrągłej linijki Różnica kątów łuków: &1= &k-&p [ ] &k &p cięciwa łuku 4 SZKIC RIENTACJI PRZESTRZENNEJ ***KULA*** Patrzymy aktywna (+)Z (+)X (-)Y (+)Y (-)X (-)Z MAPA Na str.1 nie napisałem, co jeszcze podpowiada mi moja wyobraźnia, odnośnie wydrążonego koryta w grubym walcu. Gdybym w to koryto włożył kartkę kolorową do wycinanek dla dzieci, w taki sposób, że przylegałaby idealnie do tego koryta, a następnie odciął wystające fragmenty, wówczas po rozwinięciu wyciętej figury wskaże - ELIPSĘ. Podobnie moja wyobraźnia podpowiada mi o rozwinięciu, nie rzutu prostokątnego koryta, lecz jego cienia. Chodzi o to, że rozwinięcie obrysu koryta na grubym walcu - wykaże także ELIPSĘ. Reasumując myśl wynikającą z mojej wyobraźni stawiam tezę, iż będą to trzy ELIPSY. Pisząc to, poddaję ocenie swoją wyobraźnię. Nie każdego na to stać. Ale, jest to potrzebne, by mieć własne zdanie o postępie, doskonaleniu własnej wyobraźni. Zastanawiam się rysując rys.3, czy ewentualne ELIPSY będą zachowywać podobieństwo wg ()? A, gdybym wydrążył koryto w grubym walcu na pełną średnicę tj. 2* 3, to też byłaby ELIPSA? Wiem już teraz, że czeka mnie dużo pracy związanej z tym plikiem. T Projekt: Magazyn Wiedzy z (). Pomnik. Koszalin dnia 03 stycznia 2015r
3 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). Rys.3 Po obróceniu w prawo, wokół osi Z o kąt 90 str.3 SZKIC RIENTACJI PRZESTRZENNEJ ***KULA*** aktywna (+)Z (-)Y (+)X Patrzymy (+)Y (-)X (-)Z MAPA T Projekt: Magazyn Wiedzy o (). Pomnik.
4 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). Rys.4 PWIĘKSZ D 200% P DDATKWYM BRCIE KĄT 180. str.4 () Rys.4 jest obrócony o kąt 180 w porównaniu do rys.3. Natomiast do narysowania kształtu owala skorzystałem z wymiarów rzeczywistych rys.2. Są to linie rysowane pionowo, które zamieniłem na przyrządy - funkcja linie. Potem je obróciłem poziomując z funkcji obróć 90. Następnie skorzystałem z półkola skopiowanego z rys.1, gdzie są rozmieszczone punkty na okręgu koła (przyrząd). Przenosiłem wymiary powtarzającymi się parami z rys.2 na rys.4 o czym już wspomniałem. Teraz w centralnym rys.4 umieściłem okrąg i ELIPSĘ. Niestety, nie jest to ELIPSA, lecz zwykły owal. wal ten jest efektem rzutu na i nie jest on rozwinięciem żadnej innej figury geometrycznej. Z wyglądu przypomina krzyżówkę - KŁA i ELIPSY. Na tym programie komputerowym nie da się wykreślić rozwinięcia cienia owalu na grubym walcu. Po to wymyśliłem okrągłą linijkę, by temu sprostać, tak jak w wielu innych przypadkach. Na str.5 chcę pokazać to samo, lecz inaczej. Czysto. T Projekt: Magazyn Wiedzy o (). Pomnik.
5 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). Rys.4 PWIĘKSZ D 200% P DDATKWYM BRCIE KĄT 180. str.5 () Rys.4 jest obrócony o kąt 180 w porównaniu do rys.3. Natomiast do narysowania kształtu owala skorzystałem z wymiarów rzeczywistych rys.2. Są to linie rysowane pionowo, które zamieniłem na przyrządy - funkcja linie. Potem je obróciłem poziomując z funkcji obróć 90. Następnie skorzystałem z półkola skopiowanego z rys.1, gdzie są rozmieszczone punkty na okręgu koła (przyrząd). Przenosiłem wymiary powtarzającymi się parami z rys.2 na rys.4 o czym już wspomniałem. Teraz w centralnym rys.4 umieściłem okrąg i ELIPSĘ. Niestety, nie jest to ELIPSA, lecz zwykły owal. wal ten jest efektem rzutu na i nie jest on rozwinięciem żadnej innej figury geometrycznej. Z wyglądu przypomina krzyżówkę - KŁA i ELIPSY. Na tym programie komputerowym nie da się wykreślić rozwinięcia cienia owalu na grubym walcu. Po to wymyśliłem okrągłą linijkę, by temu sprostać, tak jak w wielu innych przypadkach. Na str.5 chcę pokazać to samo, lecz inaczej. Czysto. Tabela obliczeniowa wymaga więcej miejsca, Projekt: Magazyn Wiedzy o (). Pomnik. stąd Cz.I. Magazynu Wiedzy o () kończę tu. T
gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii
![gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii](/thumbs/103/159774468.jpg) Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
gk T Rozwiązanie Zadania nr1 - uzupełnienie
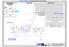 TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
TABELA PRZELICZENIOWA
 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
gk T Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (gk), w sposób praktyczny. Rys.2a
 Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
400% Rys.2a Negatyw *** ZASADA *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na OPIS WYKONYWANYCH CZYNNOŚCI.
 Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5
 Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
WYKŁAD 2 Znormalizowane elementy rysunku technicznego. Przekroje.
 WYKŁAD 2 Znormalizowane elementy rysunku technicznego. Przekroje. Tworzenie z formatu A4 formatów podstawowych. Rodzaje linii Najważniejsze zastosowania linii: - ciągła gruba do rysowania widocznych krawędzi
WYKŁAD 2 Znormalizowane elementy rysunku technicznego. Przekroje. Tworzenie z formatu A4 formatów podstawowych. Rodzaje linii Najważniejsze zastosowania linii: - ciągła gruba do rysowania widocznych krawędzi
Rys.1. str.1. 48h;0h 18h 19h 20h 21h 22h 46h. 44h r1 4h. 10h. 38h. 34h 14h. 32h 16h. 24h jest linią do przenoszenia szablonów
 Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
gk T Okrąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 Rys.2
 krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
Rys 3-1. Rysunek wałka
 Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
Rys.1 pomocniczy. Okrąg z którego powstały łuki na rys.1b.
 OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
W module Część-ISO wykonać kubek jak poniżej
 W module Część-ISO wykonać kubek jak poniżej rozpoczniemy od wyciągnięcia walca o średnicy 75mm i wysokości 90mm z płaszczyzny xy wykonujemy szkic do wyciągnięcia zamykamy szkic, oraz wprowadzamy wartość
W module Część-ISO wykonać kubek jak poniżej rozpoczniemy od wyciągnięcia walca o średnicy 75mm i wysokości 90mm z płaszczyzny xy wykonujemy szkic do wyciągnięcia zamykamy szkic, oraz wprowadzamy wartość
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył
 Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
3.3. dwie płaszczyzny równoległe do siebie α β Dwie płaszczyzny równoległe do siebie mają ślady równoległe do siebie
 Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
Nr3 JEDNOPŁASZCZYZNOWY
 Ruch obrotwy południkowy kul widocznych FRAKTALA KULOWEGO, jednopłaszczyznowego - z pliku B.Zeszyt.030. pł.(yz) pł.(yz) pł.(yz) FRAKTAL KULOWY Nr2 FRAKTAL KULOWY Nr3 FRAKTAL KULOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY
Ruch obrotwy południkowy kul widocznych FRAKTALA KULOWEGO, jednopłaszczyznowego - z pliku B.Zeszyt.030. pł.(yz) pł.(yz) pł.(yz) FRAKTAL KULOWY Nr2 FRAKTAL KULOWY Nr3 FRAKTAL KULOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY
Wymiarowanie jest to podawanie wymiarów przedmiotów na rysunkach technicznych za pomocą linii, liczb i znaków wymiarowych.
 WYMIAROWANIE (w rys. technicznym maszynowym) 1. Co to jest wymiarowanie? Aby rysunek techniczny mógł stanowić podstawę do wykonania jakiegoś przedmiotu nie wystarczy bezbłędne narysowanie go w rzutach
WYMIAROWANIE (w rys. technicznym maszynowym) 1. Co to jest wymiarowanie? Aby rysunek techniczny mógł stanowić podstawę do wykonania jakiegoś przedmiotu nie wystarczy bezbłędne narysowanie go w rzutach
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
INSTYTUT INFORMATYKI STOSOWANEJ MODELOWANIE CZĘŚCI Z WYKORZYSTANIEM PROGRAMU SOLID EDGE
 INSTYTUT INFORMATYKI STOSOWANEJ MODELOWANIE CZĘŚCI Z WYKORZYSTANIEM PROGRAMU SOLID EDGE Łódź 2012 1 Program Solid Edge ST (Synchronous Technology) umożliwia projektowanie urządzeń technicznych w środowisku
INSTYTUT INFORMATYKI STOSOWANEJ MODELOWANIE CZĘŚCI Z WYKORZYSTANIEM PROGRAMU SOLID EDGE Łódź 2012 1 Program Solid Edge ST (Synchronous Technology) umożliwia projektowanie urządzeń technicznych w środowisku
G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm
![G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm](/thumbs/71/64805542.jpg) Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
(a) (b) (c) o1" o2" o3" o1'=o2'=o3'
 Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Pokrywka. Rysunek 1. Projekt - wynik końcowy. Rysunek 2. Pierwsza linia łamana szkicu
 Pokrywka Rysunek 1. Projekt - wynik końcowy Projekt rozpoczynamy od narysowania zamkniętego szkicu. 1. Narysujemy i zwymiarujmy linię łamaną jako część szkicu (nie zamknięty), rys. 2. Uwaga: a) Dodajmy
Pokrywka Rysunek 1. Projekt - wynik końcowy Projekt rozpoczynamy od narysowania zamkniętego szkicu. 1. Narysujemy i zwymiarujmy linię łamaną jako część szkicu (nie zamknięty), rys. 2. Uwaga: a) Dodajmy
Geometria wykreślna. 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław. Politechnika Gdańska, Wydział Architektury
 Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
gk T MAŁA C 18h O 6h F
 ROZWIĄZANIE ZADANIA TPO.Nr 1. (TYLKO PRZEZ ORŁÓW) Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). TO JEST MÓJ I TWÓJ EGZAMIN Z MYŚLENIA (). str.25 1 Plik cz.i. rozwiązania zadania jest przeciążony ilością
ROZWIĄZANIE ZADANIA TPO.Nr 1. (TYLKO PRZEZ ORŁÓW) Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). TO JEST MÓJ I TWÓJ EGZAMIN Z MYŚLENIA (). str.25 1 Plik cz.i. rozwiązania zadania jest przeciążony ilością
gk T GEOMETRIA WYKREŚLNA PRZESTRZENNA T (GK) W PRAKTYCE. SZTUKA TRASOWANIA CZ.1. Rys.3. Rys.4. Rysunek jest zbyt duży, zmniejszę go na str.2.
 GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
1/4(koła; okrągu) A A' P'(x)
 skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
RZUTOWANIE PROSTOKĄTNE
 RZUTOWANIE PROSTOKĄTNE WPROWADZENIE Wykonywanie rysunku technicznego - zastosowanie Rysunek techniczny przedmiotu jest najczęściej podstawą jego wykonania, dlatego odwzorowywany przedmiot nie powinien
RZUTOWANIE PROSTOKĄTNE WPROWADZENIE Wykonywanie rysunku technicznego - zastosowanie Rysunek techniczny przedmiotu jest najczęściej podstawą jego wykonania, dlatego odwzorowywany przedmiot nie powinien
1. Przykładowy test nr 1
 1. Przykładowy test nr 1 Nr Treść zad. zad. 1 Proszę podać wymiary formatu arkusza A1 Odpowiedź 2 Proszę podać przykład typowej podziałki zwiększającej 3 Proszę podać zastosowanie linii ciągłej, cienkiej
1. Przykładowy test nr 1 Nr Treść zad. zad. 1 Proszę podać wymiary formatu arkusza A1 Odpowiedź 2 Proszę podać przykład typowej podziałki zwiększającej 3 Proszę podać zastosowanie linii ciągłej, cienkiej
gk T Rzutowanie walców w geometrii wykreśl.wg (gk).
 Dodatkowe przyrządy stosow.w (), do przyspieszenia prac kreślarskich rzutowania walców. Format ark. A4 : 14,25*1,75 str.1 Rys.1 Sprawdzenie średnicy KULI ϕ13,12 cm, na podstawie okrągłej linijki. UWAGA:
Dodatkowe przyrządy stosow.w (), do przyspieszenia prac kreślarskich rzutowania walców. Format ark. A4 : 14,25*1,75 str.1 Rys.1 Sprawdzenie średnicy KULI ϕ13,12 cm, na podstawie okrągłej linijki. UWAGA:
PODSTAWY GRAFIKI INŻYNIERSKIEJ projektowanie SZKICOWANIE TECHNICZNE
 MATERIAŁY POMOCNICZE Zajęcia 5 Temat: Szkic techniczny. Kompozycja rysunku. Widoki SZKICOWANIE TECHNICZNE 1. Rodzaje linii i ich podstawowe zastosowanie Linia ciągła gruba widoczne krawędzie i wyraźne
MATERIAŁY POMOCNICZE Zajęcia 5 Temat: Szkic techniczny. Kompozycja rysunku. Widoki SZKICOWANIE TECHNICZNE 1. Rodzaje linii i ich podstawowe zastosowanie Linia ciągła gruba widoczne krawędzie i wyraźne
Narysujemy uszczelkę podobną do pokazanej na poniższym rysunku. Rys. 1
 Narysujemy uszczelkę podobną do pokazanej na poniższym rysunku. Rys. 1 Jak zwykle, podczas otwierania nowego projektu, zaczynamy od ustawienia warstw. Poniższy rysunek pokazuje kolejne kroki potrzebne
Narysujemy uszczelkę podobną do pokazanej na poniższym rysunku. Rys. 1 Jak zwykle, podczas otwierania nowego projektu, zaczynamy od ustawienia warstw. Poniższy rysunek pokazuje kolejne kroki potrzebne
Kolektor. Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk. Wykonajmy model kolektora jak na rys. 1.
 Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
SZa 98 strona 1 Rysunek techniczny
 Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
X Olimpiada Matematyczna Gimnazjalistów
 www.omg.edu.pl X Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część korespondencyjna (10 listopada 01 r. 15 grudnia 01 r.) Szkice rozwiązań zadań konkursowych 1. nia rozmieniła banknot
www.omg.edu.pl X Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część korespondencyjna (10 listopada 01 r. 15 grudnia 01 r.) Szkice rozwiązań zadań konkursowych 1. nia rozmieniła banknot
gk T Zadania nr 2. opracował: inż. Kazimierz Barski dla wszystkich ludzi świata TECHNIKA Koszalin dnia r
 ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
Ćwiczenie nr 3 Edycja modeli bryłowych
 Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
Pytania do spr / Własności figur (płaskich i przestrzennych) (waga: 0,5 lub 0,3)
 Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
4.2. ELIPSA. 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie:
 4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
RZUTOWANIE PROSTOKĄTNE
 RZUTOWANIE PROSTOKĄTNE wg PN-EN ISO 5456-2 rzutowanie prostokątne (przedstawienie prostokątne) stanowi odwzorowanie geometrycznej postaci konstrukcji w postaci rysunków dwuwymiarowych. Jest to taki rodzaj
RZUTOWANIE PROSTOKĄTNE wg PN-EN ISO 5456-2 rzutowanie prostokątne (przedstawienie prostokątne) stanowi odwzorowanie geometrycznej postaci konstrukcji w postaci rysunków dwuwymiarowych. Jest to taki rodzaj
Obiekt 2: Świątynia Zeusa
 Obiekt 2: Świątynia Zeusa Rys 2-1. Wyobrażenie greckiej świątyni ku czci Zeusa Prezentowane w tym dokumencie zadanie polega na narysowaniu bryły, będącej wyobrażeniem greckiej świątyni ku czci Zeusa. Poniżej
Obiekt 2: Świątynia Zeusa Rys 2-1. Wyobrażenie greckiej świątyni ku czci Zeusa Prezentowane w tym dokumencie zadanie polega na narysowaniu bryły, będącej wyobrażeniem greckiej świątyni ku czci Zeusa. Poniżej
Zastosowania informatyki w geologii ćwiczenia 1,2 INKSCAPE 1
 INKSCAPE 1 Zadanie 1 (Ctrl + shift + c konwersja kształtu na scieżkę) Narysuj kształty: Usuń cały prostokąt i połowę gwiazdy Zadanie 2 Narysuj prostokąt o wymiarach: 40x20pikseli (wysokość, szerokość),
INKSCAPE 1 Zadanie 1 (Ctrl + shift + c konwersja kształtu na scieżkę) Narysuj kształty: Usuń cały prostokąt i połowę gwiazdy Zadanie 2 Narysuj prostokąt o wymiarach: 40x20pikseli (wysokość, szerokość),
METODA RZUTÓW MONGE A (II CZ.)
 RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
O kula. w (gks). Rzutnie: (XZ); (YZ); (XY). A B (YZ) (XY) D sześciana
 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ
 Zapis i Podstawy Konstrukcji Widoki i przekroje przedmiotów 1 WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ Rzutami przedmiotów mogą być zarówno widoki przestawiające zewnętrzne kształty przedmiotów
Zapis i Podstawy Konstrukcji Widoki i przekroje przedmiotów 1 WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ Rzutami przedmiotów mogą być zarówno widoki przestawiające zewnętrzne kształty przedmiotów
Płaszczyzny, Obrót, Szyk
 Płaszczyzny, Obrót, Szyk Zagadnienia. Szyk kołowy, tworzenie brył przez Obrót. Geometria odniesienia, Płaszczyzna. Wykonajmy model jak na rys. 1. Wykonanie korpusu pokrywki Rysunek 1. Model pokrywki (1)
Płaszczyzny, Obrót, Szyk Zagadnienia. Szyk kołowy, tworzenie brył przez Obrót. Geometria odniesienia, Płaszczyzna. Wykonajmy model jak na rys. 1. Wykonanie korpusu pokrywki Rysunek 1. Model pokrywki (1)
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
PYTANIA TEORETYCZNE Z MATEMATYKI
 Zbiory liczbowe: 1. Wymień znane Ci zbiory liczbowe. 2. Co to są liczby rzeczywiste? 3. Co to są liczby naturalne? 4. Co to są liczby całkowite? 5. Co to są liczby wymierne? 6. Co to są liczby niewymierne?
Zbiory liczbowe: 1. Wymień znane Ci zbiory liczbowe. 2. Co to są liczby rzeczywiste? 3. Co to są liczby naturalne? 4. Co to są liczby całkowite? 5. Co to są liczby wymierne? 6. Co to są liczby niewymierne?
OBLICZENIE PRZEKROJU WALCA PO CIĘCIU SKOŚNYM. Rysunki i obliczenia dotyczą walca
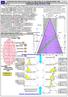 Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Rysujemy. Rysunek techniczny Odwzoruj to co widzisz. rzutowanie, Wymiarowanie, linie i łańcuchy
 Rysujemy Dr inż. Hieronim Piotr Janecki Miłe spotkanie wyższego rzędu No 10 Rysunek techniczny Odwzoruj to co widzisz rzutowanie, Wymiarowanie, linie i łańcuchy 1 Rzutowanie rzut prostokątny Definicja
Rysujemy Dr inż. Hieronim Piotr Janecki Miłe spotkanie wyższego rzędu No 10 Rysunek techniczny Odwzoruj to co widzisz rzutowanie, Wymiarowanie, linie i łańcuchy 1 Rzutowanie rzut prostokątny Definicja
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
Nauka, poprzez zabawę w swoim domu. Rodzice z dziećmi. Rzutowanie bryły geometrycznej. Format ark.a4 12,75*1,75 str.1. "TABLICZKA MNOśENIA AWERS * A
 dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
Przeciąganie, rzutowanie, płaszczyzna konstrukcyjna
 Przeciąganie, rzutowanie, płaszczyzna konstrukcyjna Wykonajmy projekt tłumika z elementami rur wydechowych, rys. 1 Rys. 1. Efekt końcowy projektu Przyjmując jako płaszczyznę szkicu płaszczyznę XY, narysujmy
Przeciąganie, rzutowanie, płaszczyzna konstrukcyjna Wykonajmy projekt tłumika z elementami rur wydechowych, rys. 1 Rys. 1. Efekt końcowy projektu Przyjmując jako płaszczyznę szkicu płaszczyznę XY, narysujmy
Kurs Rysunku Starpak4kids
 www.starpak4kids.pl Kurs Rysunku Starpak4kids Lekcja 1 podstawy i kreska Podczas naszego kursu nie będziemy rysować na płaskim biurku, tylko w pozycji pionowej lub pod kątem trzymając podstawkę na kolanach.
www.starpak4kids.pl Kurs Rysunku Starpak4kids Lekcja 1 podstawy i kreska Podczas naszego kursu nie będziemy rysować na płaskim biurku, tylko w pozycji pionowej lub pod kątem trzymając podstawkę na kolanach.
WYDZIAŁ OCEANOTECHNIKI I OKRĘTOWNICTWA. Katedra Hydromechaniki i Hydroakustyki
 WYDZIAŁ OCEANOTECHNIKI I OKRĘTOWNICTWA Katedra Hydromechaniki i Hydroakustyki ĆWICZENIA LABORATORYJNE Z HYDROMECHANIKI OKRĘTU Ćwiczenie Nr 12 Pomiar charakterystyk geometrycznych śruby Opracował: dr inż.
WYDZIAŁ OCEANOTECHNIKI I OKRĘTOWNICTWA Katedra Hydromechaniki i Hydroakustyki ĆWICZENIA LABORATORYJNE Z HYDROMECHANIKI OKRĘTU Ćwiczenie Nr 12 Pomiar charakterystyk geometrycznych śruby Opracował: dr inż.
Zajęcia techniczne kl. I - Gimnazjum w Tęgoborzy
 Temat 14 : Podstawowe wiadomości o rysunku technicznym. Prezentacja Pismo techniczne.pps 1. - język porozumiewawczy między inżynierem a konstruktorem. Jest znormalizowany, tzn. istnieją normy (przepisy)
Temat 14 : Podstawowe wiadomości o rysunku technicznym. Prezentacja Pismo techniczne.pps 1. - język porozumiewawczy między inżynierem a konstruktorem. Jest znormalizowany, tzn. istnieją normy (przepisy)
Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks.
 1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
Kolektor. Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk. Wykonajmy model kolektora jak na rys. 1.
 Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leŝącej w płaszczyźnie symetrii kolektora
Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leŝącej w płaszczyźnie symetrii kolektora
Co należy zauważyć Rzuty punktu leżą na jednej prostej do osi rzutów x 12, którą nazywamy prostą odnoszącą Wysokość punktu jest odległością rzutu
 Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
OPŁYW PROFILU. Ciała opływane. profile lotnicze łopatki. Rys. 1. Podział ciał opływanych pod względem aerodynamicznym
 OPŁYW PROFILU Ciała opływane Nieopływowe Opływowe walec kula profile lotnicze łopatki spoilery sprężarek wentylatorów turbin Rys. 1. Podział ciał opływanych pod względem aerodynamicznym Płaski np. z blachy
OPŁYW PROFILU Ciała opływane Nieopływowe Opływowe walec kula profile lotnicze łopatki spoilery sprężarek wentylatorów turbin Rys. 1. Podział ciał opływanych pod względem aerodynamicznym Płaski np. z blachy
23h 24h;0h(koła) 24[h]*15[ /h]=360[ ]
![23h 24h;0h(koła) 24[h]*15[ /h]=360[ ] 23h 24h;0h(koła) 24[h]*15[ /h]=360[ ]](/thumbs/53/31835593.jpg) Dla młodzieży. brót w kole dużych kropek w prawo, po jego obwodzie. Koło jest odchylone od pionu. W tym opracowaniu będę posługiwał się swoimi przyrządami stosowanymi w geometrii kulowej (). Nabyłem na
Dla młodzieży. brót w kole dużych kropek w prawo, po jego obwodzie. Koło jest odchylone od pionu. W tym opracowaniu będę posługiwał się swoimi przyrządami stosowanymi w geometrii kulowej (). Nabyłem na
Rok akademicki 2005/2006
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
Grafika inżynierska geometria wykreślna. 5a. Obroty i kłady. Rozwinięcie wielościanu.
 Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
COMENIUS PROJEKT ROZWOJU SZKOŁY. Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów.
 COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2007 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STOLIKÓW
COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2007 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STOLIKÓW
Wymiarowanie. Wymiarowanie jest to podawanie wymiarów przedmiotów na rysunkach technicznych za pomocą linii, liczb i znaków wymiarowych.
 Wymiarowanie Wymiarowanie jest to podawanie wymiarów przedmiotów na rysunkach technicznych za pomocą linii, liczb i znaków wymiarowych. Wymiarowanie: -jedna z najważniejszych rzeczy na rysunku technicznym
Wymiarowanie Wymiarowanie jest to podawanie wymiarów przedmiotów na rysunkach technicznych za pomocą linii, liczb i znaków wymiarowych. Wymiarowanie: -jedna z najważniejszych rzeczy na rysunku technicznym
ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (gk).
 ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). str.1 patrzymy Stożek prosty nr1 Rys.1 m k ELIPSA jest cieniem, czyli rzutem prostopadłym na. Zatem nie podlega odchyleniom od pionu. Co nie
ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). str.1 patrzymy Stożek prosty nr1 Rys.1 m k ELIPSA jest cieniem, czyli rzutem prostopadłym na. Zatem nie podlega odchyleniom od pionu. Co nie
dla symboli graficznych O bardzo dużej liczbie szczegółów 0,18 0,35 0,70 0,25 A3 i A4 O dużej liczbie szczegółów
 6/ LINIE RYSUNKOWE Normy rysunkowe PN-EN ISO 128-20:2002 Rysunek techniczny. Zasady ogólne przedstawiania Część 20: Wymagania podstawowe dotyczące linii PN-ISO 128-23:2002 Rysunek techniczny. Ogólne zasady
6/ LINIE RYSUNKOWE Normy rysunkowe PN-EN ISO 128-20:2002 Rysunek techniczny. Zasady ogólne przedstawiania Część 20: Wymagania podstawowe dotyczące linii PN-ISO 128-23:2002 Rysunek techniczny. Ogólne zasady
Koło zębate wału. Kolejnym krokiem będzie rozrysowanie zębatego koła przeniesienia napędu na wał.
 Witam w kolejnej części kursu modelowania 3D. Jak wspomniałem na forum, dalsze etapy będą przedstawiały terminy i nazwy opcji, ustawień i menu z polskojęzycznego interfejsu programu. Na początek dla celów
Witam w kolejnej części kursu modelowania 3D. Jak wspomniałem na forum, dalsze etapy będą przedstawiały terminy i nazwy opcji, ustawień i menu z polskojęzycznego interfejsu programu. Na początek dla celów
4.2. ELIPSA. 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie:
 4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
4.2. ELIPSA 1. W linii statusowej włączamy siatkę i skok, które ułatwią rysowanie: 2. Rysujemy Elipsę (_Ellipse) zaczynając w dowolnym punkcie, koniec osi definiujemy np. za pomocą współrzędnych względnych
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3
 DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
Zadanie I. 2. Gdzie w przestrzeni usytuowane są punkty (w której ćwiartce leży dany punkt): F x E' E''
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
Polecenie LUSTRO _MIRROR Lustro Pasek narzędzi: Menu: Klawiatura: UWAGA
 Polecenie LUSTRO _MIRROR Symetria osiowa obiektów względem dowolnej osi. Otrzymane obiekty są odbiciem oryginałów. Lustro Pasek narzędzi: Zmiana > Lustro; Menu: Zmiana > Lustro; Klawiatura: LUSTRO, _MIRROR
Polecenie LUSTRO _MIRROR Symetria osiowa obiektów względem dowolnej osi. Otrzymane obiekty są odbiciem oryginałów. Lustro Pasek narzędzi: Zmiana > Lustro; Menu: Zmiana > Lustro; Klawiatura: LUSTRO, _MIRROR
WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA
 WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA WALEC powstaje w wyniku obrotu prostokąta wokół prostej zawierającej jeden z jego boków WALEC oś obrotu podstawa wysokość
WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA WALEC powstaje w wyniku obrotu prostokąta wokół prostej zawierającej jeden z jego boków WALEC oś obrotu podstawa wysokość
WIDOKI I PRZEKROJE PRZEDMIOTÓW
 WIDOKI I PRZEKROJE PRZEDMIOTÓW Rzutami przedmiotów mogą być zarówno widoki przedstawiające zewnętrzne kształty przedmiotów jak i przekroje, które pokazują budowę wewnętrzną przedmiotów wydrążonych. Rys.
WIDOKI I PRZEKROJE PRZEDMIOTÓW Rzutami przedmiotów mogą być zarówno widoki przedstawiające zewnętrzne kształty przedmiotów jak i przekroje, które pokazują budowę wewnętrzną przedmiotów wydrążonych. Rys.
X = r cosα = (R+r sinα) cosβ = (R+r sinα) sinβ
 Krzywe Krzywa przez punkty XYZ Rysunek 18.1. Schemat wymiarów torusa i wynik nawinięcia W rozdziale zostanie przedstawiony przykład nawinięcia krzywej na ścianę torusa. Poniżej (rysunek 18.1) schemat wymiarów
Krzywe Krzywa przez punkty XYZ Rysunek 18.1. Schemat wymiarów torusa i wynik nawinięcia W rozdziale zostanie przedstawiony przykład nawinięcia krzywej na ścianę torusa. Poniżej (rysunek 18.1) schemat wymiarów
Chropowatości powierzchni
 Chropowatość powierzchni Chropowatość lub chropowatość powierzchni cecha powierzchni ciała stałego, oznacza rozpoznawalne optyczne lub wyczuwalne mechanicznie nierówności powierzchni, niewynikające z jej
Chropowatość powierzchni Chropowatość lub chropowatość powierzchni cecha powierzchni ciała stałego, oznacza rozpoznawalne optyczne lub wyczuwalne mechanicznie nierówności powierzchni, niewynikające z jej
ROZWINIĘCIA POWIERZCHNI STOPNIA DRUGIEGO W OPARCIU O MIEJSCA GEOMETRYCZNE Z ZA- STOSOWANIEM PROGRAMU CABRI II PLUS.
 Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
Rozkład figury symetrycznej na dwie przystające
 Rozkład figury symetrycznej na dwie przystające Tomasz Tkocz 10 X 2010 Streszczenie Tekst zawiera notatki do referatu z seminarium monograficznego Wybrane zagadnienia geometrii. Całość jest oparta na artykule
Rozkład figury symetrycznej na dwie przystające Tomasz Tkocz 10 X 2010 Streszczenie Tekst zawiera notatki do referatu z seminarium monograficznego Wybrane zagadnienia geometrii. Całość jest oparta na artykule
KURS MATURA PODSTAWOWA Część 2
 KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
KURS MATURA PODSTAWOWA Część 2 LEKCJA 7 Planimetria ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kąt na poniższym rysunku ma miarę:
aksonometrie trójosiowe odmierzalne odwzorowania na płaszczyźnie
 aksonometrie trójosiowe odmierzalne odwzorowania na płaszczyźnie Przykładowy rzut (od lewej) izometryczny, dimetryczny ukośny i dimetryczny prostokątny Podział aksonometrii ze względu na kierunek rzutowania:
aksonometrie trójosiowe odmierzalne odwzorowania na płaszczyźnie Przykładowy rzut (od lewej) izometryczny, dimetryczny ukośny i dimetryczny prostokątny Podział aksonometrii ze względu na kierunek rzutowania:
WYMAGANIA EDUKACYJNE Przedmiot: Pracownia dokumentacji Klasa: I Podstawa opracowania: PROGRAM NAUCZANIA DLA ZAWODU TECHNIK DROGOWNICTWA
 WYMAGANIA EDUKACYJNE Przedmiot: Pracownia dokumentacji Klasa: I Podstawa opracowania: PROGRAM NAUCZANIA DLA ZAWODU TECHNIK DROGOWNICTWA 311206 Lp Wiadomości wstępne, normy rysunkowe 1 Lekcja organizacyjna
WYMAGANIA EDUKACYJNE Przedmiot: Pracownia dokumentacji Klasa: I Podstawa opracowania: PROGRAM NAUCZANIA DLA ZAWODU TECHNIK DROGOWNICTWA 311206 Lp Wiadomości wstępne, normy rysunkowe 1 Lekcja organizacyjna
Łożysko z pochyleniami
 Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
Wymiarowanie. Wymiary normalne. Elementy wymiaru rysunkowego Znak ograniczenia linii wymiarowej
 Wymiary normalne Wymiarowanie Elementy wymiaru rysunkowego Znak ograniczenia linii wymiarowej 1. Linia wymiarowa 2. Znak ograniczenia linii wymiarowej 3. Liczba wymiarowa 4. Pomocnicza linia wymiarowa
Wymiary normalne Wymiarowanie Elementy wymiaru rysunkowego Znak ograniczenia linii wymiarowej 1. Linia wymiarowa 2. Znak ograniczenia linii wymiarowej 3. Liczba wymiarowa 4. Pomocnicza linia wymiarowa
1. OPEN OFFICE RYSUNKI
 1. 1 1. OPEN OFFICE RYSUNKI 1.1 Wiadomości podstawowe Po uruchomieniu programu Draw okno aplikacji wygląda jak na poniższym rysunku. Składa się ono z głównego okna, w którym edytuje się rysunek oraz czterech
1. 1 1. OPEN OFFICE RYSUNKI 1.1 Wiadomości podstawowe Po uruchomieniu programu Draw okno aplikacji wygląda jak na poniższym rysunku. Składa się ono z głównego okna, w którym edytuje się rysunek oraz czterech
Wymagania edukacyjne dla klasy VI z matematyki. Opracowane na podstawie programu nauczania Matematyka z plusem LICZBY NATURALNE I UŁAMKI
 Wymagania edukacyjne dla klasy VI z matematyki. Opracowane na podstawie programu nauczania Matematyka z plusem LICZBY NATURALNE I UŁAMKI Ocena dopuszczająca: - nazwy działań - algorytm mnożenia i dzielenia
Wymagania edukacyjne dla klasy VI z matematyki. Opracowane na podstawie programu nauczania Matematyka z plusem LICZBY NATURALNE I UŁAMKI Ocena dopuszczająca: - nazwy działań - algorytm mnożenia i dzielenia
Stożkiem nazywamy bryłę obrotową, która powstała przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych.
 1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
Internetowe Ko³o M a t e m a t yc z n e
 Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 2 szkice rozwiązań zadań 1. Dana jest taka liczba rzeczywista, której rozwinięcie dziesiętne jest nieskończone
Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 2 szkice rozwiązań zadań 1. Dana jest taka liczba rzeczywista, której rozwinięcie dziesiętne jest nieskończone
LICZBY I WYRAŻENIA ALGEBRAICZNE
 LICZBY I WYRAŻENIA ALGEBRAICZNE KLASA III GIMNAZJUM DZIAŁ PROGRAMOWY WYMAGANIA KONIECZNE (K) PODSTAWOWE (P) ROZSZERZAJĄCE (R) DOPEŁNIAJĄCE (D) UCZEŃ: - zna pojęcie liczby naturalnej, całkowitej, wymiernej,
LICZBY I WYRAŻENIA ALGEBRAICZNE KLASA III GIMNAZJUM DZIAŁ PROGRAMOWY WYMAGANIA KONIECZNE (K) PODSTAWOWE (P) ROZSZERZAJĄCE (R) DOPEŁNIAJĄCE (D) UCZEŃ: - zna pojęcie liczby naturalnej, całkowitej, wymiernej,
Matematyka z plusem Klasa IV
 Matematyka z plusem Klasa IV KLASA IV SZCZEGÓŁOWE CELE EDUKACYJNE KSZTAŁCENIE Rozwijanie sprawności rachunkowej Wykonywanie jednodziałaniowych obliczeń pamięciowych na liczbach naturalnych. Stosowanie
Matematyka z plusem Klasa IV KLASA IV SZCZEGÓŁOWE CELE EDUKACYJNE KSZTAŁCENIE Rozwijanie sprawności rachunkowej Wykonywanie jednodziałaniowych obliczeń pamięciowych na liczbach naturalnych. Stosowanie
ROZKŁAD MATERIAŁU Z MATEMATYKI DO KLASY V I (5 godz. tygodn.) NA ROK SZKOLNY 2002/2003 WG PROGRAMU MATEMATYKA Z PLUSEM DKW /99
 ROZKŁAD MATERIAŁU Z MATEMATYKI DO KLASY V I (5 godz. tygodn.) NA ROK SZKOLNY 00/00 WG PROGRAMU MATEMATYKA Z PLUSEM DKW-404-8/99 I PROCENTY 5 PODSTAWOWE ZAGADNIENIA Procent jako ułamek. - procent jako setna
ROZKŁAD MATERIAŁU Z MATEMATYKI DO KLASY V I (5 godz. tygodn.) NA ROK SZKOLNY 00/00 WG PROGRAMU MATEMATYKA Z PLUSEM DKW-404-8/99 I PROCENTY 5 PODSTAWOWE ZAGADNIENIA Procent jako ułamek. - procent jako setna
KRZYŻÓWKA 2. 11. Może być np. równoboczny lub rozwartokątny. Jego pole to a b HASŁO:
 KRZYŻÓWKA.Wyznaczają ją dwa punkty.. Jego pole to π r² 3. Jego pole to a a 4.Figura przestrzenna, której podstawą jest dowolny wielokąt, a ściany boczne są trójkątami o wspólnym wierzchołku. 5.Prosta mająca
KRZYŻÓWKA.Wyznaczają ją dwa punkty.. Jego pole to π r² 3. Jego pole to a a 4.Figura przestrzenna, której podstawą jest dowolny wielokąt, a ściany boczne są trójkątami o wspólnym wierzchołku. 5.Prosta mająca
Tematy lekcji informatyki klasa 4a styczeń 2013
 Tematy lekcji informatyki klasa 4a styczeń 2013 temat 7. z podręcznika (str. 70-72); sztuczki 4. i 5. (str. 78); Narysuj ikony narzędzi do zaznaczania i opisz je. 19 Zaznaczamy fragment rysunku i przenosimy
Tematy lekcji informatyki klasa 4a styczeń 2013 temat 7. z podręcznika (str. 70-72); sztuczki 4. i 5. (str. 78); Narysuj ikony narzędzi do zaznaczania i opisz je. 19 Zaznaczamy fragment rysunku i przenosimy
Matura z matematyki 1920 r.
 Matura z matematyki 1920 r. (źródło: Sprawozdanie Dyrekcji Państwowego Gimnazjum im. Karola Marcinkowskiego w Poznaniu: za 1-sze dziesięciolecie zakładu w niepodległej i wolnej ojczyźnie: 1919-1929) Żelazna
Matura z matematyki 1920 r. (źródło: Sprawozdanie Dyrekcji Państwowego Gimnazjum im. Karola Marcinkowskiego w Poznaniu: za 1-sze dziesięciolecie zakładu w niepodległej i wolnej ojczyźnie: 1919-1929) Żelazna
Geometria odwzorowań inżynierskich. Zadania 10A
 Scriptiones Geometrica Volumen I (2014), No. Z10A, 1 7. Geometria odwzorowań inżynierskich. Zadania 10A Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Twierdzenia o rozpadzie linii przenikania W
Scriptiones Geometrica Volumen I (2014), No. Z10A, 1 7. Geometria odwzorowań inżynierskich. Zadania 10A Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Twierdzenia o rozpadzie linii przenikania W
POMIAR KÓŁ ZĘBATYCH WALCOWYCH cz. 1.
 I. Cel ćwiczenia: POMIAR KÓŁ ZĘBATYCH WALCOWYCH cz. 1. 1. Zidentyfikować koło zębate przeznaczone do pomiaru i określić jego podstawowe parametry 2. Dokonać pomiaru grubości zęba suwmiarką modułową lub
I. Cel ćwiczenia: POMIAR KÓŁ ZĘBATYCH WALCOWYCH cz. 1. 1. Zidentyfikować koło zębate przeznaczone do pomiaru i określić jego podstawowe parametry 2. Dokonać pomiaru grubości zęba suwmiarką modułową lub
Przykładowe plany zajęć lekcyjnych Design the Future Poland
 Przykładowe plany zajęć lekcyjnych Design the Future Poland 1 Spis treści Plik projektu... 3 Brelok Krok po kroku... 5 Tron dla komórki krok po kroku... 15 Plik projektu... 15 Tron na komórkę... 17 Figury
Przykładowe plany zajęć lekcyjnych Design the Future Poland 1 Spis treści Plik projektu... 3 Brelok Krok po kroku... 5 Tron dla komórki krok po kroku... 15 Plik projektu... 15 Tron na komórkę... 17 Figury
Wymagania z matematyki na poszczególne oceny III klasy gimnazjum
 Wymagania z matematyki na poszczególne oceny III klasy gimnazjum Opracowano na podstawie planu realizacji materiału nauczania matematyki Matematyka Podręcznik do gimnazjum Nowa wersja Praca zbiorowa pod
Wymagania z matematyki na poszczególne oceny III klasy gimnazjum Opracowano na podstawie planu realizacji materiału nauczania matematyki Matematyka Podręcznik do gimnazjum Nowa wersja Praca zbiorowa pod
Układ scalony UL 1111
 1 Układ scalony UL 1111 Punkty lutownicze prostokątne najczęściej wykorzystujemy do projektowania punktów lutowniczych na płytce drukowanej służące najczęściej do wlutowywania podstawek lub układów scalonych
1 Układ scalony UL 1111 Punkty lutownicze prostokątne najczęściej wykorzystujemy do projektowania punktów lutowniczych na płytce drukowanej służące najczęściej do wlutowywania podstawek lub układów scalonych
