Rachunek wektorowy. I. Notacja i terminologia: a,a,x,y, y R n wektorywprzestrzenin-wymiarowej, A,B,R,T macierze(zazwyczajowymiarzen n)
|
|
|
- Sylwia Tomaszewska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Wstęp do Robotyki c W. Szynkiewicz, 9 I. Notacja i terminologia: Rachunek wektorowy a,a,x,y, y R n wektorywprzestrzenin-wymiarowej, A,B,R,T macierze(zazwyczajowymiarzen n) R zbiór liczb rzeczywistych R n = R R... R iloczyn kartezjański }{{} nrazy Wektorkolumnowyx R n jestpostaci: x= x. x n ; x=[x,...,x n ] T ; x i R Długośćlubnormaeuklidesowawektorax R n x = x = x +...+x n Wstęp do Robotyki c W. Szynkiewicz, 9 Rodzaje współrzędnych:. Współrzędne punktu uporządkowana kolumna dwóch(dla płaszczyzny) lub trzech(przestrzeni trójwymiarowej) liczb reprezentujących wektor(odcinek skierowany) o początku w początku układu odniesienia i końcu w danym punkcie. Zarówno punkt, jak jego współrzędne często tak samo oznacza się,np.p.. Współrzędne uogólnione uporządkowana kolumna trzech lub czterech liczb reprezentujących współrzędnepunktup=[p x,p y,] T lubodpowiedniop=[p x,p y,p z,] T. 3. Współrzędne wektora uporządkowana kolumna dwóch lub trzech liczb reprezentujących wektor w pewnymukładzieodniesieniar=[r x,r y,r z ] T. 4. Współrzędne wektora swobodnego wektor o określonym kierunku i zwrocie oraz wielkości lecz, którego punkt zaczepienia nie ma fizycznego znaczenia. Układy współrzędnych będą oznaczane jako{f},{},{}.
2 Wstęp do Robotyki c W. Szynkiewicz, 9 3 II. Iloczyn skalarny: Iloczynskalarny x,y dwóchwektorówx,y R n jestliczbąrzeczywistą x,y =x T y=x y=x y +...+x n y n wówczas x = x,x x = x,x Własności iloczynu skalarnego: a) x,y = y,x przemienność, b) x,y x y nierównośćcauchy ego-schwartz a, c) x+y x + y nierównośćtrójkąta, d)m x,y = mx,y łącznośćwzględemmnożeniaprzezliczbę, e) (x+y),z = x,z + y,z rozdzielnośćwzględemdodawania Wstęp do Robotyki c W. Szynkiewicz, 9 4 Dlawektorówx,y R 3 x,y = x y cosθ,gdzieθ= (x,y) Dla wersorów osi(wektorów jednostkowych) î= ; ĵ= ; ˆk= układu ortokartezjańskiego Oxyz mamy î,î = ĵ,ĵ = ˆk,ˆk = î,ĵ = ĵ,ˆk = ˆk,î = wtymukładziewektora=[a x,a y,a z ] T możnazapisać a=a x î+a y ĵ+a zˆk
3 Wstęp do Robotyki c W. Szynkiewicz, 9 5 Iloczynskalarnydwóchwektorówa,b R 3 a,b =a x b x +a y b y +a z b z Jeślia ib tokątmiędzytymiwektoramispełniazwiązek cos (a,b)= a,b a b Współrzędną wektora a względem osi s(α, β, γ) można zapisać a s = a,s =a x cosα+a y cosβ+a z cosγ stąd w szczególności wynika, że a x = a,î ; a y = a,ĵ ; a z = a,ˆk Wektory a, b nazywamy ortogonalnymi jeśli a,b = ajeśliponadtoa ib towektorytesąprostopadłea b. Wstęp do Robotyki c W. Szynkiewicz, 9 6 III. Iloczyn wektorowy(wewnętrzny) Iloczynwektorowya buporządkowanejparywektorów(a,b)jestwektoremc=a b. Jeśli wektory a i b są kolinearne wówczas iloczyn wektorowy jest wektorem zerowym, w przeciwnym przypadku jest wektorem, którego: modułjestdanyjako: a b = a b sin (a,b)ijestpolemrównoległobokurozpiętegonatych wektorach kierunekjestprostopadłydokażdegozwektorówtj. a,(a b) =; b,(a b) =ijestto kierunek prostopadły do płaszczyzny rozpiętej na tych wektorach zwrottaki,żeuporządkowanatrójka(a,b,a b)matęsamąorientacjęcoprzestrzeńwktórej zdefiniowany jest iloczyn wektorowy. ax b b O a Rysunek : Iloczyn wektorowy
4 Wstęp do Robotyki c W. Szynkiewicz, 9 7 Własności iloczynu wektorowego: a)a b= (b a) antyprzemienność, b)m(a b)=(ma) b łącznośćwzględemmnożeniaprzezliczbę, c)(a+b) c=a c+b c rozdzielnośćwzględemdodawania Jeślia ib to sin (a,b)= a b a b W układzie ortokartezjańskim mamy î î=ĵ ĵ=ˆk ˆk= î ĵ=ˆk, ĵ ˆk=î, ˆk î=ĵ Wstęp do Robotyki c W. Szynkiewicz, 9 8 IloczynwektorowywR 3 wyznaczamyzewzoru a b=(a y b z a z b y )î+(a z b x a x b z )ĵ+(a x b y a y b x )ˆk= a y a z b y b z î+ a z a x b z b x ĵ+ a x a y b x b y ˆk albo a b= î ĵ ˆk a x a y a z b x b y b z =det î ĵ ˆk a x a y a z b x b y b z Moduł iloczynu wektorowego a b = a y a z b y b z + a z a x b z b x + a x a y b x b y
5 Wstęp do Robotyki c W. Szynkiewicz, 9 9 Macierze Macierzowymiarach(m n) A=[a ij ] n m= Własności: a... a n... a m... a mn Dodawanie macierzy jest łączne i przemienne (A+B)+C=A+(B+C) A+B=B+A Mnożenie macierzy jest łączne A(BC) =(AB)C Mnożenie macierzy w ogólnym przypadku nie jest przemienne AB BA Transpozycja macierzy (A+B) T =A T +B T (A T ) T =A (AB) T =B T A T Wstęp do Robotyki c W. Szynkiewicz, 9 Obrót układu współrzędnych: Opis położenia i orientacji na płaszczyźnie y y j j i x {} i x sin cos Rysunek:ObrótwR î = cosϕ sinϕ, ĵ = stąd otrzymujemy macierz rotacji R= cosϕ sinϕ sinϕ cosϕ sinϕ cosϕ () ()
6 Wstęp do Robotyki c W. Szynkiewicz, 9 Ten sam wynik można uzyskać wiedząc, że iloczyn skalarny wersorów układu{} i układu{} odpowiada rzutowaniu jednych wersorów na drugie: î = î î î, ĵ = ĵ ĵ î (3) ĵ ĵ zatem macierz rotacji R= î î ĵ î î ĵ ĵ ĵ (4) Własności macierzy obrotu(rotacji): macierzrjestortogonalna:rr T =R T R=I,czylikolumny(takżewiersze)macierzyRsą wzajemnieortogonalne,stądwynika,żer T =R Każda kolumna(wiersz) macierzy R jest wektorem jednostkowym detr=+(dlaukładówprawoskrętnych) Macierze R tworzą specjalną grupę obrotów SO() tzn. R SO(). Wstęp do Robotyki c W. Szynkiewicz, 9 y y P x d y p p d {} {} d x x Rysunek3:ObrótiprzesunięciewR p x p = y cosϕ sinϕ sinϕ cosϕ p x p + d x y d y (5) p x p = y cosϕ sinϕ sinϕ cosϕ p x p d x y d y (6)
7 Wstęp do Robotyki c W. Szynkiewicz, 9 3 Postać zwarta p =Rp +d p =R (p d) (7) gdzie R= cosϕ sinϕ d= sinϕ cosϕ d x d y Przykład : Układ{}obróconywzględem{}okąt π 4 iprzesuniętyowektord=[ ] T.Wukładzie{}dany jestwektorp =[ ] T,przedstawićtenwektorwukładzie{} p = cos π 4 sin π 4 sin π 4 cos π 4 + = Wstęp do Robotyki c W. Szynkiewicz, 9 4 MacierzprzekształceniajednorodnegowR P = p x p y p x p y = ; P = p x p y cosϕ sinϕ d x sinϕ cosϕ d y ;P,P współrzędnejednorodne p x p y (8) p x p y = cosϕ sinϕ d x cosϕ d y sinϕ sinϕ cosϕ d x sinϕ d y cosϕ p x p y (9) P = R d P = HP () P = R T R T d P = H P = HP ()
8 Wstęp do Robotyki c W. Szynkiewicz, 9 5 Obroty w przestrzeni trójwymiarowej z z P y x k k j i j i y x Rysunek4:ObrótwR 3 W układzie{} p =p x î +p y ĵ +p zˆk W układzie{} p =p x î +p y ĵ +p zˆk () (3) Wstęp do Robotyki c W. Szynkiewicz, 9 6 p x =p î =p î =p x î î +p y ĵ î +p zˆk î (4) p y =p ĵ =p ĵ =p x î ĵ +p y ĵ ĵ +p zˆk ĵ (5) p z =p ˆk =p ˆk =p x î ˆk +p y ĵ ˆk +p zˆk ˆk (6) Równanie w postaci wektorowej gdzie p = Rp R= î î ĵ î ˆk î î ĵ ĵ ĵ ˆk ĵ î ˆk ĵ ˆk ˆk ˆk (7) (8) podobnie gdzie p = Rp R= î î ĵ î ˆk î î ĵ ĵ ĵ ˆk ĵ î ˆk ĵ ˆk ˆk ˆk (9) ()
9 Wstęp do Robotyki c W. Szynkiewicz, 9 7 ponieważiloczynskalarnyjestprzemiennytzn.î ĵ =ĵ î,więc R= R = R T () Własności macierzy obrotu(rotacji): macierzrjestortogonalna:rr T =R T R=I 3,czylikolumny(takżewiersze)macierzyRsą wzajemnieortogonalne,stądwynika,żer T =R Każda kolumna(wiersz) macierzy R jest wektorem jednostkowym R(u w)=(ru) (Rw) detr=((rî) (Rĵ)) ((Rˆk))= (Rˆk) =+(dlaukładówprawoskrętnych) Macierze R tworzą specjalną grupę obrotów SO(3). Wstęp do Robotyki c W. Szynkiewicz, 9 8 Składanie obrotów: p = Rp,p = Rp,p = Rp Względem osi bieżącego układu: stąd p = R Rp R= R R kolejne macierze mnożymy prawostronnie. Względem osi układu ustalonego: R= R R kolejne macierze mnożymy lewostronnie.
10 Wstęp do Robotyki c W. Szynkiewicz, 9 9 Przykład : Składanie obrotów nie jest przemienne. z z y x y z y x y O x O x z Rysunek5:Obrótwokółosiz,anastępniey z y y z z y O x z y O x x x Rysunek6:Obrótwokółosiy,anastępniez Wstęp do Robotyki c W. Szynkiewicz, 9 Przykład3:Układ{}jestobróconywzględem{}okątϕwokółosiz.Znaleźćmacierz R z z j O j i i y y x x Rysunek7:Obrótwokółosiz î î =cosϕ,ĵ î = sinϕ,ĵ ĵ =cosϕ,î ĵ =sinϕ,ˆk ˆk =
11 Wstęp do Robotyki c W. Szynkiewicz, 9 Macierz R=R z,ϕ = R z, = I 3 R z,ϕ R z,θ =R z,ϕ+θ R z,ϕ=r z, ϕ cosϕ sinϕ sinϕ cosϕ Podobnie można wyznaczyć macierze obrotu odpowiednio wokół osi x oraz y R x,ϕ = cosϕ sinϕ sinϕ cosϕ R y,ϕ = cosϕ sinϕ sinϕ cosϕ Wstęp do Robotyki c W. Szynkiewicz, 9 Inne wybrane reprezentacje obrotu: reprezentacja oś-kąt(obrót wokół dowolnej osi) obroty wokół osi układu bieżącego kąty Euler a( zestawów) np. kąty Eulera Z-Y-Z obroty wokół osi układu ustalonego np. roll-pitch-yaw(kołysanie-kiwanie-myszkowanie) parametry Eulera(kwaternion jednostkowy) Dalej omówimy trzy pierwsze reprezentacje obrotu.
12 Wstęp do Robotyki c W. Szynkiewicz, 9 3 Obrót wokół dowolnej osi: Mającdanywektora R 3,wektorjednostkowyk, k =ikątϕznaleźćwektorb R 3 powstaływ wynikuobrotuawokółkokątϕ. k x (k x a) C k oœ obrotu k x a k(k a) a b O Rysunek8:Obrótwokółosikokątϕ Wektoramożnazdekomponowaćnaskładowąrównoległąa iskładowąprostopadłąa doosiobrotu a=k(k a) k (k a) }{{}}{{} a a Tylkoskładowaa jestzmienianawwynikuobrotu. Wstęp do Robotyki c W. Szynkiewicz, 9 4 Wektor b można wyznaczyć ze wzoru Rodrigues a: b=k(k a)+sinϕ(k a) cosϕk (k a) () lub innej jego postaci: b=a+(sinϕ)k a+( cosϕ)k (k a) (3) Definiując operator macierzowy iloczynu wektorowego w postaci macierzy K K= taki, że k z k y k z k x k y k x Ka=k a a następnie podstawiając macierz K do wzoru(3) otrzymamy b=a+(sinϕ)ka+( cosϕ)k a stąd wyciągając a można wyznaczyć macierz obrotu R R=I+(sinϕ)K+( cosϕ)k (4)
13 Wstęp do Robotyki c W. Szynkiewicz, 9 5 InnysposóbobliczeniaobliczeniamacierzyR k,ϕ : Znającwektork=[k x,k y,k z ] T definiującyośobrotuikątϕmożnawyprowadzićmacierzobrotur k,ϕ. z k z k x O k k y y x Rysunek 9: Obrót wokół dowolnej osi Obrót wokół dowolnej osi można przedstawić jako złożenie następujących obrotów: R k,ϕ =R z,α R y,β R z,ϕ R y, β R z, α (5) Wstęp do Robotyki c W. Szynkiewicz, 9 6 Obroty wykonywane są wokół osi układu ustalonego. sinα= k y, cosα= k x +ky k x k x +k y sinβ= k x+k y, cosβ=k z cosϕ c ϕ, sinϕ s ϕ, v ϕ =versϕ= c ϕ podstawiając powyższe zależności do(5) mamy R k,ϕ = k xv ϕ +c ϕ k x k y v ϕ k z s ϕ k x k z v ϕ +k y s ϕ k x k y v ϕ +k z s ϕ k yv ϕ +c ϕ k y k z v ϕ k x s ϕ k x k z v ϕ k y s ϕ k y k z v ϕ +k x s ϕ k zv ϕ +c ϕ (6)
14 Wstęp do Robotyki c W. Szynkiewicz, 9 7 Macierz obrotu R SO(3) można zawsze wyrazić w postaci pojedynczego obrotu wokół odpowiedniej osi o odpowiedni kąt R=R k,ϕ gdziekwektorjednostkowydefiniującyoś,zaśϕkątobrotuwokółtejosi.znającelementyr i,j macierzyr kąt ϕ obliczamy Tr(R) ϕ=arccos =arccos r +r +r 33 oraz k= sinϕ r 3 r 3 r 3 r 3 r r Reprezentacja oś-kąt nie jest jednoznaczna ponieważ R k,ϕ =R k, ϕ Jeśliϕ=toR=I,aośobrotujestnieokreślona. Reprezentację oś-kąt można przedstawić w postaci R=[r x,r y,r z ] T =[ϕk x,ϕk y,ϕk z ] T Długość wektora R jest równa mierze kąta ϕ. Wstęp do Robotyki c W. Szynkiewicz, 9 8 Przykład4:MacierzRpowstałazobrotuokąt9 wokółosiz,następnieokąt6 wokółosiy orazo kąt3 wokółosix.obliczyćwynikowąmacierzobrotuorazodpowiadającąjejparametryzacjęoś-kąt. Wynikowa macierz obrotu ma postać R=R x,3 R y,6 R z,9 = Odpowiadająca tej macierzy reprezentacja oś-kąt jest następująca: Kąt obrotu jest równy ϕ=arccos = zaś oś określa wektor k=, 3 3, 3 T
15 Wstęp do Robotyki c W. Szynkiewicz, 9 9 Zadanie : Danesądwaukładyortokartezjańskie{}=(O,x,y,z )i{}=(o,x,y,z ).Kątmiędzyosiami x,y jestrówny 3 π,kątmiędzyosiamix,z jestrówny π 6 orazkątmiędzyosiamiy,z jestrówny π 3. Obliczyćelementymacierzyrotacji R(przejściezukładu{}do{}).Czyjesttylkojednorozwiązanie tego zadania? z x y 6 3 z _ 3 y x Rysunek:Obrotywprzestrzeni R 3 Wstęp do Robotyki c W. Szynkiewicz, 9 3 Obroty wokół osi układu bieżącego: Kąty Eulera Z-Y-Z: z z z z y x O y y x x x y Rysunek : Reprezentacja kątów Eulera ZestawkątówEuleraZ-Y-Zotrzymamyprzeztrzyobroty:wokółosiz okątϕ,następniewokółosiy o kątθiwokółosiz okątψ.
16 Wstęp do Robotyki c W. Szynkiewicz, 9 3 Wynikowa macierz obrotu: R=R z,ϕ R y,θ R z,ψ = c ϕ c θ c ψ s ϕ s ψ c ϕ c θ s ψ s ϕ c ψ c ϕ s θ s ϕ c θ c ψ +c ϕ s ψ s ϕ c θ s ψ +c ϕ c ψ s ϕ s θ s θ c ψ s θ s ψ c θ (7) Problemodwrotny:Mającdanewartościr i,j elementówmacierzyrznaleźćkątyϕ,θ,ψ. Jeślisinθ θ=atan ϕ=atan ( ) ± r3+r 3,r 33 r 3 s θ s θ, r 3 r 3 ψ=atan, r 3 s θ s θ Jeżeliθ=lubθ=πwówczasmożnawyznaczyćjedyniesumęalboróżnicękatówϕ±ψ. Kiedyr 33 =,wówczasc θ =is θ =,zatemθ=. ϕ+ψ=atan(r,r )=atan( r,r ) Kiedyr 33 =,wówczasc θ = is θ =,zatemθ=π ϕ ψ=atan( r, r )=atan( r, r ) W obu przypadkach mamy nieskończenie wiele rozwiązań. Wstęp do Robotyki c W. Szynkiewicz, 9 3 Obroty wokół osi układu ustalonego: Kołysanie-kiwanie-myszkowanie(roll-pitch-yaw): x myszkowanie (yaw) z ko³ysanie (roll) O kiwanie (pitch) y Rysunek : Obroty wokół osi układu ustalonego R=R z,ϕ R y,θ R x,ψ = c ϕ c θ s ϕ c ψ +c ϕ s θ s ψ s ϕ s ψ +c ϕ s θ c ψ s ϕ c θ c ϕ c ψ +s ϕ s θ s ψ c ϕ s ψ +s ϕ s θ c ψ s θ c θ s ψ c θ c ψ określone na zbiorze V= {(ϕ,θ,ψ) π } θπ,<ϕ<π, ψ<π (8)
17 Wstęp do Robotyki c W. Szynkiewicz, 9 33 Przekształcenie odwrotne: Dlaθ ± π mamy ϕ=atan(r,r ), ϕ=ϕ+π (9) θ=atan( r 3,cosϕr +sinϕr ) (3) ψ=atan(sinϕr 3 cosϕr 3, sinϕr +cosϕr ) (3) Jeśliθ=± π wówczasrozwiązaniedegenerujesięimożemyobliczyćtylkosumęlubróżnicękątówϕiψ. Zazwyczaj przyjmuje się ϕ = i rozwiązanie znajduje się z zależności: Dlaθ= π θ= π, ϕ=, ψ=atan(r,r ) Dlaθ= π θ= π, ϕ=, ψ= atan(r,r ) Wstęp do Robotyki c W. Szynkiewicz, 9 34 P= p x p y p z = p MacierzprzekształceniajednorodnegowR 3 p R d R d R d p = = Rp+d R R Rd+ d =HP (3) (33) R d = R T R T d (34) H= R 3 3 d 3 f 3 s = obrót przesunięcie perspektywa skalowanie (35)
18 Wstęp do Robotyki c W. Szynkiewicz, 9 35 Zbiór elementarnych przekształceń jednorodnych Zbiór wszystkich macierzy jednorodnych H stanowi specjalną grupę euklidesową izometrii przestrzeni trójwymiarowej. Zbiór podstawowych przekształceń jednorodnych generujących tę grupę jest następujący: Trans x,a = a Trans y,b = b Trans z,c = c dla translacji odpowiednio wzdłuż osi x, y, z, Rot x,α = cα sα sα cα Rot y,ϕ = cϕ sϕ sϕ cϕ Rot z,θ = cθ i sθ i sθ i cθ i dlaobrotuodpowiedniowokółosix,y,z(gdzies() sin()orazc() cos()). Wstęp do Robotyki c W. Szynkiewicz, 9 36 Interpretacje macierzy przekształcenia jednorodnego: {} z P P z k k d P O j y x i {} O j i y T= R d x. Jako opis układu opisuje układ{} względem układu{}. Kolumny macierzy rotacji(macierzy kosinusówkierunkowych) Rsąwersoramiokreślającymikierunkiosiukładu{}wukładzie{}. Wektor dokreślapołożeniepoczątkuukładu{}wukładzie{}..jakoprzekształcenieodwzorowujące.macierz Todwzorowuje P P. 3.Jakooperatorprzekształcenia.MacierzTdziałanawektor P tworzącwektor P (przesuniętyi obrócony w układzie{})
19 Wstęp do Robotyki c W. Szynkiewicz, 9 37 Przykład 5: Układortokartezjański{}=(O,x,y,z )początkowopokrywałsięzukładem{}=(o,x,y,z ), następniezostałobróconyokątϕ= π 6 wokółosiz iprzesuniętyod=6wzdłużosix.punktpma współrzędnewukładzie{}współrzędne P=[,,3] T.ObliczyćwspółrzędnepunktuPwukładzie{}. Rozwiązanie: Transformacja współrzędnych z układu{} do{} opisana jest wzorem: P= T P Macierz przekształcenia jednorodnego ma postać: T= cosϕ sinϕ d sinϕ cosϕ Zapisując we współrzędnych jednorodnych współrzędne punktu P, możemy obliczyć P= T 3 P= = Wstęp do Robotyki c W. Szynkiewicz, 9 38 Ruch ciała sztywnego: Ruch ciała(bryły) sztywnego w przestrzeni euklidesowej można przedstawić jako gładkie odwzorowanie czasuwgrupęprzesunięć R 3 orazspecjalnągrupęobrotów SO(3) c: R R 3 SO(3) = SE(3), H SE(3), (36) które opisuje w każdej chwili czasu położenie i orientację układu związanego z ciałem względem układu przestrzeni(układu odniesienia). KażdyelementH SE(3)formalnienależydo R : H R (R R 9 d R 3 ) przy czym macierz rotacji R spełnia 6 niezależnych warunków ortogonalności R T R=I 3 stąd wymiar specjalnej grupy euklidesowej dim SE(3) = 6, czyli ciało swobodne ma 6 stopni swobody.
20 Wstęp do Robotyki c W. Szynkiewicz, 9 39 Macierze skośniesymetryczne S T +S= (37) dlamacierzysowymiarze3 3oelementachs ij,i,j=,,3mamy9równań s ij +s ji = (38) ponieważs ii =orazdlai js ij = s ji tomacierzs 3 3 S= s s s s 3 s s 3 Jeśliwektora=[a x,a y,a z ] T tos(a) S(a)=[a ]= a z a y a z a x a y a x Macierzeskośnie-symetryczneS(î),S(ĵ),S(ˆk)dlawersorówî,ĵ,ˆk S(î)= ; S(ĵ)= ; S(ˆk)= (39) (4) (4) Wstęp do Robotyki c W. Szynkiewicz, 9 4 Własności macierzy skośniesymetrycznych: dladowolnychwektorówa,b R 3 orazskalarówα,βmamys(αa+βb)=αs(a)+βs(b) liniowość dladowolnegowektorap R 3 mamys(a)p=a p dladowolnychprzekształceńr,s SO(3)idowolnychwektorówa,b R 3 zpoprzednichwłasności wynika, iż RS(a)R T b = R(a R T b)=(ra) (RR T b) = (Ra) b = S(Ra)b (4) Stąd wynika, że RS(a)R T =S(Ra) (43) Lewa strona równania reprezentuje przekształcenie macierzy S(a) przez podobieństwo. Niech macierz obrotu będzie funkcją jednego kąta θ, stąd R = R(θ) SO(3). Pochodna macierzy względem θ dana jest wzorem dr dθ =SR(θ) (44)
21 Wstęp do Robotyki c W. Szynkiewicz, 9 4 Przykład:6JeśliR=R x,θ jestpodstawowąmacierząobrotutomożnapokazać,że S= dr dθ RT = sinθ cosθ cosθ sinθ = cosθ sinθ sinθ cosθ =S(î) (45) stąd otrzymujemy dr x,θ dθ =S(î)R x,θ podobnie dostajemy pozostałe pochodne (46) dr y,θ dθ =S(ĵ)R y,θ ; dr z,θ dθ =S(ˆk)R z,θ (47) Wstęp do Robotyki c W. Szynkiewicz, 9 4 Prędkość kątowa i liniowa z s Z b y b s k b {s} O s s d b {b} O b x b s v b y s x s Rysunek 3: Ruch ciała sztywnego prędkości Prędkość kątowa: Załóżmy,żemacierzobrotujestzmiennawczasieR=R(t) SO(3).PonieważmacierzR(t)jest ortogonalna, więc R(t)R(t) T =I różniczkując obustronnie względem t jako pochodną iloczynu otrzymamy dr dt R(t)T +R(t) drt dt (48) = (49)
22 Wstęp do Robotyki c W. Szynkiewicz, 9 43 Definiujemy macierz S dr dt R(t)T wówczas transpozycja macierzy S S T = dr dt R(t)T ) T =R(t) drt dt równanie(49) oznacza wówczas, że (5) (5) S+S T = (5) zatem macierz S zdefiniowana wzorem(5) jest skośniesymetryczna. Mnożąc obie strony równania(5) przezr(t)iwiedząc,żer(t)jestmacierząortogonalnąotrzymujemypochodnąṙ(t)macierzyr(t) względem czasu dr(t) dt =Ṙ(t)=S(t)R(t) (53) Macierz S(t) może być jednoznacznie reprezentowana w postaci S(ω(t)) przez wektor prędkości kątowej ω(t) układu obracającego się względem układu ustalonego w chwili t. Pochodną macierzy R(t) względem czasu wyrazić Ṙ(t) = S(t)R(t) = S(ω(t))R(t) (54) gdzie ω(t) wektor prędkości kątowej. Wstęp do Robotyki c W. Szynkiewicz, 9 44 Niech c(t)= R(t) d(t) ċ(t) = Ṙ(t) ḋ(t) Prędkość(macierz prędkości) w układzie przestrzeni V s =ċ(t)c (t)= Ω s ḋ Ω s d gdzieω s =ṘRT prędkośćkątowawukładzieinercjalnym (55) Prędkość(macierz prędkości) w układzie ciała(związanym z ciałem) V b =c (t)ċ(t)= Ω b R T ḋ gdzieω b =R T Ṙ prędkośćkątowawukładzieciała. MacierzeprędkościkątowychΩ s iω b sąokreśloneprzezwektoryprędkościkątowychω s orazω b ω ω ω 3 =ω [ω ]=Ω= ω 3 ω ω 3 ω ω ω (56) (57)
23 Wstęp do Robotyki c W. Szynkiewicz, 9 45 odwzorowanie jest wzajemnie jednoznaczne i określa wektorową reprezentację prędkości kątowej Ω s =[ω s ] Ω b =[ω b ] (58) MacierzeprędkościV s iv b możnazatemzastąpićwektorami v s = ν s ω s, vb = ν b ω b (59) gdzie ν s =ḋ+d ωs, ν b =R T ḋ prędkość liniowa odpowiednio w układzie przestrzeni i układzie ciała. Wstęp do Robotyki c W. Szynkiewicz, 9 46 Interpretacja prędkości ciała sztywnego w układzie przestrzeni i układzie ciała: DanyjestpunktowspółrzędnychjednorodnychP= [ p T, ] T wukładzieciała.współrzędnetegopunktuw układzie przestrzeni w chwili t: r(t) = R(t) d(t) p(t) (6) prędkość punktu P względem układu przestrzeni ṙ(t) = Ṙ(t) ḋ(t) p (6) prędkość punktu P wyrażona w układzie ciała R(t) d(t) Ṙ(t) ḋ(t) p =Vb p = ω b p+rḋ (6) prędkość w układzie ciała jest prędkością ruchu względem układu przestrzeni punktu P którego współrzędne w układzie ciała są ustalone widzianą z układu ciała. (Uwaga: Punkt P nie porusza się względem układu ciała.)
24 Wstęp do Robotyki c W. Szynkiewicz, 9 47 Prędkość punktu P w układzie przestrzeni ṙ(t) = =V s Ṙ(t) ḋ(t) r(t) = R(t) d(t) r(t) ω s (r(t) d(t))+ḋ(t) = (63) prędkość punktu P w układzie przestrzeni ma składową pochodzącą od obrotu wektora(r d) z prędkością kątowąω s orazskładowąwynikającązruchupoczątkuukładuciałaḋ.
Podstawy robotyki. Wykład II. Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska
 Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
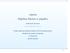
i = [ 0] j = [ 1] k = [ 0]
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I
![2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I 2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I](/thumbs/88/115575416.jpg) Liniowa niezależno ność wektorów Przykład: Sprawdzić czy następujące wektory z przestrzeni 3 tworzą bazę: e e e3 3 Sprawdzamy czy te wektory są liniowo niezależne: 3 c + c + c3 0 c 0 c iei 0 c + c + 3c3
Liniowa niezależno ność wektorów Przykład: Sprawdzić czy następujące wektory z przestrzeni 3 tworzą bazę: e e e3 3 Sprawdzamy czy te wektory są liniowo niezależne: 3 c + c + c3 0 c 0 c iei 0 c + c + 3c3
Iloczyn skalarny, wektorowy, mieszany. Ortogonalność wektorów. Metoda ortogonalizacji Grama-Schmidta. Małgorzata Kowaluk semestr X
 Iloczyn skalarny, wektorowy, mieszany. Ortogonalność wektorów. Metoda ortogonalizacji Grama-Schmidta. Małgorzata Kowaluk semestr X ILOCZYN SKALARNY Iloczyn skalarny operator na przestrzeni liniowej przypisujący
Iloczyn skalarny, wektorowy, mieszany. Ortogonalność wektorów. Metoda ortogonalizacji Grama-Schmidta. Małgorzata Kowaluk semestr X ILOCZYN SKALARNY Iloczyn skalarny operator na przestrzeni liniowej przypisujący
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Algebra liniowa. 1. Macierze.
 Algebra liniowa 1 Macierze Niech m oraz n będą liczbami naturalnymi Przestrzeń M(m n F) = F n F n będącą iloczynem kartezjańskim m egzemplarzy przestrzeni F n z naturalnie określonymi działaniami nazywamy
Algebra liniowa 1 Macierze Niech m oraz n będą liczbami naturalnymi Przestrzeń M(m n F) = F n F n będącą iloczynem kartezjańskim m egzemplarzy przestrzeni F n z naturalnie określonymi działaniami nazywamy
Zadania egzaminacyjne
 Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora.
 1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
Wektory. Algebra. Aleksander Denisiuk. Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi Gdańsk
 Algebra Wektory Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wektory Najnowsza wersja
Algebra Wektory Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wektory Najnowsza wersja
Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem.
 1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
cx cx 1,cx 2,cx 3,...,cx n. Przykład 4, 5
 Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
Matematyka stosowana i metody numeryczne
 Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 14 Rachunekwektorowy W celu zdefiniowania wektora a należy podać: kierunek(prostą na której leży wektor)
Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 14 Rachunekwektorowy W celu zdefiniowania wektora a należy podać: kierunek(prostą na której leży wektor)
Mechanika. Wykład 2. Paweł Staszel
 Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn x 1 x 2... x m ...
 Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
macierze jednostkowe (identyczności) macierze diagonalne, które na przekątnej mają same
 1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład II
 Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
TENSOMETRIA ZARYS TEORETYCZNY
 TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A
 PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej
PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej
Przekształcenia geometryczne. Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej
 Przekształcenia geometryczne Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Akademia Górniczo Hutnicza w Krakowie Przekształcenia elementarne w przestrzeni D Punkty p w E na płaszczyźnie
Przekształcenia geometryczne Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Akademia Górniczo Hutnicza w Krakowie Przekształcenia elementarne w przestrzeni D Punkty p w E na płaszczyźnie
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
A,B M! v V ; A + v = B, (1.3) AB = v. (1.4)
 Rozdział 1 Prosta i płaszczyzna 1.1 Przestrzeń afiniczna Przestrzeń afiniczna to matematyczny model przestrzeni jednorodnej, bez wyróżnionego punktu. Można w niej przesuwać punkty równolegle do zadanego
Rozdział 1 Prosta i płaszczyzna 1.1 Przestrzeń afiniczna Przestrzeń afiniczna to matematyczny model przestrzeni jednorodnej, bez wyróżnionego punktu. Można w niej przesuwać punkty równolegle do zadanego
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
= i Ponieważ pierwiastkami stopnia 3 z 1 są (jak łatwo wyliczyć) liczby 1, 1+i 3
 ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
Geometria Lista 0 Zadanie 1
 Geometria Lista 0 Zadanie 1. Wyznaczyć wzór na pole równoległoboku rozpiętego na wektorach u, v: (a) nie odwołując się do współrzędnych tych wektorów; (b) odwołując się do współrzędnych względem odpowiednio
Geometria Lista 0 Zadanie 1. Wyznaczyć wzór na pole równoległoboku rozpiętego na wektorach u, v: (a) nie odwołując się do współrzędnych tych wektorów; (b) odwołując się do współrzędnych względem odpowiednio
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Elementy geometrii analitycznej w R 3
 Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
1 Zbiory i działania na zbiorach.
 Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
Układy równań liniowych, macierze, Google
 Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ
 METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
Baza w jądrze i baza obrazu ( )
 Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
Jakobiany. Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA
 OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA Wprowadzenie W robotyce przez pojęcie manipulacji rozumiemy przemieszczanie w przestrzeni przedmiotów i narzędzi za pomocą specjalnego mechanizmu. W związku z tym pojawia
OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA Wprowadzenie W robotyce przez pojęcie manipulacji rozumiemy przemieszczanie w przestrzeni przedmiotów i narzędzi za pomocą specjalnego mechanizmu. W związku z tym pojawia
Przekształcenia geometryczne w grafice komputerowej. Marek Badura
 Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
Fizyka 1(mechanika) AF14. Wykład 5
 Fizyka 1(mechanika) 1100-1AF14 Wykład 5 Jerzy Łusakowski 30.10.2017 Plan wykładu Ziemia jako układ nieinercjalny Fizyka 1(mechanika) 1100-1AF14 Wykład 5 Dwaj obserwatorzy- związek między mierzonymi współrzędnymi
Fizyka 1(mechanika) 1100-1AF14 Wykład 5 Jerzy Łusakowski 30.10.2017 Plan wykładu Ziemia jako układ nieinercjalny Fizyka 1(mechanika) 1100-1AF14 Wykład 5 Dwaj obserwatorzy- związek między mierzonymi współrzędnymi
Algebra linowa w pigułce
 Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ
 ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 10. Homomorfizmy Definicja 1. Niech V, W będą dwiema przestrzeniami liniowymi nad ustalonym ciałem, odwzorowanie ϕ : V W nazywamy homomorfizmem
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 10. Homomorfizmy Definicja 1. Niech V, W będą dwiema przestrzeniami liniowymi nad ustalonym ciałem, odwzorowanie ϕ : V W nazywamy homomorfizmem
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ. 1. Ciała
 ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 1. Ciała Definicja 1. Układ { ; 0, 1; +, } złożony ze zbioru, dwóch wyróżnionych elementów 0, 1 oraz dwóch działań +:, : nazywamy ciałem
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 1. Ciała Definicja 1. Układ { ; 0, 1; +, } złożony ze zbioru, dwóch wyróżnionych elementów 0, 1 oraz dwóch działań +:, : nazywamy ciałem
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
Analiza stanu naprężenia - pojęcia podstawowe
 10. ANALIZA STANU NAPRĘŻENIA - POJĘCIA PODSTAWOWE 1 10. 10. Analiza stanu naprężenia - pojęcia podstawowe 10.1 Podstawowy zapisu wskaźnikowego Elementy konstrukcji znajdują się w przestrzeni fizycznej.
10. ANALIZA STANU NAPRĘŻENIA - POJĘCIA PODSTAWOWE 1 10. 10. Analiza stanu naprężenia - pojęcia podstawowe 10.1 Podstawowy zapisu wskaźnikowego Elementy konstrukcji znajdują się w przestrzeni fizycznej.
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Przekształcenia liniowe
 Przekształcenia liniowe Zadania Które z następujących przekształceń są liniowe? (a) T : R 2 R 2, T (x, x 2 ) = (2x, x x 2 ), (b) T : R 2 R 2, T (x, x 2 ) = (x + 3x 2, x 2 ), (c) T : R 2 R, T (x, x 2 )
Przekształcenia liniowe Zadania Które z następujących przekształceń są liniowe? (a) T : R 2 R 2, T (x, x 2 ) = (2x, x x 2 ), (b) T : R 2 R 2, T (x, x 2 ) = (x + 3x 2, x 2 ), (c) T : R 2 R, T (x, x 2 )
Drgania układu o wielu stopniach swobody
 Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
Układy współrzędnych
 Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
D l. D p. Rodzaje baz jezdnych robotów mobilnych
 ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
III.4 Ruch względny w przybliżeniu nierelatywistycznym. Obroty.
 III.4 Ruch względny w przybliżeniu nierelatywistycznym. Obroty. Newtonowskie absolutna przestrzeń i absolutny czas. Układy inercjalne Obroty Układów Współrzędnych Opis ruchu w UO obracających się względem
III.4 Ruch względny w przybliżeniu nierelatywistycznym. Obroty. Newtonowskie absolutna przestrzeń i absolutny czas. Układy inercjalne Obroty Układów Współrzędnych Opis ruchu w UO obracających się względem
1 Tensory drugiego rzędu jako odwzorowanie liniowe
 TNSORY Tensory drugiego rzędu jako odwzorowanie liniowe RozważmyzbiórLin n wszystkichliniowychodwzorowańwektorawwektorgdzieobawektorynależądo n ( n -nwymiarowaprzestrzeńukidesowa)takieodwzorowaniemożebyć
TNSORY Tensory drugiego rzędu jako odwzorowanie liniowe RozważmyzbiórLin n wszystkichliniowychodwzorowańwektorawwektorgdzieobawektorynależądo n ( n -nwymiarowaprzestrzeńukidesowa)takieodwzorowaniemożebyć
1 Przestrzeń liniowa. α 1 x α k x k = 0
 Z43: Algebra liniowa Zagadnienie: przekształcenie liniowe, macierze, wyznaczniki Zadanie: przekształcenie liniowe, jądro i obraz, interpretacja geometryczna. Przestrzeń liniowa Już w starożytności człowiek
Z43: Algebra liniowa Zagadnienie: przekształcenie liniowe, macierze, wyznaczniki Zadanie: przekształcenie liniowe, jądro i obraz, interpretacja geometryczna. Przestrzeń liniowa Już w starożytności człowiek
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
Wprowadzenie do grafiki maszynowej. Wprowadenie do geometrii maszynowej
 Wprowadzenie do grafiki maszynowej. Wprowadenie do geometrii maszynowej Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 61 Wprowadenie do geometrii
Wprowadzenie do grafiki maszynowej. Wprowadenie do geometrii maszynowej Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 61 Wprowadenie do geometrii
ALGEBRA z GEOMETRIA, ANALITYCZNA,
 ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
Lista nr 1 - Liczby zespolone
 Lista nr - Liczby zespolone Zadanie. Obliczyć: a) ( 3 i) 3 ( 6 i ) 8 c) (+ 3i) 8 (i ) 6 + 3 i + e) f*) g) ( 3 i ) 77 ( ( 3 i + ) 3i 3i h) ( + 3i) 5 ( i) 0 i) i ( 3 i ) 4 ) +... + ( 3 i ) 0 Zadanie. Przedstawić
Lista nr - Liczby zespolone Zadanie. Obliczyć: a) ( 3 i) 3 ( 6 i ) 8 c) (+ 3i) 8 (i ) 6 + 3 i + e) f*) g) ( 3 i ) 77 ( ( 3 i + ) 3i 3i h) ( + 3i) 5 ( i) 0 i) i ( 3 i ) 4 ) +... + ( 3 i ) 0 Zadanie. Przedstawić
Elementy grafiki komputerowej. Elementy geometrii afinicznej
 Elementy grafiki komputerowej. Elementy geometrii j Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 28 Elementy geometrii j Najnowsza wersja
Elementy grafiki komputerowej. Elementy geometrii j Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 28 Elementy geometrii j Najnowsza wersja
Informatyka Stosowana. a b c d a a b c d b b d a c c c a d b d d c b a
 Działania na zbiorach i ich własności Informatyka Stosowana 1. W dowolnym zbiorze X określamy działanie : a b = b. Pokazać, że jest to działanie łączne. 2. W zbiorze Z określamy działanie : a b = a 2 +
Działania na zbiorach i ich własności Informatyka Stosowana 1. W dowolnym zbiorze X określamy działanie : a b = b. Pokazać, że jest to działanie łączne. 2. W zbiorze Z określamy działanie : a b = a 2 +
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
1. Liczby zespolone i
 Zadania podstawowe Liczby zespolone Zadanie Podać część rzeczywistą i urojoną następujących liczb zespolonych: z = ( + 7i)( + i) + ( 5 i)( + 7i), z = + i, z = + i i, z 4 = i + i + i i Zadanie Dla jakich
Zadania podstawowe Liczby zespolone Zadanie Podać część rzeczywistą i urojoną następujących liczb zespolonych: z = ( + 7i)( + i) + ( 5 i)( + 7i), z = + i, z = + i i, z 4 = i + i + i i Zadanie Dla jakich
Met Me ody numer yczne Wykład ykład Dr inż. Mic hał ha Łanc Łan zon Instyt Ins ut Elektr Elektr echn iki echn i Elektrot Elektr echn olo echn
 Metody numeryczne Wykład 3 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Pojęcia podstawowe Algebra
Metody numeryczne Wykład 3 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Pojęcia podstawowe Algebra
Drgania i fale II rok Fizyk BC
 00--07 5:34 00\FIN00\Drgzlo00.doc Drgania złożone Zasada superpozycji: wychylenie jest sumą wychyleń wywołanych przez poszczególne czynniki osobno. Zasada wynika z liniowości związku między wychyleniem
00--07 5:34 00\FIN00\Drgzlo00.doc Drgania złożone Zasada superpozycji: wychylenie jest sumą wychyleń wywołanych przez poszczególne czynniki osobno. Zasada wynika z liniowości związku między wychyleniem
Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Zajmijmy się najpierw pierwszym równaniem. Zapiszmy je w postaci trygonometrycznej, podstawiając z = r(cos ϕ + i sin ϕ).
 Zad (0p) Zaznacz na płaszczyźnie zespolonej wszystkie z C, które spełniają równanie ( iz 3 z z ) Re [(z + 3) ( z 3) = 0 Szukane z C spełniają: iz 3 = z z Re [(z + 3) ( z 3) = 0 Zajmijmy się najpierw pierwszym
Zad (0p) Zaznacz na płaszczyźnie zespolonej wszystkie z C, które spełniają równanie ( iz 3 z z ) Re [(z + 3) ( z 3) = 0 Szukane z C spełniają: iz 3 = z z Re [(z + 3) ( z 3) = 0 Zajmijmy się najpierw pierwszym
Więzy i ich klasyfikacja Wykład 2
 Więzy i ich klasyfikacja Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
Więzy i ich klasyfikacja Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
MECHANIKA 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO. Wykład Nr 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
1 Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych
 Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych 2. Wektory. 2.. Wektor jako n ka liczb W fizyce mamy do czynienia z pojęciami lub obiektami o różnym charakterze. Są np. wielkości,
Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych 2. Wektory. 2.. Wektor jako n ka liczb W fizyce mamy do czynienia z pojęciami lub obiektami o różnym charakterze. Są np. wielkości,
Przestrzenie liniowe
 Rozdział 4 Przestrzenie liniowe 4.1. Działania zewnętrzne Niech X oraz F będą dwoma zbiorami niepustymi. Dowolną funkcję D : F X X nazywamy działaniem zewnętrznym w zbiorze X nad zbiorem F. Przykład 4.1.
Rozdział 4 Przestrzenie liniowe 4.1. Działania zewnętrzne Niech X oraz F będą dwoma zbiorami niepustymi. Dowolną funkcję D : F X X nazywamy działaniem zewnętrznym w zbiorze X nad zbiorem F. Przykład 4.1.
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki opracowanie Spis treści I Wyrażenia algebraiczne, indukcja matematyczna 2 II Geometria analityczna w R 2 4 III Liczby zespolone 5
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki opracowanie Spis treści I Wyrażenia algebraiczne, indukcja matematyczna 2 II Geometria analityczna w R 2 4 III Liczby zespolone 5
Macierze i Wyznaczniki
 dr Krzysztof Żyjewski MiBM; S-I 0.inż. 0 października 04 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Definicja. Iloczynem macierzy A = [a ij m n, i macierzy B = [b ij n p nazywamy macierz
dr Krzysztof Żyjewski MiBM; S-I 0.inż. 0 października 04 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Definicja. Iloczynem macierzy A = [a ij m n, i macierzy B = [b ij n p nazywamy macierz
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
13 Układy równań liniowych
 13 Układy równań liniowych Definicja 13.1 Niech m, n N. Układem równań liniowych nad ciałem F m równaniach i n niewiadomych x 1, x 2,..., x n nazywamy koniunkcję równań postaci a 11 x 1 + a 12 x 2 +...
13 Układy równań liniowych Definicja 13.1 Niech m, n N. Układem równań liniowych nad ciałem F m równaniach i n niewiadomych x 1, x 2,..., x n nazywamy koniunkcję równań postaci a 11 x 1 + a 12 x 2 +...
Dr inż. Janusz Dębiński Mechanika ogólna Wykład 2 Podstawowe wiadomości z matematyki Kalisz
 Dr inż. Janusz Dębiński Mechanika ogólna Wykład 2 Podstawowe wiadomości z matematyki Kalisz Dr inż. Janusz Dębiński 1 2.1. Przestrzeń i płaszczyzna Podstawowe definicje Punkt - najmniejszy bezwymiarowy
Dr inż. Janusz Dębiński Mechanika ogólna Wykład 2 Podstawowe wiadomości z matematyki Kalisz Dr inż. Janusz Dębiński 1 2.1. Przestrzeń i płaszczyzna Podstawowe definicje Punkt - najmniejszy bezwymiarowy
Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u
 Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u W ) Rzeczywiście U W jest podprzetrzenią przestrzeni
Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u W ) Rzeczywiście U W jest podprzetrzenią przestrzeni
Rachunek wektorowy - wprowadzenie. dr inż. Romuald Kędzierski
 Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Zagadnienie dwóch ciał
 Zagadnienie dwóch ciał Rysunek : Rysunek ilustrujący zagadnienie dwóch ciał. Wektor R określa położenie środka masy, wektor x położenie masy m, a wektor x 2 położenie masy m 2. Położenie masy m 2 względem
Zagadnienie dwóch ciał Rysunek : Rysunek ilustrujący zagadnienie dwóch ciał. Wektor R określa położenie środka masy, wektor x położenie masy m, a wektor x 2 położenie masy m 2. Położenie masy m 2 względem
Przestrzeń unitarna. Jacek Kłopotowski. 23 października Katedra Matematyki i Ekonomii Matematycznej SGH
 Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora
 Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
Liczby zespolone. Magdalena Nowak. 23 marca Uniwersytet Śląski
 Uniwersytet Śląski 23 marca 2012 Ciało liczb zespolonych Rozważmy zbiór C = R R, czyli C = {(x, y) : x, y R}. W zbiorze C definiujemy następujące działania: dodawanie: mnożenie: (a, b) + (c, d) = (a +
Uniwersytet Śląski 23 marca 2012 Ciało liczb zespolonych Rozważmy zbiór C = R R, czyli C = {(x, y) : x, y R}. W zbiorze C definiujemy następujące działania: dodawanie: mnożenie: (a, b) + (c, d) = (a +
Ćwiczenia nr 4. TEMATYKA: Rzutowanie
 TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
1 Macierze i wyznaczniki
 1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
Podstawy robotyki wykład V. Jakobian manipulatora. Osobliwości
 Podstawy robotyki Wykład V Jakobian manipulatora i osobliwości Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Metoda bezpośrednia uzyskania macierzy
Podstawy robotyki Wykład V Jakobian manipulatora i osobliwości Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Metoda bezpośrednia uzyskania macierzy
DB Algebra liniowa semestr zimowy 2018
 DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Pokazać, że wyżej zdefiniowana struktura algebraiczna jest przestrzenią wektorową nad ciałem
 Zestaw zadań 9: Przestrzenie wektorowe. Podprzestrzenie () Wykazać, że V = C ze zwykłym dodawaniem jako dodawaniem wektorów i operacją mnożenia przez skalar : C C C, (z, v) z v := z v jest przestrzenią
Zestaw zadań 9: Przestrzenie wektorowe. Podprzestrzenie () Wykazać, że V = C ze zwykłym dodawaniem jako dodawaniem wektorów i operacją mnożenia przez skalar : C C C, (z, v) z v := z v jest przestrzenią
Układy równań liniowych
 Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
3 1 + i 1 i i 1 2i 2. Wyznaczyć macierze spełniające własność komutacji: [A, X] = B
![3 1 + i 1 i i 1 2i 2. Wyznaczyć macierze spełniające własność komutacji: [A, X] = B 3 1 + i 1 i i 1 2i 2. Wyznaczyć macierze spełniające własność komutacji: [A, X] = B](/thumbs/73/69286698.jpg) 1. Dla macierzy a) A = b) A = c) A = d) A = 3 1 + i 1 i i i 0 i i 0 1 + i 1 i 0 0 0 0 1 0 1 0 1 + i 1 i Wyznaczyć macierze spełniające własność komutacji: A, X = B. Obliczyć pierwiaski z macierzy: A =
1. Dla macierzy a) A = b) A = c) A = d) A = 3 1 + i 1 i i i 0 i i 0 1 + i 1 i 0 0 0 0 1 0 1 0 1 + i 1 i Wyznaczyć macierze spełniające własność komutacji: A, X = B. Obliczyć pierwiaski z macierzy: A =
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..)
 Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie Teoria sprężystości jest działem mechaniki, zajmującym się bryłami sztywnymi i ciałami plastycznymi. Sprężystość zajmuje się odkształceniami
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie Teoria sprężystości jest działem mechaniki, zajmującym się bryłami sztywnymi i ciałami plastycznymi. Sprężystość zajmuje się odkształceniami
n=0 (n + r)a n x n+r 1 (n + r)(n + r 1)a n x n+r 2. Wykorzystując te obliczenia otrzymujemy, że lewa strona równania (1) jest równa
 Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Układy fizyczne z więzami Wykład 2
 Układy fizyczne z więzami Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
Układy fizyczne z więzami Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
ALGEBRA LINIOWA 2. Lista zadań 2003/2004. Opracowanie : dr Teresa Jurlewicz, dr Zbigniew Skoczylas
 ALGEBRA LINIOWA 2 Lista zadań 23/24 Opracowanie : dr Teresa Jurlewicz dr Zbigniew Skoczylas Lista pierwsza Zadanie Uzasadnić z definicji że zbiór wszystkich rzeczywistych macierzy trójkątnych górnych stopnia
ALGEBRA LINIOWA 2 Lista zadań 23/24 Opracowanie : dr Teresa Jurlewicz dr Zbigniew Skoczylas Lista pierwsza Zadanie Uzasadnić z definicji że zbiór wszystkich rzeczywistych macierzy trójkątnych górnych stopnia
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
Pole magnetyczne magnesu w kształcie kuli
 napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
Podstawy elektromagnetyzmu. Wykład 1. Rachunek wektorowy
 Podstawy elektromagnetyzmu Wykład 1 Rachunek wektorowy Co to jest,,pole? Matematyka: odwzorowanie Rn Rm które przypisuje każdemu punktowi wartość (skalarną lub wektorową). Fizyka: Własność przestrzeni
Podstawy elektromagnetyzmu Wykład 1 Rachunek wektorowy Co to jest,,pole? Matematyka: odwzorowanie Rn Rm które przypisuje każdemu punktowi wartość (skalarną lub wektorową). Fizyka: Własność przestrzeni
Symetrie i prawa zachowania Wykład 6
 Symetrie i prawa zachowania Wykład 6 Karol Kołodziej Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna 1/29 Rola symetrii Największym
Symetrie i prawa zachowania Wykład 6 Karol Kołodziej Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna 1/29 Rola symetrii Największym
WEKTORY I MACIERZE. Strona 1 z 11. Lekcja 7.
 Strona z WEKTORY I MACIERZE Wektory i macierze ogólnie nazywamy tablicami. Wprowadzamy je:. W sposób jawny: - z menu Insert Matrix, - skrót klawiszowy: {ctrl}+m, - odpowiedni przycisk z menu paska narzędziowego
Strona z WEKTORY I MACIERZE Wektory i macierze ogólnie nazywamy tablicami. Wprowadzamy je:. W sposób jawny: - z menu Insert Matrix, - skrót klawiszowy: {ctrl}+m, - odpowiedni przycisk z menu paska narzędziowego
Laboratorium z Krystalografii. 2 godz.
 Uniwersytet Śląski - Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40-006 Katowice tel. 0323591627, e-mail: ewa.malicka@us.edu.pl opracowanie: dr Ewa Malicka Laboratorium z Krystalografii
Uniwersytet Śląski - Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40-006 Katowice tel. 0323591627, e-mail: ewa.malicka@us.edu.pl opracowanie: dr Ewa Malicka Laboratorium z Krystalografii
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
21 Symetrie Grupy symetrii Grupa translacji
 21 Symetrie 21.1 Grupy symetrii Spróbujmy odpowiedzieć sobie na pytanie, jak zmienia się stan układu kwantowego pod wpływem transformacji układu współrzędnych. Najprostszą taką transformacją jest np. przesunięcie
21 Symetrie 21.1 Grupy symetrii Spróbujmy odpowiedzieć sobie na pytanie, jak zmienia się stan układu kwantowego pod wpływem transformacji układu współrzędnych. Najprostszą taką transformacją jest np. przesunięcie
