PORÓWNANIE METOD ESTYMACJI ZMIENNYCH STANU W UKŁADZIE KASKADOWYM DWÓCH ZBIORNIKÓW
|
|
|
- Stanisław Brzeziński
- 8 lat temu
- Przeglądów:
Transkrypt
1 Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki Politechniki Gdańskiej Nr 3 XXII Seminarium ZASOSOWANIE KOMPUERÓW W NAUCE I ECHNICE 1 Oddział Gdański PEiS Referat nr 9 PORÓWNANIE MEOD ESYMACJI ZMIENNYCH SANU W UKŁADZIE KASKADOWYM DWÓCH ZBIORNIKÓW Mirosław OMERA 1, Karol POZORSKI 1. Akademia Morska w Gdyni, Wydział Elektryczny, ul. Morska 83, 81-5 Gdynia tel: fax: tomera@am.gdynia.pl. Venture Industries Sp. z o.o., ul. Mokra 7, 5-9 Łomianki-Kiełpin tel: fax: karol.pozorski@venture.pl Streszczenie: W pracy przedstawiona została analiza porównawcza dokonana pomiędzy trzema obserwatorami stanu: obserwatorem liniowym Luengergera oraz dwoma filtrami Kalmana: liniowym i rozszerzonym (EKF Extended Kalman Filter) opierająca się ocenie dokładności estymacji zmiennych stanu. Analizowany obiekt w którym estymowane są zmienne stanu, składa się z dwóch zbiorników zawieszonych kaskadowo. Rozpatrzony został przypadek w którym pomiar poziomu wody odbywa się tylko w dolnym zbiorniku, natomiast informacja o poziomie wody w górnym zbiorniku uzyskiwana jest w wyniku estymacji. Analizowane obserwatory wykorzystane zostały w układzie sterowania poziomem wody w dolnym zbiorniku przy użyciu regulatora stanu, który wymaga znajomości poziomu wody w obydwu zbiornikach. Dodatkowo dokonano porównania jakości sterowania układów regulacji z wykorzystaniem regulatora stanu w konfiguracji z wyżej wymienionymi obserwatorami oraz z użyciem regulatora PID, który wykorzystuje tylko pomiar poziomu wody w dolnym zbiorniku i nie potrzebuje obserwatora. Wstępnie przeprowadzone zostały badania symulacyjne z wykorzystaniem środowiska obliczeniowego MALAB/Simulink. Badania docelowe wykonane zostały w układzie rzeczywistym, gdzie zaprojektowane obserwatory wraz z regulatorami zaprogramowane zostały w mikrokontrolerze sygnałowym MS3F8335, wykorzystanym do automatycznego sterowania poziomem wody w zbiorniku dolnym. Słowa kluczowe: obserwatory, regulator stanu, regulator PID 1. WPROWADZENIE Pojęcie obserwatorów często utożsamiane jest tzw. estymatorami, czyli układami śledzącymi zmienność stanu procesów dynamicznych na podstawie wiedzy o aktualnym stanie wejść i wyjść. Model matematyczny, służący do właściwego odwzorowania zachowań procesu jest podstawą działania obserwatora [1]. Rozważone zostały trzy obserwatory: liniowy obserwator Luenbergera oraz dwa obserwatory wykorzystujące filtr Kalmana: liniowy i rozszerzony. Ze względu na docelową implementację obserwatorów w cyfrowym procesorze sygnałowym przyjęto od początku rozważania w dziedzinie czasu dyskretnego. W niniejszej pracy przedstawione obserwatory zostały wykorzystane do estymacji poziomów wody w układzie Rys. 1. Struktura układu kaskadowego dwóch zbiorników kaskadowym dwóch zbiorników, schematycznie pokazanym na rysunku 1. Rozpatrzony został przypadek estymacji poziomu w zbiorniku górnym i dodatkowo zaprojektowane obserwatory wykorzystane zostały w układzie regulacji z regulatorem stanu do sterowania poziomem wody w dolnym zbiorniku. W praktyce, najczęściej stosowanym regulatorem w układach sterowania automatycznego jest regulator PID. Regulator ten również został wykorzystany do sterowania poziomem wody w dolnym zbiorniku i nie wymaga stosowania obserwatora, wystarczy tylko pomiar poziomu wody w dolnym zbiorniku. W ten sposób zostały uzyskane dwa typy układów sterowania, obydwa wykorzystujące pomiar poziomu wody w dolnym zbiorniku. Pierwszy typ uzyskanego układu sterowania wykorzystujący zmienne stanu, pokazany został na rysunku, natomiast drugi typ układu sterowania z regulatorem PID na rysunku 3. Zaprojektowane obserwatory wraz z regulatorami zaprogramowane zostały w mikrokontrolerze sygnałowym MS3F8335 W układzie sterowania z rysunku, regulator stanu wraz z obserwatorami projektowane były metodą bezpośrednią w dziedzinie czasu dyskretnego z okresem próbkowania = 1 [s], natomiast regulator PID pracujący Recenzent: Dr hab. inż. Kazimierz Duzinkiewicz Wydział Elektrotechniki i Automatyki Politechnika Gdańska
2 Rys.. Struktura projektowanego układu sterowania z obserwatorem i regulatorem stanu Rys. 3. Struktura projektowanego układu sterowania z regulatorem PID w układzie z rysunku 3, zaprojektowany został metodą emulacji. Metoda emulacji polega na tym, że projektowanie przeprowadzane jest w dziedzinie czasu ciągłego i następnie uzyskany algorytm sterowania konwertowany jest w dziedzinę czasu dyskretnego, w tym przypadku również z okresem próbkowania = 1 [s]. Szczegóły związane z projektowaniem regulatorów zastosowanych w układach sterowania pokazanych na rysunkach i 3 nie zostaną tutaj przedstawione. Opis syntezy regulatora PID zastosowanego do sterowania poziomem w dolnym zbiorniku można znaleźć w pracy [], natomiast regulatora stanu zastosowanego w układzie sterowania z rysunku znajduje się w pracy [3].. MODEL MAEMAYCZNY OBIEKU SEROWANIA Szczegółowy sposób wyznaczenia modelu matematycznego, rozważanego tutaj układu kaskadowego dwóch zbiorników można znaleźć w pracy [3]. utaj przedstawione zostaną najważniejsze równania, niezbędne przy projektowaniu regulatorów i obserwatorów stanu. Układ kaskadowy dwóch zbiorników opisany jest nieliniowymi równaniami różniczkowymi. Dynamika zmian poziomu wody w zbiornikach: górnym i dolnym opisana jest następującymi wzorami dh1 1 gh1 u( U min (1) dt dh 1 gh1 gh () dt gdzie: 1 =.6, =.18, =.3737 współczynniki, g = 981 [cm/s] przyśpieszenie ziemskie, U min = [V] próg minimalny zadziałania pompy, h 1 poziom wody w górnym zbiorniku, h poziom wody w dolnym zbiorniku, u sygnał sterujący pompą, wyjście w regulatora. Charakterystyka czujnika pomiaru poziomu wody w dolnym zbiorniku aproksymowana jest wzorem y c (3) k h b gdzie k c =.583 wzmocnienie, b =.8666 współczynnik przesunięcia. Projektowanie obserwatorów wymagało liniowego modelu matematycznego obiektu i w tym celu dokonana została linearyzacja modelu opisanego wzorami (1), () i (3) w otoczeniu następującego punktu pracy 1 u, h, h, y = (3.6; 11.3; 1.; 1.4) (4) Pozwoliło to wyznaczyć ciągły model liniowy opisanymi następującymi równaniami stanu d dt 1 x1( 1 x ( ) 1 t 1 x1( k u( 1 x gdzie: x 1 (= h 1 (, x ( = h ( zmienne stanu, u( sygnał sterujący, 1 = [s], = [s] stałe czasowe, k =.1679 wzmocnienie. i równaniem wyjścia (5) x1( y.14 (6) x gdzie: y( sygnał powierzony, wyjście z czujnika. Aby obserwatory stanu na swoich wyjściach wyznaczały wysokości poziomów wody wyrażone w centymetrach to pomierzony sygnał wejściowy z czujnika wyrażony w woltach, na wejściu obserwatorów został przeskalowany przez odwrotną charakterystykę czujnika h k y b (7) zm o o gdzie k o = , b o = Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN , Nr 31/1
3 Charakterystyka ta umieszczona na wejściu obserwatora stanu znosi charakterystykę czujnika i powoduje, że zmianie ulega równanie wyjścia (6) i po tej korekcie przyjmuje postać x1( y( Cx 1 (8) x Obserwatory stanu, docelowo będą implementowane w cyfrowym procesorze sygnałowym, dlatego też projektowane ich przeprowadzone zostało w przestrzeni czasu dyskretnego. W tym celu uzyskany ciągły model liniowy opisany wzorami (5) i (8) został przekonwertowany do postaci dyskretnej z okresem próbkowania = 1 [s]. x ( k 1) F x( G u( (9) y( H x( (1) gdzie F dyskretna macierz stanu, G dyskretna macierz wejścia, H dyskretna macierz wyjścia F G (11).1 H C 1 (1) Szczegóły dotyczące konwersji równań dynamicznych ciągłych do postaci dyskretnej można znaleźć w pracy [3]. 3. OBSERWAORY SANU Regulator stanu, zastosowany w układzie sterowania pokazanym na rysunku wymaga znajomości wszystkich zmiennych stanu, w tym przypadku są to poziomy wody w zbiornikach górnym i dolnym. W układzie tym mierzony jest poziom tylko w zbiorniku dolnym i brakujący poziom wody w górnym zbiorniku musi być rekonstruowany na podstawie znajomości modelu matematycznego obiektu przez obserwator stanu Obserwator liniowy Luenbergera Pierwszy z projektowanych obserwatorów wykorzystuje liniowy model matematyczny obiektu opisany równaniami (9), (1) i równanie estymacji wektora stanu przyjmuje postać xˆ ( k 1) Fxˆ( Gu( (13) Rys. 4. Obserwator liniowy pracujący w pętli otwartej wówczas rozbieżność powinna zostać zminimalizowana. Idea ta służy do skonstruowania układu ze sprzężeniem wokół obserwatora pracującego w otwartej pętli z estymowanym błędem wyjściowym jako sprzężeniem. Schemat ten pokazany został na rysunku 5, równanie dla tego układu ma postać [1] xˆ ( k 1) Fxˆ( Gu( L y( Hxˆ( (14) gdzie L l1 l jest wektorem wzmocnień sprzężenia obserwatora. Po przekształceniu równania (14) xˆ ( k 1) [ F LH] xˆ( Gu( Ly( (15) wyznaczona zostaje macierz stanu obserwatora [FLH]. Jeśli układ ten będzie asymptotycznie stabilny to wówczas błąd estymacji obserwatora będzie zanikał do zera. Macierz wzmocnień L obserwatora liniowego składa się z dwóch elementów i wyznaczana jest w taki sposób aby wartości własne macierzy [FLH] pokrywały się z pożądanymi położeniami 1, na płaszczyźnie z celem uzyskania pożądanego równania charakterystycznego estymatora e ( 1 e1 e z) ( z )( z ) z z (16) Pożądane położenia biegunów obserwatora wyrażają jego dynamikę i określają jak szybko wektor stanu obserwatora zbiega się z wektorem stanu obiektu. W projektowanym obserwatorze liniowym Luenbergera przyjęto, że bieguny będą miały odpowiedź impulsową cztery razy szybszą od zanikania odpowiedzi impulsowej biegunów regulatora stanu. gdzie ˆ ˆ ˆ ˆ ˆ x x1 x h1 h estymowany wektor zmiennych stanu. Znając macierze F, G oraz wejście u( można zbudować obserwator, który będzie poprawnie pracował jeśli otrzyma warunki początkowe xˆ, równe wartościom początkowym obiektu. Na rysunku 4 przedstawiony został obserwator pracujący w pętli otwartej. Jeśli obserwator pracuje w pętli otwartej i nie wykorzystuje żadnych pomiarów o zachowaniu obiektu to można się spodziewać, że estymowany wektor zmiennych stanu będzie się różnił od wartości poprawnych. Jeśli natomiast do obserwatora wprowadzona zostanie różnica pomiędzy wyjściami: pomierzonymi i estymowanymi oraz będzie ciągle korygować model tym sygnałem błędu to Rys. 5. Obserwator liniowy pracujący w pętli zamkniętej Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN , Nr 31/1 133
4 gdzie =.6, 1, n jn 1 s (17) n =.14. Bieguny te zostały przekonwertowane na płaszczyznę z przy użyciu przekształcenia gdzie = 1 [s] okres próbkowania. s i i e, i = 1, (18) Wyznaczenie macierzy L można to uzyskać dwoma metodami: lokowania biegunów i Ackermana. Poniżej przedstawione zostały obydwie te metody. Metoda lokowania biegunów Postać równania charakterystycznego uzyskiwana z opisu macierzowego obserwatora (13) jest następująca z I F LH (19) Równania (16) oraz (19) muszą być identyczne. Dlatego też współczynniki każdej potęgi zmiennej z muszą być takie same, uzyska się w ten sposób w rozważanym przypadku dwa równania z dwoma nieznanymi elementami wektora wzmocnień L. W wyniku przeprowadzonych obliczeń, metodą lokowania biegunów uzyskane zostały następujące wartości wzmocnień regulatora stanu L () Metoda Ackermana Inną metodą wyznaczania wzmocnień L dla obserwatora liniowego jest metoda Ackermana, która opiera się na następującym wzorze 1 L e ( F) O (1) 1 procesu sterowanego, modelowanego przez liniowe, stochastyczne równanie różnicowe. W tym celu równanie (9) zostanie zapisane jako x( k 1) Fx( k 1) Gu( Ew( (5) Obserwacje (pomiary) procesu dokonywane są w dyskretnych chwilach czasowych i opisane są przez równanie (1) rozszerzone do postaci y ( Hx( v( (6) gdzie w ( są zakłóceniami przypadkowymi wpływającymi na proces, v ( błędy pomiarowe. Zakłada się, że sygnały w ( oraz v ( są o zerowej wartości średniej i nie ma żadnej korelacji pomiędzy tymi sygnałami. Macierze kowariancji dla sygnałów stochastycznych w ( i v ( opisane są następująco Q i k Ew( w( i) (7), i k R i k Ev ( v( i) (8), i k w ( v( i) E (9) Zakłada się, że znane są wartości początkowe estymat procesu w pewnej chwili czasu t ( i ta estymata będzie oznaczana jako x ( gdzie kreska będzie oznaczała, że jest to najlepsza estymata przed pomiarem w chwili t (. eraz zdefiniowany zostanie błąd estymacji jako e( x( x( (3) i powiązana z tą różnicą macierz kowariancji błędu gdzie e (F ) jest macierzą zdefiniowaną następująco e ( F e1 e ) F F I () ei są pożądanymi współczynnikami wielomianu charakterystycznego (16), O jest macierzą obserwowalności składającą się z następujących wierszy H O (3) HF Warunkiem istnienia rozwiązania jest obserwowalność układu, czyli wyznacznik macierzy obserwowalności O musi być różny od zera. W wyniku przeprowadzonych tą metodą obliczeń uzyskano identyczne rozwiązanie jak metodą lokowania biegunów L (4) x( x( x( ( k P ( k ) E e( e ( E x ) (31) W chwilach próbkowania t (, w których dokonywany będzie pomiar y, posiadana estymata x ( będzie korygowana według następującej zależności [1] P( k ) E e( e ( E x( xˆ( x( xˆ( (33) 3.. Filtr Kalmana W sposób ogólny można stwierdzić, że filtr Kalmana Estymaty w czasie pomiędzy chwilami próbkowania próbuje wyestymować w sposób optymalny wektor stanu 134 Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN , Nr 31/1 xˆ ( x( L( y( Hx( (3) gdzie x ˆ( estymata zauktualizowana o dokonany pomiar, L( wzmocnienie skalujące. eraz problemem jest znalezienie takich wzmocnień wektora L ( które będą aktualizować estymatę w sposób optymalny. W tym celu przeprowadzona zostanie minimalizacja błędu średnio kwadratowego. Zdefiniowana zostanie macierz kowariancji błędu związanego z estymatą zaktualizowaną przez uzyskany pomiar
5 Na rysunku 6, w postaci schematu blokowego przedstawiony został rekurencyjny algorytm obliczeniowy, oparty na równaniach (3), (34), (35), (38), (39) powszechnie znany jako filtr Kalmana Rozszerzony filtr Kalmana Rozszerzony filtr Kalmana (EKF Extended Kalman Filter) działa w oparciu o zasadę pokazaną na rysunku 6, z tą różnicą, że w bloku oznaczonym jako Prognoza w przód, zamiast równania (34) wykorzystywany jest nieliniowy model matematyczny obiektu opisany równaniami (1) i (). Stan x ( k 1) wyznaczany jest przez zastosowanie całkowania numerycznego gdzie f x( k 1) xˆ( xˆ(, u( (4) 1 gxˆ 1( u( U min f (ˆ( x, u( ) (41) 1 gxˆ 1( gxˆ ( Rys. 6. Algorym filtru Kalmana wyznaczane będą z następującego wzoru x( k 1) Fxˆ( Gu( (34) W pierwszej kolejności wyznaczona zostanie macierz kowariancji P ( k 1) w oparciu o wzór (33) po skorygowaniu jej o jedną próbkę do przodu x( k 1) x( k 1) x( k 1) ( k 1 P ( k 1) E x ) (35) Po podstawieniu do wzoru (35) zależności (5) i (34) po przekształceniach uzyskuje się P( k 1) FP( F EQE (36) Po podstawieniu do wzoru (33) zależności (3) otrzymuje się P( P( L( HP( P( H L( HP ( H R L ( L ( (37) Poszukiwana jest taka wartość wektora wzmocnień L (, która zminimalizuje macierz P (, będącą sumą błędów średnio-kwadratowych estymat wszystkich elementów wektora stanu. Po zróżniczkowaniu macierzy P ( w odniesieniu do macierzy L ( i przyrównaniu uzyskanego wyniku do zera uzyskuje się wyrażenie na macierz wzmocnień filtru Kalmana HP( H R 1 L ( P( H (38) Podstawienie uzyskanego wyrażenia (38) do wzoru (37), upraszcza macierz kowariancji błędu estymacji do postaci I L( H P( ) P( P( L( HP( k (39) 4. BADANIA UKŁADÓW SEROWANIA I OBSERWAORÓW SANU W pierwszej kolejności, zaprojektowane układy obserwatorów stanu zostały zaimplementowane w środowisku obliczeniowym MALAB/Simulink w postaci S-funkcji, zapisanych w kodzie języka C w układzie sterowania pokazanym na rysunku. Etap miał za zadanie przygotowanie kodów źródłowych algorytmów, które następnie były implementowane w procesorze sygnałowym. Przebadane zostały cztery układy sterowania, trzy z nich zawierały zaprojektowane obserwatory pracujące w układzie z regulatorem stanu (Rys. ), natomiast czwarty układ sterowania wykorzystywał sam regulator PID bez obserwatora. Wszystkie te układy sterowania działały w oparciu o poziom wody pomierzony w dolnym zbiorniku. Uzyskane wyniki sterowania pokazane zostały na rysunkach 7 1. Ocena jakości sterowania rozważanych układów regulacji polegała na ocenie wskaźników jakości definiowanych na podstawie odpowiedzi skokowej i były to: maksymalne przeregulowanie M p, czas regulacji t R mierzony przy strefie dokładności = 5%. Dodatkowo na każdym odcinku stabilizacji poziomu, na podstawie pomierzonych wartości poziomu i sygnału sterującego wyznaczany był funkcjonał J N e u ( k (, N = 4/.5 = 16 (4) gdzie: e(=h zad (h ( uchyb regulacji, u( sygnał sterujący pompą, wyjście w regulatora Uzyskane wyniki parametrów oceny jakości sterowania na poszczególnych odcinkach stabilizacji poziomu wody w dolnym zbiorniku, zawarte są w tabeli 1. W układzie rzeczywistym dodatkowo mierzony był poziom wody w górnym zbiorniku, który posłużył do oceny dokładności estymacji poziomu w zbiorniku górnym. Sygnały pomierzone przez czujniki poziomu wymagały filtracji w celu wyeliminowania z nich szumów pomiarowych [1, 3]. Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN , Nr 31/1 135
6 Regulator stanu + Rys. 7 Wyniki sterowania poziomem wody w dolnym zbiorniku użyciem regulatora PID w układzie z rysunku 3 Rys 8. Wyniki sterowania poziomem wody w dolnym zbiorniku z użyciem regulatora stanu i estymatora liniowego Luenbergera abela 1 Wskaźniki oceny jakości sterowania z wykresów czasowych pokazanych na rysunkach 7-1 yp układu Odcinek 1 ( s 4 s) Odcinek (4 s 8 s) Odcinek 3 (8 s 1 s) M p t R J M p t R J M p t R J J c [%] [s] [-] [%] [s] [-] [%] [s] [-] [-] Regulator PID 18,53, 186,8 47, - 834,9 4,8 39,5 1845, 6487, estymator liniowy 1,7 16,5 665,4 7,71 195, 781, 3,79 137,5 5,3 7496,7 filtr Kalmana 3,91 17, 95,8 7,34, 314,9,5 135, 13,9 8143,7 rozszerzony filtr Kalmana (EKF),35 5, 3136,4, 13,5 3685,6 1,38 135, 86,6 918,6 136 Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN , Nr 31/1
7 Rys. 9. Wyniki sterowania poziomem wody w dolnym zbiorniku z użyciem regulatora stanu i filtrem Kalmana w układzie z rys. Rys. 1. Wyniki sterowania poziomem wody w dolnym zbiorniku z użyciem regulatora stanu i rozszerzonym filtrem Kalmana (EKF) Przebiegi czasowe poziomu wody w górnym zbiorniku: pomierzonego h 1 zm i estymowanego ĥ 1 pokazane zostały na rysunku 11. Ocena dokładności estymacji polegała na wyznaczeniu pierwiastka błędu średniokwadratowego (RMSE - Root Mean Square Error) RMSE 1 N N k ( h1 zm h ˆ 1), N = 1/.5 = 48 (43) abela. Wskaźniki oceny dokładności estymacji poziomu w zbiorniku górnym (RMSE) Estymator liniowy Filtr Kalmana Rozszerzony filtr Kalmana [cm] [cm] [cm] Symulacje Weryfikacje Uzyskane wyniki zawarte zostały w tabeli. Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN , Nr 31/1 137
8 Rys. 11. Wyniki estymacji poziomu wody w zbiorniku górnym (linia ciągła poziom pomierzony h 1, linia przerywana poziom estymowany h 1 e ) 5. WNIOSKI KOŃCOWE Badania zaprojektowanych obserwatorów stanu przeprowadzone zostały w układzie sterowania poziomem wody w dolnym zbiorniku. Jako obserwatory stanu niemierzonego rozpatrzone zostały trzy układy: obserwator liniowy Luenbergera, filtr Kalmana i rozszerzony filtr Kalmana. Przeprowadzone badania pokazały, że regulator stanu we współpracy z obserwatorami stanu niemierzonego pozwala na uzyskanie zdecydowanie lepszej jakości sterowania (Rys. 8-1) niż regulator PID (Rys. 7). Przedstawione wyniki badań pokazały, że największą dokładność estymacji poziomu wody w górnym zbiorniku uzyskano przy wykorzystaniu rozszerzonego filtru Kalmana (EKF). Największa dokładność estymacji tego obserwatora przełożyła się również na najlepszą jakość sterowania poziomem wody w dolnym zbiorniku. 6. BIBLIOGRAFIA 1. Pozorski K.: Filtracja optymalna sygnałów pomierzonych w układzie kaskadowym dwóch zbiorników, Praca magisterska, Akademia Morska, Gdynia 11.. omera M., Kaczmarczyk M.: Komputerowy układ sterowania poziomem wody w kaskadzie dwóch zbiorników, Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki Politechniki Gdańskiej, Nr 8, s , 1, ISSN omera M., Kęska J., Kasprowicz A.: Sterowanie poziomem wody w kaskadzie dwóch zbiorników przy użyciu mikrokontrolera MS3F8335, Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki Politechniki Gdańskiej, Nr 3, s , ISSN COMPARISON OF SAE VARIABLE ESIMAION MEHODS IN A DOUBLE ANK CASCADE SYSEM Key-words: observers, state controller, PID control he paper presents the comparative analysis made between the linear observer and two linear Kalman filters: linear and extended Kalman filter (EKF), which is based assessment of the accuracy of estimation of state variables. he analyzed object in the estimated state variables are composed of two cascaded tanks suspended. Was examined in a case in which the measurement of the water level takes place only in the botom tank, and information about the water level in the top tank is obtained by the estimation. Observers analyzed were used in the control water level in the lower tank with the control condition, which requires the knowledge of the water level in both tanks. In addition, a comparison of the quality control using the control systems of the controller with the above configuration, observers, and using the PID controller, which uses only the measurement of the water level in the bottom tank, and does not require the observer. Pre-simulation study was carried out using the computational environment MALAB/Simulink. he research targets were made in a real time system, where the observers designed with controls are programmed in a digital signal processor MS3F8335, deployed to automatically control the water level in the bottom tank. 138 Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN , Nr 31/1
KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK
 Inżynieria Rolnicza 8(117)/2009 KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK Ewa Wachowicz, Piotr Grudziński Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy
Inżynieria Rolnicza 8(117)/2009 KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK Ewa Wachowicz, Piotr Grudziński Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy
Filtr Kalmana. Struktury i Algorytmy Sterowania Wykład 1-2. prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz
 Filtr Kalmana Struktury i Algorytmy Sterowania Wykład 1-2 prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz Politechnika Gdańska, Wydział Elektortechniki i Automatyki 2013-10-09, Gdańsk Założenia
Filtr Kalmana Struktury i Algorytmy Sterowania Wykład 1-2 prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz Politechnika Gdańska, Wydział Elektortechniki i Automatyki 2013-10-09, Gdańsk Założenia
Estymacja wektora stanu w prostym układzie elektroenergetycznym
 Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Automatyka i sterowania
 Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Systemy. Krzysztof Patan
 Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Sreszczenie. Słowa kluczowe: sterowanie, poziom cieczy, regulator rozmyty
 Ewa Wachowicz Katedra Systemów Sterowania Politechnika Koszalińska STEROWANIE POZIOMEM CIECZY W ZBIORNIKU Z WYKORZYSTANIEM REGULATORA ROZMYTEGO Sreszczenie W pracy omówiono układ regulacji poziomu cieczy,
Ewa Wachowicz Katedra Systemów Sterowania Politechnika Koszalińska STEROWANIE POZIOMEM CIECZY W ZBIORNIKU Z WYKORZYSTANIEM REGULATORA ROZMYTEGO Sreszczenie W pracy omówiono układ regulacji poziomu cieczy,
Estymacja częstotliwości podstawowej sieci energetycznej na podstawie scałkowanego sygnału napięcia
 SIWOŃ Cezary 1 Estymacja częstotliwości podstawowej sieci energetycznej na podstawie scałkowanego sygnału napięcia WSTĘP Utrzymanie stałej częstotliwości napięcia w sieci energetycznej jest jednym z najważniejszych
SIWOŃ Cezary 1 Estymacja częstotliwości podstawowej sieci energetycznej na podstawie scałkowanego sygnału napięcia WSTĘP Utrzymanie stałej częstotliwości napięcia w sieci energetycznej jest jednym z najważniejszych
Obserwatory stanu, zasada separowalności i regulator LQG
 Obserwatory stanu, zasada separowalności i regulator LQG Zaawansowane Techniki Sterowania Wydział Mechatroniki Politechniki Warszawskiej Anna Sztyber ZTS (IAiR PW) LQR Anna Sztyber / 29 Plan wykładu Obserwatory
Obserwatory stanu, zasada separowalności i regulator LQG Zaawansowane Techniki Sterowania Wydział Mechatroniki Politechniki Warszawskiej Anna Sztyber ZTS (IAiR PW) LQR Anna Sztyber / 29 Plan wykładu Obserwatory
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Wpływ częstotliwości taktowania układu FPGA na dokładność estymacji prędkości silnika prądu stałego
 Tomasz BINKOWSKI Politechnika Rzeszowska, Polska Bogdan KWIATKOWSKI Uniwersytet Rzeszowski, Polska Wpływ częstotliwości taktowania układu FPGA na dokładność estymacji prędkości silnika prądu stałego Wstęp
Tomasz BINKOWSKI Politechnika Rzeszowska, Polska Bogdan KWIATKOWSKI Uniwersytet Rzeszowski, Polska Wpływ częstotliwości taktowania układu FPGA na dokładność estymacji prędkości silnika prądu stałego Wstęp
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Regulacja temperatury z wykorzystaniem sterownika PLC Zadania do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Regulacja temperatury z wykorzystaniem sterownika PLC Zadania do ćwiczeń laboratoryjnych
Rys. 1 Otwarty układ regulacji
 Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI
 WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
Filtracja pomiarów z głowic laserowych
 dr inż. st. of. Paweł Zalewsi Filtracja pomiarów z głowic laserowych słowa luczowe: filtracja pomiaru odległości, PNDS Założenia filtracji pomiaru odległości. Problem wyznaczenia odległości i parametrów
dr inż. st. of. Paweł Zalewsi Filtracja pomiarów z głowic laserowych słowa luczowe: filtracja pomiaru odległości, PNDS Założenia filtracji pomiaru odległości. Problem wyznaczenia odległości i parametrów
Podstawy Automatyki. wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak. Politechnika Wrocławska. Instytut Technologii Maszyn i Automatyzacji (I-24)
 Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Problemy optymalizacji układów napędowych w automatyce i robotyce
 Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Katedra Automatyki Autoreferat rozprawy doktorskiej Problemy optymalizacji układów napędowych
Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Katedra Automatyki Autoreferat rozprawy doktorskiej Problemy optymalizacji układów napędowych
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych
 XXXVIII MIĘDZYUCZELNIANIA KONFERENCJA METROLOGÓW MKM 06 Warszawa Białobrzegi, 4-6 września 2006 r. Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych Eligiusz PAWŁOWSKI Politechnika
XXXVIII MIĘDZYUCZELNIANIA KONFERENCJA METROLOGÓW MKM 06 Warszawa Białobrzegi, 4-6 września 2006 r. Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych Eligiusz PAWŁOWSKI Politechnika
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku
 Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Algorytmy ze skończoną pamięcią dla przetwarzania sygnałów w diagnostyce procesów.
 Mgr inż. Jędrzej Byrski 28.11.2014 Katedra Informatyki Stosowanej Wydział EAIiIB, AGH 1. Tezy i zakres rozprawy AUTOREFERAT PRACY DOKTORSKIEJ Algorytmy ze skończoną pamięcią dla przetwarzania sygnałów
Mgr inż. Jędrzej Byrski 28.11.2014 Katedra Informatyki Stosowanej Wydział EAIiIB, AGH 1. Tezy i zakres rozprawy AUTOREFERAT PRACY DOKTORSKIEJ Algorytmy ze skończoną pamięcią dla przetwarzania sygnałów
Fuzja sygnałów i filtry bayesowskie
 Fuzja sygnałów i filtry bayesowskie Roboty Manipulacyjne i Mobilne dr inż. Janusz Jakubiak Katedra Cybernetyki i Robotyki Wydział Elektroniki, Politechnika Wrocławska Wrocław, 10.03.2015 Dlaczego potrzebna
Fuzja sygnałów i filtry bayesowskie Roboty Manipulacyjne i Mobilne dr inż. Janusz Jakubiak Katedra Cybernetyki i Robotyki Wydział Elektroniki, Politechnika Wrocławska Wrocław, 10.03.2015 Dlaczego potrzebna
Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Automatyka i robotyka ETP2005L. Laboratorium semestr zimowy
 Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
AUTOMATYKA. h 1 Q 1. y 2 Q 2
 - ELEKRYKA - ZAKŁÓCENIA NR 6/ Porównanie jakości pracy trzech algorytmów typu PID: liniowego, rozmytego i neuronowego dr inż. Mirosław OMERA Akademia Morska w Gdyni, e:mail:tomera@am.gdynia.pl Comparison
- ELEKRYKA - ZAKŁÓCENIA NR 6/ Porównanie jakości pracy trzech algorytmów typu PID: liniowego, rozmytego i neuronowego dr inż. Mirosław OMERA Akademia Morska w Gdyni, e:mail:tomera@am.gdynia.pl Comparison
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Obiekt. Obiekt sterowania obiekt, który realizuje proces (zaplanowany).
 SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Algorytmy sztucznej inteligencji
 Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Politechnika Gdańska Wydział Elektrotechniki i Automatyki. Automatyka i Robotyka Systemy Sterowania i Wspomagania Decyzji
 Monitorowanie i Diagnostyka w Systemach Sterowania (MiDwSS) Podstawowe sposoby opisu niepewności, wybrane zagadnienia zastosowania estymacji rekursywnej dla potrzeb monitorowania i diagnostyki w systemach
Monitorowanie i Diagnostyka w Systemach Sterowania (MiDwSS) Podstawowe sposoby opisu niepewności, wybrane zagadnienia zastosowania estymacji rekursywnej dla potrzeb monitorowania i diagnostyki w systemach
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD I PSPICE
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
Regulacja dwupołożeniowa.
 Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
Ćwiczenie nr 3 Układy sterowania w torze otwartym i zamkniętym
 Ćwiczenie nr 3 Układy sterowania w torze otwartym i zamkniętym 1. Cel ćwiczenia Celem ćwiczenia jest analiza właściwości układu sterowania w torze otwartym, zamkniętym oraz zamkniętym z kompensacją zakłóceń.
Ćwiczenie nr 3 Układy sterowania w torze otwartym i zamkniętym 1. Cel ćwiczenia Celem ćwiczenia jest analiza właściwości układu sterowania w torze otwartym, zamkniętym oraz zamkniętym z kompensacją zakłóceń.
AUTO-STROJENIE REGULATORA TYPU PID Z WYKORZYSTANIEM LOGIKI ROZMYTEJ
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 75 Electrical Engineering 2013 Łukasz NIEWIARA* Krzysztof ZAWIRSKI* AUTO-STROJENIE REGULATORA TYPU PID Z WYKORZYSTANIEM LOGIKI ROZMYTEJ Zagadnienia
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 75 Electrical Engineering 2013 Łukasz NIEWIARA* Krzysztof ZAWIRSKI* AUTO-STROJENIE REGULATORA TYPU PID Z WYKORZYSTANIEM LOGIKI ROZMYTEJ Zagadnienia
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania KOMPUTEROWE SYSTEMY STEROWANIA (KSS)
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania KOMPUTEROWE SYSTEMY STEROWANIA (KSS) Temat: Budowa pętli sprzętowej (ang. Hardware In the Loop) w oparciu
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania KOMPUTEROWE SYSTEMY STEROWANIA (KSS) Temat: Budowa pętli sprzętowej (ang. Hardware In the Loop) w oparciu
Regulator liniowo kwadratowy na przykładzie wahadła odwróconego
 Regulator liniowo kwadratowy na przykładzie wahadła odwróconego kwiecień 2012 Sterowanie Teoria Przykład wahadła na wózku Dany jest system dynamiczny postaci: ẋ = f (x, u) (1) y = h(x) (2) Naszym zadaniem
Regulator liniowo kwadratowy na przykładzie wahadła odwróconego kwiecień 2012 Sterowanie Teoria Przykład wahadła na wózku Dany jest system dynamiczny postaci: ẋ = f (x, u) (1) y = h(x) (2) Naszym zadaniem
Podstawy automatyki. Energetyka Sem. V Wykład 1. Sem /17 Hossein Ghaemi
 Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Podstawy Automatyki. Wykład 6 - Miejsce i rola regulatora w układzie regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
INSTRUKCJA DO ĆWICZENIA NR 7
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
Metody numeryczne Wykład 4
 Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
WPŁYW OPÓŹNIENIA NA DYNAMIKĘ UKŁADÓW Z REGULACJĄ KLASYCZNĄ I ROZMYTĄ
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 65 Politechniki Wrocławskiej Nr 65 Studia i Materiały Nr 31 2011 Kinga GÓRNIAK* układy z opóźnieniem, regulacja rozmyta, model Mamdaniego,
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 65 Politechniki Wrocławskiej Nr 65 Studia i Materiały Nr 31 2011 Kinga GÓRNIAK* układy z opóźnieniem, regulacja rozmyta, model Mamdaniego,
Praca dyplomowa magisterska
 Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Wprowadzenie do technik regulacji automatycznej. prof nzw. dr hab. inż. Krzysztof Patan
 Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter)
 Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter) 1. WSTĘP W wielu złożonych układach mechanicznych elementy występują połączenia elastyczne (długi
Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter) 1. WSTĘP W wielu złożonych układach mechanicznych elementy występują połączenia elastyczne (długi
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji
 Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Inżynieria Systemów Dynamicznych (5)
 Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Metodyka projektowania systemów sterowania Uwagi wstępne
 Uwagi wstępne Inżynieria sterowania (Control Engineering) odgrywa dziś fundamentalną rolę w nowoczesnych systemach technologicznych, Korzyści ze sterowania w przemyśle,. mogą być wielorakie - poprawa jakości
Uwagi wstępne Inżynieria sterowania (Control Engineering) odgrywa dziś fundamentalną rolę w nowoczesnych systemach technologicznych, Korzyści ze sterowania w przemyśle,. mogą być wielorakie - poprawa jakości
Prof. dr hab. inż. Lech M. Grzesiak Politechnika Warszawska, Wydział Elektryczny
 Prof. dr hab. inż. Lech M. Grzesiak Politechnika Warszawska, Wydział Elektryczny Recenzja rozprawy doktorskiej mgr. inż. Karola Tatara pt. Synteza regulatorów ślizgowych dla przetworników energoelektronicznych
Prof. dr hab. inż. Lech M. Grzesiak Politechnika Warszawska, Wydział Elektryczny Recenzja rozprawy doktorskiej mgr. inż. Karola Tatara pt. Synteza regulatorów ślizgowych dla przetworników energoelektronicznych
PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM
 Mostefa Mohamed-Seghir Akademia Morska w Gdyni PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM W artykule przedstawiono propozycję zastosowania programowania dynamicznego do rozwiązywania
Mostefa Mohamed-Seghir Akademia Morska w Gdyni PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM W artykule przedstawiono propozycję zastosowania programowania dynamicznego do rozwiązywania
Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej
 Marcin Szega Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej (Monografia habilitacyjna nr 193. Wydawnictwo Politechniki
Marcin Szega Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej (Monografia habilitacyjna nr 193. Wydawnictwo Politechniki
Analityczne metody detekcji uszkodzeń
 Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania. Studia: I stopnia (inżynierskie)
 Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Skalowanie czujników prędkości kątowej i orientacji przestrzennej 1. Analiza właściwości czujników i układów
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Skalowanie czujników prędkości kątowej i orientacji przestrzennej 1. Analiza właściwości czujników i układów
Badanie stabilności liniowych układów sterowania
 Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Dla naszego obiektu ciągłego: przy czasie próbkowania T p =2.
 1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
Przekształcanie równań stanu do postaci kanonicznej diagonalnej
 Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
Model Predictive Control
 Model Predictive Control podstawy Politechnika Gdańska Wydział Elektrotechniki i Automatyki Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania 2014/2015 1 Plan wykładu Część I:
Model Predictive Control podstawy Politechnika Gdańska Wydział Elektrotechniki i Automatyki Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania 2014/2015 1 Plan wykładu Część I:
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
I. KARTA PRZEDMIOTU CEL PRZEDMIOTU
 I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: SYSTEMY DYNAMICZNE 2. Kod przedmiotu: Esd 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Techniki Komputerowe
I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: SYSTEMY DYNAMICZNE 2. Kod przedmiotu: Esd 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Techniki Komputerowe
Porównanie wyników symulacji wpływu kształtu i amplitudy zakłóceń na jakość sterowania piecem oporowym w układzie z regulatorem PID lub rozmytym
 ARCHIVES of FOUNDRY ENGINEERING Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 15 Special Issue 4/2015 133 138 28/4 Porównanie wyników
ARCHIVES of FOUNDRY ENGINEERING Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 15 Special Issue 4/2015 133 138 28/4 Porównanie wyników
ANALIZA PORÓWNAWCZA METOD POMIARU IMPEDANCJI PĘTLI ZWARCIOWEJ PRZY ZASTOSOWANIU PRZETWORNIKÓW ANALOGOWYCH
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 54 Politechniki Wrocławskiej Nr 54 Studia i Materiały Nr 23 2003 Andrzej STAFINIAK * metody pomiarowe,impedancje pętli zwarciowej impedancja
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 54 Politechniki Wrocławskiej Nr 54 Studia i Materiały Nr 23 2003 Andrzej STAFINIAK * metody pomiarowe,impedancje pętli zwarciowej impedancja
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
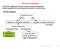 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
PL B1. Sposób regulacji prądu silnika asynchronicznego w układzie bez czujnika prędkości obrotowej. POLITECHNIKA GDAŃSKA, Gdańsk, PL
 PL 224167 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 224167 (13) B1 (21) Numer zgłoszenia: 391278 (51) Int.Cl. H02P 27/06 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia:
PL 224167 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 224167 (13) B1 (21) Numer zgłoszenia: 391278 (51) Int.Cl. H02P 27/06 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia:
STEROWANIE TEMPERATURĄ W DRUKARCE 3D
 MODELOWANIE INŻYNIERSKIE nr 54, ISSN 1896-771X STEROWANIE TEMPERATURĄ W DRUKARCE 3D Marek Surmak 1a, Robert Piotrowski 1b 1 Wydział Elektrotechniki i Automatyki, Politechnika Gdańska a marek.surmak@gmail.com,
MODELOWANIE INŻYNIERSKIE nr 54, ISSN 1896-771X STEROWANIE TEMPERATURĄ W DRUKARCE 3D Marek Surmak 1a, Robert Piotrowski 1b 1 Wydział Elektrotechniki i Automatyki, Politechnika Gdańska a marek.surmak@gmail.com,
WYKŁAD 9 METODY ZMIENNEJ METRYKI
 WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie)
 Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Pomiar prędkości kątowych samolotu przy pomocy czujnika ziemskiego pola magnetycznego 1. Analiza właściwości
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Pomiar prędkości kątowych samolotu przy pomocy czujnika ziemskiego pola magnetycznego 1. Analiza właściwości
MODEL OBSERWATORA ZMIENNYCH STANU DLA UKŁADU Z NIELINIOWYM WAŁEM MECHANICZNYM
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 63 Politechniki Wrocławskiej Nr 63 Studia i Materiały Nr 9 9 Krzysztof SZABAT* układ dwumasowy, nieliniowość wału estymacja, obserwator
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 63 Politechniki Wrocławskiej Nr 63 Studia i Materiały Nr 9 9 Krzysztof SZABAT* układ dwumasowy, nieliniowość wału estymacja, obserwator
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4
 Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Wykład z Technologii Informacyjnych. Piotr Mika
 Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
WYDZIAŁ ELEKTRYCZNY KATEDRA AUTOMATYKI I ELEKTRONIKI. Badanie układu regulacji dwustawnej
 POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
ZASTOSOWANIE SIECI NEURONOWYCH W BEZCZUJNIKOWYM UKŁADZIE NAPĘDOWYM Z POŁĄCZENIEM SPRĘŻYSTYM
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 58 Politechniki Wrocławskiej Nr 58 Studia i Materiały Nr 25 2005 Sebastian RAKOCZY *, Krzysztof SZABAT * układ dwumasowy, estymacja zmiennych
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 58 Politechniki Wrocławskiej Nr 58 Studia i Materiały Nr 25 2005 Sebastian RAKOCZY *, Krzysztof SZABAT * układ dwumasowy, estymacja zmiennych
Rys 1 Schemat modelu masa- sprężyna- tłumik
 Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
Modelowanie jako sposób opisu rzeczywistości. Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka
 Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Prowadzący: Prof. PWr Jan Syposz
 Automatyzacja w inżynierii środowiska Prowadzący: Wykład 1 Prof. PWr Jan Syposz Zakres tematyczny wykładu Wprowadzenie do techniki regulacji i sterowania Regulatory Programowanie sterowników swobodnie
Automatyzacja w inżynierii środowiska Prowadzący: Wykład 1 Prof. PWr Jan Syposz Zakres tematyczny wykładu Wprowadzenie do techniki regulacji i sterowania Regulatory Programowanie sterowników swobodnie
