Kilka spraw prak- Uproszczenia, cd. Symetria konstrukcji. Zasada nr 1. Uwzględniamy symetrię. Nawet jeżeli jej nie ma:-)
|
|
|
- Jadwiga Adamczyk
- 6 lat temu
- Przeglądów:
Transkrypt
1 Kilka spraw prak- MES-2 5 tycznych Część I Uproszczenia, cd. Symetria konstrukcji Zasada nr. Uwzględniamy symetrię. Nawet jeżeli jej nie ma:-) Kiedy możemy zastosować symetrię automatycznie Model ma być symetryczny Ma być symetrycznie umocowany Ma być symetrycznie obciążony Symetria w SWS Dla płaskiego modelu można automatycznie uwzględnić maksymalnie 2 prostopadłe osie symetrii, czyli rozważyć /4 modelu. Dla przestrzennego modelu - maksymalnie 3 prostopadłe płaszczyzny symetrii albo /8 modelu. Dla symetrycznych części SWS pozwala pracować /2 lub /4 śruby, robi to trochę dziwnie. Najpierw przy definicji śruby w zaawansowanych opcjach trzeba zaznaczyć, że jest to tylko /2 lub /4. Siłę docisku lub odpowiedni moment podajemy jednak dla całej śruby. Ale wynik obliczeń (siły dla każdej śruby) podawane są tylko dla /2 lub /4 śruby. rak z -displ. y-displ.=z-displ. z z y y z y rak z-displ. rak z-displ. W tym przypadku wystarczy przeprowadzić obliczenia dla /8 konstrukcji. W wielu programach MES można określić warunki brzegowe w dodatkowym układzie współrzędnych. Najprościej zrobić to w układzie biegunowym lub cylindrycznym (brak przemieszczeń obwodowych lub stała wartość kąta wzdłuż odpowiednich linii lub powierzchni). W programach zaawansowanych również używamy constrains ograniczeń na przemieszczenia zapisywanych w postaci dowolnego (realnie tylko liniowego) równania. W większości przypadków dla /N modelu najprostszym rozwiązaniem jest używanie warunku brzegowego Przesuwanie (Roller/Slider) na odpowiednich ścianach. Symetria cykliczna, wykrzywione granice części W tym przypadku warunek brzegowy przemieszczenia na wszystkich liniach podziału konstrukcji na symetryczne części są jednakowe (po obróceniu o 360/N stopni)
2 W tym miejscu był przykład pokazany bezpośrednio w SW Symetria cykliczna, uwagi końcowe Symetria cykliczna to nie to samo, co zwykła symetria osiowa, chociaż czasem obydwa podejścia dają ten sam wynik. Zasadnicza różnica pomiędzy symetrią cykliczną a zwykłą polega na tym, że pierwsza pozwala na odkształcenie modelu w kierunku obwodowym (prostopadłym do powierzchni użytej do wycięcia /N modelu). Ograniczenia SWS przy modelowaniu symetrii cyklicznej:. Oś symetrii musi być zdefiniowana jawnie (np. przez Przygotowywanie analizy/geometria odniesienia/oś) 2. Przy definicji symetrii jednocześnie można zaznaczyć tylko parę powierzchni granicznych. Jeżeli nasze przekroje graniczne zawierają N par powierzchni, to w SWS musimy definiować symetrię cykliczną N razy. Dlaczego? T! Antysymetria obciążenia /2 rak obrotu Przy obciążeniu symetrycznym wszystkie wyniki dla drugiej połowy konstrukcji są lustrzanym odbiciem tych dla pierwszej połowy. Przy obciążeniu antysymetrycznym, wyniki dla drugiej połowy = (wyniki dla pierwszej połowy) ( ) rak ugięcia Antysymetria w 2D Symetryczna konstrukcja, niesymetryczne obciążenie /2 /2 /2 /2 = + Krok Podziel obciążenie na pół Krok 2 Przyłóż 2 połówki obciążenia symetrycznie. To będzie pierwszy schemat (symetryczny) I.Rokach,
3 Krok 3 Przyłóż 2 połówki obciążenia antysymetrycznie. To będzie schemat drugi. W sumie dają model wejściowy. Wnioski Każde niesymetryczne obciążenie, które działa na symetryczną konstrukcję można zastąpić sumą symetrycznego i antysymetrycznego obciążenia. To szczególnie opłaca się dla konstrukcji z dużą ilością osi lub płaszczyzn symetrii (koła zębate, turbiny, itp.). N razy mniejsza ilość węzłów = co najmniej N 2... N 3 szybsze obliczenia. Jeszcze jeden przykład Symetria 2/3 /2 /2 /3 /3 5/6 5/6 2/3 /2 Antysymetria /3 /3 /2 /6 /6 rak symetrii obciążenia, symetryczna konstrukcja Nawet w przypadku braku symetrii obciążenia dobry program MES (np. ADINA, Nastran) pozwala analizować tylko /N część symetrycznej konstrukcji. Przy pełnej symetrii rozwiązujemy układ równań N razy mniejszy od układu dla całej konstrukcji, w przypadku braku symetrii obciążenia dwa takie układy. Część II Elementy na sterydach niekompatybilne funkcje kształtu Próba zginania elementu Q4 (albo pary elementów T3) Stopień zawyżenia sztywności elementu do osiągnięcia θ = θ 2 potrzebujemy M 2 = ( + ν ν + ( a ) ) 2 M 2 b a/b = 2 3 ν=0,2,46 2,7 4,79 ν=0,3,48 2,64 4, I.Rokach,
4 Zależność M 2 /M od a/b dla różnych wartości ν Dlaczego to nazywa się shear locking (blokada sztywnosciowa)? Czyste zginanie = brak naprężeń/odkształceń stycznych ponieważ kąty w każdym elemencie nie zmieniają się w czasie odkształcenia, a w Q4 one są niezerowe tu kąty zmieniają: przed odkształceniem mamy prostokąt, po odkształceniu trapez. Te niefizyczne naprężenia styczne znacznie zwiększają energię wymaganą dla odkształcenia elementu, czyli jego sztywność. Na czym polega problem Tradycyjne funkcje kształtu zapewniają ciągle pole przemieszczeń w całym modelu (na którym nam nie zbyt mocno zależy), ale jednocześnie produkują pole naprężeń (na którym nam bardzo zależy) ze skokami na granicach elementów. Tradycyjne elementy liniowe sztucznie usztywniają model poddany zginaniu, bo nie są w stanie zamodelować zmiennych naprężeń. Oni nadają się tylko w tych miejscach modelu, gdzie dominuje rozciąganie lub ściskanie i naprężenia są prawie niezmienne. (Nieco szatański) pomysł Dodać nowe bezwęzłowe kwadratowe funkcje kształtu do tradycyjnego elementu Q4 do modelowania tych wygibasów. Koszt: przemieszczenia na granicach elementów już nie będą ciągle. Zysk: lepsze modelowanie zginania w ramach bardzo prostych i powszechnie używanych elementów Q4. Dlaczego po prostu (jak w SWS) nie użyć elementów kwadratowych? Elementy kwadratowe są bardziej kosztowne obliczniowo Zwykła zamiana liniowych funkcji kształtu na kwadratowe prowadzi do problemów na granicach elementów różnych typów Zadanie domowe A jak to będzie dla elementów trójkątnych: T3, T6 i T7? Elementy Q4 i Q8 nie są przyjaciółmi C C I.Rokach,
5 Pomysł na dodatkowe wewnętrzne funkcje kształtu Cztery standardowe poliliniowe funkcje kształtu uzupełniamy 2 funkcjami kwadratowymi, z których każda zanika tylko na 2 granicach elementu N 5 (ξ) = ξ 2, N 6 (η) = η 2 Nowe funkcji nie mają swoich węzłów, aproksymacja funkcji f(ξ, η) wewnątrz elementu ma postać f(ξ, η) 4 f i N i (ξ, η) + αn 5 (ξ) + βn 6 (η) i= przy czym, w odróżnieniu od f i, współczynniki α i β nie mają klarownego sensu fizycznego. Dlatego dodatkowe funkcje kształtu uważa się za niekompatybilne z pozostałymi. Takie elementy mają ogólną nazwę niekompatybilne. Element Q4 z dwoma dodatkowymi niekompatybilnymi funkcjami kształtu nazywa się albo Q4/Q6 albo Q4/6 albo Q6. Przemieszczenia poza węzłami już nie są ciągle Elementy Q4/Q6 Elementy Q4 To samo jeszcze raz Widzimy, że element Q6 jest w stanie poprawnie modelować zginanie, ale kosztem powstawania szczelin pomiędzy elementami. Na tym właśnie polega niekompatybilność elementów Q6. Ale każdy program MES, w obawie o zdrowie psychiczne użytkownika szczeliny te dyskretnie ukrywa I.Rokach,
6 Wpływ dodatkowych funkcji kształtu Cena obliczeniowa różnych elementów Zależność ilości węzłów N w od ilości elementów dla siatki z n n = n 2 elementów N w = (n + ) 2 N w = (n + ) 2 N w = (2n + ) 2 n 2 N w = (2n + ) 2 Q4, N w n 2 Q4/6, N w n 2 Q8, N w 3n 2 Q9, N w 4n 2 Wnioski Elementy Q4/6 nic nie kosztują, bo zmienne α i β są kondensowane (element ten w zasadzie jest superelementem) Elementy Q4/6 zdecydowanie lepiej od tradycyjnych Q4 modelują naprężenia pochodzące od zginania We wszystkich programach komercyjnych praktycznie już nie ma tradycyjnych elementów Q4, domyślnie zamiast nich używane są elementy typu Q4/6. Ale każdy producent programów MES wprowadza swoje elementy niekompatybilne. Dlatego różne programy dają różne wyniki dla tych samych siatek. WAŻNE! Nigdy nie używamy tradycyjnych elementów liniowych (przede wszystkim T3 i Q4) w modelach z dużymi gradientami (zmianami) naprężeń i/lub odkształceń (np. modelowanie plastyczności). Można to robić tylko w celu szybkiego sprawdzenia poprawności umocowania/obciążenia lub przy wstępnej jakościowej analizie konstrukcji I.Rokach,
7 Część III Ekstrapolacja Richardsona, albo jak pozbyć się grzechów (czyli błędów obliczeniowych) nie będąc Papieżem Teoria w pigułce y(h) y(h/2) y(0) h/2 Ah/2 Niech y(0) jest dokładną wartością, y(h) i y(h/2) - wartości przybliżone i { y(h) = y(0) + Ah { y(h) = y(0) + Ah y(h/2) = y(0) + /2Ah 2y(h/2) = 2y(0) + Ah Ah (2)-() y(0) = 2y(h/2) y(h) h Teoria w pigułce 2 y(h) y(h/2) y(0) h/2 A(h/2) 2 Niech y(0) jest dokładną wartością, y(h) i y(h/2) - wartości przybliżone i { y(h) = y(0) + Ah 2 y(h/2) = y(0) + A(h/2) 2 Ah 2 (2)-() y(0) = y(h/2) y(h) h 3 4y lepszych ygorsze y dokł 3 { 4y(h/2) y(h) 3 y(h) = y(0) + Ah 2 4y(h/2) = 4y(0) + Ah 2 = y(h/2) = + + Realnie wszystko jest bardziej skomplikowane. Zwykle jest kilka źródeł błędu i pełny wzór na wartość przybliżoną ma postać y(h) = y(0) + Ah + h 2 + Ch 3... przy czym mnożniki A,, C nie są stałymi lecz funkcjami h. Dlatego wzór Richardsona praktycznie nigdy nie pozwala otrzymać dokładnej wartości y(0). Ale w większości realnych sytuacji pozwala bardzo mocno poprawić wynik. Ekstrapolacja Richardsona, wzór ogólny W ogólnym przypadku y(h) = y(0) + Ah n y(0) = 2n y(h/2) y(h) 2 n Najczęściej używane wzory = y(h/2) + y(h/2) y(h) 2 n I.Rokach,
8 n Wzór Zastosowanie y = 2y(h/2) y(h) MES: przemieszczenia u i w el. liniowych, naprężenia σ ij w el. kwadratowych 2 4y(h/2) y(h) y = 3 MES: przemieszczenia u i w el. kwadratowych 4 6y(h/2) y(h) y = 5 Całkowanie: metoda Gaussa 2-punktowa Zagadnienie do rozwiązania 5 Dane wejściowe Wymiary belki 5, przekrój kwadratowy, E = 333 /3 Amplituda rozłożonego obciążenia, siła wypadkowa = 2 /3 Rozwiązania teoretyczne Rozkład naprężeń stycznych σ yz jest stały dla wszystkich przekrojów i odpowiada kształtowi obciążenia Rozkład naprężeń normalnych w każdym przekroju jest liniowy. Amplituda σ yy rośnie od 0 na prawym końcu belki do 20 w zamocowaniu. Maksymalne ugięcie belki δ E = PL3 3EI = (Euler-ernoulli), δ T = δ E ν P 0( + ν) Gbh,0295 (Timoszenko), δ 2D = δ E ν P,04 (płaski stan 2 Gbh naprężeń) Naprężenia σ yy Naprężenia σ yz Na czym polega wredność zagadnienia MES najgorzej radzi sobie z naprężeniami stycznymi. Tu na dodatek ich rozkład jest paraboliczny. To leży poza możliwościami aproksymacyjnymi elementów liniowych i kwadratowych. Rozkład naprężeń normalnych jest podwójnie liniowy. Elementy liniowe będą mieć problem z interpolacją tego kształtu. Jakie ES zostaną użyte. Elementy trójkątne: liniowy T3 (3-węzłowy) kwadratowe: T6 i T7 2. Elementy czworokątne: liniowy Q4 liniowy Q4/6, niekompatybilny kwadratowe: Q8 i Q I.Rokach,
9 Wyniki: ugięcie Ugięcie: element T3, schemat: N Dokładność wyników dla siatki N dla elementów T3 jest wyjątkowo niska. Sztywność belki jest zawyżona 3- krotnie Stopnie swobody Ugięcie: schemat: N Teoria Timoszenki Teoria Eulera-ernoulliego 2D Element Q4 lepszy od T3, lecz gorszy od pozostałych Element Q4/6 najbardziej efektywny Stopnie swobody Q4 Q4/6 Q8 Q9 T6 T7 Elementy T6 i T7 są nieznacznie gorsze od wszystkich elementów kwadratowych. iorąc pod uwagę łatwość generacji siatek trójkątnych, to jest bardzo pozytywny wynik. Wyniki dla Q8 i Q9 są porównywalne Ugięcie dla T3, inne podejście Ugięcie: element T3, schemat: N Wykres we współrzędnych względnych pokazuje, że zbieżność przemieszczeń w przypadku elementu T3 jest liniową funkcją /n. Oznacza to, że dla znalezienia dokładnej wartości ugięcia można było zastosować ekstrapolację Richardsona dla n =. Ale nie tym razem Względny krok siatki wzdłuż belki Ugięcie dla Q4, inne podejście I.Rokach,
10 Ugięcie: element Q4, schemat: N Zbieżność przemieszczeń w przypadku elementu Q4 jest liniową funkcją h = /n. Ekstrapolacja liniowa (n = we wzorze Richardsona) tym razem pozwala znaleźć dokładniejsze rozwiązanie. Przykład: u(0,5) = u 2 = 0,288, u(0,25) = u 4 = 0,607 u = 2u 4 u 2 = 2 0,607 0,288 = 0, Względny krok siatki wzdłuż belki Ugięcie dla Q4/6, inne podejście Ugięcie: element Q4/6: N D Teoria Timoszenki Zbieżność przemieszczeń w przypadku niekompatybilnego elementu Q4 jest liniową funkcją h = /n, ale tylko na samym początku. Szybko osiągamy stabilne rozwiązanie. Wzór Richardsona również działa: u(0,5) = u 2 = 0,963, u(0,25) = u 4 =,00 u = 2u 4 u 2 = 2,00 0,963 =, Względny krok siatki wzdłuż belki Ugięcie dla elementów kwadratowych, inne podejście Ugięcie, elementy kwadratowe, schemat: N 0.9 2D Teoria Timoszenki Teoria Eulera-ernoulliego Q8 Q9 T6 T7 Zbieżność przemieszczeń w przypadku elementu kwadratowych jest kwadratową funkcją h = /n albo liniową funkcją h 2 = /n 2. Tu można było skorzystać z ekstrapolacji Richardsona dla n = 2. Przykład dla T6: u 2 = 0,803, u 4 = 0,972 u = /3(4u 4 u 2 ) = /3(4 0,972 0,803) =, Wnioski końcowe (Względny krok siatki wzdłuż belki) 2 Każde zagadnienie zawsze rozwiązujemy kilkakrotnie: albo używając jakościowo różnych modeli, albo zagęszczając siatkę (najczęściej 2-krotnie) I.Rokach,
11 Możliwe są 2 scenariusze: albo przy zmianie modelu wynik zmienia się nieznacznie, albo zmiany są duże W pierwszym przypadku sprawdzamy co się dzieje z energią modelu i (jeżeli tam też nie ma zmian) zachowujemy najbardziej dokładny wynik. Który? O tym też może zadecydować energia lub częstotliwość własnych drgań W drugim przypadku można zastosować ekstrapolację Richardsona, żeby zobaczyć jak daleko jest do dokładnego rozwiązania. Literatura [] oeraeve Ir.P., Introduction to the inite Element Method (EM), Institut Gramme - Liege, 200. [2] ADINA Theory and Modeling Guide, ADINA R&D, Watertown, 202. [3] Wpis z blogu technicznego SOLIDWORKS: SOLIDWORKS Simulation: The mystery of symmetry, Part, Part 2. Wykład został opracowany w LATEXe za pomocą klasy EAMER, graficznego pakietu PG/TikZ i pakietu do tworzenia wykresów PGPLOTS. Obliczenia wewnątrz dokumentu zostały przeprowadzone za pomocą EQC I.Rokach,
Kilka spraw praktycz-
 Kilka spraw praktycz- MES2 2 nych Część I Uproszczenia, cd. Symetria konstrukcji Zasada nr. Uwzględniamy symetrię rakz -displ. y-displ.=z-displ. z z y y z y rak z-displ. rak z-displ. W tym przypadku wystarczy
Kilka spraw praktycz- MES2 2 nych Część I Uproszczenia, cd. Symetria konstrukcji Zasada nr. Uwzględniamy symetrię rakz -displ. y-displ.=z-displ. z z y y z y rak z-displ. rak z-displ. W tym przypadku wystarczy
Modelowanie w MES. Kolejność postępowania w prostej analizie MES w SWS
 MES 5 Modelowanie w MES Część I Kolejność postępowania w prostej analizie MES w SWS Kroki analizy Zakładamy, że model już jest uproszczony, zdefiniowany został materiał, obciążenie i umocowanie (krok 0).
MES 5 Modelowanie w MES Część I Kolejność postępowania w prostej analizie MES w SWS Kroki analizy Zakładamy, że model już jest uproszczony, zdefiniowany został materiał, obciążenie i umocowanie (krok 0).
Najprostszy element. F+R = 0, u A = 0. u A = 0. Mamy problem - równania zawierają siły, a warunek umocowania - przemieszczenia
 MES skończony Najprostszy element Część I Najprostszy na świecie przykład rozwiązania zagadnienia za pomocą MES Dwie sprężyny Siły zewnętrzne i wewnętrzne działające na element A B R F F+R, u A R f f F
MES skończony Najprostszy element Część I Najprostszy na świecie przykład rozwiązania zagadnienia za pomocą MES Dwie sprężyny Siły zewnętrzne i wewnętrzne działające na element A B R F F+R, u A R f f F
F + R = 0, u A = 0. u A = 0. f 0 f 1 f 2. Relację pomiędzy siłami zewnętrznymi i wewnętrznymi
 MES Część I Najprostszy na świecie przykład rozwiązania zagadnienia za pomocą MES Dwie sprężyny Siły zewnętrzne i wewnętrzne działające na element A B R F F + R, u A R f f F R + f, f + f, f + F, u A Równania
MES Część I Najprostszy na świecie przykład rozwiązania zagadnienia za pomocą MES Dwie sprężyny Siły zewnętrzne i wewnętrzne działające na element A B R F F + R, u A R f f F R + f, f + f, f + F, u A Równania
Modelowanie w MES. Kroki analizy Zakładamy, że model już jest uproszczony, zdefiniowane są materiał, obciążenie i umocowanie (krok 0).
 MES 5 Modelowanie w MES Część I Kolejność postępowania w prostej analizie MES w SWS Kroki analizy Zakładamy, że model już jest uproszczony, zdefiniowane są materiał, obciążenie i umocowanie (krok 0). Krok
MES 5 Modelowanie w MES Część I Kolejność postępowania w prostej analizie MES w SWS Kroki analizy Zakładamy, że model już jest uproszczony, zdefiniowane są materiał, obciążenie i umocowanie (krok 0). Krok
[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)
![[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia) [ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)](/thumbs/88/115575588.jpg) PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
Al.Politechniki 6, Łódź, Poland, Tel/Fax (48) (42) Mechanika Budowli. Inżynieria Środowiska, sem. III
 KATEDRA MECHANIKI MATERIAŁÓW POLITECHNIKA ŁÓDZKA DEPARTMENT OF MECHANICS OF MATERIALS TECHNICAL UNIVERSITY OF ŁÓDŹ Al.Politechniki 6, 93-590 Łódź, Poland, Tel/Fax (48) (42) 631 35 51 Mechanika Budowli
KATEDRA MECHANIKI MATERIAŁÓW POLITECHNIKA ŁÓDZKA DEPARTMENT OF MECHANICS OF MATERIALS TECHNICAL UNIVERSITY OF ŁÓDŹ Al.Politechniki 6, 93-590 Łódź, Poland, Tel/Fax (48) (42) 631 35 51 Mechanika Budowli
Elementy belkowe i. Brak źródeł koncentracji naprężeń (chyba, że jest możliwość ich uwzględnienia).
 MES1 11 powłokowe Elementy belkowe i Część I Elementy belkowe Kiedy używamy modeli belkowe? Elementy konstrukcyjne, w których jeden z wymiarów jest wielokrotnie (> 4 razy) większy od innych i zginanie
MES1 11 powłokowe Elementy belkowe i Część I Elementy belkowe Kiedy używamy modeli belkowe? Elementy konstrukcyjne, w których jeden z wymiarów jest wielokrotnie (> 4 razy) większy od innych i zginanie
Kolejność postępowania w prostej analizie MES w SWS
 MES-1 10 Część I Kolejność postępowania w prostej analizie MES w SWS Kroki analizy Zakładamy, że model już jest uproszczony, zdefiniowane są materiał, obciążenie i umocowanie (krok 0). Krok 1. Wstępna
MES-1 10 Część I Kolejność postępowania w prostej analizie MES w SWS Kroki analizy Zakładamy, że model już jest uproszczony, zdefiniowane są materiał, obciążenie i umocowanie (krok 0). Krok 1. Wstępna
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Osiadanie kołowego fundamentu zbiornika
 Przewodnik Inżyniera Nr 22 Aktualizacja: 01/2017 Osiadanie kołowego fundamentu zbiornika Program: MES Plik powiązany: Demo_manual_22.gmk Celem przedmiotowego przewodnika jest przedstawienie analizy osiadania
Przewodnik Inżyniera Nr 22 Aktualizacja: 01/2017 Osiadanie kołowego fundamentu zbiornika Program: MES Plik powiązany: Demo_manual_22.gmk Celem przedmiotowego przewodnika jest przedstawienie analizy osiadania
Defi f nicja n aprę r żeń
 Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
Pytania przygotowujące do egzaminu z Wytrzymałości Materiałów sem. I studia niestacjonarne, rok ak. 2015/16
 Pytania przygotowujące do egzaminu z Wytrzymałości Materiałów sem. I studia niestacjonarne, rok ak. 2015/16 1. Warunkiem koniecznym i wystarczającym równowagi układu sił zbieżnych jest, aby a) wszystkie
Pytania przygotowujące do egzaminu z Wytrzymałości Materiałów sem. I studia niestacjonarne, rok ak. 2015/16 1. Warunkiem koniecznym i wystarczającym równowagi układu sił zbieżnych jest, aby a) wszystkie
MES 4. 1 Przykłady błędów MES. 2 Proces V&V. Weryfikacja i walidacja. Czy MES jest nieomylny?
 MES 4 błędu Zbieżność. Wskaźniki 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi (3
MES 4 błędu Zbieżność. Wskaźniki 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi (3
Obsługa programu Soldis
 Obsługa programu Soldis Uruchomienie programu Po uruchomieniu, program zapyta o licencję. Można wybrać licencję studencką (trzeba założyć konto na serwerach soldisa) lub pracować bez licencji. Pliki utworzone
Obsługa programu Soldis Uruchomienie programu Po uruchomieniu, program zapyta o licencję. Można wybrać licencję studencką (trzeba założyć konto na serwerach soldisa) lub pracować bez licencji. Pliki utworzone
MES Przykłady błędów MES. 2 Proces V&V. Weryfikacja i walidacja. Czy MES jest nieomylny?
 Zbieżność. Wskaź- MES1 05 niki błędu 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi
Zbieżność. Wskaź- MES1 05 niki błędu 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi
Podsumowanie trzech podstawowych modeli używanych w wytrzymałości materiałów Nazwa teorii. Podstawowe wyniki
 Elementy belkowe i powło- MES-1 11 kowe Część I Elementy belkowe Podsumowanie trzech podstawowych modeli używanych w wytrzymałości materiałów Nazwa teorii Prętów Wałów Belek Rodzaj odkształcenia Rozciąganie,
Elementy belkowe i powło- MES-1 11 kowe Część I Elementy belkowe Podsumowanie trzech podstawowych modeli używanych w wytrzymałości materiałów Nazwa teorii Prętów Wałów Belek Rodzaj odkształcenia Rozciąganie,
Ć w i c z e n i e K 4
 Akademia Górniczo Hutnicza Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości, Zmęczenia Materiałów i Konstrukcji Nazwisko i Imię: Nazwisko i Imię: Wydział Górnictwa i Geoinżynierii Grupa
Akademia Górniczo Hutnicza Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości, Zmęczenia Materiałów i Konstrukcji Nazwisko i Imię: Nazwisko i Imię: Wydział Górnictwa i Geoinżynierii Grupa
7. ELEMENTY PŁYTOWE. gdzie [N] oznacza przyjmowane funkcje kształtu, zdefinować odkształcenia i naprężenia: zdefiniować macierz sztywności:
![7. ELEMENTY PŁYTOWE. gdzie [N] oznacza przyjmowane funkcje kształtu, zdefinować odkształcenia i naprężenia: zdefiniować macierz sztywności: 7. ELEMENTY PŁYTOWE. gdzie [N] oznacza przyjmowane funkcje kształtu, zdefinować odkształcenia i naprężenia: zdefiniować macierz sztywności:](/thumbs/93/113319619.jpg) 7. ELEMENTY PŁYTOWE 1 7. 7. ELEMENTY PŁYTOWE Rys. 7.1. Element płytowy Aby rozwiązać zadanie płytowe należy: zdefiniować geometrię płyty, dokonać podziału płyty na elementy, zdefiniować węzły, wprowadzić
7. ELEMENTY PŁYTOWE 1 7. 7. ELEMENTY PŁYTOWE Rys. 7.1. Element płytowy Aby rozwiązać zadanie płytowe należy: zdefiniować geometrię płyty, dokonać podziału płyty na elementy, zdefiniować węzły, wprowadzić
MECHANIKA PRĘTÓW CIENKOŚCIENNYCH
 dr inż. Robert Szmit Przedmiot: MECHANIKA PRĘTÓW CIENKOŚCIENNYCH WYKŁAD nr Uniwersytet Warmińsko-Mazurski w Olsztynie Katedra Geotechniki i Mechaniki Budowli Opis stanu odkształcenia i naprężenia powłoki
dr inż. Robert Szmit Przedmiot: MECHANIKA PRĘTÓW CIENKOŚCIENNYCH WYKŁAD nr Uniwersytet Warmińsko-Mazurski w Olsztynie Katedra Geotechniki i Mechaniki Budowli Opis stanu odkształcenia i naprężenia powłoki
4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ
 4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 1 4. 4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 4.1. Elementy trójkątne Do opisywania dwuwymiarowego kontinuum jako jeden z pierwszych elementów
4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 1 4. 4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 4.1. Elementy trójkątne Do opisywania dwuwymiarowego kontinuum jako jeden z pierwszych elementów
MES 4. 1 Przykłady błędów MES. 2 Proces V&V. Weryfikacja i walidacja. Czy MES jest nieomylny?
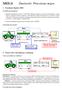 MES 4 Zbieżność. Wskaźniki błędu 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi (3
MES 4 Zbieżność. Wskaźniki błędu 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi (3
Zbieżność. Wskaźniki błędu MES Przykłady błędów MES. 2 Proces V&V. Weryfikacja i walidacja. Czy MES jest nieomylny?
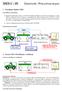 MES-1 05 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi (3 stopnie w skali Richtera),
MES-1 05 1 Przykłady błędów MES Czy MES jest nieomylny? Katastrofa platformy Sleipner A 23.08.1991. Skutki: kompletne zniszczenie konstrukcji o wadzę 97K ton, trzęsienie ziemi (3 stopnie w skali Richtera),
Wytrzymałość Materiałów
 Wytrzymałość Materiałów Zginanie Wyznaczanie sił wewnętrznych w belkach i ramach, analiza stanu naprężeń i odkształceń, warunek bezpieczeństwa Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości,
Wytrzymałość Materiałów Zginanie Wyznaczanie sił wewnętrznych w belkach i ramach, analiza stanu naprężeń i odkształceń, warunek bezpieczeństwa Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości,
Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie
 Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie Rozciąganie lub ściskanie Zginanie Skręcanie Ścinanie 1. Pręt rozciągany lub ściskany
Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie Rozciąganie lub ściskanie Zginanie Skręcanie Ścinanie 1. Pręt rozciągany lub ściskany
TARCZE PROSTOKĄTNE Charakterystyczne wielkości i równania
 TARCZE PROSTOKĄTNE Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika
TARCZE PROSTOKĄTNE Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika
Liczba godzin Liczba tygodni w tygodniu w semestrze
 15. Przedmiot: WYTRZYMAŁOŚĆ MATERIAŁÓW Kierunek: Mechatronika Specjalność: mechatronika systemów energetycznych Rozkład zajęć w czasie studiów Liczba godzin Liczba godzin Liczba tygodni w tygodniu w semestrze
15. Przedmiot: WYTRZYMAŁOŚĆ MATERIAŁÓW Kierunek: Mechatronika Specjalność: mechatronika systemów energetycznych Rozkład zajęć w czasie studiów Liczba godzin Liczba godzin Liczba tygodni w tygodniu w semestrze
Materiały pomocnicze do wykładów z wytrzymałości materiałów 1 i 2 (299 stron)
 Jerzy Wyrwał Materiały pomocnicze do wykładów z wytrzymałości materiałów 1 i 2 (299 stron) Uwaga. Załączone materiały są pomyślane jako pomoc do zrozumienia informacji podawanych na wykładzie. Zatem ich
Jerzy Wyrwał Materiały pomocnicze do wykładów z wytrzymałości materiałów 1 i 2 (299 stron) Uwaga. Załączone materiały są pomyślane jako pomoc do zrozumienia informacji podawanych na wykładzie. Zatem ich
8. Metody rozwiązywania układu równań
 8. Metody rozwiązywania układu równań [K][u e ]=[F e ] Błędy w systemie MES Etapy modelowania metodami komputerowymi UKŁAD RZECZYWISTY MODEL FIZYCZNY MODEL DYSKRETNY Weryfikacja modelu fiz. Weryfikacja
8. Metody rozwiązywania układu równań [K][u e ]=[F e ] Błędy w systemie MES Etapy modelowania metodami komputerowymi UKŁAD RZECZYWISTY MODEL FIZYCZNY MODEL DYSKRETNY Weryfikacja modelu fiz. Weryfikacja
Metoda elementów skończonych
 Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
8. PODSTAWY ANALIZY NIELINIOWEJ
 8. PODSTAWY ANALIZY NIELINIOWEJ 1 8. 8. PODSTAWY ANALIZY NIELINIOWEJ 8.1. Wprowadzenie Zadania nieliniowe mają swoje zastosowanie na przykład w rozwiązywaniu cięgien. Przyczyny nieliniowości: 1) geometryczne:
8. PODSTAWY ANALIZY NIELINIOWEJ 1 8. 8. PODSTAWY ANALIZY NIELINIOWEJ 8.1. Wprowadzenie Zadania nieliniowe mają swoje zastosowanie na przykład w rozwiązywaniu cięgien. Przyczyny nieliniowości: 1) geometryczne:
Linie wpływu w belce statycznie niewyznaczalnej
 Prof. Mieczysław Kuczma Poznań, styczeń 215 Zakład Mechaniki Budowli, PP Linie wpływu w belce statycznie niewyznaczalnej (Przykład liczbowy) Zacznijmy od zdefiniowania pojęcia linii wpływu (używa się też
Prof. Mieczysław Kuczma Poznań, styczeń 215 Zakład Mechaniki Budowli, PP Linie wpływu w belce statycznie niewyznaczalnej (Przykład liczbowy) Zacznijmy od zdefiniowania pojęcia linii wpływu (używa się też
Informacje ogólne. Rys. 1. Rozkłady odkształceń, które mogą powstać w stanie granicznym nośności
 Informacje ogólne Założenia dotyczące stanu granicznego nośności przekroju obciążonego momentem zginającym i siłą podłużną, przyjęte w PN-EN 1992-1-1, pozwalają na ujednolicenie procedur obliczeniowych,
Informacje ogólne Założenia dotyczące stanu granicznego nośności przekroju obciążonego momentem zginającym i siłą podłużną, przyjęte w PN-EN 1992-1-1, pozwalają na ujednolicenie procedur obliczeniowych,
WYMAGANIA EDUKACYJNE Z PRZEDMIOTU: KONSTRUKCJE BUDOWLANE klasa III Podstawa opracowania: PROGRAM NAUCZANIA DLA ZAWODU TECHNIK BUDOWNICTWA 311204
 WYMAGANIA EDUKACYJNE Z PRZEDMIOTU: KONSTRUKCJE BUDOWLANE klasa III Podstawa opracowania: PROGRAM NAUCZANIA DLA ZAWODU TECHNIK BUDOWNICTWA 311204 1 DZIAŁ PROGRAMOWY V. PODSTAWY STATYKI I WYTRZYMAŁOŚCI MATERIAŁÓW
WYMAGANIA EDUKACYJNE Z PRZEDMIOTU: KONSTRUKCJE BUDOWLANE klasa III Podstawa opracowania: PROGRAM NAUCZANIA DLA ZAWODU TECHNIK BUDOWNICTWA 311204 1 DZIAŁ PROGRAMOWY V. PODSTAWY STATYKI I WYTRZYMAŁOŚCI MATERIAŁÓW
Rachunek całkowy - całka oznaczona
 SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
Mechanika teoretyczna
 Wypadkowa -metoda analityczna Mechanika teoretyczna Wykład nr 2 Wypadkowa dowolnego układu sił. Równowaga. Rodzaje sił i obciążeń. Rodzaje ustrojów prętowych. Składowe poszczególnych sił układu: Składowe
Wypadkowa -metoda analityczna Mechanika teoretyczna Wykład nr 2 Wypadkowa dowolnego układu sił. Równowaga. Rodzaje sił i obciążeń. Rodzaje ustrojów prętowych. Składowe poszczególnych sił układu: Składowe
Pytania przygotowujące do egzaminu z Wytrzymałości Materiałów sem. I studia niestacjonarne, rok ak. 2014/15
 Pytania przygotowujące do egzaminu z Wytrzymałości Materiałów sem. I studia niestacjonarne, rok ak. 2014/15 1. Warunkiem koniecznym i wystarczającym równowagi układu sił zbieżnych jest, aby a) wszystkie
Pytania przygotowujące do egzaminu z Wytrzymałości Materiałów sem. I studia niestacjonarne, rok ak. 2014/15 1. Warunkiem koniecznym i wystarczającym równowagi układu sił zbieżnych jest, aby a) wszystkie
Mechanika i Budowa Maszyn
 Mechanika i Budowa Maszyn Materiały pomocnicze do ćwiczeń Wyznaczanie sił wewnętrznych w belkach statycznie wyznaczalnych Andrzej J. Zmysłowski Andrzej J. Zmysłowski Wyznaczanie sił wewnętrznych w belkach
Mechanika i Budowa Maszyn Materiały pomocnicze do ćwiczeń Wyznaczanie sił wewnętrznych w belkach statycznie wyznaczalnych Andrzej J. Zmysłowski Andrzej J. Zmysłowski Wyznaczanie sił wewnętrznych w belkach
STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH
 Część. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH.. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH Rozwiązując układy niewyznaczalne dowolnie obciążone, bardzo często pomijaliśmy wpływ sił normalnych i
Część. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH.. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH Rozwiązując układy niewyznaczalne dowolnie obciążone, bardzo często pomijaliśmy wpływ sił normalnych i
9. PODSTAWY TEORII PLASTYCZNOŚCI
 9. PODSTAWY TEORII PLASTYCZNOŚCI 1 9. 9. PODSTAWY TEORII PLASTYCZNOŚCI 9.1. Pierwsze kroki Do tej pory zajmowaliśmy się w analizie ciał i konstrukcji tylko analizą sprężystą. Nie zastanawialiśmy się, co
9. PODSTAWY TEORII PLASTYCZNOŚCI 1 9. 9. PODSTAWY TEORII PLASTYCZNOŚCI 9.1. Pierwsze kroki Do tej pory zajmowaliśmy się w analizie ciał i konstrukcji tylko analizą sprężystą. Nie zastanawialiśmy się, co
Pręt nr 1 - Element żelbetowy wg. PN-B-03264
 Pręt nr 1 - Element żelbetowy wg. PN-B-03264 Informacje o elemencie Nazwa/Opis: element nr 5 (belka) - Brak opisu elementu. Węzły: 13 (x6.000m, y24.000m); 12 (x18.000m, y24.000m) Profil: Pr 350x900 (Beton
Pręt nr 1 - Element żelbetowy wg. PN-B-03264 Informacje o elemencie Nazwa/Opis: element nr 5 (belka) - Brak opisu elementu. Węzły: 13 (x6.000m, y24.000m); 12 (x18.000m, y24.000m) Profil: Pr 350x900 (Beton
Siły wewnętrzne - związki różniczkowe
 Siły wewnętrzne - związki różniczkowe Weźmy dowolny fragment belki obciążony wzdłuż osi obciążeniem n(x) oraz poprzecznie obciążeniem q(x). Na powyższym rysunku zwroty obciążeń są zgodne z dodatnimi zwrotami
Siły wewnętrzne - związki różniczkowe Weźmy dowolny fragment belki obciążony wzdłuż osi obciążeniem n(x) oraz poprzecznie obciążeniem q(x). Na powyższym rysunku zwroty obciążeń są zgodne z dodatnimi zwrotami
Pręt nr 1 - Element żelbetowy wg. EN :2004
 Pręt nr 1 - Element żelbetowy wg. EN 1992-1-1:2004 Informacje o elemencie Nazwa/Opis: element nr 5 (belka) - Brak opisu elementu. Węzły: 13 (x6.000m, y24.000m); 12 (x18.000m, y24.000m) Profil: Pr 350x800
Pręt nr 1 - Element żelbetowy wg. EN 1992-1-1:2004 Informacje o elemencie Nazwa/Opis: element nr 5 (belka) - Brak opisu elementu. Węzły: 13 (x6.000m, y24.000m); 12 (x18.000m, y24.000m) Profil: Pr 350x800
Spis treści. Wstęp Część I STATYKA
 Spis treści Wstęp... 15 Część I STATYKA 1. WEKTORY. PODSTAWOWE DZIAŁANIA NA WEKTORACH... 17 1.1. Pojęcie wektora. Rodzaje wektorów... 19 1.2. Rzut wektora na oś. Współrzędne i składowe wektora... 22 1.3.
Spis treści Wstęp... 15 Część I STATYKA 1. WEKTORY. PODSTAWOWE DZIAŁANIA NA WEKTORACH... 17 1.1. Pojęcie wektora. Rodzaje wektorów... 19 1.2. Rzut wektora na oś. Współrzędne i składowe wektora... 22 1.3.
Wzór Żurawskiego. Belka o przekroju kołowym. Składowe naprężenia stycznego można wyrazić następująco (np. [1,2]): T r 2 y ν ) (1) (2)
![Wzór Żurawskiego. Belka o przekroju kołowym. Składowe naprężenia stycznego można wyrazić następująco (np. [1,2]): T r 2 y ν ) (1) (2) Wzór Żurawskiego. Belka o przekroju kołowym. Składowe naprężenia stycznego można wyrazić następująco (np. [1,2]): T r 2 y ν ) (1) (2)](/thumbs/101/149183432.jpg) Przykłady rozkładu naprężenia stycznego w przekrojach belki zginanej nierównomiernie (materiał uzupełniający do wykładu z wytrzymałości materiałów I, opr. Z. Więckowski, 11.2018) Wzór Żurawskiego τ xy
Przykłady rozkładu naprężenia stycznego w przekrojach belki zginanej nierównomiernie (materiał uzupełniający do wykładu z wytrzymałości materiałów I, opr. Z. Więckowski, 11.2018) Wzór Żurawskiego τ xy
Przykład 4.1. Ściag stalowy. L200x100x cm 10 cm I120. Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym
 Przykład 4.1. Ściag stalowy Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym rysunku jeśli naprężenie dopuszczalne wynosi 15 MPa. Szukana siła P przyłożona jest
Przykład 4.1. Ściag stalowy Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym rysunku jeśli naprężenie dopuszczalne wynosi 15 MPa. Szukana siła P przyłożona jest
{H B= 6 kn. Przykład 1. Dana jest belka: Podać wykresy NTM.
 Przykład 1. Dana jest belka: Podać wykresy NTM. Niezależnie od sposobu rozwiązywania zadania, zacząć należy od zastąpienia podpór reakcjami. Na czas obliczania reakcji można zastąpić obciążenie ciągłe
Przykład 1. Dana jest belka: Podać wykresy NTM. Niezależnie od sposobu rozwiązywania zadania, zacząć należy od zastąpienia podpór reakcjami. Na czas obliczania reakcji można zastąpić obciążenie ciągłe
gruparectan.pl 1. Metor Strona:1 Dla danego układu wyznaczyć MTN metodą przemieszczeń Rys. Schemat układu Współrzędne węzłów:
 1. Metor Dla danego układu wyznaczyć MTN metodą przemieszczeń Rys. Schemat układu Współrzędne węzłów: węzeł 1 x=[0.000][m], y=[0.000][m] węzeł 2 x=[2.000][m], y=[0.000][m] węzeł 3 x=[2.000][m], y=[2.000][m]
1. Metor Dla danego układu wyznaczyć MTN metodą przemieszczeń Rys. Schemat układu Współrzędne węzłów: węzeł 1 x=[0.000][m], y=[0.000][m] węzeł 2 x=[2.000][m], y=[0.000][m] węzeł 3 x=[2.000][m], y=[2.000][m]
Wytrzymałość Konstrukcji I - MEiL część II egzaminu. 1. Omówić wykresy rozciągania typowych materiałów. Podać charakterystyczne punkty wykresów.
 Wytrzymałość Konstrukcji I - MEiL część II egzaminu 1. Omówić wykresy rozciągania typowych materiałów. Podać charakterystyczne punkty wykresów. 2. Omówić pojęcia sił wewnętrznych i zewnętrznych konstrukcji.
Wytrzymałość Konstrukcji I - MEiL część II egzaminu 1. Omówić wykresy rozciągania typowych materiałów. Podać charakterystyczne punkty wykresów. 2. Omówić pojęcia sił wewnętrznych i zewnętrznych konstrukcji.
TENSOMETRIA ZARYS TEORETYCZNY
 TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A
 PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej
PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej
Wprowadzenie do MES. Dla każdego ES, w oparciu o przemieszczenia w węzłach, wyznaczamy siły działające na niego, odkształcenia, naprężenia, itp.
 MES 2 Wprowadzenie do MES Everything important is simple! Podstawowe zasady MES Dzielimy konstrukcję na proste fragmenty (analogia klocki Lego, cegły), które nazywamy elementami skończonymi (ES). ES są
MES 2 Wprowadzenie do MES Everything important is simple! Podstawowe zasady MES Dzielimy konstrukcję na proste fragmenty (analogia klocki Lego, cegły), które nazywamy elementami skończonymi (ES). ES są
Wyboczenie ściskanego pręta
 Wszelkie prawa zastrzeżone Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: 1. Wstęp Wyboczenie ściskanego pręta oprac. dr inż. Ludomir J. Jankowski Zagadnienie wyboczenia
Wszelkie prawa zastrzeżone Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: 1. Wstęp Wyboczenie ściskanego pręta oprac. dr inż. Ludomir J. Jankowski Zagadnienie wyboczenia
Modelowanie Wspomagające Projektowanie Maszyn
 Modelowanie Wspomagające Projektowanie Maszyn TEMATY ĆWICZEŃ: 1. Metoda elementów skończonych współczynnik kształtu płaskownika z karbem a. Współczynnik kształtu b. MES i. Preprocesor ii. Procesor iii.
Modelowanie Wspomagające Projektowanie Maszyn TEMATY ĆWICZEŃ: 1. Metoda elementów skończonych współczynnik kształtu płaskownika z karbem a. Współczynnik kształtu b. MES i. Preprocesor ii. Procesor iii.
7.0. Fundament pod słupami od stropu nad piwnicą. Rzut fundamentu. Wymiary:
 7.0. Fundament pod słupami od stropu nad piwnicą. Rzut fundamentu Wymiary: B=1,2m L=4,42m H=0,4m Stan graniczny I Stan graniczny II Obciążenie fundamentu odporem gruntu OBCIĄŻENIA: 221,02 221,02 221,02
7.0. Fundament pod słupami od stropu nad piwnicą. Rzut fundamentu Wymiary: B=1,2m L=4,42m H=0,4m Stan graniczny I Stan graniczny II Obciążenie fundamentu odporem gruntu OBCIĄŻENIA: 221,02 221,02 221,02
CIENKOŚCIENNE KONSTRUKCJE METALOWE
 CIENKOŚCIENNE KONSTRUKCJE METALOWE Wykład 6: Wymiarowanie elementów cienkościennych o przekroju w ujęciu teorii Własowa INFORMACJE OGÓLNE Ścianki rozważanych elementów, w zależności od smukłości pod naprężeniami
CIENKOŚCIENNE KONSTRUKCJE METALOWE Wykład 6: Wymiarowanie elementów cienkościennych o przekroju w ujęciu teorii Własowa INFORMACJE OGÓLNE Ścianki rozważanych elementów, w zależności od smukłości pod naprężeniami
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
ALGORYTM STATYCZNEJ ANALIZY MES DLA KRATOWNICY
 ALGORYTM STATYCZNEJ ANALIZY MES DLA RATOWNICY Piotr Pluciński e-mail: p.plucinski@l5.pk.edu.pl Jerzy Pamin e-mail: jpamin@l5.pk.edu.pl Instytut Technologii Informatycznych w Inżynierii Lądowej Wydział
ALGORYTM STATYCZNEJ ANALIZY MES DLA RATOWNICY Piotr Pluciński e-mail: p.plucinski@l5.pk.edu.pl Jerzy Pamin e-mail: jpamin@l5.pk.edu.pl Instytut Technologii Informatycznych w Inżynierii Lądowej Wydział
Analiza stateczności zbocza
 Przewodnik Inżyniera Nr 25 Aktualizacja: 06/2017 Analiza stateczności zbocza Program: MES Plik powiązany: Demo_manual_25.gmk Celem niniejszego przewodnika jest analiza stateczności zbocza (wyznaczenie
Przewodnik Inżyniera Nr 25 Aktualizacja: 06/2017 Analiza stateczności zbocza Program: MES Plik powiązany: Demo_manual_25.gmk Celem niniejszego przewodnika jest analiza stateczności zbocza (wyznaczenie
9.0. Wspornik podtrzymujący schody górne płytowe
 9.0. Wspornik podtrzymujący schody górne płytowe OBCIĄŻENIA: 55,00 55,00 OBCIĄŻENIA: ([kn],[knm],[kn/m]) Pręt: Rodzaj: Kąt: P(Tg): P2(Td): a[m]: b[m]: Grupa: A "" Zmienne γf=,0 Liniowe 0,0 55,00 55,00
9.0. Wspornik podtrzymujący schody górne płytowe OBCIĄŻENIA: 55,00 55,00 OBCIĄŻENIA: ([kn],[knm],[kn/m]) Pręt: Rodzaj: Kąt: P(Tg): P2(Td): a[m]: b[m]: Grupa: A "" Zmienne γf=,0 Liniowe 0,0 55,00 55,00
8. WIADOMOŚCI WSTĘPNE
 Część 2 8. MECHNIK ELEMENTÓW PRĘTOWYCH WIDOMOŚCI WSTĘPNE 1 8. WIDOMOŚCI WSTĘPNE 8.1. KLSYFIKCJ ZSDNICZYCH ELEMENTÓW KONSTRUKCJI Podstawą klasyfikacji zasadniczych elementów konstrukcji jest kształt geometryczny
Część 2 8. MECHNIK ELEMENTÓW PRĘTOWYCH WIDOMOŚCI WSTĘPNE 1 8. WIDOMOŚCI WSTĘPNE 8.1. KLSYFIKCJ ZSDNICZYCH ELEMENTÓW KONSTRUKCJI Podstawą klasyfikacji zasadniczych elementów konstrukcji jest kształt geometryczny
Metoda Elementów Skończonych - Laboratorium
 Metoda Elementów Skończonych - Laboratorium Laboratorium 5 Podstawy ABAQUS/CAE Analiza koncentracji naprężenia na przykładzie rozciąganej płaskiej płyty z otworem. Główne cele ćwiczenia: 1. wykorzystanie
Metoda Elementów Skończonych - Laboratorium Laboratorium 5 Podstawy ABAQUS/CAE Analiza koncentracji naprężenia na przykładzie rozciąganej płaskiej płyty z otworem. Główne cele ćwiczenia: 1. wykorzystanie
Element cięgnowy. Rysunek: Element LINK1. Jakub J. Słowiński (IMMT PWr) Wykład 4 09 i 16.03.2012 51 / 74
 Elementy 1D Element cięgnowy Element LINK1 jest elementem 2D, dwuwęzłowym, posiadającym jedynie dwa stopnie swobody - translację w kierunku x oraz y. Można zadeklarować pole jego przekroju oraz odkształcenie
Elementy 1D Element cięgnowy Element LINK1 jest elementem 2D, dwuwęzłowym, posiadającym jedynie dwa stopnie swobody - translację w kierunku x oraz y. Można zadeklarować pole jego przekroju oraz odkształcenie
Wprowadzenie do WK1 Stan naprężenia
 Wytrzymałość materiałów i konstrukcji 1 Wykład 1 Wprowadzenie do WK1 Stan naprężenia Płaski stan naprężenia Dr inż. Piotr Marek Wytrzymałość Konstrukcji (Wytrzymałość materiałów, Mechanika konstrukcji)
Wytrzymałość materiałów i konstrukcji 1 Wykład 1 Wprowadzenie do WK1 Stan naprężenia Płaski stan naprężenia Dr inż. Piotr Marek Wytrzymałość Konstrukcji (Wytrzymałość materiałów, Mechanika konstrukcji)
Wpływ podpory ograniczającej obrót pasa ściskanego na stateczność słupa-belki
 Wpływ podpory ograniczającej obrót pasa ściskanego na stateczność słupa-belki Informacje ogólne Podpora ograniczająca obrót pasa ściskanego słupa (albo ramy) może znacząco podnieść wielkość mnożnika obciążenia,
Wpływ podpory ograniczającej obrót pasa ściskanego na stateczność słupa-belki Informacje ogólne Podpora ograniczająca obrót pasa ściskanego słupa (albo ramy) może znacząco podnieść wielkość mnożnika obciążenia,
2. Pręt skręcany o przekroju kołowym
 2. Pręt skręcany o przekroju kołowym Przebieg wykładu : 1. Sformułowanie zagadnienia 2. Warunki równowagi kąt skręcenia 3. Warunek geometryczny kąt odkształcenia postaciowego 4. Związek fizyczny Prawo
2. Pręt skręcany o przekroju kołowym Przebieg wykładu : 1. Sformułowanie zagadnienia 2. Warunki równowagi kąt skręcenia 3. Warunek geometryczny kąt odkształcenia postaciowego 4. Związek fizyczny Prawo
Zestaw pytań z konstrukcji i mechaniki
 Zestaw pytań z konstrukcji i mechaniki 1. Układ sił na przedstawionym rysunku a) jest w równowadze b) jest w równowadze jeśli jest to układ dowolny c) nie jest w równowadze d) na podstawie tego rysunku
Zestaw pytań z konstrukcji i mechaniki 1. Układ sił na przedstawionym rysunku a) jest w równowadze b) jest w równowadze jeśli jest to układ dowolny c) nie jest w równowadze d) na podstawie tego rysunku
10.1 Płyta wspornikowa schodów górnych wspornikowych w płaszczyźnie prostopadłej.
 10.1 Płyta wspornikowa schodów górnych wspornikowych w płaszczyźnie prostopadłej. OBCIĄŻENIA: 6,00 6,00 4,11 4,11 1 OBCIĄŻENIA: ([kn],[knm],[kn/m]) Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]: Grupa:
10.1 Płyta wspornikowa schodów górnych wspornikowych w płaszczyźnie prostopadłej. OBCIĄŻENIA: 6,00 6,00 4,11 4,11 1 OBCIĄŻENIA: ([kn],[knm],[kn/m]) Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]: Grupa:
1. Obciążenie statyczne
 . Obciążenie statyczne.. Obliczenie stopnia kinematycznej niewyznaczalności n = Σ ϕ + Σ = + = p ( ) Σ = w p + d u = 5 + 5 + 0 0 =. Schemat podstawowy metody przemieszczeń . Schemat odkształceń łańcucha
. Obciążenie statyczne.. Obliczenie stopnia kinematycznej niewyznaczalności n = Σ ϕ + Σ = + = p ( ) Σ = w p + d u = 5 + 5 + 0 0 =. Schemat podstawowy metody przemieszczeń . Schemat odkształceń łańcucha
Politechnika Krakowska im. Tadeusza Kościuszki. Karta przedmiotu. obowiązuje studentów rozpoczynających studia w roku akademickim 2015/2016
 Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 015/016 Kierunek studiów: Mechanika i Budowa Maszyn Forma
Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 015/016 Kierunek studiów: Mechanika i Budowa Maszyn Forma
1. Połączenia spawane
 1. Połączenia spawane Przykład 1a. Sprawdzić nośność spawanego połączenia pachwinowego zakładając osiową pracę spoiny. Rysunek 1. Przykład zakładkowego połączenia pachwinowego Dane: geometria połączenia
1. Połączenia spawane Przykład 1a. Sprawdzić nośność spawanego połączenia pachwinowego zakładając osiową pracę spoiny. Rysunek 1. Przykład zakładkowego połączenia pachwinowego Dane: geometria połączenia
Wyznaczanie modułu Younga metodą strzałki ugięcia
 Ćwiczenie M12 Wyznaczanie modułu Younga metodą strzałki ugięcia M12.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie wartości modułu Younga różnych materiałów poprzez badanie strzałki ugięcia wykonanych
Ćwiczenie M12 Wyznaczanie modułu Younga metodą strzałki ugięcia M12.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie wartości modułu Younga różnych materiałów poprzez badanie strzałki ugięcia wykonanych
FUNKCJE. Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 5 Teoria funkcje cz.1. Definicja funkcji i wiadomości podstawowe
 1 FUNKCJE Definicja funkcji i wiadomości podstawowe Jeżeli mamy dwa zbiory: zbiór X i zbiór Y, i jeżeli każdemu elementowi ze zbioru X przyporządkujemy dokładnie jeden element ze zbioru Y, to takie przyporządkowanie
1 FUNKCJE Definicja funkcji i wiadomości podstawowe Jeżeli mamy dwa zbiory: zbiór X i zbiór Y, i jeżeli każdemu elementowi ze zbioru X przyporządkujemy dokładnie jeden element ze zbioru Y, to takie przyporządkowanie
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
pt.: KOMPUTEROWE WSPOMAGANIE PROCESÓW OBRÓBKI PLASTYCZNEJ
 Ćwiczenie audytoryjne pt.: KOMPUTEROWE WSPOMAGANIE PROCESÓW OBRÓBKI PLASTYCZNEJ Autor: dr inż. Radosław Łyszkowski Warszawa, 2013r. Metoda elementów skończonych MES FEM - Finite Element Method przybliżona
Ćwiczenie audytoryjne pt.: KOMPUTEROWE WSPOMAGANIE PROCESÓW OBRÓBKI PLASTYCZNEJ Autor: dr inż. Radosław Łyszkowski Warszawa, 2013r. Metoda elementów skończonych MES FEM - Finite Element Method przybliżona
Tra r n a s n fo f rm r a m c a ja a na n p a rę r ż ę eń e pomi m ę i d ę zy y uk u ł k a ł d a am a i m i obr b ó r cony n m y i m
 Wytrzymałość materiałów Naprężenia główne na przykładzie płaskiego stanu naprężeń 1 Tensor naprężeń Naprężenia w stanie przestrzennym: τ τxz τ yx τ yz τzx τzy zz Układ współrzędnych jest zwykle wybrany
Wytrzymałość materiałów Naprężenia główne na przykładzie płaskiego stanu naprężeń 1 Tensor naprężeń Naprężenia w stanie przestrzennym: τ τxz τ yx τ yz τzx τzy zz Układ współrzędnych jest zwykle wybrany
WIADOMOŚCI WSTĘPNE, PRACA SIŁ NA PRZEMIESZCZENIACH
 Część 1 1. WIADOOŚCI WSTĘNE, RACA SIŁ NA RZEIESZCZENIAC 1 1.. 1. WIADOOŚCI WSTĘNE, RACA SIŁ NA RZEIESZCZENIAC 1.1. Wstęp echanika budowli stanowi dział mechaniki technicznej zajmującej się statyką, dynamiką,
Część 1 1. WIADOOŚCI WSTĘNE, RACA SIŁ NA RZEIESZCZENIAC 1 1.. 1. WIADOOŚCI WSTĘNE, RACA SIŁ NA RZEIESZCZENIAC 1.1. Wstęp echanika budowli stanowi dział mechaniki technicznej zajmującej się statyką, dynamiką,
MES1 Metoda elementów skończonych - I Finite Element Method - I. Mechanika i Budowa Maszyn I stopień ogólnoakademicki
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2016/2017 MES1 Metoda elementów skończonych - I Finite Element Method - I A. USYTUOWANIE
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2016/2017 MES1 Metoda elementów skończonych - I Finite Element Method - I A. USYTUOWANIE
Mechanika teoretyczna
 Inne rodzaje obciążeń Mechanika teoretyczna Obciążenie osiowe rozłożone wzdłuż pręta. Obciążenie pionowe na pręcie ukośnym: intensywność na jednostkę rzutu; intensywność na jednostkę długości pręta. Wykład
Inne rodzaje obciążeń Mechanika teoretyczna Obciążenie osiowe rozłożone wzdłuż pręta. Obciążenie pionowe na pręcie ukośnym: intensywność na jednostkę rzutu; intensywność na jednostkę długości pręta. Wykład
10.0. Schody górne, wspornikowe.
 10.0. Schody górne, wspornikowe. OBCIĄŻENIA: Grupa: A "obc. stałe - pł. spocznik" Stałe γf= 1,0/0,90 Q k = 0,70 kn/m *1,5m=1,05 kn/m. Q o1 = 0,84 kn/m *1,5m=1,6 kn/m, γ f1 = 1,0, Q o = 0,63 kn/m *1,5m=0,95
10.0. Schody górne, wspornikowe. OBCIĄŻENIA: Grupa: A "obc. stałe - pł. spocznik" Stałe γf= 1,0/0,90 Q k = 0,70 kn/m *1,5m=1,05 kn/m. Q o1 = 0,84 kn/m *1,5m=1,6 kn/m, γ f1 = 1,0, Q o = 0,63 kn/m *1,5m=0,95
gruparectan.pl 1. Silos 2. Ustalenie stopnia statycznej niewyznaczalności układu SSN Strona:1 Dla danego układu wyznaczyć MTN metodą sił
 1. Silos Dla danego układu wyznaczyć MTN metodą sił Rys. Schemat układu Przyjęto przekrój podstawowy: I= 3060[cm4] E= 205[GPa] Globalne EI= 6273[kNm²] Globalne EA= 809750[kN] 2. Ustalenie stopnia statycznej
1. Silos Dla danego układu wyznaczyć MTN metodą sił Rys. Schemat układu Przyjęto przekrój podstawowy: I= 3060[cm4] E= 205[GPa] Globalne EI= 6273[kNm²] Globalne EA= 809750[kN] 2. Ustalenie stopnia statycznej
ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI
 10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI 1 10. 10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI 10.1. Zastosowanie funkcji Airy'ego =0 (10.1) Zakładamy, że istnieje funkcja F(x,y) spełniająca następujące
10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI 1 10. 10. ROZWIĄZYWANIE ZADAŃ Z TEORII SPRĘŻYSTOŚCI 10.1. Zastosowanie funkcji Airy'ego =0 (10.1) Zakładamy, że istnieje funkcja F(x,y) spełniająca następujące
Ścinanie i skręcanie. dr hab. inż. Tadeusz Chyży
 Ścinanie i skręcanie dr hab. inż. Tadeusz Chyży 1 Ścinanie proste Ścinanie czyste Ścinanie techniczne 2 Ścinanie Czyste ścinanie ma miejsce wtedy, gdy na czterech ścianach prostopadłościennej kostki występują
Ścinanie i skręcanie dr hab. inż. Tadeusz Chyży 1 Ścinanie proste Ścinanie czyste Ścinanie techniczne 2 Ścinanie Czyste ścinanie ma miejsce wtedy, gdy na czterech ścianach prostopadłościennej kostki występują
Wprowadzenie do MES. Dla każdego ES, w oparciu o przemieszczenia w węzłach, wyznaczamy siły działające na niego, odkształcenia, naprężenia, itp.
 MES 2 Everything important is simple! odstawowe zasady MES Dzielimy konstrukcję na proste fragmenty (analogia klocki Lego, cegły), które nazywamy elementami skończonymi (ES). ES są połączone w węzłach
MES 2 Everything important is simple! odstawowe zasady MES Dzielimy konstrukcję na proste fragmenty (analogia klocki Lego, cegły), które nazywamy elementami skończonymi (ES). ES są połączone w węzłach
Dr inż. Janusz Dębiński
 Wytrzymałość materiałów ćwiczenia projektowe 5. Projekt numer 5 przykład 5.. Temat projektu Na rysunku 5.a przedstawiono belkę swobodnie podpartą wykorzystywaną w projekcie numer 5 z wytrzymałości materiałów.
Wytrzymałość materiałów ćwiczenia projektowe 5. Projekt numer 5 przykład 5.. Temat projektu Na rysunku 5.a przedstawiono belkę swobodnie podpartą wykorzystywaną w projekcie numer 5 z wytrzymałości materiałów.
Metody numeryczne. materiały do wykładu dla studentów. 7. Całkowanie numeryczne
 Metody numeryczne materiały do wykładu dla studentów 7. Całkowanie numeryczne 7.1. Całkowanie numeryczne 7.2. Metoda trapezów 7.3. Metoda Simpsona 7.4. Metoda 3/8 Newtona 7.5. Ogólna postać wzorów kwadratur
Metody numeryczne materiały do wykładu dla studentów 7. Całkowanie numeryczne 7.1. Całkowanie numeryczne 7.2. Metoda trapezów 7.3. Metoda Simpsona 7.4. Metoda 3/8 Newtona 7.5. Ogólna postać wzorów kwadratur
FUNKCJE I RÓWNANIA KWADRATOWE. Lekcja 78. Pojęcie i wykres funkcji kwadratowej str
 FUNKCJE I RÓWNANIA KWADRATOWE Lekcja 78. Pojęcie i wykres funkcji kwadratowej str. 178-180. Funkcja kwadratowa to taka, której wykresem jest parabola. Definicja Funkcją kwadratową nazywamy funkcje postaci
FUNKCJE I RÓWNANIA KWADRATOWE Lekcja 78. Pojęcie i wykres funkcji kwadratowej str. 178-180. Funkcja kwadratowa to taka, której wykresem jest parabola. Definicja Funkcją kwadratową nazywamy funkcje postaci
Styczeń wzoru 6.10a i 6.10b, zadawać współczynniki. współczynniki redukcyjne dla obciążeń
 Styczeń 2016 105. Wprowadzono przycisk [K] - jak kasuj, którym można usunąć wszystkie dane o żelbecie. Można go użyć w sytuacji, kiedy każda próba wywołania menu Wymiar kończy się komunikatem błędu z angielskim
Styczeń 2016 105. Wprowadzono przycisk [K] - jak kasuj, którym można usunąć wszystkie dane o żelbecie. Można go użyć w sytuacji, kiedy każda próba wywołania menu Wymiar kończy się komunikatem błędu z angielskim
Symulacja Analiza_wytrz_kor_ra my
 Symulacja Analiza_wytrz_kor_ra my Data: 19 września 2016 Projektant: Nazwa badania: Analiza statyczna 1 Typ analizy: Analiza statyczna Opis Brak danych Spis treści Opis... 1 Założenia... 2 Informacje o
Symulacja Analiza_wytrz_kor_ra my Data: 19 września 2016 Projektant: Nazwa badania: Analiza statyczna 1 Typ analizy: Analiza statyczna Opis Brak danych Spis treści Opis... 1 Założenia... 2 Informacje o
Modelowanie układów prętowych
 Modelowanie kładów prętowych Elementy prętowe -definicja Elementami prętowymi można modelować - elementy konstrkcji o stosnk wymiarów poprzecznych do podłżnego poniżej 0.1, - elementy, które są wąskie
Modelowanie kładów prętowych Elementy prętowe -definicja Elementami prętowymi można modelować - elementy konstrkcji o stosnk wymiarów poprzecznych do podłżnego poniżej 0.1, - elementy, które są wąskie
Lista 6. Kamil Matuszewski 13 kwietnia D n =
 Lista 6 Kamil Matuszewski 3 kwietnia 6 3 4 5 6 7 8 9 Zadanie Mamy Pokaż, że det(d n ) = n.... D n =.... Dowód. Okej. Dla n =, n = trywialne. Załóżmy, że dla n jest ok, sprawdzę dla n. Aby to zrobić skorzystam
Lista 6 Kamil Matuszewski 3 kwietnia 6 3 4 5 6 7 8 9 Zadanie Mamy Pokaż, że det(d n ) = n.... D n =.... Dowód. Okej. Dla n =, n = trywialne. Załóżmy, że dla n jest ok, sprawdzę dla n. Aby to zrobić skorzystam
WYZNACZANIE MODUŁU YOUNGA METODĄ STRZAŁKI UGIĘCIA
 Ćwiczenie 58 WYZNACZANIE MODUŁU YOUNGA METODĄ STRZAŁKI UGIĘCIA 58.1. Wiadomości ogólne Pod działaniem sił zewnętrznych ciała stałe ulegają odkształceniom, czyli zmieniają kształt. Zmianę odległości między
Ćwiczenie 58 WYZNACZANIE MODUŁU YOUNGA METODĄ STRZAŁKI UGIĘCIA 58.1. Wiadomości ogólne Pod działaniem sił zewnętrznych ciała stałe ulegają odkształceniom, czyli zmieniają kształt. Zmianę odległości między
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia. Wytrzymałość materiałów Rodzaj przedmiotu: obowiązkowy Kod przedmiotu:
 Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Wytrzymałość materiałów Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 3 19-0_1 Rok: II Semestr: 3 Forma studiów:
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Wytrzymałość materiałów Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 3 19-0_1 Rok: II Semestr: 3 Forma studiów:
Analiza fundamentu na mikropalach
 Przewodnik Inżyniera Nr 36 Aktualizacja: 09/2017 Analiza fundamentu na mikropalach Program: Plik powiązany: Grupa pali Demo_manual_en_36.gsp Celem niniejszego przewodnika jest przedstawienie wykorzystania
Przewodnik Inżyniera Nr 36 Aktualizacja: 09/2017 Analiza fundamentu na mikropalach Program: Plik powiązany: Grupa pali Demo_manual_en_36.gsp Celem niniejszego przewodnika jest przedstawienie wykorzystania
Narysować wykresy momentów i sił tnących w belce jak na rysunku. 3ql
 Narysować wykresy momentów i sił tnących w belce jak na rysunku. q l Określamy stopień statycznej niewyznaczalności: n s = r - 3 - p = 5-3 - 0 = 2 Przyjmujemy schemat podstawowy: X 2 X Zakładamy do obliczeń,
Narysować wykresy momentów i sił tnących w belce jak na rysunku. q l Określamy stopień statycznej niewyznaczalności: n s = r - 3 - p = 5-3 - 0 = 2 Przyjmujemy schemat podstawowy: X 2 X Zakładamy do obliczeń,
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne.
 Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
2kN/m Zgodnie z wyznaczonym zadaniem przed rozpoczęciem obliczeń dobieram wstępne przekroje prętów.
 2kN/m -20 C D 5kN 0,006m A B 0,004m +0 +20 0,005rad E 4 2 4 [m] Układ prętów ma dwie tarcze i osiem reakcji w podporach. Stopień statycznej niewyznaczalności SSN= 2, ponieważ, przy dwóch tarczach powinno
2kN/m -20 C D 5kN 0,006m A B 0,004m +0 +20 0,005rad E 4 2 4 [m] Układ prętów ma dwie tarcze i osiem reakcji w podporach. Stopień statycznej niewyznaczalności SSN= 2, ponieważ, przy dwóch tarczach powinno
Pręt nr 0 - Płyta żelbetowa jednokierunkowo zbrojona wg PN-EN :2004
 Pręt nr 0 - Płyta żelbetowa jednokierunkowo zbrojona wg PN-EN 1992-1- 1:2004 Informacje o elemencie Nazwa/Opis: element nr 0 (belka) - Brak opisu elementu. Węzły: 0 (x0.000m, y0.000m); 1 (x6.000m, y0.000m)
Pręt nr 0 - Płyta żelbetowa jednokierunkowo zbrojona wg PN-EN 1992-1- 1:2004 Informacje o elemencie Nazwa/Opis: element nr 0 (belka) - Brak opisu elementu. Węzły: 0 (x0.000m, y0.000m); 1 (x6.000m, y0.000m)
Pierwsze komputery, np. ENIAC w 1946r. Obliczenia dotyczyły obiektów: o bardzo prostych geometriach (najczęściej modelowanych jako jednowymiarowe)
 METODA ELEMENTÓW W SKOŃCZONYCH 1 Pierwsze komputery, np. ENIAC w 1946r. Obliczenia dotyczyły obiektów: o bardzo prostych geometriach (najczęściej modelowanych jako jednowymiarowe) stałych własnościach
METODA ELEMENTÓW W SKOŃCZONYCH 1 Pierwsze komputery, np. ENIAC w 1946r. Obliczenia dotyczyły obiektów: o bardzo prostych geometriach (najczęściej modelowanych jako jednowymiarowe) stałych własnościach
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
