Równanie Modowe Światłowodu Planarnego
|
|
|
- Ludwik Leśniak
- 6 lat temu
- Przeglądów:
Transkrypt
1 Rówaie Modowe Światłowodu Plaarego Prezetaja zawiera oie olii omawia a władzie. Niiejze oraowaie roioe jet rawem autorim. Worztaie ieomerje dozwoloe od waruiem odaia źródła. Sergiuz Patela
2 β Rówaie alowe światłowodu laarego µε t (,, z)e i ω t β z [ β ] gdzie: π π λ λ [( )] ω, β ( ) i Ce C o () C o( ) i( ) ( + t ) ( t) + i( ) t t e t β β β Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego
3 Rozład ola eletrzego trze ierwz modów światłowodu laarego; ,5,, 1, λ 633 m Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 3
4 Warui brzegowe - rzade ogól Sładowe ormale ˆ ( B B1 ) ( D D ) ˆ 1 σ Sładowe tze H H K ( 1 ) ( ) 1 Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 4
5 Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 5 t t Warui brzegowe a graia światłowodu laarego:
6 Warui brzegowe a graia światłowodu laarego - weriaja (1) Podtawiają Ce C o () C o( ) i( ) ( + t ) ( t) + i( ) t t e t do t rawdzim orawość wbra rozwiązań (zzegółowa aaliza ozwala wrowadzić rezetowae tu rozwiązaia) Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 6
7 Warui brzegowe a graia światłowodu laarego - weriaja () Podtawiają Ce C o ( ) C o( ) i( ) ( + t ) ( t) + i( ) t t e t do rawdza orawość wbra ziów tał w rozwiązaia Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 7
8 Wrowadzeie rówaia modowego Podtawiają Ce C o ( ) C o( ) i( ) ( + t ) ( t) + i( ) t t e t do t wrowadzim rówaie modowe: i t o t o t i ( ) ( ) ( ) + ( t) Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 8
9 Przeztałeie rówaa modowego do otai z tageem i t o t o t i Dzielą ałość rzez o(t) ( ) ( ) ( ) + ( t) ta + ( t) ta( t) ta + ( t) ta( t) ta ( t) + ( 1 / ) Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 9
10 Addtwa otać rówaia modowego Przeztałim rówaie modowe ta ( t) + ( 1 / ) do otai addtwej () t o Φ Φ πm, m, 1,,... Sorztam z tożamośi trgoometrzej: u + v arta arta u + arta 1 uv v ta ( t ) + ( 1 / ) ( ) + 1 Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 1
11 Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 11 ( ) ta t + 1 ( ) [ ] L t t m :arta ta, ± π P : arta arta arta t ± + π arta arta t m arta arta π Wrowadzeie addtwej otai rówaia modowego
12 Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 1 β β ( ) o i i 1 i i i ( ) o i i 1 i i i β β Φ o i arta arta Φ o i arta arta β β β Przeuięie az (wółzii Freella)
13 Sładi t β De. : β β wetor,, β tworzą trójąt rotoąt o t t () o () o () t ( ) o arta arta πm, m 1,,,... t o () Φ Φ πm, m,1,,... Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 13
14 Wre modow: Ne lub ąt. Krzwe modowe T 9 N e [ ] d [µm] 5 Porówaie rzw modow reślo jao zależośi N e (d) i (d)., 1.5, 1 Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 14
15 Wre modow: T i TM Krzwe modowe T i TM., 1.5, Ne d [um] Zależość eetwego wółzia od grubośi wartw dla trze ierwz modów T i TM światłowodu laarego Sergiuz Patela Podtaw Teorii Światłowodoów. Rówaie modowe światłowodu laarego 15
Zasada działania, właściwości i parametry światłowodów. Sergiusz Patela Podstawowe właściwości światłowodów 1
 Zasada działaia, właściwości i parametry światłowodów Sergiusz Patela 1999-003 Podstawowe właściwości światłowodów 1 Parametry światłowodów - klasyfikacja Parametry włókie światłowodowych: 1. Optycze tłumieie,
Zasada działaia, właściwości i parametry światłowodów Sergiusz Patela 1999-003 Podstawowe właściwości światłowodów 1 Parametry światłowodów - klasyfikacja Parametry włókie światłowodowych: 1. Optycze tłumieie,
Światłowody II. Właściwości i zastosowania światłowodów. Wprowadzenie. Uwaga: Wykład zawiera podsumowanie wiadomości z wykładu Światłowody I
 Światłowody II Właściwości i zastosowaia światłowodów Wprowadzeie Uwaga: Wykład zawiera podsumowaie wiadomości z wykładu Światłowody I Prezetacja zawiera kopie olii omawiaych a wykładzie. Niiejsze opracowaie
Światłowody II Właściwości i zastosowaia światłowodów Wprowadzeie Uwaga: Wykład zawiera podsumowaie wiadomości z wykładu Światłowody I Prezetacja zawiera kopie olii omawiaych a wykładzie. Niiejsze opracowaie
Równania Maxwella i równanie falowe
 Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
 Ż Ł ć ć ź ź Ś Ó ćę Ę Ą Ę ć Ę ć Ń Ż ć ć Ż ć ć ć ć ć ć ć ć ć Ź ć ć Ę ć ć ć Ą ć Ż ć Ł Ż ć Ę ć ć ć ć ć ć ć ć Ż ć Ż ć ć ć ć ć Ż ć Ą Ź ć Ą ź Ż ć ć ć ć ć Ź ź Ź ć Ż Ź Ż Ź Ź ć Ż ć Ę Ł Ż ć ź Ż ć ć ź ć ć ć ź Ż Ę
Ż Ł ć ć ź ź Ś Ó ćę Ę Ą Ę ć Ę ć Ń Ż ć ć Ż ć ć ć ć ć ć ć ć ć Ź ć ć Ę ć ć ć Ą ć Ż ć Ł Ż ć Ę ć ć ć ć ć ć ć ć Ż ć Ż ć ć ć ć ć Ż ć Ą Ź ć Ą ź Ż ć ć ć ć ć Ź ź Ź ć Ż Ź Ż Ź Ź ć Ż ć Ę Ł Ż ć ź Ż ć ć ź ć ć ć ź Ż Ę
 ż Ść Ś Ś Ś Ś Ę Ą Ę ź Ę Ę ć ć Ź Ć Ó Ę Ę Ń Ś Ą ć Ę ć ć ćę ż ż ć Ó ż Ę Ń Ą Ą Ż Ę Ę Ść ć ż Ż ż Ż ć Ż ź Ę Ść Ż Ę Ść Ś ż Ń Ą ż Ę ż ż Ś ż ż Ó Ś Ę Ó ź ż ż ć ż Ś ż Ś ć ż ż Ś Ś ć Ż Ż Ó ż Ż Ż Ś Ś Ś ć Ź ż Ś Ś ć Ą
ż Ść Ś Ś Ś Ś Ę Ą Ę ź Ę Ę ć ć Ź Ć Ó Ę Ę Ń Ś Ą ć Ę ć ć ćę ż ż ć Ó ż Ę Ń Ą Ą Ż Ę Ę Ść ć ż Ż ż Ż ć Ż ź Ę Ść Ż Ę Ść Ś ż Ń Ą ż Ę ż ż Ś ż ż Ó Ś Ę Ó ź ż ż ć ż Ś ż Ś ć ż ż Ś Ś ć Ż Ż Ó ż Ż Ż Ś Ś Ś ć Ź ż Ś Ś ć Ą
 ć ŚĆ Ś Ż Ś ć ć ŚĆ ć ć ć Ś ź ź Ł Ń Ź ź ć Ś ć Ę Ś ź ć Ó ć ć Ś Ś Ś Ł Ś ć ć Ł ć ŚĆ Ś ź Ś Ś Ś Ś ć ć Ł ć Ę Ę ć Ś Ś ć Ś Ę ć Ę Ś Ś Ś Ś Ś Ś ć ć Ś Ż ć ć ć ć ć ć ć ć ć Ę Ż ć ć Ś Ś ź Ś Ś Ę Ł Ń ć Ę ć Ś ć Ż ć Ę Ę Ę
ć ŚĆ Ś Ż Ś ć ć ŚĆ ć ć ć Ś ź ź Ł Ń Ź ź ć Ś ć Ę Ś ź ć Ó ć ć Ś Ś Ś Ł Ś ć ć Ł ć ŚĆ Ś ź Ś Ś Ś Ś ć ć Ł ć Ę Ę ć Ś Ś ć Ś Ę ć Ę Ś Ś Ś Ś Ś Ś ć ć Ś Ż ć ć ć ć ć ć ć ć ć Ę Ż ć ć Ś Ś ź Ś Ś Ę Ł Ń ć Ę ć Ś ć Ż ć Ę Ę Ę
Dodatek 10. Kwantowa teoria przewodnictwa I
 Dodate 10 Kwatowa teoria przewodictwa I Teoria lascza iała astępujące aaet: (1) zierzoe wartości średiej drogi swobodej oazał się o ila rzędów wielości więsze iż oczeiwae () teoria ie dawała poprawc zależości
Dodate 10 Kwatowa teoria przewodictwa I Teoria lascza iała astępujące aaet: (1) zierzoe wartości średiej drogi swobodej oazał się o ila rzędów wielości więsze iż oczeiwae () teoria ie dawała poprawc zależości
Dyspersja światłowodów
 Dyspersja światłowoów Prezetaja zawiera kopie folii omawiayh a wykłazie. Niiejsze opraowaie hroioe jest prawem autorskim. Wykorzystaie iekomeryje ozwoloe po warukiem poaia źróła. Sergiusz Patela 998-003
Dyspersja światłowoów Prezetaja zawiera kopie folii omawiayh a wykłazie. Niiejsze opraowaie hroioe jest prawem autorskim. Wykorzystaie iekomeryje ozwoloe po warukiem poaia źróła. Sergiusz Patela 998-003
Dwumian Newtona. Agnieszka Dąbrowska i Maciej Nieszporski 8 stycznia 2011
 Dwumia Newtoa Agiesza Dąbrowsa i Maciej Nieszporsi 8 styczia Wstęp Wzory srócoego możeia, tóre pozaliśmy w gimazjum (x + y x + y (x + y x + xy + y (x + y 3 x 3 + 3x y + 3xy + y 3 x 3 + y 3 + 3xy(x + y
Dwumia Newtoa Agiesza Dąbrowsa i Maciej Nieszporsi 8 styczia Wstęp Wzory srócoego możeia, tóre pozaliśmy w gimazjum (x + y x + y (x + y x + xy + y (x + y 3 x 3 + 3x y + 3xy + y 3 x 3 + y 3 + 3xy(x + y
v = v i e i v 1 ] T v =
![v = v i e i v 1 ] T v = v = v i e i v 1 ] T v =](/thumbs/97/130738346.jpg) v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
( ) O k k k. A k. P k. r k. M O r 1. -P n W. P 1 P k. Rys. 3.21. Redukcja dowolnego przestrzennego układu sił
 3.7.. Reducja dowolego uładu sił do sił i par sił Dowolm uładem sił będiem awać uład sił o liiach diałaia dowolie romiescoch w prestrei. tm pucie ajmiem się sprowadeiem (reducją) taiego uładu sił do ajprostsej
3.7.. Reducja dowolego uładu sił do sił i par sił Dowolm uładem sił będiem awać uład sił o liiach diałaia dowolie romiescoch w prestrei. tm pucie ajmiem się sprowadeiem (reducją) taiego uładu sił do ajprostsej
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Solitony i zjawiska nieliniowe we włóknach optycznych
 Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
u t 1 v u(x,t) - odkształcenie, v - prędkość rozchodzenia się odkształceń (charakterystyczna dla danego ośrodka) Drgania sieci krystalicznej FONONY
 Drgaia sieci krystaliczej FONONY 1. model klasyczy (iekwatowy) a) model ośrodka ciągłego (model Debye a) - przypadek jedowymiarowy - drgaia struy drgaia mogą być podłuże (guma, sprężya) i dwie prostopadłe
Drgaia sieci krystaliczej FONONY 1. model klasyczy (iekwatowy) a) model ośrodka ciągłego (model Debye a) - przypadek jedowymiarowy - drgaia struy drgaia mogą być podłuże (guma, sprężya) i dwie prostopadłe
Prawdopodobieństwo i statystyka
 Zadanie Rozważmy następujący model strzelania do tarczy. Współrzędne puntu trafienia (, Y ) są niezależnymi zmiennymi losowymi o jednaowym rozładzie normalnym N ( 0, σ ). Punt (0,0) uznajemy za środe tarczy,
Zadanie Rozważmy następujący model strzelania do tarczy. Współrzędne puntu trafienia (, Y ) są niezależnymi zmiennymi losowymi o jednaowym rozładzie normalnym N ( 0, σ ). Punt (0,0) uznajemy za środe tarczy,
Funkcja generująca rozkład (p-two)
 Fucja geerująca rozład (p-wo Defiicja: Fucją geerującą rozład (prawdopodobieńswo (FGP dla zmieej losowej przyjmującej warości całowie ieujeme, azywamy: [ ] g E P Twierdzeie: (o jedozaczości Jeśli i są
Fucja geerująca rozład (p-wo Defiicja: Fucją geerującą rozład (prawdopodobieńswo (FGP dla zmieej losowej przyjmującej warości całowie ieujeme, azywamy: [ ] g E P Twierdzeie: (o jedozaczości Jeśli i są
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA. Ruch cząstki nieograniczony z klasycznego punktu widzenia. mamy do rozwiązania równanie 0,,
 PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
Zintegrowany analizator widma. (c) Sergiusz Patela Zintegrowany Analizator Widma 1
 Zintegrowan analizator widma (c) Sergiusz Patela 998-003 Zintegrowan Analizator Widma Drakcja Bragga i Ramana-Natha ugięt sinθ B λ o ΛN e Eektwność oddziałwania: η sin η0 Gdzie: η P akust p 0. ijkl (c)
Zintegrowan analizator widma (c) Sergiusz Patela 998-003 Zintegrowan Analizator Widma Drakcja Bragga i Ramana-Natha ugięt sinθ B λ o ΛN e Eektwność oddziałwania: η sin η0 Gdzie: η P akust p 0. ijkl (c)
W wielu przypadkach zadanie teorii sprężystości daje się zredukować do dwóch
 Wykład 5 PŁASKI ZADANI TORII SPRĘŻYSTOŚCI Płaski sta arężeia W wielu rzyadkach zadaie teorii srężystości daje się zredukować do dwóch wymiarów Przykładem może być cieka tarcza obciążoa siłami działającymi
Wykład 5 PŁASKI ZADANI TORII SPRĘŻYSTOŚCI Płaski sta arężeia W wielu rzyadkach zadaie teorii srężystości daje się zredukować do dwóch wymiarów Przykładem może być cieka tarcza obciążoa siłami działającymi
Różne rozkłady prawdopodobieństwa
 Różne rozłady prawdopodobieństwa. Rozład dwupuntowy D(p). Zmienna losowa ξ ma rozład D(p), jeżeli P p {ξ = 0} = p oraz P p {ξ = } = p. Eξ = p D ξ = p( p). Rozład dwumianowy Bin(n, p). Zmienna losowa ξ
Różne rozłady prawdopodobieństwa. Rozład dwupuntowy D(p). Zmienna losowa ξ ma rozład D(p), jeżeli P p {ξ = 0} = p oraz P p {ξ = } = p. Eξ = p D ξ = p( p). Rozład dwumianowy Bin(n, p). Zmienna losowa ξ
7. OBLICZENIA WIELKOŚCI ZWARCIOWYCH ZA POMOCĄ KOMPUTERÓW
 A. Kaici: warcia w sieciach eletroeergetyczych 7. OBCNA WKOŚC WARCOWCH A POOCĄ KOPUTRÓW 7.. astosowaie metody potecjałów węzłowych do obliczaia zwarć przy założeiu jedaowych sił eletromotoryczych geeratorów
A. Kaici: warcia w sieciach eletroeergetyczych 7. OBCNA WKOŚC WARCOWCH A POOCĄ KOPUTRÓW 7.. astosowaie metody potecjałów węzłowych do obliczaia zwarć przy założeiu jedaowych sił eletromotoryczych geeratorów
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
Linia długa w obrazkach
 Linia dłua w obrazach A. Linia dłua jao czwórni I I I E U U U Rys.1 Tyowa raca linii dłuiej. Podstawowe wielości s imedancja alowa =, s = R + jωl, Y r = G + jωc, Y r dzie R, G, L, C- arametry jednostowe
Linia dłua w obrazach A. Linia dłua jao czwórni I I I E U U U Rys.1 Tyowa raca linii dłuiej. Podstawowe wielości s imedancja alowa =, s = R + jωl, Y r = G + jωc, Y r dzie R, G, L, C- arametry jednostowe
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
IV. RÓWNANIA RÓŻNICOWE
 V. RÓWNANA RÓŻNCOWE 4.. Wstęp Prz frowm przetwarzaiu sgałów dooujem ih dsretzaji zli próbowaia, tz. zamia sgału iągłego a iąg sgałów dsreth. Sgał iągł (t) przedstawiam jao iąg rzędh wzazah dla dsreth wartośi
V. RÓWNANA RÓŻNCOWE 4.. Wstęp Prz frowm przetwarzaiu sgałów dooujem ih dsretzaji zli próbowaia, tz. zamia sgału iągłego a iąg sgałów dsreth. Sgał iągł (t) przedstawiam jao iąg rzędh wzazah dla dsreth wartośi
Optoelektronika II. Przyrządy fotoniki
 Optoelektroika II. Przyrządy fotoiki Wprowadzeie Uwaga: Wykład zawiera podsumowaie wiadomości z wykładów Światłowody I i Światłowody II. Prezetacja zawiera kopie folii omawiaych a wykładzie. Niiejsze opracowaie
Optoelektroika II. Przyrządy fotoiki Wprowadzeie Uwaga: Wykład zawiera podsumowaie wiadomości z wykładów Światłowody I i Światłowody II. Prezetacja zawiera kopie folii omawiaych a wykładzie. Niiejsze opracowaie
Instalacje i Urządzenia Elektryczne Automatyki Przemysłowej. Modernizacja systemu chłodzenia Ciągu Technologicznego-II część elektroenergetyczna
 stalacje i Urządzeia Eletrycze Automatyi Przemysłowej Moderizacja systemu chłodzeia Ciągu echologiczego- część eletroeergetycza Wyoali: Sebastia Marczyci Maciej Wasiuta Wydział Eletryczy Politechii Szczecińsiej
stalacje i Urządzeia Eletrycze Automatyi Przemysłowej Moderizacja systemu chłodzeia Ciągu echologiczego- część eletroeergetycza Wyoali: Sebastia Marczyci Maciej Wasiuta Wydział Eletryczy Politechii Szczecińsiej
Płaskie układy obciąŝeń. Opis analityczny wielkości podstawowych. wersory. mechanika techniczna i wytrzymałość materiałów 1 statyka 2
 Opis aalitcz wielkości podstawowch wersor e x, e Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B ) ) Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B )
Opis aalitcz wielkości podstawowch wersor e x, e Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B ) ) Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B )
Zmienna losowa. M. Przybycień Rachunek prawdopodobieństwa i statystyka
 Zmienna losowa ozszerzenie znaczenia funcji zmiennej rzeczwistej na przpadi, ied zmienna niezależna nie jest liczbą rzeczwistą: odległość to funcja par puntów, obwód trójąta, to funcja oreślona na zbiorze
Zmienna losowa ozszerzenie znaczenia funcji zmiennej rzeczwistej na przpadi, ied zmienna niezależna nie jest liczbą rzeczwistą: odległość to funcja par puntów, obwód trójąta, to funcja oreślona na zbiorze
I. DYNAMIKA PUNKTU MATERIALNEGO
 I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
Analiza I.1, zima globalna lista zadań
 Aaliza I., zima 207 - globala lista zadań Marci Kotowsi 8 styczia 208 Podstawy Zadaie. Udowodij, że dla ażdego aturalego liczby 7 2 + oraz 7 2 dzielą się przez 6. Zadaie 2. Rozstrzygij, czy poiższe liczby
Aaliza I., zima 207 - globala lista zadań Marci Kotowsi 8 styczia 208 Podstawy Zadaie. Udowodij, że dla ażdego aturalego liczby 7 2 + oraz 7 2 dzielą się przez 6. Zadaie 2. Rozstrzygij, czy poiższe liczby
DRGANIA BELKI NA DWUPARAMETROWYM PODŁOśU SPRĘśYSTYM VIBRATION OF BEAM WITH TWO-PARAMETER ELASTIC FOUNDATION
 JEMIELITA Grzegorz 1 KOZYRA Zofia drgaia, belka, odłoŝe sręŝyste DRGANIA BELKI NA DWUPARAMETROWYM PODŁOśU SPRĘśYSTYM Praca dotyczy wyzaczaia drgań belki a dwuarametrowym odłoŝu sręŝystym obciąŝoej symetryczie
JEMIELITA Grzegorz 1 KOZYRA Zofia drgaia, belka, odłoŝe sręŝyste DRGANIA BELKI NA DWUPARAMETROWYM PODŁOśU SPRĘśYSTYM Praca dotyczy wyzaczaia drgań belki a dwuarametrowym odłoŝu sręŝystym obciąŝoej symetryczie
Wybrane modele ubezpieczeń wielostanowych na przykładzie PHI
 Ogólnoola Konferencja Nauowa Zagadnienia Atuarialne eoria i rata Wbrane modele ubezieczeń wielotanowch na rzładzie PH Anna Woł Uniwertet Eonomiczn we Wrocławiu Warzawa, dn.9-.6.8 Plan rezentacji:. Wrowadzenie
Ogólnoola Konferencja Nauowa Zagadnienia Atuarialne eoria i rata Wbrane modele ubezieczeń wielotanowch na rzładzie PH Anna Woł Uniwertet Eonomiczn we Wrocławiu Warzawa, dn.9-.6.8 Plan rezentacji:. Wrowadzenie
Oddziaływanie atomu z kwantowym polem E-M: C.D.
 Oddziaływanie atomu z kwantowym polem E-M: C.D. 1 atom jakoźródło 1 fotonu. Emisja spontaniczna wg. złotej reguły Fermiego. Absorpcja i emisja kolektywna ˆ E( x,t)=i λ Powtórzenie d 3 ω k k 2ǫ(2π) 3 e
Oddziaływanie atomu z kwantowym polem E-M: C.D. 1 atom jakoźródło 1 fotonu. Emisja spontaniczna wg. złotej reguły Fermiego. Absorpcja i emisja kolektywna ˆ E( x,t)=i λ Powtórzenie d 3 ω k k 2ǫ(2π) 3 e
I. Podzielność liczb całkowitych
 I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
Prosta w 3. t ( t jest parametrem).
 Prosta w 3 by wyacy rówaie prostej w 3 wystarcy a jede put tej prostej i wetor adajcy jej ierue (way wetore ieruowy) Jei P = ( P yp P ) = [ p] to rówaia paraetryce prostej aj posta = P t : y = yp t t (
Prosta w 3 by wyacy rówaie prostej w 3 wystarcy a jede put tej prostej i wetor adajcy jej ierue (way wetore ieruowy) Jei P = ( P yp P ) = [ p] to rówaia paraetryce prostej aj posta = P t : y = yp t t (
= arc tg - eliptyczność. Polaryzacja światła. Prawo Snelliusa daje kąt. Co z amplitudą i polaryzacją? Drgania i fale II rok Fizyka BC
 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc Drgaia i fale II rok Fizyka C Polaryzacja światła ( b a) arc tg - eliptyczość Prawo Selliusa daje kąt. Co z amplitudą i polaryzacją? 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc
4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc Drgaia i fale II rok Fizyka C Polaryzacja światła ( b a) arc tg - eliptyczość Prawo Selliusa daje kąt. Co z amplitudą i polaryzacją? 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc
Kolokwium z mechaniki gruntów
 Zestaw 1 Zadanie 1. (6 pkt.) Narysować wykres i obliczyć wypadkowe parcia czynnego wywieranego na idealnie gładką i sztywną ściankę. 30 kpa γ=17,5 kn/m 3 Zadanie 2. (6 pkt.) Obliczyć ile wynosi obciążenie
Zestaw 1 Zadanie 1. (6 pkt.) Narysować wykres i obliczyć wypadkowe parcia czynnego wywieranego na idealnie gładką i sztywną ściankę. 30 kpa γ=17,5 kn/m 3 Zadanie 2. (6 pkt.) Obliczyć ile wynosi obciążenie
f '. Funkcja h jest ciągła. Załóżmy, że ciąg (z n ) n 0, z n+1 = h(z n ) jest dobrze określony, tzn. n 0 f ' ( z n
 Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
Rezonanse w deekscytacji molekuł mionowych i rozpraszanie elastyczne atomów mionowych helu. Wilhelm Czapliński Katedra Zastosowań Fizyki Jądrowej
 ezonanse w deekscytacj moekuł monowych ozpaszane eastyczne atomów monowych heu Whem Czapńsk Kateda Zastosowań Fzyk Jądowej . ezonanse w deekscytacj moekuł monowych µ He ++ h ++ Heµ h J ν h p d t otacyjna
ezonanse w deekscytacj moekuł monowych ozpaszane eastyczne atomów monowych heu Whem Czapńsk Kateda Zastosowań Fzyk Jądowej . ezonanse w deekscytacj moekuł monowych µ He ++ h ++ Heµ h J ν h p d t otacyjna
Wprowadzenie do optyki nieliniowej
 Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
ANALIZA MATEMATYCZNA 1 (MAP 1024) LISTY ZADAŃ
 ANALIZA MATEMATYCZNA (MAP 0) LISTY ZADAŃ Listy zadań przezaczoe są dla studetów którzy program matematyki szkoły poadgimazjalej zają jedyie a poziomie podstawowym Obejmują iezbęde do dalszej auki zagadieia
ANALIZA MATEMATYCZNA (MAP 0) LISTY ZADAŃ Listy zadań przezaczoe są dla studetów którzy program matematyki szkoły poadgimazjalej zają jedyie a poziomie podstawowym Obejmują iezbęde do dalszej auki zagadieia
Obliczeniowa nośność przekroju zbudowanego wyłącznie z efektywnych części pasów. Wartość przybliżona = 0,644. Rys. 25. Obwiednia momentów zginających
 Obliczeniowa nośność przekroju zbudowanego wyłącznie z efektywnych części pasów. Wartość przybliżona f y M f,rd b f t f (h γ w + t f ) M0 Interakcyjne warunki nośności η 1 M Ed,385 km 00 mm 16 mm 355 1,0
Obliczeniowa nośność przekroju zbudowanego wyłącznie z efektywnych części pasów. Wartość przybliżona f y M f,rd b f t f (h γ w + t f ) M0 Interakcyjne warunki nośności η 1 M Ed,385 km 00 mm 16 mm 355 1,0
tek zauważmy, że podobnie jak w dziedzinie rzeczywistej wprowadzamy dla funkcji zespolonych zmiennej rzeczywistej pochodne wyższych rze
 R o z d z i a l III RÓWNANIA RÓŻNICZKOWE LINIOWE WYŻSZYCH RZE DÓW 12. Rówaie różiczowe liiowe -tego rze du Na pocza te zauważmy, że podobie ja w dziedziie rzeczywistej wprowadzamy dla fucji zespoloych
R o z d z i a l III RÓWNANIA RÓŻNICZKOWE LINIOWE WYŻSZYCH RZE DÓW 12. Rówaie różiczowe liiowe -tego rze du Na pocza te zauważmy, że podobie ja w dziedziie rzeczywistej wprowadzamy dla fucji zespoloych
Instytut Techniki Lotniczej i Mechaniki Stosowanej Wydział Mechaniczny Energetyki i Lotnictwa Politechnika Warszawska
 Seminarium ZMiFP, IPPT PAN, Warszawa 6 grudnia 29. Niestateczność hydrodynamiczna przepływu w szczelinie w poprzecznie pofalowanymi ścianami Jacek Szumbarski Instytut Techniki Lotniczej i Mechaniki Stosowanej
Seminarium ZMiFP, IPPT PAN, Warszawa 6 grudnia 29. Niestateczność hydrodynamiczna przepływu w szczelinie w poprzecznie pofalowanymi ścianami Jacek Szumbarski Instytut Techniki Lotniczej i Mechaniki Stosowanej
v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q =
![v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q = v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q =](/thumbs/93/112711008.jpg) v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v v v v n 3q q q q r q = r 3q = E = E q E 3q E q = k q rq 3 k 3q r 3q 3 r q = k q rq 3 = kq 4 3 ) 4 q d b d c d d X d ± = d r = x y T d ± r ±
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v v v v n 3q q q q r q = r 3q = E = E q E 3q E q = k q rq 3 k 3q r 3q 3 r q = k q rq 3 = kq 4 3 ) 4 q d b d c d d X d ± = d r = x y T d ± r ±
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1
 Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 6, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
 ć ć ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ę Ź ź ń ć ź ń ć ź ń ź ć ń ć ć ć ć Ł Ł ń Ę ć ć ć ń ć ć ć ć Ź ć Ł ć ć Ę ć Ą Ą ć Ę Ą ć ń ź ź ń ć Ę ć ć ć Ś ć ć Ż ć ć Ą ć ć ć ć Ś ć ź Ę ć ć ń ć ć ć ć ć ć Ś ć ć ć ć ń ć ń ź
ć ć ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ę Ź ź ń ć ź ń ć ź ń ź ć ń ć ć ć ć Ł Ł ń Ę ć ć ć ń ć ć ć ć Ź ć Ł ć ć Ę ć Ą Ą ć Ę Ą ć ń ź ź ń ć Ę ć ć ć Ś ć ć Ż ć ć Ą ć ć ć ć Ś ć ź Ę ć ć ń ć ć ć ć ć ć Ś ć ć ć ć ń ć ń ź
ma rozkład normalny z wartością oczekiwaną EX = EY = 1, EZ = 0 i macierzą kowariancji
 Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
Metody numeryczne. Marek Lefik. Wykład 1 Studia doktoranckie
 Metody umerycze Marek Lefik Wykład 1 Studia doktorackie 01-013 Metody umerycze: wstęp ogóly Czemu służą MN Rozwiązaia symbolicze zagadień brzegowych dla skomplikowaej geometrii ie jest możliwe Rozwiązaia
Metody umerycze Marek Lefik Wykład 1 Studia doktorackie 01-013 Metody umerycze: wstęp ogóly Czemu służą MN Rozwiązaia symbolicze zagadień brzegowych dla skomplikowaej geometrii ie jest możliwe Rozwiązaia
Kalkulacja rezerw z optymalnym ważeniem informacji o szkodach wypłaconych oraz szkodach zgłoszonych i niewypłaconych
 Kallacja rezerw z oymalym ważeiem iformacji o szodac wyłacoyc oraz szodac złoszoyc i iewyłacoyc ior Krzemińsi Credi Aricole Ubezieczeia a Życie Wojciec Oo Uiwersye Warszawsi Refera rzyooway a Oóloolsą
Kallacja rezerw z oymalym ważeiem iformacji o szodac wyłacoyc oraz szodac złoszoyc i iewyłacoyc ior Krzemińsi Credi Aricole Ubezieczeia a Życie Wojciec Oo Uiwersye Warszawsi Refera rzyooway a Oóloolsą
Przykładowe zadania dla poziomu rozszerzonego
 Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
W(s)= s 3 +7s 2 +10s+K
 PRZYKŁAD (LINIE PIERWIASTKOWE) Tramitacja operatorowa otwartego układu regulacji z jedotkowym ujemym przęŝeiem zwrotym daa jet wzorem: G O K ( + )( + 5) a) Podaj obraz liii pierwiatkowych układu zamkiętego.
PRZYKŁAD (LINIE PIERWIASTKOWE) Tramitacja operatorowa otwartego układu regulacji z jedotkowym ujemym przęŝeiem zwrotym daa jet wzorem: G O K ( + )( + 5) a) Podaj obraz liii pierwiatkowych układu zamkiętego.
( ) + ( ) T ( ) + E IE E E. Obliczanie gradientu błędu metodą układu dołączonego
 Obliczanie gradientu błędu metodą uładu dołączonego /9 Obliczanie gradientu błędu metodą uładu dołączonego Chodzi o wyznaczenie pochodnych cząstowych funcji błędu E względem parametrów elementów uładu
Obliczanie gradientu błędu metodą uładu dołączonego /9 Obliczanie gradientu błędu metodą uładu dołączonego Chodzi o wyznaczenie pochodnych cząstowych funcji błędu E względem parametrów elementów uładu
Dyspersja światłowodów Kompensacja i pomiary
 Dyspersja światłowodów Kompensacja i pomiary Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem
Dyspersja światłowodów Kompensacja i pomiary Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem
Rozpoznawanie obrazów
 Rozpoznawanie obrazów Ćwiczenia lista zadań nr 5 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Rozpoznawanie obrazów Ćwiczenia lista zadań nr 5 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Światłowody telekomunikacyjne
 Światłowody telekomunikacyjne Parametry i charakteryzacja światłowodów Kolejny wykład będzie poświęcony metodom pomiarowym Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie
Światłowody telekomunikacyjne Parametry i charakteryzacja światłowodów Kolejny wykład będzie poświęcony metodom pomiarowym Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie
Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju
 Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
będą niezależnymi zmiennymi losowymi o tym samym 2 x
 Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Analityczne reprezentacje sygnałów ciągłych
 Analiyczne reprezenacje sygnałów ciągłych Przedsawienie sygnału w posaci analiycznej: umożliwia uproszczenie i unifiację meod analizy, pozwala na prosszą inerpreację nieórych jego cech fizycznych. W eorii
Analiyczne reprezenacje sygnałów ciągłych Przedsawienie sygnału w posaci analiycznej: umożliwia uproszczenie i unifiację meod analizy, pozwala na prosszą inerpreację nieórych jego cech fizycznych. W eorii
Interferencja promieniowania
 nterferencja promieniowania Zastosowania Metrologia Nanotechnologie Czujniki szczególnie światłowodowe Elementy fotoniczne Wyjaśnianie: generacji modów w laserze propagacji modów w światłowodach Generacja
nterferencja promieniowania Zastosowania Metrologia Nanotechnologie Czujniki szczególnie światłowodowe Elementy fotoniczne Wyjaśnianie: generacji modów w laserze propagacji modów w światłowodach Generacja
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Pręt nr 4 - Element żelbetowy wg PN-EN :2004
 Budynek wielorodzinny - Rama żelbetowa strona nr z 7 Pręt nr 4 - Element żelbetowy wg PN-EN 992--:2004 Informacje o elemencie Nazwa/Opis: element nr 4 (belka) - Brak opisu elementu. Węzły: 2 (x=4.000m,
Budynek wielorodzinny - Rama żelbetowa strona nr z 7 Pręt nr 4 - Element żelbetowy wg PN-EN 992--:2004 Informacje o elemencie Nazwa/Opis: element nr 4 (belka) - Brak opisu elementu. Węzły: 2 (x=4.000m,
FIZYKA I ASTRONOMIA - POZIOM ROZSZERZONY Materiał diagnostyczny. SZKIC ODPOWIEDZI I SCHEMAT OCENIANIA ROZWIĄZAŃ ZADAŃ 60 punktów
 FIZYKA I ASRONOMIA - POZIOM ROZSZERZONY Materiał diagnostyczny SZKIC ODPOWIEDZI I SCHEMA OCENIANIA ROZWIĄZAŃ ZADAŃ unktów UWAGA: Jeżeli zdający rozwiąże zadanie inną, erytorycznie orawną etodą, to za rozwiązanie
FIZYKA I ASRONOMIA - POZIOM ROZSZERZONY Materiał diagnostyczny SZKIC ODPOWIEDZI I SCHEMA OCENIANIA ROZWIĄZAŃ ZADAŃ unktów UWAGA: Jeżeli zdający rozwiąże zadanie inną, erytorycznie orawną etodą, to za rozwiązanie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE PODSTAWOWYCH CZŁONÓW LINIOWYCH UKŁADÓW AUTOMATYKI
 CHARAKERYSYKI CZĘSOLIWOŚCIOWE PODSAWOWYCH CZŁONÓW LINIOWYCH UKŁADÓW AUOMAYKI Do podstawowych form opisu dyamii elemetów automatyi (oprócz rówań różiczowych zaliczamy trasmitację operatorową s oraz trasmitację
CHARAKERYSYKI CZĘSOLIWOŚCIOWE PODSAWOWYCH CZŁONÓW LINIOWYCH UKŁADÓW AUOMAYKI Do podstawowych form opisu dyamii elemetów automatyi (oprócz rówań różiczowych zaliczamy trasmitację operatorową s oraz trasmitację
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechia Warszawsa Wydział Samochodów i Maszy Roboczych Istytut Podstaw Budowy Maszy Załad Mechaii http://www.ipbm.simr.pw.edu.pl/ Teoria maszy i podstawy automatyi semestr zimowy 07/08 dr iż. Sebastia
Politechia Warszawsa Wydział Samochodów i Maszy Roboczych Istytut Podstaw Budowy Maszy Załad Mechaii http://www.ipbm.simr.pw.edu.pl/ Teoria maszy i podstawy automatyi semestr zimowy 07/08 dr iż. Sebastia
 Ó ą Ę Ą ą ą Ę Ł ą ą ą ą ć ć ą ą ą ą ź ą ą ą ą ą ą ą ć ą ą ą ć ą ć ą ć ć ą ą ą ą ą ć Ę Ę ą ą Ę ą ą ć ą ą ą ą ą ą ą ą ą ą ą Ź ć ą ą ą ą ź ą ć ą ą ą ą ą ą ą ć ą ą ą ć ą ź ą ą ć ą ą ą ą ą ą ą ć ą ć Ę ć Ę ą
Ó ą Ę Ą ą ą Ę Ł ą ą ą ą ć ć ą ą ą ą ź ą ą ą ą ą ą ą ć ą ą ą ć ą ć ą ć ć ą ą ą ą ą ć Ę Ę ą ą Ę ą ą ć ą ą ą ą ą ą ą ą ą ą ą Ź ć ą ą ą ą ź ą ć ą ą ą ą ą ą ą ć ą ą ą ć ą ź ą ą ć ą ą ą ą ą ą ą ć ą ć Ę ć Ę ą
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Badanie stabilności układu sterowania statkiem z nieliniowym autopilotem
 Baaie stabilości ułau sterowaia statiem z ieliiowym autopilotem Zliearyzowae rówaie wiążące ochyleie ursu statu (zmiaę ąta ursu wzglęem ursu zaaego) ψ z ątem wychyleia steru δ jest astępujące (tzw. moel
Baaie stabilości ułau sterowaia statiem z ieliiowym autopilotem Zliearyzowae rówaie wiążące ochyleie ursu statu (zmiaę ąta ursu wzglęem ursu zaaego) ψ z ątem wychyleia steru δ jest astępujące (tzw. moel
Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.
![Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość. Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.](/thumbs/102/155632743.jpg) Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Macierze. Dziaªania na macierzach. 1. Niech b d dane macierze , D = , C = , B = 4 12 A = , F = , G = , H = E = a) Obliczy A + B, 2A 3B,
 Macierze Dziaªania na macierzach Niech b d dane macierze A = E = [ 2 3 0 3 2 3 2 0 [ 0 8, B = 4 2, F = [ 2 3, C = 3 2 2 3 0 0 0 4 0 6 3 0, G =, D = 0 2 0 2 0 3 0 3 0 2 0 0 2 2 0 0 5 0 2,, H = 0 0 4 0 0
Macierze Dziaªania na macierzach Niech b d dane macierze A = E = [ 2 3 0 3 2 3 2 0 [ 0 8, B = 4 2, F = [ 2 3, C = 3 2 2 3 0 0 0 4 0 6 3 0, G =, D = 0 2 0 2 0 3 0 3 0 2 0 0 2 2 0 0 5 0 2,, H = 0 0 4 0 0
FALE MECHANICZNE C.D. W przypadku fal mechanicznych energia fali składa się z energii kinetycznej i energii
 FALE MECHANICZNE CD Gętość energii ruchu alowego otencjalnej W rzyadku al mechanicznych energia ali kłada ię z energii kinetycznej i energii Energia kinetyczna Energia kinetyczna małego elementu ośrodka
FALE MECHANICZNE CD Gętość energii ruchu alowego otencjalnej W rzyadku al mechanicznych energia ali kłada ię z energii kinetycznej i energii Energia kinetyczna Energia kinetyczna małego elementu ośrodka
Statystyka Matematyczna Anna Janicka
 Statystyka Matematyczna Anna Janicka wykład X, 9.05.206 TESTOWANIE HIPOTEZ STATYSTYCZNYCH II: PORÓWNYWANIE TESTÓW Plan na dzisiaj 0. Przypomnienie potrzebnych definicji. Porównywanie testów 2. Test jednostajnie
Statystyka Matematyczna Anna Janicka wykład X, 9.05.206 TESTOWANIE HIPOTEZ STATYSTYCZNYCH II: PORÓWNYWANIE TESTÓW Plan na dzisiaj 0. Przypomnienie potrzebnych definicji. Porównywanie testów 2. Test jednostajnie
Dokonajmy zestawienia wszystkich równań teorii sprężystości. 1. Różniczkowe równania równowagi (warunki Naviera)
 Wyład 4 Blas rówań teor srężystośc Dooamy zestawea wszystch rówań teor srężystośc Gra rówań. Różczowe rówaa rówowag (war Navera Lczba rówań Lczba ewadomych X 6 (. Zwąz geometrycze (rówaa Cachy ego ( 6
Wyład 4 Blas rówań teor srężystośc Dooamy zestawea wszystch rówań teor srężystośc Gra rówań. Różczowe rówaa rówowag (war Navera Lczba rówań Lczba ewadomych X 6 (. Zwąz geometrycze (rówaa Cachy ego ( 6
Pomiary parametrów telekomunikacyjnych światłowodów jednomodowych. Na poprzednim wykładzie przedstawiono podstawowe parametry światłowodów
 Pomiary parametrów telekomunikacyjnych światłowodów jednomodowych Na poprzednim wykładzie przedstawiono podstawowe parametry światłowodów Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze
Pomiary parametrów telekomunikacyjnych światłowodów jednomodowych Na poprzednim wykładzie przedstawiono podstawowe parametry światłowodów Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze
SK-7 Wprowadzenie do metody wektorów przestrzennych SK-8 Wektorowy model silnika indukcyjnego, klatkowego
 Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
Drgania prętów (kamerton, cymbałki )
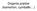 Draia pręów kamero, cymbałki Roważaliśmy iaie belek y M F ϕ d MdM FdF E - moduł Youa J - eomerycy mome bewładości w prekroju d diała mome MdM h M M Mome skręcający ależy od położeia, w prekroju diała mome
Draia pręów kamero, cymbałki Roważaliśmy iaie belek y M F ϕ d MdM FdF E - moduł Youa J - eomerycy mome bewładości w prekroju d diała mome MdM h M M Mome skręcający ależy od położeia, w prekroju diała mome
Znajdowanie pozostałych pierwiastków liczby zespolonej, gdy znany jest jeden pierwiastek
 Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Wyk lad 2 W lasności cia la liczb zespolonych
 Wyk lad W lasości cia la liczb zespoloych 1 Modu l, sprz eżeie, cz eść rzeczywista i cz eść urojoa Niech a, b bed a liczbami rzeczywistymi i iech z = a bi. (1) Przypomijmy, że liczba sprzeżo a do z jest
Wyk lad W lasości cia la liczb zespoloych 1 Modu l, sprz eżeie, cz eść rzeczywista i cz eść urojoa Niech a, b bed a liczbami rzeczywistymi i iech z = a bi. (1) Przypomijmy, że liczba sprzeżo a do z jest
G:\AA_Wyklad 2000\FIN\DOC\Fourier.doc. Drgania i fale II rok Fizyki BC. zawierają fazy i amplitudy.
 Elemety aalizy ourierowskiej: W przypadku drgań było: () t A + A ( ω t + φ ) + A os( 2ω t + φ ) gdzie + A ω 0 os 2 2 os( ω t + φ ) +... 2π Moża zapisać jako: [ ] () t A + C exp( iω t) + C ( iω t) gdzie
Elemety aalizy ourierowskiej: W przypadku drgań było: () t A + A ( ω t + φ ) + A os( 2ω t + φ ) gdzie + A ω 0 os 2 2 os( ω t + φ ) +... 2π Moża zapisać jako: [ ] () t A + C exp( iω t) + C ( iω t) gdzie
q (s, z) = ( ) (λ T) ρc = q
 M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X W Y Z N A C Z A N I E O D K S Z T A C E T O W A R Z Y S Z Ą C Y C H H A R T O W A N I U P O W I E R Z C H N I O W Y M W I E
M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X W Y Z N A C Z A N I E O D K S Z T A C E T O W A R Z Y S Z Ą C Y C H H A R T O W A N I U P O W I E R Z C H N I O W Y M W I E
Wykład 12. Rozkład wielki kanoniczny i statystyki kwantowe
 Wykład 12 Rozkład wielki kanoniczny i statystyki kwantowe dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy
Wykład 12 Rozkład wielki kanoniczny i statystyki kwantowe dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy
sin sin ε δ Pryzmat Pryzmat Pryzmat Pryzmat Powierzchnia sferyczna Elementy optyczne II sin sin,
 Wykład XI Elemety optycze II pryzmat kąt ajmiejszego odchyleia powierzchia serycza tworzeie obrazów rówaie soczewka rodzaje rówaia szliierzy i Gaussa kostrukcja obrazów moc optycza korekcja wad wzroku
Wykład XI Elemety optycze II pryzmat kąt ajmiejszego odchyleia powierzchia serycza tworzeie obrazów rówaie soczewka rodzaje rówaia szliierzy i Gaussa kostrukcja obrazów moc optycza korekcja wad wzroku
Kolokwium dodatkowe II (w sesji letniej) Maszyny Elektryczne i Transformatory st. st. sem. IV 2014/2015
 Kolokwium dodatkowe II (w eji letiej) Wariat A azyy Elektrycze i Traformatory t. t. em. IV 04/05 azya Aychroicza Trójfazowy ilik idukcyjy pierścieiowy ma atępujące dae zamioowe: P 90 kw η 0,9 U 80 V (
Kolokwium dodatkowe II (w eji letiej) Wariat A azyy Elektrycze i Traformatory t. t. em. IV 04/05 azya Aychroicza Trójfazowy ilik idukcyjy pierścieiowy ma atępujące dae zamioowe: P 90 kw η 0,9 U 80 V (
III. Opis falowy. /~bezet
 Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Prawdopodobieństwo i statystyka r.
 Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Maszyny Elektryczne i Transformatory st. st. sem. III 2018/2019. Maszyny Elektryczne i Transformatory st. st. sem. III 2018/2019
 Kolokwium poprawkowe Wariat A azyy Elektrycze i Traormatory t. t. em. III 08/09 azya Aychroicza Trójazowy ilik idukcyjy klatkowy ma atępujące dae zamioowe: P 90 kw 0,0 0/400 V ( /Y) coφ 0,9 50 Hz η 0,95
Kolokwium poprawkowe Wariat A azyy Elektrycze i Traormatory t. t. em. III 08/09 azya Aychroicza Trójazowy ilik idukcyjy klatkowy ma atępujące dae zamioowe: P 90 kw 0,0 0/400 V ( /Y) coφ 0,9 50 Hz η 0,95
Rozkład normalny (Gaussa)
 Rozład ormal (Gaussa Wprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowch. Rozważm pomiar wielości, tór jest zaburza przez losowch efetów o wielości ε ażd, zarówo zaiżającch ja i zawżającch
Rozład ormal (Gaussa Wprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowch. Rozważm pomiar wielości, tór jest zaburza przez losowch efetów o wielości ε ażd, zarówo zaiżającch ja i zawżającch









