1. Podstawy matematyczne programowania grafiki 3D
|
|
|
- Martyna Klimek
- 7 lat temu
- Przeglądów:
Transkrypt
1 Podstaw programowania gier 3D Podstaw atematki. Podstaw matematcne programowania grafiki 3D Analię agadnień dotcącch grafiki komputerowej acniem od elementów matematki niebędnch do roumienia omawianch tematów. To matematka daje podstaw do opisu trójwmiarowego świata gier, obiektów wstępującch w tworonch światach ora relacje w nich achodące. W grafice komputerowej użwa się wielu mechanimów matematcnch ponanch w skole średniej a także na wkładach algebr. Omówim astosowanie w grafice macier, wektorów, kwaternionów, jak roumieć układ współrędnch, jak posługiwać się układami współrędnch do identfikowania obiektów w świecie, ora relacji międ nimi. Ze wględu na skomplikowanie omawianch agadnień, niektóre temat omówim pobieżnie, scegółowe wjaśnienie danego agadnienia umieściliśm pr konkretnm astosowaniu.. Wektor (Vectors W grafice trójwmiarowej wektor posiadają wiele astosowań: od predstawiania kierunków po repreentacje punktów w prestreni. Wektor, jakich będiem użwać, składają się trech składowch: [ X Y Z ] się wektorami cterema składowmi [ X Y Z W ]. ożna też spotkać. Ponieważ do operacji w układie współrędnch (prestreni trójwmiarowej wstarcą nam tr składowe, dlatego W będie się równać. ożna w tm momencie adać ptanie, dlacego W ogóle ostało wspomniane o wektorach trójwmiarowch a wektorach cterowmiarowch. Jest to pewna niekonsekwencja towarsąca grafice od dłużsego casu. Tak jak wspominaliśm, wstarcą tlko tr komponent do więksości operacji, dopiero umiejscowienie wektora w tw. układie jednorodnm wmaga użcia współrędnej W. Użcie atem trójwmiarowch wektorów albo cterowmiarowch jest poostawione programiście. prjmiem, że nase wektor są trójwmiarowe, mając w pamięci, że mogą się stać cterowmiarowe pre dodanie składowej W. Łukas igas,
2 Podstaw programowania gier 3D Podstaw atematki Oto lista operacji na wektorach, które będą nam potrebne: - Dodawanie wektorów (Vector Addition. Prkładow kod najduje się na listingu. CVector operator+ ( CVector& v, CVector& u return CVector( v.m_fx + u.m_fx, v.m_fy + u.m_fy, v.m_fz + u.m_fz ; Listing CVector::operator+, Źródło własne - Odejmowanie wektorów (Vector Subtraction. Prkładow kod najduje się na listingu 2. CVector operator- (CVector& v, CVector& u return CVector( v.m_fx-u.m_fx, v.m_fy-u.m_fy, v.m_fz-u.m_fz ; Listing 2 CVector::operator-, Źródło własne - Ilocn wektorow (Cross product. Prkładow kod najduje się na listingu 3. CVector veccross(cvector &v, CVector &u CVector vectmp; vectmp.m_fx v.m_fy*u.m_fz - v.m_fz*u.m_fy; vectmp.m_fy v.m_fz*u.m_fx - v.m_fx*u.m_fz; vectmp.m_fz v.m_fx*u.m_fy - v.m_fy*u.m_fx; return vectmp; Listing 3 veccross, Źródło własne - Ilocn skalarn (Dot product. Prkładow kod najduje się na listingu 4. float vecdot(cvector &v, CVector &u return (v.m_fx*u.m_fx + v.m_fy*u.m_fy + v.m_fz*u.m_fz; Listing 4 vecdot, Źródło własne Łukas igas, 2
3 Podstaw programowania gier 3D Podstaw atematki - Interpolacja liniowa (Linear Interpolation, LERP. Prkładow kod najduje się na listingu 5. CVector veclerp(cvector &v, CVector &u, float ft CVector vectmp; float ftemp.f - ft; vectmp.m_fx ftemp*v.m_fx + ft*u.m_fx; vectmp.m_fy ftemp*v.m_fy + ft*u.m_fy; vectmp.m_fz ftemp*v.m_fz + ft*u.m_fz; return vectmp; Listing 5 veclerp, Źródło własne - Oblicanie długości wektora (Vector Length. Prkładow kod najduje się na listingu 6. float CVector::Length( return( (floatsqrtf(m_fx*m_fx + m_fy*m_fy + m_fz*m_fz ; Listing 6 CVector::Length, Źródło własne - Normaliacja wektora (Vector Normaliation. Prkładow kod najduje się na listingu 7. void CVector::Normalie( float flen Length(; if ( flen.f return; flen.f / flen; m_fx * flen; m_fy * flen; m_fz * flen; Listing 7 CVector::Normalie, Źródło własne Istotną kwestią jest apiswanie wektorów. Na wielu wkładach matematcnch wektor jest pionow i umiescan a macierą w operacji mnożenia macier pre wektor. W bibliotece D3D wektor jest leżąc poiom. Co a tm idie, kolejność prekstałceń się mienia. nożm wektor pre macier. Łukas igas, 3
4 Podstaw programowania gier 3D Podstaw atematki.2 aciere (atri/atrices W grafice komputerowej użwa się rożnch rodajów macier. Najbardiej popularne są maciere o wmiarach 44. Dlatego ajmiem się właśnie macierami 44, aciere dają nam bardo wgodn w użciu sstem do apiswania prekstałceń. Definicja - translacja. Weźm punkt [ X Y Z ] współrędnch. Chcąc presunąć punkt P o wektor T[ X Y Z ] P leżąc w pocątku układu apisujem tę operacje następująco (prjmując, że P, P, P to wektor P, a T, T, T to wektor T: T T T Ta samą operacje można apisać pr pomoc macier. Zatem wkonajm operacje: T T T P P ( ( ( 3 ( ( 22 + ( 32 ( ( 23 + ( 33 w ( ( 24 + ( Łukas igas, 4
5 Podstaw programowania gier 3D Podstaw atematki Jak widać, potrebna tutaj jest współrędna W. Ponieważ W i najcęściej będie będne atem możem je opuścić. ( + ( ( 3 ( ( 22 ( 32 ( ( 23 ( Zatem:,,,,,,,, , nastę pnie: 4 T, 42 T, T Stąd: + T + + Ostatecnie dosliśm do apisu wjściowego. Prkładow kod implementując m acier presunięcia najduje się na listingu 8. T T void Catri::Setove(float, float, float LoadIdentit(; matri[3][]; matri[3][]; matri[3][2]; Listing 8 Catri::Setove, Źródło własne Prkładowe astosowanie może bć następujące: Definicja T T T [ ] [ ] 2 - skalowanie. Weźm seścian położon w pocątku układu współrędnch, o długości krawędi równej 2. Tera mniejsam seścian o połowę, tak ab długość krawędi bła. Zatem, jeżeli mam wartości skalowania apisane w Łukas igas, 5
6 Podstaw programowania gier 3D Podstaw atematki wektore S ( gdie.5 (prjmując że aktualnie prekstałcan punkt ma współrędne P, P, P a wartości skalowania to S, S, S, to: S S S A tera to samo apisujem macierą: S S S Zatem: P P Następnie oblicając: ( + + ( 2 + ( 3 ( ( 22 + ( 32 ( ( 23 + ( Podstawiając wartości macier dostajem: S + S + S + cli apis, od którego acęliśm. Łukas igas, 6
7 Podstaw programowania gier 3D Podstaw atematki Prkład: [ ] [ ] S S S Prkładowa implementacja skalowania najduje się na listingu 9. void Catri::SetScale(float,float,float LoadIdentit(; matri[][]; matri[][]; matri[2][2]; Listing 9 Catri::SetScale, Źródło własne Definicja 3 - obrot. Ponieważ obrot nie są tak łatwe do wobrażenia, jak presuwanie c skalowanie, atem wor podane będiem musieli na raie prjąć jako pewniki. Każd nich ostanie w rodiale poświęconm importowaniu geometrii/animacji scegółowo omówion. Definicja 4 - obrót wględem osi X. Oto wór obracając punkt o adan kąt jako parametr: θ cosθ sin + θ sin θ cos A oto macier repreentująca prekstałcenie obrotu wględem osi X: cos sin sin cos θ θ θ θ Prkład: [ ] [ ] cos sin sin cos θ θ θ θ Łukas igas, 7
8 Podstaw programowania gier 3D Podstaw atematki Dowód, że pierws apis jest taki sam jak apis P P, gdie P to punkt prekstałcan P, P, P, będie analogicne do dwóch poprednich cęści poświęconch presunięciu i skalowaniu. Prkładow kod implementując obrót wględem osi X najduje się na listingu. void Catri::SetRotateX(float rad float cosa(floatcos(rad; float sina(floatsin(rad; LoadIdentit(; matri[][]cosa; matri[2][2]cosa; matri[][2]sina; matri[2][]-sina; Listing Catri::SetRotateX, Źródło własne jako parametr: Definicja 5 - obrót wględem osi Y. Oto wór obracając punkt o adan kąt cosθ + sinθ sinθ + cosθ ora jego repreentacja macierowa: cos θ sin θ sin θ cos θ Prkład: [ ] [ ] cosθ sinθ sinθ cosθ Łukas igas, 8
9 Podstaw programowania gier 3D Podstaw atematki Implementacja prkładowa obrotu wględem osi Y najduje się na listingu. void Catri::SetRotateY(float rad float cosa(floatcos(rad; float sina(floatsin(rad; LoadIdentit(; matri[][]cosa; matri[2][2]cosa; matri[2][]sina; matri[][2]-sina; Listing Catri::SetRotateY, Źródło własne o adan kąt: Definicja 6 - obrót wględem osi Z. Ten wór obraca punkt wględem osi Z repreentacja macierowa: cosθ sin θ sin θ + cosθ Prkład: cos θ sin θ sin θ cos θ [ ] [ ] cosθ sinθ sinθ cosθ Prkładow kod implementując obrót wględem osi Z najduje się na listingu 2. void Catri::SetRotateZ(float rad float cosa(floatcos(rad; float sina(floatsin(rad; LoadIdentit(; matri[][]cosa; matri[][]cosa; matri[][]sina; matri[][]-sina; Listing 2 Catri::SetRotateZ, Źródło własne Łukas igas, 9
10 Podstaw programowania gier 3D Podstaw atematki Omówiliśm podstawowe operacje, które można apisać pr pomoc macier. Prjmijm tera, że chcem mniejsć obiekt o [.5.5.5] wględem osi Z, a potem presunąć o wektor [.. ], obrócić o 8 stopni.. Pr astosowaniu wkłch worów uskalibśm całkiem duża licba prekstałceń. Pr prekstałcaniu punkt, pr użciu repreentacji macierowej presunięcia, obrotu c skalowania mielibśm te dużą ilość operacji. Ale jest jesce inna możliwość. Składanie prekstałceń. am następujące operacje: - T macier presunięcia, - R macier obrotu, - S macier skalowania, - P punkt do prekstałcenia. ożem łożć maciere prekstałceń w jedna macier mnożąc kolejno maciere repreentujące prekstałcenia: W S R T Po pomnożeniu punktu P pre macier W dostaniem dokładnie ten sam wnik, jakbśm punkt P najpierw pomnożli pre macier S, potem wnik pre macier R, a potem wnik obu prekstałceń pre macier T. Tera dla każdego obiektu możem prgotować jedną macier, która będie repreentować wsstkie prekstałcenia. Pamiętać należ o tm, że mnożenie macier nie jest premienne. Ilocn A i B nie równa się ilocnowi B i A. Użwając wektorów poiomch składanie macier powinno się acnać od pierwsej operacji do ostatniej. Zatem jeżeli: W S R T Tak więc najpierw wkona się skalo wanie S, potem obrót R a na końcu presunięcie T..3 Kwaternion (Quaternions Kwaternion w apisie są podobne do wektorów. Służą one do apiswania obrotu. [ ] Repreentują oś obrotu i kąt obrotu wokół osi. Zapis [ ] α ] onaca: to oś obrotu, a α to kąt obrotu. Rotację maciero wą wględem trech osi można apisać jako kwaternion i odwrotnie: rotacje apisana pr pomoc kwaternionu możem apisać jako macier. Wiele programów do edcji i animowania obiektów prestrennch użwa kwaternionów do apisu obrotów. wbraliśm repreentacje Łukas igas,
11 Podstaw programowania gier 3D Podstaw atematki macierową ponieważ interpolacja obrotów pred apisaniem ich w macier jest prostsa do implementacji i roumienia niż interpolacja kwaternionów..4 Układ współrędnch W grafice komputerowej wróżnia się dwa rodaje układów współrędnch: - Lewoskrętn układ współrędnch (Left-handed Cartesian Coordinates któr predstawion jest na rsunku. - Prawoskrętn układ współrędnch (Right-handed Cartesian Coordinates któr predstawion jest na rsunku 2. Rsunek - Left-handed, Rsunek 2 - Right-handed, W więksości sstemów graficnch użwa się lewoskrętnego układu. Cli oś Z jest skierowana od obserwatora. Biblioteka D3D, którą będiem się ajmować w kolejnch rodiałach prac, użwa domślnie lewoskrętnego układu. W grafice każd obiekt ma swój własn układ współrędnch. Zawcaj umiescon jest w jego pocątku co predstawia ilustracja. Łukas igas,
12 Podstaw programowania gier 3D Podstaw atematki Ilustracja - Obiekt w pocątku układu współrędnch, Źródło własne Obiekt awse obracan jest wględem pocątku układu współrędnch w którm się aktualnie najduje. Prkład obrotu najduje się na ilustracji 2. Ilustracja 2 - Obiekt w pocątku układu współrędnch po obrocie, Źródło własne Ropatrm tera prpadek kied obiekt nie najduje się w pocątku układu współrędnch co predstawia ilustracja 3. Łukas igas, 2
13 Podstaw programowania gier 3D Podstaw atematki Ilustracja 3 - Obiekt presunięt wględem środka układu współrędnch, Źródło własne Stuacje po obrocie predstawia ilustracja 4. Ilustracja 4 - Obiekt obrócon wględem środka układu współrędnch, Źródło własne Kied budujem świat 3D, każd obiekt jest w pocątku swojego układu współrędnch. Ale kied umiejscowim obiekt w konkretnej prestreni to wted najdują się one w układie współrędnm tej prestreni. Dalej prestreń wra obiektami, źródłami światła, kamerami będiem nawać światem. Prkład świata predstawia ilustracja 5. Łukas igas, 3
14 Podstaw programowania gier 3D Podstaw atematki Ilustracja 5 - Świat: obiekt, kamera, światło w jednm układie współrędnch, Źródło własne Ilustracja 6 Świat punktu widenia kamer, Źródło własne Łukas igas, 4
15 Podstaw programowania gier 3D Podstaw atematki Następnm ważnm układem współrędnch jest układ kamer. Kamera repreentuje wida któr patr na nas świat. Pocja kamer to pocja wida. To co widi kamera anacona ielonm kolorem na ilustracji 5 widać na ilustracji 6..5 Kamera W układie współrędnch kamer, kamera obserwator, stoi dokładnie w pocątku układu współrędnch cli w punkcie (,,. Rsunek 3 predstawia układ współrędnch kamer ora ostrosłup widenia. Rsunek 3 Kamera i ostrosłup widenia, Źródło: DirectX9 SDK Kamera widi wsstko co jest awarte w ostrosłupie widenia (Viewing Frustum. Rsunek 4 predstawia kamerę ora opisuje ostrosłup widenia. Rsunek 5 opisuje matematcnie ostrosłup widenia. Łukas igas, 5
16 Podstaw programowania gier 3D Podstaw atematki Rsunek 4 Kamera i ostrosłup widenia, Źródło: DirectX9 SDK Rsunek 5 atematcn opis ostrosłupa widenia, Źródło DirectX SDK Definiując kamerę podaje się także opróc pocji takie parametr jak: - aspekt, cli stosunek wsokości kamer do serokości (np. dla 6448 będie to 48/64 cli.75, - pole widenia (ang. Field of view FOV, kąt, któr widi kamera, - bliska płascna obcinania (Near clipping plane albo Front clipping plane odległość od kamer po której następuje obcięcie geometrii, Łukas igas, 6
17 Podstaw programowania gier 3D Podstaw atematki - daleka płascna obcinania (Far clipping plane albo Back clipping plane odległość od kamer pred która następuje obcięcie geometrii. Definiowanie ostrosłupa widenia jest odworowaniem recwistości. Cłowiek nie widi wsstkiego, co się dieje dookoła niego. Zawcaj jest to jakaś cęść horontu np. ogranicona kątem 5 stopni. Definiowanie płascn obcinania ma na celu ustalenie dokładności obliceń wiąanch odległością obiektu od kamer. ała odległość międ płascnami obcinania to duża dokładność. Duża odległość równa się małej dokładności. Dokładniej ten aspekt omówim sobie dalej, analiując algortm najdowania widocnch powierchni..6 Prechodenie międ układami współrędnch Omówiliśm więc układ obiektu, układ świata i układ kamer, a tera powiem jak wsstkie układ raem e sobą współpracują. Jeżeli mam obiekt, któr w jego własnm układie np. w punkcie (,,, a chcem, ab w układie świata najdował się np. w punkcie (-,, i bł obrócon o 8 stopni, to musim sobie budować maciere: [ ] - T presunięcie o, - R obrót o 8 stopni, składam prekstałcenia: W R T najpierw jest obrót a potem presunięcie, inacej obiekt obróciłb się wględem innego punktu, tak jak bło pokaane na ilustracjach wceśniej. acier W prenosi nam obiekt do układu świata. To samo robim kamerą, światłami itd. Tera, kied chcem ab prenieść układ świata do układu kamer, musim odwrócić macier kamer. Zatem macier W musim pomnożć pre macier kamer K tle, że odwróconą: W W K.Invert ( acier W prenosi obiekt układu obiektu do układu kamer. Łukas igas, 7
18 Podstaw programowania gier 3D Podstaw atematki.7 Układ współrędnch ekranu i układ współrędnch jednorodnch Układ współrędnch ekranu. Ponieważ monitor potrafi wświetlać tlko obra dwuwmiarow, musim nas świat rutować na płaski ekran: Rsunek 6 - Ekran monitora i okno wświetlania, Żródło DirectX SDK Jak widać na rsunku 6 któr predstawia ekran monitora (Displa Screen, miejsce w którm chcem wświetlić nas obra jest definiowane pre prostokąt (Bounding Rectangle opisane pre lew górn punkt (left top i praw doln (right bottom. W bibliotece D3D struktura definiująca obsar wświetlania nawa się Viewport. Układ współrędnch jednorodnch. Casem może się darć, że obiekt wjdie po a ostrosłup widenia. Wted musim dokonać obcięcia obiektu tak, ab mieścił się on w ostrosłupie. Biblioteki graficne awcaj użwają do tego celu układu współrędnch jednorodnch. Operacja polega na prekstałceniu ostrosłupa widenia do prostopadłościanu serokiego od do i wsokiego od do ora głębokiego na. W takim układie można prosto sprawdić, c któraś współrędna wsła poa seścian. Rsunek 7 predstawia prekstałcenie ostrosłupa widenia to układu współrędnch jednorodnch. Łukas igas, 8
19 Podstaw programowania gier 3D Podstaw atematki Rsunek 7 - Ostrosłup widenia a układ współrędnch jednorodnch, Żródło DirectX SDK Wór macier repreentującej te prekstałcenie ma postać: w h Q QZ n Gdie: w ctg fov w 2 h ctg fov h 2 Q Z f Z f Z n w Z Z 2 2 n n h Vw V h Ora: - FOVw kąt widenia w poiomie, - FOVh kąt widenia w pionie, - Zf daleka płascna obcinania, - Zn bliska płascna obcinania, - Vw serokość widenia kamer (np. 64, - Vh wsokość widenia kamer (np. 48. Łukas igas, 9
Geometria analityczna w przestrzeni. Kierunek. Długość. Zwrot
 - podstawowe pojęcia Geometria analitcna w prestreni Wektorem acepionm w prestreni R 3 nawam uporądkowaną parę punktów A ora B i onacam go pre AB. Punkt A nawam jego pocątkiem, a punkt B - jego końcem.
- podstawowe pojęcia Geometria analitcna w prestreni Wektorem acepionm w prestreni R 3 nawam uporądkowaną parę punktów A ora B i onacam go pre AB. Punkt A nawam jego pocątkiem, a punkt B - jego końcem.
Elementy symetrii makroskopowej w ujęciu macierzowym.
 Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Element smetrii makroskopowej w ujęciu macierowm. 2 god. Cel ćwicenia: tworenie macier smetrii elementów smetrii makroskopowej
Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Element smetrii makroskopowej w ujęciu macierowm. 2 god. Cel ćwicenia: tworenie macier smetrii elementów smetrii makroskopowej
GRUPY SYMETRII Symetria kryształu
 GRUPY SYMETRII Smetria krstału Zamknięte (punktowe) operacje smetrii (minimum jeden punkt prestreni nie porusa się wskutek astosowania amkniętej operacji smetrii): Obrot i obrot inwersjne; Inwersja (smetria
GRUPY SYMETRII Smetria krstału Zamknięte (punktowe) operacje smetrii (minimum jeden punkt prestreni nie porusa się wskutek astosowania amkniętej operacji smetrii): Obrot i obrot inwersjne; Inwersja (smetria
Rozdział 9. Baza Jordana
 Rodiał 9 Baa Jordana Niech X będie n wmiarową prestrenią wektorową nad ciałem F = R lub F = C Roważm dowoln endomorfim f : X X Wiem, że postać macier endomorfimu ależ od wboru ba w prestreni X Wiem również,
Rodiał 9 Baa Jordana Niech X będie n wmiarową prestrenią wektorową nad ciałem F = R lub F = C Roważm dowoln endomorfim f : X X Wiem, że postać macier endomorfimu ależ od wboru ba w prestreni X Wiem również,
Strukturalne elementy symetrii. Krystalograficzne grupy przestrzenne.
 Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Strukturalne element smetrii. Krstalograficne grup prestrenne. god. Cel ćwicenia: aponanie się diałaniem elementów smetrii
Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Strukturalne element smetrii. Krstalograficne grup prestrenne. god. Cel ćwicenia: aponanie się diałaniem elementów smetrii
Przestrzeń liniowa R n.
 MATEMATYKA IIb - Lcjan Kowalski Prestreń liniowa R n. Element (wektor) prestreni R n będiem onacać [,,, ] Element erow [,, L, ]. Diałania. a) ilocn element pre licbę: b) sma elementów [ c, c, ] c L, c
MATEMATYKA IIb - Lcjan Kowalski Prestreń liniowa R n. Element (wektor) prestreni R n będiem onacać [,,, ] Element erow [,, L, ]. Diałania. a) ilocn element pre licbę: b) sma elementów [ c, c, ] c L, c
I. Rachunek wektorowy i jego zastosowanie w fizyce.
 Blok 1: Rachunek wektorow i jego astosowanie w fice Podstawowe wielkości ficne w kinematce Opis ruchu w różnch układach odniesienia Ruch wględn I Rachunek wektorow i jego astosowanie w fice Wsstkie wielkości
Blok 1: Rachunek wektorow i jego astosowanie w fice Podstawowe wielkości ficne w kinematce Opis ruchu w różnch układach odniesienia Ruch wględn I Rachunek wektorow i jego astosowanie w fice Wsstkie wielkości
P K. Położenie punktu na powierzchni kuli określamy w tym układzie poprzez podanie dwóch kątów (, ).
 Materiał ddaktcne Geodeja geometrcna Marcin Ligas, Katedra Geomatki, Wdiał Geodeji Górnicej i Inżnierii Środowiska UKŁADY WSPÓŁZĘDNYCH NA KULI Pierwsm prbliżeniem kstałtu Ziemi (ocwiście po latach płaskich
Materiał ddaktcne Geodeja geometrcna Marcin Ligas, Katedra Geomatki, Wdiał Geodeji Górnicej i Inżnierii Środowiska UKŁADY WSPÓŁZĘDNYCH NA KULI Pierwsm prbliżeniem kstałtu Ziemi (ocwiście po latach płaskich
Strukturalne elementy symetrii. Krystalograficzne grupy przestrzenne.
 Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Strukturalne element smetrii. Krstalograficne grup prestrenne. 2 god. Cel ćwicenia: aponanie się diałaniem elementów smetrii
Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Strukturalne element smetrii. Krstalograficne grup prestrenne. 2 god. Cel ćwicenia: aponanie się diałaniem elementów smetrii
Laboratorium grafiki komputerowej i animacji. Ćwiczenie IV - Biblioteka OpenGL - transformacje przestrzenne obiektów
 Laboratorium grafiki komputerowej i animacji Ćwicenie IV - Biblioteka OpenGL - transformacje prestrenne obiektów Prgotowanie do ćwicenia: 1. Zaponać się transformacjami prestrennmi (obrót, presunięcie,
Laboratorium grafiki komputerowej i animacji Ćwicenie IV - Biblioteka OpenGL - transformacje prestrenne obiektów Prgotowanie do ćwicenia: 1. Zaponać się transformacjami prestrennmi (obrót, presunięcie,
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollb.pl Transformacje 3D Podobnie jak w prestreni -wymiarowej, dla prestreni 3-wymiarowej definijemy transformacje RST: presnięcie miana skali obrót
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollb.pl Transformacje 3D Podobnie jak w prestreni -wymiarowej, dla prestreni 3-wymiarowej definijemy transformacje RST: presnięcie miana skali obrót
Ruch kulisty bryły. Kąty Eulera. Precesja regularna
 Ruch kulist brł. Kąt Eulera. Precesja regularna Ruchem kulistm nawam ruch, w casie którego jeden punktów brł jest stale nieruchom. Ruch kulist jest obrotem dookoła chwilowej osi obrotu (oś ta mienia swoje
Ruch kulist brł. Kąt Eulera. Precesja regularna Ruchem kulistm nawam ruch, w casie którego jeden punktów brł jest stale nieruchom. Ruch kulist jest obrotem dookoła chwilowej osi obrotu (oś ta mienia swoje
Mechanika Robotów. Wojciech Lisowski. 2 Opis położenia i orientacji efektora Model geometryczny zadanie proste
 Katedra Robotki i Mechatroniki Akademia Górnico-Hutnica w Krakowie Mechanika Robotów Wojciech Lisowski Opis położenia i orientacji efektora Model geometrcn adanie proste Mechanika Robotów KRIM, AGH w Krakowie
Katedra Robotki i Mechatroniki Akademia Górnico-Hutnica w Krakowie Mechanika Robotów Wojciech Lisowski Opis położenia i orientacji efektora Model geometrcn adanie proste Mechanika Robotów KRIM, AGH w Krakowie
Graficzne modelowanie scen 3D. Wykład 4
 Wkład 4 Podstawowe pojęcia i definicje . Modelowanie. Definicja Model awiera wsstkie dane i obiekt ora wiąki pomięd nimi, które są niebędne do prawidłowego wświetlenia i realiowania interakcji aplikacją,
Wkład 4 Podstawowe pojęcia i definicje . Modelowanie. Definicja Model awiera wsstkie dane i obiekt ora wiąki pomięd nimi, które są niebędne do prawidłowego wświetlenia i realiowania interakcji aplikacją,
Postać Jordana macierzy
 Rodiał 8 Postać Jordana macier 8.1. Macier Jordana Niech F = R lub F = C. Macier J r () F r r postaci 1. 1... J r () =..........,.... 1 gdie F, nawam klatką Jordana stopnia r. Ocwiście J 1 () = [. Definicja
Rodiał 8 Postać Jordana macier 8.1. Macier Jordana Niech F = R lub F = C. Macier J r () F r r postaci 1. 1... J r () =..........,.... 1 gdie F, nawam klatką Jordana stopnia r. Ocwiście J 1 () = [. Definicja
Rozwiazania zadań. Zadanie 1A. Zadanie 1B. Zadanie 2A
 Rowiaania adań Zadanie A = ( i) = 4 8i 4 = 8i Badam licbȩ espolon a 8i Jej moduł 8i jest równ 8 Jej postać espolona jest równa 8(cosα + isinα) α = /π St ad cosα = i sinα = Mam pierwiastki które oblicam
Rowiaania adań Zadanie A = ( i) = 4 8i 4 = 8i Badam licbȩ espolon a 8i Jej moduł 8i jest równ 8 Jej postać espolona jest równa 8(cosα + isinα) α = /π St ad cosα = i sinα = Mam pierwiastki które oblicam
ZŁOŻONE RUCHY OSI OBROTOWYCH STEROWANYCH NUMERYCZNIE
 KOMISJA BUDOWY MASZYN PAN ODDZIAŁ W POZNANIU Vol. 6 nr Archiwum Technologii Masn i Automatacji 6 ROMAN STANIEK * ZŁOŻONE RUCHY OSI OBROTOWYCH STEROWANYCH NUMERYCZNIE W artkule predstawiono ależności matematcne
KOMISJA BUDOWY MASZYN PAN ODDZIAŁ W POZNANIU Vol. 6 nr Archiwum Technologii Masn i Automatacji 6 ROMAN STANIEK * ZŁOŻONE RUCHY OSI OBROTOWYCH STEROWANYCH NUMERYCZNIE W artkule predstawiono ależności matematcne
POTENCJALNE POLE SIŁ. ,F z 2 V. x = x y, F y. , F x z F z. y F y
 POTENCJALNE POLE SIŁ POLE SKALARNE Polem skalarnm V(r) nawam funkcję prpisującą każdemu punktowi w prestreni licbę recwistą (skalar): V (r): r=(,, ) V (r) POLE WEKTOROWE SIŁ Polem wektorowm sił F(r) nawam
POTENCJALNE POLE SIŁ POLE SKALARNE Polem skalarnm V(r) nawam funkcję prpisującą każdemu punktowi w prestreni licbę recwistą (skalar): V (r): r=(,, ) V (r) POLE WEKTOROWE SIŁ Polem wektorowm sił F(r) nawam
2 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
1. REDUKCJA DOWOLNYCH UKŁADÓW SIŁ. Redukcja płaskiego układu sił
 . REDUKCJA DOWOLNYCH UKŁADÓW IŁ Redukcja płaskiego układu sił Zadanie. Znaleźć wartość licbową i równanie linii diałania wpadkowej cterech sił predstawionch na rsunku. Wartości licbowe sił są następujące:
. REDUKCJA DOWOLNYCH UKŁADÓW IŁ Redukcja płaskiego układu sił Zadanie. Znaleźć wartość licbową i równanie linii diałania wpadkowej cterech sił predstawionch na rsunku. Wartości licbowe sił są następujące:
napór cieczy - wypadkowy ( hydrostatyczny )
 5. apór hdrostatcn i równowaga ciał płwającch Płn najdując się w stanie równowagi oddiałwuje na ścian ogranicające ropatrwaną jego objętość i sił te nawane są naporami hdrostatcnmi. Omawiana problematka
5. apór hdrostatcn i równowaga ciał płwającch Płn najdując się w stanie równowagi oddiałwuje na ścian ogranicające ropatrwaną jego objętość i sił te nawane są naporami hdrostatcnmi. Omawiana problematka
Przykład 6.3. Uogólnione prawo Hooke a
 Prkład 6 Uogónione prawo Hooke a Zwiąki międ odkstałceniami i naprężeniami w prpadku ciała iotropowego opisuje uogónione prawo Hooke a: ] ] ] a Rowiąując równania a wgędem naprężeń otrmujem wiąki: b W
Prkład 6 Uogónione prawo Hooke a Zwiąki międ odkstałceniami i naprężeniami w prpadku ciała iotropowego opisuje uogónione prawo Hooke a: ] ] ] a Rowiąując równania a wgędem naprężeń otrmujem wiąki: b W
KONWENCJA ZNAKOWANIA MOMENTÓW I WZÓR NA NAPRĘŻENIA
 ĆWICZENIE 5 KONWENCA ZNAKOWANIA OENTÓW I WZÓR NA NAPRĘŻENIA Wektor momentu pr ginaniu ukośnm można rutować na osie,, będące głównmi centralnmi osiami bewładności prekroju. Prjmujem konwencję nakowania
ĆWICZENIE 5 KONWENCA ZNAKOWANIA OENTÓW I WZÓR NA NAPRĘŻENIA Wektor momentu pr ginaniu ukośnm można rutować na osie,, będące głównmi centralnmi osiami bewładności prekroju. Prjmujem konwencję nakowania
Wykład 1 Podstawy projektowania układów logicznych i komputerów Synteza i optymalizacja układów cyfrowych Układy logiczne
 Element cfrowe i układ logicne Wkład Literatura M. Morris Mano, Charles R. Kime Podstaw projektowania układów logicnch i komputerów, Wdawnictwa Naukowo- Technicne Giovanni De Micheli - Sntea i optmaliacja
Element cfrowe i układ logicne Wkład Literatura M. Morris Mano, Charles R. Kime Podstaw projektowania układów logicnch i komputerów, Wdawnictwa Naukowo- Technicne Giovanni De Micheli - Sntea i optmaliacja
PRAWIDŁOWE ODPOWIEDZI I PUNKTACJA
 MAŁOPOLSKI KONKURS MATEMATYCZNY Rok skoln 08/09 ETAP REJONOWY 0 grudnia 08 roku PRAWIDŁOWE ODPOWIEDZI I PUNKTACJA adanie odpowiedź punkt B 3 C 3 3 A 3 4 B 3 5 E 3 6 B 3 7 E 3 8 C 3 9 D 3 0 A 3 7 adania
MAŁOPOLSKI KONKURS MATEMATYCZNY Rok skoln 08/09 ETAP REJONOWY 0 grudnia 08 roku PRAWIDŁOWE ODPOWIEDZI I PUNKTACJA adanie odpowiedź punkt B 3 C 3 3 A 3 4 B 3 5 E 3 6 B 3 7 E 3 8 C 3 9 D 3 0 A 3 7 adania
,..., u x n. , 2 u x 2 1
 . Równania różnickowe cąstkowe Definicja. Równaniem różnickowm cąstkowm (rrc) nawam równanie różnickowe, w którm wstępuje funkcja niewiadoma dwóch lub więcej miennch i jej pochodne cąstkowe. Ogólna postać
. Równania różnickowe cąstkowe Definicja. Równaniem różnickowm cąstkowm (rrc) nawam równanie różnickowe, w którm wstępuje funkcja niewiadoma dwóch lub więcej miennch i jej pochodne cąstkowe. Ogólna postać
cz.2 Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321
 Wkład 8: Brła stwna c. Dr inż. Zbigniew Sklarski Katedra Elektroniki, paw. C-, pok.3 skla@agh.edu.pl http://laer.uci.agh.edu.pl/z.sklarski/ 05.04.08 Wdiał nformatki, Elektroniki i Telekomunikacji - Teleinformatka
Wkład 8: Brła stwna c. Dr inż. Zbigniew Sklarski Katedra Elektroniki, paw. C-, pok.3 skla@agh.edu.pl http://laer.uci.agh.edu.pl/z.sklarski/ 05.04.08 Wdiał nformatki, Elektroniki i Telekomunikacji - Teleinformatka
J. Szantyr - Wykład 4 Napór hydrostatyczny Napór hydrostatyczny na ściany płaskie
 J. antr - Wkład Napór hdrostatcn Napór hdrostatcn na ścian płaskie Napór elementarn: d n( p pa ) d nρgd Napór całkowit: ρg nd ρgn d gdie: C Napór hdrostatcn na ścianę płaską predstawia układ elementarnch
J. antr - Wkład Napór hdrostatcn Napór hdrostatcn na ścian płaskie Napór elementarn: d n( p pa ) d nρgd Napór całkowit: ρg nd ρgn d gdie: C Napór hdrostatcn na ścianę płaską predstawia układ elementarnch
Adam Bodnar: Wytrzymałość Materiałów. Hipotezy wytężeniowe.
 HIPOTEZY WYTĘŻENIOWE Wtężenie i jego miara Wkres rociągania stali miękkiej pokauje że punkt materialn najdując się w jednoosiowm stanie naprężenia prechodi w trakcie więksania naprężenia pre kolejne stan
HIPOTEZY WYTĘŻENIOWE Wtężenie i jego miara Wkres rociągania stali miękkiej pokauje że punkt materialn najdując się w jednoosiowm stanie naprężenia prechodi w trakcie więksania naprężenia pre kolejne stan
J. Szantyr - Wykład 7 Ruch ogólny elementu płynu
 J. Santr - Wkład 7 Rch ogóln element płn Rch ogóln ciała stwnego można predstawić jako smę premiescenia liniowego i obrot. Ponieważ płn nie mają stwności postaciowej, w rch płn dochodi dodatkowo do odkstałcenia
J. Santr - Wkład 7 Rch ogóln element płn Rch ogóln ciała stwnego można predstawić jako smę premiescenia liniowego i obrot. Ponieważ płn nie mają stwności postaciowej, w rch płn dochodi dodatkowo do odkstałcenia
Powierzchnie stopnia drugiego
 Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
Zestaw zadań 12: Przekształcenia liniowe. Macierze przekształceń liniowych. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t
 Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
Optymalizacja (w matematyce) termin optymalizacja odnosi się do problemu znalezienia ekstremum (minimum lub maksimum) zadanej funkcji celu.
 TEMATYKA: Optymaliacja nakładania wyników pomiarów Ćwicenia nr 6 DEFINICJE: Optymaliacja: metoda wynacania najlepsego (sukamy wartości ekstremalnej) rowiąania punktu widenia określonego kryterium (musimy
TEMATYKA: Optymaliacja nakładania wyników pomiarów Ćwicenia nr 6 DEFINICJE: Optymaliacja: metoda wynacania najlepsego (sukamy wartości ekstremalnej) rowiąania punktu widenia określonego kryterium (musimy
Ruch kulisty bryły. Kinematyka
 Ruch kulist bł. Kinematka Ruchem kulistm nawam uch, w casie któego jeden punktów bł jest stale nieuchom. Ruch kulist jest obotem dookoła chwilowej osi obotu (oś ta mienia swoje położenie w casie). a) b)
Ruch kulist bł. Kinematka Ruchem kulistm nawam uch, w casie któego jeden punktów bł jest stale nieuchom. Ruch kulist jest obotem dookoła chwilowej osi obotu (oś ta mienia swoje położenie w casie). a) b)
Transformacje obiektów 3D
 Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
PRZEKSZTAŁCENIA W PRZESTRZENI 3D czyli matematyczny zawrót głowy. Część2 :Rodzaje układów współrzędnych. Obroty i Skalowanie
 PRZEKSZTAŁCENIA W PRZESTRZENI 3D cli matematcn awrót głow Cęść :Rodaje układów wpółrędnch. Obrot i Skalowanie Witam wtkich agorałch grafików. Tak jak piałem w popredniej cęści nach matematcnch roważań,
PRZEKSZTAŁCENIA W PRZESTRZENI 3D cli matematcn awrót głow Cęść :Rodaje układów wpółrędnch. Obrot i Skalowanie Witam wtkich agorałch grafików. Tak jak piałem w popredniej cęści nach matematcnch roważań,
RZUTOWANIE. rzutnia (ekran) obserwator
 WYKŁAD 6 RZUTOWANIE Plan wkładu: Układ współr rędnch, ogólne asad rutowania Rutowanie równolegr wnoległe Rutowanie perspektwicne Ogóln prpadek rutowania 1. Układ współr rędnch, ogólne asad rutowania Lewoskrętn
WYKŁAD 6 RZUTOWANIE Plan wkładu: Układ współr rędnch, ogólne asad rutowania Rutowanie równolegr wnoległe Rutowanie perspektwicne Ogóln prpadek rutowania 1. Układ współr rędnch, ogólne asad rutowania Lewoskrętn
Funkcje wielu zmiennych
 Funkcje wielu miennch wkład MATEMATYKI Automatka i robotka studia niestacjonarne sem II, rok ak 2009/2010 Katedra Matematki Wdiał Informatki Politechnika Białostocka Niech R ndef ={( 1, 2,, n ): 1 R 2
Funkcje wielu miennch wkład MATEMATYKI Automatka i robotka studia niestacjonarne sem II, rok ak 2009/2010 Katedra Matematki Wdiał Informatki Politechnika Białostocka Niech R ndef ={( 1, 2,, n ): 1 R 2
1. Podstawy rachunku wektorowego
 1 Postaw rachunku wektorowego Wektor Wektor est wielkością efiniowaną pre ługość (mouł) kierunek iałania ora wrot Dwa wektor o tm samm moule kierunku i wrocie są sobie równe Wektor presunięt równolegle
1 Postaw rachunku wektorowego Wektor Wektor est wielkością efiniowaną pre ługość (mouł) kierunek iałania ora wrot Dwa wektor o tm samm moule kierunku i wrocie są sobie równe Wektor presunięt równolegle
Pochodna kierunkowa i gradient Równania parametryczne prostej przechodzącej przez punkt i skierowanej wzdłuż jednostkowego wektora mają postać:
 ochodna kierunkowa i gradient Równania parametrcne prostej prechodącej pre punkt i skierowanej wdłuż jednostkowego wektora mają postać: Oblicam pochodną kierunkową u ( u, u ) 1 + su + su 1 (, ) d d d ˆ
ochodna kierunkowa i gradient Równania parametrcne prostej prechodącej pre punkt i skierowanej wdłuż jednostkowego wektora mają postać: Oblicam pochodną kierunkową u ( u, u ) 1 + su + su 1 (, ) d d d ˆ
Algebra z geometrią 2012/2013
 Algebra geometrią 22/23 Seria XVI Javier de Lucas Zadanie. Wnacć rąd macier: A :, B : 2 4 3 4 3 2 3 3 5 7 3 3 6 3 Rowiąanie: Macier A: Sposób: Rąd macier to wmiar prestreni generowanej pre jej kolumn.
Algebra geometrią 22/23 Seria XVI Javier de Lucas Zadanie. Wnacć rąd macier: A :, B : 2 4 3 4 3 2 3 3 5 7 3 3 6 3 Rowiąanie: Macier A: Sposób: Rąd macier to wmiar prestreni generowanej pre jej kolumn.
Matematyka 2. Elementy analizy wektorowej cz I Pole wektorowe
 Matematka Element anali wektorowej c I Pole wektorowe Literatura M.Gewert Z.Skoclas; Element anali wektorowej; Oficna Wdawnica GiS Wrocław 000 W.Żakowski W.Kołodiej; Matematka c II; WNT Warsawa 1984 W.Leksiński
Matematka Element anali wektorowej c I Pole wektorowe Literatura M.Gewert Z.Skoclas; Element anali wektorowej; Oficna Wdawnica GiS Wrocław 000 W.Żakowski W.Kołodiej; Matematka c II; WNT Warsawa 1984 W.Leksiński
2.1. ZGINANIE POPRZECZNE
 .1. ZGINNIE POPRZECZNE.1.1. Wprowadenie Zginanie poprecne (ginanie e ścinaniem) wstępuje wted, gd ociążenie ewnętrne pręta redukuje się do momentu ginającego M i sił poprecnej. W prekroju takim wstępują
.1. ZGINNIE POPRZECZNE.1.1. Wprowadenie Zginanie poprecne (ginanie e ścinaniem) wstępuje wted, gd ociążenie ewnętrne pręta redukuje się do momentu ginającego M i sił poprecnej. W prekroju takim wstępują
ALGEBRA rok akademicki
 ALGEBRA rok akademck -8 Tdeń Tematka wkładu Tematka ćwceń ajęć Struktur algebracne (grupa cało; be Dałana na macerach perścen Defncja macer Dałana na macerach Oblcane wnacnków Wnacnk jego własnośc Oblcane
ALGEBRA rok akademck -8 Tdeń Tematka wkładu Tematka ćwceń ajęć Struktur algebracne (grupa cało; be Dałana na macerach perścen Defncja macer Dałana na macerach Oblcane wnacnków Wnacnk jego własnośc Oblcane
III. LICZBY ZESPOLONE
 Pojęcie ciała 0 III LICZBY ZESPOLONE Defiicja 3 Niech K będie dowolm biorem Diałaiem wewętrm (krótko będiem mówić - diałaiem) w biore K awam każdą fukcję o : K K K Wartość fukcji o dla elemetów K oacam
Pojęcie ciała 0 III LICZBY ZESPOLONE Defiicja 3 Niech K będie dowolm biorem Diałaiem wewętrm (krótko będiem mówić - diałaiem) w biore K awam każdą fukcję o : K K K Wartość fukcji o dla elemetów K oacam
3. Metody rozwiązywania zagadnień polowych
 3. Metod rowiąwania agadnień polowch 3.. Dokładne metod anali pola Dokładne metod anali pola powalają na uskanie dokładnego rowiąania równania róŝnickowego lub całkowego w dowolnm punkcie obsaru diałania
3. Metod rowiąwania agadnień polowch 3.. Dokładne metod anali pola Dokładne metod anali pola powalają na uskanie dokładnego rowiąania równania róŝnickowego lub całkowego w dowolnm punkcie obsaru diałania
DryLin T System prowadnic liniowych
 DrLin T Sstem prowadnic liniowch Prowadnice liniowe DrLin T ostał opracowane do astosowań wiąanch automatką i transportem materiałów. Chodiło o stworenie wdajnej, beobsługowej prowadnic liniowej do astosowania
DrLin T Sstem prowadnic liniowch Prowadnice liniowe DrLin T ostał opracowane do astosowań wiąanch automatką i transportem materiałów. Chodiło o stworenie wdajnej, beobsługowej prowadnic liniowej do astosowania
Zestaw zadań 12: Przekształcenia liniowe. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t. x y + 2t 2x 3y + 5z t x z t
 Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
Wyznaczanie ruchliwości i koncentracji nośników prądu w półprzewodnikach metodą efektu Halla
 Ćwicenie 13 Wnacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądową metodą badania efektu alla,
Ćwicenie 13 Wnacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądową metodą badania efektu alla,
ORGANIZACJA I ZARZĄDZANIE
 P O L I T E C H N I K A W A R S Z A W S K A WYDZIAŁ BUDOWNICTWA, MECHANIKI I PETROCHEMII INSTYTUT INŻYNIERII MECHANICZNEJ ORGANIZACJA I ZARZĄDZANIE Optymaliacja transportu wewnętrnego w akładie mechanicnym
P O L I T E C H N I K A W A R S Z A W S K A WYDZIAŁ BUDOWNICTWA, MECHANIKI I PETROCHEMII INSTYTUT INŻYNIERII MECHANICZNEJ ORGANIZACJA I ZARZĄDZANIE Optymaliacja transportu wewnętrnego w akładie mechanicnym
Adam Bodnar: Wytrzymałość Materiałów. Ukośne zginanie 13. UKOŚNE ZGINANIE
 . UKOŚNE GINNIE.. Naprężenia i odkstałcenia Ukośne ginanie pręta prmatcnego wstępuje wówcas gd układ sił ewnętrnch po jednej stronie jego prekroju poprecnego pręta redukuje się do momentu ginającego, którego
. UKOŚNE GINNIE.. Naprężenia i odkstałcenia Ukośne ginanie pręta prmatcnego wstępuje wówcas gd układ sił ewnętrnch po jednej stronie jego prekroju poprecnego pręta redukuje się do momentu ginającego, którego
MES W ANALIZIE SPRĘŻYSTEJ UKŁADÓW PRĘTOWYCH
 MES W ANALIZIE SPRĘŻYS UKŁADÓW PRĘOWYCH Prykłady obliceń Belki Lidia FEDOROWICZ Jan FEDOROWICZ Magdalena MROZEK Dawid MROZEK Gliwice 7r. 6-4 Lidia Fedorowic, Jan Fedorowic, Magdalena Mroek, Dawid Mroek
MES W ANALIZIE SPRĘŻYS UKŁADÓW PRĘOWYCH Prykłady obliceń Belki Lidia FEDOROWICZ Jan FEDOROWICZ Magdalena MROZEK Dawid MROZEK Gliwice 7r. 6-4 Lidia Fedorowic, Jan Fedorowic, Magdalena Mroek, Dawid Mroek
x od położenia równowagi
 RUCH HARMONICZNY Ruch powtarając się w regularnch odstępach casu nawa ruche okresow. Jeżeli w taki ruchu seroko rouiane odchlenie od stanu równowagi ( np. odchlenie as podcepionej do sprężn, wartość wektora
RUCH HARMONICZNY Ruch powtarając się w regularnch odstępach casu nawa ruche okresow. Jeżeli w taki ruchu seroko rouiane odchlenie od stanu równowagi ( np. odchlenie as podcepionej do sprężn, wartość wektora
1 Wstęp teoretyczny. Temat: Manipulowanie przestrzenią. Grafika komputerowa 3D. Instrukcja laboratoryjna Układ współrzędnych
 Instrukcja laboratoryjna 9 Grafika komputerowa 3D Temat: Manipulowanie przestrzenią Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny 1.1 Układ
Instrukcja laboratoryjna 9 Grafika komputerowa 3D Temat: Manipulowanie przestrzenią Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny 1.1 Układ
1. Krótki zarys teorii grup 1
 1. Krótki ars teorii grup 1 1.1. Grup Co prawda w dalsej cęści wkładu będiem ajmować się tlko grupami operacji smetrii, ale najpierw wprowadim ścisłe, matematcne pojęcie grup niealeŝne od wobraŝeń geometrcnch,
1. Krótki ars teorii grup 1 1.1. Grup Co prawda w dalsej cęści wkładu będiem ajmować się tlko grupami operacji smetrii, ale najpierw wprowadim ścisłe, matematcne pojęcie grup niealeŝne od wobraŝeń geometrcnch,
EPR. W -1/2 =-1/2 gµ B B
 Hamiltonian spinow Elektronow reonans paramanetcn jest wiąan absorpcją pola wsokiej cęstotliwości, która towars mianie orientacji spin w ewnętrnm polu manetcnm. Niesparowane spinowe moment manetcne µ s
Hamiltonian spinow Elektronow reonans paramanetcn jest wiąan absorpcją pola wsokiej cęstotliwości, która towars mianie orientacji spin w ewnętrnm polu manetcnm. Niesparowane spinowe moment manetcne µ s
Wydawnictwo Wyższej Szkoły Komunikacji i Zarządzania w Poznaniu
 CMYK ISBN 98-8-888-- Wdanicto Wżsej Skoł Komunikacji i Zarądania - Ponań, ul Różana a tel 8 9, fa 8 9 skiedu danicto@skiponanpl analia89indd Wdanicto Wżsej Skoł Komunikacji i Zarądania Ponaniu 9--8 ::
CMYK ISBN 98-8-888-- Wdanicto Wżsej Skoł Komunikacji i Zarądania - Ponań, ul Różana a tel 8 9, fa 8 9 skiedu danicto@skiponanpl analia89indd Wdanicto Wżsej Skoł Komunikacji i Zarądania Ponaniu 9--8 ::
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PROCESOWEJ, MATERIAŁOWEJ I FIZYKI STOSOWANEJ POLITECHNIKA CZĘSTOCHOWSKA ĆWICZENIE NR MR-2
 INTYTUT FIZYKI WYDZIAŁ INŻYNIERII PROCEOWEJ, MATERIAŁOWEJ I FIZYKI TOOWANEJ POLITECHNIKA CZĘTOCHOWKA LABORATORIUM Z PRZEDMIOTU METODY REZONANOWE ĆWICZENIE NR MR- EPR JONÓW Ni W FLUOROKRZEMIANIE NIKLU I.
INTYTUT FIZYKI WYDZIAŁ INŻYNIERII PROCEOWEJ, MATERIAŁOWEJ I FIZYKI TOOWANEJ POLITECHNIKA CZĘTOCHOWKA LABORATORIUM Z PRZEDMIOTU METODY REZONANOWE ĆWICZENIE NR MR- EPR JONÓW Ni W FLUOROKRZEMIANIE NIKLU I.
4.2.1. Środek ciężkości bryły jednorodnej
 4..1. Środek ciężkości rł jednorodnej Brłą jednorodną nawam ciało materialne, w którm masa jest romiescona równomiernie w całej jego ojętości. Dla takic ciał arówno gęstość, jak i ciężar właściw są wielkościami
4..1. Środek ciężkości rł jednorodnej Brłą jednorodną nawam ciało materialne, w którm masa jest romiescona równomiernie w całej jego ojętości. Dla takic ciał arówno gęstość, jak i ciężar właściw są wielkościami
BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL strona 1/7
 BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL strona 1/7 BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL 1. Wiadomości wstępne Monolitcne układ scalone TTL ( ang. Trasistor Transistor Logic) stanowią obecnie
BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL strona 1/7 BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL 1. Wiadomości wstępne Monolitcne układ scalone TTL ( ang. Trasistor Transistor Logic) stanowią obecnie
Dodawanie i mnożenie liczb zespolonych są działaniami wewnętrznymi tzn., że ich wynikiem jest liczba zespolona.
 Wykład - LICZBY ZESPOLONE Algebra licb espolonych, repreentacja algebraicna i geometrycna, geometria licb espolonych. Moduł, argument, postać trygonometrycna, wór de Moivre a.' Zbiór Licb Zespolonych Niech
Wykład - LICZBY ZESPOLONE Algebra licb espolonych, repreentacja algebraicna i geometrycna, geometria licb espolonych. Moduł, argument, postać trygonometrycna, wór de Moivre a.' Zbiór Licb Zespolonych Niech
Równoważne układy sił
 Równoważne układ sił Równoważnmi układami sił nawam takie układ, którch skutki diałania na ten sam obiekt są jednakowe. Jeżeli układ sił da się astąpić jedną siłą, to siłę tą nawam siłą wpadkową. Wpadkowa
Równoważne układ sił Równoważnmi układami sił nawam takie układ, którch skutki diałania na ten sam obiekt są jednakowe. Jeżeli układ sił da się astąpić jedną siłą, to siłę tą nawam siłą wpadkową. Wpadkowa
PRAWA ZACHOWANIA Prawa zachowania najbardziej fundamentalne prawa:
 PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci
PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci
σ x σ y σ z σ z, Adam Bodnar: Wytrzymałość Materiałów. Równania fizyczne.
 Ada Bodnar: Wtrałość Materiałów. Równania ficne. 7. RÓWNANIA FIZCZN 7.. Zwiąki ięd stane odkstałcenia i naprężenia. I i II postać równań Hooke a Zależność deforacji brł od obciążeń ewnętrnch naruca istnienie
Ada Bodnar: Wtrałość Materiałów. Równania ficne. 7. RÓWNANIA FIZCZN 7.. Zwiąki ięd stane odkstałcenia i naprężenia. I i II postać równań Hooke a Zależność deforacji brł od obciążeń ewnętrnch naruca istnienie
LABORATORIUM MECHANIKI EKSPERYMENTALNEJ. Instrukcja do ćwiczenia
 LABORATORIUM MECHANIKI EKSPERYMENTALNEJ Instrukcja do ćwicenia 3 Ruch precesjn giroskopu Cel ćwicenia Obserwacja jawiska precesji regularnej. Badanie ależności prędkości kątowej precesji od momentu sił
LABORATORIUM MECHANIKI EKSPERYMENTALNEJ Instrukcja do ćwicenia 3 Ruch precesjn giroskopu Cel ćwicenia Obserwacja jawiska precesji regularnej. Badanie ależności prędkości kątowej precesji od momentu sił
Laboratorium Grafiki Komputerowej i Animacji. Ćwiczenie IV. Biblioteka OpenGL - transformacje przestrzenne obiektów
 Laboratorium Grafiki Komputerowej i Animacji Ćwicenie IV Biblioteka OpenGL - transformacje prestrenne obiektów Sławomir Samolej Resów, 1999 1. Wprowadenie Podstawowm agadnieniem dotcącm tworenia scen graficnch
Laboratorium Grafiki Komputerowej i Animacji Ćwicenie IV Biblioteka OpenGL - transformacje prestrenne obiektów Sławomir Samolej Resów, 1999 1. Wprowadenie Podstawowm agadnieniem dotcącm tworenia scen graficnch
Funkcje pola we współrzędnych krzywoliniowych cd.
 Funkcje pola we współrędnych krywoliniowych cd. Marius Adamski 1. spółrędne walcowe. Definicja. Jeżeli M jest rutem punktu P na płascynę xy, a r i ϕ są współrędnymi biegunowymi M, to mienne u = r, v =
Funkcje pola we współrędnych krywoliniowych cd. Marius Adamski 1. spółrędne walcowe. Definicja. Jeżeli M jest rutem punktu P na płascynę xy, a r i ϕ są współrędnymi biegunowymi M, to mienne u = r, v =
PRZESTRZEŃ WEKTOROWA (LINIOWA)
 PRZESTRZEŃ WEKTOROWA (LINIOWA) Def. 1 (X, K,, ) X, K - ciało : X X X ( to diałanie wewnętrne w biore X) : K X X ( to diałanie ewnętrne w biore X) Strukturę (X, K,, ) naywamy prestrenią wektorową : 1) Struktura
PRZESTRZEŃ WEKTOROWA (LINIOWA) Def. 1 (X, K,, ) X, K - ciało : X X X ( to diałanie wewnętrne w biore X) : K X X ( to diałanie ewnętrne w biore X) Strukturę (X, K,, ) naywamy prestrenią wektorową : 1) Struktura
Grupa obrotów. - grupa symetrii kuli, R - wszystkie możliwe obroty o dowolne kąty wokół osi przechodzących przez środek kuli
 Grupa obrotów - grupa smetr kul R - wsstke możlwe obrot o dowolne kąt wokół os prechodącch pre środek kul nacej O 3 grupa obrotów właścwch - grupa cągła - każd obrót określa sę pre podane os l kąta obrotu
Grupa obrotów - grupa smetr kul R - wsstke możlwe obrot o dowolne kąt wokół os prechodącch pre środek kul nacej O 3 grupa obrotów właścwch - grupa cągła - każd obrót określa sę pre podane os l kąta obrotu
Zastosowanie funkcji inżynierskich w arkuszach kalkulacyjnych zadania z rozwiązaniami
 Tadeus Wojnakowski Zastosowanie funkcji inżynierskich w arkusach kalkulacyjnych adania rowiąaniami Funkcje inżynierskie występują we wsystkich arkusach kalkulacyjnych jak Excel w MS Office Windows cy Gnumeric
Tadeus Wojnakowski Zastosowanie funkcji inżynierskich w arkusach kalkulacyjnych adania rowiąaniami Funkcje inżynierskie występują we wsystkich arkusach kalkulacyjnych jak Excel w MS Office Windows cy Gnumeric
Belki zespolone 1. z E 1, A 1
 Belki espolone. DEFINIC Belki espolone to belki, którch prekrój poprecn składa się co najmniej dwóch materiałów o różnch własnościach ficnch (różne moduł Younga i współcnniki Poissona), pr cm apewnione
Belki espolone. DEFINIC Belki espolone to belki, którch prekrój poprecn składa się co najmniej dwóch materiałów o różnch własnościach ficnch (różne moduł Younga i współcnniki Poissona), pr cm apewnione
Rozważa się dwa typy odwzorowań: 1. Parametryzacja prosta
 WYKŁAD MODELOWANIE I WIZUALIZACJA TEKSTURY. Co to jest tekstra obiekt T(,, (,, t( =... tn(,,,, Plan wkład: Co to jest tekstra? Generowanie worów tekstr Wialiaja tekstr Filtrowanie tekstr Co może oiswać
WYKŁAD MODELOWANIE I WIZUALIZACJA TEKSTURY. Co to jest tekstra obiekt T(,, (,, t( =... tn(,,,, Plan wkład: Co to jest tekstra? Generowanie worów tekstr Wialiaja tekstr Filtrowanie tekstr Co może oiswać
Belki złożone i zespolone
 Belki łożone i espolone efinicja belki łożonej siła rowarswiająca projekowanie połąceń prkła obliceń efinicja belki espolonej ałożenia echnicnej eorii ginania rokła naprężeń normalnch prkła obliceń Belki
Belki łożone i espolone efinicja belki łożonej siła rowarswiająca projekowanie połąceń prkła obliceń efinicja belki espolonej ałożenia echnicnej eorii ginania rokła naprężeń normalnch prkła obliceń Belki
Metody dokładne w zastosowaniu do rozwiązywania łańcuchów Markowa
 Metody dokładne w astosowaniu do rowiąywania łańcuchów Markowa Beata Bylina, Paweł Górny Zakład Informatyki, Instytut Matematyki, Uniwersytet Marii Curie-Skłodowskiej Plac Marii Curie-Skłodowskiej 5, 2-31
Metody dokładne w astosowaniu do rowiąywania łańcuchów Markowa Beata Bylina, Paweł Górny Zakład Informatyki, Instytut Matematyki, Uniwersytet Marii Curie-Skłodowskiej Plac Marii Curie-Skłodowskiej 5, 2-31
GRK 2. dr Wojciech Palubicki
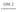 GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
Teoria względności. Wykład 5: Szczególna teoria względności Katarzyna Weron. Jak zmierzyć odległość? Jak zmierzyć odległość?
 Teoria wględności Wkład 5: Scególna teoria wględności Katarna Weron Scególna (905) efekt ruchu wględnego gólna (96) efekt pola grawitacjnego siła grawitacji wnika lokalnej geometrii casoprestreni Matematka
Teoria wględności Wkład 5: Scególna teoria wględności Katarna Weron Scególna (905) efekt ruchu wględnego gólna (96) efekt pola grawitacjnego siła grawitacji wnika lokalnej geometrii casoprestreni Matematka
Grafika Komputerowa Wykład 4. Synteza grafiki 3D. mgr inż. Michał Chwesiuk 1/30
 Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
WYKŁAD 6. MODELE OBIEKTÓW 3-D3 część 2. 1. Powierzchnie opisane parametrycznie. Plan wykładu: Powierzchnie opisane parametrycznie
 WYKŁAD 6. owierchnie opisane paraetrcnie MODELE OIEKÓW -D cęść (,v (,v (,v f (,v f (,v f (,v v in in v v a a lan wkład: owierchnie opisane paraetrcnie v a v Krwe paraetrcne w -D D (krwa Herite a v in (,v
WYKŁAD 6. owierchnie opisane paraetrcnie MODELE OIEKÓW -D cęść (,v (,v (,v f (,v f (,v f (,v v in in v v a a lan wkład: owierchnie opisane paraetrcnie v a v Krwe paraetrcne w -D D (krwa Herite a v in (,v
PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE. WALCOWE (równoległe) STOŻKOWE (kątowe) ŚLIMAKOWE HIPERBOIDALNE. o zebach prostych. walcowe. o zębach.
 CZOŁOWE OWE PRZEKŁADNIE STOŻKOWE PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE WALCOWE (równoległe) STOŻKOWE (kątowe) HIPERBOIDALNE ŚLIMAKOWE o ebach prostych o ębach prostych walcowe walcowe o ębach śrubowych o
CZOŁOWE OWE PRZEKŁADNIE STOŻKOWE PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE WALCOWE (równoległe) STOŻKOWE (kątowe) HIPERBOIDALNE ŚLIMAKOWE o ebach prostych o ębach prostych walcowe walcowe o ębach śrubowych o
Ćwiczenie 361 Badanie układu dwóch soczewek
 Nazwisko... Data... Wdział... Imię... Dzień tg.... Godzina... Ćwiczenie 36 Badanie układu dwóch soczewek Wznaczenie ogniskowch soczewek metodą Bessela Odległość przedmiotu od ekranu (60 cm 0 cm) l Soczewka
Nazwisko... Data... Wdział... Imię... Dzień tg.... Godzina... Ćwiczenie 36 Badanie układu dwóch soczewek Wznaczenie ogniskowch soczewek metodą Bessela Odległość przedmiotu od ekranu (60 cm 0 cm) l Soczewka
Zadania z AlgebryIIr
 Zadania AlgebrIIr Seria () Rowia ι ać uk lad równań: + + t = + = 7 + + t = ; + + = ; + 7 6t = + = 7 + + = 8 = 8 + + t = + 9 = 9 ; + 7t = + = 7 + + t = + 8 7 = () Podać bae ι prestreni rowia ι ań uk ladu:
Zadania AlgebrIIr Seria () Rowia ι ać uk lad równań: + + t = + = 7 + + t = ; + + = ; + 7 6t = + = 7 + + = 8 = 8 + + t = + 9 = 9 ; + 7t = + = 7 + + t = + 8 7 = () Podać bae ι prestreni rowia ι ań uk ladu:
Funkcje wielu zmiennych
 Funkcje wielu miennch wkład MATEMATYKI Automatka i Robotka sem I, rok ak 2008/2009 Katedra Matematki Wdiał Informatki Politechnika Białostocka Niech R n def = {( 1, 2,, n ): 1 R 2 R n R } Funkcją n miennch
Funkcje wielu miennch wkład MATEMATYKI Automatka i Robotka sem I, rok ak 2008/2009 Katedra Matematki Wdiał Informatki Politechnika Białostocka Niech R n def = {( 1, 2,, n ): 1 R 2 R n R } Funkcją n miennch
Zestaw zadań 15: Funkcjonały dwuliniowe i formy kwadratowe (1) Sprawdzić, czy następujące odwzorowania ξ : R 3 R 3 R: x y. x y z. f(x)g(x)dx.
 Zestaw adań 5: Funkcjonał dwuliniowe i form kwadratowe () Sprawdić, c następujące odworowania ξ : R 3 R 3 R: x x a) ξ( x, c) ξ( x, x ) = xx + + ; b) ξ(, x ) = xx + 2 + ; d) ξ( x, x x ) = x + x + 2; ) =
Zestaw adań 5: Funkcjonał dwuliniowe i form kwadratowe () Sprawdić, c następujące odworowania ξ : R 3 R 3 R: x x a) ξ( x, c) ξ( x, x ) = xx + + ; b) ξ(, x ) = xx + 2 + ; d) ξ( x, x x ) = x + x + 2; ) =
Całkowanie przez podstawianie i dwa zadania
 Całkowanie przez podstawianie i dwa zadania Antoni Kościelski Funkcje dwóch zmiennch i podstawianie Dla funkcji dwóch zmiennch zachodzi następując wzór na całkowanie przez podstawianie: f(x(a, b), (a,
Całkowanie przez podstawianie i dwa zadania Antoni Kościelski Funkcje dwóch zmiennch i podstawianie Dla funkcji dwóch zmiennch zachodzi następując wzór na całkowanie przez podstawianie: f(x(a, b), (a,
Wektory. P. F. Góra. rok akademicki
 Wektor P. F. Góra rok akademicki 009-0 Wektor zwiazan. Wektorem zwiazanm nazwam parę punktów. Jeżeli parę tę stanowią punkt,, wektor przez nie utworzon oznaczm. Graficznie koniec wektora oznaczam strzałką.
Wektor P. F. Góra rok akademicki 009-0 Wektor zwiazan. Wektorem zwiazanm nazwam parę punktów. Jeżeli parę tę stanowią punkt,, wektor przez nie utworzon oznaczm. Graficznie koniec wektora oznaczam strzałką.
TEORIA SPRĘŻYSTOŚCI 10
 W YKŁ ADY Z T EOII S ĘŻYSTOŚCI ZADANIE BOUSSINESQA I FLAMANTA olitechnika onańska Kopac, Kawck, Łodgowski, łotkowiak, Świtek, Tmpe Olga Kopac, Kstof Kawck, Adam Łodgowski, Michał łotkowiak, Agnieska Świtek,
W YKŁ ADY Z T EOII S ĘŻYSTOŚCI ZADANIE BOUSSINESQA I FLAMANTA olitechnika onańska Kopac, Kawck, Łodgowski, łotkowiak, Świtek, Tmpe Olga Kopac, Kstof Kawck, Adam Łodgowski, Michał łotkowiak, Agnieska Świtek,
ANALIZA KONSTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY
 Cw3_biornik.doc ANALIZA KONTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY 1. W P R O W A D Z E N I E Ciało utworone pre dwie akrwione powierchnie nawane jest powłoką, jeśli preciętna odlełość pomięd
Cw3_biornik.doc ANALIZA KONTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY 1. W P R O W A D Z E N I E Ciało utworone pre dwie akrwione powierchnie nawane jest powłoką, jeśli preciętna odlełość pomięd
KINEMATYKA. Pojęcia podstawowe
 KINEMTYK Pojęcia podstawowe Kinematka jest diałem mechaniki ajmującm się badaniem uchu ciał be uwględniania pcn wwołującch ten uch. Jej celem jest opis tego uchu. Ruchem nawam mianę położenia ciała w odniesieniu
KINEMTYK Pojęcia podstawowe Kinematka jest diałem mechaniki ajmującm się badaniem uchu ciał be uwględniania pcn wwołującch ten uch. Jej celem jest opis tego uchu. Ruchem nawam mianę położenia ciała w odniesieniu
PITAGORAS ARYSTOTELES ERATOSTENES. Wprowadzenie. O kulistości Ziemi. Starożytni postulatorzy kulistości Ziemi
 O kulistości Ziemi Starożtni postulator kulistości Ziemi Wprowaenie PITAGOAS sugerował, iż Ziemia jest kstałtu kulistego. Jenak postulat ten opierał się racej na tm, iż kula bła uważana a figurę oskonałą,
O kulistości Ziemi Starożtni postulator kulistości Ziemi Wprowaenie PITAGOAS sugerował, iż Ziemia jest kstałtu kulistego. Jenak postulat ten opierał się racej na tm, iż kula bła uważana a figurę oskonałą,
Przykład 3.7. Naprężenia styczne przy zginaniu belki cienkościennej.
 Prkład.7. Naprężenia tcne pr ginaniu belki cienkościennej. Wnac rokład naprężenia tcnego w prekroju podporowm belki wpornikowej o prekroju cienkościennm obciążonej na wobodnm końcu pionową iłą P. Siła
Prkład.7. Naprężenia tcne pr ginaniu belki cienkościennej. Wnac rokład naprężenia tcnego w prekroju podporowm belki wpornikowej o prekroju cienkościennm obciążonej na wobodnm końcu pionową iłą P. Siła
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Płaska fala monochromatyczna
 Płaska fala onochroatcna Fala płaska propagująca się w owoln kierunku s P s s - fragent coła fali płaskiej propagującej się w kierunku efiniowan pre wersor s O r,, prawoskrętn ukła współręnch kartejańskich
Płaska fala onochroatcna Fala płaska propagująca się w owoln kierunku s P s s - fragent coła fali płaskiej propagującej się w kierunku efiniowan pre wersor s O r,, prawoskrętn ukła współręnch kartejańskich
i = [ 0] j = [ 1] k = [ 0]
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 INSTRUKCJA DO ĆWICZENIA NR 3. Optymalizacja wielowarstwowych płyt laminowanych
 Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 PRZEDMIOT TEMAT KATEDRA MECHANIKI STOSOWANEJ Wydiał Mechanicny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 3 1. CEL ĆWICZENIA Wybrane
Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 PRZEDMIOT TEMAT KATEDRA MECHANIKI STOSOWANEJ Wydiał Mechanicny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 3 1. CEL ĆWICZENIA Wybrane
WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASACH I - III GIMNAZJUM. Rok szkolny 2015/16
 WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASACH I - III GIMNAZJUM Rok skolny 2015/16 POZIOMY WYMAGAŃ EDUKACYJNYCH: (2) - ocena dopscająca (2); (3) - ocena dostatecna (3); (4) - ocena dobra (4);
WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASACH I - III GIMNAZJUM Rok skolny 2015/16 POZIOMY WYMAGAŃ EDUKACYJNYCH: (2) - ocena dopscająca (2); (3) - ocena dostatecna (3); (4) - ocena dobra (4);
Wielokryteriowa optymalizacja liniowa (WPL)
 arek isyński BO UŁ 007 - Wielokryteriowa optymaliaja liniowa (WPL) -. Wielokryteriowa optymaliaja liniowa (WPL) Zadaniem WPL naywamy następująe adanie optymaliaji liniowej: a a m L O L L O L L a a n n
arek isyński BO UŁ 007 - Wielokryteriowa optymaliaja liniowa (WPL) -. Wielokryteriowa optymaliaja liniowa (WPL) Zadaniem WPL naywamy następująe adanie optymaliaji liniowej: a a m L O L L O L L a a n n
Układy równań - Przykłady
 Układy równań - Prykłady Dany układ równań rowiąać trea sposobai: (a) korystając e worów Craera, (b) etodą aciery odwrotnej, (c) etodą eliinacji Gaussa, + y + = y = y = (a) Oblicy wynacnik deta aciery
Układy równań - Prykłady Dany układ równań rowiąać trea sposobai: (a) korystając e worów Craera, (b) etodą aciery odwrotnej, (c) etodą eliinacji Gaussa, + y + = y = y = (a) Oblicy wynacnik deta aciery
Adam Bodnar: Wytrzymałość Materiałów. Proste zginanie
 dam Bodnar: trmałość ateriałów. Proste ginanie. PROSTE GINNIE.. Naprężenia i odkstałcenia Proste ginanie pręta prmatcnego wstępuje wówcas gd układ sił ewnętrnch po jednej stronie jego prekroju poprecnego
dam Bodnar: trmałość ateriałów. Proste ginanie. PROSTE GINNIE.. Naprężenia i odkstałcenia Proste ginanie pręta prmatcnego wstępuje wówcas gd układ sił ewnętrnch po jednej stronie jego prekroju poprecnego
Przekształcenia geometryczne w grafice komputerowej. Marek Badura
 Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
Narzędzia kontroli wersji Subversion
 Narędia kontroli wersji Subversion Łukas Krak Akademia Górnico-Hutnica im. Stanisława Stasica w Krakowie, Wdiał Informatki, Elektroniki i Telekomunikacji Katedra Elektroniki www.wsn.agh.edu.pl Problem
Narędia kontroli wersji Subversion Łukas Krak Akademia Górnico-Hutnica im. Stanisława Stasica w Krakowie, Wdiał Informatki, Elektroniki i Telekomunikacji Katedra Elektroniki www.wsn.agh.edu.pl Problem
