Analiza szeregów czasowych: 4. Filtry liniowe
|
|
|
- Krzysztof Barański
- 8 lat temu
- Przeglądów:
Transkrypt
1 Analiza szeregów czasowych: 4. Filtry liniowe P. F. Góra semestr letni 2007/08
2 Filtry liniowe W dziedzinie fourierowskiej filtruje się bardzo prosto: oblicza się iloczyn transformat sygnału wejściowego i funkcji przejścia. W dziedzinie sygnału może to być bardziej skomplikowane: filtr FIR: x(t) r(t) y(t) filtr IIR: x(t) r(t) y(t) 4. Filtry liniowe 2
3 Funkcja przejścia Nawet jeśli filtr jest realizowany w dziedzinie sygnału, wygodnie jest go analizować w dziedzinie fourierowskiej. Każdy filtr liniowy w dziedzinie fourierowskiej przedstawiamy jako Y (f) = H(f)X(f). (1) Funkcję H(f) nazywam funkcja przejścia lub funkcja przenoszenia (transfer function). 4. Filtry liniowe 3
4 Terminologia H(f) = 0 dla f f 0 filtr dolnoprzepustowy. H(f) = 0 dla f f 0 filtr górnoprzepustowy. H(f) 0 dla f 1 f f 2 filtr pasmowo przepuszczajacy (bandpass). H(f) = 0 dla f 1 f f 2 filtr pasmowo zatrzymujacy (bandstop); jeżeli szerokość wycinanego pasma f 2 f 1 jest mała, zwany także notch filter. 4. Filtry liniowe 4
5 Ogólny filtr liniowy w dziedzinie sygnału ma postać y n = q k= s α k x n k + p k=1 β k y n k (2) x n jest (dyskretnym) sygnałem wejściowym, y n sygnałem wyjściowym. Jeśli s > 0, przyszłe wartości sygnału wejściowego sa potrzebne do określenia sygnału wyjściowego taki filtr nazywamy akauzalnym. Nie może on być zrealizowany on-line. Jeśli p = 0, filtr nazywa się filtrem FIR (ang. Finite Impulse Response) lub też filtrem średniej ruchomej (ang. moving average). Jeśli p > 0, filtr nazywa się filtrem IIR (ang. Infinite Impulse Response) lub też filtrem autoregresywnym (ang. autoregressive). 4. Filtry liniowe 5
6 Kauzalne filtry FIR Kauzalny filtr FIR ma postać y n = q k=0 α k x n k. (3) Jeżeli sygnał wejściowy jest stacjonarny, sygnał wyjściowy także jest stacjonarny. Liczbę q nazywamy rzędem filtru. 4. Filtry liniowe 6
7 Aby znaleźć funkcję przejścia filtru, liczymy transformatę Fouriera wyrażenia (3). Otrzymujemy = q k=0 Y m = 1 N 1 N N 1 1 α k N n=0 n=0 e 2πimn/N y n = 1 N 1 N e 2πimn/N x n k = q k=0 n=0 e 2πimn/N N 1 k 1 α k N n = k q k=0 α k x n k e 2πim(n +k)/n x n. (4) 4. Filtry liniowe 7
8 Na mocy założenia o okresowości wejściowego sygnału, x l x N l. Z drugiej strony, exp(2πim(n l)/n) = exp(2πim) exp(2πim( l)/n) = exp(2πim( l)/n). A zatem Y m = q k=0 α k e 2πimk/N 1 N 1 N e 2πimn /N x n } n =0 {{ } X m = q α k e 2πimk/N k=0 } {{ } H m X m. (5) m/n = m/(n ) = f m, gdzie f m jest m-ta dyskretna częstotliwościa fourierowska. Zatem 4. Filtry liniowe 8
9 Funkcja przejścia kauzalnego filtru FIR ma postać H(f m ) = q k=0 gdzie α(z) jest wielomianem stopnia q postaci α k ( e 2πif m ) k = α ( e 2πif m ), (6) α(z) = q k=0 α k z k. (7) Często dla wygody przyjmuje się, że = 1, czyli że krok próbkowania jest jednostka czasu. Wówczas można pominać w (6); należy jednak pamiętać, iż w tej konwencji częstotliwości sa wielkościami bezwymiarowymi, a przedziałem Nyquista jest [ 1/2, 1/2]. 4. Filtry liniowe 9
10 Funkcja przejścia filtru FIR Powyższe wyrazenie można bardzo łatwo uogólnić, rachunek jest niemalże taki sam: Funkcja przejścia dowolnego filtru FIR ma postać H(f m ) = q k= s α k ( e 2πif m ) k = α ( e 2πif m ), (8) gdzie α( ) oznacza teraz odpowiednia funkcję wymierna. 4. Filtry liniowe 10
11 Proste filtry dolno i górnoprzepustowe Rozważmy filtr Jego funkcja przejścia jest y n = 1 4 x n x n x n+1. (9) H c (f) = 1 4 e2πif e 2πif = cos 2πf = cos2 πf. (10) Analogicznie, funkcja przejścia filtru jest y n = 1 4 x n x n 1 4 x n+1. (11) H s (f) = 1 4 e2πif e 2πif = cos 2πf = sin2 πf. (12) 4. Filtry liniowe 11
12 1 Filtr (9) jest (kiepskim) filtrem dolnoprzepustowym. Filtr (11) jest (kiepskim) filtrem górnoprzepustowym. Funkcje przejścia: cos 2 πf 0.5 sin 2 πf f f 4. Filtry liniowe 12
13 Zwykła średnia ruchoma Również nieważona średnia ruchoma y n = 1 2l + 1 o funkcji przejścia ( xn l + x n l x n + + x n+l 1 + x n+l ), (13) H MA (f) = 1 2l + 1 jest kiepskim filtrem dolnoprzepustowym. (1 + 2 cos 2πf + 2 cos 4πf cos 2lπf) (14) 4. Filtry liniowe 13
14 Funkcje przejścia dla filtrów nieważonej średniej ruchomej 1 l=1 l=2 l=3 l= H MA (f) f 4. Filtry liniowe 14
15 Przykład zastosowania średniej ruchomej (szum porównywalny z sygnałem) Moving Averages l= 0 l= 1 l= 5 l=16 4. Filtry liniowe 15
16 Filtry różniczkujace Pierwsza pochodna: dg dx 1 ( g(x) g(x ) x 2 + ) g(x + ) g(x) = 1 1 g(x + ) g(x ) (15a) 2 2 y n = 1 2 x n x n 1 H(f) = i sin(2πf ) (15b) (15c) Druga pochodna: y n = 1 4 2x n x n x n 1 H(f) = 1 2 sin(πf ) (16a) (16b) 4. Filtry liniowe 16
17 Sygnal Pierwsza pochodna Druga pochodna y n n 4. Filtry liniowe 17
18 Sygnal Pierwsza pochodna Druga pochodna y n n 4. Filtry liniowe 18
19 Rola fazy funkcji przenoszenia W dziedzinie fourierowskiej Y (f) = H(f)X(f). (17) H(f) = R(f)e iφ(f), R(f) 0. Moduł funkcji przejścia osłabia/wzmacnia poszczególne częstości. Za co odpowiada faza φ(f)? Zauważmy, że filtr (9) jest filtrem akauzalnym, bardzo łatwo jednak znaleźć jego kauzalna wersję, wprowadzajac opóźnienie w czasie: y n = 1 4 x n x n x n (18) o funkcji przejścia H(f) = e 2πif cos 2 πf. (19) 4. Filtry liniowe 19
20 Funkcja ta różni się od funkcji przejścia filtru (9) tylko czynnikiem fazowym, sam zaś filtr (18) różni się od filtru (9) jedynie przesunięciem w czasie. Stad wniosek, iż czynnik fazowy w (19) odpowiada za to przesunięcie w czasie. Tak jest w istocie! Załóżmy, że faza funkcji przejścia zależy liniowo od częstotliwości, φ(f) = af. Obliczajac transformatę odwrotna znajdziemy y k (t) n H(f n )X(f n )e 2πif nk = n R(f n )e iaf n X(f n )e 2πif nk = n R(f n )X(f n )e 2πif n(k a), (20) co odpowiada przesunięciu w czasie o a kanałów. Zatem filtry o liniowej fazie wprowadzaja jednorodne przesunięcie w czasie. Filtry, które nie maja liniowej fazy, wprowadzaja różnice fazowe pomiędzy poszczególnymi składowymi fourierowskimi, co może być niepożadane. 4. Filtry liniowe 20
21 Projektowanie filtrów FIR Jeśli dany jest filtr FIR y n = q k=0 to wiadomo, że jego funkcja przejścia ma postać H(f m ) = q k=0 α k x n k, (21) α k ( e 2πif m ) k. (22) Zauważmy, że (22) jest (z dokładnościa do stałej) dyskretna transformata Fouriera filtru w dziedzinie czasowej. 4. Filtry liniowe 21
22 Problem odwrotny Na ogół mamy jednak do czynienia z problemem odwrotnym : Majac dana idealna funkcję przejścia H(f), dobrać współczynniki α k i rzad q filtru (21) tak, aby jego funkcja przejścia była możliwie najbliższa zakładanej funkcji idealnej. Problem odwrotny (ang. an inverse problem) to nazwa techniczna! 4. Filtry liniowe 22
23 Podejście intuicyjne Weź idealna funkcję przejścia H(f). Oblicz odwrotna transformatę Fouriera h(t) = 1/2 1/2 H(f)e 2πift df. (23) Zdyskretyzuj h(t) w tylu punktach, ile wynosi rzad filtru. To podejście na ogół nie działa. Na ogół dyskretyzuje się idealna funkcję przejścia i odwraca dyskretna transformatę celem znalezienia współczynników filtru, ale za cenę zniekształcenia funkcji przejścia. Dla = 1 częstość Nyquista wynosi 1/2. 4. Filtry liniowe 23
24 Przykład: Filtr dolnoprzepustowy Idealna funkcja przejścia wynosi H(f) = 1 f f 0 < 1/2, 0 f > f 0. (24) Funkcja przejścia w dziedzinie czasowej wynosi zatem h(t) = 1/2 1/2 H(f)e 2πift df = f 0 f 0 e 2πift df = sin 2πf 0 t πt. (25) Amplituda h(t) maleje bardzo powoli. Ostra krawędź zawiera wszystkie składowe fourierowskie. Trzeba albo wprowadzić arbitralne obcięcie, albo kombinować, na ogół domnażajac idealna funkcję przejścia przez pewna funkcję okna. 4. Filtry liniowe 24
25 0.4 Współczynniki dolnoprzepustowego filtru FIR a n n 4. Filtry liniowe 25
26 Współczynniki dolnoprzepustowych filtrów FIR z oknem Hanninga a n n 4. Filtry liniowe 26
27 Dolnoprzepustowe filtry FIR dyskretyzowane w różnej ilości punktów n= 8 n= 16 n= 32 n= 64 n= H(f) square Hanning 0.4 square Hanning 0.4 square Hanning 0.4 square Hanning 0.4 square Hanning f f f f f 4. Filtry liniowe 27
28 Uwagi Na ogół potrzeba wysokiego rzędu, aby filtr FIR był przyzwoity. Wprowadzenie funkcji okna zmniejsza gwałtowne oscylacje w pobliżu krawędzi (ripple), ale zwiększa obszar spadku/narastania funkcji przejścia (rolloff ). Projektowanie filtrów jest tyleż nauka, co sztuka. Projektujac filtr trzeba zwracać uwagę na ripple, roll-off, (nie)liniowość fazy, wymagania odnośnie pamięci i czasu przetwarzania. Zazwyczaj nie da się zoptymalizować wszystkich wymagań jednocześnie. Istnieje bardzo bogata literatura dotyczaca projektowania filtrów. 4. Filtry liniowe 28
29 Liniowy filtr IIR ma postać y n = q k= s α k x n k + p k=1 β k y n k, (26) gdzie p 1, x n jest (dyskretnym) sygnałem wejściowym, y n sygnałem wyjściowym. Dla wygody zapisu przyjmujemy, że filtr jest kauzalny (s = 0); dopuszczenie akauzalności niewiele zmienia w naszych rozważaniach. 4. Filtry liniowe 29
30 Problem Filtr IIR ma sprzężenie zwrotne. Oznacza to, że, w zasadzie, może on dawać niezerowe wyjście nieskończenie długo po ustaniu sygnału wejściowego. Jak temu zapobiec? Czy możemy być pewni, że jeśli sygnał wejściowy jest stacjonarny, to stacjonarny jest również sygnał wyjściowy? 4. Filtry liniowe 30
31 Liniowe równania różnicowe Jednorodne liniowe równanie różnicowe: z n = β 1 z n 1 + β 2 z n β p z n p (27) Niejednorodne liniowe równanie różnicowe: z n = β 1 z n 1 + β 2 z n β p z n p + ϕ (28) Twierdzenie: Rzowiazanie ogólne niejednorodnego liniowego równania różnicowego jest równe sumie rowiazania szczegółowego równania niejednorodnego i rozwiazania ogólnego równania jednorodnego. Dla badania stabilności filtrów IIR wystarczy zatem zajać się równaniami jednorodnymi. 4. Filtry liniowe 31
32 Zanurzenie w przestrzeni wielowymiarowej Zdefiniujmy z n = [z n, z n 1,..., z n p+1 ] T R p. Wówczas równanie (27) możemy zapisać w postaci z n = β 1 β 2 β 3 β p 1 β p z n 1. (29) Widać, że rozwiazanie równania (29) będzie stabilne (nie będzie wybuchać), jeśli wszystkie wartości własne będa na moduł mniejsze od Filtry liniowe 32
33 Wyznacznik charakterystyczny ma postać W p = det β 1 λ β 2 β 3 β p 1 β p 1 λ λ λ = λw p 1 + ( 1) p+1 β p = λ 2 W p 2 + ( 1) p+1 β p 1 λ + ( 1) p+1 β p =... = ( 1) p+1 ( λ p + β 1 λ p 1 + β 2 λ p 2 ) + + β p (30) Widzimy zatem, że Filtry liniowe 33
34 Warunek stabilności filtru IIR Filtr IIR (26) jest stabilny wtedy i tylko wtedy gdy pierwiastki równania λ p β 1 λ p 1 β 2 λ p 2 β p = 0 (31) leża wewnatrz okręgu jednostkowego. 4. Filtry liniowe 34
35 Konfuzja terminologiczna Czasami z powodów, które już za chwilę stana się oczywiste powyższy warunek formułuje się dla odwrotności λ, a zatem Filtr IIR (26) jest stabilny wtedy i tylko wtedy gdy pierwiastki równania 1 β 1 u β 2 u 2 β p u p = 0 (32) leża na zewnatrz okręgu jednostkowego. Warunki (31), (32) sa równoważne, ale trzeba uważać, żeby się nie pomylić. 4. Filtry liniowe 35
36 Przykład Rozważmy filtr y n = β 1 y n 1 + x n. (33) Jego wielomianem charaktesrystycznym jest β(z) = 1 β 1 z. (34) Widać, że jeśli β 1 > 1, y n wybucha, musi zatem być β 1 < 1, jednak w takiej sytuacji jedyny pierwiastek wielomianu charakterystycznego (34), równy 1/β 1, leży na zewnatrz przedziału (a więc i okręgu) jednostkowego. 4. Filtry liniowe 36
37 Funkcja przejścia filtru IIR Przekształcam wyrażenie (26) do postaci y n β 1 y n 1 β p y n p = α 0 x n + α 1 x n α q x n q, (35) a następnie, tak jak dla filtrów FIR, biorę transformatę Fouriera. Ostatecznie jako funkcję przejścia dostaję ( jest krokiem próbkowania) H(f m ) = q k=0 1 p j=1 α k ( e 2πif m ) k β j ( e 2πif m ) j. (36) Często przyjmuje się = 1. Wówczas przedział Nyquista wynosi [ 1/2, 1/2]. 4. Filtry liniowe 37
38 Projektowanie filtrów IIR Trudność w projektowaniu filtrów IIR polega na unikaniu biegunów prowadza- cych do niestabilności. Na ogół nie jest łatwo stwierdzić czy biegun leży na zewnatrz, czy też wewnatrz okręgu jednostkowego. Dlatego też używa się następujacej transformacji biliniowej: Obliczmy z 2 = 1 iw 1 + iw 1 + i w 1 i w z = 1 iw 1 + iw czyli w = i z 1 z + 1. (37) = 1 + i w iw + w 2 1 i w + iw + w 2 = 1 + w Im w 1 + w 2 2 Im w. (38) Dla stabilności filtru, dopuszczamy bieguny z 2 > 1. Z (38) wynika, że musi być Im w > 0. Po zastosowaniu transformacji (37), dopuszczamy jedynie bieguny leżace na górnej półpłaszczyźnie. 4. Filtry liniowe 38
39 Procedura projektowania filtru IIR Dana jest idealna funkcja przejścia H(f). Znajdujemy funkcję wymierna dostatecznie dobrze przybliżajac a H(f). Oznaczamy ja H(f). Musi być ona rzeczywista, nieujemna i ograniczona. Traktujemy ja jako funkcję zmiennej w, f w. Znajdujemy bieguny H(f). Połowa leżeć będzie na górnej, połowa na dolnej półpłaszczyźnie. Bierzemy tylko iloczyn członów z biegunami górnej półpłaszczyzny, podstawiamy f = i(z 1)/(z + 1), upraszczamy, identyfikujemy współczynniki. 4. Filtry liniowe 39
40 Przykład: Filt Butterwortha rzędu N Jak poprzednio, projektujemy filtr dolnoprzepustowy. Schodkowa funkcję przejścia przybliżamy za pomoca H(f) = ( f f 0 ) 2N, (39) gdzie f 0 jest częstotliwościa obcięcia. Filtr oparty na funkcji (39) nazywa się filtrem Butterwortha rzędu N. Bieguny funkcji (39) leża na okręgu o promieniu f 0, symetrycznie względem osi rzeczywistej. 4. Filtry liniowe 40
41 Najprostszym przybliżeniem jest przypadek N = 1. Mamy Bierzemy zatem ( f f ) 2 = i f 0 f + i 0 i f f 0 i. (40) if 0 f if 0 = if 0 i z 1 z+1 if 0 = f 0 f 0 z z 1 f 0 z f 0 = = f 0 1+f 0 + f 0 1+f 0 z 1 1 f 0 1+f 0 z f 0 f 0 z (1 + f 0 ) + (1 f 0 )z (41) Współczynnikami filtru sa α 0 = α 1 = f 0 /(1 + f 0 ), β 1 = (1 f 0 )/(1 + f 0 ). 4. Filtry liniowe 41
42 Po lewej: funkcja przejścia filtru Butterwortha rzędu pierwszego. W środku: funkcja przejścia filtru Butterwortha rzędu czwartego. Po prawej: faza filtru Butterwortha rzędu czwartego H(f) H(f) φ(f) f f f 4. Filtry liniowe 42
43 Najbardziej popularne typy filtrów 1. Filtr Butterwortha Zobacz wyżej (39). Pierwszych 2N 1 pochodnych H(f) znika w f = 0 filtr Butterwortha jest maksymalnie płaski. Bieguny leża na okręgu. Używany w zastosowaniach audio. 4. Filtry liniowe 43
44 2. Filtry Czebyszewa. Ma znacznie bardziej stromy spadek (rolloff ), ale pojawiaja się ripple. Sa dwa typy filtrów Czebyszewa, w zależności od tego, gdzie dopuszczamy ripple: Ripple w paśmie przenoszenia (passband): H(f) = Ripple w paśmie zatrzymywanym (stopband): H(f) = [T N (f/f p )] 2. (42) [ TN (f s /f p ) T N (f s /f) ] 2. (43) W powyższych wyrażeniach T N oznacza wielomian Czebyszewa stopnia N, f p oznacza (górna) granicę pasma przenoszenia, f s > f p oznacza (dolna) granicę pasma zatrzymywanego. 4. Filtry liniowe 44
45 Z uwagi na ripple, nie używa się go w zastosowaniach audio. Jest znakomity, jeśli pasmo przenoszenia obejmuje tylko jedna interesujac a częstotliwość na przykład gdy trzeba wyciać wyższe harmoniczne. 3. Filtry eliptyczne H(f) = [R N (f/f p )] 2, (44) gdzie R N jest pewna funkcja wymierna, w której zera licznika leża w przedziale [ 1/2, 1/2], zaś zera mianownika leża poza tym przedziałem, przy czym R N (1/z) = 1/R N (z). Bieguny takiego filtru leża na elipsie. 4. Filtry Bessela, o stałym opóźnieniu w paśmie przenoszenia. 4. Filtry liniowe 45
46 Wszystkie powyższe filtry daje się zrealizować analogowo. Projektowanie analogowych i cyfrowych filtrów IIR jest bardzo ważnym zagadnieniem w elektronice, telekomunikacji itp. Filtry IIR wymagaja znacznie niższego rzędu niż filtry FIR o podobnej dokładności. Bierze się to stad, że aproksymacja funkcjami wymiernymi jest lepsza od aproksymacji wielomianowej. 4. Filtry liniowe 46
Transformata Laplace a to przekształcenie całkowe funkcji f(t) opisane następującym wzorem:
 PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
Wprowadzenie. Spis treści. Analiza_sygnałów_-_ćwiczenia/Filtry
 Analiza_sygnałów_-_ćwiczenia/Filtry Spis treści 1 Wprowadzenie 2 Filtry cyfrowe: powtórka z wykładu 2.1 Działanie filtra w dziedzinie czasu 2.2 Nazewnictwo 2.3 Przejście do dziedziny częstości 2.3.1 Działanie
Analiza_sygnałów_-_ćwiczenia/Filtry Spis treści 1 Wprowadzenie 2 Filtry cyfrowe: powtórka z wykładu 2.1 Działanie filtra w dziedzinie czasu 2.2 Nazewnictwo 2.3 Przejście do dziedziny częstości 2.3.1 Działanie
Analiza szeregów czasowych: 7. Liniowe modele stochastyczne
 Analiza szeregów czasowych: 7. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Liniowe modele stochastyczne Niech {y n } N n=1 będzie pewnym ciagiem danych
Analiza szeregów czasowych: 7. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Liniowe modele stochastyczne Niech {y n } N n=1 będzie pewnym ciagiem danych
Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI)
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH
 ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
b n y k n T s Filtr cyfrowy opisuje się również za pomocą splotu dyskretnego przedstawionego poniżej:
 1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
Stabilność. Krzysztof Patan
 Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Analiza szeregów czasowych: 5. Liniowe modele stochastyczne
 Analiza szeregów czasowych: 5. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Dwa rodzaje modelowania 1. Modelowanie z pierwszych zasad. Znamy prawa
Analiza szeregów czasowych: 5. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Dwa rodzaje modelowania 1. Modelowanie z pierwszych zasad. Znamy prawa
Analiza szeregów czasowych: 2. Splot. Widmo mocy.
 Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
Filtrowanie a sploty. W powyższym przykładzie proszę zwrócić uwagę na efekty brzegowe. Wprowadzenie Projektowanie filtru Zadania
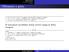 Filtrowanie a sploty idea x=[2222222222] %sygnałstochastycznyodługości5próbek h=[1111]/4; %Filtruśredniającypo4sąsiednichelementach y=conv(h,x)%zaaplikowaniefiltruhdosygnałux W powyższym przykładzie proszę
Filtrowanie a sploty idea x=[2222222222] %sygnałstochastycznyodługości5próbek h=[1111]/4; %Filtruśredniającypo4sąsiednichelementach y=conv(h,x)%zaaplikowaniefiltruhdosygnałux W powyższym przykładzie proszę
Przetwarzanie sygnałów
 Przetwarzanie sygnałów Ćwiczenie 5 Filtry o nieskończonej odpowiedzi impulsowej (NOI) Spis treści 1 Wprowadzenie 1 1.1 Filtry jednobiegunowe....................... 1 1.2 Filtry wąskopasmowe........................
Przetwarzanie sygnałów Ćwiczenie 5 Filtry o nieskończonej odpowiedzi impulsowej (NOI) Spis treści 1 Wprowadzenie 1 1.1 Filtry jednobiegunowe....................... 1 1.2 Filtry wąskopasmowe........................
Analiza szeregów czasowych: 2. Splot. Widmo mocy.
 Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
2. Próbkowanie Sygnały okresowe (16). Trygonometryczny szereg Fouriera (17). Częstotliwość Nyquista (20).
 SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
Wykład 3 Równania rózniczkowe cd
 7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Podstawowe człony dynamiczne
 . Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
. Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
Przetwarzanie sygnałów
 Przetwarzanie sygnałów Ćwiczenie 3 Filtry o skończonej odpowiedzi impulsowej (SOI) Spis treści 1 Filtracja cyfrowa podstawowe wiadomości 1 1.1 Właściwości filtru w dziedzinie czasu............... 1 1.2
Przetwarzanie sygnałów Ćwiczenie 3 Filtry o skończonej odpowiedzi impulsowej (SOI) Spis treści 1 Filtracja cyfrowa podstawowe wiadomości 1 1.1 Właściwości filtru w dziedzinie czasu............... 1 1.2
Przekształcanie równań stanu do postaci kanonicznej diagonalnej
 Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Wstęp do metod numerycznych Dyskretna transformacja Fouriera. P. F. Góra
 Wstęp do metod numerycznych Dyskretna transformacja Fouriera P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 01 Problem Majac dany szereg czasowy {x i } N i=1 = {x 1, x,..., x N } (zazwyczaj nieciekawy),
Wstęp do metod numerycznych Dyskretna transformacja Fouriera P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 01 Problem Majac dany szereg czasowy {x i } N i=1 = {x 1, x,..., x N } (zazwyczaj nieciekawy),
Analiza matematyczna dla informatyków 3 Zajęcia 14
 Analiza matematyczna dla informatyków 3 Zajęcia 14 Metoda rozwiązywania (Jednorodne równanie różniczkowe liniowe rzędu n o stałych współczynnikach). gdzie a 0,..., a n 1 C. Wielomian charakterystyczny:
Analiza matematyczna dla informatyków 3 Zajęcia 14 Metoda rozwiązywania (Jednorodne równanie różniczkowe liniowe rzędu n o stałych współczynnikach). gdzie a 0,..., a n 1 C. Wielomian charakterystyczny:
Równania różniczkowe liniowe wyższych rzędów o stałych współcz
 Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
FFT i dyskretny splot. Aplikacje w DSP
 i dyskretny splot. Aplikacje w DSP Marcin Jenczmyk m.jenczmyk@knm.katowice.pl Wydział Matematyki, Fizyki i Chemii 10 maja 2014 M. Jenczmyk Sesja wiosenna KNM 2014 i dyskretny splot 1 / 17 Transformata
i dyskretny splot. Aplikacje w DSP Marcin Jenczmyk m.jenczmyk@knm.katowice.pl Wydział Matematyki, Fizyki i Chemii 10 maja 2014 M. Jenczmyk Sesja wiosenna KNM 2014 i dyskretny splot 1 / 17 Transformata
Interpolacja. Marcin Orchel. Drugi przypadek szczególny to interpolacja trygonometryczna
 Interpolacja Marcin Orchel 1 Wstęp Mamy daną funkcję φ (x; a 0,..., a n ) zależną od n + 1 parametrów a 0,..., a n. Zadanie interpolacji funkcji φ polega na określeniu parametrów a i tak aby dla n + 1
Interpolacja Marcin Orchel 1 Wstęp Mamy daną funkcję φ (x; a 0,..., a n ) zależną od n + 1 parametrów a 0,..., a n. Zadanie interpolacji funkcji φ polega na określeniu parametrów a i tak aby dla n + 1
Akwizycja i przetwarzanie sygnałów cyfrowych
 Akwizycja i przetwarzanie sygnałów cyfrowych Instytut Teleinformatyki ITI PK Kraków 21 luty 2011 Analiza czas - częstotliwość analiza częstotliwościowa: problem dla sygnału niestacjonarnego zwykła transformata
Akwizycja i przetwarzanie sygnałów cyfrowych Instytut Teleinformatyki ITI PK Kraków 21 luty 2011 Analiza czas - częstotliwość analiza częstotliwościowa: problem dla sygnału niestacjonarnego zwykła transformata
Transformaty. Kodowanie transformujace
 Transformaty. Kodowanie transformujace Kodowanie i kompresja informacji - Wykład 10 10 maja 2009 Szeregi Fouriera Każda funkcję okresowa f (t) o okresie T można zapisać jako f (t) = a 0 + a n cos nω 0
Transformaty. Kodowanie transformujace Kodowanie i kompresja informacji - Wykład 10 10 maja 2009 Szeregi Fouriera Każda funkcję okresowa f (t) o okresie T można zapisać jako f (t) = a 0 + a n cos nω 0
Równania różnicowe. Dodatkowo umawiamy się, że powyższy iloczyn po pustym zbiorze indeksów, czyli na przykład 0
 Równania różnicowe 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp Zamiast tego pisać będziemy x (n), y (n) itp Ponadto
Równania różnicowe 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp Zamiast tego pisać będziemy x (n), y (n) itp Ponadto
Analiza szeregów czasowych: 6. Liniowe modele niestacjonarne
 Analiza szeregów czasowych: 6. Liniowe modele niestacjonarne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Warunki stacjonarności modelu AR(p) y n = β 1 y n 1 + β 2 y n 2 + + β
Analiza szeregów czasowych: 6. Liniowe modele niestacjonarne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Warunki stacjonarności modelu AR(p) y n = β 1 y n 1 + β 2 y n 2 + + β
Liczby zespolone. x + 2 = 0.
 Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 7a. Metody wielokrokowe
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 7a. Metody wielokrokowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Motywacja Metody wielokrokowe sa
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 7a. Metody wielokrokowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Motywacja Metody wielokrokowe sa
1 Równania różniczkowe zwyczajne o rozdzielonych zmiennych
 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transform
 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. March 20, 2013 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. Sygnał i system Sygnał jest opisem
Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. March 20, 2013 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. Sygnał i system Sygnał jest opisem
Przetwarzanie sygnałów dyskretnych
 Przetwarzanie sygnałów dyskretnych System dyskretny p[ n ] r[ n] Przykłady: [ ] = [ ] + [ ] r n a p n a p n [ ] r n = 2 [ + ] + p[ n ] p n 2 r[ n] = a p[ n] + b n [ ] = [ ] r n a p n n [ ] = [ + ] r n
Przetwarzanie sygnałów dyskretnych System dyskretny p[ n ] r[ n] Przykłady: [ ] = [ ] + [ ] r n a p n a p n [ ] r n = 2 [ + ] + p[ n ] p n 2 r[ n] = a p[ n] + b n [ ] = [ ] r n a p n n [ ] = [ + ] r n
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Kompresja Danych. Streszczenie Studia Dzienne Wykład 13, f(t) = c n e inω0t, T f(t)e inω 0t dt.
 1 Kodowanie podpasmowe Kompresja Danych Streszczenie Studia Dzienne Wykład 13, 18.05.2006 1.1 Transformaty, próbkowanie i filtry Korzystamy z faktów: Każdą funkcję okresową można reprezentować w postaci
1 Kodowanie podpasmowe Kompresja Danych Streszczenie Studia Dzienne Wykład 13, 18.05.2006 1.1 Transformaty, próbkowanie i filtry Korzystamy z faktów: Każdą funkcję okresową można reprezentować w postaci
9. Dyskretna transformata Fouriera algorytm FFT
 Transformata Fouriera ma szerokie zastosowanie w analizie i syntezie układów i systemów elektronicznych, gdyż pozwala na połączenie dwóch sposobów przedstawiania sygnałów reprezentacji w dziedzinie czasu
Transformata Fouriera ma szerokie zastosowanie w analizie i syntezie układów i systemów elektronicznych, gdyż pozwala na połączenie dwóch sposobów przedstawiania sygnałów reprezentacji w dziedzinie czasu
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
Filtracja. Krzysztof Patan
 Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
Technika audio część 2
 Technika audio część 2 Wykład 12 Projektowanie cyfrowych układów elektronicznych Mgr inż. Łukasz Kirchner lukasz.kirchner@cs.put.poznan.pl http://www.cs.put.poznan.pl/lkirchner Wprowadzenie do filtracji
Technika audio część 2 Wykład 12 Projektowanie cyfrowych układów elektronicznych Mgr inż. Łukasz Kirchner lukasz.kirchner@cs.put.poznan.pl http://www.cs.put.poznan.pl/lkirchner Wprowadzenie do filtracji
Równania różniczkowe liniowe II rzędu
 Równania różniczkowe liniowe II rzędu Definicja równania różniczkowego liniowego II rzędu Warunki początkowe dla równania różniczkowego II rzędu Równania różniczkowe liniowe II rzędu jednorodne (krótko
Równania różniczkowe liniowe II rzędu Definicja równania różniczkowego liniowego II rzędu Warunki początkowe dla równania różniczkowego II rzędu Równania różniczkowe liniowe II rzędu jednorodne (krótko
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Metoda eliminacji Gaussa. Autorzy: Michał Góra
 Metoda eliminacji Gaussa Autorzy: Michał Góra 9 Metoda eliminacji Gaussa Autor: Michał Góra Przedstawiony poniżej sposób rozwiązywania układów równań liniowych jest pewnym uproszczeniem algorytmu zwanego
Metoda eliminacji Gaussa Autorzy: Michał Góra 9 Metoda eliminacji Gaussa Autor: Michał Góra Przedstawiony poniżej sposób rozwiązywania układów równań liniowych jest pewnym uproszczeniem algorytmu zwanego
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Liczby zespolone. P. F. Góra (w zastępstwie prof. K. Rościszewskiego) 27 lutego 2007
 Liczby zespolone P. F. Góra (w zastępstwie prof. K. Rościszewskiego) http://th-www.if.uj.edu.pl/zfs/gora/ 27 lutego 2007 Definicja C zbiór par liczb rzeczywistych w którym określono następujace działania:
Liczby zespolone P. F. Góra (w zastępstwie prof. K. Rościszewskiego) http://th-www.if.uj.edu.pl/zfs/gora/ 27 lutego 2007 Definicja C zbiór par liczb rzeczywistych w którym określono następujace działania:
KOMPUTEROWE SYSTEMY POMIAROWE
 KOMPUTEROWE SYSTEMY POMIAROWE Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMST - ITwE Semestr zimowy Wykład nr 12 Prawo autorskie Niniejsze
KOMPUTEROWE SYSTEMY POMIAROWE Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMST - ITwE Semestr zimowy Wykład nr 12 Prawo autorskie Niniejsze
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
WSTĘP DO ELEKTRONIKI
 WSTĘP DO ELEKTRONIKI Część VI Sprzężenie zwrotne Wzmacniacz operacyjny Wzmacniacz operacyjny w układach z ujemnym i dodatnim sprzężeniem zwrotnym Janusz Brzychczyk IF UJ Sprzężenie zwrotne Sprzężeniem
WSTĘP DO ELEKTRONIKI Część VI Sprzężenie zwrotne Wzmacniacz operacyjny Wzmacniacz operacyjny w układach z ujemnym i dodatnim sprzężeniem zwrotnym Janusz Brzychczyk IF UJ Sprzężenie zwrotne Sprzężeniem
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Systemy. Krzysztof Patan
 Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Wykład z równań różnicowych
 Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Własności wyznacznika
 Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
13.2. Filtry cyfrowe
 Bibliografia: 1. Chassaing Rulph, Digital Signal Processing and Applications with the C6713 and C6416 DSK, Wiley-Interscience 2005. 2. Borodziewicz W., Jaszczak K., Cyfrowe Przetwarzanie sygnałów, Wydawnictwo
Bibliografia: 1. Chassaing Rulph, Digital Signal Processing and Applications with the C6713 and C6416 DSK, Wiley-Interscience 2005. 2. Borodziewicz W., Jaszczak K., Cyfrowe Przetwarzanie sygnałów, Wydawnictwo
Spis treści. Metody nieparametryczne. Transformacja Fouriera
 Spis treści 1 Metody nieparametryczne 1.1 Transformacja Fouriera 1.2 Bliżej życia 1.3 Splot 2 Transformacja Z 3 Filtry 4 Metody parametryczne 5 Analiza danych wielokanałowych 5.1 Koherencje 5.2 Związki
Spis treści 1 Metody nieparametryczne 1.1 Transformacja Fouriera 1.2 Bliżej życia 1.3 Splot 2 Transformacja Z 3 Filtry 4 Metody parametryczne 5 Analiza danych wielokanałowych 5.1 Koherencje 5.2 Związki
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Algebra liniowa II. Lista 1. 1 u w 0 1 v 0 0 1
 Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
A-2. Filtry bierne. wersja
 wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
INTERPOLACJA I APROKSYMACJA FUNKCJI
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Wprowadzenie Na czym polega interpolacja? Interpolacja polega
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Wprowadzenie Na czym polega interpolacja? Interpolacja polega
Kartkówka 1 Opracowanie: Próbkowanie częstotliwość próbkowania nie mniejsza niż podwojona szerokość przed spróbkowaniem.
 Znowu prosta zasada - zbierzmy wszystkie zagadnienia z tych 3ech kartkówek i opracujmy - może się akurat przyda na dopytkę i uda się zaliczyć labki :) (dodatkowo można opracowania z tych rzeczy z doc ów
Znowu prosta zasada - zbierzmy wszystkie zagadnienia z tych 3ech kartkówek i opracujmy - może się akurat przyda na dopytkę i uda się zaliczyć labki :) (dodatkowo można opracowania z tych rzeczy z doc ów
Podstawy Automatyki. wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak. Politechnika Wrocławska. Instytut Technologii Maszyn i Automatyzacji (I-24)
 Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych
 Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Równania poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie = Rozwiąż układ równań: (( + 1 ( + 2 = = 1
 Równania poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/). Rozwiąż układ równań: (( + ( + 2 = 3 = 4. http://www.zadania.info/d38/2287 2. Rozwiąż układ równań: ( + 2 (
Równania poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/). Rozwiąż układ równań: (( + ( + 2 = 3 = 4. http://www.zadania.info/d38/2287 2. Rozwiąż układ równań: ( + 2 (
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa. P. F. Góra
 Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
DYSKRETNE PRZEKSZTAŁCENIE FOURIERA C.D.
 CPS 6 DYSKRETE PRZEKSZTAŁCEIE FOURIERA C.D. Twierdzenie o przesunięciu Istnieje ważna właściwość DFT, znana jako twierdzenie o przesunięciu. Mówi ono, że: Przesunięcie w czasie okresowego ciągu wejściowego
CPS 6 DYSKRETE PRZEKSZTAŁCEIE FOURIERA C.D. Twierdzenie o przesunięciu Istnieje ważna właściwość DFT, znana jako twierdzenie o przesunięciu. Mówi ono, że: Przesunięcie w czasie okresowego ciągu wejściowego
VI. Równania różniczkowe liniowe wyższych rzędów
 VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
8. Realizacja projektowanie i pomiary filtrów IIR
 53 8. Realizacja projektowanie i pomiary filtrów IIR Cele ćwiczenia Realizacja na zestawie TMX320C5515 ezdsp prostych liniowych filtrów cyfrowych. Pomiary charakterystyk amplitudowych zrealizowanych filtrów
53 8. Realizacja projektowanie i pomiary filtrów IIR Cele ćwiczenia Realizacja na zestawie TMX320C5515 ezdsp prostych liniowych filtrów cyfrowych. Pomiary charakterystyk amplitudowych zrealizowanych filtrów
Przekształcenia widmowe Transformata Fouriera. Adam Wojciechowski
 Przekształcenia widmowe Transformata Fouriera Adam Wojciechowski Przekształcenia widmowe Odmiana przekształceń kontekstowych, w których kontekstem jest w zasadzie cały obraz. Za pomocą transformaty Fouriera
Przekształcenia widmowe Transformata Fouriera Adam Wojciechowski Przekształcenia widmowe Odmiana przekształceń kontekstowych, w których kontekstem jest w zasadzie cały obraz. Za pomocą transformaty Fouriera
Równania różniczkowe liniowe rzędu pierwszego
 Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Laboratorium nr 4: Porównanie filtrów FIR i IIR. skończonej odpowiedzi impulsowej (FIR) zawsze stabilne, mogą mieć liniową charakterystykę fazową
 Teoria Sygnałów sprawozdanie z zajęć laboratoryjnych Zajęcia z dnia 07.01.2009 Prowadzący: dr inż. Stanisław Nuckowski Sprawozdanie wykonał: Tomasz Witka Laboratorium nr 4: Porównanie filtrów FIR i IIR
Teoria Sygnałów sprawozdanie z zajęć laboratoryjnych Zajęcia z dnia 07.01.2009 Prowadzący: dr inż. Stanisław Nuckowski Sprawozdanie wykonał: Tomasz Witka Laboratorium nr 4: Porównanie filtrów FIR i IIR
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM
 ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
Wykład z równań różnicowych
 Wykład z równań różnicowych Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp. Definicja 1. Operatorem
Wykład z równań różnicowych Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp. Definicja 1. Operatorem
Cyfrowe przetwarzanie sygnałów Jacek Rezmer -1-
 Cyfrowe przetwarzanie sygnałów Jacek Rezmer -1- Filtry cyfrowe cz. Zastosowanie funkcji okien do projektowania filtrów SOI Nierównomierności charakterystyki amplitudowej filtru cyfrowego typu SOI można
Cyfrowe przetwarzanie sygnałów Jacek Rezmer -1- Filtry cyfrowe cz. Zastosowanie funkcji okien do projektowania filtrów SOI Nierównomierności charakterystyki amplitudowej filtru cyfrowego typu SOI można
Zmiany fazy/okresu oscylacji Chandlera i rocznej we współrzędnych bieguna ziemskiego.
 Strona 1 z 27 Zmiany fazy/okresu oscylacji Chandlera i rocznej we współrzędnych bieguna ziemskiego. Alicja Rzeszótko Wiesław Kosek Waldemar Popiński Seminarium Sekcji Dynamiki Ziemi Komitetu Geodezji PAN
Strona 1 z 27 Zmiany fazy/okresu oscylacji Chandlera i rocznej we współrzędnych bieguna ziemskiego. Alicja Rzeszótko Wiesław Kosek Waldemar Popiński Seminarium Sekcji Dynamiki Ziemi Komitetu Geodezji PAN
Rozwiązania zadań z kolokwium w dniu r. Zarządzanie Inżynierskie, WDAM, grupy I i II
 Rozwiązania zadań z kolokwium w dniu 10.1.010r. Zarządzanie Inżynierskie, WDAM, grupy I i II Zadanie 1. Wyznacz dziedzinę naturalną funkcji f (x) = x 4x + 3 x + x + log arc sin 1 x. Rozwiązanie. Wymagane
Rozwiązania zadań z kolokwium w dniu 10.1.010r. Zarządzanie Inżynierskie, WDAM, grupy I i II Zadanie 1. Wyznacz dziedzinę naturalną funkcji f (x) = x 4x + 3 x + x + log arc sin 1 x. Rozwiązanie. Wymagane
uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem próbkowania t takim, że T = t N 1 t
 4. 1 3. " P r ze c ie k " w idm ow y 1 0 2 4.13. "PRZECIEK" WIDMOWY Rozważmy szereg czasowy {x r } dla r = 0, 1,..., N 1 uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem
4. 1 3. " P r ze c ie k " w idm ow y 1 0 2 4.13. "PRZECIEK" WIDMOWY Rozważmy szereg czasowy {x r } dla r = 0, 1,..., N 1 uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem
Rozwiązaniem jest zbiór (, ] (5, )
![Rozwiązaniem jest zbiór (, ] (5, ) Rozwiązaniem jest zbiór (, ] (5, )](/thumbs/62/48086093.jpg) FUNKCJE WYMIERNE Definicja Miech L() i M() będą niezerowymi wielomianami i niech D { R : M( ) 0 } Funkcję (*) D F : D R określoną wzorem F( ) L( ) M( ) nazywamy funkcją wymierną Funkcja wymierna, to iloraz
FUNKCJE WYMIERNE Definicja Miech L() i M() będą niezerowymi wielomianami i niech D { R : M( ) 0 } Funkcję (*) D F : D R określoną wzorem F( ) L( ) M( ) nazywamy funkcją wymierną Funkcja wymierna, to iloraz
Zaawansowane metody numeryczne
 Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
SYNTEZA obwodów. Zbigniew Leonowicz
 SYNTEZA obwodów Zbigniew Leonowicz Literatura: [1]. S. Bolkowski Elektrotechnika teoretyczna. Tom I. WNT Warszawa 1982 (s.420-439) [2]. A. Cichocki, K.Mikołajuk, S. Osowski, Z. Trzaska: Zbiór zadań z elektrotechniki
SYNTEZA obwodów Zbigniew Leonowicz Literatura: [1]. S. Bolkowski Elektrotechnika teoretyczna. Tom I. WNT Warszawa 1982 (s.420-439) [2]. A. Cichocki, K.Mikołajuk, S. Osowski, Z. Trzaska: Zbiór zadań z elektrotechniki
Promieniowanie dipolowe
 Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Teoria sygnałów Signal Theory. Elektrotechnika I stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny)
 . KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Teoria sygnałów Signal Theory A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Teoria sygnałów Signal Theory A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
LINIOWE UKŁADY DYSKRETNE
 LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
Analiza szeregów czasowych: 3. Filtr Wienera
 Analiza szeregów czasowych: 3. Filtr Wienera P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Filtr Wienera ( filtr optymalny ) Przypuśćmy, że pewien układ (fizyczny, biologiczny,
Analiza szeregów czasowych: 3. Filtr Wienera P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Filtr Wienera ( filtr optymalny ) Przypuśćmy, że pewien układ (fizyczny, biologiczny,
Ćwiczenie 3. Właściwości przekształcenia Fouriera
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Liniowe układy scalone. Filtry aktywne w oparciu o wzmacniacze operacyjne
 Liniowe układy scalone Filtry aktywne w oparciu o wzmacniacze operacyjne Wiadomości ogólne (1) Zadanie filtrów aktywnych przepuszczanie sygnałów znajdujących się w pewnym zakresie częstotliwości pasmo
Liniowe układy scalone Filtry aktywne w oparciu o wzmacniacze operacyjne Wiadomości ogólne (1) Zadanie filtrów aktywnych przepuszczanie sygnałów znajdujących się w pewnym zakresie częstotliwości pasmo
Rozwiązania zadań z kolokwium w dniu r. Zarządzanie Licencjackie, WDAM, grupy I i II
 Rozwiązania zadań z kolokwium w dniu 15.1.010r. Zarządzanie Licencjackie, WDAM, grupy I i II Zadanie 1. Wyznacz dziedzinę naturalną funkcji f x) = arc cos x x + x 5 ) ) log x + 5. Rozwiązanie. Wymagane
Rozwiązania zadań z kolokwium w dniu 15.1.010r. Zarządzanie Licencjackie, WDAM, grupy I i II Zadanie 1. Wyznacz dziedzinę naturalną funkcji f x) = arc cos x x + x 5 ) ) log x + 5. Rozwiązanie. Wymagane
Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems)
 Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems) P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Wprowadzenie Rozważmy
Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems) P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Wprowadzenie Rozważmy
Funkcje wymierne. Jerzy Rutkowski. Działania dodawania i mnożenia funkcji wymiernych określa się wzorami: g h + k l g h k.
 Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
Wstęp do metod numerycznych Rozwiazywanie równań algebraicznych. P. F. Góra
 Wstęp do metod numerycznych Rozwiazywanie równań algebraicznych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2010 Co to znaczy rozwiazać równanie? Przypuśmy, że postawiono przed nami problem rozwiazania
Wstęp do metod numerycznych Rozwiazywanie równań algebraicznych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2010 Co to znaczy rozwiazać równanie? Przypuśmy, że postawiono przed nami problem rozwiazania
CZWÓRNIKI KLASYFIKACJA CZWÓRNIKÓW.
 CZWÓRNK jest to obwód elektryczny o dowolnej wewnętrznej strukturze połączeń elementów, mający wyprowadzone na zewnątrz cztery zaciski uporządkowane w dwie pary, zwane bramami : wejściową i wyjściową,
CZWÓRNK jest to obwód elektryczny o dowolnej wewnętrznej strukturze połączeń elementów, mający wyprowadzone na zewnątrz cztery zaciski uporządkowane w dwie pary, zwane bramami : wejściową i wyjściową,
