Przetwarzanie sygnałów
|
|
|
- Izabela Murawska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Przetwarzanie sygnałów Ćwiczenie 5 Filtry o nieskończonej odpowiedzi impulsowej (NOI) Spis treści 1 Wprowadzenie Filtry jednobiegunowe Filtry wąskopasmowe Filtry Czebyszewa Pytania na kartkówkę 4 3 Zadania do realizacji Implementacja filtra NOI Funkcje obliczające odpowiedzi filtra Funkcje wyliczające współczynniki filtrów NOI Filtry Czebyszewa Filtr sinc dr hab. inż. Grzegorz Jóźwiak, dr hab. inż. Tomasz Piasecki (tomasz.piasecki@pwr.edu.pl)
2 1 Wprowadzenie Do realizacji ćwiczenia 5 niezbędne są podstawowe wiadomości o filtracji cyfrowej zawarte w rozdziale 1 instrukcji do ćwiczenia 4. Zasadniczą różnicą między filtrami o nieskończonej odpowiedzi impulsowej (NOI) a filtrami o skończonej odpowiedzi impulsowej (SOI) jest fakt, że do filtracji za pomocą filtrów SOI wykorzystuje się tylko próbki pobudzenia, natomiast filtry NOI wykorzystują do obliczeń wartości próbek odpowiedzi, które algorytm filtracji wygenerował w przeszłości. Stąd filtry NOI nazywane są często filtrami rekursywnymi. Poniższe równanie jest jedną z możliwych wyrażeń definiujących sposób przetwarzania informacji przez filtr NOI. a 0 y[n] = b 0 x[n] + b 1 x[n 1] + + b Ma x[n M a ]+ a 1 y[n 1] a 2 y[n 2] a Mb y[n M b ] gdzie: n numer próbki, b k współczynnik k dla sygnału wejściowego, a k współczynnik k dla sygnału wyjściowego. Ta postać jest wykorzystywana przez funkcje pakietu Origin związane z projektowaniem filtrów NOI. Filtry NOI charakteryzują się gorszymi parametrami użytkowymi takimi jak tłumienie w paśmie zaporowym czy zafalowania w paśmie przepustowym, ale ze względu na niewielką liczbę współczynników, redukującą znacznie ilość niezbędnych obliczeń, odznaczają się znacznie większą szybkością działania w porównaniu z filtrami SOI. Cyfrowe filtry rekursywne projektowane są z wykorzystaniem transformaty Z. Transformata ta umożliwia przekształcenie równań różnicowych (takich jak (1)) na równania algebraiczne. Jest to możliwe dzięki podanej niżej właściwości przekształcenia Z. jeżeli Z{x[n]} = X(z), to Z{x[n k]} = z k X(z) (2) Wówczas równanie zapisane w dziedzinie czasu (numerów próbek) w postaci: może być przekształcone do postaci w dziedzinie zmiennej z: y[n] = 0, 1x[n] + 0, 9y[n 1] (3) Y (z) = 0, 1X(z) + 0, 9z 1 Y (z) (4) Wyrażenie to można następnie przekształcić w taki sposób, aby uzyskać transmitancję H(z) = Y (z)/x(z): 0, 1 0, 1z H(z) = = (5) 1 0, 9z 1 z 0, 9 Transmitancja H(z) jest zespoloną funkcją wymierną (zarówno z jak i H(z) są liczbami zespolonymi). Wielomiany licznika i mianownika mają swoje miejsca zerowe. Położenie tych punktów osobliwych w przestrzeni zmiennej z wpływa na odpowiedź częstotliwościową filtru. W przestrzeni zmiennej z odpowiedź częstotliwościowa znajduje się na okręgu jednostkowym o promieniu 1 (rys. 1). 1.1 Filtry jednobiegunowe Filtr jednobiegunowy posiada jeden biegun na płaszczyźnie transformaty Z. Do jego budowy za pomocą metody rekursywnej stosuje się tylko dwa współczynniki dla filtru dolnoprzepustowego: b 0 = 1 x a 1 = x 1 (1) (6)
3 H(z) = 0, z 1 H(z) = 0, z 1 H(z) = 0, z 1 H(f) = H(z = e j2πf = 0, e j2πf H(f) = H(z = e j2πf = 0, e j2πf H(f) = H(z = e j2πf = 0, e j2πf Rysunek 1: Ilustracja wpływu położenia bieguna filtru na charakterystykę częstotliwościową H(f) (wykresy przedstawiają moduł transmitancji i odpowiedzi częstotliwościowej): z lewej strony biegun położony jest najbliżej linii okręgu jednostkowego, z prawej strony najdalej. Żeby filtr był stabilny, wszystkie jego bieguny muszą znajdować wewnątrz tego okręgu. Im więcej biegunów, tym łatwiej kształtować charakterystykę filtru. oraz trzy współczynniki dla filtru górnoprzepustowego: b 0 = (1 + x)/2 b 1 = (1 + x)/2 a 1 = x (7) gdzie parametr x opisuje szybkość zmian między kolejnymi próbkami i powinien mieścić się w przedziale (0, 1). Z częstotliwością odcięcia f c (równą od 0 do 0,5 częstotliwości próbkowania) filtru łączy go zależność w postaci x = e 2πfc (8) Odpowiedź skokowa tego filtru nie ma przerzutu i dzwonienia. Parametr x umożliwia projektowanie filtru o zadanej stałej czasowej narastania d: x = e 1 d (9) wyrażonej w liczbie próbek. Aby poprawić charakterystykę częstotliwościową filtru jednobiegunowego można przeprowadzić filtrację wielokrotną. 1.2 Filtry wąskopasmowe Filtry wąskopasmowe należą do grupy filtrów NOI, które umożliwiają wydzielenie bardzo wąskiego pasma częstotliwości z widma sygnału wejściowego. Dzielą się na filtry pasmowoprzepustowe i pasmowozaporowe. Ich współczynniki można wyznaczyć ze wzorów: 1 2R cos(2πf) + R2 K = 2 2 cos(2πf) (10) R = 1 3BW (11) 2
4 Parametry filtru pasmowoprzepustowego: Parametry filtru pasmowozaporowego: b 0 = 1 K b 0 = K b 1 = 2(K R) cos(2πf) b 1 = 2K cos(2πf) b 2 = R 2 K (12) b 2 = K (13) a 1 = 2R cos(2πf) a 1 = 2R cos(2πf) a 2 = R 2 a 2 = R 2 gdzie: BW - szerokość pasma (zaporowego lub przepustowego), f - częstotliwość środkowa filtru (częstotliwość środka pasma zaporowego lub przepustowego). Podobnie jak w przypadku filtrów jednobiegunowych, w celu poprawienia charakterystyki częstotliwościowej filtrów wąskopasmowych można łączyć je kaskadowo. UWAGA: Zarówno częstotliwość odcięcia, jak i pasmo przenoszenia filtru definiuje się jako ułamek częstotliwości próbkowania, więc ich wartości muszą mieścić się w przedziale od 0 do 0, Filtry Czebyszewa Filtry Czebyszewa charakteryzują się szybką charakterystyką opadania (wąskim pasmem przejściowym) i często są wykorzystywane do rozdzielania pasm częstotliwości. Niekorzystnym zjawiskiem występującym w odpowiedzi częstotliwościowej filtru Czebyszewa są zafalowania w paśmie przepustowym, przy czym im większe są zafalowania, tym węższe jest pasmo przejściowe filtru. Bez zwiększania poziomu zafalowań można zmniejszyć szerokość pasma przejściowego poprzez zwiększenie liczby biegunów filtru. Filtry Czebyszewa projektowane są metodą transformacji biliniowej na podstawie ich analogowych prototypów. Z kolei analogowy filtr Czebyszewa to filtr, który posiada bieguny rozmieszczone równomiernie na lewym półokręgu o środku w punkcie (0,0) przestrzeni s transformaty Laplace a. Procedura projektowania może być zrealizowana przez algorytm numeryczny, dlatego filtry tego typu projektuje się z wykorzystaniem specjalistycznego oprogramowania. W środowisku Octave można wykorzystać funkcję cheby1. Projekt filtru Czebyszewa wymaga podania czterech parametrów: rodzaju odpowiedzi (dolno lub górnoprzepustowej, pasmowoprzepustowej czy pasmowo zaporowej), częstotliwości odcięcia (definiowana od 0 do 0,5 częstotliwości próbkowania), poziomu zafalowań w paśmie przepustowym wyrażonej w db lub %, liczby biegunów. Poniżej przedstawiono przykłady użycia funkcji cheby1 środowiska Octave. [b, a] = cheby1(n, Rp, Wc) projektuje filtr dolnoprzepustowy przy czym: n - rząd filtru, Rp- poziom zafalowań w db, W c- częstotliwość odcięcia jako ułamek połowy częstotliwości próbkowania (np. 0,5 oznacza 0,25 częstotliwości próbkowania), [b, a] = cheby1(n, Rp, Wc, high ) filtr górnoprzepustowy. [b, a] = cheby1(n, Rp, [Wl, Wh]) projektuje filtr pasmowoprzepustowy, w którym pasmo przepustowe jest od W l do W h (wyrażone w ułamku połowy częstotliwości próbkowania, wartości 0,4 i 0,6 oznaczają pasmo przepustowe od 0,2 do 0,3 częstotliwości próbkowania), [b, a] = cheby1(n, Rp, [Wl, Wh], stop ) filtr pasmowozaporowy. Najczęściej zawartość procentową ustala się na poziomie 0,5%, natomiast w skali logarytmicznej typowo stosuje się 0,05 db. 3
5 2 Pytania na kartkówkę 1. Jakie wartości będą na osi odciętych dla charakterystyk czasowych a jakie dla częstotliwościowych? 2. Jak będą wyglądały osie odciętych charakterystyk czasowych i częstotliwościowych filtrów cyfrowych przetwarzających sygnały próbkowane z częstotliwością 1 khz? 3. Jaką częstotliwość odcięcia w hercach będzie miał dolnoprzepustowy filtr NOI, jeżeli zaprojektowano go dla częstotliwości odcięcia znormalizowanej fc=0,1, a częstotliwość próbkowania filtrowanego sygnału wynosi fs=1khz? 4. Dla jakiej częstotliwości odcięcia należy zaprojektować dolnoprzepustowy filtr NOI, aby z sygnału próbkowanego z częstotliwością fs=1khz usunąć wszystkie składowe powyżej 200 Hz? 5. Jak poprawić tłumienie w paśmie zaporowym filtru jednobiegunowego? 6. Zaprojektuj filtr jednobiegunowy górnoprzepustowy o częstotliwości odcięcia 0,1. 7. Zaprojektuj filtr jednobiegunowy dolnoprzepustowy o częstotliwości odcięcia 0,2. 8. Zaprojektuj filtr jednobiegunowy górnoprzepustowy o stałej czasowej równej 3 próbkom. 9. Zaprojektuj filtr jednobiegunowy dolnoprzepustowy o stałej czasowej równej 2 próbkom. 10. Jak zmniejszyć szerokość pasma przejściowego filtru Czebyszewa bez zwiększania poziomu zafalowań? 11. Jakiego filtru rekursywnego należy użyć, aby uniknąć przerzutu i dzwonienia odpowiedzi skokowej? 3 Zadania do realizacji W trakcie zajęć należy rozwiązać pięć podanych poniżej zadań. Za każde zadanie można otrzymać jeden punkt pod warunkiem, że zostanie ono całkowicie poprawnie zrealizowane. 3.1 Implementacja filtra NOI Zadanie polega na napisaniu funkcji postaci: function y = iir_filter(b, a, x) która będzie realizowała filtrowanie rekursywne próbek wejściowych x z wykorzystaniem współczynników a oraz b. Wyniki działania funkcji należy przedstawić prezentując charakterystyki filtrów projektowanych w zadaniu Funkcje obliczające odpowiedzi filtra Należy napisać następujące funkcje: function [y,t]=iir_step_resp(b, a, N, fs) #definicja ciała funkcji obliczającą odpowiedź skokową filtru NOI o współczynnikach podanych w tablicach a i b. Długość odpowiedzi skokowej (ilość próbek) określa argument N, natomiast fs jest częstotliwością próbkowania. t powinno być osią odciętych/poziomą odpowiedzi skokowej. 4
6 function [y,t]=iir_imp_resp(b, a, N, fs) #definicja ciała funkcji obliczającą odpowiedź impulsową filtru NOI o współczynnikach podanych w tablicach a i b. Ilość próbek odpowiedzi impulsowej określa argument N, natomiast fs jest częstotliwością próbkowania. t powinno być osią odciętych/poziomą odpowiedzi impulsowej. function [mh,fih, mhdb, f]=iir_freq_resp(b, a, #definicja ciała funkcji N, fs) obliczającą odpowiedź częstotliwościową filtru NOI o współczynnikach podanych w tablicach a i b (mh- odpowiedź amplitudowa liniowa, mhdb- odpowiedź amplitudowa w db, fih- odpowiedź fazowa z fazą rozwiniętą, f- wspólna oś odciętych/pozioma wszystkich odpowiedzi częstotliwościowych). Liczba próbek odpowiedzi określa argument N, natomiast fs jest częstotliwością próbkowania. Do rozwijania fazy można wykorzystać funkcję z ćwiczenia 3. Wyniki działania funkcji należy przedstawić prezentując charakterystyki filtrów projektowanych w zadaniu Funkcje wyliczające współczynniki filtrów NOI Napisać funkcje w postaci: function [b, a] = iir_onepole_lpf(fc) która będzie wyznaczać współczynniki dolnoprzepustowego filtru jednobiegunowego. function [b, a] = iir_onepole_hpf(fc) zwracającą współczynniki górnoprzepustowego filtru jednobiegunowego o częstotliwości odcięcia fc. function [b, a] = iir_narrow_bf(f,bw) wyznaczającej współczynniki pasmowoprzepustowego filtru wąskopasmowego function [b, a] = iir_narrow_nf(f,bw) wyznaczającą współczynnik pasmowozaporowego filtru wąskopasmowego, gdzie f to częstotliwość środkowa, a BW to szerokość pasma przenoszenia filtru. Należy zaprezentować wszystkie charakterystyki filtrów dla parametrów wskazanych przez prowadzącego. 5
7 3.4 Filtry Czebyszewa Zadanie czwarte polega na porównaniu amplitudowych charakterystyk częstotliwościowych filtrów dwu-, cztero- i sześciobiegunowych Czebyszewa o zafalowaniach w paśmie przepustowym na poziomie 0,05 db. Częstotliwość odcięcia ustala prowadzący zajęcia. Wszystkie charakterystyki należy zaprezentować na jednym wykresie w decybelach. 3.5 Filtr sinc W zadaniu piątym należy porównać wszystkie rodzaje odpowiedzi filtru utworzonego z okienkowanej funkcji sinc oraz sześciobiegunowego filtru Czebyszewa dla ustalonej przez prowadzącego częstotliwości odcięcia oraz zadanego poziomu zafalowań wyrażonego w decybelach. Należy dobrać odpowiednią długość odpowiedzi impulsowej filtru typu sinc tak, aby uzyskać zbliżone właściwości. Odpowiedzi częstotliwościowe należy wykreślić w decybelach. 6
Przetwarzanie sygnałów
 Przetwarzanie sygnałów Ćwiczenie 3 Filtry o skończonej odpowiedzi impulsowej (SOI) Spis treści 1 Filtracja cyfrowa podstawowe wiadomości 1 1.1 Właściwości filtru w dziedzinie czasu............... 1 1.2
Przetwarzanie sygnałów Ćwiczenie 3 Filtry o skończonej odpowiedzi impulsowej (SOI) Spis treści 1 Filtracja cyfrowa podstawowe wiadomości 1 1.1 Właściwości filtru w dziedzinie czasu............... 1 1.2
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI)
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Transformata Laplace a to przekształcenie całkowe funkcji f(t) opisane następującym wzorem:
 PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
b n y k n T s Filtr cyfrowy opisuje się również za pomocą splotu dyskretnego przedstawionego poniżej:
 1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
8. Realizacja projektowanie i pomiary filtrów IIR
 53 8. Realizacja projektowanie i pomiary filtrów IIR Cele ćwiczenia Realizacja na zestawie TMX320C5515 ezdsp prostych liniowych filtrów cyfrowych. Pomiary charakterystyk amplitudowych zrealizowanych filtrów
53 8. Realizacja projektowanie i pomiary filtrów IIR Cele ćwiczenia Realizacja na zestawie TMX320C5515 ezdsp prostych liniowych filtrów cyfrowych. Pomiary charakterystyk amplitudowych zrealizowanych filtrów
A-2. Filtry bierne. wersja
 wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
Wprowadzenie. Spis treści. Analiza_sygnałów_-_ćwiczenia/Filtry
 Analiza_sygnałów_-_ćwiczenia/Filtry Spis treści 1 Wprowadzenie 2 Filtry cyfrowe: powtórka z wykładu 2.1 Działanie filtra w dziedzinie czasu 2.2 Nazewnictwo 2.3 Przejście do dziedziny częstości 2.3.1 Działanie
Analiza_sygnałów_-_ćwiczenia/Filtry Spis treści 1 Wprowadzenie 2 Filtry cyfrowe: powtórka z wykładu 2.1 Działanie filtra w dziedzinie czasu 2.2 Nazewnictwo 2.3 Przejście do dziedziny częstości 2.3.1 Działanie
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej
 Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
Podstawy Przetwarzania Sygnałów
 Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
ĆWICZENIE 5 EMC FILTRY AKTYWNE RC. 1. Wprowadzenie. f bez zakłóceń. Zasilanie FILTR Odbiornik. f zakłóceń
 ĆWICZENIE 5 EMC FILTRY AKTYWNE RC. Wprowadzenie Filtr aktywny jest zespołem elementów pasywnych RC i elementów aktywnych (wzmacniających), najczęściej wzmacniaczy operacyjnych. Właściwości wzmacniaczy,
ĆWICZENIE 5 EMC FILTRY AKTYWNE RC. Wprowadzenie Filtr aktywny jest zespołem elementów pasywnych RC i elementów aktywnych (wzmacniających), najczęściej wzmacniaczy operacyjnych. Właściwości wzmacniaczy,
Laboratorium nr 4: Porównanie filtrów FIR i IIR. skończonej odpowiedzi impulsowej (FIR) zawsze stabilne, mogą mieć liniową charakterystykę fazową
 Teoria Sygnałów sprawozdanie z zajęć laboratoryjnych Zajęcia z dnia 07.01.2009 Prowadzący: dr inż. Stanisław Nuckowski Sprawozdanie wykonał: Tomasz Witka Laboratorium nr 4: Porównanie filtrów FIR i IIR
Teoria Sygnałów sprawozdanie z zajęć laboratoryjnych Zajęcia z dnia 07.01.2009 Prowadzący: dr inż. Stanisław Nuckowski Sprawozdanie wykonał: Tomasz Witka Laboratorium nr 4: Porównanie filtrów FIR i IIR
x(n) x(n-1) x(n-2) D x(n-n+1) h N-1
 Laboratorium Układy dyskretne LTI projektowanie filtrów typu FIR Z1. apisać funkcję y = filtruj(x, h), która wyznacza sygnał y będący wynikiem filtracji sygnału x przez filtr FIR o odpowiedzi impulsowej
Laboratorium Układy dyskretne LTI projektowanie filtrów typu FIR Z1. apisać funkcję y = filtruj(x, h), która wyznacza sygnał y będący wynikiem filtracji sygnału x przez filtr FIR o odpowiedzi impulsowej
Liniowe układy scalone. Filtry aktywne w oparciu o wzmacniacze operacyjne
 Liniowe układy scalone Filtry aktywne w oparciu o wzmacniacze operacyjne Wiadomości ogólne (1) Zadanie filtrów aktywnych przepuszczanie sygnałów znajdujących się w pewnym zakresie częstotliwości pasmo
Liniowe układy scalone Filtry aktywne w oparciu o wzmacniacze operacyjne Wiadomości ogólne (1) Zadanie filtrów aktywnych przepuszczanie sygnałów znajdujących się w pewnym zakresie częstotliwości pasmo
Cyfrowe przetwarzanie sygnałów Jacek Rezmer -1-
 Cyfrowe przetwarzanie sygnałów Jacek Rezmer -1- Filtry cyfrowe cz. Zastosowanie funkcji okien do projektowania filtrów SOI Nierównomierności charakterystyki amplitudowej filtru cyfrowego typu SOI można
Cyfrowe przetwarzanie sygnałów Jacek Rezmer -1- Filtry cyfrowe cz. Zastosowanie funkcji okien do projektowania filtrów SOI Nierównomierności charakterystyki amplitudowej filtru cyfrowego typu SOI można
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów
 ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
Ćwiczenie 3. Właściwości przekształcenia Fouriera
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Filtry elektroniczne sygnałów ciągłych - cz.1
 Filtry elektroniczne sygnałów ciągłych - cz.1 Wprowadzenie Podstawowe pojęcia Klasyfikacje, charakterystyki częstotliwościowe filtrów Właściwości filtrów w dziedzinie czasu Realizacje elektroniczne filtrów
Filtry elektroniczne sygnałów ciągłych - cz.1 Wprowadzenie Podstawowe pojęcia Klasyfikacje, charakterystyki częstotliwościowe filtrów Właściwości filtrów w dziedzinie czasu Realizacje elektroniczne filtrów
2. Próbkowanie Sygnały okresowe (16). Trygonometryczny szereg Fouriera (17). Częstotliwość Nyquista (20).
 SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
BADANIE FILTRÓW. Instytut Fizyki Akademia Pomorska w Słupsku
 BADANIE FILTRÓW Cel ćwiczenia. Celem ćwiczenia jest zapoznanie się z właściwościami filtrów. Zagadnienia teoretyczne. Filtry częstotliwościowe Filtrem nazywamy układ o strukturze czwórnika, który przepuszcza
BADANIE FILTRÓW Cel ćwiczenia. Celem ćwiczenia jest zapoznanie się z właściwościami filtrów. Zagadnienia teoretyczne. Filtry częstotliwościowe Filtrem nazywamy układ o strukturze czwórnika, który przepuszcza
5 Filtry drugiego rzędu
 5 Filtry drugiego rzędu Cel ćwiczenia 1. Zrozumienie zasady działania i charakterystyk filtrów. 2. Poznanie zalet filtrów aktywnych. 3. Zastosowanie filtrów drugiego rzędu z układem całkującym Podstawy
5 Filtry drugiego rzędu Cel ćwiczenia 1. Zrozumienie zasady działania i charakterystyk filtrów. 2. Poznanie zalet filtrów aktywnych. 3. Zastosowanie filtrów drugiego rzędu z układem całkującym Podstawy
CZWÓRNIKI KLASYFIKACJA CZWÓRNIKÓW.
 CZWÓRNK jest to obwód elektryczny o dowolnej wewnętrznej strukturze połączeń elementów, mający wyprowadzone na zewnątrz cztery zaciski uporządkowane w dwie pary, zwane bramami : wejściową i wyjściową,
CZWÓRNK jest to obwód elektryczny o dowolnej wewnętrznej strukturze połączeń elementów, mający wyprowadzone na zewnątrz cztery zaciski uporządkowane w dwie pary, zwane bramami : wejściową i wyjściową,
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH
 ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
AKADEMIA MORSKA KATEDRA NAWIGACJI TECHNICZEJ
 AKADEMIA MORSKA KATEDRA NAWIGACJI TECHNICZEJ ELEMETY ELEKTRONIKI LABORATORIUM Kierunek NAWIGACJA Specjalność Transport morski Semestr II Ćw. 2 Filtry analogowe układy całkujące i różniczkujące Wersja opracowania
AKADEMIA MORSKA KATEDRA NAWIGACJI TECHNICZEJ ELEMETY ELEKTRONIKI LABORATORIUM Kierunek NAWIGACJA Specjalność Transport morski Semestr II Ćw. 2 Filtry analogowe układy całkujące i różniczkujące Wersja opracowania
H f = U WY f U WE f =A f e j f. 1. Cel ćwiczenia. 2. Wprowadzenie. H f
 . el ćwiczenia elem ćwiczenia jest zapoznanie studentów z podstawowymi pojęciami dotyczącymi czwórników i pomiarem ich charakterystyk czestotliwościowych na przykładzie filtrów elektrycznych. 2. Wprowadzenie
. el ćwiczenia elem ćwiczenia jest zapoznanie studentów z podstawowymi pojęciami dotyczącymi czwórników i pomiarem ich charakterystyk czestotliwościowych na przykładzie filtrów elektrycznych. 2. Wprowadzenie
Analiza właściwości filtrów dolnoprzepustowych
 Ćwiczenie Analiza właściwości filtrów dolnoprzepustowych Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra dolnoprzepustowego (DP) rzędu i jego parametrami.. Analiza widma sygnału prostokątnego.
Ćwiczenie Analiza właściwości filtrów dolnoprzepustowych Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra dolnoprzepustowego (DP) rzędu i jego parametrami.. Analiza widma sygnału prostokątnego.
POLITECHNIKA WROCŁAWSKA, WYDZIAŁ PPT I-21 LABORATORIUM Z PODSTAW ELEKTRONIKI Ćwiczenie nr 4. Czwórniki bierne - charakterystyki częstotliwościowe
 . el ćwiczenia elem ćwiczenia jest zapoznanie studentów z podstawowymi pojęciami dotyczącymi czwórników i pomiarem ich charakterystyk czestotliwościowych na przykładzie filtrów elektrycznych. 2. Wprowadzenie
. el ćwiczenia elem ćwiczenia jest zapoznanie studentów z podstawowymi pojęciami dotyczącymi czwórników i pomiarem ich charakterystyk czestotliwościowych na przykładzie filtrów elektrycznych. 2. Wprowadzenie
PROCESORY SYGNAŁOWE - LABORATORIUM. Ćwiczenie nr 04
 PROCESORY SYGNAŁOWE - LABORATORIUM Ćwiczenie nr 04 Obsługa buforów kołowych i implementacja filtrów o skończonej i nieskończonej odpowiedzi impulsowej 1. Bufor kołowy w przetwarzaniu sygnałów Struktura
PROCESORY SYGNAŁOWE - LABORATORIUM Ćwiczenie nr 04 Obsługa buforów kołowych i implementacja filtrów o skończonej i nieskończonej odpowiedzi impulsowej 1. Bufor kołowy w przetwarzaniu sygnałów Struktura
Temat: Filtracja cyfrowa okresowych sygnałów deterministycznych Ćwiczenie 3
 CYFROWE PRZETWARZANIE SYGNAŁÓW Laboratorium Inżynieria Biomedyczna, studia stacjonarne pierwszego stopnia imei Instytut Metrologii, Elektroniki i Informatyki Temat: Filtracja cyfrowa okresowych sygnałów
CYFROWE PRZETWARZANIE SYGNAŁÓW Laboratorium Inżynieria Biomedyczna, studia stacjonarne pierwszego stopnia imei Instytut Metrologii, Elektroniki i Informatyki Temat: Filtracja cyfrowa okresowych sygnałów
Przetwarzanie sygnałów
 Spis treści Przetwarzanie sygnałów Ćwiczenie 3 Właściwości przekształcenia Fouriera 1 Podstawowe właściwości przekształcenia Fouriera 1 1.1 Kompresja i ekspansja sygnału................... 2 1.2 Właściwości
Spis treści Przetwarzanie sygnałów Ćwiczenie 3 Właściwości przekształcenia Fouriera 1 Podstawowe właściwości przekształcenia Fouriera 1 1.1 Kompresja i ekspansja sygnału................... 2 1.2 Właściwości
Temat: Filtracja cyfrowa okresowych sygnałów deterministycznych Ćwiczenie 3
 CYFROWE PRZETWARZANIE SYGNAŁÓW Laboratorium Informatyka, studia stacjonarne drugiego stopnia imei Instytut Metrologii, Elektroniki i Informatyki Temat: Filtracja cyfrowa okresowych sygnałów deterministycznych
CYFROWE PRZETWARZANIE SYGNAŁÓW Laboratorium Informatyka, studia stacjonarne drugiego stopnia imei Instytut Metrologii, Elektroniki i Informatyki Temat: Filtracja cyfrowa okresowych sygnałów deterministycznych
Dynamiczne badanie wzmacniacza operacyjnego- ćwiczenie 8
 Dynamiczne badanie wzmacniacza operacyjnego- ćwiczenie 8 1. Cel ćwiczenia Celem ćwiczenia jest dynamiczne badanie wzmacniacza operacyjnego, oraz zapoznanie się z metodami wyznaczania charakterystyk częstotliwościowych.
Dynamiczne badanie wzmacniacza operacyjnego- ćwiczenie 8 1. Cel ćwiczenia Celem ćwiczenia jest dynamiczne badanie wzmacniacza operacyjnego, oraz zapoznanie się z metodami wyznaczania charakterystyk częstotliwościowych.
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej
 Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej 1. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej 1. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
Przetwarzanie sygnałów dyskretnych
 Przetwarzanie sygnałów dyskretnych System dyskretny p[ n ] r[ n] Przykłady: [ ] = [ ] + [ ] r n a p n a p n [ ] r n = 2 [ + ] + p[ n ] p n 2 r[ n] = a p[ n] + b n [ ] = [ ] r n a p n n [ ] = [ + ] r n
Przetwarzanie sygnałów dyskretnych System dyskretny p[ n ] r[ n] Przykłady: [ ] = [ ] + [ ] r n a p n a p n [ ] r n = 2 [ + ] + p[ n ] p n 2 r[ n] = a p[ n] + b n [ ] = [ ] r n a p n n [ ] = [ + ] r n
Kartkówka 1 Opracowanie: Próbkowanie częstotliwość próbkowania nie mniejsza niż podwojona szerokość przed spróbkowaniem.
 Znowu prosta zasada - zbierzmy wszystkie zagadnienia z tych 3ech kartkówek i opracujmy - może się akurat przyda na dopytkę i uda się zaliczyć labki :) (dodatkowo można opracowania z tych rzeczy z doc ów
Znowu prosta zasada - zbierzmy wszystkie zagadnienia z tych 3ech kartkówek i opracujmy - może się akurat przyda na dopytkę i uda się zaliczyć labki :) (dodatkowo można opracowania z tych rzeczy z doc ów
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 4 WYZNACZANIE CHARAKTERYSTYK CZĘSTOTLIWOŚCIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia jest doświadczalne
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 4 WYZNACZANIE CHARAKTERYSTYK CZĘSTOTLIWOŚCIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia jest doświadczalne
13.2. Filtry cyfrowe
 Bibliografia: 1. Chassaing Rulph, Digital Signal Processing and Applications with the C6713 and C6416 DSK, Wiley-Interscience 2005. 2. Borodziewicz W., Jaszczak K., Cyfrowe Przetwarzanie sygnałów, Wydawnictwo
Bibliografia: 1. Chassaing Rulph, Digital Signal Processing and Applications with the C6713 and C6416 DSK, Wiley-Interscience 2005. 2. Borodziewicz W., Jaszczak K., Cyfrowe Przetwarzanie sygnałów, Wydawnictwo
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC.
 Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC. Spis treści 1 Cel ćwiczenia 2 2 Podstawy teoretyczne 2 2.1 Charakterystyki częstotliwościowe..........................
Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC. Spis treści 1 Cel ćwiczenia 2 2 Podstawy teoretyczne 2 2.1 Charakterystyki częstotliwościowe..........................
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1C400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1C400027 Temat ćwiczenia:
Przetwarzanie sygnałów z czasem ciągłym
 Przetwarzanie sygnałów z czasem ciągłym Model systemowy układu p( t ) r ( t) wejście Układ wyjście p( t ) pobudzenie r ( t) reakcja Układ wykonuje pewną operację { i } na sygnale wejściowym p t (pobudzeniu),
Przetwarzanie sygnałów z czasem ciągłym Model systemowy układu p( t ) r ( t) wejście Układ wyjście p( t ) pobudzenie r ( t) reakcja Układ wykonuje pewną operację { i } na sygnale wejściowym p t (pobudzeniu),
Wykonawcy: Data Wydział Elektryczny Studia dzienne Nr grupy:
 POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI I ELEKTRONIKI PRZEMYSŁOWEJ Zakład Elektrotechniki Teoretycznej i Stosowanej Laboratorium Podstaw Telekomunikacji Ćwiczenie nr 2 Temat: Projektowanie i analiza
POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI I ELEKTRONIKI PRZEMYSŁOWEJ Zakład Elektrotechniki Teoretycznej i Stosowanej Laboratorium Podstaw Telekomunikacji Ćwiczenie nr 2 Temat: Projektowanie i analiza
Filtracja. Krzysztof Patan
 Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
KOMPUTEROWE SYSTEMY POMIAROWE
 KOMPUTEROWE SYSTEMY POMIAROWE Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMST - ITwE Semestr zimowy Wykład nr 12 Prawo autorskie Niniejsze
KOMPUTEROWE SYSTEMY POMIAROWE Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMST - ITwE Semestr zimowy Wykład nr 12 Prawo autorskie Niniejsze
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Laboratorium Przetwarzania Sygnałów Biomedycznych
 Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 3 Analiza sygnału o nieznanej strukturze Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik Politechnika Warszawska,
Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 3 Analiza sygnału o nieznanej strukturze Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik Politechnika Warszawska,
Filtrowanie a sploty. W powyższym przykładzie proszę zwrócić uwagę na efekty brzegowe. Wprowadzenie Projektowanie filtru Zadania
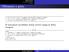 Filtrowanie a sploty idea x=[2222222222] %sygnałstochastycznyodługości5próbek h=[1111]/4; %Filtruśredniającypo4sąsiednichelementach y=conv(h,x)%zaaplikowaniefiltruhdosygnałux W powyższym przykładzie proszę
Filtrowanie a sploty idea x=[2222222222] %sygnałstochastycznyodługości5próbek h=[1111]/4; %Filtruśredniającypo4sąsiednichelementach y=conv(h,x)%zaaplikowaniefiltruhdosygnałux W powyższym przykładzie proszę
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Przekształcenie Z. Krzysztof Patan
 Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
Przykładowe pytania 1/11
 Parametry sygnałów Przykładowe pytania /. Dla okresowego przebiegu sinusoidalnego sterowanego fazowo (jak na rys) o kącie przewodzenia θ wyprowadzić zależność wartości skutecznej od kąta przewodzenia θ.
Parametry sygnałów Przykładowe pytania /. Dla okresowego przebiegu sinusoidalnego sterowanego fazowo (jak na rys) o kącie przewodzenia θ wyprowadzić zależność wartości skutecznej od kąta przewodzenia θ.
Charakterystyka amplitudowa i fazowa filtru aktywnego
 1 Charakterystyka amplitudowa i fazowa filtru aktywnego Charakterystyka amplitudowa (wzmocnienie amplitudowe) K u (f) jest to stosunek amplitudy sygnału wyjściowego do amplitudy sygnału wejściowego w funkcji
1 Charakterystyka amplitudowa i fazowa filtru aktywnego Charakterystyka amplitudowa (wzmocnienie amplitudowe) K u (f) jest to stosunek amplitudy sygnału wyjściowego do amplitudy sygnału wejściowego w funkcji
ZASTOSOWANIA PRZEKSZTAŁCENIA ZET
 CPS - - ZASTOSOWANIA PRZEKSZTAŁCENIA ZET Rozwiązywanie równań różnicowych Dyskretny system liniowy-stacjonarny można opisać równaniem różnicowym w postaci ogólnej N M aky[ n k] bkx[ n k] k k Przekształcenie
CPS - - ZASTOSOWANIA PRZEKSZTAŁCENIA ZET Rozwiązywanie równań różnicowych Dyskretny system liniowy-stacjonarny można opisać równaniem różnicowym w postaci ogólnej N M aky[ n k] bkx[ n k] k k Przekształcenie
Analiza właściwości filtra selektywnego
 Ćwiczenie 2 Analiza właściwości filtra selektywnego Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra selektywnego 2 rzędu i zakresami jego parametrów. 2. Analiza widma sygnału prostokątnego..
Ćwiczenie 2 Analiza właściwości filtra selektywnego Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra selektywnego 2 rzędu i zakresami jego parametrów. 2. Analiza widma sygnału prostokątnego..
WOJSKOWA AKADEMIA TECHNICZNA
 WOJSKOWA AKADEMIA TECHNICZNA LABORATORIUM CYFROWE PRZETWARZANIE SYGNAŁÓW Stopień, imię i nazwisko prowadzącego Imię oraz nazwisko słuchacza Grupa szkoleniowa Data wykonania ćwiczenia dr inż. Andrzej Wiśniewski
WOJSKOWA AKADEMIA TECHNICZNA LABORATORIUM CYFROWE PRZETWARZANIE SYGNAŁÓW Stopień, imię i nazwisko prowadzącego Imię oraz nazwisko słuchacza Grupa szkoleniowa Data wykonania ćwiczenia dr inż. Andrzej Wiśniewski
Wydział Elektryczny. Katedra Telekomunikacji i Aparatury Elektronicznej. Konstrukcje i Technologie w Aparaturze Elektronicznej.
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Konstrukcje i Technologie w Aparaturze Elektronicznej Ćwiczenie nr 5 Temat: Przetwarzanie A/C. Implementacja
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Konstrukcje i Technologie w Aparaturze Elektronicznej Ćwiczenie nr 5 Temat: Przetwarzanie A/C. Implementacja
3. Przetwarzanie analogowo-cyfrowe i cyfrowo-analogowe... 43
 Spis treści 3 Przedmowa... 9 Cele książki i sposoby ich realizacji...9 Podziękowania...10 1. Rozległość zastosowań i głębia problematyki DSP... 11 Korzenie DSP...12 Telekomunikacja...14 Przetwarzanie sygnału
Spis treści 3 Przedmowa... 9 Cele książki i sposoby ich realizacji...9 Podziękowania...10 1. Rozległość zastosowań i głębia problematyki DSP... 11 Korzenie DSP...12 Telekomunikacja...14 Przetwarzanie sygnału
Zjawisko aliasingu. Filtr antyaliasingowy. Przecieki widma - okna czasowe.
 Katedra Mechaniki i Podstaw Konstrukcji Maszyn POLITECHNIKA OPOLSKA Komputerowe wspomaganie eksperymentu Zjawisko aliasingu.. Przecieki widma - okna czasowe. dr inż. Roland PAWLICZEK Zjawisko aliasingu
Katedra Mechaniki i Podstaw Konstrukcji Maszyn POLITECHNIKA OPOLSKA Komputerowe wspomaganie eksperymentu Zjawisko aliasingu.. Przecieki widma - okna czasowe. dr inż. Roland PAWLICZEK Zjawisko aliasingu
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
Realizacja filtrów cyfrowych z buforowaniem próbek
 str. 1 Realizacja filtrów cyfrowych z buforowaniem próbek 1. Filtry Cyfrowe Zadaniem filtracji jest przepuszczanie (tłumienie) składowych sygnału leŝących w określonym paśmie częstotliwości. Ogólnie filtr
str. 1 Realizacja filtrów cyfrowych z buforowaniem próbek 1. Filtry Cyfrowe Zadaniem filtracji jest przepuszczanie (tłumienie) składowych sygnału leŝących w określonym paśmie częstotliwości. Ogólnie filtr
Ćwiczenie - 7. Filtry
 LABOATOIUM ELEKTONIKI Ćwiczenie - 7 Filtry Spis treści 1 el ćwiczenia 1 2 Podstawy teoretyczne 2 2.1 Transmitancja filtru dolnoprzepustowego drugiego rzędu............. 2 2.2 Aktywny filtr dolnoprzepustowy
LABOATOIUM ELEKTONIKI Ćwiczenie - 7 Filtry Spis treści 1 el ćwiczenia 1 2 Podstawy teoretyczne 2 2.1 Transmitancja filtru dolnoprzepustowego drugiego rzędu............. 2 2.2 Aktywny filtr dolnoprzepustowy
Transmitancje i charakterystyki częstotliwościowe. Krzysztof Patan
 Transmitancje i charakterystyki częstotliwościowe Krzysztof Patan Transmitancja systemu czasu ciągłego Przekształcenie Laplace a systemu czasu ciągłego jest superpozycją składowych pochodzących od wymuszenia
Transmitancje i charakterystyki częstotliwościowe Krzysztof Patan Transmitancja systemu czasu ciągłego Przekształcenie Laplace a systemu czasu ciągłego jest superpozycją składowych pochodzących od wymuszenia
Filtry aktywne filtr górnoprzepustowy
 . el ćwiczenia. Filtry aktywne filtr górnoprzepustowy elem ćwiczenia jest praktyczne poznanie właściwości filtrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów filtru.. Budowa
. el ćwiczenia. Filtry aktywne filtr górnoprzepustowy elem ćwiczenia jest praktyczne poznanie właściwości filtrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów filtru.. Budowa
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Filtry cyfrowe. h(n) odpowiedź impulsowa. Filtr cyfrowy. Procesory sygnałowe (DSP), układy programowalne
 Filtry cyfrowe Procesory sygnałowe (DSP), układy programowalne x(n) Filtr cyfrowy y(n) h(n) odpowiedź impulsowa x(n) y(n) y(n) = x(n) h(n) 1 Filtry cyfrowe Po co filtrujemy sygnały? Aby uzyskać: redukcję
Filtry cyfrowe Procesory sygnałowe (DSP), układy programowalne x(n) Filtr cyfrowy y(n) h(n) odpowiedź impulsowa x(n) y(n) y(n) = x(n) h(n) 1 Filtry cyfrowe Po co filtrujemy sygnały? Aby uzyskać: redukcję
1. Modulacja analogowa, 2. Modulacja cyfrowa
 MODULACJA W16 SMK 2005-05-30 Jest operacja mnożenia. Jest procesem nakładania informacji w postaci sygnału informacyjnego m.(t) na inny przebieg o wyższej częstotliwości, nazywany falą nośną. Przyczyna
MODULACJA W16 SMK 2005-05-30 Jest operacja mnożenia. Jest procesem nakładania informacji w postaci sygnału informacyjnego m.(t) na inny przebieg o wyższej częstotliwości, nazywany falą nośną. Przyczyna
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Ćwiczenie: "Obwody prądu sinusoidalnego jednofazowego"
 Ćwiczenie: "Obwody prądu sinusoidalnego jednofazowego" Opracowane w ramach projektu: "Informatyka mój sposób na poznanie i opisanie świata realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres
Ćwiczenie: "Obwody prądu sinusoidalnego jednofazowego" Opracowane w ramach projektu: "Informatyka mój sposób na poznanie i opisanie świata realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres
Technika analogowa. Problematyka ćwiczenia: Temat ćwiczenia:
 Technika analogowa Problematyka ćwiczenia: Pomiędzy urządzeniem nadawczym oraz odbiorczym przesyłany jest sygnał użyteczny w paśmie 10Hz 50kHz. W trakcie odbioru sygnału po stronie odbiorczej stwierdzono
Technika analogowa Problematyka ćwiczenia: Pomiędzy urządzeniem nadawczym oraz odbiorczym przesyłany jest sygnał użyteczny w paśmie 10Hz 50kHz. W trakcie odbioru sygnału po stronie odbiorczej stwierdzono
Akwizycja i przetwarzanie sygnałów cyfrowych
 Akwizycja i przetwarzanie sygnałów cyfrowych Instytut Teleinformatyki ITI PK Kraków 21 luty 2011 Projektowania filtrów IIR Metoda niezmienności odpowiedzi impulsowej Podstawowa zasada określajaca: projektujemy
Akwizycja i przetwarzanie sygnałów cyfrowych Instytut Teleinformatyki ITI PK Kraków 21 luty 2011 Projektowania filtrów IIR Metoda niezmienności odpowiedzi impulsowej Podstawowa zasada określajaca: projektujemy
Technika audio część 2
 Technika audio część 2 Wykład 12 Projektowanie cyfrowych układów elektronicznych Mgr inż. Łukasz Kirchner lukasz.kirchner@cs.put.poznan.pl http://www.cs.put.poznan.pl/lkirchner Wprowadzenie do filtracji
Technika audio część 2 Wykład 12 Projektowanie cyfrowych układów elektronicznych Mgr inż. Łukasz Kirchner lukasz.kirchner@cs.put.poznan.pl http://www.cs.put.poznan.pl/lkirchner Wprowadzenie do filtracji
CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera)
 I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
rezonansu rezonansem napięć rezonansem szeregowym rezonansem prądów rezonansem równoległym
 Lekcja szósta poświęcona będzie analizie zjawisk rezonansowych w obwodzie RLC. Zjawiskiem rezonansu nazywamy taki stan obwodu RLC przy którym prąd i napięcie są ze sobą w fazie. W stanie rezonansu przesunięcie
Lekcja szósta poświęcona będzie analizie zjawisk rezonansowych w obwodzie RLC. Zjawiskiem rezonansu nazywamy taki stan obwodu RLC przy którym prąd i napięcie są ze sobą w fazie. W stanie rezonansu przesunięcie
Podstawowe człony dynamiczne
 . Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
. Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
Szybkie metody projektowania filtrów aktywnych
 Szybkie metody projektowania filtrów aktywnych Aby szybko rozpocząć projektowanie układów filtrów aktywnych należy znać: Wartości dostępnych źródeł zasilania: zasilanie plus/minus (symetryczne) czy tylko
Szybkie metody projektowania filtrów aktywnych Aby szybko rozpocząć projektowanie układów filtrów aktywnych należy znać: Wartości dostępnych źródeł zasilania: zasilanie plus/minus (symetryczne) czy tylko
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Rys. 1. Wzmacniacz odwracający
 Ćwiczenie. 1. Zniekształcenia liniowe 1. W programie Altium Designer utwórz schemat z rys.1. Rys. 1. Wzmacniacz odwracający 2. Za pomocą symulacji wyznaczyć charakterystyki częstotliwościowe (amplitudową
Ćwiczenie. 1. Zniekształcenia liniowe 1. W programie Altium Designer utwórz schemat z rys.1. Rys. 1. Wzmacniacz odwracający 2. Za pomocą symulacji wyznaczyć charakterystyki częstotliwościowe (amplitudową
SPRZĘTOWA REALIZACJA FILTRÓW CYFROWYCH TYPU SOI
 1 ĆWICZENIE VI SPRZĘTOWA REALIZACJA FILTRÓW CYFROWYCH TYPU SOI (00) Celem pracy jest poznanie sposobu fizycznej realizacji filtrów cyfrowych na procesorze sygnałowym firmy Texas Instruments TMS320C6711
1 ĆWICZENIE VI SPRZĘTOWA REALIZACJA FILTRÓW CYFROWYCH TYPU SOI (00) Celem pracy jest poznanie sposobu fizycznej realizacji filtrów cyfrowych na procesorze sygnałowym firmy Texas Instruments TMS320C6711
AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT. Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA
 AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA II rok Kierunek Transport Temat: Transmitancja operatorowa. Badanie odpowiedzi układów automatyki. Opracował
AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA II rok Kierunek Transport Temat: Transmitancja operatorowa. Badanie odpowiedzi układów automatyki. Opracował
STUDIA MAGISTERSKIE DZIENNE LABORATORIUM SYGNAŁÓW, SYSTEMÓW I MODULACJI. Filtracja cyfrowa. v.1.0
 Politechnika Warszawska Instytut Radioelektroniki Zakład Radiokomunikacji SUDIA MAGISERSKIE DZIENNE LABORAORIUM SYGNAŁÓW, SYSEMÓW I MODULACJI Filtracja cyfrowa v.1. Opracowanie: dr inż. Wojciech Kazubski,
Politechnika Warszawska Instytut Radioelektroniki Zakład Radiokomunikacji SUDIA MAGISERSKIE DZIENNE LABORAORIUM SYGNAŁÓW, SYSEMÓW I MODULACJI Filtracja cyfrowa v.1. Opracowanie: dr inż. Wojciech Kazubski,
Stabilność. Krzysztof Patan
 Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Filtry aktywne filtr środkowoprzepustowy
 Filtry aktywne iltr środkowoprzepustowy. Cel ćwiczenia. Celem ćwiczenia jest praktyczne poznanie właściwości iltrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów iltru.. Budowa
Filtry aktywne iltr środkowoprzepustowy. Cel ćwiczenia. Celem ćwiczenia jest praktyczne poznanie właściwości iltrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów iltru.. Budowa
DYSKRETNE PRZEKSZTAŁCENIE FOURIERA C.D.
 CPS 6 DYSKRETE PRZEKSZTAŁCEIE FOURIERA C.D. Twierdzenie o przesunięciu Istnieje ważna właściwość DFT, znana jako twierdzenie o przesunięciu. Mówi ono, że: Przesunięcie w czasie okresowego ciągu wejściowego
CPS 6 DYSKRETE PRZEKSZTAŁCEIE FOURIERA C.D. Twierdzenie o przesunięciu Istnieje ważna właściwość DFT, znana jako twierdzenie o przesunięciu. Mówi ono, że: Przesunięcie w czasie okresowego ciągu wejściowego
Filtry IIR. Zadania Przepróbkowywanie. Filtry IIR
 Filtry IIR Filtry IIR mają zazwyczaj dużo niższe rzędy przy osiągach takich jak FIR z dużo wyższymi rzędami. W matlabie mamy zaimplementowane kilka funkcji do projektowania óptymalnych pod różnymi względami
Filtry IIR Filtry IIR mają zazwyczaj dużo niższe rzędy przy osiągach takich jak FIR z dużo wyższymi rzędami. W matlabie mamy zaimplementowane kilka funkcji do projektowania óptymalnych pod różnymi względami
Ćwiczenie nr 11. Projektowanie sekcji bikwadratowej filtrów aktywnych
 Ćwiczenie nr 11 Projektowanie sekcji bikwadratowej filtrów aktywnych 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi filtrami elektrycznymi o charakterystyce dolno-, środkowo- i górnoprzepustowej,
Ćwiczenie nr 11 Projektowanie sekcji bikwadratowej filtrów aktywnych 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi filtrami elektrycznymi o charakterystyce dolno-, środkowo- i górnoprzepustowej,
Politechnika Łódzka. Instytut Systemów Inżynierii Elektrycznej
 Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium komputerowych systemów pomiarowych Ćwiczenie 4 Filtracja sygnałów dyskretnych 1. Opis stanowiska Ćwiczenie jest realizowane w
Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium komputerowych systemów pomiarowych Ćwiczenie 4 Filtracja sygnałów dyskretnych 1. Opis stanowiska Ćwiczenie jest realizowane w
PORÓWNANIE METOD PROJEKTOWANIA FILTRÓW CYFROWYCH
 POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0029 Dominik MATECKI * PORÓWNANIE METOD PROJEKTOWANIA FILTRÓW CYFROWYCH W artykule zostały
POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0029 Dominik MATECKI * PORÓWNANIE METOD PROJEKTOWANIA FILTRÓW CYFROWYCH W artykule zostały
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
A3 : Wzmacniacze operacyjne w układach liniowych
 A3 : Wzmacniacze operacyjne w układach liniowych Jacek Grela, Radosław Strzałka 2 kwietnia 29 1 Wstęp 1.1 Wzory Poniżej zamieszczamy podstawowe wzory i definicje, których używaliśmy w obliczeniach: 1.
A3 : Wzmacniacze operacyjne w układach liniowych Jacek Grela, Radosław Strzałka 2 kwietnia 29 1 Wstęp 1.1 Wzory Poniżej zamieszczamy podstawowe wzory i definicje, których używaliśmy w obliczeniach: 1.
LINIOWE UKŁADY DYSKRETNE
 LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
1 Dana jest funkcja logiczna f(x 3, x 2, x 1, x 0 )= (1, 3, 5, 7, 12, 13, 15 (4, 6, 9))*.
 EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 0/0 Odpowiedzi do zadań dla grupy elektronicznej na zawody II stopnia (okręgowe) Dana jest funkcja logiczna f(x 3, x,
EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 0/0 Odpowiedzi do zadań dla grupy elektronicznej na zawody II stopnia (okręgowe) Dana jest funkcja logiczna f(x 3, x,
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Projekt z Układów Elektronicznych 1
 Projekt z Układów Elektronicznych 1 Lista zadań nr 4 (liniowe zastosowanie wzmacniaczy operacyjnych) Zadanie 1 W układzie wzmacniacza z rys.1a (wzmacniacz odwracający) zakładając idealne parametry WO a)
Projekt z Układów Elektronicznych 1 Lista zadań nr 4 (liniowe zastosowanie wzmacniaczy operacyjnych) Zadanie 1 W układzie wzmacniacza z rys.1a (wzmacniacz odwracający) zakładając idealne parametry WO a)
A-4. Filtry aktywne RC
 A-4. A-4. wersja 4 4. Wstęp Filtry aktywne II rzędu RC to układy liniowe, stacjonarne realizowane za pomocą elementu aktywnego jakim jest wzmacniacz, na który załoŝono sprzęŝenie zwrotne zbudowane z elementów
A-4. A-4. wersja 4 4. Wstęp Filtry aktywne II rzędu RC to układy liniowe, stacjonarne realizowane za pomocą elementu aktywnego jakim jest wzmacniacz, na który załoŝono sprzęŝenie zwrotne zbudowane z elementów
Detekcja zespołów QRS w sygnale elektrokardiograficznym
 Detekcja zespołów QRS w sygnale elektrokardiograficznym 1 Wprowadzenie Zadaniem algorytmu detekcji zespołów QRS w sygnale elektrokardiograficznym jest określenie miejsc w sygnale cyfrowym w których znajdują
Detekcja zespołów QRS w sygnale elektrokardiograficznym 1 Wprowadzenie Zadaniem algorytmu detekcji zespołów QRS w sygnale elektrokardiograficznym jest określenie miejsc w sygnale cyfrowym w których znajdują
analogowego regulatora PID doboru jego nastaw i przetransformowanie go na cyfrowy regulator PID, postępując według następujących podpunktów:
 Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
