TwierdzeniePoincaré 1 Bendixsona 2
|
|
|
- Renata Rybak
- 7 lat temu
- Przeglądów:
Transkrypt
1 Twierdzenie Poincaré Bendixsona 1 TwierdzeniePoincaré 1 Bendixsona 2 1 TwierdzeniePoincaré Bendixsona W bieżącym podrozdziale zakładamy, że U jest otwartym podzbiorem płaszczyzny R 2 if:u R 2 jestpolemwektorowymklasyc 1,generującym lokalny potok ϕ. Twierdzenie 1(Twierdzenie Poincaré Bendixsona). Niech dla pewnego x U zbiór ω(x) będzie niepustym zbiorem zwartym nie zawierającym punktów stacjonarnych. Wówczas ω(x) jest orbitą okresową. W dowodzie twierdzenia Poincaré Bendixsona wykorzystuje się następujący wynik: Twierdzenie 2(TwierdzenieJordana 3 orozcinaniupłaszczyzny).niech J R 2 będziekrzywązwykłązamkniętą(tzn.zbioremhomeomorficznymz okręgiem).wówczasdopełnienie R 2 \Jmadwieskładowespójności,jedną ograniczoną(wnętrze krzywej J), i drugą nieograniczoną(zewnętrze krzywej J). Ponadto, J jest wspólnym brzegiem swojego wnętrza i zewnętrza. Przystępujemy teraz do dowodu twierdzenia Poincaré Bendixsona. Jeśli O(x) jest orbitą okresową, to nie ma czego dowodzić. Załóżmy zatem, że x nie jest punktem okresowym, oraz że ω(x) jest niepustym zbiorem zwartym nie zawierającym punktów stacjonarnych. Przypomnijmy dwuwymiarową wersję twierdzenia o lokalnym prostowaniu pola wektorowego: Twierdzenie 3(Twierdzenie o prostowaniu pola wektorowego wersja dwuwymiarowa).niechf:u R 2 będziepolemwektorowymklasyc 1 i niech u U będzie punktem regularnym pola F. Wówczas istnieją: transwersalalpolafwpunkcieu, otoczenie otwarte V punktu u, 1 HenriPoincaré( ),matematykfrancuski,wedługkompilatora(J.M.)jeden z najwybitniejszych matematyków wszech czasów 2 IvarOttoBendixson( ),matematykszwedzki 3 (MarieEnnemond)CamilleJordan( ),matematykfrancuski(odjegonazwiska pochodzi też postać Jordana macierzy; nie należy go mylić z Wilhelmem Jordanem ( ), geodetą i matematykiem niemieckim, od którego nazwiska pochodzi algorytm Gaussa Jordana)
2 Twierdzenie Poincaré Bendixsona 2 liczby dodatnie ε, δ, oraz dyfeomorfizm klasyc 1 o następujących własnościach: M:V 1 1 na ( δ,δ) ( ε,ε) (i)m(l)=( δ,δ) {0};ponadtoM(u)=(0,0), (ii)dlakażdegov V istniejedokładniejednapara(w,t) L ( ε,ε) taka,żev=ϕ t (w);ponadto,m(v)=(ξ,t),gdziem(w)=(ξ,0). OznaczmyM=(M 1,M 2 ). Fakt1.Niechy ω(x).wówczasistniejątranswersalalpolafwpunkcie yorazciąg(ϕ tk (x)) L,t k gdyk,zbieżnydoy. Dowód.Niechs k będzieciągiemtakim,żeϕ sk (x)dążydoy.oznaczmy przezl(odp.v)transwersalę(odp.otoczenie)punktuyjakwtwierdzeniuo lokalnym prostowaniu(tw. 3). Odrzucając skończenie wiele wyrazów, można założyć,żewszystkieϕ sk (x)należądov.określmyt k :=s k M 2 (ϕ sk (x)). Po pierwsze, zauważmy że, na podstawie Tw. 3(ii), ϕ tk (x)=ϕ sk M 2 (ϕ sk (x))(x) L. Dalej, korzystając z własności(pl2) oraz z ciągłości potoku lokalnego(patrz, np., wykład o lokalnym prostowaniu), widzimy, że ϕ sk M 2 (ϕ sk (x))(x)=ϕ M2 (ϕ sk (x))(ϕ sk (x)) dąży,przyk,doϕ M2 (y)(y),którejestrówne,znównapodstawie(znów na podstawie Tw. 3(ii)), y. Wystarczyterazzauważyć,żet k s k ε,zatemt k gdyk. Fakt2.Niechy ω(x).wówczasdlakażdejtranswersalilpolafwpunkcie yjakwfakcie1,każdyciąg(ϕ tk (x)) k=1 Lzbieżnydoyitaki,że0<t 1< t 2 < <t k <t k+1 <,jestmonotoniczny. Monotonicznośćrozumiemywnastępującysposób:ciąg(M 1 (ϕ tk (x))) k=1 jest monotoniczny.
3 Twierdzenie Poincaré Bendixsona 3 DowódFaktu2.Załóżmynajpierwniewprost,żeM 1 (ϕ tk (x))im 1 (ϕ tk+1 (x)) są,dlapewnegok N,przeciwnychznaków. WówczaszbiórJ,będącysumąodcinkatranswersaliLokońcachϕ tk (x) iϕ tk+1 (x),i kawałka orbity{ϕ t (x):t [t k,t k+1 ]},jestkrzywązwykłą zamkniętą(patrzponiższyrysunek,gdziex 1 :=ϕ tk (x),x 2 :=ϕ tk+1 (x)). x 1 y x 2 y 1 Zauważmy,żenaodcinkutranswersaliLłączącympunktyx 1 ix 2 pole wektorowe F skierowane jest na zewnątrz krzywej J. Wynika stąd, że dla s<0dostateczniebliskichzerupunktϕ s (y)jestpołożonywewnątrzkrzywej J.Ustalmytakies,ioznaczmyy 1 :=ϕ s (y).leczy 1 ω(x),zatemistnieje ϑ>t k+1 takie,żeϕ ϑ (x)leżywewnątrzkrzywejj.leczjesttoniemożliwe, bododatniapółorbitapunktux 2 niemajakwejśćdownętrzakrzywejj:nie możeprzeciąćzbioru{ϕ t (x):t [t k,t k+1 ]}(przeczyłobytozałożeniu,żex niejestpunktemokresowym),iniemożewejśćdownętrzakrzywejjprzez odcinek transwersali(gdyż tam pole wektorowe skierowane jest na zewnątrz). Załóżmyterazniewprost,że,naprzykład,0<M 1 (ϕ tk (x))<m 1 (ϕ tk+1 (x)) dlapewnegok N. WówczaszbiórJ,będącysumąodcinkatranswersaliLokońcachϕ tk (x) iϕ tk+1 (x),i kawałka orbity{ϕ t (x):t [t k,t k+1 ]},jestkrzywązwykłą zamkniętą(patrzponiższyrysunek,gdziex 1 :=ϕ tk (x),x 2 :=ϕ tk+1 (x)).
4 Twierdzenie Poincaré Bendixsona 4 y x 1 x 2 TerazpunktyleżywewnątrzkrzywejJ.Leczjesttoniemożliwe,bo (takjakwpoprzedniejczęścidowodu)dodatniapółorbitapunktux 2 niema którędy wejść do wnętrza krzywej J. Lemat1.Niechy ω(x).wówczasdlakażdejtranswersalilpolafw punkcieyjakwfakcie1zachodziω(x) L={y}. Dowód.Załóżmyniewprost,żeξ y ω(x) L.ZachodziM 1 (ξ) 0= M 1 (y).załóżmy,że0 s <s sątakie,żeϕ s (x) Liϕ s (x) L. Z twierdzenia o lokalnym prostowaniu pola wektorowego(tw. 3) wynika, żes s >2ε.Zatemzbiórtychchwilt 0,dlaktórychϕ t (x)należy do transwersali L, jest co najwyżej przeliczalny. Zbiór ten(oznaczany przez (t k ))jestwistocieprzeliczalny,gdyży ω(x).dlapewnegopodciągu(t kl ) zachodziϕ tkl (x) y,czylim 1 (ϕ tkl (x)) 0,zaśdlainnegopodciągu(t k l ) zachodziϕ tk l (x) ξ,czylim 1 (ϕ tk l (x)) M 1 (ξ) 0.Lecz,napodstawie Faktu2,ciąg(M 1 (ϕ tk (x))jestmonotoniczny,sprzeczność. Lemat2.Niechy ω(x).wówczasyjestpunktemokresowym. Dowód.Ztego,żeω(x)jestzwartyiniezmienniczywynika,że ω(y) ω(x).ustalmyz ω(y).fakt1zastosowanydoz ω(y)gwarantujenam istnienietranswersalilpolafwpunkcieziciągu(t k )rozbieżnegodo
5 Twierdzenie Poincaré Bendixsona 5 takiego,żeϕ tk (y) Lorazϕ tk (y)dążydozgdyk.ociągu(t k ) możemyzałożyć,żejestrosnący.leczzlematu1(zastosowanegodoz ω(x))wynika,żeϕ t1 (y)=ϕ t2 (y)=z,gdziet 1 <t 2,zatemyjestpunktem okresowym. Wykazaliśmy zatem, że ω(x) jest sumą orbit okresowych. Aby dokończyć dowód twierdzenia Poincaré Bendixsona, ustalmy y ω(x),ioznaczmyprzezt>0okrespodstawowyorbityokresowejγ=o(y) (oczywiście Γ ω(x)). Rozważmy znów transwersalę L w punkcie y i otoczenie V. Z ciągłej zależności rozwiązania od warunków początkowych wynika, żedlakażdegoη>0istniejeotoczenieotwartev Vpunktuytakie,że (i) ϕ t (z) ϕ t (y) <ηdladowolnegoz V iwszystkicht [0,T+ε], (ii)ϕ T (V ) V. Załóżmydalej,żeotoczenieotwarteV jestwypukłe. Ustalmyη>0,idobierzmyV doη.istniejes>0takie,żeϕ s (x) L V.Z(ii)wynika,żepunktϕ s+t (x) V.Ztwierdzeniaoprostowaniu pola wektorowego(twierdzenie 3) wynika istnienie ϑ ( ε, ε) takiego, że ϕ s+t+ϑ (x) L.Z(i)wynika,że ϕ t+s (x) ϕ t (y) <ηdlawszystkicht [0,T+ε]. Zmonotoniczności(Fakt2)wynika,żepunktϕ s+t+ϑ (x)musileżećna transwersalilpomiędzypunktamiϕ s (x)iy.ponieważotoczeniev jest wypukłe,punktϕ s+t+ϑ (x)należydov.powtarzamyterazpowyższerozumowanie,otrzymując,żedlawszystkicht spunktϕ t (x)jestwodległości mniejszejniżηodorbityokresowejγ.wynikastąd,żeω(x) Γ,cokończy dowód twierdzenia Poincaré Bendixsona. OrbitęokresowąO(y)taką,żeistniejex / O(y),dlaktóregoω(x)= O(y), nazywamy cyklem granicznym. 2 Dalsze własności pól wektorowych na płaszczyźnie Sformułujemy teraz dwa twierdzenia z topologii, które będą potrzebne w późniejszych rozważaniach. Twierdzenie4(TwierdzenieSchönfliesa 4 ).NiechJ R 2 będziekrzywą zwykłązamkniętąiniechh:j T,gdzie T={x R 2 : x =1},będziehomeomorfizmem.WówczasistniejehomeomorfizmH: R 2 R 2 będący rozszerzeniemhomeomorfizmuh(tzn.h J =hih 1 T =h 1 ). 4 ArthurMoritzSchönflies( ),matematykniemiecki
6 Twierdzenie Poincaré Bendixsona 6 Przed sformułowaniem następnego twierdzenia, przypomnijmy, że punktemstałymodwzorowaniaf:x X(Xjestdowolnymzbiorem)nazywamy x Xtaki,żef(x)=x.JeśliXjestprzestrzeniąmetryzowalną(ogólniej: przestrzenią topologiczną Hausdorffa) i f jest odwzorowaniem ciągłym, to zbiór punktów stałych odwzorowania f(być może pusty!) jest domknięty. Przestrzeń metryzowalną homeomorficzną z domkniętą kulą jednostkową w n-wymiarowej przestrzeni euklidesowej nazywamy dyskiem n-wymiarowym. Twierdzenie5(TwierdzenieBrouwera 5 opunkciestałym).ciągłeodwzorowanie dysku n-wymiarowego w siebie ma punkt stały. Twierdzenie6.NiechF:U R 2 będziepolemwektorowymklasyc 1,i niechγbędzieorbitąokresowąpolaftaką,żejejwnętrzezawartejestwu. WówczaswewnątrzΓistniejeytaki,żeF(y)=0. Dowód.JakożeΓjestpodzbiorempłaszczyzny R 2 homeomorficznymzokręgiem, na podstawie twierdzenia Schönfliesa istnieje homeomorfizm płaszczyzny R 2 na R 2 przeprowadzającysumędkrzywejγijejwnętrzad 0 na(domknięte) koło jednostkowe. Wobec tego, D jest dyskiem dwuwymiarowym. Oznaczmy przez Φ potok lokalny generowany przez pole wektorowe F. Dlakażdegox D 0 orbitao(x)jest,jakozbiórspójny,zawartawd 0. Wynikastąd,żeD 0 jestzbioremniezmienniczym,i,cozatymidzie,dysk dwuwymiarowy D też jest zbiorem niezmienniczym. Ponieważ D jest zbiorem zwartym,ϕ t (x)jestokreślonedlakażdegot Rikażdegox D. Dlak NoznaczmyprzezE k zbiórpunktówstałychodwzorowania Ψ k :D D,Ψ k (x):=ϕ 1/2 k(x).ztwierdzeniabrouweraopunkciestałym wynika,żezbiorye k,k NsąniepustePonadto,zbiorytesądomknięte, zatemzwarte.dalej,e k+1 E k.wynikastąd,żee:= k=1 E k jest,jako przekrój zstępującej rodziny niepustych zbiorów zwartych, też niepusty i zwarty. Weźmyy E.ZdefinicjizbioruEwynika,żeϕ t (y)=ydlat>0 dwójkowowymiernych.leczodwzorowanie R t ϕ t (x)jestciągłe,zatem ϕ t (x)=ydlakażdegot>0,czylif(y)=0. Fakt,żeE Γ=,jestoczywisty. Wniosek.NiechF: R 2 R 2 będziepolemwektorowymklasyc 1 takim,że O + (x)mazwartedomknięcie,dlapewnegox.wówczasistniejeytakie,że F(y)=0. Dowód. Zbiór ω(x) jest zwarty i niepusty. Jeśli ω(x) zawiera punkt stacjonarny y, to teza wniosku jest spełniona. Jeśli nie, to na podstawie twierdzenia 5 LuitzenEgbertusJanBrouwer( ),matematykholenderski
7 Twierdzenie Poincaré Bendixsona 7 Poincaré Bendixsona(Tw. 1) ω(x) jest orbitą okresową Γ. Lecz z Tw. 6 wynika istnienie(wewnątrz krzywej Γ) punktu y takiego, że F(y) = 0.
ϕ(t k ; p) dla pewnego cigu t k }.
 VI. Trajektorie okresowe i zbiory graniczne. 1. Zbiory graniczne. Rozważamy równanie (1.1) x = f(x) z funkcją f : R n R n określoną na całej przestrzeni R n. Będziemy zakładać, że funkcja f spełnia założenia,
VI. Trajektorie okresowe i zbiory graniczne. 1. Zbiory graniczne. Rozważamy równanie (1.1) x = f(x) z funkcją f : R n R n określoną na całej przestrzeni R n. Będziemy zakładać, że funkcja f spełnia założenia,
II. Równania autonomiczne. 1. Podstawowe pojęcia.
 II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
Topologia - Zadanie do opracowania. Wioletta Osuch, Magdalena Żelazna, Piotr Kopyrski
 Topologia - Zadanie do opracowania Wioletta Osuch, Magdalena Żelazna, Piotr Kopyrski 5 grudnia 2013 Zadanie 1. (Topologie na płaszczyźnie) Na płaszczyźnie R 2 rozważmy następujące topologie: a) Euklidesową
Topologia - Zadanie do opracowania Wioletta Osuch, Magdalena Żelazna, Piotr Kopyrski 5 grudnia 2013 Zadanie 1. (Topologie na płaszczyźnie) Na płaszczyźnie R 2 rozważmy następujące topologie: a) Euklidesową
zbiorów domkniętych i tak otrzymane zbiory domknięte ustawiamy w ciąg. Oznaczamy
 5. Funkcje 1 klasy Baire a. Pod koniec XIX i początkiem XX wieku kilku matematyków zajmowało się problemami dotyczącymi klasyfikacji funkcji borelowskich: między innymi R. Baire, E. Borel, H. Lebesgue
5. Funkcje 1 klasy Baire a. Pod koniec XIX i początkiem XX wieku kilku matematyków zajmowało się problemami dotyczącymi klasyfikacji funkcji borelowskich: między innymi R. Baire, E. Borel, H. Lebesgue
TEST A. A-1. Podaj aksjomaty przestrzeni topologicznej według W. Sierpińskiego: aksjomaty
 TEST A A-1. Podaj aksjomaty przestrzeni topologicznej według W. Sierpińskiego: aksjomaty T 1 przestrzeni. Czym ta aksjomatyka różni się od aksjomatyki zbiorów otwartych? A-2. Ile różnych zbiorów otwartych
TEST A A-1. Podaj aksjomaty przestrzeni topologicznej według W. Sierpińskiego: aksjomaty T 1 przestrzeni. Czym ta aksjomatyka różni się od aksjomatyki zbiorów otwartych? A-2. Ile różnych zbiorów otwartych
A-1. Podaj aksjomaty przestrzeni topologicznej według W. Sierpińskiego: aksjomaty
 A-1. Podaj aksjomaty przestrzeni topologicznej według W. Sierpińskiego: aksjomaty T 1 przestrzeni. Czym ta aksjomatyka różni się od aksjomatyki zbiorów otwartych? A-2. Wyprowadź z aksjomatów topologii
A-1. Podaj aksjomaty przestrzeni topologicznej według W. Sierpińskiego: aksjomaty T 1 przestrzeni. Czym ta aksjomatyka różni się od aksjomatyki zbiorów otwartych? A-2. Wyprowadź z aksjomatów topologii
2 Rodziny zbiorów. 2.1 Algebry i σ - algebry zbiorów. M. Beśka, Wstęp do teorii miary, rozdz. 2 11
 M. Beśka, Wstęp do teorii miary, rozdz. 2 11 2 Rodziny zbiorów 2.1 Algebry i σ - algebry zbiorów Niech X będzie niepustym zbiorem. Rodzinę indeksowaną zbiorów {A i } i I 2 X nazywamy rozbiciem zbioru X
M. Beśka, Wstęp do teorii miary, rozdz. 2 11 2 Rodziny zbiorów 2.1 Algebry i σ - algebry zbiorów Niech X będzie niepustym zbiorem. Rodzinę indeksowaną zbiorów {A i } i I 2 X nazywamy rozbiciem zbioru X
Wykład 10. Stwierdzenie 1. X spełnia warunek Borela wtedy i tylko wtedy, gdy każda scentrowana rodzina zbiorów domkniętych ma niepusty przekrój.
 Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
1 Zbiory. 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =.
 1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
ZADANIA PRZYGOTOWAWCZE DO EGZAMINU Z UKŁADÓW DYNAMICZNYCH
 ZADANIA PRZYGOTOWAWCZE DO EGZAMINU Z UKŁADÓW DYNAMICZNYCH Punkty okresowe, zbiory graniczne, sprzężenia Zadanie 1. Pokazać, że trajektoria (w przód) punktu x w przestrzeni metrycznej X pod działaniem ciągłego
ZADANIA PRZYGOTOWAWCZE DO EGZAMINU Z UKŁADÓW DYNAMICZNYCH Punkty okresowe, zbiory graniczne, sprzężenia Zadanie 1. Pokazać, że trajektoria (w przód) punktu x w przestrzeni metrycznej X pod działaniem ciągłego
(b) Suma skończonej ilości oraz przekrój przeliczalnej ilości zbiorów typu G α
 FUNKCJE BORELOWSKIE Rodzinę F podzbiorów zbioru X (tzn. F X) będziemy nazywali ciałem gdy spełnione są warunki: (1) Jeśli zbiór Y F, to dopełnienie X \ Y też należy do rodziny F. (2) Jeśli S F jest skończoną
FUNKCJE BORELOWSKIE Rodzinę F podzbiorów zbioru X (tzn. F X) będziemy nazywali ciałem gdy spełnione są warunki: (1) Jeśli zbiór Y F, to dopełnienie X \ Y też należy do rodziny F. (2) Jeśli S F jest skończoną
Rozdział 6. Ciągłość. 6.1 Granica funkcji
 Rozdział 6 Ciągłość 6.1 Granica funkcji Podamy najpierw dwie definicje granicy funkcji w punkcie i pokażemy ich równoważność. Definicja Cauchy ego granicy funkcji w punkcie. Niech f : X R, gdzie X R oraz
Rozdział 6 Ciągłość 6.1 Granica funkcji Podamy najpierw dwie definicje granicy funkcji w punkcie i pokażemy ich równoważność. Definicja Cauchy ego granicy funkcji w punkcie. Niech f : X R, gdzie X R oraz
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
Zad.3. Jakub Trojgo i Jakub Wieczorek. 14 grudnia 2013
 Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Topologia I Wykład 4.
 Topologia I Wykład 4. Stefan Jackowski 24 października 2012 Przeciąganie topologii przez rodzinę przekształceń X zbiór. f = {f i : X Y i } i I rodziną przekształceń o wartościach w przestrzeniach topologicznych
Topologia I Wykład 4. Stefan Jackowski 24 października 2012 Przeciąganie topologii przez rodzinę przekształceń X zbiór. f = {f i : X Y i } i I rodziną przekształceń o wartościach w przestrzeniach topologicznych
Wykład z modelowania matematycznego.
 Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
Krzywa uniwersalna Sierpińskiego
 Krzywa uniwersalna Sierpińskiego Małgorzata Blaszke Karol Grzyb Streszczenie W niniejszej pracy omówimy krzywą uniwersalną Sierpińskiego, zwaną również dywanem Sierpińskiego. Pokażemy klasyczną metodę
Krzywa uniwersalna Sierpińskiego Małgorzata Blaszke Karol Grzyb Streszczenie W niniejszej pracy omówimy krzywą uniwersalną Sierpińskiego, zwaną również dywanem Sierpińskiego. Pokażemy klasyczną metodę
Całki powierzchniowe w R n
 Całki powierzchniowe w R n Na początek małe uzupełnienie z algebry liniowej. Niech R n k oznacza przestrzeń liniową macierzy o n wierszach i k kolumnach. Dla dowolnej macierzy A R n k, gdzie k n, połóżmy
Całki powierzchniowe w R n Na początek małe uzupełnienie z algebry liniowej. Niech R n k oznacza przestrzeń liniową macierzy o n wierszach i k kolumnach. Dla dowolnej macierzy A R n k, gdzie k n, połóżmy
Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki.
 3. Funkcje borelowskie. Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki. (1): Jeśli zbiór Y należy do rodziny F, to jego dopełnienie X
3. Funkcje borelowskie. Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki. (1): Jeśli zbiór Y należy do rodziny F, to jego dopełnienie X
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Teoria miary i całki
 Teoria miary i całki Spis treści 1 Wstęp 3 2 lgebra zbiorów 5 3 Pierścienie, ciała, σ ciała zbiorów. 7 3.1 Definicja pierścienia ciała i σ ciała............... 7 3.2 Pierścień, ciało i σ ciało generowane
Teoria miary i całki Spis treści 1 Wstęp 3 2 lgebra zbiorów 5 3 Pierścienie, ciała, σ ciała zbiorów. 7 3.1 Definicja pierścienia ciała i σ ciała............... 7 3.2 Pierścień, ciało i σ ciało generowane
Definicja odwzorowania ciągłego i niektóre przykłady
 Odwzorowania Pojęcie odwzorowania pomiędzy dwoma zbiorami było już definiowane, ale dawno, więc nie od rzeczy będzie przypomnieć, że odwzorowaniem nazywamy sposób przyporządkowania (niekoniecznie każdemu)
Odwzorowania Pojęcie odwzorowania pomiędzy dwoma zbiorami było już definiowane, ale dawno, więc nie od rzeczy będzie przypomnieć, że odwzorowaniem nazywamy sposób przyporządkowania (niekoniecznie każdemu)
. : a 1,..., a n F. . a n Wówczas (F n, F, +, ) jest przestrzenią liniową, gdzie + oraz są działaniami zdefiniowanymi wzorami:
 9 Wykład 9: Przestrzenie liniowe i podprzestrzenie Definicja 9 Niech F będzie ciałem Algebrę (V, F, +, ), gdzie V, + jest działaniem w zbiorze V zwanym dodawaniem wektorów, a jest działaniem zewnętrznym
9 Wykład 9: Przestrzenie liniowe i podprzestrzenie Definicja 9 Niech F będzie ciałem Algebrę (V, F, +, ), gdzie V, + jest działaniem w zbiorze V zwanym dodawaniem wektorów, a jest działaniem zewnętrznym
VI. Równania różniczkowe liniowe wyższych rzędów
 VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
Informacja o przestrzeniach Sobolewa
 Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Uniwersytet Mikołaja Kopernika Wydział Matematyki i Informatyki
 Uniwersytet Mikołaja Kopernika Wydział Matematyki i Informatyki Stabilność rozwiązań równań różniczkowych w ujęciu lokalnych układów dynamicznych. Adam Kanigowski Toruń 2010 1 Spis treści 1 Wprowadzenie
Uniwersytet Mikołaja Kopernika Wydział Matematyki i Informatyki Stabilność rozwiązań równań różniczkowych w ujęciu lokalnych układów dynamicznych. Adam Kanigowski Toruń 2010 1 Spis treści 1 Wprowadzenie
Weronika Siwek, Metryki i topologie 1. (ρ(x, y) = 0 x = y) (ρ(x, y) = ρ(y, x))
 Weronika Siwek, Metryki i topologie 1 Definicja 1. Załóżmy, że X, ρ: X X [0, ). Funkcja ρ spełnia następujące warunki: 1. x,y X (ρ(x, y) = 0 x = y) 2. 3. (ρ(x, y) = ρ(y, x)) x,y X (ρ(x, y) ρ(x, z) + ρ(z,
Weronika Siwek, Metryki i topologie 1 Definicja 1. Załóżmy, że X, ρ: X X [0, ). Funkcja ρ spełnia następujące warunki: 1. x,y X (ρ(x, y) = 0 x = y) 2. 3. (ρ(x, y) = ρ(y, x)) x,y X (ρ(x, y) ρ(x, z) + ρ(z,
Zdzisław Dzedzej. Politechnika Gdańska. Gdańsk, 2013
 Zdzisław Dzedzej Politechnika Gdańska Gdańsk, 2013 1 PODSTAWY 2 3 Definicja. Przestrzeń metryczna (X, d) jest zwarta, jeśli z każdego ciągu {x n } w X można wybrać podciąg zbieżny {x nk } w X. Ogólniej
Zdzisław Dzedzej Politechnika Gdańska Gdańsk, 2013 1 PODSTAWY 2 3 Definicja. Przestrzeń metryczna (X, d) jest zwarta, jeśli z każdego ciągu {x n } w X można wybrać podciąg zbieżny {x nk } w X. Ogólniej
4 Równania różniczkowe w postaci Leibniza, równania różniczkowe zupełne
 Równania w postaci Leibniza 4 1 4 Równania różniczkowe w postaci Leibniza, równania różniczkowe zupełne 4.1 Równania różniczkowe w postaci Leibniza Załóżmy, że P : D R i Q: D R są funkcjami ciągłymi określonymi
Równania w postaci Leibniza 4 1 4 Równania różniczkowe w postaci Leibniza, równania różniczkowe zupełne 4.1 Równania różniczkowe w postaci Leibniza Załóżmy, że P : D R i Q: D R są funkcjami ciągłymi określonymi
Korzystając z własności metryki łatwo wykazać, że dla dowolnych x, y, z X zachodzi
 M. Beśka, Wstęp do teorii miary, Dodatek 158 10 Dodatek 10.1 Przestrzenie metryczne Niech X będzie niepustym zbiorem. Funkcję d : X X [0, ) spełniającą dla x, y, z X warunki (i) d(x, y) = 0 x = y, (ii)
M. Beśka, Wstęp do teorii miary, Dodatek 158 10 Dodatek 10.1 Przestrzenie metryczne Niech X będzie niepustym zbiorem. Funkcję d : X X [0, ) spełniającą dla x, y, z X warunki (i) d(x, y) = 0 x = y, (ii)
Całki krzywoliniowe skierowane
 Całki krzywoliniowe skierowane Zamiana całki krzywoliniowej skierowanej na całkę pojedyńcza. Twierdzenie Greena. Zastosowania całki krzywoliniowej skierowanej. Małgorzata Wyrwas Katedra Matematyki Wydział
Całki krzywoliniowe skierowane Zamiana całki krzywoliniowej skierowanej na całkę pojedyńcza. Twierdzenie Greena. Zastosowania całki krzywoliniowej skierowanej. Małgorzata Wyrwas Katedra Matematyki Wydział
n=0 Dla zbioru Cantora prawdziwe są wersje lematu 3.6 oraz lematu 3.8 przy założeniu α = :
 4. Zbiory borelowskie. Zbiór wszystkich podzbiorów liczb naturalnych będziemy oznaczali przez ω. Najmniejszą topologię na zbiorze ω, w której zbiory {A ω : x A ω \ y}, gdzie x oraz y są zbiorami skończonymi,
4. Zbiory borelowskie. Zbiór wszystkich podzbiorów liczb naturalnych będziemy oznaczali przez ω. Najmniejszą topologię na zbiorze ω, w której zbiory {A ω : x A ω \ y}, gdzie x oraz y są zbiorami skończonymi,
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
Fale biegnące w równaniach reakcji-dyfuzji
 Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
PRACA MAGISTERSKA DYSKRETNY NIELINIOWY UKŁAD SEMIDYNAMICZNY UNIWERSYTET JAGIELLOŃSKI
 UNIWERSYTET JAGIELLOŃSKI Wydział Matematyki i Fizyki Kierunek: Matematyka Sekcja teoretyczna PRACA MAGISTERSKA DYSKRETNY NIELINIOWY UKŁAD SEMIDYNAMICZNY NA PŁASZCZYŹNIE Zbigniew Galias opiekun: doc. Jerzy
UNIWERSYTET JAGIELLOŃSKI Wydział Matematyki i Fizyki Kierunek: Matematyka Sekcja teoretyczna PRACA MAGISTERSKA DYSKRETNY NIELINIOWY UKŁAD SEMIDYNAMICZNY NA PŁASZCZYŹNIE Zbigniew Galias opiekun: doc. Jerzy
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Notatki z Analizy Matematycznej 2. Jacek M. Jędrzejewski
 Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
II. FUNKCJE WIELU ZMIENNYCH
 II. FUNKCJE WIELU ZMIENNYCH 1. Zbiory w przestrzeni R n Ustalmy dowolne n N. Definicja 1.1. Zbiór wszystkich uporzadkowanych układów (x 1,..., x n ) n liczb rzeczywistych, nazywamy przestrzenią n-wymiarową
II. FUNKCJE WIELU ZMIENNYCH 1. Zbiory w przestrzeni R n Ustalmy dowolne n N. Definicja 1.1. Zbiór wszystkich uporzadkowanych układów (x 1,..., x n ) n liczb rzeczywistych, nazywamy przestrzenią n-wymiarową
Ośrodkowość procesów, proces Wienera. Ośrodkowość procesów, proces Wienera Procesy Stochastyczne, wykład, T. Byczkowski,
 Procesy Stochastyczne, wykład, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 27 luty, 2012 Ośrodkowość procesów Dalej zakładamy, że (Ω, Σ, P) jest zupełną przestrzenią miarową. Definicja.
Procesy Stochastyczne, wykład, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 27 luty, 2012 Ośrodkowość procesów Dalej zakładamy, że (Ω, Σ, P) jest zupełną przestrzenią miarową. Definicja.
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Twierdzenie Banacha-Tarskiego z punktu widzenia algebraika
 Instytut Matematyczny PAN Konwersatorium dla doktorantów Twierdzenie Banacha-Tarskiego z punktu widzenia algebraika Joanna Jaszuńska IM PAN Warszawa, 10 listopada 2006 Twierdzenie Banacha-Tarskiego z punktu
Instytut Matematyczny PAN Konwersatorium dla doktorantów Twierdzenie Banacha-Tarskiego z punktu widzenia algebraika Joanna Jaszuńska IM PAN Warszawa, 10 listopada 2006 Twierdzenie Banacha-Tarskiego z punktu
Ciągłość i topologia. Rozdział Ciągłość funkcji wg. Cauchy
 Rozdział 1 Ciągłość i topologia Nadanie precyzyjnego sensu intiucyjnemu pojęciu ciągłości jest jednym z głównych tematów dziedziny matematyki, zwanej topologią. Definicja funkcji ciągłej znana z podstawowego
Rozdział 1 Ciągłość i topologia Nadanie precyzyjnego sensu intiucyjnemu pojęciu ciągłości jest jednym z głównych tematów dziedziny matematyki, zwanej topologią. Definicja funkcji ciągłej znana z podstawowego
Zbiór zadań z Układów Dynamicznych. Krzysztof Barański Michał Krych Anna Zdunik
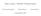 Zbiór zadań z Układów Dynamicznych Krzysztof Barański Michał Krych Anna Zdunik 9 października 2017 2 c Krzysztof Barański, Michał Krych i Anna Zdunik 2015 Spis treści 1 Punkty okresowe, zbiory graniczne,
Zbiór zadań z Układów Dynamicznych Krzysztof Barański Michał Krych Anna Zdunik 9 października 2017 2 c Krzysztof Barański, Michał Krych i Anna Zdunik 2015 Spis treści 1 Punkty okresowe, zbiory graniczne,
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
28 maja, Problem Dirichleta, proces Wienera. Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Analiza funkcjonalna 1.
 Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Temperatura w atmosferze (czy innym ośrodku) jako funkcja dł. i szer. geogr. oraz wysokości.
 Własności Odległości i normy w Będziemy się teraz zajmować funkcjami od zmiennych, tzn. określonymi na (iloczyn kartezja/nski egzemplarzy ). Punkt należący do będziemy oznaczać jako Przykł. Wysokość terenu
Własności Odległości i normy w Będziemy się teraz zajmować funkcjami od zmiennych, tzn. określonymi na (iloczyn kartezja/nski egzemplarzy ). Punkt należący do będziemy oznaczać jako Przykł. Wysokość terenu
Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/
 Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Akademicka 15, p.211a, bud. Agro
Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Akademicka 15, p.211a, bud. Agro
Rodzinę spełniającą trzeci warunek tylko dla sumy skończonej nazywamy ciałem (algebrą) w zbiorze X.
 1 σ-ciała Definicja 1.1 (σ - ciało) σ - ciałem (σ - algebrą) w danym zbiorze X (zwanym przestrzenią) nazywamy rodzinę M pewnych podzbiorów zbioru X, spełniającą trzy warunki: 1 o M; 2 o jeśli A M, to X
1 σ-ciała Definicja 1.1 (σ - ciało) σ - ciałem (σ - algebrą) w danym zbiorze X (zwanym przestrzenią) nazywamy rodzinę M pewnych podzbiorów zbioru X, spełniającą trzy warunki: 1 o M; 2 o jeśli A M, to X
Wstęp do przestrzeni metrycznych i topologicznych oraz ich zastosowań w ekonomii
 Wstęp do przestrzeni metrycznych i topologicznych oraz ich zastosowań w ekonomii Mirosław Sobolewski 25 maja 2010 Definicja. Przestrzenią metryczną nazywamy zbiór X z funkcją ρ : X X R przyporządkowującą
Wstęp do przestrzeni metrycznych i topologicznych oraz ich zastosowań w ekonomii Mirosław Sobolewski 25 maja 2010 Definicja. Przestrzenią metryczną nazywamy zbiór X z funkcją ρ : X X R przyporządkowującą
F t+ := s>t. F s = F t.
 M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
13 Równanie struny drgającej. Równanie przewodnictwa ciepła.
 Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Przestrzenie metryczne. Elementy Topologii. Zjazd 2. Elementy Topologii
 Zjazd 2 Przestrzenia metryczna (X, d) nazywamy parę złożona ze zbioru X i funkcji d : X X R, taka, że 1 d(x, y) 0 oraz d(x, y) = 0 wtedy i tylko wtedy, gdy x = y, 2 d(x, y) = d(y, x), 3 d(x, z) d(x, y)
Zjazd 2 Przestrzenia metryczna (X, d) nazywamy parę złożona ze zbioru X i funkcji d : X X R, taka, że 1 d(x, y) 0 oraz d(x, y) = 0 wtedy i tylko wtedy, gdy x = y, 2 d(x, y) = d(y, x), 3 d(x, z) d(x, y)
Zagadnienia stacjonarne
 Zagadnienia stacjonarne Karol Hajduk 19 grudnia 2012 Nierówność wariacyjna (u (t), v u(t)) + a(u, v u) + Ψ(v) Ψ(u) (f, v u), v V. Zagadnienie stacjonarne ma postać (u (t) = 0): a(u, v u) + Ψ(v) Ψ(u) (f,
Zagadnienia stacjonarne Karol Hajduk 19 grudnia 2012 Nierówność wariacyjna (u (t), v u(t)) + a(u, v u) + Ψ(v) Ψ(u) (f, v u), v V. Zagadnienie stacjonarne ma postać (u (t) = 0): a(u, v u) + Ψ(v) Ψ(u) (f,
Geometria Różniczkowa II wykład piąty
 Geometria Różniczkowa II wykład piąty Wykład piąty poświęcony będzie pojęciu całkowalności dystrybucji oraz fundamentalnemu dal tego zagadnienia twierdzeniu Frobeniusa. Przy okazji postanowiłam sprawdzić
Geometria Różniczkowa II wykład piąty Wykład piąty poświęcony będzie pojęciu całkowalności dystrybucji oraz fundamentalnemu dal tego zagadnienia twierdzeniu Frobeniusa. Przy okazji postanowiłam sprawdzić
Grupa klas odwzorowań powierzchni
 Grupa klas odwzorowań powierzchni Błażej Szepietowski Uniwersytet Gdański Horyzonty matematyki 2014 Błażej Szepietowski (UG) Grupa klas odwzorowań Horyzonty matematyki 2014 1 / 36 Grupa klas odwzorowań
Grupa klas odwzorowań powierzchni Błażej Szepietowski Uniwersytet Gdański Horyzonty matematyki 2014 Błażej Szepietowski (UG) Grupa klas odwzorowań Horyzonty matematyki 2014 1 / 36 Grupa klas odwzorowań
Wykłady... b i a i. i=1. m(d k ) inf
 Wykłady... CŁKOWNIE FUNKCJI WIELU ZMIENNYCH Zaczniemy od konstrukcji całki na przedziale domkniętym. Konstrukcja ta jest, w gruncie rzeczy, powtórzeniem definicji całki na odcinku domkniętym w R 1. Przedziałem
Wykłady... CŁKOWNIE FUNKCJI WIELU ZMIENNYCH Zaczniemy od konstrukcji całki na przedziale domkniętym. Konstrukcja ta jest, w gruncie rzeczy, powtórzeniem definicji całki na odcinku domkniętym w R 1. Przedziałem
Analiza matematyczna 1 - test egzaminacyjny wersja do ćwiczeń
 Analiza matematyczna 1 - test egzaminacyjny wersja do ćwiczeń Leszek Skrzypczak 1. Niech E = {x [0, 1] : x = k 2 n k = 1, 2,... 2 n, n = 1, 2, 3,...} Wówczas: (a) Dla dowolnych liczb wymiernych p, q [0,
Analiza matematyczna 1 - test egzaminacyjny wersja do ćwiczeń Leszek Skrzypczak 1. Niech E = {x [0, 1] : x = k 2 n k = 1, 2,... 2 n, n = 1, 2, 3,...} Wówczas: (a) Dla dowolnych liczb wymiernych p, q [0,
Informacja o przestrzeniach Hilberta
 Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Całka podwójna po prostokącie
 Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
3 Abstrakcyjne kompleksy symplicjalne.
 3 Abstrakcyjne kompleksy symplicjalne. Uwaga 3.1. Niech J będzie dowolnym zbiorem indeksów, niech R J = {(x α ) α J J α x α R} będzie produktem kartezjańskim J kopii R, niech E J = {(x α ) α J R J x α
3 Abstrakcyjne kompleksy symplicjalne. Uwaga 3.1. Niech J będzie dowolnym zbiorem indeksów, niech R J = {(x α ) α J J α x α R} będzie produktem kartezjańskim J kopii R, niech E J = {(x α ) α J R J x α
B jest liniowo niezależny V = lin (B) 1. Układ pusty jest bazą przestrzeni trywialnej {θ}. a i v i = i I. b i v i, (a i b i ) v i = θ.
 8 Baza i wymiar Definicja 8.1. Bazą przestrzeni liniowej nazywamy liniowo niezależny układ jej wektorów, który generuję tę przestrzeń. Innymi słowy, układ B = (v i ) i I wektorów z przestrzeni V jest bazą
8 Baza i wymiar Definicja 8.1. Bazą przestrzeni liniowej nazywamy liniowo niezależny układ jej wektorów, który generuję tę przestrzeń. Innymi słowy, układ B = (v i ) i I wektorów z przestrzeni V jest bazą
Twierdzenie 2: Własności pola wskazujące na istnienie orbit
 Cykle graniczne Dotychczas zajmowaliśmy się głównie znajdowaniem i badaniem stabilności punktów stacjonarnych. Wiele ciekawych procesów ma naturę cykliczną. Umiemy już sobie poradzić z cyklicznością występującą
Cykle graniczne Dotychczas zajmowaliśmy się głównie znajdowaniem i badaniem stabilności punktów stacjonarnych. Wiele ciekawych procesów ma naturę cykliczną. Umiemy już sobie poradzić z cyklicznością występującą
O ROZMAITOŚCIACH TORYCZNYCH
 O ROZMAITOŚCIACH TORYCZNYCH NA PODSTAWIE REFERATU NGUYEN QUANG LOCA Przez cały referat K oznaczać będzie ustalone ciało algebraicznie domknięte. 1. Przez cały referat N oznaczać będzie ustaloną kratę izomorficzną
O ROZMAITOŚCIACH TORYCZNYCH NA PODSTAWIE REFERATU NGUYEN QUANG LOCA Przez cały referat K oznaczać będzie ustalone ciało algebraicznie domknięte. 1. Przez cały referat N oznaczać będzie ustaloną kratę izomorficzną
Topologia I*, jesień 2012 Zadania omawiane na ćwiczeniach lub zadanych jako prace domowe, grupa 1 (prowadzący H. Toruńczyk).
 Topologia I*, jesień 2012 Zadania omawiane na ćwiczeniach lub zadanych jako prace domowe, grupa 1 (prowadzący H. Toruńczyk). Zadania w dużej mierze pochodzą z zestawu zadań w rozdziale 8 skryptu autorów
Topologia I*, jesień 2012 Zadania omawiane na ćwiczeniach lub zadanych jako prace domowe, grupa 1 (prowadzący H. Toruńczyk). Zadania w dużej mierze pochodzą z zestawu zadań w rozdziale 8 skryptu autorów
Układy równań i nierówności liniowych
 Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Zadania z analizy matematycznej - sem. II Funkcje, ich granice i ciągłość
 Zadania z analizy matematycznej - sem II Funkcje ich granice i ciągłość Zadanie 1 Wyznaczyć i naszkicować dziedziny naturalne podanych funkcji: a f y = 2 y 3 25 2 +y 2 16 b g y = ln1 2 y 2 c h y = ln 2
Zadania z analizy matematycznej - sem II Funkcje ich granice i ciągłość Zadanie 1 Wyznaczyć i naszkicować dziedziny naturalne podanych funkcji: a f y = 2 y 3 25 2 +y 2 16 b g y = ln1 2 y 2 c h y = ln 2
Analiza matematyczna. 1. Ciągi
 Analiza matematyczna 1. Ciągi Definicja 1.1 Funkcję a: N R odwzorowującą zbiór liczb naturalnych w zbiór liczb rzeczywistych nazywamy ciągiem liczbowym. Wartość tego odwzorowania w punkcie n nazywamy n
Analiza matematyczna 1. Ciągi Definicja 1.1 Funkcję a: N R odwzorowującą zbiór liczb naturalnych w zbiór liczb rzeczywistych nazywamy ciągiem liczbowym. Wartość tego odwzorowania w punkcie n nazywamy n
A i. i=1. i=1. i=1. i=1. W dalszej części skryptu będziemy mieli najczęściej do czynienia z miarami określonymi na rodzinach, które są σ - algebrami.
 M. Beśka, Wstęp do teorii miary, rozdz. 3 25 3 Miara 3.1 Definicja miary i jej podstawowe własności Niech X będzie niepustym zbiorem, a A 2 X niepustą rodziną podzbiorów. Wtedy dowolne odwzorowanie : A
M. Beśka, Wstęp do teorii miary, rozdz. 3 25 3 Miara 3.1 Definicja miary i jej podstawowe własności Niech X będzie niepustym zbiorem, a A 2 X niepustą rodziną podzbiorów. Wtedy dowolne odwzorowanie : A
Zbiory liczbowe widziane oczami topologa
 Zbiory liczbowe widziane oczami topologa Aleksander Błaszczyk Instytut Matematyki Uniwersytetu Ślaskiego Brenna, 25 wrzesień 2018 Aleksander Błaszczyk (UŚ) Zbiory liczbowe widziane oczami topologa Brenna,
Zbiory liczbowe widziane oczami topologa Aleksander Błaszczyk Instytut Matematyki Uniwersytetu Ślaskiego Brenna, 25 wrzesień 2018 Aleksander Błaszczyk (UŚ) Zbiory liczbowe widziane oczami topologa Brenna,
Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. u = 0, (6.1) jest operatorem Laplace a. (x,y)
 Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Część wspólna (przekrój) A B składa się z wszystkich elementów, które należą jednocześnie do zbioru A i do zbioru B:
 Zbiory 1 Rozważmy dowolne dwa zbiory A i B. Suma A B składa się z wszystkich elementów, które należą do zbioru A lub do zbioru B: (x A B) (x A x B). Część wspólna (przekrój) A B składa się z wszystkich
Zbiory 1 Rozważmy dowolne dwa zbiory A i B. Suma A B składa się z wszystkich elementów, które należą do zbioru A lub do zbioru B: (x A B) (x A x B). Część wspólna (przekrój) A B składa się z wszystkich
Indukcja. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Układy autonomiczne. Rozdział Stabilność w sensie Lapunowa. Przedmiotem analizy w tym rozdziale będą układy równań autonomicznych
 Rozdział 5 Układy autonomiczne 5.1 Stabilność w sensie Lapunowa Przedmiotem analizy w tym rozdziale będą układy równań autonomicznych ẋ = f(x), (5.1) z funkcją f : Q R m, gdzie Q jest otwartym zbiorem
Rozdział 5 Układy autonomiczne 5.1 Stabilność w sensie Lapunowa Przedmiotem analizy w tym rozdziale będą układy równań autonomicznych ẋ = f(x), (5.1) z funkcją f : Q R m, gdzie Q jest otwartym zbiorem
Wyk lad 9 Baza i wymiar przestrzeni liniowej
 Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
jest ciągiem elementów z przestrzeni B(R, R)
 Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych
 Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
(c) Wykazać, że (X, ϱ) jest spójna wtedy i tylko wtedy, gdy (X j, ϱ j ) jest spójna, j = 1,..., N.
 1. Przestrzenie metryczne Zadanie 1.1. Czy może się zdarzyć, że B(a, r) B(a, r)? Zadanie 1.2. Czy może się zdarzyć, że kula nie jest zbiorem spójnym? Zadanie 1.3. Niech (X, d) będzie przestrzenią metryczną
1. Przestrzenie metryczne Zadanie 1.1. Czy może się zdarzyć, że B(a, r) B(a, r)? Zadanie 1.2. Czy może się zdarzyć, że kula nie jest zbiorem spójnym? Zadanie 1.3. Niech (X, d) będzie przestrzenią metryczną
Geometria Lista 0 Zadanie 1
 Geometria Lista 0 Zadanie 1. Wyznaczyć wzór na pole równoległoboku rozpiętego na wektorach u, v: (a) nie odwołując się do współrzędnych tych wektorów; (b) odwołując się do współrzędnych względem odpowiednio
Geometria Lista 0 Zadanie 1. Wyznaczyć wzór na pole równoległoboku rozpiętego na wektorach u, v: (a) nie odwołując się do współrzędnych tych wektorów; (b) odwołując się do współrzędnych względem odpowiednio
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Stanisław Betley, Józef Chaber, Elżbieta Pol i Roman Pol TOPOLOGIA I. wykłady i zadania
 Stanisław Betley, Józef Chaber, Elżbieta Pol i Roman Pol TOPOLOGIA I wykłady i zadania WSTĘP. Materiał w skrypcie odpowiada programowi zajęć z Topologii I w trzecim semestrze studiów na Wydziale MIM Uniwersytetu
Stanisław Betley, Józef Chaber, Elżbieta Pol i Roman Pol TOPOLOGIA I wykłady i zadania WSTĘP. Materiał w skrypcie odpowiada programowi zajęć z Topologii I w trzecim semestrze studiów na Wydziale MIM Uniwersytetu
1 Elementy analizy funkcjonalnej
 M. Beśka, Dodatek 1 1 Elementy analizy funkcjonalnej 1.1 Twierdzenia o reprezentacji Zaczniemy od znanego twierdzenia Riesza Twierdzenie 1.1 (Riesz) Niech będzie zwartą przestrzenią metryczną i załóżmy,
M. Beśka, Dodatek 1 1 Elementy analizy funkcjonalnej 1.1 Twierdzenia o reprezentacji Zaczniemy od znanego twierdzenia Riesza Twierdzenie 1.1 (Riesz) Niech będzie zwartą przestrzenią metryczną i załóżmy,
Wykład 11 i 12. Matematyka 3, semestr zimowy 2011/ i 18 listopada 2011
 Wykład 11 i 12 Matematyka 3, semestr zimowy 2011/2012 15 i 18 listopada 2011 Zanim przejdziemy do formułowaniu lematu Poincaré musimy zdefiniować pojęcie transportu formy. Dyskutowaliśmy już wcześniej
Wykład 11 i 12 Matematyka 3, semestr zimowy 2011/2012 15 i 18 listopada 2011 Zanim przejdziemy do formułowaniu lematu Poincaré musimy zdefiniować pojęcie transportu formy. Dyskutowaliśmy już wcześniej
Paradoksalny rozkład kuli
 Wydział Fizyki UW Katedra Metod Matematycznych Fizyki Paradoksalny rozkład kuli Joanna Jaszuńska Centrum Studiów Zaawansowanych Politechniki Warszawskiej Warszawa, 9 grudnia 2010 Paradoksalny rozkład kuli
Wydział Fizyki UW Katedra Metod Matematycznych Fizyki Paradoksalny rozkład kuli Joanna Jaszuńska Centrum Studiów Zaawansowanych Politechniki Warszawskiej Warszawa, 9 grudnia 2010 Paradoksalny rozkład kuli
21 maja, Mocna własność Markowa procesu Wienera. Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Różniczkowalna zależność rozwiązania od warunków początkowych i parametrów
 Różniczkowalna zależność 1 Różniczkowalna zależność rozwiązania od warunków początkowych i parametrów Rozważmy zagadnienie początkowe x =f(t,x,p) (1) x()=ξ. Funkcjafjestokreślonanazbiorze(a,b) R S,gdzieRjestwnętrzem
Różniczkowalna zależność 1 Różniczkowalna zależność rozwiązania od warunków początkowych i parametrów Rozważmy zagadnienie początkowe x =f(t,x,p) (1) x()=ξ. Funkcjafjestokreślonanazbiorze(a,b) R S,gdzieRjestwnętrzem
Analiza Funkcjonalna - Zadania
 Analiza Funkcjonalna - Zadania 1 Wprowadzamy następujące oznaczenia. K oznacza ciało liczb rzeczywistych lub zespolonych. Jeżeli T jest dowolnym zbiorem niepustym, to l (T ) = {x : E K : x funkcja ograniczona}.
Analiza Funkcjonalna - Zadania 1 Wprowadzamy następujące oznaczenia. K oznacza ciało liczb rzeczywistych lub zespolonych. Jeżeli T jest dowolnym zbiorem niepustym, to l (T ) = {x : E K : x funkcja ograniczona}.
2 Równania różniczkowe zwyczajne o rozdzielonych zmiennych
 2. Równania o rozdzielonych zmiennych 2 1 2 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Równaniem różniczkowym zwyczajnym pierwszego rzędu o rozdzielonych zmiennych nazywamy równanie różniczkowe
2. Równania o rozdzielonych zmiennych 2 1 2 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Równaniem różniczkowym zwyczajnym pierwszego rzędu o rozdzielonych zmiennych nazywamy równanie różniczkowe
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
O geometrii semialgebraicznej
 Inauguracja roku akademickiego 2018/2019 na Wydziale Matematyki i Informatyki Uniwersytetu Łódzkiego O geometrii semialgebraicznej Stanisław Spodzieja Łódź, 28 września 2018 Wstęp Rozwiązywanie równań
Inauguracja roku akademickiego 2018/2019 na Wydziale Matematyki i Informatyki Uniwersytetu Łódzkiego O geometrii semialgebraicznej Stanisław Spodzieja Łódź, 28 września 2018 Wstęp Rozwiązywanie równań
sa dzie metryka z euklidesowa, to znaczy wyznaczaja ca cki, Wojciech Suwiński)
 Zadanie 1 Pokazać, że dowolne dwie kule w R z metryka sa homeomorficzne Niech ρ be dzie metryka równoważna z, to znaczy wyznaczaja ca topologie na R Czy wynika z tego, że dowolne dwie kule w metryce ρ
Zadanie 1 Pokazać, że dowolne dwie kule w R z metryka sa homeomorficzne Niech ρ be dzie metryka równoważna z, to znaczy wyznaczaja ca topologie na R Czy wynika z tego, że dowolne dwie kule w metryce ρ
Stanisław Betley, Józef Chaber, Elżbieta Pol i Roman Pol TOPOLOGIA I. wykłady i zadania. luty 2013
 Stanisław Betley, Józef Chaber, Elżbieta Pol i Roman Pol TOPOLOGIA I wykłady i zadania luty 2013 WSTĘP. Materiał w skrypcie odpowiada programowi zajęć z Topologii I w trzecim semestrze studiów na Wydziale
Stanisław Betley, Józef Chaber, Elżbieta Pol i Roman Pol TOPOLOGIA I wykłady i zadania luty 2013 WSTĘP. Materiał w skrypcie odpowiada programowi zajęć z Topologii I w trzecim semestrze studiów na Wydziale
n=0 (n + r)a n x n+r 1 (n + r)(n + r 1)a n x n+r 2. Wykorzystując te obliczenia otrzymujemy, że lewa strona równania (1) jest równa
 Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
Postać Jordana macierzy
 Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I
![2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I 2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I](/thumbs/88/115575416.jpg) Liniowa niezależno ność wektorów Przykład: Sprawdzić czy następujące wektory z przestrzeni 3 tworzą bazę: e e e3 3 Sprawdzamy czy te wektory są liniowo niezależne: 3 c + c + c3 0 c 0 c iei 0 c + c + 3c3
Liniowa niezależno ność wektorów Przykład: Sprawdzić czy następujące wektory z przestrzeni 3 tworzą bazę: e e e3 3 Sprawdzamy czy te wektory są liniowo niezależne: 3 c + c + c3 0 c 0 c iei 0 c + c + 3c3
Topologia kombinatoryczna zadania kwalifikacyjne
 Topologia kombinatoryczna zadania kwalifikacyjne Piotr Suwara 9 czerwca 2013 Nie ma wyznaczonego progu na kwalifikację na zajęcia. Gorąco zachęcam do wysyłania rozwiązań dużo przed terminem wtedy będzie
Topologia kombinatoryczna zadania kwalifikacyjne Piotr Suwara 9 czerwca 2013 Nie ma wyznaczonego progu na kwalifikację na zajęcia. Gorąco zachęcam do wysyłania rozwiązań dużo przed terminem wtedy będzie
