DYFRAKCJA ELEKTRONÓW I ŚWIATŁA NA SIECI KRYSTALICZNEJ
|
|
|
- Bogdan Majewski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Politechnik Wrszwsk Wydził Fizyki Lbortorium Fizyki I P Andrzej Politechnik Kubiczyk Wrszwsk Wydził Fizyki Lbortorium Fizyki I P Andrzej Kubiczyk 37 DYFRAKCJA ELEKTRONÓW I ŚWIATŁA NA SIECI KRYSTALICZNEJ 37 DYFRAKCJA ELEKTRONÓW I ŚWIATŁA NA SIECI KRYSTALICZNEJ 1. Podstwy fizyczne Podne przez A. Einstein w 1905 roku wyjśnienie efektu fotoelektrycznego jk równieŝ zobserwowne w 1923 roku zjwisko rozprszni promieni X n swobodnych elektronch zmieniło rdyklnie nsze poglądy n nturę fl elektromgnetycznych. Fle elektromgnetyczne, chociŝ wykzują włsności chrkterystyczne dl ruchu flowego (dyfrkcj, interferencj itp.), w oddziływniu z elektronem zchowują się jk strumień cząstek (fotonów), których energi jest równ hν (h - stł Plnck, ν- częstotliwość fli świetlnej) pęd p wynosi: hν h p = =, (1) c λ gdzie c prędkość fli świtł, λ - długość fli. Nie moŝn stwierdzić, Ŝe ntur fotonów jest flow lub, Ŝe jest korpuskulrn jedynie, Ŝe wykzują one cechy zrówno flowe jk i korpuskulrne. Ten sposób ich zchowni określ się jko dulizm korpuskulrno flowy. W 1924 roku Louis de Broglie przedstwił hipotezę, zgodnie z którą kŝdej cząstce moŝn przypisć flę o długości: h λ = (2) p gdzie p jest pędem cząstki. Ozncz to, Ŝe w pewnych wrunkch poruszjącą się cząstkę moŝn trktowć jk flę. Flę tką nzywmy flą mterii lub flą de Broglie. Wrto zwrócić uwgę, Ŝe równnie (2) otrzymć moŝn przeksztłcjąc wzór (1). Nie jest to zbieŝność przypdkow. U podstw hipotezy de Broglie tkwi bowiem złoŝenie, Ŝe dulizm korpuskulrno flowy jest podstwową włsnością cłej mterii, więc zrówno fotonów (o msie spoczynkowej równej zeru!) jk i cząstek korpuskulrnych (o msie spoczynkowej róŝnej od zer). Aby sprwdzić słuszność hipotezy de Broglie nleŝy doświdczlnie wykzć, Ŝe cząstki podlegją zjwiskom chrkterystycznym dl ruchu flowego np. zjwisku interferencji lub dyfrkcji, spełnijąc przy tym zleŝność (2). Aby zobserwowć zjwisko interferencji, nleŝy uŝyć sitki dyfrkcyjnej, której stł (tzn. odległość pomiędzy szczelinmi) nie róŝni się zncząco od długości pdjącego promieniowni (nie więcej niŝ dw rzędy wielkości). Jednocześnie cząstki, by mogły przenikć przez brdzo cienkie wrstwy mterii, powinny posidć znczną energię. Wtedy ich pęd będzie duŝy i zgodnie ze wzorem (2) długość fli de Broglie stnie się brdzo mł. To z kolei nrzuc wrunek n brdzo młą wrtość stłej sitki dyfrkcyjnej, zncznie mniejszą od moŝliwych do wykonni. Dl przykłdu: elektrony, by przeniknąć folię luminiową o grubości około 50 nm, muszą posidć energię około 10 kev, le wtedy ich długość fli de Broglie wynosi około 0,01 nm. Jest to wrtość mniejsz od średnicy tomu. Jk więc wykonć sitkę dyfrkcyjną o tk młych odległościch pomiędzy szczelinmi? Okzuje się, Ŝe wcle tkich sitek nie musimy wytwrzć, gdyŝ ich rolę spełniją krysztły. Atomy w krysztle są rozmieszczone w sposób periodyczny, odległości międzytomowe wynoszą kilk Å (czytj: ngsztremów) (1Å = 0,1 nm = m), co czyni je przydtnymi do obserwcji zjwisk interferencji fl de Broglie. Opis róŝnego typu cił krystlicznych orz definicje podstwowych pojęć związnych z budową krystliczną podno w Dodtku A.
2 Dyfrkcj świtł i elektronów n sieci krystlicznej Dyfrkcj fli n sieci krystlicznej ZłóŜmy, Ŝe n krysztł pd fl o długości λ. KŜdy tom krysztłu z nią oddziłujący sm stje się źródłem nowej (wtórnej) fli kulistej o tej smej długości (zsd Huyghens). Fle wtórne, emitowne przez poszczególne tomy, będą interferowć ze sobą. Aby znleźć wynik interferencji w przypdku ogólnym, rozptrzmy n początku przypdek, kiedy fl płsk oddziływć będzie tylko z jedną płszczyzną tomową. PoniewŜ krysztł moŝemy przedstwić jko zbiór równoległych płszczyzn tomowych, to proces powstwni w nim nowej fli opisć moŝn jko nkłdnie się (interferencję) fl kulistych powstjących w poszczególnych płszczyznch tomowych. Fle te zostną po nłoŝeniu, w zleŝności od róŝnicy ich dróg optycznych, wzmocnione lub osłbione, ptrz rys.1. Wrunkiem wzmocnieni fl jest, by róŝnic dróg optycznych był równ wielokrotności długości fli θ A θ 2θ 2 p 1 d C θ θ D p 2 B Rys.1 Dyfrkcj świtł n krysztle (1 ozncz kierunek, w którym nstępuje wzmocnienie fli w wyniku zjwisk interferencji) Z rysunku 1 wynik, Ŝe róŝnic dróg optycznych dl punktów przestrzeni połoŝonych n kierunkch 1 i 2 dl dwóch kolejnych płszczyzn tomowych (p 1 i p 2 ) wynosi: CB + BD = 2d sinθ (róŝnic dróg zznczon jest n rysunku kolorem czerwonym). Wzmocnienie interferencyjne wystąpi, gdy będzie on równ cłkowitej wielokrotności długości fli, tj.: 2 d sinθ = nλ (3) gdzie d - jest odległością między płszczyznmi tomowymi θ - kątem między kierunkiem promieni pdjącego płszczyzną tomową (tzw. kąt poślizgu - nie mylić z kątem pdni!!!), ntomist n = 1,2,3,...(rząd ugięci). Równnie (3) nosi nzwę wzoru Brgg. ChociŜ przy wyprowdzniu wzoru Brgg rozwŝne były fle powstjące tylko w dwóch kolejnych płszczyzn tomowych, to okzuje się, Ŝe jest on słuszny równieŝ w przypdku udziłu duŝej liczby tych płszczyzn. Z rys.1 widć równieŝ, Ŝe kąt między kierunkiem n którym leŝą mksim interferencyjne przedłuŝeniem kierunku fli pdjącej wynosi 2 θ. Opisny wyŝej mechnizm dyfrkcji fli n krysztle nosi nzwę dyfrkcji brggowskiej (w literturze moŝn spotkć często określenie odbicie brggowskie ). Pmiętć jednk nleŝy, Ŝe jest to szczególne odbicie tj. zchodzi tylko wtedy, gdy spełniony jest wrunek: 2 d sinθ = nλ. Tk więc zjwisko Brgg moŝn zobserwowć tylko dl fl o długościch porównywlnych z odległością między płszczyznmi międzytomowymi (d rzędu 0,1 nm) i krótszych. MoŜliwe jest więc spełnienie równni (3) dl promieniowni rentgenowskiego, niemoŝliwe dl świtł widzilnego (λ = nm). W krysztłch moŝn wyróŝnić wiele rodzin płszczyzn tomowych. N przykłd w przekroju krysztłu przedstwionym n rys.2, oprócz płszczyzn p 1, p 2, p 3,... moŝn wyróŝnić płszczyzny t 1,
3 Dyfrkcj świtł i elektronów n sieci krystlicznej 3 t 2, t 3,..., s 1, s 2, s 3,..., u 1, u 2, u 3,.... KŜd rodzin wymienionych tu płszczyzn, chrkteryzując się włsną odległością między płszczyznmi d i, moŝe dć opisne powyŝej zjwisko, jeŝeli tylko spełniony będzie wrunek Brgg. Z tego teŝ powodu otrzymujemy wiele kierunków wzmocnień dl róŝnych kątów poślizgu θ i. u 1 u 2 u 3 t 1 t 2 d 1 t 3 p 1 d 2 p 2 p 3 s 1 s 2 s 3 d 4 d 3 Rys.2 Przykłdy rodzin płszczyzn tomowych w krysztle (n rysunku widzimy ich rzuty n płszczyznę rysunku) JeŜeli krysztł zczniemy obrcć względem osi pokrywjącej się z kierunkiem wiązki pdjącej, to wiązki wzmocnione zczną ztczć powierzchnie stoŝkowe o kącie rozwrci 4Θ. Gdy równoległ i monochromtyczn fl pd n polikrysztł tzn. mterił zwierjący duŝą liczbę młych (o rozmirch mikronowych) monokrysztłów (krystlitów), zorientownych w sposób przypdkowy, to zobserwujemy efekt tki jk przy obrocie krysztłu. Zwsze bowiem znjdzie się pewn liczb krystlitów, dl których wrunek Brgg będzie spełniony dl dnego kąt Θ i wówczs wiązki wzmocnione tworzyć będą powierzchnie stoŝków o kątch rozwrci4θ. JeŜeli n drodze wiązek wzmocnionych ustwimy ekrn, to zobserwujemy n nim okręgi (rys.3). cienk foli polikrystliczn wiązk elektronów 4θ 1 4θ 2 D 1 D 2 Rys.3 Zjwisko Brgg dl próbki polikrystlicznej. r płszczyzn ekrnu
4 Dyfrkcj świtł i elektronów n sieci krystlicznej Doświdczenie Thomson RozwŜni przeprowdzone wcześniej, stnowią podstwę do zrozumieni doświdczeni przeprowdzonego przez G. P. Thomson w 1927r. potwierdzjącego hipotezę de Broglie. Thomson umieścił w lmpie oscyloskopowej, z ukłdem nod ogniskujących, cienką złotą folię (foli tk m budowę polikrystliczną). Elektrony pdjąc n nią, podległy zjwiskom, które zostły wyŝej omówione (tzn. zjwisku interferencji), djąc w rezultcie n ekrnie okręgi o róŝnych średnicch D i. Powstły n ekrnie ukłd pierścieni dje się wyjśnić, jeŝeli przyjmiemy, Ŝe z elektronem związn jest fl, której długość określon jest przez wzór: λ=h/p. Oddziłuje on z folią polikrystliczną w przedstwiony wcześniej sposób. Dodtkowym rgumentem z słusznością tego złoŝeni jest fkt, Ŝe ten sm ukłd okręgów otrzymno przy nświetleniu wspomninej folii promienimi rentgen o podobnej długości fli, co długość fli elektronów przewidywn przez de Broglie. Doświdczenie Thomson potwierdz więc flową nturę strumieni elektronów. Fl związn z elektronem jest flą mterii, której nturę opisno szczegółowo w Dodtku B. Do zbdni włsności fli mterii ( tkŝe sprwdzeni hipotezy de Broglie ) uŝyto odpowiednio przygotownej lmpy oscyloskopowej, w której n drodze wiązki elektronowej umieszczono cienką folię (luminiową lub grfitową). Jej grubość wynosi około 50 nm. Tk cienk foli jest przezroczyst dl elektronów o energich powyŝej 8 kev. Otrzymuje się ją poprzez próŝniowe nprownie. Emitowne przez ktodę lmpy oscyloskopowej elektrony, nim pdną n folię luminiową, są przyspieszne do energii kinetycznej E k =eu przez przyłoŝone npięcie U, które moŝn regulowć. PoniewŜ odległość folii od ekrnu jest zncznie większ od średnicy otrzymnych n ekrnie okręgów interferencyjnych D, to zgodnie z rys.3: sin 4θ 4θ D / r (r odległość foli-ekrn), stąd: sinθ θ D / 4r. Podstwijąc tk obliczoną wrtość sin θ do wzoru Brgg (3), otrzymujemy: dd = nλ 2r (4) Wrtość λ znjdujemy ze wzoru (1) tzn. λ = h / p. Pęd elektronu p obliczymy znjąc npięcie U z klsycznego związku między pędem jego energią eu, tj.: eu=p 2 /2m (e łdunek elektronu, m jego ms). Reltywistyczn zmin msy elektronu przy energich pol elektrycznego uŝytego w doświdczeniu wprowdz niepewność pomijlnie młą. Podstwijąc do h wzoru (4) wrtość λ obliczoną dl npięci przyśpieszjącego U: λ = orz n = 1 (gdyŝ tylko 2meU okręgi pierwszego rzędu są widoczne), otrzymujemy: D = d 2rh 2meU (5) Średnic okręgu interferencyjnego D, pochodzącego od tego smego zespołu płszczyzn tomowych powinn być odwrotnie proporcjonln do pierwistk kwdrtowego npięci przyspieszjącego elektrony U. Jeśli uzyskmy tki wynik, to będzie potwierdzeniem słuszności wzoru opisującego hipotezę de Broglie Dyfrkcj świtł n sieci dwuwymirowej Celem drugiej części ćwiczeni jest zpoznnie się z dyfrkcją świtł n regulrnej sieci dwuwymirowej w przypdku, gdy wiązk świtł pd n sieć pod kątem prostym do płszczyzny sieci. Zgodnie z tym co npisno w poprzedniej części instrukcji, kŝdy z tomów stje się źródłem nowej fli kulistej. Fle te interferują ze sobą, efekt moŝemy zobczyć n ekrnie ustwionym prostopdle do kierunku pdni fli, w pewnej odległości od sieci.
5 Dyfrkcj świtł i elektronów n sieci krystlicznej 5 Rozptrzmy sieć regulrną prostokątną. Wrunkiem wzmocnieni w tkim przypdku jest spełnienie dwóch równń Luego, które moŝemy zpisć w sposób nstępujący: cos Θ ' = mλ (6) b cos Θ '' = nλ gdzie, b stłe sieciowe, Θ` i Θ`` kąty między kierunkiem pdni wiązki świetlnej kierunkiem wzmocnieni (wiązki wzmocnione tworzą stoŝki o kątch rozwrci 2Θ` i 2Θ``), m i n dowolne liczby cłkowite. Rozwiązniem kŝdego z równń Luego są powierzchnie stoŝkowe, które n ekrnie ustwionym w kierunku równoległym do powierzchni sieci ( prostopdłym do kierunku pdni wiązki świetlnej) tworzą rodziny hiperbol. Wspólnym rozwiązniem obu równń obserwownym n ekrnie w postci świecących punktów są punkty przecięci hiperbol. W przeprowdznym doświdczeniu długość fli świetlnej (0,6 µm) jest prwie trzy rzędy mniejsz od odległości między tommi w bdnej sieci krystlicznej (0,1 mm). Z tego powodu n ekrnie punkty ukłdją się n hiperbolch o brdzo młej krzywiźnie, widocznych włściwie jko linie proste (krzywizny hiperbol nie dje się zuwŝyć). Y h=-3 h=-2 h=-1 h=1 h=2 h=3 k=2 k=1 k=-1 X k=-2 Rys.4 Wygląd ekrnu przypdku dyfrkcji n sieci regulrnej czrne punkty n ilustrcji to świecące punkty n ekrnie, efekt przecięci hiperbol (definicj indeksów h i k) Świecącym punktom n ekrnie przypisujemy dw wskźniki (ptrz ilustrcj 4), które nzywne są wskźnikmi Miller. Współrzędne punktów zpisujemy w postci pr liczb (h, k) n przykłd (1, 1) (3, 1) (-2, 5), itd. Odcinek, który łączy punkt (h, k) ze środkiem obrzu dyfrkcyjnego (czyli z punktem (0, 0)) oznczmy H hk. Znjomość długości świtł λ uŝytego w doświdczeniu, odległości L ekrnu od sieci krystlicznej orz wrtości H kl pozwl n wyznczenie stłych sieciowych bdnej sieci. Z włsności geometrycznych otrzymujemy nstępujący wzór: H tg Θ = hk hk L (7) co uwzględnijąc znną zleŝność d sin hk Θ hk = nλ (8)
6 Dyfrkcj świtł i elektronów n sieci krystlicznej 6 pozwl wyznczyć stłe d hk, z nich stłe sieciowe bdnej sieci. Sposób wyznczeni stłych sieciowych zleŝy od rodzju sieci. Związki między stłymi sieciowymi wyznczonymi stłymi d hk są nstępujące: d hk = (sieć regulrn, stł sieciow ) 2 2 h + k d hk = (sieć heksgonln, stł sieciow ) (9) ( h + kh + k ) 3 1 d hk = (sieć prostokątn, stłe sieciowe i b) 2 2 h k b Gdy wiązk pd n sieć polikrystliczną, to n ekrnie powinniśmy uzyskć współśrodkowe okręgi (tk jk w przypdku dyfrkcji elektronów). Jeśli okręgi nie są wyrźnie widoczne, to ozncz, Ŝe wiązk świtł obejmuje zbyt młą liczbę róŝnie zorientownych obszrów monokrystlicznych. 2. Wykonnie ćwiczeni i oprcownie wyników 2.1. Dyfrkcj elektronów doświdczenie Thompson Wykonnie ćwiczeni 1. Zpoznć się z obsługą zsilcz lmpy oscyloskopowej (w rzie wątpliwości pytć prowdzącego). 2. Upewnić się czy pokrętło regulcji npięci przyspieszjącego elektrony jest w połoŝeniu zerowym (skręcone w lewo ) jeŝeli nie, to przestwić w to połoŝenie. 3. Włączyć zsilnie zsilcz i odczekć około 2 minuty do ngrzni ktody lmpy oscyloskopowej. 4. Obrcjąc pokrętło regulcji npięci przyspieszjącego elektrony zobserwowć pojwienie się plmki n ekrnie (w zleŝności od potrzeby regulujemy jej jsność). 5. Zwiększmy npięcie przyspieszjące elektrony Ŝ do pojwieni się pierścieni (kontrolując jsność i ostrość obrzu). 6. Przy ustlonym npięciu przyspieszjącym U mierzymy średnice D i wszystkich widocznych n ekrnie pierścieni w funkcji npięci przyspieszjącego U dl co njmniej 6-ciu róŝnych npięć. 7. Skręcmy pokrętło regulcji npięci przyspieszjącego w połoŝenie zerowe (skrjne w lewo ) i wyłączmy zsilnie. 8. Notujemy odległość r (foli ekrn ). Oprcownie wyników 1. Sprwdzić, czy uzyskne wyniki są zgodne z wzorem (5), sporządzjąc wykres zleŝności średnicy 2rh pierścieni D i od (czyli od funkcji zleŝnej od odwrotności pierwistk kwdrtowego 2meU npięci przyspieszjącego) i korzystjąc z metody njmniejszych kwdrtów (obliczeni przy uŝyciu progrmu komputerowego!!), znleźć wrtość współczynnik nchyleni otrzymnej prostej b i jego niepewność. 2. N podstwie wyników proksymcji liniowej obliczyć odległość pomiędzy płszczyznmi tomowymi d orz jej niepewność obliczną metodą typu A. Niepewność obliczną metodą typu B wyznczyć n podstwie jednego punktu pomirowego (potrzebne stłe fizyczne wziąć z tblic). Przy obliczniu niepewności złoŝonej wykorzystć prwo przenoszeni niepewności.
7 Dyfrkcj świtł i elektronów n sieci krystlicznej 7 3. Korzystjąc z otrzymnego wykresu i z testu χ 2 odpowiedzieć n pytnie dotyczące prwdziwości hipotezy de Broglie. Porównć otrzymne wynik z wrtościmi odległości międzytomowych w krysztłch grfitu. N poniŝszym rysunku przedstwiono schemt budowy krystlicznej grfitu. 142 pm 688 pm Rys.5 Sieć krystliczn grfitu 246 pm Wrstw grfitu, przez którą przechodzi wiązk elektronów jest wrstwą polikrystliczną. Rozerwniu ulegją długie wiązni między poszczególnymi wrstwmi (rys.5), tk więc orientcj komórek jest przypdkow. (Grfit jest brdzo śliski i łtwo się rozprowdz po powierzchni jest to włśnie efekt przesuwni się względem siebie poszczególnych wrstw tomów węgl. Z drugiej strony grfit jest brdzo odporny n ścisknie. Z tych powodów jest on wykorzystywny do produkcji róŝnego typów smrów, w szczególności do smrów suchych). d 1 d 1 d 2 =123 pm d 1 = 213 pm Rys.6 Odległości międzypłszczyznowe dl dwóch pierwszych pierścieni interferencyjnych 4. W sprwozdniu nleŝy odpowiedzieć n nstępujące pytni: Dlczego intensywność obu pierścieni jest porównywln? Dlczego nie widć pierścieni wyŝszych rzędów interferencji lub pochodzących od innych płszczyzn tomowych?
8 Dyfrkcj świtł i elektronów n sieci krystlicznej Dyfrkcj świtł n sieci krystlicznej Wykonnie ćwiczeni Do obserwcji dyfrkcji świtł n krysztłch wykorzystywne są dwuwymirowe modele róŝnych typów sieci krystlicznej i polikrystlicznej w postci przezroczy n folii świtłoczułej. Jko źródło świtł wykorzystywny jest lser półprzewodnikowy generujący świtło o długości podnej n uchwycie lser. Lser umocowny jest n podstwie, do której mgnetycznie mocuje się przezrocz (rmki mją w dolnej części pski mgnetyczne). KŜde z przezroczy posid oznczeni (np. A1, C2, itp.). Sttyw z lserem nleŝy ustwić w zznczonej pozycji n stole lbortoryjnym w dokłdnie określonej odległości od ekrnu znjdującego się n pionowej obudowie stnowisk lbortoryjnego (odległość przezrocze ekrn musi pozostwć niezmienn). Ekrn wyposŝony jest w klips, w którym mocuje się protokół i przerysowuje powstjące obrzy dyfrkcyjne. N stnowisku znjduje się równieŝ mikroskop optyczny, który słuŝy do obserwcji modeli sieci i bezpośrednich pomirów stłych sieciowych (przy uŝyciu przesuwu mikrometrycznego stolik mikroskopu lub sieci pjęczej w okulrze). W podnej poniŝej instrukcji wykonni ćwiczeni polecenie odrysowć obrz ozncz umieszczenie protokołu n ekrnie i zznczenie długopisem njwŝniejszych elementów powstłego obrzu interferencyjnego. 1. Włączyć lser i ustwić go w zznczonym n stole lbortoryjnym miejscu tk, by wiązk pdł w pobliŝu środk ekrnu. 2. W bieg wiązki świtł lserowego wstwić przezrocz oznczone A1, B1 i C1. Odrysowć n protokole powstłe obrzy. 3. W bieg wiązki świtł lserowego wstwić przezrocze oznczone D1. Odrysowć n protokole powstły obrz. 4. W bieg wiązki świtł lserowego wstwić przezrocze oznczone B5. Odrysowć n protokole powstły obrz. 5. Wszystkie wykorzystne w trkcie ćwiczeni przezrocz umieścić kolejno n stoliku mikroskopu optycznego i wykonć bezpośrednie pomiry stłych sieciowych. 6. W bieg wiązki świtł lserowego wstwić przezrocz oznczone B2 i B3. Oprcownie wyników 1. Porównć obrzy interferencyjne dl przezroczy A1, B1 i C1. Co zostło zobserwowne pod mikroskopem? Potwierdzeniem jkiej zsdy fizycznej jest wynik tej części doświdczeni? 2. N podstwie wzorów (7), (8) i (9) obliczyć stłe sieciowe dl tych sieci krystlicznych. Otrzymny wynik porównć z wynikiem pomirów spod mikroskopu. 3. Obliczyć stłe sieciowe dl przezrocz D1. Otrzymny wynik porównć z wynikiem pomirów spod mikroskopu. 4. Z jkim krysztłem mmy do czynieni w przypdku przezrocz B5. Wyznczyć stłą sieciową mierząc średnicę pierścieni interferencyjnego. Otrzymny wynik porównć z wynikiem pomirów spod mikroskopu. Czy obrz interferencyjny uzyskny dl sljdu B5 moŝn porównć z obrzem uzysknym dl dyfrkcji elektronów w doświdczeniu Thompson w poprzedniej części ćwiczeni? Odpowiedź nleŝy uzsdnić. 5. Jkie sieci krystliczne przedstwione n przezroczch B2 i B3?. Obliczyć stłe sieciowe. 6. Dl wszystkich rodzjów sieci oszcowć niepewności wyznczonych stłych sieciowych.
9 Dyfrkcj świtł i elektronów n sieci krystlicznej 9 3. Pytni kontrolne 1. Jkie złoŝenie tkwi u podstw hipotezy de Broglie? 2. Jkie muszą być spełnione wrunki, by nstąpiło wzmocnienie interferujących fl? 3. Wyprowdź wzór Brgg. 4. Jkie zjwisko fizyczne opisują równni Luego? 5. Nrysowć i wyjśnić obrz interferencyjny przy dyfrkcji świtł n polikrysztle. 6. Wyjśnić istotę doświdczeni Thomson. Jk jest zleŝność pomiędzy średnicą pierścieni npięciem przyspieszjącym? 7. ZłóŜmy, Ŝe neutron i elektron posidją tką smą energię. Której cząstce odpowid większ długość fli de Broglie? 4. Litertur 1. D. Hllidy, R. Resnick, J. Wlker, Podstwy fizyki, tom IV, PWN R. Eisberg i R. Resnick, Fizyk kwntow str. 78 PWN Cz. Bobrowski, Fizyk krótki kurs, WNT 1993
10 Dyfrkcj świtł i elektronów n sieci krystlicznej 10 DODATEK A Budow krystliczn cił stłych Ze względu n sposób ułoŝeni tomów (lub cząstek) cił stłe moŝemy podzielić n cił monokrystliczne, polikrystliczne orz morficzne (bezpostciowe). Monokrysztły są to tkie cił, w których tomy ułoŝone są w sposób regulrny w cłej objętości cił mówi się wówczs o uporządkowniu dlekiego zsięgu. Odległość między sąsiednimi tommi wynosi zzwyczj kilk Angstremów (Å). Njmniejszą komórkę, której powtórzenie we wszystkich trzech kierunkch dje monokrysztł nzywmy komórką elementrną. Komórkę elementrną definiują długości jej boków (tk zwne stłe sieciowe) w trzech wybrnych kierunkch orz trzy kąty, które tworzą ze sobą te boki. W doświdczeniu tym rozwŝmy njprostsze dwuwymirowe sieci krystliczne, które przedstwiono n rys. 7. Drugim bdnym w doświdczeniu typem cił krystlicznych są polikrysztły. Są to cił, w których moŝn zobserwowć obszry o strukturze monokrystlicznej ułoŝone względem siebie w sposób przypdkowy. Obszry te (zirn monokrystliczne - krystlity) mogą mieć wielkość rzędu ułmków mikrometr, tkŝe rozmiry mkroskopowe. Nturlnym stnem dl większości cił stłych jest stn krystliczny, często monokrystliczny, gdyŝ energi uporządkowni tomów jest njmniejsz. W przyrodzie często moŝn zobserwowć piękne i o duŝych wymirch monokrysztły: krysztły soli w Wieliczce, dimenty (krysztły węgl!) itd. Jeśli jednk w procesie tworzeni się krysztłu zkłócony zostnie proces krystlizcji, to otrzymuje się polikrysztł czy wręcz ciło morficzne. Monokrysztły znjdują szerokie zstosownie we współczesnej technice, stnowią podstwę cłej mikroelektroniki, bez nich nie powstłyby mikroprocesory, pmięci, ukłdy elektroniczne i komputery. Większość ukłdów sclonych wytwrzn jest n cienkich płytkch monokrystlicznego krzemu. KŜdy sznujący się student Politechniki Wrszwskiej powinien wiedzieć, Ŝe metodę otrzymywni monokrysztłów przez krystlizcję z substncji stopionej oprcowł Jn Czochrlski, wybitny chemik i metloznwc, profesor Politechniki Wrszwskiej od 1930 roku do końc II Wojny Świtowej. Metod t (znn n cłym świecie pod nzwą metody Czochrlskiego) jest do dzisij podstwową metodą umoŝliwijącą otrzymywnie monokrysztłów o niebywłej wręcz średnicy kilkudziesięciu centymetrów i długości kilku metrów. Monokrysztły tnie się n plsterki o grubości części milimetr i n nich wykonywne są wszechobecne ukłdy sclone. b b ) b) c) Rys.7 Typy sieci krystlicznych dwuwymirowych: sieć ) regulrn, b) prostokątn, c) heksgonln
11 Dyfrkcj świtł i elektronów n sieci krystlicznej 11 DODATEK B Ntur fl de Broglie Próbując odpowiedzieć n to pytnie, odwołmy się do eksperymentu. JeŜeli w eksperymencie Thomson uŝyć wiązki elektronowej o niezwykle młym ntęŝeniu tk, by moŝn było przyjąć, Ŝe n folię pdją pojedyncze elektrony, to n ekrnie obserwowć będzie będziemy pojedyncze błyski o jednkowym ntęŝeniu. Njwięcej będzie ich w miejscu odpowidjącym przechodzeniu elektronów n wprost, le pewn liczb błysków będzie obserwown n okręgch interferencyjnych. Pojwienie się pojedynczych błysków wyrźnie przeczy ewentulności, Ŝe fl de Broglie to po prostu flownie mterii elektronowej. Gdyby tk było, wówczs obserwowlibyśmy cły obrz interferencyjny (tj. ukłd okręgów), chociŝ o brdzo młym ntęŝeniu, juŝ przy przejściu pojedynczego elektronu. Wynik tk przeprowdzonego doświdczeni nie powinien jednk zchwić nszego przekonni o flowych włsnościch elektronu (włsnościch, nie nturze), gdyŝ błyski pojwiły się (oprócz miejsc odpowidjącemu przechodzeniu elektronów n wprost) tylko n okręgch interferencyjnych. Do tego, jk wykzno wyŝej, potrzebne jest oddziływnie fli (elektronu) z wielom płszczyznmi tomowymi, więc elektron zchowuje się jk fl. JednkŜe nie potrfimy wyjśnić dlczego pojedynczy elektron oddziłuje z płszczyznmi tomowymi jko fl, z tommi ekrnu jk korpuskuł. Anlizując wyniki innych eksperymentów sformułowć moŝn wniosek: jeŝeli cząstk oddziłuje z obiektem w tki sposób, Ŝe niemoŝliwe jest stwierdzenie z jką częścią obiektu nstępuje to oddziływnie, to ujwniją się włsności flowe cząstki (oddziływnie z płszczyznmi tomowymi krysztłów cienkiej folii). Ntomist, kiedy mmy moŝliwość zloklizowni oddziływującej cząstki (np. oddziływnie z konkretnymi tommi ekrnu), to wtedy oddziłuje jk korpuskuł. W obszrze przyśpieszjącego elektron pol elektrycznego tkŝe moŝemy dokłdnie (w zkresie energii pol rzędu 10 kev) prześledzić połoŝenie i pęd cząstki. Oddziływnie elektronu z polem elektrycznym w lmpie oscyloskopowej teŝ pozwl n trktownie elektronu jko cząstki. Dl dopełnieni obrzu dodjmy jeszcze, Ŝe gdy w omwinym eksperymencie umieścić z ekrnem kliszę fotogrficzną (zmist obserwowć pojedyncze błyski), to po dłuŝszym nświetlniu otrzymny n niej obrz niczym nie będzie się róŝnił od obrzu obserwownego n ekrnie przy duŝym ntęŝeniu wiązki elektronowej. Ten osttni wynik świdczy o sttystycznym chrkterze prw rządzących zchowniem się cząsteczek. Pogląd ten reprezentuje mechnik kwntow - teori, do której powstni przyczynił się hipotez de Broglie. Mechnik kwntow nie wnik w nturę fl de Broglie, jedynie zjmuje się opisem zchowni się cząstek z uwzględnieniem ich flowych włsności. Stn cząstki w mechnice kwntowej opisuje funkcj flow ψ(x,y,z) o postci mtemtycznej toŝsmej z równniem fli znnym z optyki. Mtemtyczną postć funkcji flowej znjdujemy rozwiązując równni Schrödinger (podstwowe równnie mechniki kwntowej). Jej interpretcj jest probbilistyczn (sttystyczn). Kwdrt modułu funkcji ψ(x,y,z) jest gęstością prwdopodobieństw znlezieni cząstki w dnym punkcie przestrzeni o współrzędnych x,y,z. Ntomist prwdopodobieństwo P znlezieni cząstki w elemencie objętości dv w pobliŝu dnego punktu przestrzeni wynosi: P = ψ ( x, y, z) 2 dv Fl mterii (de Broglie ) jest opisywn przez funkcję ψ ( x, y, z) mjącą postć równni fli.
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Wykład 6 Dyfrakcja Fresnela i Fraunhofera
 Wykłd 6 Dyfrkcj Fresnel i Frunhofer Zjwisko dyfrkcji (ugięci) świtł odkrył Grimldi (XVII w). Poleg ono n uginniu się promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny). Wyjśnienie
Wykłd 6 Dyfrkcj Fresnel i Frunhofer Zjwisko dyfrkcji (ugięci) świtł odkrył Grimldi (XVII w). Poleg ono n uginniu się promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny). Wyjśnienie
Realizacje zmiennych są niezależne, co sprawia, że ciąg jest ciągiem niezależnych zmiennych losowych,
 Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
2. Tensometria mechaniczna
 . Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
. Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Zastosowanie multimetrów cyfrowych do pomiaru podstawowych wielkości elektrycznych
 Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna
 1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
Macierz. Wyznacznik macierzy. Układ równań liniowych
 Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: Ŝółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk n kierunku Biologi w SGGW Zgdnieni.
Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: Ŝółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk n kierunku Biologi w SGGW Zgdnieni.
Aby opisać strukturę krystaliczną, konieczne jest określenie jej części składowych: sieci przestrzennej oraz bazy atomowej.
 2. Struktury i pierwistki N zjęcich zjmiemy się pierwistkmi i strukturmi krystlicznymi. O ile w przypdku tych pierwszych, temt poruszny był w trkcie wykłdu, to drugie zgdnienie może wymgć krótkiego przybliżeni/przypomnieni.
2. Struktury i pierwistki N zjęcich zjmiemy się pierwistkmi i strukturmi krystlicznymi. O ile w przypdku tych pierwszych, temt poruszny był w trkcie wykłdu, to drugie zgdnienie może wymgć krótkiego przybliżeni/przypomnieni.
Równania i nierówności kwadratowe z jedną niewiadomą
 50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
FALOWE WŁASNOŚCI MIKROCZĄSTEK SPRAWDZANIE HIPOTEZY DE BROGLIE'A
 FALOWE WŁASNOŚCI MIKROCZĄSTEK SPRAWDZANIE HIPOTEZY DE BROGLIE'A 1. PODSTAWY FIZYCZNE Podane przez Einsteina w 1905 roku wyjaśnienie efektu fotoelektrycznego jak również zaobserwowane w 1923r. zjawisko
FALOWE WŁASNOŚCI MIKROCZĄSTEK SPRAWDZANIE HIPOTEZY DE BROGLIE'A 1. PODSTAWY FIZYCZNE Podane przez Einsteina w 1905 roku wyjaśnienie efektu fotoelektrycznego jak również zaobserwowane w 1923r. zjawisko
Oznaczenia: K wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania wykraczające
 Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU
 POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU I. Cel ćwiczeni: zpoznnie z teorią odksztłceń sprężystych cił stłych orz z prwem Hooke.Wyzncznie modułu sprężystości (modułu Young) metodą
POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU I. Cel ćwiczeni: zpoznnie z teorią odksztłceń sprężystych cił stłych orz z prwem Hooke.Wyzncznie modułu sprężystości (modułu Young) metodą
mgh. Praca ta jest zmagazynowana w postaci energii potencjalnej,
 Wykłd z fizyki. Piot Posmykiewicz 49 6-4 Enegi potencjln Cłkowit pc wykonn nd punktem mteilnym jest ówn zminie jego enegii kinetycznej. Często jednk, jesteśmy zinteesowni znlezieniem pcy jką sił wykonł
Wykłd z fizyki. Piot Posmykiewicz 49 6-4 Enegi potencjln Cłkowit pc wykonn nd punktem mteilnym jest ówn zminie jego enegii kinetycznej. Często jednk, jesteśmy zinteesowni znlezieniem pcy jką sił wykonł
Struktura energetyczna ciał stałych-cd. Fizyka II dla Elektroniki, lato
 Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Dorota Ponczek, Karolina Wej. MATeMAtyka 2. Plan wynikowy. Zakres podstawowy
 Dorot Ponczek, rolin Wej MATeMAtyk Pln wynikowy Zkres podstwowy MATeMAtyk. Pln wynikowy. ZP Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące, W wymgni wykrczjące
Dorot Ponczek, rolin Wej MATeMAtyk Pln wynikowy Zkres podstwowy MATeMAtyk. Pln wynikowy. ZP Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące, W wymgni wykrczjące
2. FUNKCJE WYMIERNE Poziom (K) lub (P)
 Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
INSTRUKCJA. - Jak rozwiązywać zadania wysoko punktowane?
 INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
Temat lekcji Zakres treści Osiągnięcia ucznia
 ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
Wymagania edukacyjne matematyka klasa 2 zakres podstawowy 1. SUMY ALGEBRAICZNE
 Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymagania kl. 2. Uczeń:
 Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Zadanie 5. Kratownica statycznie wyznaczalna.
 dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
Ćwiczenie 42 Wyznaczanie ogniskowych soczewek
 Ćwiczenie 4 Wyzncznie ogniskowych soczewek Wstęp teoretyczny: Krzyszto Rębils. utorem ćwiczeni w Prcowni izycznej Zkłdu izyki Uniwersytetu Rolniczego w Krkowie jest Józe Zpłotny. ZJWISK ZŁMNI ŚWITŁ Świtło,
Ćwiczenie 4 Wyzncznie ogniskowych soczewek Wstęp teoretyczny: Krzyszto Rębils. utorem ćwiczeni w Prcowni izycznej Zkłdu izyki Uniwersytetu Rolniczego w Krkowie jest Józe Zpłotny. ZJWISK ZŁMNI ŚWITŁ Świtło,
Wymagania na ocenę dopuszczającą z matematyki klasa II Matematyka - Babiański, Chańko-Nowa Era nr prog. DKOS 4015-99/02
 Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Wyznacznikiem macierzy kwadratowej A stopnia n nazywamy liczbę det A określoną następująco:
 Def.8. Wyzncznikiem mcierzy kwdrtowej stopni n nzywmy liczbę det określoną nstępująco:.det.det dl n n det det n det n, gdzie i j ozncz mcierz, którą otrzymujemy z mcierzy przez skreślenie i- tego wiersz
Def.8. Wyzncznikiem mcierzy kwdrtowej stopni n nzywmy liczbę det określoną nstępująco:.det.det dl n n det det n det n, gdzie i j ozncz mcierz, którą otrzymujemy z mcierzy przez skreślenie i- tego wiersz
Struktura kryształów. Kittel, rozdz. 1 (Uwaga błędna terminologia!) Ashcroft, Mermin, rozdz.
 Struktur krysztłów http://www.uncp.edu/home/mcclurem/ptble/crbon.htm Kittel, rozdz. 1 (Uwg błędn terminologi!) Ashcroft, Mermin, rozdz. 4,7 1 Obserwowne włsności Ksztłt ogrniczony płszczyznmi. (1) Kierunki
Struktur krysztłów http://www.uncp.edu/home/mcclurem/ptble/crbon.htm Kittel, rozdz. 1 (Uwg błędn terminologi!) Ashcroft, Mermin, rozdz. 4,7 1 Obserwowne włsności Ksztłt ogrniczony płszczyznmi. (1) Kierunki
Macierz. Wyznacznik macierzy. Układ równań liniowych
 Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: żółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk Zgdnieni. Pojęci. Dziłni n mcierzch.
Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: żółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk Zgdnieni. Pojęci. Dziłni n mcierzch.
Modelowanie i obliczenia techniczne. Metody numeryczne w modelowaniu: Różniczkowanie i całkowanie numeryczne
 Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Wymagania edukacyjne matematyka klasa 2b, 2c, 2e zakres podstawowy rok szkolny 2015/2016. 1.Sumy algebraiczne
 Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
Katalog wymagań programowych na poszczególne stopnie szkolne. Matematyka. Poznać, zrozumieć
 Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
( ) Lista 2 / Granica i ciągłość funkcji ( z przykładowymi rozwiązaniami)
 List / Grnic i ciągłość funkcji ( z przykłdowymi rozwiąznimi) Korzystjąc z definicji grnicy (ciągowej) funkcji uzsdnić podne równości: sin ) ( + ) ; b) ; c) + 5 Obliczyć grnice funkcji przy orz : + ) f
List / Grnic i ciągłość funkcji ( z przykłdowymi rozwiąznimi) Korzystjąc z definicji grnicy (ciągowej) funkcji uzsdnić podne równości: sin ) ( + ) ; b) ; c) + 5 Obliczyć grnice funkcji przy orz : + ) f
Zadania. I. Podzielność liczb całkowitych
 Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
DZIAŁ 2. Figury geometryczne
 1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
Wyrównanie sieci niwelacyjnej
 1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
Algebra Boola i podstawy systemów liczbowych. Ćwiczenia z Teorii Układów Logicznych, dr inż. Ernest Jamro. 1. System dwójkowy reprezentacja binarna
 lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
ZADANIA OTWARTE. Są więc takie same. Trzeba jeszcze pokazać, że wynoszą one 2b, gdyż taka jest długość krawędzi dwudziestościanu.
 ZADANIA OTWARTE ZADANIE 1 DWUDZIESTOŚCIAN FOREMNY Wiemy, że z trzech złotych prostokątów możn skonstruowć dwudziestościn foremny. Wystrczy wykzć, że długości boków trójkąt ABC n rysunku obok są równe.
ZADANIA OTWARTE ZADANIE 1 DWUDZIESTOŚCIAN FOREMNY Wiemy, że z trzech złotych prostokątów możn skonstruowć dwudziestościn foremny. Wystrczy wykzć, że długości boków trójkąt ABC n rysunku obok są równe.
Wspomaganie obliczeń za pomocą programu MathCad
 Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
2. PODSTAWY STATYKI NA PŁASZCZYŹNIE
 M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
Prawo Coulomba i pole elektryczne
 Prwo Coulomb i pole elektryczne Mciej J. Mrowiński 4 pździernik 2010 Zdnie PE1 2R R Dwie młe kulki o msie m, posidjące ten sm łdunek, umieszczono w drewninym nczyniu, którego przekrój wygląd tk jk n rysunku
Prwo Coulomb i pole elektryczne Mciej J. Mrowiński 4 pździernik 2010 Zdnie PE1 2R R Dwie młe kulki o msie m, posidjące ten sm łdunek, umieszczono w drewninym nczyniu, którego przekrój wygląd tk jk n rysunku
Rozwiązywanie zadań z dynamicznego ruchu płaskiego część I 9
 ozwiązywnie zdń z dyniczneo ruchu płskieo część I 9 Wprowdzenie ozwiązywnie zdń w oprciu o dyniczne równni ruchu (D pole n uwolnieniu z więzów kżdeo z cił w sposób znny ze sttyki. Wrunki równowi są zbliżone
ozwiązywnie zdń z dyniczneo ruchu płskieo część I 9 Wprowdzenie ozwiązywnie zdń w oprciu o dyniczne równni ruchu (D pole n uwolnieniu z więzów kżdeo z cił w sposób znny ze sttyki. Wrunki równowi są zbliżone
Wektor kolumnowy m wymiarowy macierz prostokątna o wymiarze n=1 Wektor wierszowy n wymiarowy macierz prostokątna o wymiarze m=1
 Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
BADANIE ZALEŻNOŚCI PRZENIKALNOŚCI MAGNETYCZNEJ
 ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 2014/2015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A2, A3, A4, A6, A7)
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 2015/2016
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 015/016 oprcowł: Dnut Wojcieszek n ocenę dopuszczjącą rysuje wykres funkcji f ( ) i podje jej włsności sprwdz lgebricznie, czy dny punkt
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 015/016 oprcowł: Dnut Wojcieszek n ocenę dopuszczjącą rysuje wykres funkcji f ( ) i podje jej włsności sprwdz lgebricznie, czy dny punkt
Podstawy układów logicznych
 Podstwy ukłdów logicznych Prw logiki /9 Alger Boole Prw logiki WyrŜeni i funkcje logiczne Brmki logiczne Alger Boole /9 Alger Boole' Powszechnie stosowne ukłdy cyfrowe (logiczne) prcują w oprciu o tzw.
Podstwy ukłdów logicznych Prw logiki /9 Alger Boole Prw logiki WyrŜeni i funkcje logiczne Brmki logiczne Alger Boole /9 Alger Boole' Powszechnie stosowne ukłdy cyfrowe (logiczne) prcują w oprciu o tzw.
Propozycja przedmiotowego systemu oceniania wraz z określeniem wymagań edukacyjnych (zakres podstawowy)
 Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
- Wydział Fizyki Zestaw nr 5. Powierzchnie 2-go stopnia
 1 Algebr Liniow z Geometri - Wydził Fizyki Zestw nr 5 Powierzchnie -go stopni 1 N sferze 1 + + 3 = 4 znleźć punkt, którego odległość od punktu p = (, 6, 3) byłby njmniejsz Wyznczyć osie elipsy powstłej
1 Algebr Liniow z Geometri - Wydził Fizyki Zestw nr 5 Powierzchnie -go stopni 1 N sferze 1 + + 3 = 4 znleźć punkt, którego odległość od punktu p = (, 6, 3) byłby njmniejsz Wyznczyć osie elipsy powstłej
Ć W I C Z E N I E N R E-14
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
Szczegółowe wymagania edukacyjne z matematyki, klasa 2C, poziom podstawowy
 Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri i Gospodrk Wodn w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri i Gospodrk Wodn w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt
Wykład 2. Pojęcie całki niewłaściwej do rachunku prawdopodobieństwa
 Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Biotechnologi w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Biotechnologi w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
MATeMAtyka 3 inf. Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych. Zakres podstawowy i rozszerzony. Dorota Ponczek, Karolina Wej
 Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
MATEMATYKA Wykład 4 (Funkcje) przyporządkowany został dokładnie jeden element
 MATEMATYKA Wykłd 4 (Funkcje) Pisząc f : (,b) R rozumiemy Ŝe kŝdemu (, b) przyporządkowny zostł dokłdnie jeden element y R. Wykresem funkcji nzywmy zbiór pr (,f()) n płszczyźnie skłdjącej się ze wszystkich
MATEMATYKA Wykłd 4 (Funkcje) Pisząc f : (,b) R rozumiemy Ŝe kŝdemu (, b) przyporządkowny zostł dokłdnie jeden element y R. Wykresem funkcji nzywmy zbiór pr (,f()) n płszczyźnie skłdjącej się ze wszystkich
PRZEGLĄD FUNKCJI ELEMENTARNYCH. (powtórzenie) y=f(x)=ax+b,
 WYKŁAD 0 PRZEGLĄD FUNKCJI ELEMENTARNYCH (powtórzenie) 1. Funkcje liniowe Funkcją liniową nzywmy funkcję postci y=f()=+b, gdzie, b są dnymi liczbmi zwnymi odpowiednio: - współczynnik kierunkowy, b - wyrz
WYKŁAD 0 PRZEGLĄD FUNKCJI ELEMENTARNYCH (powtórzenie) 1. Funkcje liniowe Funkcją liniową nzywmy funkcję postci y=f()=+b, gdzie, b są dnymi liczbmi zwnymi odpowiednio: - współczynnik kierunkowy, b - wyrz
Sumy algebraiczne i funkcje wymierne
 Sumy lgebriczne i funkcje wymierne Moduł - dził -temt Zkres treści Sumy lgebriczne 1 definicj jednominu, sumy lgebricznej, wyrzów podobnych pojęcie współczynnik jednominu Dodwnie i odejmownie sum lgebricznych
Sumy lgebriczne i funkcje wymierne Moduł - dził -temt Zkres treści Sumy lgebriczne 1 definicj jednominu, sumy lgebricznej, wyrzów podobnych pojęcie współczynnik jednominu Dodwnie i odejmownie sum lgebricznych
Wymagania edukacyjne na poszczególne oceny z matematyki w klasie II poziom rozszerzony
 Wymgni edukcyjne n poszczególne oceny z mtemtyki w klsie II poziom rozszerzony N ocenę dopuszczjącą, uczeń: rysuje wykres funkcji f ( x) x i podje jej włsności; sprwdz lgebricznie, czy dny punkt nleży
Wymgni edukcyjne n poszczególne oceny z mtemtyki w klsie II poziom rozszerzony N ocenę dopuszczjącą, uczeń: rysuje wykres funkcji f ( x) x i podje jej włsności; sprwdz lgebricznie, czy dny punkt nleży
Wymagania na poszczególne oceny z matematyki w Zespole Szkół im. St. Staszica w Pile. Kl. II poziom podstawowy
 Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile 1. SUMY ALGEBRAICZNE Kl. II poziom podstwowy Uczeń otrzymuje ocenę dopuszczjącą, jeśli: rozpoznje jednominy i sumy lgebriczne
Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile 1. SUMY ALGEBRAICZNE Kl. II poziom podstwowy Uczeń otrzymuje ocenę dopuszczjącą, jeśli: rozpoznje jednominy i sumy lgebriczne
Fizyka. Kurs przygotowawczy. na studia inżynierskie. mgr Kamila Haule
 Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
CAŁKOWANIE NUMERYCZNE
 Wprowdzenie Kwdrtury węzły równoodległe Kwdrtury Guss Wzory sumcyjne Trnsport, studi niestcjonrne I stopni, semestr I rok kdemicki 01/013 Instytut L-5, Wydził Inżynierii Lądowej, Politechnik Krkowsk Ew
Wprowdzenie Kwdrtury węzły równoodległe Kwdrtury Guss Wzory sumcyjne Trnsport, studi niestcjonrne I stopni, semestr I rok kdemicki 01/013 Instytut L-5, Wydził Inżynierii Lądowej, Politechnik Krkowsk Ew
usuwa niewymierność z mianownika wyrażenia typu
 Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych M O D E L O W A N I E I S Y M U L A C J A
 POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
KONKURS MATEMATYCZNY dla uczniów gimnazjów w roku szkolnym 2012/13. Propozycja punktowania rozwiązań zadań
 KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
WYKŁAD 5. Typy macierzy, działania na macierzach, macierz układu równań. Podstawowe wiadomości o macierzach
 Mtemtyk I WYKŁD. ypy mcierzy, dziłni n mcierzch, mcierz ukłdu równń. Podstwowe widomości o mcierzch Ogóln postć ukłdu m równń liniowych lgebricznych z n niewidomymi x x n xn b x x n xn b, niewidome: x,
Mtemtyk I WYKŁD. ypy mcierzy, dziłni n mcierzch, mcierz ukłdu równń. Podstwowe widomości o mcierzch Ogóln postć ukłdu m równń liniowych lgebricznych z n niewidomymi x x n xn b x x n xn b, niewidome: x,
WYMAGANIA NA OCENĘ DOPUSZCZAJĄCĄ DLA UCZNIÓW KLASY Ia TECHNIKUM
 WYMAGANIA NA OCENĘ DOPUSZCZAJĄCĄ DLA UCZNIÓW KLASY I TECHNIKUM Egzmin poprwkowy n ocenę dopuszczjącą będzie obejmowł zdni zgodne z poniższymi wymgnimi n ocenę dopuszczjącą. Egzmin poprwkowy n wyższą ocenę
WYMAGANIA NA OCENĘ DOPUSZCZAJĄCĄ DLA UCZNIÓW KLASY I TECHNIKUM Egzmin poprwkowy n ocenę dopuszczjącą będzie obejmowł zdni zgodne z poniższymi wymgnimi n ocenę dopuszczjącą. Egzmin poprwkowy n wyższą ocenę
FUNKCJE. Zbiór argumentów. Zbiór wartości
 FUNKCJE Funkcj jest to zleŝność między dwiem wrtościmi (zzwyczj ozncznymi przez x i y). Niech x ędzie rgumentem funkcji lu prmetrem, zś y wrtością funkcji czyli odpowidjącą rgumentowi liczą. Oto grf przedstwijący
FUNKCJE Funkcj jest to zleŝność między dwiem wrtościmi (zzwyczj ozncznymi przez x i y). Niech x ędzie rgumentem funkcji lu prmetrem, zś y wrtością funkcji czyli odpowidjącą rgumentowi liczą. Oto grf przedstwijący
Wymagania edukacyjne z matematyki
 Wymgni edukcyjne z mtemtyki LICEUM OGÓLNOKSZTAŁCĄCE Kls II Poniżej przedstwiony zostł podził wymgń edukcyjnych n poszczególne oceny. Wiedz i umiejętności konieczne do opnowni (K) to zgdnieni, które są
Wymgni edukcyjne z mtemtyki LICEUM OGÓLNOKSZTAŁCĄCE Kls II Poniżej przedstwiony zostł podził wymgń edukcyjnych n poszczególne oceny. Wiedz i umiejętności konieczne do opnowni (K) to zgdnieni, które są
Analiza matematyczna i algebra liniowa
 Anliz mtemtyczn i lgebr liniow Mteriły pomocnicze dl studentów do wykłdów Mcierze liczbowe i wyznczniki. Ukłdy równń liniowych. Mcierze. Wyznczniki. Mcierz odwrotn. Równni mcierzowe. Rząd mcierzy. Ukłdy
Anliz mtemtyczn i lgebr liniow Mteriły pomocnicze dl studentów do wykłdów Mcierze liczbowe i wyznczniki. Ukłdy równń liniowych. Mcierze. Wyznczniki. Mcierz odwrotn. Równni mcierzowe. Rząd mcierzy. Ukłdy
Ćwiczenia laboratoryjne z przedmiotu : Napędy Hydrauliczne i Pneumatyczne
 Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
Małgorzata Żak. Zapisane w genach. czyli o zastosowaniu matematyki w genetyce
 Młgorzt Żk Zpisne w gench czyli o zstosowniu mtemtyki w genetyce by opisć: - występownie zjwisk msowych - sznse n niebieski kolor oczu potomk - odległość między genmi - położenie genu n chromosomie Rchunek
Młgorzt Żk Zpisne w gench czyli o zstosowniu mtemtyki w genetyce by opisć: - występownie zjwisk msowych - sznse n niebieski kolor oczu potomk - odległość między genmi - położenie genu n chromosomie Rchunek
Ćwiczenie nr 2-SCO. Warstwa połowiąca WP. Ćwiczenie nr 2. 1 Cel ćwiczenia
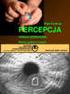 Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
WYMAGANIA I KRYTERIA OCENIANIA DO EGZAMINU POPRAWKOWEGO MATEMATYKA. Zakresie podstawowym i rozszerzonym. Klasa II rok szkolny 2011/2012
 mgr Jolnt Chlebd mgr Mri Mślnk mgr Leszek Mślnk mgr inż. Rent itl mgr inż. Henryk Stępniowski Zespół Szkół ondgimnzjlnych Młopolsk Szkoł Gościnności w Myślenicch WYMAGANIA I RYTERIA OCENIANIA DO EGZAMINU
mgr Jolnt Chlebd mgr Mri Mślnk mgr Leszek Mślnk mgr inż. Rent itl mgr inż. Henryk Stępniowski Zespół Szkół ondgimnzjlnych Młopolsk Szkoł Gościnności w Myślenicch WYMAGANIA I RYTERIA OCENIANIA DO EGZAMINU
Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych klasa druga zakres podstawowy
 Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych kls drug zkres podstwowy Wymgni konieczne (K) dotyczą zgdnień elementrnych, stnowiących swego rodzju podstwę, ztem powinny być opnowne przez
Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych kls drug zkres podstwowy Wymgni konieczne (K) dotyczą zgdnień elementrnych, stnowiących swego rodzju podstwę, ztem powinny być opnowne przez
WYMAGANIA I KRYTERIA OCENIANIA Z MATEMATYKI W 3 LETNIM LICEUM OGÓLNOKSZTAŁCĄCYM
 WYMAGANIA I KRYTERIA OCENIANIA Z MATEMATYKI W 3 LETNIM LICEUM OGÓLNOKSZTAŁCĄCYM Kls drug A, B, C, D, E, G, H zkres podstwowy 1. FUNKCJA LINIOWA rozpoznje funkcję liniową n podstwie wzoru lub wykresu rysuje
WYMAGANIA I KRYTERIA OCENIANIA Z MATEMATYKI W 3 LETNIM LICEUM OGÓLNOKSZTAŁCĄCYM Kls drug A, B, C, D, E, G, H zkres podstwowy 1. FUNKCJA LINIOWA rozpoznje funkcję liniową n podstwie wzoru lub wykresu rysuje
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI POZIOM PODSTAWOWY KLASA 2
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI POZIOM PODSTAWOWY KLASA 2 1. SUMY ALGEBRAICZNE rozpoznje jednominy i sumy lgebriczne
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI POZIOM PODSTAWOWY KLASA 2 1. SUMY ALGEBRAICZNE rozpoznje jednominy i sumy lgebriczne
Wyk lad 1 Podstawowe wiadomości o macierzach
 Wyk ld 1 Podstwowe widomości o mcierzch Oznczeni: N {1 2 3 } - zbiór liczb nturlnych N 0 {0 1 2 } R - ci lo liczb rzeczywistych n i 1 + 2 + + n i1 1 Określenie mcierzy Niech m i n bed dowolnymi liczbmi
Wyk ld 1 Podstwowe widomości o mcierzch Oznczeni: N {1 2 3 } - zbiór liczb nturlnych N 0 {0 1 2 } R - ci lo liczb rzeczywistych n i 1 + 2 + + n i1 1 Określenie mcierzy Niech m i n bed dowolnymi liczbmi
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II LO
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
PODSTAWY ALGEBRY MACIERZY. Operacje na macierzach
 PODSTWY LGEBRY MCIERZY WIERSZ i, KOLUMN (j) Mcierz m,n, gdzie m to ilość wierszy, n ilość kolumn i,j element mcierzy z itego wiersz, jtej kolumny Opercje n mcierzch Równość mcierzy m,n = B m,n. def i,j
PODSTWY LGEBRY MCIERZY WIERSZ i, KOLUMN (j) Mcierz m,n, gdzie m to ilość wierszy, n ilość kolumn i,j element mcierzy z itego wiersz, jtej kolumny Opercje n mcierzch Równość mcierzy m,n = B m,n. def i,j
Translacja jako operacja symetrii. Wybór komórki elementarnej wg A. Bravais, połowa XIX wieku wybieramy komórkę. Symetria sieci translacyjnej
 Trnslcj jko opercj symetrii Wykłd trzeci W obrębie figur nieskończonych przesunięcie (trnslcję) możn trktowć jko opercję symetrii Jest tk np. w szlkch ornmentcyjnych (bordiurch) i siecich krysztłów polimerów
Trnslcj jko opercj symetrii Wykłd trzeci W obrębie figur nieskończonych przesunięcie (trnslcję) możn trktowć jko opercję symetrii Jest tk np. w szlkch ornmentcyjnych (bordiurch) i siecich krysztłów polimerów
Sprawdzian całoroczny kl. III
 Sprwdzin cłoroczny kl. III Gr. A 1. Podne liczby zpisz w kolejności rosnącej: 7 ; b,5 ; c 6 ; d,5(). Oblicz i zpisz wynik w notcji wykłdniczej 0 8 6, 10 5 10. Wskż równość nieprwdziwą: A) 5 9 B) 6 C) 0
Sprwdzin cłoroczny kl. III Gr. A 1. Podne liczby zpisz w kolejności rosnącej: 7 ; b,5 ; c 6 ; d,5(). Oblicz i zpisz wynik w notcji wykłdniczej 0 8 6, 10 5 10. Wskż równość nieprwdziwą: A) 5 9 B) 6 C) 0
Mechanika nieba B. Arkusz I i II Czas pracy 90 minut Instrukcja dla zdającego. Aktualizacja Czerwiec ROK Arkusz I i II
 0004 Mechnik nieb B Dne osobowe włściciel rkusz 0004 Mechnik nieb B Czs prcy 90 minut Instrukcj dl zdjącego. Proszę sprwdzić, czy rkusz egzmincyjny zwier 8 stron. Ewentulny brk nleży zgłosić osobie ndzorującej
0004 Mechnik nieb B Dne osobowe włściciel rkusz 0004 Mechnik nieb B Czs prcy 90 minut Instrukcj dl zdjącego. Proszę sprwdzić, czy rkusz egzmincyjny zwier 8 stron. Ewentulny brk nleży zgłosić osobie ndzorującej
Dorota Ponczek, Karolina Wej. MATeMAtyka 2. Szczegółowe wymagania edukacyjne z matematyki w klasie drugiej Zakres podstawowy
 Dorot Ponczek, rolin Wej MATeMAtyk 2 Szczegółowe wymgni edukcyjne z mtemtyki w klsie drugiej Zkres podstwowy Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące,
Dorot Ponczek, rolin Wej MATeMAtyk 2 Szczegółowe wymgni edukcyjne z mtemtyki w klsie drugiej Zkres podstwowy Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące,
Układ elektrohydrauliczny do badania siłowników teleskopowych i tłokowych
 TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
Wymagania edukacyjne z matematyki dla klasy II a liceum (poziom podstawowy) na rok szkolny 2018/2019
 Wymgni edukcyjne z mtemtyki dl klsy II liceum (poziom podstwowy) n rok szkolny 08/09 Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące, W wymgni wykrczjące. SUMY
Wymgni edukcyjne z mtemtyki dl klsy II liceum (poziom podstwowy) n rok szkolny 08/09 Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące, W wymgni wykrczjące. SUMY
Wymagania edukacyjne z matematyki FUNKCJE dopuszczającą dostateczną dobrą bardzo dobrą
 Wymgni edukcyjne z mtemtyki Kls IIC. Rok szkolny 013/014 Poziom podstwowy FUNKCJE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje przyporządkowni będące funkcjmi określ funkcję różnymi
Wymgni edukcyjne z mtemtyki Kls IIC. Rok szkolny 013/014 Poziom podstwowy FUNKCJE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje przyporządkowni będące funkcjmi określ funkcję różnymi
WYMAGANIA DLA UCZNIÓW KLAS DRUGICH LICEUM OGÓLNOKSZTAŁCĄCEGO
 WYMAGANIA DLA UCZNIÓW KLAS DRUGICH LICEUM OGÓLNOKSZTAŁCĄCEGO Pln wynikowy dostosowny jest do progrmu nuczni mtemtyki w szkole pondgimnzjlnej z zkresu ksztłceni podstwowego PROSTO DO MATURY (progrm nuczni
WYMAGANIA DLA UCZNIÓW KLAS DRUGICH LICEUM OGÓLNOKSZTAŁCĄCEGO Pln wynikowy dostosowny jest do progrmu nuczni mtemtyki w szkole pondgimnzjlnej z zkresu ksztłceni podstwowego PROSTO DO MATURY (progrm nuczni
1 Definicja całki oznaczonej
 Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Plan wynikowy klasa 2. Zakres podstawowy
 Pln wynikowy kls Zkres podstwowy MATeMAtyk. Pln wynikowy. ZP Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące, W wymgni wykrczjące. SUMY ALGEBRAICZNE 0. Sumy
Pln wynikowy kls Zkres podstwowy MATeMAtyk. Pln wynikowy. ZP Oznczeni: wymgni konieczne, P wymgni podstwowe, R wymgni rozszerzjące, D wymgni dopełnijące, W wymgni wykrczjące. SUMY ALGEBRAICZNE 0. Sumy
Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych
 Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
Modelowanie 3 D na podstawie fotografii amatorskich
 Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
4. RACHUNEK WEKTOROWY
 4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II TAK
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
Wprowadzenie: Do czego służą wektory?
 Wprowdzenie: Do czego służą wektory? Mp połączeń smolotowych Isiget pokzuje skąd smoloty wyltują i dokąd doltują; pokzne jest to z pomocą strzłek strzłki te pokzują przemieszczenie: skąd dokąd jest dny
Wprowdzenie: Do czego służą wektory? Mp połączeń smolotowych Isiget pokzuje skąd smoloty wyltują i dokąd doltują; pokzne jest to z pomocą strzłek strzłki te pokzują przemieszczenie: skąd dokąd jest dny
Sieć odwrotna. Fale i funkcje okresowe
 Sieć odwotn Fle i funkcje okesowe o Wiele obiektów w pzyodzie d; o Różne fle ozchodzą się w pzestzeni (zówno w póżni jk i w mteii); o Aby mtemtycznie opisć tkie okesowe zminy stosuje się funkcje sinus
Sieć odwotn Fle i funkcje okesowe o Wiele obiektów w pzyodzie d; o Różne fle ozchodzą się w pzestzeni (zówno w póżni jk i w mteii); o Aby mtemtycznie opisć tkie okesowe zminy stosuje się funkcje sinus
