Sterowanie napędów maszyn i robotów
|
|
|
- Fabian Biernacki
- 6 lat temu
- Przeglądów:
Transkrypt
1 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2014
2 Identyfikacja Identyfikacja systemów lub procesów Zespół metod, narzędzi i algorytmów mających na celu zbudować dynamiczny model systemu lub procesu na podstawie danych pomiarowych zebranych z wejścia i wyjścia. Model taki może opisywać: właściwości wejściowo-wyjściowe systemu - tworzony w oparciu o sekwencje sygnałów wejściowych i towarzyszące im sekwencje sygnałów wyjściowych, przebieg wyjścia systemu o wejściach pomiarowo niedostępnych - tworzony tylko w oparciu o mierzoną sekwencję sygnału wyjściowego. Model budowany jest poprzez wyszukiwanie zależności i relacji pomiędzy zmierzonymi danymi bez analizy systemu lub procesu (brak szczegółowego badania zjawisk fizycznych zachodzących w systemie lub procesie). System lub proces czarna skrzynka.
3 Etapy identyfikacji (1-5) Identyfikacja jest procesem iteracyjnym, który może posiadać następujące etapy: 1 Przygotowanie eksperymentu identyfikacyjnego: Generacja pobudzeń wejść systemu, aby zebrać odpowiednie dane pomiarowe. 2 Przeprowadzenie eksperymentu identyfikacyjnego: Zebranie pomiarów. 3 Wstępne przetwarzanie danych pomiarowych: np. eliminacja błędów grubych, skalowanie, filtrowanie. 4 Wybór klasy dopuszczalnych modeli: Wybiera się klasę modeli deterministycznych lub stochastycznych, ciągłych lub dyskretnych, liniowych lub nieliniowych, stacjonarnych bądź niestacjonarnych. 5 Wybór typu modelu z wybranej klasy: W każdej klasie modeli istnieją modele różnych typów. Wybór konkretnego modelu może być poprzedzony wstępną, zgrubną analizą modelowanego systemu bądź pochodzących z niego sygnałów.
4 Etapy identyfikacji (6-8) 1 Wybór struktury modelu (dla modeli parametrycznych): Jest to bardzo trudny etap, który często sprowadza się do pełnego lub ograniczonego przeglądu wszystkich dopuszczalnych (i rozsądnych) struktur modeli danego typu. 2 Estymacja parametrów danego modelu: Na tym etapie wybiera się odpowiedni algorytm estymacji, pozwalający na wyznaczenie parametrów wybranego uprzednio modelu. 3 Weryfikacja modelu: Kończy pojedynczą iterację procesu identyfikacji. Na tym etapie należy rozstrzygnąć, czy wynik identyfikacji jest zadowalający. Można w tym celu: porównać sygnał wyjściowy modelu z sygnałem rzeczywistym (najlepiej dla innego zbioru danych - zbioru danych testowych), sprawdzić, czy model ma zbyt bogatą strukturę (nadmiar parametrów), sprawdzić inne cechy modelu, decydujące o jego przydatności (np. stabilność, odwracalność).
5 Modele parametryczne Model AR (ang.autoregressive) Model auto-regresyjny, zawiera wyłącznie wyrazy pomierzonego wcześniej sygnału wyjściowego ŷ(k) = a 1 y(k 1) a 2 y(k 1)... a n y(k n) (1) gdzie: y - sygnał wyjściowy, k - czas dyskretny, T = kt p, n - szerokość okna pomiarowego, a i, i = 1,.., n - współczynniki modelu. Stosowany, gdy: nie można pomierzyć sygnału wejściowego sygnał wejściowy jest bliżej nie określony
6 Modele parametryczne Model ARX (ang.autoregressive with exogenous input) Model auto-regresyjny z zewnętrznym wejściem (z dołączonym sygnałem zakłócającym) ŷ(k) = a 1 y(k 1)... a n y(k n) + c 1ˆη(k 1) c n ˆη(k n) (2) gdzie: ˆη(k) - zakłócenie (szacowanie wpływu zakłócenia), a i, c i i = 1,.., n - współczynniki modelu.
7 Modele parametryczne Model MA (ang.moving Average) model ruchomej średniej, jest uśrednionym (za pomocą wagowych współczynników b) wpływem sygnału wejściowego ŷ(k) = b 0 u(k d) b n u(k n d) (3) gdzie: u(k) - sygnał sterujący (wejściowy), d - dyskretna wartość opóźnienia.
8 Modele parametryczne Model MAX (ang. Moving Average with exogenous input) Model MA z zewnętrznym wejściem (z dołączonym sygnałem zakłócającym) ŷ(k) = b 0 u(k d)+...+b n u(k n d)+c 1ˆη(k 1)+...+c n ˆη(k n) (4)
9 Modele parametryczne Model ARMA (ang. Auto-Regressive with Moving Average) Model stanowiący połączenie modelu AR z modelem MA (zawiera zarówno sygnał wejściowy jak i przeszłe wartości wyjścia z procesu) ŷ(k) = a 1 y(k 1)... a n y(k n)+b 0 u(k d)+...+b n u(k n d) (5)
10 Modele parametryczne Model ARMAX (ang. Auto-Regressive Moving Average with exogenous input) model ARMA z zewnętrznym wejściem (z dołączonym sygnałem zakłócającym) ŷ(k) = a 1 y(k 1)... a n y(k n)+ +b 0 u(k d) b n u(k n d)+ +c 1ˆη(k 1) c n ˆη(k n) (6)
11 Algorytmy stosowane w identyfikacji Do algorytmów powszechnie stosowanych w identyfikacji systemów (procesów), do szacowania współczynników modeli parametrycznych należą: metoda najmniejszych kwadratów LS (ang. Least Squares) z odmianami: rekurencyjna metoda LS RLS (ang. Recursive Least Squares) rozszerzona macierzowa metoda ELS (ang. Extendend Least Squares) metoda zmiennych instrumentalnych IV (ang. Instrumental Variable) metoda największej wiarygodności ML (ang. Maximum Likelihood)
12 Metoda najmniejszych kwadratów LS Jest to najszybsza i najprostsza metoda szacowania współczynników modelu. Jego cechą charakterystyczną jest brak iteracji w przypadku obliczeń modeli o strukturach AR, MA, ARMA. Ze względu na formę modelu oszacowanie LS istnieje praktycznie zawsze (z wyjątkiem stałych wartości sygnałów wejść do modelu). Algorytm tej metody jest prosty i w wersji off-line ma postać: Θ LS = [V T V ] 1 V T Y (7) gdzie: V - wektor wejść modelu, Y - wektor wyjść modelu. W wielu przypadkach pomiary wartości są dokonywane sekwencyjnie w trybie ciągłym on line. Wówczas szacowanie parametrów obliczane jest dla coraz większej liczby danych co wymaga coraz większego nakładu obliczeniowego i czasu. Algorytm LS wymaga odwracania macierzy [V T V ], co wpływa na stabilność i dokładnośc rozwiązania.
13 Metoda najmniejszych kwadratów rekurencyjny RLS Aby przyspieszyć obliczenia on-line opracowano wersję algorytmu LS, w której po każdym kolejnym pomiarze ma miejsce aktualizacja poprzednio wyznaczonych wartości parametrów P(k) = [V (k) T V (k)] 1 (8) Θ RLS (k) = P(k)V T (k)y (k) (9) Θ RLS (k + 1) = P(k + 1)V T (k + 1)Y (k + 1) = = P(k + 1)[V T (k)y (k) + v T (k + 1)y(k + 1)] Θ RLS (k + 1) = Θ RLS (k) + Θ RLS (k) = = Θ(k) + P T (k + 1)[y(k + 1) v(k + 1)Θ(k)] Wartość parametrów w chwili k + 1 równa się wartości parametrów w chwili k z poprawką wynikającą z sygnałów wejść i wyjścia w chwili k + 1. Algorytm ten nie wymaga odwracania macierzy, tak jak ma to miejsce w przypadku metody LS (7). (10) (11)
14 Metoda najmniejszych kwadratów rozszerzona macierzowa ELS Metoda rozszerzona macierzowa ELS jest rozszerzeniem metody LS dla układów, w których błędy pomiarowe są ze sobą skorelowane. Układy tego typu są modelowane między innymi jako modele typu ARMAX.
15 Metoda zmiennych instrumentalnych IV Gdy w zadaniu identyfikacji liniowego obiektu dynamicznego występuje skorelowanie zakłóceń można zastosować metodę zmiennych instrumentalnych (IV). Polega ona na częściowym zastąpieniu w estymatorze LS macierzy wejść do modelu V przez macierz wielkości pomocniczych W (instrumentalnych) Θ IV = [W T V ] 1 W T Y (12) Macierz W zmiennych pomocniczych z definicji nie powinna zawierać wartości skorelowanych z wektorem błędów modelu, co powinno zapewnić nieobciążenie oszacowania współczynników modelu, również w przypadku zakłóceń skorelowanych. Utworzenie dobrej macierzy zmiennych instrumentalnych nie jest proste, ale metoda ma wyraźnie lepsze właściwości od metody najmniejszej sumy kwadratów.
16 Metoda największej wiarygodności ML Metoda największej wiarygodności (ML) pozwala wyprowadzić najbardziej efektywne estymatory, przy czym jest ona dostosowana do procesów, dla których adekwatny jest opis w formie modeli ARMAX. W wyniku oszacowań powinien powstać model, który zapewnia właściwości białego szumu dla oszacowanych błędów wyjścia modelu. Estymator jest najbardziej złożony (z dotychczas omawianych) i jest realizowany iteracyjnie. Θ ML (k + 1) = Θ ML (k) + κ(k)l T ΘΘ(Θ(k)) 1 L T Θ(Θ(k)) (13) gdzie: Θ ML (k) - kolejna iteracja wektora współczynników modelu, L T Θ - wektor pierwszych pochodnych funkcji wiarygodności, L T ΘΘ - macierz drugich pochodnych funkcji wiarygodności, κ(k) - wartość długości kroku. Przybliżeniem początkowym Θ(0) wektora współczynników modelu jest zwykle oszacowanie uzyskane metodą LS.
17 Identyfikacja statystyczna struktury i parametrów modelu serownapędu pneumatycznego Podstawowe znaczenie dla udanej identyfikacji modelu procesu ruchu ma rozwiązanie następujących problemów: Wybór metody identyfikacji: studium przydatności trzech podstawowych metod statystycznych dla estymacji modeli zachowań dynamicznych napędu wykazało, że pod względem niezawodności i efektywności w obszarze techniki napędowej najbardziej przydatna jest metoda LS, w dwóch wersjach: w wersji podstawowej (LS) podczas uruchomienia napędu, (Off-line), w wersji rekurencyjnej (RLS) podczas normalnej pracy napędu.
18 Identyfikacja statystyczna struktury i parametrów modelu serownapędu pneumatycznego Zastosowanie metody najmniejszych kwadratów daje: w trakcie identyfikacji uruchomieniowej napędu i dużej liczby danych pomiarowych, zwłaszcza wielokrotnych eksperymentów (brak ograniczeń czasowych), zbieżne i względnie dobrze powtarzalne oszacowanie współczynników tego modelu (a i, b i ), w trakcie identyfikacji prowadzonej podczas normalnej pracy napędu otrzymuje się zdecydowanie gorsze wyniki. Powodowane są one małą liczbą danych pomiarowych (od kilkunastu do kilkudziesięciu pomiarów krótki przedział czasowy estymacji), silnymi oscylacjami wartości współczynników w początkowej fazie szacowania powodowanymi procedurą rekurencyjną oraz ograniczonym zakresem zmian prędkości ruchu. Są to przyczyny występowania wyraźnej wariancji i względnie dużych wartości błędu szacowania.
19 Identyfikacja statystyczna struktury i parametrów modelu serownapędu pneumatycznego wybór struktury modelu: przeprowadzony eksperyment czynny identyfikacji modeli w dwóch podstawowych dla sterowanego napędu fazach ruchu: rozbiegu i hamowania, doprowadził do sformułowania następujących wniosków: modele fazy rozbiegu mają charakter aperiodyczny, przeważnie 4-go rzędu z opóźnieniem (d) równym jednemu lub dwóm okresom próbkowania (przy T p = 2ms): pewne właściwości oscylacyjne, ujawniają się tylko przy niskim wysterowaniu, poniżej 30[%] nominalnej wartości sygnału u, modele fazy hamowania charakteryzują się właściwościami oscylacyjnymi 3-go rzędu z krótszym opóźnieniem d w stosunku do fazy rozbiegu - przeważnie o okres T p; właściwości te ustępują ponownie zachowaniom inercyjnym w zakresie malejących wysterowań, szczególnie poniżej 20 10[%] wartości u max.
20 Identyfikacja statystyczna struktury i parametrów modelu serownapędu pneumatycznego wybór postaci modelu: ograniczając zachowania napędu do modelu zachowań oscylacyjnego członu 2-go rzędu z pominięciem astatyczności, transmitancja i równanie różnicowe identyfikacji, podane są - w przypadku prędkościowego modelu ARMA - w postaci oraz ˆv(k) = G v (z) = b 1z 1 + b 2 z a 1 z 1 + a 2 z 2 z d (14) 2 a i v(k i) + i=1 2 b j u(k d j) (15) j=1
21 Identyfikacja statystyczna struktury i parametrów modelu serownapędu pneumatycznego wybór okresu próbkowania: znane zalecenia (określone względem czasów narastania odpowiedzi skokowej identyfikowanego obiektu) zakładają, że okres próbkowania T p powinien zawierać się w granicach od kilku do kilkudziesięciu ms. Problem próbkowania Element ruchomy napędu przy maksymalnej prędkości ruchu przebywa w czasie 1[ms] drogę rzędu 5[mm]. Powstaje tu konflikt pomiędzy koniecznością zmniejszania okresu próbkowania dla zapewnienia żądanej dokładności pozycjonowania a zachowaniem akceptowalnej jakości identyfikowanego modelu. Rozwiązanie problemu próbkowania W stosunku do wartości T p (0, 8; 1, 2)[ms], stosowanych w sterowaniu pozycyjnym rozwiązaniem konfliktu jest wprowadzenie oddzielnego okresu próbkowania T pident = nt p, n C przeznaczonego do identyfikacji.
22 Procedury identyfikacji statystycznej modelu serownapędu pneumatycznego Wybierając model przyspieszeniowy procesu ruchu napędu, podstawą procedur metody LS jest oszacowanie w chwili dyskretnej k wektora parametrów modelu ˆΘ a (k) ˆΘ a (k) = [V T (k)v (k)] 1 V T (k)a(k) = ˆΘ a (k 1) + ˆΘ a (k) (16) który minimalizuje zakłócenie ˆη a (k) (utożsamiane z błędem szacowania). ˆη a (k) = a(k) â(k) (17) gdzie: a(k) - sygnał przyspieszenia w rzeczywistym napędzie, â(k) - sygnał przyspieszenia w modelu.
23 Procedury identyfikacji statystycznej modelu serownapędu pneumatycznego W zapisie (16) kryją się dwa podejścia do identyfikacji metodą najmniejszych kwadratów: w wersji podstawowej metody LS - wykorzystywane są na raz wszystkie zebrane w chwilach k = 1, 2,..., m pomiarowe dane wejściowe v(k), a(k) i u(k d) V (m) = v(1) a(1) u(1) v(m) a(m) u(m), a(m) = a(1)... a(m) (18) Prowadzi to do oszacowania wektora parametrów modelu za pomocą wyrażenia ˆΘ LS a (m) = [V T (m)v (m)] 1 V T (m)a(m) (19) minimalizującego kryteria jakości w postaci Ia LS (m) = 1 m m i=1 ˆη 2 a(i) min, I LS amod(m) = 1 m m ˆη a (i) min (20) i=1
24 Procedury identyfikacji statystycznej modelu w wersji rekurencyjnej (RLS), w której korekcyjny - względem RLS RLS wektora parametrów modelu ˆΘ a (k) - wektor ˆΘ a (k) określają zależności RLS ˆΘ a (k) = γ a (k)ˆη a (k) = γ a (k)[a(k) â(k)] = γ a (k)[a(k) RLS ˆΘ a (k 1)w(k)] (21) gdzie γ a (k) - współczynnikiem szacowania, tzn. zmianę wartości parametrów modelu wywołuje tylko różny od zera błąd szacowania, η a (k) 0. W procedurze tej, inaczej niż w wersji podstawowej, w każdej kolejnej chwili k macierze V i a uzupełniane są o nowy niezerowy wiersz (wiersze k < i m pozostają zerowe), co pozwala na szacowanie wektora parametrów modelu w postaci ˆΘ RLS a (k) = [V T (k 1)V (k 1)+w T (k)w(k)] 1 [V T (k 1)a(k 1)+w T (k)a(k)] (22) Postać ta pozwala na wykorzystanie obliczeniowo oszczędnej techniki pseudoinwersji macierzy.
25 Procedury identyfikacji statystycznej modelu Pseudoinwersja macierzy polega ona na zastąpieniu odwracanej macierzy następująco: [V T (k 1)V (k 1) + w T (k)w(k)] 1 = [V T (k 1)V (k 1)] 1 + µ(k)[v T (k 1)V (k 1)] 1 w T (k)w(k)[v T (k 1)V (k 1)] 1 (23) 1 µ(k) = w(k)[v T (k 1)V (k 1)] 1 w t (24) (k) + λ gdzie: λ - współczynnik zapominania (λ = 1 przy równym traktowaniu wszystkich danych pomiarowych). Macierz odwracana w chwili k daje się obliczyć ze znanej już dla chwili poprzedniej (k 1) macierzy odwrotnej. W tej procedurze minimalizowane jest kryterium jakości w postaci Ia LS (m) = 1 k k λ k 1ˆη a (i) 2 (i) min (25) i=1
26 Konwersja parametrów modelu dyskretnego w parametry modelu ciągłego Konwersja parametrów modelu dyskretnego w parametry modelu ciągłego polega odwrócenie przyporządkowania parametrów modelu ciągłego zachowań ruchowych napędu (C m, ω om, D m ) elementom wektora szacowania ˆθ v lub ˆθ a modelu dyskretnego. W celu poprawienia niezawodności numerycznej konwersji przez lepsze uwarunkowania równań procedury i dla zmniejszenia nakładu obliczeń zdecydowano się na kolejne uproszczenie uzasadnione zakresami zmian wartości współczynników α i β dla potencjalnego zbioru modeli. Dla siłowników pneumatycznych stosowanych w układach pozycyjnych wartości parametrów modelu ciągłego mieszczą się w zakresach C m (0, 15; 1, 5)[m/sV ], ω om (10; 60)[rad/s] oraz D m (0, 1; 1, 5) - co prowadzi, w następstwie uśrednionego zakresu wartości wyrażenia D m ω om T p (0, 0008; 0, 18)[rad] dla okresu próbkowania T p (0, 8, 2)[ms] i przyjęcia wartości D m ω om T p 0, do uproszczonych równań konwersji.
27 Konwersja parametrów modelu dyskretnego w parametry modelu ciągłego Uproszczone równania konwersji dla modelu prędkościowego C m = ˆθ v3 1 ˆθ v1, ω om dla modelu przyspieszeniowego C m = ˆθ a3 θ, ω om ˆ a1 ˆθ a1 2(1 ˆθ v1 ) T p, D m 1 ω om T p (1 ˆθ v2 T p ) (26) T p D m 1 (1 ω2 omtp 2 2ω om T p 2 ˆθ a2 ) (27)
28 Konwersja parametrów modelu dyskretnego w parametry modelu ciągłego W przypadku ostatniej zależności (27) błąd wynikający z przyjęcia wartości zerowej dla wyrażenia D m ω om T p nie przekracza 2 3% wartości pulsacji drgań swobodnych ω om oraz współczynnika tłumienia D m liczonych bez uproszczeń i w stosunku do wspomnianej zmienności zachowań ruchowych samego napędu może być całkowicie zaniedbany. W celu zmniejszenia wpływu chwilowych odchyłek aktualnie szacowanych wartości parametrów modelu na wynik konwersji zastosowano następujący filtr: Φ usr (k) = νφa akt (k) + (1 ν)φ usr (k 1), Φ = [C m ω om D m ] T (28) gdzie: v - współczynnik filtracji, ν << 1, Φ akt - bieżąca wartość parametrów i Φ usr - uśredniona wartość parametrów modelu ciągłego, np. dla współczynnika v = 0, 1 wynik wcześniejszy o pięć okresów próbkowania względem chwili k ma już tylko połowę tej wagi, co aktualny (0, 9 5 0, 59).
29 Realizacja identyfikacji statystycznej modelu ETAP 1: Identyfikacja w trakcie uruchomienia napędu dla wyznaczenia deskryptorów, charakterystyk i modeli układu napędowego: zakresu ruchu (siły, momentu) i jego korelacji z szerokością zakresu pomiarowego zastosowanego przetwornika pomiarowego, tzn. rzeczywistej charakterystyki pomiaru kontrolowanego parametru w układzie napędowym, biegunowości podłączenia elektrycznego, błędu punktu zerowego i histerezy wysterowania nastawnika, charakterystyki prędkościowej ruchu i charakterystyki kompensacyjnej jej nieliniowości w układzie nastawnik - siłownik, parametrów modelu zakłóceniowego (np. zmian obciążenia masowego, siłowego) układu napędowego, parametrów modelu zachowań ruchowych (siłowych, momentowych) układu napędowego; parametry te są wykorzystywane dla doboru nastaw startowych sterowania oraz jako parametry startowe szacowanego w trybie on-line modelu.
30 Identyfikacja uruchomieniowa napędu Rysunek 1. Identyfikacja uruchomieniowa napędu.
31 Realizacja identyfikacji statystycznej modelu ETAP 2: Identyfikacja w trakcie normalnej pracy napędu służy do: wyznaczenia lokalnych (chwilowych) modeli zachowań układu napędowego; jest prowadzona równolegle do sterowania pozycyjnego: szacowanie wektora parametrów modelu dyskretnego (ˆθ) i potem modelu ciągłego (Φ) przebiega w każdym okresie T pident w trzech kolejnych krokach obliczeniowych, w powtarzalnych ciągach po kilkadziesiąt szacowań kończonych każdorazowo modyfikacji nastaw sterowania przez szacowanie obciążenia masowego i identyfikację on-line modelu procesu ruchu.
32 Identyfikacja w trakcie normalnej pracy napędu Rysunek 2. Identyfikacja w trakcie normalnej pracy napędu.
33 Uwagi - sterowanie pozycyjne napędów pneumatycznych W trakcie identyfikacji uruchomieniowej ograniczenia działań rozruchowych układu napędowego narzucają zastosowanie w procedurze identyfikacyjnej modelu planowanego eksperymentu czynnego z możliwością pobudzenia pseudoprzypadkowym sygnałem binarnym (PRBS Pseudorandom Binary Sequence) o właściwościach zbliżonych do białego szumu, wytwarzanym przez generator w postaci rejestru przesuwnego z wejściem przez sprzężenia z wybranych pozycji; przy amplitudzie równej aktualnemu wysterowaniu u pozostałe parametry generatora dobiera się eksperymentalnie np. dla napędu pneumatycznego i okresu próbkowania T p < 0, 8, 2 > ms oraz przewidywanego zbioru identyfikowanych napędów wybrano jako długość rejestru n = 4 i jako minimalną wartość przedziału czasowego sygnału mt p, m(2; 9), optymalnie m = 6.
34 Uwagi - sterowanie pozycyjne napędów pneumatycznych Identyfikacja uruchomieniowa prowadzona jest po rozpędzeniu siłownika (silnika) do bezpiecznej wartości prędkości v bezp i następnie wyhamowaniu przy pomocy sygnału PRBS dla obydwu kierunków ruchu (istotne dla siłowników i niehoryzontalnych położeń napędu), różnych obciążeń masowych m obc, wybranych położeń s i wysterowań u. W najprostszym przypadku identyfikowane są cztery modele: dla dwóch kierunków ruchu oraz minimalnego i maksymalnego obciążenia masowego dla wybranego, np. środkowego, położenia elementu ruchomego napędu (siłownika).
35 Uwagi - sterowanie pozycyjne napędów pneumatycznych W porównaniu do modelu obliczeniowego (bilansowego), gorzej szacowany jest wpływ obciążenia masowego. Tak więc dla bardziej zaawansowanych metod sterowania (np. adaptacyjnego) konieczne może być stosowanie specjalnej procedury identyfikacyjnej. Obserwowane rozbieżności w przypadku współczynnika tłumienia D m wynikają z trudności analitycznego określenia zachowań ciernych napędu pneumatycznego: współczynnik tarcia jest przyjmowany w praktyce według katalogowych danych producenta, z reguły jako pewna wartość stała dla całego typoszeregu siłowników (silników, przekładni), bez uwzględnienia rzeczywistych oporów ruchu w kompletnym układzie napędowym. W stosunku do uśrednionych wyników modelowania analitycznego i uruchomieniowego (metoda LS), różnice w odniesieniu do identyfikacji w trakcie normalnej pracy, zwłaszcza zmniejszenie wzmocnienia obiektowego C m, wywołane są dwoma czynnikami: zapewnieniem procedurze RLS charakteru silnie bieżącego szacowania oraz wpływu tarcia przylgowego w przypadku małych przemieszczeń i prędkości ruchu.
36 Uwagi W trakcie normalnej pracy układu napędowego są identyfikowane charakterystyczne dla napędów przebiegi zależności parametrów zachowań modelu oscylacyjnego od parametrów ruchu i wysterowania: dotyczy to charakterystyk pulsacji drgań swobodnych ω om i tłumienia D m w funkcji położenia s. Spośród działań o charakterze ulepszeń numerycznych zmniejszających wrażliwość identyfikacji i konwersji parametrów na zakłócenia i zniekształcenia pomiarowe, dyskretyzacyjne i rekonstrukcyjne wykorzystywanych sygnałów, jak np. skalowanie ich wartości dla poprawy uwarunkowań równań procedur lub dopasowania czasu próbkowania, szczególne znaczenie przypisać należy działaniom filtracyjnym zarówno na sygnałach wejściowych, jak i na estymowanych parametrach modeli.
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Sterowanie Napędów Maszyn i Robotów
 Wykład 3 - Metodyka projektowania sterowania. Opis bilansowy Instytut Automatyki i Robotyki Warszawa, 2015 Metodyka projektowania sterowania Zrozumienie obiektu, możliwości, ograniczeń zapoznanie się z
Wykład 3 - Metodyka projektowania sterowania. Opis bilansowy Instytut Automatyki i Robotyki Warszawa, 2015 Metodyka projektowania sterowania Zrozumienie obiektu, możliwości, ograniczeń zapoznanie się z
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Sterowanie napędów maszyn i robotów
 Wykład 6 - odtwarzanie zmiennych stanu przez obserwację Instytut Automatyki i Robotyki Warszawa, 2014 Odtwarzanie zmiennych stanu Wykorzystanie układów sterowania od zmiennych stanu wymaga uzyskania dodatkowych
Wykład 6 - odtwarzanie zmiennych stanu przez obserwację Instytut Automatyki i Robotyki Warszawa, 2014 Odtwarzanie zmiennych stanu Wykorzystanie układów sterowania od zmiennych stanu wymaga uzyskania dodatkowych
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Sterowanie Napędów Maszyn i Robotów
 Wykład 4 - Model w przestrzeni stanów Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Do zaprojektowania układu regulacji pozycji siłownika pneumatycznego, poszukiwany jest model dynamiki układu w
Wykład 4 - Model w przestrzeni stanów Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Do zaprojektowania układu regulacji pozycji siłownika pneumatycznego, poszukiwany jest model dynamiki układu w
Sterowanie napędów maszyn i robotów
 Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 1 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 1 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Sterowanie napędów maszyn i robotów
 Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 3 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 3 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Filtr Kalmana. Struktury i Algorytmy Sterowania Wykład 1-2. prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz
 Filtr Kalmana Struktury i Algorytmy Sterowania Wykład 1-2 prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz Politechnika Gdańska, Wydział Elektortechniki i Automatyki 2013-10-09, Gdańsk Założenia
Filtr Kalmana Struktury i Algorytmy Sterowania Wykład 1-2 prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz Politechnika Gdańska, Wydział Elektortechniki i Automatyki 2013-10-09, Gdańsk Założenia
Analityczne metody detekcji uszkodzeń
 Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Rozdział 2: Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów
 Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
#09. Systemy o złożonej strukturze
 #09 Systemy o złożonej strukturze system składa się z wielu elementów, obiekty (podsystemy) wchodzące w skład systemu są ze sobą połączone i wzajemnie od siebie zależne mogą wystąpić ograniczenia w dostępności
#09 Systemy o złożonej strukturze system składa się z wielu elementów, obiekty (podsystemy) wchodzące w skład systemu są ze sobą połączone i wzajemnie od siebie zależne mogą wystąpić ograniczenia w dostępności
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Sterowanie Napędów Maszyn i Robotów
 Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Sterowanie Napędów Maszyn i Robotów
 Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Estymacja wektora stanu w prostym układzie elektroenergetycznym
 Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Obiekt. Obiekt sterowania obiekt, który realizuje proces (zaplanowany).
 SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
x x 1. Przedmiot identyfikacji System x (1) x (2) : x (s) a 1 a 2 : a s mierzone, a = zestaw współczynników konkretyzujacych F ()
 . Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
. Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH
 Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11; środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11; środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
POMIARY WIELKOŚCI NIEELEKTRYCZNYCH
 POMIARY WIELKOŚCI NIEELEKTRYCZNYCH Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMST Semestr letni Wykład nr 3 Prawo autorskie Niniejsze
POMIARY WIELKOŚCI NIEELEKTRYCZNYCH Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMST Semestr letni Wykład nr 3 Prawo autorskie Niniejsze
Sterowanie napędów maszyn i robotów
 Wykład 8 - zaawansowane układy sterowania Instytut Automatyki i Robotyki Warszawa, 2014 adaptacyjne (ang. adaptive control) z dostosowaniem się do aktualnych warunków pracy napędu - koncepcje: ze wstępnie
Wykład 8 - zaawansowane układy sterowania Instytut Automatyki i Robotyki Warszawa, 2014 adaptacyjne (ang. adaptive control) z dostosowaniem się do aktualnych warunków pracy napędu - koncepcje: ze wstępnie
Regulacja dwupołożeniowa (dwustawna)
 Regulacja dwupołożeniowa (dwustawna) I. Wprowadzenie Regulacja dwustawna (dwupołożeniowa) jest często stosowaną metodą regulacji temperatury w urządzeniach grzejnictwa elektrycznego. Polega ona na cyklicznym
Regulacja dwupołożeniowa (dwustawna) I. Wprowadzenie Regulacja dwustawna (dwupołożeniowa) jest często stosowaną metodą regulacji temperatury w urządzeniach grzejnictwa elektrycznego. Polega ona na cyklicznym
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI
 WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Liniowe układy scalone w technice cyfrowej
 Liniowe układy scalone w technice cyfrowej Wykład 6 Zastosowania wzmacniaczy operacyjnych: konwertery prąd-napięcie i napięcie-prąd, źródła prądowe i napięciowe, przesuwnik fazowy Konwerter prąd-napięcie
Liniowe układy scalone w technice cyfrowej Wykład 6 Zastosowania wzmacniaczy operacyjnych: konwertery prąd-napięcie i napięcie-prąd, źródła prądowe i napięciowe, przesuwnik fazowy Konwerter prąd-napięcie
Drgania wymuszone - wahadło Pohla
 Zagadnienia powiązane Częstość kołowa, częstotliwość charakterystyczna, częstotliwość rezonansowa, wahadło skrętne, drgania skrętne, moment siły, moment powrotny, drgania tłumione/nietłumione, drgania
Zagadnienia powiązane Częstość kołowa, częstotliwość charakterystyczna, częstotliwość rezonansowa, wahadło skrętne, drgania skrętne, moment siły, moment powrotny, drgania tłumione/nietłumione, drgania
POMIARY WIELKOŚCI NIEELEKTRYCZNYCH
 POMIARY WIELKOŚCI NIEELEKTRYCZNYCH Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMNS Semestr zimowy studia niestacjonarne Wykład nr
POMIARY WIELKOŚCI NIEELEKTRYCZNYCH Dr inż. Eligiusz PAWŁOWSKI Politechnika Lubelska Wydział Elektrotechniki i Informatyki Prezentacja do wykładu dla EMNS Semestr zimowy studia niestacjonarne Wykład nr
Analiza szeregów czasowych: 6. Liniowe modele niestacjonarne
 Analiza szeregów czasowych: 6. Liniowe modele niestacjonarne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Warunki stacjonarności modelu AR(p) y n = β 1 y n 1 + β 2 y n 2 + + β
Analiza szeregów czasowych: 6. Liniowe modele niestacjonarne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Warunki stacjonarności modelu AR(p) y n = β 1 y n 1 + β 2 y n 2 + + β
Ekonometria. Prognozowanie ekonometryczne, ocena stabilności oszacowań parametrów strukturalnych. Jakub Mućk. Katedra Ekonomii Ilościowej
 Ekonometria Prognozowanie ekonometryczne, ocena stabilności oszacowań parametrów strukturalnych Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Wykład 4 Prognozowanie, stabilność 1 / 17 Agenda
Ekonometria Prognozowanie ekonometryczne, ocena stabilności oszacowań parametrów strukturalnych Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Wykład 4 Prognozowanie, stabilność 1 / 17 Agenda
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji
 Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
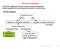 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Ćw. 18: Pomiary wielkości nieelektrycznych II
 Wydział: EAIiE Kierunek: Imię i nazwisko (e mail): Rok:. (../..) Grupa: Zespół: Data wykonania: Zaliczenie: Podpis prowadzącego: Uwagi: LABORATORIUM METROLOGII Ćw. 18: Pomiary wielkości nieelektrycznych
Wydział: EAIiE Kierunek: Imię i nazwisko (e mail): Rok:. (../..) Grupa: Zespół: Data wykonania: Zaliczenie: Podpis prowadzącego: Uwagi: LABORATORIUM METROLOGII Ćw. 18: Pomiary wielkości nieelektrycznych
Przetwarzanie A/C i C/A
 Przetwarzanie A/C i C/A Instrukcja do ćwiczenia laboratoryjnego opracował: Łukasz Buczek 05.2015 Rev. 204.2018 (KS) 1 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z przetwornikami: analogowo-cyfrowym
Przetwarzanie A/C i C/A Instrukcja do ćwiczenia laboratoryjnego opracował: Łukasz Buczek 05.2015 Rev. 204.2018 (KS) 1 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z przetwornikami: analogowo-cyfrowym
[d(i) y(i)] 2. Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) i=1. λ n i [d(i) y(i)] 2 λ (0, 1]
![[d(i) y(i)] 2. Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) i=1. λ n i [d(i) y(i)] 2 λ (0, 1] [d(i) y(i)] 2. Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) i=1. λ n i [d(i) y(i)] 2 λ (0, 1]](/thumbs/72/67682252.jpg) Algorytm RLS Recursive Least Squares Ogólna postać kryterium LS: J = i e 2 (i) = i [d(i) y(i)] 2 Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) Zmodyfikowane kryterium
Algorytm RLS Recursive Least Squares Ogólna postać kryterium LS: J = i e 2 (i) = i [d(i) y(i)] 2 Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) Zmodyfikowane kryterium
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
(86) Data i numer zgłoszenia międzynarodowego: , PCT/DE03/00923 (87) Data i numer publikacji zgłoszenia międzynarodowego:
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 204399 (21) Numer zgłoszenia: 370760 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia: 20.03.2003 (86) Data i numer zgłoszenia
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 204399 (21) Numer zgłoszenia: 370760 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia: 20.03.2003 (86) Data i numer zgłoszenia
PODSTAWY AUTOMATYKI. Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
Automatyka i sterowania
 Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
WYDZIAŁ PPT / KATEDRA INŻYNIERII BIOMEDYCZNEJ D-1 LABORATORIUM Z MIERNICTWA I AUTOMATYKI Ćwiczenie nr 7. Badanie jakości regulacji dwupołożeniowej.
 Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
Ekonometria. Dobór postaci analitycznej, transformacja liniowa i estymacja modelu KMNK. Paweł Cibis 9 marca 2007
 , transformacja liniowa i estymacja modelu KMNK Paweł Cibis pawel@cibis.pl 9 marca 2007 1 Miary dopasowania modelu do danych empirycznych Współczynnik determinacji Współczynnik zbieżności Skorygowany R
, transformacja liniowa i estymacja modelu KMNK Paweł Cibis pawel@cibis.pl 9 marca 2007 1 Miary dopasowania modelu do danych empirycznych Współczynnik determinacji Współczynnik zbieżności Skorygowany R
Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych
 Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych Cel ćwiczenia Celem ćwiczenia jest poznanie podstawowych własności członów liniowych
Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych Cel ćwiczenia Celem ćwiczenia jest poznanie podstawowych własności członów liniowych
Analiza właściwości filtrów dolnoprzepustowych
 Ćwiczenie Analiza właściwości filtrów dolnoprzepustowych Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra dolnoprzepustowego (DP) rzędu i jego parametrami.. Analiza widma sygnału prostokątnego.
Ćwiczenie Analiza właściwości filtrów dolnoprzepustowych Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra dolnoprzepustowego (DP) rzędu i jego parametrami.. Analiza widma sygnału prostokątnego.
Metoda najmniejszych kwadratów
 Metoda najmniejszych kwadratów Przykład wstępny. W ekonomicznej teorii produkcji rozważa się funkcję produkcji Cobba Douglasa: z = AL α K β gdzie z oznacza wielkość produkcji, L jest nakładem pracy, K
Metoda najmniejszych kwadratów Przykład wstępny. W ekonomicznej teorii produkcji rozważa się funkcję produkcji Cobba Douglasa: z = AL α K β gdzie z oznacza wielkość produkcji, L jest nakładem pracy, K
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Własności dynamiczne przetworników pierwszego rzędu
 1 ĆWICZENIE 7. CEL ĆWICZENIA. Własności dynamiczne przetworników pierwszego rzędu Celem ćwiczenia jest poznanie własności dynamicznych przetworników pierwszego rzędu w dziedzinie czasu i częstotliwości
1 ĆWICZENIE 7. CEL ĆWICZENIA. Własności dynamiczne przetworników pierwszego rzędu Celem ćwiczenia jest poznanie własności dynamicznych przetworników pierwszego rzędu w dziedzinie czasu i częstotliwości
Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów
 Laboratorium Metod Optymalizacji 216 Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów 1. Za pomocą funkcji lsqcurvefit dobrać parametry a i b funkcji: Posiadając następujące dane pomiarowe:
Laboratorium Metod Optymalizacji 216 Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów 1. Za pomocą funkcji lsqcurvefit dobrać parametry a i b funkcji: Posiadając następujące dane pomiarowe:
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Podstawy Automatyki. Wykład 6 - Miejsce i rola regulatora w układzie regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Spis treści Przedmowa
 Spis treści Przedmowa 1. Wprowadzenie do problematyki konstruowania - Marek Dietrich (p. 1.1, 1.2), Włodzimierz Ozimowski (p. 1.3 -i-1.7), Jacek Stupnicki (p. l.8) 1.1. Proces konstruowania 1.2. Kryteria
Spis treści Przedmowa 1. Wprowadzenie do problematyki konstruowania - Marek Dietrich (p. 1.1, 1.2), Włodzimierz Ozimowski (p. 1.3 -i-1.7), Jacek Stupnicki (p. l.8) 1.1. Proces konstruowania 1.2. Kryteria
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
 Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Odchudzamy serię danych, czyli jak wykryć i usunąć wyniki obarczone błędami grubymi
 Odchudzamy serię danych, czyli jak wykryć i usunąć wyniki obarczone błędami grubymi Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska D syst D śr m 1 3 5 2 4 6 śr j D 1
Odchudzamy serię danych, czyli jak wykryć i usunąć wyniki obarczone błędami grubymi Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska D syst D śr m 1 3 5 2 4 6 śr j D 1
Wzmacniacze operacyjne
 Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
Automatyka i Robotyka II stopień ogólno akademicki studia niestacjonarne. wszystkie Katedra Automatyki i Robotyki Dr inż.
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Identyfikacja obiektów sterowania Identification of Control Systems A.
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Identyfikacja obiektów sterowania Identification of Control Systems A.
Przetwarzanie AC i CA
 1 Elektroniki Elektroniki Elektroniki Elektroniki Elektroniki Katedr Przetwarzanie AC i CA Instrukcja do ćwiczenia laboratoryjnego opracował: Łukasz Buczek 05.2015 1. Cel ćwiczenia 2 Celem ćwiczenia jest
1 Elektroniki Elektroniki Elektroniki Elektroniki Elektroniki Katedr Przetwarzanie AC i CA Instrukcja do ćwiczenia laboratoryjnego opracował: Łukasz Buczek 05.2015 1. Cel ćwiczenia 2 Celem ćwiczenia jest
Przetworniki cyfrowo analogowe oraz analogowo - cyfrowe
 Przetworniki cyfrowo analogowe oraz analogowo - cyfrowe Przetworniki cyfrowo / analogowe W cyfrowych systemach pomiarowych często zachodzi konieczność zmiany sygnału cyfrowego na analogowy, np. w celu
Przetworniki cyfrowo analogowe oraz analogowo - cyfrowe Przetworniki cyfrowo / analogowe W cyfrowych systemach pomiarowych często zachodzi konieczność zmiany sygnału cyfrowego na analogowy, np. w celu
WYDZIAŁ PPT / KATEDRA INŻYNIERII BIOMEDYCZNEJ D-1 LABORATORIUM Z AUTOMATYKI I ROBOTYKI Ćwiczenie nr 4. Badanie jakości regulacji dwupołożeniowej.
 Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 1. Modelowanie i analiza widmowa dyskretnych sygnałów losowych
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 1 Modelowanie i analiza widmowa dyskretnych sygnałów losowych 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie studentów z wybranymi algorytmami
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 1 Modelowanie i analiza widmowa dyskretnych sygnałów losowych 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie studentów z wybranymi algorytmami
WZMACNIACZ NAPIĘCIOWY RC
 WZMACNIACZ NAPIĘCIOWY RC 1. WSTĘP Tematem ćwiczenia są podstawowe właściwości jednostopniowego wzmacniacza pasmowego z tranzystorem bipolarnym. Zadaniem ćwiczących jest dokonanie pomiaru częstotliwości
WZMACNIACZ NAPIĘCIOWY RC 1. WSTĘP Tematem ćwiczenia są podstawowe właściwości jednostopniowego wzmacniacza pasmowego z tranzystorem bipolarnym. Zadaniem ćwiczących jest dokonanie pomiaru częstotliwości
Modele DSGE. Jerzy Mycielski. Maj Jerzy Mycielski () Modele DSGE Maj / 11
 Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Filtry aktywne filtr górnoprzepustowy
 . el ćwiczenia. Filtry aktywne filtr górnoprzepustowy elem ćwiczenia jest praktyczne poznanie właściwości filtrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów filtru.. Budowa
. el ćwiczenia. Filtry aktywne filtr górnoprzepustowy elem ćwiczenia jest praktyczne poznanie właściwości filtrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów filtru.. Budowa
Spis treści. Przedmowa 11
 Podstawy konstrukcji maszyn. T. 1 / autorzy: Marek Dietrich, Stanisław Kocańda, Bohdan Korytkowski, Włodzimierz Ozimowski, Jacek Stupnicki, Tadeusz Szopa ; pod redakcją Marka Dietricha. wyd. 3, 2 dodr.
Podstawy konstrukcji maszyn. T. 1 / autorzy: Marek Dietrich, Stanisław Kocańda, Bohdan Korytkowski, Włodzimierz Ozimowski, Jacek Stupnicki, Tadeusz Szopa ; pod redakcją Marka Dietricha. wyd. 3, 2 dodr.
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Metody Prognozowania
 Wprowadzenie Ewa Bielińska 3 października 2007 Plan 1 Wprowadzenie Czym jest prognozowanie Historia 2 Ciągi czasowe Postępowanie prognostyczne i prognozowanie Predykcja długo- i krótko-terminowa Rodzaje
Wprowadzenie Ewa Bielińska 3 października 2007 Plan 1 Wprowadzenie Czym jest prognozowanie Historia 2 Ciągi czasowe Postępowanie prognostyczne i prognozowanie Predykcja długo- i krótko-terminowa Rodzaje
Tranzystory bipolarne. Właściwości dynamiczne wzmacniaczy w układzie wspólnego emitera.
 ĆWICZENIE 5 Tranzystory bipolarne. Właściwości dynamiczne wzmacniaczy w układzie wspólnego emitera. I. Cel ćwiczenia Badanie właściwości dynamicznych wzmacniaczy tranzystorowych pracujących w układzie
ĆWICZENIE 5 Tranzystory bipolarne. Właściwości dynamiczne wzmacniaczy w układzie wspólnego emitera. I. Cel ćwiczenia Badanie właściwości dynamicznych wzmacniaczy tranzystorowych pracujących w układzie
Spis treści 3 SPIS TREŚCI
 Spis treści 3 SPIS TREŚCI PRZEDMOWA... 1. WNIOSKOWANIE STATYSTYCZNE JAKO DYSCYPLINA MATEMATYCZNA... Metody statystyczne w analizie i prognozowaniu zjawisk ekonomicznych... Badania statystyczne podstawowe
Spis treści 3 SPIS TREŚCI PRZEDMOWA... 1. WNIOSKOWANIE STATYSTYCZNE JAKO DYSCYPLINA MATEMATYCZNA... Metody statystyczne w analizie i prognozowaniu zjawisk ekonomicznych... Badania statystyczne podstawowe
Automatyka i robotyka ETP2005L. Laboratorium semestr zimowy
 Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Manipulatory i roboty mobilne AR S1 semestr 5
 Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa. P. F. Góra
 Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
Analiza korelacyjna i regresyjna
 Podstawy Metrologii i Technik Eksperymentu Laboratorium Analiza korelacyjna i regresyjna Instrukcja do ćwiczenia nr 5 Zakład Miernictwa i Ochrony Atmosfery Wrocław, kwiecień 2014 Podstawy Metrologii i
Podstawy Metrologii i Technik Eksperymentu Laboratorium Analiza korelacyjna i regresyjna Instrukcja do ćwiczenia nr 5 Zakład Miernictwa i Ochrony Atmosfery Wrocław, kwiecień 2014 Podstawy Metrologii i
Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transform
 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. March 20, 2013 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. Sygnał i system Sygnał jest opisem
Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. March 20, 2013 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. Sygnał i system Sygnał jest opisem
Wykład 9. Terminologia i jej znaczenie. Cenzurowanie wyników pomiarów.
 Wykład 9. Terminologia i jej znaczenie. Cenzurowanie wyników pomiarów.. KEITHLEY. Practical Solutions for Accurate. Test & Measurement. Training materials, www.keithley.com;. Janusz Piotrowski: Procedury
Wykład 9. Terminologia i jej znaczenie. Cenzurowanie wyników pomiarów.. KEITHLEY. Practical Solutions for Accurate. Test & Measurement. Training materials, www.keithley.com;. Janusz Piotrowski: Procedury
Spis treści Wstęp Estymacja Testowanie. Efekty losowe. Bogumiła Koprowska, Elżbieta Kukla
 Bogumiła Koprowska Elżbieta Kukla 1 Wstęp Czym są efekty losowe? Przykłady Model mieszany 2 Estymacja Jednokierunkowa klasyfikacja (ANOVA) Metoda największej wiarogodności (ML) Metoda największej wiarogodności
Bogumiła Koprowska Elżbieta Kukla 1 Wstęp Czym są efekty losowe? Przykłady Model mieszany 2 Estymacja Jednokierunkowa klasyfikacja (ANOVA) Metoda największej wiarogodności (ML) Metoda największej wiarogodności
INSTRUKCJA DO ĆWICZENIA NR 7
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Filtry aktywne filtr środkowoprzepustowy
 Filtry aktywne iltr środkowoprzepustowy. Cel ćwiczenia. Celem ćwiczenia jest praktyczne poznanie właściwości iltrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów iltru.. Budowa
Filtry aktywne iltr środkowoprzepustowy. Cel ćwiczenia. Celem ćwiczenia jest praktyczne poznanie właściwości iltrów aktywnych, metod ich projektowania oraz pomiaru podstawowych parametrów iltru.. Budowa
Metody numeryczne. Janusz Szwabiński. Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/50
 Metody numeryczne Układy równań liniowych, część II Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/50 Układy równań liniowych, część II 1. Iteracyjne poprawianie
Metody numeryczne Układy równań liniowych, część II Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/50 Układy równań liniowych, część II 1. Iteracyjne poprawianie
b n y k n T s Filtr cyfrowy opisuje się również za pomocą splotu dyskretnego przedstawionego poniżej:
 1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
Katedra Metrologii i Systemów Diagnostycznych Laboratorium Metrologii II. 2013/14. Grupa: Nr. Ćwicz.
 Politechnika Rzeszowska Katedra Metrologii i Systemów Diagnostycznych Laboratorium Metrologii II WYZNACZANIE WŁAŚCIWOŚCI STATYCZNYCH I DYNAMICZNYCH PRZETWORNIKÓW Grupa: Nr. Ćwicz. 9 1... kierownik 2...
Politechnika Rzeszowska Katedra Metrologii i Systemów Diagnostycznych Laboratorium Metrologii II WYZNACZANIE WŁAŚCIWOŚCI STATYCZNYCH I DYNAMICZNYCH PRZETWORNIKÓW Grupa: Nr. Ćwicz. 9 1... kierownik 2...
Sterowanie napędów maszyn i robotów
 Wykład 7 - układy sterowania zwykłego Instytut Automatyki i Robotyki Warszawa, 2014 Kryteria oceny jakości sterowania Kryteria oceny jakości sterowania Standardowe miary jakości sterowania Modyfikacje
Wykład 7 - układy sterowania zwykłego Instytut Automatyki i Robotyki Warszawa, 2014 Kryteria oceny jakości sterowania Kryteria oceny jakości sterowania Standardowe miary jakości sterowania Modyfikacje
