ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 1. Modelowanie i analiza widmowa dyskretnych sygnałów losowych
|
|
|
- Aleksander Lisowski
- 6 lat temu
- Przeglądów:
Transkrypt
1 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 1 Modelowanie i analiza widmowa dyskretnych sygnałów losowych 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie studentów z wybranymi algorytmami filtracji adaptacyjnej stosowanymi do estymacji parametrów sygnałów modelowanych procesami ARMA oraz przedstawienie nowoczesnych metod analizy widmowej opartych na liniowym modelowaniu dyskretnych procesów losowych. 2. ZAKRES BADAŃ W pierwszej części ćwiczenia badane są dwa algorytmy adaptacyjnej identyfikacji modeli ARMA sygnału losowego: blokowy transwersalny algorytm typu LS w wersji Kay a; rekursywny transwersalny algorytm oparty na kryterium największej wiarygodności (tzw. algorytm Friedlandera). W drugiej części ćwiczenia badane są natomiast metody analizy widmowej oparte na autoregresyjnym modelu dyskretnego procesu losowego. Badania szerokiej klasy algorytmów modelowania AR zaimplementowanych w pakiecie AFRICA przeprowadzone są dla różnych typów sygnałów syntetycznych i rzeczywistych (sygnał EEG). W szczególności badane są adaptacyjne właściwości algorytmów na przykładzie sygnałów niestacjonarnych (sygnał sinusoidalny o liniowo narastającej częstotliwości (chirp) oraz sygnał EEG). 3. PODSTAWY TEORETYCZNE 3.1 Model ARMA dyskretnego procesu losowego Losowy proces autoregresji z ruchomą średnią ARMA (AutoRegressive Moving Average) opisany jest następującym równaniem różnicowym: p q X(n) = a i X(n i) + W (n) + b j W (n j), (1) i=1 j=1 gdzie W (n) jest szumem białym, a liczby p i q określają rząd modelu ozn. ARMA(p, q). Innymi słowy jest to proces otrzymywany na wyjściu filtru liniowego o transmitancji H(z), pobudzanego szumem W (n). Transmitancja H(z) ma przy tym postać: H(z) = B(z) A(z) = 1 + b 1z b q z q. (2) 1 a 1 z 1 a p z p 1
2 Filtr o transmitancji H(z) nazywany jest filtrem modelującym. Jeśli filtr ten spełnia warunek minimalnofazowości, to wówczas sensownym staje zagadnienie filtru odwrotnego, rozumianego jako filtr o transmitancji G(z) = 1/H(z) = A(z)/B(z). Jeśli na wejście takiego filtru podamy sygnał X(n), to na jego wyjściu otrzymamy szum biały. Mamy wtedy do czynienia z problemem wybielania sygnałów, który sprowadza się do znalezienia transmitancji filtru odwrotnego. Jeśli transmitancja H(z) filtru modelującego jest znana lub inaczej znany jest model sygnału X(n), to tak postawione zadanie jest trywialne. W praktyce jednak model sygnału X(n) nie jest znany. Co więcej nie ma żadnej pewności, że obserwowany sygnał spełnia równanie modelu ARMA (1). W takiej sytuacji problem wybielania sygnału wiąże się nierozerwalnie z problemem modelowania, tzn. znalezienia takiego filtru liniowego o transmitancji ˆB(z)/ Â(z), którego wyjście przy pobudzaniu szumem białym na wejściu jest w jakimś sensie przybliżeniem obserwowanego sygnału X(n). Filtr wybielający ma wówczas transmitancję Ĝ(z) = Â(z)/ ˆB(z). Przedstawiony powyżej schemat rozwiązania problemu wybielania poprzez uprzednie modelowanie ma znaczenie czysto teoretyczne i wyłącznie poglądowe. W praktyce bowiem zdecydowana większość algorytmów znajdowania modelu ARMA dla obserwowanego sygnału pracuje w odwróconej kolejności. Model znajdowany jest poprzez uprzednie wybielanie sygnału, którego obserwowane próbki przetwarzane są przez filtr adaptacyjny w taki sposób, aby na wyjściu tego filtru pojawił się sygnał błędu o właściwościach możliwie najbardziej zbliżonych do szumu białego. Filtr modelujący uzyskuje się wtedy poprzez odpowiednie odwrócenie filtru wybielającego. Dowodzi to, że z praktycznego punktu widzenia problemy wybielania i modelowania sygnałów są ze sobą nierozerwalnie związane i należy je traktować łącznie. 3.2 Adaptacyjne algorytmy modelowania procesów losowych ARMA W ćwiczeniu badane są dwa algorytmy modelowania ARMA. Pierwszym z nich jest blokowy algorytm transwersalny oparty na kryterium LS. Istotą tego algorytmu jest połączenie rozwiązania nadokreślonego układu zmodyfikowanych równań Yula-Walkera (estymacja parametrów AR) z metodą Kay a estymacji parametrów MA w modelu ARMA. Algorytm ten jest opisany szczegółowo w [1, 2]. Drugim algorytmem jest rekursywny algorytm oparty na kryterium największej wiarygodności [3]. Ze względu na duże znaczenie praktyczne w klasie algorytmów estymacji parametrów procesów ARMA zostanie on omówiony dokładniej. Przyjmujemy następujące oznaczenia: θ = [ a 1,..., a p, b 1,..., b q ] T - wektor parametrów modelu, ˆθ n = [ â 1 (n),..., â p (n), ˆb 1 (n),..., ˆb q (n)] T - wektor estymat parametrów modelu, ν n = [x(n 1),..., x(n p), e(n 1),..., e(n q) T - wektor danych (obserwacji), ν n = [ x(n 1),..., x(n p), ẽ(n 1),..., ẽ(n q) T - wektor danych po filtracji. Zakładając, że znamy już wektor estymat parametrów ˆθ n 1 wyznaczony dla poprzednich obserwacji możemy, zgodnie z ogólną zasadą algorytmów rekursywnych, wyznaczyć wektor estymat ˆθ n po zarejestrowaniu obserwacji x(n). Bezpośrednio przed zarejestrowaniem obserwacji x(n) dostępne są następujące wielkości: ˆθ n 1, ν n, ν n oraz macierz Q n 1 = E[(ˆθ n 1 θ)(ˆθ n 1 θ) T ], (3) będąca macierzą kowariancji błędu. Po zarejestrowaniu próbki x(n) możemy zatem wyznaczyć błąd predykcji: ε(n) = x(n) ν T n ˆθ n 1 (4) 2
3 oraz macierz kowariancji błędu w chwili n: Q n = 1 λ n Qn 1 Q n 1 ν n ν T nq n 1 λ n + ν T n 1Q n 1 ν n 1. (5) Rola parametru λ n zostanie wyjaśniona niżej. Główna rekursja na parametry modelu przyjmuje postać: ˆθ n = ˆθ n 1 + Q n ν n ε(n). (6) Po wyznaczeniu bieżącej wartości wektora estymat ˆθ n możemy wyznaczyć błąd resztkowy: e(n) = x(n) ν T n ˆθ n, (7) który występuje w wektorze obserwacji ν n+1. Mając z kolei wektor ν n+1 możemy wyznaczyć wektor danych po filtracji ν n+1 do następnej iteracji. W tym celu należy dokonać następującej operacji filtracji: x n (z) = 1 ˆB n (kz 1 ) x n(z), ẽ n (z) = 1 ˆB n (kz 1 ) e n(z), (8) gdzie ˆB n (kz 1 ) = 1 + kˆb 1 (n)z 1 + k 2ˆb2 (n)z k qˆbq (n)z q. (9) Rolą stałej k jest zapewnienie stabilności filtru. W wersji algorytmu zaimplementowanej w pakiecie AFRICA wartość tej stałej jest dobierana automatycznie. Występujący wcześniej parametr λ n jest pewnym parametrem wagowym nazywanym również wykładniczym współczynnikiem zapominania. Często przyjmuje się, że λ n = const. W wersji algorytmu badanej w ćwiczeniu przyjęto jednak, że λ n = (1 β)λ n 1 + β, gdzie λ 0 = 0, 95, β zaś jest stałą dodatnią o małej wartości (β < 1), która ma jednakże istotny wpływ na szybkość zbieżności algorytmu. 3.3 Analiza widmowa oparta na modelowaniu autoregresyjnym Proces autoregresyjny AR jest szczególnym przypadkiem procesu ARMA rozważanego w punkcie 3.1. Losowy dyskretny proces autoregresji opisany jest następującym równaniem: p X(n) = a i X(n i) + W (n). (10) i=1 Podobnie jak dla procesu ARMA, proces AR otrzymywany jest na wyjściu filtru liniowego o transmitancji H(z) pobudzanego szumem W (n) z tą różnicą, że tym razem transmitancja ta ma postać: H(z) = 1 A(z) = 1. (11) 1 a 1 z 1 a p z p Zgodnie z właściwościami transmisyjnymi układów liniowych widmowa gęstość mocy sygnału na wyjściu filtru, a więc procesu autoregresyjnego jest dana zależnością: S XX (e jθ ) = σ 2 W 1 1 a 1 e jθ a p e jpθ 2. (12) 3
4 Oczywiście podaną zależność widmową można bez trudu uogólnić na przypadek procesu ARMA. Wówczas otrzymujemy S XX (e jθ ) = σw b 1 e jθ + + b q e jqθ 1 a 1 e jθ a p e jpθ 2. (13) Przedstawione zależności widmowe stanowią podstawę analizowanych w ćwiczeniu nowoczesnych metod estymacji widma opartych na modelowaniu procesów losowych. Zgodnie z zależnościami (12) i (13), znając parametry modelu, możemy bez trudu wyznaczyć widmową gęstość mocy obserwowanego procesu. Oczywiście w praktyce parametry modelu nie są znane i należy je estymować na podstawie próbek pojedynczej realizacji obserwowanego sygnału losowego. W tym miejscu należy podkreślić, że w porównaniu z klasycznymi metodami estymacji widma takimi jak metoda periodogramów, metody oparte na modelowaniu sygnałów charakteryzują się znacznie lepszą rozdzielczością, a także lepszymi właściwościami statystycznymi estymatora, takimi jak obciążenie czy wariancja. Cena jaką trzeba zapłacić za taką poprawę to znaczne zwiększenie złożoności obliczeniowej algorytmów estymacji widma mocy. 4. BADANIA EKSPERYMENTALNE 4.1 Badanie algorytmów estymacji parametrów procesu ARMA Wygenerować 500 próbek sygnału ARMA(2, 2) o współczynnikach b = [1-1,7150 0,9810] T oraz a = [1-0,9500 0,9025] T, wykorzystując do tego celu następującą sekwencję instrukcji: rand( normal ); x = rand(1,500); y = filter(b,a,x); 1. Wyestymować widmo sygnału za pomocą blokowego algorytmu Kay a BLK i porównać je na jednym wykresie logarytmicznym z charakterystyką amplitudową filtru modelującego. Skorzystać z funkcji freqz. Skomentować wyniki. 2. Wybielić sygnał za pomocą estymowanego i idealnego filtru odwrotnego. Porównać i skomentować wyniki na podstawie oceny widma mocy i funkcji autokorelacji wybielonych sygnałów. 3. Wygenerowany sygnał ARMA(2, 2) poddać filtracji za pomocą rekursywnego algorytmu Friedlandera RML dla kilku wartości stałej β (β = 0, 3; 0, 1; 0, 05; 0, 01; 0), badając jednocześnie wpływ tej stałej na jakość estymacji widma oraz dokładność estymacji współczynników. 4. Porównać jakość wybielania sygnału dla trzech wybranych wartości stałej β. 4.2 Estymacja widma zaszumionych sygnałów sinusoidalnych 1. Wygenerować sygnał o długości 500 próbek będący sumą dwóch składowych harmonicznych o jednostkowych amplitudach oraz częstotliwościach unormowanych 0,20 i 0,30 zakłóconych addytywnym szumem białym. Wyestymować widmo takiego sygnału za pomocą algorytmu BLK, zakładając jednocześnie, że sygnał ten jest dobrze 4
5 modelowany procesem ARMA(4, 4). Zbadać jakość estymacji widma w zależności od wariancji szumu zakłócającego. 2. Powtórzyć badania z punktu 1 zbliżając do siebie częstotliwości unormowane składowych sinusoidalnych (przyjąć wartości 0,20 i 0,21). 4.3 Estymacja widma sygnału zespolonego za pomocą modelowania AR Ten punkt ćwiczenia został zrealizowany w pakiecie AFRICA jako program demo 6. Sygnał zespolony, którego widmo będzie estymowane za pomocą różnych algorytmów AR dostępnych w pakiecie AFRICA jest krótkim 64 punktowym ciągiem danych. Zawiera on w swoim widmie dwie silne blisko siebie położone sinusoidy zespolone o częstotliwościach unormowanych 0,20 i 0,21, a także dwie słabsze o 20 db sinusoidy o częstotliwościach -0,15 i 0,10. Sygnał użyteczny składający się z tych czterech zespolonych sinusoid zakłócony jest szumem kolorowym występującym w pasmach częstotliwości od -0,50 do -0,20 oraz od 0,20 do 0,50. Widma będą estymowane kolejno za pomocą następujących algorytmów: BLT, BLL, GAT, GAL, LST. Rząd modelu AR ustalono na 15. Oglądając kolejno estymowane widma porównać i skomentować rezultaty pod kątem rozdzielenia dwóch bliskich składowych sinusoidalnych, skuteczności wychwycenia składowych o mniejszych amplitudach oraz obecności ewentualnych artefaktów. 4.4 Zastosowanie algorytmów rekursywnych do estymacji charakterystyk procesu niestacjonarnego Wygenerować 100 próbek sygnału sinusoidalnego o liniowo narastającej częstotliwości unormowanej w zakresie od 0,16 do 0,32 zakłócanego szumem białym o odchyleniu standardowym σ W = 0, 1 (program demonstracyjny demo 4). 1. Wyznaczyć widmo takiego sygnału metodą FFT oraz blokowym algorytmem AR wysokiego rzędu (np. 32). Skomentować wyniki. 2. Do estymacji widma zastosować rekursywny algorytm rzędu 4 (np. LST). Za pomocą odpowiednich procedur wizualizacji wyników dostępnych w pakiecie AFRICA zbadać możliwość śledzenia widma chwilowego sygnału niestacjonarnego przez algorytm rekursywny. Sformułować wnioski ogólne. 4.5 Zastosowanie algorytmów rekursywnych do estymacji widma chwilowego sygnału EEG Rekursywna estymacja widma chwilowego sygnału EEG została zaimplementowana jako program demonstracyjny pakietu AFRICA o nazwie demo 5. Sygnał EEG wykorzystany w tym pokazowym programie jest fragmentem sygnału rzeczywistego nagranego podczas całonocnego badania pacjenta w szpitalu. Podobnie jak w poprzednim punkcie jest to sygnał niestacjonarny. Analiza widmowa tego sygnału służy do rozpoznawania faz snu, a w szczególności tzw. wrzecion sennych, które stanowią istotną informację diagnostyczną dla lekarzy. Szczegóły dotyczące analizowanego przebiegu EEG podane zostaną jako komentarze w trakcie kolejnych kroków wykonywania się programu demo 5. 5
6 4.6 Zastosowanie algorytmów AR do estymacji widma procesów ARMA Wygenerować sygnał ARMA(2, 2) o dowolnych (ale sensownych) wymyślonych przez ćwiczących parametrach. Dokonać estymacji widma tego sygnału za pomocą kilku wybranych algorytmów AR. Zbadać wpływ rzędu algorytmu AR na jakość estymacji. LITERATURA [1] M. L. Hönig and D. G. Messerschmitt, Adaptive Filters. Kluwer Academic Publishers, [2] B. Widrow and S. D. Stearns, Adaptive Signal Processing. Englewood Cliffs: Prentice- Hall, [3] B. Friedlander, Recursive Maximum Likelihood Algorithm for ARMA Spectral Estimation, IEEE Trans. on Information Theory, July [4] P. M. Clarkson, Optimal and Adaptive Signal Processing. CRC Press,
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 2. Badanie algorytmów adaptacyjnych LMS i RLS
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 2. Badanie algorytmów adaptacyjnych LMS i RLS
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
Rozdział 2: Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów
 Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Egzamin / zaliczenie na ocenę*
 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim CYFROWE PRZETWARZANIE SYGNAŁÓW Nazwa w języku angielskim DIGITAL SIGNAL PROCESSING Kierunek studiów
WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim CYFROWE PRZETWARZANIE SYGNAŁÓW Nazwa w języku angielskim DIGITAL SIGNAL PROCESSING Kierunek studiów
Laboratorium Przetwarzania Sygnałów Biomedycznych
 Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 1 Wydobywanie sygnałów z szumu z wykorzystaniem uśredniania Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik
Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 1 Wydobywanie sygnałów z szumu z wykorzystaniem uśredniania Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik
Adaptacyjne Przetwarzanie Sygnałów. Filtracja adaptacyjna w dziedzinie częstotliwości
 W Filtracja adaptacyjna w dziedzinie częstotliwości Blokowy algorytm LMS (BLMS) N f n+n = f n + α x n+i e(n + i), i= N L Slide e(n + i) =d(n + i) f T n x n+i (i =,,N ) Wprowadźmy nowy indeks: n = kn (
W Filtracja adaptacyjna w dziedzinie częstotliwości Blokowy algorytm LMS (BLMS) N f n+n = f n + α x n+i e(n + i), i= N L Slide e(n + i) =d(n + i) f T n x n+i (i =,,N ) Wprowadźmy nowy indeks: n = kn (
Ćwiczenie 3,4. Analiza widmowa sygnałów czasowych: sinus, trójkąt, prostokąt, szum biały i szum różowy
 Ćwiczenie 3,4. Analiza widmowa sygnałów czasowych: sinus, trójkąt, prostokąt, szum biały i szum różowy Grupa: wtorek 18:3 Tomasz Niedziela I. CZĘŚĆ ĆWICZENIA 1. Cel i przebieg ćwiczenia. Celem ćwiczenia
Ćwiczenie 3,4. Analiza widmowa sygnałów czasowych: sinus, trójkąt, prostokąt, szum biały i szum różowy Grupa: wtorek 18:3 Tomasz Niedziela I. CZĘŚĆ ĆWICZENIA 1. Cel i przebieg ćwiczenia. Celem ćwiczenia
CYFROWE PRZETWARZANIE SYGNAŁÓW
 POLITECHNIKA RZESZOWSKA im. I. Łukasiewicza WYDZIAŁ ELEKTROTECHNIKI I INFORMATYKI Katedra Metrologii i Systemów Diagnostycznych CYFROWE PRZETWARZANIE SYGNAŁÓW Analiza korelacyjna sygnałów dr hab. inż.
POLITECHNIKA RZESZOWSKA im. I. Łukasiewicza WYDZIAŁ ELEKTROTECHNIKI I INFORMATYKI Katedra Metrologii i Systemów Diagnostycznych CYFROWE PRZETWARZANIE SYGNAŁÓW Analiza korelacyjna sygnałów dr hab. inż.
Analiza szeregów czasowych: 7. Liniowe modele stochastyczne
 Analiza szeregów czasowych: 7. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Liniowe modele stochastyczne Niech {y n } N n=1 będzie pewnym ciagiem danych
Analiza szeregów czasowych: 7. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Liniowe modele stochastyczne Niech {y n } N n=1 będzie pewnym ciagiem danych
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 3. Adaptacyjne usuwanie szumów i interferencji
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 3 Adaptacyjne usuwanie szumów i interferencji 1. CEL ĆWICZENIA Usuwanie szumów i interferencji to jeden z pierwszych obszarów, można rzec klasyczny,
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 3 Adaptacyjne usuwanie szumów i interferencji 1. CEL ĆWICZENIA Usuwanie szumów i interferencji to jeden z pierwszych obszarów, można rzec klasyczny,
Analiza szeregów czasowych: 5. Liniowe modele stochastyczne
 Analiza szeregów czasowych: 5. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Dwa rodzaje modelowania 1. Modelowanie z pierwszych zasad. Znamy prawa
Analiza szeregów czasowych: 5. Liniowe modele stochastyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Dwa rodzaje modelowania 1. Modelowanie z pierwszych zasad. Znamy prawa
Ćwiczenie 3. Właściwości przekształcenia Fouriera
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Sposoby opisu i modelowania zakłóceń kanałowych
 INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
REGRESJA LINIOWA Z UOGÓLNIONĄ MACIERZĄ KOWARIANCJI SKŁADNIKA LOSOWEGO. Aleksander Nosarzewski Ekonometria bayesowska, prowadzący: dr Andrzej Torój
 1 REGRESJA LINIOWA Z UOGÓLNIONĄ MACIERZĄ KOWARIANCJI SKŁADNIKA LOSOWEGO Aleksander Nosarzewski Ekonometria bayesowska, prowadzący: dr Andrzej Torój 2 DOTYCHCZASOWE MODELE Regresja liniowa o postaci: y
1 REGRESJA LINIOWA Z UOGÓLNIONĄ MACIERZĄ KOWARIANCJI SKŁADNIKA LOSOWEGO Aleksander Nosarzewski Ekonometria bayesowska, prowadzący: dr Andrzej Torój 2 DOTYCHCZASOWE MODELE Regresja liniowa o postaci: y
LABORATORIUM PODSTAW TELEKOMUNIKACJI
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego w Warszawie Wydział Elektroniki LABORATORIUM PODSTAW TELEKOMUNIKACJI Grupa Podgrupa Data wykonania ćwiczenia Ćwiczenie prowadził... Skład podgrupy:
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego w Warszawie Wydział Elektroniki LABORATORIUM PODSTAW TELEKOMUNIKACJI Grupa Podgrupa Data wykonania ćwiczenia Ćwiczenie prowadził... Skład podgrupy:
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 3. Adaptacyjne usuwanie szumów i interferencji
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 3 Adaptacyjne usuwanie szumów i interferencji 1. CEL ĆWICZENIA Usuwanie szumów i interferencji to jeden z pierwszych obszarów, można rzec klasyczny,
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 3 Adaptacyjne usuwanie szumów i interferencji 1. CEL ĆWICZENIA Usuwanie szumów i interferencji to jeden z pierwszych obszarów, można rzec klasyczny,
Podstawy Przetwarzania Sygnałów
 Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
Algorytmy detekcji częstotliwości podstawowej
 Algorytmy detekcji częstotliwości podstawowej Plan Definicja częstotliwości podstawowej Wybór ramki sygnału do analizy Błędy oktawowe i dokładnej estymacji Metody detekcji częstotliwości podstawowej czasowe
Algorytmy detekcji częstotliwości podstawowej Plan Definicja częstotliwości podstawowej Wybór ramki sygnału do analizy Błędy oktawowe i dokładnej estymacji Metody detekcji częstotliwości podstawowej czasowe
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI)
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
[d(i) y(i)] 2. Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) i=1. λ n i [d(i) y(i)] 2 λ (0, 1]
![[d(i) y(i)] 2. Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) i=1. λ n i [d(i) y(i)] 2 λ (0, 1] [d(i) y(i)] 2. Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) i=1. λ n i [d(i) y(i)] 2 λ (0, 1]](/thumbs/72/67682252.jpg) Algorytm RLS Recursive Least Squares Ogólna postać kryterium LS: J = i e 2 (i) = i [d(i) y(i)] 2 Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) Zmodyfikowane kryterium
Algorytm RLS Recursive Least Squares Ogólna postać kryterium LS: J = i e 2 (i) = i [d(i) y(i)] 2 Do wyprowadzenia algorytmu RLS posłuży kryterium autokorelacyjne: J n = e 2 (i) Zmodyfikowane kryterium
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
DYSKRETNA TRANSFORMACJA FOURIERA
 Laboratorium Teorii Sygnałów - DFT 1 DYSKRETNA TRANSFORMACJA FOURIERA Cel ćwiczenia Celem ćwiczenia jest przeprowadzenie analizy widmowej sygnałów okresowych za pomocą szybkiego przekształcenie Fouriera
Laboratorium Teorii Sygnałów - DFT 1 DYSKRETNA TRANSFORMACJA FOURIERA Cel ćwiczenia Celem ćwiczenia jest przeprowadzenie analizy widmowej sygnałów okresowych za pomocą szybkiego przekształcenie Fouriera
8. Analiza widmowa metodą szybkiej transformaty Fouriera (FFT)
 8. Analiza widmowa metodą szybkiej transformaty Fouriera (FFT) Ćwiczenie polega na wykonaniu analizy widmowej zadanych sygnałów metodą FFT, a następnie określeniu amplitud i częstotliwości głównych składowych
8. Analiza widmowa metodą szybkiej transformaty Fouriera (FFT) Ćwiczenie polega na wykonaniu analizy widmowej zadanych sygnałów metodą FFT, a następnie określeniu amplitud i częstotliwości głównych składowych
Model autoregresyjny stochastycznego szeregu czasowego
 Pracownia EEG / Widmowa analiza parametryczna Spis treści 1 Model autoregresyjny stochastycznego szeregu czasowego 1.1 Wstęp 1.2 Parametryczna analiza widmowa 1.3 Wybór rzędu modelu 1.4 Sygnały wielokanałowe
Pracownia EEG / Widmowa analiza parametryczna Spis treści 1 Model autoregresyjny stochastycznego szeregu czasowego 1.1 Wstęp 1.2 Parametryczna analiza widmowa 1.3 Wybór rzędu modelu 1.4 Sygnały wielokanałowe
Praca dyplomowa magisterska
 Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera)
 I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
b n y k n T s Filtr cyfrowy opisuje się również za pomocą splotu dyskretnego przedstawionego poniżej:
 1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
1. FILTRY CYFROWE 1.1 DEFIICJA FILTRU W sytuacji, kiedy chcemy przekształcić dany sygnał, w inny sygnał niezawierający pewnych składowych np.: szumów mówi się wtedy o filtracji sygnału. Ogólnie Filtracją
Ekonometria. Prognozowanie ekonometryczne, ocena stabilności oszacowań parametrów strukturalnych. Jakub Mućk. Katedra Ekonomii Ilościowej
 Ekonometria Prognozowanie ekonometryczne, ocena stabilności oszacowań parametrów strukturalnych Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Wykład 4 Prognozowanie, stabilność 1 / 17 Agenda
Ekonometria Prognozowanie ekonometryczne, ocena stabilności oszacowań parametrów strukturalnych Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Wykład 4 Prognozowanie, stabilność 1 / 17 Agenda
Przekształcenia sygnałów losowych w układach
 INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Sygnały i kodowanie Przekształcenia sygnałów losowych w układach Warszawa 010r. 1. Cel ćwiczenia: Ocena wpływu charakterystyk
INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Sygnały i kodowanie Przekształcenia sygnałów losowych w układach Warszawa 010r. 1. Cel ćwiczenia: Ocena wpływu charakterystyk
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Systemy. Krzysztof Patan
 Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Automatyczne rozpoznawanie mowy - wybrane zagadnienia / Ryszard Makowski. Wrocław, Spis treści
 Automatyczne rozpoznawanie mowy - wybrane zagadnienia / Ryszard Makowski. Wrocław, 2011 Spis treści Przedmowa 11 Rozdział 1. WPROWADZENIE 13 1.1. Czym jest automatyczne rozpoznawanie mowy 13 1.2. Poziomy
Automatyczne rozpoznawanie mowy - wybrane zagadnienia / Ryszard Makowski. Wrocław, 2011 Spis treści Przedmowa 11 Rozdział 1. WPROWADZENIE 13 1.1. Czym jest automatyczne rozpoznawanie mowy 13 1.2. Poziomy
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Kartkówka 1 Opracowanie: Próbkowanie częstotliwość próbkowania nie mniejsza niż podwojona szerokość przed spróbkowaniem.
 Znowu prosta zasada - zbierzmy wszystkie zagadnienia z tych 3ech kartkówek i opracujmy - może się akurat przyda na dopytkę i uda się zaliczyć labki :) (dodatkowo można opracowania z tych rzeczy z doc ów
Znowu prosta zasada - zbierzmy wszystkie zagadnienia z tych 3ech kartkówek i opracujmy - może się akurat przyda na dopytkę i uda się zaliczyć labki :) (dodatkowo można opracowania z tych rzeczy z doc ów
x x 1. Przedmiot identyfikacji System x (1) x (2) : x (s) a 1 a 2 : a s mierzone, a = zestaw współczynników konkretyzujacych F ()
 . Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
. Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
Teoria sygnałów Signal Theory. Elektrotechnika I stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny)
 . KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Teoria sygnałów Signal Theory A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Teoria sygnałów Signal Theory A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
KARTA MODUŁU / KARTA PRZEDMIOTU
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Cyfrowe przetwarzanie sygnałów pomiarowych_e2s
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Cyfrowe przetwarzanie sygnałów pomiarowych_e2s
Szeregi czasowe, analiza zależności krótkoi długozasięgowych
 Szeregi czasowe, analiza zależności krótkoi długozasięgowych Rafał Weron rweron@im.pwr.wroc.pl Definicje Mając dany proces {X t } autokowariancję definiujemy jako : γ(t, t ) = cov(x t, X t ) = = E[(X t
Szeregi czasowe, analiza zależności krótkoi długozasięgowych Rafał Weron rweron@im.pwr.wroc.pl Definicje Mając dany proces {X t } autokowariancję definiujemy jako : γ(t, t ) = cov(x t, X t ) = = E[(X t
Laboratorium Przetwarzania Sygnałów
 PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 4 Transformacja falkowa Opracował: - prof. dr hab. inż. Krzysztof Kałużyński Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii
PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 4 Transformacja falkowa Opracował: - prof. dr hab. inż. Krzysztof Kałużyński Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii
Politechnika Łódzka. Instytut Systemów Inżynierii Elektrycznej. Laboratorium cyfrowej techniki pomiarowej. Ćwiczenie 3
 Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium cyfrowej techniki pomiarowej Ćwiczenie 3 Przetwarzanie danych pomiarowych w programie LabVIEW 1. Generator harmonicznych Jako
Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium cyfrowej techniki pomiarowej Ćwiczenie 3 Przetwarzanie danych pomiarowych w programie LabVIEW 1. Generator harmonicznych Jako
Metody matematyczne w analizie danych eksperymentalnych - sygnały, cz. 2
 Metody matematyczne w analizie danych eksperymentalnych - sygnały, cz. 2 Dr hab. inż. Agnieszka Wyłomańska Faculty of Pure and Applied Mathematics Hugo Steinhaus Center Wrocław University of Science and
Metody matematyczne w analizie danych eksperymentalnych - sygnały, cz. 2 Dr hab. inż. Agnieszka Wyłomańska Faculty of Pure and Applied Mathematics Hugo Steinhaus Center Wrocław University of Science and
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji
 Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3.
 Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3. Sygnały deterministyczne 4 1.3.1. Parametry 4 1.3.2. Przykłady 7 1.3.3. Sygnały
Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3. Sygnały deterministyczne 4 1.3.1. Parametry 4 1.3.2. Przykłady 7 1.3.3. Sygnały
Transformata Laplace a to przekształcenie całkowe funkcji f(t) opisane następującym wzorem:
 PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
8. Realizacja projektowanie i pomiary filtrów IIR
 53 8. Realizacja projektowanie i pomiary filtrów IIR Cele ćwiczenia Realizacja na zestawie TMX320C5515 ezdsp prostych liniowych filtrów cyfrowych. Pomiary charakterystyk amplitudowych zrealizowanych filtrów
53 8. Realizacja projektowanie i pomiary filtrów IIR Cele ćwiczenia Realizacja na zestawie TMX320C5515 ezdsp prostych liniowych filtrów cyfrowych. Pomiary charakterystyk amplitudowych zrealizowanych filtrów
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 4. Wybrane telekomunikacyjne zastosowania algorytmów adaptacyjnych
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 4 Wybrane telekomunikacyjne zastosowania algorytmów adaptacyjnych 1. CEL ĆWICZENIA Celem niniejszego ćwiczenia jest zapoznanie studentów z dwoma
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 4 Wybrane telekomunikacyjne zastosowania algorytmów adaptacyjnych 1. CEL ĆWICZENIA Celem niniejszego ćwiczenia jest zapoznanie studentów z dwoma
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 1
 Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 1 Konrad Miziński, nr albumu 233703 1 maja 2015 Zadanie 1 Parametr λ wyestymowano jako średnia z próby: λ = X n = 3.73 Otrzymany w
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 1 Konrad Miziński, nr albumu 233703 1 maja 2015 Zadanie 1 Parametr λ wyestymowano jako średnia z próby: λ = X n = 3.73 Otrzymany w
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 7 i 8 - Efektywność estymatorów, przedziały ufności
 WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 7 i 8 - Efektywność estymatorów, przedziały ufności Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 7 i 8 1 / 9 EFEKTYWNOŚĆ ESTYMATORÓW, próba
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 7 i 8 - Efektywność estymatorów, przedziały ufności Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 7 i 8 1 / 9 EFEKTYWNOŚĆ ESTYMATORÓW, próba
Filtrowanie a sploty. W powyższym przykładzie proszę zwrócić uwagę na efekty brzegowe. Wprowadzenie Projektowanie filtru Zadania
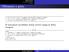 Filtrowanie a sploty idea x=[2222222222] %sygnałstochastycznyodługości5próbek h=[1111]/4; %Filtruśredniającypo4sąsiednichelementach y=conv(h,x)%zaaplikowaniefiltruhdosygnałux W powyższym przykładzie proszę
Filtrowanie a sploty idea x=[2222222222] %sygnałstochastycznyodługości5próbek h=[1111]/4; %Filtruśredniającypo4sąsiednichelementach y=conv(h,x)%zaaplikowaniefiltruhdosygnałux W powyższym przykładzie proszę
Metody Prognozowania
 Wprowadzenie Ewa Bielińska 3 października 2007 Plan 1 Wprowadzenie Czym jest prognozowanie Historia 2 Ciągi czasowe Postępowanie prognostyczne i prognozowanie Predykcja długo- i krótko-terminowa Rodzaje
Wprowadzenie Ewa Bielińska 3 października 2007 Plan 1 Wprowadzenie Czym jest prognozowanie Historia 2 Ciągi czasowe Postępowanie prognostyczne i prognozowanie Predykcja długo- i krótko-terminowa Rodzaje
Andrzej Leśnicki Laboratorium CPS Ćwiczenie 9 1/5 ĆWICZENIE 9. Kwantowanie sygnałów
 Andrzej Leśnicki Laboratorium CP Ćwiczenie 9 1/5 ĆWICZEIE 9 Kwantowanie sygnałów 1. Cel ćwiczenia ygnał przesyłany w cyfrowym torze transmisyjnym lub przetwarzany w komputerze (procesorze sygnałowym) musi
Andrzej Leśnicki Laboratorium CP Ćwiczenie 9 1/5 ĆWICZEIE 9 Kwantowanie sygnałów 1. Cel ćwiczenia ygnał przesyłany w cyfrowym torze transmisyjnym lub przetwarzany w komputerze (procesorze sygnałowym) musi
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1C400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1C400027 Temat ćwiczenia:
Metoda momentów i kwantyli próbkowych. Wrocław, 7 listopada 2014
 Metoda momentów i kwantyli próbkowych Wrocław, 7 listopada 2014 Metoda momentów Momenty zmiennych losowych X 1, X 2,..., X n - próba losowa. Momenty zmiennych losowych X 1, X 2,..., X n - próba losowa.
Metoda momentów i kwantyli próbkowych Wrocław, 7 listopada 2014 Metoda momentów Momenty zmiennych losowych X 1, X 2,..., X n - próba losowa. Momenty zmiennych losowych X 1, X 2,..., X n - próba losowa.
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
Modele zapisane w przestrzeni stanów
 Modele zapisane w przestrzeni stanów Modele Przestrzeni Stanów (State Space Models) sa to modele, w których część parametrów jest nieobserwowalna i losowa. Zachowanie wielowymiarowej zmiennej y t zależy
Modele zapisane w przestrzeni stanów Modele Przestrzeni Stanów (State Space Models) sa to modele, w których część parametrów jest nieobserwowalna i losowa. Zachowanie wielowymiarowej zmiennej y t zależy
2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
 Sprawdzanie założeń przyjętych o modelu (etap IIIC przyjętego schematu modelowania regresyjnego) 1. Szum 2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
Sprawdzanie założeń przyjętych o modelu (etap IIIC przyjętego schematu modelowania regresyjnego) 1. Szum 2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
Metody systemowe i decyzyjne w informatyce
 Metody systemowe i decyzyjne w informatyce Laboratorium JAVA Zadanie nr 2 Rozpoznawanie liter autorzy: A. Gonczarek, J.M. Tomczak Cel zadania Celem zadania jest zapoznanie się z problemem klasyfikacji
Metody systemowe i decyzyjne w informatyce Laboratorium JAVA Zadanie nr 2 Rozpoznawanie liter autorzy: A. Gonczarek, J.M. Tomczak Cel zadania Celem zadania jest zapoznanie się z problemem klasyfikacji
ANALIZA WIDMOWA SYGNAŁÓW (1) Podstawowe charakterystyki widmowe, aliasing
 POLITECHNIKA RZESZOWSKA KATEDRA METROLOGII I SYSTEMÓW DIAGNOSTYCZNYCH LABORATORIUM PRZETWARZANIA SYGNAŁÓW ANALIZA WIDMOWA SYGNAŁÓW (1) Podstawowe charakterystyki widmowe, aliasing I. Cel ćwiczenia Celem
POLITECHNIKA RZESZOWSKA KATEDRA METROLOGII I SYSTEMÓW DIAGNOSTYCZNYCH LABORATORIUM PRZETWARZANIA SYGNAŁÓW ANALIZA WIDMOWA SYGNAŁÓW (1) Podstawowe charakterystyki widmowe, aliasing I. Cel ćwiczenia Celem
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/
 Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Przetwarzanie sygnałów
 Przetwarzanie sygnałów Ćwiczenie 5 Filtry o nieskończonej odpowiedzi impulsowej (NOI) Spis treści 1 Wprowadzenie 1 1.1 Filtry jednobiegunowe....................... 1 1.2 Filtry wąskopasmowe........................
Przetwarzanie sygnałów Ćwiczenie 5 Filtry o nieskończonej odpowiedzi impulsowej (NOI) Spis treści 1 Wprowadzenie 1 1.1 Filtry jednobiegunowe....................... 1 1.2 Filtry wąskopasmowe........................
Wzmacniacze operacyjne
 Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Wprowadzenie. Spis treści. Analiza_sygnałów_-_ćwiczenia/Filtry
 Analiza_sygnałów_-_ćwiczenia/Filtry Spis treści 1 Wprowadzenie 2 Filtry cyfrowe: powtórka z wykładu 2.1 Działanie filtra w dziedzinie czasu 2.2 Nazewnictwo 2.3 Przejście do dziedziny częstości 2.3.1 Działanie
Analiza_sygnałów_-_ćwiczenia/Filtry Spis treści 1 Wprowadzenie 2 Filtry cyfrowe: powtórka z wykładu 2.1 Działanie filtra w dziedzinie czasu 2.2 Nazewnictwo 2.3 Przejście do dziedziny częstości 2.3.1 Działanie
x(n) x(n-1) x(n-2) D x(n-n+1) h N-1
 Laboratorium Układy dyskretne LTI projektowanie filtrów typu FIR Z1. apisać funkcję y = filtruj(x, h), która wyznacza sygnał y będący wynikiem filtracji sygnału x przez filtr FIR o odpowiedzi impulsowej
Laboratorium Układy dyskretne LTI projektowanie filtrów typu FIR Z1. apisać funkcję y = filtruj(x, h), która wyznacza sygnał y będący wynikiem filtracji sygnału x przez filtr FIR o odpowiedzi impulsowej
Analiza szeregów czasowych: 2. Splot. Widmo mocy.
 Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
ĆWICZENIE III ANALIZA WIDMOWA SYGNAŁÓW DYSKRETNYCH. ver.3
 1 Zakład Elektrotechniki Teoretycznej ver.3 ĆWICZEIE III AALIZA WIDMOWA SYGAŁÓW DYSKRETYCH (00) Celem ćwiczenia jest przeprowadzenie analizy widmowej dyskretnych sygnałów okresowych przy zastosowaniu szybkiego
1 Zakład Elektrotechniki Teoretycznej ver.3 ĆWICZEIE III AALIZA WIDMOWA SYGAŁÓW DYSKRETYCH (00) Celem ćwiczenia jest przeprowadzenie analizy widmowej dyskretnych sygnałów okresowych przy zastosowaniu szybkiego
POLITECHNIKA POZNAŃSKA
 POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI I ELEKTRONIKI PRZEMYSŁOWEJ Zakład Elektrotechniki Teoretycznej i Stosowanej Laboratorium Podstaw Telekomunikacji Ćwiczenie nr 1 Temat: Pomiar widma częstotliwościowego
POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI I ELEKTRONIKI PRZEMYSŁOWEJ Zakład Elektrotechniki Teoretycznej i Stosowanej Laboratorium Podstaw Telekomunikacji Ćwiczenie nr 1 Temat: Pomiar widma częstotliwościowego
Analizy Ilościowe EEG QEEG
 Analizy Ilościowe EEG QEEG Piotr Walerjan PWSIM MEDISOFT 2006 Piotr Walerjan MEDISOFT Jakościowe vs. Ilościowe EEG Analizy EEG na papierze Szacunkowa ocena wartości częstotliwości i napięcia Komputerowy
Analizy Ilościowe EEG QEEG Piotr Walerjan PWSIM MEDISOFT 2006 Piotr Walerjan MEDISOFT Jakościowe vs. Ilościowe EEG Analizy EEG na papierze Szacunkowa ocena wartości częstotliwości i napięcia Komputerowy
Ekonometria. Dobór postaci analitycznej, transformacja liniowa i estymacja modelu KMNK. Paweł Cibis 9 marca 2007
 , transformacja liniowa i estymacja modelu KMNK Paweł Cibis pawel@cibis.pl 9 marca 2007 1 Miary dopasowania modelu do danych empirycznych Współczynnik determinacji Współczynnik zbieżności Skorygowany R
, transformacja liniowa i estymacja modelu KMNK Paweł Cibis pawel@cibis.pl 9 marca 2007 1 Miary dopasowania modelu do danych empirycznych Współczynnik determinacji Współczynnik zbieżności Skorygowany R
Zastosowanie modelu regresji logistycznej w ocenie ryzyka ubezpieczeniowego. Łukasz Kończyk WMS AGH
 Zastosowanie modelu regresji logistycznej w ocenie ryzyka ubezpieczeniowego Łukasz Kończyk WMS AGH Plan prezentacji Model regresji liniowej Uogólniony model liniowy (GLM) Ryzyko ubezpieczeniowe Przykład
Zastosowanie modelu regresji logistycznej w ocenie ryzyka ubezpieczeniowego Łukasz Kończyk WMS AGH Plan prezentacji Model regresji liniowej Uogólniony model liniowy (GLM) Ryzyko ubezpieczeniowe Przykład
Politechnika Łódzka. Instytut Systemów Inżynierii Elektrycznej
 Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium komputerowych systemów pomiarowych Ćwiczenie 3 Analiza częstotliwościowa sygnałów dyskretnych 1. Opis stanowiska Ćwiczenie jest
Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium komputerowych systemów pomiarowych Ćwiczenie 3 Analiza częstotliwościowa sygnałów dyskretnych 1. Opis stanowiska Ćwiczenie jest
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Zjawisko aliasingu. Filtr antyaliasingowy. Przecieki widma - okna czasowe.
 Katedra Mechaniki i Podstaw Konstrukcji Maszyn POLITECHNIKA OPOLSKA Komputerowe wspomaganie eksperymentu Zjawisko aliasingu.. Przecieki widma - okna czasowe. dr inż. Roland PAWLICZEK Zjawisko aliasingu
Katedra Mechaniki i Podstaw Konstrukcji Maszyn POLITECHNIKA OPOLSKA Komputerowe wspomaganie eksperymentu Zjawisko aliasingu.. Przecieki widma - okna czasowe. dr inż. Roland PAWLICZEK Zjawisko aliasingu
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH
 ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Metody analizy zapisu EEG. Piotr Walerjan
 Metody analizy zapisu EEG Piotr Walerjan Metody automatyczne i semiautomatyczne w EEG automatyczna detekcja (i zliczanie) zdarzeń wykrywanie wyładowań, napadów tworzenie hipnogramów analizy widmowe, wykresy
Metody analizy zapisu EEG Piotr Walerjan Metody automatyczne i semiautomatyczne w EEG automatyczna detekcja (i zliczanie) zdarzeń wykrywanie wyładowań, napadów tworzenie hipnogramów analizy widmowe, wykresy
Optymalizacja ciągła
 Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
ĆWICZENIE nr 3. Badanie podstawowych parametrów metrologicznych przetworników analogowo-cyfrowych
 Politechnika Łódzka Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych WWW.DSOD.PL LABORATORIUM METROLOGII ELEKTRONICZNEJ ĆWICZENIE nr 3 Badanie podstawowych parametrów metrologicznych przetworników
Politechnika Łódzka Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych WWW.DSOD.PL LABORATORIUM METROLOGII ELEKTRONICZNEJ ĆWICZENIE nr 3 Badanie podstawowych parametrów metrologicznych przetworników
STUDIA MAGISTERSKIE DZIENNE LABORATORIUM SYGNAŁÓW, SYSTEMÓW I MODULACJI. Filtracja cyfrowa. v.1.0
 Politechnika Warszawska Instytut Radioelektroniki Zakład Radiokomunikacji SUDIA MAGISERSKIE DZIENNE LABORAORIUM SYGNAŁÓW, SYSEMÓW I MODULACJI Filtracja cyfrowa v.1. Opracowanie: dr inż. Wojciech Kazubski,
Politechnika Warszawska Instytut Radioelektroniki Zakład Radiokomunikacji SUDIA MAGISERSKIE DZIENNE LABORAORIUM SYGNAŁÓW, SYSEMÓW I MODULACJI Filtracja cyfrowa v.1. Opracowanie: dr inż. Wojciech Kazubski,
BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO
 ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
Analiza szeregów czasowych: 2. Splot. Widmo mocy.
 Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
Analiza szeregów czasowych: 2. Splot. Widmo mocy. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2006/07 Splot Jedna z najważniejszych własności transformaty Fouriera jest to, że transformata
Analiza sygnałów biologicznych
 Analiza sygnałów biologicznych Paweł Strumiłło Zakład Elektroniki Medycznej Instytut Elektroniki PŁ Co to jest sygnał? Funkcja czasu x(t) przenosząca informację o stanie lub działaniu układu (systemu),
Analiza sygnałów biologicznych Paweł Strumiłło Zakład Elektroniki Medycznej Instytut Elektroniki PŁ Co to jest sygnał? Funkcja czasu x(t) przenosząca informację o stanie lub działaniu układu (systemu),
ZAJĘCIA II. Zmienne losowe, sygnały stochastyczne, zakłócenia pomiarowe
 ZAJĘCIA II Zmienne losowe, sygnały stochastyczne, zakłócenia pomiarowe Po co statystyka w identyfikacji? Zmienne losowe i ich parametry Korelacja zmiennych losowych Rozkłady wielowymiarowe i sygnały stochastyczne
ZAJĘCIA II Zmienne losowe, sygnały stochastyczne, zakłócenia pomiarowe Po co statystyka w identyfikacji? Zmienne losowe i ich parametry Korelacja zmiennych losowych Rozkłady wielowymiarowe i sygnały stochastyczne
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 5 - suplement
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 5 - suplement Realizacja na procesorze sygnałowym adaptacyjnego usuwania echa w łączu telefonicznym 1. SYMULACJA ECHA W ŁĄCZU TELEFONICZNYM I JEGO
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 5 - suplement Realizacja na procesorze sygnałowym adaptacyjnego usuwania echa w łączu telefonicznym 1. SYMULACJA ECHA W ŁĄCZU TELEFONICZNYM I JEGO
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych
 Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych Cel ćwiczenia Celem ćwiczenia jest poznanie podstawowych własności członów liniowych
Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych Cel ćwiczenia Celem ćwiczenia jest poznanie podstawowych własności członów liniowych
WYZNACZANIE CECH PUNKTOWYCH SYGNAŁÓW POMIAROWYCH
 PODSTAWY SYGNAŁÓW POMIAROWYCH I METROLOGII WYZNACZANIE CECH PUNKTOWYCH SYGNAŁÓW POMIAROWYCH WSTĘP TEORETYCZNY Sygnałem nazywamy przebieg dowolnej wielkości fizycznej mogącej być nośnikiem informacji Opis
PODSTAWY SYGNAŁÓW POMIAROWYCH I METROLOGII WYZNACZANIE CECH PUNKTOWYCH SYGNAŁÓW POMIAROWYCH WSTĘP TEORETYCZNY Sygnałem nazywamy przebieg dowolnej wielkości fizycznej mogącej być nośnikiem informacji Opis
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
