Zagadnienia normalizacji kryteriów w analizach wielokryterialnych w projektowaniu dróg

Transkrypt

1 Budowictwo i Architektura 3(4) (204) Zagadieia ormalizaci kryteriów w aalizach wielokryterialych w proektowaiu dróg Piotr Żabicki, Władysław Gardzieczyk 2,2 Zakład Iżyierii Drogowe, Wydział Budowictwa i Iżyierii Środowiska, Politechika Białostocka, trafficpz@o2.pl, 2 w.gardzieczyk@pb.edu.pl, Streszczeie: Aaliza wielokryteriala to metoda wspomagaia procesu decyzyego w sytuaci gdy aalizowaych est wiele wariatów przebiegu tras drogowych a etapie przygotowywaia dokumetaci proektowych autostrad, dróg ekspresowych czy obwodic miescowości. Polega oa a odpowiedim doborze kryteriów ocey oraz wag im przypisaych. Celem aalizy wielokryteriale est wybór wariatu akorzystieszego aczęście z puktu widzeia kryteriów o charakterze trasportowym, środowiskowym, ekoomiczym i społeczym. Kryteria przyęte do aalizy wielokryteriale mogą być wyrażoe za pomocą parametrów mierzalych bądź iemierzalych. Aby możliwe było porówaie i ocea wariatów wszystkim kryteriom ależy adać wartości liczbowe iemiaowae. Proces zastąpieia wartości miaowae a iemiaowaą azywa się ormalizacą. Normalizaca może przebiegać w oparciu o maksymalizacę zmieych (stymulaty) lub miimalizacę zmieych (destymulaty). W aalizach prezetowaych w artykule zbadao wpływ przyęte metody ormalizaci kryteriów oraz zastosowaych wag poszczególych kryteriów a wybór wariatu przebiegu trasy drogowe. Słowa kluczowe: trasa drogowa, aaliza wielokryteriala, metody ormalizaci, kryteria ocey wariatów. Wprowadzeie Aaliza wielokryteriala to zestaw algorytmów stosowaych przy wyborze rozwiązaia akorzystieszego wariatu przebiegu trasy drogowe a etapie przygotowywaia dokumetaci proektowych autostrad, dróg ekspresowych czy obwodic miescowości. Wybór metody zależy między iymi od zróżicowaia liczby daych iezbędych do wprowadzeia w dae metodzie, etapu przygotowaia dokumetaci, skali i rodzau przedsięwzięcia. Naczęście są uwzględiae kryteria o charakterze trasportowym, środowiskowym, ekoomiczym i społeczym [,2,3]. Istotą rolę w oceie poszczególych wariatów przebiegu tras drogowych maą przyęte kryteria ocey oraz przypisae im wagi puktowe. Przyęte kryteria tworzą macierz daych, w które ity wiersz charakteryzue wariat i według koleych (wszystkich) kryteriów, a ta koluma opisue kolee (wszystkie) wariaty według określoego kryterium. Kryteria przyęte do aalizy wielokryteriale wyrażoe są za pomocą parametrów mierzalych (p. kryterium długości drogi wyrażaa est w kilometrach) oraz iemierzalych, opisuących wariaty bez ich ocey ilościowe (p. wpływ a kraobraz). W odiesieiu do tych ostatich dokoue się ich kwatyfikaci (adaia wartości liczbowych). Aby możliwe było porówaie i ocea wariatów wszystkim kryteriom adae się wartości liczbowe iemiaowae. Proces zastąpieia wartości miaowae a iemiaowaą azywa się ormalizacą [4,5]. Normalizaca może przebiegać w oparciu o maksymalizacę zmieych (stymulaty) lub miimalizacę zmieych (destymulaty) [6].

2 326 Piotr Żabicki, Władysław Gardzieczyk Celem prowadzoych aaliz est zbadaie wpływu metody ormalizaci kryteriów oraz zastosowaych wag, w odiesieiu do poszczególych kryteriów, a wybór wariatu przebiegu trasy drogowe. 2. Aaliza wielokryteriala założeia Rozpatryway est zbiór określoych wariatów rozwiązań W{W i : i,2,3,}, dla których przymue się zbiór kryteriów K{K :,2,3,m}, według których oceiae są poszczególe wariaty. Dla każdego wariatu wyzacza się wartości x (miara wariatu W i według kryterium K ), tworzące macierz daych: X{x : i,2,3,,;,2,3,,m}. W macierzy daych ity wiersz przedstawia charakterystykę wariatu i według koleych (wszystkich) kryteriów, a ta koluma opisue kolee wariaty według kryterium. W zapisie tablicowym macierz ma postać (): éx K x K x mù ê ú ê M O M K M ú êxi K K x ú im ê ú ê M K M O M ú êx x x ú ë K K m û Zaych est wiele metod ormalizaci kryteriów. Normalizacę Va Delfta i Nkampa oraz Peldschusa zastosowao do wyboru proektu autostrady [7]. W pracy [8] wykorzystao metodę Weitedorfa do ormalizaci kryteriów w oceie egatywych oddziaływań trasportu drogowego a środowisko przyrodicze. W pracy [9] przedstawioo wybór wariatu korytarza drogowego za pomocą maksymale stadaryzaci. Szwabowski i ii [6] zastosowali róże metody ormalizaci kryteriów (ormowaie, stadaryzacę, ormalizacę Weitedorfa, Patter) w budowictwie ogólym. Aalizę metod ormalizaci w teorii gier przedstawioo w pracy [0]. W artykule przeaalizowao 2 metod ormalizaci przyętych kryteriów ocey wariatów (tabela ) [4,6,7,8,9,0]. Każda z wymieioych metod ormalizaci ma swoe zalety ak i wady, est mie lub bardzie przydata przy wyborze przebiegu trasy drogowe. Rakig aalizowaych wariatów ustala się a podstawie obliczoych oce sytetyczych S i. Do obliczeia ocey sytetycze wariatu stosue się wskaźik sumowaia bez lub z uwzględieiem wag ω poszczególych kryteriów, obliczoy odpowiedio według wzoru (2) i wzoru (3): S i m m i S x w Oceę końcową aalizowaych wariatów oblicza się poprzez sprowadzeie sumy wartości S i do edości według wzoru (4): i i / i i S S S () (2) (3) (4)

3 Iżyieria Komuikacya Drogi Zagadieia ormalizaci kryteriów w którym i S est zormalizowaą oceą sytetyczą wariatu S i, ( ). Nakorzystieszym wariatem est wariat charakteryzuący się awyższą wartością Tabela. Metody ormalizaci kryteriów Lp. 2 3 Metoda ormalizaci Normalizaca Va Delfta i Nkampa Normalizaca Weitedorfa Normalizaca Peldschusa 4 Normalizaca Jüttlera 5 Normalizaca Stoppa Normalizaca Jüttlera i Körtha Normalizaca logarytmicza Normalizaca sumowaie 9 Normalizaca Patter 0 Normowaie Stadaryzaca 2 Maksymala stadaryzaca Normalizaca maksymalizuąca (stymulaty) 2 i x + x x 2 æ x ö ç ç x + è ø + x + x i S i S i. Normalizaca miimalizuąca (destymulaty) 2 i + x + x x 3 æ x ö ç ç è ø x x 00 x x + 00 x + x + x x x l( x l( ) ) l( l( Õ ) Õ ) i i x x i i i x + x s x + + i x + x () s

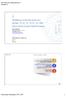
4 328 Piotr Żabicki, Władysław Gardzieczyk Ozaczeia podae w tabeli określaą: według kryterium tego, zormalizowaą wartość wariatu itego wartość wariatu itego według kryterium tego, x + max( x ), x mi( x ) maksymalą bądź miimalą wartość wariatu itego i według kryterium tego, i x / x, kryterium tego po maksymalizaci, x tego kryterium, x /, s odchyleie stadardowe, s i x + maksymalą wartość wariatu itego według wartość średią aalizowaych wariatów według ( x x )/. i 3. Normalizaca kryteriów ocey wariatów opis wariatów i przyęte kryteria ocey Aalizę wpływu metody ormalizaci kryteriów ocey oraz wag a wybór wariatu przebiegu trasy drogowe przeprowadzoo a przykładzie pokazaym a rysuku. Przyęty układ wariatów est często spotykay w warukach polskich i dotyczy w szczególości obwodic i obeść miescowości. Plaowae owe odciki tras drogowych koliduą z obszarami chroioymi i igeruą w istieące zagospodarowaie obszaru. Rozwiązaie problemu wymaga ustaleia wariatu, który w amieszym stopiu uemie wpływa a obszary chroioe oraz przyległą zabudowę mieszkalą. Wariaty przyęte do aalizy scharakteryzowao w astępuący sposób: wariat przebieg obwodicy po półoce stroie miescowości A, proektowaa droga arusza obszar Natura 2000, długość obwodicy wyosi 3,88 km, wariat 2 przebieg proektowae drogi pomiędzy zabudową mieszkaiową, długość proektowaego odcika drogi wyosi 3,82 km, wariat 3 przebieg obwodicy po stroie połudiowe, proektowaa droga oma zabudową mieszkaiową, długość obwodicy wyosi 4,794 km. Rys.. Schemat przebiegu wariatów obwodicy miescowości A Aalizę wielokryterialą obwodicy miescowości A przeprowadzoo w oparciu o osiem kryteriów cząstkowych przypisaych do kryteriów główych o charakterze trasportowym, środowiskowym, ekoomiczym i społeczym (tabela 2). Wartości

5 Iżyieria Komuikacya Drogi Zagadieia ormalizaci kryteriów poszczególych kryteriów zostały ustaloe przez autorów a podstawie własych obliczeń, oszacowań i kalkulaci. W celu lepszego wyaśieia wpływu metody ormalizaci a wyik aalizy liczbę kryteriów cząstkowych w poszczególych kryteriach główych ograiczoo do dwóch. W kryteriach trasportowych uwzględioo długość drogi oraz liczbę węzłów drogowych. Kryteria środowiskowe uwzględiaą: kolizę proektowaych wariatów z obszarem Natura 2000 i długość przebiegu drogi przez terey leśe. Kryteria ekoomicze obemuą koszty budowy drogi oraz ekoomiczą wartość bieżącą etto (ENPV). Koszty budowy drogi oszacowao w oparciu o ceę budowy edego kilometra a poziomie 27 ml PLN w przypadku drogi klasy S 2x2. Kryteria społecze obemuą liczbę budyków mieszkalych do wyburzeia oraz liczbę osób arażoych a poadormatywy hałas. W tabeli 2 wskazao także kryteria będące stymulatami ( + ENPV) i destymulatami ( pozostałe kryteria). W przypadku stymulat zastosowao ormalizacę maksymalizuącą, a w przypadku destymulat ormalizacę miimalizuącą. Tabela 2. Kryteria przyęte do aalizy Lp. Kryteria Jedostka Wariat Wariat 2 Wariat 3 TRANSPORTOWE K Długość drogi [km] 3,880 3,820 4,794 K2 Liczb węzłów drogowych [liczba] 2 ŚRODOWISKOWE K3 Koliza z obszarem Natura 2000 [ha] 8, 2,,9 K4 Długość przebiegu drogi przez lasy [km] 2,5,0 2, EKONOMICZNE K5 Koszty budowy [0 6 PLN] 04,76 03,4 29,44 K6 Ekoomicza wartość bieżąca etto ENPV + [0 6 PLN] 32,4 27,5 9,5 SPOŁECZNE K7 Liczba domów do wyburzeia [liczba] K8 Liczba osób arażoych a poadormatywy hałas 4. Wyiki obliczeń i ich aaliza [liczba] Wpływ metody ormalizaci kryteriów ocey, podaych w tabeli, a wybór akorzystieszego wariatu przebiegu trasy drogowe poprzedzoo aalizą metod ormalizaci przedstawioych w tabeli 2 (bez uwzględieia wag poszczególych kryteriów). Wyiki obliczeń w odiesieiu do 2 metod ormalizaci oraz studia literatury [4,6,7,9,0] pozwoliły a sformułowaie poiższych wiosków (a rysuku 2 pokazao uzyskae wartości edyie dla 4 przykładowych metod ormalizaci): Do ormalizaci kryteriów abardzie są przydate metody: Va Delfta i Nkampa (rys. 2a), Peldschusa, Stoppa, logarytmicza, sumowaia, Patter, ormowaia. Zaletą tych metod ormalizaci est możliwość porówywaia dowole liczby kryteriów, a zormalizowae wartości zawieraą się w przedziale (0,). Metody te maą zastosowaie do obliczeń ocey sytetycze wariatów z uwzględieiem wag ω kryteriów. Zastosowaie metody Weitedorfa (rys. 2b), ze względu a otrzymae wartości "0" i "" wśród zormalizowaych kryteriów, może w końcowe oceie ie uwzględiać we właściwy sposób zebraych iformaci w odiesieiu do poszczególych wariatów.

6 330 Piotr Żabicki, Władysław Gardzieczyk Metody Jüttlera (rys. 2c), Jüttlera i Körha oraz metoda stadaryzaci, ze względu a występowaie wartości uemych, ie maą zastosowaia w sytuaci, gdy est wymagae aby wartości zormalizowae x > 0. Jest to istota wada tych metod. Metoda maksymale stadaryzaci (rys. 2d), ze względu a wartości "0" wśród zormalizowaych kryteriów ie może być wykorzystaa w aalizach wielokryterialych uwzględiaących wagi puktowe poszczególych kryteriów. W takie sytuaci moża wprowadzić wartość bliską 0, ale dodatią. Działaie takie edak ie wpływa a czytelość i przerzystość ormalizaci kryteriów. Jest to istota wada te metody. Na podstawie obliczeń z wykorzystaiem metod ormalizaci: Jüttlera, Jüttlera i Körha oraz stadaryzaci w końcowe oceie wariatów otrzymao wartości ueme (tabela 3). Potwierdza to ieprzydatość tych metod w aalizach wielokryterialych przy podemowaiu decyzi o przebiegu trasy drogowe. Rakig wariatów przebiegu obwodicy miescowości A według rozpatrywaych metod ormalizaci (bez uwzględieia wag kryteriów ocey) przedstawioo w tabeli 3. Wyiki przeprowadzoych obliczeń, przy wykorzystaiu metod ormalizaci, uzaych ako abardzie przydate przy kształtowaiu przebiegu tras drogowych (wiosek r ), ie wskazały edozaczie akorzystieszego wariatu przebiegu obwodicy. Przy zastosowaiu metody Peldschusa i logarytmicze za alepszy uzao wariat 2, a w przypadku metod: Va Delfta i Nkampa, Stoppa, sumowaia, Patter, ormowaia wariat 3. Wariat 2 charakteryzue się zdecydowaie akrótszym prześciem przez obszary leśe oraz amieszą długością obwodicy. Wariat 3 wyróżia się amieszą kolizyością z obszarem Natura 2000, amieszą liczbą domów do wyburzeia i amieszą liczbą osób arażoych a poadormatywy hałas. Rys. 2. Normalizaca kryteriów według przykładowych metod

7 Iżyieria Komuikacya Drogi Zagadieia ormalizaci kryteriów Tabela 3. Wyiki aalizy wariatów obwodicy miescowości bez uwzględieia wag kryteriów Lp. Metoda ormalizaci Wariat Wariat 2 Wariat 3 Va Delfta i Nkampa 0,338 0,393 0,3489 Rakig Weitedorfa 0,3683 0,360 0,2707 Rakig Peldschusa 0,3023 0,3789 0,388 Rakig Jüttlera 0,3803 0,492 0,285 Rakig Stoppa 0,370 0,3407 0,3423 Rakig Jüttlera i Körha 0,2558 0,329 0,8772 Rakig Logarytmicza 0,3305 0,3709 0,2986 Rakig Sumowaia 0,3309 0,3227 0,3463 Rakig Patter 0,3085 0,3303 0,362 Rakig Normowaia 0,370 0,3407 0,3423 Rakig 3 2 Stadaryzaca,696,72 3,338 Rakig Maksymala stadaryzaca 0,2895 0,395 0,390 Rakig 3 2 W praktyce przymoway układ wag charakteryzuących poszczególe kryteria est aczęście róży od podeścia zrówoważoego. Przeprowadzoo więc obliczeia dla czterech przykładowych sceariuszy prefereci, przy astępuącym układzie wag: 55% (kryterium preferowae 55%):5%:5%:5% (trzy pozostałe kryteria: 3x5%). Zastosowao przy tym metody ormalizaci kryteriów wskazae powyże ako abardzie przydate w tego typu aalizach, rezyguąc edak z metody ormowaia (takie same wyiki uzyskue się przy zastosowaiu metody Stoppa). Wyiki obliczeń pozwoliły określić akorzystiesze wariaty przebiegu obwodicy miescowości A w ramach poszczególych sceariuszy prefereci przy przyętych metodach ormalizaci kryteriów (tabela 4). Tabela 4. Nakorzystieszy wariat przebiegu drogi (bez uwzględieia wag i przy założoych sceariuszach prefereci) Lp. Metoda Bez wag Sceariusz prefereci ormalizaci kryteriów trasportowy środowiskowy ekoomiczy społeczy Va Delfta i Nkampa W3 W W2 W W3 2 Peldschusa W2 W2 W2 W2 W3 3 Stoppa W3 W2 W2 W2 W3 4 Logarytmicza W2 W2 W2 W2 W 5 Sumowaia W3 W W2 W W3 6 Patter W3 W2 W2 W2 W3

8 332 Piotr Żabicki, Władysław Gardzieczyk Wyiki aaliz przedstawioe w tabeli 4 ie pozwalaą w edozaczy sposób wskazać optymale metody ormalizaci kryteriów ocey wariatów. Zarówo w przypadku podeścia zrówoważoego (rówe wartości wag poszczególych kryteriów) ak i przy założoych przykładowych sceariuszach prefereci za akorzystiesze rozwiązaie uzawao róże wariaty przebiegu obwodicy miescowości A. Jedyie w przypadku kryterium środowiskowego wariat 2 określoo ako akorzystieszy iezależie od metody ormalizaci kryteriów. Wyika to edak ze zdecydowaie korzystieszych wartości kryteriów cząstkowych charakteryzuących te wariat. Nabardzie zbliżoe rozwiązaia uzyskao przy zastosowaiu ormalizaci metodą Peldschusa i metodą logarytmiczą. Stwierdzoo przy tym także istoty wpływ przyętego sceariusza prefereci a wyik aalizy. 5. Podsumowaie Aaliza wielokryteriala est metodą wspomagaia procesu decyzyego w sytuaci gdy rozważaych est wiele wariatów przebiegu trasy drogowe. Na podstawie przeprowadzoych aaliz stwierdzoo, że ie wszystkie zae metody ormalizaci kryteriów ocey wariatów mogą być przydate przy wyborze akorzystieszego wariatu przebiegu trasy drogowe. Za abardzie właściwe moża uzao metody: Va Delfta i Nkampa, Peldschusa, Stoppa, logarytmiczą, sumowaia, Patter i ormowaia, ze względu a możliwość porówywaia dowole liczby kryteriów, a zormalizowae wartości zawieraą się w przedziale (0,). Metody te pozwalaą obliczyć ocey sytetycze w odiesieiu do rozważaych wariatów z uwzględieiem wag poszczególych kryteriów. Jako ieprzydate w rozwiązywaiu zagadień kształtowaia tras drogowych uzao ormalizacę kryteriów metodami: Weitedorfa, Jüttlera oraz Jüttlera i Körha, ze względu a występowaie wartości uemych i wartości zerowych, co uiemożliwia uwzględieie wag kryteriów. Ustaloo także, że a rakig wariatów istoty wpływ maą przyęte sceariusze prefereci, opisae poprzez wagi przyętych kryteriów. Dokoae ustaleia wskazuą, że problem wyboru metody ormalizaci kryteriów ocey wariatów ma istoty wpływ a wyik aalizy wielokryteriale w procesie decyzyym przy wyborze przebiegu tras drogowych i powiie być adal baday. Literatura Bohatkiewicz J. Podręczik dobrych praktyk wykoywaia opracowań środowiskowych dla dróg kraowych. GDDKiA/EKKOM Sp. z o.o., Kraków De Silva, H., Tatam, CH., 996. A empirical procedure for ehacig the impact of road ivestmets. Trasport Policy 3 (4), Kalamaras, G.S., Brio, L., Carrieri, G., Plie, C., Grasso, P., Applicatio of multicriteria aalysis to select the best highway aligmet. Tuelig ad Udergroud Space Techology 5 (4), Hwag C.L, Yoo K. Multiple attribute decisio makig methods ad applicatios. A state of the art survey. Spriger Verlag, Berli, Heidelberg, New York, Gievicius R. Normalizatio of quatities of various dimesios. Joural of Busiess Ecoomics ad Maagemet 9(), (2008), Szwabowski J., Deszcz J. Metody wielokryteriale aalizy porówawcze, Wydawictwo Politechiki Śląskie, Gliwice Brauers W.K. M., Zavadskas E.K., Peldschus F., Turskis Z. Multi obective decisio makig for road desig. Trasport 23(3), (2008), Gadziński J. Ocea egatywych oddziaływań trasportu drogowego a środowisko przyrodicze. Przegląd komuikacyy (202), 49.

9 Iżyieria Komuikacya Drogi Zagadieia ormalizaci kryteriów Geeletti D. Multicriteria aalysis to compare the impact of alterative road corridors: a case study i orther Italy. Impact Assessmet ad Proect Appraisal 23(2) (2005), Zavadskas E.K., Turskis Z. A ew logarithmic ormalizatio method i games theory. Iformatica 9(2), (2008), Issues of criteria ormalizatio i the multicriteria aalyzes i the desig of roads Piotr Żabicki, Władysław Gardzieczyk 2,2 Divisio of Road Egieerig, Faculty of Civil ad Evirometal Egieerig, Bialystok Uiversity of Techology, trafficpz@o2.pl, 2 w.gardzieczyk@pb.edu.pl Abstract: Multicriteria aalysis is a method for supportig the decisio process i a situatio where there are may variats of road aligmets aalyzed durig the preparatio of proect documetatio of motorways, expressways ad bypasses. It is based o a appropriate choice of assessmet criteria ad weights assiged to them. The aim of the multicriteria aalysis is choose the most beeficial variat for road aligmet from the poit of view of trasport, evirometal, ecoomic ad social criteria. The criteria adopted for the multicriteria aalysis ca be expressed by usig measurable or immeasurable parameters. I order to be able to compare ad assess the variats, dimesioless quatities must be assiged to the all criteria. The process of replacig a dimesio quatity with a dimesioless oe is called ormalizatio. Normalizatio may be performed o the basis of maximizig the variables (stimulats) or to miimize the variables (destimulats). The aalyses preseted i the article examie the impact of the adopted method of criteria ormalizatio ad the weights of the criteria used for the selectio of a road variat. Keywords: road, multicriteria aalysis, method of ormalizatio, evaluatio of variats

10