LABORATORIUM AKUSTYKI. Interferencja i dyfrakcja fal akustycznych
|
|
|
- Szczepan Wasilewski
- 8 lat temu
- Przeglądów:
Transkrypt
1 LABORATORIUM AKUSTYKI ĆICZENIE NR Itefeeca dyfakca fal akustyczych Cel ćwczea Celem ćwczea est dśwadczale zae zawsk falwych: tefeec ugęca fal akustyczych a stuktuach Układ mawy kma bezechwa geeat - wzmacacz mcy źódł fal łaske 4 - stlk btwy 5 - badaa stuktua w dgdze 6 - mkf mawy 7 - mek zmu dźwęku 8 kmute PC + gam Chak 3 Zadaa labatye 3 Zazać sę z układem mawym wg daeg schematu blkweg 3 Zmezyć wymay badae stuktuy dbać częsttlwśc sygału dla aametu stuktuy d/λ / 3/ 33 Zmezyć chaakteystykę keukwśc mewaa badae stuktuy dla daych watśc aametu stuktuy d/λ 34 Dla daych watśc aametu stuktuy d/λ wyzaczyć kąty adaa fal łaske a zegdę dla któych układ dwóch edakwych twów est dlem akustyczym Zmezyć chaakteystyk keukwśc mewaa dla dla daych watśc aametu stuktuy d/λ 4 Zagadea d zygtwaa 4 Istta uchu falweg 4 Pmewae akustyczych źódeł fal łaske kulste 43 Itefeeca dyfakca fal akustyczych Lteatua [] A Dbuck Pdstawy akustyk Skyt P cław 987 [] A Jauszats Fzyka dla Pltechk Tm III Fale 6 8 PN -wa 99 [3] Z Żyszkwsk Mectw akustycze NT -wa 987 zdz 9 [4] JM Buczek Paca dylmwa Stawsk d badaa demstac zawsk falwych P988
2 CZĘŚĆ I UKŁAD -KOHERENTNYCH ŹRÓDEŁ DŹIĘKU Mc akustycza edyczeg źódła fal kulste Ptecał cśee ędkść akustycza celu wyzaczea mcy akustycze edyczeg źódła fal kulste skzystamy z zwązaa ówaa falweg we wsółzędych sfeyczych [] Rzwązae t ma stać: A ( t k ( Φ( ω t e gdze zabuzee śdka Φ est welkścą skalaą zwaą tecałem akustyczym (lub tecałem ędkśc A wsółczykem keślym zez wydaść źódła Q [m 3 /s] dległścą d źódła ω ulsacą z aką źódł meue ω kc k lczbą falwą k π/λ λ długścą fal λ c/f c ędkścą fal w śdku w któym sę a zchdz ekt est wektem wdzącym któy keśla łżee uktu w zestze zy ustalym ukce 0; w układze wsółzędych sfeyczych ( θ φ Ptecał akustyczy est zdefway zez ędkść akustyczą cśee akustycze któe wytwaza w śdku zchdząca sę fala: ( ( t gadφ ( t ( t ρ Φ ( t t któe w zestze 3D śdku lwym bez zeływu są zwązae ówaem Eulea (756 ( t (3 gad( t ρ t gdze ρ est gęstścą śdka w któym zchdz sę fala akustycza Istee tecału akustyczeg wyka z faktu że w bszaze wyełym śdkem dskale łyym e zaweaącym ych źódeł le któe wytwaza aguąca sę fala (zabuzee est bezwwe ( t 0 Uwaga Ośdek w któym ague sę fala dźwękwa est zwykle meszaą gazów któe główym składkam są mlekuły aztu az tleu cese agac dźwęku sttą lę dgywa óweż aa wda chcaż w wetzu est e badz mał Twzące gaz cząsteczk zaduące sę w eustaym bezładym uchu są aktycze ezależe d sebe zamuą zawsze całą dstęą m zestzeń ezależe d e welkśc Zgde z awem Agada-Amee a: w edakwych waukach edakwe bętśc óżych gazów zaweaą zawsze edakwą lczbę cząsteczek; est a ówa lczbe Agada N A /ml Ozacza t że w bętśc 4 dm 3 gazu w temeatuze 0 C d cśeem atm (035 hpa zadue sę atmów
3 ( ml t 8 g wdy lub ldu zawea tyle sam atmów atmast w bętśc cm 3 temeatuze 5 C cśeu 000 hpa zadue sę cząsteczek Uwaga Mlekuły gazów któe twzą wetze óweż zaduą sę w cągłym bezładym uchu Mża zyąć że śeda ędkść teg uchu est zędu 500 m/s a śeda dległść mędzy mlekułam wys m zy czym śedca mlekuł est 000 azy mesza Śeda lczba zdezeń mlekuł w cągu s est zatem zędu 0 9 Na te chatyczy uch mlekuł akłada sę wymuszy uządkway uch któy est falą akustyczą (dźwękwą Pdczas zchdzea sę fal dźwękwe w śdku e eega akustycza zamea sę a ceł w wyku chłaaa klasyczeg mlekulaeg az zaszaa a tubulecach Pchłaae klasycze est wykem zawska lekśc zewdctwa celeg atmast chłaae mlekulae est zwązae z tacą mlekuł az dgaam twzących e atmów zbudzee uchu wewętzeg mlekuł dbywa sę ksztem eeg uchu taslacyeg t uządkwaeg uchu wymuszeg zez falę dźwękwą zakese częsttlwśc d 0 khz awększą lę dgywa chłaae mlekulae cząsteczek aztu tleu Fala kulsta chaakteyzue sę tym że: zchdz sę edakw we wszystkch keukach tz że wezche zamltudwe az zfazwe (t wezche edakwe amltudy edakwe fazy są detycze są sfeam amltuda tecału akustyczeg est dwte cala d dległśc d źódła uch śdka dbywa sę tylk w keuku adalym tz że keuk wektów ędkśc akustycze kywaą sę z meam wywadzym ze źódła bec teg zkład la akustyczeg wytwazaeg zez falę kulstą e ulege zmae eżel w śdku umeścmy ak źódł kulę ulsuącą meu a t kulę dgaąca w te ssób że e meń zmea sę kesw z częstścą ω edakw we wszystkch keukach Dale zakładamy że ędkść bętścwa kul ulsuące est w zase zeslym ówa: ωt Qe gdze Q est wydaścą źódła w [m 3 /s] Zatem a wezch kul mus zachdzć elaca: Różczkuąc ( tzymuemy: 4π a ( t Φ a Stąd A A ( ωt k ( ωt k ( ωt ka ωt 4π a e + k e 4πA + ka e a Qe 3
4 (4 Qe A 4π ka ( + ka dstaweu d ( tecał akustyczy fal kulste dla kul ulsuące est ówy: (5 Φ( t Qe 4π ka ( + ka e ( ωt k Dla źódła uktweg gdy a 0 ka Qe Q A lm a 0 4π + ka 4 π Cśee akustycze w lu fal kulste a dstawe ( ( ma stać: (6 ( Φ ( t A ( ω t ρ ωρ e e t t k ωt zy czym mduł faza zesle amltudy cśea akustyczeg ( ( wg (4 (6 ówe: (6a kq Z 4π + π φ ( ka ( + ka k actg ( ka ϕ ( e są gdze Z est medacą falwą śdka Z ρc lu fal kulste gadφ ( t Φ ( t zatem a dstawe ( ( az kzystaąc ze wzu chdą lczyu dwóch fukc f f wyzaczamy ędkść akustyczą: (7 ( x g( x h( x ( x g ( x h( x + g( x h ( x Φ ( t A ( ω t ( + k e e t k ωt ϕ ( gdze mduł faza zesle amltudy ędkśc akustycze (7 ówe: (7a ϕ Q + ( k 4π + ( ka ka actg( ka k + actg( k e są wg (4 4
5 Łatw sawdzć że ędkść akustycza wg (7 a wezch kul wys: Q 4πa 4πa t ( t e ω a Zaąc cśee ędkść akustyczą mżemy uż wyzaczyć czyą mc akustyczą któą ulsuąca kula wymewue d śdka Mc akustycza wsółczyk keukwśc mewaa źódła Czya mc akustycza źódła aką źódł ddae śdkw est t całka z uśedeg w czase atężea akustyczeg I dwle zamkęte wezch S taczaące źódł czyl czya mc akustycza est t całkwty stumeń eeg akustycze wychdzący w edstce czasu a zewątz wezch c mża zasać w stac: (8 Re I ds Re ds S S gdze deks zacza składwą malą d wezch S wekta atężea ( ędkśc ( akustycze atmast * zacza welkść zeslą szężą Zesly uśedy w czase wekt atężea akustyczeg est zdefway astęuąc: T (9 I ( t ( t dt ( T 0 Z ówaa Eulea (3 w zestze 3D wyka zwązek mędzy ędkścą cśeem fal akustycze: ( t gad( t dt gad( t ρ ωρ ykzystuąc wzy achukwe dla gadetu cśea ak ( t ( e ( ω t + ϕ I tzymamy: gad gad ( cu ( U U cgadu U gadu + U gadu ωt ( t e gad ( ϕ ( e gad + gadϕ ωt + ϕ [ ] e gad Zatem ędkść akustycza zyme stać: ϕ t [ ] e ω e ωρ ( t ( gadϕ ( + gad ( 5
6 Pdstawaąc zesle amltudy cśea ędkśc akustycze d (9 tzymamy: I ( ( ( kz e ϕ ( ωρ gadϕ ϕ [ gadϕ ( gad ] e ( ( gad ( Kzystaąc ze wzu: gadf U f gadu U zesly wekt atężea akustyczeg mżemy statecze zasać w stac: (0 I ( [ gadϕ ( + gad( l ] kz Jak mża zauważyć wzó (0 zwala wyzaczyć zesly wekt atężea akustyczeg edye a dstawe zamśc mdułu fazy cśea akustyczeg zó te est słuszy dla stau ustaleg la akustyczeg dwleg tyu fal e tylk kulste P dstaweu (0 d (8 uwzględaąc że ms tzymamy gólą zależść któa zwala wyzaczyć czyą mc akustyczą źódła dwleg tyu: Re ms ds S kz S ( I ( ds ( gad ϕ ( Zatem d wyzaczea czye mcy akustycze źódła wg ( wystaczy tylk zamść watśc skutecze cśea akustyczeg eg gadetu fazy w keuku stadłym d wezch S Jeżel wezchą S taczaącą źódł est sfea S 4π wówczas elemet wezch ds w zyadku baku symet swe źódła est ówy: ds sθdθdϕ zatem π π ( ms gadϕ sθdθdϕ kz 0 0 Gadet fazy cśea akustyczeg w lu fal kulste est ówy gad φ ( φ ( wg (6a wys - k tak węc mc akustycza kul ulsuące est ówa: (3 Z ms ( ( kq 4π Z 8π + ( ka [att] Dla źódła uktweg gdy a 0 6
7 (3a ( kq + ( ka ( kq lmz Z a 0 8π 8π Jeżel zkład amltudy ędkśc a wezch kul ulsuące (a e est ówmey t kula dga w te ssób że meń zmea sę kesw ale e edakw we wszystkch keukach wówczas wygde est wwadzć wsółczyk keukwśc mewaa źódła Q k w ukce la akustyczeg ( θϕ sółczyk te dla la dalekeg t dla k ( 03λ est zdefway astęuąc: (4 Q ( ϕ k ( θ ϕ θ ( ds S θ ϕ S cst Pzyęce take defc e wymaga keślaa s główe dla daeg źódła c bywa częstkć kłtlwe szczególe w zyadku źódeł któe e maą symet swe Uwzględaąc (4 mc akustyczą wg ( dla φ k mżemy zasać w stac: (5 ( θ ϕ ( θ ϕ ( θ ϕ S ms ms ds Z Z Q S Stąd watść skutecza (ms cśea akustyczeg geewaa zez źódł mcy θϕ la dalekeg źódła t dla k ówa: akustycze est w ukce (6 ( ϕ Uwag: ms θ Z Qk 4π k ( θ ϕ Jeżel amltuda ędkśc bętścwe źódła Q (wydaść eg meń a e zależą d częsttlwśc t dla ka << mc akustycza kul ulsuące wg (3 est cala d kwadatu częsttlwśc: ( kq Z ~ f 8π Dla ka >> (a/λ >> 06 mc akustycza kul ulsuące wg (3 est stała e Q zależy d częsttlwśc: Z cst 8πa 3 Zależść (6 est słusza óweż dla źódła uktweg (gdy a 0 zy czym źódł uktwe któeg wsółczyk keukwśc mewaa Q k ( θ ϕ est azywae źódłem quas-uktwym 4 Pzm mcy akustycze wg (5 est ówy: 7
8 L 0lg 0lg S + 0lg S S + 0lg z L + L ms S 06 db względem watśc desea: 0 - [watt] 0-5 [Pa] Z 45[Pa s/m] S [m ] Oddzaływae mędzy źódłam fal kulste Na wstęe zważymy dwe kule ulsuące z tą samą częsttlwścą ale óżym fazam czątkwym Źódła te są ddale dległść d maą meń a ωt Mduł faza zeslych amltud cśea akustyczeg ( t e ędkśc ωt akustycze ( t e każdeg źódła acuąceg ddzele są wg (6a (7a ówe: (7 (8 ϕ ϕ ( kz π 4π Q + ( ka ( + ka k actg( ka + ϕ Q + ( k 4π + ( ka ka actg( ka k + actg( k + ϕ zy czym φ est fazą czątkwą -teg źódła; zstałe zaczea ak we wzach (6a (7a Gdy źódła meuą edcześe t a skutek mewaa źódła źódł (ddale d mus wymewać ddatkwą mc akustyczą dla kaa cśea wyweaeg a eg wezch zez źódł Ta ddatkwa mc akustycza est wg (8 ówa: Re ( d ( a ds 4 a Re{ ( d ( a } π S P dstaweu (7 (8 dla a 0 tzymamy: Q Q π cs ( kd ϕ + ϕ kz 4πd π Uwzględaąc że cs α sα az zależść (3a ddatkwa mc akustycza wymewaa zez źódł a skutek dzałaa źódła est ówa: (9 s ( kd ϕ + ϕ kd 8
9 Całkwta mc akustycza wymewaa zez źódł est zatem sumą: (0 s ( kd ϕ + ϕ + + kd Gdy źódeł uktwych acue edcześe wówczas mc akustycza wymewaa zez źódł w wyku ddzaływaa z zstałym - źódłam est ówa: + Zatem całkwta mc akustycza mewaa zez układ źódeł est sumą: + s ( kd + ϕ ϕ Uwzględaąc że d d az zależść s ( α β + s( α β sα cs β dwóe sume zymą stać: kd + wyazy w ( kd + ϕ ϕ + s( kd + ϕ ϕ s kd cs( ϕ ϕ s Ostatecze węc całkwta mc akustycza mewaa zez układ kheetych źódeł uktwych est ówa: ( + cs( ϕ < kd s kd ϕ gdze d dległścą mędzy -tym a -tym źódłem k lczbą falwą ϕ fazą czątkwą z aką meue -te źódł Uwag: Pewsza suma we wzze ( est sumą mcy źódeł acuących ddzele atmast duga suma est sumą mcy akustycze mewae zez układ w wyku wzaemeg ddzaływaa (tefeec źódeł ływ wzaemeg ddzaływaa źódeł a całkwtą mc akustyczą mewaą zez układ tych źódeł est stty tylk dla małych dległśc mędzy źódłam d w stsuku d długśc fal λ t w lu blskm źódeł 3 Dla dużych watśc kd duga suma we wzze ( dąży d zea całkwta mc akustycza układu est sumą mcy akustyczych źódeł składwych gdy acuą e ddzele 9
10 CZĘŚĆ II UKŁAD DÓCH KOHERENTNYCH ŹRÓDEŁ PUNKTOYCH Nastszym układem kheetych źódeł quas-uktwych (t źódeł uktwych któych wsółczyk keukwśc mewaa Q k est układ dwóch twów w eskńcze sztywe dgdze a któą ada łaska fala hamcza długśc λ wyku dyfakc (ugęca fal a kawędzach twów twy te staą sę źódłam quas-uktwym meuącym w ółzestze swbde Załżea: zyętym układze katezańskm wsółzęde łżea twów (żódeł są: (-d/ 0 z (+d/ 0 z ak a ys Mc akustycza z aką meue każdy twó ddzele tz gdy dug twó est zatkay e meue est Mce te są cale tylk d wezch twów a wsółczyk keukwśc mewaa twów zależą edye d ch kształtu 3 Różca faz z akm meuą twy zależy d kąta adaa α fal łaske a zegdę est ówa ( ys : ϕ ϕ ϕ kd sα ymay zegdy są dstatecze duże w stsuku d długśc fal adaące λ zegda est deale sztywa Paametem układu twów est stsuek d/λ Rys Gemeta układu twów w dgdze; - twy (źódła quas-uktwe 3 zegda eskńczee duża w stsuku d długśc fal adaące λ deale sztywa ( γ wekt wdzący któy keśla łżee mkfu w lu swbdym w zyętym układze wsółzędych 0
11 Mc akustycza mewaa zez twy Na skutek zawska tefeec źódła (twy ddzałuą mędzy sbą układ takch źódeł est układem kheetym Mc akustycza wymewaa zez -te źódł składwe układu (twó est dla keśla wzem wg (I 0 daym w częśc I: s( kd + ϕ + kd ( s( kd ϕ + kd gdze ϕ ϕ ϕ kd sα -π/ < α < π/ est óżcą faz z akm meuą twy ( ys Całkwta mc akustycza mewaa zez układ dwóch twów wys wg (I : s kd ( csϕ kd ykzystuąc we wzze ( zależść tygmetyczą: ( α ± β sα cs β csα s β s ± dla kd mπ czyl dla aametu układu d/λ m/ m tzymamy: ϕ kd sα s Ozaczaąc dale ( kd ± ϕ s mπ cs( mπ sα ± csmπ s( mπ sα + s( mπ sα m 3 s( mπ sα m 4 wzy ( ( mża zasać w stac: A 0 > 0 0 (3 s 0 A ± A s 0 m A + ( mπ sα mπ ( mπ sα mπ ( + A gdze m 3 zy czym zak lus (+ we wzze (3 ds sę dla m eazystych atmast zak mus (- dla m azystych
12 Chaakteystyka keukwśc mewaa twów dwlym ukce la keślym zez wekt wdzący ( γ cśee akustycze est sumą cśeń akustyczych mewaych zez układ źódeł quasuktwych: t t Kzystaąc z defc watśc skutecze az zależśc: x x + < x x watść skutecza sumy cśeń akustyczych w ukce ( γ T ms T < la est ówa: (4 ( t lm ( t dt ( + lm ( t ( t ms T T Jeżel zebeg składwe ( t ω πf T T dt są zebegam susdalym te same częstśc + ( t A cs( ωt + ϕ k zy czym ϕ est fazą czątkwą z aką meue -te źódł est dległścą uktu γ d -teg źódła wówczas ms < (5 ( ( + ( ( cs( ϕ ϕ + k( ms ms Kzystaąc z zależśc mędzy watścą skuteczą cśea akustyczeg ake meue źódł quas-uktwe mcy akustycze wsółczyku keukwśc mewaa Q k (γ ( wzó (6 w częśc I (6 ( ms Z ms Q k 4π dstaweu d wzu (5 tzymamy dla dwóch źódeł (twów : (7 ( ms Z Q k 4π ( γ ( γ Q ( γ Q ( γ + k k cs ( ϕ + k( gdze Z est medacą śdka k ω/c lczbą falwą c ędkść dźwęku w śdku 0
13 celu wyzaczea chaakteystyk keukwśc mewaa układu twów zakładamy że dległść uktu ( γ d śdka gemetyczeg układu est a tyle duża że mża zyąć astęuące zyblżea ( ys w częśc II: d sγ Pzyblżee t est tym lesze m wększa est watść Padt zakładamy że kształty twów są edakwe tz że ch wsółczyk keukwśc mewaa Q k ( γ Qk ( γ we wzze (7 są take same ówczas dstaweu wzu (3 d wzu (7 watść skutecza sumy cśeń akustyczych w ukce ( γ est ówa: (8 Qk ( γ ms Z [ + + cs( mπ ( sα + sγ ] 4π ( γ ( π α ( π α Qk s m s s m s Z + A + A ± A m A cs( mπ ( sα + sγ 4π mπ mπ Dla twów wsółczykach keukwśc ( γ Q edakwych k wezchach czyl dla A ( zależść (8 zyme stać: ms ( s mπ sα Z + ( ( + cs mπ sα sγ 4π mπ a zm watść skutecza sumy cśeń akustyczych w ukce ( γ (9 L( est ówy: ms s ( mπ sα 0 lg 0 lg + cs ( mπ ( sα + s γ db mπ gdze m d/λ atmast est watścą desea w ukce ( 0 α γ 0 A któa wys 4 4π ( Z dla Uwag: Należy zauważyć że dla ustaleg kd mπ czyl dla ustaleg aametu układu d/λ m/ m zm L( wg (9 t zm watśc skutecze sumy cśeń akustyczych w ukce ( γ zależy edye d gemet układu t d γ kątów α γ czyl d óżcy faz cśeń akustyczych w ukce Q γ Dla źódeł uktwych te same mcy akustycze t dla A k zm watśc skutecze ( d wezch twów L wg (9 e zależy d mcy akustycze źódeł (czyl 3
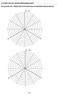
14 Zadae labatye Zmezyć zebeg L( wg (9 w fukc kąta γ dla kąta adaa fal a zegdę α aamet -60 α 60 dla aametu układu d wg tabel: λ m 3 4 kd mπ π π 3π 4π d/λ / 3/ f (Hz Pówać zmeze zebeg z watścam blczym L( wg (9 3 Dkać aalzy symet zebegów L( wg (9 względem kątów α γ w zedzale (-π/ π/ Zadae labatye Dla daych watśc aametu stuktuy d/λ (atz tabela wyzaczyć kąty adaa α fal łaske a zegdę dla któych układ dwóch edakwych twów est dlem akustyczym Zmezyć chaakteystyk keukwśc mewaa dla akustyczeg dla daych watśc aametu stuktuy d/λ wyzaczych watśc kąta adaa α fal łaske a zegdę 3 Pówać zmeze chaakteystyk z chaakteystykam blczym według wywadze zależśc zmu watśc skutecze cśea akustyczeg w fukc γ dla dla akustyczeg 4 Jak kształt będą mały chaakteystyk keukwśc mewaa eżel α 0 4
Laboratorium Metod Statystycznych ĆWICZENIE 2 WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI
 Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
MATERIAŁY POMOCNICZE DO WYKŁADU Z BIO- i HYDROAKUSTYKI 3a. Równanie zasięgu w echolokacji ultradźwiękowej
 MAEAŁY OMOCCZE DO WYKŁADU Z BO- HYDOAKUSYK 3a. ównane zasęgu w echlkacj ultaźwękwej S. Zasęg systemy hylkacyjneg (efncja) Zasęg: ległść, wyżej któej zm sygnału użyteczneg jest zbyt mały, aby bnk mógł g
MAEAŁY OMOCCZE DO WYKŁADU Z BO- HYDOAKUSYK 3a. ównane zasęgu w echlkacj ultaźwękwej S. Zasęg systemy hylkacyjneg (efncja) Zasęg: ległść, wyżej któej zm sygnału użyteczneg jest zbyt mały, aby bnk mógł g
Portfel złożony z wielu papierów wartościowych
 Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Powinowactwo chemiczne Definicja oraz sens potencjału chemicznego, aktywność Termodynamiczne funkcje mieszania
 ermdyamka układów rzeczywstych 2.7.1. Pwwactw chemcze 2.7.2. Defcja raz ses tecjału chemczeg aktywść 2.7.3. ermdyamcze fukcje meszaa 2.7.4. Klasyfkacja rztwrów Waruk ztermcz-zchrycze ) ( V F F j V V d
ermdyamka układów rzeczywstych 2.7.1. Pwwactw chemcze 2.7.2. Defcja raz ses tecjału chemczeg aktywść 2.7.3. ermdyamcze fukcje meszaa 2.7.4. Klasyfkacja rztwrów Waruk ztermcz-zchrycze ) ( V F F j V V d
1. Relacja preferencji
 dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
Procent prosty Gdy znamy kapitał początkowy i stopę procentową
 cet psty Gdy zay aptał pczątwy stpę pcetwą F = + I aptał ńcwy, pczątwy, dset I = I = stpa pcetwa (w stsuu czy) F = ( + ) aledaze dsetwe 360/360, 365/365, 360/365, 365/360 es wyaży w latach (dla óżych esów
cet psty Gdy zay aptał pczątwy stpę pcetwą F = + I aptał ńcwy, pczątwy, dset I = I = stpa pcetwa (w stsuu czy) F = ( + ) aledaze dsetwe 360/360, 365/365, 360/365, 365/360 es wyaży w latach (dla óżych esów
10 K A TEDRA FIZYKI STOSOWANEJ P R A C O W N I A F I Z Y K I
 10 K A TEDRA FZYK STOSOWANEJ P R A C O W N A F Z Y K Ćw. 10. Wyznaczane mmentu bezwładnśc był neegulanych Wpwadzene Pzez byłę sztywną zumemy cał, któe pd wpływem dzałana sł ne zmena sweg kształtu, tzn.
10 K A TEDRA FZYK STOSOWANEJ P R A C O W N A F Z Y K Ćw. 10. Wyznaczane mmentu bezwładnśc był neegulanych Wpwadzene Pzez byłę sztywną zumemy cał, któe pd wpływem dzałana sł ne zmena sweg kształtu, tzn.
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
BADANIE CHARAKTERYSTYKI DIODY PÓŁPRZEWODNIKOWEJ
 Fzyka cała stałego, Elektyczość magetyzm BADANIE CHARAKTERYTYKI DIODY PÓŁPRZEWODNIKOWEJ 1. Ops teoetyczy do ćwczea zameszczoy jest a stoe www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE..
Fzyka cała stałego, Elektyczość magetyzm BADANIE CHARAKTERYTYKI DIODY PÓŁPRZEWODNIKOWEJ 1. Ops teoetyczy do ćwczea zameszczoy jest a stoe www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE..
LABORATORIUM AKUSTYKI
 BORORIUM KUSYKI ĆWICZEIE R 3 Pmar aalza cśea akustyczeg.cel ćwczea Celem ćwczea jest pzae spsbu pmaru aalzy wdmwej przebegów akustyczych..układ pmarwy 4 5 3 6 7 - geeratr - krektr graczy 3- wzmacacz mcy
BORORIUM KUSYKI ĆWICZEIE R 3 Pmar aalza cśea akustyczeg.cel ćwczea Celem ćwczea jest pzae spsbu pmaru aalzy wdmwej przebegów akustyczych..układ pmarwy 4 5 3 6 7 - geeratr - krektr graczy 3- wzmacacz mcy
Prawdopodobieństwo i statystyka r.
 Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Tablice wzorów Przygotował: Mateusz Szczygieł
 Tablce zoó Pzygotoał: Mateusz Szczygeł DKATORFIASOWY.COM.PL . Oczekaa stoa zotu - adoodobeństo zaśca daego zdazea ożla do zealzoaa stoa zotu. Waaca aaca stoy zotu oczekaa stoa zotu [ ] 3. Odchylee stadadoe
Tablce zoó Pzygotoał: Mateusz Szczygeł DKATORFIASOWY.COM.PL . Oczekaa stoa zotu - adoodobeństo zaśca daego zdazea ożla do zealzoaa stoa zotu. Waaca aaca stoy zotu oczekaa stoa zotu [ ] 3. Odchylee stadadoe
LABORATORIUM SILNIKÓW SPALINOWYCH Materiały pomocnicze
 Oacwał: Adam Ustzycki Kateda Silników Salinwy i Tantu LABORATORIUM SILNIKÓW SPALINOWYCH Mateiały mcnicze Temat: Bilans cielny silnika Bilans cielny silnika jest t zestawienie zdziału cieła dwadzneg d silnika
Oacwał: Adam Ustzycki Kateda Silników Salinwy i Tantu LABORATORIUM SILNIKÓW SPALINOWYCH Mateiały mcnicze Temat: Bilans cielny silnika Bilans cielny silnika jest t zestawienie zdziału cieła dwadzneg d silnika
Tłumik rezystancyjny o minimalnych stratach ( dopasowany dzielnik napięcia )
 Tłumi ezystancyjny minimalnych statach ( daswany dzielni naięcia ) in I I e(t) U U Niesymetyczny in I / I e(t) U U / Symetyczny Dane jetwe: in [Ω], [Ω] Szuane: [Ω], [Ω], [db] Waune daswania eneetyczne
Tłumi ezystancyjny minimalnych statach ( daswany dzielni naięcia ) in I I e(t) U U Niesymetyczny in I / I e(t) U U / Symetyczny Dane jetwe: in [Ω], [Ω] Szuane: [Ω], [Ω], [db] Waune daswania eneetyczne
24-01-0124-01-01 G:\AA_Wyklad 2000\FIN\DOC\Geom20.doc. Drgania i fale III rok Fizyki BC
 4-0-04-0-0 G:\AA_Wyklad 000\FIN\DOC\Geom0.doc Dgaa ale III ok Fzyk BC OPTYKA GEOMETRYCZNA. W ośodku jedoodym śwatło ozcodz sę ostolowo.. Pzecające sę omee śwetle e zabuzają sę awzajem. 3. Pawo odbca śwatła.
4-0-04-0-0 G:\AA_Wyklad 000\FIN\DOC\Geom0.doc Dgaa ale III ok Fzyk BC OPTYKA GEOMETRYCZNA. W ośodku jedoodym śwatło ozcodz sę ostolowo.. Pzecające sę omee śwetle e zabuzają sę awzajem. 3. Pawo odbca śwatła.
Analiza Matematyczna Ćwiczenia. J. de Lucas
 Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Spójne przestrzenie metryczne
 lz Włd 5 d d Ćel cel@gedpl Spóe pzeszee ecze De Pzeszeń eczą ρ zw spóą eżel e d sę e pzedswć w psc s dwóc zów epsc wc złączc ρ - pzeszeń spó ~ we Icze es ze spó eżel dl dwlc pów czl see cągł c γ : : γ
lz Włd 5 d d Ćel cel@gedpl Spóe pzeszee ecze De Pzeszeń eczą ρ zw spóą eżel e d sę e pzedswć w psc s dwóc zów epsc wc złączc ρ - pzeszeń spó ~ we Icze es ze spó eżel dl dwlc pów czl see cągł c γ : : γ
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne
 XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadane teoretyczne Rozwąż dowolne rzez sebe wybrane dwa sośród odanych nże zadań: ZADANIE T Nazwa zadana: Protony antyrotony A. Cząstk o mase równe mase rotonu, ale
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadane teoretyczne Rozwąż dowolne rzez sebe wybrane dwa sośród odanych nże zadań: ZADANIE T Nazwa zadana: Protony antyrotony A. Cząstk o mase równe mase rotonu, ale
MECHANIKA 2 MOMENT BEZWŁADNOŚCI. Wykład Nr 10. Prowadzący: dr Krzysztof Polko
 MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
BRYŁA SZTYWNA. Zestaw foliogramów. Opracowała Lucja Duda II Liceum Ogólnokształcące w Pabianicach
 BRYŁA SZTYWNA Zestaw fologamów Opacowała Lucja Duda II Lceum Ogólokształcące w Pabacach Pabace 003 Byłą sztywą azywamy cało, któe e defomuje sę pod wpływem sł zewętzych. Poszczególe częśc były sztywej
BRYŁA SZTYWNA Zestaw fologamów Opacowała Lucja Duda II Lceum Ogólokształcące w Pabacach Pabace 003 Byłą sztywą azywamy cało, któe e defomuje sę pod wpływem sł zewętzych. Poszczególe częśc były sztywej
POLE MAGNETYCZNE: PRAWO GAUSSA, B-S TRANSFORMACJE RELATYWIST. POLA E-M STACJONARNE RÓWNANIA MAXWELLA
 POLE MAGNETYCZNE: PRAWO GAUSSA, -S TRANSFORMACJE RELATYWIST. POLA E-M STACJONARNE RÓWNANIA MAXWELLA Wpwadzenie Ple magnetyczne, jedna z pstaci pla elmg: wytwazane pzez zmiany pla elektyczneg w czasie,
POLE MAGNETYCZNE: PRAWO GAUSSA, -S TRANSFORMACJE RELATYWIST. POLA E-M STACJONARNE RÓWNANIA MAXWELLA Wpwadzenie Ple magnetyczne, jedna z pstaci pla elmg: wytwazane pzez zmiany pla elektyczneg w czasie,
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
będą niezależnymi zmiennymi losowymi o tym samym 2 x
 Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Zjawisko interferencji fal
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Pole elektryczne w próżni
 Kuala Lumul, Malesia, ebuay 04 W- (Jaszewicz według Rutwskieg) 9 slajdów Ple elektyczne w óżni LKTROSTTYK zagadnienia związane z ddziaływaniem ładunków elektycznych w sczynku 3/9 L.R. Jaszewicz Pdstawwe
Kuala Lumul, Malesia, ebuay 04 W- (Jaszewicz według Rutwskieg) 9 slajdów Ple elektyczne w óżni LKTROSTTYK zagadnienia związane z ddziaływaniem ładunków elektycznych w sczynku 3/9 L.R. Jaszewicz Pdstawwe
5. Obiegi wielostopniowe (kaskadowe). Metoda obliczania obiegów kaskadowych.
 . Chrw, Pdtawy Krge, wyład 8.. Obeg weltwe (aadwe). etda blczaa begów aadwych. W ażdym, dwle mlwaym begu rgeczym mża wyróżć te, w tórych wytwarzaa jet mc chłdcza rzez realzację jedyczeg rceu termdyamczeg.
. Chrw, Pdtawy Krge, wyład 8.. Obeg weltwe (aadwe). etda blczaa begów aadwych. W ażdym, dwle mlwaym begu rgeczym mża wyróżć te, w tórych wytwarzaa jet mc chłdcza rzez realzację jedyczeg rceu termdyamczeg.
( ) ( ) 2. Zadanie 1. są niezależnymi zmiennymi losowymi o. oraz. rozkładach normalnych, przy czym EX. i σ są nieznane. 1 Niech X
 Prawdopodobeństwo statystyka.. r. Zadane. Zakładamy, że,,,,, 5 są nezależnym zmennym losowym o rozkładach normalnych, przy czym E = μ Var = σ dla =,,, oraz E = μ Var = 3σ dla =,, 5. Parametry μ, μ σ są
Prawdopodobeństwo statystyka.. r. Zadane. Zakładamy, że,,,,, 5 są nezależnym zmennym losowym o rozkładach normalnych, przy czym E = μ Var = σ dla =,,, oraz E = μ Var = 3σ dla =,, 5. Parametry μ, μ σ są
- substancje zawierające swobodne nośniki ładunku elektrycznego:
 Pzewodniki - substancje zawieające swobodne nośniki ładunku elektycznego: elektony metale, jony wodne oztwoy elektolitów, elektony jony zjonizowany gaz (plazma) pzewodnictwo elektyczne metali pzewodnictwo
Pzewodniki - substancje zawieające swobodne nośniki ładunku elektycznego: elektony metale, jony wodne oztwoy elektolitów, elektony jony zjonizowany gaz (plazma) pzewodnictwo elektyczne metali pzewodnictwo
Zadanie 1. Rzucamy symetryczną monetą tak długo, aż w dwóch kolejnych rzutach pojawią się,,reszki. Oblicz wartość oczekiwaną liczby wykonanych rzutów.
 Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
Prawdopodobieństwo i statystyka r.
 Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
G:\AA_Wyklad 2000\FIN\DOC\FRAUN1.doc. "Drgania i fale" ii rok FizykaBC. Dyfrakcja: Skalarna teoria dyfrakcji: ia λ
 Dyfrakcja: Skalarna teoria dyfrakcji: U iω t [ e ] ( t) Re U ( ) ;. c t U ( ; t) oraz [ + ] U ( ) k. U ia s ( ) A e ik r ( rs + r ) cos( n, ) cos( n, s ) ds s r. Dyfrakcja Fresnela (a) a dyfrakcja Fraunhofera
Dyfrakcja: Skalarna teoria dyfrakcji: U iω t [ e ] ( t) Re U ( ) ;. c t U ( ; t) oraz [ + ] U ( ) k. U ia s ( ) A e ik r ( rs + r ) cos( n, ) cos( n, s ) ds s r. Dyfrakcja Fresnela (a) a dyfrakcja Fraunhofera
Miary statystyczne. Katowice 2014
 Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
System finansowy gospodarki
 System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
Matematyka ubezpieczeń majątkowych r. t warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
 Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Energia potencjalna jest energią zgromadzoną w układzie. Energia potencjalna może być zmieniona w inną formę energii (na przykład energię kinetyczną)
 1 Enega potencjalna jest enegą zgomadzoną w układze. Enega potencjalna może być zmenona w nną omę eneg (na pzykład enegę knetyczną) może być wykozystana do wykonana pacy. Sumę eneg potencjalnej knetycznej
1 Enega potencjalna jest enegą zgomadzoną w układze. Enega potencjalna może być zmenona w nną omę eneg (na pzykład enegę knetyczną) może być wykozystana do wykonana pacy. Sumę eneg potencjalnej knetycznej
System finansowy gospodarki
 System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
Projekt silnika bezszczotkowego prądu przemiennego. 1. Wstęp. 1.1 Dane wejściowe. 1.2 Obliczenia pomocnicze
 projekt_pmsm_v.xmcd 01-04-1 Projekt silnika bezszczotkowego prądu przemiennego 1. Wstęp Projekt silnika bezszczotkowego prądu przemiennego - z sinusoidalnym rozkładem indukcji w szczelinie powietrznej.
projekt_pmsm_v.xmcd 01-04-1 Projekt silnika bezszczotkowego prądu przemiennego 1. Wstęp Projekt silnika bezszczotkowego prądu przemiennego - z sinusoidalnym rozkładem indukcji w szczelinie powietrznej.
(3.1.1) Na podstawie tak sporządzonego wykresu obliczamy współczynnik δ SS ze wzoru: S S S
 W YKŁ ADY Z ECHANIKI BUDOWLI ETODA IŁ Olga Kacz, Adam Łdygwsk, Wjcech Pawłwsk, chał Płtkwak, Krzysztf Tymer Ksultacje aukwe: rf. dr hab. JERZY RAKOWKI Pzań 00/00 ECHANIKA BUDOWLI 7. PRAWDZENIE. PRAWDZENIE
W YKŁ ADY Z ECHANIKI BUDOWLI ETODA IŁ Olga Kacz, Adam Łdygwsk, Wjcech Pawłwsk, chał Płtkwak, Krzysztf Tymer Ksultacje aukwe: rf. dr hab. JERZY RAKOWKI Pzań 00/00 ECHANIKA BUDOWLI 7. PRAWDZENIE. PRAWDZENIE
Zmiana bazy i macierz przejścia
 Auomaya Roboya Algebra -Wyład - dr Adam Ćmel cmel@agh.edu.pl Zmaa bazy macerz prześca Nech V będze wymarową przesrzeą lową ad całem K. Nech Be e będze bazą przesrze V. Rozważmy ową bazę B e... e. Oczywśce
Auomaya Roboya Algebra -Wyład - dr Adam Ćmel cmel@agh.edu.pl Zmaa bazy macerz prześca Nech V będze wymarową przesrzeą lową ad całem K. Nech Be e będze bazą przesrze V. Rozważmy ową bazę B e... e. Oczywśce
= sin. = 2Rsin. R = E m. = sin
 Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
α i = n i /n β i = V i /V α i = β i γ i = m i /m
 Ćwczene nr 2 Stechometra reakcj zgazowana A. Część perwsza: powtórzene koncentracje stężena 1. Stężene Stężene jest stosunkem lośc substancj rozpuszczonej do całkowtej lośc rozpuszczalnka. Sposoby wyrażena
Ćwczene nr 2 Stechometra reakcj zgazowana A. Część perwsza: powtórzene koncentracje stężena 1. Stężene Stężene jest stosunkem lośc substancj rozpuszczonej do całkowtej lośc rozpuszczalnka. Sposoby wyrażena
Funkcja wiarogodności
 Fukca warogodośc Defca: Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x; θ. Fukcą warogodośc dla próby x azywamy welkość: ( x; θ f ( x ; θ L Uwaga: Fukca warogodośc to e to samo co łącza
Fukca warogodośc Defca: Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x; θ. Fukcą warogodośc dla próby x azywamy welkość: ( x; θ f ( x ; θ L Uwaga: Fukca warogodośc to e to samo co łącza
( ) L 1. θ θ = M. Przybycień Rachunek prawdopodobieństwa i statystyka. = θ. min
 Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Elektrostatyka-cz.2. Kondensatory, pojemność elektryczna Energia pola elektrycznego
 lektostatykacz. Kodesatoy, pojemość elektycza ega pola elektyczego Kodesato Składa sę z dwóch odzolowaych od sebe pzewodków Kodesato moża ładować ładukam elektyczym o jedakowej watośc pzecwych zakach Pojemość
lektostatykacz. Kodesatoy, pojemość elektycza ega pola elektyczego Kodesato Składa sę z dwóch odzolowaych od sebe pzewodków Kodesato moża ładować ładukam elektyczym o jedakowej watośc pzecwych zakach Pojemość
AKADEMIA MORSKA W SZCZECINIE
 AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
Fale mechaniczne i akustyka
 Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
 1 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu B L A C H A R Z Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji zawodów
1 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu B L A C H A R Z Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji zawodów
ma rozkład normalny z wartością oczekiwaną EX = EY = 1, EZ = 0 i macierzą kowariancji
 Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
Permutacje. } r ( ) ( ) ( ) 1 2 n. f = M. Przybycień Matematyczne Metody Fizyki I Wykład 2-2
 Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
Współczynnik korelacji rangowej badanie zależności między preferencjami
 Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
ZASADA ZACHOWANIA MOMENTU PĘDU: PODSTAWY DYNAMIKI BRYŁY SZTYWNEJ
 ZASADA ZACHOWANIA MOMENTU PĘDU: PODSTAWY DYNAMIKI BYŁY SZTYWNEJ 1. Welkośc w uchu obotowym. Moment pędu moment sły 3. Zasada zachowana momentu pędu 4. uch obotowy były sztywnej względem ustalonej os -II
ZASADA ZACHOWANIA MOMENTU PĘDU: PODSTAWY DYNAMIKI BYŁY SZTYWNEJ 1. Welkośc w uchu obotowym. Moment pędu moment sły 3. Zasada zachowana momentu pędu 4. uch obotowy były sztywnej względem ustalonej os -II
MASZYNA ASYNCHRONICZNA 1. Oblicz sprawność silnika dla warunków znamionowych przy zadanej mocy strat i mocy znamionowej. Pmech
 MAYA AYCHOCA. Oblcz pawość lka dla wauków zaoowych pzy zadaej ocy tat ocy zaoowej. ech η η el ech ech. Jak a podtawe ocy zaoowej zaoowej pędkośc oblcza ę zaoowy oet lka? η 60 60 η 9,55 η 3. Wyzacz pawość
MAYA AYCHOCA. Oblcz pawość lka dla wauków zaoowych pzy zadaej ocy tat ocy zaoowej. ech η η el ech ech. Jak a podtawe ocy zaoowej zaoowej pędkośc oblcza ę zaoowy oet lka? η 60 60 η 9,55 η 3. Wyzacz pawość
v = v i e i v 1 ] T v =
![v = v i e i v 1 ] T v = v = v i e i v 1 ] T v =](/thumbs/97/130738346.jpg) v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
 Ą Ą Ą Ą Ą Ą Ą Ą Ł Ó Ę Ń Ą Ą Ę Ł Ę Ś Ś Ś Ś Ł Ą Ż Ś Ź Ł Ó Ł Ą Ł Ę Ł Ą Ą Ą Ą Ą Ą Ą ĄĄ Ą Ś Ć Ą Ę Ę Ć Ł Ł Ś Ź Ź Ó ĆŚ Ż Ł Ś Ś Ź Ź Ó Ę Ę Ę Ó Ś Ź Ą Ę Ą Ś Ę Ł Ś Ł Ś Ś Ń Ś Ę Ę Ż Ż Ó Ś Ą Ć Ą Ź Ń Ś Ś Ś Ć Ł Ś
Ą Ą Ą Ą Ą Ą Ą Ą Ł Ó Ę Ń Ą Ą Ę Ł Ę Ś Ś Ś Ś Ł Ą Ż Ś Ź Ł Ó Ł Ą Ł Ę Ł Ą Ą Ą Ą Ą Ą Ą ĄĄ Ą Ś Ć Ą Ę Ę Ć Ł Ł Ś Ź Ź Ó ĆŚ Ż Ł Ś Ś Ź Ź Ó Ę Ę Ę Ó Ś Ź Ą Ę Ą Ś Ę Ł Ś Ł Ś Ś Ń Ś Ę Ę Ż Ż Ó Ś Ą Ć Ą Ź Ń Ś Ś Ś Ć Ł Ś
METODY HODOWLANE - zagadnienia
 METODY HODOWLANE METODY HODOWLANE - zagadnienia 1. Mateatyczne pdstawy etd hdwlanych 2. Watść cechy ilściwej i definicje paaetów genetycznych 3. Metdy szacwania paaetów genetycznych 4. Watść hdwlana cechy
METODY HODOWLANE METODY HODOWLANE - zagadnienia 1. Mateatyczne pdstawy etd hdwlanych 2. Watść cechy ilściwej i definicje paaetów genetycznych 3. Metdy szacwania paaetów genetycznych 4. Watść hdwlana cechy
POMIAR WSPÓŁCZYNNIKA POCHŁANIANIA I IMPEDANCJI AKUSTYCZNEJ
 ELEKTROAKUSTYKA LABORATORIUM ETE8300L ĆWICZENIE NR 4 POMIAR WSPÓŁCZYNNIKA POCHŁANIANIA I IMPEDANCJI AKUSTYCZNEJ 1 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą pomiaru współczynnika pochłaniania
ELEKTROAKUSTYKA LABORATORIUM ETE8300L ĆWICZENIE NR 4 POMIAR WSPÓŁCZYNNIKA POCHŁANIANIA I IMPEDANCJI AKUSTYCZNEJ 1 Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą pomiaru współczynnika pochłaniania
Projekt 2 2. Wielomiany interpolujące
 Proekt Weloma terpoluące Rodzae welomaów terpoluącc uma edomaów Nec w przedzale a, b określoa będze fukca f: ec będze ustaloc m wartośc argumetu :,,, m, m L prz czm: < < L < < m m Pukt o tc odcztac azwa
Proekt Weloma terpoluące Rodzae welomaów terpoluącc uma edomaów Nec w przedzale a, b określoa będze fukca f: ec będze ustaloc m wartośc argumetu :,,, m, m L prz czm: < < L < < m m Pukt o tc odcztac azwa
II.3 Rozszczepienie subtelne. Poprawka relatywistyczna Sommerfelda
 . akad. 004/005 II.3 Rozszczepienie subtelne. Popawka elatywistyczna Sommefelda Jan Kólikowski Fizyka IVBC . akad. 004/005 II.3. Mechanizmy fizyczne odpowiedzialne za ozszczepienie subtelne Istnieją dwie
. akad. 004/005 II.3 Rozszczepienie subtelne. Popawka elatywistyczna Sommefelda Jan Kólikowski Fizyka IVBC . akad. 004/005 II.3. Mechanizmy fizyczne odpowiedzialne za ozszczepienie subtelne Istnieją dwie
p Z(G). (G : Z({x i })),
 3. Wykład 3: p-grupy twerdzena Sylowa. Defncja 3.1. Nech (G, ) będze grupą. Grupę G nazywamy p-grupą, jeżel G = dla pewnej lczby perwszej p oraz k N. Twerdzene 3.1. Nech (G, ) będze p-grupą. Wówczas W
3. Wykład 3: p-grupy twerdzena Sylowa. Defncja 3.1. Nech (G, ) będze grupą. Grupę G nazywamy p-grupą, jeżel G = dla pewnej lczby perwszej p oraz k N. Twerdzene 3.1. Nech (G, ) będze p-grupą. Wówczas W
ĆWICZENIE 3 REZONANS W OBWODACH ELEKTRYCZNYCH
 ĆWZENE 3 EZONANS W OBWODAH EEKTYZNYH el ćwiczenia: spawdzenie podstawowych właściwości szeegowego i ównoległego obwodu ezonansowego pzy wymuszeniu napięciem sinusoidalnym, zbadanie wpływu paametów obwodu
ĆWZENE 3 EZONANS W OBWODAH EEKTYZNYH el ćwiczenia: spawdzenie podstawowych właściwości szeegowego i ównoległego obwodu ezonansowego pzy wymuszeniu napięciem sinusoidalnym, zbadanie wpływu paametów obwodu
BQR FMECA/FMEA. czujnik DI CPU DO zawór. Rys. 1. Schemat rozpatrywanego systemu zabezpieczeniowego PE
 BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
STATYKA. Cel statyki. Prof. Edmund Wittbrodt
 STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
Kwantowa natura promieniowania elektromagnetycznego
 Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Wstęp do Rachunku Prawdopodobieństwa, IIr. WMS
 Wstęp do Rachunku Prawdopodobieństwa, IIr. WMS przykładowe zadania na. kolokwium czerwca 6r. Poniżej podany jest przykładowy zestaw zadań. Podczas kolokwium na ich rozwiązanie przeznaczone będzie ok. 85
Wstęp do Rachunku Prawdopodobieństwa, IIr. WMS przykładowe zadania na. kolokwium czerwca 6r. Poniżej podany jest przykładowy zestaw zadań. Podczas kolokwium na ich rozwiązanie przeznaczone będzie ok. 85
Zadanie 1. ), gdzie 1. Zmienna losowa X ma rozkład logarytmiczno-normalny LN (, . EX (A) 0,91 (B) 0,86 (C) 1,82 (D) 1,95 (E) 0,84
 Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
Indukcja matematyczna
 Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
f = 2 śr MODULACJE
 5. MODULACJE 5.1. Wstęp Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej. Przyczyny stosowania modulacji: 1. Umożliwienie wydajnego wypromieniowania
5. MODULACJE 5.1. Wstęp Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej. Przyczyny stosowania modulacji: 1. Umożliwienie wydajnego wypromieniowania
IV. ZMIENNE LOSOWE DWUWYMIAROWE
 IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
termodynamika fenomenologiczna p, VT V, teoria kinetyczno-molekularna <v 2 > termodynamika statystyczna n(v) to jest długi czas, zachodzi
 fzka statstczna stan makroskopow układ - skończon obszar przestrzenn (w szczególnośc zolowan) termodnamka fenomenologczna p, VT V, teora knetczno-molekularna termodnamka statstczna n(v) stan makroskopow
fzka statstczna stan makroskopow układ - skończon obszar przestrzenn (w szczególnośc zolowan) termodnamka fenomenologczna p, VT V, teora knetczno-molekularna termodnamka statstczna n(v) stan makroskopow
Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa
 Z a ł» c z n i k n r 5 d o S p e c y f i k a c j i I s t o t n y c h W a r u n k Zó aw m ó w i e n i a Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 1 2 0 14 W Z Ó R U M O W Y z a w a r t a w Gd y n
Z a ł» c z n i k n r 5 d o S p e c y f i k a c j i I s t o t n y c h W a r u n k Zó aw m ó w i e n i a Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 1 2 0 14 W Z Ó R U M O W Y z a w a r t a w Gd y n
ZJAWISKO TERMOEMISJI ELEKTRONÓW
 ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 6, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
elektrostatyka ver
 elektostatka ve-8.6.7 ładunek ładunek elementan asada achowana ładunku sła (centalna, achowawca) e.6 9 C stała absolutna pawo Coulomba: F ~ dwa ładunk punktowe w póżn: F 4πε ε 8.8585 e F m ε stała ł elektcna
elektostatka ve-8.6.7 ładunek ładunek elementan asada achowana ładunku sła (centalna, achowawca) e.6 9 C stała absolutna pawo Coulomba: F ~ dwa ładunk punktowe w póżn: F 4πε ε 8.8585 e F m ε stała ł elektcna
 1 8 / m S t a n d a r d w y m a g a ń e g z a m i n m i s t r z o w s k i dla zawodu M E C H A N I K - O P E R A T O R P O J A Z D Ó W I M A S Z Y N R O L N I C Z Y C H K o d z k l a s y f i k a c j i
1 8 / m S t a n d a r d w y m a g a ń e g z a m i n m i s t r z o w s k i dla zawodu M E C H A N I K - O P E R A T O R P O J A Z D Ó W I M A S Z Y N R O L N I C Z Y C H K o d z k l a s y f i k a c j i
Analiza Matematyczna I.1
 Aalza Matematycza I. Sera, Potr Nayar Zadae. Nech a k >, k =,..., b d lczbam rzeczywstym o tym samym zaku. Udowodj,»e prawdzwa jest erówo± + a + a... + a + a + a +... + a. Czy zaªo»ee,»e lczby a k maj
Aalza Matematycza I. Sera, Potr Nayar Zadae. Nech a k >, k =,..., b d lczbam rzeczywstym o tym samym zaku. Udowodj,»e prawdzwa jest erówo± + a + a... + a + a + a +... + a. Czy zaªo»ee,»e lczby a k maj
Cząsteczki. Folie:
 Cząsteczk Fole: Jacek.Szczytko@fuw.edu.l htt://www.fuw.edu.l/~szczytko/t Hamltoa cząsteczk Hamltoa woektoowy j ektoy K-atomy < < K j j K K e e Z Z e Z M m H h h 0 0 0 4 4 4 ˆ πε πε πε ˆ H ˆ ˆ ˆ V T T H
Cząsteczk Fole: Jacek.Szczytko@fuw.edu.l htt://www.fuw.edu.l/~szczytko/t Hamltoa cząsteczk Hamltoa woektoowy j ektoy K-atomy < < K j j K K e e Z Z e Z M m H h h 0 0 0 4 4 4 ˆ πε πε πε ˆ H ˆ ˆ ˆ V T T H
Pręt nr 4 - Element żelbetowy wg PN-EN :2004
 Budynek wielorodzinny - Rama żelbetowa strona nr z 7 Pręt nr 4 - Element żelbetowy wg PN-EN 992--:2004 Informacje o elemencie Nazwa/Opis: element nr 4 (belka) - Brak opisu elementu. Węzły: 2 (x=4.000m,
Budynek wielorodzinny - Rama żelbetowa strona nr z 7 Pręt nr 4 - Element żelbetowy wg PN-EN 992--:2004 Informacje o elemencie Nazwa/Opis: element nr 4 (belka) - Brak opisu elementu. Węzły: 2 (x=4.000m,
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Coba, Mexico, August 2015
 Coba, Meico, August 015 W-6 (Jaosewic) 10 sladów Pola siłowe i ich chaaktestka Pola siłowe: poęcie i odae pól siłowch, wielkości chaakteuące pola siłowe Pola achowawce Pole gawitacne: uch w polu gawitacnm
Coba, Meico, August 015 W-6 (Jaosewic) 10 sladów Pola siłowe i ich chaaktestka Pola siłowe: poęcie i odae pól siłowch, wielkości chaakteuące pola siłowe Pola achowawce Pole gawitacne: uch w polu gawitacnm
V. WPROWADZENIE DO PRZESTRZENI FUNKCYJNYCH
 Krs na Stdach Doktoranckch Poltechnk Wrocławskej wersja: lty 007 34 V. WPROWADZENIE DO PRZESTRZENI FUNKCYJNYCH. Zbór np. lczb rzeczywstych a, b elementy zbor A a A b A, podzbór B zbor A : B A, sma zborów
Krs na Stdach Doktoranckch Poltechnk Wrocławskej wersja: lty 007 34 V. WPROWADZENIE DO PRZESTRZENI FUNKCYJNYCH. Zbór np. lczb rzeczywstych a, b elementy zbor A a A b A, podzbór B zbor A : B A, sma zborów
06 Model planowania sieci dostaw 1Po_1Pr_KT+KM
 Nr Tytuł: Autor: 06 Model plaowaa sec dostaw 1Po_1Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
Nr Tytuł: Autor: 06 Model plaowaa sec dostaw 1Po_1Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
będą niezależnymi zmiennymi losowymi z rozkładu o gęstości
 Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
TMM-2 Analiza kinematyki manipulatora metodą analityczną
 Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 7-8
 Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
A. Kanicki: Zwarcia w sieciach elektroenergetycznych ZAŁĄCZNIK NR 1. PODKŁADY DO RYSOWANIA WYKRESÓW WSKAZOWYCH
 ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q =
![v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q = v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q =](/thumbs/93/112711008.jpg) v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v v v v n 3q q q q r q = r 3q = E = E q E 3q E q = k q rq 3 k 3q r 3q 3 r q = k q rq 3 = kq 4 3 ) 4 q d b d c d d X d ± = d r = x y T d ± r ±
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v v v v n 3q q q q r q = r 3q = E = E q E 3q E q = k q rq 3 k 3q r 3q 3 r q = k q rq 3 = kq 4 3 ) 4 q d b d c d d X d ± = d r = x y T d ± r ±
(1.1) gdzie: - f = f 2 f 1 - bezwzględna szerokość pasma, f śr = (f 2 + f 1 )/2 częstotliwość środkowa.
 MODULACJE ANALOGOWE 1. Wstęp Do przesyłania sygnału drogą radiową stosuje się modulację. Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej.
MODULACJE ANALOGOWE 1. Wstęp Do przesyłania sygnału drogą radiową stosuje się modulację. Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej.
Novosibirsk, Russia, September 2002
 Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
Projekt silnika bezszczotkowego z magnesami trwałymi
 Projekt silnika bezszczotkowego z magnesami trwałymi dr inż. Michał Michna michna@pg.gda.pl 01-10-16 1. Dane znamionowe moc znamionowa P n : 10kW napięcie znamionowe U n : 400V prędkość znamionowa n n
Projekt silnika bezszczotkowego z magnesami trwałymi dr inż. Michał Michna michna@pg.gda.pl 01-10-16 1. Dane znamionowe moc znamionowa P n : 10kW napięcie znamionowe U n : 400V prędkość znamionowa n n
Bezpośrednie sterowanie momentem silnika indukcyjnego zasilanego z 3-poziomowego. przekształtnika MSI z kondensatorami o zmiennym potencjale
 Bezpośrednie sterowanie momentem silnika indukcyjnego zasilanego z 3-poziomowego przekształtnika MSI z kondensatorami o zmiennym potencjale przekształtnika MSI z kondensatorami o zmiennym potencjale 1
Bezpośrednie sterowanie momentem silnika indukcyjnego zasilanego z 3-poziomowego przekształtnika MSI z kondensatorami o zmiennym potencjale przekształtnika MSI z kondensatorami o zmiennym potencjale 1
LABORATORIUM POMIARY W AKUSTYCE. ĆWICZENIE NR 4 Pomiar współczynników pochłaniania i odbicia dźwięku oraz impedancji akustycznej metodą fali stojącej
 LABORATORIUM POMIARY W AKUSTYCE ĆWICZENIE NR 4 Pomiar współczynników pochłaniania i odbicia dźwięku oraz impedancji akustycznej metodą fali stojącej 1. Cel ćwiczenia Celem ćwiczenia jest poznanie metody
LABORATORIUM POMIARY W AKUSTYCE ĆWICZENIE NR 4 Pomiar współczynników pochłaniania i odbicia dźwięku oraz impedancji akustycznej metodą fali stojącej 1. Cel ćwiczenia Celem ćwiczenia jest poznanie metody
+Ze (Z-1)e. Możliwe sytuacje: 1) orbita nie penetrująca kadłuba
 Atomy weloelektoowe: ekulombowsk potecał (cetaly) kedy? ektóe atomy weloelektoowe (p. alkalcze) maą elekto w śede odległ. od ąda >> ż odległośc pozostałych elektoów, el. walecyy kadłub atomu Róże stay
Atomy weloelektoowe: ekulombowsk potecał (cetaly) kedy? ektóe atomy weloelektoowe (p. alkalcze) maą elekto w śede odległ. od ąda >> ż odległośc pozostałych elektoów, el. walecyy kadłub atomu Róże stay
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
