Tablice wzorów Przygotował: Mateusz Szczygieł

Portfel złożony z wielu papierów wartościowych

Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe

Dywersyfikacja jako metoda zabezpieczania się przed ryzykiem

ywesyfkaca ako metoda zabezeczaa sę zed yzykem otfel dwuskładkowy Jedą z metod zabezeczaa sę zed yzykem est dywesyfkaca. W sytuac gdy decydet sto zed wyboem edego z klku dostęych yzykowych waatów, okazue

Laboratorium Metod Statystycznych ĆWICZENIE 2 WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI

Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze

3. Optymalizacja portfela inwestycyjnego Model Markowitza Model jednowskaźnikowy Sharpe a Model wyceny aktywów kapitałowych CAPM

3. Optymalizacja portfela inwestycyjnego Model Markowitza Model jednowskaźnikowy Sharpe a Model wyceny aktywów kapitałowych CAPM Oczekiwana stopa zwrotu portfela dwóch akcji: E(r p ) = w 1 E(R 1 ) + w

MATEMATYKA FINANSOWA - WZORY LOKATY

Stoa ocetowa Z Dysoto ateatycze D M Dysoto halowe D H MAMAYA FINANSOA - ZORY LOAY stoa ysotowa atalzacja zgoa osta z ołu atał o oesach: P Oset: ( Z P Oblczae atału a ostawe P : P P P P atalzacja zgoa złożoa

ĆWICZENIE 3 ANALIZA WSPÓŁZALEŻNOŚCI ZJAWISK MASOWYCH

Laboaoum eod aczch ĆWICZENIE 3 ANALIZA WPÓŁZALEŻNOŚCI ZJAWIK AOWCH Jedo wozące zboowość chaaezowae ą zazwcza za pomocą welu cech óe wzaeme ę wauuą. Celem aalz wpółzależośc e wedzee cz mędz badam cecham

Ó Ć Ó Ż Ó Ó Ó Ó Ż Ó Ę Ę Ę Ó Ź Ź Ę Ź Ź Ó Ź Ż Ó Ó Ę Ó Ń Ą Ó Ą Ź Ź Ó Ę Ź Ó Ż Ń Ź Ż Ż Ź Ę Ż Ł Ó Ź Ó Ń Ż Ę Ó Ź Ó Ż Ó Ć Ę Ó Ó Ó Ć Ż Ę Ę Ó ÓĘ Ż Ź Ż Ę Ó Ź Ź Ą Ó Ę Ź Ó Ź Ł Ń Ę Ę Ń Ó Ó Ę Ó Ó Ź Ż Ó Ó Ź Ź Ó Ó Ż Ó

Ę Ą Ę Ł Ł Ę ż Ł ż Ą ż ż ż ć ż ć Ł ż Ę Ą Ę Ł ż Ó ć ŚĆ Ś Ś Ń ż ż Ż Ć Ń Ę Ę ÓĘ ć ż ż Ó Ę Ó ć ć ż ż ż ż ż Ą ć Ł ż Ó ć ć Ł Ś ć Ż Ź Ś ć ć ż Ę ż ć ć ż ć Ą ż Ś Ł Ł ż ć ż ć Ą ż ć Ś ż ż ż ć ć ć ć Ć ż ć ż ć ż ż ż

STATYSTYKA PODSTAWOWE WZORY DOZWOLONE NA EGZAMINIE NA STUDIACH LICENCJACKICH

STATYSTYKA PODSTAWOWE WZORY DOZWOLONE NA EGZAMNE NA STUDACH LCENCJACKCH Oacoa zgooa zz d Maę Wczo a oda:. P. Kuz, J. Podgó: Saa. Wzo ablc. SGH, Wazaa, 8. M. Wczo: Saa. Lubę o! Zbó zadań. SGH, Wazaa 3 .

STATYSTYKA PODSTAWOWE WZORY DOZWOLONE NA EGZAMINIE NA STUDIACH LICENCJACKICH

STATYSTYKA PODSTAWOWE WZORY DOZWOLONE NA EGZAMNE NA STUDACH LCENCJACKCH Oacoa zgooa zz d Maę Wczo a oda:. P. Kuz, J. Podgó: Saa. Wzo ablc. SGH, Wazaa, 8. M. Wczo: Saa. Lubę o! Zbó zadań. SGH, Wazaa 6 .

STATYSTYKA PODSTAWOWE WZORY DOZWOLONE NA EGZAMINIE NA STUDIACH LICENCJACKICH

STATYSTYKA PODSTAWOWE WZORY DOZWOLONE NA EGZAMNE NA STUDACH LCENCJACKCH Oacoa zgotoa zz d Maę Wczo a odta:. P. Kuz, J. Podgó: Statta. Wzo tablc. SGH, Wazaa, 8. M. Wczo: Statta. Lubę to! Zbó zadań. SGH,

Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż

Ł Ł Ś Ę ź ń ź ź Ś Ę Ę Ś Ą Ś Ę Ż Ł ń Ę Ś ć ć ń ć ń ń ń ź ń Ę ź ń ń ń ź ź Ś ź ź ć ń ń ń ń Ś ć Ś ń ń Ś ź ń Ę ń Ś ź ź ź ź ź Ę Ę Ę Ś ń Ś ć ń ń ń ń ń ń Ę ń ń ń ń ć ń ń ń ń ć ń Ś ć Ł ń ń ń ć ń ć ź ń ź ć ń ń ć

Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż

Ł Ł Ś ź ń ź ź ź Ś Ł Ę Ę Ś ż Ś ń Ą Ś Ą Ł ż ż ń ż ć ż ż ż ź ż ć ź Ę Ę ń ć ż Ł ń ż ż ż Ś ż Ś ż ż ż ż ż ż ż ń ń ż ż ż ć ż ń ż ń ź ż ć ż ż ć ń ż Ę Ę ć ń Ę ż ż ń ń ź Ę ź ż ń ż ń ź ż ż ż ń ż ż ż ż ż ż ż ż ń ń

= σ σ. 5. CML Capital Market Line, Rynkowa Linia Kapitału

5 CML Catal Market Lne, ynkowa Lna Katału Zbór ortolo o nalny odchylenu standardowy zbór eektywny ozważy ortolo złożone ze wszystkch aktywów stnejących na rynku Załóży, że jest ch N A * P H P Q P 3 * B

L.Kowalski zadania ze statystyki opisowej-zestaw 5. ZADANIA Zestaw 5

L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk

Portfel. Portfel pytania. Portfel pytania. Analiza i Zarządzanie Portfelem cz. 2. Katedra Inwestycji Finansowych i Zarządzania Ryzykiem

Katedra Ietycj Faoych Zarządzaa yzykem Aalza Zarządzae Portfelem cz. Dr Katarzya Kuzak Co to jet portfel? Portfel grupa aktyó (trumetó faoych, aktyó rzeczoych), które zotały yelekcjooae, którym ależy zarządzać

będą niezależnymi zmiennymi losowymi o tym samym 2 x

Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka

ź Ł Ą Ę Ź Ę Ę Ą Ę Ę Ę Ę Ę Ź Ą Ę Ą Ź Ę Ź Ó ć Ź Ó Ę Ź Ź ć ć Ę ć Ó Ó Ę Ę Ę Ę Ó Ę Ę ć Ć Ł Ó Ź ć ć ć Ę ć Ę Ł Ź Ź Ł ć ź ź Ę ć Ś Ą ć ć Ą ć Ś Ę Ź Ę Ź Ę ć Ó Ń Ę Ś Ę ź Ź Ę Ę Ć Ę Ń Ę Ę ć Ą Ę ć Ę ć Ę Ź Ę Ć Ę ź ć

Monika Jeziorska-Pąpka Uniwersytet Mikołaja Kopernika w Toruniu. Zastosowanie progowego modelu Sharpe a w analizie szeregów rynku kapitałowego

DYNAMICZNE MODELE EKONOMETRYCZNE IX Ogólnoolske Semnaum Naukowe, 6 8 wześna 005 w Tounu Kateda Ekonomet Statystyk, Unwesytet Mkołaja Koenka w Tounu Monka Jezoska-Pąka Unwesytet Mkołaja Koenka w Tounu Zastosowane

α i = n i /n β i = V i /V α i = β i γ i = m i /m

Ćwczene nr 2 Stechometra reakcj zgazowana A. Część perwsza: powtórzene koncentracje stężena 1. Stężene Stężene jest stosunkem lośc substancj rozpuszczonej do całkowtej lośc rozpuszczalnka. Sposoby wyrażena

dr hab. Renata Karkowska 1

dr hab. Renata Karkowska 1 Miary zmienności: obrazują zmiany cen, stóp zwrotu instrumentów finansowych, opierają się na rozproszeniu ich rozkładu, tym samym uśredniają ryzyko: wariancja stopy zwrotu, odchylenie

ć Ę ó ó Ź ó ó ć ź ć ć Ś ć Ź ó Ó ó ó Ś ó ó ć ó ć Ź ź ć ó ź ć ó ź ó ó ó ó ć Ą ó ó ź ó ó ó ć ź ć ć ź ź Ś ó ó ó ć ó Ź ó ó ć ó ó ó ó Ę ó ó ź Ę ó ó ó ć ó ó ź Ć Ź ź ó ó ó ó ó ó ó óź ź ó ź ó ó ó ó ć ó ó ć ó ó

Spalanie. 1. Skład paliw. 1.1. Paliwa gazowe (1) kmol C. kmol H 2. gdzie: H. , itd. udziały molowe składników paliwa w gazie. suchym. kmol.

Salae / 1 Salae Salae jet zybko rzebegającym roceem utleaa ołączoym z ydzelaem ę ceła. Salau z reguły toarzyzy emja śatła. Podtaoym eratkam alym alach ą ęgel odór. W ale moża yróżć część alą ealy balat.

Ó Ś Ą ŚĆ Ą Ś Ś ż Ó Ą Ś Ó Ż Ó Ó ć ć ć Ó Ó Ń Ś Ó ć Ś Ó Ń Ą Ś ć Ó Ó ć Ź ć ć Ź ż Ź ć ż ć ż ż ż ż ć ć ć Ó Ó Ó ć ż ż ż Ó Ó Ó Ń ż ć ć ż ż Ż ć Ó Ó ć ć ć ć ć ż ż Ó Ó ć ć Ó Ą Ź Ź Ó Ó Ó Ń ć ż ć ż Ó ż ć Ź ć ć Ż ż

Tradycyjne mierniki ryzyka

Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%

WSPOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LABORATORIUM II PROGRAMOWANIE CELOWE, ILORAZOWE I MIN-MAX. min. min

WSPOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LABORAORIUM II PROGRAMOWANIE CELOWE, ILORAZOWE I MIN-MAX Probley prograowae celowego lorazowego to probley prograowae ateatyczego elowego, który oża sktecze zlearyzować

ń óź óź Ę ć Ą Ą ó Ę ć ć Ł Ś Ł Ą ź ó Ź ź ń ó ź ź ź ó ó ź ź ź ź ó ć ź ó ć ó Ź ź ń Ę ó Ź ź ź Ę ź ó Ź ź ź Ź ź ń Ą Ą Ę Ą Ę ć Ą Ą Ę Ą Ź Ą ź Ł Ę Ł ó ź ć ć Ę Źó ó ó ź Ś Ą ź ó ó ń ź Ę ó Ą Ś ź ó Ę ó ź ó ź ź ź ź

Statystyka opisowa. W szeregu tym prezentowana jest ilość wystąpień w próbie każdej wartości cechy.

Statystyka osowa Statystyka osowa óż sę od statystyk matematyczej tym, że óy statystyczej dotyczącej daej cechy, e wykozystuje sę do woskowaa a temat oulacj, z któej óa ta została wylosowaa, a jedye aalzuje

Przejmowanie ciepła przy kondensacji pary

d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej

Prawdopodobieństwo i statystyka r.

Prawdopodobeństwo statystya.05.00 r. Zadane Zmenna losowa X ma rozład wyładnczy o wartośc oczewanej, a zmenna losowa Y rozład wyładnczy o wartośc oczewanej. Obe zmenne są nezależne. Oblcz E( Y X + Y =

Ź ź Ę Ś Ś Ń ę ę ż Ę ż ę ż ę ż ę ż ż ę ż ż Ń ź ę ę Ę Ć ż Ź Ś ę ż ż ę ż Ź Ó ę Ź ż Ś ż ę ż Ź ę Ę Ź ż ę ę ż Ś ę ę Ó Ś ę Ę ę ę ę Ą Ę Ą Ę Ś ę ż ż Ź ę Ń Ź Ś Ś ę Ź ż Ź ź ę ć Ó ż ż Ę Ó ę ż Ń ż ę Ź ę Ź Ą ę ż ż Źę

Ćwiczenia nr 3 Finanse II Robert Ślepaczuk. Teoria portfela papierów wartościowych

Ćczea r 3 Fae II obert Ślepaczuk Teora portfela paperó artoścoych Teora portfela paperó artoścoych jet jedym z ajażejzych dzałó ooczeych faó. Dotyczy oa etycj faoych, a przede zytkm etycj dokoyaych a ryku

Arytmetyka finansowa Wykład 1 Dr Wioletta Nowak

Aytmetyka fiasowa Wykład D Wioletta Nowak Sylabus Watość ieiądza jako fukcja czasu. Oocetowaie lokaty. aitalizacja osta, złożoa z dołu i z góy, ciągła. aitalizacja zgoda i iezgoda. Rówoważość oocetowaia.

Matematyka ubezpieczeń majątkowych r.

Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady

11/22/2014 STRATEGIE MIESZANE - MOTYWACJA. ROZWAśMY PRZYKŁAD:

//4 Gry o sue zero - gry rozgrywae w strategach eszaych STRATEGIE IESZANE - OTYWACJA. ROZWAśY PRZYKŁAD: 5 DEFINICJA..6 Strategą eszaą π gracza P azyway kaŝdy rozkład prawdopodobeństwa określoy a zborze

Zarządzanie ryzykiem w przedsiębiorstwie i jego wpływ na analizę opłacalności przedsięwzięć inwestycyjnych

dr nż Andrze Chylńsk Katedra Bankowośc Fnansów Wyższa Szkoła Menedżerska w Warszawe Zarządzane ryzykem w rzedsęborstwe ego wływ na analzę ołacalnośc rzedsęwzęć nwestycynych w w w e - f n a n s e c o m

Procent prosty Gdy znamy kapitał początkowy i stopę procentową

cet psty Gdy zay aptał pczątwy stpę pcetwą F = + I aptał ńcwy, pczątwy, dset I = I = stpa pcetwa (w stsuu czy) F = ( + ) aledaze dsetwe 360/360, 365/365, 360/365, 365/360 es wyaży w latach (dla óżych esów

135 X 4000 135 X 2500 185 X

eveling diesel rzekładnia hydrostatyczna z dyferencjałami 4W ZTRY KOŁ SKRĘT eveling 135 X 4000 eveling 135 X 2500 eveling 185 X 3000 eveling eveling eveling 135 x 4000 O 2500-3000 beta 8,5 8,5 6 2080 1620

Ś Ś Ś Ś Ś Ś Ę Ą Ę ŚĘ Ę Ś ń Ę Ę Ą Ł Ż Ń Ł ć Ą ć Ł Ę Ó ć Ź ć ź ń Ń ń Ś Ą Ę Ł Ę Ą Ę ń ć ń Ź ć ń ć ń Ś ń ŚĆ ć ź Ł Ę Ę Ś Ę Ę Ę ń ŚĘ Ń Ę Ę ń ŚĘ Ę Ę Ś Ś ć ń Ę ń Ś Ę ć ć Ę Ę ć ź ć ń Ę Ń ń ć Ł Ę Ę Ę Ę ć Ę ć ć ź

GEOMETRIA PŁASZCZYZNY

GEOMETRIA PŁASZCZYZNY. Oblicz pole tapezu ównoamiennego, któego podstawy mają długość cm i 0 cm, a pzekątne są do siebie postopadłe.. Dany jest kwadat ABCD. Punkty E i F są śodkami boków BC i CD. Wiedząc,

Ł ś ą ś ż ą Ż ż ż ó ó ó ó ś ą ą Ś ą ą ó ą ś Ż ą ż ż ż ą ą Ś ą ą ą ż ś ą ó ą Ę ą ą ś ą ą ó ś ą ś Ą ż ż ą ą Ś ą Ż ą ż Ł ó ą ś ą ó ó Ę ą ą Ś ą ą ó ą ą ż ś ą ą Ę ż Ąą ą ś ą ą ą ą ś Ż ó ą ą ż ż ą ą Ś ą Ę ó

Ą Ś Ś ż Ż ć Ś Ż Ś Ń Ó Ż ć Ź ć ć Ż Ź Ś Ą Ą Ż Ś Ą ĘĄ Ś Ę ŚĘ Ę Ó Ś Ą ć Ś ź Ś ż Ż Ź ć ć ć Ą ć ć Ź ć ć ć ć Ś ć Ż ć ć Ą ć Ż ć Ż ć Ż Ż Ż ć Ż ć Ż ć Ż ż ź Ą ż ć Ż Ź Ż Ś Ż Ś Ą ż Ą Ż ź Ż ż ć Ż Ż Ą Ś Ź ć Ś ż Ź ż Ł

Zadanie 1. Rzucamy symetryczną monetą tak długo, aż w dwóch kolejnych rzutach pojawią się,,reszki. Oblicz wartość oczekiwaną liczby wykonanych rzutów.

Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer

Ł Ś Ą ó ó ó ś ó ó ś ó ó ó ó ó Ó ś ó ś ó ó ś Ó ó Ó ś ó ś ó ó ó Ź ó ó ś ó ó ó ś ó ść ó ó ó Ą ó ś ó ó ó ś śó ó ó ź ó ó ś ó Ź ś ó ć ó ś Ę Ą ó ś óź ó ó ś ó ś Ę ó Ó ź ść ó ó ś ś ś Ó ó ź ó ś Ó ó ó ó ó ó ś Ó ó

Ć ź Ą Ć ź ź Ę Ę Ę Ę Ń Ą Ę ź ź Ó Ę Ę Ć Ę Ó ź ź ź ź Ń ź ź Ę Ę Ó ź Ć Ę ź ź Ą Ć Ę Ę Ę Ą Ć Ć Ż Ż Ó Ó Ą Ą Ą Ź Ą ź Ę Ą Ę Ó Ę ź Ę Ą Ś Ń Ż Ś Ó Ó Ó Ż Ę Ę Ę Ż Ź Ę Ę Ę Ę Ę Ę Ż Ż Ę Ę Ę Ę Ę Ę Ę Ż Ż Ń Ę Ś Ę Ę ĘĘ ÓŚ Ę

2. GAZY DOSKONAŁE I PÓŁDOSKONAŁE

Gazy doskoałe ółdoskoałe /. GZY DOSKONŁE I PÓŁDOSKONŁE Gazy wystęujące w zyodze składają sę z ooej lośc cząsteczek, któe zajdują sę w cąły uchu. ząsteczk wykoują uchy taslacyje (zeeszczea ostolowe), otacyje

Rachunek prawdopodobieństwa i statystyka matematyczna. Estymacja przedziałowa parametrów strukturalnych zbiorowości generalnej

Rachek prawdopodobeńswa saysyka maemaycza Esymacja przedzałowa paramerów srkralych zborowośc geeralej Częso zachodz syacja, że koecze jes zbadae ogół poplacj pod pewym kąem p. średa oce z pewego przedmo.

www.bdas.pl Rozdział 3 Zastosowanie języka SQL w statystyce opisowej 1 Wprowadzenie

Rozdzał moogaf: 'Bazy Daych: Nowe Techologe', Kozelsk S., Małysak B., Kaspowsk P., Mozek D. (ed.), WKŁ 007 Rozdzał 3 Zastosowae języka SQL w statystyce opsowej Steszczee. Relacyje bazy daych staową odpowede

AKADEMIA MORSKA W SZCZECINIE

AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych

dev = y y Miary położenia rozkładu Wykład 9 Przykład: Przyrost wagi owiec Odchylenia Mediana próbkowa: Przykłady Statystyki opisowe Σ dev i =?

Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych

Symulacja czasu ładowania zasobnika C.W.U

Por Prybyc Syulacja casu łaoaa asobka C.W. Syulacja casu łaoaa asobka C.W. Do cgo służy Progra: Progra służy o sybkgo okrśla casu łaoaa asobka C.W. ry ałożoych arukach brgoych aruk brgo fuj rogra użykok

COLLEGIUM MAZOVIA INNOWACYJNA SZKOŁA WYŻSZA WYDZIAŁ NAUK STOSOWANYCH. Kierunek: Finanse i rachunkowość. Robert Bąkowski Nr albumu: 9871

COLLEGIUM MAZOVIA INNOWACYJNA SZKOŁA WYŻSZA WYDZIAŁ NAUK STOSOWANYCH Kieruek: Fiase i rachukowość Robert Bąkowski Nr albumu: 9871 Projekt: Badaie statystycze cey baryłki ropy aftowej i wartości dolara

Obliczanie średniej, odchylenia standardowego i mediany oraz kwartyli w szeregu szczegółowym i rozdzielczym?

Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)

WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA

WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA Powtórka Powtórki Kowiariancja cov xy lub c xy - kierunek zależności Współczynnik korelacji liniowej Pearsona r siła liniowej zależności Istotność

WIELOWYMIAROWE REGUŁY ASOCJACJI W MODELOWANIU TENDENCJI ROZWOJOWYCH MSP

KATARZYNA BŁASZCZYK BOGDAN RUSZCZAK Poltecha Opolsa WIELOWYMIAROWE REGUŁY ASOCJACJI W MODELOWANIU TENDENCJI ROZWOJOWYCH MSP Wstęp Esploraca daych (ag. data g) zaue sę efetywy zadowae ezaych dotychczas

Analiza wariancji w analizie regresji - weryfikacja prawdziwości przyjętego układu ograniczeń Problem Przykłady

Analiza wariancji w analizie regresji - weryfikacja prawdziwości przyjętego układu ograniczeń 1. Problem ozwaŝamy zjawisko (model): Y = β 1 X 1 X +...+ β k X k +Z Ηβ = w r Hipoteza alternatywna: Ηβ w r

Wynik finansowy transakcji w momencie jej zawierania jest nieznany z uwagi na zmienność ceny przedmiotu transakcji, czyli instrumentu bazowego

.Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je

Ze względu na sposób zapisu wielkości błędu rozróżnia się błędy bezwzględne i względne.

Katedra Podsta Systemó Techczych - Podstay metrolog - Ćczee 3. Dokładość pomaró, yzaczae błędó pomaroych Stroa:. BŁĘDY POMIAROWE, PODSTAWOWE DEFINICJE Każdy yk pomaru bez określea dokładośc pomaru jest

y Y : r R ; n Dobór zmiennych objaśniających do modelu ekonometrycznego Oznaczenia: Y - zmienna objaśniana, Postać macierzowa:

Dobó zec objaśającc do odeu eooetczego Ozaczea Y - zea objaśaa,,.,, - potecjae zee objaśające. Postać acezowa Y,. Współcz oeacj R, R, gdze ;,.,, ; ;,.,,, Postuat dotczące zec objaśającc Wso pozo zeośc

Statystyka Wykład 3 Adam Ćmiel A3-A4 311a

styaca uktowa Podstawowe oęca estyac uktowe Nech B P={P :} będze zestzeą statystyczą. Na odstawe obsewac oszacować g Y gdze g: Y est zaą fukcą. Watość g est ezaa gdyż e zay. Rozwązae tego obleu będze ewa

Ł Ł Ó Ś Ż Ł Ń Ż Ż ć Ż Ł Ż Ż Ż Ż Ż Ż Ż Ż Ż Ż Ż Ł ć Ż Ż ć ć Ź Ł Ż Ż Ż ć ź Ż ń Ż Ż Ż Ż ć ń ć ń ć Ł Ż ć Ż Ł Ś ŻŻ Ł Ż Ń Ł ź Ź Ż Ź Ł Ż Ł Ł Ń ć Ó Ż Ń Ń Ł ź ź Ż Ż Ż Ś Ć Ż Ć Ł Ł Ł Ż Ż Ś ŚĆ Ś Ś ć ć Ż Ż ŚĆ Ś Ś ŚĆ

EKONOMETRIA. Liniowy model ekonometryczny (regresji) z jedną zmienną objaśniającą

EKONOMETRIA Tema wykładu: Liiowy model ekoomeryczy (regresji z jedą zmieą objaśiającą Prowadzący: dr iż. Zbigiew TARAPATA e-mail: Zbigiew.Tarapaa Tarapaa@isi.wa..wa.edu.pl hp:// zbigiew.arapaa.akcja.pl/p_ekoomeria/

Korelacja i regresja. Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych. Wykład 12

Wykład Korelacja i regresja Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Wykład 8. Badaie statystycze ze względu

Zarządzanie portfelem inwestycyjnym

Zarządzanie portfelem inwestycyjnym Dr hab. Renata Karkowska Wykład 3, 4 Renata Karkowska, Wydział Zarządzania 1 Wykład 3 - cel 3. Konstrukcja i zarządzanie portfelem inwestycyjnym 1. Cele i ograniczenia

Ś Ś Ł ć Ś ć Ś ć Ż Ż Ż Ę ć Ż Ś Ś Ś Ś Ś ć Ę Ł Ń ć ć Ź ć Ś Ż Ż Ą Ż Ż Ę Ś ć Ł Ż Ż Ż Ę Ś Ś Ś Ś Ż Ż Ę Ż Ż Ś Ż ŚĘ Ż ć Ż ć Ł Ę Ż Ń Ń ć ć Ż Ż Ż Ń Ę Ę Ź Ż Ż Ż ź Ż Ż Ę ź Ż Ń Ę Ż Ł Ż Ż Ł Ż ź Ś Ś ź Ę ź Ś Ę ź Ż ć Ż

Prawdopodobieństwo i statystyka r.

Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta

Ą Ż Ą Ś ĄŻ ź Ś Ś ż Ł Ś Ą Ą Ś ż ż Ł Ż ż ż Ą Ś Ś ż Ś Ż ż ż Ż Ó ż Ś ż Ż ż Ś ż Ż ź Ż Ż Ł Ą Ł ż Ż Ś Ś Ś Ś Ż Ż Ś Ż ż Ó Ż ż Ś Ó Ą ź Ć Ż Ą ź Ś ż Ć ż Ł Ż Ż ż ż Ś ź Ó ż Ż Ć Ż Ó ż ż Ą Ś ż ż Ó Ł Ś ż ż ż ż Ż ż Ś ź

BQR FMECA/FMEA. czujnik DI CPU DO zawór. Rys. 1. Schemat rozpatrywanego systemu zabezpieczeniowego PE

BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.

DYNAMIKA. Dynamika jest działem mechaniki zajmującym się badaniem ruchu ciał z uwzględnieniem sił działających na ciało i wywołujących ten ruch.

DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża

PROJEKT I WALIDACJA URZĄDZEŃ POMIAROWYCH

M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X P R O J E K T I W A L I D A C J A U R Z Ą D Z E P O M I A R O W Y C H a S I Y W L I N I E I K Ą T A W Y C H Y L E N I A L I

W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:

Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,

Ę ĘŃ ć Ą Ś ć ć ć ć ć ć Ń Ł ć Ń Ą ć ć Ę ć Ń ć Ń ć ź Ę Ń ć Ę ć ć ć ć ź ć ć ć ć ć ĄĄ Ę Ą ź ć Ą ć ć ź ź Ń Ą Ą Ę Ę Ę ć źć Ń Ą Ń ć Ł ź ź ć ć Ł ć Ę ć Ń Ń ź Ę ź ć Ę Ś Ń ć Ą Ń Ń Ń Ą Ą ź Ą Ę Ł ć Ń Ń ć ź Ń Ą Ę Ę

M{ZD{ CX-5 zoo} z 202670 MME_CX-5_COVER_14R1_V2.indd 1 09/01/2014 16:52:10

BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ

Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB WYKŁAD 2 BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB Przkład.

Zarządzanie ryzykiem. Lista 3

Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa

f f x f, f, f / / / METODA RÓŻNIC SKOŃCZONYCH niech N = 2 (2 równania różniczkowe zwyczajne liniowe I-rz.) lub jedno II-rzędu

METODA RÓŻIC SKOŃCZOYCH (omówee a przykładze rówań lowych) ech ( rówaa różczkowe zwyczaje lowe I-rz.) lub jedo II-rzędu f / / p( x) f / + q( x) f + r( x) a x b, f ( a) α, f ( b) β dea: a satce argumetu

MODELE OBIEKTÓW W 3-D3 część

WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego

Modelowanie niepewności przy użyciu przybliżonych miar prawdopodobieństwa

Modelowae epewośc pzy użycu pzyblżoych ma pawdopodobeństwa d ż. Mosław Kweselewcz Wydzał Elektotechk utomatyk Kateda utomatyk Gdańsk, lstopad 998 . Wpowadzee Tadycyje do modelowaa epewośc stosoway był

Równania różniczkowe. y xy (1.1) x y (1.2) z xyz (1.3)

ownn oznczkowe Równn óżnczkowe. Wstę Równne óżnczkow nzw ównne zwejące funkcje newdoe zenne nezleżne oz ocodne funkcj newdoc lu c óżnczk. Pzkłd d 5 d d sn d. d d e d d d. z z z z. ównne óżnczkowe zwczjne

Projekt 3 Analiza masowa

Wydzał Mechaczy Eergetyk Lotctwa Poltechk Warszawskej - Zakład Saolotów Śgłowców Projekt 3 Aalza asowa Nejszy projekt składa sę z dwóch częśc. Perwsza polega projekce wstępy wętrza kaby (kadłuba). Druga

F : R 0;1 rozkład prawdopodobieństwa stopy zwrotu.

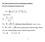Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu

Novosibirsk, Russia, September 2002

Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego

1. Relacja preferencji

dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x

Zawansowane modele wyborów dyskretnych

Zawansowane modele wyborów dyskretnych Jerzy Mycielski Uniwersytet Warszawski grudzien 2013 Jerzy Mycielski (Uniwersytet Warszawski) Zawansowane modele wyborów dyskretnych grudzien 2013 1 / 16 Model efektów

Stacjonarność Integracja. Integracja. Integracja

Biały szum AR(1) Słaba stacjonarność Szereg czasowy nazywamy słabo (wariancyjnie) stacjonarnym jeżeli: Biały szum AR(1) Słaba stacjonarność Szereg czasowy nazywamy słabo (wariancyjnie) stacjonarnym jeżeli:

Statystyka Wzory I. Analiza struktury

Uiwersytet Ekooiczy w Katowicach Wzory I. Aaliza struktury 1. Miary tedecji cetralej (średie, przecięte Średia arytetycza Dla sz. ważoego Dla sz. ważoego dla z. ciągłej Dla szeregu wyliczającego: dla zieej

teorii optymalizacji

Poltechka Gdańska Wydzał Oceaotechk Okrętowctwa St. II stop. se. I Podstawy teor optyalzac wykład 7 M. H. Ghae Ma 5 Podstawy teor optyalzac Oceaotechka II stop. se. I 5 Podstawy teor optyalzac Oceaotechka

ρ (6) przy czym ρ ij to współczynnik korelacji, wyznaczany na podstawie następującej formuły: (7)

PROCES ZARZĄDZANIA PORTFELEM PAPIERÓW WARTOŚCIOWYCH WSPOMAGANY PRZEZ ŚRODOWISKO AUTOMATÓW KOMÓRKOWYCH Ageszka ULFIK Streszczee: W pracy przedstawoo sposób zarządzaa portfelem paperów wartoścowych wspomagay

POLE MAGNETYCZNE W PRÓŻNI - CD. Zjawisko indukcji elektromagnetycznej polega na powstawaniu prądu elektrycznego w

POL AGNTYCZN W PRÓŻNI - CD Indukcja elektomagnetyczna Zjawsko ndukcj elektomagnetycznej polega na powstawanu pądu elektycznego w zamknętym obwodze wskutek zmany stumena wektoa ndukcj magnetycznej. Np.

FINANSE II. Model jednowskaźnikowy Sharpe a.

ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy

BADANIE STATYSTYCZNEJ CZYSTOŚCI POMIARÓW

INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII RODUKCJI I TECHNOLOGII MATERIAŁÓW OLITECHNIKA CZĘSTOCHOWSKA RACOWNIA DETEKCJI ROMIENIOWANIA JĄDROWEGO Ć W I C Z E N I E N R J-6 BADANIE STATYSTYCZNEJ CZYSTOŚCI OMIARÓW

Wykład 8. Prawo Hooke a

Wykład 8 Pawo Hooke a Pod działaiem apężeń ciało tałe zmieia wó kztałt. Z doświadczeń wyika, że eżeli wielkość apężeia et mieza od pewe watości, zwae gaicą pężytości, to odkztałceie et odwacale i po uuięciu

Trzeba pokazać, że dla każdego c 0 c Mc 0. ) = oraz det( ) det( ) det( ) jest macierzą idempotentną? Proszę odpowiedzieć w

Zad Dae są astępujące macierze: A =, B, C, D, E 0. 0 = = = = 0 Wykoaj astępujące działaia: a) AB, BA, C+E, DE b) tr(a), tr(ed), tr(b) c) det(a), det(c), det(e) d) A -, C Jeśli działaia są iewykoale, to

Matematyka ubezpieczeń majątkowych r. t warunkowo niezależne i mają (brzegowe) rozkłady Poissona:

Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t