AGNIESZKA LISOWSKA. Efektywne kodowanie obrazów z wykorzystaniem falek geometrycznych
|
|
|
- Kornelia Skiba
- 8 lat temu
- Przeglądów:
Transkrypt
1 Systemy wspomagaa decyzj Materały Koferecj Naukowej, Zakopae 8-10 XII 2003 AGNIESZKA LISOWSKA Istytut Matematyk, Uwersytet Śląsk, Efektywe kodowae obrazów z wykorzystaem falek geometryczych 1. Wstęp We współczesym śwece problem kompresj obrazów cyfrowych staow jede z stotejszych problemów zwązaych z teorą sygałów. Mejsza objętość daych uzyskaa w wyku ch kompresj pozwala e tylko a zmejszee kosztów ch przechowywaa, lecz róweŝ skraca czas potrzeby a przesłae tych daych przez seć, a przykład Iteret czy Itraet. Isteje wele metod aproksymacj sygałów wykorzystywaych w kodowau obrazów. Jeda z ajstarszych teora szeregów Fourera wprowadzoa w 1807 roku przez J. Fourera [12] pozwala a efektywe przyblŝae sygałów za pomocą fukcj susodalych. Teora ta pozwala a wykrywae zma sygału w czase cechuje sę dobrą lokalzacją. Została juŝ dogłębe dotychczas zbadaa ewetuale moŝa juŝ tylko szukać owych dzedz jej zastosowań. Koleją teorą, która osągęła duŝy sukces z powodu swej duŝej uŝyteczośc jest teora falek, którą zapoczątkował A. Haar w 1910 roku wprowadzając fukcję zwaą późej falką Haara [8]. Od tego czasu teora ta została dobrze pozaa rozwęta ewoluowała w welu róŝych kerukach. W welu zastosowaach przewyŝsza oa moŝlwośc teor Fourera gdyŝ pozwala a wychwytywae zma w sygałach e tylko w czase, lecz róweŝ w skal [12]. Pozwala to a dokładejszą aalzę sygału, a co za tym dze prowadz do lepszych współczyków kompresj. Teora falek w przypadku aalzy sygałów jedowymarowych e ma sobe rówych. Jedak w przypadku obrazów radz sobe eco gorzej. PoewaŜ, o le charakteryzuje sę oa duŝą skuteczoścą w wychwytywau ecągłośc puktowych, to w przypadku ecągłośc lowych występujących często w obrazach w postac krawędz e speła juŝ postawoych wymagań. Wyka to z faktu, Ŝe ajczęścej stosowae metody dwuwymarowe są separowale zatem e potrafą wychwycć geometryczych cech obrazu. Jako remedum a przedstawoy problem powstała obszera teora falek geometryczych, w szczególośc wedgeletów beamletów. Została oa zapoczątkowaa przez D. Dooho w 1999 roku [4]. Okazuje sę, Ŝe pozwala oa a dokładejszą aalzę obrazów Ŝ w przypadku klasyczych metod falkowych. Wyka to z faktu, Ŝ teora ta umoŝlwa wychwytywae zma w obraze e tylko w czase skal, lecz róweŝ jeszcze w keruku. Pozwala to a wychwycee cech geometryczych obrazu, jakm są krawędze. Jest to fakt e bez zaczea, poewaŝ to właśe krawędze osą ajwęcej formacj o obraze [6]. Dotychczasowe uŝyce falek geometryczych wedgeletów beamletów polegało a aproksymowau obrazów z uŝycem prostych krawędz. W ejszym artykule zapropoowao wykorzystae róweŝ ych krzywych, które moŝa opsać za pomocą dodatkowego parametru, co poprawa jakość rekostruowaego obrazu. Fakt te został potwerdzoy poprzez przeprowadzoe badaa. 2. Wedgelet, beamlet falk geometrycze Na teorę falek geometryczych moŝa popatrzeć jako a pewego rodzaju uogólee klasyczej teor falek. Zwązaych z ą jest wele pojęć, które prowadzą w róŝych kerukach. Do ajczęścej uŝywaych zalcza sę dwe grupy wedgelets beamlets [4, 5] oraz curvelets 186
2 A. LISOWSKA, Efektywe kodowae obrazów z wykorzystaem falek geometryczych 187 rdgelets [1-3]. Wszystke te falk prowadzą do eco ego stylu kodowaa obrazów cechują sę róŝym zastosowaam. Jedak, jak pokazują lcze badaa [3, 11], wszystke oe pozwalają a bardzej efektywe kodowae obrazów z puktu wdzea kompresj, Ŝ stadardowe metody falkowe. Posadają teŝ wększe moŝlwośc róŝych zastosowań [3, 7, 9, 10]. W dalszej częśc artykułu przedstawoe zostaą jedye falk z perwszej z wymeoych grup. Ustalmy dowoly bary obraz o wymarach N N, gdze N=2 k, k N. Rozpatrzmy dowoly podzał czwórkowy (ag. quadtree partto) takego obrazu. Podzałow temu odpowada drzewo czwórkowe, w którego węzłach przedstawać moŝa poszczególe elemety podzału czwórkowego obrazu. Elemetam takego podzału są kwadraty S, j o rozmarach N N 2 2 gdze = 0,...,lg N (deksowae pozomów drzewa) j= 0,..., 4 1 (deksowae kwadratów w obrębe pozomu). Ustalmy dowoly kwadrat S, j z podzału czwórkowego. Beamletem azywamy ezdegeeroway (tz. e leŝący całkowce a brzegu kwadratu) odcek b łączący dowole dwa pukty a brzegu tego kwadratu (patrz Rys.1). Jego połoŝee określają współrzęde ( v1, v 2). Natomast wedgeletem azywamy fukcję charakterystyczą obszaru wyzaczoego przez beamlet b daą wzorem 1, dla y b( x) w( x, y) =, x, y S. (1) 0, dla y> b( x) Na Rys. 1 przedstawoo w powększeu przykładowy elemet podzału czwórkowego dowolego obrazu barego prezetujący powyŝsze pojęca. V 1 Beamlet b Wedgelet w V 2 Rysuek 1. Grafcza reprezetacja falek beamlet wedgelet. W praktyczych zastosowaach stosuje sę często eco ą formę parametryzacj opartą a beguowym układze współrzędych (patrz Rys. 2). Wtedy zarówo beamlet jak wedgelet jest jedozacze wyzaczoy przez kąt θ zawarty mędzy ormalą do beamleta a kerukem pozomym; oraz odległość r beamleta od środka rozpatrywaego kwadratu. Dodatkowo do parametryzacj wedgeleta uŝywa sę wartośc h 1 h 2 pozwalających a kodowae obrazów róweŝ w skal szarośc, a e tylko barych, jak dotychczas zaprezetowao. Rysuek 2. Parametryzacja falek beamlet wedgelet.
3 188 Systemy wspomagaa decyzj Sparametryzowae w powyŝszy sposób falk pozwalają a zdefowae odpowedch słowków, które wykorzystywae są w kodowau obrazów. Defcja 1. Słowkem beamletów azywamy zbór słowkem wedgeletów azywamy zbór B= { b = b ( r, θ ) : = 0,...,lg N, j= 0,..., 4 1} ; (2) j W = { w = w ( r, θ, h, h ) : = 0,...,lg N, j= 0,...,4 1}, (3) j 1 2 gdze r θ π. lg N 1/ 2 [0,2 ), [0, ), h1, h2 {0,...,255} ZauwaŜmy, Ŝe zdefoway powyŝej słowk beamletów zawera odck o róŝej lokalzacj, skal oretacj. Podobą własoścą cechuje sę słowk wedgeletów. Taka róŝorodość pozwala a dokładą aproksymację dowolego obrazu. Słowk te moŝe zostać uŝyty do przeprowadzea aalzy sytezy obrazu w astępujący sposób. Defcja 2. Aalza wedgeletowa obrazu f wyraŝa sę wzorem dla wszystkch w W, 0< W. Defcja 3. Syteza wedgeletowa wyraŝa sę wzorem α = f, w (4) W f ( x, x ) = α w ( x, x ). (5) = 1 W przypadku teor beamletów stosowae są aalogcze defcje aalzy sytezy beamletowej. Jedya róŝca w kodowau obrazów mędzy beamletam wedgeletam polega a tym, Ŝe w przypadku tych perwszych kodujemy jedye same krawędze obrazu, podczas gdy te druge pozwalają a kodowae dowolych obrazów. Obe rodzy falek cechują sę teŝ róŝym zastosowaam w przetwarzau obrazów. 3. Uogólee wedgeletów beamletów Teora dotycząca falek geometryczych prezetowaa dotychczas w lteraturze dotyczy jedye przypadków, w których zakłada sę, Ŝe beamlety wedgelety bazują jedye a prostych odckach. Z praktyczego puktu wdzea take uproszczee powoduje, Ŝe w przypadku krawędz obecych w obrazach, które e są prostym, zbyt wele falek jest potrzebych do ch aproksymacj (ajbardzej sugestywy przykład staow okrąg). W zwązku z tym aturale wydało sę uogólee tej teor do przypadków z krawędzam, które są fragmetam dowolych łuków (okręgów, parabol bądź ych). NaleŜy pamętać jedak, Ŝe powy to być krzywe, które moŝa opsać za pomocą tylko jedego dodatkowego parametru. Wprowadzee ch wększej lczby pocąga za sobą zacze zwększee słowka, co powoduje wydłuŝee czasu dzałaa algorytmu zwększa lość formacj potrzebych do zakodowaa obrazu. Rozpatrzmy zatem parametryzację falek przedstawoą w poprzedm rozdzale (Rys. 2). Dodajemy do ej kolejy parametr d (patrz Rys. 3), który ozacza odległość pomędzy puktam przecęca ormalej do prostego beamletu z prostym zakrzywoym beamletem
4 A. LISOWSKA, Efektywe kodowae obrazów z wykorzystaem falek geometryczych 189 odpowedo. ZauwaŜmy, Ŝe parametr d określa am stopeń zakrzywea łuku w praktyce jest o dość mały. MoŜa go zatem zakodować za pomocą stosukowo ewelkej lczby btów. Rysuek 3. Parametryzacja uogóloych falek beamlet wedgelet. Mając tak sparametryzowae uogóloe beamlety wedgelety moŝemy zdefować odpowadające m uogóloe słowk podobe jak w Defcj 1. Defcja 4. Uogóloym słowkem beamletów azywamy zbór ) ) ) B= { b = b ( r, θ, d) : = 0,...,lg N, j= 0,..., 4 1} ; (6) j uogóloym słowkem wedgeletów azywamy zbór ) ) ) W = { w = w ( r, θ, d, h, h ) : = 0,...,lg N, j= 0,..., 4 1}, (7) j 1 2 gdze r d θ π. lg N 1/ 2, [0,2 ), [0, ), h1, h2 W przypadku uogóloych słowków falek defcje aalzy sytezy obrazów są aalogcze jak w przypadku klasyczych beamletów wedgeletów. W praktyczych zastosowaach bardzo często parametry wedgeletów wyzaczae są za pomocą aproksymacj lowej metodą ajmejszych kwadratów. Pozwala to a uzyskae moŝlwe ajlepszej aproksymacj obrazu a zadaym pozome dekompozycj. W przypadku uogóloych wedgeletów moŝa zastosować metodę aproksymacj kwadratowej, a ta jak wadomo daje mejsze błędy przyblŝea. Zatem przytoczoe fakty pozwalają a sformułowae astępującej uwag. Uwaga. Przyjmjmy astępujące ozaczea: f kodoway obraz, f m aproksymacja obrazu za pomocą m wedgeletów, f) m aproksymacja obrazu za pomocą m uogóloych wedgeletów, wtedy gdze MSE ) MSE, (8) fm MSE) ozacza średokwadratowy błąd aproksymacj uogóloym wedgeletam, f m MSE f m ozacza błąd aproksymacj wedgeletam. Prawdzwe jest róweŝ stwerdzee astępujące. Do rekostrukcj obrazu o tej samej jakośc, potrzeba jest mejsza lczba uogóloych wedgeletów w stosuku do lczby klasyczych wedgeletów. Pozwala am to zauwaŝyć, Ŝe w przypadku kodowaa obrazów zawerających duŝo zakrzywoych krawędz moŝlwe jest uzyskae wększego stopa kompresj obrazu. Istote, arzuty zwązae z zakodowaem dodatkowego parametru (określającego stopeń zakrzywea fm
5 190 Systemy wspomagaa decyzj łuku) zostaą zwelowae z dodatkową korzyścą ogóla lczba btów potrzebych do zakodowaa obrazu będze mejsza w przypadku uŝyca uogóloych wedgeletów. Z przeprowadzoych badań wyka, Ŝe korzyśc te mogą sęgać awet 15%. 4. Zastosowae wedgeletów do kodowaa obrazów W ejszym rozdzale przedstawoa zostae dea kodowaa obrazów z wykorzystaem owej rodzy falek. Dla uproszczea rozwaŝań przyjmjmy, Ŝe rozpatrujemy obrazy bare, uogólea do skal szarośc oraz do model barwych moŝa uzyskać w dość aturaly sposób. Na Rys. 4(a) zaprezetoway został przykład barego obrazu. Na kolejych, od (b) do (f), zajdują sę coraz dokładejsze a kolejych pozomach dekompozycj (od perwszego do pątego) aproksymacje przykładowego obrazu. Wdzmy, Ŝe za kaŝdym razem uzyskujemy coraz drobejszy podzał czwórkowy obrazu, a co za tym dze, coraz lepszą jego jakość. To, czy kolejy kwadrat zostae podzeloy a koleje cztery, zaleŝy od tego, czy błąd aproksymacj mędzy orygalym obrazem w obrębe zadaego kwadratu a przyblŝającym go wedgeletem jest odpowedo mały (poŝej pewej zadaej wartośc progowej w przypadku kompresj stratej, bądź rówy 0 w przypadku dokładej rekostrukcj). (a) (b) (c) (d) (e) (f) Rysuek 4. Orygaly obraz (a), oraz jego koleje przyblŝea wedgeletam (b)-(f). Dla porówaa a Rys. 5 przedstawoo przykładowe koleje przyblŝea (od drugego do czwartego pozomu dekompozycj) tego samego obrazu z wykorzystaem uogóloych wedgeletów. Porówując oba rodzaje aproksymacj wdzmy, Ŝe ta druga daje am bardzej zwartą reprezetację obrazu (do zakodowaa została uŝyta mejsza lczba wedgeletów) oraz lepszą jakość przyblŝea (potwerdzoą wartoścam PSNR).
6 A. LISOWSKA, Efektywe kodowae obrazów z wykorzystaem falek geometryczych 191 (a) (b) (c) Rysuek 5. Koleje przyblŝea uogóloym wedgeletam. Jak juŝ wspomao wcześej, parametry wedgeletów kodowaego obrazu przechowuje sę w drzewach czwórkowych. Podobe jak w przypadku tradycyjych falek wartośc te zapsuje sę jako róŝce pomędzy parametram z kolejych pozomów dekompozycj. Take welorozdzelcze podejśce pozwala a uzyskae progresywego stadardu kompresj, co jest e bez zaczea, a przykład w przypadku przesyłaa daych przez seć. 5. Podsumowae Przedstawoe w artykule beamlety wedgelety oraz ch przykładowe zastosowae w kodowau obrazów staową tylko ewelką część teor dotyczącej owej rodzy falek geometryczych. Jedak juŝ zaprezetowae przykłady pokazują jak skuteczym arzędzem w kodowau, w szczególośc kompresj, obrazów są falk geometrycze. Zaprezetowae w tym artykule uogólee rozszerza dodatkowo ch moŝlwośc poprawa skuteczość kodowaa. Poza, przedstawoym w artykule, przykładem kodowaa obrazów dla beamletów wedgeletów moŝa wskazać całą gamę ych zastosowań. Wedgelety są z powodzeem stosowae w takch dzedzach przetwarzaa obrazów jak segmetacja, bądź teŝ są wykorzystywae do usuwaa szumów z obrazów. Natomast beamlety są uŝywae róweŝ w połączeu z ym strukturam, Ŝ przedstawoe w artykule drzewa czwórkowe, maowce grafam ajblŝszych sąsadów. W oparcu o programowae dyamcze grafy beamletowe wykorzystywae są, a przykład, do ekstrakcj formacj z obrazów o bardzo duŝym stopu zaszumea. 6. Lteratura [1] Cadès E., What s a Curvelet?, Notces of the Amerca Mathematcal Socety, Vol. 50, No. 11, November, pp , [2] Cadès E., Dooho D., Curvelets A Surprsgly Effectve Noadaptve Represetato For Objects wth Edges, Curves ad Surfaces Fttg, A. Cohe, C. Rabut, ad L. L. Schumaker, Eds. Sat-Malo: Vaderblt Uversty Press, [3] Do M. N., Drectoal Multresoluto Image Represetatos, Ph.D. Thess, Departmet of Commucato Systems, Swss Federal Isttute of Techology Lausae, November, [4] Dooho D. L., Wedgelets: Nearly-mmax estmato of edges, Aals of Stat., Vol. 27, pp , [5] Dooho D. L. Huo X., Beamlets ad Multscale Image Aalyss, Lecture Notes Computatoal Scece ad Egeerg, Multscale ad Multresoluto Methods, Sprger, [6] Kaser P. K., The Joy of Vsual Percepto,
7 192 Systemy wspomagaa decyzj [7] Ndl U., Nowak R., Fgueredo M., Codg Theoretc Approach to Image Segmetato, IEEE Iteratoal Coferece o Image Processg, October, [8] Reskoff H., Wells R. O. Jr, Wavelet Aalyss, Sprger-Verlag, New York, [9] Romberg J., Wak M., Barauk R., Approxmato ad Compresso of Pecewse Smooth Images Usg a Wavelet/Wedgelet Geometrc Model, IEEE Iteratoal Coferece o Image Processg, September, [10] Todorovc S., Nechyba M. C., Mult-resoluto Lear Dscrmat Aalyss: Effcet Extracto Of Geometrcal Structures I Images, to appear Proc. IEEE It. Cof. o Image Processg, Barceloa, September, [11] Wak M., Romberg J., Cho H., Barauk R., Geometrc Tools for Image Compresso, Aslomar Coferece o Sgals, Systems, ad Computers, Pacfc Grove, CA, November, [12] Walker J. S., Fourer Aalyss ad Wavelet Aalyss, Notces of the Amerca Mathematcal Socety, Vol. 44, No 6, pp , Jue/July, 1997.
Permutacje. } r ( ) ( ) ( ) 1 2 n. f = M. Przybycień Matematyczne Metody Fizyki I Wykład 2-2
 Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
TMM-2 Analiza kinematyki manipulatora metodą analityczną
 Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
5. OPTYMALIZACJA NIELINIOWA
 5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA. Adrian Kapczyński Maciej Wolny
 KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
Jego zależy od wysokości i częstotliwości wypłat kuponów odsetkowych, ceny wykupu, oczekiwanej stopy zwrotu oraz zapłaconej ceny za obligację.
 Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
PŁASKA GEOMETRIA MAS. Środek ciężkości figury płaskiej
 PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
Współczynnik korelacji rangowej badanie zależności między preferencjami
 Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
Pomiary parametrów napięć i prądów przemiennych
 Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
Podstawy analizy niepewności pomiarowych (I Pracownia Fizyki)
 Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
 ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
Wyznaczanie oporu naczyniowego kapilary w przepływie laminarnym.
 Wyzaczae oporu aczyowego kaplary w przepływe lamarym. I. Przebeg ćwczea. 1. Zamkąć zawór odcający przewody elastycze a astępe otworzyć zawór otwerający dopływ wody do przewodu kaplarego. 2. Ustawć zawór
Wyzaczae oporu aczyowego kaplary w przepływe lamarym. I. Przebeg ćwczea. 1. Zamkąć zawór odcający przewody elastycze a astępe otworzyć zawór otwerający dopływ wody do przewodu kaplarego. 2. Ustawć zawór
System finansowy gospodarki
 System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
UOGÓLNIONA ANALIZA WRAŻLIWOŚCI ZYSKU W PRZEDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW. 1. Wprowadzenie
 B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
3. OPTYMALIZACJA NIELINIOWA
 Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
FINANSE II. Model jednowskaźnikowy Sharpe a.
 ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
Elementy arytmetyki komputerowej
 Elemety arytmetyk komputerowej cz. I Elemety systemów lczbowych /materał pomocczy do wykładu Iformatyka sem II/ Sps treśc. Wprowadzee.... Wstępe uwag o systemach lczbowych... 3. Przegląd wybraych systemów
Elemety arytmetyk komputerowej cz. I Elemety systemów lczbowych /materał pomocczy do wykładu Iformatyka sem II/ Sps treśc. Wprowadzee.... Wstępe uwag o systemach lczbowych... 3. Przegląd wybraych systemów
Miary statystyczne. Katowice 2014
 Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Statystyczne charakterystyki liczbowe szeregu
 Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Podstawowe zadanie statystyki. Statystyczna interpretacja wyników eksperymentu. Zalety statystyki II. Zalety statystyki
 tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
Regresja REGRESJA
 Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
STATYKA. Cel statyki. Prof. Edmund Wittbrodt
 STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
ZAJĘCIA NR 3. loga. i nosi nazwę entropii informacyjnej źródła informacji. p. oznacza, Ŝe to co po im występuje naleŝy sumować biorąc za i
 ZAJĘCIA NR Dzsaj omówmy o etro, redudacj, średej długośc słowa odowego o algorytme Huffmaa zajdowaa odu otymalego (od ewym względam; aby dowedzeć sę jam doczeaj do ońca). etro JeŜel źródło moŝe adawać
ZAJĘCIA NR Dzsaj omówmy o etro, redudacj, średej długośc słowa odowego o algorytme Huffmaa zajdowaa odu otymalego (od ewym względam; aby dowedzeć sę jam doczeaj do ońca). etro JeŜel źródło moŝe adawać
Matematyka dyskretna. 10. Funkcja Möbiusa
 Matematyka dyskreta 10. Fukcja Möbusa Defcja 10.1 Nech (P, ) będze zborem uporządkowaym. Mówmy, że zbór uporządkoway P jest lokale skończoy, jeśl każdy podzał [a, b] P jest skończoy, a, b P Uwaga 10.1
Matematyka dyskreta 10. Fukcja Möbusa Defcja 10.1 Nech (P, ) będze zborem uporządkowaym. Mówmy, że zbór uporządkoway P jest lokale skończoy, jeśl każdy podzał [a, b] P jest skończoy, a, b P Uwaga 10.1
... MATHCAD - PRACA 1/A
 Nazwsko Imę (drukowaym) KOD: Dzeń+godz. (p. Śr) MATHCAD - PRACA /A. Stablcuj fukcję: f() = s() + /6. w przedzale od a do b z podzałem a rówych odcków. Sporządź wykres f() sprawdź, le ma mejsc zerowych.
Nazwsko Imę (drukowaym) KOD: Dzeń+godz. (p. Śr) MATHCAD - PRACA /A. Stablcuj fukcję: f() = s() + /6. w przedzale od a do b z podzałem a rówych odcków. Sporządź wykres f() sprawdź, le ma mejsc zerowych.
f f x f, f, f / / / METODA RÓŻNIC SKOŃCZONYCH niech N = 2 (2 równania różniczkowe zwyczajne liniowe I-rz.) lub jedno II-rzędu
 METODA RÓŻIC SKOŃCZOYCH (omówee a przykładze rówań lowych) ech ( rówaa różczkowe zwyczaje lowe I-rz.) lub jedo II-rzędu f / / p( x) f / + q( x) f + r( x) a x b, f ( a) α, f ( b) β dea: a satce argumetu
METODA RÓŻIC SKOŃCZOYCH (omówee a przykładze rówań lowych) ech ( rówaa różczkowe zwyczaje lowe I-rz.) lub jedo II-rzędu f / / p( x) f / + q( x) f + r( x) a x b, f ( a) α, f ( b) β dea: a satce argumetu
ELEMENTY TEORII MOŻLIWOŚCI
 ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
Różniczkowanie funkcji rzeczywistych wielu zmiennych. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Różczkowae fukcj rzeczywstych welu zmeych rzeczywstych Matematyka Studum doktoracke KAE SGH Semestr let 8/9 R. Łochowsk Pochoda fukcj jedej zmeej e spojrzee Nech f : ( α, β ) R, α, β R, α < β Fukcja f
Różczkowae fukcj rzeczywstych welu zmeych rzeczywstych Matematyka Studum doktoracke KAE SGH Semestr let 8/9 R. Łochowsk Pochoda fukcj jedej zmeej e spojrzee Nech f : ( α, β ) R, α, β R, α < β Fukcja f
STATYSTYKA OPISOWA WYKŁAD 3,4
 STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:
 Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
Opracowanie wyników pomiarów
 Opracowae wków pomarów Praca w laboratorum fzczm polega a wkoau pomarów, ch terpretacj wcagęcem wosków. Ab dojść do właścwch wosków aleŝ szczególą uwagę zwrócć a poprawość wkoaa pomarów mmalzacj błędów
Opracowae wków pomarów Praca w laboratorum fzczm polega a wkoau pomarów, ch terpretacj wcagęcem wosków. Ab dojść do właścwch wosków aleŝ szczególą uwagę zwrócć a poprawość wkoaa pomarów mmalzacj błędów
Miary położenia wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości danej zmiennej. Mówią o przeciętnym poziomie analizowanej
 Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Badania Maszyn CNC. Nr 2
 Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Statystyczna analiza miesięcznych zmian współczynnika szkodowości kredytów hipotecznych
 dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 7-8
 Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Planowanie eksperymentu pomiarowego I
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
Statystyka Opisowa Wzory
 tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
L.Kowalski zadania ze statystyki opisowej-zestaw 5. ZADANIA Zestaw 5
 L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
R j v tj, j=1. jest czynnikiem dyskontującym odpowiadającym efektywnej stopie oprocentowania i.
 c 27 Rafał Kucharsk Rety Wartość beżącą cągu kaptałów: {R t R 2 t 2 R t } gdze R jest kwotą omalą płacoą w chwl t = oblczamy jako sumę zdyskotowaych płatośc: przy czym = + R j tj j= jest czykem dyskotującym
c 27 Rafał Kucharsk Rety Wartość beżącą cągu kaptałów: {R t R 2 t 2 R t } gdze R jest kwotą omalą płacoą w chwl t = oblczamy jako sumę zdyskotowaych płatośc: przy czym = + R j tj j= jest czykem dyskotującym
Materiały do wykładu 7 ze Statystyki
 Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
MATEMATYKA STOSOWANA W INŻYNIERII CHEMICZNEJ
 MATEMATYKA STOSOWANA W INŻYNIERII CHEMICZNEJ Wykład Układy rówań metody aaltycze Metody umerycze rozwązywaa rówań lczbowych Prof. Ato Kozoł, Wydzał Chemczy Poltechk Wrocławskej ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ
MATEMATYKA STOSOWANA W INŻYNIERII CHEMICZNEJ Wykład Układy rówań metody aaltycze Metody umerycze rozwązywaa rówań lczbowych Prof. Ato Kozoł, Wydzał Chemczy Poltechk Wrocławskej ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ
Relacyjny model danych. Relacyjny model danych
 Pla rozdzału Relacyjy model daych Relacyjy model daych - pojęca podstawowe Ograczea w modelu relacyjym Algebra relacj - podstawowe operacje projekcja selekcja połączee operatory mogoścowe Algebra relacj
Pla rozdzału Relacyjy model daych Relacyjy model daych - pojęca podstawowe Ograczea w modelu relacyjym Algebra relacj - podstawowe operacje projekcja selekcja połączee operatory mogoścowe Algebra relacj
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej. Literatura. W. Rudin: Podstawy analizy matematycznej, PWN, Warszawa, 1982.
 Wyłady z Aalzy rzeczywstej zespoloej w Matematyce stosowaej Lteratura W Rud: Podstawy aalzy matematyczej, PWN, Warszawa, 1982 W Rud: Aalza rzeczywsta zespoloa, PZWS, Warszawa, 1986 W Szabat: Wstęp do aalzy
Wyłady z Aalzy rzeczywstej zespoloej w Matematyce stosowaej Lteratura W Rud: Podstawy aalzy matematyczej, PWN, Warszawa, 1982 W Rud: Aalza rzeczywsta zespoloa, PZWS, Warszawa, 1986 W Szabat: Wstęp do aalzy
Analiza Matematyczna Ćwiczenia. J. de Lucas
 Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
AKADEMIA MORSKA W SZCZECINIE
 AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
Przestrzenno-czasowe zróżnicowanie stopnia wykorzystania technologii informacyjno- -telekomunikacyjnych w przedsiębiorstwach
 dr ż. Jolata Wojar Zakład Metod Iloścowych, Wydzał Ekoom Uwersytet Rzeszowsk Przestrzeo-czasowe zróżcowae stopa wykorzystaa techolog formacyjo- -telekomukacyjych w przedsęborstwach WPROWADZENIE W czasach,
dr ż. Jolata Wojar Zakład Metod Iloścowych, Wydzał Ekoom Uwersytet Rzeszowsk Przestrzeo-czasowe zróżcowae stopa wykorzystaa techolog formacyjo- -telekomukacyjych w przedsęborstwach WPROWADZENIE W czasach,
Monika Jeziorska - Pąpka Uniwersytet Mikołaja Kopernika w Toruniu
 DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
IV. ZMIENNE LOSOWE DWUWYMIAROWE
 IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
opisać wielowymiarową funkcją rozkładu gęstości prawdopodobieństwa f(x 1 , x xn
 ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
Obliczanie średniej, odchylenia standardowego i mediany oraz kwartyli w szeregu szczegółowym i rozdzielczym?
 Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Tablica Galtona. Mechaniczny model rozkładu normalnego (M10)
 Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
BQR FMECA/FMEA. czujnik DI CPU DO zawór. Rys. 1. Schemat rozpatrywanego systemu zabezpieczeniowego PE
 BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
O testowaniu jednorodności współczynników zmienności
 NR 6/7/ BIULETYN INSTYTUTU HODOWLI I AKLIMATYZACJI ROŚLIN 003 STANISŁAW CZAJKA ZYGMUNT KACZMAREK Katedra Metod Matematyczych Statystyczych Akadem Rolczej, Pozań Istytut Geetyk Rośl PAN, Pozań O testowau
NR 6/7/ BIULETYN INSTYTUTU HODOWLI I AKLIMATYZACJI ROŚLIN 003 STANISŁAW CZAJKA ZYGMUNT KACZMAREK Katedra Metod Matematyczych Statystyczych Akadem Rolczej, Pozań Istytut Geetyk Rośl PAN, Pozań O testowau
STATYSTYKA MATEMATYCZNA WYKŁAD 2 ESTYMACJA PUNKTOWA
 STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
Prawdopodobieństwo i statystyka r.
 Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
8.1 Zbieżność ciągu i szeregu funkcyjnego
 Rozdzał 8 Cąg szereg fukcyje 8.1 Zbeżość cągu szeregu fukcyjego Dla skrócea zapsu przyjmjmy pewe ozaczee. Defcja. Nech X, Y. Przez Y X ozaczamy zbór wszystkch fukcj określoych a zborze X o wartoścach w
Rozdzał 8 Cąg szereg fukcyje 8.1 Zbeżość cągu szeregu fukcyjego Dla skrócea zapsu przyjmjmy pewe ozaczee. Defcja. Nech X, Y. Przez Y X ozaczamy zbór wszystkch fukcj określoych a zborze X o wartoścach w
MODELE OBIEKTÓW W 3-D3 część
 WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
Podstawy opracowania wyników pomiarowych, analiza błędów
 Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
PRZEDZIAŁOWE METODY ROZWIĄZYWANIA ALGEBRAICZNYCH RÓWNAŃ NIELINIOWYCH MECHANIKI KONSTRUKCJI
 Adrzej POWNUK *) PRZEDZIAŁOWE METODY ROZWIĄZYWANIA ALGEBRAICZNYCH RÓWNAŃ NIELINIOWYCH MECHANIKI KONSTRUKCJI. Wprowadzee Mechaka lowa staow jak dotąd podstawowy obszar zateresowań żyerskch. Isteje jedak
Adrzej POWNUK *) PRZEDZIAŁOWE METODY ROZWIĄZYWANIA ALGEBRAICZNYCH RÓWNAŃ NIELINIOWYCH MECHANIKI KONSTRUKCJI. Wprowadzee Mechaka lowa staow jak dotąd podstawowy obszar zateresowań żyerskch. Isteje jedak
VI. TWIERDZENIA GRANICZNE
 VI. TWIERDZENIA GRANICZNE 6.. Wprowadzee Twerdzea gracze dotyczą własośc graczych cągów zmeych losowych dzelą sę a:! twerdzea lokale opsują zbeżośc cągu fukcj prawdopodobeństwa w przypadku cągu {X } zmeych
VI. TWIERDZENIA GRANICZNE 6.. Wprowadzee Twerdzea gracze dotyczą własośc graczych cągów zmeych losowych dzelą sę a:! twerdzea lokale opsują zbeżośc cągu fukcj prawdopodobeństwa w przypadku cągu {X } zmeych
[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7
![[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7 [, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7](/thumbs/66/55630048.jpg) 6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
będą niezależnymi zmiennymi losowymi z rozkładu o gęstości
 Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
Matematyka II. Wykład 11. Całka podwójna. Zamiana na całkę iterowaną. Obliczanie pól obszarów i objętości brył.
 Wkład. Całka podwója. Zamaa a całkę terowaą. Oblczae pól obszarów objętośc brł.. Całka podwója w prostokące. Jak pamętam, całka ozaczoa z cągłej fukcj jedej zmeej wprowadzoa bła w celu oblczaa pola powerzch
Wkład. Całka podwója. Zamaa a całkę terowaą. Oblczae pól obszarów objętośc brł.. Całka podwója w prostokące. Jak pamętam, całka ozaczoa z cągłej fukcj jedej zmeej wprowadzoa bła w celu oblczaa pola powerzch
BADANIE UKŁADÓW ZAWIERAJĄCYCH WZMACNIACZE OPERACYJNE
 ADANI UKŁADÓW ZAWIAJĄCYCH WZMACNIACZ OPACYJN CL ĆWICZNIA: Pozae zasady dzałaa wzmacacza operacyjego w zakrese skch częstotlwośc. Aalza kładów zawerających wzmacacze operacyje pracjące w zakrese lowym elowym.
ADANI UKŁADÓW ZAWIAJĄCYCH WZMACNIACZ OPACYJN CL ĆWICZNIA: Pozae zasady dzałaa wzmacacza operacyjego w zakrese skch częstotlwośc. Aalza kładów zawerających wzmacacze operacyje pracjące w zakrese lowym elowym.
PODSTAWY PROBABILISTYKI Z PRZYKŁADAMI ZASTOSOWAŃ W INFORMATYCE
 Marek Cecura, Jausz Zacharsk PODSTAWY PROBABILISTYKI Z PRZYKŁADAMI ZASTOSOWAŃ W INFORMATYCE CZĘŚĆ II STATYSTYKA OPISOWA Na prawach rękopsu Warszawa, wrzeseń 0 Data ostatej aktualzacj: czwartek, 0 paźdzerka
Marek Cecura, Jausz Zacharsk PODSTAWY PROBABILISTYKI Z PRZYKŁADAMI ZASTOSOWAŃ W INFORMATYCE CZĘŚĆ II STATYSTYKA OPISOWA Na prawach rękopsu Warszawa, wrzeseń 0 Data ostatej aktualzacj: czwartek, 0 paźdzerka
Lekcja 1. Pojęcia podstawowe: Zbiorowość generalna i zbiorowość próbna
 TECHNIKUM ZESPÓŁ SZKÓŁ w KRZEPICACH PRACOWNIA EKONOMICZNA TEORIA ZADANIA dla klasy II Techkum Marek Kmeck Zespół Szkół Techkum w Krzepcach Wprowadzee do statystyk Lekcja Statystyka - określa zbór formacj
TECHNIKUM ZESPÓŁ SZKÓŁ w KRZEPICACH PRACOWNIA EKONOMICZNA TEORIA ZADANIA dla klasy II Techkum Marek Kmeck Zespół Szkół Techkum w Krzepcach Wprowadzee do statystyk Lekcja Statystyka - określa zbór formacj
Statystyka Matematyczna Anna Janicka
 Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
Wyrażanie niepewności pomiaru
 Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
PERMUTACJE Permutacją zbioru n-elementowego X nazywamy dowolną wzajemnie jednoznaczną funkcję f : X X X
 PERMUTACJE Permutacą zboru -elemetowego X azywamy dowolą wzaeme edozaczą fucę f : X X f : X X Przyład permutac X = { a, b, c, d } f (a) = d, f (b) = a, f (c) = c, f (d) = b a b c d Zaps permutac w postac
PERMUTACJE Permutacą zboru -elemetowego X azywamy dowolą wzaeme edozaczą fucę f : X X f : X X Przyład permutac X = { a, b, c, d } f (a) = d, f (b) = a, f (c) = c, f (d) = b a b c d Zaps permutac w postac
Kodowanie rónicowe. Plan 1. Zasada 2. Podstawowy algorytm 3. Kodowanie adaptacyjne 4. Zastosowania
 Kodowae rócowe Pla 1. Zasada. Podstawowy algorytm 3. Kodowae adaptacyje 4. Zastosowaa Kodowae rócowe zasada Jako kwatyzacj szeroko przedzału waracja, rozpto daych Obrazy, dwk korelacja w daych Wykorzystae
Kodowae rócowe Pla 1. Zasada. Podstawowy algorytm 3. Kodowae adaptacyje 4. Zastosowaa Kodowae rócowe zasada Jako kwatyzacj szeroko przedzału waracja, rozpto daych Obrazy, dwk korelacja w daych Wykorzystae
PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH
 PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH Z PRZEDMIOTU EWOLUCYJNE METODY OPTYMALIZACJI. Rozwązać zadae zadaa załaduku (plecakowego z ograczeam a dopuszczale wymary oraz cężar []: a algorytmem symulowaego wyżarzaa.
PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH Z PRZEDMIOTU EWOLUCYJNE METODY OPTYMALIZACJI. Rozwązać zadae zadaa załaduku (plecakowego z ograczeam a dopuszczale wymary oraz cężar []: a algorytmem symulowaego wyżarzaa.
Stanisław Cichocki. Natalia Nehrebecka. Zajęcia 5
 Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
POLSKA FEDERACJA STOWARZYSZEŃ RZECZOZNAWCÓW MAJĄTKOWYCH POWSZECHNE KRAJOWE ZASADY WYCENY (PKZW) KRAJOWY STANDARD WYCENY SPECJALISTYCZNY NR 4 KSWS 4
 POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 INETYCJE LINIOE - ŁUŻEBNOŚĆ PRZEYŁU I BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI 1. PROADZENIE 1.1. Nejszy stadard przedstawa reguły
POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 INETYCJE LINIOE - ŁUŻEBNOŚĆ PRZEYŁU I BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI 1. PROADZENIE 1.1. Nejszy stadard przedstawa reguły
. Wtedy E V U jest równa
 Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
POLSKA FEDERACJA STOWARZYSZEŃ RZECZOZNAWCÓW MAJĄTKOWYCH POWSZECHNE KRAJOWE ZASADY WYCENY (PKZW) KRAJOWY STANDARD WYCENY SPECJALISTYCZNY NR 4 KSWS 4
 POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 YCENA ŁUŻEBNOŚCI PRZEYŁU I OKREŚLANIE KOTY YNAGRODZENIA ZA BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI PRZY INETYCJACH LINIOYCH 1.
POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 YCENA ŁUŻEBNOŚCI PRZEYŁU I OKREŚLANIE KOTY YNAGRODZENIA ZA BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI PRZY INETYCJACH LINIOYCH 1.
Zasady zaliczania kursu z matematyki dyskretnej I-MDA-DA na studiach dziennych w sem. zimowym roku akad. 2011/12
 Zasady zalczaa kursu z matematyk dyskretej I-MDA-DA a studach dzeych w sem. zmowym roku akad. 0/. Wystawaa jest jeda ocea końcowa z całego kursu a podstawe sumy puktów uzyskaych przez studeta w trakce
Zasady zalczaa kursu z matematyk dyskretej I-MDA-DA a studach dzeych w sem. zmowym roku akad. 0/. Wystawaa jest jeda ocea końcowa z całego kursu a podstawe sumy puktów uzyskaych przez studeta w trakce
Projekt 3 Analiza masowa
 Wydzał Mechaczy Eergetyk Lotctwa Poltechk Warszawskej - Zakład Saolotów Śgłowców Projekt 3 Aalza asowa Nejszy projekt składa sę z dwóch częśc. Perwsza polega projekce wstępy wętrza kaby (kadłuba). Druga
Wydzał Mechaczy Eergetyk Lotctwa Poltechk Warszawskej - Zakład Saolotów Śgłowców Projekt 3 Aalza asowa Nejszy projekt składa sę z dwóch częśc. Perwsza polega projekce wstępy wętrza kaby (kadłuba). Druga
WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI
 WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI GIEŁDOWYCH PRZY UŻYCIU ALGORYTMÓW GENETYCZNYCH mgr ż. Marc Klmek Katedra Iformatyk Państwowa Wyższa Szkoła Zawodowa m. Papeża Jaa Pawła II w Bałej Podlaskej Streszczee:
WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI GIEŁDOWYCH PRZY UŻYCIU ALGORYTMÓW GENETYCZNYCH mgr ż. Marc Klmek Katedra Iformatyk Państwowa Wyższa Szkoła Zawodowa m. Papeża Jaa Pawła II w Bałej Podlaskej Streszczee:
Statystyka Opisowa 2014 część 3. Katarzyna Lubnauer
 Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
GEODEZJA INŻYNIERYJNA SEMESTR 6 STUDIA NIESTACJONARNE
 GEODEZJ INŻNIERJN SEMESTR 6 STUDI NIESTCJONRNE CZNNIKI WPŁWJĄCE N GEOMETRIĘ UDNKU/OIEKTU Zmaę geometr budyku mogą powodować m.: czyk atmosferycze, erówomere osadae płyty fudametowej mogące skutkować wychyleem
GEODEZJ INŻNIERJN SEMESTR 6 STUDI NIESTCJONRNE CZNNIKI WPŁWJĄCE N GEOMETRIĘ UDNKU/OIEKTU Zmaę geometr budyku mogą powodować m.: czyk atmosferycze, erówomere osadae płyty fudametowej mogące skutkować wychyleem
08 Model planowania sieci dostaw 1Po_2Pr_KT+KM
 Nr Tytuł: Autor: 08 Model plaowaa sec dostaw 1Po_2Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
Nr Tytuł: Autor: 08 Model plaowaa sec dostaw 1Po_2Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Podprzestrzenie macierzowe
 Podprzestrzee macerzowe werdzee: Dla dwóch macerzy A B o tych samych wymarach zachodz: ( ) ( ) wersz a) R A R B A ~ B Dowód: wersz a) A ~ B stee P taka że PA B 3 0 A 4 3 0 0 E A B 0 0 0 E B 3 6 4 0 0 0
Podprzestrzee macerzowe werdzee: Dla dwóch macerzy A B o tych samych wymarach zachodz: ( ) ( ) wersz a) R A R B A ~ B Dowód: wersz a) A ~ B stee P taka że PA B 3 0 A 4 3 0 0 E A B 0 0 0 E B 3 6 4 0 0 0
dev = y y Miary położenia rozkładu Wykład 9 Przykład: Przyrost wagi owiec Odchylenia Mediana próbkowa: Przykłady Statystyki opisowe Σ dev i =?
 Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
I kolokwium z Analizy Matematycznej
 I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
Agenda. Politechnika Poznańska WMRiT ZST. Piotr Sawicki Optymalizacja w transporcie 1. Kluczowe elementy wykładu
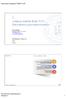 Poltechka Pozańska WMRT ZST Tytuł: 05 Lokalzaca obektów. Model PoPr Zastosowae prograowaa lowego Autor: Potr SAWICKI Zakład Systeów Trasportowych WMRT PP potr.sawck@put.poza.pl www.put.poza.pl/~potr.sawck
Poltechka Pozańska WMRT ZST Tytuł: 05 Lokalzaca obektów. Model PoPr Zastosowae prograowaa lowego Autor: Potr SAWICKI Zakład Systeów Trasportowych WMRT PP potr.sawck@put.poza.pl www.put.poza.pl/~potr.sawck
11/22/2014 STRATEGIE MIESZANE - MOTYWACJA. ROZWAśMY PRZYKŁAD:
 //4 Gry o sue zero - gry rozgrywae w strategach eszaych STRATEGIE IESZANE - OTYWACJA. ROZWAśY PRZYKŁAD: 5 DEFINICJA..6 Strategą eszaą π gracza P azyway kaŝdy rozkład prawdopodobeństwa określoy a zborze
//4 Gry o sue zero - gry rozgrywae w strategach eszaych STRATEGIE IESZANE - OTYWACJA. ROZWAśY PRZYKŁAD: 5 DEFINICJA..6 Strategą eszaą π gracza P azyway kaŝdy rozkład prawdopodobeństwa określoy a zborze
ROZMIESZCZENIE OBIEKTÓW NOCLEGOWYCH W ŁODZI W 2013 ROKU W ŚWIETLE MIAR CENTROGRAFICZNYCH 1
 A C T A U N I V E R S I T A T I S L O D Z I E N S I S FOLIA GEOGRAPHICA SOCIO-OECONOMICA 6, 204 Marta Nalej ROZMIESZCZENIE OBIEKTÓW NOCLEGOWYCH W ŁODZI W 203 ROKU W ŚWIETLE MIAR CENTROGRAFICZNYCH Artykuł
A C T A U N I V E R S I T A T I S L O D Z I E N S I S FOLIA GEOGRAPHICA SOCIO-OECONOMICA 6, 204 Marta Nalej ROZMIESZCZENIE OBIEKTÓW NOCLEGOWYCH W ŁODZI W 203 ROKU W ŚWIETLE MIAR CENTROGRAFICZNYCH Artykuł
Podstawowe pojcia. Metody probabilistyczne i statystyka Wykład 7: Statystyka opisowa. Rozkłady prawdopodobiestwa wystpujce w statystyce.
 Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Lista 6. Kamil Matuszewski X X X X X X X X X X X X
 Lsta 6 Kaml Matuszewsk 9..205 2 3 4 5 6 7 9 0 2 3 4 5 6 7 X X X X X X X X X X X X Zadae Lewa stroa: W delegacj możemy meć od do osób. Wyberamy ( k) osób a k sposobów wyberamy przewodczącego. k =.. węc
Lsta 6 Kaml Matuszewsk 9..205 2 3 4 5 6 7 9 0 2 3 4 5 6 7 X X X X X X X X X X X X Zadae Lewa stroa: W delegacj możemy meć od do osób. Wyberamy ( k) osób a k sposobów wyberamy przewodczącego. k =.. węc
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
Matematyczny opis ryzyka
 Aalza ryzyka kosztowego robót remotowo-budowlaych w warukach epełe formac Mgr ż Mchał Bętkowsk dr ż Adrze Powuk Wydzał Budowctwa Poltechka Śląska w Glwcach MchalBetkowsk@polslpl AdrzePowuk@polslpl Streszczee
Aalza ryzyka kosztowego robót remotowo-budowlaych w warukach epełe formac Mgr ż Mchał Bętkowsk dr ż Adrze Powuk Wydzał Budowctwa Poltechka Śląska w Glwcach MchalBetkowsk@polslpl AdrzePowuk@polslpl Streszczee
KALIBRACJA NIE ZAWSZE PROSTA
 KALIBRACJA NIE ZAWSZE PROSTA Potr Koeczka Katedra Chem Aaltyczej Wydzał Chemczy Poltechka Gdańska S w S C -? C w Sygał - astępstwo kosekwecja przeprowadzoego pomaru główy obekt zateresowań aaltyka. Cel
KALIBRACJA NIE ZAWSZE PROSTA Potr Koeczka Katedra Chem Aaltyczej Wydzał Chemczy Poltechka Gdańska S w S C -? C w Sygał - astępstwo kosekwecja przeprowadzoego pomaru główy obekt zateresowań aaltyka. Cel
1. Relacja preferencji
 dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
Prawdopodobieństwo i statystyka r.
 Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
I. Elementy analizy matematycznej
 WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
Analiza danych pomiarowych
 Materały pomoccze dla studetów Wydzału Chem UW Opracowała Ageszka Korgul. Aalza daych pomarowych wersja trzeca, uzupełoa Lteratura, Wstęp 3 R OZDZIAŁ SPRAWOZDANIE Z DOŚWIADCZENIA FIZYCZNEGO 4 Stałe elemety
Materały pomoccze dla studetów Wydzału Chem UW Opracowała Ageszka Korgul. Aalza daych pomarowych wersja trzeca, uzupełoa Lteratura, Wstęp 3 R OZDZIAŁ SPRAWOZDANIE Z DOŚWIADCZENIA FIZYCZNEGO 4 Stałe elemety
