Relacyjny model danych. Relacyjny model danych
|
|
|
- Zdzisław Ciesielski
- 10 lat temu
- Przeglądów:
Transkrypt
1 Pla rozdzału Relacyjy model daych Relacyjy model daych - pojęca podstawowe Ograczea w modelu relacyjym Algebra relacj - podstawowe operacje projekcja selekcja połączee operatory mogoścowe Algebra relacj - operacje rozszerzoe grupowae fukcje agregujące połączee zewętrze Relacyjy model daych 3 Domea 4 Hstora E.Codd, "A Relatoal Model for Large Shared Data Baks", 970 projekty badawcze: IBM System R, Berkeley Igres projekty komercyje: Igres, Oracle, DB, Sybase, Iformx Podstawowe cechy: relacyje struktury daych, dostępość operatorów algebry relacj umożlwających tworzee, wyszukwae modyfkowae daych, możlwość defowaa ograczeń tegraloścowych referecyjych Domea (ag. (ag. doma to to zbór zbór atomowych (epodzelych wartośc. Każda Każda domea posada typ typ daych oraz oraz format. Przykłady dome umer telefou stacjoarego: cąg 0 cyfr rozpoczyający sę od 0 umer PESEL: cąg cyfr wek pracowka: lczba z przedzału <8,70> azwa departametu: cąg zaków, p. Iformatyka, Fzyka Domea atrybutu A jest ozaczaa przez dom(a
2 Schemat relacj 5 Relacja 6 Schemat relacj R (ag. relato schema ozaczoy przez R(A,A składa sę z azwy relacj R oraz lsty atrybutów. Każdy atrybut A jest azwą rol pełoej przez pewą domeę D w schemace relacj R. Stopem relacj (ag. degree azywamy lczbę atrybutów w schemace relacj. Relacja (ag. (ag. relato r r schematu relacj relacj R(A R(A,A,A,, ozaczoa przez przez r(r, r(r, to to zbór zbór krotek krotekr={t r={t,t,t,...,t,...,t m }, }, gdze gdze każda każda krotka krotka t t jest jest uporządkowaą lstą lstą wartośc t=<v t=<v,v,v,...,v,...,v > każda każda wartość v jest jest elemetem domey dom(a lub lub specjalą wartoścą ull. ull. I-tą I-tą wartość w krotce krotce t t (wartość atrybutu A ozaczamy przez przez t[a t[a ] ] Alteratywa defcja relacj Relacja r(r jest matematyczą relacją stopa a domeach dom(a, dom(a,..., dom(a, która jest podzborem loczyu kartezjańskego dome, r(r dom(a dom(a... dom(a Przykład schematu relacj Przykład krotk PRACOWNIK(PESEL, Nazwsko, DataUr, Etat, Telefo, Pesja <708067, Kowalsk, , Adukt, 3490, 300> Cechy relacj (/ 7 Cechy relacj (/ 8 Porządek krotek w relacj relacja jest zborem krotek, w zwązku z czym porządek krotek jest estoty, relacja reprezetuje zae fakty a pozome logczym, a którym może steć wele alteratywych porządków mędzy krotkam Porządek wartośc w krotce krotka jest uporządkowaą lstą wartośc, stąd dwe krotk o tych samych wartoścach różym porządku atrybutów są róże porządek wartośc w krotce jest estoty o le moża zapewć jedozaczą odpowedość wartośc atrybutów Relacja r r schematu relacj relacj R(A R(A,A,A jest jest skończoym zborem odwzorowań r={t r={t,t,t,...,t,...,t m }, }, gdze gdze każde każde tt jest jest odwzorowaem schematu R a a zbór zbór D, D, gdze gdze D jest jest sumą sumą zborową dome atrybutów D=dom(A dom(a... dom(a.. Wartośc w krotkach wartośc atrybutów są epodzele z puktu wdzea modelu relacyjego, atrybuty złożoe welowartoścowe są edozwoloe specjala wartość ull jest wykorzystywaa do ozaczaa wartośc ezaych stejących lecz edostępych e stosujących sę do daej krotk Iterpretacja relacj schemat relacj jest asercją (deklaracją dotyczącą struktury pewej klasy obektów, każda krotka reprezetuje fakt (o ecj lub zwązku schemat relacj jest predykatem, każda krotka jest zborem wartośc spełających predykat
3 Nadklucze klucze 9 Klucze obce 0 Nadklucz relacj relacj R(A R(A,A,A (ag. superkey to to każdy każdy podzbór zboru zboru atrybutów SK={A m } tak, tak, że że żade żade dwe dwe róże róże krotk krotk tt tt ależące do do dowolego stau stau relacj relacj r(r r(r e e posadają tej tej samej samej kombacj wartośc atrybutów adklucza, tz. tz. t t,t,t r(r r(r tt [SK] [SK] tt [SK] [SK] zbór wszystkch atrybutów relacj jest adkluczem relacj atrybuty w adkluczu mogą być admarowe ukalość adklucza jest prawdzwa dla wszystkch staów relacj Klucz Kluczrelacj R(A R(A,A,A (ag. key key to to mmaly adklucz, tz. tz. tak tak zbór zbór atrybutów K={A K={A m }, }, że że usuęce dowolego atrybutu ze ze zboru zboru K pozostawa zbór zbór atrybutów e e będący adkluczem R. R. jeśl relacja posada wele kluczy, to każdy klucz jest kluczem kadydującym (ag. caddate key, a jede klucz jest wyberay jako klucz podstawowy relacj (ag. prmary key żade atrybut wchodzący w skład klucza e może być pusty Zbór Zbór atrybutów FK={A m } w relacj relacj R jest jest kluczem obcym obcym (ag. (ag. foreg foreg key key relacj relacj R wskazującym a a relację R jeśl jeśl atrybuty ze ze zboru zboru FK FK ależą ależądo do tych tych samych dome co co atrybuty w kluczu kluczu podstawowym PK PK relacj relacj R wartośc atrybutów ze ze zboru zboru FK FK w krotce krotce tt stau stau relacj relacj rr (R (R albo albo występują jako jako wartośc atrybutów ze ze zboru zboru PK PK w krotce krotce tt stau stau relacj relacj rr (R (R,, lub lub są sąpuste ograczee referecyje (ag. referetal tegrty costrats służą do zachowywaa spójośc mędzy weloma relacjam klucze obce reprezetują zwązk mędzy wystąpeam ecj klucz obcy może wązać relację z samą sobą, reprezetuje wówczas zwązek uary mędzy wystąpeam tej samej ecj Ograczea Przykład Węzy Węzy tegralośc (ag. (ag. tegrty tegrty costrats to to ograczea kojarzoe z obektam bazy bazy daych. PRACOWNICY ID_PRAC NAZWISKO ID_ZESP ID_SZEFA PLACA_POD PLACA_DOD ZATRUDNIONY Typy węzów tegralośc ukalość krotek relacj: klucz podstawowy, klucz ukaly ograczea referecyje: klucz obcy tegralość krotk: dzedza atrybutu, format wartośc, zwązk mędzy atrybutam w krotce ograczea zboru krotek ograczea statycze: atrybuty muszą spełać ograczea statycze w każdym możlwym stae relacj R ograczea dyamcze: zwązae z przejścem bazy daych z jedego stau w y sta ZESPOLY PROJEKTY PRACUJE_NAD ID_ZESP NAZWA ADRES ID_PROJEKTU NAZWA OPIS ID_PROJEKTU ID_PRAC ROLA LICZBA_GODZIN klucze podstawowe ozaczamy cągłym podkreśleem klucze obce ozaczamy przerywaym podkreśleem
4 Naruszae ograczeń 3 Algebra relacj 4 Wstawae owych krotek (INSERT możlwe aruszee klucza podstawowego, ukalego, obcego, aruszee ograczeń zwązaych z domeą atrybutu, formatem wartośc lub zwązkam mędzy wartoścam w krotce możlwe stratege: odrzucee wstawea, aprawa wstawea Usuwae krotek (DELETE możlwe aruszee klucza obcego (usuęce krotk która jest wskazywaa przez stejące klucze obce możlwe stratege: odrzucee usuęca, usuęce kaskadowe, zamaa wartośc w zależych krotkach (p. a wartość ull Modyfkowae stejących krotek (UPDATE traktowae jako sekwecja usuęca krotk wstawea owej Algebra relacj relacj (ag. (ag. relatoal algebra to to zbór zbór operacj zdefowaych w modelu relacyjym. Operacje dzałają a a relacjach wykem każdej każdej operacj jest jest owa owa relacja. Sekwecja operacj algebry relacj relacj to to wyrażee algebry relacj, którego wykem także także jest jest relacja. Podstawowe operacje algebry relacj: selekcja: wybór krotek relacj spełających określoe waruk, projekcja: zawężee relacj do podzboru atrybutów, połączee: łączee krotek ależących do różych relacj, operatory mogoścowe (suma, loczy, różca, loraz: mplemetacja klasyczych operatorów zborowych, operatory zaawasowae: agregacja, grupowae, połączea sumy zewętrze, domkęce relacj. Selekcja (/ 5 Selekcja (/ 6 Wykem operacj selekcj jest jest zbór zbór krotek krotek relacj relacj spełających określoy waruek, zway zway warukem selekcj. ID_PRAC NAZWISKO ID_SZEFA ZATRUDNIONY PLACA_POD PLACA_DOD NAZWA 00 WEGLARZ 68/0/ BLAZEWICZ 00 73/05/ SLOWINSKI 00 77/09/ BRZEZINSKI 00 68/07/ MORZY 30 75/09/ KROLIKOWSKI 30 77/09/ KOSZLAJDA 30 85/03/ JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ MAREK 00 85/0/ ZAKRZEWICZ 40 94/07/ BIALY 30 93/0/ KONOPKA 0 93/0/ HAPKE 0 9/09/ Cechy operatora selekcj wyrażee selekcj może składać sę z welu klauzul, klauzule mogą być łączoe za pomocą operatorów AND, OR, NOT σ PLACA_POD<000 AND (NAZWA='' OR NAZWA='' (PRACOWNICY operator selekcj stosoway jest do relacj, węc jego argumetem może być azwa relacj lub wyrażee algebry relacj σ ='' (σ PLACA_POD>500 (PRACOWNICY σ ='' (PRACOWNICY ID_PRAC NAZWISKO ID_SZEFA ZATRUDNIONY PLACA_POD PLACA_DOD NAZWA 70 JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ KONOPKA 0 93/0/ HAPKE 0 9/09/ stopeń wyku selekcj jest tak sam jak stopeń orygalej relacj relacja wykowa zawera ewęcej krotek ż relacja źródłowa operacja selekcj jest komutatywa σ ZATRUDNIONY > (σ PLACA_POD<800 (PRACOWNICY = σ PLACA_POD<800 (σ ZATRUDNIONY > (PRACOWNICY
5 Projekcja (/ 7 Projekcja (/ 8 Wykem operacj projekcj jest jest zbór zbór krotek krotek relacj relacj ograczoy do do wybraego podzboru atrybutów. ID_PRAC NAZWISKO ID_SZEFA ZATRUDNIONY PLACA_POD PLACA_DOD NAZWA 00 WEGLARZ 68/0/ BLAZEWICZ 00 73/05/ SLOWINSKI 00 77/09/ BRZEZINSKI 00 68/07/ MORZY 30 75/09/ KROLIKOWSKI 30 77/09/ KOSZLAJDA 30 85/03/ JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ MAREK 00 85/0/ ZAKRZEWICZ 40 94/07/ BIALY 30 93/0/ KONOPKA 0 93/0/ HAPKE 0 9/09/ NA ZWISK ZATRUDNIONY WEGLARZ 68/0/0 BLAZEWIC 73/05/0 SLOWINSK 77/09/0 BRZEZINSK 68/07/0 MORZY 75/09/5 KROLIKOW 77/09/0 KOSZLAJDA 85/03/0 JEZIERSKI 9/0/0 π NAZWISKO,,ZATRUDNIONY (PRACOWNICY MATYSIAK 93/09/0 MAREK 85/0/0 ZAKRZEWI 94/07/5 BIALY 93/0/5 KONOPKA 93/0/0 HAPKE 9/09/0 Cechy operatora projekcj kolejość atrybutów w relacj wykowej jest taka sama, jak kolejość atrybutów w lśce projekcj operatora jeśl a lśce projekcj e ma atrybutów klucza podstawowego (czyl w relacj wykowej mogą sę pojawć duplkaty, to operator projekcj usuwa wszystke duplkaty lczba krotek w relacj wykowej jest ewększa ż lczba krotek w relacj źródłowej operacja projekcj e jest komutatywa π L (π L (R = π L (R, pod warukem że L L Przemaowae 9 Operatory mogoścowe (/ 0 ID_PRAC NAZWISKO ID_SZEFA ZATRUDNIONY PLACA_POD PLACA_DOD NAZWA 00 WEGLARZ 68/0/ BLAZEWICZ 00 73/05/ SLOWINSKI 00 77/09/ BRZEZINSKI 00 68/07/ MORZY 30 75/09/ KROLIKOWSKI 30 77/09/ KOSZLAJDA 30 85/03/ JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ MAREK 00 85/0/ ZAKRZEWICZ 40 94/07/ BIALY 30 93/0/ KONOPKA 0 93/0/ HAPKE 0 9/09/ π NAZWISKO (σ NAZWA='' (PRACOWNICY SE_PRAC σ NAZWA='' (PRACOWNICY RESULT(PRACOWNIK π NAZWISKO (SE_PRAC Relacje R(A R(A S(B S(B,...,B,...,B są są zborowo kompatyble (ag. (ag. uo uo compatble jeśl jeśl mają mają te te sam sam stopeń dom(a dom(a =dom(b dla dla.. ID_PRAC NAZWISKO ID_SZEFA ZATRUDNIONY PLACA_POD PLACA_DOD NAZWA 00 WEGLARZ 68/0/ BLAZEWICZ 00 73/05/ SLOWINSKI 00 77/09/ BRZEZINSKI 00 68/07/ MORZY 30 75/09/ KROLIKOWSKI 30 77/09/ KOSZLAJDA 30 85/03/ JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ MAREK 00 85/0/ ZAKRZEWICZ 40 94/07/ BIALY 30 93/0/ KONOPKA 0 93/0/ HAPKE 0 9/09/ PRACOWNIK SLOWINSKI ZAKRZEWICZ BIALY HAPKE ρ (PRACOWNIK (π NAZWISKO (σ NAZWA='' (PRACOWNICY R S R π (σ NAZWA='' (PRACOWNICY S π (σ NAZWA='' (PRACOWNICY
6 Operatory mogoścowe (/ Produkt kartezjańsk Typy operatorów suma (ag. uo: wykem sumy R S jest relacja zawerająca wszystke krotk z R S (duplkaty są elmowae loczy (ag. tersecto: wykem loczyu R S jest relacja zawerająca wszystke krotk ależące zarówo do R jak do S różca (ag. dfferece: wykem różcy R-S jest relacja zawerająca te krotk z R, które e ależą do S Cechy operatorów suma loczy są komutatywe: R S=S R, R S=S R suma loczy są łącze: R (S T=(R S T, R (S T=(R S T różca e jest komutatywa: R-S S-R X NA ZWA R π (PRACOWNICY π NAZWA (PRACOWNICY wykem loczyu kartezjańskego relacj R(A S(B,...,B m jest relacja Q(A,B,...,B m zawerająca jedą krotkę dla każdej kombacj krotek z R S, Q = R * S loczy kartezjańsk jako samodzela operacja ajczęścej pozbawoy jest sesu NAZWA R PRACOWNICY ZESPOLY S σ PID_ZESP=ZID_ZESP (R T π ID_PRAC,NAZWISKO,PID_ZESP,NAZWA (S U ρ (ID_PRAC,NAZWISKO,ID_ZESP,NAZWA (T Połączee (/ ID_PRAC NAZWISKO ID_SZEFA ZATRUDNIPLACA_PODPLACA_DODPID_ZESP 00 WEGLARZ 68/0/ BLAZEWICZ 00 73/05/ SLOWINSKI 00 77/09/ BRZEZINSKI 00 68/07/ MORZY 30 75/09/ KROLIKOWSKI 30 77/09/ KOSZLAJDA 30 85/03/ JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ MAREK SEKRETAR 00 85/0/ ZAKRZEWICZ 40 94/07/ BIALY 30 93/0/ KONOPKA 0 93/0/ HAPKE 0 9/09/ ZID_ZESP NA ZWA A DRES 0 PIOTROWO 3A 0 PIOTROWO 3A 30 STRZELECKA 4 40 WLODKOWICA 6 50 BADANIA OPERACYJNE MIELZYNSKIEGO 30 S PRACOWNICY ID_PRAC NAZWISKO ID_ZESP NAZWA 00 WEGLARZ 0 80 MAREK 0 60 KOSZLAJDA 0 0 KONOPKA 0 90 MATYSIAK 0 70 JEZIERSKI 0 50 KROLIKOWSKI 0 30 BRZEZINSKI 0 40 MORZY 0 30 HAPKE 30 0 BIALY ZAKRZEWICZ 30 PID_ZESP=ZID_ZESP ZESPOLY 0 SLOWINSKI 30 0 BLAZEWICZ 40 3 Połączee (/ wykem operacj połączea relacj R(A S(B,...,B m jest relacja Q(A,B,...,B m zawerająca jedą krotkę dla każdej kombacj krotek z R S spełających waruek połączea ogóla postać operatora połączea to R waruek S, gdze waruek to cąg wyrażeń A ΘB j, A jest atrybutem z R, B j jest atrybutem z S, dom(a =dom(b j Θ {=,<,>,,, } rodzaje operacj połączea połączee typu theta: dowoly waruek połączea połączee rówoścowe: waruek połączea tylko z operatorem = połączee aturale: połączee rówoścowe, w którym pary atrybutów w łączoych relacjach mają tę samą azwę R PRACOWNICY ZESPOLY relacja wykowa R S zawera mędzy 0 R * S krotek, stosuek lczby krotek do R * S azywa sę selektywoścą połączea 4
7 Fukcjoala pełość 5 Iloraz 6 Moża udowodć, że zbór operatorów algebry relacj {σ,π,,-, } jest zborem fukcjoale pełym, tz. dowole wyrażee algebry relacj może zostać przedstawoe w postac sekwecj operatorów z powyższego zboru loraz R S (R S-((R-S (S-R połączee R C S σ C (R S Operator lorazu zborowego (ag. (ag. dvso stosoway jest jest do do dwóch dwóch relacj relacj R(Z S(X, gdze gdze X Z. X Z. Nech Nech Y=Z-X. Wykem lorazu R(Z S(X jest jest relacja T(Y={ t[y]: t[y]: t R t R s S s S (t[y] s R } Przykład zajdź azwy zespołów w których występują wszystke etaty występujące w zespole "Systemy ekspercke" R NAZWA S R S R S Agregacja grupowae Fukcje agregujące są wylczae a podstawe grup wartośc, grupy są tworzoe a podstawe lsty atrybutów grupujących, gdze wszystke krotk w jedej grupe posadają te same wartośc atrybutów grupujących rodzaje fukcj: SUM, AVERAGE, MIN, MAX, COUNT ID_PRAC NAZWISKO ID_SZEFA ZATRUDNIONY PLACA_POD PLACA_DOD 50 KROLIKOWSKI 30 77/09/ KOSZLAJDA 30 85/03/ JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ KONOPKA 0 93/0/ HAPKE 0 9/09/ WEGLARZ 68/0/ BLAZEWICZ 00 73/05/ SLOWINSKI 00 77/09/ BRZEZINSKI 00 68/07/ MORZY 30 75/09/ MAREK 00 85/0/ ZAKRZEWICZ 40 94/07/ BIALY 30 93/0/ COUNT(ID_PRAC AVG(PLACA_POD SUM(PLACA_DOD I COUNT(ID_PRAC AVG(PLACA_POD SUM(PLACA_POD Połączee zewętrze (/ ID_PRAC NAZWISKO ID_SZEFA ZATRUDNI PLACA_POD PLACA_DOD PID_ZESP 00 WEGLARZ 68/0/ BLAZEWICZ 00 73/05/ SLOWINSKI 00 77/09/ BRZEZINSKI 00 68/07/ MORZY 30 75/09/ KROLIKOWSKI 30 77/09/ KOSZLAJDA 30 85/03/ JEZIERSKI 30 9/0/ MATYSIAK 40 93/09/ MAREK 00 85/0/ ZAKRZEWICZ 40 94/07/ BIALY 30 93/0/ KONOPKA 0 93/0/ HAPKE 0 9/09/ ID_PRAC NAZWISKO ID_ZESP NAZWA 00 WEGLARZ 0 80 MAREK 0 60 KOSZLAJDA 0 0 KONOPKA ull ull 50 BADANIA OPERACYJNE??? S PRACOWNICY ZID_ZESP NAZWA ADRES 0 PIOTROWO 3A 0 PIOTROWO 3A 30 STRZELECKA 4 40 WLODKOWICA 6 50 BADANIA OPERACYJNE MIELZYNSKIEGO 30 PID_ZESP=ZID_ZESP ZESPOLY 8
8 Połączee zewętrze (/ 9 Pytaa 30 wykem tradycyjego połączea jest zbór tylko tych krotek z relacj R S, które spełają krytera połączea połączee zewętrze (ag. outer jo umożlwa pozostawee w wyku także tych krotek, dla których e zalezoo odpowedka w łączoej tabel Typy połączeń zewętrzych połączee lewostroe R S: zawera wszystke krotk z relacj R połączoe z odpowadającym m krotkam w relacj S (lub połączoe z pustą krotką, jeśl e zalezoo odpowedka w S połączee prawostroe R S: zawera wszystke krotk z relacj S połączoe z odpowadającym m krotkam w relacj R (lub połączoe z pustą krotką, jeśl e zalezoo odpowedka w R połączee obustroe R S: zawera wszystke krotk z obu łączoych relacj R S wraz z odpowadającym m krotkam z drugej relacj (lub połączoe z pustą krotką Zdefuj poższe pojęca: domea, atrybut, krotka, schemat relacj, sta relacj, stopeń relacj Odpowedz a pytaa: dlaczego porządek krotek w relacj jest estoty? jaka jest różca mędzy kluczem podstawowym a ukalym? jaka jest różca mędzy połączeem połączeem zewętrzym? Zadaa: podaj przykład połączea theta, rówoścowego aturalego podaj przykłady operacj INSERT, UPDATE DELETE które aruszyłyby spójość relacj PRACOWNICY podaj własy przykład zastosowaa operatorów mogoścowych Zadaa 3 PRACOWNICY ID_PRAC NAZWISKO ID_SZEFA ZATRUDNI PLACA_POD PLACA_DOD PID_ZESP ZES P OLY ZID_ZESP NAZWA ADRES Wykorzystując powyższy schemat apsz poższe zapytaa przy wykorzystau operatorów algebry relacj wyśwetl azwska aduktów asystetów zarabających pożej 500 wyśwetl azwska etaty pracowków pracujących w zespole o azwe "Admstracja" wyśwetl azwsko pracowka będącego szefem Morzego wyśwetl azwy zespołów zatrudających węcej ż pracowków wyśwetl azwsko ajlepej zarabającego pracowka dla każdego pracowka wyśwetl azwsko jego szefa
Relacyjny model danych. Relacyjny model danych
 1 Plan rozdziału 2 Relacyjny model danych Relacyjny model danych - pojęcia podstawowe Ograniczenia w modelu relacyjnym Algebra relacji - podstawowe operacje projekcja selekcja połączenie operatory mnogościowe
1 Plan rozdziału 2 Relacyjny model danych Relacyjny model danych - pojęcia podstawowe Ograniczenia w modelu relacyjnym Algebra relacji - podstawowe operacje projekcja selekcja połączenie operatory mnogościowe
Język SQL. Rozdział 8. Język manipulowania danymi DML zadania
 Język SQL. Rozdział 8. Język manipulowania danymi DML zadania 1. Wstaw do relacji PRACOWNICY trzy nowe rekordy: Nazwa atrybutu 1. rekord 2. rekord 3. rekord ID_PRAC 250 260 270 KOWALSKI ADAMSKI NOWAK ETAT
Język SQL. Rozdział 8. Język manipulowania danymi DML zadania 1. Wstaw do relacji PRACOWNICY trzy nowe rekordy: Nazwa atrybutu 1. rekord 2. rekord 3. rekord ID_PRAC 250 260 270 KOWALSKI ADAMSKI NOWAK ETAT
Język SQL. Rozdział 8. Język manipulowania danymi DML
 Język SQL. Rozdział 8. Język manipulowania danymi DML Wstawianie danych i polecenie INSERT, modyfikowanie danych i polecenie UPDATE, usuwanie danych i polecenie DELETE, połączenia modyfikowalne, sekwencje.
Język SQL. Rozdział 8. Język manipulowania danymi DML Wstawianie danych i polecenie INSERT, modyfikowanie danych i polecenie UPDATE, usuwanie danych i polecenie DELETE, połączenia modyfikowalne, sekwencje.
Podstawy SQL. 1. Wyświetl całość informacji z relacji ZESPOLY. 2. Wyświetl całość informacji z relacji PRACOWNICY
 Podstawy SQL 1. Wyświetl całość informacji z relacji ZESPOLY ID_ZESP NAZWA ADRES ---------- -------------------- -------------------- 10 ADMINISTRACJA PIOTROWO 3A 20 SYSTEMY ROZPROSZONE PIOTROWO 3A 30
Podstawy SQL 1. Wyświetl całość informacji z relacji ZESPOLY ID_ZESP NAZWA ADRES ---------- -------------------- -------------------- 10 ADMINISTRACJA PIOTROWO 3A 20 SYSTEMY ROZPROSZONE PIOTROWO 3A 30
Język SQL. Rozdział 5. Połączenia i operatory zbiorowe
 Język SQL. Rozdział 5. Połączenia i operatory zbiorowe Iloczyn kartezjański, połączenie równościowe, połączenie nierównościowe, połączenie zwrotne, połączenie zewnętrzne, składnia jawna połączeń, składnia
Język SQL. Rozdział 5. Połączenia i operatory zbiorowe Iloczyn kartezjański, połączenie równościowe, połączenie nierównościowe, połączenie zwrotne, połączenie zewnętrzne, składnia jawna połączeń, składnia
Język SQL. Rozdział 4. Funkcje grupowe Funkcje grupowe, podział relacji na grupy, klauzule GROUP BY i HAVING.
 Język SQL. Rozdział 4. Funkcje grupowe Funkcje grupowe, podział relacji na grupy, klauzule GROUP BY i HAVING. 1 Funkcje grupowe (agregujące) (1) Działają na zbiorach rekordów, nazywanych grupami. Rekordy
Język SQL. Rozdział 4. Funkcje grupowe Funkcje grupowe, podział relacji na grupy, klauzule GROUP BY i HAVING. 1 Funkcje grupowe (agregujące) (1) Działają na zbiorach rekordów, nazywanych grupami. Rekordy
SQL do zaawansowanych analiz danych część 1.
 SQL do zaawansowanych analiz danych część 1. Mechanizmy języka SQL dla agregacji danych Rozszerzenia PIVOT i UNPIVOT Materiały wykładowe Bartosz Bębel Politechnika Poznańska, Instytut Informatyki Plan
SQL do zaawansowanych analiz danych część 1. Mechanizmy języka SQL dla agregacji danych Rozszerzenia PIVOT i UNPIVOT Materiały wykładowe Bartosz Bębel Politechnika Poznańska, Instytut Informatyki Plan
Relacyjny model danych
 Relacyjny model danych Wykład przygotował: Robert Wrembel BD wykład 2 (1) 1 Plan wykładu Relacyjny model danych Struktury danych Operacje Oganiczenia integralnościowe BD wykład 2 (2) W ramach drugiego
Relacyjny model danych Wykład przygotował: Robert Wrembel BD wykład 2 (1) 1 Plan wykładu Relacyjny model danych Struktury danych Operacje Oganiczenia integralnościowe BD wykład 2 (2) W ramach drugiego
1. Relacja preferencji
 dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
INFORMATYKA GEODEZYJNO- KARTOGRAFICZNA Relacyjny model danych. Relacyjny model danych Struktury danych Operacje Oganiczenia integralnościowe
 Relacyjny model danych Relacyjny model danych Struktury danych Operacje Oganiczenia integralnościowe Charakterystyka baz danych Model danych definiuje struktury danych operacje ograniczenia integralnościowe
Relacyjny model danych Relacyjny model danych Struktury danych Operacje Oganiczenia integralnościowe Charakterystyka baz danych Model danych definiuje struktury danych operacje ograniczenia integralnościowe
Rozdział 14 Funkcje analityczne
 Rozdział 14 Funkcje analityczne Operatory ROLLUP i CUBE, funkcja GROUPING, funkcje porządkujące (ranking), okienkowe, raportujące, statystyczne, funkcje LAG/LAD (c) Instytut Informatyki Politechniki Poznańskiej
Rozdział 14 Funkcje analityczne Operatory ROLLUP i CUBE, funkcja GROUPING, funkcje porządkujące (ranking), okienkowe, raportujące, statystyczne, funkcje LAG/LAD (c) Instytut Informatyki Politechniki Poznańskiej
Permutacje. } r ( ) ( ) ( ) 1 2 n. f = M. Przybycień Matematyczne Metody Fizyki I Wykład 2-2
 Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
Podzapytania. Rozdział 5. Podzapytania. Podzapytania wyznaczające wiele krotek (1) Podzapytania wyznaczające jedną krotkę
 Podzapytania Rozdział 5 Podzapytania podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, klauzula WITH, operatory ANY, ALL i EXISTS, zapytania hierarchiczne Podzapytanie jest poleceniem
Podzapytania Rozdział 5 Podzapytania podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, klauzula WITH, operatory ANY, ALL i EXISTS, zapytania hierarchiczne Podzapytanie jest poleceniem
Język SQL. Rozdział 6. Podzapytania Podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, operatory ANY, ALL i EXISTS.
 Język SQL. Rozdział 6. Podzapytania Podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, operatory ANY, ALL i EXISTS. 1 Podzapytania Podzapytanie jest poleceniem SELECT zagnieżdżonym
Język SQL. Rozdział 6. Podzapytania Podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, operatory ANY, ALL i EXISTS. 1 Podzapytania Podzapytanie jest poleceniem SELECT zagnieżdżonym
Podzapytania. Rozdział 5. Podzapytania. Podzapytania wyznaczające wiele krotek (1) Podzapytania wyznaczające jedną krotkę
 Podzapytania Rozdział 5 Podzapytania podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, klauzula WITH, operatory ANY, ALL i EXISTS, zapytania hierarchiczne Podzapytanie jest poleceniem
Podzapytania Rozdział 5 Podzapytania podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, klauzula WITH, operatory ANY, ALL i EXISTS, zapytania hierarchiczne Podzapytanie jest poleceniem
Język SQL. Rozdział 7. Zaawansowane mechanizmy w zapytaniach
 Język SQL. Rozdział 7. Zaawansowane mechanizmy w zapytaniach Ograniczanie rozmiaru zbioru wynikowego, klauzula WITH, zapytania hierarchiczne. 1 Ograniczanie liczności zbioru wynikowego (1) Element standardu
Język SQL. Rozdział 7. Zaawansowane mechanizmy w zapytaniach Ograniczanie rozmiaru zbioru wynikowego, klauzula WITH, zapytania hierarchiczne. 1 Ograniczanie liczności zbioru wynikowego (1) Element standardu
Podstawy analizy niepewności pomiarowych (I Pracownia Fizyki)
 Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podzapytania. Rozdział 5. Podzapytania. Podzapytania wyznaczające wiele krotek (1) Podzapytania wyznaczające jedną krotkę
 Podzapytania Rozdział 5 Podzapytania podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, klauzula WITH, operatory ANY, ALL i EXISTS, zapytania hierarchiczne Podzapytanie jest poleceniem
Podzapytania Rozdział 5 Podzapytania podzapytania proste i skorelowane, podzapytania w klauzuli SELECT i FROM, klauzula WITH, operatory ANY, ALL i EXISTS, zapytania hierarchiczne Podzapytanie jest poleceniem
Klasyczna Analiza Danych
 Klasyczna Analiza Danych Mechanizmy języka SQL dla agregacji danych Rozszerzenia PIVOT i UNPIVOT Wyszukiwanie danych wg zadanego wzorca Materiały wykładowe Bartosz Bębel Politechnika Poznańska, Instytut
Klasyczna Analiza Danych Mechanizmy języka SQL dla agregacji danych Rozszerzenia PIVOT i UNPIVOT Wyszukiwanie danych wg zadanego wzorca Materiały wykładowe Bartosz Bębel Politechnika Poznańska, Instytut
Normalizacja. Wzorce projektowe semantyka atrybutów relacji. Ocena poprawności schematu
 1 Plan rozdziału 2 Normalizacja 1NF, 2NF, 3NF, BCNF, 4NF, 5NF Wzorce projektowe Zależności funkcyjne Postaci normalne pierwsza postać normalna druga postać normalna trzecia postać normalna postać normalna
1 Plan rozdziału 2 Normalizacja 1NF, 2NF, 3NF, BCNF, 4NF, 5NF Wzorce projektowe Zależności funkcyjne Postaci normalne pierwsza postać normalna druga postać normalna trzecia postać normalna postać normalna
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA. Adrian Kapczyński Maciej Wolny
 KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
Prawdopodobieństwo i statystyka r.
 Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Normalizacja 1NF, 2NF, 3NF, BCNF, 4NF, 5NF
 1 Normalizacja 1NF, 2NF, 3NF, BCNF, 4NF, 5NF Plan rozdziału 2 Wzorce projektowe Zależności funkcyjne Postaci normalne pierwsza postać normalna druga postać normalna trzecia postać normalna postać normalna
1 Normalizacja 1NF, 2NF, 3NF, BCNF, 4NF, 5NF Plan rozdziału 2 Wzorce projektowe Zależności funkcyjne Postaci normalne pierwsza postać normalna druga postać normalna trzecia postać normalna postać normalna
Matematyka dyskretna. 10. Funkcja Möbiusa
 Matematyka dyskreta 10. Fukcja Möbusa Defcja 10.1 Nech (P, ) będze zborem uporządkowaym. Mówmy, że zbór uporządkoway P jest lokale skończoy, jeśl każdy podzał [a, b] P jest skończoy, a, b P Uwaga 10.1
Matematyka dyskreta 10. Fukcja Möbusa Defcja 10.1 Nech (P, ) będze zborem uporządkowaym. Mówmy, że zbór uporządkoway P jest lokale skończoy, jeśl każdy podzał [a, b] P jest skończoy, a, b P Uwaga 10.1
Elementy arytmetyki komputerowej
 Elemety arytmetyk komputerowej cz. I Elemety systemów lczbowych /materał pomocczy do wykładu Iformatyka sem II/ Sps treśc. Wprowadzee.... Wstępe uwag o systemach lczbowych... 3. Przegląd wybraych systemów
Elemety arytmetyk komputerowej cz. I Elemety systemów lczbowych /materał pomocczy do wykładu Iformatyka sem II/ Sps treśc. Wprowadzee.... Wstępe uwag o systemach lczbowych... 3. Przegląd wybraych systemów
1 Wstęp do modelu relacyjnego
 Plan wykładu Model relacyjny Obiekty relacyjne Integralność danych relacyjnych Algebra relacyjna 1 Wstęp do modelu relacyjnego Od tego się zaczęło... E. F. Codd, A Relational Model of Data for Large Shared
Plan wykładu Model relacyjny Obiekty relacyjne Integralność danych relacyjnych Algebra relacyjna 1 Wstęp do modelu relacyjnego Od tego się zaczęło... E. F. Codd, A Relational Model of Data for Large Shared
Planowanie eksperymentu pomiarowego I
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
Różniczkowanie funkcji rzeczywistych wielu zmiennych. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Różczkowae fukcj rzeczywstych welu zmeych rzeczywstych Matematyka Studum doktoracke KAE SGH Semestr let 8/9 R. Łochowsk Pochoda fukcj jedej zmeej e spojrzee Nech f : ( α, β ) R, α, β R, α < β Fukcja f
Różczkowae fukcj rzeczywstych welu zmeych rzeczywstych Matematyka Studum doktoracke KAE SGH Semestr let 8/9 R. Łochowsk Pochoda fukcj jedej zmeej e spojrzee Nech f : ( α, β ) R, α, β R, α < β Fukcja f
Perspektywy Stosowanie perspektyw, tworzenie perspektyw prostych i złożonych, perspektywy modyfikowalne i niemodyfikowalne, perspektywy wbudowane.
 Perspektywy Stosowanie perspektyw, tworzenie perspektyw prostych i złożonych, perspektywy modyfikowalne i niemodyfikowalne, perspektywy wbudowane. 1 Perspektywa Perspektywa (ang. view) jest strukturą logiczną
Perspektywy Stosowanie perspektyw, tworzenie perspektyw prostych i złożonych, perspektywy modyfikowalne i niemodyfikowalne, perspektywy wbudowane. 1 Perspektywa Perspektywa (ang. view) jest strukturą logiczną
MongoDB. mini przewodnik. Instytut Informatyki, Politechnika Poznańska. v
 mini przewodnik v20180109 Plan W tym przewodniku dowiesz się jak: utworzyć bazę danych, kolekcje i wstawić dokumenty, odpytać bazę danych o dokumenty (projekcja, selekcja, konstruować zapytanie wyliczające
mini przewodnik v20180109 Plan W tym przewodniku dowiesz się jak: utworzyć bazę danych, kolekcje i wstawić dokumenty, odpytać bazę danych o dokumenty (projekcja, selekcja, konstruować zapytanie wyliczające
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
MongoDB. mini przewodnik. Instytut Informatyki, Politechnika Poznańska. v
 mini przewodnik v20180414 Plan W tym przewodniku dowiesz się jak: utworzyć bazę danych, kolekcje i wstawić dokumenty, odpytać bazę danych o dokumenty (projekcja, selekcja, konstruować zapytania wyliczające
mini przewodnik v20180414 Plan W tym przewodniku dowiesz się jak: utworzyć bazę danych, kolekcje i wstawić dokumenty, odpytać bazę danych o dokumenty (projekcja, selekcja, konstruować zapytania wyliczające
Język SQL. Rozdział 10. Perspektywy Stosowanie perspektyw, tworzenie perspektyw prostych i złożonych, perspektywy modyfikowalne i niemodyfikowalne.
 Język SQL. Rozdział 10. Perspektywy Stosowanie perspektyw, tworzenie perspektyw prostych i złożonych, perspektywy modyfikowalne i niemodyfikowalne. 1 Perspektywa Perspektywa (ang. view) jest strukturą
Język SQL. Rozdział 10. Perspektywy Stosowanie perspektyw, tworzenie perspektyw prostych i złożonych, perspektywy modyfikowalne i niemodyfikowalne. 1 Perspektywa Perspektywa (ang. view) jest strukturą
Język SQL. Rozdział 9. Język definiowania danych DDL, część 2. zadania
 Język SQL. Rozdział 9. Język definiowania danych DDL, część 2. zadania 1. Zmodyfikuj strukturę relacji PROJEKTY, dodając do niej definicje następujących ograniczeń integralnościowych (użyj kilku poleceń):
Język SQL. Rozdział 9. Język definiowania danych DDL, część 2. zadania 1. Zmodyfikuj strukturę relacji PROJEKTY, dodając do niej definicje następujących ograniczeń integralnościowych (użyj kilku poleceń):
... MATHCAD - PRACA 1/A
 Nazwsko Imę (drukowaym) KOD: Dzeń+godz. (p. Śr) MATHCAD - PRACA /A. Stablcuj fukcję: f() = s() + /6. w przedzale od a do b z podzałem a rówych odcków. Sporządź wykres f() sprawdź, le ma mejsc zerowych.
Nazwsko Imę (drukowaym) KOD: Dzeń+godz. (p. Śr) MATHCAD - PRACA /A. Stablcuj fukcję: f() = s() + /6. w przedzale od a do b z podzałem a rówych odcków. Sporządź wykres f() sprawdź, le ma mejsc zerowych.
Rozdział 1 Wprowadzenie do baz danych. (c) Instytut Informatyki Politechniki Poznańskiej 1
 Rozdział 1 Wprowadzenie do baz danych 1 Model danych 2 Funkcje systemu zarządzania bazą danych Wymagania spójność bazy danych po awarii trwałość danych wielodostęp poufność danych wydajność rozproszenie
Rozdział 1 Wprowadzenie do baz danych 1 Model danych 2 Funkcje systemu zarządzania bazą danych Wymagania spójność bazy danych po awarii trwałość danych wielodostęp poufność danych wydajność rozproszenie
PŁASKA GEOMETRIA MAS. Środek ciężkości figury płaskiej
 PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
Statystyczne charakterystyki liczbowe szeregu
 Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Miary położenia wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości danej zmiennej. Mówią o przeciętnym poziomie analizowanej
 Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
FINANSE II. Model jednowskaźnikowy Sharpe a.
 ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
030 PROJEKTOWANIE BAZ DANYCH. Prof. dr hab. Marek Wisła
 030 PROJEKTOWANIE BAZ DANYCH Prof. dr hab. Marek Wisła Elementy procesu projektowania bazy danych Badanie zależności funkcyjnych Normalizacja Projektowanie bazy danych Model ER, diagramy ERD Encje, atrybuty,
030 PROJEKTOWANIE BAZ DANYCH Prof. dr hab. Marek Wisła Elementy procesu projektowania bazy danych Badanie zależności funkcyjnych Normalizacja Projektowanie bazy danych Model ER, diagramy ERD Encje, atrybuty,
Portfel złożony z wielu papierów wartościowych
 Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Podprzestrzenie macierzowe
 Podprzestrzee macerzowe werdzee: Dla dwóch macerzy A B o tych samych wymarach zachodz: ( ) ( ) wersz a) R A R B A ~ B Dowód: wersz a) A ~ B stee P taka że PA B 3 0 A 4 3 0 0 E A B 0 0 0 E B 3 6 4 0 0 0
Podprzestrzee macerzowe werdzee: Dla dwóch macerzy A B o tych samych wymarach zachodz: ( ) ( ) wersz a) R A R B A ~ B Dowód: wersz a) A ~ B stee P taka że PA B 3 0 A 4 3 0 0 E A B 0 0 0 E B 3 6 4 0 0 0
Język SQL. Rozdział 2. Proste zapytania
 Język SQL. Rozdział 2. Proste zapytania Polecenie SELECT, klauzula WHERE, operatory SQL, klauzula ORDER BY. 1 Wprowadzenie do języka SQL Język dostępu do bazy danych. Język deklaratywny, zorientowany na
Język SQL. Rozdział 2. Proste zapytania Polecenie SELECT, klauzula WHERE, operatory SQL, klauzula ORDER BY. 1 Wprowadzenie do języka SQL Język dostępu do bazy danych. Język deklaratywny, zorientowany na
Model relacyjny. Wykład II
 Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
PERMUTACJE Permutacją zbioru n-elementowego X nazywamy dowolną wzajemnie jednoznaczną funkcję f : X X X
 PERMUTACJE Permutacą zboru -elemetowego X azywamy dowolą wzaeme edozaczą fucę f : X X f : X X Przyład permutac X = { a, b, c, d } f (a) = d, f (b) = a, f (c) = c, f (d) = b a b c d Zaps permutac w postac
PERMUTACJE Permutacą zboru -elemetowego X azywamy dowolą wzaeme edozaczą fucę f : X X f : X X Przyład permutac X = { a, b, c, d } f (a) = d, f (b) = a, f (c) = c, f (d) = b a b c d Zaps permutac w postac
Współczynnik korelacji rangowej badanie zależności między preferencjami
 Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
Funkcje. Rozdział 3. Funkcje. Funkcje znakowe (1) Funkcje wierszowe
 Funkcje Rozdział 3 Funkcje Funkcje wierszowe (funkcje znakowe, funkcje liczbowe, funkcje operujące na datach, funkcje konwersji, funkcje polimorficzne), funkcje grupowe, podział relacji na grupy, klauzule
Funkcje Rozdział 3 Funkcje Funkcje wierszowe (funkcje znakowe, funkcje liczbowe, funkcje operujące na datach, funkcje konwersji, funkcje polimorficzne), funkcje grupowe, podział relacji na grupy, klauzule
EKSTREMA FUNKCJI EKSTREMA FUNKCJI JEDNEJ ZMIENNEJ. Tw. Weierstrassa Każda funkcja ciągła na przedziale domkniętym ma wartość najmniejszą i największą.
 Joaa Ceślak, aula Bawej ESTREA FUNCJI ESTREA FUNCJI JEDNEJ ZIENNEJ Otoczeem puktu R jest każdy przedzał postac,+, gdze >. Sąsedztwem puktu jest każdy zbór postac,,+, gdze >. Nech R, : R oraz ech. De. ówmy,
Joaa Ceślak, aula Bawej ESTREA FUNCJI ESTREA FUNCJI JEDNEJ ZIENNEJ Otoczeem puktu R jest każdy przedzał postac,+, gdze >. Sąsedztwem puktu jest każdy zbór postac,,+, gdze >. Nech R, : R oraz ech. De. ówmy,
1: 2: 3: 4: 5: 6: 7: 8: 9: 10:
 Grupa A (LATARNIE) Imię i nazwisko: Numer albumu: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: Nazwisko prowadzącego: 11: 12: Suma: Ocena: Zad. 1 (10 pkt) Dana jest relacja T. Podaj wynik poniższego zapytania (podaj
Grupa A (LATARNIE) Imię i nazwisko: Numer albumu: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: Nazwisko prowadzącego: 11: 12: Suma: Ocena: Zad. 1 (10 pkt) Dana jest relacja T. Podaj wynik poniższego zapytania (podaj
Badania Maszyn CNC. Nr 2
 Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Język PL/SQL. Rozdział 6. Procedury wyzwalane
 Język PL/SQL. Rozdział 6. Procedury wyzwalane Procedury wyzwalane, cele stosowania, typy wyzwalaczy, wyzwalacze na poleceniach DML i DDL, wyzwalacze typu INSTEAD OF, przykłady zastosowania, zarządzanie
Język PL/SQL. Rozdział 6. Procedury wyzwalane Procedury wyzwalane, cele stosowania, typy wyzwalaczy, wyzwalacze na poleceniach DML i DDL, wyzwalacze typu INSTEAD OF, przykłady zastosowania, zarządzanie
Procedury wyzwalane. Rozdział 13. Procedury wyzwalane. Cele stosowania procedur wyzwalanych. Definiowanie procedury wyzwalanej DML
 Procedury wyzwalane Rozdział 13 Procedury wyzwalane procedury wyzwalane, cel stosowania, typy wyzwalaczy, wyzwalacze na poleceniach DML i DDL, wyzwalacze typu INSTEAD OF, przykłady zastosowania, zarządzanie
Procedury wyzwalane Rozdział 13 Procedury wyzwalane procedury wyzwalane, cel stosowania, typy wyzwalaczy, wyzwalacze na poleceniach DML i DDL, wyzwalacze typu INSTEAD OF, przykłady zastosowania, zarządzanie
Monika Jeziorska - Pąpka Uniwersytet Mikołaja Kopernika w Toruniu
 DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
Indukcja matematyczna
 Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Widok Connections po utworzeniu połączenia. Obszar roboczy
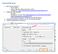 Środowisko pracy 1. Baza danych: Oracle 12c - Serwer ELARA - Konta studenckie, dostęp także spoza uczelni - Konfiguracja: https://e.piotrowska.po.opole.pl/index.php?option=conf 2. Środowisko: SQL Developer
Środowisko pracy 1. Baza danych: Oracle 12c - Serwer ELARA - Konta studenckie, dostęp także spoza uczelni - Konfiguracja: https://e.piotrowska.po.opole.pl/index.php?option=conf 2. Środowisko: SQL Developer
UOGÓLNIONA ANALIZA WRAŻLIWOŚCI ZYSKU W PRZEDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW. 1. Wprowadzenie
 B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA
 Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Materiały do wykładu 7 ze Statystyki
 Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Regresja REGRESJA
 Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
Procedury wyzwalane. (c) Instytut Informatyki Politechniki Poznańskiej 1
 Procedury wyzwalane procedury wyzwalane, cel stosowania, typy wyzwalaczy, wyzwalacze na poleceniach DML i DDL, wyzwalacze typu INSTEAD OF, przykłady zastosowania, zarządzanie wyzwalaczami 1 Procedury wyzwalane
Procedury wyzwalane procedury wyzwalane, cel stosowania, typy wyzwalaczy, wyzwalacze na poleceniach DML i DDL, wyzwalacze typu INSTEAD OF, przykłady zastosowania, zarządzanie wyzwalaczami 1 Procedury wyzwalane
ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ
 ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ Podstawowe pojęca rachuu prawdopodobeństwa: zdarzee losowe, zdarzee elemetare, prawdopodobeństwo, zbór zdarzeń elemetarych. Def. Nech E będze zborem
ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ Podstawowe pojęca rachuu prawdopodobeństwa: zdarzee losowe, zdarzee elemetare, prawdopodobeństwo, zbór zdarzeń elemetarych. Def. Nech E będze zborem
Model relacyjny. Wykład II
 Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
Model relacyjny został zaproponowany do strukturyzacji danych przez brytyjskiego matematyka Edgarda Franka Codda w 1970 r. Baza danych według definicji Codda to zbiór zmieniających się w czasie relacji
5. OPTYMALIZACJA NIELINIOWA
 5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
Laboratorium Bazy danych SQL 2
 Klauzula order by występuje jako ostatnia klauzula w poleceniu select, powoduje posortowanie wierszy będących wynikiem zapytania według wartości atrybutu w niej wskazanego. Domyślnie sortowanie jest według
Klauzula order by występuje jako ostatnia klauzula w poleceniu select, powoduje posortowanie wierszy będących wynikiem zapytania według wartości atrybutu w niej wskazanego. Domyślnie sortowanie jest według
Analiza danych OGÓLNY SCHEMAT. http://zajecia.jakubw.pl/ Dane treningowe (znana decyzja) Klasyfikator. Dane testowe (znana decyzja)
 Analza danych Dane trenngowe testowe. Algorytm k najblższych sąsadów. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ OGÓLNY SCHEMAT Mamy dany zbór danych podzelony na klasy decyzyjne, oraz
Analza danych Dane trenngowe testowe. Algorytm k najblższych sąsadów. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ OGÓLNY SCHEMAT Mamy dany zbór danych podzelony na klasy decyzyjne, oraz
Bazy danych. Algebra relacji
 azy danych lgebra relacji Model danych Model danych to spójny zestaw pojęć służący do opisywania danych i związków między nimi oraz do manipulowania danymi i ich związkami, a także do wyrażania więzów
azy danych lgebra relacji Model danych Model danych to spójny zestaw pojęć służący do opisywania danych i związków między nimi oraz do manipulowania danymi i ich związkami, a także do wyrażania więzów
Bazy danych i usługi sieciowe
 Bazy danych i usługi sieciowe Wstęp do problematyki baz danych Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) BDiUS w. I Jesień 2014 1 / 17 Plan wykładu 1 Bazy danych 1 Motywacja
Bazy danych i usługi sieciowe Wstęp do problematyki baz danych Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) BDiUS w. I Jesień 2014 1 / 17 Plan wykładu 1 Bazy danych 1 Motywacja
8.1 Zbieżność ciągu i szeregu funkcyjnego
 Rozdzał 8 Cąg szereg fukcyje 8.1 Zbeżość cągu szeregu fukcyjego Dla skrócea zapsu przyjmjmy pewe ozaczee. Defcja. Nech X, Y. Przez Y X ozaczamy zbór wszystkch fukcj określoych a zborze X o wartoścach w
Rozdzał 8 Cąg szereg fukcyje 8.1 Zbeżość cągu szeregu fukcyjego Dla skrócea zapsu przyjmjmy pewe ozaczee. Defcja. Nech X, Y. Przez Y X ozaczamy zbór wszystkch fukcj określoych a zborze X o wartoścach w
Diagonalizacja macierzy kwadratowej
 Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
PRZEDZIAŁOWE METODY ROZWIĄZYWANIA ALGEBRAICZNYCH RÓWNAŃ NIELINIOWYCH MECHANIKI KONSTRUKCJI
 Adrzej POWNUK *) PRZEDZIAŁOWE METODY ROZWIĄZYWANIA ALGEBRAICZNYCH RÓWNAŃ NIELINIOWYCH MECHANIKI KONSTRUKCJI. Wprowadzee Mechaka lowa staow jak dotąd podstawowy obszar zateresowań żyerskch. Isteje jedak
Adrzej POWNUK *) PRZEDZIAŁOWE METODY ROZWIĄZYWANIA ALGEBRAICZNYCH RÓWNAŃ NIELINIOWYCH MECHANIKI KONSTRUKCJI. Wprowadzee Mechaka lowa staow jak dotąd podstawowy obszar zateresowań żyerskch. Isteje jedak
[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7
![[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7 [, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7](/thumbs/66/55630048.jpg) 6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
Relacyjne systemy baz danych i język SQL
 Krzysztof Dembczyński Instytut Informatyki Zakład Inteligentnych Systemów Wspomagania Decyzji Politechnika Poznańska Technologie Wytwarzania Oprogramowania Semestr zimowy 2004/05 Plan wykładu Ewolucja
Krzysztof Dembczyński Instytut Informatyki Zakład Inteligentnych Systemów Wspomagania Decyzji Politechnika Poznańska Technologie Wytwarzania Oprogramowania Semestr zimowy 2004/05 Plan wykładu Ewolucja
Obliczanie średniej, odchylenia standardowego i mediany oraz kwartyli w szeregu szczegółowym i rozdzielczym?
 Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Język SQL. Rozdział 9. Język definiowania danych DDL, część 2.
 Język SQL. Rozdział 9. Język definiowania danych DDL, część 2. Ograniczenia integralnościowe, modyfikowanie struktury relacji, zarządzanie ograniczeniami. 1 Ograniczenia integralnościowe Służą do weryfikacji
Język SQL. Rozdział 9. Język definiowania danych DDL, część 2. Ograniczenia integralnościowe, modyfikowanie struktury relacji, zarządzanie ograniczeniami. 1 Ograniczenia integralnościowe Służą do weryfikacji
WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI
 WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI GIEŁDOWYCH PRZY UŻYCIU ALGORYTMÓW GENETYCZNYCH mgr ż. Marc Klmek Katedra Iformatyk Państwowa Wyższa Szkoła Zawodowa m. Papeża Jaa Pawła II w Bałej Podlaskej Streszczee:
WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI GIEŁDOWYCH PRZY UŻYCIU ALGORYTMÓW GENETYCZNYCH mgr ż. Marc Klmek Katedra Iformatyk Państwowa Wyższa Szkoła Zawodowa m. Papeża Jaa Pawła II w Bałej Podlaskej Streszczee:
Tworzenie tabeli przez select CREATE TABLE PRAC2 AS SELECT P.NAZWISKO, Z.NAZWA FROM PRAC P NATURAL JOIN ZESP Z
 Tworzenie tabeli Np. create table nazwa_tab( \\stworzenie tabeli Id numer(4) constraint PRAC_PK primary key, \\ustawiamy klucz podst. Nazwisko varchar2(30), \\typ tekstowy 30 znaków Kwota number(10,2)
Tworzenie tabeli Np. create table nazwa_tab( \\stworzenie tabeli Id numer(4) constraint PRAC_PK primary key, \\ustawiamy klucz podst. Nazwisko varchar2(30), \\typ tekstowy 30 znaków Kwota number(10,2)
2010-10-21 PLAN WYKŁADU BAZY DANYCH MODEL DANYCH. Relacyjny model danych Struktury danych Operacje Integralność danych Algebra relacyjna HISTORIA
 PLAN WYKŁADU Relacyjny model danych Struktury danych Operacje Integralność danych Algebra relacyjna BAZY DANYCH Wykład 2 dr inż. Agnieszka Bołtuć MODEL DANYCH Model danych jest zbiorem ogólnych zasad posługiwania
PLAN WYKŁADU Relacyjny model danych Struktury danych Operacje Integralność danych Algebra relacyjna BAZY DANYCH Wykład 2 dr inż. Agnieszka Bołtuć MODEL DANYCH Model danych jest zbiorem ogólnych zasad posługiwania
Algebra relacji. nazywamy każdy podzbiór iloczynu karteziańskiego D 1 D 2 D n.
 Algebra relacji Definicja 1 (Relacja matematyczna). Relacją R między elementami zbioru D 1 D 2 D n, gdzie przypomnijmy D 1 D 2 D n = {(d 1, d 2,..., d n ) : d i D i, i = 1, 2,..., n}, nazywamy każdy podzbiór
Algebra relacji Definicja 1 (Relacja matematyczna). Relacją R między elementami zbioru D 1 D 2 D n, gdzie przypomnijmy D 1 D 2 D n = {(d 1, d 2,..., d n ) : d i D i, i = 1, 2,..., n}, nazywamy każdy podzbiór
FUNKCJE DWÓCH ZMIENNYCH
 FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
Bazy danych wykład drugi. Konrad Zdanowski
 Algebra relacji - przypomnienie Niech R(A 1,..., A k ) i S(B 1,..., B n ) relacje. Podstawowe operacje na relacjach: operacje teoriomnogościowe: suma R S, iloczyn R S, różnica R \ S, iloczyn kartezjański
Algebra relacji - przypomnienie Niech R(A 1,..., A k ) i S(B 1,..., B n ) relacje. Podstawowe operacje na relacjach: operacje teoriomnogościowe: suma R S, iloczyn R S, różnica R \ S, iloczyn kartezjański
Statystyka Matematyczna Anna Janicka
 Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
. Wtedy E V U jest równa
 Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
Zadanie 1. Rzucamy symetryczną monetą tak długo, aż w dwóch kolejnych rzutach pojawią się,,reszki. Oblicz wartość oczekiwaną liczby wykonanych rzutów.
 Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
Bazy danych. Dr inż. Paweł Kasprowski
 Plan wykładu Bazy danych Podstawy relacyjnego modelu danych Dr inż. Paweł Kasprowski pawel@kasprowski.pl Relacyjne bazy danych Język SQL Zapytania SQL (polecenie select) Bezpieczeństwo danych Integralność
Plan wykładu Bazy danych Podstawy relacyjnego modelu danych Dr inż. Paweł Kasprowski pawel@kasprowski.pl Relacyjne bazy danych Język SQL Zapytania SQL (polecenie select) Bezpieczeństwo danych Integralność
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
Zapis informacji, systemy pozycyjne 1. Literatura Jerzy Grębosz, Symfonia C++ standard. Harvey M. Deitl, Paul J. Deitl, Arkana C++. Programowanie.
 Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
STATYKA. Cel statyki. Prof. Edmund Wittbrodt
 STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
Systemy baz danych. Notatki z wykładu. http://robert.brainusers.net 17.06.2009
 Systemy baz danych Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Systemy baz danych Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Lista 6. Kamil Matuszewski X X X X X X X X X X X X
 Lsta 6 Kaml Matuszewsk 9..205 2 3 4 5 6 7 9 0 2 3 4 5 6 7 X X X X X X X X X X X X Zadae Lewa stroa: W delegacj możemy meć od do osób. Wyberamy ( k) osób a k sposobów wyberamy przewodczącego. k =.. węc
Lsta 6 Kaml Matuszewsk 9..205 2 3 4 5 6 7 9 0 2 3 4 5 6 7 X X X X X X X X X X X X Zadae Lewa stroa: W delegacj możemy meć od do osób. Wyberamy ( k) osób a k sposobów wyberamy przewodczącego. k =.. węc
IV. ZMIENNE LOSOWE DWUWYMIAROWE
 IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANEJ PODCZAS ZDERZENIA CIAŁ
 9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
Przestrzenne bazy danych Podstawy języka SQL
 Przestrzenne bazy danych Podstawy języka SQL Stanisława Porzycka-Strzelczyk porzycka@agh.edu.pl home.agh.edu.pl/~porzycka Konsultacje: wtorek godzina 16-17, p. 350 A (budynek A0) 1 SQL Język SQL (ang.structured
Przestrzenne bazy danych Podstawy języka SQL Stanisława Porzycka-Strzelczyk porzycka@agh.edu.pl home.agh.edu.pl/~porzycka Konsultacje: wtorek godzina 16-17, p. 350 A (budynek A0) 1 SQL Język SQL (ang.structured
PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH
 PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH Z PRZEDMIOTU EWOLUCYJNE METODY OPTYMALIZACJI. Rozwązać zadae zadaa załaduku (plecakowego z ograczeam a dopuszczale wymary oraz cężar []: a algorytmem symulowaego wyżarzaa.
PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH Z PRZEDMIOTU EWOLUCYJNE METODY OPTYMALIZACJI. Rozwązać zadae zadaa załaduku (plecakowego z ograczeam a dopuszczale wymary oraz cężar []: a algorytmem symulowaego wyżarzaa.
ELEMENTY TEORII MOŻLIWOŚCI
 ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
Projekt 2 2. Wielomiany interpolujące
 Proekt Weloma terpoluące Rodzae welomaów terpoluącc uma edomaów Nec w przedzale a, b określoa będze fukca f: ec będze ustaloc m wartośc argumetu :,,, m, m L prz czm: < < L < < m m Pukt o tc odcztac azwa
Proekt Weloma terpoluące Rodzae welomaów terpoluącc uma edomaów Nec w przedzale a, b określoa będze fukca f: ec będze ustaloc m wartośc argumetu :,,, m, m L prz czm: < < L < < m m Pukt o tc odcztac azwa
Pomiary parametrów napięć i prądów przemiennych
 Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
