3. Zjawisko wzmocnienia i nasycenia. Rozkład mocy w przekroju poprzecznym (TEM)

Transkrypt

1 3. Zjawisko wzmocieia i asyceia. Rozkład mocy w przekroju poprzeczym (TEM) 3.. Zjawisko wzmocieia i asyceia W staie rówowagi termodyamiczej obsadzaie staów eergetyczych opisae jest rozkładem Boltzmaa. Ozacza to, że dla każdej temperatury większość cząsteczek przebywa w iższych staach eergetyczych tylko dla poziomów rotacyjych stwierdzeie to ie jest zawsze prawdziwe. Tak więc, przy jedakowym prawdopodobieństwie przejść wymuszoych ze stau o iższej eergii do stau o wyższej eergii (absorpcja) i ze stau o wyższej eergii do stau o iższej eergii (emisja), całkowita liczba przejść z poziomów iższych a wyższe jest większa iż liczba przejść odwrotych, czyli układ pochłaia eergię promieiowaia ρ ω < 0. (3.) t ρ Aby padające promieiowaie zostało wzmocioe (czyli ω > 0 ), musi astąpić, t jak już powiedzieliśmy wcześiej, iwersja obsadzeń czyli >. (3.) g g α l = I e Z prawa Lamberta - Beera I 0 musiałoby więc wyikać, że współczyik absorpcji α jest ujemy. Ozacza to, że tradycyje rówaie Lamberta - Beera traci tutaj ses, jest oo bowiem wyprowadzoe dla α = cost, czyli dla zakresu optyki liiowej, gdy atężeie padającego promieiowaia jest małe. Promieiowaie o iewielkim atężeiu ie powoduje odchyleń od stau rówowagi termodyamiczej dla obsadzaia poziomów eergetyczych przez cząsteczki. Gdy a układ pada promieiowaie o dużym atężeiu, arusza oo paującą rówowagę termodyamiczą. Ilość pochłaiaej eergii zmiejsza się, a współczyik absorpcji maleje, coraz więcej bowiem cząsteczek zostaje przeiesioych a wyższy poziom eergetyczy. Gdy atężeie padającego promieiowaia adal rośie, układ osiąga sta asyceia czyli =. (3.3) g g 30

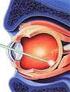
2 Ozacza to, że układ wybiela się, ie ma bowiem ai pochłaiaia, ai emitowaia eergii (α = 0). Przy dalszym wzroście atężeia padającego promieiowaia układ osiąga sta zway iwersją obsadzeń, czyli >. Układ zaczya emitować więcej g g eergii iż absorbować (α<0). Rys. 3.. Zależość współczyika absorpcji od atężeia padającego promieiowaia w zakresie optyki ieliiowej Oszacujmy, jak duże muszą być moce wiązki pompującej, aby został osiągięty sta asyceia. Rozważmy układ dwupoziomowy m. Jak już powiedzieliśmy wcześiej, w warukach rówowagi w układzie dwupoziomowym możemy osiągąć jedyie sta asyceia =, ie moża zaś osiągąć stau iwersji obsadzeń. g g Niech N 0 =N +N m będzie liczbą cząsteczek w jedostce objętości, N i N m są liczbami cząsteczek a poziomie i poziomie m. Zmiaa obsadzaia poziomu m w czasie wyosi dnm N ( ) m = W N Nm, (3.4) dt τ gdzie W = B m ρ ω. (3.5) We wzorze (3.4) pierwszy czło charakteryzuje procesy absorpcji wymuszoej, zaś czło drugi spotaicze opróżiaie poziomu wyższego m w sposób promieisty lub bezpromieisty z czasem życia a poziomie wzbudzoym τ. Wyraźmy N m za pomocą N=N -N m, czyli ( N Nm ) + Nm = N Nm N = (3.6) 0 N + Nm = + i podstawmy do wzoru (3.4). Otrzymujemy: d N N0 N N = W N + = N W (3.7) dt τ τ τ τ d N Załóżmy, że osiągięty został sta stacjoary = 0. Z rówaia (3.7) dt otrzymujemy więc 3

3 N N W τ τ =, (3.8) czyli N0 N =. (3.9) Wτ + Gdy wzrasta atężeie światła wywołującego przejścia, rośie W, a maleje N. Prawdopodobieństwo W związae jest z gęstością promieiowaia padającego zgodie ze wzorem (3.5). Moża pokazać, że W wiąże się z atężeiem promieiowaia I (czyli strumieiem eergii a powierzchię cm w czasie s) astępująco: σ I W =, (3.0) gdzie σ jest przekrojem czyym a absorpcję. Przekrój czyy σ jest związay ze współczyikiem absorpcji α zależością α =σν, gdzie N jest liczbą cząsteczek w cm 3. Jedostką przekroju czyego σ jest cm, a typowe przekroje czye mieszczą się w zakresie cm w zależości od zakresu widmowego. Dla obszaru widzialego są oe rzędu 0-6 cm. Podstawiając (3.0) do (3.9), otrzymujemy N0 N =. (3.) σ I τ + Ozaczając =, (3.) στ otrzymujemy N0 N =. (3.3) I + Wielkość osi azwę parametru asyceia i jest ważym parametrem pozwalającym określić wartość atężeia wiązki pompującej I, przy której rozpoczya się efekt asyceia, choć jest to oczywiście graica umowa. Gdy I=, ze wzoru (3.3) 3 otrzymujemy N = N 0, czyli N = N 0, N = N 0. Ozacza to, że choć 4 4 iwersja obsadzeń jeszcze ie astąpiła, to jedak zacząca część cząsteczek zajduje się a poziomie wzbudzoym N. Sta pełego asyceia osiągamy przy dalszym wzroście wartości I, gdy bowiem I>> wówczas, N 0 i N =N. Parametr asyceia ma prostą iterpretację fizyczą, wzór (3.) bowiem moża przekształcić tak, aby σ =. (3.4) τ I σ Czło s ozacza średią szybkość absorpcji a jedostkę eergii, zaś opisuje τ średią szybkość relaksacji spotaiczej. Parametr asyceia ozacza więc takie 3

4 atężeie padającego światła, przy którym szybkość pompowaia układu (przejścia do staów o wyższej eergii) zdołała się zrówać z szybkością opróżiaia poziomu wyższego (przejścia do stau o iższej eergii). Gdy to się staie, sta asyceia zaczya być dostrzegaly. Zakładając, że σ = 0-6 cm, a szybkość relaksacji jest rzędu τ = 0-6 s, otrzymamy atężeie asyceia około - kw/cm. Tak więc a przykład typowy laser argoowy o iezbyt dużej mocy 4 W używay do pomiarów spotaiczego rozpraszaia Ramaa wysyła wiązkę o atężeiu rzędu I = 4 W/(0, mm) = 0,4 kw/cm. Natężeie to jest więc za małe, aby wywoływać iwersję obsadzeń i pompować p. laser barwikowy lub szafirowy, ale lasery argoowe o mocy W mogą już być użyte do takich celów. Waruek (3.4) określa parametr asyceia dla laserów pracujących w reżimie pracy ciągłej. Waruek asyceia dla laserów pracujących jako lasery impulsowe jest trochę iy, miaowicie τ imp =, (3.5) σ gdzie τ imp jest czasem trwaia impulsu. Wyika to z faktu, że τ imp jest dużo krótszy od τ i dlatego czas charakteryzujący relaksację układu τ przestaje być istoty. 3.. Rozkład mocy w przekroju poprzeczym Do tej pory zakładaliśmy, że rezoator optyczy jest rezoatorem płaskim (rys.3.a). W rezoatorze płaskim powstaje fala płaska, tworząca z falą odbitą falę stojącą. O rozkładzie atężeia wzdłuż osi rezoatora decyduje waruek geeracji fali stojącej λ q = L, (3.6) gdzie q jest liczbą całkowitą. Aby powstała fala stojąca o długości λ, w rezoatorze optyczym o długości L musi się zmieścić wielokrotość połówek długości fali. Ozacza to, że dla różych liczb całkowitych q powstają fale o różej częstotliwości, zwae modami podłużym lub osiowymi charakteryzowae liczbą q (we wcześiejszych ozaczeiach używao symbolu, patrz wzór (.)). Trzeba zdawać sobie jedak sprawę, że w rzeczywistości rozkład atężeia promieiowaia wewątrz rezoatora jest bardziej skomplikoway. Przede wszystkim akcja laserowa rozpoczya się w dowolym miejscu rezoatora (w środku lub w pobliżu lustra) i dociera do lustra jako fala płaska lub fala kulista. Płaszczyza zwierciadła staje się źródłem promieiowaia i wskutek dyfrakcji wiązka ulega poszerzeiu. Stabilość rezoatora zależy od jego zdolości do utrzymaia promiei świetlych w jego wętrzu po wielokrotych odbiciach od zwierciadeł. Budowa rezoatorów optyczych decyduje o sposobie odbijaia światła we węce. Najczęściej spotykae rezoatory to: a) płaski, b) kofokaly (współogiskowy), c) hemisferyczy, d) iestabily (rys. 3.). W rezoatorze płaskim i kofokalym akcja rozwija się główie w obszarze przyosiowym. W rezoatorze kofokalym czoło fali kulistej jest dobrze dopasowae do kształtu zwierciadła, w 33

5 rezoatorze iestabilym zaś akcja rozwija się w całym obszarze czyym lasera. Rezoator iestabily ie ma więc zdolości do utrzymaia promiei świetlych we wętrzu przez dłuższy czas, ale pozwala a wysyłaie impulsu o gigatyczej mocy, poieważ akcja rozwija się w całym obszarze czyym. Rys.3.. Typy rezoatorów: a) płaski, b) kofokaly, c) hemisferyczy, d) iestabily Dotychczas iteresowaliśmy się rozkładem atężeia wzdłuż osi z. Należy jedak pamiętać, że wiązka wychodząca z lasera jest rozbieża (rys. 3.3) (choć odchyleie kątowe jest zwykle iewielkie) i ma pewie rozkład atężeia wzdłuż osi x i y, czyli w płaszczyźie prostopadłej do kieruku propagacji. Na rysuku 3.4 przedstawioo ajbardziej typowe rozkłady atężeń światła w płaszczyźie prostopadłej do kieruku rozchodzeia się wiązki laserowej. Rys Rozkład atężeia w kieruku poprzeczym 34

6 Rys Róże typy rozkładu atężeń w kieruku poprzeczym: a) TEM 00, b)tem 0, TEM 0, c) TEM 0, TEM 0 Rozkład atężeia w płaszczyźie xy prostopadłej do kieruku propagacji wiązki jest róży dla różego typu rezoatorów i wiele z takich rozkładów zostało policzoych przez Li i Foxa (teoria rezoatorów optyczych Li i Foxa). Omówieie teorii rezoatorów optyczych Li i Foxa zajdzie czytelik w podręcziku F. Kaczmarka, Wstęp do fizyki laserów, PWN, Warszawa 986. Uwzględieie rozkładu atężeń w płaszczyźie xy powoduje, że a mody geerowae w rezoatorze ałożoe są ie waruki iż dla fali stojącej. Moża pokazać, że dla rezoatora kofokalego (rys. 3.b) rozkład atężeń określoy jest astępującym warukiem 4L q m λ = + ( + + ), (3.7) zamiast waruku, który obowiązywał dla modów podłużych 4L q λ =. (3.8) Wielkości m i przybierają wartości całkowite, q zaś ozacza, jak poprzedio, liczbę połówek długości fali mieszczących się w długości rezoatora L. Mody charakteryzowae za pomocą liczb m i azywa się modami poprzeczymi i ozacza symbolem TEM m (ag. trasverse electromagetic mode). Mody określoe za pomocą tych samych m i, a różiące się q (czyli częstotliwościami) są różymi modami podłużymi o tym samym rozkładzie w kieruku poprzeczym. Mody poprzecze o różych wartościach ideksów m i różią się rozkładem atężeia w przekroju poprzeczym. Tak więc dla modu TEM 00 a ekraie umieszczoym prostopadle do kieruku rozchodzeia się wiązki widzimy okrągłą plamkę o malejącym atężeiu względem środka okręgu, dla modu TEM 0 i TEM 0 otrzymujemy a ekraie dwie plamki, dla modu TEM 0 i TEM 0 cztery itd. Na rysuku 3.5 przedstawioo rozkład atężeia pola elektryczego S(x,y) w płaszczyźie xy dla rezoatora kofokalego. Mod podstawowy TEM 00 jest symetryczy względem osi rezoatora i jego atężeie ma rozkład gaussowski. W płaszczyźie xy prostopadłej do kieruku propagacji wiązki obserwujemy w tym wypadku okrągłą plamkę o atężeiu malejącym w kieruku zewętrzym w sposób opisay przez fukcję Gaussa. Dla wyższych modów otrzymujemy rozkład kilku plamek i efekt te jest ajczęściej iepożąday. Poieważ dla modów wyższych iż TEM 00 atężeie w pukcie przecięcia płaszczyzy xy z osią z wyosi zero, więc ajprostszym sposobem wydzieleia TEM 00 i usuięcia wyższych modów jest diafragmowaie wiązki laserowej. Podsumujmy zagadieia omawiae w tym rozdziale: ) Parametrem, który charakteryzuje iwersję obsadzeń układu jest parametr asyceia = dla pracy w reżimie ciągłym, (3.9) στ τ imp = dla pracy w reżimie impulsowy. (3.0) σ 35

7 ) W rezoatorze optyczym lasera wyróżia się dwa typy modów: mody osiowe (podłuże) i mody poprzecze. Mody podłuże różią się od siebie jedyie wartościami częstotliwości. Różym modom podłużym odpowiadają te same rozkłady pól w przekroju poprzeczym. Mody poprzecze różią się między sobą ie tylko częstotliwością, ale rówież rozkładami pól w przekroju poprzeczym. Do tego samego modu poprzeczego ależy pewa liczba modów podłużych, które różią się częstotliwościami, ale rozkład pola w płaszczyźie poprzeczej jest dla tych modów jedakowy. Rys Rozkład amplitudy pola elektryczego dla różych modów poprzeczych 36