Metody Obliczeniowe Mikrooptyki i Fotoniki
|
|
|
- Gabriela Karczewska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM cd wyznaczanie modów metodą urojonej długości i korelacyjną operowanie efektywnym współczynnikiem załamania metoda FT-BPM metoda split-step dla nieliniowego r. Schödingera trójwymiarowa metoda ADI-BPM szerokokątowa trójwymiarowa metoda BPM
2 Równanie BPM Równanie Helmholtza: Rozwiązanie zapisujemy jako: r =A r exp i k z n k 0 =0 k=n k0 Fala nośna Amplituda zespolona A ℂ / z k n k 0 i k / z A=0 Przybliżenie paraboliczne (wolnozmiennej obwiedni) A/ z k / z, k A Podstawowe równanie metody propagacji wiązki (BPM- beam propagation method): A 1 = ( k n k 0) A z i k
3 Znajdowanie modów światłowodów i falowodów metodami propagacyjnymi Metoda imaginary distance (urojonej długości) z=i z ' R. Scarmozzino, A. Gopinath, R. Pregla Numerical Techniques for Modeling Guided-Wave Photonic Devices, IEEE JQE 60, 150 (000) A x, y,i z ' = m cm m x, y exp n m n k 0 z ' 1. Propagujemy pole wzdłuż kierunku iz', zaczynając od rozkładu losowego. Amplituda modu podstawowego wzrasta wykładniczo najszybciej i w krótkim czasie pozostałe mody stają się zaniedbywalne z' A x, y, i z ' c1 exp n1 n k 0 z ' 1 x, y c1 z ' n1 n ln A x, y,i z ' z ' A x, y, i z ' / k0 z ' Dokładność można podwyższyć przez kilkukrotnie powtarzanie procedury, za każdym razem przyjmując, że: n 1 n
4 Znajdowanie modów światłowodów i falowodów metodami propagacyjnymi Metoda imaginary distance (urojonej długości) Wyższe mody znajdujemy tak samo, zaczynając od rozkładu losowego, ale ortogonalnego do modów już znalezionych (ze względu na kumulację błędów w trakcie propagacji wskazane jest powtarzanie ortogonalizacji co jakiś czas) Ortogonalizacja (w pętli po wyznaczonych modach):
5 Znajdowanie modów światłowodów i falowodów metodami propagacyjnymi Metoda korelacyjna r = m c m m x, y exp i m z 1. Propagujemy pole wzdłuż kierunku z, zaczynając od rozkładu losowego. W trakcie propagacji obliczamy korelacje: P z = we x, y x, y, z dx dy R. Scarmozzino, A. Gopinath, R. Pregla Numerical Techniques for Modeling Guided-Wave Photonic Devices, IEEE JQE 60, 150 (000)
6 Znajdowanie modów światłowodów i falowodów metodami propagacyjnymi Metoda korelacyjna r = m c m m x, y exp i m z 1. Propagujemy pole wzdłuż kierunku z, zaczynając od rozkładu losowego. W trakcie propagacji obliczamy korelacje: P z = we x, y x, y, z dx dy FFT Piki korelacyjne wyznaczają wartości stałych propagacji 3. Odfiltrowujemy pola modów L m x, y = 0 x, y, z exp i m z dz R. Scarmozzino, A. Gopinath, R. Pregla Numerical Techniques for Modeling Guided-Wave Photonic Devices, IEEE JQE 60, 150 (000)
7 Mod podstawowy falowodu Rdzeń Płaszcz 1.0 Natężenie A x Amplituda A x Mod podstawowy zawsze istnieje
8 Pierwszy mod wyższego rzędu Pierwszy mod nieparzysty Mody wyższego rzędu istnieją powyżej kolejnych częstości odcięcia
9 Pierwszy mod wyższego rzędu
10 Pierwszy mod wyższego rzędu
11 Mody płaszczowe
12 Metoda efektywnego współczynnika załamania Idea: fragment falowodu, w którym występuje mikrostruktura, zastępujemy w obliczeniach materiałem jednorodnym o pewnej efektywnej wartości współczynnika załamania, który trzeba najpierw wyznaczyć. W rezultacie dochodzimy do prostszego niż pierwotny problemu obliczeniowego, czasem o znanych rozwiązaniach, lub o niższej wymiarowości. Wynik jest jednak przybliżony. Przykłady: 1. Falowody planarne z wieloma cienkimi warstwami można zredukować liczbę warstw w obliczeniach i np. sprowadzić obliczenia do falowodu trójwarstwowego o znanym związku dyspersyjnym. Falowody paskowe (np. grzebieniowe) można sprowadzić do falowodu planarnego '. Układy planarne o naprawdę skończonej wysokości można analizować jako układy dwuwymiarowe 3. Światłowody fotoniczne (ale nie wykorzystujące przerwy wzbronionej do prowadzenia) można sprowadzić do światłowodu skokowego
13 Metoda efektywnego współczynnika załamania 1. Falowody planarne z cienkimi warstwami z x d i λ Homogenizacja: ϵ eff y =ϵ ϵ eff x = ( eff z = d 1 ϵ1 + d ϵ d 1+ d 1 d 1 ϵ d ϵ d 1+ d ) 1 Uwaga: polaryzacje TE i TM widzą różne składowe tensora przenikalności elektrycznej = ϵ eff n eff TM = ϵ x n eff TE eff y
14 Metoda efektywnego współczynnika załamania M. Karpierz, E. Weinert-Rączka, Nieliniowa Optyka Światłowodowa, WNT 009
15 Metoda efektywnego współczynnika załamania jako sposób na redukcję wymiarowości problemu. Falowody paskowe Embedded strip (pol. grzebieniowy) Strip Rib/ ridge Strip loaded
16 Metoda efektywnego współczynnika załamania jako sposób na redukcję wymiarowości problemu
17
18 Fourier Transform BPM A 1 ^ S^ ) A = ( k n k 0) ( D+ z i k i ^ D= k where n= n + Δ n Δ n 1 S^ = i k Δ n założenie, że oba operatory nie zależą od z ^ S^ dz ) A(x, y, z ) exp ( D dz ^ A( x, y, z + dz)=exp ( D+ ) exp ( S^ dz ) A(x, y, z )
19 Fourier Transform BPM ^ A( x, y, z + dz) exp ( S^ dz ) exp ( D dz ) A(x, y, z) Krok iteracyjny dla metody FT-BPM: A(x, y, z + dz)=e i k Δ n( x, y) dz IFT exp (i dz (k x + k y )/( k )) FT A(x, y, z)
20 Nieliniowe równanie Schrödingera Równanie na obwiednię impulsu w ośrodku o współczynniku dyspersji β i nieliniowości Kerra γ ma strukturę przypominającą równanie BPM: A i β A ^ N^ ) A = + i γ A A=( D+ z t Metoda split step polega na naprzemiennym rozwiązywaniu dwóch równań dla kolejnych warstw wzdłuż z: AN AD i β A ^ ^ =i γ A A= N A = A= D A z z t
21
22 3-wymiarowy BPM (ADI -Alternate Direction Implicit) Równanie BPM na zespoloną amplitudę pola A: A 1 = ( k n k 0 ) A z i k wprowadzamy operatory pomocnicze Lx, Ly: i k 1. w kierunku z: 1 1 z = L x L y A Li = k =k 0 n n k 0 k xi A kj, l A k,l, j z Dyskretyzacja: A k 0 = / i k Lx L x 1 A j 1 A j z x j 1 y j A z r= L y A L L A = j 1 L y A = 1 j 1 = 1 i k L x L x 1 L y A j j L y A r 4 4 L x L y A j 1 A j 3
23 3-wymiarowy BPM (ADI) Alternate Directions Implicit: Równanie: 1 L x 1 L y A j 1= 1 L x 1 L y A j Zastępujemy przez: r r j 1 1 L y A = 1 L x A j 1 / 1 r L x A j 1/ = 1 r L y A j Warstwa pomocnicza (niefizyczna) Wykazanie równoważności : 1 L x 1 L y A j 1 = 1 L x 1 L x A j 1 / = = 1 L x 1 L x A j 1 / = 1 L x 1 Przez pomnożenie obu równań stronami dostajemy równanie wyjściowe L y A j
24 3-wymiarowy BPM (ADI) Rozwiązanie ADI polega na rozwiązywaniu obu równań na przemian 1 1 L y A j 1 L x A j 1/ = 1 = 1 L x A j 1 / L y A j Dyskretyzacja po x i y z użyciem centralnego ilorazu różnicowego Równanie 1: 1 k r n k 0 j 1 A = 1 y n k 0 k j 1/ A x r r j 1 j 1/ j 1 j 1 j 1 / j 1/ j 1 / j 1 / r Ak, l 1 r n k, l k 0 k A k, l r Ak, l 1 = r A k 1,l r n k, l k 0 k A k, l r Ak 1,l Równanie : j 1 / r Ak 1,l r r k r n k 0 r n k 0 k j 1/ 1 A = 1 A j x y r j 1 / j 1 / j j 1 / j j k 0 k A k, l r Ak 1,l = r Ak, l 1 r n k,l k 0 k Ak,l r Ak,l 1 j 1/ n k, l Dla obu równań -> seria układów trójdiagonalnych
25 Nieprzyosiowy ADI-BPM -na podst. art. C. Ma and E. Van Keuren, "A simple three dimensional wide-angle beam propagation method," Opt. Express 14, 4668 (006) Równanie Helmholtza: n k 0 E =0 E r = r exp i k 0 n 0 z SVEA (slowly varying envelope approximation) + paraxial approximation Podstawowe równanie metody propagacji wiązki (BPM): ADI W poprzednich oznaczeniach to równanie miało następującą postać: równania 1-wym A 1 = ( k n k 0 ) A z i k
26 1. Dyskretyzacja w kierunku z l m, j = m x, j y, l z
27 Szerokokątowy BPM -Oznaczenia zgodne z artykułem C. Ma and E. Van Keuren, "A simple three dimensional wide-angle beam propagation method," Opt. Express 14, 4668 (006) Równanie Helmholtza: n k 0 E =0 E r = r exp i k 0 n 0 z SVEA (slowly varying envelope approximation) W szerokokątowym BPM zostawiamy ten wyraz
28 1. Dyskretyzacja w kierunku z
29 Szerokokątowy BPM Ostateczna postać dla obu kroków algorytmu (po rozpisaniu na poszczególne elementy obu trójdiagonalnych macierzy): l m, j = m x, j y, l z
30 C. Ma and E. Van Keuren, "A simple three dimensional wide-angle beam propagation method," Opt. Express 14, 4668 (006)
31 Ćwiczenia Zadanie 1. Użyć metody propagacji w urojonym kierunku w falowodzie do wyznaczania: modu podstawowego w falowodzie (rozkład pola oraz efektywny współczynnik załamania) najniższego modu parzystego i nieparzystego w falowodzie charakteryzującym się parzystym rozkładem współczynnika załamania. Zadanie. Dla zadanego falowodu, wyznaczyć wszystkie mody prowadzone (metoda BPM + urojony kierunek propagacji+ortogonalizacja). Zadania na 5 : Zrealizować metodę BPM dla struktur trójwymiarowych (ADI). Napisać funkcje do wyznaczania struktury modowej dla falowodów lub włókien światłowodowych (o przekroju dwuwymiarowym). Napisać funkcje do wyznaczania struktury modowej metodą korelacyjną.
Metody Obliczeniowe Mikrooptyki i Fotoniki. Metoda propagacji wiązki BPM Modelowanie propagacji
 Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
III. Opis falowy. /~bezet
 Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
KATEDRA TELEKOMUNIKACJI I FOTONIKI
 ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji
 Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 6, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
IV. Transmisja. /~bezet
 Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Fotonika. Plan: Wykład 3: Polaryzacja światła
 Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Metody Obliczeniowe Mikrooptyki i Fotoniki. Podstawy metody różnic skończonych Podstawy metody FDTD
 Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody różnic skończonych Podstawy etody FDTD M. N. Sadiku, Nuerical Techniques in Electroagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Coputational
Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody różnic skończonych Podstawy etody FDTD M. N. Sadiku, Nuerical Techniques in Electroagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Coputational
Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji
 Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Solitony i zjawiska nieliniowe we włóknach optycznych
 Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki Kod USOS: 1103-4Fot4 Wykład (30h): R. Kotyński Wtorki 9:15-11:00, s.1.38 lub B4.17(ul. Pasteura 5) Ćwiczenia (45h): Wtorki, w godz. 14.15-16.30, s.1.7 lub B4.17
Metody Obliczeniowe Mikrooptyki i Fotoniki Kod USOS: 1103-4Fot4 Wykład (30h): R. Kotyński Wtorki 9:15-11:00, s.1.38 lub B4.17(ul. Pasteura 5) Ćwiczenia (45h): Wtorki, w godz. 14.15-16.30, s.1.7 lub B4.17
Propagacja w przestrzeni swobodnej (dyfrakcja)
 Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Propagacja
Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Propagacja
Fizyka Laserów wykład 5. Czesław Radzewicz
 Fizyka Laserów wykład 5 Czesław Radzewicz rezonatory optyczne, optyczne wnęki rezonansowe rezonatory otwarte: Fabry-Perot E t E 0 R 0.99 T 1 0 E r R R R 0. R 0.9 E t = TE 0 e iδφ R 0.5 R 0.9 E t Gires-Tournois
Fizyka Laserów wykład 5 Czesław Radzewicz rezonatory optyczne, optyczne wnęki rezonansowe rezonatory otwarte: Fabry-Perot E t E 0 R 0.99 T 1 0 E r R R R 0. R 0.9 E t = TE 0 e iδφ R 0.5 R 0.9 E t Gires-Tournois
Różne reżimy dyfrakcji
 Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Różne reżimy
Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Różne reżimy
Metody Obliczeniowe Mikrooptyki i Fotoniki. - Dyfrakcja różne reżimy - Obliczanie elementów dyfrakcyjnych
 Metody Obliczeniowe Mikrooptyki i Fotoniki - Dyfrakcja różne reżimy - Obliczanie elementów dyfrakcyjnych Elementy dyfrakcyjne - idea d1 Wiązka padająca Ψ i ( x,y ) DOE (diffractive optical element) d Oczekiwany
Metody Obliczeniowe Mikrooptyki i Fotoniki - Dyfrakcja różne reżimy - Obliczanie elementów dyfrakcyjnych Elementy dyfrakcyjne - idea d1 Wiązka padająca Ψ i ( x,y ) DOE (diffractive optical element) d Oczekiwany
Wprowadzenie do optyki nieliniowej
 Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
Podstawy prowadzenia światła we włóknach oraz ich budowa. Light-Guiding Fundamentals and Fiber Design
 Podstawy prowadzenia światła we włóknach oraz ich budowa Light-Guiding Fundamentals and Fiber Design Rozchodzenie się liniowo-spolaryzowanego światła w światłowodzie Robocza definicja długości fali odcięcia
Podstawy prowadzenia światła we włóknach oraz ich budowa Light-Guiding Fundamentals and Fiber Design Rozchodzenie się liniowo-spolaryzowanego światła w światłowodzie Robocza definicja długości fali odcięcia
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
Pomiary parametrów telekomunikacyjnych światłowodów jednomodowych. Na poprzednim wykładzie przedstawiono podstawowe parametry światłowodów
 Pomiary parametrów telekomunikacyjnych światłowodów jednomodowych Na poprzednim wykładzie przedstawiono podstawowe parametry światłowodów Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze
Pomiary parametrów telekomunikacyjnych światłowodów jednomodowych Na poprzednim wykładzie przedstawiono podstawowe parametry światłowodów Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Fotonika kurs magisterski grupa R41 semestr VII Specjalność: Inżynieria fotoniczna. Egzamin ustny: trzy zagadnienia do objaśnienia
 Dr inż. Tomasz Kozacki Prof. dr hab.inż. Romuald Jóźwicki Zakład Techniki Optycznej Instytut Mikromechaniki i Fotoniki pokój 513a ogłoszenia na tablicach V-tego piętra kurs magisterski grupa R41 semestr
Dr inż. Tomasz Kozacki Prof. dr hab.inż. Romuald Jóźwicki Zakład Techniki Optycznej Instytut Mikromechaniki i Fotoniki pokój 513a ogłoszenia na tablicach V-tego piętra kurs magisterski grupa R41 semestr
Metody numeryczne w przykładach
 Metody numeryczne w przykładach Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Regionalne Koło Matematyczne 8 kwietnia 2010 r. Bartosz Ziemkiewicz (WMiI UMK) Metody numeryczne w przykładach
Metody numeryczne w przykładach Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Regionalne Koło Matematyczne 8 kwietnia 2010 r. Bartosz Ziemkiewicz (WMiI UMK) Metody numeryczne w przykładach
Ośrodki dielektryczne optycznie nieliniowe
 Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Laboratorium techniki światłowodowej. Ćwiczenie 5. Badanie wpływu periodycznych zgięd na tłumiennośd światłowodu
 Laboratorium techniki światłowodowej Ćwiczenie 5. Badanie wpływu periodycznych zgięd na tłumiennośd Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie
Laboratorium techniki światłowodowej Ćwiczenie 5. Badanie wpływu periodycznych zgięd na tłumiennośd Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie
Fizyczna struktura włókna optycznego Propagacja światła liniowo spolaryzowanego
 Światłowody włókniste podstawy fizyczne Fizyczna struktura włókna optycznego Propagacja światła liniowo spolaryzowanego Fizyczna struktura włókna optycznego Światłowody włókniste są wytwarzane poprzez
Światłowody włókniste podstawy fizyczne Fizyczna struktura włókna optycznego Propagacja światła liniowo spolaryzowanego Fizyczna struktura włókna optycznego Światłowody włókniste są wytwarzane poprzez
Fotonika. Wykład (30h): R. Kotyński Wtorki 15:15-17:00, s. 1.40
 Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
Uniwersytet Warszawski Wydział Fizyki. Światłowody
 Uniwersytet Warszawski Wydział Fizyki Marcin Polkowski 251328 Światłowody Pracownia Fizyczna dla Zaawansowanych ćwiczenie L6 w zakresie Optyki Streszczenie Celem wykonanego na Pracowni Fizycznej dla Zaawansowanych
Uniwersytet Warszawski Wydział Fizyki Marcin Polkowski 251328 Światłowody Pracownia Fizyczna dla Zaawansowanych ćwiczenie L6 w zakresie Optyki Streszczenie Celem wykonanego na Pracowni Fizycznej dla Zaawansowanych
Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych
 Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych Piotr Modliński Wydział Geodezji i Kartografii PW 13 stycznia 2012 P. Modliński, GiK PW Rozw.
Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych Piotr Modliński Wydział Geodezji i Kartografii PW 13 stycznia 2012 P. Modliński, GiK PW Rozw.
Wykład 3 Równania rózniczkowe cd
 7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
Teoria falowa Równania Maxwella
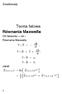 Teoria falowa Równania Maxwella Oś falowodu oś z Równania Maxwella E B, t H J D t, D, B 0. Jeżeli E x,y,z,t Re E x,y,z e i t 1 2 E x,y,z e i t E x,y,z e i t, 1 W postaci zespolonej: E i B, prawo indukcji
Teoria falowa Równania Maxwella Oś falowodu oś z Równania Maxwella E B, t H J D t, D, B 0. Jeżeli E x,y,z,t Re E x,y,z e i t 1 2 E x,y,z e i t E x,y,z e i t, 1 W postaci zespolonej: E i B, prawo indukcji
UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać układu równań liniowych Układ liniowych równań algebraicznych
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać układu równań liniowych Układ liniowych równań algebraicznych
Motywacja Podstawy. Historia Teoria 2D PhC Podsumowanie. Szymon Lis Photonics Group szymon.lis@pwr.wroc.pl C-2 p.305. Motywacja.
 Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
WYKŁAD 8 ANALIZA REGRESJI
 WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
Fotonika. Wykład (30h): Rafał Kotyński, wtorki 15:15-17:00, s. 1.40
 Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
METODY NUMERYCZNE. wykład. konsultacje: wtorek 10:00-11:30 środa 10:00-11:30. dr inż. Grażyna Kałuża pokój
 METODY NUMERYCZNE wykład dr inż. Grażyna Kałuża pokój 103 konsultacje: wtorek 10:00-11:30 środa 10:00-11:30 www.kwmimkm.polsl.pl Program przedmiotu wykład: 15 godzin w semestrze laboratorium: 30 godzin
METODY NUMERYCZNE wykład dr inż. Grażyna Kałuża pokój 103 konsultacje: wtorek 10:00-11:30 środa 10:00-11:30 www.kwmimkm.polsl.pl Program przedmiotu wykład: 15 godzin w semestrze laboratorium: 30 godzin
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Fotonika. Plan: Wykład 11: Kryształy fotoniczne
 Fotonika Wykład 11: Kryształy fotoniczne Plan: Kryształy fotoniczne Homogenizacja długofalowa Prawo załamania dla kryształów fotonicznych, superkolimacja Tw. Blocha, kryształy, kryształy fotoniczne, kryształy
Fotonika Wykład 11: Kryształy fotoniczne Plan: Kryształy fotoniczne Homogenizacja długofalowa Prawo załamania dla kryształów fotonicznych, superkolimacja Tw. Blocha, kryształy, kryształy fotoniczne, kryształy
Obliczenia Naukowe. Wykład 12: Zagadnienia na egzamin. Bartek Wilczyński
 Obliczenia Naukowe Wykład 12: Zagadnienia na egzamin Bartek Wilczyński 6.6.2016 Tematy do powtórki Arytmetyka komputerów Jak wygląda reprezentacja liczb w arytmetyce komputerowej w zapisie cecha+mantysa
Obliczenia Naukowe Wykład 12: Zagadnienia na egzamin Bartek Wilczyński 6.6.2016 Tematy do powtórki Arytmetyka komputerów Jak wygląda reprezentacja liczb w arytmetyce komputerowej w zapisie cecha+mantysa
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
KADD Minimalizacja funkcji
 Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość
 Fotonika Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość S. Maier Plasmonics fundamentals and applications (Springer, 007). Plan: związek dyspersyjny
Fotonika Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość S. Maier Plasmonics fundamentals and applications (Springer, 007). Plan: związek dyspersyjny
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
Propagacja światła we włóknie obserwacja pól modowych.
 Propagacja światła we włóknie obserwacja pól modowych. Przy pomocy optyki geometrycznej łatwo można przedstawić efekty propagacji światła tylko w ośrodku nieograniczonym. Nie ukazuje ona jednak interesujących
Propagacja światła we włóknie obserwacja pól modowych. Przy pomocy optyki geometrycznej łatwo można przedstawić efekty propagacji światła tylko w ośrodku nieograniczonym. Nie ukazuje ona jednak interesujących
Zawansowane modele wyborów dyskretnych
 Zawansowane modele wyborów dyskretnych Jerzy Mycielski Uniwersytet Warszawski grudzien 2013 Jerzy Mycielski (Uniwersytet Warszawski) Zawansowane modele wyborów dyskretnych grudzien 2013 1 / 16 Model efektów
Zawansowane modele wyborów dyskretnych Jerzy Mycielski Uniwersytet Warszawski grudzien 2013 Jerzy Mycielski (Uniwersytet Warszawski) Zawansowane modele wyborów dyskretnych grudzien 2013 1 / 16 Model efektów
Defi f nicja n aprę r żeń
 Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
Optyka instrumentalna
 Optyka instrumentalna wykład 12 25 maja 2017 Wykład 11 Wiązki przyosiowe Wyższego rzędu TEM mn (Gaussa-Hermite a) Elementy optyczne w działaniu na wiązki Prawo ABCD dla wiązek gaussowskich Ogniskowanie
Optyka instrumentalna wykład 12 25 maja 2017 Wykład 11 Wiązki przyosiowe Wyższego rzędu TEM mn (Gaussa-Hermite a) Elementy optyczne w działaniu na wiązki Prawo ABCD dla wiązek gaussowskich Ogniskowanie
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Światłowody telekomunikacyjne
 Światłowody telekomunikacyjne Parametry i charakteryzacja światłowodów Kolejny wykład będzie poświęcony metodom pomiarowym Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie
Światłowody telekomunikacyjne Parametry i charakteryzacja światłowodów Kolejny wykład będzie poświęcony metodom pomiarowym Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie
5. Twierdzenie Weierstrassa
 Pytania egzaminacyjne z Metod Numerycznych 1. Jaką największą liczbę można zapisać w postaci znormalizowanej w dwójkowym systemie liczenia na 8-miu bitach podzielonych 4 + 4 na mantysę i cechę, jeśli zarówno
Pytania egzaminacyjne z Metod Numerycznych 1. Jaką największą liczbę można zapisać w postaci znormalizowanej w dwójkowym systemie liczenia na 8-miu bitach podzielonych 4 + 4 na mantysę i cechę, jeśli zarówno
5. Rozwiązywanie układów równań liniowych
 5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
Rozkłady wielu zmiennych
 Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Układy równań liniowych i metody ich rozwiązywania
 Układy równań liniowych i metody ich rozwiązywania Łukasz Wojciechowski marca 00 Dany jest układ m równań o n niewiadomych postaci: a x + a x + + a n x n = b a x + a x + + a n x n = b. a m x + a m x +
Układy równań liniowych i metody ich rozwiązywania Łukasz Wojciechowski marca 00 Dany jest układ m równań o n niewiadomych postaci: a x + a x + + a n x n = b a x + a x + + a n x n = b. a m x + a m x +
Systemy laserowe. dr inż. Adrian Zakrzewski dr inż. Tomasz Baraniecki
 Systemy laserowe dr inż. Adrian Zakrzewski dr inż. Tomasz Baraniecki Metody analizy i kształtowania wiązki laserowej Źródło: Beyer Wiązka gaussowska Natężenia promieniowania poprzecznie do kierunku propagacji
Systemy laserowe dr inż. Adrian Zakrzewski dr inż. Tomasz Baraniecki Metody analizy i kształtowania wiązki laserowej Źródło: Beyer Wiązka gaussowska Natężenia promieniowania poprzecznie do kierunku propagacji
Zaawansowane metody numeryczne
 Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
3. Umiejętność obsługi prostych przyrządów optycznych (UMIEJĘTNOŚĆ)
 Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Światłowody Nazwa w języku angielskim Optical waveguides Kierunek studiów (jeśli dotyczy): Inżynieria Kwantowa Specjalność (jeśli
Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Światłowody Nazwa w języku angielskim Optical waveguides Kierunek studiów (jeśli dotyczy): Inżynieria Kwantowa Specjalność (jeśli
KADD Minimalizacja funkcji
 Minimalizacja funkcji n-wymiarowych Forma kwadratowa w n wymiarach Procedury minimalizacji Minimalizacja wzdłuż prostej w n-wymiarowej przestrzeni Metody minimalizacji wzdłuż osi współrzędnych wzdłuż kierunków
Minimalizacja funkcji n-wymiarowych Forma kwadratowa w n wymiarach Procedury minimalizacji Minimalizacja wzdłuż prostej w n-wymiarowej przestrzeni Metody minimalizacji wzdłuż osi współrzędnych wzdłuż kierunków
Fotonika. Plan: Wykład 9: Interferencja w układach warstwowych
 Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
SZYBKI ALGORYTM Z MACIERZĄ SHURA DLA MACIERZY TRÓJDIAGONALNYCH
 SZYBKI ALGORYTM Z MACIERZĄ SHURA DLA MACIERZY TRÓJDIAGONALNYCH Rozwiązujemy układ z macierzą trójdiagonalną. Założymy dla prostoty opisu, że macierz ma stałe współczynniki, to znaczy, że na głównej diagonali
SZYBKI ALGORYTM Z MACIERZĄ SHURA DLA MACIERZY TRÓJDIAGONALNYCH Rozwiązujemy układ z macierzą trójdiagonalną. Założymy dla prostoty opisu, że macierz ma stałe współczynniki, to znaczy, że na głównej diagonali
Podpis prowadzącego SPRAWOZDANIE
 Imię i nazwisko.. Grupa. Data. Podpis prowadzącego. SPRAWOZDANIE LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1 Zadanie nr 1 (plik strip.pro,nazwa ośrodka wypełniającego prowadnicę - "airlossy") Rozważamy przypadek
Imię i nazwisko.. Grupa. Data. Podpis prowadzącego. SPRAWOZDANIE LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1 Zadanie nr 1 (plik strip.pro,nazwa ośrodka wypełniającego prowadnicę - "airlossy") Rozważamy przypadek
http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet
 IV. Światłowody BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Literatura 2 3 Historia i uwarunkowania Podstawowe elementy: 1. Rozwój techniki laserowej (lasery półprzewodnikowe, modulacja,
IV. Światłowody BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Literatura 2 3 Historia i uwarunkowania Podstawowe elementy: 1. Rozwój techniki laserowej (lasery półprzewodnikowe, modulacja,
Tydzień nr 9-10 (16 maja - 29 maja), Równania różniczkowe, wartości własne, funkcja wykładnicza od operatora - Matematyka II 2010/2011L
 Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
Technika laserowa, otrzymywanie krótkich impulsów Praca impulsowa
 Praca impulsowa Impuls trwa określony czas i jest powtarzany z pewną częstotliwością; moc w pracy impulsowej znacznie wyższa niż w pracy ciągłej (pomiędzy impulsami może magazynować się energia) Ablacja
Praca impulsowa Impuls trwa określony czas i jest powtarzany z pewną częstotliwością; moc w pracy impulsowej znacznie wyższa niż w pracy ciągłej (pomiędzy impulsami może magazynować się energia) Ablacja
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 17, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 17, 01.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 16 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 17, 01.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 16 - przypomnienie
Metody Obliczeniowe Mikrooptyki i Fotoniki. Program mpb i wyznaczanie struktury pasmowej kryształów fotonicznych
 Metody Obliczeniowe Mikrooptyki i Fotoniki Program mpb i wyznaczanie struktury pasmowej kryształów fotonicznych Kryształy fotoniczne metoda fal płaskich Periodyczność i brak własności magnetycznych i strat:
Metody Obliczeniowe Mikrooptyki i Fotoniki Program mpb i wyznaczanie struktury pasmowej kryształów fotonicznych Kryształy fotoniczne metoda fal płaskich Periodyczność i brak własności magnetycznych i strat:
Równania Maxwella. roth t
 , H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
OBLICZANIE POCHODNYCH FUNKCJI.
 OBLICZANIE POCHODNYCH FUNKCJI. ROZWIĄZYWANIE RÓWNAŃ RÓŻNICZKOWYCH. ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ LINIOWYCH. Obliczanie pochodnych funkcji. Niech będzie dana funkcja y(x określona i różniczkowalna na przedziale
OBLICZANIE POCHODNYCH FUNKCJI. ROZWIĄZYWANIE RÓWNAŃ RÓŻNICZKOWYCH. ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ LINIOWYCH. Obliczanie pochodnych funkcji. Niech będzie dana funkcja y(x określona i różniczkowalna na przedziale
MODEL CZUJNIKA ŚWIATŁOWODOWEGO NA BAZIE WIELOMODOWYCH STRUKTUR INTERFERENCYJNYCH MODEL OF WAVEGUIDE SENSOR BASED ON MULTIMODE INTERFERENCE STRUCTURES
 ELEKTRYKA 2015 Zeszyt 2 (234) Rok LXI Artur SZEWCZUK, Marek BŁAHUT Katedra Optoelektroniki, Politechnika Śląska w Gliwicach MODEL CZUJNIKA ŚWIATŁOWODOWEGO NA BAZIE WIELOMODOWYCH STRUKTUR INTERFERENCYJNYCH
ELEKTRYKA 2015 Zeszyt 2 (234) Rok LXI Artur SZEWCZUK, Marek BŁAHUT Katedra Optoelektroniki, Politechnika Śląska w Gliwicach MODEL CZUJNIKA ŚWIATŁOWODOWEGO NA BAZIE WIELOMODOWYCH STRUKTUR INTERFERENCYJNYCH
Metoda elementów skończonych
 Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
Algebra liniowa II. Lista 1. 1 u w 0 1 v 0 0 1
 Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
WYKŁAD 9 METODY ZMIENNEJ METRYKI
 WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
Iteracje. Algorytm z iteracją to taki, w którym trzeba wielokrotnie powtarzać instrukcję, aby warunek został spełniony.
 Iteracje Algorytm z iteracją to taki, w którym trzeba wielokrotnie powtarzać instrukcję, aby warunek został spełniony. Iteracja inaczej zwana jest pętlą i oznacza wielokrotne wykonywanie instrukcji. Iteracje
Iteracje Algorytm z iteracją to taki, w którym trzeba wielokrotnie powtarzać instrukcję, aby warunek został spełniony. Iteracja inaczej zwana jest pętlą i oznacza wielokrotne wykonywanie instrukcji. Iteracje
Fala EM w izotropowym ośrodku absorbującym
 Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Całkowanie numeryczne
 Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Uczenie sieci typu MLP
 Uczenie sieci typu MLP Przypomnienie budowa sieci typu MLP Przypomnienie budowy neuronu Neuron ze skokową funkcją aktywacji jest zły!!! Powszechnie stosuje -> modele z sigmoidalną funkcją aktywacji - współczynnik
Uczenie sieci typu MLP Przypomnienie budowa sieci typu MLP Przypomnienie budowy neuronu Neuron ze skokową funkcją aktywacji jest zły!!! Powszechnie stosuje -> modele z sigmoidalną funkcją aktywacji - współczynnik
Wstęp do optyki i fizyki materii skondensowanej. O: Wojciech Wasilewski FMS: Mateusz Goryca
 Wstęp do optyki i fizyki materii skondensowanej O: Wojciech Wasilewski FMS: Mateusz Goryca 1 Zasady części O Wykład przeglądowy Ćwiczenia rozszerzające lub ilustrujące Sprawdzane prace domowe psi.fuw.edu.pl/main/wdoifms
Wstęp do optyki i fizyki materii skondensowanej O: Wojciech Wasilewski FMS: Mateusz Goryca 1 Zasady części O Wykład przeglądowy Ćwiczenia rozszerzające lub ilustrujące Sprawdzane prace domowe psi.fuw.edu.pl/main/wdoifms
Obliczanie niepewności rozszerzonej metodą analityczną opartą na splocie rozkładów wielkości wejściowych
 Obliczanie niepewności rozszerzonej metodą analityczną opartą na splocie rozkładów wejściowych Paweł Fotowicz * Przedstawiono ścisłą metodę obliczania niepewności rozszerzonej, polegającą na wyznaczeniu
Obliczanie niepewności rozszerzonej metodą analityczną opartą na splocie rozkładów wejściowych Paweł Fotowicz * Przedstawiono ścisłą metodę obliczania niepewności rozszerzonej, polegającą na wyznaczeniu
Analiza numeryczna Lista nr 3 (ćwiczenia) x x 2 n x.
 Analiza numeryczna Lista nr 3 (ćwiczenia) Sprawdzić że macierz ma wartości własne2+ 222 2 2 Niechx R n Udowodnić że 2 0 0 x x 2 n x 3 NiechA R n n będzie macierzą symetryczną Wiadomo że wówczas istnieje
Analiza numeryczna Lista nr 3 (ćwiczenia) Sprawdzić że macierz ma wartości własne2+ 222 2 2 Niechx R n Udowodnić że 2 0 0 x x 2 n x 3 NiechA R n n będzie macierzą symetryczną Wiadomo że wówczas istnieje
Bernard Ziętek OPTOELEKTRONIKA
 Uniwersytet Mikołaja Kopernika Bernard Ziętek OPTOELEKTRONIKA Wydanie III, uzupełnione i poprawione Toruń 2011 SPIS TREŚCI PRZEDMOWA DO III WYDANIA 1 PRZEDMOWA DO II WYDANIA 3 PRZEDMOWA DO I WYDANIA 4
Uniwersytet Mikołaja Kopernika Bernard Ziętek OPTOELEKTRONIKA Wydanie III, uzupełnione i poprawione Toruń 2011 SPIS TREŚCI PRZEDMOWA DO III WYDANIA 1 PRZEDMOWA DO II WYDANIA 3 PRZEDMOWA DO I WYDANIA 4
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 18, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
n=0 (n + r)a n x n+r 1 (n + r)(n + r 1)a n x n+r 2. Wykorzystując te obliczenia otrzymujemy, że lewa strona równania (1) jest równa
 Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu
 1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
Modelowanie rynków finansowych z wykorzystaniem pakietu R
 Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
UKŁADY RÓWNAŃ LINIOWYCH -Metody dokładne
 UKŁADY RÓWNAŃ LINIOWYCH -Metody dokładne Układy równań liniowych Rozpatruje się układ n równań liniowych zawierających n niewiadomych: a + a +... + ann b a + a +... + ann b... an + an+... + annn bn który
UKŁADY RÓWNAŃ LINIOWYCH -Metody dokładne Układy równań liniowych Rozpatruje się układ n równań liniowych zawierających n niewiadomych: a + a +... + ann b a + a +... + ann b... an + an+... + annn bn który
LASERY NA CIELE STAŁYM BERNARD ZIĘTEK
 LASERY NA CIELE STAŁYM BERNARD ZIĘTEK TEK Lasery na ciele stałym lasery, których ośrodek czynny jest: -kryształem i ciałem amorficznym (również proszkiem), - dielektrykiem i półprzewodnikiem. 2 Podział
LASERY NA CIELE STAŁYM BERNARD ZIĘTEK TEK Lasery na ciele stałym lasery, których ośrodek czynny jest: -kryształem i ciałem amorficznym (również proszkiem), - dielektrykiem i półprzewodnikiem. 2 Podział
Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką
 Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Instytut Podstawowych Problemów Techniki PAN Zakład Teorii Ośrodków
Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Instytut Podstawowych Problemów Techniki PAN Zakład Teorii Ośrodków
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 17, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 17, 0.04.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 16 - przypomnienie dyfrakcja
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 17, 0.04.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 16 - przypomnienie dyfrakcja
Układy równań liniowych. Krzysztof Patan
 Układy równań liniowych Krzysztof Patan Motywacje Zagadnienie kluczowe dla przetwarzania numerycznego Wiele innych zadań redukuje się do problemu rozwiązania układu równań liniowych, często o bardzo dużych
Układy równań liniowych Krzysztof Patan Motywacje Zagadnienie kluczowe dla przetwarzania numerycznego Wiele innych zadań redukuje się do problemu rozwiązania układu równań liniowych, często o bardzo dużych
Technika falo- i światłowodowa
 Technika falo- i światłowodowa Falowody elementy planarne (płytki, paski) Światłowody elementy cylindryczne (włókna światłowodowe) płytkowy paskowy włókno optyczne Rdzeń o wyższym współczynniku załamania
Technika falo- i światłowodowa Falowody elementy planarne (płytki, paski) Światłowody elementy cylindryczne (włókna światłowodowe) płytkowy paskowy włókno optyczne Rdzeń o wyższym współczynniku załamania
y i b) metoda różnic skończonych nadal problem nieliniowy 2 go rzędu z warunkiem Dirichleta
 b) metoda różnic skończonych nadal problem nieliniowy 2 go rzędu z warunkiem Dirichleta przedział (a,b) dzielimy na siatkę, powiedzmy o stałym kroku: punkty siatki: u A y i w metodzie strzałów używamy
b) metoda różnic skończonych nadal problem nieliniowy 2 go rzędu z warunkiem Dirichleta przedział (a,b) dzielimy na siatkę, powiedzmy o stałym kroku: punkty siatki: u A y i w metodzie strzałów używamy
1 Równania nieliniowe
 1 Równania nieliniowe 1.1 Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym jest numeryczne poszukiwanie rozwiązań równań nieliniowych, np. algebraicznych (wielomiany),
1 Równania nieliniowe 1.1 Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym jest numeryczne poszukiwanie rozwiązań równań nieliniowych, np. algebraicznych (wielomiany),
Rachunek prawdopodobieństwa i statystyka
 Rachunek prawdopodobieństwa i statystyka Momenty Zmienna losowa jest wystarczająco dokładnie opisana przez jej rozkład prawdopodobieństwa. Względy praktyczne dyktują jednak potrzebę znalezienia charakterystyk
Rachunek prawdopodobieństwa i statystyka Momenty Zmienna losowa jest wystarczająco dokładnie opisana przez jej rozkład prawdopodobieństwa. Względy praktyczne dyktują jednak potrzebę znalezienia charakterystyk
Laboratorium techniki światłowodowej. Ćwiczenie 2. Badanie apertury numerycznej światłowodów
 Laboratorium techniki światłowodowej Ćwiczenie 2. Badanie apertury numerycznej światłowodów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie Światłowody
Laboratorium techniki światłowodowej Ćwiczenie 2. Badanie apertury numerycznej światłowodów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie Światłowody
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Równania Maxwella. Wstęp E B H J D
 Równania Maxwella E B t, H J D t, D, B 0 Równania materiałowe B 0 H M, D 0 E P, J E, gdzie: 0 przenikalność elektryczną próżni ( 0 8854 10 1 As/Vm), 0 przenikalność magetyczną próżni ( 0 4 10 7 Vs/Am),
Równania Maxwella E B t, H J D t, D, B 0 Równania materiałowe B 0 H M, D 0 E P, J E, gdzie: 0 przenikalność elektryczną próżni ( 0 8854 10 1 As/Vm), 0 przenikalność magetyczną próżni ( 0 4 10 7 Vs/Am),
