Zastosowanie metody VFO do sterowania pojazdami N-przyczepowymi
|
|
|
- Krzysztof Mróz
- 6 lat temu
- Przeglądów:
Transkrypt
1 Zastosowanie metody VFO do sterowania pojazdami N-przyczepowymi Naukowe seminarium wyjazdowe Szklarska Poręba, 5-8 V 211 Praca naukowa finansowana ze środków na naukę w latach jako projekt badawczy nr N N Maciej Michałek Katedra Sterowania i Inżynierii Systemów Politechnika Poznańska M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 1 / 42
2 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 2 / 42
3 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 3 / 42
4 Zasadnicze rozróżnienie dwa sposoby mocowania przyczep segment i-1 segment i-1 L hi i i segment i segment i L i i-ty przegub pasywny L i i-ty przegub pasywny L hi > mocowanie pozaosiowe (po) (ang. off-axle) L hi = mocowanie osiowe (O) (ang. on-axle) Rodzaje pojazdów N-przyczepowych: Ogólny Pojazd N-Przyczepowy (OPNP): ciagnik (monocykl) + po/o po po/o Standardowy Pojazd N-Przyczepowy (SPNP): ciagnik (monocykl) + O + O O M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 4 / 42
5 Sterowanie pojazdami N-przyczepowymi motywacja 1 Argumenty teoretyczne SPNP i OPNP trudnymi obiektami sterowania (nieliniowe, nieholonomiczne, niestabilne w ruchu tyłem) dla SPNP większość rozwiazań wynika transformacji modelu do postaci łańcuchowej (lokalność metody, potencjalne trudności w strojeniu sterownika problem jakości sterowania w przestrzeni oryginalnej) szczególne trudności dla modelu OPNP (model nie jest linearyzowalny sprzężeniem zwrotnym dla N 2, nieminimalnofazowość w ruchu przodem) otwarte problemy (sterowanie z ograniczeniami na stan, odporność, uniwersalność sterowników, sterowanie OPNP dla N 1... ) 2 Argumenty praktyczne liczne zastosowania pojazdów przegubowych (w tym z przyczepami) manewry pojazdami przegubowymi częste i uciażliwe w praktyce nieintuicyjne i złożone manewry pojazdami wielosegmentowymi SPNP: Standardowy Pojazd N-Przyczepowy (ang. standard N-trailer vehicle) OPNP: Ogólny Pojazd N-Przyczepowy (ang. general N-trailer vehicle) M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 5 / 42
6 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 6 / 42
7 Ogólny pojazd N-przyczepowy (OPNP): podstawowe definicje v Y y tractor (segment 1) 1 L h1 Wektor konfiguracji pojazdu q = [β 1... β N θ N x N y N ] T R N+3 (1) 1 y 1 trailer 1 (segment 2) v L 1 Wektor konfiguracji ostatniego segmentu q = [θ N x N y N ] T R 3 (2) L h2 y 2 trailer N (segment N+1) v N trailer 2 (segment 3) N 2 v L 2 Wektor wejść sterujacych u = [ω v ] T R 2 (3) Punkt wyróżniony P (ang. guidance point) y N P guidance point N L N L h3 X P = (x N, y N ) (4) x N x 2 x 1 L i > długość i-tej przyczepy L hi odsunięcie i-tego przegubu x OPNP L hi= i SPNP M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 7 / 42
8 Rekurencyjna (kaskadowa) postać modelu OPNP Y tractor (segment 1) v 1 Równania kinematyki OPNP: y L h1 θ i = ω i (5) y 1 trailer 1 (segment 2) 1 v L 1 ẋ i = v i cos θ i (6) ẏ i = v i sin θ i (7) y 2 y N trailer N (segment N+1) P guidance point v N trailer 2 (segment 3) N N L N 2 v 2 3 x N x 2 x 1 2 L h3 L 2 x L h2 X [ ] ωi = v i ω i, v i wirtualne sterowania i-tego segmentu [ ] L hi 1 cos β L i sin β i L i i L hi sin β i cos β i }{{} J i (β i ) odwracalna β i [ ] ωi 1 v i 1 (8) β i = θ i 1 θ i (9) β 1 β 2 β N θ + - θ θ N ω v = ẋ =v c ẏ =v s tractor β 1 J 1 (β 1 ) ω 1 v 1 1 = 1 ẋ 1 =v 1 c 1 ẏ 1 =v 1 s 1 trailer 1 β 2 J 2 (β 2 ) ω N-1 v N-1 N 1 = N 1 ẋ N 1 =v N 1 c N 1 ẏ N 1 =v N 1 s N 1 trailer N-1 β N J N (β N ) ω N v N N = N ẋ N =v N c N ẏ N =v N s N trailer N θ N x N y N general N-trailer vehicle M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 8 / 42
9 Rekurencyjna (kaskadowa) postać modelu SPNP Y y y 1 y 2 y N trailer N (segment N+1) P guidance point v N N N L N L 2 tractor (segment 1) 2 v 2 3 v 1 v 1 x N x 2 x trailer 2 (segment 3) x L 1 trailer 1 (segment 2) X Równania kinematyki SPNP: θ i = ω i (1) ẋ i = v i cos θ i (11) ẏ i = v i sin θ i (12) ω i, v i wirtualne sterowania i-tego segmentu [ ] ωi = v i [ ] 1 sin β L i i cos β }{{} J i (β i ) osobliwa β i [ ] ωi 1 v i 1 (13) β i = θ i 1 θ i (14) ω v = 1 = 1 ẋ =v c ω 1 ẋ 1 =v 1 c 1 ẏ J 1 (β 1 ) =v s J 2 (β 2 ) v ẏ 1 =v 1 s 1 1 tractor β 1 β 2 β N θ θ 1 β 1 trailer 1 β ω N-1 v N-1 θ N-1 N 1 = N 1 ẋ N 1 =v N 1 c N 1 ẏ N 1 =v N 1 s N 1 trailer N β N J N (β N ) ω N v N N = N ẋ N =v N c N ẏ N =v N s N trailer N θ N x N y N standard N-trailer vehicle M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 9 / 42
10 SPNP cechy modelu kinematyki sterowalny w krótkim czasie* (spełnia LARC) Y y tractor (segment 1) v 1 1 silnie nieliniowy nieholonomiczny: ẋ i sin θ i ẏ i cos θ i =, i [,N] 1 v 2 1 L 1 DOF = dim(q) (N + 1) = N + 3 N 1 = 2 y 1 y 2 y N trailer N (segment N+1) P guidance point v N N N L N L 2 2 v 2 3 x N x 2 x 1 2 trailer 2 (segment 3) x trailer 1 (segment 2) X ubogi w sterowanie: dim(q) dim(u ) = n m = N = N + 1 osobliwy**, gdy i [1;N 1] : β i = π/2 (zmiana stopnia nieholonomiczności) strukturalnie niestabilny dla v < (efekt składania się pojazdu oraz efekt scyzoryka ang. jacknifing phenomenon) różniczkowo płaski***: wyścia płaskie x N i y N (linearyzowalny sprzężeniem zwrotnym) *J.P. Laumond: Controllability of a multibody mobile robot, IEEE Trans. Robotics and Automation, 9(6), 1993 **F. Jean: The car with N trailers: characterization of the singular configurations, ESAIM: Control, Optim. Calc. Variations, Vol.1, 1996 *** P. Rouchon et al.: Flatness, motion planning and trailer systems, Proc. of 32nd CDC Conf., San Antonio USA, 1993 M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 1 / 42
11 OPNP specyficzne cechy modelu kinematyki Y y tractor (segment 1) v 1 L h1 osobliwy*, gdy: i [1;N 1] : β i = π/2 lub j : γ j = π/2, gdzie: γ i = θ i θ i+1 + arc tg( θ i L hi /v i ) segment i 1 v i i y 1 trailer 1 (segment 2) v L 1 segment i+1 L i i L hi y 2 y N trailer N (segment N+1) P guidance point v N trailer 2 (segment 3) N N L N 2 v 2 3 x N x 2 x 1 2 L h3 L 2 x L h2 X (zmiana stopnia nieholonomiczności) i 1 wirtualne koło skrętne dynamika w torze ω i 1 θ i nieminimalnofazowa**: G(s) θ i(s) ω i 1 (s) v i 1 :=V > nie jest różniczkowo płaski*** dla N 2 (nie jest linearyzowalny sprzężeniem zwrotnym, gdy N 2) = 1 L hi V s s(1 + L i V s) *C. Altafini: Some properties of the general n-trailer, Int. Journal of Control 74(4), 21 ** M. Michałek, K. Kozłowski: VFO tracking and set-point control for an articulated vehicle with off-axle hitched trailer, Proc. of ECC, Budapeszt, 29 *** P. Rouchon et al.: Flatness, motion planning and trailer systems, Proc. of 32nd CDC Conf., San Antonio USA, 1993 M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 11 / 42
12 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 12 / 42
13 Definicje zwiazane z zadaniem sterowania Wektor konfiguracji referencyjnej: [ ] qβt q t = = [β t1... β tn θ tn x tn y tn ] T R N+3 q t Wektor błędu konfiguracji: [ ] eβ e = = [e β1 ē... e βn e θ e x e y] T q t q (15) Wektor błędów katów w przegubach: e β [β t1 β 1... β tn β N ] T R N (16) Wektor błędu położenia (orientacji i pozycji) ostatniego segmentu: e θ θ tn θ N ē = e x qt q = x tn x N R 3 e y y tn y N (17) M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 13 / 42
14 Zadanie sterowania Śledzenie trajektorii Dane: q t (τ) C d (dopuszczalna) Założenia: At1. At2. At3. trajektoria q t (τ) jest ustawicznie pobudzajaca: τ ẋ 2 tn (τ) + ẏ2 tn (τ) wszystkie elementy wektora q mierzalne wartości parametrów L i, L hi dokładnie znane Sterowanie do punktu Dane: q t = [... q T t ]T = const Założenia: Ap1. dla ostatniego segmentu: ē() Ap2. Ap3. wszystkie elementy wektora q mierzalne wartości parametrów L i, L hi dokładnie znane Zadanie sterowania polega na zaprojektowaniu reguły sterowania ze sprzężeniem zwrotnym u = u (q t, q, ), która zastosowana do kinematyki robota reprezentowanej równaniami (1)-(14) zapewnia zbieżność błędu e = [e T β ēt ] T w takim sensie, że: Śledzenie trajektorii lim ē(τ) δ 1 oraz lim eβi (τ) δ2, τ τ Sterowanie do punktu lim ē(τ) δ 1 oraz lim eβi (τ) = kπ τ τ przy czym: δ 1, δ 2 to założone otoczenia zera w przestrzeni uchybu oraz k {, 1, 2,...}. zadanie = stabilizacja N-tej przyczepy + układanie/prostowanie łańcucha M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 14 / 42
15 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 15 / 42
16 SPNP: propagacja prędkości wzdłuż łańcucha kinematycznego Propagacja prędkości w kierunku ciagnik przyczepy (na podstawie kinematyki (1)-(14)): oraz ω i = (1/L i )v i 1 sin β i (18) v i = v i 1 cos β i (19) β i = θ i 1 θ i βi = θ i 1 θ i = ω i 1 ω i (2) Propagacja prędkości w kierunku przyczepy ciagnik (na podstawie (18)-(2)): oraz ω i 1 = ω i + β i (21) v i 1 = L i ω i sin β i + v i cos β i (22) β i = Atan2c (L i ω i v i 1, v i v i 1 ) R (23) Atan2c (, ) : R R R M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 16 / 42
17 SPNP: wyprowadzenie sterownika kaskadowego (pętla zewnętrzna) Eksperyment myślowy: uwalniamy ostatnia przyczepę i traktujemy ja jak pojazd typu monocykl o wejściach sterujacych ω N i v N. Zakładamy, że dane sa funkcje sterujace Φ ω(ē, ), Φ v(ē, ), które zapewniaja asymptotyczne śledzenie trajektorii lub asymptotyczna stabilizację w punkcie dla pojazdu typu monocykl: LTPT: ω N = Φ ω(ē, ), v N = Φ v(ē, ) lim ē(τ) = qt(τ) q(τ) = τ LTPS: ω N = Φ ω(ē, ), v N = Φ v(ē, ) lim ē(τ) = qt q(τ) = τ Y y N trailer N (segment N+1) P v N = v N N = X x N LTPT: Last-Trailer Posture Tracker, LTPS: Last-Trailer Posture Stabilizer M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 17 / 42
18 SPNP: wyprowadzenie sterownika kaskadowego (pętla zewnętrzna) Skoro w SPNP nie możemy bezpośrednio wymusić spełnienia równań ω N = Φ ω(ē, ) oraz v N = Φ v(ē, ), zatem proponujemy przyjać: ω dn := Φ ω(ē, ), v dn := Φ v(ē, ) (24) q t q LTPT / LTPS ω dn := Φ ω ( e,.) v dn := Φ v ( e,.)...?... ω v kinematyka SPNP q pętla zewnętrzna Jak zapewnić, aby (ω dn ω N ) oraz (v dn v N )? Realizacja (ω dn ω N ) oraz (v dn v N ) możliwa poprzez odpowiedni ruch segmentu N 1, który wynika z ruchu segmentu N 2..., który ostatecznie wynika z ruchu modułu czyli modułu ciagnika (aktywny segment pojazdu SPNP). M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 18 / 42
19 SPNP: wyprowadzenie sterownika kaskadowego (pętle wewnętrzne) Propozycja procedury projektowej K1. propagacja prędkości zadanych oraz k [ at zadany w złaczu (na podstawie (21)-(23)): ] ω di 1 ω di + βi d (25) v di 1 L i ω di sin β i + v di cos β i (26) β di Atan2c (L i ω di v di 1, v di v di 1 ) R (27) K2. konstrukcja i-tej wewnętrznej pętli sprzężenia zwrotnego: [ βi ] d k i(β di β i ) + β di = k i e di + β di, k i > (28) ω di v di (26) v di-1 β di e di (27) - d/dτ k i ω di ω di-1 v di-1 JCM i Joint Control Module β i k i > parametr projektowy M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 19 / 42
20 SPNP: schemat układu sterowania kaskadowego Równania sterownika: q t q LTPT / LTPS ω dn v dn JCM N... ω d2... v d2 JCM 2 ω d1 v d1 JCM 1 ω d v d kinematyka SPNP β N q wyjście systemu β i wyjścia pomocnicze... β 2 pętle wewnętrzne pętla zewnętrzna β 1 q v dn := Φ v(ē, ) (29) ω dn := Φ ω(ē, ) (3) v dn 1 := L N ω dn sin β N + v dn cos β N (31) ) β dn := Atan2c (L N ω dn v dn 1, v dn v dn 1 (32) ω dn 1 := k N (β dn β N ) + β dn + ω dn (33). v d1 := L 2 ω d2 sin β 2 + v d2 cos β 2 (34) β d2 := Atan2c (L 2 ω d2 v d1, v d2 v d1 ) (35) ω d1 := k 2 (β d2 β 2 ) + β d2 + ω d2 (36) v d := L 1 ω d1 sin β 1 + v d1 cos β 1 (37) β d1 := Atan2c (L 1 ω d1 v d, v d1 v d ) (38) ω d := k 1 (β d1 β 1 ) + β d1 + ω d1 (39) Pozostaja do określenia jawne postaci funkcji sterujacych Φ v(ē, ) oraz Φ ω(ē, )... M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 2 / 42
21 Efekt składania łańcucha kinematycznego pojazdu SPNP A 1 R d 2 R D tractor (segment 1) trailer 1 (segment 2) tractor (segment 1) trailer 2 (segment 3) B 1 R 2 Q R tractor (segment 1) trailer 1 (segment 2) trailer 2 (segment 3) A: kostrukcja mechanicznie dopuszczajaca składanie się pojazdu (β 1, β 2 R) B: kostrukcja z mechanicznym ograniczeniem drugiego kata skręcenia (β 2 Q β R) M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 21 / 42
22 Efekt składania łańcucha kinematycznego pojazdu SPNP Przedstawiona postać równań dopuszcza występowanie efektu składania pojazdu, ponieważ: β di Atan2c Li ω di v di 1, v di v di 1 R }{{}}{{} R R Propozycja unikania efektu składania: wówczas v di 1 σ L i ω di sin β i + v di cos β i, σ { 1, +1} (4) β di Atan2c L i ω di v di 1, v di v di 1 }{{}}{{} R R + gdy sgn(v di )=σ? Skuteczność propozycji (4) zależy od własności sterownika pętli zewnętrznej (LTPT/LTPS). Poza modyfikacja (4) pozostałe równania sterownika nie ulegaja zmianie. σ to zmienna decyzyjna, której wartość wybierana jest w odniesieniu do własności sterownika pętli zewnętrznej (LTPT/LTPS) M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 22 / 42
23 Kwestie implementacyjne 1 Nieciagłość algorytmu Definicja β di (τ I ) = Atan2c (A(τ I ), B(τ I )) nieokreślona, gdy A(τ I ) = B(τ I ) =. Propozycja: w chwilach τ I przyjać β di (τ I ) := β di = lim τ τ β di (τ). Alternatywnie: I IF (A 2 + B 2 ɛ) AND ( ē ɛ e) THEN β di := β di 2 Realizacja sprzężeń wyprzedzajacych β di analityczna wynikajaca z formalnego zróżniczkowania β di (wymaga pochodnych ω di oraz v di ) numeryczna z zastosowaniem dokładnych odpornych różniczkowatorów (ang. exact robust differentiators*) numeryczna aproksymacja poprzez filtrację: β di β dif = L 1 {sβ di (s)/(1 + st F )} (aproksymacja zwykle pogarsza dokładność śledzenia w stanie ustalonym) 3 Zasada syntezy pętli wewnętrznych reguła heurystyczna: k i > k i+1 (41) Wybór wartości k i > jako kompromis między sztywnościa pętli wewnętrznych a wrażliwościa układu zamkniętego na szumy pomiarowe oraz tolerancja ograniczeń sygnałów sterujacych (prędkości kół ciagnika). * A. Levant: Robust exact differentiation via sliding mode technique, Automatica, 34(3), 1998 M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 23 / 42
24 Ograniczenia sterowania ω k max maksymalna dopuszczalna prędkość katowa koła ciagnika (kinematyka (2,)) przestrzeń prędkości kół ciągnika L kmax s u 2 przestrzeń prędkości platformy ciągnika u 2dop u 2max D P kinematyka u 1 kmax kmax (2,) u 1max u 1dop u 1max Ω = kmax u 2max [ ] b/(2r) 1/r u b/(2r) 1/r, u = [u 1 u 2 ] T = [ω v ] T, Ω = [ω P ω L ] T b: rozstaw kół ciagnika, r: promień koła ciagnika Procedura skalowania prędkości: u s = 1 s u, { s max 1; ω P ω k max ; } ω L 1 (42) ω k max Składowe przeskalowanego sterowania u s sa już realizowalne fizycznie. M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 24 / 42
25 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 25 / 42
26 Sterownik VFO jako LTPT lub LTPS - równania Równania sterownika VFO zapisane dla ostatniej (N-tej) przyczepy: Φ ω k ae a + θ a (43) Φ v h x cos θ N + h y sin θ N (44) Śledzenie trajektorii (LTPT) Sterowanie do punktu (LTPS) h x = k pe x + v x, v x = ẋ t (45) h y = k pe y + v y, v y = ẏ t (46) e x = x tn x N, e y = y tn y N (47) e a = θ a θ N (48) θ a = Atan2c (σ h y, σ h x) (49) θ a = (ḣyhx hyḣx)/(h2 x + h2 y ) (5) σ sgn(u 2t (τ)) (51) h x = k pe x + v x, v x = ησ ē cos θ tn (52) h y = k pe y + v y, v y = ησ ē sin θ tn (53) e x = x tn x N, e y = y tn y N (54) e a = θ a θ N (55) θ a = Atan2c (σ h y, σ h x) (56) θ a = (ḣyhx hyḣx)/(h2 x + h 2 y) (57) σ sgn(e x cos θ tn + e y sin θ tn ) (58) Współczynniki projektowe: k a, k p >, η (, k p) Postaci zmiennej decyzyjnej σ zdefiniowane w (51) i (58) sa wykorzystywane w ramach modyfikacji (4) algorytmu sterowania kaskadowego. M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 26 / 42
27 Sterownik VFO jako LTPT lub LTPS - interpretacje geometryczne śledzenie trajektorii k p =1 sterowanie do punktu k p =1 y tn y N y G wirtualna N-ta przyczepa referencyjna P x N e * e a q * t q * t * h x tn q * trajektoria referencyjna a N x G tn P x N * h q * ea a N * v e * y G wirtualna N-ta przyczepa referencyjna x G tn * g 2t przyjęte 2ε otoczenie pozycji y referencyjnej dla N N-tej przyczepy q * t = h = [h x h y] T, ē = [e x e y] T, v = [v x v y] T, q = [ẋ N ẏ N ] T, ḡ 2t = [cos θ tn sin θ tn ] T M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 27 / 42
28 Sterownik VFO jako LTPT lub LTPS - motywacja Gwarancja ruchu nieoscylacyjnego, prawie bez zmiany znaku prędkości postępowej (możliwa co najwyżej jedna zmiana znaku w stanie przejściowym skuteczność propozycji (4)) Efekt naprowadzania N-tej przyczepy przydatny w prostowaniu łańcucha SPNP Prostota strojenia sterownika VFO: K1. k p (, 5] jako kompromis między szybkościa zbieżności a wrażliwościa na szumy pomiarowe i opóźnienia w pętli sprzężenia K2. k a := 2k p ponieważ proces orientowania jest kluczowy i istotniejszy od procesu popychania K3. η (, k p) zgodnie z żadan a intensywnościa efektu naprowadzania (tym większa intensywność im mniejsze k p η) Gwarancja asymptotycznej zbieżności błędów do zera dla zadania śledzenia oraz sterowania do punktu* *M. Michałek, K. Kozłowski: Vector-Field-Orientation feedback control method for a differentially driven vehicle, IEEE Trans. Control Sys. Techn., 18(1), 21 M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 28 / 42
29 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 29 / 42
30 SPNP: śledzenie trajektorii złożonej (ruch tyłem) TRAJECTORY TRACKING + VFO for LTPT Warunki symulacji 2 q() = [ π/2.3] T q t () = [ π/2 1 ] T ω 3t =.15(1 + sin.5τ) rad/s, v 3t =.2 m/s β d1 := β d1f, T F =.5 s βd2,3 := Wartości parametrów L 1 = L 2 = L 3 =.25 m k 1 = 5, k 2 = 2, k 3 = 5, ɛ =.1 k a = 2, k p = 1, ɛ h =.1 ω k max = 8π rad/s, b =.17 m, r =.25 m y G [m] q t () Animacje: S2RMPMovie.gif S2FoldRMPMovie.gif x G [m] 1 e θ [rad] e x [m] e y [m] 2 1 β 1 [rad] β 2 [rad] β 3 [rad] 1 5 ω [rad/s] v [m/s] time [s] time [s] time [s] M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 3 / 42 5
31 SPNP: sterowanie do punktu (parkowanie równoległe tyłem) Warunki symulacji 1.5 SET POINT REGULATION + VFO for LTPS q() = [ π/2 ] T q t = [ π/2 1 ] T ω 3t = v 3t β d1 := β d1f, T F =.5 s βd2,3 := 1 Wartości parametrów y G [m].5 L 1 = L 2 = L 3 =.25 m k 1 = 5, k 2 = 2, k 3 = 5, ɛ =.1 k a = 2, k p = 1, η =.8, ɛ h =. ω k max = 8π rad/s, b =.17 m, r =.25 m q t.5 Animacje: S3RMPMovie.gif S3FoldRMPMovie.gif x G [m] e θ [rad] e x [m] e y [m] 2 1 β 1 [rad] β 2 [rad] β 3 [rad] 5 ω [rad/s] v [m/s] time [s] time [s] time [s] M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 31 / 42
32 SPNP: wpływ efektu naprowadzania na prostowanie pojazdu SET POINT REGULATION + VFO: k p =1., η=.1 SET POINT REGULATION + VFO: k p =1., η=.3 SET POINT REGULATION + VFO: k p =1., η= y G [m].5 y G [m].5 y G [m] x G [m] x G [m] x G [m] SET POINT REGULATION + VFO: k p =1., η=.6 SET POINT REGULATION + VFO: k p =1., η=.8 SET POINT REGULATION + VFO: k p =1., η= y G [m].5 y G [m].5 y G [m] x G [m] x G [m] x G [m] Czasy trwania poszczególnych symulacji: τ h 29 s dla η =.1, η =.3, η =.4 oraz τ h = 4 s dla η =.6, η =.8, η =.9. M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 32 / 42
33 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 33 / 42
34 OPNP: propagacja prędkości wdłuż łańcucha kinematycznego Propagacja prędkości w kierunku ciagnik przyczepy (na podstawie kinematyki (8)): [ ] ωi = v i ] [ L hi cos β L i i 1 sin β L i i } L hi sin β i {{ cos β i } J i (β i ) [ ] ωi 1 v i 1 (59) Propagacja prędkości w kierunku przyczepy ciagnik (na podstawie (59)): [ ] [ ] ωi 1 L i 1 cos β = L i sin β hi L i hi v i 1 L i sin β i cos β i }{{} J 1 (β i i ) [ ] ωi v i (6) det(j i (β i )) = L hi /L i M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 34 / 42
35 OPNP: modyfikacja pętli wewnętrznych dla przegubów typu po Transformacja prędkości zadanych (na podstawie (6)): [ ] [ ] ωdi 1 L i 1 [ωdi ] [ ] cos β = L i sin β hi L i hi = J 1 ωdi v di 1 L i sin β i cos β i v i (β i ) di v di (61) ω di v di J i -1 (β i ) ω di-1 v di-1 JTM i Joint Transformation Module β i JTM i odwzorowanie algebraiczne (brak dynamiki) M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 35 / 42
36 OPNP: schemat układu sterowania w przypadku N po Równania sterownika: q t q LTPT / LTPS ω dn v dn JTM N J N -1 (β N ) β N q wyjście systemu β i wyjścia pomocnicze ω d2 JTM v 2 d2-1 J 2 (β 2 ) β 2 ω d1 v d1 pętle wewnętrzne pętla zewnętrzna JTM 1 J 1-1 (β 1 ) β 1 ω d v d kinematyka W tym przypadku obwody podrzędne nie wprowadzaja dodatkowej dynamiki nieliniowe odwzorowanie statyczne zależne od bieżacej konfiguracji. OPNP q v dn := Φ v(ē, ) (62) ω dn := Φ ω(ē, ) (63) [ ] [ ] ω dn 1 := J 1 v dn 1 N (β ω N ) dn v dn. [ ] ω d := J 1 v 1 (β 1) d [ ] ω d1 v d1 ( [ ] N [ ] ω d = J 1 Φ (β v i i )) ω(ē, ) d Φ v(ē, ) i=1 (64) (65) (66) M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 36 / 42
37 OPNP (SPNP): schemat układu sterowania w przypadku ogólnym q t q LTPT / LTPS ω dn v dn JTM N / JCM N β N ω d2 v d2 JTM 2 / JCM 2 β 2 ω d1 v d1 JTM 1 / JCM 1 β 1 ω d v d kinematyka OPNP (SPNP) q pętle wewnętrzne pętla zewnętrzna JTM i gdy i-ty przegub jest typu po JCM i gdy i-ty przegub jest typu O M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 37 / 42
38 OPNP: śledzenie trajektorii złożonej (ruch tyłem dla N po) TRAJECTORY TRACKING + VFO for LTPT Warunki symulacji q() = [ 2π 1.5.5] T q t () = [ π/2 1 ] T ω 3t =.15(1 + sin.5τ) rad/s, v 3t =.2 m/s Wartości parametrów L 1 =.35 m, L 2 = L 3 =.25 m L h1 =.1 m, L h2 =.2 m, L h3 =.1 m k a = 2, k p = 1, ɛ h =.1 ω k max = 8π rad/s, b =.17 m, r =.25 m y G [m].5.5 q t () Animacje: S6RMPMovie.gif S6FoldRMPMovie.gif* * ruch przodem przyczepy referencyjnej (v 3t = +.2 m/s) x G [m] e θ [rad] e x [m] e y [m] time [s] time [s] β 1 [rad] β 2 [rad] β 3 [rad] ω [rad/s] v [m/s] time [s] M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 38 / 42
39 OPNP: sterowanie do punktu (parkowanie prostopadłe tyłem dla N po) Warunki symulacji q() = [ π 2 ] T q t = [ π/2 1 ] T ω 3t = v 3t SET POINT REGULATION + VFO for LTPS Wartości parametrów L 1 =.35 m, L 2 = L 3 =.25 m L h1 =.1 m, L h2 =.2 m, L h3 =.1 m k a = 2, k p = 1, η =.8, ɛ h =. ω k max = 8π rad/s, b =.17 m, r =.25 m y G [m] Animacje: S7RMPMovie.gif S7FoldRMPMovie.gif* * żadany ruch przodem dla ostatniej przyczepy (σ := +1) q t x G [m] e θ [rad] e x [m] e y [m] β 1 [rad] β 2 [rad] β 3 [rad] 5 5 ω [rad/s] v [m/s] time [s] time [s] time [s] M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 39 / 42
40 Plan 1 Wprowadzenie 2 Modele kinematyki pojazdów N-przyczepowych 3 Definicja zadania sterowania 4 Kaskadowa struktura sterowania dla SPNP 5 Wykorzystanie metody VFO 6 Wyniki symulacji dla SPNP 7 Zastosowanie metody dla OPNP 8 Uwagi końcowe M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 4 / 42
41 Problemy otwarte i przyszłe prace 1 Ograniczenie skutków wrażliwości układu zamkniętego w otoczeniu punktu q t (skutek nieciagłości algorytmu) 2 Modyfikacja sterownika dla OPNP w ruchu przodem (skutek nieminimalnofazowości w ruchu przodem dla L hi > ) 3 Badania w zakresie odporności układu zamkniętego (niepewność parametryczna: L si L i oraz L shi L hi, szumy pomiarowe w sprzężeniu zwrotnym: q n = q + n) 4 Przeprowadzenie formalnej analizy stabilności i zbieżności (twierdzenie o stabilności systemów wzajemnie połaczonych interconnected systems) 5 Sterowanie z ograniczeniami na stan (ograniczone katy w złaczach) 6 Eksperymentalna weryfikacja metody (stanowisko laboratoryjne RMP-SW) 7 Wykorzystanie metody do realizacji systemu wsparcia kierowców M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 41 / 42
42 ... Dziękuję za uwagę! M. Michałek (KSIS-PP) Metoda VFO dla pojazdów N-przyczepowych 42 / 42
Kaskadowa metoda sterowania standardowym pojazdem N-przyczepowym z zastosowaniem algorytmu VFO
 Kaskadowa metoda sterowania standardowym pojazdem N-przyczepowym z zastosowaniem algorytmu VFO Seminarium naukowe KSIS Poznań, kwiecień 2 Praca naukowa finansowana ze środków na naukę w latach 2-22 jako
Kaskadowa metoda sterowania standardowym pojazdem N-przyczepowym z zastosowaniem algorytmu VFO Seminarium naukowe KSIS Poznań, kwiecień 2 Praca naukowa finansowana ze środków na naukę w latach 2-22 jako
Kaskadowe sterowanie przegubowym robotem mobilnym w systemie RMP-SW
 Kaskadowe sterowanie przegubowym robotem mobilnym w systemie RMP-SW Maciej Michałek, Marcin Kiełczewski, Tomasz Jedwabny Streszczenie Artykuł poświęcony jest problemowi sterowania przegubowym robotem mobilnym
Kaskadowe sterowanie przegubowym robotem mobilnym w systemie RMP-SW Maciej Michałek, Marcin Kiełczewski, Tomasz Jedwabny Streszczenie Artykuł poświęcony jest problemowi sterowania przegubowym robotem mobilnym
Planowanie przejazdu przez zbiór punktów. zadania zrobotyzowanej inspekcji
 dla zadania zrobotyzowanej inspekcji Katedra Sterowania i Inżynierii Systemów, Politechnika Poznańska 3 lipca 2014 Plan prezentacji 1 Wprowadzenie 2 3 4 Postawienie problemu Założenia: Rozpatrujemy kinematykę
dla zadania zrobotyzowanej inspekcji Katedra Sterowania i Inżynierii Systemów, Politechnika Poznańska 3 lipca 2014 Plan prezentacji 1 Wprowadzenie 2 3 4 Postawienie problemu Założenia: Rozpatrujemy kinematykę
Metoda VFO i jej zastosowanie do sterowania potrójnym integratorem
 Metoda VFO i jej zastosowanie do sterowania potrójnym integratorem Maciej Michałek i Krzysztof Kozłowski Katedra Sterowania i Inżynierii Systemów Politechnika Poznańska Piotrowo 3a, 6-965 Poznań {maciej.michalek/krzysztof.kozlowski}@put.poznan.pl
Metoda VFO i jej zastosowanie do sterowania potrójnym integratorem Maciej Michałek i Krzysztof Kozłowski Katedra Sterowania i Inżynierii Systemów Politechnika Poznańska Piotrowo 3a, 6-965 Poznań {maciej.michalek/krzysztof.kozlowski}@put.poznan.pl
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Numeryczne metody optymalizacji Optymalizacja w kierunku. informacje dodatkowe
 Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Kinematyka robotów mobilnych
 Kinematyka robotów mobilnych Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course:
Kinematyka robotów mobilnych Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course:
Planowanie i realizacja ruchu z wykorzystaniem własności stabilizatora VFO dla robota z napędem różnicowym
 Planowanie i realizacja ruchu z wykorzystaniem własności stabilizatora VFO dla robota z napędem różnicowym Maciej Michałek 1, Krzysztof Kozłowski 1 Streszczenie Artykuł prezentuje propozycję strategii
Planowanie i realizacja ruchu z wykorzystaniem własności stabilizatora VFO dla robota z napędem różnicowym Maciej Michałek 1, Krzysztof Kozłowski 1 Streszczenie Artykuł prezentuje propozycję strategii
Laboratorium Podstaw Robotyki ĆWICZENIE 4
 Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 4 System sterowania robotem mobilnym MTracker Celem ćwiczenia jest poznanie sposobów sterowania nieholonomicznym,
Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 4 System sterowania robotem mobilnym MTracker Celem ćwiczenia jest poznanie sposobów sterowania nieholonomicznym,
Laboratorium Podstaw Robotyki ĆWICZENIE 4
 Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 4 System sterowania robotem mobilnym MTracker 1 Celem ćwiczenia jest poznanie sposobów sterowania
Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 4 System sterowania robotem mobilnym MTracker 1 Celem ćwiczenia jest poznanie sposobów sterowania
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Podstawy robotyki wykład V. Jakobian manipulatora. Osobliwości
 Podstawy robotyki Wykład V Jakobian manipulatora i osobliwości Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Metoda bezpośrednia uzyskania macierzy
Podstawy robotyki Wykład V Jakobian manipulatora i osobliwości Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Metoda bezpośrednia uzyskania macierzy
2.9. Kinematyka typowych struktur manipulatorów
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
Strategia śledzenia trajektorii z unikaniem kolizji dla robota mobilnego klasy (2,0)
 Strategia śledzenia trajektorii z unikaniem kolizji dla robota mobilnego klasy (2,) Maciej Michałek 1, Wojciech Kowalczyk 1, Krzysztof Kozłowski 1 Streszczenie Artykuł przedstawia koncepcję sterowania
Strategia śledzenia trajektorii z unikaniem kolizji dla robota mobilnego klasy (2,) Maciej Michałek 1, Wojciech Kowalczyk 1, Krzysztof Kozłowski 1 Streszczenie Artykuł przedstawia koncepcję sterowania
2.12. Zadania odwrotne kinematyki
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej
 MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Hybrydowy stabilizator odporny dla robota mobilnego o kinematyce (2,0)
 Hybrydowy stabilizator odporny dla robota mobilnego o kinematyce (2,) Maciej Michałek 1, Dariusz Pazderski 1 Streszczenie Artykuł przedstawia propozycję nowego algorytmu stabilizacji dla robota mobilnego
Hybrydowy stabilizator odporny dla robota mobilnego o kinematyce (2,) Maciej Michałek 1, Dariusz Pazderski 1 Streszczenie Artykuł przedstawia propozycję nowego algorytmu stabilizacji dla robota mobilnego
Laboratorium Podstaw Robotyki ĆWICZENIE 4
 Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 4 System sterowania robotem mobilnym MiniTracker V3 Celem ćwiczenia jest poznanie sposobów sterowania
Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 4 System sterowania robotem mobilnym MiniTracker V3 Celem ćwiczenia jest poznanie sposobów sterowania
Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Stabilność II Metody Lapunowa badania stabilności
 Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Mechanika Robotów. Wojciech Lisowski. 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej
 Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Manipulatory i roboty mobilne AR S1 semestr 5
 Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej
 mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-28.06.07 współrzędne uogólnione punkt materialny... wektor wodzący: prędkość: przyspieszenie: liczba
mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-28.06.07 współrzędne uogólnione punkt materialny... wektor wodzący: prędkość: przyspieszenie: liczba
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
3.1. Jakobian geometryczny
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 3. Kinematyki różniczkowa i statyka 3.1. Jakobian geometryczny Pozycja i orientacja x manipulatora o n stopniach swobody zależy od
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 3. Kinematyki różniczkowa i statyka 3.1. Jakobian geometryczny Pozycja i orientacja x manipulatora o n stopniach swobody zależy od
Kompensacja wyprzedzająca i opóźniająca fazę. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
#09. Systemy o złożonej strukturze
 #09 Systemy o złożonej strukturze system składa się z wielu elementów, obiekty (podsystemy) wchodzące w skład systemu są ze sobą połączone i wzajemnie od siebie zależne mogą wystąpić ograniczenia w dostępności
#09 Systemy o złożonej strukturze system składa się z wielu elementów, obiekty (podsystemy) wchodzące w skład systemu są ze sobą połączone i wzajemnie od siebie zależne mogą wystąpić ograniczenia w dostępności
INSTRUKCJA DO ĆWICZENIA NR 7
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
6. Zagadnienie parkowania ciężarówki.
 6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
Jakobiany. Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Projektowanie układów regulacji w dziedzinie częstotliwości. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Z poprzedniego wykładu:
 Z poprzedniego wykładu: Człon: Ciało stałe posiadające możliwość poruszania się względem innych członów Para kinematyczna: klasy I, II, III, IV i V (względem liczby stopni swobody) Niższe i wyższe pary
Z poprzedniego wykładu: Człon: Ciało stałe posiadające możliwość poruszania się względem innych członów Para kinematyczna: klasy I, II, III, IV i V (względem liczby stopni swobody) Niższe i wyższe pary
7. Zagadnienie parkowania ciężarówki.
 7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 7 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
KARTA OPISU MODUŁU KSZTAŁCENIA
 Nazwa modułu: Kierunek studiów KARTA OPISU MODUŁU KSZTAŁCENIA Sterowanie robotów mobilnych Profil kształcenia (ogólnoakademicki, praktyczny) Kod Rok / Semestr Automatyka i Robotyka ogólnoakademicki 1 /
Nazwa modułu: Kierunek studiów KARTA OPISU MODUŁU KSZTAŁCENIA Sterowanie robotów mobilnych Profil kształcenia (ogólnoakademicki, praktyczny) Kod Rok / Semestr Automatyka i Robotyka ogólnoakademicki 1 /
Obiekt. Obiekt sterowania obiekt, który realizuje proces (zaplanowany).
 SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Sekantooptyki owali i ich własności
 Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI. Robot do pokrycia powierzchni terenu
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI Robot do pokrycia powierzchni terenu Zadania robota Zadanie całkowitego pokrycia powierzchni na podstawie danych sensorycznych Zadanie unikania przeszkód
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI Robot do pokrycia powierzchni terenu Zadania robota Zadanie całkowitego pokrycia powierzchni na podstawie danych sensorycznych Zadanie unikania przeszkód
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji.
 I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
Inżynieria Systemów Dynamicznych (4)
 Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
D l. D p. Rodzaje baz jezdnych robotów mobilnych
 ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
Modelowanie i Wizualizowanie 3W grafiki. Łańcuchy kinematyczne
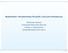 Modelowanie i Wizualizowanie 3W grafiki. Łańcuchy kinematyczne Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 31 Łańcuchy kinematyczne Najnowsza
Modelowanie i Wizualizowanie 3W grafiki. Łańcuchy kinematyczne Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 31 Łańcuchy kinematyczne Najnowsza
Sterowanie w programie ADAMS regulator PID. Przemysław Sperzyński
 Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Podstawowe pojęcia wytrzymałości materiałów. Statyczna próba rozciągania metali. Warunek nośności i użytkowania. Założenia
 Wytrzymałość materiałów dział mechaniki obejmujący badania teoretyczne i doświadczalne procesów odkształceń i niszczenia ciał pod wpływem różnego rodzaju oddziaływań (obciążeń) Podstawowe pojęcia wytrzymałości
Wytrzymałość materiałów dział mechaniki obejmujący badania teoretyczne i doświadczalne procesów odkształceń i niszczenia ciał pod wpływem różnego rodzaju oddziaływań (obciążeń) Podstawowe pojęcia wytrzymałości
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Modele DSGE. Jerzy Mycielski. Maj Jerzy Mycielski () Modele DSGE Maj / 11
 Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Właściwości dynamiczne kolektora słonecznego a efektywność instalacji grzewczej
 Właściwości dynamiczne kolektora słonecznego a efektywność instalacji grzewczej mgr inż. Joanna Aleksiejuk 2016-09-19 Problemy gospodarki energią i środowiskiem w rolnictwie, leśnictwie i przemyśle spożywczym
Właściwości dynamiczne kolektora słonecznego a efektywność instalacji grzewczej mgr inż. Joanna Aleksiejuk 2016-09-19 Problemy gospodarki energią i środowiskiem w rolnictwie, leśnictwie i przemyśle spożywczym
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Podstawy Automatyki. Wykład 2 - modelowanie matematyczne układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
ROZWIĄZANIE PROBLEMU NIELINIOWEGO
 Budownictwo, studia I stopnia, semestr VII przedmiot fakultatywny rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Jerzy Pamin Tematyka zajęć 1 Dyskretyzacja
Budownictwo, studia I stopnia, semestr VII przedmiot fakultatywny rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Jerzy Pamin Tematyka zajęć 1 Dyskretyzacja
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wprowadzenie do technik regulacji automatycznej. prof nzw. dr hab. inż. Krzysztof Patan
 Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter)
 Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter) 1. WSTĘP W wielu złożonych układach mechanicznych elementy występują połączenia elastyczne (długi
Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter) 1. WSTĘP W wielu złożonych układach mechanicznych elementy występują połączenia elastyczne (długi
Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
I. DYNAMIKA PUNKTU MATERIALNEGO
 I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
Laboratorium Podstaw Robotyki ĆWICZENIE 3
 Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 3 Kinematyka i lokalizacja dwukołowego robota mobilnego Celem ćwiczenia jest wyprowadzenie modelu
Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 3 Kinematyka i lokalizacja dwukołowego robota mobilnego Celem ćwiczenia jest wyprowadzenie modelu
Plan wykładu. Własności statyczne i dynamiczne elementów automatyki:
 Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Janusz Adamowski METODY OBLICZENIOWE FIZYKI Kwantowa wariacyjna metoda Monte Carlo. Problem własny dla stanu podstawowego układu N cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 9 AiR III
 1 Na podstawie materiałów autorstwa dra inż. Marka Wnuka. Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania
1 Na podstawie materiałów autorstwa dra inż. Marka Wnuka. Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania
WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ DYNAMICZNĄ
 ĆWICZENIE 12 WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ DYNAMICZNĄ Cel ćwiczenia: Wyznaczanie modułu sztywności drutu metodą sprężystych drgań obrotowych. Zagadnienia: sprężystość, naprężenie ścinające, prawo
ĆWICZENIE 12 WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ DYNAMICZNĄ Cel ćwiczenia: Wyznaczanie modułu sztywności drutu metodą sprężystych drgań obrotowych. Zagadnienia: sprężystość, naprężenie ścinające, prawo
Wprowadzenie do WK1 Stan naprężenia
 Wytrzymałość materiałów i konstrukcji 1 Wykład 1 Wprowadzenie do WK1 Stan naprężenia Płaski stan naprężenia Dr inż. Piotr Marek Wytrzymałość Konstrukcji (Wytrzymałość materiałów, Mechanika konstrukcji)
Wytrzymałość materiałów i konstrukcji 1 Wykład 1 Wprowadzenie do WK1 Stan naprężenia Płaski stan naprężenia Dr inż. Piotr Marek Wytrzymałość Konstrukcji (Wytrzymałość materiałów, Mechanika konstrukcji)
Wykład 5. Zagadnienia omawiane na wykładzie w dniu r
 Wykład 5. Zagadnienia omawiane na wykładzie w dniu 14.11.2018r Definicja (iloraz różnicowy) Niech x 0 R oraz niech funkcja f będzie określona przynajmnniej na otoczeniu O(x 0 ). Ilorazem różnicowym funkcji
Wykład 5. Zagadnienia omawiane na wykładzie w dniu 14.11.2018r Definicja (iloraz różnicowy) Niech x 0 R oraz niech funkcja f będzie określona przynajmnniej na otoczeniu O(x 0 ). Ilorazem różnicowym funkcji
II. Równania autonomiczne. 1. Podstawowe pojęcia.
 II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
MECHANIKA 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Prowadzący: dr Krzysztof Polko PLAN WYKŁADÓW 1. Podstawy kinematyki 2. Ruch postępowy i obrotowy bryły 3. Ruch płaski bryły 4. Ruch złożony i ruch względny 5. Ruch kulisty i ruch ogólny bryły
MECHANIKA 2 Prowadzący: dr Krzysztof Polko PLAN WYKŁADÓW 1. Podstawy kinematyki 2. Ruch postępowy i obrotowy bryły 3. Ruch płaski bryły 4. Ruch złożony i ruch względny 5. Ruch kulisty i ruch ogólny bryły
R o z d z i a ł 2 KINEMATYKA PUNKTU MATERIALNEGO
 R o z d z i a ł KINEMATYKA PUNKTU MATERIALNEGO Kinematyka zajmuje się opisem ruchu ciał bez uwzględniania ich masy i bez rozpatrywania przyczyn, które ten ruch spowodowały. Przez punkt materialny rozumiemy
R o z d z i a ł KINEMATYKA PUNKTU MATERIALNEGO Kinematyka zajmuje się opisem ruchu ciał bez uwzględniania ich masy i bez rozpatrywania przyczyn, które ten ruch spowodowały. Przez punkt materialny rozumiemy
Modelowanie wybranych. urządzeń mechatronicznych
 Modelowanie wybranych elementów torów pomiarowych urządzeń mechatronicznych Pomiary - element sterowania napędem mechatronicznym Układ napędowy - Zintegrowane czujniki Zewnetrzne sygnały sterujące Sprzężenia
Modelowanie wybranych elementów torów pomiarowych urządzeń mechatronicznych Pomiary - element sterowania napędem mechatronicznym Układ napędowy - Zintegrowane czujniki Zewnetrzne sygnały sterujące Sprzężenia
Regulator liniowo kwadratowy na przykładzie wahadła odwróconego
 Regulator liniowo kwadratowy na przykładzie wahadła odwróconego kwiecień 2012 Sterowanie Teoria Przykład wahadła na wózku Dany jest system dynamiczny postaci: ẋ = f (x, u) (1) y = h(x) (2) Naszym zadaniem
Regulator liniowo kwadratowy na przykładzie wahadła odwróconego kwiecień 2012 Sterowanie Teoria Przykład wahadła na wózku Dany jest system dynamiczny postaci: ẋ = f (x, u) (1) y = h(x) (2) Naszym zadaniem
Dynamika manipulatora. Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska. Podstawy robotyki wykład VI
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
Rys 1 Schemat modelu masa- sprężyna- tłumik
 Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
FUNKCJE ZESPOLONE Lista zadań 2005/2006
 FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Podstawy Automatyki. Wykład 2 - modelowanie matematyczne układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
WYKŁAD 2 KINEMATYKA PŁYNÓW CZĘŚĆ 1 1/14
 WYKŁAD 2 KINEMATYKA PŁYNÓW CZĘŚĆ 1 1/14 OPISY LAGRANGE A I EULERA. PRĘDKOŚĆ I PRZYSPIESZENIE PŁYNU. Elementem płynu nazywamy indywidualną i x 3, nieskończenie małą porcę płynu. Każdy element płynu ma przypisane
WYKŁAD 2 KINEMATYKA PŁYNÓW CZĘŚĆ 1 1/14 OPISY LAGRANGE A I EULERA. PRĘDKOŚĆ I PRZYSPIESZENIE PŁYNU. Elementem płynu nazywamy indywidualną i x 3, nieskończenie małą porcę płynu. Każdy element płynu ma przypisane
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Analityczna postać równowagi Nasha w postaci sprzężenia zwrotnego w modelu Lanchestera
 Analityczna postać równowagi Nasha w postaci sprzężenia zwrotnego w modelu Lanchestera Dominika Machowska dominika.machowska@uni.lodz.pl Katedra Ekonometrii, Wydział Ekonomiczno-Socjologiczny, Uniwersytet
Analityczna postać równowagi Nasha w postaci sprzężenia zwrotnego w modelu Lanchestera Dominika Machowska dominika.machowska@uni.lodz.pl Katedra Ekonometrii, Wydział Ekonomiczno-Socjologiczny, Uniwersytet
