KONCEPCJA SYSTEMU DO WSPOMAGANIA DECYZJI ZARZĄDZANIA ŁAŃCUCHEM DOSTAW
|
|
|
- Aneta Skiba
- 6 lat temu
- Przeglądów:
Transkrypt
1 SITEK Paweł Optymalzacja dyskretna, modelowane, wspomagane decyzj, łańcuch dostaw KONCEPCJA SYSTEMU DO WSPOMAGANIA DECYZJI ZARZĄDZANIA ŁAŃCUCHEM DOSTAW Skuteczne efektywne zarządzane łańcuchem dostaw w dobe globalzacj, szybko zmenających sę potrzeb rynkowych oraz rozproszonych zasobów jest kluczowym problemem do rozwązana dla kaŝdego przedsęborstwa. Jest to koneczne aby utrzymać konkurencyjność przy realzacj zleceń klentów. Ze względu na lczbę złoŝoność problemów decyzyjnych występujących podczas realzacj zleceń klentów nezbędne jest dostarczene efektywnych rozwązań nformatycznych do wspomagana decyzj. W artykule przedstawono koncepcje systemu wspomagana decyzj zarządzana łańcuchem dostaw w postac dodatkowych warstw nformacyjno-decyzyjnych dla zntegrowanego systemu zarządzana przedsęborstwem. MoŜlwośc zaproponowanej koncepcj systemu przedstawono na przykładze modelu kosztowego zarządzana dwupozomowym łańcuchem dostaw (two-ter Supply Chan []). THE CONCEPT OF DECISION SUPPORT SYSTEM FOR SUPPLY CHAIN MANAGEMENT Effectve and effcent supply chan management n the era of globalzaton, rapdly changng market needs and dstrbuted resources s a key problem to be solved for each company. Due to the number and complexty of decson problems that occur when executng clent orders, t s necessary to provde effectve solutons for decson support. The paper presents the concept of decson support system for supply chan management n the form of addtonal nformaton and decson-makng layers for the ERP (Enterprse Resource Plannng). The concept has been shown for two-ter supply chan management as an example.. WPROWADZENIE Obecne przedsęborstwa zmuszone są do dzałana w szybko zmenającym sę otoczenu w ramach globalnej konkurencj. Dlatego muszą posadać zdolnośc narzędza do zarządzana przedsęborstwem na neprzewdywalnych rynkach, przy posadanu rozproszonych zasobów jednocześne mnmalzując koszty czas realzacj zamóweń klentów. Poltechnka Śwętokrzyska, Wydzał Elektrochnk Automatyk Informatyk; Kelce, Al. 000 PP 7. tel: Fax: , e-mal: stek@tu.kelce.pl
2 2672 Paweł SITEK W ostatnch latach wele frm o zasęgu globalnym jak równeŝ małych średnch przedsęborstw (MŚP), zdaje sobe sprawę, Ŝe skuteczność ch dzałań jest w duŝym stopnu zaleŝna od odpowednej współpracy koordynacj z ch dostawcam, jak równeŝ z odborcam czy bezpośredno klentam końcowym [2]. Ten rodzaj wzajemnych zaleŝnośc uwarunkowań jest znany w lteraturze jako koncepcja zarządzana łańcuchem dostaw (Supply Chan Management (SCM)). Wprowadzene SCM umoŝlwa synchronzację przepływu nformacj materałów pomędzy poszczególnym kooperantam, co wyraźne ułatwa frme dostosowane sę do określonego popytu rynkowego. Wewnętrzne SCM obejmuje zagadnena zwązane z zaopatrzenem, produkcją dystrybucją. Zewnętrzne SCM ntegruje przedsęborstwo z jego dostawcam klentam. Dzsaj ryzyko zarządzana łańcuchem jest neporównane wększe nŝ klka/klkanaśce lat temu. Główna przyczyna takego stanu rzeczy to postępująca globalzacja powodująca rozcągnęce skomplkowane łańcucha dostaw cągłe podnoszene efektywnośc frm. Dzęk globalzacj, produkt dowolnej frmy moŝe dotrzeć na kaŝdy rynek na śwece. Lczba problemów decyzyjnych w SCM jest bardzo duŝa dotyczy zarówno realzacj wewnętrznego łańcucha dostaw w przedsęborstwe jak zewnętrznego, gdze dane przedsęborstwo jest tylko jednym z ognw. W artykule przedstawono koncepcję oraz moŝlwośc zastosowana systemu wspomagana decyzj dla jednego z problemów ogólnych występujących w SCM ( dwuwarstwowy model kosztowy zarządzana łańcuchem dostaw). NaleŜy podkreślć, Ŝe załoŝena systemu wspomagana decyzj umoŝlwają jego zastosowana dla welu problemów decyzyjnych zarówno w obszarze produkcj, dystrybucj, magazynowana, transportu td. 2. PODSTAWOWE ZAŁOśENIA SYSTEMU WSPOMAGANIA DECYZJI Informatyczne systemy zarządzana (ISZ) klasy ERP (Enterprse Resource Plannng), DRP (Dstrbuton Resource Plannng), MRP II (Manufacturng Resource Plannng) oparte są najczęścej na zntegrowanej baze danych. Zwykle jest to baza danych wykorzystująca model relacyjny [3]. Jest to najbardzej rozpowszechnony model organzacj danych bazujący na matematycznej teor mnogośc, w szczególnośc na pojęcu relacj. W najprostszym ujęcu w modelu relacyjnym dane grupowane są w relacje, które reprezentowane są przez tabele. Relacje są pewnym zborem rekordów o dentycznej strukturze wewnętrzne powązanych za pomocą zwązków zachodzących pomędzy danym. Model relacyjny moŝna traktować równeŝ jako modelu logk perwszego rzędu. Językem zwązanym z tym modelem jest SQL (Structured Query Language)-strukturalny język zapytań uŝywany do tworzena, modyfkowana baz danych oraz do umeszczana poberana danych z baz danych. Język SQL jest językem deklaratywnym. Dlatego przy opracowanu koncepcj systemu wspomagana decyzj wykorzystano relacyjny model danych, gdze zapsano nformacje o modelach decyzyjnych (zarówno danych jak ch strukturze). System wspomagana decyzj został zaproponowany w postac dodatkowych warstw nformacyjnych ISZ (Rys.). Warstwy te są wzajemne zntegrowane umoŝlwają automatyczną generację model decyzyjnych na podstawe odpowednch danych w tabelach bazy danych systemu
3 KONCEPCJA SYSTEMU DO WSPOMAGANIA DECYZJI wspomagana decyzj oraz ch rozwązane za pomocą narzędz CLP (Constrant Logc Programmng) oraz MIP (Mxed Integer Programmng). Rys. Schemat koncepcj systemu wspomagana decyzj dla SCM
4 2674 Paweł SITEK Sposób dzałana Systemu Wspomagana Decyzj (SWD) przedstawono na rys. (cyfram oznaczono w kolejnośc wykonywana - poszczególne procesy):. Mapowane-uzupełnane danych model decyzyjnych (TM) na podstawe bazy danych nformatycznego systemu zarządzana np. klasy ERP/MRP II (BD). 2. Pobrane nformacj - o strukturze model decyzyjnych z tabel systemowych (TS) SWD. 3. Pobrane danych - dla model decyzyjnych z tabel z danym model (TM). 4. Generacja model decyzyjnych - w postac plków tekstowych (T) w odpowednm formace (metajęzyku programu optymalzacyjnego). 5. Przesłane - plków z modelam do programu/paketu optymalzacyjnego, uruchomene optymalzacj. (S) 6. Zaps -uzyskanych wynków (decyzj ) do bazy danych (TM) SWD. 7. Transfer danych z bazy danych (TM) SWD do bazy danych systemu ERP/MRP II (BD). Najcekawszym rozwązanem proponowanym w całej koncepcj jest mechanzm automatycznej generacj model decyzyjnych (4). Jego nnowacyjność polega na automatyzacj samego procesu tzn. modele są generowane na podstawe odpowednch wpsów w dwóch zborach tabel (TM) (TS) bazy danych SWD. Dodatkowo zmana parametrów model jest jedyne zmaną danych w tabelach (TM), bez konecznośc zman struktur model. Jeśl nawet koneczna jest zmaną struktur model ch parametrów to wystarczą odpowedne wpsy w tabelach (TM) (TS) bez pracochłonnego skomplkowanego procesu budowy kompletnych model. Modele są generowane w postac plków tekstowych (T). Następne są przesyłane do oprogramowana optymalzacyjnego (S) po rozwązanu uzyskwane są odpowedno decyzję optymalne bądź dopuszczalne, które zapsywane są w baze danych SWD. W prezentowanej wersj SWD zastosowano dwa środowska optymalzacyjne. Jedno klasyczne oparte na optymalzacj całkowtolczbowej (MIP-Mxed Integer Programmng) [4]. Druge to środowsko oparte na paradygmace programowana w logce z ogranczenam (CLP-Constrant Logc Programmng) [5]. Szczegóły mplementacyjne SWD oraz podstawowe struktury danych przedstawono w [6]. 3. MODEL MATEMATYCZNY ŁAŃCUCHA DOSTAW Jako przykład zastosowana SWD przedstawono model kosztowy zarządzana łańcuchem dostaw. W lteraturze jest on przedstawany jako ogólny dwuwarstwowy lub dwupozomowy (two-ter Supply Chan) model łańcucha dostaw []. Znany z lteratury model został rozbudowany o funkcjonalność, umoŝlwającą szczegółowe określene, które z produktów mogą być dostarczane przez wybrane punkty dystrybucyjne (centra dystrybucj/magazyny). W modelu [] wszystke punkty dystrybucyjne są unwersalne mogą uczestnczyć w dostawach wszystkch produktów do wszystkch klentów. W rzeczywstych warunkach ze względu na gabaryty, parametry przechowywana, typy produktów oraz np. posadane odpowednej floty transportowej td. ne wszystke punkty dystrybucyjne są w stane zapewnać dostawę wszystkch produktów do wszystkch klentów. Model metamatematyczny został sformułowany w postac zadana programowana lnowego całkowtolczbowego [3][4]. Jako funkcje celu przyjęto koszty realzacj
5 KONCEPCJA SYSTEMU DO WSPOMAGANIA DECYZJI dostaw. Zmennym decyzyjnym modelu są (X jk ) określająca udzał (procentowy) dostaw produktu j (j=..n) realzowany dla klenta k (k=..q) przez punkt (=..M) oraz (Z ) wskazująca czy dany punkt berze udzał w dostawach czy ne (zmenna bnarna). Funkcja celu posada dwe składowe. Perwsza określa koszt punktów dystrybucyjnych (magazynów, centrów dystrybucyjnych). Druga określa koszty dostarczana produktów przez poszczególne punkty dystrybucyjne do klentów. Ogranczena modelu matematycznego ().. (6) moŝna nterpretować następująco. Ogranczene () zapewna, Ŝe dostawa wszystkch zamówonych produktów, dla wszystkch klentów będze zrealzowana w pełn przez punkty dystrybucyjne. Ogranczene to zostało zmodyfkowane w tak sposób (przy pomocy parametru R j ) aby uwzględnć specyfkę poszczególnych punktów dystrybucyjnych. W praktyce bowem ne kaŝdy magazyn czy centrum dystrybucyjne, moŝe dokonywać dostawy danego produktu. Ogranczene (2) zapewna realzowalność dostaw ze względu na pojemność danego punktu dystrybucyjnego. Kolejne ogranczene (3) zapewna ne przekraczane dopuszczalnej lczby punktów dystrybucyjnych zaangaŝowanych w dostawy. Ogranczena (4),(5),(6) określają charakter zmennych decyzyjnych jak równeŝ ch wzajemną zaleŝność. W tabel przedstawono wszystke dane modelu optymalzacyjnego oraz zmenne decyzyjne. Tab.. Parametry oraz zmenne decyzyjne modelu matematycznego Symbol Ops Indeksy uŝywane w modelu j ndeks produktu ndeks punktu dystrybucyjnego (centrum dystrybucyjnego/magazynu) k ndeks odborcy/klenta N lczba produktów M lczba punktów dystrybucyjnych Q lczba odborców klentów Parametry modelu F koszt centrum dystrybucyjnego (=..M). S j przestrzeń/objętość zajmowana przez produkt j (j=..n) maksymalna lczba punktów dystrybucyjnych borących udzał w P dostawach. W maksymalna pojemność punktu dystrybucyjnego (l=..o). D jk zapotrzebowane odborcy k na produkt j w danym okrese czasu (k=..q) (j=..n) R j Wartość bnarna jest -jeśl dany punkt dystrybucyjny moŝe dystrybuować produkt j lub jest 0 w przecwnym przypadku. C jk koszt dostawy produktu j (j =.. N) dla klenta k (k=..q) przez punkt dystrybucyjny (=..M). Zmenne decyzyjne X jk udzał rynku (procent) dostaw produktu j (j=..n) realzowana dla klenta k (k=..q) przez punkt (=..M). Z bnarna zmenna decyzyjna przyjmuje wartość - jeśl dany punkt berze udzał w dostawach 0- w przecwnym przypadku.
6 2676 Paweł SITEK Funkcja celu mnmalzacja kosztów punktów dystrybucyjnych dostaw Ogranczena M M = F * Z + M N Q = j= k= X, j, k * C, j, k X * R = dla k =..Q, j..n (), j, k, j = = N Q, j, k j, k = j= k= X * D * S W dla..m (2) M = Z P Z + 0dla =..N j =..M k..q (4) X, j, k = (3) Z { 0,}dla =..N (5) 0, j, k = 4. PRZYKŁADY LICZBOWE X dla =..N j =..M k..q (6) Po dokonanu mplementacj podstawowych struktur funkcj SWD [6] zgodne z załoŝenam z rozdz. 2 sprawdzono moŝlwośc systemu w praktyce. Zgodne z załoŝenam SWD moŝe wsperać wele decyzj z róŝnych obszarów szeroko rozumanego zarządzana łańcuchem dostaw. System moŝe wykorzystywać wele róŝnych co do zakresu jak charakteru model decyzyjnych. Jednym z perwszych był przedstawony w rozdz. 4 dwuwarstwowy model kosztowy łańcucha dostaw sformułowany w postac zadana programowana lnowego całkowtolczbowego (MIP). Pommo tego, ze model ten posada stosunkowo prostą funkcję celu, to odpowada na następujące pytana: Jak jest mnmalny koszt realzacj dostaw poprzez seć punktów dystrybucyjnych? Które punkty dystrybucyjne borą udzał w realzacj dostaw? Jake jest wykorzystane poszczególnych punktów dystrybucyjnych? Jak jest szczegółowy rozdzał dostarczanych produktów dla poszczególnych klentów kto pośrednczy? Oprócz jednoznacznych odpowedz na te nne pytana tego typu, SWD moŝna wykorzystać do zadawana nnego typu pytań (zwązanych z symulacją podejmowana decyzj przy zmenających sę parametrach np. pojemnośc magazynów, unwersalnośc td.): Jak wpływ na koszt dostaw będze mała zmana pojemnośc poszczególnych punktów? Czy lepej dąŝyć do unwersalnośc czy specjalzacj punktów?
7 KONCEPCJA SYSTEMU DO WSPOMAGANIA DECYZJI Eksperymenty oblczenowe oparto na danych zapsanych w tabelach (TM) SWD, których wartośc lczbowe w notacj z rozdz.4 są wdoczne w Tab. 2. Wartość parametru C jk (koszt dostaw produktu j dla klenta k przez punkt ) wynos 2 dla =,3,4 j=..0, k=..8 oraz 3 dla =2 j=..0, k=..8. Tab. 2. Fragmenty tabel z danym lczbowym do eksperymentów oblczenowych D jk - zapotrzebowane klenta k na produkt j, R j -czy dany punkt moŝe dystrybuować produkt j j k D jk j k D jk j k D jk j k D jk j k D jk j R j j R j j R j j 9 0 R j S j -pojemność, którą zajmuje produkt j, W -pojemność punktu, F -koszt punktu j S j F W Przy wykorzystanu SWD dla danych z Tab. 2. uzyskano następujące odpowedz. Po perwsze optymalny-mnmalny koszt dostaw wynos f c =200 62, wszystke punkty dystrybucyjne brały udzał w dostawach. Punkty o ndeksach =,3,4 były w pełn wykorzystane, natomast punkt o ndekse =2 w 3%. Odpowedn udzał w dostawach
8 2678 Paweł SITEK produktów dla klentów przez odpowedne punkty dystrybucyjne (wartośc zmennych X jk ) przedstawono w Tab. 3. Tab.III Wynk-udzał w dostawach poszczególnych punktów dystrybucyjnych. j k X jk 0, j k X jk 0,05 0, j k X jk 0, j k X jk W drugm etape eksperymentów postanowono zadać pytana zwązane z symulacją decyzj przy zmenających sę parametrach. Zapytano jake będze wykorzystane punktów dystrybucyjnych oraz koszt realzacj dostaw jeśl zmen sę pojemność punktu dystrybucyjnego (W ) o ndekse = dokładne o 3% (czyl o zakres realzowanych dostaw przez punkt o ndekse =2). Okazało sę, Ŝe dalej w dostawach borą udzał wszystke punkty dystrybucyjne. Pojemnośc punktów dystrybucyjnych o ndeksach =3,4 są w pełn wykorzystane. Pojemność punktu o ndekse =2 w 2% natomast punkt o zwększonej pojemnośc (=) w 9%. Uzyskano wartość funkcj celu fc=200 6, czyl praktyczne dentyczną jak dla eksperymentu perwszego. W kolejnym etape zmenono pojemność punktu dystrybucyjnego o ndekse =3 równeŝ o 3% przy pozostawenu standardowej pojemnośc pozostałych punktów (Tab. 2.). Trzec eksperyment pokazał, Ŝe w dostawach ne berze udzału punkt dystrybucyjny o ndekse =2. Pozostałe są w pełn wykorzystane. Dodatkowo wartość funkcj celu znaczne sę obnŝyła wynosła fc= Jak wdać tylko na podstawe zaprezentowanego w rozdz.4 modelu, który został zamplementowany w SWD [6] moŝna dokonać, jeszcze welu symulacj decyzj np. przy zmane parametrów F, C jk oraz wzajemnych ch kombnacj. 5. WNIOSKI Zaproponowana koncepcja systemu wspomagana decyzj zarządzana łańcuchem dostaw poprzez perwsze eksperymenty lczbowe oraz mplementację [6] pokazuje duŝą elastyczność praktyczne neogranczone moŝlwośc. Zaproponowane rozwązana umoŝlwają wykorzystane welu model decyzyjnych dotyczących całego łańcucha dostaw jak równeŝ bardzej szczegółowych model zwązanych z produkcją, dystrybucją, transportem td. W obecnej wersj zaproponowano modele rozwązywane
9 KONCEPCJA SYSTEMU DO WSPOMAGANIA DECYZJI w dwóch środowskach. Perwsze to standardowe środowsko MIP druge to CLP. W obu moŝna wypracowywać rozwązana (decyzje) optymalne dopuszczalne zaleŝne od potrzeb złoŝonośc problemów decyzyjnych. Prezentowana koncepcja opera sę na powszechnym modelu relacyjnym bazy danych. To w baze danych zapsane są nformacje o strukturach model decyzyjnych jak ch parametrach. To właśne na podstawe odpowednch wpsów w baze danych moŝna automatyczne generować pełne modele decyzyjne przesyłać do środowsk gdze są rozwązywane - czyl uzyskwane optymalne bądź dopuszczalne decyzje. Jednocześne oparce sę na relacyjnej baze danych daje praktyczne neogranczone moŝlwośc mplementacj model decyzyjnych. MoŜna bowem za pomocą odpowednch wpsów do tabel systemowych (TS) SWD wpsywać struktury model ogólnych szczegółowych dla produkcj, dystrybucj, transportu, całego łańcucha dostaw td. Z drugej strony raz wpsane struktury model mogą być podstawą do wygenerowana neskończene welu przypadków juŝ konkretnych decyzj w zaleŝnośc od wartośc parametrów, które mogą sę zmenać, aktualzować na podstawe bazy danych ISZ a są poberane z tabel (TM) SWD. Dalsze prace zwązane będą z mplementacją w ramach struktur SWD zarówno autorskch jak znanych z lteratury model decyzyjnych z zakresu sterowana zarządza produkcją, logstyk, dystrybucj, planowana harmonogramowana, zarządzana projektowego td. 6. BIBLIOGRAFIA [] Huang Xao-yuan, Lu Zhen. Applcaton of two-stages by supply chan model n server and dstrbuton system. Systems engneerng-theory methodology applcatons, 2(3), p , [2] Terz S., Cavaler S.: Smulaton n the Supply Chan, Context: A Survery, Computers n Industry, vol. 53, no., pp. 3 6, [3] Date C. J., An Introducton to Database System, vol. II, Adson-Wesley Pub. Comp., równeŝ WNT W-wa, (sera: Klasyka Informatyk), [4] Sysło M.M., Deo M., Kowalk J.S.: Algorytmy optymalzacj dyskretnej z programam w języku PASCAL, PWN, 993. [5] K. Apt, Prncples of constrant programmng, Cambrdge Unversty, [6] Wkarek J., Aspekty mplementacyjne systemu wspomagana decyzj zarządzana łańcuchem dostaw, Transcomp 20, LOGISTYKA (w druku).
Rozwiązywanie zadań optymalizacji w środowisku programu MATLAB
 Rozwązywane zadań optymalzacj w środowsku programu MATLAB Zagadnene optymalzacj polega na znajdowanu najlepszego, względem ustalonego kryterum, rozwązana należącego do zboru rozwązań dopuszczalnych. Standardowe
Rozwązywane zadań optymalzacj w środowsku programu MATLAB Zagadnene optymalzacj polega na znajdowanu najlepszego, względem ustalonego kryterum, rozwązana należącego do zboru rozwązań dopuszczalnych. Standardowe
Zapis informacji, systemy pozycyjne 1. Literatura Jerzy Grębosz, Symfonia C++ standard. Harvey M. Deitl, Paul J. Deitl, Arkana C++. Programowanie.
 Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 15. ALGORYTMY GENETYCZNE Częstochowa 014 Dr hab. nż. Grzegorz Dudek Wydzał Elektryczny Poltechnka Częstochowska TERMINOLOGIA allele wartośc, waranty genów, chromosom - (naczej
SZTUCZNA INTELIGENCJA WYKŁAD 15. ALGORYTMY GENETYCZNE Częstochowa 014 Dr hab. nż. Grzegorz Dudek Wydzał Elektryczny Poltechnka Częstochowska TERMINOLOGIA allele wartośc, waranty genów, chromosom - (naczej
WikiWS For Business Sharks
 WkWS For Busness Sharks Ops zadana konkursowego Zadane Opracowane algorytmu automatyczne przetwarzającego zdjęce odręczne narysowanego dagramu na tablcy lub kartce do postac wektorowej zapsanej w formace
WkWS For Busness Sharks Ops zadana konkursowego Zadane Opracowane algorytmu automatyczne przetwarzającego zdjęce odręczne narysowanego dagramu na tablcy lub kartce do postac wektorowej zapsanej w formace
SZACOWANIE NIEPEWNOŚCI POMIARU METODĄ PROPAGACJI ROZKŁADÓW
 SZACOWANIE NIEPEWNOŚCI POMIARU METODĄ PROPAGACJI ROZKŁADÓW Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskego 8, 04-703 Warszawa tel.
SZACOWANIE NIEPEWNOŚCI POMIARU METODĄ PROPAGACJI ROZKŁADÓW Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskego 8, 04-703 Warszawa tel.
Prawdziwa ortofotomapa
 Prawdzwa ortofotomapa klasyczna a prawdzwa ortofotomapa mnmalzacja przesunęć obektów wystających martwych pól na klasycznej ortofotomape wpływ rodzaju modelu na wynk ortorektyfkacj budynków stratege opracowana
Prawdzwa ortofotomapa klasyczna a prawdzwa ortofotomapa mnmalzacja przesunęć obektów wystających martwych pól na klasycznej ortofotomape wpływ rodzaju modelu na wynk ortorektyfkacj budynków stratege opracowana
Kształtowanie się firm informatycznych jako nowych elementów struktury przestrzennej przemysłu
 PRACE KOMISJI GEOGRAFII PRZEMY SŁU Nr 7 WARSZAWA KRAKÓW 2004 Akadema Pedagogczna, Kraków Kształtowane sę frm nformatycznych jako nowych elementów struktury przestrzennej przemysłu Postępujący proces rozwoju
PRACE KOMISJI GEOGRAFII PRZEMY SŁU Nr 7 WARSZAWA KRAKÓW 2004 Akadema Pedagogczna, Kraków Kształtowane sę frm nformatycznych jako nowych elementów struktury przestrzennej przemysłu Postępujący proces rozwoju
Zaawansowane metody numeryczne
 Wykład 9. jej modyfkacje. Oznaczena Będzemy rozpatrywać zagadnene rozwązana następującego układu n równań lnowych z n newadomym x 1... x n : a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x
Wykład 9. jej modyfkacje. Oznaczena Będzemy rozpatrywać zagadnene rozwązana następującego układu n równań lnowych z n newadomym x 1... x n : a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x
Oligopol dynamiczny. Rozpatrzmy model sekwencyjnej konkurencji ilościowej jako gra jednokrotna z pełną i doskonalej informacją
 Olgopol dynamczny Rozpatrzmy model sekwencyjnej konkurencj loścowej jako gra jednokrotna z pełną doskonalej nformacją (1934) Dwa okresy: t=0, 1 tzn. frma 2 podejmując decyzję zna decyzję frmy 1 Q=q 1 +q
Olgopol dynamczny Rozpatrzmy model sekwencyjnej konkurencj loścowej jako gra jednokrotna z pełną doskonalej nformacją (1934) Dwa okresy: t=0, 1 tzn. frma 2 podejmując decyzję zna decyzję frmy 1 Q=q 1 +q
Minimalizacja globalna, algorytmy genetyczne i zastosowanie w geotechnice
 Mnmalzacja globalna, algorytmy genetyczne zastosowane w geotechnce Metoda sejsmczna Metoda geoelektryczna Podstawowy podzał ZAGADNIENIE PROSTE (ang. forward problem) model + parametry modelu dane (ośrodek,
Mnmalzacja globalna, algorytmy genetyczne zastosowane w geotechnce Metoda sejsmczna Metoda geoelektryczna Podstawowy podzał ZAGADNIENIE PROSTE (ang. forward problem) model + parametry modelu dane (ośrodek,
Minimalizacja globalna. Algorytmy genetyczne i ewolucyjne.
 Mnmalzacja globalna Algorytmy genetyczne ewolucyjne. Lnearyzacja nelnowego operatora g prowadz do przyblżonych metod rozwązywana zagadnena odwrotnego. Wynk takej nwersj jest slne uzależnony od wyboru modelu
Mnmalzacja globalna Algorytmy genetyczne ewolucyjne. Lnearyzacja nelnowego operatora g prowadz do przyblżonych metod rozwązywana zagadnena odwrotnego. Wynk takej nwersj jest slne uzależnony od wyboru modelu
BADANIA OPERACYJNE. Podejmowanie decyzji w warunkach niepewności. dr Adam Sojda
 BADANIA OPERACYJNE Podejmowane decyzj w warunkach nepewnośc dr Adam Sojda Teora podejmowana decyzj gry z naturą Wynk dzałana zależy ne tylko od tego, jaką podejmujemy decyzję, ale równeż od tego, jak wystąp
BADANIA OPERACYJNE Podejmowane decyzj w warunkach nepewnośc dr Adam Sojda Teora podejmowana decyzj gry z naturą Wynk dzałana zależy ne tylko od tego, jaką podejmujemy decyzję, ale równeż od tego, jak wystąp
8. Optymalizacja decyzji inwestycyjnych
 dr nż. Zbgnew Tarapata: Optymalzacja decyzj nwestycyjnych, cz.ii 8. Optymalzacja decyzj nwestycyjnych W rozdzale 8, część I przedstawono elementarne nformacje dotyczące metod oceny decyzj nwestycyjnych.
dr nż. Zbgnew Tarapata: Optymalzacja decyzj nwestycyjnych, cz.ii 8. Optymalzacja decyzj nwestycyjnych W rozdzale 8, część I przedstawono elementarne nformacje dotyczące metod oceny decyzj nwestycyjnych.
Regulamin promocji 14 wiosna
 promocja_14_wosna strona 1/5 Regulamn promocj 14 wosna 1. Organzatorem promocj 14 wosna, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa od 01 lutego 2014 do 30
promocja_14_wosna strona 1/5 Regulamn promocj 14 wosna 1. Organzatorem promocj 14 wosna, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa od 01 lutego 2014 do 30
Optymalizacja belki wspornikowej
 Leszek MIKULSKI Katedra Podstaw Mechank Ośrodków Cągłych, Instytut Mechank Budowl, Poltechnka Krakowska e mal: ps@pk.edu.pl Optymalzacja belk wspornkowej 1. Wprowadzene RozwaŜamy zadane optymalnego kształtowana
Leszek MIKULSKI Katedra Podstaw Mechank Ośrodków Cągłych, Instytut Mechank Budowl, Poltechnka Krakowska e mal: ps@pk.edu.pl Optymalzacja belk wspornkowej 1. Wprowadzene RozwaŜamy zadane optymalnego kształtowana
Usługi KPMG oferowane polskim przedsiębiorcom
 Usług KPMG oferowane polskm przedsęborcom Czyl jak w czym pomagamy polskm frmom kpmg.pl 1 Usług KPMG oferowane polskm przedsęborcom 2013 Usług KPMG oferowane polskm przedsęborcom Doradztwo fnansowe ksęgowe
Usług KPMG oferowane polskm przedsęborcom Czyl jak w czym pomagamy polskm frmom kpmg.pl 1 Usług KPMG oferowane polskm przedsęborcom 2013 Usług KPMG oferowane polskm przedsęborcom Doradztwo fnansowe ksęgowe
KRZYWA BÉZIERA TWORZENIE I WIZUALIZACJA KRZYWYCH PARAMETRYCZNYCH NA PRZYKŁADZIE KRZYWEJ BÉZIERA
 KRZYWA BÉZIERA TWORZENIE I WIZUALIZACJA KRZYWYCH PARAMETRYCZNYCH NA PRZYKŁADZIE KRZYWEJ BÉZIERA Krzysztof Serżęga Wyższa Szkoła Informatyk Zarządzana w Rzeszowe Streszczene Artykuł porusza temat zwązany
KRZYWA BÉZIERA TWORZENIE I WIZUALIZACJA KRZYWYCH PARAMETRYCZNYCH NA PRZYKŁADZIE KRZYWEJ BÉZIERA Krzysztof Serżęga Wyższa Szkoła Informatyk Zarządzana w Rzeszowe Streszczene Artykuł porusza temat zwązany
Analiza danych OGÓLNY SCHEMAT. http://zajecia.jakubw.pl/ Dane treningowe (znana decyzja) Klasyfikator. Dane testowe (znana decyzja)
 Analza danych Dane trenngowe testowe. Algorytm k najblższych sąsadów. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ OGÓLNY SCHEMAT Mamy dany zbór danych podzelony na klasy decyzyjne, oraz
Analza danych Dane trenngowe testowe. Algorytm k najblższych sąsadów. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ OGÓLNY SCHEMAT Mamy dany zbór danych podzelony na klasy decyzyjne, oraz
2012-10-11. Definicje ogólne
 0-0- Defncje ogólne Logstyka nauka o przepływe surowców produktów gotowych rodowód wojskowy Utrzyywane zapasów koszty zwązane.n. z zarożene kaptału Brak w dostawach koszty zwązane.n. z przestoje w produkcj
0-0- Defncje ogólne Logstyka nauka o przepływe surowców produktów gotowych rodowód wojskowy Utrzyywane zapasów koszty zwązane.n. z zarożene kaptału Brak w dostawach koszty zwązane.n. z przestoje w produkcj
Zadanie na wykonanie Projektu Zespołowego
 Zadane na wykonane Projektu Zespołowego Celem projektu jest uzyskane następującego szeregu umejętnośc praktycznych: umejętnośc opracowana równoległych wersj algorytmów (na przykładze algorytmów algebry
Zadane na wykonane Projektu Zespołowego Celem projektu jest uzyskane następującego szeregu umejętnośc praktycznych: umejętnośc opracowana równoległych wersj algorytmów (na przykładze algorytmów algebry
OPTYMALIZACJA PROCESU PRZESIEWANIA W PRZESIEWACZACH WIELOPOKŁADOWYCH
 Prace Naukowe Instytutu Górnctwa Nr 136 Poltechnk Wrocławskej Nr 136 Studa Materały Nr 43 2013 Jerzy MALEWSKI* Marta BASZCZYŃSKA** przesewane, jakość produktów, optymalzacja OPTYMALIZACJA PROCESU PRZESIEWANIA
Prace Naukowe Instytutu Górnctwa Nr 136 Poltechnk Wrocławskej Nr 136 Studa Materały Nr 43 2013 Jerzy MALEWSKI* Marta BASZCZYŃSKA** przesewane, jakość produktów, optymalzacja OPTYMALIZACJA PROCESU PRZESIEWANIA
KURS STATYSTYKA. Lekcja 6 Regresja i linie regresji ZADANIE DOMOWE. www.etrapez.pl Strona 1
 KURS STATYSTYKA Lekcja 6 Regresja lne regresj ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 Funkcja regresj I rodzaju cechy Y zależnej
KURS STATYSTYKA Lekcja 6 Regresja lne regresj ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 Funkcja regresj I rodzaju cechy Y zależnej
A O n RZECZPOSPOLITA POLSKA. Gospodarki Narodowej. Warszawa, dnia2/stycznia 2014
 Warszawa, dna2/styczna 2014 r, RZECZPOSPOLITA POLSKA MINISTERSTWO ADMINISTRACJI I CYFRYZACJI PODSEKRETARZ STANU Małgorzata Olsze wska BM-WP 005.6. 20 14 Pan Marek Zółkowsk Przewodnczący Komsj Gospodark
Warszawa, dna2/styczna 2014 r, RZECZPOSPOLITA POLSKA MINISTERSTWO ADMINISTRACJI I CYFRYZACJI PODSEKRETARZ STANU Małgorzata Olsze wska BM-WP 005.6. 20 14 Pan Marek Zółkowsk Przewodnczący Komsj Gospodark
Wprowadzenie do Sieci Neuronowych Sieci rekurencyjne
 Wprowadzene do Sec Neuronowych Sec rekurencyjne M. Czoków, J. Persa 2010-12-07 1 Powtórzene Konstrukcja autoasocjatora Hopfelda 1.1 Konstrukcja Danych jest m obrazów wzorcowych ξ 1..ξ m, gdze każdy pojedynczy
Wprowadzene do Sec Neuronowych Sec rekurencyjne M. Czoków, J. Persa 2010-12-07 1 Powtórzene Konstrukcja autoasocjatora Hopfelda 1.1 Konstrukcja Danych jest m obrazów wzorcowych ξ 1..ξ m, gdze każdy pojedynczy
Laboratorium ochrony danych
 Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
D Archiwum Prac Dyplomowych - Instrukcja dla studentów
 Kraków 01.10.2015 D Archwum Prac Dyplomowych - Instrukcja dla studentów Procedura Archwzacj Prac Dyplomowych jest realzowana zgodne z zarządzenem nr 71/2015 Rektora Unwersytetu Rolnczego m. H. Kołłątaja
Kraków 01.10.2015 D Archwum Prac Dyplomowych - Instrukcja dla studentów Procedura Archwzacj Prac Dyplomowych jest realzowana zgodne z zarządzenem nr 71/2015 Rektora Unwersytetu Rolnczego m. H. Kołłątaja
MATEMATYKA POZIOM ROZSZERZONY Kryteria oceniania odpowiedzi. Arkusz A II. Strona 1 z 5
 MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
D Archiwum Prac Dyplomowych - Instrukcja dla opiekunów/promotorów/recenzentów
 D Archwum Prac Dyplomowych - Instrukcja dla opekunów/promotorów/recenzentów Kraków 13.01.2016 r. Procedura Archwzacj Prac Dyplomowych jest realzowana zgodne z zarządzenem nr 71/2015 Rektora Unwersytetu
D Archwum Prac Dyplomowych - Instrukcja dla opekunów/promotorów/recenzentów Kraków 13.01.2016 r. Procedura Archwzacj Prac Dyplomowych jest realzowana zgodne z zarządzenem nr 71/2015 Rektora Unwersytetu
Weryfikacja hipotez dla wielu populacji
 Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
TRANSCOMP INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT
 TRANSCOP INTERNATIONAL CONFERENCE COPUTER SYSTES AIDED SCIENCE, INDUSTRY AND TRANSPORT Paweł SITEK Jarosław WIKAREK Optymalizacja dyskretna, modelowanie, wspomaganie decyzji, centra dystrybucyjne, łańcuch
TRANSCOP INTERNATIONAL CONFERENCE COPUTER SYSTES AIDED SCIENCE, INDUSTRY AND TRANSPORT Paweł SITEK Jarosław WIKAREK Optymalizacja dyskretna, modelowanie, wspomaganie decyzji, centra dystrybucyjne, łańcuch
TRANSCOMP INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT
 TRANSCOMP INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT Paweł SITEK 1 Jarosław WIKAREK 1 Bazy danych, modelowanie, wspomaganie decyzji, centra dystrybucyjne, łańcuch dostaw
TRANSCOMP INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT Paweł SITEK 1 Jarosław WIKAREK 1 Bazy danych, modelowanie, wspomaganie decyzji, centra dystrybucyjne, łańcuch dostaw
5. OPTYMALIZACJA GRAFOWO-SIECIOWA
 . OPTYMALIZACJA GRAFOWO-SIECIOWA Defncja grafu Pod pojęcem grafu G rozumemy następującą dwójkę uporządkowaną (defncja grafu Berge a): (.) G W,U gdze: W zbór werzchołków grafu, U zbór łuków grafu, U W W,
. OPTYMALIZACJA GRAFOWO-SIECIOWA Defncja grafu Pod pojęcem grafu G rozumemy następującą dwójkę uporządkowaną (defncja grafu Berge a): (.) G W,U gdze: W zbór werzchołków grafu, U zbór łuków grafu, U W W,
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 1. Układy równań liniowych
 Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
KURS STATYSTYKA. Lekcja 1 Statystyka opisowa ZADANIE DOMOWE. www.etrapez.pl Strona 1
 KURS STATYSTYKA Lekcja 1 Statystyka opsowa ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 W statystyce opsowej mamy pełne nformacje
KURS STATYSTYKA Lekcja 1 Statystyka opsowa ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 W statystyce opsowej mamy pełne nformacje
-ignorowanie zmiennej wartości pieniądza w czasie, -niemoŝność porównywania projektów o róŝnych klasach ryzyka.
 Podstawy oceny ekonomcznej przedsęwzęć termo-modernzacyjnych modernzacyjnych -Proste (statyczne)-spb (prosty czas zwrotu nakładów nwestycyjnych) -ZłoŜone (dynamczne)-dpb, NPV, IRR,PI Cechy metod statycznych:
Podstawy oceny ekonomcznej przedsęwzęć termo-modernzacyjnych modernzacyjnych -Proste (statyczne)-spb (prosty czas zwrotu nakładów nwestycyjnych) -ZłoŜone (dynamczne)-dpb, NPV, IRR,PI Cechy metod statycznych:
Stanisław Cichocki. Natalia Nehrebecka. Wykład 6
 Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Interpretacja parametrów przy zmennych objaśnających cągłych Semelastyczność 2. Zastosowane modelu potęgowego Model potęgowy 3. Zmenne cągłe za zmenne dyskretne
Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Interpretacja parametrów przy zmennych objaśnających cągłych Semelastyczność 2. Zastosowane modelu potęgowego Model potęgowy 3. Zmenne cągłe za zmenne dyskretne
Stanisław Cichocki. Natalia Nehrebecka. Wykład 6
 Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Model potęgowy Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych
Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Model potęgowy Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych
Regulamin promocji upalne lato 2014 2.0
 upalne lato 2014 2.0 strona 1/5 Regulamn promocj upalne lato 2014 2.0 1. Organzatorem promocj upalne lato 2014 2.0, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa
upalne lato 2014 2.0 strona 1/5 Regulamn promocj upalne lato 2014 2.0 1. Organzatorem promocj upalne lato 2014 2.0, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa
Systemy Just-in-time. Sterowanie produkcją
 Systemy Just-n-tme Sterowane proukcją MRP MRP II Just n tme OPT 1 Sterowane proukcją MRP MRP II Just n tme OPT Koszty opóźneń Kary umowne Utrata zamówena Utrata klenta Utrata t reputacj 2 Problemy z zapasam
Systemy Just-n-tme Sterowane proukcją MRP MRP II Just n tme OPT 1 Sterowane proukcją MRP MRP II Just n tme OPT Koszty opóźneń Kary umowne Utrata zamówena Utrata klenta Utrata t reputacj 2 Problemy z zapasam
Wykład IX Optymalizacja i minimalizacja funkcji
 Wykład IX Optymalzacja mnmalzacja funkcj Postawene zadana podstawowe dee jego rozwązana Proste metody mnmalzacj Metody teracj z wykorzystanem perwszej pochodnej Metody teracj z wykorzystanem drugej pochodnej
Wykład IX Optymalzacja mnmalzacja funkcj Postawene zadana podstawowe dee jego rozwązana Proste metody mnmalzacj Metody teracj z wykorzystanem perwszej pochodnej Metody teracj z wykorzystanem drugej pochodnej
Analiza ryzyka jako instrument zarządzania środowiskiem
 WARSZTATY 2003 z cyklu Zagrożena naturalne w górnctwe Mat. Symp. str. 461 466 Elżbeta PILECKA, Małgorzata SZCZEPAŃSKA Instytut Gospodark Surowcam Mneralnym Energą PAN, Kraków Analza ryzyka jako nstrument
WARSZTATY 2003 z cyklu Zagrożena naturalne w górnctwe Mat. Symp. str. 461 466 Elżbeta PILECKA, Małgorzata SZCZEPAŃSKA Instytut Gospodark Surowcam Mneralnym Energą PAN, Kraków Analza ryzyka jako nstrument
Natalia Nehrebecka. Zajęcia 3
 St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 3 1. Dobroć dopasowana równana regresj. Współczynnk determnacj R Dk Dekompozycja warancj zmennej zależnej ż Współczynnk determnacj R. Zmenne cągłe a
St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 3 1. Dobroć dopasowana równana regresj. Współczynnk determnacj R Dk Dekompozycja warancj zmennej zależnej ż Współczynnk determnacj R. Zmenne cągłe a
ZASTOSOWANIE MODELU MOTAD DO TWORZENIA PORTFELA AKCJI KLASYFIKACJA WARUNKÓW PODEJMOWANIA DECYZJI
 Krzysztof Wsńsk Katedra Statystyk Matematycznej, AR w Szczecne e-mal: kwsnsk@e-ar.pl ZASTOSOWANIE MODELU MOTAD DO TWORZENIA PORTFELA AKCJI Streszczene: W artykule omówono metodologę modelu MOTAD pod kątem
Krzysztof Wsńsk Katedra Statystyk Matematycznej, AR w Szczecne e-mal: kwsnsk@e-ar.pl ZASTOSOWANIE MODELU MOTAD DO TWORZENIA PORTFELA AKCJI Streszczene: W artykule omówono metodologę modelu MOTAD pod kątem
EKONOMETRIA I Spotkanie 1, dn. 05.10.2010
 EKONOMETRIA I Spotkane, dn. 5..2 Dr Katarzyna Beń Program ramowy: http://www.sgh.waw.pl/nstytuty/e/oferta_dydaktyczna/ekonometra_stacjonarne_nest acjonarne/ Zadana, dane do zadań, ważne nformacje: http://www.e-sgh.pl/ben/ekonometra
EKONOMETRIA I Spotkane, dn. 5..2 Dr Katarzyna Beń Program ramowy: http://www.sgh.waw.pl/nstytuty/e/oferta_dydaktyczna/ekonometra_stacjonarne_nest acjonarne/ Zadana, dane do zadań, ważne nformacje: http://www.e-sgh.pl/ben/ekonometra
ASPEKTY IMPLEMENTACYJNE SYSTEMU DO WSPOMAGANIA DECYZJI
 WIKAREK Jarosław 1 Bazy danych, systemy wspomagania decyzji, łańcuch dostaw ASPEKTY IMPLEMENTACYJNE SYSTEMU DO WSPOMAGANIA DECYZJI W artykule przedstawiono załoŝenia i podstawowe struktury systemu wspomagania
WIKAREK Jarosław 1 Bazy danych, systemy wspomagania decyzji, łańcuch dostaw ASPEKTY IMPLEMENTACYJNE SYSTEMU DO WSPOMAGANIA DECYZJI W artykule przedstawiono załoŝenia i podstawowe struktury systemu wspomagania
Stanisław Cichocki. Natalia Nehrebecka. Wykład 7
 Stansław Cchock Natala Nehrebecka Wykład 7 1 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy zmennych dyskretnych 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy
Stansław Cchock Natala Nehrebecka Wykład 7 1 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy zmennych dyskretnych 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy
liniowym w przeciwnym przypadku mówimy o programowaniu nieliniowym.
 =DGDQLHSROHJDMFHQDSRV]XNLZDQLXPDNV\PDOQHMOXEPLQLPDOQHMZDUWRFLIXQNFMLZLHOX ]PLHQQ\FKSU]\MHGQRF]HVQ\PVSHáQLHQLXSHZQHMLORFLQDáR*RQ\FKZDUXQNyZ UyZQDOXE QLHUyZQRFLQRVLQD]Z]DGDQLDRSW\PDOL]DF\MQHJROXE]DGDQLDSURJUDPRZDQLD
=DGDQLHSROHJDMFHQDSRV]XNLZDQLXPDNV\PDOQHMOXEPLQLPDOQHMZDUWRFLIXQNFMLZLHOX ]PLHQQ\FKSU]\MHGQRF]HVQ\PVSHáQLHQLXSHZQHMLORFLQDáR*RQ\FKZDUXQNyZ UyZQDOXE QLHUyZQRFLQRVLQD]Z]DGDQLDRSW\PDOL]DF\MQHJROXE]DGDQLDSURJUDPRZDQLD
Stanisław Cichocki. Natalia Nehrebecka. Wykład 6
 Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych 1. Zastosowane
Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych 1. Zastosowane
Wielokryterialny Trójwymiarowy Problem Pakowania
 Łukasz Kacprzak, Jarosław Rudy, Domnk Żelazny Instytut Informatyk, Automatyk Robotyk, Poltechnka Wrocławska Welokryteralny Trójwymarowy Problem Pakowana 1. Wstęp Problemy pakowana należą do klasy NP-trudnych
Łukasz Kacprzak, Jarosław Rudy, Domnk Żelazny Instytut Informatyk, Automatyk Robotyk, Poltechnka Wrocławska Welokryteralny Trójwymarowy Problem Pakowana 1. Wstęp Problemy pakowana należą do klasy NP-trudnych
Regulamin promocji zimowa piętnastka
 zmowa pętnastka strona 1/5 Regulamn promocj zmowa pętnastka 1. Organzatorem promocj zmowa pętnastka, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa od 01 grudna
zmowa pętnastka strona 1/5 Regulamn promocj zmowa pętnastka 1. Organzatorem promocj zmowa pętnastka, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa od 01 grudna
Modele wieloczynnikowe. Modele wieloczynnikowe. Modele wieloczynnikowe ogólne. α β β β ε. Analiza i Zarządzanie Portfelem cz. 4.
 Modele weloczynnkowe Analza Zarządzane Portfelem cz. 4 Ogólne model weloczynnkowy można zapsać jako: (,...,,..., ) P f F F F = n Dr Katarzyna Kuzak lub (,...,,..., ) f F F F = n Modele weloczynnkowe Można
Modele weloczynnkowe Analza Zarządzane Portfelem cz. 4 Ogólne model weloczynnkowy można zapsać jako: (,...,,..., ) P f F F F = n Dr Katarzyna Kuzak lub (,...,,..., ) f F F F = n Modele weloczynnkowe Można
STATECZNOŚĆ SKARP. α - kąt nachylenia skarpy [ o ], φ - kąt tarcia wewnętrznego gruntu [ o ],
![STATECZNOŚĆ SKARP. α - kąt nachylenia skarpy [ o ], φ - kąt tarcia wewnętrznego gruntu [ o ], STATECZNOŚĆ SKARP. α - kąt nachylenia skarpy [ o ], φ - kąt tarcia wewnętrznego gruntu [ o ],](/thumbs/27/11347185.jpg) STATECZNOŚĆ SKARP W przypadku obektu wykonanego z gruntów nespostych zaprojektowane bezpecznego nachylena skarp sprowadza sę do przekształcena wzoru na współczynnk statecznośc do postac: tgφ tgα = n gdze:
STATECZNOŚĆ SKARP W przypadku obektu wykonanego z gruntów nespostych zaprojektowane bezpecznego nachylena skarp sprowadza sę do przekształcena wzoru na współczynnk statecznośc do postac: tgφ tgα = n gdze:
Typy systemów informacyjnych
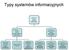 Typy systemów informacyjnych Information Systems Systemy Informacyjne Operations Support Systems Systemy Wsparcia Operacyjnego Management Support Systems Systemy Wspomagania Zarzadzania Transaction Processing
Typy systemów informacyjnych Information Systems Systemy Informacyjne Operations Support Systems Systemy Wsparcia Operacyjnego Management Support Systems Systemy Wspomagania Zarzadzania Transaction Processing
ZASTOSOWANIE PROGRAMOWANIA DYNAMICZNEGO DO OPRACOWANIA STRATEGII REDUKCJI EMISJI GAZÓW
 ZASTOSOWANIE PROGRAOWANIA DYNAICZNEGO DO OPRACOWANIA STRATEGII REDUKCJI EISJI GAZÓW ANDRZEJ KAŁUSZKO Instytut Bada Systemowych Streszczene W pracy opsano zadane efektywnego przydzału ogranczonych rodków
ZASTOSOWANIE PROGRAOWANIA DYNAICZNEGO DO OPRACOWANIA STRATEGII REDUKCJI EISJI GAZÓW ANDRZEJ KAŁUSZKO Instytut Bada Systemowych Streszczene W pracy opsano zadane efektywnego przydzału ogranczonych rodków
RÓWNOLEGŁY ALGORYTM POPULACYJNY DLA PROBLEMU GNIAZDOWEGO Z RÓWNOLEGŁYMI MASZYNAMI
 RÓWNOLEGŁY ALGORYTM POPULACYJNY DLA PROBLEMU GNIAZDOWEGO Z RÓWNOLEGŁYMI MASZYNAMI Wojcech BOŻEJKO, Marusz UCHROŃSKI, Meczysław WODECKI Streszczene: W pracy rozpatrywany jest ogólny problem kolejnoścowy
RÓWNOLEGŁY ALGORYTM POPULACYJNY DLA PROBLEMU GNIAZDOWEGO Z RÓWNOLEGŁYMI MASZYNAMI Wojcech BOŻEJKO, Marusz UCHROŃSKI, Meczysław WODECKI Streszczene: W pracy rozpatrywany jest ogólny problem kolejnoścowy
METODY PLANOWANIA EKSPERYMENTÓW. dr hab. inż. Mariusz B. Bogacki
 Metody Planowana Eksperymentów Rozdzał 1. Strona 1 z 14 METODY PLANOWANIA EKSPERYMENTÓW dr hab. nż. Marusz B. Bogack Marusz.Bogack@put.poznan.pl www.fct.put.poznan.pl/cv23.htm Marusz B. Bogack 1 Metody
Metody Planowana Eksperymentów Rozdzał 1. Strona 1 z 14 METODY PLANOWANIA EKSPERYMENTÓW dr hab. nż. Marusz B. Bogack Marusz.Bogack@put.poznan.pl www.fct.put.poznan.pl/cv23.htm Marusz B. Bogack 1 Metody
Regulamin promocji fiber xmas 2015
 fber xmas 2015 strona 1/5 Regulamn promocj fber xmas 2015 1. Organzatorem promocj fber xmas 2015, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa od 01 grudna 2015
fber xmas 2015 strona 1/5 Regulamn promocj fber xmas 2015 1. Organzatorem promocj fber xmas 2015, zwanej dalej promocją, jest JPK Jarosław Paweł Krzymn, zwany dalej JPK. 2. Promocja trwa od 01 grudna 2015
Sieci Neuronowe 1 Michał Bereta
 Wprowadzene Zagadnena Sztucznej Intelgencj laboratorum Sec Neuronowe 1 Mchał Bereta Sztuczne sec neuronowe można postrzegać jako modele matematyczne, które swoje wzorce wywodzą z bolog obserwacj ludzkch
Wprowadzene Zagadnena Sztucznej Intelgencj laboratorum Sec Neuronowe 1 Mchał Bereta Sztuczne sec neuronowe można postrzegać jako modele matematyczne, które swoje wzorce wywodzą z bolog obserwacj ludzkch
BADANIE DRGAŃ WŁASNYCH NAPĘDU ROBOTA KUCHENNEGO Z SILNIKIEM SRM
 Zeszyty Problemowe Maszyny Elektryczne Nr 88/2010 13 Potr Bogusz Marusz Korkosz Jan Prokop POLITECHNIKA RZESZOWSKA Wydzał Elektrotechnk Informatyk BADANIE DRGAŃ WŁASNYCH NAPĘDU ROBOTA KUCHENNEGO Z SILNIKIEM
Zeszyty Problemowe Maszyny Elektryczne Nr 88/2010 13 Potr Bogusz Marusz Korkosz Jan Prokop POLITECHNIKA RZESZOWSKA Wydzał Elektrotechnk Informatyk BADANIE DRGAŃ WŁASNYCH NAPĘDU ROBOTA KUCHENNEGO Z SILNIKIEM
MINISTER EDUKACJI NARODOWEJ
 4 MINISTER EDUKACJI NARODOWEJ DWST WPZN 423189/BSZI13 Warszawa, 2013 -Q-4 Pan Marek Mchalak Rzecznk Praw Dzecka Szanowny Pane, w odpowedz na Pana wystąpene z dna 28 czerwca 2013 r. (znak: ZEW/500127-1/2013/MP),
4 MINISTER EDUKACJI NARODOWEJ DWST WPZN 423189/BSZI13 Warszawa, 2013 -Q-4 Pan Marek Mchalak Rzecznk Praw Dzecka Szanowny Pane, w odpowedz na Pana wystąpene z dna 28 czerwca 2013 r. (znak: ZEW/500127-1/2013/MP),
Realizacja logiki szybkiego przeniesienia w prototypie prądowym układu FPGA Spartan II
 obert Berezowsk Natala Maslennkowa Wydzał Elektronk Poltechnka Koszalńska ul. Partyzantów 7, 75-4 Koszaln Mchał Bałko Przemysław Sołtan ealzacja logk szybkego przenesena w prototype prądowym układu PG
obert Berezowsk Natala Maslennkowa Wydzał Elektronk Poltechnka Koszalńska ul. Partyzantów 7, 75-4 Koszaln Mchał Bałko Przemysław Sołtan ealzacja logk szybkego przenesena w prototype prądowym układu PG
Proste modele ze złożonym zachowaniem czyli o chaosie
 Proste modele ze złożonym zachowanem czyl o chaose 29 kwetna 2014 Komputer jest narzędzem coraz częścej stosowanym przez naukowców do ukazywana skrzętne ukrywanych przez naturę tajemnc. Symulacja, obok
Proste modele ze złożonym zachowanem czyl o chaose 29 kwetna 2014 Komputer jest narzędzem coraz częścej stosowanym przez naukowców do ukazywana skrzętne ukrywanych przez naturę tajemnc. Symulacja, obok
APROKSYMACJA QUASIJEDNOSTAJNA
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 73 Electrcal Engneerng 213 Jan PURCZYŃSKI* APROKSYMACJA QUASIJEDNOSTAJNA W pracy wykorzystano metodę aproksymacj średnokwadratowej welomanowej, przy
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 73 Electrcal Engneerng 213 Jan PURCZYŃSKI* APROKSYMACJA QUASIJEDNOSTAJNA W pracy wykorzystano metodę aproksymacj średnokwadratowej welomanowej, przy
Pattern Classification
 attern Classfcaton All materals n these sldes were taken from attern Classfcaton nd ed by R. O. Duda,. E. Hart and D. G. Stork, John Wley & Sons, 000 wth the permsson of the authors and the publsher Chapter
attern Classfcaton All materals n these sldes were taken from attern Classfcaton nd ed by R. O. Duda,. E. Hart and D. G. Stork, John Wley & Sons, 000 wth the permsson of the authors and the publsher Chapter
Spis treści. Wstęp 11
 Spis treści Wstęp 11 Rozdział 1. Znaczenie i cele logistyki 15 1.1. Definicje i etapy rozwoju logistyki 16 1.2. Zarządzanie logistyczne 19 1.2.1. Zarządzanie przedsiębiorstwem 20 1.2.2. Czynniki stymulujące
Spis treści Wstęp 11 Rozdział 1. Znaczenie i cele logistyki 15 1.1. Definicje i etapy rozwoju logistyki 16 1.2. Zarządzanie logistyczne 19 1.2.1. Zarządzanie przedsiębiorstwem 20 1.2.2. Czynniki stymulujące
OPTYMALIZACJA WARTOŚCI POLA MAGNETYCZNEGO W POBLIŻU LINII NAPOWIETRZNEJ Z WYKORZYSTANIEM ALGORYTMU GENETYCZNEGO
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 81 Electrcal Engneerng 015 Mkołaj KSIĄŻKIEWICZ* OPTYMALIZACJA WARTOŚCI POLA MAGNETYCZNEGO W POLIŻU LINII NAPOWIETRZNEJ Z WYKORZYSTANIEM ALGORYTMU
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 81 Electrcal Engneerng 015 Mkołaj KSIĄŻKIEWICZ* OPTYMALIZACJA WARTOŚCI POLA MAGNETYCZNEGO W POLIŻU LINII NAPOWIETRZNEJ Z WYKORZYSTANIEM ALGORYTMU
3. ŁUK ELEKTRYCZNY PRĄDU STAŁEGO I PRZEMIENNEGO
 3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH
 Metrologa Wspomagana Komputerowo - Zegrze, 9-22 05.997 WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH dr nż. Jan Ryszard Jask, dr nż. Elgusz Pawłowsk POLITECHNIKA lubelska
Metrologa Wspomagana Komputerowo - Zegrze, 9-22 05.997 WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH dr nż. Jan Ryszard Jask, dr nż. Elgusz Pawłowsk POLITECHNIKA lubelska
Model IS-LM-BP. Model IS-LM-BP jest wersją modelu ISLM w gospodarce otwartej. Pokazuje on zatem jak
 Ćwczena z Makroekonom II Model IS-LM- Model IS-LM- jest wersją modelu ISLM w gospodarce otwartej. Pokazuje on zatem jak gospodarka taka zachowuje sę w krótkm okrese, w efekce dzałań podejmowanych w ramach
Ćwczena z Makroekonom II Model IS-LM- Model IS-LM- jest wersją modelu ISLM w gospodarce otwartej. Pokazuje on zatem jak gospodarka taka zachowuje sę w krótkm okrese, w efekce dzałań podejmowanych w ramach
MPEC wydaje warunki techniczne KONIEC
 1 2 3 1 2 2 1 3 MPEC wydaje warunk technczne 4 5 6 10 9 8 7 11 12 13 14 15 KONIEC 17 16 4 5 Chcesz wedzeć, czy masz możlwość przyłączena budynku Możlwośc dofnansowana wymany peców węglowych do sec mejskej?
1 2 3 1 2 2 1 3 MPEC wydaje warunk technczne 4 5 6 10 9 8 7 11 12 13 14 15 KONIEC 17 16 4 5 Chcesz wedzeć, czy masz możlwość przyłączena budynku Możlwośc dofnansowana wymany peców węglowych do sec mejskej?
Sztuczne sieci neuronowe. Krzysztof A. Cyran POLITECHNIKA ŚLĄSKA Instytut Informatyki, p. 311
 Sztuczne sec neuronowe Krzysztof A. Cyran POLITECHNIKA ŚLĄSKA Instytut Informatyk, p. 311 Wykład 6 PLAN: - Repetto (brevs) - Sec neuronowe z radalnym funkcjam bazowym Repetto W aspekce archtektury: zajmowalśmy
Sztuczne sec neuronowe Krzysztof A. Cyran POLITECHNIKA ŚLĄSKA Instytut Informatyk, p. 311 Wykład 6 PLAN: - Repetto (brevs) - Sec neuronowe z radalnym funkcjam bazowym Repetto W aspekce archtektury: zajmowalśmy
WIELOKRYTERIALNE WSPOMAGANIE DECYZJI W HARMONOGRAMOWANIU PROJEKTÓW 1
 DECYZJE nr 13 czerwec 2010 WIELOKRYTERIALNE WSPOMAGANIE DECYZJI W HARMONOGRAMOWANIU PROJEKTÓW 1 Tomasz Błaszczyk* Akadema Ekonomczna w Katowcach Macej Nowak** Akadema Ekonomczna w Katowcach Streszczene:
DECYZJE nr 13 czerwec 2010 WIELOKRYTERIALNE WSPOMAGANIE DECYZJI W HARMONOGRAMOWANIU PROJEKTÓW 1 Tomasz Błaszczyk* Akadema Ekonomczna w Katowcach Macej Nowak** Akadema Ekonomczna w Katowcach Streszczene:
XXX OLIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne
 XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
SYSTEMY UCZĄCE SIĘ WYKŁAD 7. KLASYFIKATORY BAYESA. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska.
 SYSTEMY UCZĄCE SIĘ WYKŁAD 7. KLASYFIKATORY BAYESA Częstochowa 4 Dr hab. nż. Grzegorz Dudek Wydzał Elektryczny Poltechnka Częstochowska TWIERDZENIE BAYESA Wedza pozyskwana przez metody probablstyczne ma
SYSTEMY UCZĄCE SIĘ WYKŁAD 7. KLASYFIKATORY BAYESA Częstochowa 4 Dr hab. nż. Grzegorz Dudek Wydzał Elektryczny Poltechnka Częstochowska TWIERDZENIE BAYESA Wedza pozyskwana przez metody probablstyczne ma
ZASTOSOWANIE ANALIZY HARMONICZNEJ DO OKREŚLENIA SIŁY I DŁUGOŚCI CYKLI GIEŁDOWYCH
 Grzegorz PRZEKOTA ZESZYTY NAUKOWE WYDZIAŁU NAUK EKONOMICZNYCH ZASTOSOWANIE ANALIZY HARMONICZNEJ DO OKREŚLENIA SIŁY I DŁUGOŚCI CYKLI GIEŁDOWYCH Zarys treśc: W pracy podjęto problem dentyfkacj cykl gełdowych.
Grzegorz PRZEKOTA ZESZYTY NAUKOWE WYDZIAŁU NAUK EKONOMICZNYCH ZASTOSOWANIE ANALIZY HARMONICZNEJ DO OKREŚLENIA SIŁY I DŁUGOŚCI CYKLI GIEŁDOWYCH Zarys treśc: W pracy podjęto problem dentyfkacj cykl gełdowych.
Model systemu informatycznego monitorowania jakości produktu poligraficznego na poziomie operacyjnym
 Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Informatyk ROZPRAWA DOKTORSKA Agneszka Olejnk-Krugły Model systemu nformatycznego montorowana jakośc produktu polgrafcznego na pozome operacyjnym
Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Informatyk ROZPRAWA DOKTORSKA Agneszka Olejnk-Krugły Model systemu nformatycznego montorowana jakośc produktu polgrafcznego na pozome operacyjnym
TRANZYSTOR BIPOLARNY CHARAKTERYSTYKI STATYCZNE
 POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
Komputerowe generatory liczb losowych
 . Perwszy generator Komputerowe generatory lczb losowych 2. Przykłady zastosowań 3. Jak generuje sę lczby losowe przy pomocy komputera. Perwszy generator lczb losowych L. H. C. Tppet - 927 Ksąż ążka -
. Perwszy generator Komputerowe generatory lczb losowych 2. Przykłady zastosowań 3. Jak generuje sę lczby losowe przy pomocy komputera. Perwszy generator lczb losowych L. H. C. Tppet - 927 Ksąż ążka -
Szkolimy z pasją. tel.(012)2623040; 0601457926; 0602581731 www.aiki-management.pl
 Szkolmy z pasją Warsztaty Samura Game Godność Przywództwo Integracja Komunkacja Budowane Zespołu Honor Samura Game www.samuragame.org jest unkalną rzucającą wyzwane symulacją z obszaru budowana zespołu
Szkolmy z pasją Warsztaty Samura Game Godność Przywództwo Integracja Komunkacja Budowane Zespołu Honor Samura Game www.samuragame.org jest unkalną rzucającą wyzwane symulacją z obszaru budowana zespołu
na zabezpieczeniu z połączeniu
 2011 Montorng Zabezpeczane obektów Jesteśmy zespołem fachowców, którzy dostarczają wysokej jakośc usług. Nasza dzałalnośćć koncentruje sę przede wszystkm na doskonałym zabezpeczenu państwa dóbr. Dostarczamy
2011 Montorng Zabezpeczane obektów Jesteśmy zespołem fachowców, którzy dostarczają wysokej jakośc usług. Nasza dzałalnośćć koncentruje sę przede wszystkm na doskonałym zabezpeczenu państwa dóbr. Dostarczamy
Zobacz jak sam możesz stworzyć skuteczny e-mailing krok po kroku
 Stwórz skuteczny e-malng krok po kroku Zobacz jak sam możesz stworzyć skuteczny e-malng krok po kroku JAK ZAROBIĆ NA E-MAIL MARKETINGU I WZMOCNIĆ RELACJE Z ODBIORCAMI? E-MAILING W BRANŻY EDUKACYJNEJ Branża
Stwórz skuteczny e-malng krok po kroku Zobacz jak sam możesz stworzyć skuteczny e-malng krok po kroku JAK ZAROBIĆ NA E-MAIL MARKETINGU I WZMOCNIĆ RELACJE Z ODBIORCAMI? E-MAILING W BRANŻY EDUKACYJNEJ Branża
35-105 Rzeszów, Tel +48 17 740 00 38 fax +48 17 740 00 18. www.bmm.com.pl
 2015,,Zdolność uczena sę szybcej od swojej konkurencj może być długotrwałą przewagą, BMM Sp. z o.o. 35-105 Rzeszów, jaką nad nm posadasz. Are de Gaus ul. Przemysłowa 4a Tel +48 17 740 00 38 fax +48 17
2015,,Zdolność uczena sę szybcej od swojej konkurencj może być długotrwałą przewagą, BMM Sp. z o.o. 35-105 Rzeszów, jaką nad nm posadasz. Are de Gaus ul. Przemysłowa 4a Tel +48 17 740 00 38 fax +48 17
Bonus! Odpowiedzi do zadań na FTP. Pewnie wkrocz w świat baz danych z programem Access 2010!
 Pewne wkrocz w śwat baz danych z programem Access 2010! Poznaj zasady rządzące systemam baz danych Naucz sę nstalować program Access korzystać z jego możlwośc Dowedz sę, jak defnować modyfkować strukturę
Pewne wkrocz w śwat baz danych z programem Access 2010! Poznaj zasady rządzące systemam baz danych Naucz sę nstalować program Access korzystać z jego możlwośc Dowedz sę, jak defnować modyfkować strukturę
Automatyzacja Procesów Biznesowych. Systemy Informacyjne Przedsiębiorstw
 Automatyzacja Procesów Biznesowych Systemy Informacyjne Przedsiębiorstw Rodzaje przedsiębiorstw Produkcyjne największe zapotrzebowanie na kapitał, największe ryzyko Handlowe kapitał obrotowy, średnie ryzyko
Automatyzacja Procesów Biznesowych Systemy Informacyjne Przedsiębiorstw Rodzaje przedsiębiorstw Produkcyjne największe zapotrzebowanie na kapitał, największe ryzyko Handlowe kapitał obrotowy, średnie ryzyko
Problem plecakowy (KNAPSACK PROBLEM).
 Problem plecakowy (KNAPSACK PROBLEM). Zagadnene optymalzac zwane problemem plecakowym swą nazwę wzęło z analog do sytuac praktyczne podobne do problemu pakowana plecaka. Chodz o to, by zapakować maksymalne
Problem plecakowy (KNAPSACK PROBLEM). Zagadnene optymalzac zwane problemem plecakowym swą nazwę wzęło z analog do sytuac praktyczne podobne do problemu pakowana plecaka. Chodz o to, by zapakować maksymalne
Zapytanie ofertowe nr 4/2016/Młodzi (dotyczy zamówienia na usługę ochrony)
 Fundacja na Rzecz Rozwoju Młodzeży Młodz Młodym ul. Katedralna 4 50-328 Wrocław tel. 882 021 007 mlodzmlodym@archdecezja.wroc.pl, www.sdm2016.wroclaw.pl Wrocław, 24 maja 2016 r. Zapytane ofertowe nr 4/2016/Młodz
Fundacja na Rzecz Rozwoju Młodzeży Młodz Młodym ul. Katedralna 4 50-328 Wrocław tel. 882 021 007 mlodzmlodym@archdecezja.wroc.pl, www.sdm2016.wroclaw.pl Wrocław, 24 maja 2016 r. Zapytane ofertowe nr 4/2016/Młodz
Podstawy teorii falek (Wavelets)
 Podstawy teor falek (Wavelets) Ψ(). Transformaca Haara (97).. Przykład pewne metody zapsu obrazu Transformaca Haara Przykład zapsu obrazu -D Podstawy matematyczne transformac Algorytmy rozkładana funkc
Podstawy teor falek (Wavelets) Ψ(). Transformaca Haara (97).. Przykład pewne metody zapsu obrazu Transformaca Haara Przykład zapsu obrazu -D Podstawy matematyczne transformac Algorytmy rozkładana funkc
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY. Zakład Budowy i Eksploatacji Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA
 PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy Eksploatacj Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwczena: PRAKTYCZNA REALIZACJA PRZEMIANY ADIABATYCZNEJ.
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy Eksploatacj Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwczena: PRAKTYCZNA REALIZACJA PRZEMIANY ADIABATYCZNEJ.
RODO final countdown - nowa jakość w ochronie danych osobowych
 RODO fnal countdown - nowa jakość w ochrone danych osobowych TEMAT WYSTĄPIENIA: Ocena wprowadzana obowązków RODO w JST PRELEGENT Arkadusz ŚPIEWAKOWSKI PRELEGENT VIOLETTA DĄBROWSKA członek SIODO WSPÓŁAUTOR
RODO fnal countdown - nowa jakość w ochrone danych osobowych TEMAT WYSTĄPIENIA: Ocena wprowadzana obowązków RODO w JST PRELEGENT Arkadusz ŚPIEWAKOWSKI PRELEGENT VIOLETTA DĄBROWSKA członek SIODO WSPÓŁAUTOR
 Klasyfkator lnowy Wstęp Klasyfkator lnowy jest najprostszym możlwym klasyfkatorem. Zakłada on lnową separację lnowy podzał dwóch klas mędzy sobą. Przedstawa to ponższy rysunek: 5 4 3 1 0-1 - -3-4 -5-5
Klasyfkator lnowy Wstęp Klasyfkator lnowy jest najprostszym możlwym klasyfkatorem. Zakłada on lnową separację lnowy podzał dwóch klas mędzy sobą. Przedstawa to ponższy rysunek: 5 4 3 1 0-1 - -3-4 -5-5
Modelowanie i obliczenia techniczne. Metody numeryczne w modelowaniu: Optymalizacja
 Modelowane oblczena technczne Metody numeryczne w modelowanu: Optymalzacja Zadane optymalzacj Optymalzacja to ulepszane lub poprawa jakośc danego rozwązana, projektu, opracowana. Celem optymalzacj jest
Modelowane oblczena technczne Metody numeryczne w modelowanu: Optymalzacja Zadane optymalzacj Optymalzacja to ulepszane lub poprawa jakośc danego rozwązana, projektu, opracowana. Celem optymalzacj jest
Model oceny ryzyka w działalności firmy logistycznej - uwagi metodyczne
 Magdalena OSIŃSKA Unwersytet Mkołaja Kopernka w Torunu Model oceny ryzyka w dzałalnośc frmy logstycznej - uwag metodyczne WSTĘP Logstyka w cągu ostatnch 2. lat stała sę bardzo rozbudowaną dzedzną dzałalnośc
Magdalena OSIŃSKA Unwersytet Mkołaja Kopernka w Torunu Model oceny ryzyka w dzałalnośc frmy logstycznej - uwag metodyczne WSTĘP Logstyka w cągu ostatnch 2. lat stała sę bardzo rozbudowaną dzedzną dzałalnośc
Ocena jakościowo-cenowych strategii konkurowania w polskim handlu produktami rolno-spożywczymi. dr Iwona Szczepaniak
 Ocena jakoścowo-cenowych strateg konkurowana w polskm handlu produktam rolno-spożywczym dr Iwona Szczepanak Ekonomczne, społeczne nstytucjonalne czynnk wzrostu w sektorze rolno-spożywczym w Europe Cechocnek,
Ocena jakoścowo-cenowych strateg konkurowana w polskm handlu produktam rolno-spożywczym dr Iwona Szczepanak Ekonomczne, społeczne nstytucjonalne czynnk wzrostu w sektorze rolno-spożywczym w Europe Cechocnek,
Diagnostyka układów kombinacyjnych
 Dagnostyka układów kombnacyjnych 1. Wprowadzene Dagnostyka obejmuje: stwerdzene stanu układu, systemu lub ogólne sec logcznej. Jest to tzw. kontrola stanu wykrywająca czy dzałane sec ne jest zakłócane
Dagnostyka układów kombnacyjnych 1. Wprowadzene Dagnostyka obejmuje: stwerdzene stanu układu, systemu lub ogólne sec logcznej. Jest to tzw. kontrola stanu wykrywająca czy dzałane sec ne jest zakłócane
Uchwała Senatu Uniwersytetu Kazimierza Wielkiego. Nr 110/2016/2017. z dnia 27 czerwca 2017 r.
 Uchwała Senatu Unwersytetu Kazmerza Welkego Nr 110/2016/2017 z dna 27 czerwca 2017 r. w sprawe określena zakładanych efektów kształcena dla kerunku studów nformacja naukowa bblotekoznawstwo studa perwszego
Uchwała Senatu Unwersytetu Kazmerza Welkego Nr 110/2016/2017 z dna 27 czerwca 2017 r. w sprawe określena zakładanych efektów kształcena dla kerunku studów nformacja naukowa bblotekoznawstwo studa perwszego
KONCEPCJA SYSTEMU WSPOMAGANIA DECYZJI LOGISTYCZNYCH
 STUDIA INFORMATICA 2011 Volume 32 Number 2B (97) Paweł SITK, Jarosław WIKARK Politechnika Świętokrzyska, Katedra Systemów Sterowania i Zarządzania KONCPCJA SYSTMU WSPOMAGANIA DCYZJI LOGISTYCZNYCH Streszczenie.
STUDIA INFORMATICA 2011 Volume 32 Number 2B (97) Paweł SITK, Jarosław WIKARK Politechnika Świętokrzyska, Katedra Systemów Sterowania i Zarządzania KONCPCJA SYSTMU WSPOMAGANIA DCYZJI LOGISTYCZNYCH Streszczenie.
Kierownik Katedry i Kliniki: prof. dr hab. Bernard Panaszek, prof. zw. UMW. Recenzja
 KATEDRA KLINIKA CHORÓB WEWNĘTRZNYCHYCH GERIATRII ALERGOLOGU Unwersytet Medyczny m. Pastów Śląskch we Wrocławu 50-367 Wrocław, ul. Cure-Skłodowskej 66 Tel. 71/7842521 Fax 71/7842529 E-mal: bernard.panaszek@umed.wroc.pl
KATEDRA KLINIKA CHORÓB WEWNĘTRZNYCHYCH GERIATRII ALERGOLOGU Unwersytet Medyczny m. Pastów Śląskch we Wrocławu 50-367 Wrocław, ul. Cure-Skłodowskej 66 Tel. 71/7842521 Fax 71/7842529 E-mal: bernard.panaszek@umed.wroc.pl
Modelowanie systemu zarządzania przepływem materiałów i oceny efektywności procesów. Redakcja naukowa Bogusław Śliwczyoski
 BOGUSŁAW ŚLIWCZYŃSKI (RED.) MODELOWANIE SYSTEMU ZARZĄDZANIA PRZEPŁYWEM MATERIAŁÓW I OCENY EFEKTYWNOŚCI PROCESÓW Modelowane systemu zarządzana przepływem materałów oceny efektywnośc procesów Redakcja naukowa
BOGUSŁAW ŚLIWCZYŃSKI (RED.) MODELOWANIE SYSTEMU ZARZĄDZANIA PRZEPŁYWEM MATERIAŁÓW I OCENY EFEKTYWNOŚCI PROCESÓW Modelowane systemu zarządzana przepływem materałów oceny efektywnośc procesów Redakcja naukowa
Komputerowe wspomaganie procesów decyzyjnych w sklepach wielkopowierzchniowych z wykorzystaniem optymalizacji wielokryterialnej i metod przybliżonych
 Instytut Badań Systemowych Polskej Akadem Nauk Janusz Mrofords Komputerowe wspomagane procesów decyzyjnych w sklepach welkopowerzchnowych z wykorzystanem optymalzacj welokryteralnej metod przyblżonych
Instytut Badań Systemowych Polskej Akadem Nauk Janusz Mrofords Komputerowe wspomagane procesów decyzyjnych w sklepach welkopowerzchnowych z wykorzystanem optymalzacj welokryteralnej metod przyblżonych
Badania operacyjne w logistyce i zarządzaniu produkcją
 Państwowa Wyższa Szkoła Zawodowa w Nowym Sączu Badana operacyne w logstyce zarządzanu produkcą cz. I Andrze Woźnak Nowy Sącz Komtet Redakcyny doc. dr Zdzsława Zacłona przewodncząca, prof. dr hab. nż. Jarosław
Państwowa Wyższa Szkoła Zawodowa w Nowym Sączu Badana operacyne w logstyce zarządzanu produkcą cz. I Andrze Woźnak Nowy Sącz Komtet Redakcyny doc. dr Zdzsława Zacłona przewodncząca, prof. dr hab. nż. Jarosław
