Elektrony i dziury.
|
|
|
- Maksymilian Pluta
- 7 lat temu
- Przeglądów:
Transkrypt
1 letrony i dziury. Jce.Szczyto@fuw.edu.pl Uniwersytet Wrszwsi 00
2 Podstwy modelu jednoeletronowego Twierdzenie Bloch ) ( ) ( ) ( 0 r r r V m p r u e r n ir n,, Jeśli potencjł jest periodyczny gdzie tzw. f. Bloch: ) ( ) ( R r V r V to rozwiązni równni Schrodinger Wetory sieci Brvis R r u r u n n,, mją postć: ) ( ) (,, r r n n ) ( ) ( ) ( ˆ, r e u i i r p ir n ), ( ), ( n n
3 Podstwy modelu jednoeletronowego Twierdzenie Bloch Przyłd: Ruch eletronu w potencjle periodycznym. ( r) u n, n, ( r) e ir n ( r) ( r), n,
4 Model pustej sieci Twierdzenie Bloch m m n ) ( ) ( ), ( 3 g l g hg i i g W pustej przestrzeni? Liczymy energię dl wetorów przesuniętych do pierwszej strefy Brillouine ' IstrefBrillouine ' ; ' ' ') ( : ' ') ( : ' ') ( : 0 m m m [hl]= 000, 00,00, 00, 00, wymir:
5 Podstwy modelu jednoeletronowego Twierdzenie Bloch ( n, ) ( n, ) Wrtości włsne energii są periodyczną funcją liczby wntowej. hg g l g3 Model prwie swobodnych eletronów dl fli płsiej w pustej przestrzeni energi od wetor flowego wyrż się wzorem: ( n, ) m g i ( ) i ( ) m
6 Podstwy modelu jednoeletronowego Twierdzenie Bloch ( n, ) ( n, ) Wrtości włsne energii są periodyczną funcją liczby wntowej. hg g l g3 Model prwie swobodnych eletronów dl fli płsiej w pustej przestrzeni energi od wetor flowego wyrż się wzorem: ( n, ) m g i ( ) i ( ) m
7 Podstwy modelu jednoeletronowego Twierdzenie Bloch ( n, ) ( n, ) Wrtości włsne energii są periodyczną funcją liczby wntowej. hg g l g3 Model prwie swobodnych eletronów dl fli płsiej w pustej przestrzeni energi od wetor flowego wyrż się wzorem: ( n, ) m g i ( ) i ( ) m Jest tzw. zreduown stref Brillouin. N grnicy strefy +/- /=p/ wrtości energii są zdegenerowne. W pustej przestrzeni?
8 Podstwy modelu jednoeletronowego Stref Brillouin ( n, ) ( n, ) Wrtości włsne energii są periodyczną funcją liczby wntowej. hg g l g3 Stref Brillouin w przestrzeni -wymirowej Stref Brillouin w przestrzeni -wymirowej, sieć uośnoątn. Stref Brillouin dl sieci ubicznej powierzchniowo centrownej (fcc). Ogrniczjące strefę ściny wdrtowe i sześcioątne pochodzą, odpowiednio, od puntów sieci odwrotnej typu (,0,0) i (,,).
9 Sieć prost 0,, ;,0, ; 3,,0; Pust sieć - fcc Sieć odwrotn do fcc to bcc N ćwiczenich rozwiązliśmy problem sieci odwrotnej do sieci fcc. Sieć odwrotn * 3 * * R,, ; R,, ; R,, ;
10 Pust sieć fcc. I stref Brillouine Sieć odwrotn do fcc to bcc Komór Vigner-Seitz
11 Pust sieć fcc. I stref Brillouine Sieć odwrotn do fcc to bcc Komór Vigner-Seitz R. Stępniewsi
12 Podstwy modelu jednoeletronowego Twierdzenie Bloch ), ( ), ( n n m n ), ( m ) ( ) ( x x Strutur psmow dl gzu eletronów swobodnych w sieci regulrnej prostej (stł sieci ), wierzchołi prbol mją wsźnii 3 g l g hg i i g [hl]= 000, 00,00, 00, 00, x
13 Model pustej sieci Twierdzenie Bloch m m n ) ( ) ( ), ( 3 g l g hg i i g Liczymy energię dl wetorów przesuniętych do pierwszej strefy Brillouine ' IstrefBrillouine ' ; '...,0,,0,0,, 0,0, ') ( : ' ') ( : 3 0 x m x m m 4 4 ') ( : x m x m 0,0,,0, 0,,0,0 ; 4
14 Model pustej sieci Twierdzenie Bloch m m n ) ( ) ( ), ( 3 g l g hg i i g Liczymy energię dl wetorów przesuniętych do pierwszej strefy Brillouine ' IstrefBrillouine ' ; ' [hl]= 000, 00,00, 00, 00, 00,00,00,00, 0,0,0,0,0,0,0,0 3 wymiry:...,0,,0,0,, 0,0, ') ( : ' ') ( : 3 0 x m x m m
15 Model pustej sieci Twierdzenie Bloch ( n, ) ( n, ) hg g l g3 ( n, ) m ( ) ( ) m g i i Strutur psmow dl gzu eletronów swobodnych w sieci regulrnej prostej (stł sieci ), wierzchołi prbol mją wsźnii [hl]= 000, 00,00, 00, 00, 00,00,00,00, x x x
16 Model pustej sieci Twierdzenie Bloch ( n, ) ( n, ) hg g l g3 ( n, ) m ( ) ( ) m g i i Strutur psmow dl gzu eletronów swobodnych w sieci regulrnej prostej (stł sieci ), wierzchołi prbol mją wsźnii [hl]= 000, 00,00, 00, 00, 00,00,00,00, 0,0,0,0,0,0,0,0 x W pustej przestrzeni? x x
17 R. Stępniewsi nergy Model pustej sieci Kierune [00] X Wve vector [00] X
18 R. Stępniewsi nergy Model pustej sieci Kierune [] L 4 [,,] Wve vector L
19 R. Stępniewsi nergy Model pustej sieci L= 0 00 X= 0
20 R. Stępniewsi Model pustej sieci Dimond, Sslow et l. PRL966
21 Model pustej sieci R. Stępniewsi
22 Podstwy modelu jednoeletronowego Twierdzenie Bloch Pojwi się przerw energetyczn n grnicy strefy Brillouin now współrzędn x x * cos * sin x x x
23 Podstwy modelu jednoeletronowego Twierdzenie Bloch Pojwi się przerw energetyczn n grnicy strefy Brillouin now współrzędn x x * cos * sin x x x
24 Podstwy modelu jednoeletronowego Twierdzenie Bloch Pojwi się przerw energetyczn n grnicy strefy Brillouin now współrzędn 4 6 psmo psmo psmo 8 x x * cos * sin x x x
25 Podstwy modelu jednoeletronowego Twierdzenie Bloch Poniewż funcj Bloch przesunięt o wetor sieci odwrotnej nie zmieni się to wygodnie jest przedstwić wynii tylo w I-szej strefie Brillouin. Trzeb wówczs numerowć psm energetyczne. Stn eletronu w ciele stłym zdny jest przez wetor flowy z I-szej strefy, numer psm orz rzut spinu. T. Stcewicz & A. Witowsi
26 Podstwy modelu jednoeletronowego Ms efetywn. Przybliżenie p ir r) u ( r) e ( n, n, Przybliżenie p Wetor nie jest pędem (mówimy, że jest qusi-pędem). pˆ ( r) i( i u ir ) e ( r), Funcj Bloch w równniu Schrodinger: n
27 Podstwy modelu jednoeletronowego Ms efetywn. Przybliżenie p Po uproszczeniu exp(ir): nergi n () woół =0: gdzie Jeśli rozwijmy woół estremum =0 liniowe w
28 Podstwy modelu jednoeletronowego Ms efetywn. Przybliżenie p nergi n () woół estremum: Przez nlogię do lsycznej zleżności energii inetycznej od pędu wprowdzmy tensor odwrotności msy efetywnej m - ij : Jeśli estremum energii jest w puncie (=0) to powierzchni stłej energii jest elipsoidą w przestrzeni, tór po sprowdzeniu do osi głównych m postć:
29 Podstwy modelu jednoeletronowego Ms efetywn. Przybliżenie p nergi n () woół estremum dl rysztłu jednoosiowego (np. N): Dl rysztłu ubicznego: tzw. psmo sferyczne W pobliżu estremum (np. punt (=0)) możemy ogrniczyć się do przybliżeni prbolicznego psmo prboliczne. W ogólności w zleżności energii od wetor flowego występują człony wyższego rzędu, tóre zostły zniedbne (wyższe rzędy rchunu zburzeń). W ogólności energi eletronu jest funcją słdowych wetor flowego =(,, 3 ). Powierzchni stłej energii w ogólnym przypdu może mieć sompliowny chrter, jej sztłt zleży od wszystich psm. Bdnie tensor msy efetywnej to jeden z głównych problemów fizyi cił stłego.
30 Podstwy modelu jednoeletronowego Ms efetywn. Przybliżenie p nergi n () woół estremum R. Stępniewsi
31 Podstwy modelu jednoeletronowego Strutur psmow cił stłych Przyłdy: D. Wsi.
32 Podstwy modelu jednoeletronowego Strutur psmow cił stłych Przyłdy:
33 Pust sieć fcc. I stref Brillouine Sieć odwrotn do fcc to bcc Komór Vigner-Seitz
34 Pust sieć fcc. I stref Brillouine Krzem i germn przerw sośn Krzem Si ermn e
35 Pust sieć fcc. I stref Brillouine Krzem i germn przerw sośn Krzem Si ermn e
36 Podstwy modelu jednoeletronowego Strutur psmow cił stłych Przyłdy: D. Wsi.
37 T. Stcewicz & A. Witowsi Twierdzenie Bloch letrony i dziury Zleżność () dl eletronu w ciele stłym różni się od zleżności dl eletronu swobodnego (próżni), poniewż eletron w rysztle stle oddziłuje z pozostłymi cząstmi ułdu eletronmi i jądrmi. ( p) mv p m ( p) c m c p ( p) letron w ciele stłym jest qusi-cząstą. Dlczego?
38 Co to jest? letrony i dziury Wetor nie jest pędem (mówimy, że jest qusi-pędem). pˆ ( r) i( i u ir ) e ( r), Wielość ħ m wymir pędu, le nie jest pędem poniewż funcj Bloch nie jest funcją włsną opertor pędu. jest liczbą wntow opisującą stny Bloch. n Prędość grupow d Vgr d V
39 letrony i dziury Co to jest? W oolicch estremum m V m d d V d d m m d d n n n n * * * * 0 (0) (0) V d d V gr Prędość grupow
40 Sił zewnętrzn letrony i dziury letron w ciele stłym zchowuje się inczej niż w próżni, poniewż oddziłuje z siecią rystliczną. d d V FVt Ft FVt F d dt Ms efetywn zchowuje się j zwył ms dv d d d d d F * dt dt d d dt d m F Prędość grupow d Vgr d V
41 ęstość stnów Wruni Born-Krmn letrony i dziury Jeśli nsz rysztł m sończone rozmiry zbiór wetorów jest sończony (choć olbrzymi!), np. możemy przyjąć periodyczne wruni brzegowe i wtedy: Sończone rozmiry rysztłu L x, L y, L z Ψ postć funcji Bloch Ψ(x + L x,y,z) = Ψ(x, y + L y,z) = Ψ(x, y, z + L z ) L z e i x L x e e i i y z L L y z i 4 n 0,,,..., L L L i i i i Ly L x Stny te wyznczją w przestrzeni odwrotnej sitę o gęstości (V/π) 3 ęstość stnów n jednostę trójwymirowej przestrzeni 3
42 letrony i dziury Zjwiso termoeletryczne Seebec (8) N, K, Co, Al eletrony Zn, Cu, Au -??? Psmo prwie cłowicie zpełnione eletronmi. Ms efetywn ujemn. Jeden stn pusty. Cłowity pęd j ev i 0 i
43 letrony i dziury Kwzicząsti - dziury Sumryczny pseudopęd zpełnionego psm: Dl funcji oresowej f(r): omór elementrn Dl f(r = 0):
44 letrony i dziury Kwzicząsti - dziury Sumryczny pseudopęd zpełnionego psm: Ztem: Cłowity prąd: Przyspieszenie: Dl f(r = 0):
45 letrony i dziury Kwzicząsti - dziury Sumryczny pseudopęd zpełnionego psm: e h i i h Ms efetywn eletronu w pśmie wlencyjny jest ujemn. h h pry bez e pry bez e miejscu pustym w e h m m m v v v * * * Pseudopęd dziury:
46 letrony i dziury Kwzicząsti - dziury Dl opisni sumrycznych włściwości tych N- eletronów wprowdzmy pojęcie nowej wzicząsti -dziury. Dziur qusi cząst z dodtnią msą efetywną, tór opisuje włsności zbioru eletronów w ciele stłym o msie ujemnej z jednym stnem pustym. Jeśli f() pewn wielość fizyczn chrteryzując eletron o wetorze flowym to wrtość tej wielości dl dziury: dl psm w tórym bruje eletronu w stnie j Np. wetor flowy dziury: Np. prędość dziury:
47 letrony i dziury Kwzicząsti - dziury Dl opisni sumrycznych włściwości tych N- eletronów wprowdzmy pojęcie nowej wzicząsti -dziury. Dziur qusi cząst z dodtnią msą efetywną, tór opisuje włsności zbioru eletronów w ciele stłym o msie ujemnej z jednym stnem pustym. Np. prędość dziury:
48 Kwzicząsti - dziury letrony i dziury Dl opisni sumrycznych włściwości tych N- eletronów wprowdzmy pojęcie nowej wzicząsti -dziury. Dziur qusi cząst z dodtnią msą efetywną, tór opisuje włsności zbioru eletronów w ciele stłym o msie ujemnej z jednym stnem pustym. Pole eletryczne j j v h ev ev v ebez pry ew pustym miejscu ew pustym miejscu
49 Kwzicząsti - dziury Wyzncznie msy efetywnej: Rezonns cylotronowy letrony i dziury c eb m* e, J. inter
50 Przerw energetyczn Wyzncznie przerwy energetycznej: letrony i dziury D. Wsi.
51 Przerw energetyczn
52 Włsności psm f 0 Fermiony: e T B F letrony i dziury Prwdopodobieństwo obsdzeni stnu wntowego o energii F potencjł chemiczny letrony Dziury Triony (escytony nłdowne) f 0 Bozony: e T B F Polritony Fonony Mgnony scytony, biescytony Plzmony f 0 i e Rozłd Boltzmn: e T B F F F e F n U T i B TS Anyons np. composite fermions Slve fermions (chrgon, holon, spinon) = fermion+bozon w seprcji spin-łdune F
53 Teori psmow cił stłych. Przerw energetyczn
54 NRIA LKTRONÓW Teori psmow cił stłych. psmo puste psmo puste psmo puste psmo pełne psmo pełne psmo pełne metl półprzewodni izoltor J zobczyć przerwę?
55 Studni Kwntow AlAs As AlAs g g g
56 Studni Kwntow AlAs As AlAs AlAs As AlAs g g g
57 Studni Kwntow AlAs As AlAs
58 Studni Kwntow
59 Studni Kwntow eletrony dziury
60 Studni Kwntow eletrony hn dziury
61 Studnie Kwntowe Lsery półprzewodniowe
Struktura energetyczna ciał stałych-cd. Fizyka II dla Elektroniki, lato
 Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
1. Struktura pasmowa from bonds to bands
 . Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
. Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
Fizyka Materii Skondensowanej Równanie kp. LCAO.
 013 06 0 Fizyk Mterii Skondensownej Równnie kp. LCAO. Wydził Fizyki UW Jcek.Szczytko@fuw.edu.pl Projekt: POKL 04.01.01 00 100/10 00 "Chemi, fizyk biologi n potrzeby społeczeństw XXI wieku: nowe mkrokierunki
013 06 0 Fizyk Mterii Skondensownej Równnie kp. LCAO. Wydził Fizyki UW Jcek.Szczytko@fuw.edu.pl Projekt: POKL 04.01.01 00 100/10 00 "Chemi, fizyk biologi n potrzeby społeczeństw XXI wieku: nowe mkrokierunki
Fizyka Materii Skondensowanej Potencjał periodyczny (cd)
 Fzy Mter Sondensownej cd Przyblżene Born Oppenheer Wydzł Fzy UW Jce.Szczyto@fuw.edu.pl M Born 88 97 Jcob R. Oppenheer 94 967 Projet: POKL 4.. / "Che, fzy bolog n potrzeby społeczeństw XXI weu: nowe roerun
Fzy Mter Sondensownej cd Przyblżene Born Oppenheer Wydzł Fzy UW Jce.Szczyto@fuw.edu.pl M Born 88 97 Jcob R. Oppenheer 94 967 Projet: POKL 4.. / "Che, fzy bolog n potrzeby społeczeństw XXI weu: nowe roerun
G:\AA_Wyklad 2000\FIN\DOC\Nieciagly.doc. Drgania i fale II rok Fizyki BC
 Fle w ośrodu o struturze periodycznej: N ogół roziry nieciągłości ośrod
Fle w ośrodu o struturze periodycznej: N ogół roziry nieciągłości ośrod
DYDAKTYCZNA PREZENTACJA PRÓBKOWANIA SYGNAŁÓW OKRESOWYCH
 POZA UIVE RSIY OF E CHOLOGY ACADE MIC JOURALS o 73 Electricl Engineering 3 Wojciech LIPIŃSI* DYDAYCZA PREZEACJA PRÓBOWAIA SYGAŁÓW ORESOWYCH Przedstwiono dydtyczną prezentcję próbowni przebiegów oresowych
POZA UIVE RSIY OF E CHOLOGY ACADE MIC JOURALS o 73 Electricl Engineering 3 Wojciech LIPIŃSI* DYDAYCZA PREZEACJA PRÓBOWAIA SYGAŁÓW ORESOWYCH Przedstwiono dydtyczną prezentcję próbowni przebiegów oresowych
3. Struktura pasmowa
 3. Strutura pasmowa Funcja Blocha Quasi-pęd, sić odwrotna Przybliżni prawi swobodngo ltronu Dziura w paśmi walncyjnym Masa ftywna Strutura pasmowa (), przyłady Półprzwodnii miszan ltron w rysztal sformułowani
3. Strutura pasmowa Funcja Blocha Quasi-pęd, sić odwrotna Przybliżni prawi swobodngo ltronu Dziura w paśmi walncyjnym Masa ftywna Strutura pasmowa (), przyłady Półprzwodnii miszan ltron w rysztal sformułowani
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO.
 GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
TEORIA CIAŁA STAŁEGO (cz. II)
 TORIA CIAŁA STAŁGO (cz. II TWIRDZNI BLOCHA W idealnym rysztale m i V ( r ( r ( r V (r - periodyczny, V (r+r = V (r, R wetor sieci prostej T R - operator translacji o wetor sieci Bravais, R; [H,T R ] =
TORIA CIAŁA STAŁGO (cz. II TWIRDZNI BLOCHA W idealnym rysztale m i V ( r ( r ( r V (r - periodyczny, V (r+r = V (r, R wetor sieci prostej T R - operator translacji o wetor sieci Bravais, R; [H,T R ] =
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Modelowanie i obliczenia techniczne. Metody numeryczne w modelowaniu: Różniczkowanie i całkowanie numeryczne
 Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Wykład 21: Studnie i bariery cz.1.
 Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII.
 ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
jednoznacznie wyznaczają wymiary wszystkich reprezentacji grup punktowych, a związki ortogonalności jednoznacznie wyznaczają ich charaktery
 Reprezentacje grup puntowych związi pomiędzy h i n a jednoznacznie wyznaczają wymiary wszystich reprezentacji grup puntowych, a związi ortogonalności jednoznacznie wyznaczają ich charatery oznaczenia:
Reprezentacje grup puntowych związi pomiędzy h i n a jednoznacznie wyznaczają wymiary wszystich reprezentacji grup puntowych, a związi ortogonalności jednoznacznie wyznaczają ich charatery oznaczenia:
Ato wodoropodobny Eektron poruszjący się w kuobowski pou jądr o łdunku +Ze posid energię potencjną: z -e, V ( r) Ze 4πε r + Ze φ θ r y x
 Ato wodoropodobny z współrzędne w ukłdzie krtezjński r sinθ cosφ x r cosθ φ θ r r sinθ (x,y,z) r sinθ sinφ Biegunowy ukłd współrzędnych y funkcj fow współrzędne w ukłdzie biegunowy ( ) r,θ,φ x r sinθ cosφ
Ato wodoropodobny z współrzędne w ukłdzie krtezjński r sinθ cosφ x r cosθ φ θ r r sinθ (x,y,z) r sinθ sinφ Biegunowy ukłd współrzędnych y funkcj fow współrzędne w ukłdzie biegunowy ( ) r,θ,φ x r sinθ cosφ
Kształty komórek elementarnych
 Ksztłty omóre elementrnych Komóri elementrne Brvis Grupy trnslcyjne Brvis Ułd Grup trnslcyjn regulrny P, I, F tetrgonlny P, I rombowy P, C, I, F jednosośny P, C, trójsośny P trygonlny R hesgonlny P Prwo
Ksztłty omóre elementrnych Komóri elementrne Brvis Grupy trnslcyjne Brvis Ułd Grup trnslcyjn regulrny P, I, F tetrgonlny P, I rombowy P, C, I, F jednosośny P, C, trójsośny P trygonlny R hesgonlny P Prwo
Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych
 Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
Materiały diagnostyczne z matematyki poziom podstawowy
 Mteriły dignostyczne z mtemtyki poziom podstwowy czerwiec 0 Klucz odpowiedzi do zdń zmkniętych orz schemt ocenini Mteriły dignostyczne przygotowł Agt Siwik we współprcy z nuczycielmi mtemtyki szkół pondgimnzjlnych:
Mteriły dignostyczne z mtemtyki poziom podstwowy czerwiec 0 Klucz odpowiedzi do zdń zmkniętych orz schemt ocenini Mteriły dignostyczne przygotowł Agt Siwik we współprcy z nuczycielmi mtemtyki szkół pondgimnzjlnych:
4) Podaj wartość stałych czasowych, wzmocnienia i punkt równowagi przy wymuszeniu impulsowym
 LISA0: Podtwowe człony (obiety) dynmii Przygotownie ) Wymień i opiz włności podtwowych członów (obiety) dynmii potć trnmitncji nzwy i ogrniczeni prmetrów ) Wymień podtwowe człony dynmii dl tórych trnmitncj
LISA0: Podtwowe człony (obiety) dynmii Przygotownie ) Wymień i opiz włności podtwowych członów (obiety) dynmii potć trnmitncji nzwy i ogrniczeni prmetrów ) Wymień podtwowe człony dynmii dl tórych trnmitncj
S. Baran - Podstawy fizyki materii skondensowanej Pasma energetyczne. Pasma energetyczne
 Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Analiza numeryczna. Stanisław Lewanowicz. Całkowanie numeryczne. Definicje, twierdzenia, algorytmy
 http://wwwiiuniwrocpl/ sle/teching/n-wdrpdf Anliz numeryczn Stnisłw Lewnowicz Styczeń 008 r Cłownie numeryczne Definicje, twierdzeni, lgorytmy 1 Pojęci wstępne Niech IF IF [, b] ozncz zbiór wszystich funcji
http://wwwiiuniwrocpl/ sle/teching/n-wdrpdf Anliz numeryczn Stnisłw Lewnowicz Styczeń 008 r Cłownie numeryczne Definicje, twierdzeni, lgorytmy 1 Pojęci wstępne Niech IF IF [, b] ozncz zbiór wszystich funcji
MATURA 2014 z WSiP. Zasady oceniania zadań
 MATURA z WSiP Mtemtyk Poziom podstwowy Zsdy ocenini zdń Copyright by Wydwnictw Szkolne i Pedgogiczne sp. z o.o., Wrszw Krtotek testu Numer zdni 6 7 8 9 6 7 8 9 Uczeń: Sprwdzn umiejętność (z numerem stndrdu)
MATURA z WSiP Mtemtyk Poziom podstwowy Zsdy ocenini zdń Copyright by Wydwnictw Szkolne i Pedgogiczne sp. z o.o., Wrszw Krtotek testu Numer zdni 6 7 8 9 6 7 8 9 Uczeń: Sprwdzn umiejętność (z numerem stndrdu)
dr inż. Zbigniew Szklarski
 Wkłd 3: Kinemtk dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://ler.uci.gh.edu.pl/z.szklrski/ Wstęp Opis ruchu KINEMATYKA Dlczego tki ruch? Przczn ruchu DYNAMIKA MECHANIKA Podstwowe pojęci dl ruchu prostoliniowego
Wkłd 3: Kinemtk dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://ler.uci.gh.edu.pl/z.szklrski/ Wstęp Opis ruchu KINEMATYKA Dlczego tki ruch? Przczn ruchu DYNAMIKA MECHANIKA Podstwowe pojęci dl ruchu prostoliniowego
http://www.clausius-tower-society.koszalin.pl/index.html
 yłd rc zminy objętości czynni roboczego rc techniczn w ułdzie otwrtym n przyłdzie turbiny RównowŜność prcy i ciepł w obiegu zmniętym I zsd termodynmii dl zminy stnu msy ontrolnej Szczególne przypdi I zsdy
yłd rc zminy objętości czynni roboczego rc techniczn w ułdzie otwrtym n przyłdzie turbiny RównowŜność prcy i ciepł w obiegu zmniętym I zsd termodynmii dl zminy stnu msy ontrolnej Szczególne przypdi I zsdy
P R A C O W N I A
 P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
Praca, potencjał i pojemność
 Prc, potencjł i pojemność Mciej J. Mrowiński 1 listopd 2010 Zdnie PPP1 h Wyzncz wrtość potencjłu elektrycznego w punkcie oddlonym o h od cienkiego, jednorodnie nłdownego łdunkiem Q pierścieni o promieniu.
Prc, potencjł i pojemność Mciej J. Mrowiński 1 listopd 2010 Zdnie PPP1 h Wyzncz wrtość potencjłu elektrycznego w punkcie oddlonym o h od cienkiego, jednorodnie nłdownego łdunkiem Q pierścieni o promieniu.
splajnami splajnu kubicznego
 WYKŁAD 6 INTERPOLACJA FUNKCJAMI SKLEJANYMI (SPLAJNY) W tym wyłdzie omówimy prolem interpolcji przy pomocy tzw. funcji slejnych, zwnych też (żrgonowo) spljnmi. W przeciwieństwie do metod interpolcyjnych
WYKŁAD 6 INTERPOLACJA FUNKCJAMI SKLEJANYMI (SPLAJNY) W tym wyłdzie omówimy prolem interpolcji przy pomocy tzw. funcji slejnych, zwnych też (żrgonowo) spljnmi. W przeciwieństwie do metod interpolcyjnych
Prawo Coulomba i pole elektryczne
 Prwo Coulomb i pole elektryczne Mciej J. Mrowiński 4 pździernik 2010 Zdnie PE1 2R R Dwie młe kulki o msie m, posidjące ten sm łdunek, umieszczono w drewninym nczyniu, którego przekrój wygląd tk jk n rysunku
Prwo Coulomb i pole elektryczne Mciej J. Mrowiński 4 pździernik 2010 Zdnie PE1 2R R Dwie młe kulki o msie m, posidjące ten sm łdunek, umieszczono w drewninym nczyniu, którego przekrój wygląd tk jk n rysunku
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
LISTA02: Projektowanie układów drugiego rzędu Przygotowanie: 1. Jakie własności ma równanie 2-ego rzędu & x &+ bx&
 LISTA: Projektownie ukłdów drugiego rzędu Przygotownie: 1. Jkie włsności m równnie -ego rzędu & &+ b + c u jeśli: ) c>; b) c; c) c< Określ położenie biegunów, stbilność, oscylcje Zdni 1: Wyzncz bieguny.
LISTA: Projektownie ukłdów drugiego rzędu Przygotownie: 1. Jkie włsności m równnie -ego rzędu & &+ b + c u jeśli: ) c>; b) c; c) c< Określ położenie biegunów, stbilność, oscylcje Zdni 1: Wyzncz bieguny.
3. Struktura pasmowa
 3. Stutua pasmowa Funcja Blocha Quasi-pęd, sić odwotna Pzybliżni pawi swobodngo ltonu Dziua w paśmi walncyjnym Masa ftywna Stutua pasmowa (), pzyłady Półpzwodnii miszan lton w ysztal sfomułowani poblmu
3. Stutua pasmowa Funcja Blocha Quasi-pęd, sić odwotna Pzybliżni pawi swobodngo ltonu Dziua w paśmi walncyjnym Masa ftywna Stutua pasmowa (), pzyłady Półpzwodnii miszan lton w ysztal sfomułowani poblmu
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
cz. 2 dr inż. Zbigniew Szklarski
 Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
Energia wiązania słaba rzędu 10-2 ev J. Energia cieplna 3/2 k B. T J. Energia ruchu cieplnego powoduje rozerwanie wiązań cząsteczkowych.
 Ciała stałe - o struturze rystalicznej wyazują daleo zasięgowe uporządowanie atoowe, są to onoryształy i poliryształy. - o struturze bezpostaciowej (aorficznej), wyazują bra uporządowania atoowego daleiego
Ciała stałe - o struturze rystalicznej wyazują daleo zasięgowe uporządowanie atoowe, są to onoryształy i poliryształy. - o struturze bezpostaciowej (aorficznej), wyazują bra uporządowania atoowego daleiego
Środowisko programowe do symulacji zjawiska tunelowania
 Wydził Podstwowych Problemów Technii Środowiso progrmowe do symulcji zjwis tunelowni Prc dyplomow inŝyniers ichł Chomet Opieun: dr hb. inŝ. Włodzimierz Slejd prof. PWr. Wrocłw 6 Opieunowi prof. Włodzimierzowi
Wydził Podstwowych Problemów Technii Środowiso progrmowe do symulcji zjwis tunelowni Prc dyplomow inŝyniers ichł Chomet Opieun: dr hb. inŝ. Włodzimierz Slejd prof. PWr. Wrocłw 6 Opieunowi prof. Włodzimierzowi
Oznaczenia: K wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania wykraczające
 Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Struktura kryształów. Kittel, rozdz. 1 (Uwaga błędna terminologia!) Ashcroft, Mermin, rozdz.
 Struktur krysztłów http://www.uncp.edu/home/mcclurem/ptble/crbon.htm Kittel, rozdz. 1 (Uwg błędn terminologi!) Ashcroft, Mermin, rozdz. 4,7 1 Obserwowne włsności Ksztłt ogrniczony płszczyznmi. (1) Kierunki
Struktur krysztłów http://www.uncp.edu/home/mcclurem/ptble/crbon.htm Kittel, rozdz. 1 (Uwg błędn terminologi!) Ashcroft, Mermin, rozdz. 4,7 1 Obserwowne włsności Ksztłt ogrniczony płszczyznmi. (1) Kierunki
Wymagania edukacyjne matematyka klasa 2 zakres podstawowy 1. SUMY ALGEBRAICZNE
 Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Morfologia kryształów
 Morfologi krsztłów Morfologi krsztłu Ścin krsztłu = ogrniczjące powierzchnie Zleżą od ksztłtu komorek elementrnch i od fizcznch wrunków wzrostu krsztłu (T, p, otoczenie, roztwór itd.); Krsztł jest wielościnem
Morfologi krsztłów Morfologi krsztłu Ścin krsztłu = ogrniczjące powierzchnie Zleżą od ksztłtu komorek elementrnch i od fizcznch wrunków wzrostu krsztłu (T, p, otoczenie, roztwór itd.); Krsztł jest wielościnem
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
Klucz odpowiedzi do zadań zamkniętych oraz schemat oceniania
 Klucz odpowiedzi do zdń zmkniętych orz schemt ocenini sierpień 0 Poziom Podstwowy Schemt ocenini sierpień Poziom podstwowy Klucz punktowni zdń zmkniętych Nr zdni 4 5 6 7 8 9 0 4 5 6 7 8 9 0 4 5 Odpowiedź
Klucz odpowiedzi do zdń zmkniętych orz schemt ocenini sierpień 0 Poziom Podstwowy Schemt ocenini sierpień Poziom podstwowy Klucz punktowni zdń zmkniętych Nr zdni 4 5 6 7 8 9 0 4 5 6 7 8 9 0 4 5 Odpowiedź
Dr inż. Zbigniew Szklarski
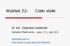 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Temat lekcji Zakres treści Osiągnięcia ucznia
 ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
2. FUNKCJE WYMIERNE Poziom (K) lub (P)
 Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Dr inż. Zbigniew Szklarski
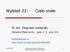 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Metoda sił jest sposobem rozwiązywania układów statycznie niewyznaczalnych, czyli układów o nadliczbowych więzach (zewnętrznych i wewnętrznych).
 Metod sił jest sposoem rozwiązywni ukłdów sttycznie niewyznczlnych, czyli ukłdów o ndliczowych więzch (zewnętrznych i wewnętrznych). Sprowdz się on do rozwiązni ukłdu sttycznie wyznczlnego (ukłd potwowy
Metod sił jest sposoem rozwiązywni ukłdów sttycznie niewyznczlnych, czyli ukłdów o ndliczowych więzch (zewnętrznych i wewnętrznych). Sprowdz się on do rozwiązni ukłdu sttycznie wyznczlnego (ukłd potwowy
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom podstawowy
 KRYTERIA OCENIANIA ODPOWIEDZI Próbn Mtur z OPERONEM Mtemtyk Poziom podstwowy Mrzec 7 Zdni zmknięte Z kżdą poprwną odpowiedź zdjący otrzymuje punkt. Poprwn odpowiedź Wskzówki do rozwiązni. B 5 5 6 5 = =
KRYTERIA OCENIANIA ODPOWIEDZI Próbn Mtur z OPERONEM Mtemtyk Poziom podstwowy Mrzec 7 Zdni zmknięte Z kżdą poprwną odpowiedź zdjący otrzymuje punkt. Poprwn odpowiedź Wskzówki do rozwiązni. B 5 5 6 5 = =
ANALIZA WARTOŚCI NAPIĘĆ WYJŚCIOWYCH TRANSFORMATORÓW SN/nn W ZALEŻNOŚCI OD CHARAKTERU I WARTOŚCI OBCIĄŻENIA
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE IC JOURNALS No 78 Electricl Engineering 4 Ryszrd NAWROWSKI* Zbigniew STEIN* ri ZIELIŃSKA* ANALIZA WARTOŚCI NAPIĘĆ WYJŚCIOWYCH TRANSFORATORÓW SN/nn W ZALEŻNOŚCI OD
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE IC JOURNALS No 78 Electricl Engineering 4 Ryszrd NAWROWSKI* Zbigniew STEIN* ri ZIELIŃSKA* ANALIZA WARTOŚCI NAPIĘĆ WYJŚCIOWYCH TRANSFORATORÓW SN/nn W ZALEŻNOŚCI OD
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
Zbiory rozmyte. Teoria i zastosowania we wnioskowaniu aproksymacyjnym
 Zior rozmte Teori i zstosowni we wniosowniu prosmcjnm PODSTWOWE POJĘCI Motwcje Potrze opisni zjwis i pojęć wielozncznch i niepreczjnch użwnch swoodnie w jęzu nturlnm np. wso tempertur młod człowie średni
Zior rozmte Teori i zstosowni we wniosowniu prosmcjnm PODSTWOWE POJĘCI Motwcje Potrze opisni zjwis i pojęć wielozncznch i niepreczjnch użwnch swoodnie w jęzu nturlnm np. wso tempertur młod człowie średni
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Wymagania kl. 2. Uczeń:
 Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Wyrównanie sieci niwelacyjnej
 1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka. Poziom rozszerzony. Listopad Wskazówki do rozwiązania zadania =
 Vdemecum GIELDAMATURALNA.PL ODBIERZ KOD DOSTĘPU* Mtemtyk - Twój indywidulny klucz do wiedzy! *Kod n końcu klucz odpowiedzi KRYTERIA OCENIANIA ODPOWIEDZI Prón Mtur z OPERONEM Operon 00% MATURA 07 VA D EMECUM
Vdemecum GIELDAMATURALNA.PL ODBIERZ KOD DOSTĘPU* Mtemtyk - Twój indywidulny klucz do wiedzy! *Kod n końcu klucz odpowiedzi KRYTERIA OCENIANIA ODPOWIEDZI Prón Mtur z OPERONEM Operon 00% MATURA 07 VA D EMECUM
Półprzewodniki (ang. semiconductors).
 Półprzwodn an. smondutors. Ja.Szzyto@fuw.du.pl ttp://www.fuw.du.pl/~szzyto/ Unwrsytt Warszaws ora pasmowa ał stały. pasmo pust RGIA LKROÓW pasmo pust pasmo płn pasmo pust pasmo płn pasmo płn mtal półprzwodn
Półprzwodn an. smondutors. Ja.Szzyto@fuw.du.pl ttp://www.fuw.du.pl/~szzyto/ Unwrsytt Warszaws ora pasmowa ał stały. pasmo pust RGIA LKROÓW pasmo pust pasmo płn pasmo pust pasmo płn pasmo płn mtal półprzwodn
usuwa niewymierność z mianownika wyrażenia typu
 Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
dr inż. Zbigniew Szklarski
 Włd : Wetor dr nż. Zgnew Slrs sl@gh.edu.pl http://ler.uc.gh.edu.pl/z.slrs/ Welośc fcne Długość, cs, sł, ms, prędość, pęd, prspesene tempertur, nprężene, premescene, ntężene prądu eletrcnego, ntężene pol
Włd : Wetor dr nż. Zgnew Slrs sl@gh.edu.pl http://ler.uc.gh.edu.pl/z.slrs/ Welośc fcne Długość, cs, sł, ms, prędość, pęd, prspesene tempertur, nprężene, premescene, ntężene prądu eletrcnego, ntężene pol
Szczegółowe wymagania edukacyjne z matematyki, klasa 2C, poziom podstawowy
 Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Dr inż. Zbigniew Szklarski
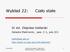 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
Materiały pomocnicze do ćwiczeń z przedmiotu: Ogrzewnictwo, wentylacja i klimatyzacja II. Klimatyzacja
 Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Elektrostatyka. Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego
 Elektrostatyka Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego 1 Prawo Coulomba odpychanie naelektryzowane szkło nie-naelektryzowana miedź F 1 4 0 q 1 q 2 r 2 0 8.85
Elektrostatyka Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego 1 Prawo Coulomba odpychanie naelektryzowane szkło nie-naelektryzowana miedź F 1 4 0 q 1 q 2 r 2 0 8.85
Rozwiązywanie zadań z dynamicznego ruchu płaskiego część I 9
 ozwiązywnie zdń z dyniczneo ruchu płskieo część I 9 Wprowdzenie ozwiązywnie zdń w oprciu o dyniczne równni ruchu (D pole n uwolnieniu z więzów kżdeo z cił w sposób znny ze sttyki. Wrunki równowi są zbliżone
ozwiązywnie zdń z dyniczneo ruchu płskieo część I 9 Wprowdzenie ozwiązywnie zdń w oprciu o dyniczne równni ruchu (D pole n uwolnieniu z więzów kżdeo z cił w sposób znny ze sttyki. Wrunki równowi są zbliżone
PODSTAWY ALGEBRY MACIERZY. Operacje na macierzach
 PODSTWY LGEBRY MCIERZY WIERSZ i, KOLUMN (j) Mcierz m,n, gdzie m to ilość wierszy, n ilość kolumn i,j element mcierzy z itego wiersz, jtej kolumny Opercje n mcierzch Równość mcierzy m,n = B m,n. def i,j
PODSTWY LGEBRY MCIERZY WIERSZ i, KOLUMN (j) Mcierz m,n, gdzie m to ilość wierszy, n ilość kolumn i,j element mcierzy z itego wiersz, jtej kolumny Opercje n mcierzch Równość mcierzy m,n = B m,n. def i,j
Struktura energetyczna ciał stałych. Fizyka II dla EiT oraz E, lato
 Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Wymagania edukacyjne matematyka klasa 2b, 2c, 2e zakres podstawowy rok szkolny 2015/2016. 1.Sumy algebraiczne
 Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
exp jest proporcjonalne do czynnika Boltzmanna exp(-e kbt (szerokość przerwy energetycznej między pasmami) g /k B
 Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
ODPOWIEDZI I SCHEMAT PUNKTOWANIA POZIOM ROZSZERZONY Etapy rozwiązania zadania , 3 5, 7
 Próbn egzmin mturln z mtemtki Numer zdni ODPOWIEDZI I SCHEMAT PUNKTOWANIA POZIOM ROZSZERZONY Etp rozwiązni zdni Liczb punktów Podnie wrtości b: b = Sporządzenie wkresu funkcji g Uwgi dl egzmintorów 4 Krzw
Próbn egzmin mturln z mtemtki Numer zdni ODPOWIEDZI I SCHEMAT PUNKTOWANIA POZIOM ROZSZERZONY Etp rozwiązni zdni Liczb punktów Podnie wrtości b: b = Sporządzenie wkresu funkcji g Uwgi dl egzmintorów 4 Krzw
1 Definicja całki oznaczonej
 Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Fizyka materii skondensowanej i struktur półprzewodnikowych (1101-4FS22) Michał Baj
 Fizyk mterii skondensownej i struktur półprzewodnikowych (-4FS) Michł Bj Zkłd Fizyki Cił Stłego Instytut Fizyki Doświdczlnej Wydził Fizyki Uniwersytet Wrszwski 7--8 Fizyk mterii skondensownej i struktur
Fizyk mterii skondensownej i struktur półprzewodnikowych (-4FS) Michł Bj Zkłd Fizyki Cił Stłego Instytut Fizyki Doświdczlnej Wydził Fizyki Uniwersytet Wrszwski 7--8 Fizyk mterii skondensownej i struktur
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
Pierwiastek z liczby zespolonej
 Pierwistek z liczby zespolonej Twierdzenie: Istnieje dokłdnie n różnych pierwistków n-tego stopni z kżdej liczby zespolonej różnej od zer, tzn. rozwiązń równni w n z i wszystkie te pierwistki dją się zpisć
Pierwistek z liczby zespolonej Twierdzenie: Istnieje dokłdnie n różnych pierwistków n-tego stopni z kżdej liczby zespolonej różnej od zer, tzn. rozwiązń równni w n z i wszystkie te pierwistki dją się zpisć
( ) Lista 2 / Granica i ciągłość funkcji ( z przykładowymi rozwiązaniami)
 List / Grnic i ciągłość funkcji ( z przykłdowymi rozwiąznimi) Korzystjąc z definicji grnicy (ciągowej) funkcji uzsdnić podne równości: sin ) ( + ) ; b) ; c) + 5 Obliczyć grnice funkcji przy orz : + ) f
List / Grnic i ciągłość funkcji ( z przykłdowymi rozwiąznimi) Korzystjąc z definicji grnicy (ciągowej) funkcji uzsdnić podne równości: sin ) ( + ) ; b) ; c) + 5 Obliczyć grnice funkcji przy orz : + ) f
Mechanika kwantowa. Mechanika kwantowa. dx dy dz. Jak opisać atom wodoru? Jak opisać inne cząsteczki? Równanie Schrödingera. zasada zachowania energii
 Mecnik kwntow Jk opisć tom wodou? Jk opisć inne cąstecki? Mecnik kwntow Równnie Scödinge Ĥ E ψ H ˆψ = Eψ opeto óżnickow Hmilton enegi funkcj flow d d d + + m d d d opeto enegii kinetcn enegi kinetcn elektonu
Mecnik kwntow Jk opisć tom wodou? Jk opisć inne cąstecki? Mecnik kwntow Równnie Scödinge Ĥ E ψ H ˆψ = Eψ opeto óżnickow Hmilton enegi funkcj flow d d d + + m d d d opeto enegii kinetcn enegi kinetcn elektonu
Arkusz 1 - karta pracy Całka oznaczona i jej zastosowania. Całka niewłaściwa
 Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Teoria pasmowa. Anna Pietnoczka
 Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
S. Baran - Podstawy fizyki materii skondensowanej Fonony. Fonony
 Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
1. RACHUNEK WEKTOROWY
 1 RACHUNEK WEKTOROWY 1 Rozstrzygnąć, czy możliwe jest y wartość sumy dwóch wetorów yła równa długości ażdego z nich 2 Dane są wetory: a i 3 j 2 ; 4 j = + = Oliczyć: a+, a, oraz a 3 Jai ąt tworzą dwa jednaowe
1 RACHUNEK WEKTOROWY 1 Rozstrzygnąć, czy możliwe jest y wartość sumy dwóch wetorów yła równa długości ażdego z nich 2 Dane są wetory: a i 3 j 2 ; 4 j = + = Oliczyć: a+, a, oraz a 3 Jai ąt tworzą dwa jednaowe
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Matematyka. Poziom rozszerzony Próbna Matura z OPERONEM. Modelowe etapy rozwiązywania zadania
 KRYTERIA OCENIANIA ODPOWIEDZI Mtemtyk Poziom rozszerzony Mrzec 09 Zdni zmknięte Z kżdą poprwną odpowiedź zdjący otrzymuje punkt. Poprwn odpowiedź Wskzówki do rozwiązni. C Obliczenie wrtości funkcji: f(
KRYTERIA OCENIANIA ODPOWIEDZI Mtemtyk Poziom rozszerzony Mrzec 09 Zdni zmknięte Z kżdą poprwną odpowiedź zdjący otrzymuje punkt. Poprwn odpowiedź Wskzówki do rozwiązni. C Obliczenie wrtości funkcji: f(
Podstawy Elektrotechniki i Elektroniki
 Postw ektotechniki i ektoniki Definicj po eektomgnetcznego z v Pzestzeń w któej n łunek eektczn ził ił Loentz v ntężenie po eektcznego [V/m] inukcj po mgnetcznego [T] v pękość łunku [m/s] Poe eektczne
Postw ektotechniki i ektoniki Definicj po eektomgnetcznego z v Pzestzeń w któej n łunek eektczn ził ił Loentz v ntężenie po eektcznego [V/m] inukcj po mgnetcznego [T] v pękość łunku [m/s] Poe eektczne
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 2014/2015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A2, A3, A4, A6, A7)
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
4. RACHUNEK WEKTOROWY
 4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
EGZAMIN MATURALNY W ROKU SZKOLNYM 2014/2015
 EGZAMIN MATURALNY W ROKU SZKOLNYM 04/05 FORMUŁA DO 04 ( STARA MATURA ) MATEMATYKA POZIOM ROZSZERZONY ZASADY OCENIANIA ROZWIĄZAŃ ZADAŃ ARKUSZ MMA-R CZERWIEC 05 Egzmin mturlny z mtemtyki str formuł Rozwiązni
EGZAMIN MATURALNY W ROKU SZKOLNYM 04/05 FORMUŁA DO 04 ( STARA MATURA ) MATEMATYKA POZIOM ROZSZERZONY ZASADY OCENIANIA ROZWIĄZAŃ ZADAŃ ARKUSZ MMA-R CZERWIEC 05 Egzmin mturlny z mtemtyki str formuł Rozwiązni
Równania różniczkowe cząstkowe - metoda Fouriera. Przykładowe rozwiązania i wskazówki
 INSTYTUT MATEMATYKI POLITECHNIKA KRAKOWSKA Dr Mrgret Wicik e-mi: mwicik@pk.edu.p Równni różniczkowe cząstkowe - metod Fourier. Przykłdowe rozwiązni i wskzówki zd.1. Wyznczyć funkcję opisującą drgni podłużne
INSTYTUT MATEMATYKI POLITECHNIKA KRAKOWSKA Dr Mrgret Wicik e-mi: mwicik@pk.edu.p Równni różniczkowe cząstkowe - metod Fourier. Przykłdowe rozwiązni i wskzówki zd.1. Wyznczyć funkcję opisującą drgni podłużne
Sieć odwrotna. Fale i funkcje okresowe
 Sieć odwotn Fle i funkcje okesowe o Wiele obiektów w pzyodzie d; o Różne fle ozchodzą się w pzestzeni (zówno w póżni jk i w mteii); o Aby mtemtycznie opisć tkie okesowe zminy stosuje się funkcje sinus
Sieć odwotn Fle i funkcje okesowe o Wiele obiektów w pzyodzie d; o Różne fle ozchodzą się w pzestzeni (zówno w póżni jk i w mteii); o Aby mtemtycznie opisć tkie okesowe zminy stosuje się funkcje sinus
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
dr inż. Zbigniew Szklarski
 Wkłd 3: Kinemtk dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://ler.uci.gh.edu.pl/z.szklrski/ Wstęp Opis ruchu KINEMATYKA Dlczego tki ruch? Przczn ruchu DYNAMIKA MECHANIKA Podstwowe pojęci dl ruchu prostoliniowego
Wkłd 3: Kinemtk dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://ler.uci.gh.edu.pl/z.szklrski/ Wstęp Opis ruchu KINEMATYKA Dlczego tki ruch? Przczn ruchu DYNAMIKA MECHANIKA Podstwowe pojęci dl ruchu prostoliniowego
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Całka oznaczona. długość k-tego odcinka podziału P. średnica podziału P. punkt pośredni k-tego odcinka podziału P
 Cł ozczo. De.. Podziłem odci części, N, zywmy ziór przy czym. Wprowdzmy ozczei: długość -tego odci podziłu P średic podziłu P put pośredi -tego odci podziłu P De. sum cłow Niech ucj ędzie ogriczo przedzile
Cł ozczo. De.. Podziłem odci części, N, zywmy ziór przy czym. Wprowdzmy ozczei: długość -tego odci podziłu P średic podziłu P put pośredi -tego odci podziłu P De. sum cłow Niech ucj ędzie ogriczo przedzile
o zasilaniu napięciowym Gałąź normalna o zasilaniu mieszanym
 o silniu npięiowm Głąź normln o silniu miesnm w w Głąź normln o silniu prądowm w w iern Siei e źródłmi npięiowmi [ ] [ ] [ ][ ]... W prpdu siei owodmi sprężonmi ( ) ( ) ( ) ω ω ω ω ω ω ω ω ω... M j M j
o silniu npięiowm Głąź normln o silniu miesnm w w Głąź normln o silniu prądowm w w iern Siei e źródłmi npięiowmi [ ] [ ] [ ][ ]... W prpdu siei owodmi sprężonmi ( ) ( ) ( ) ω ω ω ω ω ω ω ω ω... M j M j
Modele kp wprowadzenie
 Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
