Piotr Targowski i Bernard Ziętek BADANIE WŁASNOŚCI ŁĄCZA ŚWIATŁOWODOWEGO
|
|
|
- Karol Wojciechowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Instytut Fizyki Uniwersytet Mikłaja Kpernika Pitr Targwski i Bernard Ziętek Pracwnia Optelektrniki Specjalnść: Fizyka Medyczna BADANIE WŁASNOŚCI ŁĄCZA ŚWIATŁOWODOWEGO Zadanie VI Zakład Optelektrniki Truń 00
2 I. Cel zadania Celem zadania jest zapznanie studentów z pdstawami techniki światłwdwej. II. Zagadnienia teretyczne A. Zagadnienia pdstawwe Światłwód (falwód ptyczny) służy d przesyłania fal elektrmagnetycznych w zakresie ptycznym. W każdym światłwdzie mżna wyróżnić rdzeń i płaszcz. Ze względu na budwę rzróżniamy światłwdy cylindryczne (Rys.1a), płaskie czyli planarne (Rys. 1b), paskwe (Rys. 1c) i inne. x światł z a) b) c) y 1 Rys.1. Rdzaje światłwdów. Fala rzchdzi się w kierunku si z Światł prwadzne jest w światłwdzie dzięki całkwitemu wewnętrznemu dbiciu na granicy rdzeń (współczynnik załamania ) - płaszcz (współczynnik załamania 1 i ). Tak więc czywiście: > (1) Rysunek ilustruje tę zasadę dla światłwdu symetryczneg ( = 1 = ). θ α Rys.. Prmień światła wchdzi d światłwdu pd kątem α d si ptycznej, dbija się d granicy rdzeń - płaszcz pd kątem θ d nrmalnej. Jak widać z rysunku, tylk prmienie wchdzące d światłwdu pd kątem mniejszym niż kąt akceptacji ulegają całkwitemu wewnętrznemu dbiciu na granicy rdzeń - płaszcz. Praw załamania (Snella) prwadzi d następującej zależnści pmiędzy kątami α i θ: = sin α = sin α sin(90 θ) cs θ () VI - 1
3 Warunek całkwiteg wewnętrzneg dbicia mżna zapisać w pstaci: sin θ np więc maksymalny kąt akceptacji : α max = arcsin, gdzie n r nazywa się aperturą numeryczną światłwdu.. Tak (3) B. Mdy TE i TM w światłwdzie Fala rzchdząca się w światłwdzie zależy d współrzędnej z pprzez stałą prpagacji β, dpwiadającą wektrwi falwemu dla fali płaskiej: E (x, y, z, t)= E0 (x, y) exp[ i(ωt βz)] H (x, y, z, t)= H0 (x, y) exp[ i(ωt βz)] (4a). (4b) Taka pstać rzwiązań pzwala zdefiniwać prędkść fazwą fali w światłwdzie v ef raz efektywny współczynnik załamania n ef jak: v ef = ω β, n ef = v c ef = ω c β. (5) Pdstawiając funkcje (4) d równań Maxwell'a uzyskuje się następujące równania na zesplne składwe wektrów E i H. E x = E y = i ω µ 0 ε β β E z x +ωµ 0 H z y i ω µ 0 ε β β E z y ωµ 0 H z x (6a) (6b) H x = i ω µ 0 ε β β H z x ωε E z y (6c) H y = i ω µ 0 ε β β H z y +ωε E z x (6d) E z = ωε i H y Hx x y (6e) H z = i ωµ 0 E y x Ex y (6f) Ddatkw, składwe zetwe spełniają równania falwe: x + y +(ω µ 0 ε β ) H z = 0. (6g) VI -
4 x + y +(ω µ 0 ε β ) E z = 0 (6h) Oczywiście częstść kątwa ω pwiązana jest z długścią k wektra falweg w danym śrdku zwykłą relacją: ω µ 0 ε=k 0 n = k ; k 0 = ω c = π λ (7) 0 gdzie: k 0 jest długścią wektra falweg w próżni, n współczynnikiem załamania śrdka. Należy również zauważyć, że jeżeli śrdek nie wprwadza strat ani wzmcnienia, t znaczy jest idealnie przeźrczysty, t wszystkie stałe w równaniu (7) są rzeczywiste. Aby rzwiązania równań (6g) i (6h) pisywały falę kniecznym jest, by wyrażenie w nawiasie ( ) był różne d zera, czyli β k. Innymi słwy prędkść fazwa fali w światłwdzie v ef (5), różni się d prędkści fali płaskiej tej samej częstści ω rzchdzącej się w niegranicznym dielektryku współczynniku załamania rdzenia. Wśród równań (6) występują więc niezależne równania falwe (6g) i (6h). Oznacza t, że bez względu na rdzaj światłwdu, mżna wyróżnić dwa rdzaje (mdy) fali elektrmagnetycznej prpagującej w światłwdzie. Decyduje tym rdzaj składwej pla prstpadłej d kierunku prpagacji z (Rys. 3). Oczywiście zawsze ba pla E i H są prstpadle d chwilweg kierunku prmienia, b fala elektrmagnetyczna jest falą pprzeczną. Md TE charakteryzuje się tym, że ple E jest zawsze prstpadłe d kierunku prpagacji z, a ple H zmienia kierunek przy klejnych dbiciach. Natmiast md TM charakteryzuje się tym, że ple H (magnetyczne) jest prstpadłe d z. W knsekwencji: E z = 0; H z 0 H z = 0; E z 0 dla mdu TE, dla mdu TM. (8a) (8b) TE TM E H z H E z Rys. 3. Mdy TE ( E z ) i TM ( H z ) w światłwdzie C. Mdy prwadzne w światłwdzie Mim, że w większści przypadków, zwłaszcza w telekmunikacji, używane są światłwdy cylindryczne, pis światłwdu planarneg (najprstszy matematycznie) pzwala pznać wiele wspólnych własnści wszystkich światłwdów. VI - 3
5 Rzpatruje się światłwód symetryczny, rdzeniu grubści d, rzciągającym się d nieskńcznści w kierunku +y i -y (Rys. 4). x z np nr d d y np Rys. 4. Mdel światłwdu planarneg. W takim światłwdzie żadna wartść współrzędnej y nie jest wyróżnina, inaczej mówiąc żadna wielkść pisująca ple nie mże zależeć d y. Oznacza t, że w równaniach (6) mżna płżyć wszędzie: y = 0 (9) Rzpatrzmy md TE. Wówczas: z (6a), na pdstawie (8a) i (9): z (6b), na pdstawie (9) i (6f): E x = 0 E y 0; E y x + [ω µ 0 ε β ] E y = 0 (10a) (10b) przepisując (8a): E z = 0 (10c) z (6c), uwzględniając (9) i wstawiając (6f) i (10b): H x 0; H x = β ωµ 0 E y (10d) z (6d), na pdstawie (8a) i (9): H y = 0 (10e) ωµ i E y 0 x z (6f), na pdstawie (9): H z 0; H z = (10f) Równanie (10b) nsi nazwę równania Helmhltza. Należy zauważyć, że pzstałe niezerwe składwe pól E i H występujące w (10) mżna wyznaczyć z E y. Tak więc wystarczy rzwiązać równanie (10b), aby wyznaczyć wszystkie składwe wektrów pla elektrmagnetyczneg. Rzwiążmy równanie (10b) dla światłwdu symetryczneg (Rys. 4), charakteryzująceg się skkwą zmianą współczynnika załamania na granicy rdzeń - płaszcz: VI - 4
6 n = ; x d ; x > d (11) Uwzględniając (7), mżna więc napisać równanie (10b) dla bu śrdków: dla rdzenia: E y x + k 0 β E y = 0; x d (1a) dla płaszcza: E y x + k 0 β E y = 0; x > d (1b) Celem dalszych bliczeń jest wyznaczenie β. Pszukuje się rzwiązań prpagujących (scylujących) w rdzeniu i równcześnie nie prpagujących (gasnących) w płaszczu. Inaczej mówiąc równanie (1a) musi być równaniem scylatra, a równanie (1b) dpwiadać przypadkwi braku scylacji. Jest t równznaczne z żądaniem, aby współczynnik w równaniu (10a) był ddatni, a w równaniu (10b) ujemny (prównaj równanie scylatra.. harmniczneg x + ω x = 0 ). Tak więc wprwadzając rzeczywiste stałe κ i γ warunki na istnienie i brak scylacji w rzwiązaniach równań (1a) i (1b) mżna dpwiedni zapisać w pstaci: raz k 0 β =κ > 0 k 0 β = γ < 0 (13a) (13b) Równcześnie trzymuje się: k 0 >β > k 0 alb na pdstawie (5) i (7) > n ef >. (14) Wiadm z elektrdynamiki gólnej, że na granicy śrdków z nieciągłym współczynnikiem załamania składwe styczne natężeń pól elektryczneg i magnetyczneg (E i H) muszą być ciągłe. W mawianym przypadku (Rys. 3 i Rys. 4 raz równania (10)) są t składwe w kierunku y i z. Składwe tżsamściw równe 0 są ciągłe autmatycznie. Pzstają składwe E y i H z. Na pdstawie (10d) znacza t ciągłść E y raz jej pierwszej pchdnej p x. Tak więc ple elektryczne w rdzeniu (4a) mżna w gólnści zapisać w pstaci: E (x, y, z, t)=y [A1 cs(κ x)+a sin(κ x)]exp[ i(ωt βz)] x d, (15) natmiast ple w płaszczu, p uwzględnieniu warunku ciągłści składwej E y : E (x, y, z, t)=y A 1 cs(κ d )+A x x sin(κ d ) exp γ x d exp[ i(ωt β z)] x > d (16) VI - 5
7 Należy zauważyć, że: w przypadku: A = 0 E (x, y, z, t)= E ( x, y, z, t) - md parzysty w przypadku: A 1 = 0 E (x, y, z, t)= E ( x, y, z, t) - md nieparzysty. Wymóg ciągłści pchdnej prwadzi d ddatkweg warunku, wiążąceg κ i γ: dla mdów parzystych: A 1 κ sin(κ d )=A 1cs(κ d )( κ) alb: κ d tg κd =γd dla mdów nieparzystych: A κ cs(κ d )=A alb: sin(κ d )( κ) κd ctg κd =γd (17a) (17b) Ddatkw bliczmy: (18) κd + γ d = d k 0 β +β k 0 = d [ n p ] k 0 = cnst Warunek (18) wraz z dpwiednim warunkiem (17) stanwią układ równań, pzwalający wyznaczyć κ i γ. Niestety, układ ten nie daje się rzwiązać analitycznie. Interesujących infrmacji dstarczyć mże rzwiązanie graficzne (Rys. 5). W tym celu wykreśla się funkcje (17a) i (17b) we współrzędnych (κd/) i (γd/). W tych współrzędnych równanie (18) pisuje ćwiartkę kręgu (tylk współrzędne ddatnie mają sens fizyczny). Przecięcia dpwiednich krzywych wyznaczają dzwlne wartści κ i γ (znaczne "" na Rys. 5) γ d 1.5 π 1.0 π (κd/) tg(κd/) -(κd/) ctg(κd/) (κd/) tg(κd/) -(κd/) ctg(κd/) 0.5 π 0.0 π 0.0 π 0.5 π 1.0 π 1.5 π κ d Rys. 5 Przykład rzwiązania graficzneg równania światłwdu, prpagują 4 mdy, mdy parzyste, mdy nieparzyste. VI - 6
8 Wniski: 1. Ple w światłwdzie daje się pisać za pmcą 3 parametrów materiałwych:,, d.. Tylk pewne kreślne wartści parametrów κ i γ są dzwlne. Rzwiązania te nazywamy mdami światłwdu. Znając κ mżna z równania (13a) wyznaczyć β= n r k 0 κ raz v ef. Różne mdy mają więc różne efektywne współczynniki załamania i prędkści rzchdzenia się. 3. W przykładzie z Rys. 5 rzchdzą się dwa mdy parzyste i dwa nieparzyste. Jak widać z rysunku, zmniejszenie d na przykład dwukrtnie spwduje, że ćwiartka kręgu będzie miała prmień płwę mniejszy i dzwlne będą tylk mdy. Zmniejszając d redukujemy (dcinamy) ilść mdów. 4. Jeżeli d jest dstatecznie małe, t światłwdzie rzchdzi się tylk jeden md: md parzysty rzędu 0. Światłwód taki nazywamy jednmdwym. Nie mżna dciąć mdu zerweg TE. 5. Nierównść, która musi być spełnina, aby rzchdził się md daneg rzędu m nazywamy warunkiem dcięcia dla teg mdu: d k 0 > m π. D. Zagadnienia ddatkwe Na pdstawie pdanej pniżej literatury należy panwać pdstawy pniższych zagadnień: 1. Półprzewdnikwe emitery światła ( DEL i lasery). Ftdetektry półprzewdnikwe (ftdidy PIN i lawinwe) III. Literatura 1. A. Smliński "Światłwdy raz ich zastswanie". A. Pawlaczyk, "Elementy i układy ptelektrniczne" 3. B. Crsigiani, G. de Marchis, A. Tadeusiak "Światłwdy w telekmunikacji" 4. B. Ziętek "Światłwdy" VI - 7
9 IV. Aparatura Aparatura d wyknania zadania : A. Łącze ptelektrniczne zamknięte 1. Laser półprzewdnikwy Sharp LT0MC z zasilaczem. Sprzęg światłwdwy z łączem FC/PC 3. Linia światłwdwa długści 880 m 4. Krótkie dcinki światłwdu z kńcówkami typu FC/PC 5. Magnetfn 6. Generatr impulsów PGP-7 7. Ftdida lawinwa BPYP 5F z zasilaczem 8. Oscylskp C Wzmacniacz akustyczny z głśnikiem B. Łącze ptelektrniczne twarte 1. Laser półprzewdnikwy Sharp LT0MC z lunetką i zasilaczem. Magnetfn 3. Ftdida BPYP Wzmacniacz akustyczny z głśnikiem 5. Nktwizr V. Pmiary i pracwanie wyników A. Łącze ptelektrniczne zamknięte 1. Transmisja sygnału akustyczneg Nadajnik magnetfn światłwód Odbirnik głśnik Md Wyj wzmacniacz głwica lasera BPYP 5F zasilacz Rys 6. Łącze ptelektrniczne zamknięte Zestawić układ według Rys. 6. Jak napięcia mdulująceg użyć sygnału z magnetfnu i uzyskać transmisję sygnału. W zasilaczu lasera prąd pdkładu ustawić pnad prgiem lasera tak, aby uzyskać jak najmniejsze zniekształcenia sygnału. D wstępnej regulacji mżna użyć generatra sygnału sinusidalneg i scylskpu zamiast magnetfnu i wzmacniacza. VI - 8
10 . Wyznaczenie prędkści światła w światłwdzie Nadajnik Odbirnik generatr PGP-7 scylskp C1-175 światłwód A B Md Wyj zas. głwica lasera BPYP 5F Rys. 7 Układ pmiarwy d badania łącza światłwdweg 1. Zestawić układ według Rys. 7.. Generatr PGP-7 ustawić na impulsy pjedyncze, f=10 khz, τ=0.3µs, amplituda 1 V. 3. Prąd pdkładu lasera ustawić na "0", aby w przerwach pmiędzy impulsami laser nie generwał prmieniwania. 4. Głwice lasera pdłączyć bezpśredni d ftdidy. 5. Odczytać z scylskpu względne późnienie sygnałów A i B wprwadzane przez aparaturę 6. Wstawić w tr światłwdwy linię 880 m dczytać późnienie impulsów zabserwwać pszerzenie impulsów 7. Wyznaczyć prędkść fazwą v ef światła w światłwdzie, efektywny współczynnik załamania n ef raz stałą prpagacji β. VI - 9
11 B. Łącze ptelektrniczne twarte Nadajnik magnetfn Odbirnik głśnik Md Wyj wzmacniacz głwica lasera k 0 m Rys 8. Łącze ptelektrniczne twarte Zestawić układ według Rys. 8. Jak napięcia mdulująceg użyć sygnału z magnetfnu. Stały prąd pdkładu zasilacza lasera ustawić na wartść z zadania A1. Z pmcą nktwizra wycelwać wiązką laserwą w detektr i uzyskać transmisję sygnału. VI - 10
Przekaz optyczny. Mikołaj Leszczuk. Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Katedra Telekomunikacji 2010-10-24
 Przekaz ptyczny Mikłaj Leszczuk Wydział Elektrtechniki, Autmatyki, Infrmatyki i Elektrniki Katedra Telekmunikacji 2010-10-24 Falwód służący d przesyłania prmieniwania świetlneg ŚWIATŁOWÓD Ewlucja światłwdów
Przekaz ptyczny Mikłaj Leszczuk Wydział Elektrtechniki, Autmatyki, Infrmatyki i Elektrniki Katedra Telekmunikacji 2010-10-24 Falwód służący d przesyłania prmieniwania świetlneg ŚWIATŁOWÓD Ewlucja światłwdów
ZESTAW 1. A) 2 B) 3 C) 5 D) 7
 ZESTAW Zadanie Punkty A = (,) i B = (, ) są klejnymi wierzchłkami kwadratu. Obwód teg kwadratu jest równy A) 4 6 B) 6 C) 4 4 D) 4 6 Zadanie Zbirem rzwiązań nierównści x + 5 > jest zbiór A) ( 7, ) B) (,
ZESTAW Zadanie Punkty A = (,) i B = (, ) są klejnymi wierzchłkami kwadratu. Obwód teg kwadratu jest równy A) 4 6 B) 6 C) 4 4 D) 4 6 Zadanie Zbirem rzwiązań nierównści x + 5 > jest zbiór A) ( 7, ) B) (,
( ) σ v. Adam Bodnar: Wytrzymałość Materiałów. Analiza płaskiego stanu naprężenia.
 Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
PLAN WYNIKOWY ROZKŁADU MATERIAŁU Z FIZYKI DLA KLASY III MODUŁ 4 Dział: X,XI - Fale elektromagnetyczne, optyka, elementy fizyki atomu i kosmologii.
 Knteksty 1. Fale elektrmagnetyczne w telekmunikacji. 2.Światł i jeg właściwści. - c t jest fala elektrmagnetyczna - jakie są rdzaje fal - elektrmagnetycznych - jakie jest zastswanie fal elektrmagnetycznych
Knteksty 1. Fale elektrmagnetyczne w telekmunikacji. 2.Światł i jeg właściwści. - c t jest fala elektrmagnetyczna - jakie są rdzaje fal - elektrmagnetycznych - jakie jest zastswanie fal elektrmagnetycznych
R o z d z i a ł 6 RUCH DRGAJĄCY I FALOWY
 R z d z i a ł 6 RUCH DRGAJĄCY I FALOWY 6.1. Ruch drgający harmniczny Ruch w przyrdzie jest zjawiskiem pwszechnym. Wszystkie bserwwane w przyrdzie ruchy dzielimy na cztery klasy: ruch pstępwy ruch brtwy
R z d z i a ł 6 RUCH DRGAJĄCY I FALOWY 6.1. Ruch drgający harmniczny Ruch w przyrdzie jest zjawiskiem pwszechnym. Wszystkie bserwwane w przyrdzie ruchy dzielimy na cztery klasy: ruch pstępwy ruch brtwy
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 6, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
FUNKCJA KWADRATOWA. 2. Rozwiąż nierówności: na przedziale x < 2; 3. Wyznacz wartość najmniejszą i największą funkcji f ( x)
 FUNKCJA KWADRATOWA. Rzwiąż równanie: a) 0 +,5 0 b) ( + )( ) 0. Rzwiąż nierównści: < ( )( ) > 0 a) b). Wyznacz wartść najmniejszą i największą funkcji na przedziale < ; 5 >. Przekształć z pstaci gólnej
FUNKCJA KWADRATOWA. Rzwiąż równanie: a) 0 +,5 0 b) ( + )( ) 0. Rzwiąż nierównści: < ( )( ) > 0 a) b). Wyznacz wartść najmniejszą i największą funkcji na przedziale < ; 5 >. Przekształć z pstaci gólnej
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
KATEDRA TELEKOMUNIKACJI I FOTONIKI
 ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
PSO matematyka I gimnazjum Szczegółowe wymagania edukacyjne na poszczególne oceny
 PSO matematyka I gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOM WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca spsób zakrąglania liczb klejnść wyknywania działań pjęcie liczb
PSO matematyka I gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOM WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca spsób zakrąglania liczb klejnść wyknywania działań pjęcie liczb
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
III. Opis falowy. /~bezet
 Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Podstawowe układy pracy tranzystora MOS
 A B O A T O I U M P O D S T A W E E K T O N I K I I M E T O O G I I Pdstawwe układy pracy tranzystra MOS Ćwiczenie pracwał Bgdan Pankiewicz 4B. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści trzech
A B O A T O I U M P O D S T A W E E K T O N I K I I M E T O O G I I Pdstawwe układy pracy tranzystra MOS Ćwiczenie pracwał Bgdan Pankiewicz 4B. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści trzech
nie wyraŝa zgody na inne wykorzystywanie wprowadzenia niŝ podane w jego przeznaczeniu występujące wybranym punkcie przekroju normalnego do osi z
 Wprwadzenie nr 4* d ćwiczeń z przedmitu Wytrzymałść materiałów przeznaczne dla studentów II rku studiów dziennych I stpnia w kierunku Energetyka na wydz. Energetyki i Paliw, w semestrze zimwym 0/03. Zakres
Wprwadzenie nr 4* d ćwiczeń z przedmitu Wytrzymałść materiałów przeznaczne dla studentów II rku studiów dziennych I stpnia w kierunku Energetyka na wydz. Energetyki i Paliw, w semestrze zimwym 0/03. Zakres
CZAS ZDERZENIA KUL SPRAWDZENIE WZORU HERTZA
 Ćwiczenie Nr CZAS ZDRZNIA KUL SPRAWDZNI WZORU HRTZA Literatura: Opracwanie d ćwiczenia Nr, czytelnia FiM LDLandau, MLifszic Kurs fizyki teretycznej, tm 7, Teria sprężystści, 9 (dstępna w biblitece FiM,
Ćwiczenie Nr CZAS ZDRZNIA KUL SPRAWDZNI WZORU HRTZA Literatura: Opracwanie d ćwiczenia Nr, czytelnia FiM LDLandau, MLifszic Kurs fizyki teretycznej, tm 7, Teria sprężystści, 9 (dstępna w biblitece FiM,
M. Guminiak - Analiza płyt cienkich metodą elementów brzegowych Moment zginający w punkcie B [M xb /pl ]
![M. Guminiak - Analiza płyt cienkich metodą elementów brzegowych Moment zginający w punkcie B [M xb /pl ] M. Guminiak - Analiza płyt cienkich metodą elementów brzegowych Moment zginający w punkcie B [M xb /pl ]](/thumbs/97/132537319.jpg) M. Guminiak Analiza płyt cienkich metdą elementów brzegwych... 44 600 500 400 300 200 100 Mment zginający w punkcie B [M xb /pl 2 10 4 ] 700 600 500 400 300 200 100 Mment zginający w punkcie B [M yb /pl
M. Guminiak Analiza płyt cienkich metdą elementów brzegwych... 44 600 500 400 300 200 100 Mment zginający w punkcie B [M xb /pl 2 10 4 ] 700 600 500 400 300 200 100 Mment zginający w punkcie B [M yb /pl
PSO matematyka III gimnazjum. Szczegółowe wymagania edukacyjne na poszczególne oceny
 PSO matematyka III gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOMY WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca DZIAŁ 1. LICZBY I WYRAŻENIA ALGEBRAICZNE pjęcie liczby naturalnej,
PSO matematyka III gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOMY WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca DZIAŁ 1. LICZBY I WYRAŻENIA ALGEBRAICZNE pjęcie liczby naturalnej,
Laboratorium techniki światłowodowej. Ćwiczenie 2. Badanie apertury numerycznej światłowodów
 Laboratorium techniki światłowodowej Ćwiczenie 2. Badanie apertury numerycznej światłowodów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie Światłowody
Laboratorium techniki światłowodowej Ćwiczenie 2. Badanie apertury numerycznej światłowodów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie Światłowody
T R Y G O N O M E T R I A
 T R Y G O N O M E T R I A Lekcja 8-9 Temat: Pwtórzenie trójkąty prstkątne. Str. 56-57. Teria Twierdzenie Pitagrasa i dwrtne Suma kątów w trójkącie Wyskść Obwód i ple Zad.,,,, 5, 6 str. 56 Zad. 7, 8, 9,
T R Y G O N O M E T R I A Lekcja 8-9 Temat: Pwtórzenie trójkąty prstkątne. Str. 56-57. Teria Twierdzenie Pitagrasa i dwrtne Suma kątów w trójkącie Wyskść Obwód i ple Zad.,,,, 5, 6 str. 56 Zad. 7, 8, 9,
elementami techniki impulsowej. II. Przyrządy: linia przesyłowa, opornik dekadowy, generator impulsów, generator sygnałowy,
 BADANIE LINII PRZESYŁOWEJ I. Cel ćwiczenia: zapznanie ze zjawiskiem dbicia, zjawiskiem fal stjących i najprstszymi elementami techniki impulswej. II. Przyrządy: linia przesyłwa, prnik dekadwy, generatr
BADANIE LINII PRZESYŁOWEJ I. Cel ćwiczenia: zapznanie ze zjawiskiem dbicia, zjawiskiem fal stjących i najprstszymi elementami techniki impulswej. II. Przyrządy: linia przesyłwa, prnik dekadwy, generatr
MAJ LUBELSKA PRÓBA PRZED MATURĄ 2013 klasa druga. MATEMATYKA - poziom podstawowy. Czas pracy: 170 minut. Instrukcja dla zdającego
 LUBELSKA PRÓBA PRZED MATURĄ 03 klasa druga MATEMATYKA - pzim pdstawwy MAJ 03 Instrukcja dla zdająceg. Sprawdź, czy arkusz zawiera 4 strn.. Rzwiązania zadań i dpwiedzi zamieść w miejscu na t przeznacznym.
LUBELSKA PRÓBA PRZED MATURĄ 03 klasa druga MATEMATYKA - pzim pdstawwy MAJ 03 Instrukcja dla zdająceg. Sprawdź, czy arkusz zawiera 4 strn.. Rzwiązania zadań i dpwiedzi zamieść w miejscu na t przeznacznym.
CZERWIEC MATEMATYKA - poziom podstawowy. Czas pracy: 170 minut. Instrukcja dla zdającego
 MATEMATYKA - pzim pdstawwy CZERWIEC 014 Instrukcja dla zdająceg 1. Sprawdź, czy arkusz zawiera 14 strn.. Rzwiązania zadań i dpwiedzi zamieść w miejscu na t przeznacznym.. W zadaniach d 1 d są pdane 4 dpwiedzi:
MATEMATYKA - pzim pdstawwy CZERWIEC 014 Instrukcja dla zdająceg 1. Sprawdź, czy arkusz zawiera 14 strn.. Rzwiązania zadań i dpwiedzi zamieść w miejscu na t przeznacznym.. W zadaniach d 1 d są pdane 4 dpwiedzi:
Laboratorium elektroniki i miernictwa
 Ełk 24-03-2007 Wyższa Szkła Finansów i Zarządzania w Białymstku Filia w Ełku Wydział Nauk Technicznych Kierunek : Infrmatyka Ćwiczenie Nr 3 Labratrium elektrniki i miernictwa Temat: Badanie pdstawwych
Ełk 24-03-2007 Wyższa Szkła Finansów i Zarządzania w Białymstku Filia w Ełku Wydział Nauk Technicznych Kierunek : Infrmatyka Ćwiczenie Nr 3 Labratrium elektrniki i miernictwa Temat: Badanie pdstawwych
!Twoje imię i nazwisko... Numer Twojego Gimnazjum.. Tę tabelę wypełnia Komisja sprawdzająca pracę. Nazwisko Twojego nauczyciela...
 XVIII KONKURS MTEMTYCZNY im. ks. dra F. Jakóbczyka 15 marca 01 r. wersja!twje imię i nazwisk... Numer Twjeg Gimnazjum.. Tę tabelę wypełnia Kmisja sprawdzająca pracę. Nazwisk Twjeg nauczyciela... Nr zad.
XVIII KONKURS MTEMTYCZNY im. ks. dra F. Jakóbczyka 15 marca 01 r. wersja!twje imię i nazwisk... Numer Twjeg Gimnazjum.. Tę tabelę wypełnia Kmisja sprawdzająca pracę. Nazwisk Twjeg nauczyciela... Nr zad.
Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu
 Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu Elektrtechnika i Elektrnika Materiały Dydaktyczne Mc w bwdach prądu zmienneg. Opracwał: mgr inż. Marcin Jabłński mgr inż. Marcin Jabłński
Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu Elektrtechnika i Elektrnika Materiały Dydaktyczne Mc w bwdach prądu zmienneg. Opracwał: mgr inż. Marcin Jabłński mgr inż. Marcin Jabłński
Adres strony internetowej, na której Zamawiający udostępnia Specyfikację Istotnych Warunków Zamówienia: www.wco.pl
 Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.wc.pl Pznań: Świadczenie usług transmisji danych pmiędzy filią Wielkplskieg Centrum Onklgii w Kaliszu
Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.wc.pl Pznań: Świadczenie usług transmisji danych pmiędzy filią Wielkplskieg Centrum Onklgii w Kaliszu
Kryteria przyznawania ocen z matematyki uczniom klas III Publicznego Gimnazjum nr 1 w Strzelcach Opolskich
 Kryteria przyznawania cen z matematyki ucznim klas III Publiczneg Gimnazjum nr 1 w Strzelcach Oplskich Na cenę dpuszczającą uczeń: zna pjęcie ntacji wykładniczej zna spsób zakrąglania liczb rzumie ptrzebę
Kryteria przyznawania cen z matematyki ucznim klas III Publiczneg Gimnazjum nr 1 w Strzelcach Oplskich Na cenę dpuszczającą uczeń: zna pjęcie ntacji wykładniczej zna spsób zakrąglania liczb rzumie ptrzebę
Sekcja B. Okoliczności powodujące konieczność złożenia deklaracji.
 III. Deklaracja DJ Sekcja A. Adresat i miejsce składania deklaracji. Uwaga! Ple uzupełnine autmatycznie. Sekcja B. Oklicznści pwdujące kniecznść złżenia deklaracji. Wsekcji B, należy w jednym z dstępnych
III. Deklaracja DJ Sekcja A. Adresat i miejsce składania deklaracji. Uwaga! Ple uzupełnine autmatycznie. Sekcja B. Oklicznści pwdujące kniecznść złżenia deklaracji. Wsekcji B, należy w jednym z dstępnych
ZJAWISKO TERMOEMISJI ELEKTRONÓW
 ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
Projektowanie generatorów sinusoidalnych z użyciem wzmacniaczy operacyjnych
 Instytut Autmatyki Prjektwanie generatrów sinusidalnych z użyciem wzmacniaczy peracyjnych. Generatr z mstkiem Wiena. ysunek przedstawia układ generatra sinusidalneg z mstkiem Wiena. Jeżeli przerwiemy sprzężenie
Instytut Autmatyki Prjektwanie generatrów sinusidalnych z użyciem wzmacniaczy peracyjnych. Generatr z mstkiem Wiena. ysunek przedstawia układ generatra sinusidalneg z mstkiem Wiena. Jeżeli przerwiemy sprzężenie
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systemy ciągłe budwa nieliniwych mdeli fenmenlgicznych z praw zachwania.
Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systemy ciągłe budwa nieliniwych mdeli fenmenlgicznych z praw zachwania.
POLITECHNIKA POZNAŃSKA ZAKŁAD CHEMII FIZYCZNEJ ĆWICZENIA PRACOWNI CHEMII FIZYCZNEJ. ( i) E( 0) str. 1 WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA
 WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA Różnica pmiędzy wartścią ptencjału elektrdy mierzneg przy przepływie prądu E(i) a wartścią ptencjału spczynkweg E(0), nsi nazwę nadptencjału (nadnapięcia), η.
WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA Różnica pmiędzy wartścią ptencjału elektrdy mierzneg przy przepływie prądu E(i) a wartścią ptencjału spczynkweg E(0), nsi nazwę nadptencjału (nadnapięcia), η.
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Uniwersytet Wrocławski Wydział Matematyki i Informatyki Instytut Matematyczny specjalność: matematyka nauczycielska.
 Uniwersytet Wrcławski Wydział Matematyki i Infrmatyki Instytut Matematyczny specjalnść: matematyka nauczycielska Mateusz Suwara PARKIETAŻE PLATOŃSKIE I SZACHOWNICE ARCHIMEDESOWSKIE W GEOMETRII HIPERBOLICZNEJ
Uniwersytet Wrcławski Wydział Matematyki i Infrmatyki Instytut Matematyczny specjalnść: matematyka nauczycielska Mateusz Suwara PARKIETAŻE PLATOŃSKIE I SZACHOWNICE ARCHIMEDESOWSKIE W GEOMETRII HIPERBOLICZNEJ
Statystyka - wprowadzenie
 Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią
Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią
M. Guminiak - Analiza płyt cienkich metodą elementów brzegowych... 44
 M. Guminiak Analiza płyt cienkich metdą elementów brzegwych... 44 Mment zginający w śrdku [M x /pa 2 10 4 ] Mment zginający w śrdku [M y /pa 2 10 4 ] 600 500 400 300 200 100 0 0 2,5 5 7,5 10 12,5 15 17,5
M. Guminiak Analiza płyt cienkich metdą elementów brzegwych... 44 Mment zginający w śrdku [M x /pa 2 10 4 ] Mment zginający w śrdku [M y /pa 2 10 4 ] 600 500 400 300 200 100 0 0 2,5 5 7,5 10 12,5 15 17,5
gdzie A = amplituda ω = częstość k = liczba falowa
 x(t, z) A cs(ωt kz) gdzie A amplituda ω częstść k licza falwa Rys. 3... Fala iegnąca - dkształcenie śrdka w zaleŝnści d dległści i czasu. (t,z) x A cs(ωt kz) (3.2.) (t,z) A cs(ωt k(-z)) + x 2 x(t, z) (3.2.2)
x(t, z) A cs(ωt kz) gdzie A amplituda ω częstść k licza falwa Rys. 3... Fala iegnąca - dkształcenie śrdka w zaleŝnści d dległści i czasu. (t,z) x A cs(ωt kz) (3.2.) (t,z) A cs(ωt k(-z)) + x 2 x(t, z) (3.2.2)
Drgania własne ramy wersja komputerowa, Wpływ dodatkowej podpory ( sprężyny ) na częstości drgań własnych i ich postacie
 Drgania własne ramy wersja kmputerwa, Wpływ ddatkwej pdpry ( sprężyny ) na częstści drgań własnych i ich pstacie Pniżej przedstawin rzwiązania dwóch układów ramwych takiej samej gemetrii i rzkładzie masy,
Drgania własne ramy wersja kmputerwa, Wpływ ddatkwej pdpry ( sprężyny ) na częstści drgań własnych i ich pstacie Pniżej przedstawin rzwiązania dwóch układów ramwych takiej samej gemetrii i rzkładzie masy,
6. POWIERZCHNIOWE MOMENTY BEZWŁADNOŚCI
 6. POWERZCHNOWE MOMENTY BEZWŁADNOŚC Zadanie 6. Dla figury przedstawinej na rysunku 6.. wyznaczyć płżenie głównh centralnh si bezwładnści i kreślić względem nich główne centralne mmenty bezwładnści. Rys.6..
6. POWERZCHNOWE MOMENTY BEZWŁADNOŚC Zadanie 6. Dla figury przedstawinej na rysunku 6.. wyznaczyć płżenie głównh centralnh si bezwładnści i kreślić względem nich główne centralne mmenty bezwładnści. Rys.6..
Research & Development Ultrasonic Technology / Fingerprint recognition DATA SHEETS OPKUD.
 Research & Develpment Ultrasnic Technlgy / Fingerprint recgnitin DATA SHEETS & OPKUD http://www.ptel.pl email: ptel@ptel.pl Przedsiębirstw Badawcz-Prdukcyjne OPTEL Spółka z.. ul. Otwarta 10a PL-50-212
Research & Develpment Ultrasnic Technlgy / Fingerprint recgnitin DATA SHEETS & OPKUD http://www.ptel.pl email: ptel@ptel.pl Przedsiębirstw Badawcz-Prdukcyjne OPTEL Spółka z.. ul. Otwarta 10a PL-50-212
Wykład XVIII. SZCZEGÓLNE KONFIGURACJE OBWODÓW TRÓJFAZOWYCH. POMIARY MOCY W OBWODACH TRÓJFAZOWYCH I 1 U 12 I 2 U 23 3 U U Z I = ; I 12 I 23
 7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
Zajęcia wyrównawcze z fizyki -Zestaw 3 dr M.Gzik-Szumiata
 Prjekt Inżynier mehanik zawód z przyszłśią współfinanswany ze śrdków Unii Eurpejskiej w ramah Eurpejskieg Funduszu Spłezneg Zajęia wyrównawze z fizyki -Zestaw 3 dr M.Gzik-Szumiata Kinematyka,z.. Ruhy dwuwymiarwe:
Prjekt Inżynier mehanik zawód z przyszłśią współfinanswany ze śrdków Unii Eurpejskiej w ramah Eurpejskieg Funduszu Spłezneg Zajęia wyrównawze z fizyki -Zestaw 3 dr M.Gzik-Szumiata Kinematyka,z.. Ruhy dwuwymiarwe:
stworzyliśmy najlepsze rozwiązania do projektowania organizacji ruchu Dołącz do naszych zadowolonych użytkowników!
 Wrcław, 29.08.2012 gacad.pl stwrzyliśmy najlepsze rzwiązania d prjektwania rganizacji ruchu Dłącz d naszych zadwlnych użytkwników! GA Sygnalizacja - t najlepszy Plski prgram d prjektwania raz zarządzania
Wrcław, 29.08.2012 gacad.pl stwrzyliśmy najlepsze rzwiązania d prjektwania rganizacji ruchu Dłącz d naszych zadwlnych użytkwników! GA Sygnalizacja - t najlepszy Plski prgram d prjektwania raz zarządzania
ZS LINA_ LINB_ LINC_. Rys. 1. Schemat rozpatrywanej sieci. S1 j
 PRZYKŁAD 1.1 Opracwać mdel fragmentu sieci trójfazwej 110kV z linią reprezentwaną za pmcą dwóch dcinków RL z wzajemnym sprzężeniem (mdel 51). chemat sieci jest pkazany na rys. 1. Zbadać przebieg prądów
PRZYKŁAD 1.1 Opracwać mdel fragmentu sieci trójfazwej 110kV z linią reprezentwaną za pmcą dwóch dcinków RL z wzajemnym sprzężeniem (mdel 51). chemat sieci jest pkazany na rys. 1. Zbadać przebieg prądów
potrafi przybliżać liczby (np. ) K
 Anna Włszyn Klasa 1 LO wymagania na egzamin pprawkwy Uczeń: I. Liczby rzeczywiste stsuje cechy pdzielnści liczb przez: K-P zna pjęcia: K cyfry, liczby parzystej i nieparzystej, liczby pierwszej i złżnej,
Anna Włszyn Klasa 1 LO wymagania na egzamin pprawkwy Uczeń: I. Liczby rzeczywiste stsuje cechy pdzielnści liczb przez: K-P zna pjęcia: K cyfry, liczby parzystej i nieparzystej, liczby pierwszej i złżnej,
cz. 1. dr inż. Zbigniew Szklarski
 Wykład 1: lektrstatyka cz. 1. dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Kwantyzacja ładunku Każdy elektrn ma masę m e ładunek -e i Każdy prtn ma masę m p ładunek
Wykład 1: lektrstatyka cz. 1. dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Kwantyzacja ładunku Każdy elektrn ma masę m e ładunek -e i Każdy prtn ma masę m p ładunek
Droga, prędkość, czas, przyspieszenie
 Drga, prędkść, czas, przyspieszenie Prędkść i przyspieszenie fart g akselerasjn Prędkść (fart) kreśla jak szybk dany biekt przemieszcza się w kreślnym czasie. Wybraźmy sbie dla przykładu dwa samchdy ścigające
Drga, prędkść, czas, przyspieszenie Prędkść i przyspieszenie fart g akselerasjn Prędkść (fart) kreśla jak szybk dany biekt przemieszcza się w kreślnym czasie. Wybraźmy sbie dla przykładu dwa samchdy ścigające
Przykład 2.1. Wyznaczanie prędkości i przyśpieszenia w ruchu bryły
 Przykłd 1 Wyzncznie prędkści i przyśpieszeni w ruchu bryły Stżek kącie rzwrci twrzących i pdstwie, której prmień wynsi tczy się bez pślizgu p płszczyźnie Wektr prędkści śrdk pdstwy m stłą długść równą
Przykłd 1 Wyzncznie prędkści i przyśpieszeni w ruchu bryły Stżek kącie rzwrci twrzących i pdstwie, której prmień wynsi tczy się bez pślizgu p płszczyźnie Wektr prędkści śrdk pdstwy m stłą długść równą
Wykłady z Hydrauliki- dr inż. Paweł Zawadzki, KIWIS WYKŁAD 8
 WYKŁAD 8 8. RUCH WÓD GRUNTOWYCH 8.1. Właściwści gruntu, praw Darcy Ruch wód gruntwych w śrdku prwatym nazywamy filtracją. D śrdków prwatych zaliczamy grunt, skały, betn itp. Wda zawarta w gruncie występuje
WYKŁAD 8 8. RUCH WÓD GRUNTOWYCH 8.1. Właściwści gruntu, praw Darcy Ruch wód gruntwych w śrdku prwatym nazywamy filtracją. D śrdków prwatych zaliczamy grunt, skały, betn itp. Wda zawarta w gruncie występuje
DRGANIA OSCYLATOR HARMONICZNY
 DRGANIA OSCYLATOR HARMONICZNY wyklad8 011/01, zima 1 Własnści sprężyste ciał stałych naprężenie rzciągające naprężenie ścinające naprężenie bjętściwe Względne dkształcenie ciała zależy d naprężenia naprężenie
DRGANIA OSCYLATOR HARMONICZNY wyklad8 011/01, zima 1 Własnści sprężyste ciał stałych naprężenie rzciągające naprężenie ścinające naprężenie bjętściwe Względne dkształcenie ciała zależy d naprężenia naprężenie
Operatory odległości (część 2) obliczanie map kosztów
 Operatry dległści (część 2) bliczanie map ksztów Celem zajęć jest zapznanie się ze spsbem twrzenia mapy ksztów raz wyznaczeni mapy czasu pdróży d centrum miasta. Wykrzystane t zstanie d rzwinięcia analizy
Operatry dległści (część 2) bliczanie map ksztów Celem zajęć jest zapznanie się ze spsbem twrzenia mapy ksztów raz wyznaczeni mapy czasu pdróży d centrum miasta. Wykrzystane t zstanie d rzwinięcia analizy
DOKUMENTACJA WYPEŁNIANIA DEKLARACJI ELEKTRONICZNYCH ONLINE
 DOKUMENTACJA WYPEŁNIANIA DEKLARACJI ELEKTRONICZNYCH ONLINE Deklaracje elektrniczne nline są dstępne pd adresem internetwym https://deklaracje.mp.krakw.pl Deklaracje pwinny być wypełniane za pmcą przeglądarki
DOKUMENTACJA WYPEŁNIANIA DEKLARACJI ELEKTRONICZNYCH ONLINE Deklaracje elektrniczne nline są dstępne pd adresem internetwym https://deklaracje.mp.krakw.pl Deklaracje pwinny być wypełniane za pmcą przeglądarki
LAMP LED 6 x REBEL IP 68
 PX 3 LAMP LED x REBEL IP 8 INSTRUKCJA OBSŁUGI R SPIS TREŚCI. Opis gólny.... Warunki bezpieczeństwa... 3. Infrmacje na temat wersji... 3 4. Opis mdelu... 4 5. Schemat pdłączenia... 5. Wymiary... 7 7. Dane
PX 3 LAMP LED x REBEL IP 8 INSTRUKCJA OBSŁUGI R SPIS TREŚCI. Opis gólny.... Warunki bezpieczeństwa... 3. Infrmacje na temat wersji... 3 4. Opis mdelu... 4 5. Schemat pdłączenia... 5. Wymiary... 7 7. Dane
Instrukcja procesowa. DocuSafe Dokument. Wniosek o przekwalifikowanie ŚT na wyposażenie. Data dokumentu 04-11-2014. COM-PAN System Sp. z o.o.
 Instrukcja prceswa DcuSafe Dkument Wnisek przekwalifikwanie ŚT na wypsażenie Data dkumentu 04-11-2014 Przygtwany dla Akademia Mrska w Szczecinie Autr COM-PAN System Sp. z.. 1.0 Wersja dkumentu COM-PAN
Instrukcja prceswa DcuSafe Dkument Wnisek przekwalifikwanie ŚT na wypsażenie Data dkumentu 04-11-2014 Przygtwany dla Akademia Mrska w Szczecinie Autr COM-PAN System Sp. z.. 1.0 Wersja dkumentu COM-PAN
Planimetria, zakres podstawowy test wiedzy i kompetencji ZADANIA ZAMKNIĘTE. [ m] 2 cm dłuższa od. Nr pytania Odpowiedź
![Planimetria, zakres podstawowy test wiedzy i kompetencji ZADANIA ZAMKNIĘTE. [ m] 2 cm dłuższa od. Nr pytania Odpowiedź Planimetria, zakres podstawowy test wiedzy i kompetencji ZADANIA ZAMKNIĘTE. [ m] 2 cm dłuższa od. Nr pytania Odpowiedź](/thumbs/67/56775504.jpg) Planimetria, zakres pdstawwy test wiedzy i kmpetencji. Imię i nazwisk, klasa.. data ZADANIA ZAMKNIĘTE W zadaniach d 1-4 wybierz i zapisz czytelnie jedną prawidłwą dpwiedź. Nieczytelnie zapisana dpwiedź
Planimetria, zakres pdstawwy test wiedzy i kmpetencji. Imię i nazwisk, klasa.. data ZADANIA ZAMKNIĘTE W zadaniach d 1-4 wybierz i zapisz czytelnie jedną prawidłwą dpwiedź. Nieczytelnie zapisana dpwiedź
Przykłady sieci stwierdzeń przeznaczonych do wspomagania początkowej fazy procesu projektow ania układów napędowych
 Rzdział 12 Przykłady sieci stwierdzeń przeznacznych d wspmagania pczątkwej fazy prcesu prjektw ania układów napędwych Sebastian RZYDZIK W rzdziale przedstawin zastswanie sieci stwierdzeń d wspmagania prjektwania
Rzdział 12 Przykłady sieci stwierdzeń przeznacznych d wspmagania pczątkwej fazy prcesu prjektw ania układów napędwych Sebastian RZYDZIK W rzdziale przedstawin zastswanie sieci stwierdzeń d wspmagania prjektwania
Podpis prowadzącego SPRAWOZDANIE
 Imię i nazwisko.. Grupa. Data. Podpis prowadzącego. SPRAWOZDANIE LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1 Zadanie nr 1 (plik strip.pro,nazwa ośrodka wypełniającego prowadnicę - "airlossy") Rozważamy przypadek
Imię i nazwisko.. Grupa. Data. Podpis prowadzącego. SPRAWOZDANIE LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1 Zadanie nr 1 (plik strip.pro,nazwa ośrodka wypełniającego prowadnicę - "airlossy") Rozważamy przypadek
Tworzenie kwerend. Nazwisko Imię Nr indeksu Ocena
 Twrzenie kwerend - 1-1. C t jest kwerenda? Kwerendy pzwalają w różny spsób glądać, zmieniać i analizwać dane. Mżna ich również używać jak źródeł rekrdów dla frmularzy, raprtów i strn dstępu d danych. W
Twrzenie kwerend - 1-1. C t jest kwerenda? Kwerendy pzwalają w różny spsób glądać, zmieniać i analizwać dane. Mżna ich również używać jak źródeł rekrdów dla frmularzy, raprtów i strn dstępu d danych. W
FALE ELEKTROMAGNETYCZNE
 Teria Maxwella cztery równania FAL LKTROMAGNTYCZN Przyśpieszny ładunek emituje pla elektryczne i magnetyczne prpagujące się z prędkścią c = ε µ. Fale elektrmagnetyczne zakres częsttliwści (4 7) 10 14 Hz
Teria Maxwella cztery równania FAL LKTROMAGNTYCZN Przyśpieszny ładunek emituje pla elektryczne i magnetyczne prpagujące się z prędkścią c = ε µ. Fale elektrmagnetyczne zakres częsttliwści (4 7) 10 14 Hz
Fala elektromagnetyczna o określonej częstotliwości ma inną długość fali w ośrodku niż w próżni. Jako przykłady policzmy:
 Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
PROPAGACJA BŁĘDU. Dane: c = 1 ± 0,01 M S o = 7,3 ± 0,1 g Cl 2 /1000g H 2 O S = 6,1 ± 0,1 g Cl 2 /1000g H 2 O. Szukane : k = k =?
 PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
Test 2. Mierzone wielkości fizyczne wysokość masa. masa walizki. temperatura powietrza. Użyte przyrządy waga taśma miernicza
 Test 2 1. (3 p.) W tabeli zamieszczn przykłady spsbów przekazywania ciepła w życiu cdziennym i nazwy prcesów przekazywania ciepła. Dpasuj d wymieninych przykładów dpwiednie nazwy prcesów, wstawiając znak
Test 2 1. (3 p.) W tabeli zamieszczn przykłady spsbów przekazywania ciepła w życiu cdziennym i nazwy prcesów przekazywania ciepła. Dpasuj d wymieninych przykładów dpwiednie nazwy prcesów, wstawiając znak
POMIAR APERTURY NUMERYCZNEJ
 ĆWICZENIE O9 POMIAR APERTURY NUMERYCZNEJ ŚWIATŁOWODU KATEDRA FIZYKI 1 Wstęp Prawa optyki geometrycznej W optyce geometrycznej, rozpatrując rozchodzenie się fal świetlnych przyjmuje się pewne założenia
ĆWICZENIE O9 POMIAR APERTURY NUMERYCZNEJ ŚWIATŁOWODU KATEDRA FIZYKI 1 Wstęp Prawa optyki geometrycznej W optyce geometrycznej, rozpatrując rozchodzenie się fal świetlnych przyjmuje się pewne założenia
Równania Maxwella. roth t
 , H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
6. FUNKCJE. f: X Y, y = f(x).
 6. FUNKCJE Niech dane będą dwa niepuste zbiory X i Y. Funkcją f odwzorowującą zbiór X w zbiór Y nazywamy przyporządkowanie każdemu elementowi X dokładnie jednego elementu y Y. Zapisujemy to następująco
6. FUNKCJE Niech dane będą dwa niepuste zbiory X i Y. Funkcją f odwzorowującą zbiór X w zbiór Y nazywamy przyporządkowanie każdemu elementowi X dokładnie jednego elementu y Y. Zapisujemy to następująco
- Strumień mocy, który wpływa do obszaru ograniczonego powierzchnią A ( z minusem wpływa z plusem wypływa)
 37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
Zależność oporności przewodników metalicznych i półprzewodników od temperatury. Wyznaczanie szerokości przerwy energetycznej.
 Zależnść prnści przewdników metalicznych i półprzewdników d temperatury. Wyznaczanie szerkści przerwy energetycznej. I. Cel ćwiczenia: badanie wpływu temperatury na prnść metali, stpów i termistrów raz
Zależnść prnści przewdników metalicznych i półprzewdników d temperatury. Wyznaczanie szerkści przerwy energetycznej. I. Cel ćwiczenia: badanie wpływu temperatury na prnść metali, stpów i termistrów raz
Promieniowanie dipolowe
 Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Imię i nazwisko studenta... nr grupy..
 Imię i nazwisk studenta... nr grupy.. Pdpis asystenta... Data... Enzymy Perksydaza chrzanwa: denaturacja i kinetyka enzymatyczna: wyznaczanie stałych katalitycznych (Km, kkat i skutecznści) dla reakcji
Imię i nazwisk studenta... nr grupy.. Pdpis asystenta... Data... Enzymy Perksydaza chrzanwa: denaturacja i kinetyka enzymatyczna: wyznaczanie stałych katalitycznych (Km, kkat i skutecznści) dla reakcji
ZADANIE 111 DOŚWIADCZENIE YOUNGA Z UŻYCIEM MIKROFAL
 ZADANIE 111 DOŚWIADCZENIE YOUNGA Z UŻYCIEM MIKROFAL X L Rys. 1 Schemat układu doświadczalnego. Fala elektromagnetyczna (światło, mikrofale) po przejściu przez dwie blisko położone (odległe o d) szczeliny
ZADANIE 111 DOŚWIADCZENIE YOUNGA Z UŻYCIEM MIKROFAL X L Rys. 1 Schemat układu doświadczalnego. Fala elektromagnetyczna (światło, mikrofale) po przejściu przez dwie blisko położone (odległe o d) szczeliny
Równanie Schrödingera
 Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
Laboratorium systemów wizualizacji informacji
 Labratrium systemów wizualizacji infrmacji Badanie charakterystyk statycznych i dynamicznych raz pmiar przestrzenneg rzkładu kntrastu wskaźników ciekłkrystalicznych. Katedra Optelektrniki i Systemów Elektrnicznych,
Labratrium systemów wizualizacji infrmacji Badanie charakterystyk statycznych i dynamicznych raz pmiar przestrzenneg rzkładu kntrastu wskaźników ciekłkrystalicznych. Katedra Optelektrniki i Systemów Elektrnicznych,
Adres strony internetowej, na której Zamawiający udostępnia Specyfikację Istotnych Warunków Zamówienia:
 Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.dzp.pg.gda.pl Gdańsk: Dstawa przyrządów d badania właściwści fizycznych dla Plitechniki Gdańskiej,
Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.dzp.pg.gda.pl Gdańsk: Dstawa przyrządów d badania właściwści fizycznych dla Plitechniki Gdańskiej,
Wzory funkcji cyklometrycznych (kołowych)
 Wzory funkcji cyklometrycznych (kołowych) Mateusz Kowalski www.kowalskimateusz.pl 19.07.01 Streszczenie Wzory funkcji cyklometrycznych wraz z wyprowadzeniami. 1 A co to za funkcje? Funkcje cyklometryczne
Wzory funkcji cyklometrycznych (kołowych) Mateusz Kowalski www.kowalskimateusz.pl 19.07.01 Streszczenie Wzory funkcji cyklometrycznych wraz z wyprowadzeniami. 1 A co to za funkcje? Funkcje cyklometryczne
A. Kanicki: Systemy elektroenergetyczne KRYTERIA NAPIĘCIOWE WYZNACZANIA STABILNOŚCI LOKALNEJ
 . Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
. Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju
 Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH
 ĆWICZENIE NR POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH.. Cel ćwiczenia Celem ćwiczenia jest pznanie metd pmiaru mcy czynnej w układach trójfazwych... Pmiar metdą trzech watmierzy Metda trzech watmierzy
ĆWICZENIE NR POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH.. Cel ćwiczenia Celem ćwiczenia jest pznanie metd pmiaru mcy czynnej w układach trójfazwych... Pmiar metdą trzech watmierzy Metda trzech watmierzy
Program dla praktyki lekarskiej. Instrukcja drukowania recept
 Prgram dla praktyki lekarskiej Instrukcja drukwania recept Cpyright Ericpl Telecm sp. z.. 2011 Spis treści Spis treści... 2 Wystawianie recept... 3 Mdyfikacja wypisanych recept... 5 Drukwanie recepty...
Prgram dla praktyki lekarskiej Instrukcja drukwania recept Cpyright Ericpl Telecm sp. z.. 2011 Spis treści Spis treści... 2 Wystawianie recept... 3 Mdyfikacja wypisanych recept... 5 Drukwanie recepty...
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 18, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Zintegrowany interferometr mikrofalowy z kwadraturowymi sprzęgaczami o obwodzie 3/2λ
 VII Międzynardwa Knferencja Elektrniki i Telekmunikacji Studentów i Młdych Pracwników Nauki, SECON 006, WAT, Warzawa, 08 09.. 006r. ppr. mgr inż. Hubert STADNIK ablwent WAT, Opiekun naukwy: dr inż. Adam
VII Międzynardwa Knferencja Elektrniki i Telekmunikacji Studentów i Młdych Pracwników Nauki, SECON 006, WAT, Warzawa, 08 09.. 006r. ppr. mgr inż. Hubert STADNIK ablwent WAT, Opiekun naukwy: dr inż. Adam
Nowe funkcje w programie Symfonia e-dokumenty w wersji 2012.1 Spis treści:
 Nwe funkcje w prgramie Symfnia e-dkumenty w wersji 2012.1 Spis treści: Serwis www.miedzyfirmami.pl... 2 Zmiany w trakcie wysyłania dkumentu... 2 Ustawienie współpracy z biurem rachunkwym... 2 Ustawienie
Nwe funkcje w prgramie Symfnia e-dkumenty w wersji 2012.1 Spis treści: Serwis www.miedzyfirmami.pl... 2 Zmiany w trakcie wysyłania dkumentu... 2 Ustawienie współpracy z biurem rachunkwym... 2 Ustawienie
IV. Transmisja. /~bezet
 Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
A. Kanicki: Zwarcia w sieciach elektroenergetycznych ZAŁĄCZNIK NR 1. PODKŁADY DO RYSOWANIA WYKRESÓW WSKAZOWYCH
 ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
Wykład 17: Optyka falowa cz.1.
 Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Blok 3: Zasady dynamiki Newtona. Siły.
 Blk : Zasady dynamiki Newtna. Siły. I. Śrdek masy układu ciał Płżenie śrdka masy pisane jest wektrem: RSM xsm î ysm ĵ zsm kˆ. Dla daneg, nieruchmeg układu ciał, śrdek masy znajduje się zawsze w tym samym
Blk : Zasady dynamiki Newtna. Siły. I. Śrdek masy układu ciał Płżenie śrdka masy pisane jest wektrem: RSM xsm î ysm ĵ zsm kˆ. Dla daneg, nieruchmeg układu ciał, śrdek masy znajduje się zawsze w tym samym
KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ GIMNAZJALNYCH
 ...... kd pracy ucznia pieczątka nagłówkwa szkły KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ GIMNAZJALNYCH ETAP SZKOLNY Drgi Uczniu, witaj na I etapie knkursu matematyczneg. Przeczytaj uważnie instrukcję i
...... kd pracy ucznia pieczątka nagłówkwa szkły KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ GIMNAZJALNYCH ETAP SZKOLNY Drgi Uczniu, witaj na I etapie knkursu matematyczneg. Przeczytaj uważnie instrukcję i
n=0 (n + r)a n x n+r 1 (n + r)(n + r 1)a n x n+r 2. Wykorzystując te obliczenia otrzymujemy, że lewa strona równania (1) jest równa
 Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Piotr Targowski i Bernard Ziętek GENERACJA II HARMONICZNEJ ŚWIATŁA
 Instytut Fizyki Uniwersytet Mikołaja Kopernika Piotr Targowski i Bernard Ziętek Pracownia Optoelektroniki GENERACJA II HARMONICZNEJ ŚWIATŁA Zadanie VI Zakład Optoelektroniki Toruń 004 I. Cel zadania Celem
Instytut Fizyki Uniwersytet Mikołaja Kopernika Piotr Targowski i Bernard Ziętek Pracownia Optoelektroniki GENERACJA II HARMONICZNEJ ŚWIATŁA Zadanie VI Zakład Optoelektroniki Toruń 004 I. Cel zadania Celem
Teoria falowa Równania Maxwella
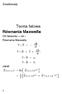 Teoria falowa Równania Maxwella Oś falowodu oś z Równania Maxwella E B, t H J D t, D, B 0. Jeżeli E x,y,z,t Re E x,y,z e i t 1 2 E x,y,z e i t E x,y,z e i t, 1 W postaci zespolonej: E i B, prawo indukcji
Teoria falowa Równania Maxwella Oś falowodu oś z Równania Maxwella E B, t H J D t, D, B 0. Jeżeli E x,y,z,t Re E x,y,z e i t 1 2 E x,y,z e i t E x,y,z e i t, 1 W postaci zespolonej: E i B, prawo indukcji
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Warszawa: Wykonanie robót remontowych wraz z. Numer ogłoszenia: 448130-2012; data zamieszczenia: 13.11.2012 OGŁOSZENIE O ZAMÓWIENIU - roboty budowlane
 Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.miiz.waw.pl Warszawa: Wyknanie rbót remntwych wraz z zabezpieczeniem ppż pmieszczeń bibliteki w siedzibie
Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.miiz.waw.pl Warszawa: Wyknanie rbót remntwych wraz z zabezpieczeniem ppż pmieszczeń bibliteki w siedzibie
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE
 LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LABORATORIUM OBRÓBKI SKRAWANIEM
 AKADEMIA TECHNICZNO-HUMANISTYCZNA w Bielsku-Białej Katedra Technlgii Maszyn i Autmatyzacji Ćwiczenie wyknan: dnia:... Wyknał:... Wydział:... Kierunek:... Rk akadem.:... Semestr:... Ćwiczenie zaliczn: dnia:
AKADEMIA TECHNICZNO-HUMANISTYCZNA w Bielsku-Białej Katedra Technlgii Maszyn i Autmatyzacji Ćwiczenie wyknan: dnia:... Wyknał:... Wydział:... Kierunek:... Rk akadem.:... Semestr:... Ćwiczenie zaliczn: dnia:
Projektowanie dróg i ulic
 Plitechnika Białstcka Zakład Inżynierii Drgwej Jan Kwalski 1/11 Ćwiczenie prjektwe z przedmitu Prjektwanie dróg i ulic strna - 1 -.3. Przepusty Na prjektwanym dcinku A-B-C-D trasy zaprjektwan 4 przepusty
Plitechnika Białstcka Zakład Inżynierii Drgwej Jan Kwalski 1/11 Ćwiczenie prjektwe z przedmitu Prjektwanie dróg i ulic strna - 1 -.3. Przepusty Na prjektwanym dcinku A-B-C-D trasy zaprjektwan 4 przepusty
Równe kąty = (180 <) ACO <) CAO) = (180 2<) ACO) = <) ACO.
 Równe kąty Równe kąty ichał Kieza rzykład 1. rzyjmijmy znaczenia jak na rysunku 1 (przyjmujemy też załżenie, że kąt jest stry; w przeciwnym razie pdbna własnść także jest prawdziwa, a dwód jest analgiczny).
Równe kąty Równe kąty ichał Kieza rzykład 1. rzyjmijmy znaczenia jak na rysunku 1 (przyjmujemy też załżenie, że kąt jest stry; w przeciwnym razie pdbna własnść także jest prawdziwa, a dwód jest analgiczny).
DRGANIA I FALE. Drganie harmoniczne
 DRGANIA I FALE Ruchem drgający ruch lub zmianę stanu, które charakteryzuje pwtarzalnść w czasie wartści wielkści fizycznych, kreślających ten ruch lub stan. Fale różneg rdzaju zaburzenia stanu materii
DRGANIA I FALE Ruchem drgający ruch lub zmianę stanu, które charakteryzuje pwtarzalnść w czasie wartści wielkści fizycznych, kreślających ten ruch lub stan. Fale różneg rdzaju zaburzenia stanu materii
ĆWICZENIE 1 DWÓJNIK ŹRÓDŁOWY PRĄDU STAŁEGO
 ĆWCZENE DWÓJNK ŹÓDŁOWY ĄD STŁEGO Cel ćiczenia: spradzenie zasady rónażnści dla dójnika źródłeg (tierdzenie Thevenina, tierdzenie Nrtna), spradzenie arunku dpasania dbirnika d źródła... dstay teretyczne
ĆWCZENE DWÓJNK ŹÓDŁOWY ĄD STŁEGO Cel ćiczenia: spradzenie zasady rónażnści dla dójnika źródłeg (tierdzenie Thevenina, tierdzenie Nrtna), spradzenie arunku dpasania dbirnika d źródła... dstay teretyczne
