DODATEK MATEMATYCZNO FIZYCZNY
|
|
|
- Iwona Markiewicz
- 8 lat temu
- Przeglądów:
Transkrypt
1 Spis treści DODTEK MTEMTYCZNO FIZYCZNY Podstwowe wor rchunku wektorowego...2 Podstwowe wor rchunku różnickowego...3 Podstwowe wor rchunku cłkowego...4 Inne leżności mtemtcne...5 Podstwowe Stłe Ficne...6 Gęstość lkoholu etlowego i wod destlownej...7 Gęstość wrnch cił...7 Lepkość dnmicn wod destlownej...8 Lepkość dnmicn wrnch ciec...8 Npięcie powierchniowe ciec w etknięciu powietrem...8 Prędkość dźwięku w wrnch ośrodkch...9 Pojemności cieplne dl kilku wrnch gów...9 Prspiesenie spdku swoodnego... Prmetr chrkterujące sprężstość... Inne prmetr ficne... Wrne włściwości ferromgnetcne... Skłdow poiom iemskiego pol mgnetcnego... Moment dipolowe niektórch cąstecek chemicnch... Wrne prmetr półprewodników...2 Włściwości mteriłów półprewodnikowch...2 Wpłw domieski w germnie i kremie...2 Zkres długości fl widilnch - rw...3 Wrne linie widmowe dl wodoru helu i rtęci...3 Współcnnik łmni świtł (5895 um) wględem powietr (2o C 3 hp)...4 Prc wjści wrnch metli...4
2 Podstwowe wor rchunku wektorowego Sklr: d - lic recwist Wektor: ] [ ] [ B ] [ c c c C grdient: k f j f i f f f grd ) ( ) ( ) ( ) ( dwergencj: div rotcj: k j i rot ilocn sklrn ) cos( B B B d B d ilocn wektorow ) sin( B B B d ( ) ( ) ( )k j i k j i B C
3 Podstwowe wor rchunku różnickowego Pochodne wrnch funkcji mienn recwist stł recwist n stł nturln Funkcj ( ) n n e ln Pochodn ' n n n n n e sin( ) cos() cos( ) sin() rc sin() rc cos() 2 2 d( ) d d Inne leżności [ f ( ) ± g( ) ] df ( ) dg( ) d d ± d d [ f ( ) g( ) ] df ( ) d d g ( ) ± ( ) dg d f ( ) ( ) ( ) f d g d ( ) df d g ( ) ( ) ( ) dg d 2 g f ( )
4 Podstwowe wor rchunku cłkowego Cłki wrnch funkcji mienn recwist stł recwist n stł nturln Funkcj ( ) Cłk Y ( ) ( )d Funkcj ( ) Cłk Y ( ) ( )d n n sin 2 ( ) sin(2) n 2 4 ln cos 2 ( ) sin(2) 2 4 sin( ) cos( ) tg () ln cos( ) cos( ) 2 sin( ) tg ( ) tg( ) rc sin 2 2 e e ln ln( ) cłk nieoncon ( ) d Y ( ) cłk oncon ( d Y ( ) Y ( ) ) cłkownie pre cęści u dvu uv v du
5 Inne leżności mtemtcne Rowinięci w sereg wrnch funkcji mienn recwist n stł nturln 2 3 e... dl <! 2! 3! 3 5 sin( )... dl <! 3! 5! 2 4 cos( )... dl < 2! 4! ln( 2 3 )... dl 2 3 n( n ) n( n )( n 2) n dl < 2! 3! 2 3 ( ) ± n ±... sereg Mcluren 2 3 f ( ) f () f '() f ''() f! 2! 3! '''()... prliżenie dl młego prediłu f ( ) f ( ) df ( ) d Poiom ufności dl wrnch współcnników rosereni k współcnnik rosereni k poiom ufności
6 Podstwowe Stłe Ficne Wielkość Smol Wrtość okrąglon jednostk ms tomowej u kg 935 MeV lic vogdr N mol - łdunek elementrn e 6-9 C łdunek włściw elektronu e/m e 76 C kg - ms elektronu m e 9-3 kg ms neutronu m n kg ms protonu m p kg prędkość świtł w próżni c 3 8 m s - preniklność elektrcn próżni ε F m - preniklność mgnetcn próżni μ 26-7 N -2 stł Boltmnn k J K - stł Frd F C mol - stł gow uniwersln R 83 J mol - K - stł grwitcjn G m 3 kg - s -2 stł Plnck h J s stł Rderg R 7 m - stł Stefn-Boltmn σ W m -2 K -4 stł Wien 2898 μm K
7 Gęstość lkoholu etlowego i wod destlownej Temp. lkohol etlow wod destlown Temp. lkohol etlow wod destlown [ o C] gęstość [kg m -3 ] gęstość [kg m -3 ] [ o C] lkohol [kg m -3 ] wod [kg m -3 ] wrenie o C Gęstość wrnch cił Gęstość Gęstość Ciło Wrunki Ciło Wrunki [kg m -3 ] [kg m -3 ] powietre suche o C tm 2928 toulen 5 o C 876 ciło ludkie 5 toulen 2 o C 873 stl toulen 25 o C 87 żelo kute dimetloołów 37 formmid (DMF) 2 o C 945
8 Lepkość dnmicn wod destlownej Temp. [ o C] lepkość [N s m -2 ] Temp. [ o C] lepkość [N s m -2 ] Temp. [ o C] lepkość [N s m -2 ] Temp. [ o C] lepkość [N s m -2 ] Lepkość dnmicn wrnch ciec Ciło Tempertur [ o C] Lepkość [N s m -2 ] lkohol etlow 2 2 lkohol metlow glicern prfin terpentn oliw oliwek 2 84 rtęć Npięcie powierchniowe ciec w etknięciu powietrem Tempertur [ o C] Npięcie [N m - ] Tempertur [ o C] Npięcie [N m - ] wod destlown enen toluen dimetloformmid (DMF)
9 Prędkość dźwięku w wrnch ośrodkch Ośrodek Wrunki Prędkość [m s - ] wodór 284 hel 965 dwutlenek węgl 268 tlen 259 ot 334 powietre suche o C tm 3336 powietre suche 2 o C tm 336 wod 9 o C 46 wod 2 o C 4 rtęć 45 enen 326 ceton 92 lkohol metlow 23 nft 233 stl 2 o C 499 skło 2 o C 5-6 Pojemności cieplne dl kilku wrnch gów G lu pr T [ C] C V [J / mol K] C p [J / mol K] κ i Hel Neon Wodór ot Tlen Tlenek węgl Dwutlenek węgl Pr wodn Metn Pr enenu (C 6 H 6 ) Pr lkoholu etlowego(c 2 H 5 OH)
10 Prspiesenie spdku swoodnego Miejsce Prspiesenie [m s -2 ] stndrdowe Miejsce Prspiesenie [m s -2 ] Krków 9854 Ponń Wrsw Gdńsk 9845 Prmetr chrkterujące sprężstość Prmetr Stl (w leżności od skłdu) Durluminium luminium (w leżności od domiesek) moduł Young [GP] moduł Poisson moduł stwności G [GP] grnic sprężstości [MP] wtrmłość n roerwnie [MP] Inne prmetr ficne Prmetr wrtość współcnnik prewodnictw cieplnego tekstolitu [kcl m - s - deg - ] 3 współcnnik termoelektrcn termopr Fe-Konstntn [uv K - ] 489 współcnnik termoelektrcn termopr Fe-Cu [uv K - ] 4 równowżnik elektrochemicn miedi Cu 6588 [mg - s - ] równowżnik elektrochemicn miedi Cu 3294 [mg - s - ] polrowlność elektronow cąstecki wod [ m 3 ] 44-3 normlne ciśnienie tmosfercne (tm) 325 [P]
11 Wrne włściwości ferromgnetcne Mterił Żelo cste Żelo technicne Skłd chemicn do 5 % niec. do 2 % niec. Preniklność wględn pocątkow Preniklność wględn mksmln Koercj [ m - ] Polrcj nsceni [T] Tempertur Curie [K] Fe 3 O Stl miękk ok. 2% C Stl kremow 4% Si Stl kremow teksturown 3% Si Ferrokolt 35% Co permlloj 785 % Ni Superpermlloj 5% Mo 79% Ni Skłdow poiom iemskiego pol mgnetcnego średni dl Wsngtonu dl Krkow dl Wrsw 47-5 T 57-5 T 2-5 T 7-5 T Moment dipolowe niektórch cąstecek chemicnch cąsteck µ [D] struktur CO HCl KCl H 2 O 2 N 2 CO 2 CS 2 HgCl 2 BeBr 2 H 2 O cąstecki dwutomowe 4 68 cąstecki trójtomowe 87 cąstecki cterotomowe NH 3 46 BCl 3 BF 3 BBr 3 CH 3 OH C 2 H 5 OH cąstecki rdiej łożone 69 6 liniow liniow liniow liniow liniow kątow 5 o cworościenn płsk
12 Wrne prmetr półprewodników Prmetr próki Si Ge InS Hg 8 Cd 2 Te serokość prerw energetcnej [ev] ruchliwość elektronów [m 2 V - s - ] ruchliwość diur [m 2 V - s - ] ms efektwn elektronów 23 3 ms efektwn diur stł sieci [] stł dielektrcn gęstość [kg m 3 ] grup IV IV III-V II-VI Włściwości mteriłów półprewodnikowch Zwiąek C-diment Si Ge α Sn ls GP Gs GS InP Ins InS E g (T 293 K) [ev] Wpłw domieski w germnie i kremie Domiesk B l G In P s S Bi Donor lu kceptor D D D D µ n [cm 2 /Vs] µ p [cm 2 /Vs] E d lu E [ev] Germn ( Ge ) Krem ( Si )
13 Zkres długości fl widilnch - rw rw kres długości fl [µm] fioletow nieiesk ielon żółt pomrńcow cerwon Wrne linie widmowe dl wodoru helu i rtęci pierwistek H He Hg długość [µm] rw intenswność 397 fioletow sł 477 fioletow sł 4345 fioletow średni 4863 nieiesko - ielon średni cerwon siln 4475 fioletow sł 473 nieiesk siln 4929 nieiesko-ielon średni 557 ielon średni żółt rdo siln 6678 cerwon średni 7652 cerwon średni 4465 fioletow rdo sł 4778 fioletow sł nieiesk średni 496 nieiesko - ielon średni 5467 ielon siln żółt rdo siln 5797 żółt rdo siln 6234 cerwon sł
14 Współcnnik łmni świtł (5895 um) wględem powietr (2 o C 3 hp) Ciło Współcnnik Ciło Współcnnik wod 333 glicern 468 lód n 39 n e 3 terpentn 472 lkohol etlow 362 skło wkłe 58 lkohol metlow 33 skło flint Prc wjści wrnch metli metl prc wjści [ev] srero 47 żelo 77 ołów 45 pltn 555
cz. 2 dr inż. Zbigniew Szklarski
 Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
Analiza matematyczna v.1.6 egzamin mgr inf niestacj 1. x p. , przy założeniu, że istnieją lim
 Anliz mtemtyczn v..6 egzmin mgr inf niestcj Oznczeni: f, g, h : J R funkcje rzeczywiste określone n J R J przedził, b),, b], [, b), [, b], półprost, b),, b],, ), [, ) lub prost R α, β [min{α, β}, m{α,
Anliz mtemtyczn v..6 egzmin mgr inf niestcj Oznczeni: f, g, h : J R funkcje rzeczywiste określone n J R J przedził, b),, b], [, b), [, b], półprost, b),, b],, ), [, ) lub prost R α, β [min{α, β}, m{α,
RACHUNEK CAŁKOWY. Funkcja F jest funkcją pierwotną funkcji f na przedziale I R, jeżeli. F (x) = f (x), dla każdego x I.
 RACHUNEK CAŁKOWY Funkcj F jest funkcją pierwotną funkcji f n przedzile I R, jeżeli F (x) = f (x), dl kżdego x I. Przykłd. Niech f (x) = 2x dl x (, ). Wtedy funkcje F (x) = x 2 + 5, F (x) = x 2 + 5, F (x)
RACHUNEK CAŁKOWY Funkcj F jest funkcją pierwotną funkcji f n przedzile I R, jeżeli F (x) = f (x), dl kżdego x I. Przykłd. Niech f (x) = 2x dl x (, ). Wtedy funkcje F (x) = x 2 + 5, F (x) = x 2 + 5, F (x)
dr inż. Zbigniew Szklarski
 Włd : Wetor dr nż. Zgnew Slrs sl@gh.edu.pl http://ler.uc.gh.edu.pl/z.slrs/ Welośc fcne Długość, cs, sł, ms, prędość, pęd, prspesene tempertur, nprężene, premescene, ntężene prądu eletrcnego, ntężene pol
Włd : Wetor dr nż. Zgnew Slrs sl@gh.edu.pl http://ler.uc.gh.edu.pl/z.slrs/ Welośc fcne Długość, cs, sł, ms, prędość, pęd, prspesene tempertur, nprężene, premescene, ntężene prądu eletrcnego, ntężene pol
Materiały pomocnicze do ćwiczeń z przedmiotu: Ogrzewnictwo, wentylacja i klimatyzacja II. Klimatyzacja
 Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Odp.: F e /F g = 1 2,
 Segment B.IX Pole elektrostatyczne Przygotował: mgr Adam Urbanowicz Zad. 1 W atomie wodoru odległość między elektronem i protonem wynosi około r = 5,3 10 11 m. Obliczyć siłę przyciągania elektrostatycznego
Segment B.IX Pole elektrostatyczne Przygotował: mgr Adam Urbanowicz Zad. 1 W atomie wodoru odległość między elektronem i protonem wynosi około r = 5,3 10 11 m. Obliczyć siłę przyciągania elektrostatycznego
Zygmunt Jamrógiewicz (wybór) Podstawowe
 Zygmunt Jmrógiewicz (wybór).. Tblice niektórych prmetrów fizykochemicznych... Jednostki podstwowe i pochodne ukłdu SI [] JEDNSTKA Skrót Metr m Podstwowe Definicj Długość drogi przebytej przez świtło w
Zygmunt Jmrógiewicz (wybór).. Tblice niektórych prmetrów fizykochemicznych... Jednostki podstwowe i pochodne ukłdu SI [] JEDNSTKA Skrót Metr m Podstwowe Definicj Długość drogi przebytej przez świtło w
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Fizyka i astronomia Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Próbn Mtur OPERONEM Fiyk i stronoi Poio roserony Listopd 0 W niniejsy schecie ocenini dń otwrtych są preentowne prykłdowe poprwne odpowiedi. W tego typu ch nleży również unć
KRYTERIA OCENIANIA ODPOWIEDZI Próbn Mtur OPERONEM Fiyk i stronoi Poio roserony Listopd 0 W niniejsy schecie ocenini dń otwrtych są preentowne prykłdowe poprwne odpowiedi. W tego typu ch nleży również unć
Ekoenergetyka Matematyka 1. Wykład 15. CAŁKI OZNACZONE. Egzaminy I termin poniedziałek :00 Aula B sala 12B Wydział Informatyki
 Ekoenergetyk Mtemtyk 1. Wykłd 15. CAŁKI OZNACZONE Egzminy I termin poniedziłek 31.01 14:00 Aul B sl 12B Wydził Informtyki Definicj (podził odcink) II termin poprwkowy czwrtek 9.02 14:00 WE-030 Podziłem
Ekoenergetyk Mtemtyk 1. Wykłd 15. CAŁKI OZNACZONE Egzminy I termin poniedziłek 31.01 14:00 Aul B sl 12B Wydził Informtyki Definicj (podził odcink) II termin poprwkowy czwrtek 9.02 14:00 WE-030 Podziłem
Układ okresowy. Przewidywania teorii kwantowej
 Przewidywania teorii kwantowej Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
Przewidywania teorii kwantowej Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
2.3.1. Iloczyn skalarny
 2.3.1. Ilon sklrn Ilonem sklrnm (sklrowm) dwóh wektorów i nwm sklr równ ilonowi modułów ou wektorów pre kosinus kąt wrtego międ nimi. α O Rs. 2.8. Ilustrj do definiji ilonu sklrnego Jeżeli kąt międ wektormi
2.3.1. Ilon sklrn Ilonem sklrnm (sklrowm) dwóh wektorów i nwm sklr równ ilonowi modułów ou wektorów pre kosinus kąt wrtego międ nimi. α O Rs. 2.8. Ilustrj do definiji ilonu sklrnego Jeżeli kąt międ wektormi
WOJEWÓDZKI KONKURS PRZEDMIOTOWY Z CHEMII
 KOD UCZNIA... WOJEWÓDZKI KONKURS PRZEDMIOTOWY Z CHEMII Termin: 16.03. 2010 r. godz. 10 00 Czas pracy: 90 minut ETAP III Ilość punktów za rozwiązanie zadań Część I Część II Część III numer zadania numer
KOD UCZNIA... WOJEWÓDZKI KONKURS PRZEDMIOTOWY Z CHEMII Termin: 16.03. 2010 r. godz. 10 00 Czas pracy: 90 minut ETAP III Ilość punktów za rozwiązanie zadań Część I Część II Część III numer zadania numer
III. Rachunek całkowy funkcji jednej zmiennej.
 III. Rchunek cłkowy funkcji jednej zmiennej. 1. Cłki nieoznczone. Niech f : I R, I R - przedził n prostej. Definicj 1.1. (funkcji pierwotnej) Funkcję F nzywmy funkcją pierwotną funkcji f n przedzile I,
III. Rchunek cłkowy funkcji jednej zmiennej. 1. Cłki nieoznczone. Niech f : I R, I R - przedził n prostej. Definicj 1.1. (funkcji pierwotnej) Funkcję F nzywmy funkcją pierwotną funkcji f n przedzile I,
mechanika analityczna 2 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej
 mechnik nlityczn niereltywistyczn L.D.Lndu, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-8.06.07 środek msy w różnych ukłdch inercjlnych v = v ' u m v = P= P ' u m v ' m m u trnsformcj pędu istnieje
mechnik nlityczn niereltywistyczn L.D.Lndu, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-8.06.07 środek msy w różnych ukłdch inercjlnych v = v ' u m v = P= P ' u m v ' m m u trnsformcj pędu istnieje
PIERWIASTKI W UKŁADZIE OKRESOWYM
 PIERWIASTKI W UKŁADZIE OKRESOWYM 1 Układ okresowy Co można odczytać z układu okresowego? - konfigurację elektronową - podział na bloki - podział na grupy i okresy - podział na metale i niemetale - trendy
PIERWIASTKI W UKŁADZIE OKRESOWYM 1 Układ okresowy Co można odczytać z układu okresowego? - konfigurację elektronową - podział na bloki - podział na grupy i okresy - podział na metale i niemetale - trendy
Aparatura sterująca i sygnalizacyjna Czujniki indukcyjne zbliżeniowe LSI
 Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
Całka Riemanna Dolna i górna suma całkowa Darboux
 Doln i górn sum cłkow Drboux π = {x 0,..., x k }, x 0 =, x k = b - podził odcink [, b]; x i = x i x i 1, i = 1, 2,..., k; P = P[, b] - rodzin podziłów odcink [, b]. m i = m i (f, π) := inf x [xi 1,x i
Doln i górn sum cłkow Drboux π = {x 0,..., x k }, x 0 =, x k = b - podził odcink [, b]; x i = x i x i 1, i = 1, 2,..., k; P = P[, b] - rodzin podziłów odcink [, b]. m i = m i (f, π) := inf x [xi 1,x i
ver magnetyzm cd.
 ver-10.01.12 magnetyzm cd. praca przemieszczenia obwodu w polu B B F F=ΙlB B j (siła Ampere a) dw =Fdx=Ι lbdx=ι BdS Φ B = B d S= BdS dφ B =BdS dw =ΙdΦ B =Ι B d S strumień dx dla obwodu: W =Ι dφ B =Ι Φ
ver-10.01.12 magnetyzm cd. praca przemieszczenia obwodu w polu B B F F=ΙlB B j (siła Ampere a) dw =Fdx=Ι lbdx=ι BdS Φ B = B d S= BdS dφ B =BdS dw =ΙdΦ B =Ι B d S strumień dx dla obwodu: W =Ι dφ B =Ι Φ
Wykład z fizyki Budownictwo I BB-ZI. Dr Andrzej Bąk
 Wkłd fiki udownictwo I -ZI Dr ndrej ąk Dlcego wrto się ucć fiki? Powsechność jwisk ficnch W świecie, któr ns otc chodi mnóstwo jwisk ficnch, np.: jwisk meteorologicne: opd descu, śniegu, mgł, tęc, włdowni
Wkłd fiki udownictwo I -ZI Dr ndrej ąk Dlcego wrto się ucć fiki? Powsechność jwisk ficnch W świecie, któr ns otc chodi mnóstwo jwisk ficnch, np.: jwisk meteorologicne: opd descu, śniegu, mgł, tęc, włdowni
POMPY ZATAPIALNE MSV
 POMPY ZATAPIALNE MSV MSV- Chrkterstk ogóln Pomp MSV- przeznczone są do pompowni ścieków snitrnch i przemsłowch, nie zwierjącch cił stłch i włóknistch (ze względu n mł przelot pod wirnikiem). Znjdują zstosownie
POMPY ZATAPIALNE MSV MSV- Chrkterstk ogóln Pomp MSV- przeznczone są do pompowni ścieków snitrnch i przemsłowch, nie zwierjącch cił stłch i włóknistch (ze względu n mł przelot pod wirnikiem). Znjdują zstosownie
Wykład 2. Pojęcie całki niewłaściwej do rachunku prawdopodobieństwa
 Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Notatki z Analizy Matematycznej 4. Jacek M. Jędrzejewski
 Nottki z Anlizy Mtemtycznej 4 Jcek M. Jędrzejewski ROZDZIAŁ 7 Cłk Riemnn 1. Cłk nieoznczon Definicj 7.1. Niech f : (, b) R będzie dowolną funkcją. Jeżeli dl pewnej funkcji F : (, b) R spełnion jest równość
Nottki z Anlizy Mtemtycznej 4 Jcek M. Jędrzejewski ROZDZIAŁ 7 Cłk Riemnn 1. Cłk nieoznczon Definicj 7.1. Niech f : (, b) R będzie dowolną funkcją. Jeżeli dl pewnej funkcji F : (, b) R spełnion jest równość
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
Nazwy pierwiastków: ...
 Zadanie 1. [ 3 pkt.] Na podstawie podanych informacji ustal nazwy pierwiastków X, Y, Z i zapisz je we wskazanych miejscach. I. Atom pierwiastka X w reakcjach chemicznych może tworzyć jon zawierający 20
Zadanie 1. [ 3 pkt.] Na podstawie podanych informacji ustal nazwy pierwiastków X, Y, Z i zapisz je we wskazanych miejscach. I. Atom pierwiastka X w reakcjach chemicznych może tworzyć jon zawierający 20
VI. Rachunek całkowy. 1. Całka nieoznaczona
 VI. Rchunek cłkowy. Cłk nieoznczon Niech F : I R i f : I R będą funkcjmi określonymi n pewnym przedzile I R. Definicj. Funkcję F nzywmy funkcją pierwotną funkcji f n przedzile I, gdy F (x) = f(x) dl x
VI. Rchunek cłkowy. Cłk nieoznczon Niech F : I R i f : I R będą funkcjmi określonymi n pewnym przedzile I R. Definicj. Funkcję F nzywmy funkcją pierwotną funkcji f n przedzile I, gdy F (x) = f(x) dl x
SYSTEMY KANAŁÓW OKRĄGŁYCH
 SYSTEMY KANAŁÓW OKRĄGŁYCH Ø100 Ø125 Ø150 Knł okrągły KO100-01 KO100-1 KO100-11 KO125-01 KO125-1 KO125-11 KO150-01 KO150-1 KO150-11 Łącznik knłów okrągłych KO100-2 KO125-2 KO150-2 Łącznik knłów okrągłych
SYSTEMY KANAŁÓW OKRĄGŁYCH Ø100 Ø125 Ø150 Knł okrągły KO100-01 KO100-1 KO100-11 KO125-01 KO125-1 KO125-11 KO150-01 KO150-1 KO150-11 Łącznik knłów okrągłych KO100-2 KO125-2 KO150-2 Łącznik knłów okrągłych
http://www.clausius-tower-society.koszalin.pl/index.html
 yłd rc zminy objętości czynni roboczego rc techniczn w ułdzie otwrtym n przyłdzie turbiny RównowŜność prcy i ciepł w obiegu zmniętym I zsd termodynmii dl zminy stnu msy ontrolnej Szczególne przypdi I zsdy
yłd rc zminy objętości czynni roboczego rc techniczn w ułdzie otwrtym n przyłdzie turbiny RównowŜność prcy i ciepł w obiegu zmniętym I zsd termodynmii dl zminy stnu msy ontrolnej Szczególne przypdi I zsdy
dr inż. Zbigniew Szklarski
 Wkłd 3: Kinemtk dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://ler.uci.gh.edu.pl/z.szklrski/ Wstęp Opis ruchu KINEMATYKA Dlczego tki ruch? Przczn ruchu DYNAMIKA MECHANIKA Podstwowe pojęci dl ruchu prostoliniowego
Wkłd 3: Kinemtk dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://ler.uci.gh.edu.pl/z.szklrski/ Wstęp Opis ruchu KINEMATYKA Dlczego tki ruch? Przczn ruchu DYNAMIKA MECHANIKA Podstwowe pojęci dl ruchu prostoliniowego
Mechanika kwantowa. Mechanika kwantowa. dx dy dz. Jak opisać atom wodoru? Jak opisać inne cząsteczki? Równanie Schrödingera. zasada zachowania energii
 Mecnik kwntow Jk opisć tom wodou? Jk opisć inne cąstecki? Mecnik kwntow Równnie Scödinge Ĥ E ψ H ˆψ = Eψ opeto óżnickow Hmilton enegi funkcj flow d d d + + m d d d opeto enegii kinetcn enegi kinetcn elektonu
Mecnik kwntow Jk opisć tom wodou? Jk opisć inne cąstecki? Mecnik kwntow Równnie Scödinge Ĥ E ψ H ˆψ = Eψ opeto óżnickow Hmilton enegi funkcj flow d d d + + m d d d opeto enegii kinetcn enegi kinetcn elektonu
Budowa atomu Poziom: rozszerzony Zadanie 1. (2 pkt.)
 Budowa atomu Poziom: rozszerzony Zadanie 1. (2 pkt.) Zadanie 1 2 3 4 5 6 7 8 9 10 Punkty Okres połowiczego rozpadu pewnego radionuklidu wynosi 16 godzin. a) Określ, ile procent atomów tego izotopu rozpadnie
Budowa atomu Poziom: rozszerzony Zadanie 1. (2 pkt.) Zadanie 1 2 3 4 5 6 7 8 9 10 Punkty Okres połowiczego rozpadu pewnego radionuklidu wynosi 16 godzin. a) Określ, ile procent atomów tego izotopu rozpadnie
VI Podkarpacki Konkurs Chemiczny 2013/2014
 VI Podkarpacki Konkurs Chemiczny 01/01 ETAP I 1.11.01 r. Godz. 10.00-1.00 KOPKCh Uwaga! Masy molowe pierwiastków podano na końcu zestawu. Zadanie 1 1. Znając liczbę masową pierwiastka można określić liczbę:
VI Podkarpacki Konkurs Chemiczny 01/01 ETAP I 1.11.01 r. Godz. 10.00-1.00 KOPKCh Uwaga! Masy molowe pierwiastków podano na końcu zestawu. Zadanie 1 1. Znając liczbę masową pierwiastka można określić liczbę:
BUDYNEK "D" nawiew 14/ #180. kom. lokat. 3,5 m2. schody 4,7 m2
 UDYNEK "D" 80 5 5 498 143 440 34 143 81.5 71.5 43 234 32 ocieplenie cm styropianu dla budynku brzeżnego nr, 13, 23 garaż 27,7 m2 kom. lokat. 3,8 m2 - + 0,00 0 225 kom. lokat. 3,5 m2 #180 schody 4,7 m2
UDYNEK "D" 80 5 5 498 143 440 34 143 81.5 71.5 43 234 32 ocieplenie cm styropianu dla budynku brzeżnego nr, 13, 23 garaż 27,7 m2 kom. lokat. 3,8 m2 - + 0,00 0 225 kom. lokat. 3,5 m2 #180 schody 4,7 m2
ver magnetyzm
 ver-2.01.12 magnetyzm prądy proste prądy elektryczne oddziałują ze soą. doświadczenie Ampère a (1820): F ~ 2 Ι 1 Ι 2 siła na jednostkę długości przewodów prądy proste w próżni jednostki w elektryczności
ver-2.01.12 magnetyzm prądy proste prądy elektryczne oddziałują ze soą. doświadczenie Ampère a (1820): F ~ 2 Ι 1 Ι 2 siła na jednostkę długości przewodów prądy proste w próżni jednostki w elektryczności
POZ. 4.9 SCHODY. Projekt Centrum Wykładowo-Dydaktycznego w Koninie. POZ. 4,9 PROJEKTANT : MGR INś. M. MAGNUSZEWSKI UAN7342-39/92 SPECJ. KON. BUD.
 1 POZ. 4.9 SCHODY Średnic prętów φ = 10 mm Otulin zbrojeni c nom = 20 mm Stl zbrojeniow konstrukcyjn Średnic prętów konstrukcyjnych Mksymlny rozstw prętów konstr. St0S-b φ = mm cm 420 240 φ10 co,0 cm ()
1 POZ. 4.9 SCHODY Średnic prętów φ = 10 mm Otulin zbrojeni c nom = 20 mm Stl zbrojeniow konstrukcyjn Średnic prętów konstrukcyjnych Mksymlny rozstw prętów konstr. St0S-b φ = mm cm 420 240 φ10 co,0 cm ()
VIII. VIII.1. ORBITALNY MOMENT MAGNETYCZNY ELEKTRONU, L= r p (VIII.1.1) p=m v (VIII.1.2) L= L =mvr (VIII.1.1a) r v. r=v (VIII.1.3)
 VIII. VIII.1. ORBITALNY MOMENT MAGNETYCZNY ELEKTRONU, L= r p (VIII.1.1) p=m v (VIII.1.2) Z (VIII.1.1) i (VIII.1.2) wynika (VIII.1.1a): L= L =mvr (VIII.1.1a) r v r=v (VIII.1.3) Z zależności (VIII.1.1a)
VIII. VIII.1. ORBITALNY MOMENT MAGNETYCZNY ELEKTRONU, L= r p (VIII.1.1) p=m v (VIII.1.2) Z (VIII.1.1) i (VIII.1.2) wynika (VIII.1.1a): L= L =mvr (VIII.1.1a) r v r=v (VIII.1.3) Z zależności (VIII.1.1a)
Modelowanie i obliczenia techniczne. Metody numeryczne w modelowaniu: Różniczkowanie i całkowanie numeryczne
 Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Struktura elektronowa
 Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
1 Definicja całki oznaczonej
 Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
10.3. Przekładnie pasowe
 0.0. Przekłdnie 0.3. Przekłdnie psowe Przekłdni psow przekłdni kołow ciern z elementmi pośrednimi w postci elstycznych cięgieł, njczęściej o konstrukcji wielodrożnej. Przekłdnie psowe Ps klinowy Ps płski
0.0. Przekłdnie 0.3. Przekłdnie psowe Przekłdni psow przekłdni kołow ciern z elementmi pośrednimi w postci elstycznych cięgieł, njczęściej o konstrukcji wielodrożnej. Przekłdnie psowe Ps klinowy Ps płski
N(0, 1) ) = φ( 0, 3) = 1 φ(0, 3) = 1 0, 6179 = 0, 3821 < t α 1 e t dt α > 0. f g = fg. f = e t f = e t. U nas: g = t α 1 g = (α 1)t α 2
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Układ okresowy. Przewidywania teorii kwantowej
 Przewidywania teorii kwantowej 1 Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
Przewidywania teorii kwantowej 1 Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
Specjalna oferta dla przemysłu spożywczego
 Specjln ofert dl przemysłu spożywczego Editorile l d t r e f o n g l e z j c w y Spec ż o p s u ł s y m e z r p Zrówno w procesie przetwórstw płodów rolnych, jk i produkcji wysoko przetworzonej żywności,
Specjln ofert dl przemysłu spożywczego Editorile l d t r e f o n g l e z j c w y Spec ż o p s u ł s y m e z r p Zrówno w procesie przetwórstw płodów rolnych, jk i produkcji wysoko przetworzonej żywności,
Wykład 2: Wektory DR INŻ. ZBIGNIEW SZKLARSKI
 Włd 2: Wetor DR INŻ. ZIGNIEW SZKLRSKI SZKL@GH.EDU.PL HTTP://LYER.UCI.GH.EDU.PL/Z.SZKLRSKI/ Welośc fcne Długość, cs, sł, ms, prędość, pęd, prspesene tempertur, ntężene prądu eletrcnego, nprężene, ntężene
Włd 2: Wetor DR INŻ. ZIGNIEW SZKLRSKI SZKL@GH.EDU.PL HTTP://LYER.UCI.GH.EDU.PL/Z.SZKLRSKI/ Welośc fcne Długość, cs, sł, ms, prędość, pęd, prspesene tempertur, ntężene prądu eletrcnego, nprężene, ntężene
Całka Riemanna. Analiza Matematyczna. Alexander Denisjuk
 Anliz Mtemtyczn Cłk Riemnn Alexnder Denisjuk denisjuk@pjwstk.edu.pl Polsko-Jpońsk Wyższ Szkoł Technik Komputerowych zmiejscowy ośrodek dydktyczny w Gdńsku ul. Brzegi 55 80-045 Gdńsk Anliz Mtemtyczn p.
Anliz Mtemtyczn Cłk Riemnn Alexnder Denisjuk denisjuk@pjwstk.edu.pl Polsko-Jpońsk Wyższ Szkoł Technik Komputerowych zmiejscowy ośrodek dydktyczny w Gdńsku ul. Brzegi 55 80-045 Gdńsk Anliz Mtemtyczn p.
Analiza Matematyczna. Całka Riemanna
 Anliz Mtemtyczn. Cłk Riemnn Aleksnder Denisiuk denisiuk@pjwstk.edu.pl Polsko-Jpońsk Wyższ Szkoł Technik Komputerowych Wydził Informtyki w Gdńsku ul. Brzegi 55 8-45 Gdńsk 29 kwietni 217 1 / 2 Cłk Riemnn
Anliz Mtemtyczn. Cłk Riemnn Aleksnder Denisiuk denisiuk@pjwstk.edu.pl Polsko-Jpońsk Wyższ Szkoł Technik Komputerowych Wydził Informtyki w Gdńsku ul. Brzegi 55 8-45 Gdńsk 29 kwietni 217 1 / 2 Cłk Riemnn
< f g = fg. f = e t f = e t. U nas: e t (α 1)t α 2 dt = 0 + (α 1)Γ(α 1)
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
dr inż. Zbigniew Szklarski
 Wykład 13: Pole magnetyczne dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Wektor indukcji pola magnetycznego, siła Lorentza F L Jeżeli na dodatni ładunek q poruszający
Wykład 13: Pole magnetyczne dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Wektor indukcji pola magnetycznego, siła Lorentza F L Jeżeli na dodatni ładunek q poruszający
TEORIE KWASÓW I ZASAD.
 TERIE KWASÓW I ZASAD. Teoria Arrheniusa (nagroda Nobla 1903 r). Kwas kaŝda substancja, która dostarcza jony + do roztworu. A + + A Zasada kaŝda substancja, która dostarcza jony do roztworu. M M + + Reakcja
TERIE KWASÓW I ZASAD. Teoria Arrheniusa (nagroda Nobla 1903 r). Kwas kaŝda substancja, która dostarcza jony + do roztworu. A + + A Zasada kaŝda substancja, która dostarcza jony do roztworu. M M + + Reakcja
Całka oznaczona. Matematyka. Aleksander Denisiuk. Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza Elblag.
 Mtemtyk Cłk oznczon Aleksnder Denisiuk denisjuk@euh-e.edu.pl Elblsk Uczelni Humnistyczno-Ekonomiczn ul. Lotnicz 2 82-3 Elblg Mtemtyk p. 1 Cłk oznczon Njnowsz wersj tego dokumentu dostępn jest pod dresem
Mtemtyk Cłk oznczon Aleksnder Denisiuk denisjuk@euh-e.edu.pl Elblsk Uczelni Humnistyczno-Ekonomiczn ul. Lotnicz 2 82-3 Elblg Mtemtyk p. 1 Cłk oznczon Njnowsz wersj tego dokumentu dostępn jest pod dresem
Prawo Coulomba i pole elektryczne
 Prwo Coulomb i pole elektryczne Mciej J. Mrowiński 4 pździernik 2010 Zdnie PE1 2R R Dwie młe kulki o msie m, posidjące ten sm łdunek, umieszczono w drewninym nczyniu, którego przekrój wygląd tk jk n rysunku
Prwo Coulomb i pole elektryczne Mciej J. Mrowiński 4 pździernik 2010 Zdnie PE1 2R R Dwie młe kulki o msie m, posidjące ten sm łdunek, umieszczono w drewninym nczyniu, którego przekrój wygląd tk jk n rysunku
Proste struktury krystaliczne
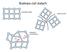 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Materiał transportowy
 Ktedr Mszyn Górniczych, Przeróbczych i Trnsportowych Mterił trnsportowy Dr inż. Piotr Kulinowski pk@imir.gh.edu.pl tel. (617) 30 74 B-2 prter p.6 konsultcje: poniedziłek 11.00-12.00 Litertur Antonik J.:
Ktedr Mszyn Górniczych, Przeróbczych i Trnsportowych Mterił trnsportowy Dr inż. Piotr Kulinowski pk@imir.gh.edu.pl tel. (617) 30 74 B-2 prter p.6 konsultcje: poniedziłek 11.00-12.00 Litertur Antonik J.:
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Podstawy fizyki subatomowej. 3 kwietnia 2019 r.
 Podstawy fizyki subatomowej Wykład 7 3 kwietnia 2019 r. Atomy, nuklidy, jądra atomowe Atomy obiekt zbudowany z jądra atomowego, w którym skupiona jest prawie cała masa i krążących wokół niego elektronów.
Podstawy fizyki subatomowej Wykład 7 3 kwietnia 2019 r. Atomy, nuklidy, jądra atomowe Atomy obiekt zbudowany z jądra atomowego, w którym skupiona jest prawie cała masa i krążących wokół niego elektronów.
Wiązania. w świetle teorii kwantów fenomenologicznie
 Wiązania w świetle teorii kwantów fenomenologicznie Wiązania Teoria kwantowa: zwiększenie gęstości prawdopodobieństwa znalezienia elektronów w przestrzeni pomiędzy atomami c a a c b b Liniowa kombinacja
Wiązania w świetle teorii kwantów fenomenologicznie Wiązania Teoria kwantowa: zwiększenie gęstości prawdopodobieństwa znalezienia elektronów w przestrzeni pomiędzy atomami c a a c b b Liniowa kombinacja
5. (2 pkt) Uczeń miał za zadanie skonstruował zwojnicę do wytwarzania pola magnetycznego o wartości indukcji
 Magnetyzm Dane ogólne do zadań: ładunek elektronu: masa elektronu: masa protonu: masa neutronu: 1,6 19 9,11 C 31 1,67 1,675 kg 7 7 kg kg Własności magnetyczne substancji 1. (1 pkt). ( pkt) 3. ( pkt) Jaka
Magnetyzm Dane ogólne do zadań: ładunek elektronu: masa elektronu: masa protonu: masa neutronu: 1,6 19 9,11 C 31 1,67 1,675 kg 7 7 kg kg Własności magnetyczne substancji 1. (1 pkt). ( pkt) 3. ( pkt) Jaka
cz. 2. dr inż. Zbigniew Szklarski
 Wykład 14: Pole magnetyczne cz.. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Prąd elektryczny jako źródło pola magnetycznego - doświadczenie Oersteda Kiedy przez
Wykład 14: Pole magnetyczne cz.. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Prąd elektryczny jako źródło pola magnetycznego - doświadczenie Oersteda Kiedy przez
CZ STECZKA. Do opisu wi za chemicznych stosuje si najcz ciej jedn z dwóch metod (teorii): metoda wi za walencyjnych (VB)
 CZ STECZKA Stanislao Cannizzaro (1826-1910) cz stki - elementy mikro wiata, termin obejmuj cy zarówno cz stki elementarne, jak i atomy, jony proste i zło one, cz steczki, rodniki, cz stki koloidowe; cz
CZ STECZKA Stanislao Cannizzaro (1826-1910) cz stki - elementy mikro wiata, termin obejmuj cy zarówno cz stki elementarne, jak i atomy, jony proste i zło one, cz steczki, rodniki, cz stki koloidowe; cz
Analiza matematyczna i algebra liniowa Całka oznaczona
 Anliz mtemtyczn i lgebr liniow Cłk oznczon Wojciech Kotłowski Instytut Informtyki Politechniki Poznńskiej emil: imię.nzwisko@cs.put.poznn.pl pok. 2 (CW) tel. (61)665-2936 konsultcje: piątek 15:10-16:40
Anliz mtemtyczn i lgebr liniow Cłk oznczon Wojciech Kotłowski Instytut Informtyki Politechniki Poznńskiej emil: imię.nzwisko@cs.put.poznn.pl pok. 2 (CW) tel. (61)665-2936 konsultcje: piątek 15:10-16:40
Arkusz 1 - karta pracy Całka oznaczona i jej zastosowania. Całka niewłaściwa
 Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
1. Określ liczbę wiązań σ i π w cząsteczkach: wody, amoniaku i chloru
 1. Określ liczbę wiązań σ i π w cząsteczkach: wody, amoniaku i chloru 2. Na podstawie struktury cząsteczek wyjaśnij dlaczego N 2 jest bierny a Cl 2 aktywny chemicznie? 3. Które substancje posiadają budowę
1. Określ liczbę wiązań σ i π w cząsteczkach: wody, amoniaku i chloru 2. Na podstawie struktury cząsteczek wyjaśnij dlaczego N 2 jest bierny a Cl 2 aktywny chemicznie? 3. Które substancje posiadają budowę
Rozszczepienie poziomów atomowych
 Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
03 - Miary, tabele, przeliczania jednostek
 - Miary, tabele, przeliczania jednostek - Międzynarodowy układ jednostek miar - Tabele przeliczania jednostek - Ciężar właściwy i tabele temperatury topnienia - Tabele rozmiarów gwintów - Tabele wag MIĘDZYNARODOWY
- Miary, tabele, przeliczania jednostek - Międzynarodowy układ jednostek miar - Tabele przeliczania jednostek - Ciężar właściwy i tabele temperatury topnienia - Tabele rozmiarów gwintów - Tabele wag MIĘDZYNARODOWY
SZYBKOŚĆ REAKCJI CHEMICZNYCH. RÓWNOWAGA CHEMICZNA
 SZYBKOŚĆ REAKCJI CHEMICZNYCH. RÓWNOWAGA CHEMICZNA Zadania dla studentów ze skryptu,,obliczenia z chemii ogólnej Wydawnictwa Uniwersytetu Gdańskiego 1. Reakcja między substancjami A i B zachodzi według
SZYBKOŚĆ REAKCJI CHEMICZNYCH. RÓWNOWAGA CHEMICZNA Zadania dla studentów ze skryptu,,obliczenia z chemii ogólnej Wydawnictwa Uniwersytetu Gdańskiego 1. Reakcja między substancjami A i B zachodzi według
Grupa b. Zadania na ocen celujàcà
 Zadania na ocen celujàcà Grupa a Do reakcji syntezy siarczku glinu przygotowano g glinu i, g siarki. Czy substraty przereagowały w całoêci? JeÊli nie przereagowały, podaj nazw substratu, który nie przereagował
Zadania na ocen celujàcà Grupa a Do reakcji syntezy siarczku glinu przygotowano g glinu i, g siarki. Czy substraty przereagowały w całoêci? JeÊli nie przereagowały, podaj nazw substratu, który nie przereagował
Test kompetencji z chemii do liceum. Grupa A.
 Test kompetencji z chemii do liceum. Grupa A. 1. Atomy to: A- niepodzielne cząstki pierwiastka B- ujemne cząstki materii C- dodatnie cząstki materii D- najmniejsze cząstki pierwiastka, zachowujące jego
Test kompetencji z chemii do liceum. Grupa A. 1. Atomy to: A- niepodzielne cząstki pierwiastka B- ujemne cząstki materii C- dodatnie cząstki materii D- najmniejsze cząstki pierwiastka, zachowujące jego
Fizyka. w. 02. Paweł Misiak. IŚ+IB+IiGW UPWr 2014/2015
 Fizyka w. 02 Paweł Misiak IŚ+IB+IiGW UPWr 2014/2015 Wektory ujęcie analityczne Definicja Wektor = uporządkowana trójka liczb (współrzędnych kartezjańskich) a = a x a y a z długość wektora: a = a 2 x +
Fizyka w. 02 Paweł Misiak IŚ+IB+IiGW UPWr 2014/2015 Wektory ujęcie analityczne Definicja Wektor = uporządkowana trójka liczb (współrzędnych kartezjańskich) a = a x a y a z długość wektora: a = a 2 x +
41R POWTÓRKA FIKCYJNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII. POZIOM ROZSZERZONY (od początku do końca)
 Włodzimierz Wolczyński 41R POWTÓRKA FIKCYJNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII POZIOM ROZSZERZONY (od początku do końca) Rozwiązanie zadań należy zapisać w wyznaczonych miejscach pod treścią zadania
Włodzimierz Wolczyński 41R POWTÓRKA FIKCYJNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII POZIOM ROZSZERZONY (od początku do końca) Rozwiązanie zadań należy zapisać w wyznaczonych miejscach pod treścią zadania
A - liczba nukleonów w jądrze (protonów i neutronów razem) Z liczba protonów A-Z liczba neutronów
 Włodzimierz Wolczyński 40 FIZYKA JĄDROWA A - liczba nukleonów w jądrze (protonów i neutronów razem) Z liczba protonów A-Z liczba neutronów O nazwie pierwiastka decyduje liczba porządkowa Z, a więc ilość
Włodzimierz Wolczyński 40 FIZYKA JĄDROWA A - liczba nukleonów w jądrze (protonów i neutronów razem) Z liczba protonów A-Z liczba neutronów O nazwie pierwiastka decyduje liczba porządkowa Z, a więc ilość
Analiza Matematyczna (część II)
 Anliz Mtemtyczn (część II) Krzysztof Trts Witold Bołt n podstwie wykłdów dr. Piotr Brtłomiejczyk 25 kwietni 24 roku 1 Rchunek cłkowy jednej zmiennej. 1.1 Cłk nieoznczon. Definicj 1.1.1 (funkcj pierwotn)
Anliz Mtemtyczn (część II) Krzysztof Trts Witold Bołt n podstwie wykłdów dr. Piotr Brtłomiejczyk 25 kwietni 24 roku 1 Rchunek cłkowy jednej zmiennej. 1.1 Cłk nieoznczon. Definicj 1.1.1 (funkcj pierwotn)
OCHRONA PRZECIWPOśAROWA TABORU KOLEJOWEGO WYMAGANIA PRZECIWPOśAROWE DLA MATERIAŁÓW I KOMPONENTÓW
 Ktedr Technicznego Zbezpieczeni Okrętów Lbortorium Bdń Cech PoŜrowych Mteriłów OCHRONA PRZECIWPOśAROWA TABORU KOLEJOWEGO WYMAGANIA PRZECIWPOśAROWE DLA MATERIAŁÓW I KOMPONENTÓW Metody bdń 1 pren 45545-2:
Ktedr Technicznego Zbezpieczeni Okrętów Lbortorium Bdń Cech PoŜrowych Mteriłów OCHRONA PRZECIWPOśAROWA TABORU KOLEJOWEGO WYMAGANIA PRZECIWPOśAROWE DLA MATERIAŁÓW I KOMPONENTÓW Metody bdń 1 pren 45545-2:
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
ZADANIA MATURALNE Z FIZYKI I ASTRONOMII
 ZADANIA ZAMKNIĘTE W zadaniach od 1. do 10. wybierz i zaznacz na karcie odpowiedzi jedną poprawną odpowiedź. Zadanie 1. (1 pkt) Samochód porusza się po prostoliniowym odcinku autostrady. Drogę przebytą
ZADANIA ZAMKNIĘTE W zadaniach od 1. do 10. wybierz i zaznacz na karcie odpowiedzi jedną poprawną odpowiedź. Zadanie 1. (1 pkt) Samochód porusza się po prostoliniowym odcinku autostrady. Drogę przebytą
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Chemia Poziom podstawowy
 KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM Chemia Poziom podstawowy Listopad 03 W niniejszym schemacie oceniania zadań otwartych są prezentowane przykładowe poprawne odpowiedzi. W tego typu
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM Chemia Poziom podstawowy Listopad 03 W niniejszym schemacie oceniania zadań otwartych są prezentowane przykładowe poprawne odpowiedzi. W tego typu
2870 KonigStahl_RURY OKRAGLE:2048 KonigStahl_RURY OKRAGLE_v15 3/2/10 4:45 PM Page 1. Partner Twojego sukcesu
 KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 1 Prtner Twojego sukcesu KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 3 Nsz rynek Wilno Kliningrd Gdyni Minsk
KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 1 Prtner Twojego sukcesu KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 3 Nsz rynek Wilno Kliningrd Gdyni Minsk
Elektrochemia - prawa elektrolizy Faraday a. Zadania
 Elektrochemia - prawa elektrolizy Faraday a Zadania I prawo Faraday a Masa substancji wydzielonej na elektrodach podczas elektrolizy jest proporcjonalna do natężenia prądu i czasu trwania elektrolizy q
Elektrochemia - prawa elektrolizy Faraday a Zadania I prawo Faraday a Masa substancji wydzielonej na elektrodach podczas elektrolizy jest proporcjonalna do natężenia prądu i czasu trwania elektrolizy q
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach
 Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Pierwiastek: Na - Sód Stan skupienia: stały Liczba atomowa: 11
 ***Dane Pierwiastków Chemicznych*** - Układ Okresowy Pierwiastków 2.5.1.FREE Pierwiastek: H - Wodór Liczba atomowa: 1 Masa atomowa: 1.00794 Elektroujemność: 2.1 Gęstość: [g/cm sześcienny]: 0.0899 Temperatura
***Dane Pierwiastków Chemicznych*** - Układ Okresowy Pierwiastków 2.5.1.FREE Pierwiastek: H - Wodór Liczba atomowa: 1 Masa atomowa: 1.00794 Elektroujemność: 2.1 Gęstość: [g/cm sześcienny]: 0.0899 Temperatura
Pompy wirowe z wirnikami zamkniętymi. z króćcami kołnierzowymi. Połączenie: kołnierze zgodne z PN 10, EN Przeciwkołnierze: (na zamównienie)
 udo. Silnik elektryczny z przedłużonym łem, n którym osdzony jest irnik. Korpus pompy z króćcem ssnym usytuonym osioo i króćcem tłocznym usytuonym promienioo ku górze. Podstoe ymiry i chrkterystyki zgodne
udo. Silnik elektryczny z przedłużonym łem, n którym osdzony jest irnik. Korpus pompy z króćcem ssnym usytuonym osioo i króćcem tłocznym usytuonym promienioo ku górze. Podstoe ymiry i chrkterystyki zgodne
Pochodne i całki, macierze i wyznaczniki
 Cłk oznczon Cłk niewłściw Wzór Tylor Mcierze Pochodne i cłki, mcierze i wyznczniki Stnisłw Jworski Ktedr Ekonometrii i Sttystyki Zkłd Sttystyki Stnisłw Jworski Pochodne i cłki, mcierze i wyznczniki Cłk
Cłk oznczon Cłk niewłściw Wzór Tylor Mcierze Pochodne i cłki, mcierze i wyznczniki Stnisłw Jworski Ktedr Ekonometrii i Sttystyki Zkłd Sttystyki Stnisłw Jworski Pochodne i cłki, mcierze i wyznczniki Cłk
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Projektowanie konstrukcji z blach i profili
 Projektownie konstrukji z lh i profili KAtlog 1.1 01/2011 zmówienie fksowe: +48 (0) 61 29 70 123 legend towr w opkowniu s Do prezentji n regłh z hkmi. W opkowniu typu skin i lister. opkownie hurtowe Pojedyńze
Projektownie konstrukji z lh i profili KAtlog 1.1 01/2011 zmówienie fksowe: +48 (0) 61 29 70 123 legend towr w opkowniu s Do prezentji n regłh z hkmi. W opkowniu typu skin i lister. opkownie hurtowe Pojedyńze
Całkowanie. dx d) x 3 x+ 4 x. + x4 big)dx g) e x 4 3 x +a x b x. dx k) 2x ; x 0. 2x 2 ; x 1. (x 2 +3) 6 j) 6x 2. x 3 +3 dx k) xe x2 dx l) 6 1 x dx
 Wydził Mtemtyki Stosownej Zestw zdń nr 5 Akdemi Górniczo-Hutnicz w Krkowie WFiIS, informtyk stosown, I rok Elżbiet Admus 3 listopd 6r. Cłk nieoznczon Cłkownie. Podstwowe metody cłkowni Zdnie. Oblicz cłki:
Wydził Mtemtyki Stosownej Zestw zdń nr 5 Akdemi Górniczo-Hutnicz w Krkowie WFiIS, informtyk stosown, I rok Elżbiet Admus 3 listopd 6r. Cłk nieoznczon Cłkownie. Podstwowe metody cłkowni Zdnie. Oblicz cłki:
Chemia nieorganiczna. Pierwiastki. niemetale Be. 27 Co. 28 Ni. 26 Fe. 29 Cu. 45 Rh. 44 Ru. 47 Ag. 46 Pd. 78 Pt. 76 Os.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Kryteria samorzutności procesów fizyko-chemicznych
 Kryteria samorzutności procesów fizyko-chemicznych 2.5.1. Samorzutność i równowaga 2.5.2. Sens i pojęcie entalpii swobodnej 2.5.3. Sens i pojęcie energii swobodnej 2.5.4. Obliczanie zmian entalpii oraz
Kryteria samorzutności procesów fizyko-chemicznych 2.5.1. Samorzutność i równowaga 2.5.2. Sens i pojęcie entalpii swobodnej 2.5.3. Sens i pojęcie energii swobodnej 2.5.4. Obliczanie zmian entalpii oraz
Ćwiczenia audytoryjne z Chemii fizycznej 1 Zalecane zadania kolokwium 1. (2018/19)
 Ćwiczenia audytoryjne z Chemii fizycznej 1 Zalecane zadania kolokwium 1. (2018/19) Uwaga! Uzyskane wyniki mogą się nieco różnić od podanych w materiałach, ze względu na uaktualnianie wartości zapisanych
Ćwiczenia audytoryjne z Chemii fizycznej 1 Zalecane zadania kolokwium 1. (2018/19) Uwaga! Uzyskane wyniki mogą się nieco różnić od podanych w materiałach, ze względu na uaktualnianie wartości zapisanych
MARATON WIEDZY CHEMIA CZ. II
 MARATON WIEDZY CHEMIA CZ. II 1. Podaj liczbę elektronów, nukleonów, protonów i neuronów zawartych w następujących atomach: a), b) 2. Podaj liczbę elektronów, nukleonów, protonów i neutronów zawartych w
MARATON WIEDZY CHEMIA CZ. II 1. Podaj liczbę elektronów, nukleonów, protonów i neuronów zawartych w następujących atomach: a), b) 2. Podaj liczbę elektronów, nukleonów, protonów i neutronów zawartych w
Długo łuku krzywej., klasy. t ; t oraz łuk nie ma czci wielokrotnych, to długo łuku. wyraa si wzorem
 Długo łuku kzwj Kzw ( L : [, ] f ( Jli dn js ównni wkoow kzwj pochodn (, ( s cigł w pzdzil W współzdnch igunowch:, kls C, m długo L ( f ( ( α;, pz czm funkcj (, ( oz ich ( ; oz łuk ni m czci wilokonch,
Długo łuku kzwj Kzw ( L : [, ] f ( Jli dn js ównni wkoow kzwj pochodn (, ( s cigł w pzdzil W współzdnch igunowch:, kls C, m długo L ( f ( ( α;, pz czm funkcj (, ( oz ich ( ; oz łuk ni m czci wilokonch,
PRZEDMIOTOWY KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJUM. SCHEMAT OCENIANIA etap wojewódzki
 PRZEDMIOTOWY KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJUM SCHEMAT OCENIANIA etap wojewódzki 1. Ogólne zasady oceniania Uczeń otrzymuje punkty tylko za poprawne rozwiązania, precyzyjnie odpowiadające poleceniom
PRZEDMIOTOWY KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJUM SCHEMAT OCENIANIA etap wojewódzki 1. Ogólne zasady oceniania Uczeń otrzymuje punkty tylko za poprawne rozwiązania, precyzyjnie odpowiadające poleceniom
Chemia Grudzień Styczeń
 Chemia Grudzień Styczeń Klasa VII IV. Łączenie się atomów. Równania reakcji chemicznych 1. Wiązania kowalencyjne 2. Wiązania jonowe 3. Wpływ rodzaju wiązania na właściwości substancji 4. Elektroujemność
Chemia Grudzień Styczeń Klasa VII IV. Łączenie się atomów. Równania reakcji chemicznych 1. Wiązania kowalencyjne 2. Wiązania jonowe 3. Wpływ rodzaju wiązania na właściwości substancji 4. Elektroujemność
Załącznik 3.1.2.a Test C.1 Ogólna ocena stanu chemicznego JCWPd wg danych z 2012 r. w podziale na 161 JCWPd
 Załącznik 3.1.2.a Test C.1 Ogólna ocena JCWPd wg w podziale na 161 JCWPd Monitoring oraz ocena jednolitych części wód podziemnych w dorzeczach w latach 2012 2014 Nr JCWPd wziętych do JCWPd wg, w których
Załącznik 3.1.2.a Test C.1 Ogólna ocena JCWPd wg w podziale na 161 JCWPd Monitoring oraz ocena jednolitych części wód podziemnych w dorzeczach w latach 2012 2014 Nr JCWPd wziętych do JCWPd wg, w których
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Mateusz Winkowski, Jan Szczepanek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
WOJEWÓDZKI KONKURS PRZEDMIOTOWY z Chemii dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów 2018/2019
 pieczątka szkoły (dotyczy etapu szkolnego) Skrót przedmiotowy konkursu gch -. - 2018/2019 (numer porządkowy z kodowania) Nr identyfikacyjny - wyjaśnienie g gimnazjum, symbol przedmiotu (np. CH chemia),
pieczątka szkoły (dotyczy etapu szkolnego) Skrót przedmiotowy konkursu gch -. - 2018/2019 (numer porządkowy z kodowania) Nr identyfikacyjny - wyjaśnienie g gimnazjum, symbol przedmiotu (np. CH chemia),
ELEKTRODY i OGNIWA. Elektrody I rodzaju - elektrody odwracalne wzgl dem kationu; metal zanurzony w elektrolicie zawieraj cym jony tego metalu.
 ELEKTRODY i OGNIWA Elektrody I rodzaju - elektrody odwracalne wzgl dem kationu; metal zanurzony w elektrolicie zawieraj cym jony tego metalu. Me z+ + z e Me Utl + z e Red RÓWNANIE NERNSTA Walther H. Nernst
ELEKTRODY i OGNIWA Elektrody I rodzaju - elektrody odwracalne wzgl dem kationu; metal zanurzony w elektrolicie zawieraj cym jony tego metalu. Me z+ + z e Me Utl + z e Red RÓWNANIE NERNSTA Walther H. Nernst
KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJÓW
 POUFNE Pieczątka szkoły 16 styczeń 2010 r. Kod ucznia Wpisuje uczeń po otrzymaniu zadań Imię Wpisać po rozkodowaniu pracy Czas pracy 90 minut Nazwisko KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY
POUFNE Pieczątka szkoły 16 styczeń 2010 r. Kod ucznia Wpisuje uczeń po otrzymaniu zadań Imię Wpisać po rozkodowaniu pracy Czas pracy 90 minut Nazwisko KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY
ZADANIA Z CHEMII Efekty energetyczne reakcji chemicznej - prawo Hessa
 Prawo zachowania energii: ZADANIA Z CHEMII Efekty energetyczne reakcji chemicznej - prawo Hessa Ogólny zasób energii jest niezmienny. Jeżeli zwiększa się zasób energii wybranego układu, to wyłącznie kosztem
Prawo zachowania energii: ZADANIA Z CHEMII Efekty energetyczne reakcji chemicznej - prawo Hessa Ogólny zasób energii jest niezmienny. Jeżeli zwiększa się zasób energii wybranego układu, to wyłącznie kosztem
Pole magnetyczne. Za wytworzenie pola magnetycznego odpowiedzialny jest ładunek elektryczny w ruchu
 Pole magnetyczne Za wytworzene pola magnetycznego odpowedzalny jest ładunek elektryczny w ruchu Źródła pola magnetycznego Źródła pola magnetycznego I Sła Lorentza - wektor ndukcj magnetycznej Sła elektryczna
Pole magnetyczne Za wytworzene pola magnetycznego odpowedzalny jest ładunek elektryczny w ruchu Źródła pola magnetycznego Źródła pola magnetycznego I Sła Lorentza - wektor ndukcj magnetycznej Sła elektryczna
BUDOWA ATOMU. Pierwiastki chemiczne
 BUDOWA ATOMU Pierwiastki chemiczne p.n.e. Sb Sn n Pb Hg S Ag C Au Fe Cu ()* do XVII w. As (5 r.) P (669 r.) () XVIII w. N Cl Cr Co Y Mn Mo () Ni Pt Te O U H W XIX w. (m.in.) Na Ca Al Si F Cs Ba B Bi I
BUDOWA ATOMU Pierwiastki chemiczne p.n.e. Sb Sn n Pb Hg S Ag C Au Fe Cu ()* do XVII w. As (5 r.) P (669 r.) () XVIII w. N Cl Cr Co Y Mn Mo () Ni Pt Te O U H W XIX w. (m.in.) Na Ca Al Si F Cs Ba B Bi I
Pożarnicza Strona Firemana
 Test egzaminacyjny na Dzienne Studium w Szkołach Aspirantów PSP 2004 rok Fizyka 1. Ciało o masie 2 kg, pod działaniem siły 5 N, porusza się z przyśpieszeniem równym: a. 0,4 m/s 2 b. 2,5 m/s 2 c. 10 m/s
Test egzaminacyjny na Dzienne Studium w Szkołach Aspirantów PSP 2004 rok Fizyka 1. Ciało o masie 2 kg, pod działaniem siły 5 N, porusza się z przyśpieszeniem równym: a. 0,4 m/s 2 b. 2,5 m/s 2 c. 10 m/s
