Wycena opcji azjatyckich metodą PDE
|
|
|
- Józef Turek
- 8 lat temu
- Przeglądów:
Transkrypt
1 Raport i dokumentacja do projektu Wycena opcji azjatyckich metodą PDE Autor: Agnieszka Ulikowska
2 1. EOREYCZNY OPIS ZAGADNIENIA Wypłata z opcji azjatyckiej zależy od ceny instrumentu podstawowego w ustalonych momentach czasu. W ramach projektu rozpatrzone zostały następujące opcje azjatyckie o wypłatach: Opcja floating strike call X =max S S, Opcja floating strike put X =max S S, Opcja fixed strike call X =max S K, Opcja fixed strike put X =max K S, gdzie S = 1 S u du Cena V =V t, S t, A t opcji azjatyckiej zależy od trzech zmiennych. t - czas S t - proces cen akcji dany wzorem S t =S exp r 1 t W t t A t - całka z funkcji procesu S t, A t = f S u,u du Dla opcji azjatyckich fixed / floating strike f S t,t =S t, t A t = S u du. Wiedząc, że da t = f S t,t dt i korzystając ze wzoru Ito zastosowanego do funkcji V =V t, S t, A t otrzymujemy równanie różniczkowe dv t = dv dt dv S ds 1 S d V dv f S,t ds da dt S dv ds dw t Używając argumentów takich jak w przypadku równania Blacka-Scholesa dla europejskich opcji waniliowych dowodzimy, że dv dt dv rs ds 1 S d V dv f S, t rv = ds da Obecność składnika f S,t dv uniemożliwia transformację do równania dyfuzji. Rozwiązanie da powyższego równania różniczkowego zdefiniowane jest na 3-wymiarowej przestrzeni S, A, t, co prowadzi do znacznych kosztów przy numerycznym rozwiązywaniu. W konkretnych przypadkach można jednak zredukować wymiar równania (do równania dwuwymiarowego) przez odpowiednią zamianę zmiennych taka zamiana zmiennych jest możliwa przy wycenie opcji floating / fixed strike.
3 *OPCJA AZJAYCKA FLOAING SRIKE CALL Wypłata z opcji floating strike call wynosi X =max S S, =S max 1 1 S S u du. Definiujemy nową zmienną R t = 1 t S S u du. t Wypłatę można wtedy zapisać jako S max 1 1 R, =S function R,. Jest to motywacja do szukania rozwiązania V =V t, S t, A t w postaci S t H R t,t, gdzie H R,t jest pewną nieznaną funkcją. Po przekształceniach otrzymujemy następujące równanie różniczkowe z warunkami terminowobrzegowymi (pełne wyprowadzenie dostępne w ools for Computational Finance, Seydel rozdział 6): dh dt 1 R d H dh 1 rr dr dr = H = dla R dh dt dh =dla R= dr H R, =max 1 R, Rozwiązując to równanie numerycznie otrzymujemy wartości funkcji mamy obliczoną także cenę opcji. H R,t - w rzeczywistości *OPCJA AZJAYCKA FIXED SRIKE CALL Wypłata z opcji azjatyckiej fixed strike call wynosi: K 1 X =max S K, = min K S, =S min S S u du, Jak poprzednio, definiujemy nową zmienną K 1 S u du. Y t = S t t Wypłatę można zapisać jako X =S min Y, =S function Y,. Jest to motywacja do szukania rozwiązania V =V t, S t, A t w postaci S t H Y t,t dla pewnej funkcji H. Można pokazać (szczegóły w artykule B.Alziary et al. / Journal of Banking & Finance 1 (1997) ), że H jest rozwiązaniem równania różniczkowego:
4 dh dt 1 Y d H dy 1 dh ry dy = H Y, = min Y,.. NUMERYCZNE ROZWIĄZANIE Do rozwiązania równań użyłam schematów: schemat Laxa Wendroffa schemat VD Przy wyborze schematów numerycznych do rozwiązywania powyższych równań, należy zwrócić szczególną uwagę na sposób przybliżenia pierwszej pochodnej zmiennej przestrzennej. Jako modelowe równanie przyjmijmy du du a x dt dx =b x d u dx Stosując standardowy schemat drugiego rzędu FCS (Forward ime Centered Scheme), tzn. przybliżając pierwszą pochodną za pomocą różnic centralnych możemy narazić się na problemy ze stabilnością i oscylacje numerycznego rozwiązania, w szczególności przy niewielkiej wartości współczynnika b x. Przy zerowym współczynniku dyfuzji w ogóle nie należy stosować powyższego schematu. Przyczyną są warunki gwarantujące stabilność nakładające ograniczenia na wielkość kroku czasowego i przestrzennego:.5, a x b, gdzie = b t x. Przy wyborze = 1, ograniczenie na krok siatki przestrzennej przybiera formę x b a. Uwaga: Ze względu na istotność problemu przybliżania pierwszej pochodnej zmiennej przestrzennej, przy analizie schematów rozważane będą równania postaci: (.1 ) du dt d dx f x =. Druga pochodna zmiennej przestrzennej przybliżana jest w programie w sposób standardowy. Oznaczenia: u j,v oznacza numeryczne rozwiązanie w punkcie j,v. Jest to aproksymacja rzeczywistego rozwiązania u x j,t v.
5 *SCHEMA LAXA WENDROFF'A Schemat Laxa-Wendroff'a oparty jest na wzorze aylora i postaci równania.1. u j,v 1 =u j,v t du j, v dt O t =u j,v t df u j, v O t dt Wykorzystuje także wartości obliczane w punktach nie będących węzłami siatki czasowoprzestrzennej, tzn. w punktach j± 1, v± 1. Formalnie, schemat można zapisać jako: u = 1 j 1, v 1 u j, v u j 1, v t x f u j 1,v f u j,v w = 1 u u t j 1, v j,v x f u f u j, v j 1, v j 1,v 1 u j,v 1 =u j,v t x f u f u j 1,v 1 j 1, v 1 *MEODY VD Idea metod VD: schemat numeryczny musi gwarantować, że całkowita wariacja rozwiązania nie będzie zwiększać się w miarę upływu czasu. Numeryczne rozwiązanie musi zatem spełniać poniższy warunek: V u n 1 V u n, gdziev u n = j u j 1,v u j,v Metoda zaimplementowana w projekcie oparta jest na odpowiednim połączeniu schematów pierwszego i drugiego rzędu. Wyjściowe równanie.1 przedstawiamy jako: du i dt f 1 f 1 i i x =, gdzie f i 1 L = f 1 i i 1 f i 1 H L f 1 i ( f i 1 zdefiniowane jest analogicznie, z odpowiednio przesuniętym indeksem powyżej składniki f i± 1 to tzw. numerical fluxes, które powstają poprzez odpowiednie i ). Występujące połączenie flux'ów niższego i wyższego rzędu. Dla ustalenia uwagi przyjmijmy, że równanie ma du du postać a =, gdzie a. dt dx Najczęściej przyjmuje się, że: f L i 1 =au i oraz f H 1=a u u i 1 i i. Po podstawieniu otrzymujemy:
6 f i =au 1 i a u i 1 i 1 u i. Funkcja (flux limiter) powinna przyjmować wartości bliskie, gdy numeryczne rozwiązanie wykazuje duże skoki gradientu (wtedy schemat jest pierwszego rzędu) i wartości bliskie 1 w przeciwnym przypadku (wtedy schemat jest drugiego rzędu). W przypadku a można zdefiniować zależność 1= r i, gdzie r i = u u i i 1. Współczynnik ten jest ujemny w i u i 1 u i pobliżu lokalnych ekstremów, stosunkowo niewielki dla gładkich danych i zwiększa się, gdy numeryczne rozwiązanie wykazuje znaczne i gwałtowne zmiany wartości. Można stosować różne limitery, w programie zostały zaimplementowane cztery rodzaje: MinMod : a,b =S a,b min a, b Van Leer : a,b =S a,b ab a b MC : a,b =S a,b min.5 a b, a, b Superbee: a,b =S a,b max min a, b,min b, a, gdzie S a, b = 1 sign a sign b, 1, r = r. Zalety metody: 1. zapobiega powstawaniu oscylacji numerycznego rozwiązania. łączy w sobie zalety schematów pierwszego i drugiego rzędu 3. prosta idea
7 3.WYNIKI *WYCENA OPCJI FIXED SRIKE CALL cena spot S: Monte Carlo PDE metoda VD PDE Lax_Wendorff 85,71,7,59 9 5,19 5,1 4, ,55 8,9 8,7 1 1,6 1,7 11, ,7 16,81 16,6 11 1,78 1,63, ,59 6,5 5, ,45 31,41 3,33 Parametry: K =9 r=.5 =. =1 cena opcji fixed strike call wycena MC wycena pde cena spot S: Monte Carlo PDE metoda VD PDE Lax_Wendorff 85 8,44 8,44 8, ,8 11,5 1, ,9 14,4 13, ,43 17,37 16, ,6 1,, ,93 4,84 4, , 8,98 8,5 1 33,9 33, 3,19 Parametry: K =9 r=.5 =.5 =1
8 cena opcji fixed strike call wycena MC pde *WYCENA OPCJI FIXED SRIKE PU Parametry: K =9 r=.5 =. =1 PDE PDE cena S Monte Carlo metoda VD Lax_Wendorff 7, 17,43 17,5 17,47 75, 1,85 13, 1,91 8, 8,75 8,91 8,8 85, 5,41 5,47 5,6 9, 3,1,91, fixed strike put wycena MC wycena pde
9 cena S Monte Carlo PDE metoda VD PDE Lax_Wendorff 7,1,5, ,79 16,9 16, ,76 13,8 13, ,14 11,1 1,7 9 8,91 8,84 8,45 Parametry: K =9 r=.5 =.5 =1 5 fixed strike put wycena MC wycena PDE 4.LIERAURA * "High-resolution FEM-VD schemes base on a fully multidimensional flux limiter", D.Kuzmin & S.urek, Institute of Applied Mathematics, University of Dortmund, rozdzial : One dimensional VD schemes. * "Comparison of sinite difference methoda for the numerical simulation of reacting flow", K. Alhumaizi, Computers & Chemical engineering 8 (4), * ools for computational finance, R.U. Seydel 5.DOKUMENACJA DANE W PLIKU wejściowym: Dane w pliku powinny mieć następującą kolejność: -> rodzaj opcji -> rodzaj schematu -> stopa % -> zmienność -> cena spot -> strike -> liczba punktów siatki przestrzennej -> liczba punktów siatki czasowej -> _min =
10 -> termin zapadalności -> R_min = -> maksymalna wartość siatki przestrzennej. Jeśli, to zostaną ustawione wartości domyślne. -> wielkość epsilona (przy liczeni pochodnych) OZNACZENIA i DOSEPNE FUNKCJE: M - ilosc wezlow siatki przestrzennej N - ilosc wezlow siatki czasowej siatka_r - siatka przestrzenna siatka_r - siatka przerstrzenna pomocnicza siatka_t - siatka czasowa delta_r - odstep miedzy punktami siatki przestrzennej delta_t - odstep miedzy punktami siatki czasowej wsp_delta - wspolczynnik pomocniczy. wsp_delta = delta_t / delta_x wsp_delta - wspolczynnik pomocniczy. wsp_delta = delta_t / delta_x^ wsp_a - wspolczynnik rownania rozniczkowego wsp_a_halfstep - wspolczynnik rownania rozniczkowego wsp_b - wspolczynnik rownania rozniczkowego wsp_v - wspolczynnik rownania rozniczkowego gamma - wspolczynnik pomocniczy. gamma = wsp_a * wsp_delta lambda - wspolczynnik pomocniczy. lambda = wsp_b * wsp_delta beta - wspolczynnik pomocniczy. beta = delta_r * (wsp_a./wsp_b) Boundary_ - warunek koncowy lo_bc_ - warunek brzegowy hi_bc_r - warunek brzegowy Option - rodzaj opcji R_min - minimalna wartosc w siatce przestrzennej R_max - maksymalna wartosc w siatce przestrzennej _min - minimalna wartosc w siatce czasowej. _min = _max - maksymalna wartosc w siatce czasowej r - stopa procentowa sigma - zmiennosc S - cena spot K - strike scheme - rodzaj schematu function [y] = SynchSigns(a) #funkcja sprawdza czy liczby/wspolrzedne wektorow sa jednakowych znakow. Jesli jednakowych znakow i dodatnie zwraca 1, jesli jednakowych znakow i ujemne zwraca -1, w przeciwnym przypadku. #na wejsciu: macierz wymiaru M na. W kolumnach porownywane liczby/wektory #przykladowe wywolanie: > a = [,-1;,1]; > SynchSigns(a); function [y] = MinMod(a) #rodzaj LIMIERA #na wejsciu: macierz wymiaru M na. W kolumnach liczby/wektory #przykladowe wywolanie: > a = [,-1;,1]; > MinMod(a); function [y] = MC(a) #rodzaj LIMIERA #na wejsciu: macierz wymiaru M na. W kolumnach liczby/wektory #przykladowe wywolanie: > a = [,-1;,1]; > MC(a); function [y] = VanLeer(a) #rodzaj LIMIERA
11 #na wejsciu: macierz wymiaru M na. W kolumnach liczby/wektory #przykladowe wywolanie: > a = [,-1;,1]; > VanLeer(a); function [y] = superbee(a) #rodzaj LIMIERA #na wejsciu: macierz wymiaru M na. W kolumnach liczby/wektory #przykladowe wywolanie: > a = [,-1;,1]; superbee(a); function [R_max] = SetMaximalGridPoint(S, K, _max, Option) #wstawia odpowiednia siatke przestrzenna w zaleznosci od rodzaju opcji function [Boundary_, lo_bc_, hi_bc_r] = SetBoundaryConditions(M, N, r, K, _max, siatka_t, siatka_r, Option) #ustawia warunki poczatkowo-brzegowe w zaleznosci o rodzaju opcji function [wsp_a, wsp_a_halfstep, wsp_b, wsp_v, gamma, lambda, beta] = Coefficients(r, sigma, _max, siatka_r, siatka_r, wsp_delta, Option) #oblicza wspolczynniki rownania rozniczkowego *** function [V] = LaxWendroff(M, N, delta_t, wsp_a, wsp_a_halfstep, wsp_b, wsp_v, wsp_delta, lambda, Boundary_, hi_bc_r, lo_bc_, Option) #implementacja schematu Laxa-Wendroffa #opis schematu w dokumencie Ulikowska_opis_problemu_i_algorytmow.txt *** function [V] = Upwind(M, N, delta_t, wsp_a, wsp_v, wsp_delta, gamma, lambda, Boundary_, hi_bc_r, lo_bc_, Option) #implementacja schematu Upwind. Uproszczona wersja funkcji HighResolution [gdy theta jest rowne zero] #opis schematu w dokumencie Ulikowska_opis_problemu_i_algorytmow.txt *** function [V] = HighResolution(M, N, delta_t, wsp_a, wsp_v, wsp_delta, gamma, lambda, Boundary_, hi_bc_r, lo_bc_, scheme, Option) #implemetacja metod HighResolution #zmienna IsPositive: okresla znak wspolczynnika przy pochodnej przestrzennej #zmienna slope: okresla stosunek gradientow w trzech kolejnych punktach siatki przestrzennej. slope = [w(j,v) - w(j-1,t)]/[w(j+1,t) - w(j,t)] #zmienna slope_final_ones: zmienna pomocnicza #zmienna theta_r: w zaleznosci od stosunku gradientow zmienna przyjmuje wartosci: # -> bliskie w okolicach znacznego stosunku gradientow [gdy theta = schemat upwind] # -> bliskie 1 gdy numeryczne rozwiazanie jest dostatecznie gladkie [gdy theta = 1 schemat roznic centralnych] #theta zalezy takze od wyboru LIMIERA #zmienna FLUX: "numerical flux" #opis schematu w dokumencie Ulikowska_opis_problemu_i_algorytmow.txt *** function [floating_put] = FloatingPutPrice(floating_call, S, _max, r) #oblicza cene opcji floating strike PU jesli znana jest cena opcji call (floating_call) function [fixed_put] = FixedPutPrice(fixed_call, S, _max, r, K) #oblicza cene opcji fixed strike PU jesli znana jest cena opcji call
12 (fixed_call) *** function [price] = OptionPrice(S, K, V, R_min, R_max,, _max, r, K, Option) #oblicza wartosc opcji na podstawie macierzy V(j, t) #wartosci V(j, _max) znajduja sie w ostaniej kolumnie #jesli wartosc opcji ma byc obliczona dla t < _max, to nalezy uzyc parametru. Moment wyceny, _max i powiazane sa rownaniem: t = _max - delta_t* *** function [price] = StartCalculatingOptionPrice(Option, scheme, r, sigma, S, K, M, N, _min, _max, R_min, R_max, h) #nadzowruje dzialanie innych funkcji: funkcja "porzadkowa" ktora wywoluje kolejno podrzedne funkcje
Dokumentacja. Opcje europejskie PDE. Michał Grzelak
 Dokumentacja Opcje europejskie PDE Michał Grzelak Spis treści 1 Ceny opcji z local volatility 2 1.1 Opcje plain vanilla z local volatility................. 2 1.2 Parametry greckie..........................
Dokumentacja Opcje europejskie PDE Michał Grzelak Spis treści 1 Ceny opcji z local volatility 2 1.1 Opcje plain vanilla z local volatility................. 2 1.2 Parametry greckie..........................
Dokumentacja. Portal Mathfinance Wycena opcji paryskich metoda. Wiktor Madejski
 Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Dokumentacja. Portal Mathfinance Wycena skomplikowanych opcji barierowych. Piotr Bochnia, Paweł Marcinkowski
 Dokumentacja Portal Mathfinance Wycena skomplikowanych opcji barierowych metoda PDE Piotr Bochnia, Paweł Marcinkowski Spis treści 1 Wstęp 2 2 Wyceniane instrumenty 2 2.1 Opcje z barierą monitorowaną dyskretnie...............
Dokumentacja Portal Mathfinance Wycena skomplikowanych opcji barierowych metoda PDE Piotr Bochnia, Paweł Marcinkowski Spis treści 1 Wstęp 2 2 Wyceniane instrumenty 2 2.1 Opcje z barierą monitorowaną dyskretnie...............
Wstęp do analitycznych i numerycznych metod wyceny opcji
 Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Dokumentacja. Opcje europejskie PDE. Zbigniew Matczak
 Dokumentacja Opcje europejskie PDE Zbigniew Matczak Spis treści 1 Model CEV 2 1.1 Cena opcji w modelu CEV...................... 2 1.2 Poprawność funkcji "option value" na podstawie funkcji delta oraz symulacji
Dokumentacja Opcje europejskie PDE Zbigniew Matczak Spis treści 1 Model CEV 2 1.1 Cena opcji w modelu CEV...................... 2 1.2 Poprawność funkcji "option value" na podstawie funkcji delta oraz symulacji
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018
 Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018 Tomasz Chwiej 22 stycznia 2019 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018 Tomasz Chwiej 22 stycznia 2019 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów
Metody redukcji wariancji
 Metody redukcji wariancji Michał Kołodziejczyk 26 maja 2009 Spis treści 1 Przedstawienie problemu 1 2 Metody redukcji - opis teoretyczny 2 2.1 Metoda Antithetic Variates...............................
Metody redukcji wariancji Michał Kołodziejczyk 26 maja 2009 Spis treści 1 Przedstawienie problemu 1 2 Metody redukcji - opis teoretyczny 2 2.1 Metoda Antithetic Variates...............................
Model Blacka-Scholesa
 WYCENA OPCJI EUROPEJSKIEJ I AMERYKAŃSKIEJ W MODELACH DWUMIANOWYCH I TRÓJMIANOWYCH COXA-ROSSA-RUBINSTEINA I JARROWA-RUDDA Joanna Karska W modelach dyskretnych wyceny opcji losowość wyrażana jest poprzez
WYCENA OPCJI EUROPEJSKIEJ I AMERYKAŃSKIEJ W MODELACH DWUMIANOWYCH I TRÓJMIANOWYCH COXA-ROSSA-RUBINSTEINA I JARROWA-RUDDA Joanna Karska W modelach dyskretnych wyceny opcji losowość wyrażana jest poprzez
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1
 Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Stochastyczne równania różniczkowe, model Blacka-Scholesa
 Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Dokumentacja. Hestona i modeli pokrewnych. Mikołaj Bińkowski Wiktor Gromniak
 Dokumentacja Wycena opcji za pomoca uogólnionego modelu Hestona i modeli pokrewnych Mikołaj Bińkowski Wiktor Gromniak Spis treści 1 Wstęp teoretyczny 3 1.1 Rozpatrywane modele stochastycznej zmienności...........
Dokumentacja Wycena opcji za pomoca uogólnionego modelu Hestona i modeli pokrewnych Mikołaj Bińkowski Wiktor Gromniak Spis treści 1 Wstęp teoretyczny 3 1.1 Rozpatrywane modele stochastycznej zmienności...........
Różniczkowanie numeryczne
 Różniczkowanie numeryczne Przyjmijmy, że funkcja ciągła y = f(x) = 4sin(3x)e -x/2, gdzie x 0,2π, dana jest w postaci dyskretnej jako ciąg wartości y odpowiadających zmiennej niezależnej x, również danej
Różniczkowanie numeryczne Przyjmijmy, że funkcja ciągła y = f(x) = 4sin(3x)e -x/2, gdzie x 0,2π, dana jest w postaci dyskretnej jako ciąg wartości y odpowiadających zmiennej niezależnej x, również danej
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje
 Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje Opracował: Zbigniew Rudnicki Powtórka z poprzedniego wykładu 2 1 Dokument, regiony, klawisze: Dokument Mathcada realizuje
Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje Opracował: Zbigniew Rudnicki Powtórka z poprzedniego wykładu 2 1 Dokument, regiony, klawisze: Dokument Mathcada realizuje
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 6. Wycena opcji modele ciągłe, metoda Monte Carlo Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na
Matematyka finansowa w pakiecie Matlab Wykład 6. Wycena opcji modele ciągłe, metoda Monte Carlo Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na
Modelowanie rynków finansowych z wykorzystaniem pakietu R
 Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
Opcje koszykowe a lokaty strukturyzowane - wycena
 Opcje koszykowe a lokaty strukturyzowane - wycena Basket options and structured deposits - pricing Janusz Gajda Promotor: dr hab. inz. Rafał Weron Politechnika Wrocławska Plan prezentacji Cel pracy Wprowadzenie
Opcje koszykowe a lokaty strukturyzowane - wycena Basket options and structured deposits - pricing Janusz Gajda Promotor: dr hab. inz. Rafał Weron Politechnika Wrocławska Plan prezentacji Cel pracy Wprowadzenie
5. Rozwiązywanie układów równań liniowych
 5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
Z52: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania, zagadnienie brzegowe.
 Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Numeryczne rozwiązywanie równań różniczkowych ( )
 Numeryczne rozwiązywanie równań różniczkowych Równanie różniczkowe jest to równanie, w którym występuje pochodna (czyli różniczka). Przykładem najprostszego równania różniczkowego może być: y ' = 2x które
Numeryczne rozwiązywanie równań różniczkowych Równanie różniczkowe jest to równanie, w którym występuje pochodna (czyli różniczka). Przykładem najprostszego równania różniczkowego może być: y ' = 2x które
FUNKCJA LINIOWA - WYKRES
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
Wykład 3 Równania rózniczkowe cd
 7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym
 Ćwiczenia ZPI 1 Współczynniki greckie Odpowiadają na pytanie o ile zmieni się wartość opcji w wyniku: Współczynnik Delta (Δ) - zmiany wartości instrumentu bazowego Współczynnik Theta (Θ) - upływu czasu
Ćwiczenia ZPI 1 Współczynniki greckie Odpowiadają na pytanie o ile zmieni się wartość opcji w wyniku: Współczynnik Delta (Δ) - zmiany wartości instrumentu bazowego Współczynnik Theta (Θ) - upływu czasu
Dokumentacja. Kalibracja parametrów modelu Hestona za rozszerzonego filtra Kalmana. Mikołaj Bińkowski Wiktor Gromniak
 Dokumentacja Kalibracja parametrów modelu Hestona za pomoca rozszerzonego filtra Kalmana Mikołaj Bińkowski Wiktor Gromniak Spis treści 1 Wstęp 2 2 Struktura katalogów 2 3 Zależności 2 4 Funkcje 3 4.1 heston_calibr_kalman..........................
Dokumentacja Kalibracja parametrów modelu Hestona za pomoca rozszerzonego filtra Kalmana Mikołaj Bińkowski Wiktor Gromniak Spis treści 1 Wstęp 2 2 Struktura katalogów 2 3 Zależności 2 4 Funkcje 3 4.1 heston_calibr_kalman..........................
Obliczenia iteracyjne
 Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Obliczanie całek. Instytut Fizyki Akademia Pomorska w Słupsku
 Obliczanie całek. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się ze sposobami i możliwościami przybliżonego obliczania całek w środowisku GNU octave. Wprowadzenie Kwadratury Zajmijmy się przybliżonym
Obliczanie całek. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się ze sposobami i możliwościami przybliżonego obliczania całek w środowisku GNU octave. Wprowadzenie Kwadratury Zajmijmy się przybliżonym
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
x y
 Przykłady pytań na egzamin końcowy: (Uwaga! Skreślone pytania nie obowiązują w tym roku.). Oblicz wartość interpolacji funkcjami sklejanymi (przypadek (case) a), dla danych i =[- 4 5], y i =[0 4 -]. Jaka
Przykłady pytań na egzamin końcowy: (Uwaga! Skreślone pytania nie obowiązują w tym roku.). Oblicz wartość interpolacji funkcjami sklejanymi (przypadek (case) a), dla danych i =[- 4 5], y i =[0 4 -]. Jaka
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Metody numeryczne Wykład 4
 Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Układy równań i nierówności liniowych
 Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Stabilność II Metody Lapunowa badania stabilności
 Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Metody numeryczne rozwiązywania równań różniczkowych
 Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
ANALIZA WRAŻLIWOŚCI CENY OPCJI O UWARUNKOWANEJ PREMII
 STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Ewa Dziawgo Uniwersytet Mikołaja Kopernika w Toruniu ANALIZA WRAŻLIWOŚCI CENY OPCJI O UWARUNKOWANEJ PREMII Streszczenie W artykule przedstawiono
STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Ewa Dziawgo Uniwersytet Mikołaja Kopernika w Toruniu ANALIZA WRAŻLIWOŚCI CENY OPCJI O UWARUNKOWANEJ PREMII Streszczenie W artykule przedstawiono
Metoda Różnic Skończonych (MRS)
 Metoda Różnic Skończonych (MRS) METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek () Równania różniczkowe zwyczajne
Metoda Różnic Skończonych (MRS) METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek () Równania różniczkowe zwyczajne
Metoda elementów skończonych
 Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
Równania różniczkowe liniowe II rzędu
 Równania różniczkowe liniowe II rzędu Definicja równania różniczkowego liniowego II rzędu Warunki początkowe dla równania różniczkowego II rzędu Równania różniczkowe liniowe II rzędu jednorodne (krótko
Równania różniczkowe liniowe II rzędu Definicja równania różniczkowego liniowego II rzędu Warunki początkowe dla równania różniczkowego II rzędu Równania różniczkowe liniowe II rzędu jednorodne (krótko
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Inżynieria Finansowa - Egzamin - 28 stycznia Rozwiązania zadań Wersja z dnia 1 marca 2005, z drobnymi poprawkami
 Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t)
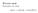 Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH
 METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH Jednym z zastosowań metod numerycznych jest wyznaczenie pierwiastka lub pierwiastków równania nieliniowego. W tym celu stosuje się szereg metod obliczeniowych np:
METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH Jednym z zastosowań metod numerycznych jest wyznaczenie pierwiastka lub pierwiastków równania nieliniowego. W tym celu stosuje się szereg metod obliczeniowych np:
Zaawansowane metody numeryczne
 Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce
 Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce Piotr Bańbuła atedra Ekonomii Ilościowej, AE Czerwiec 2017 r. Warszawa, Szkoła Główna Handlowa Wypłata Wypłata Opcja binarna 0
Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce Piotr Bańbuła atedra Ekonomii Ilościowej, AE Czerwiec 2017 r. Warszawa, Szkoła Główna Handlowa Wypłata Wypłata Opcja binarna 0
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie
 Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Dokumentacja. równań różniczkowych czastkowych
 Dokumentacja Wycena opcji za pomoca równań różniczkowych czastkowych Maria Pawłowska Mikołaj Stelmach Piotr Sulewski Spis treści 1 Opcje europejskie 2 1.1 Opis problemu..............................................
Dokumentacja Wycena opcji za pomoca równań różniczkowych czastkowych Maria Pawłowska Mikołaj Stelmach Piotr Sulewski Spis treści 1 Opcje europejskie 2 1.1 Opis problemu..............................................
METODA SYMPLEKS. Maciej Patan. Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski
 METODA SYMPLEKS Maciej Patan Uniwersytet Zielonogórski WSTĘP Algorytm Sympleks najpotężniejsza metoda rozwiązywania programów liniowych Metoda generuje ciąg dopuszczalnych rozwiązań x k w taki sposób,
METODA SYMPLEKS Maciej Patan Uniwersytet Zielonogórski WSTĘP Algorytm Sympleks najpotężniejsza metoda rozwiązywania programów liniowych Metoda generuje ciąg dopuszczalnych rozwiązań x k w taki sposób,
Tydzień nr 9-10 (16 maja - 29 maja), Równania różniczkowe, wartości własne, funkcja wykładnicza od operatora - Matematyka II 2010/2011L
 Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Opis systemów dynamicznych w przestrzeni stanu. Wojciech Kurek , Gdańsk
 Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Całkowanie numeryczne przy użyciu kwadratur
 Całkowanie numeryczne przy użyciu kwadratur Plan wykładu: 1. Kwadratury Newtona-Cotesa a) wzory: trapezów, parabol etc. b) kwadratury złożone 2. Ekstrapolacja a) ekstrapolacja Richardsona b) metoda Romberga
Całkowanie numeryczne przy użyciu kwadratur Plan wykładu: 1. Kwadratury Newtona-Cotesa a) wzory: trapezów, parabol etc. b) kwadratury złożone 2. Ekstrapolacja a) ekstrapolacja Richardsona b) metoda Romberga
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Układy równań liniowych
 Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Równania różniczkowe zwyczajne
 Równania różniczkowe zwyczajne ODE: ordinary differential equations Zbigniew Koza Wydział Fizyki i Astronomii Wrocław, 2016 RÓWNANIA RÓŻNICZKOWE JEDNEJ ZMIENNEJ Motywacja Rozwiązania równań z 1, 2 lub
Równania różniczkowe zwyczajne ODE: ordinary differential equations Zbigniew Koza Wydział Fizyki i Astronomii Wrocław, 2016 RÓWNANIA RÓŻNICZKOWE JEDNEJ ZMIENNEJ Motywacja Rozwiązania równań z 1, 2 lub
KRYTERIA ALGEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH
 KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
Wycena papierów wartościowych - instrumenty pochodne
 Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Dokumentacja. Wycena opcji europejskich. w modelu Hestona
 Dokumentacja Wycena opcji europejskich w modelu Hestona Konrad Stawski Spis treści 1 Opis problemu 2 2 Opis dyskretyzacji problemu 3 3 Zmienne wykorzystywane w programie 6 4 Spis wykorzystywanych funkcji
Dokumentacja Wycena opcji europejskich w modelu Hestona Konrad Stawski Spis treści 1 Opis problemu 2 2 Opis dyskretyzacji problemu 3 3 Zmienne wykorzystywane w programie 6 4 Spis wykorzystywanych funkcji
Przykład 4.1. Ściag stalowy. L200x100x cm 10 cm I120. Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym
 Przykład 4.1. Ściag stalowy Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym rysunku jeśli naprężenie dopuszczalne wynosi 15 MPa. Szukana siła P przyłożona jest
Przykład 4.1. Ściag stalowy Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym rysunku jeśli naprężenie dopuszczalne wynosi 15 MPa. Szukana siła P przyłożona jest
BŁĘDY OBLICZEŃ NUMERYCZNYCH
 BŁĘDY OBLICZEŃ NUMERYCZNYCH błędy zaokrągleń skończona liczba cyfr (bitów) w reprezentacji numerycznej błędy obcięcia rozwinięcia w szeregi i procesy iteracyjne - w praktyce muszą być skończone błędy metody
BŁĘDY OBLICZEŃ NUMERYCZNYCH błędy zaokrągleń skończona liczba cyfr (bitów) w reprezentacji numerycznej błędy obcięcia rozwinięcia w szeregi i procesy iteracyjne - w praktyce muszą być skończone błędy metody
Rozwiązywanie układów równań liniowych
 Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
FUNKCJA LINIOWA - WYKRES. y = ax + b. a i b to współczynniki funkcji, które mają wartości liczbowe
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
Metody iteracyjne rozwiązywania układów równań liniowych (5.3) Normy wektorów i macierzy (5.3.1) Niech. x i. i =1
 Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
3. Interpolacja. Interpolacja w sensie Lagrange'a (3.1) Dana jest funkcja y= f x określona i ciągła w przedziale [a ;b], która
![3. Interpolacja. Interpolacja w sensie Lagrange'a (3.1) Dana jest funkcja y= f x określona i ciągła w przedziale [a ;b], która 3. Interpolacja. Interpolacja w sensie Lagrange'a (3.1) Dana jest funkcja y= f x określona i ciągła w przedziale [a ;b], która](/thumbs/98/137435342.jpg) 3. Interpolacja Interpolacja w sensie Lagrange'a (3.1) Dana jest funkcja y= f x określona i ciągła w przedziale [a ;b], która przyjmuje wartości y 1, y 2,, y n, dla skończonego zbioru argumentów x 1, x
3. Interpolacja Interpolacja w sensie Lagrange'a (3.1) Dana jest funkcja y= f x określona i ciągła w przedziale [a ;b], która przyjmuje wartości y 1, y 2,, y n, dla skończonego zbioru argumentów x 1, x
Symulacyjne metody analizy ryzyka inwestycyjnego wybrane aspekty. Grzegorz Szwałek Katedra Matematyki Stosowanej Uniwersytet Ekonomiczny w Poznaniu
 Symulacyjne metody analizy ryzyka inwestycyjnego wybrane aspekty Grzegorz Szwałek Katedra Matematyki Stosowanej Uniwersytet Ekonomiczny w Poznaniu Plan prezentacji 1. Opis metody wyceny opcji rzeczywistej
Symulacyjne metody analizy ryzyka inwestycyjnego wybrane aspekty Grzegorz Szwałek Katedra Matematyki Stosowanej Uniwersytet Ekonomiczny w Poznaniu Plan prezentacji 1. Opis metody wyceny opcji rzeczywistej
Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1
 Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1 Równania różniczkowe pierwszego rzędu Równaniem różniczkowym zwyczajnym pierwszego rzędu nazywamy równanie postaci (R) y = f(x, y). Najogólniejszą
Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1 Równania różniczkowe pierwszego rzędu Równaniem różniczkowym zwyczajnym pierwszego rzędu nazywamy równanie postaci (R) y = f(x, y). Najogólniejszą
Obliczanie cen i parametrów greckich opcji walutowych w modelu Blacka-Scholesa
 Bogusław Wróblewski Obliczanie cen i parametrów greckich opcji walutowych w modelu Blacka-Scholesa Raport i dokumentacja 06.06.0 Spis treści. Opis problemu.......................................................
Bogusław Wróblewski Obliczanie cen i parametrów greckich opcji walutowych w modelu Blacka-Scholesa Raport i dokumentacja 06.06.0 Spis treści. Opis problemu.......................................................
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny
 Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Wykład z równań różnicowych
 Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Regulacja dwupołożeniowa.
 Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
1 Równania różniczkowe zwyczajne o rozdzielonych zmiennych
 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Siły wewnętrzne - związki różniczkowe
 Siły wewnętrzne - związki różniczkowe Weźmy dowolny fragment belki obciążony wzdłuż osi obciążeniem n(x) oraz poprzecznie obciążeniem q(x). Na powyższym rysunku zwroty obciążeń są zgodne z dodatnimi zwrotami
Siły wewnętrzne - związki różniczkowe Weźmy dowolny fragment belki obciążony wzdłuż osi obciążeniem n(x) oraz poprzecznie obciążeniem q(x). Na powyższym rysunku zwroty obciążeń są zgodne z dodatnimi zwrotami
Funkcje wymierne. Jerzy Rutkowski. Działania dodawania i mnożenia funkcji wymiernych określa się wzorami: g h + k l g h k.
 Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych)
 Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
OBLICZANIE POCHODNYCH FUNKCJI.
 OBLICZANIE POCHODNYCH FUNKCJI. ROZWIĄZYWANIE RÓWNAŃ RÓŻNICZKOWYCH. ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ LINIOWYCH. Obliczanie pochodnych funkcji. Niech będzie dana funkcja y(x określona i różniczkowalna na przedziale
OBLICZANIE POCHODNYCH FUNKCJI. ROZWIĄZYWANIE RÓWNAŃ RÓŻNICZKOWYCH. ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ LINIOWYCH. Obliczanie pochodnych funkcji. Niech będzie dana funkcja y(x określona i różniczkowalna na przedziale
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
PIERWSZEGO. METODA CZYNNIKA CAŁKUJĄCEGO. METODA ROZDZIELONYCH ZMIENNYCH.
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE RZĘDU PIERWSZEGO. METODA CZYNNIKA CAŁKUJĄCEGO. METODA ROZDZIELONYCH ZMIENNYCH. Równaniem różniczkowym zwyczajnym nazywamy równanie zawierające pochodne funkcji y(x) względem
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE RZĘDU PIERWSZEGO. METODA CZYNNIKA CAŁKUJĄCEGO. METODA ROZDZIELONYCH ZMIENNYCH. Równaniem różniczkowym zwyczajnym nazywamy równanie zawierające pochodne funkcji y(x) względem
numeryczne rozwiązywanie równań całkowych r i
 numeryczne rozwiązywanie równań całkowych r i Γ Ω metoda elementów brzegowych: punktem wyjściowym było rozwiązanie równania całkowego na brzegu obszaru całkowania równanie: wygenerowane z równania różniczkowego
numeryczne rozwiązywanie równań całkowych r i Γ Ω metoda elementów brzegowych: punktem wyjściowym było rozwiązanie równania całkowego na brzegu obszaru całkowania równanie: wygenerowane z równania różniczkowego
Równania różniczkowe. Notatki z wykładu.
 Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
METODY NUMERYCZNE. Wykład 3. Plan. Aproksymacja Interpolacja wielomianowa Przykłady. dr hab.inż. Katarzyna Zakrzewska, prof.agh. Met.Numer.
 METODY NUMERYCZNE Wykład 3. dr hab.inż. Katarzyna Zakrzewska, prof.agh Met.Numer. wykład 3 1 Plan Aproksymacja Interpolacja wielomianowa Przykłady Met.Numer. wykład 3 2 1 Aproksymacja Metody numeryczne
METODY NUMERYCZNE Wykład 3. dr hab.inż. Katarzyna Zakrzewska, prof.agh Met.Numer. wykład 3 1 Plan Aproksymacja Interpolacja wielomianowa Przykłady Met.Numer. wykład 3 2 1 Aproksymacja Metody numeryczne
Modelowanie ryzyka kredytowego Zadania 1.
 1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
RÓWNANIA NIELINIOWE Maciej Patan
 RÓWNANIA NIELINIOWE Maciej Patan Uniwersytet Zielonogórski Przykład 1 Prędkość v spadającego spadochroniarza wyraża się zależnością v = mg ( 1 e c t) m c gdzie g = 9.81 m/s 2. Dla współczynnika oporu c
RÓWNANIA NIELINIOWE Maciej Patan Uniwersytet Zielonogórski Przykład 1 Prędkość v spadającego spadochroniarza wyraża się zależnością v = mg ( 1 e c t) m c gdzie g = 9.81 m/s 2. Dla współczynnika oporu c
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE. Marta Zelmańska
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
Rozdziaª 9: Wycena opcji
 Rozdziaª 9: Wycena opcji MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 9) Wycena opcji 1 / 23 Denicja opcji. Opcja nansowa:. Warunkowy kontrakt terminowy na sprzeda» lub kupno instrumentu bazowego,
Rozdziaª 9: Wycena opcji MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 9) Wycena opcji 1 / 23 Denicja opcji. Opcja nansowa:. Warunkowy kontrakt terminowy na sprzeda» lub kupno instrumentu bazowego,
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Uczenie sieci typu MLP
 Uczenie sieci typu MLP Przypomnienie budowa sieci typu MLP Przypomnienie budowy neuronu Neuron ze skokową funkcją aktywacji jest zły!!! Powszechnie stosuje -> modele z sigmoidalną funkcją aktywacji - współczynnik
Uczenie sieci typu MLP Przypomnienie budowa sieci typu MLP Przypomnienie budowy neuronu Neuron ze skokową funkcją aktywacji jest zły!!! Powszechnie stosuje -> modele z sigmoidalną funkcją aktywacji - współczynnik
Równania różniczkowe zwyczajne
 Równania różniczkowe zwyczajne Zajmiemy się teraz problemem numerycznego rozwiązywania równań różniczkowych zwyczajnych o postaci: z warunkeim początkowym. Zauważmy że przykładowe równanie różniczkowe
Równania różniczkowe zwyczajne Zajmiemy się teraz problemem numerycznego rozwiązywania równań różniczkowych zwyczajnych o postaci: z warunkeim początkowym. Zauważmy że przykładowe równanie różniczkowe
Spis treści. Przedmowa 11
 Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy
 Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Wprowadzenie do Mathcada 1
 Wprowadzenie do Mathcada Ćwiczenie. - Badanie zmienności funkcji kwadratowej Ćwiczenie. pokazuje krok po kroku tworzenie prostego dokumentu w Mathcadzie. Dokument ten składa się z następujących elementów:.
Wprowadzenie do Mathcada Ćwiczenie. - Badanie zmienności funkcji kwadratowej Ćwiczenie. pokazuje krok po kroku tworzenie prostego dokumentu w Mathcadzie. Dokument ten składa się z następujących elementów:.
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 689 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 50 2012 ANALIZA WŁASNOŚCI OPCJI SUPERSHARE
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 689 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 5 212 EWA DZIAWGO ANALIZA WŁASNOŚCI OPCJI SUPERSHARE Wprowadzenie Proces globalizacji rynków finansowych stwarza
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 689 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 5 212 EWA DZIAWGO ANALIZA WŁASNOŚCI OPCJI SUPERSHARE Wprowadzenie Proces globalizacji rynków finansowych stwarza
4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ
 4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 1 4. 4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 4.1. Elementy trójkątne Do opisywania dwuwymiarowego kontinuum jako jeden z pierwszych elementów
4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 1 4. 4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ 4.1. Elementy trójkątne Do opisywania dwuwymiarowego kontinuum jako jeden z pierwszych elementów
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
