Rozdziaª 9: Wycena opcji
|
|
|
- Bożena Wróbel
- 6 lat temu
- Przeglądów:
Transkrypt
1 Rozdziaª 9: Wycena opcji MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 9) Wycena opcji 1 / 23
2 Denicja opcji. Opcja nansowa:. Warunkowy kontrakt terminowy na sprzeda» lub kupno instrumentu bazowego, który jest zawarty mi dzy wystawc i nabywc opcji. Posiadacz opcji ma prawo (nie obowi zek) nabycia instrumentu bazowego po okre±lonej cenie w okre±lonym. terminie. Aby opisa opcj nale»y okre±li : instrument bazowy (waluty, akcje, indeksy gieªdowe) rodzaj opcji (opcja kupna, opcja sprzeda»y) typ opcji (opcja europejska, opcja ameryka«ska) cen wykonania (strike price) moment wyga±ni cia opcji (expiration date) MPGzR (rozdz. 9) Wycena opcji 2 / 23
3 Opcje na WIG20 Oznaczenia opcji na WIG20 notowanych na GPW: OW20ABCCC gdzie kolejne fragmenty nazwy oznaczaj : O: dany instrument jest opcj ; W20: instrumentem bazowym jest indeks WIG20; A: miesi c terminu wykonania oraz rodzaj opcji. Litery C, F, I oraz L oznaczaj opcje kupna o terminach wyga±ni cia w trzeci pi tek marca, czerwca, wrze±nia i grudnia, za± litery O, R, U i X opisuj odpowiednie opcje sprzeda»y; B: ostatnia cyfra roku terminu wykonania opcji; CCC: cena wykonania opcji (podzielona przez 10). MPGzR (rozdz. 9) Wycena opcji 3 / 23
4 Terminologia O opcji kupna o cenie wykonania K i bie» cej cenie instrumentu bazowego P mówimy,»e: jest w cenie (in-the-money) je»eli P > K ; jest po cenie (at-the-money) je»eli P = K ; nie jest w cenie (out-of-the-money), je»eli P < K. Dla opcji sprzeda»y, nazewnictwo jest odwrotne. MPGzR (rozdz. 9) Wycena opcji 4 / 23
5 Proces stochastyczny w czasie ci gªym. Proces stochastyczny {Y t } w czasie ci gªym. Ci g zmiennych losowych Y t, gdzie indeks czasu t nale»y do zbioru liczb rzeczywistych. o warto±ciach nieujemnych. MPGzR (rozdz. 9) Wycena opcji 5 / 23
6 Proces Wienera Proces {w t } jest procesem Wienera (ruchy Browna) je»eli: 1. przyrost w t w s jest niezale»ny od w u dla dowolnych u s t 2. s t w t w s N(0, t s); 3. trajektorie procesu {w t } s ci gªe w czasie. Rozkªad procesu Wienera oraz jego przyrostów dw t = w t+dt w t : w t N(w 0, t) dw t N(0, dt) MPGzR (rozdz. 9) Wycena opcji 6 / 23
7 Uogólniony proces Wienera Dla zmiennych z dryfem i wariancj proporcjonaln do upªywu czasu stosowany jest uogólniony proces Wienera {x t } postaci: dx t = µdt + σdw t, gdzie µ okre±la dryf, za± σ odchylenie standardowe procesu x t. Rozkªad uogólnionego procesu Wienera oraz jego przyrostów: x t N(x 0 + µt, σ 2 t) dx t N(µdt, σ 2 dt) MPGzR (rozdz. 9) Wycena opcji 7 / 23
8 Proces Ito Je»eli dryf oraz zmienno± procesu s zmienne w czasie to mówimy o procesie Ito, którego przyrosty s dane przez: dx t = µ(x t, t)dt + σ(x t, t)dw t Warto± Procesu Ito jako: t t x t = x 0 + µ(x s, s)ds + σ(x s, s)dw s 0 0 MPGzR (rozdz. 9) Wycena opcji 8 / 23
9 Geometryczny proces Wienera Przykªadem procesu Ito jest geometryczny proces Wienera dla którego: µ(x t, t) = µx t σ(x t, t) = σx t Dynamika geometrycznego procesu Wienera: dx t = µx t dt + σx t dw t. MPGzR (rozdz. 9) Wycena opcji 9 / 23
10 Lemat Ito Niech x t b dzie procesem Ito postaci: dx t = µ(x t, t)dt + σ(x t, t)dw t, za± y t procesem stochastycznym: y t = f (x t, t), gdzie f jest ró»niczkowaln funkcj wzgl dem x t oraz t. Dynamika y t jest dana przez: [ f (x t, t) dy t = + f (x t, t) µ(x t, t) + 1 t x t 2 gdzie w t jest procesem Wienera. 2 f (x t, t) x 2 t ] σ 2 (x t, t) dt + f (x t, t) σ(x t, t)dw t, x t MPGzR (rozdz. 9) Wycena opcji 10 / 23
11 Lemat Ito - przykªad Jak przykªad zastosowania lematu Ito rozwa»my przypadek, gdy x t geometrycznym procesem Wienera oraz y t = f (x t, t) = ln x t, tj: jest µ(x t, t) = µx t, σ(x t, t) = σx t, f (x t, t) = 0, t f (x t, t) x t = 1 x t, 2 f (x t, t) = 1. x 2 t 2x 2 t Podstawiaj c do wzoru: [ f (x t, t) dy t = Uzyskujemy: t + f (x t, t) x t µ(x t, t) dy t = 2 f (x t, t) x 2 t ) (µ σ2 dt + σdw t. 2 ] σ 2 (x t, t) dt + f (x t, t) σ(x t, t)dw t, x t y t jest uogólnionym procesem Wienera o drye µ σ 2 /2 oraz wariancji σ 2 MPGzR (rozdz. 9) Wycena opcji 11 / 23
12 Formuªa Blacka-Scholesa - zaªo»enia cena instrumentu bazowego P t jest geometrycznym procesem Wienera nie wyst puj koszty transakcji oraz nie ma podatków rynek jest doskonale pªynny, za± wszystkie instrumenty s doskonale podzielne wszyscy uczestnicy rynku mog po»ycza i inwestowa ±rodki wedªug tej samej procentowej r MPGzR (rozdz. 9) Wycena opcji 12 / 23
13 Formuªa Blacka-Scholesa - wyprowadzenie Cena opcji: Y t = Y (P t, t) Stwórzmy portfel skªadaj cy si z krótkiej pozycji na jedn opcj oraz Y t P t sztuk instrumentu bazowego o warto±ci: Poniewa» (zgodnie z Lematem Ito): dp t = µp t dt + σp t dw t [ Yt dy t = t V t = Y t + Y t P t P t dv t = dy t + Y t + Y t P t µp t dynamika portfela jest deterministyczna: [ Yt dv t = + 1 t 2 P t dp t 2 Y t P 2 σ 2 P 2 t t MPGzR (rozdz. 9) Wycena opcji 13 / 23 ] 2 Y t P 2 σ 2 P 2 t t dt + Y t P t σp t dw t. ] dt.
14 Formuªa Blacka-Scholesa - wyprowadzenie Poniewa» stopa zwrotu z portfela V t jest deterministyczna to zgodnie z warunkiem arbitra»u powinna ona by równa stopie wolnej od ryzyka r, czyli: dv t = rv t dt. Poª czenie zale»no±ci prowadzi do uzyskania równania ró»niczkowego Blacka-Scholesa: Y t t + rp t Y t P t Y t P 2 t σ 2 P 2 t = ry t. Formuªa BS dla opcji europejskiej stanowi rozwi zanie powy»szego równania ró»niczkowego przy warunku,»e w momencie wyga±ni cia T, warto± opcji wynosi: { max(y T K, 0) dla opcji kupna Y T = max(k Y T, 0) dla opcji sprzeda»y, MPGzR (rozdz. 9) Wycena opcji 14 / 23
15 Formuªa Blacka-Scholesa Wzór na cen opcji: { P t Φ(d 1 ) e r(t t) KΦ(d 2 ) Y t = P t Φ( d 1 ) + e r(t t) KΦ( d 2 ) dla opcji kupna dla opcji sprzeda»y, gdzie Φ jest dystrybuant rozkªadu normalnego, za± warto±ci d 1 oraz d 2 wynosz : d 1 = ln(p t/k) + (r + σ 2 /2)(T t) σ T t d 2 = ln(p t/k) + (r σ 2 /2)(T t) σ. T t MPGzR (rozdz. 9) Wycena opcji 15 / 23
16 Formuªa Blacka-Scholesa - przykªad > P <- 100; sig <- 0.25; r <- 0.10; K <- 100; tau <- 0.5 > OptP <- function(type,p,k,r,sig,tau){ d1 <- (log(p/k) + (r+sig^2/2)*tau)/(sig*sqrt(tau)) d2 <- (log(p/k) + (r-sig^2/2)*tau)/(sig*sqrt(tau)) if(type == "call"){ return(p*pnorm(d1) - K*exp(-r*tau)*pnorm(d2))} if(type == "put") {return(k*exp(-r*tau)*pnorm(-d2) - P*pnorm(-d1))} } > OptP("call",P,K,r,sig,tau) > OptP("put",P,K,r,sig,tau) Wartosc opcji kupna: 9.58 Wartosc opcji sprzedazy: 4.71 MPGzR (rozdz. 9) Wycena opcji 16 / 23
17 Greckie wska¹niki w wycenie opcji Cena opcji a cena instrumentu bazowego Cena opcji a stopa procentowa Cena opcji opcja kupna opcja sprzedazy Cena opcji opcja kupna opcja sprzedazy Cena instrumentu bazowego stopa procentowa Cena opcji a zmiennosc Cena opcji a termin do wygasniecia Cena opcji opcja kupna opcja sprzedazy Cena opcji opcja kupna opcja sprzedazy zmiennosc termin do wygasniecia MPGzR (rozdz. 9) Wycena opcji 17 / 23
18 Greckie wska¹niki w wycenie opcji Cena instrumentu bazowego (delta), = Y t P t : call = Φ(d1) oraz put = Φ(d1) 1 Zauwa»my,»e call (0, 1), put ( 1, 0) oraz call put = 1 Druga pochodna (gamma), Γ = Y t = 2 Y t P 2 : t ϕ(d1) Γ call = Γ put = P tσ T t gdzie ϕ(x) = Φ (x) jest funkcj g sto±ci rozkªadu normalnego. Zmienno± (vega), ν = Y t σ : Stopa wolna od ryzyka (rho),ρ = Y t r : ν = P tϕ(d1) T t ρ call = (T t)ke r(t t) Φ(d2) oraz ρ put = (T t)ke r(t t) Φ( d2) Moment obserwacji (theta) - θ = Y t t : θ call = P tϕ(d1)σ 2 T t rke r(t t) Φ(d2) oraz θ put = P tϕ(d1)σ 2 T t + rke r(t t) Φ( d2) MPGzR (rozdz. 9) Wycena opcji 18 / 23
19 Greckie wska¹niki w wycenie opcji > library(rquantlib) > EuropeanOption("call", P, K, 0, r, tau, sig) > EuropeanOption("put", P, K, 0, r, tau, sig) Wspolczynniki greckie dla opcji kupna value delta gamma vega theta rho Wspolczynniki greckie dla opcji sprzedazy value delta gamma vega theta rho MPGzR (rozdz. 9) Wycena opcji 19 / 23
20 Przykªad - wycena opcji na WIG20 Przykªad dotyczy wyceny opcji na podstawie danych do 30 kwietnia 2010 r. na WIG20 o terminie wyga±ni cia 18 czerwca 2010 r.. Porownanie teoretycznych i rzeczywistych cen opcji Opcje kupna Opcje sprzedazy K model dane K model dane OW20F OW20R OW20F OW20R OW20F OW20R OW20F OW20R OW20F OW20R OW20F OW20R OW20F OW20R OW20F OW20R OW20R OW20R MPGzR (rozdz. 9) Wycena opcji 20 / 23
21 Przykªad - wycena opcji na WIG20 Opcja kupna Opcja sprzedazy model dane model dane cena wykonania cena wykonania MPGzR (rozdz. 9) Wycena opcji 21 / 23
22 Zmienno± implikowana Spo±ród parametrów wyst puj cych w formule Blacka-Scholesa w momencie t znane s warto±ci ceny instrumentu bazowego P t, ceny wykonania opcji K, stopy wolnej od ryzyka r oraz terminu wyga±ni cia T t. Warto± dla parametru opisuj cego zmienno±ci instrumentu bazowego σ nie jest znana Cena opcji jest funkcj prognozy zmienno±ci: Y = Y (σ P, K, r, τ) Odwracaj c zale»no± obliczymy warto± zmienno±ci implikowanej (implied volatility): σ = Y 1 (Y P, K, r, τ) MPGzR (rozdz. 9) Wycena opcji 22 / 23
23 Zmienno± implikowana - przykªad opcja kupna opcja sprzedazy cena wykonania cena wykonania MPGzR (rozdz. 9) Wycena opcji 23 / 23
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym
 Ćwiczenia ZPI 1 Współczynniki greckie Odpowiadają na pytanie o ile zmieni się wartość opcji w wyniku: Współczynnik Delta (Δ) - zmiany wartości instrumentu bazowego Współczynnik Theta (Θ) - upływu czasu
Ćwiczenia ZPI 1 Współczynniki greckie Odpowiadają na pytanie o ile zmieni się wartość opcji w wyniku: Współczynnik Delta (Δ) - zmiany wartości instrumentu bazowego Współczynnik Theta (Θ) - upływu czasu
Strategie zabezpieczaj ce
 04062008 Plan prezentacji Model binarny Model Black Scholesa Bismut- Elworthy -Li formuła Model binarny i opcja call Niech cena akcji w chwili pocz tkowej wynosi S 0 = 21 Zaªó»my,»e ceny akcji po trzech
04062008 Plan prezentacji Model binarny Model Black Scholesa Bismut- Elworthy -Li formuła Model binarny i opcja call Niech cena akcji w chwili pocz tkowej wynosi S 0 = 21 Zaªó»my,»e ceny akcji po trzech
Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce
 Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce Piotr Bańbuła atedra Ekonomii Ilościowej, AE Czerwiec 2017 r. Warszawa, Szkoła Główna Handlowa Wypłata Wypłata Opcja binarna 0
Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce Piotr Bańbuła atedra Ekonomii Ilościowej, AE Czerwiec 2017 r. Warszawa, Szkoła Główna Handlowa Wypłata Wypłata Opcja binarna 0
Stochastyczne równania różniczkowe, model Blacka-Scholesa
 Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Opcje - wprowadzenie. Mała powtórka: instrumenty liniowe. Anna Chmielewska, SGH,
 Opcje - wprowadzenie Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony wcześniej kurs terminowy. W dniu rozliczenia transakcji terminowej forward:
Opcje - wprowadzenie Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony wcześniej kurs terminowy. W dniu rozliczenia transakcji terminowej forward:
Rozdziaª 10: Portfel inwestycyjny
 Rozdziaª 10: Portfel inwestycyjny MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 10) Portfel inwestycyjny 1 / 31 Wprowadzenie Wkªad Markowitza, laureata nagrody Nobla z ekonomii w 1990 r., do teorii
Rozdziaª 10: Portfel inwestycyjny MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 10) Portfel inwestycyjny 1 / 31 Wprowadzenie Wkªad Markowitza, laureata nagrody Nobla z ekonomii w 1990 r., do teorii
Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy
 Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Inżynieria Finansowa: 8. Model Blacka-Scholesa
 Inżynieria Finansowa: 8. Model Blacka-Scholesa Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Maj 7 r. Warszawa, Szkoła Główna Handlowa Historia opcji Pierwsze użycie: Tales z Miletu Przełomowy model cen:
Inżynieria Finansowa: 8. Model Blacka-Scholesa Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Maj 7 r. Warszawa, Szkoła Główna Handlowa Historia opcji Pierwsze użycie: Tales z Miletu Przełomowy model cen:
NAJWAŻNIEJSZE CECHY OPCJI
 ABC opcji NAJWAŻNIEJSZE CECHY OPCJI Instrument pochodny, Asymetryczny profil wypłaty, Możliwość budowania portfeli o różnych profilach wypłaty, Dla nabywcy opcji z góry znana maksymalna strata, Nabywca
ABC opcji NAJWAŻNIEJSZE CECHY OPCJI Instrument pochodny, Asymetryczny profil wypłaty, Możliwość budowania portfeli o różnych profilach wypłaty, Dla nabywcy opcji z góry znana maksymalna strata, Nabywca
Wycena papierów wartościowych - instrumenty pochodne
 Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Zarządzanie portfelem inwestycyjnym
 Zarządzanie portfelem inwestycyjnym Dr hab. Renata Karkowska 1 12. Charakterystyka opcji i ich zastosowanie Rodzaje opcji Zastosowanie opcji do zabezpieczania ryzyka rynkowego 13. Wycena opcji i współczynniki
Zarządzanie portfelem inwestycyjnym Dr hab. Renata Karkowska 1 12. Charakterystyka opcji i ich zastosowanie Rodzaje opcji Zastosowanie opcji do zabezpieczania ryzyka rynkowego 13. Wycena opcji i współczynniki
Zadanie 1. Zadanie 2. Niech µ A i µ B oznaczaj stopy zwrotu odpowiednio z aktywa A i B, ªatwo obliczy,»e ,
 Zadanie 1 Niech µ A i µ B oznaczaj stopy zwrotu odpowiednio z aktywa A i B, ªatwo obliczy,»e Eµ A 0, 02, Eµ 2 A 0, 0175, V arµ A 171 10 4, Eµ B 0, 135, Eµ 2 B 0, 02275, V arµ B 181 4 10 4, Eµ A µ B 0,
Zadanie 1 Niech µ A i µ B oznaczaj stopy zwrotu odpowiednio z aktywa A i B, ªatwo obliczy,»e Eµ A 0, 02, Eµ 2 A 0, 0175, V arµ A 171 10 4, Eµ B 0, 135, Eµ 2 B 0, 02275, V arµ B 181 4 10 4, Eµ A µ B 0,
ANALIZA OPCJI ANALIZA OPCJI - WYCENA. Krzysztof Jajuga Katedra Inwestycji Finansowych i Zarządzania Ryzykiem Uniwersytet Ekonomiczny we Wrocławiu
 Krzysztof Jajuga Katedra Inwestycji Finansowych i Zarządzania Ryzykiem Uniwersytet Ekonomiczny we Wrocławiu Podstawowe pojęcia Opcja: in-the-money (ITM call: wartość instrumentu podstawowego > cena wykonania
Krzysztof Jajuga Katedra Inwestycji Finansowych i Zarządzania Ryzykiem Uniwersytet Ekonomiczny we Wrocławiu Podstawowe pojęcia Opcja: in-the-money (ITM call: wartość instrumentu podstawowego > cena wykonania
Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym. Opcje Strategie opcyjne
 Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym Opcje Strategie opcyjne 1 Współczynniki greckie Współczynniki greckie określają o ile zmieni się kurs opcji w wyniku zmiany wartości poszczególnych
Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym Opcje Strategie opcyjne 1 Współczynniki greckie Współczynniki greckie określają o ile zmieni się kurs opcji w wyniku zmiany wartości poszczególnych
Wycena opcji. Dr inż. Bożena Mielczarek
 Wycena opcji Dr inż. Bożena Mielczarek Stock Price Wahania ceny akcji Cena jednostki podlega niewielkim wahaniom dziennym (miesięcznym) wykazując jednak stały trend wznoszący. Cena może się doraźnie obniżać,
Wycena opcji Dr inż. Bożena Mielczarek Stock Price Wahania ceny akcji Cena jednostki podlega niewielkim wahaniom dziennym (miesięcznym) wykazując jednak stały trend wznoszący. Cena może się doraźnie obniżać,
OPCJE NA GPW. Zespół Rekomendacji i Analiz Giełdowych Departament Klientów Detalicznych Katowice, luty 2004
 OPCJE NA GPW Zespół Rekomendacji i Analiz Giełdowych Departament Klientów Detalicznych Katowice, luty 2004 CO TO JEST OPCJA, RODZAJE OPCJI Opcja - prawo do kupna, lub sprzedaży instrumentu bazowego po
OPCJE NA GPW Zespół Rekomendacji i Analiz Giełdowych Departament Klientów Detalicznych Katowice, luty 2004 CO TO JEST OPCJA, RODZAJE OPCJI Opcja - prawo do kupna, lub sprzedaży instrumentu bazowego po
Rozdziaª 8. Modele Krzywej Dochodowo±ci
 Rozdziaª 8. Modele Krzywej Dochodowo±ci MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 8) Krzywa dochodowo±ci 1 / 18 Denicja krzywej dochodowo±ci Krzywa dochodowo±ci (yield curve): Ilustracja graczna
Rozdziaª 8. Modele Krzywej Dochodowo±ci MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 8) Krzywa dochodowo±ci 1 / 18 Denicja krzywej dochodowo±ci Krzywa dochodowo±ci (yield curve): Ilustracja graczna
Wstęp do analitycznych i numerycznych metod wyceny opcji
 Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych
 Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Zadanie 1. Zadanie 2. Zadanie 3
 Zadanie R to rata miesi czna, odsetki w k-tej racie to ods k = R( v 8 k ), a spªata kapitaªu wyra»a si wzorem kap k = Rv 8 k, gdzie v = (, 5) /6. Dany jest ukªad nierówno±ci z którego wynika Rv 8 N R(
Zadanie R to rata miesi czna, odsetki w k-tej racie to ods k = R( v 8 k ), a spªata kapitaªu wyra»a si wzorem kap k = Rv 8 k, gdzie v = (, 5) /6. Dany jest ukªad nierówno±ci z którego wynika Rv 8 N R(
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 6. Wycena opcji modele ciągłe, metoda Monte Carlo Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na
Matematyka finansowa w pakiecie Matlab Wykład 6. Wycena opcji modele ciągłe, metoda Monte Carlo Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na
Część IV wartość opcji na zmiennym rynku - greki. Filip Duszczyk Dział Rynku Terminowego
 Część IV wartość opcji na zmiennym rynku - greki Filip Duszczyk Dział Rynku Terminowego 1. Wprowadzenie 2. Greki - Delta - Gamma - Theta - Vega - Rho 3. Stopa Dywidendy 4. Podsumowanie Agenda 2 Wprowadzenie
Część IV wartość opcji na zmiennym rynku - greki Filip Duszczyk Dział Rynku Terminowego 1. Wprowadzenie 2. Greki - Delta - Gamma - Theta - Vega - Rho 3. Stopa Dywidendy 4. Podsumowanie Agenda 2 Wprowadzenie
Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do:
 Jesteś tu: Bossa.pl Opcje na WIG20 - wprowadzenie Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do: żądania w ustalonym terminie dostawy instrumentu bazowego po określonej cenie wykonania
Jesteś tu: Bossa.pl Opcje na WIG20 - wprowadzenie Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do: żądania w ustalonym terminie dostawy instrumentu bazowego po określonej cenie wykonania
Rynkowa wycena egzotycznych instrumentów pochodnych kursów walutowych { opcje barierowe
 Rynkowa wycena egzotycznych instrumentów pochodnych kursów walutowych { opcje barierowe Ewa Kijewska BRE Bank 16 maja 2008 Ewa Kijewska (BRE Bank) Rynkowa wycena egzotycznych instrumentów pochodnych kursów
Rynkowa wycena egzotycznych instrumentów pochodnych kursów walutowych { opcje barierowe Ewa Kijewska BRE Bank 16 maja 2008 Ewa Kijewska (BRE Bank) Rynkowa wycena egzotycznych instrumentów pochodnych kursów
Konstrukcja uśmiechu zmienności. Dr Piotr Zasępa
 Konstrukcja uśmiechu zmienności Dr Piotr Zasępa Rynek opcji FX Rynek Międzybankowy Market Makerów Klientowski (bank/klient) (bank makler/bank user) Rynek opcji waniliowych Opcje egzotyczne I generacji
Konstrukcja uśmiechu zmienności Dr Piotr Zasępa Rynek opcji FX Rynek Międzybankowy Market Makerów Klientowski (bank/klient) (bank makler/bank user) Rynek opcji waniliowych Opcje egzotyczne I generacji
IRON CONDOR i IRON BUTTERFLY
 IRON CONDOR i IRON BUTTERFLY Regularnie zbieraj premię na opcjach na WIG20 Filip Duszczyk Dział Rynku Terminowego GPW Warszawa, 28 maja 2014 BULL SPREAD DŁUGI CALL SPREAD Właściwości: Bull Call Spread
IRON CONDOR i IRON BUTTERFLY Regularnie zbieraj premię na opcjach na WIG20 Filip Duszczyk Dział Rynku Terminowego GPW Warszawa, 28 maja 2014 BULL SPREAD DŁUGI CALL SPREAD Właściwości: Bull Call Spread
Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych:
 Metodologia wyznaczania greckich współczynników. (1) Dane wejściowe. Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych: S wartość zamknięcia indeksu WIG20 (pkt),
Metodologia wyznaczania greckich współczynników. (1) Dane wejściowe. Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych: S wartość zamknięcia indeksu WIG20 (pkt),
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t)
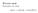 Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Opcje na akcje Zasady obrotu
 Giełda Papierów Wartościowych w Warszawie S.A. Opcje na akcje Zasady obrotu Krzysztof Mejszutowicz Zespół Instrumentów Pochodnych Dział Notowań i Rozwoju Rynku Zasady obrotu (1) Instrumenty bazowe (akcje
Giełda Papierów Wartościowych w Warszawie S.A. Opcje na akcje Zasady obrotu Krzysztof Mejszutowicz Zespół Instrumentów Pochodnych Dział Notowań i Rozwoju Rynku Zasady obrotu (1) Instrumenty bazowe (akcje
Opcje walutowe proste. 1. Czym sa opcje 2. Rodzaje opcji 3. Profile ryzyka i The Greeks 4. Hedging 5. Strategie handlowania zmiennoscia cen
 Opcje walutowe proste 1. Czym sa opcje 2. Rodzaje opcji 3. Profile ryzyka i The Greeks 4. Hedging 5. Strategie handlowania zmiennoscia cen Historia opcji Opcje byly znane od setek lat Ich natura spekulacyjna
Opcje walutowe proste 1. Czym sa opcje 2. Rodzaje opcji 3. Profile ryzyka i The Greeks 4. Hedging 5. Strategie handlowania zmiennoscia cen Historia opcji Opcje byly znane od setek lat Ich natura spekulacyjna
Opcje giełdowe. Wprowadzenie teoretyczne oraz zasady obrotu
 Opcje giełdowe Wprowadzenie teoretyczne oraz zasady obrotu NAJWAŻNIEJSZE CECHY OPCJI Instrument pochodny (kontrakt opcyjny), Asymetryczny profil wypłaty, Możliwość budowania portfeli o różnych profilach
Opcje giełdowe Wprowadzenie teoretyczne oraz zasady obrotu NAJWAŻNIEJSZE CECHY OPCJI Instrument pochodny (kontrakt opcyjny), Asymetryczny profil wypłaty, Możliwość budowania portfeli o różnych profilach
Opcje. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Opcje Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty
Opcje Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty
EGZAMIN MAGISTERSKI, r Matematyka w ekonomii i ubezpieczeniach
 EGZAMIN MAGISTERSKI, 12.09.2018r Matematyka w ekonomii i ubezpieczeniach Zadanie 1. (8 punktów) O rozkªadzie pewnego ryzyka S wiemy,»e: E[(S 20) + ] = 8 E[S 10 < S 20] = 13 P (S 20) = 3 4 P (S 10) = 1
EGZAMIN MAGISTERSKI, 12.09.2018r Matematyka w ekonomii i ubezpieczeniach Zadanie 1. (8 punktów) O rozkªadzie pewnego ryzyka S wiemy,»e: E[(S 20) + ] = 8 E[S 10 < S 20] = 13 P (S 20) = 3 4 P (S 10) = 1
Czy opcje walutowe mogą być toksyczne?
 Katedra Matematyki Finansowej Wydział Matematyki Stosowanej AGH 11 maja 2012 Kurs walutowy Kurs walutowy cena danej waluty wyrażona w innej walucie np. 1 USD = 3,21 PLN; USD/PLN = 3,21 Rodzaje kursów walutowych:
Katedra Matematyki Finansowej Wydział Matematyki Stosowanej AGH 11 maja 2012 Kurs walutowy Kurs walutowy cena danej waluty wyrażona w innej walucie np. 1 USD = 3,21 PLN; USD/PLN = 3,21 Rodzaje kursów walutowych:
Zarządzanie portfelem inwestycyjnym Opcje
 Zarządzanie portfelem inwestycyjnym Opcje 1 Opcje definicja umowa, która daje posiadaczowi prawo do kupna lub sprzedaży określonego instrumentu bazowego po z góry określonej cenie (cena wykonania) w terminie
Zarządzanie portfelem inwestycyjnym Opcje 1 Opcje definicja umowa, która daje posiadaczowi prawo do kupna lub sprzedaży określonego instrumentu bazowego po z góry określonej cenie (cena wykonania) w terminie
Projekt dyplomowy in»ynierski
 Katedra/Zakªad: Analizy Matematycznej i Numerycznej Kierunek studiów: Matematyka Specjalno± : Matematyka nansowa Rodzaj studiów: stacjonarne Imi i nazwisko: Alicja Czerwi«ska Numer albumu: 120132 Projekt
Katedra/Zakªad: Analizy Matematycznej i Numerycznej Kierunek studiów: Matematyka Specjalno± : Matematyka nansowa Rodzaj studiów: stacjonarne Imi i nazwisko: Alicja Czerwi«ska Numer albumu: 120132 Projekt
Europejska opcja kupna akcji calloption
 Europejska opcja kupna akcji callopion Nabywca holder: prawo kupna long posiion jednej akcji w okresie epiraiondae po cenie wykonania eercise price K w zamian za opłaę C Wysawca underwrier: obowiązek liabiliy
Europejska opcja kupna akcji callopion Nabywca holder: prawo kupna long posiion jednej akcji w okresie epiraiondae po cenie wykonania eercise price K w zamian za opłaę C Wysawca underwrier: obowiązek liabiliy
istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). Mała powtórka: instrumenty liniowe
 Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony
Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony
Współczynniki Greckie
 Wojciech Antniak 05.0.008r. Wstęp Współczynniki greckie określają ryzyko opcji europejskiej na zmiany rynku. ażdy z nich określa w jaki sposób wpłynie zmiana jakiegoś czynnika na cenę akcji. W dalszej
Wojciech Antniak 05.0.008r. Wstęp Współczynniki greckie określają ryzyko opcji europejskiej na zmiany rynku. ażdy z nich określa w jaki sposób wpłynie zmiana jakiegoś czynnika na cenę akcji. W dalszej
Podstawy In»ynierii Finansowej. Lista 5
 Podstawy In»ynierii Finansowej Lista 5 1. Przedstaw meechanizm marking to market dla opcji kupna i sprzeda»y na przykªadzie opcji kupna i sprzeda»y dla WIG20. Wystawca opcji deponuje depozyt pocz tkowy
Podstawy In»ynierii Finansowej Lista 5 1. Przedstaw meechanizm marking to market dla opcji kupna i sprzeda»y na przykªadzie opcji kupna i sprzeda»y dla WIG20. Wystawca opcji deponuje depozyt pocz tkowy
Dokumentacja. Portal Mathfinance Wycena opcji paryskich metoda. Wiktor Madejski
 Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). Mała powtórka: instrumenty liniowe
 Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). 1 Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony
Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). 1 Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony
Opcje. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Opcje Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty
Opcje Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty
Opcje. istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii).
 Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). 1 Mała powtórka: instrumenty liniowe Takie, w których funkcja wypłaty jest liniowa (np. forward, futures,
Opcje istota transakcji opcyjnych, rodzaje opcji, czynniki wpływające na wartość opcji (premii). 1 Mała powtórka: instrumenty liniowe Takie, w których funkcja wypłaty jest liniowa (np. forward, futures,
Beata Stolorz. Słowa kluczowe: opcje, miary wrażliwości, gamma, zomma, model wyceny opcji Blacka Scholesa.
 Zomma współczynnik wrażliwości opcji Beata Stolorz Zomma współczynnik wrażliwości opcji Streszczenie: Jednym z najlepszych narzędzi pomiaru ryzyka opcji są miary wrażliwości. Odzwierciedlają one wpływ
Zomma współczynnik wrażliwości opcji Beata Stolorz Zomma współczynnik wrażliwości opcji Streszczenie: Jednym z najlepszych narzędzi pomiaru ryzyka opcji są miary wrażliwości. Odzwierciedlają one wpływ
Opcje Giełdowe. Filip Duszczyk Dział Rynku Terminowego GPW
 Opcje Giełdowe Filip Duszczyk Dział Rynku Terminowego GPW Warszawa, 7 maja 2014 Czym są opcje indeksowe (1) Kupno opcji Koszt nabycia Zysk Strata Prawo, lecz nie obligacja, do kupna lub sprzedaży instrumentu
Opcje Giełdowe Filip Duszczyk Dział Rynku Terminowego GPW Warszawa, 7 maja 2014 Czym są opcje indeksowe (1) Kupno opcji Koszt nabycia Zysk Strata Prawo, lecz nie obligacja, do kupna lub sprzedaży instrumentu
Matematyka finansowa 2.06.2001 r.
 Matematyka finansowa 2.06.2001 r. 3. Inwe 2!%3'(!!%3 $'!%4&!! &,'! * "! &,-' ryzyko inwestycji odchyleniem standardowym stopy zwrotu ze swojego portfela. Jak *!&! $!%3$! %4 A.,. B. spadnie o 5% C. spadnie
Matematyka finansowa 2.06.2001 r. 3. Inwe 2!%3'(!!%3 $'!%4&!! &,'! * "! &,-' ryzyko inwestycji odchyleniem standardowym stopy zwrotu ze swojego portfela. Jak *!&! $!%3$! %4 A.,. B. spadnie o 5% C. spadnie
Model Blacka-Scholesa
 WYCENA OPCJI EUROPEJSKIEJ I AMERYKAŃSKIEJ W MODELACH DWUMIANOWYCH I TRÓJMIANOWYCH COXA-ROSSA-RUBINSTEINA I JARROWA-RUDDA Joanna Karska W modelach dyskretnych wyceny opcji losowość wyrażana jest poprzez
WYCENA OPCJI EUROPEJSKIEJ I AMERYKAŃSKIEJ W MODELACH DWUMIANOWYCH I TRÓJMIANOWYCH COXA-ROSSA-RUBINSTEINA I JARROWA-RUDDA Joanna Karska W modelach dyskretnych wyceny opcji losowość wyrażana jest poprzez
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty dla
Ćwiczenia ZPI 1 Kupno opcji Profil wypłaty dla nabywcy opcji kupna. Z/S Premia (P) np. 100 Kurs wykonania opcji (X) np. 2500 Punkt opłacalności X + P 2500+100=2600 WIG20 2 Kupno opcji Profil wypłaty dla
Rynek, opcje i równania SDE
 Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Strategie Opcyjne. Filip Duszczyk Dział Rynku Terminowego GPW
 Strategie Opcyjne Filip Duszczyk Dział Rynku Terminowego GPW Warszawa, 21 maj 2014 Budowanie Strategii Strategia Kombinacja dwóch lub większej liczby pozycji w opcjach, stosowana w zależności od przewidywanych
Strategie Opcyjne Filip Duszczyk Dział Rynku Terminowego GPW Warszawa, 21 maj 2014 Budowanie Strategii Strategia Kombinacja dwóch lub większej liczby pozycji w opcjach, stosowana w zależności od przewidywanych
Rynek opcji walutowych. dr Piotr Mielus
 Rynek opcji walutowych dr Piotr Mielus Rynek walutowy a rynek opcji Geneza rynku opcji walutowych Charakterystyka rynku opcji Specyfika rynku polskiego jako rynku wschodzącego 2 Geneza rynku opcji walutowych
Rynek opcji walutowych dr Piotr Mielus Rynek walutowy a rynek opcji Geneza rynku opcji walutowych Charakterystyka rynku opcji Specyfika rynku polskiego jako rynku wschodzącego 2 Geneza rynku opcji walutowych
R NKI K I F I F N N NSOW OPCJE
 RYNKI FINANSOWE OPCJE Wymagania dotyczące opcji Standard opcji Interpretacja nazw Sposoby ustalania ostatecznej ceny rozliczeniowej dla opcji na GPW OPCJE - definicja Kontrakt finansowy, w którym kupujący
RYNKI FINANSOWE OPCJE Wymagania dotyczące opcji Standard opcji Interpretacja nazw Sposoby ustalania ostatecznej ceny rozliczeniowej dla opcji na GPW OPCJE - definicja Kontrakt finansowy, w którym kupujący
OPCJE. Slide 1. This presentation or any of its parts cannot be used without prior written permission of Dom Inwestycyjny BRE Banku S..A.
 OPCJE Slide 1 Informacje ogólne definicje opcji: kupna (call)/sprzedaŝy (put) terminologia typy opcji krzywe zysk/strata Slide 2 Czym jest opcja KUPNA (CALL)? Opcja KUPNA (CALL) jest PRAWEM - nie zobowiązaniem
OPCJE Slide 1 Informacje ogólne definicje opcji: kupna (call)/sprzedaŝy (put) terminologia typy opcji krzywe zysk/strata Slide 2 Czym jest opcja KUPNA (CALL)? Opcja KUPNA (CALL) jest PRAWEM - nie zobowiązaniem
Opcje o odwrotnie uwarunkowanej premii
 ANNALES UNIVERSITATIS MARIAE CURIE-SK ODOWSKA LUBLIN POLONIA VOL. XLVI, 4 SECTIO H 212 Uniwersytet Miko aja Kopernika w Toruniu, Katedra Ekonometrii i Statystyki EWA DZIAWGO Opcje o odwrotnie uwarunkowanej
ANNALES UNIVERSITATIS MARIAE CURIE-SK ODOWSKA LUBLIN POLONIA VOL. XLVI, 4 SECTIO H 212 Uniwersytet Miko aja Kopernika w Toruniu, Katedra Ekonometrii i Statystyki EWA DZIAWGO Opcje o odwrotnie uwarunkowanej
Spis treści. Przedmowa 11
 Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
Przedmowa 11 1. Wprowadzenie 15 1.1. Początki rynków finansowych 15 1.2. Konferencja w Bretton Woods 17 1.3. Początki matematyki finansowej 19 1.4. Inżynieria finansowa 23 1.5. Nobel'97 z ekonomii 26 1.6.
Biostatystyka, # 4 /Weterynaria I/
 Biostatystyka, # 4 /Weterynaria I/ dr n. mat. Zdzisªaw Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowa«Matematyki i Informatyki ul. Gª boka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Biostatystyka, # 4 /Weterynaria I/ dr n. mat. Zdzisªaw Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowa«Matematyki i Informatyki ul. Gª boka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
ZWIĄZKI MIĘDZY WSPÓŁCZYNNIKAMI WRAŻLIWOŚCI W MODELU WYCENY OPCJI GARMANA-KOHLHAGENA
 STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR Beata Bieszk-Stolorz Uniwersytet Szczeciński ZWIĄZKI MIĘDZY WSPÓŁCZYNNIKAMI WRAŻLIWOŚCI W MODELU WYCENY OPCJI GARMANA-KOHLHAGENA Streszczenie
STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR Beata Bieszk-Stolorz Uniwersytet Szczeciński ZWIĄZKI MIĘDZY WSPÓŁCZYNNIKAMI WRAŻLIWOŚCI W MODELU WYCENY OPCJI GARMANA-KOHLHAGENA Streszczenie
Równania ró»niczkowe I rz du (RRIR) Twierdzenie Picarda. Anna D browska. WFTiMS. 23 marca 2010
 WFTiMS 23 marca 2010 Spis tre±ci 1 Denicja 1 (równanie ró»niczkowe pierwszego rz du) Równanie y = f (t, y) (1) nazywamy równaniem ró»niczkowym zwyczajnym pierwszego rz du w postaci normalnej. Uwaga 1 Ogólna
WFTiMS 23 marca 2010 Spis tre±ci 1 Denicja 1 (równanie ró»niczkowe pierwszego rz du) Równanie y = f (t, y) (1) nazywamy równaniem ró»niczkowym zwyczajnym pierwszego rz du w postaci normalnej. Uwaga 1 Ogólna
Metodologia wyznaczania greckich współczynników dla opcji na WIG20
 Metodologia wyznaczania greckich współczynników dla opcji na WIG20 (1) Dane wejściowe. Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych: S wartość indeksu WIG20
Metodologia wyznaczania greckich współczynników dla opcji na WIG20 (1) Dane wejściowe. Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych: S wartość indeksu WIG20
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Opcje koszykowe a lokaty strukturyzowane - wycena
 Opcje koszykowe a lokaty strukturyzowane - wycena Basket options and structured deposits - pricing Janusz Gajda Promotor: dr hab. inz. Rafał Weron Politechnika Wrocławska Plan prezentacji Cel pracy Wprowadzenie
Opcje koszykowe a lokaty strukturyzowane - wycena Basket options and structured deposits - pricing Janusz Gajda Promotor: dr hab. inz. Rafał Weron Politechnika Wrocławska Plan prezentacji Cel pracy Wprowadzenie
Rozdziaª 4. Jednowymiarowe modele szeregów czasowych
 Rozdziaª 4. Jednowymiarowe modele szeregów czasowych MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 4) Modele ARMA 1 / 24 Jednowymiarowe modele szeregów czasowych Jednowymiarowe modele szeregów czasowych:
Rozdziaª 4. Jednowymiarowe modele szeregów czasowych MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 4) Modele ARMA 1 / 24 Jednowymiarowe modele szeregów czasowych Jednowymiarowe modele szeregów czasowych:
Metody redukcji wariancji
 Metody redukcji wariancji Michał Kołodziejczyk 26 maja 2009 Spis treści 1 Przedstawienie problemu 1 2 Metody redukcji - opis teoretyczny 2 2.1 Metoda Antithetic Variates...............................
Metody redukcji wariancji Michał Kołodziejczyk 26 maja 2009 Spis treści 1 Przedstawienie problemu 1 2 Metody redukcji - opis teoretyczny 2 2.1 Metoda Antithetic Variates...............................
Komisja Egzaminacyjna dla Aktuariuszy. XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Zadanie 1. Zadanie 2. Zadanie 3. Zadanie 4
 Zadanie ODP = exp(, 4 )E W () = exp(, )E l (;+ ) (S()) ODP = exp(, )P (S() > ), gdzie oznacza miar martyngaªow. Przy MBS proces cen akcji ma posta S(t) = S() exp[t(µ, 5σ ) + σw t ], gdzie {W t, t } jest
Zadanie ODP = exp(, 4 )E W () = exp(, )E l (;+ ) (S()) ODP = exp(, )P (S() > ), gdzie oznacza miar martyngaªow. Przy MBS proces cen akcji ma posta S(t) = S() exp[t(µ, 5σ ) + σw t ], gdzie {W t, t } jest
Elementy Modelowania Matematycznego Wykªad 1 Prawdopodobie«stwo
 Spis tre±ci Elementy Modelowania Matematycznego Wykªad 1 Prawdopodobie«stwo Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis tre±ci Spis tre±ci 1 2 3 4 5 Spis tre±ci Spis tre±ci 1 2 3 4
Spis tre±ci Elementy Modelowania Matematycznego Wykªad 1 Prawdopodobie«stwo Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis tre±ci Spis tre±ci 1 2 3 4 5 Spis tre±ci Spis tre±ci 1 2 3 4
Inga Dębczyńska Paulina Bukowińska
 OPCJE NA WIG20 Inga Dębczyńska Paulina Bukowińska Informacje ogólne o opcjach Terminologia Opcja KUPNA (CALL) - prawo zakupu po określonej cenie Opcja SPRZEDAŻY (PUT) - prawo sprzedaży po określonej cenie
OPCJE NA WIG20 Inga Dębczyńska Paulina Bukowińska Informacje ogólne o opcjach Terminologia Opcja KUPNA (CALL) - prawo zakupu po określonej cenie Opcja SPRZEDAŻY (PUT) - prawo sprzedaży po określonej cenie
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
Opcje. Dr hab Renata Karkowska; Wydział Zarządzania UW
 Opcje 1 Opcje Narysuj: Profil wypłaty dla nabywcy opcji kupna. Profil wypłaty dla nabywcy opcji sprzedaży. Profil wypłaty dla wystawcy opcji kupna. Profil wypłaty dla wystawcy opcji sprzedaży. 2 Przykład
Opcje 1 Opcje Narysuj: Profil wypłaty dla nabywcy opcji kupna. Profil wypłaty dla nabywcy opcji sprzedaży. Profil wypłaty dla wystawcy opcji kupna. Profil wypłaty dla wystawcy opcji sprzedaży. 2 Przykład
Biostatystyka, # 5 /Weterynaria I/
 Biostatystyka, # 5 /Weterynaria I/ dr n. mat. Zdzisªaw Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowa«Matematyki i Informatyki ul. Gª boka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Biostatystyka, # 5 /Weterynaria I/ dr n. mat. Zdzisªaw Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowa«Matematyki i Informatyki ul. Gª boka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Zasady obliczania depozytów na opcje na GPW - MPKR
 Jesteś tu: Bossa.pl Zasady obliczania depozytów na opcje na GPW - MPKR Depozyt zabezpieczający dla pozycji w kontraktach opcyjnych wyznaczany jest za pomocą Modelu Portfelowej Kalkulacji Ryzyka. Czym jest
Jesteś tu: Bossa.pl Zasady obliczania depozytów na opcje na GPW - MPKR Depozyt zabezpieczający dla pozycji w kontraktach opcyjnych wyznaczany jest za pomocą Modelu Portfelowej Kalkulacji Ryzyka. Czym jest
Krzysztof Piontek MODELOWANIE I PROGNOZOWANIE ZMIENNOŚCI INSTRUMENTÓW FINANSOWYCH
 Akademia Ekonomiczna im. Oskara Langego we Wrocławiu Wydział Zarządzania i Informatyki Krzysztof Piontek MODELOWANIE I PROGNOZOWANIE ZMIENNOŚCI INSTRUMENTÓW FINANSOWYCH rozprawa doktorska Promotor: prof.
Akademia Ekonomiczna im. Oskara Langego we Wrocławiu Wydział Zarządzania i Informatyki Krzysztof Piontek MODELOWANIE I PROGNOZOWANIE ZMIENNOŚCI INSTRUMENTÓW FINANSOWYCH rozprawa doktorska Promotor: prof.
Zarządzanie portfelem inwestycyjnym
 Zarządzanie portfelem inwestycyjnym Dr hab. Renata Karkowska Strategie opcyjne Opcje egzotyczne 2 Współczynniki greckie Współczynniki greckie określają, o ile zmieni się kurs opcji w wyniku zmiany wartości
Zarządzanie portfelem inwestycyjnym Dr hab. Renata Karkowska Strategie opcyjne Opcje egzotyczne 2 Współczynniki greckie Współczynniki greckie określają, o ile zmieni się kurs opcji w wyniku zmiany wartości
Dokumentacja. Opcje europejskie PDE. Zbigniew Matczak
 Dokumentacja Opcje europejskie PDE Zbigniew Matczak Spis treści 1 Model CEV 2 1.1 Cena opcji w modelu CEV...................... 2 1.2 Poprawność funkcji "option value" na podstawie funkcji delta oraz symulacji
Dokumentacja Opcje europejskie PDE Zbigniew Matczak Spis treści 1 Model CEV 2 1.1 Cena opcji w modelu CEV...................... 2 1.2 Poprawność funkcji "option value" na podstawie funkcji delta oraz symulacji
Matematyka finansowa 08.01.2007 r. Komisja Egzaminacyjna dla Aktuariuszy. XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile
Komisja Egzaminacyjna dla Aktuariuszy XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile
Raport i dokumentacja Obliczanie Value-at-Risk portfela metodą Monte Carlo
 Raport i dokumentacja Obliczanie Value-at-Risk portfela metodą Monte Carlo 1. Opis problemu Celem pracy jest policzenie jednodniowej wartości narażonej na ryzyko (Value-at- Risk) portfela składającego
Raport i dokumentacja Obliczanie Value-at-Risk portfela metodą Monte Carlo 1. Opis problemu Celem pracy jest policzenie jednodniowej wartości narażonej na ryzyko (Value-at- Risk) portfela składającego
Ekstremalnie fajne równania
 Ekstremalnie fajne równania ELEMENTY RACHUNKU WARIACYJNEGO Zaczniemy od ogólnych uwag nt. rachunku wariacyjnego, który jest bardzo przydatnym narz dziem mog cym posªu»y do rozwi zywania wielu problemów
Ekstremalnie fajne równania ELEMENTY RACHUNKU WARIACYJNEGO Zaczniemy od ogólnych uwag nt. rachunku wariacyjnego, który jest bardzo przydatnym narz dziem mog cym posªu»y do rozwi zywania wielu problemów
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 768 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR WŁASNOŚCI OPCJI CAPPED.
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 768 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 63 213 EWA DZIAWGO Uniwersytet Mikołaja Kopernika w Toruniu WŁASNOŚCI OPCJI CAPPED Streszczenie W artykule
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 768 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 63 213 EWA DZIAWGO Uniwersytet Mikołaja Kopernika w Toruniu WŁASNOŚCI OPCJI CAPPED Streszczenie W artykule
Dokumentacja. Opcje europejskie PDE. Michał Grzelak
 Dokumentacja Opcje europejskie PDE Michał Grzelak Spis treści 1 Ceny opcji z local volatility 2 1.1 Opcje plain vanilla z local volatility................. 2 1.2 Parametry greckie..........................
Dokumentacja Opcje europejskie PDE Michał Grzelak Spis treści 1 Ceny opcji z local volatility 2 1.1 Opcje plain vanilla z local volatility................. 2 1.2 Parametry greckie..........................
Stacjonarne szeregi czasowe
 e-mail:e.kozlovski@pollub.pl Spis tre±ci 1 Denicja 1 Szereg {x t } 1 t N nazywamy ±ci±le stacjonarnym (stacjonarnym w w»szym sensie), je»eli dla dowolnych m, t 1, t 2,..., t m, τ ª czny rozkªad prawdopodobie«stwa
e-mail:e.kozlovski@pollub.pl Spis tre±ci 1 Denicja 1 Szereg {x t } 1 t N nazywamy ±ci±le stacjonarnym (stacjonarnym w w»szym sensie), je»eli dla dowolnych m, t 1, t 2,..., t m, τ ª czny rozkªad prawdopodobie«stwa
Modelowanie ryzyka kredytowego Zadania 1.
 1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Inżynieria Finansowa - Egzamin - 28 stycznia Rozwiązania zadań Wersja z dnia 1 marca 2005, z drobnymi poprawkami
 Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego
INWESTYCJE Instrumenty finansowe, ryzyko SPIS TREŚCI
 INWESTYCJE Instrumenty finansowe, ryzyko Jajuga Krzysztof, Jajuga Teresa SPIS TREŚCI Przedmowa Wprowadzenie - badania w zakresie inwestycji i finansów Literatura Rozdział 1. Rynki i instrumenty finansowe
INWESTYCJE Instrumenty finansowe, ryzyko Jajuga Krzysztof, Jajuga Teresa SPIS TREŚCI Przedmowa Wprowadzenie - badania w zakresie inwestycji i finansów Literatura Rozdział 1. Rynki i instrumenty finansowe
Wykªad 12. Transformata Laplace'a i metoda operatorowa
 Wykªad 2. Tranformata Laplace'a i metoda operatorowa Tranformata Laplace'a Dla odpowiednio okre±lonej klay funkcji zdeniujemy operator L, nazywany tranformat Laplace'a, okre±lony wzorem L[ f ]() = f(t)e
Wykªad 2. Tranformata Laplace'a i metoda operatorowa Tranformata Laplace'a Dla odpowiednio okre±lonej klay funkcji zdeniujemy operator L, nazywany tranformat Laplace'a, okre±lony wzorem L[ f ]() = f(t)e
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
Rachunek caªkowy funkcji wielu zmiennych
 Rachunek caªkowy funkcji wielu zmiennych I. Malinowska, Z. Šagodowski Politechnika Lubelska 8 czerwca 2015 Caªka iterowana podwójna Denicja Je»eli funkcja f jest ci gªa na prostok cie P = {(x, y) : a x
Rachunek caªkowy funkcji wielu zmiennych I. Malinowska, Z. Šagodowski Politechnika Lubelska 8 czerwca 2015 Caªka iterowana podwójna Denicja Je»eli funkcja f jest ci gªa na prostok cie P = {(x, y) : a x
Maksymalna liczba punktów do zdobycia: 80. Zadanie 1: a) 6 punktów, b) 3 punkty, Zadanie 2: a) 6 punktów, b) 4 punkty,
 VII Wojewódzki Konkurs Matematyczny "W ±wiecie Matematyki" im. Prof. Wªodzimierza Krysickiego Etap drugi - 17 lutego 2015 r. Maksymalna liczba punktów do zdobycia: 80. 1. Drugi etap Konkursu skªada si
VII Wojewódzki Konkurs Matematyczny "W ±wiecie Matematyki" im. Prof. Wªodzimierza Krysickiego Etap drugi - 17 lutego 2015 r. Maksymalna liczba punktów do zdobycia: 80. 1. Drugi etap Konkursu skªada si
1 Bª dy i arytmetyka zmiennopozycyjna
 1 Bª dy i arytmetyka zmiennopozycyjna Liczby w pami ci komputera przedstawiamy w ukªadzie dwójkowym w postaci zmiennopozycyjnej Oznacza to,»e s one postaci ±m c, 01 m < 1, c min c c max, (1) gdzie m nazywamy
1 Bª dy i arytmetyka zmiennopozycyjna Liczby w pami ci komputera przedstawiamy w ukªadzie dwójkowym w postaci zmiennopozycyjnej Oznacza to,»e s one postaci ±m c, 01 m < 1, c min c c max, (1) gdzie m nazywamy
Strategie inwestowania w opcje. Filip Duszczyk Dział Rynku Terminowego
 Strategie inwestowania w opcje Filip Duszczyk Dział Rynku Terminowego Agenda: Opcje giełdowe Zabezpieczenie portfela Spekulacja Strategie opcyjne 2 Opcje giełdowe 3 Co to jest opcja? OPCJA JAK POLISA Zabezpieczenie
Strategie inwestowania w opcje Filip Duszczyk Dział Rynku Terminowego Agenda: Opcje giełdowe Zabezpieczenie portfela Spekulacja Strategie opcyjne 2 Opcje giełdowe 3 Co to jest opcja? OPCJA JAK POLISA Zabezpieczenie
Metody probablistyczne i statystyka stosowana
 Politechnika Wrocªawska - Wydziaª Podstawowych Problemów Techniki - 011 Metody probablistyczne i statystyka stosowana prowadz cy: dr hab. in». Krzysztof Szajowski opracowanie: Tomasz Kusienicki* κ 17801
Politechnika Wrocªawska - Wydziaª Podstawowych Problemów Techniki - 011 Metody probablistyczne i statystyka stosowana prowadz cy: dr hab. in». Krzysztof Szajowski opracowanie: Tomasz Kusienicki* κ 17801
Modelowanie ryzyka kredytowego: MODEL BLACK-COX A
 Modelowanie ryzyka kredytowego: MODEL BLACK-COX A Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014 Niewęgłowski MiNI PW Modele wartości firmy Warszawa
Modelowanie ryzyka kredytowego: MODEL BLACK-COX A Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014 Niewęgłowski MiNI PW Modele wartości firmy Warszawa
Zastosowania matematyki
 Zastosowania matematyki Monika Bartkiewicz 1 / 126 ...czy«cie dobrze i po»yczajcie niczego si nie spodziewaj c(šk. 6,34-35) Zagadnienie pobierania procentu jest tak stare jak gospodarka pieni»na. Procent
Zastosowania matematyki Monika Bartkiewicz 1 / 126 ...czy«cie dobrze i po»yczajcie niczego si nie spodziewaj c(šk. 6,34-35) Zagadnienie pobierania procentu jest tak stare jak gospodarka pieni»na. Procent
Wykorzystanie opcji rzeczywistych
 RYNEK FINANSOWANIA NIERUCHOMOŚCI Wykorzystanie opcji rzeczywistych do modelowania wartości nieruchomości Metodologia opcji rzeczywistych jest prostą metodą do szacowania wartości nieruchomości w przyszłości.
RYNEK FINANSOWANIA NIERUCHOMOŚCI Wykorzystanie opcji rzeczywistych do modelowania wartości nieruchomości Metodologia opcji rzeczywistych jest prostą metodą do szacowania wartości nieruchomości w przyszłości.
1 Poj cia pomocnicze. Przykªad 1. A A d
 Poj cia pomocnicze Otoczeniem punktu x nazywamy dowolny zbiór otwarty zawieraj cy punkt x. Najcz ±ciej rozwa»amy otoczenia kuliste, tj. kule o danym promieniu ε i ±rodku x. S siedztwem punktu x nazywamy
Poj cia pomocnicze Otoczeniem punktu x nazywamy dowolny zbiór otwarty zawieraj cy punkt x. Najcz ±ciej rozwa»amy otoczenia kuliste, tj. kule o danym promieniu ε i ±rodku x. S siedztwem punktu x nazywamy
ANALIZA WRAŻLIWOŚCI CENY OPCJI FLOORED
 STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 36 Ewa Dziawgo * Uniwersytet Mikołaja Kopernika w Toruniu ANALIZA WRAŻLIWOŚCI CENY OPCJI FLOORED STRESZCZENIE W artykule przedstawiono charakterystykę
STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 36 Ewa Dziawgo * Uniwersytet Mikołaja Kopernika w Toruniu ANALIZA WRAŻLIWOŚCI CENY OPCJI FLOORED STRESZCZENIE W artykule przedstawiono charakterystykę
Rozdziaª 7. Modele klasy ARCH
 Rozdziaª 7. Modele klasy ARCH MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 7) Modele ARCH 1 / 24 Modele klasy ARCH Charakterystyki wi kszo±ci szeregów nansowych: Grupowanie wariancji (volatility clustering):
Rozdziaª 7. Modele klasy ARCH MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 7) Modele ARCH 1 / 24 Modele klasy ARCH Charakterystyki wi kszo±ci szeregów nansowych: Grupowanie wariancji (volatility clustering):
1) jednostka posiada wystarczające środki aby zakupić walutę w dniu podpisania kontraktu
 Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
2. (8 punktów) 3. (8 punktów) 4. (8 punktów) 5. (8 punktów) EGZAMIN MAGISTERSKI, Matematyka w ekonomii i ubezpieczeniach
 Matematyka w ekonomii i ubezpieczeniach 1. (8 punktów) Znajd¹ rozwi zanie poni»szego zagadnienia programowania liniowego: Zmaksymalizowa x 1 2x 2 + x 3 x 5 przy ograniczeniach x 1 3x 2 + x 3 + 2x 5 = 8
Matematyka w ekonomii i ubezpieczeniach 1. (8 punktów) Znajd¹ rozwi zanie poni»szego zagadnienia programowania liniowego: Zmaksymalizowa x 1 2x 2 + x 3 x 5 przy ograniczeniach x 1 3x 2 + x 3 + 2x 5 = 8
