Inżynieria Finansowa - Egzamin - 28 stycznia Rozwiązania zadań Wersja z dnia 1 marca 2005, z drobnymi poprawkami
|
|
|
- Mateusz Zalewski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Inżynieria Finansowa - Egzamin - 28 stycznia 2005 Rozwiązania zadań Wersja z dnia marca 2005, z drobnymi poprawkami Uwaga: Dla uproszczenia we wszelkich obliczeniach przyjęliśmy, że długość n-miesięcznego okresu czasu wynosi n 2 lat. Zadanie. Punktacja: (a) - 3, (b) - 7. Dane są dwie obligacje stałokuponowe, które płacą kupon co pół roku: OS: kupon - 5%, termin zapadalności - za 4 miesiące, cena czysta - 99,58; OS2: kupon - 6%, termin zapadalności - za 7 miesięcy, cena czysta - 00,6. Stopa procentowa M lokat/depozytów wynosi 5,50%. (a) Wyznacz wartości czynników dyskontowych DF (4M) oraz DF (7M). (b) Kwotowanie FRA4x7 wynosi 6,00%. Czy w tej sytuacji jest możliwość przeprowadzenia arbitrażu. Jeśli tak, skonstruuj strategię arbitrażową. Rozwiązanie Część (a). Mając stopę procentową dla depozytu/lokaty M obliczamy czynnik dyskontowy DF (M) = + 0, = 0, Do obliczenia wartości czynników dyskontowych dla 4M i 7M będą nam potrzebne ceny brudne obligacji OS i OS2. Cena brudna obligacji to cena czysta plus odsetki narosłe w bieżącym okresie odsetkowym. I tak, cena brudna P obligacji OS wynosi P = 99, , oraz analogicznie cena brudna obligacji OS2 P 2 = 00, = 00, 433, = 03, 0. Za przepływ pieniężny w chwili 4M w wysokości 02,50 z obligacji OS musimy zapłacić P. Zatem DF (4M) = P /02, 50 = 0, Czynnik DF (7M) obliczamy z równania skąd po obliczeniach P 2 = 3 DF (M) + 03 DF (7M), DF (7M) = 0, Część (b). Teraz możemy obliczyć stopę forward F (4M, 7M) implikowaną przez wartości tych czynników dyskontowych ( ) DF (4M) F (4M, 7M) = DF (7M) /( 3 ) = 3, 54283%. 2
2 Inżynieria Finansowa - Egzamin - 28 stycznia Jak widać stopa ta jest mniejsza niż stopa kwotowanego kontraktu FRA4x7. Dlatego opłaca się ulokować po stopie FRA4x7 pieniądze, których koszt finasowania (koszt ich zdobycia) będzie odpowiadał stopie F (4M, 7M). By mieć co ulokować w terminie 4M musimy kupić obligację OS (bo z niej dostaniemy wypłatę w 4M). Obligację OS kupimy za pieniądze uzyskane ze sprzedaży obligacji OS2. Ile sztuk obligacji OS2 (w stosunku do jednostki obligacji OS) powinniśmy sprzedać? Tyle, to jest x, by w terminie 7M kwota pieniędzy uzyskana z 3M lokaty, która zacznie się w 4M, kwoty 02,50 po stopie 6% (te 6% zagwarantujemy sobie sprzedając dzisiaj kontrakt FRA4x7) wystarczyła na pokrycie zobowiązania z tytułu sprzedanej x sztuk obligacji OS2. Tak więc mamy równanie 02, 50 ( + 0, 06 ) 3 = x 03, 2 skąd otrzymujemy x =, Należy jeszcze pamiętać o kuponie sprzedanej przez nas obligacji OS2, który musimy zapłacić w M. Z pieniędzy, którymi będziemy dysponować w chwili zawierania transakcji arbitrażowej, pewną część musimy przeznaczyć na wypłatę tego kuponu. Dokładniej, kwotę DF (M) x 3 = 3, powinniśmy ulokować po stopie 5,50% na okres M. Podsumujmy i sprawdźmy jak wygląda nasza strategia arbitrażowa. T=0 Sprzedajemy x =, sztuk obligacji OS2 po cenie brudnej 03,0 za sztukę - stąd otrzymujemy kwotę 04,385. Kupujemy jedną sztukę obligacji OS po cenie brudnej 00,433 - płacimy 00,433. Aby przygotować się na płatność kuponu z obligacji OS2, lokujemy kwotę DF (M) x 3 = 3, na M po stopie 5,50% - wykładamy kwotę 3, Sprzedajemy kontrakt FRA4x7 po stopie 6%. Nasz bilans wynosi zatem 04, , 433 3, = 0, 70878, i ta kwota jest naszym wolnym od ryzyka zyskiem arbitrażowym jaki wygenerowaliśmy w chwili zawierania strategii. T=M Otrzymujemy kwotę 3, = x 3 z M lokaty, która dokładnie wystarcza na uregulowanie płatności kuponowej z x sztuk sprzedanej obligacji OS2. T=4M Otrzymujemy kwotę 02,50 (z obligacji OS), którą lokujemy po 6% na 3M. Tak na prawdę lokujemy te pieniądze po rynku, ale wypłata (zainwestowana po rynku) ze sprzedanego kontraktu FRA4x7 rekompensuje odsetki od naszej lokaty tak by wynosiły one 6%.
3 Inżynieria Finansowa - Egzamin - 28 stycznia T=7M Z lokaty otrzymujemy 02, 50 ( + 0, 06 2) 3 = 04, 0375 co dokładnie wystarcza by pokryć nasze zobowiązenie z tytułu sprzedanej obligacji OS2 w kwocie x 03 = 04, Zadanie 2. Opcja lookback Punktacja: 0. Opcja sprzedaży (put) lookback to opcja, której posiadacz w chwili czasu t w trakcie trwania opcji może w przypadku zarządania wykonania opcji otrzymać kwotę max{s τ : τ [0, t]} S t gdzie czas jest mierzony od chwili zawarcia kontraktu (od t = 0) - inaczej: posiadacz opcji sprzedaży lookback może sprzedać instrument podstawowy po najwyższej zaobserwowanej od chwili zawarcia kontaktu cenie instrumentu podstawowego. Rozpatrzmy amerykańską opcję lookback na sprzedaż akcji spółki wuwu.com. Czas trwania opcji wynosi 6 miesięcy. Bieżąca cena akcji wynosi 00, a jej zmienność 36.47%. Wolna od ryzyka stopa procentowa kapitalizowana w sposób ciągły wynosi 6.62% i jest taka sama dla każdego okresu depozytowego. Wyceń tę opcję na dwuokresowym drzewie dwumianowym. Rozwiązanie Współczynniki U i D określamy w następujący sposób U = exp(+σ t) oraz D = exp( σ t), wtedy U D =. W powyższym wzorze t = 4 otrzymujemy jest długością 3M okresu. Po obliczeniach U = exp(+0, , 25) =, oraz D = /U = 0, Prawdopodobieństwo matrygnałowe wynosi p = exp(r t) D U D = exp(0, , 25) 0, 8333, , 8333 = 0, Będą nam również potrzebne czynniki, które dyskontują z końców kolejnych 3M okresów na ich początki. Ponieważ stopa wolna od ryzyka jest taka sama dla każdego okresu, czynniki dyskontowe mają taką samą wartość, która wynosi DF = exp( 0, , 25) = 0, Zaczynamy od wyznaczenia procesu cen S na drzewie. Będziemy od razu wyznaczać M = największej wartości ceny przyjętej na drodze prowadzącej do danego węzła oraz wartość wypłaty V z tytułu realizacji opcji w danym węźle (wartość wewnętrzną opcji). w t = 0
4 Inżynieria Finansowa - Egzamin - 28 stycznia S(0) = 00 M(0) = 00 V (0) = max(00 00; 0) = 0 w t = 3M S(3M, U) = 20, 0034 M(3M, U) = 20, 0034 V (3M, U) = max(20, , 0034; 0) = 0 S(3M, D) = 83, M(3M, D) = 00 V (3M, D) = max(00 83, 33096; 0) = 6, w t = 6M S(6M, UU) = 44, 0082 M(6M, UU) = 44, 0082 V (6M, UU) = max(44, , 0082; 0) = 0 S(6M, UD) = 00 M(6M, UD) = 20, 0034 V (6M, UD) = max(20, ; 0) = 20, 0034 S(6M, DU) = 00 M(6M, DU) = 00 V (6M, DU) = max(00 00; 0) = 0 S(6M, DD) = 69, M(6M, DD) = 00 V (6M, DD) = max(00 69, 44049; 0) = 30, 5595 Zauważmy, że choć drzewo z procesem cen rekombinuje się, to drzewo z procesem M (największej wartości ceny po drodze) jest rozdzielone i to po tym rozdzielonym drzewie będziemy musieli poruszać się dokonując wyceny opcji. Oczywiście wycenę przeprowadzamy zaczynając od końca, tzn. cofając się od chwili t = 6M do t = 0. W każdym węźle obliczamy zdyskontowaną wartość oczekiwaną wartości opcji widzianych z tego węzła w stanie Up i Down w następnym okresie i porównujemy ją wypłatą jaką byśmy otrzymali w przypadku realizacji opcji - wartość opcji w tym węźle jest liczbą większą z nich. w t = 3M E(3M, U) = DF (p V (6M, UU) + ( p) V (6M, UD)) = 9, P (3M, U) = max(e(3m, U); V (3M, U)) = 9, E(3M, D) = DF (p V (6M, DU) + ( p) V (6M, DD)) = 5, P (3M, D) = max(e(3m, D); V (3M, D)) = 6, w t = 0 E(0) = DF (p P (3M, U) + ( p) P (3M, D)) = 3, P (0) = max(e(0); V (0)) = 3, Cena opcji wynosi 3,03504 PLN.
5 Inżynieria Finansowa - Egzamin - 28 stycznia Zadanie 3. Punktacja: (a) - 5, (b) - 5. Aby zdobyć fundusze na inwestycje, spółka wuwu.com emituje dwuletnią obligację o rocznym kuponie, który składa się z 3/4 rynkowej stopy (typu LIBOR) dla rocznych depozytów (ustalanej na początku każdego rocznego okresu odsetkowego) plus marża m, przy czym ten składnik kuponu (to jest, część odsetek odpowiadająca tej marży) będzie wypłacana tylko wtedy, jeśli w terminie t wypłaty kuponu cena akcji będzie większa niż K t = S 0 q t, gdzie S 0 jest ceną akcji w chwili emisji obligacji, q jest współczynnikiem ustalonym w prospekcie emisyjnym obligacji, a czas t mierzymy w latach. Spółka chce wyemitować te obligacje at par, to znaczy po 00. (a) Wyprowadź formułę na wartość marży m (jako funkcję bieżącej ceny akcji S 0, jej zmienności σ i bieżącej struktury stóp procentowych danych funkcją DF (t), oraz parametru q), przy której ta obligacja będzie w chwili emisji at par. (b) Wykonaj obliczenia dla następujących danych liczbowych: cena akcji S 0 = 00, zmienność akcji σ = 20%, q =.. Załóż również, że struktura stóp procentowych (wolnych od ryzyka, kapitalizowanych w sposób ciągły) jest w chwili emisji obligacji płaska i że stopy te wynoszą 8%. Rozwiązanie Część (a). Niech L t oznacza Y stopę rynkową ustaloną w chwili t, płaconą w t. Wówczas, kupon obligacji płatny w chwili t możemy zapisać w postaci 3 4 L t + m St K t. Posiadacz obligacji, prócz odsetek po stopie rynkowej liczonych od 3/4 nominału, ma dwie europejskie binarne opcje kupna (w t = i w t = 2) na akcje spółki wuwu.com o nominale równym m nominału obligacji z cenami wykonania K t. Niech B t oznacza cenę europejskiej binarnej opcji kupna za jednostkę nominału która zapada w t i której cena wykonania wynosi K t. Ponieważ obligacja ma być wyemitowana po cenie 00 (at par), to musi zachodzić równość = DF (Y ) 3 4 L + m B + DF (2Y ) 3 4 L 2 + m B 2 + DF (2Y ), gdzie założyliśmy, że każdy roczny okres odsetkowy ma długość. Korzystając z metody wyceny obligacji o zmiennym kuponie zauważamy, że DF (Y ) 3 4 L + DF (2Y ) 3 4 L 2 + DF (2Y ) 3 4 = 3 4. Tak więc warunek na marżę m upraszcza się do następującej postaci 4 = m (B + B 2 ) + DF (2Y ) 4, skąd mamy m = 4 ( DF (2Y )). B + B 2
6 Inżynieria Finansowa - Egzamin - 28 stycznia Część (b). Obliczamy czynnik dyskontowy DF (2Y ) = exp( 0, 08 2) = 0, Teraz musimy obliczyć ceny opcji binarnych kupna. Korzystamy z następującego wzoru gdzie B = exp( rt )Φ(d 2 ), d 2 = ln(s 0/K) + rt σ 2 T/2 σ, T a Φ jest dystrybuantą standarowego rozkładu normalnego. W naszym przypadku mamy: dla opcji zapadalnej w T = z ceną wykonania K = 00, = 0 d 2 = ln(00/0) + 0, 08 0, 22 /2 0, 2 B = exp( 0, 08 )Φ( 0, 7655) = 0, = 0, 7655 dla opcji zapadalnej w T = 2 z ceną wykonania K 2 = 00, 2 = 2 Tak więc marża m wynosi d 2 = ln(00/2) + 0, , 22 2 /2 0, 2 2 B 2 = exp( 0, 08 2)Φ( 0, 24968) = 0, m = 0, (0, , ) = 0, = 5, 0023%. Zadanie 4. IRS z ograniczoną stopą zmienną Punktacja: (a) - 3, (b) - 4, (c) - 3. Rozpatrzmy n-letni kontrakt wymiany procentowej, w którym wysokość stopy zmiennej jest ograniczona z góry. Noga stała płaci odsetki co rok, a noga zmienna co sześć miesięcy. Odsetki nogi zmiennej (na jednostkę nominału) za i-ty sześciomiesięczny okres odsetkowy w tym kontrakcie wynoszą i min(l i, L max ) gdzie L i jest 6M stopą rynkową (typu LIBOR) ustalaną na początku okresu odsetkowego, i jest długością tego okresu, a L max ustaloną kontraktem maksymalną wartością płaconej stopy rynkowej. Stopa R nogi stałej tego kontraktu jest tak dobierana, by w chwili rozpoczęcia kontraktu wartość kontraktu wynosiła zero. Oznaczmy ten kontrakt symbolem IRS.
7 Inżynieria Finansowa - Egzamin - 28 stycznia (a) Przedstaw kontrakt IRS jako portfel złożony pewnego kontraktu IRS oraz odpowiedniego instrumentu pochodnego. (b) Wyprowadź formułę na wartość stopy R kontraktu IRS jako funkcję od stopy R 0 standardowego kontraktu IRS (o takim samym czasie trwania i takiej samej strukturze okresów odsetkowych jak w kontrakcie IRS ), ceny odpowiedniego instrumentu pochodnego (patrz (a)), bieżącej wartości L 0 sześciomiesięcznej stopy rynkowej oraz bieżącej wartości n-letniej zerokuponowej stopy procentowej R(nY ). (c) Wykonaj obliczenia dla następujących danych liczbowych: n = 3 (to jest dla trzyletniego kontraktu), stopa standardowego kontraktu IRS 3Y R 0 = 6% 6M stopa (typu LIBOR) L 0 = 5.70% górny poziom stopy L max = 5.50% DF (3Y ) = 0.84 caps (ceny w bp, dla danych cen wykonania) Y floors (ceny w bp, dla danych cen wykonania) Y Rozwiązanie Część (a). Ponieważ min(l i, L max ) = L i max(l i L max, 0) oraz ponieważ kontrakt cap nie obejmuje kompensaty za pierwszy sześciomiesięczny okres odsetkowy (która potencjalnie powinna nastąpić), kontrakt IRS (w którym otrzymujemy stopę stałą R) jest równoważny portfelowi złożonemu z standardowego kontraktu IRS ze stopą R (otrzymujemy stopę stałą), kupionego n-letniego kontraktu cap z ceną wykonania L max, pozycji max(l 0 L max, 0) wynikającej z potencjalnego rozliczenia różnicy między stopami L max i L 0 w pierwszym okresie odsetkowym nogi zmiennej. Część (b). Niech c n oznacza cenę za jednostkę nominału n-letniego kontraktu cap ze stopą L max, oraz niech W 0 = max(l 0 L max, 0). Wówczas R - stopa stała kontraktu IRS - spełnia równanie R Q n + DF (ny ) = (c n + DF (6M)W 0 ), gdzie n Q n = ((k )Y, ky )DF (ky ). k=
8 Inżynieria Finansowa - Egzamin - 28 stycznia Znając R 0 stopę standardowego n-letniego kontraktu IRS, wielkość Q n możemy wyznaczyć z warunku R 0 Q n + DF (ny ) =, mianowicie Q n = DF (ny ) R 0. Zatem, po prostych przekształceniach, otrzymujemy następujący wzór na stopę R kontraktu IRS ( R = R 0 c ) n + DF (6M)W 0, DF (ny ) gdzie oczywiście DF (6M) = + L 0 oraz DF (ny ) = exp( R(nY ) n). Część (c). Z podanych cen kontraktów cap wybieramy cenę kontraktu z ceną wykonania L max = 5, 50%. Tak więc c 3 = 50 bp = 0, 05. Rozliczenie w 6M wynosi W 0 = max(0, 057 0, 055; 0) = 0, 00, a wartość czynnika dyskontowego dla 6M jest równa 2 DF (6M) = + 0, = 0, Po wstawieniu tych wielkości do wyprowadzonego wzoru na stopę R, otrzymujemy ( R = 6% ) 0, , , 00 = 5, 40%. 0, 84
Inżynieria finansowa Ćwiczenia III Stopy Forward i Kontrakt FRA
 Inżynieria finansowa Ćwiczenia III Stopy Forward i Kontrakt FRA Wydział Matematyki Informatyki i Mechaniki UW 18 października 2011 Zadanie 3.1 W dniu 18 października 2004 Bank X kwotował: 3M PLN Depo -
Inżynieria finansowa Ćwiczenia III Stopy Forward i Kontrakt FRA Wydział Matematyki Informatyki i Mechaniki UW 18 października 2011 Zadanie 3.1 W dniu 18 października 2004 Bank X kwotował: 3M PLN Depo -
Egzaminy z Inżynierii Finansowej
 Egzaminy z Inżynierii Finansowej Włodzimierz Waluś Wydział Matematyki Informatyki i Mechaniki Uniwersytet Warszawski Semestr zimowy 2002/2003 Inżynieria Finansowa - Egzamin - 28 stycznia 2003 2 Egzamin
Egzaminy z Inżynierii Finansowej Włodzimierz Waluś Wydział Matematyki Informatyki i Mechaniki Uniwersytet Warszawski Semestr zimowy 2002/2003 Inżynieria Finansowa - Egzamin - 28 stycznia 2003 2 Egzamin
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS
 Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS 2 Struktura kontraktu IRS Wycena kontraktu IRS 3 Struktura kontraktu
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CRIS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS 2 Struktura kontraktu IRS Wycena kontraktu IRS 3 Struktura kontraktu
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXI Egzamin dla Aktuariuszy z 1 października 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Matematyka finansowa 26.05.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Instrumenty pochodne - Zadania
 Jerzy A. Dzieża Instrumenty pochodne - Zadania 27 marca 2011 roku Rozdział 1 Wprowadzenie 1.1. Zadania 1. Spekulant zajął krótką pozycję w kontrakcie forward USD/PLN zapadającym za 2 miesiące o nominale
Jerzy A. Dzieża Instrumenty pochodne - Zadania 27 marca 2011 roku Rozdział 1 Wprowadzenie 1.1. Zadania 1. Spekulant zajął krótką pozycję w kontrakcie forward USD/PLN zapadającym za 2 miesiące o nominale
4.5. Obligacja o zmiennym oprocentowaniu
 .5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
.5. Obligacja o zmiennym oprocentowaniu 71.5. Obligacja o zmiennym oprocentowaniu Aby wycenić kontrakt IRS musi bliżej przyjrzeć się obligacji o zmiennym oprocentowaniu (Floating Rate Note lub floater
Inżynieria Finansowa: 4. FRA i Swapy
 Inżynieria Finansowa: 4. FRA i Swapy Piotr Bańbuła Katedra Rynków i Instytucji Finansowych, KES Październik 2014 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka
Inżynieria Finansowa: 4. FRA i Swapy Piotr Bańbuła Katedra Rynków i Instytucji Finansowych, KES Październik 2014 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka
æ Inżynieria Finansowa Egzamin Wydział Matematyki, Informatyki i Mechaniki UW 28 stycznia 2003 roku
 æ Inżynieria Finansowa Egzamin Wydział Matematyki, Informatyki i Mechaniki UW 28 stycznia 2003 roku Uwagi i zasady 1. Rozwiązania zadań rachunkowych muszą zawierać objaśnienia do wykonywanych obliczeń
æ Inżynieria Finansowa Egzamin Wydział Matematyki, Informatyki i Mechaniki UW 28 stycznia 2003 roku Uwagi i zasady 1. Rozwiązania zadań rachunkowych muszą zawierać objaśnienia do wykonywanych obliczeń
Matematyka finansowa 8.12.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Inżynieria Finansowa: 4. FRA i IRS
 Inżynieria Finansowa: 4. FRA i IRS Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka sprzedaż/pożyczka
Inżynieria Finansowa: 4. FRA i IRS Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zakup syntetycznej obligacji +1 mln PLN: emisja obligacji/krótka sprzedaż/pożyczka
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXXIII Egzamin dla Aktuariuszy z 7 marca 2016 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXXIII Egzamin dla Aktuariuszy z 7 marca 2016 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXXIII Egzamin dla Aktuariuszy z 7 marca 2016 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Wykład XII. Instrumenty pochodne stopy procentowej
 Inżynieria Finansowa - Wykład XII 1 Wykład XII Instrumenty pochodne stopy procentowej Proste instrumenty pochodne stopy procentowej Instrumenty pochodne, których wypłaty zależą od struktury stóp procentowych,
Inżynieria Finansowa - Wykład XII 1 Wykład XII Instrumenty pochodne stopy procentowej Proste instrumenty pochodne stopy procentowej Instrumenty pochodne, których wypłaty zależą od struktury stóp procentowych,
Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino
 Ćwiczenia 5 Pojęcie benchmarku, tracking error Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino Renata Karkowska, Wydział Zarządzania UW 1 Współczynnik Sharpe a Renata Karkowska,
Ćwiczenia 5 Pojęcie benchmarku, tracking error Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino Renata Karkowska, Wydział Zarządzania UW 1 Współczynnik Sharpe a Renata Karkowska,
Matematyka finansowa 03.10.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVIII Egzamin dla Aktuariuszy z 3 października 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Matematyka finansowa 10.12.2012 r. Komisja Egzaminacyjna dla Aktuariuszy. LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 05.12.2005 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXVII Egzamin dla Aktuariuszy z 5 grudnia 2005 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXVII Egzamin dla Aktuariuszy z 5 grudnia 2005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XXXVII Egzamin dla Aktuariuszy z 5 grudnia 2005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 100 minut 1 1.
Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy
 Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Komisja Egzaminacyjna dla Aktuariuszy. XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Forward Rate Agreement
 Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem. Temat wykładu: Wycena kontraktów swap
 Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem Temat wykładu: Wycena kontraktów swap Podstawowe zagadnienia: 1. Wycena swapa procentowego metodą wyceny obligacji 2.
Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem Temat wykładu: Wycena kontraktów swap Podstawowe zagadnienia: 1. Wycena swapa procentowego metodą wyceny obligacji 2.
1. Charakterystyka obligacji. 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji.
 mgr Maciej Jagódka 1. Charakterystyka obligacji 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji. Wierzycielski papier wartościowy, w którym emitent obligacji jest dłużnikiem posiadacza
mgr Maciej Jagódka 1. Charakterystyka obligacji 2. Rodzaje obligacji. 3. Zadania praktyczne-duration/ceny obligacji. Wierzycielski papier wartościowy, w którym emitent obligacji jest dłużnikiem posiadacza
Matematyka finansowa 15.06.2015 r. Komisja Egzaminacyjna dla Aktuariuszy. LXXI Egzamin dla Aktuariuszy z 15 czerwca 2015 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
Matematyka finansowa 30.09.2013 r. Komisja Egzaminacyjna dla Aktuariuszy. LXV Egzamin dla Aktuariuszy z 30 września 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Papiery wartościowe o stałym dochodzie
 Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CIRS
 Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CIRS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS Struktura kontraktu OIS Wycena kontraktu OIS 2 Struktura kontraktu
Inżynieria finansowa Wykład IV Kontrakty OIS/IRS/CIRS Wydział Matematyki Informatyki i Mechaniki UW 25 października 2011 1 Kontrakty OIS Struktura kontraktu OIS Wycena kontraktu OIS 2 Struktura kontraktu
Matematyka finansowa 20.06.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVII Egzamin dla Aktuariuszy z 20 czerwca 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt)
 II Etap Maj 2013 Zadanie 1 II Etap Maj 2013 1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt) 1.1/podaj definicję składnika
II Etap Maj 2013 Zadanie 1 II Etap Maj 2013 1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt) 1.1/podaj definicję składnika
Inżynieria finansowa Ćwiczenia II Stopy Procentowe
 Inżynieria finansowa Ćwiczenia II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 Zadanie 2.1 Oprocentowanie 3M pożyczki wynosi 5.00% (ACT/365). Natomiast, 3M bon skarbowy
Inżynieria finansowa Ćwiczenia II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 Zadanie 2.1 Oprocentowanie 3M pożyczki wynosi 5.00% (ACT/365). Natomiast, 3M bon skarbowy
Inżynieria Finansowa: 5. Opcje
 Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE wiecień 2017 r. Warszawa, Szkoła Główna Handlowa Amounts outstanding of assets and derivatives Derivatives Derivatives Note:
Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE wiecień 2017 r. Warszawa, Szkoła Główna Handlowa Amounts outstanding of assets and derivatives Derivatives Derivatives Note:
Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo
 Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Dokument przedstawia zaimplementowane w systemie KDPW_CCP formuły wyceny instrumentów
Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Dokument przedstawia zaimplementowane w systemie KDPW_CCP formuły wyceny instrumentów
Matematyka finansowa 08.01.2007 r. Komisja Egzaminacyjna dla Aktuariuszy. XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile
Komisja Egzaminacyjna dla Aktuariuszy XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile
Dokumentacja Analityczna wycena instrumentów pochodnych na stopę procentową
 Dokumentacja Analityczna wycena instrumentów pochodnych na stopę procentową Tomasz Romanowski Opis wycenianych instrumentów Caplet / Floorlet Jest to pojedyncza opcja kupna/sprzedaży stopy rynkowej L(T,
Dokumentacja Analityczna wycena instrumentów pochodnych na stopę procentową Tomasz Romanowski Opis wycenianych instrumentów Caplet / Floorlet Jest to pojedyncza opcja kupna/sprzedaży stopy rynkowej L(T,
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 16 maja 2005 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE
 TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE 1 SWAP - fixed-to-floating rate IRS - swap procentowy jest umową, w której dwie strony uzgadniają, że będą w ustalonych terminach
TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE 1 SWAP - fixed-to-floating rate IRS - swap procentowy jest umową, w której dwie strony uzgadniają, że będą w ustalonych terminach
Egzamin XXVII dla Aktuariuszy z 12 października 2002 r.
 Komisja Egzaminacyjna dla Aktuariuszy Egzamin XXVII dla Aktuariuszy z 12 października 2002 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia
Komisja Egzaminacyjna dla Aktuariuszy Egzamin XXVII dla Aktuariuszy z 12 października 2002 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Opcje - wprowadzenie. Mała powtórka: instrumenty liniowe. Anna Chmielewska, SGH,
 Opcje - wprowadzenie Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony wcześniej kurs terminowy. W dniu rozliczenia transakcji terminowej forward:
Opcje - wprowadzenie Mała powtórka: instrumenty liniowe Punkt odniesienia dla rozliczania transakcji terminowej forward: ustalony wcześniej kurs terminowy. W dniu rozliczenia transakcji terminowej forward:
Matematyka finansowa 15.12.2008 r. Komisja Egzaminacyjna dla Aktuariuszy. XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Matematyka finansowa 11.10.2004 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
1) jednostka posiada wystarczające środki aby zakupić walutę w dniu podpisania kontraktu
 Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
Przykład 1 Przedsiębiorca będący importerem podpisał kontrakt na zakup materiałów (surowców) o wartości 1 000 000 euro z datą płatności za 3 miesiące. Bieżący kurs 3,7750. Pozostałe koszty produkcji (wynagrodzenia,
Instrumenty pochodne Instrumenty wbudowane
 www.pwcacademy.pl Instrumenty pochodne Instrumenty wbudowane Jan Domanik Instrumenty pochodne ogólne zasady ujmowania i wyceny 2 Instrument pochodny definicja. to instrument finansowy: którego wartość
www.pwcacademy.pl Instrumenty pochodne Instrumenty wbudowane Jan Domanik Instrumenty pochodne ogólne zasady ujmowania i wyceny 2 Instrument pochodny definicja. to instrument finansowy: którego wartość
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1. Rozważamy
Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1. Rozważamy
Powtórzenie. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
OPISY PRODUKTÓW. Rabobank Polska S.A.
 OPISY PRODUKTÓW Rabobank Polska S.A. Warszawa, marzec 2010 Wymiana walut (Foreign Exchange) Wymiana walut jest umową pomiędzy bankiem a klientem, w której strony zobowiązują się wymienić w ustalonym dniu
OPISY PRODUKTÓW Rabobank Polska S.A. Warszawa, marzec 2010 Wymiana walut (Foreign Exchange) Wymiana walut jest umową pomiędzy bankiem a klientem, w której strony zobowiązują się wymienić w ustalonym dniu
Matematyka finansowa 04.04.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Inżynieria finansowa Wykład II Stopy Procentowe
 Inżynieria finansowa Wykład II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 1 Rynkowe stopy procentowe Rodzaje stóp rynkowych Reguły rachunku stóp 2 3 Definicje stóp
Inżynieria finansowa Wykład II Stopy Procentowe Wydział Matematyki Informatyki i Mechaniki UW 11 października 2011 1 Rynkowe stopy procentowe Rodzaje stóp rynkowych Reguły rachunku stóp 2 3 Definicje stóp
Wycena papierów wartościowych - instrumenty pochodne
 Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC
 Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Załącznik przedstawia
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo 1 Wprowadzenie Załącznik przedstawia
WERSJA TESTU A. Komisja Egzaminacyjna dla Aktuariuszy. XLV Egzamin dla Aktuariuszy z 17 marca 2008 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLV Egzamin dla Aktuariuszy z 17 marca 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. RozwaŜmy
Komisja Egzaminacyjna dla Aktuariuszy XLV Egzamin dla Aktuariuszy z 17 marca 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. RozwaŜmy
Dr hab. Renata Karkowska, ćwiczenia Zarządzanie ryzykiem 1
 1 Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu. Ryzyko podstawy
1 Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu. Ryzyko podstawy
Obligacje, Swapy, FRAsy i Bob Citron
 Obligacje, Swapy, FRAsy i Bob Citron Andrzej Kulik andrzej.kulik@pioneer.com.pl +22 321 4106/ 609 691 729 1 Plan Przypomnienie informacji o rynku długu Rodzaje obligacji Ryzyko obligacji yield curve Duration
Obligacje, Swapy, FRAsy i Bob Citron Andrzej Kulik andrzej.kulik@pioneer.com.pl +22 321 4106/ 609 691 729 1 Plan Przypomnienie informacji o rynku długu Rodzaje obligacji Ryzyko obligacji yield curve Duration
Komisja Egzaminacyjna dla Aktuariuszy. XXXIX Egzamin dla Aktuariuszy z 5 czerwca 2006 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXIX Egzamin dla Aktuariuszy z 5 czerwca 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Inwestor dokonuje
Komisja Egzaminacyjna dla Aktuariuszy XXXIX Egzamin dla Aktuariuszy z 5 czerwca 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Inwestor dokonuje
Analiza instrumentów pochodnych
 Analiza instrumentów pochodnych Dr Wioletta Nowak Wykład 2-3 Kontrakt forward na przyszłą stopę procentową Kontrakty futures na długoterminowe instrumenty procentowe Swapy procentowe Przykład 1 Inwestor
Analiza instrumentów pochodnych Dr Wioletta Nowak Wykład 2-3 Kontrakt forward na przyszłą stopę procentową Kontrakty futures na długoterminowe instrumenty procentowe Swapy procentowe Przykład 1 Inwestor
- zabezpieczanie za pomocą opcji
 Ryzyko stopy procentowej - zabezpieczanie za pomocą opcji Caplets and Floorlets Opcje opiewające na wysokość terminowej stopy procentowej Alternatywa dla FRA Caplet N x M @ i% - kupno daje prawo płacić
Ryzyko stopy procentowej - zabezpieczanie za pomocą opcji Caplets and Floorlets Opcje opiewające na wysokość terminowej stopy procentowej Alternatywa dla FRA Caplet N x M @ i% - kupno daje prawo płacić
Inwestycje finansowe. Wycena obligacji. Stopa zwrotu z akcji. Ryzyko.
 Inwestycje finansowe Wycena obligacji. Stopa zwrotu z akcji. yzyko. Inwestycje finansowe Instrumenty rynku pieniężnego (np. bony skarbowe). Instrumenty rynku walutowego. Obligacje. Akcje. Instrumenty pochodne.
Inwestycje finansowe Wycena obligacji. Stopa zwrotu z akcji. yzyko. Inwestycje finansowe Instrumenty rynku pieniężnego (np. bony skarbowe). Instrumenty rynku walutowego. Obligacje. Akcje. Instrumenty pochodne.
 NOTA 6 - INSTRUMENTY POCHODNE BPH Fundusz Inwestycyjny Otwarty Parasolowy BPH Subfundusz Obligacji 2 na dzień 31.12.2012 Typ zajętej pozycji Rodzaj instrumentu pochodnego Cel otwarcia pozycji Wartość otwartej
NOTA 6 - INSTRUMENTY POCHODNE BPH Fundusz Inwestycyjny Otwarty Parasolowy BPH Subfundusz Obligacji 2 na dzień 31.12.2012 Typ zajętej pozycji Rodzaj instrumentu pochodnego Cel otwarcia pozycji Wartość otwartej
Opcje podstawowe własności.
 Opcje podstawowe własności. Opcja jest to rodzaj umowy między dwoma podmiotami i jednocześnie instrument finansowy. Opcje kupna (call) dają posiadaczowi prawo do kupienia określonego w umowie aktywa (bazowego)
Opcje podstawowe własności. Opcja jest to rodzaj umowy między dwoma podmiotami i jednocześnie instrument finansowy. Opcje kupna (call) dają posiadaczowi prawo do kupienia określonego w umowie aktywa (bazowego)
Inwestowanie w obligacje
 Inwestowanie w obligacje Ile zapłacić za obligację aby uzyskać oczekiwaną stopę zwrotu? Jaką stopę zwrotu uzyskamy kupując obligację po danej cenie? Jak zmienią się ceny obligacji, kiedy Rada olityki ieniężnej
Inwestowanie w obligacje Ile zapłacić za obligację aby uzyskać oczekiwaną stopę zwrotu? Jaką stopę zwrotu uzyskamy kupując obligację po danej cenie? Jak zmienią się ceny obligacji, kiedy Rada olityki ieniężnej
II Etap egzaminu na Doradcę Inwestycyjnego Maj 2014. Zadanie 2
 II Etap egzaminu na Doradcę Inwestycyjnego Maj 2014 Zadanie 2 1/ Analizowane są dwie spółki Alfa i Gamma. Spółka Alfa finansuje swoją działalność nie korzystając z długu, natomiast spółka Gamma finansuje
II Etap egzaminu na Doradcę Inwestycyjnego Maj 2014 Zadanie 2 1/ Analizowane są dwie spółki Alfa i Gamma. Spółka Alfa finansuje swoją działalność nie korzystając z długu, natomiast spółka Gamma finansuje
mgr Katarzyna Niewińska; Wydział Zarządzania UW Ćwiczenia 2
 Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych
 Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo Tabela zmian Wersja dokumentu Wprowadzone
Załącznik nr 6 do Szczegółowych Zasad Systemu Rozliczeń OTC Sposób wyliczania depozytów zabezpieczających oraz zasady wyceny instrumentów pochodnych i transakcji repo Tabela zmian Wersja dokumentu Wprowadzone
Inżynieria Finansowa: 5. Opcje
 Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE Listopad 2014 r. Warszawa, Szkoła Główna Handlowa Opcje - typy Opcja jest asymetrycznym instrumentem. Opcja (standardowa, prosta,
Inżynieria Finansowa: 5. Opcje Piotr Bańbuła atedra Ekonomii Ilościowej, AE Listopad 2014 r. Warszawa, Szkoła Główna Handlowa Opcje - typy Opcja jest asymetrycznym instrumentem. Opcja (standardowa, prosta,
INSTRUMENTY POCHODNE OPCJE EUROPEJSKIE OPCJE AMERYKAŃSKIE OPCJE EGZOTYCZNE
 INSTRUMENTY POCHODNE OPCJE EUROPEJSKIE OPCJE AMERYKAŃSKIE OPCJE EGZOTYCZNE OPCJE / DEFINICJA Opcja jest prawem do zakupu lub sprzedaży określonej ilości wyspecyfikowanego przedmiotu (tzw. instrumentu bazowego)
INSTRUMENTY POCHODNE OPCJE EUROPEJSKIE OPCJE AMERYKAŃSKIE OPCJE EGZOTYCZNE OPCJE / DEFINICJA Opcja jest prawem do zakupu lub sprzedaży określonej ilości wyspecyfikowanego przedmiotu (tzw. instrumentu bazowego)
Wzory matematyka finansowa
 Wzory matematyka finansowa MaciejRomaniuk 29 września 29 K(t) funkcjaopisującaakumulacjęwchwiliczasut,k() kapitał,i stopazyskuwchwilit: i= K(t) K() (1) K() K kapitał,i stałastopaprocentowadlaustalonegookresuczasut,
Wzory matematyka finansowa MaciejRomaniuk 29 września 29 K(t) funkcjaopisującaakumulacjęwchwiliczasut,k() kapitał,i stopazyskuwchwilit: i= K(t) K() (1) K() K kapitał,i stałastopaprocentowadlaustalonegookresuczasut,
Matematyka finansowa. Ćwiczenia ZPI. Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Matematyka finansowa Ćwiczenia ZPI 1 Zadanie 1. Procent składany W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku
Matematyka finansowa Ćwiczenia ZPI 1 Zadanie 1. Procent składany W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH
 O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
Forward kontrakt terminowy o charakterze rzeczywistym (z dostawą instrumentu bazowego).
 Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
Zatem, jest wartością portfela (wealth) w chwili,. j=1
 Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Uchwała Nr 10/18 Zarządu KDPW_CCP S.A. z dnia 19 marca 2018 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeń OTC
 Uchwała Nr 10/18 Zarządu KDPW_CCP S.A. z dnia 19 marca 2018 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeń OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeń Transakcji (obrót niezorganizowany)
Uchwała Nr 10/18 Zarządu KDPW_CCP S.A. z dnia 19 marca 2018 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeń OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeń Transakcji (obrót niezorganizowany)
Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych
 Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa i ubezpieczeniowa - 8 Wycena papierów wartościowych W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Zadanie 1. Zadanie 2. Zadanie 3
 Zadanie 1 Inwestor rozważa nabycie obligacji wieczystej (konsoli), od której będzie otrzymywał na koniec każdego półrocza kupon w wysokości 80 zł. Wymagana przez inwestora stopa zwrotu w terminie do wykupu
Zadanie 1 Inwestor rozważa nabycie obligacji wieczystej (konsoli), od której będzie otrzymywał na koniec każdego półrocza kupon w wysokości 80 zł. Wymagana przez inwestora stopa zwrotu w terminie do wykupu
Ostatnia aktualizacja: 18 grudnia 2011
 Zestaw zadań przygotowanych do wykładu Włodziemierza Walusia na Wydziale Matematyki, Informatyki i Mechaniki UW. Duża część z nich pochodzi ze zbiorów wykładowcy. Zadania rozgrzewkowe Ostatnia aktualizacja:
Zestaw zadań przygotowanych do wykładu Włodziemierza Walusia na Wydziale Matematyki, Informatyki i Mechaniki UW. Duża część z nich pochodzi ze zbiorów wykładowcy. Zadania rozgrzewkowe Ostatnia aktualizacja:
Zadania przygotowujące do egzaminu z wykładu Inżynieria Finansowa
 Zadania przygotowujące do egzaminu z wykładu Inżynieria Finansowa Rozpisywanie przepływów gotówkowych, zabezpieczanie, spekulacja: 1. Za 9 miesięcy musisz zapłacić za wycieczkę 1500 EUR. Posiadasz konto
Zadania przygotowujące do egzaminu z wykładu Inżynieria Finansowa Rozpisywanie przepływów gotówkowych, zabezpieczanie, spekulacja: 1. Za 9 miesięcy musisz zapłacić za wycieczkę 1500 EUR. Posiadasz konto
Prof. nadzw. dr hab. Marcin Jędrzejczyk
 Prof. nadzw. dr hab. Marcin Jędrzejczyk 1. Zakup akcji, udziałów w obcych podmiotach gospodarczych według cen nabycia. 2. Zakup akcji i innych długoterminowych papierów wartościowych, traktowanych jako
Prof. nadzw. dr hab. Marcin Jędrzejczyk 1. Zakup akcji, udziałów w obcych podmiotach gospodarczych według cen nabycia. 2. Zakup akcji i innych długoterminowych papierów wartościowych, traktowanych jako
PRODUKTY STRUKTURYZOWANE
 PRODUKTY STRUKTURYZOWANE WYŁĄCZENIE ODPOWIEDZIALNOŚCI Niniejsza propozycja nie stanowi oferty w rozumieniu art. 66 Kodeksu cywilnego. Ma ona charakter wyłącznie informacyjny. Działając pod marką New World
PRODUKTY STRUKTURYZOWANE WYŁĄCZENIE ODPOWIEDZIALNOŚCI Niniejsza propozycja nie stanowi oferty w rozumieniu art. 66 Kodeksu cywilnego. Ma ona charakter wyłącznie informacyjny. Działając pod marką New World
Dokumentacja. Portal Mathfinance Wycena opcji paryskich metoda. Wiktor Madejski
 Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
II ETAP EGZAMINU EGZAMIN PISEMNY
 II ETAP EGZAMINU NA DORADCĘ INWESTYCYJNEGO EGZAMIN PISEMNY 7 grudnia 2014 r. Warszawa Treść i koncepcja pytań zawartych w teście są przedmiotem praw autorskich i nie mogą być publikowane lub w inny sposób
II ETAP EGZAMINU NA DORADCĘ INWESTYCYJNEGO EGZAMIN PISEMNY 7 grudnia 2014 r. Warszawa Treść i koncepcja pytań zawartych w teście są przedmiotem praw autorskich i nie mogą być publikowane lub w inny sposób
3.1 Analiza zysków i strat
 3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty poniesione
3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty poniesione
8. Zarządzanie portfelem inwestycyjnym za pomocą instrumentów pochodnych Zabezpieczenie Spekulacja Arbitraż 9. Charakterystyka i teoria wyceny
 8. Zarządzanie portfelem inwestycyjnym za pomocą instrumentów pochodnych Zabezpieczenie Spekulacja Arbitraż 9. Charakterystyka i teoria wyceny kontraktów terminowych Kontrakty forward FRA 1 Zadanie 1 Profil
8. Zarządzanie portfelem inwestycyjnym za pomocą instrumentów pochodnych Zabezpieczenie Spekulacja Arbitraż 9. Charakterystyka i teoria wyceny kontraktów terminowych Kontrakty forward FRA 1 Zadanie 1 Profil
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku A ulokowano kwotę 1000 zł. Jaki kapitał należy
Ćwiczenia ZPI 1 W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku A ulokowano kwotę 1000 zł. Jaki kapitał należy
Obligacje o stałym oprocentowaniu (fixed-interest bonds)
 Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
Matematyka finansowa, rozkład normalny, Model wyceny aktywów kapitałowych, Forward, Futures
 Matematyka finansowa, rozkład normalny, Model wyceny aktywów kapitałowych, Forward, Futures 1 Inwestor ma trzyletnią obligację o wartości nominalnej 2000 zł, oprocentowaną 8% rocznie, przy czym odsetki
Matematyka finansowa, rozkład normalny, Model wyceny aktywów kapitałowych, Forward, Futures 1 Inwestor ma trzyletnią obligację o wartości nominalnej 2000 zł, oprocentowaną 8% rocznie, przy czym odsetki
MRF2019_W6. Kontrakty teminowe
 Kontrakty teminowe Transakcja (kontrakt) forward to umowa sprzedaży określonego dobra (bazowego) realizowana w z góry określonym terminie i po z góry określonej cenie. W dniu realizacji transakcji następuje
Kontrakty teminowe Transakcja (kontrakt) forward to umowa sprzedaży określonego dobra (bazowego) realizowana w z góry określonym terminie i po z góry określonej cenie. W dniu realizacji transakcji następuje
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz. II: CDS y - swapy kredytowe
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Wykład VI Kontrakty opcyjne
 Inżynieria Finansowa - Wykład VI 1 Wykład VI Kontrakty opcyjne Kontrakt opcyjny (krótko: opcja) to umowa na podstawie której jedna strona umowy (posiadacz opcji) nabywa prawo do zrealizowania opisanej
Inżynieria Finansowa - Wykład VI 1 Wykład VI Kontrakty opcyjne Kontrakt opcyjny (krótko: opcja) to umowa na podstawie której jedna strona umowy (posiadacz opcji) nabywa prawo do zrealizowania opisanej
dr hab. Marcin Jędrzejczyk
 dr hab. Marcin Jędrzejczyk Przez inwestycje należy rozumieć aktywa nabyte w celu osiągnięcia korzyści ekonomicznych, wynikających z przyrostu wartości tych zasobów, uzyskania z nich przychodów w postaci
dr hab. Marcin Jędrzejczyk Przez inwestycje należy rozumieć aktywa nabyte w celu osiągnięcia korzyści ekonomicznych, wynikających z przyrostu wartości tych zasobów, uzyskania z nich przychodów w postaci
Inwestor musi wybrać następujące parametry: instrument bazowy, rodzaj opcji (kupna lub sprzedaży, kurs wykonania i termin wygaśnięcia.
 Opcje na GPW (II) Wbrew ogólnej opinii, inwestowanie w opcje nie musi być trudne. Na rynku tym można tworzyć strategie dla doświadczonych inwestorów, ale również dla początkujących. Najprostszym sposobem
Opcje na GPW (II) Wbrew ogólnej opinii, inwestowanie w opcje nie musi być trudne. Na rynku tym można tworzyć strategie dla doświadczonych inwestorów, ale również dla początkujących. Najprostszym sposobem
Uchwała Nr 54/17 Zarządu KDPW_CCP S.A. z dnia 20 listopada 2017 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeo OTC
 Uchwała Nr 54/17 Zarządu KDPW_CCP S.A. z dnia 20 listopada 2017 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeo OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeo Transakcji (obrót niezorganizowany)
Uchwała Nr 54/17 Zarządu KDPW_CCP S.A. z dnia 20 listopada 2017 r. w sprawie zmiany Szczegółowych Zasad Systemu Rozliczeo OTC Na podstawie 3 ust. 2, 4 i 8 Regulaminu Rozliczeo Transakcji (obrót niezorganizowany)
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej
 5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
Charakterystyka i wycena kontraktów terminowych forward
 Charakterystyka i wycena kontraktów terminowych forward Profil wypłaty forward Profil wypłaty dla pozycji długiej w kontrakcie terminowym Long position Zysk/strata Cena spot Profil wypłaty dla pozycji
Charakterystyka i wycena kontraktów terminowych forward Profil wypłaty forward Profil wypłaty dla pozycji długiej w kontrakcie terminowym Long position Zysk/strata Cena spot Profil wypłaty dla pozycji
Obligacje o stałym oprocentowaniu (fixed- interest bonds) Najprostsze z nich to
 Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
Obligacje (bonds) Obligacja papier wartościowy emitowany w serii, w którym emitent stwierdza, że jest dłużnikiem obligatariusza i zobowiązuje się wobec niego do spełnienia określonego świadczenia. Najczęściej
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
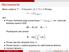 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
TRANSAKCJE KASOWE. Sekcja I (produkty inwestycyjne)
 Kwestionariusz oceny odpowiedniości w odniesieniu do transakcji skarbowych Zgodnie z Dyrektywą MIFID, Alior Bank SA, świadcząc usługi nabywania i zbywania instrumentów finansowych na własny rachunek, jest
Kwestionariusz oceny odpowiedniości w odniesieniu do transakcji skarbowych Zgodnie z Dyrektywą MIFID, Alior Bank SA, świadcząc usługi nabywania i zbywania instrumentów finansowych na własny rachunek, jest
