POWŁOKI GEOMETRIA POWIERZCHNI
|
|
|
- Dominik Jarosław Sosnowski
- 6 lat temu
- Przeglądów:
Transkrypt
1 Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydzia Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Maria Radwańska
2 Tematyka wykładu 1 Powłoka obiekt powierzchniowy 2 Opis geometryczny powierzchni definicje 3 Geometria wybranych powierzchni 4 Powierzchnia równo oddalona
3 Powłoka obiekt powierzchniowy Opis geometryczny powierzchni definicje Geometria wybranych powierzchni Konstrukcje powłokowe w przyrodzie Powierzchnia równo oddalona
4 Powłoka obiekt powierzchniowy Opis geometryczny powierzchni definicje Geometria wybranych powierzchni Powierzchnia równo oddalona Inżynierskie konstrukcje powłokowe Przekrycia dachowe Podpory platform wiertniczych Wielogałęziowe powłoki Powłoki chłodni kominowych wegrzyn/coolingt.html jako podelementy konstrukcyjne
5 Definicja powłoki Konstrukcja powłokowa to ustrój powierzchniowy zakrzywiony Powierzchnia środkowa jako dwuwymiarowy obiekt geometryczny opisany współrzędnymi krzywoliniowymi ξ 1 i ξ 2 jest modelem całej powłoki.
6 Jak określić geometrię ustroju powierzchniowego? Geometria ustroju powierzchniowego jest określona za pomocą: układu współrzędnych, kształtu powierzchni środkowej, konturu brzegowego, rozkładu grubości. Kształt powierzchni środkowej jest scharakteryzowany w odpowiednim układzie współrzędnych krzywoliniowych za pomocą: dwóch parametrów Lamègo A α, dwóch promieni głównych krzywizn R α.
7 Równanie powierzchni środkowej Powierzchnia środkowa jest scharakteryzowana w układzie współrzędnych krzywoliniowych ξ α, (α = 1, 2). Położenie punktu można określić jednoznacznie za pomocą tych współrzędnych, które są utworzone z dwóch rodzin linii. Równanie powierzchni środkowej oraz powiązanie globalnych współrzędnych kartezjańskich (X, Y, Z) i lokalnych krzywoliniowych (ξ 1, ξ 2 ) przedstawiają zależności: r = X i X + Y i Y + Zi Z X = f 1 (ξ 1, ξ 2 ) Y = f 2 (ξ 1, ξ 2 ) Z = f 3 (ξ 1, ξ 2 )
8 Powłoka obiekt powierzchniowy Opis geometryczny powierzchni definicje Geometria wybranych powierzchni Powierzchnia równo oddalona Długości łuków i parametry Lame go Dwuwymiarowy wycinek na powierzchni powstaje w wyniku przecięcia linii: ξ1 = const. ξ1 + dξ1 = const. ξ2 = const. ξ2 + dξ2 = const. Wyróżniamy krzywą l, która przechodzi przez punkty P i M. Do określenia długości łuku dsα wzdłuż linii współrzędnych ξα : dsα = Aα dξα służą parametry Lame go, równe długościom wektorów stycznych gα : Aα = ~r,α = gα gdzie α = 1, 2
9 Powłoka obiekt powierzchniowy Opis geometryczny powierzchni definicje Geometria wybranych powierzchni Powierzchnia równo oddalona I tensor metryczny i I forma kwadratowa r dξ2 r dξ1 + r = r[ξ1 (λ), ξ2 (λ)] dr = ξ ξ2 dλ dλ = r,1 dξ1 + r,2 dξ2 1 dλ Długość łuku z krzywej l, parametryzowanej współrzędną λ, pomiędzy punktami P i M obliczamy jako: ds 2 = r,1 r,1 dξ12 + 2r,1 r,2 dξ1 dξ2 + r,2 r,2 dξ22 = = A21 dξ12 + 2A1 A2 cos(g1, g2 )dξ1 dξ2 + A22 dξ22 Wersory: r eα = A,αα = Agαα e 3 = n = e1 e2 I tensor metryczny: gαβ = gα gβ = r,α r,β ds 2 = g11 dξ12 + 2g12 dξ1 dξ2 + g22 dξ22 I forma kwadratowa
10 Powłoka obiekt powierzchniowy Opis geometryczny powierzchni definicje Geometria wybranych powierzchni II tensor metryczny i II forma kwadratowa m = n r = n dr + 12 d2 r +... = 12 n d2 r +... II tensor metryczny: bαβ = r,αβ n = r,α n,β 2m = b11 dξ12 + 2b12 dξ1 dξ2 + b22 dξ22 II forma kwadratowa Promienie krzywizny lub krzywizna linii l: 1 2m n d2 r k = lim r 2 0 = 2 R r ds 2 Powierzchnia równo oddalona
11 Promienie główne krzywizn i krzywizna Gaussa Względem tzw. głównych linii wspólrzędnych, dla których g 12 = b 12 = 0, obliczamy dwa ekstremalne promienie główne krzywizn R αα, dwie krzywizny k αα : k αα = 1 = b αα = b αα, gdzie α = 1, 2. R αα g αα k 2 2 H k + K = 0 A 2 α Parametry opisujące powierzchnię: średnia krzywizna H: H = 1 2 (k 1 + k 2 ) krzywizna Gaussa: K = k 1 k 2 = 1 1 R 1 R 2 Krzywizna Gaussa jest używana do klasyfikacji typu powierzchni.
12 Powierzchnia walcowa w cylindrycznych współrzędnych r = x i i i = x i 1 + R sinθ i 2 + R cosθ i 3 [ ] [ ] g1 1 i g α = = 1 g 2 R cosθ i 2 R sinθ i 3 e α = [ e1 e 2 ] [ = n = sinθ i 2 + cosθ i 3 ] 1 i 1 cosθ i 2 sinθ i 3 A 1 = 1 A 2 = R [ ] [ ] g11 g g αβ = = g 21 g 22 0 R 2 R 1 = R 2 = R K = 0 H = 1 2R x 1 = x = ξ 1 R e 2 e 1 i 1 i 2 x 2 = y r n i 3 x 3 = z ξ 2 = θ
13 Powierzchnia kulista w układzie sferycznym r = x i i i = R sinϕ sinθ i 1 + R cosϕ i 2 + R sinϕ cosθ i 3 g α = [ g1 g 2 ] [ cosϕ sinθ i1 sinϕ i = R 2 + cosϕ cosθ i 3 sinϕ cosθ i i 2 sinϕ sinθ i 3 ] e α = 1 R g α n = sinϕ sinθ i 1 + cosϕ i 2 + sinϕ cosθ i 3 A 1 = R A 2 = R sinϕ [ ] [ g11 g g αβ = 12 R 2 0 = g 21 g 22 0 R 2 sin 2 ϕ R 1 = R 2 = R K = 1 R 2 H = 1 R ] ξ 1 = ϕ i 3 i 2 x 2 = y P r(ϕ) R i 1 e 1 n e 2 x 1 = x x 3 = z ξ 2 = θ
14 Powierzchnia hiperboliczna w układzie kartezjańskim z(x, y) = k x y k = f a b m = k x n = k y r = x i i i = x i 1 + y i 2 + k x y i 3 g α = e α = [ e1 [ g1 ] = g 2 [ ] 1 i1 + n i 3 1 i 2 + m i 3 ] 1 = e m2 + n g 2 α n = n i 1 m i 2 + i m2 + n 2 A 1 1 A 2 1 g αβ = [ ] g11 g 12 = g 21 g 22 [ ] 1 + n 2 m n m n 1 + n 2 b i 1 x b i 2 e 1 n e 2 a f y z
15 Opis geometrii ustrojów powierzchniowych za pomocą czterech parametrów geometrycznych Parametrami geometrycznymi są parametry Lamègo A α oraz promienie główne krzywizn R α, gdzie α = 1, 2. Powłoka kulista Powłoka walcowa Powłoka stożkowa Powłoki mało wyniosłe Tarcze i płyty prostokątne Tarcze i płyty kołowe lub pierścieniowe
16 Powłoka obiekt powierzchniowy Opis geometryczny powierzchni definicje Geometria wybranych powierzchni Powierzchnia równo oddalona Geometria powierzchni równo oddalonej od środkowej r(z) = r + zn (z) (z) dsα = Aα dξα (z) Aα = Aα 1 + h 2 z (z) eα = z Rα h 2 1 (z) (z) r,α Aα (z) Rα n(z) n = Rα 1 + Rzα Π (z) powierzchnia równo oddalona Π powierzchnia środkowa
1 Charakterystyka ustrojów powierzchniowych. Anna Stankiewicz
 1 Charakterystyka ustrojów powierzchniowych Anna Stankiewicz e-mail: astankiewicz@l5.pk.edu.pl Tematyka zajęć Przykłady konstrukcji inżynierskich Klasyfikacja ustrojów powierzchniowych Podstawowe pojęcia
1 Charakterystyka ustrojów powierzchniowych Anna Stankiewicz e-mail: astankiewicz@l5.pk.edu.pl Tematyka zajęć Przykłady konstrukcji inżynierskich Klasyfikacja ustrojów powierzchniowych Podstawowe pojęcia
Rozdział 3. Tensory. 3.1 Krzywoliniowe układy współrzędnych
 Rozdział 3 Tensory 3.1 Krzywoliniowe układy współrzędnych W kartezjańskim układzie współrzędnych punkty P są scharakteryzowane przez współrzędne kartezjańskie wektora wodzącego r = x 1 i 1 + x 2 i 2 +
Rozdział 3 Tensory 3.1 Krzywoliniowe układy współrzędnych W kartezjańskim układzie współrzędnych punkty P są scharakteryzowane przez współrzędne kartezjańskie wektora wodzącego r = x 1 i 1 + x 2 i 2 +
TARCZE PROSTOKĄTNE Charakterystyczne wielkości i równania
 TARCZE PROSTOKĄTNE Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika
TARCZE PROSTOKĄTNE Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika
Geometria powłoki, wg publikacji dr inż. Wiesław Baran
 Geometria powłoki, wg publikacji dr inż. Wiesław Baran Gładką i regularną powierzchnię środkową S powłoki można opisać za pomocą funkcji wektorowej (rys. 2.1) dwóch współrzędnych krzywoliniowych u 1 i
Geometria powłoki, wg publikacji dr inż. Wiesław Baran Gładką i regularną powierzchnię środkową S powłoki można opisać za pomocą funkcji wektorowej (rys. 2.1) dwóch współrzędnych krzywoliniowych u 1 i
i = [ 0] j = [ 1] k = [ 0]
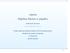
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Mechanika. Wykład 2. Paweł Staszel
 Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
PŁYTY OPIS W UKŁADZIE KARTEZJAŃSKIM Charakterystyczne wielkości i równania
 Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko
Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
PŁYTY OPIS W UKŁADZIE KARTEZJAŃSKIM Charakterystyczne wielkości i równania
 Charakterystyczne wielkości i równania PODSTAWY KOMPUTEROWEGO MODELOWANIA USTROJÓW POWIERZCHNIOWYCH Budownictwo, studia I stopnia, semestr VI przedmiot fakultatywny Instytut L-5, Wydział Inżynierii Lądowej,
Charakterystyczne wielkości i równania PODSTAWY KOMPUTEROWEGO MODELOWANIA USTROJÓW POWIERZCHNIOWYCH Budownictwo, studia I stopnia, semestr VI przedmiot fakultatywny Instytut L-5, Wydział Inżynierii Lądowej,
Mechanika ogólna. Kinematyka. Równania ruchu punktu materialnego. Podstawowe pojęcia. Równanie ruchu po torze (równanie drogi)
 Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ
 METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
Układy współrzędnych
 Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Wektory, układ współrzędnych
 Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Matematyka stosowana i metody numeryczne
 Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 14 Rachunekwektorowy W celu zdefiniowania wektora a należy podać: kierunek(prostą na której leży wektor)
Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 14 Rachunekwektorowy W celu zdefiniowania wektora a należy podać: kierunek(prostą na której leży wektor)
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Pole magnetyczne magnesu w kształcie kuli
 napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
Równa Równ n a i n e i ru r ch u u ch u po tor t ze (równanie drogi) Prędkoś ędkoś w ru r ch u u ch pros pr t os ol t i ol n i io i wym
 Mechanika ogólna Wykład nr 14 Elementy kinematyki i dynamiki 1 Kinematyka Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez
Mechanika ogólna Wykład nr 14 Elementy kinematyki i dynamiki 1 Kinematyka Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez
MECHANIKA PRĘTÓW CIENKOŚCIENNYCH
 dr inż. Robert Szmit Przedmiot: MECHANIKA PRĘTÓW CIENKOŚCIENNYCH WYKŁAD nr Uniwersytet Warmińsko-Mazurski w Olsztynie Katedra Geotechniki i Mechaniki Budowli Opis stanu odkształcenia i naprężenia powłoki
dr inż. Robert Szmit Przedmiot: MECHANIKA PRĘTÓW CIENKOŚCIENNYCH WYKŁAD nr Uniwersytet Warmińsko-Mazurski w Olsztynie Katedra Geotechniki i Mechaniki Budowli Opis stanu odkształcenia i naprężenia powłoki
Wprowadzenie do WK1 Stan naprężenia
 Wytrzymałość materiałów i konstrukcji 1 Wykład 1 Wprowadzenie do WK1 Stan naprężenia Płaski stan naprężenia Dr inż. Piotr Marek Wytrzymałość Konstrukcji (Wytrzymałość materiałów, Mechanika konstrukcji)
Wytrzymałość materiałów i konstrukcji 1 Wykład 1 Wprowadzenie do WK1 Stan naprężenia Płaski stan naprężenia Dr inż. Piotr Marek Wytrzymałość Konstrukcji (Wytrzymałość materiałów, Mechanika konstrukcji)
Lista nr 1 - Liczby zespolone
 Lista nr - Liczby zespolone Zadanie. Obliczyć: a) ( 3 i) 3 ( 6 i ) 8 c) (+ 3i) 8 (i ) 6 + 3 i + e) f*) g) ( 3 i ) 77 ( ( 3 i + ) 3i 3i h) ( + 3i) 5 ( i) 0 i) i ( 3 i ) 4 ) +... + ( 3 i ) 0 Zadanie. Przedstawić
Lista nr - Liczby zespolone Zadanie. Obliczyć: a) ( 3 i) 3 ( 6 i ) 8 c) (+ 3i) 8 (i ) 6 + 3 i + e) f*) g) ( 3 i ) 77 ( ( 3 i + ) 3i 3i h) ( + 3i) 5 ( i) 0 i) i ( 3 i ) 4 ) +... + ( 3 i ) 0 Zadanie. Przedstawić
Analiza płyt i powłok MES
 Analiza płyt i powłok MES Jerzy Pamin e-mails: JPamin@L5.pk.edu.pl Podziękowania: M. Radwańska, A. Wosatko ANSYS, Inc. http://www.ansys.com Tematyka zajęć Klasyfikacja modeli i elementów skończonych Elementy
Analiza płyt i powłok MES Jerzy Pamin e-mails: JPamin@L5.pk.edu.pl Podziękowania: M. Radwańska, A. Wosatko ANSYS, Inc. http://www.ansys.com Tematyka zajęć Klasyfikacja modeli i elementów skończonych Elementy
Kartografia matematyczna
 Wykład III Kartografia matematyczna Odwzorowania walcowe Krystian Kozioł Kraków 0 0 9 Odwzorowania walcowe Podział Ze względu na połoŝenie walca: - normalne - porzeczne - ukośne Ze względu na liczbę punktów
Wykład III Kartografia matematyczna Odwzorowania walcowe Krystian Kozioł Kraków 0 0 9 Odwzorowania walcowe Podział Ze względu na połoŝenie walca: - normalne - porzeczne - ukośne Ze względu na liczbę punktów
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Fizyka I (Mechanika) Wykład II: Pojęcia podstawowe punkt materialny, układ odniesienia, układ współrzędnych tor, prędkość, przyspieszenie Ruch jednostajny, ruch jednostajnie przyspieszony
Kinematyka: opis ruchu Fizyka I (Mechanika) Wykład II: Pojęcia podstawowe punkt materialny, układ odniesienia, układ współrzędnych tor, prędkość, przyspieszenie Ruch jednostajny, ruch jednostajnie przyspieszony
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
Dyfrakcja. Dyfrakcja to uginanie światła (albo innych fal) przez drobne obiekty (rozmiar porównywalny z długością fali) do obszaru cienia
 Dyfrakcja 1 Dyfrakcja Dyfrakcja to uginanie światła (albo innych fal) przez drobne obiekty (rozmiar porównywalny z długością fali) do obszaru cienia uginanie na szczelinie uginanie na krawędziach przedmiotów
Dyfrakcja 1 Dyfrakcja Dyfrakcja to uginanie światła (albo innych fal) przez drobne obiekty (rozmiar porównywalny z długością fali) do obszaru cienia uginanie na szczelinie uginanie na krawędziach przedmiotów
Geometria Struny Kosmicznej
 Spis treści 1 Wstęp 2 Struny kosmiczne geneza 3 Czasoprzestrzeń struny kosmicznej 4 Metryka czasoprzestrzeni struny kosmicznej 5 Wyznaczanie geodezyjnych 6 Wykresy geodezyjnych 7 Wnioski 8 Pytania Wstęp
Spis treści 1 Wstęp 2 Struny kosmiczne geneza 3 Czasoprzestrzeń struny kosmicznej 4 Metryka czasoprzestrzeni struny kosmicznej 5 Wyznaczanie geodezyjnych 6 Wykresy geodezyjnych 7 Wnioski 8 Pytania Wstęp
R o z d z i a ł 2 KINEMATYKA PUNKTU MATERIALNEGO
 R o z d z i a ł KINEMATYKA PUNKTU MATERIALNEGO Kinematyka zajmuje się opisem ruchu ciał bez uwzględniania ich masy i bez rozpatrywania przyczyn, które ten ruch spowodowały. Przez punkt materialny rozumiemy
R o z d z i a ł KINEMATYKA PUNKTU MATERIALNEGO Kinematyka zajmuje się opisem ruchu ciał bez uwzględniania ich masy i bez rozpatrywania przyczyn, które ten ruch spowodowały. Przez punkt materialny rozumiemy
II.2 Położenie i prędkość cd. Wektory styczny i normalny do toru. II.3 Przyspieszenie
 II. Położenie i prędkość cd. Wekory syczny i normalny do oru. II.3 Przyspieszenie Wersory cylindrycznego i sferycznego układu współrzędnych krzywoliniowych Wyrażenia na prędkość w układach cylindrycznym
II. Położenie i prędkość cd. Wekory syczny i normalny do oru. II.3 Przyspieszenie Wersory cylindrycznego i sferycznego układu współrzędnych krzywoliniowych Wyrażenia na prędkość w układach cylindrycznym
Mechanika Analityczna
 Mechanika Analityczna Wykład 2 - Zasada prac przygotowanych i ogólne równanie dynamiki Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej 29 lutego 2016 Plan wykładu
Mechanika Analityczna Wykład 2 - Zasada prac przygotowanych i ogólne równanie dynamiki Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej 29 lutego 2016 Plan wykładu
POD- I NADOKREŚLONE UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 POD- I NADOKREŚLONE UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko
POD- I NADOKREŚLONE UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko
Wykład 1. Wprowadzenie do przedmiotu. Powierzchnia odniesienia w pomiarach inżynierskich.
 Wykład 1 Wprowadzenie do przedmiotu. Powierzchnia odniesienia w pomiarach inżynierskich. Dr inż. Sabina Łyszkowicz Wita Studentów I Roku Inżynierii Środowiska na Pierwszym Wykładzie z Geodezji wykład 1
Wykład 1 Wprowadzenie do przedmiotu. Powierzchnia odniesienia w pomiarach inżynierskich. Dr inż. Sabina Łyszkowicz Wita Studentów I Roku Inżynierii Środowiska na Pierwszym Wykładzie z Geodezji wykład 1
ROZWINIĘCIA POWIERZCHNI STOPNIA DRUGIEGO W OPARCIU O MIEJSCA GEOMETRYCZNE Z ZA- STOSOWANIEM PROGRAMU CABRI II PLUS.
 Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
PŁYTY OPIS W UKŁADZIE KARTEZJAŃSKIM Charakterystyczne wielkości i równania
 Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko
Charakterystyczne wielkości i równania Mechanika materiałów i konstrukcji budowlanych, studia II stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko
Rozdział 2. Kinematyka
 Rozdział. Kinematyka 018 Spis treści Ruch jednowymiarowy Ruch na płaszczyźnie Rzut ukośny Ruch jednostajny po okręgu Ruch przyspieszony po okręgu Ruch krzywoliniowy Ruch jednowymiarowy Dział Fizyki zajmujący
Rozdział. Kinematyka 018 Spis treści Ruch jednowymiarowy Ruch na płaszczyźnie Rzut ukośny Ruch jednostajny po okręgu Ruch przyspieszony po okręgu Ruch krzywoliniowy Ruch jednowymiarowy Dział Fizyki zajmujący
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..)
 Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
Zagadnienie dwóch ciał
 Zagadnienie dwóch ciał Rysunek : Rysunek ilustrujący zagadnienie dwóch ciał. Wektor R określa położenie środka masy, wektor x położenie masy m, a wektor x 2 położenie masy m 2. Położenie masy m 2 względem
Zagadnienie dwóch ciał Rysunek : Rysunek ilustrujący zagadnienie dwóch ciał. Wektor R określa położenie środka masy, wektor x położenie masy m, a wektor x 2 położenie masy m 2. Położenie masy m 2 względem
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
Obliczanie indukcyjności cewek
 napisał Michał Wierzbicki Obliczanie indukcyjności cewek Indukcyjność dla cewek z prądem powierzchniowym Energia zgromadzona w polu magnetycznym dwóch cewek, przez uzwojenia których płyną prądy I 1 i I
napisał Michał Wierzbicki Obliczanie indukcyjności cewek Indukcyjność dla cewek z prądem powierzchniowym Energia zgromadzona w polu magnetycznym dwóch cewek, przez uzwojenia których płyną prądy I 1 i I
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne......................
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne......................
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN
 ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne....................
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne....................
Etap 1. Rysunek: Układy odniesienia
 Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
= sin. = 2Rsin. R = E m. = sin
 Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
RÓWNANIA RÓŻNICZKOWE WYKŁAD 15
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 15 Niech r ( t ) [ x( t), y( t), z( t)], t I ( r ( t ) x( t) i y( t) j z( t) k, t I ) będzie równaniem wektorowym krzywej w R 3. Definicja Krzywą o równaniu r ( t ) [ a cost,
RÓWNANIA RÓŻNICZKOWE WYKŁAD 15 Niech r ( t ) [ x( t), y( t), z( t)], t I ( r ( t ) x( t) i y( t) j z( t) k, t I ) będzie równaniem wektorowym krzywej w R 3. Definicja Krzywą o równaniu r ( t ) [ a cost,
Metoda elementów brzegowych
 Metoda elementów brzegowych Tomasz Chwiej, Alina Mreńca-Kolasińska 9 listopada 8 Wstęp Rysunek : a) Geometria układu z zaznaczonymi: elementami brzegu (czerwony), węzłami (niebieski). b) Numeracja: elementów
Metoda elementów brzegowych Tomasz Chwiej, Alina Mreńca-Kolasińska 9 listopada 8 Wstęp Rysunek : a) Geometria układu z zaznaczonymi: elementami brzegu (czerwony), węzłami (niebieski). b) Numeracja: elementów
Elektrostatyka, cz. 1
 Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Wykład 2. Kinematyka. Podstawowe wielkości opisujące ruch. W tekście tym przedstawię podstawowe pojecia niezbędne do opiosu ruchu:
 Wykład 2. Kinematyka. Aby prześledzić tok tego wykładu MUSISZ rozumieć pojęcie wektora, jego składowych w układzie kartezjańskim oraz w trakcie wykładu zrozumieć intuicyjnie pojęcie pochodnej funkcji jednej
Wykład 2. Kinematyka. Aby prześledzić tok tego wykładu MUSISZ rozumieć pojęcie wektora, jego składowych w układzie kartezjańskim oraz w trakcie wykładu zrozumieć intuicyjnie pojęcie pochodnej funkcji jednej
WYKŁAD 6 KINEMATYKA PRZEPŁYWÓW CZĘŚĆ 2 1/11
 WYKŁAD 6 KINEMATYKA PRZEPŁYWÓW CZĘŚĆ 1/11 DEFORMACJA OŚRODKA CIĄGŁEGO Rozważmy dwa elementy płynu położone w pewnej chwili w bliskich sobie punktach A i B. Jak zmienia się ich względne położenie w krótkim
WYKŁAD 6 KINEMATYKA PRZEPŁYWÓW CZĘŚĆ 1/11 DEFORMACJA OŚRODKA CIĄGŁEGO Rozważmy dwa elementy płynu położone w pewnej chwili w bliskich sobie punktach A i B. Jak zmienia się ich względne położenie w krótkim
Notatki do wykładu Geometria Różniczkowa I
 Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 6 stycznia 014 1 Różniczkowanie pól i form 1.1 Pochodna kowariantna Zobaczmy jak we współrzędnych wyglądać będzie równanie różniczkowe
Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 6 stycznia 014 1 Różniczkowanie pól i form 1.1 Pochodna kowariantna Zobaczmy jak we współrzędnych wyglądać będzie równanie różniczkowe
Obliczanie układów statycznie niewyznaczalnych. metodą sił
 Politechnika Poznańska Instytut Konstrukcji Budowlanych Zakład echaniki Budowli Obliczanie układów statycznie niewyznaczalnych metodą sił. Rama Dla układu pokazanego poniŝej naleŝy: - Oblicz i wykonać
Politechnika Poznańska Instytut Konstrukcji Budowlanych Zakład echaniki Budowli Obliczanie układów statycznie niewyznaczalnych metodą sił. Rama Dla układu pokazanego poniŝej naleŝy: - Oblicz i wykonać
Metoda elementów skończonych w mechanice konstrukcji / Gustaw Rakowski, Zbigniew Kacprzyk. wyd. 3 popr. Warszawa, cop
 Metoda elementów skończonych w mechanice konstrukcji / Gustaw Rakowski, Zbigniew Kacprzyk. wyd. 3 popr. Warszawa, cop. 2015 Spis treści Przedmowa do wydania pierwszego 7 Przedmowa do wydania drugiego 9
Metoda elementów skończonych w mechanice konstrukcji / Gustaw Rakowski, Zbigniew Kacprzyk. wyd. 3 popr. Warszawa, cop. 2015 Spis treści Przedmowa do wydania pierwszego 7 Przedmowa do wydania drugiego 9
Układ współrzędnych dwu trój Wykład 2 "Układ współrzędnych, system i układ odniesienia"
 Układ współrzędnych Układ współrzędnych ustanawia uporządkowaną zależność (relację) między fizycznymi punktami w przestrzeni a liczbami rzeczywistymi, czyli współrzędnymi, Układy współrzędnych stosowane
Układ współrzędnych Układ współrzędnych ustanawia uporządkowaną zależność (relację) między fizycznymi punktami w przestrzeni a liczbami rzeczywistymi, czyli współrzędnymi, Układy współrzędnych stosowane
Fizyka dla Informatyków Wykład 7 Mechanika Ośrodków Ciągłych
 Fizyka dla Informatyków Wykład 7 Mechanika Ośrodków Ciągłych Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało sprężyste Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało
Fizyka dla Informatyków Wykład 7 Mechanika Ośrodków Ciągłych Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało sprężyste Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało
Układy równań liniowych, macierze, Google
 Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)
![[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia) [ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)](/thumbs/88/115575588.jpg) PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 9, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 9, 12.03.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 8 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 9, 12.03.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 8 - przypomnienie
Opis ruchu obrotowego
 Opis ruchu obrotowego Oprócz ruchu translacyjnego ciała obserwujemy w przyrodzie inną jego odmianę: ruch obrotowy Ruch obrotowy jest zawsze względem osi obrotu W ruchu obrotowym wszystkie punkty zakreślają
Opis ruchu obrotowego Oprócz ruchu translacyjnego ciała obserwujemy w przyrodzie inną jego odmianę: ruch obrotowy Ruch obrotowy jest zawsze względem osi obrotu W ruchu obrotowym wszystkie punkty zakreślają
5.1 POJĘCIE CZASU. Rozdział należy do teorii pt. "Teoria Przestrzeni" autorstwa Dariusza Stanisława Sobolewskiego. Http:
 5.1 POJĘCIE CZASU Rozdział należy do teorii pt. "Teoria Przestrzeni" autorstwa Dariusza Stanisława Sobolewskiego. http: www.theoryofspace.info Obserwując zjawisko fizyczne w małym otoczeniu punktu charakter
5.1 POJĘCIE CZASU Rozdział należy do teorii pt. "Teoria Przestrzeni" autorstwa Dariusza Stanisława Sobolewskiego. http: www.theoryofspace.info Obserwując zjawisko fizyczne w małym otoczeniu punktu charakter
Algebra linowa w pigułce
 Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
ELEKTROSTATYKA. Zakład Elektrotechniki Teoretycznej Politechniki Wrocławskiej, I-7, W-5
 ELEKTROSTATYKA 2.1 Obliczyć siłę, z jaką działają na siebie dwa ładunki punktowe Q 1 = Q 2 = 1C umieszczone w odległości l km od siebie, a z jaką siłą - w tej samej odległości - dwie jednogramowe kulki
ELEKTROSTATYKA 2.1 Obliczyć siłę, z jaką działają na siebie dwa ładunki punktowe Q 1 = Q 2 = 1C umieszczone w odległości l km od siebie, a z jaką siłą - w tej samej odległości - dwie jednogramowe kulki
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Wstęp do Fizyki I (B+C) Wykład III: Pojęcia podstawowe punkt materialny, układ odniesienia, układ współrzędnych tor, prędkość, przyspieszenie Ruch jednostajny Pojęcia podstawowe
Kinematyka: opis ruchu Wstęp do Fizyki I (B+C) Wykład III: Pojęcia podstawowe punkt materialny, układ odniesienia, układ współrzędnych tor, prędkość, przyspieszenie Ruch jednostajny Pojęcia podstawowe
Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. u = 0, (6.1) jest operatorem Laplace a. (x,y)
 Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
2.9. Kinematyka typowych struktur manipulatorów
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
Obliczanie długości łuku krzywych. Autorzy: Witold Majdak
 Obliczanie długości łuku krzywych Autorzy: Witold Majdak 7 Obliczanie długości łuku krzywych Autor: Witold Majdak DEFINICJA Definicja : Długość łuku krzywej zadanej parametrycznie Rozważmy krzywą Γ zadaną
Obliczanie długości łuku krzywych Autorzy: Witold Majdak 7 Obliczanie długości łuku krzywych Autor: Witold Majdak DEFINICJA Definicja : Długość łuku krzywej zadanej parametrycznie Rozważmy krzywą Γ zadaną
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 9 AiR III
 1 Na podstawie materiałów autorstwa dra inż. Marka Wnuka. Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania
1 Na podstawie materiałów autorstwa dra inż. Marka Wnuka. Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania
 Ą Ż Ł ś ż ńż ż ż ś ź ź ć ź ś ń ż ć ź ź ź ż ź ś ź ń ź Ę ż ź ź ź ż ż ś ń ż ż ś ż ź ż ź źń ż ż ż ź ś ś ż ś ż ż Ż Ł ń ż ś ż ń ź ź ż żń ść ż ż ń ń ń ń ń ż ś ź ż ń ż ś ń ż ć ż ś ż ż ć ń ż ż ź ż ć ż ż ś ż ż ć
Ą Ż Ł ś ż ńż ż ż ś ź ź ć ź ś ń ż ć ź ź ź ż ź ś ź ń ź Ę ż ź ź ź ż ż ś ń ż ż ś ż ź ż ź źń ż ż ż ź ś ś ż ś ż ż Ż Ł ń ż ś ż ń ź ź ż żń ść ż ż ń ń ń ń ń ż ś ź ż ń ż ś ń ż ć ż ś ż ż ć ń ż ż ź ż ć ż ż ś ż ż ć
 Ę ć ń ż ć Ń ń ż ć ć ń ż ć ń ź ń Ę Ń ń ń ż ć ż ć ć Ń ż ć ń ć ż ń ż ć ć Ń ż ć Ń ż Ń Ń Ń ż ż Ń ż ż Ń ń ź Ń ń Ń ń ń Ą ń ń ź ń Ń Ń ć Ę ż Ń ż ć ć ć Ę ńż ń Ą ć ć Ę ż ż ć ż ć Ń ż Ń ż Ń ż ż ń ć ń Ń ń Ę ż Ł Ń ż
Ę ć ń ż ć Ń ń ż ć ć ń ż ć ń ź ń Ę Ń ń ń ż ć ż ć ć Ń ż ć ń ć ż ń ż ć ć Ń ż ć Ń ż Ń Ń Ń ż ż Ń ż ż Ń ń ź Ń ń Ń ń ń Ą ń ń ź ń Ń Ń ć Ę ż Ń ż ć ć ć Ę ńż ń Ą ć ć Ę ż ż ć ż ć Ń ż Ń ż Ń ż ż ń ć ń Ń ń Ę ż Ł Ń ż
Liczby zespolone. Magdalena Nowak. 23 marca Uniwersytet Śląski
 Uniwersytet Śląski 23 marca 2012 Ciało liczb zespolonych Rozważmy zbiór C = R R, czyli C = {(x, y) : x, y R}. W zbiorze C definiujemy następujące działania: dodawanie: mnożenie: (a, b) + (c, d) = (a +
Uniwersytet Śląski 23 marca 2012 Ciało liczb zespolonych Rozważmy zbiór C = R R, czyli C = {(x, y) : x, y R}. W zbiorze C definiujemy następujące działania: dodawanie: mnożenie: (a, b) + (c, d) = (a +
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Całka krzywoliniowa niezorientowana Niech R 3 będzie krzywą prostowalną opisywaną parametryzacją r:,α, β- γ taką, że
 Całka krzywoliniowa niezorientowana Niech R będzie krzywą prostowalną opisywaną parametryzacją r:,α, β- taką, że t α, β : r t = ( t, y t, z t ) ef. Mówimy, że krzywa jest kawałkami gładka funkcja r t ma
Całka krzywoliniowa niezorientowana Niech R będzie krzywą prostowalną opisywaną parametryzacją r:,α, β- taką, że t α, β : r t = ( t, y t, z t ) ef. Mówimy, że krzywa jest kawałkami gładka funkcja r t ma
WYDZIAŁ OCEANOTECHNIKI I OKRĘTOWNICTWA. Katedra Hydromechaniki i Hydroakustyki
 WYDZIAŁ OCEANOTECHNIKI I OKRĘTOWNICTWA Katedra Hydromechaniki i Hydroakustyki ĆWICZENIA LABORATORYJNE Z HYDROMECHANIKI OKRĘTU Ćwiczenie Nr 12 Pomiar charakterystyk geometrycznych śruby Opracował: dr inż.
WYDZIAŁ OCEANOTECHNIKI I OKRĘTOWNICTWA Katedra Hydromechaniki i Hydroakustyki ĆWICZENIA LABORATORYJNE Z HYDROMECHANIKI OKRĘTU Ćwiczenie Nr 12 Pomiar charakterystyk geometrycznych śruby Opracował: dr inż.
Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem.
 1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Atom wodoropodobny. Biegunowy układ współrzędnych. współrzędne w układzie. kartezjańskim. współrzędne w układzie. (x,y,z) biegunowym.
 Atom wodoropodobny z współrzędne w układzie kartezjańskim r sinθ cosφ x r cosθ φ θ r r sinθ (x,y,z) r sinθ sinφ Biegunowy układ współrzędnych y funkcja faowa współrzędne w układzie biegunowym ( ) r,θ,φ
Atom wodoropodobny z współrzędne w układzie kartezjańskim r sinθ cosφ x r cosθ φ θ r r sinθ (x,y,z) r sinθ sinφ Biegunowy układ współrzędnych y funkcja faowa współrzędne w układzie biegunowym ( ) r,θ,φ
Wykład z modelowania matematycznego.
 Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
WYZNACZANIE SIŁ WEWNĘTRZNYCH W BELCE
 POLITECHNIKA POZNAŃSKA INSTYTUT KONSTRUKCJI BUDOWLANYCH Zakład Mechaniki Budowli ĆWICZENIE nr 2 WYZNACZANIE SIŁ WEWNĘTRZNYCH W BELCE Prowadzący: mgr inŝ. A. Kaczor STUDIA DZIENNE MAGISTERSKIE, I ROK Wykonał:
POLITECHNIKA POZNAŃSKA INSTYTUT KONSTRUKCJI BUDOWLANYCH Zakład Mechaniki Budowli ĆWICZENIE nr 2 WYZNACZANIE SIŁ WEWNĘTRZNYCH W BELCE Prowadzący: mgr inŝ. A. Kaczor STUDIA DZIENNE MAGISTERSKIE, I ROK Wykonał:
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ zadania z odpowiedziami
 ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ zadania z odpowiedziami Maciej Burnecki opracowanie strona główna Spis treści 1 Wyrażenia algebraiczne indukcja matematyczna 1 Geometria analityczna w R 3 3 Liczby zespolone
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ zadania z odpowiedziami Maciej Burnecki opracowanie strona główna Spis treści 1 Wyrażenia algebraiczne indukcja matematyczna 1 Geometria analityczna w R 3 3 Liczby zespolone
3. Model Kosmosu A. Einsteina
 19 3. Model Kosmosu A. Einsteina Pierwszym rozwiązaniem równań pola grawitacyjnego w 1917 r. było równanie hiperpowierzchni kuli czterowymiarowej, przy założeniu, że materia kosmiczna tzw. substrat jest
19 3. Model Kosmosu A. Einsteina Pierwszym rozwiązaniem równań pola grawitacyjnego w 1917 r. było równanie hiperpowierzchni kuli czterowymiarowej, przy założeniu, że materia kosmiczna tzw. substrat jest
mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej
 mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-28.06.07 współrzędne uogólnione punkt materialny... wektor wodzący: prędkość: przyspieszenie: liczba
mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-28.06.07 współrzędne uogólnione punkt materialny... wektor wodzący: prędkość: przyspieszenie: liczba
Repetytorium z analizy i rachunku całkowego funkcji wielu zmiennych. Wiadomości wstępne.
 SPIS TREŚCI 1 Repetytorium z analizy i rachunku całkowego funkcji wielu zmiennych. Wiadomości wstępne. Spis treści 1 Repetytorium 2 2 Wiadomości wstępne 5 1 Repetytorium 2 1 Repetytorium 1. Rozwia zać
SPIS TREŚCI 1 Repetytorium z analizy i rachunku całkowego funkcji wielu zmiennych. Wiadomości wstępne. Spis treści 1 Repetytorium 2 2 Wiadomości wstępne 5 1 Repetytorium 2 1 Repetytorium 1. Rozwia zać
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Algebra liniowa i geometria analityczna II Linear algebra and geometry II Kierunek: Rodzaj przedmiotu: obowiązkowy dla wszystkich specjalności Rodzaj zajęć: wykład, ćwiczenia Matematyka
Nazwa przedmiotu: Algebra liniowa i geometria analityczna II Linear algebra and geometry II Kierunek: Rodzaj przedmiotu: obowiązkowy dla wszystkich specjalności Rodzaj zajęć: wykład, ćwiczenia Matematyka
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Fizyka Laserów wykład 5. Czesław Radzewicz
 Fizyka Laserów wykład 5 Czesław Radzewicz rezonatory optyczne, optyczne wnęki rezonansowe rezonatory otwarte: Fabry-Perot E t E 0 R 0.99 T 1 0 E r R R R 0. R 0.9 E t = TE 0 e iδφ R 0.5 R 0.9 E t Gires-Tournois
Fizyka Laserów wykład 5 Czesław Radzewicz rezonatory optyczne, optyczne wnęki rezonansowe rezonatory otwarte: Fabry-Perot E t E 0 R 0.99 T 1 0 E r R R R 0. R 0.9 E t = TE 0 e iδφ R 0.5 R 0.9 E t Gires-Tournois
ELEKTROTECHNIKA Semestr 2 Rok akad / ZADANIA Z MATEMATYKI Zestaw Oblicz pochodne cząstkowe rzędu drugiego funkcji:
 ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
1 Symulacja procesów cieplnych 1. 2 Algorytm MES 2. 3 Implementacja rozwiązania 2. 4 Całkowanie numeryczne w MES 3. k z (t) t ) k y (t) t )
 pis treści ymulacja procesów cieplnych Algorytm ME 3 Implementacja rozwiązania 4 Całkowanie numeryczne w ME 3 ymulacja procesów cieplnych Procesy cieplne opisuje równanie różniczkowe w postaci: ( k x (t)
pis treści ymulacja procesów cieplnych Algorytm ME 3 Implementacja rozwiązania 4 Całkowanie numeryczne w ME 3 ymulacja procesów cieplnych Procesy cieplne opisuje równanie różniczkowe w postaci: ( k x (t)
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 GEOMETRIA ANALITYCZNA W PRZESTRZENI Położenie punktu w przestrzeni określamy za pomocą trzech liczb (x, y, z). Liczby te odpowiadają rzutom na osie układu współrzędnych: każdy rzut wzdłuż płaszczyzny równoległej
GEOMETRIA ANALITYCZNA W PRZESTRZENI Położenie punktu w przestrzeni określamy za pomocą trzech liczb (x, y, z). Liczby te odpowiadają rzutom na osie układu współrzędnych: każdy rzut wzdłuż płaszczyzny równoległej
Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II
 Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1
Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1
TENSOMETRIA ZARYS TEORETYCZNY
 TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
Przekształcenia całkowe. Wykład 1
 Przekształcenia całkowe Wykład 1 Przekształcenia całkowe Tematyka wykładów: 1. Liczby zespolone -wprowadzenie, - funkcja zespolona zmiennej rzeczywistej, - funkcja zespolona zmiennej zespolonej. 2. Przekształcenie
Przekształcenia całkowe Wykład 1 Przekształcenia całkowe Tematyka wykładów: 1. Liczby zespolone -wprowadzenie, - funkcja zespolona zmiennej rzeczywistej, - funkcja zespolona zmiennej zespolonej. 2. Przekształcenie
Rozdział 2. Krzywe stożkowe. 2.1 Elipsa. Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie
 Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Analiza Matematyczna Praca domowa
 Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
Linie sił pola elektrycznego
 Wykład 5 5.6. Linie sił pola elektrycznego Pamiętamy, że we wzorze (5.) określiliśmy natężenie pola elektrycznego przy pomocy ładunku próbnego q 0, którego wielkość dążyła do zera. Robiliśmy to po to,
Wykład 5 5.6. Linie sił pola elektrycznego Pamiętamy, że we wzorze (5.) określiliśmy natężenie pola elektrycznego przy pomocy ładunku próbnego q 0, którego wielkość dążyła do zera. Robiliśmy to po to,
Rok akademicki: 2030/2031 Kod: DGK n Punkty ECTS: 6. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Geodezja wyższa Rok akademicki: 2030/2031 Kod: DGK-1-405-n Punkty ECTS: 6 Wydział: Geodezji Górniczej i Inżynierii Środowiska Kierunek: Geodezja i Kartografia Specjalność: - Poziom studiów:
Nazwa modułu: Geodezja wyższa Rok akademicki: 2030/2031 Kod: DGK-1-405-n Punkty ECTS: 6 Wydział: Geodezji Górniczej i Inżynierii Środowiska Kierunek: Geodezja i Kartografia Specjalność: - Poziom studiów:

