Modelowanie ryzyka kredytowego: MODEL BLACK-COX A
|
|
|
- Adam Pawłowski
- 7 lat temu
- Przeglądów:
Transkrypt
1 Modelowanie ryzyka kredytowego: MODEL BLACK-COX A Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014 Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
2 Model Blacka-Cox a - opis 1 Proces wartości firmy spełnia SDE dv t = V t r κdt + σ V dw t. 2 Klauzle bezpieczeństwa safety covenants. W B-C jest modelowane przez wprowadzenie bariery vt := Ke γt t dla t [[0, T [[ gdzie K > 0 stała. Jeżeli V uderzy w vt to posiadacze obligacji przejmuja firmę. 3 Bankructwo pojawia się także w T jeżeli V T < L. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
3 1 Moment default u jest zdefiniowany τ := inf {t [[0, T ]] : V T v t }. gdzie v t = { vt, dlat < T, L, dla t = T. 2 Proces odzysku Z i wpłata zastępcza X sa proporcjonalne do procesu wartości Z = β 2 V, X = β1 V T, dla β 1, β 2 [[0, 1]]. Stałe β 1, β 2 modeluja koszty bankructwa lub restrukturyzacji. 3 dla każdego t [[0, T ]] zakładamy vt LBt, T Ke γt t Le rt t, Bez tego założenia mogłaby zajść sytuacja że wypłata w momencie default u mogłaby przekroczyć wartość zdyskontowanego nominału!! Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
4 1 Podsumowujac w modelu Blacka-Cox a obligacja jest dana jako wypłata narażona na ryzyko kredytowe postaci X = L, A = 0, X = β1 V T, Z = β 2 V, τ = τ τ, 2 gdzie τ jest momentem wcześniejszego default u τ := inf {t [[0, T [[: V T vt} 3 natomiast τ jest momentem default u z modelu Mertona tzn. τ := T 1 {VT <L} + 1 {VT L}. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
5 1 Na zbiorze {t < τ} = {t < τ} mamy Dt, T =E Q Le rt t 1 { τ T,VT L} F t + β 1 E Q V T e rt t 1 { τ T,VT <L} F t + β 2 K E Q e γt τ e r τ t 1 {t< τ<t } F t 2 Pierwsze dwie warunkowe wartości oczekiwane można policzyć korzystajac z 3 Trzecia natomiast z QV s x, τ s F t Q τ s F t Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
6 Momenty pierwszego przejścia Niech V będzie rozwiazaniem SDE dv t = V t r κdt + σ V dw t, Dla każdego 0 t < s T, na zdarzeniu {t < τ} mamy ln vt V Q τ s F t = N t νs t σ V s t vt 2ã ln vt V + N t + νs t σ V s t V t gdzie ν = r κ γ 1 2 σ2 V, ã = ν σ 2 V Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
7 Dla t < s T i x vs na zbiorze {t < τ} lnvt /x + νs t QV s x, τ s F t = N σ V s t vt 2ã ln v 2 t lnxv t + νs t N σ V s t gdzie V t ν = r κ 1 2 σ2 V, ã = r κ γ 1 2 σ2 V σ 2 V Obydwa wzory wynikaja z dobrze znanej zasady odbicia dla procesu Wienera.. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
8 Pomocniczy lemat 1 Niech gdzie σ > 0, ν R. Lemma Dla każdego x > 0 mamy Q Y t := y 0 + X t, gdzie X t := νt + σw t sup X u x 0 u s x νs = N σ s e 2νx σ 2 N x νs σ s a dla każdego x < 0 mamy x + νs Q inf X u x = N 0 u s σ e 2νx x + νs σ 2 N s σ s Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
9 Dowód Pokazemy pierwszy wzór korzystajac z tw. Girsanov a i zasady odbicia dla procesu Wienera. Załóżmy że σ = 1. Niech P będzie miara na Ω, F s dana Wt dp dq = e νws ν 2 2 s := X t = W t + νt, t [0, s] jest standardowym procesem Wienera przy P. Ponadto możemy napisać Dla x > 0 Q sup X u x, X s x 0 u s dq dp = eνw s ν 2 2 s = E P e νw s ν2 2 s 1 {sup0 u s Wu x,ws x} Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
10 Dowód Niech τ x = inf {t 0 : W t = x}, zdefiniujmy pomocniczy proces W t := W t 1 {τx t} + 2x W t 1 {τx <t} Na mocy zasady odbicia W jest ruchem Browna. Ponadto Dla x > 0 mamy { sup W u x, W s x} = {Ws x} {τ s s} 0 u s J := Q sup X u x 0 u s = Q sup W u + νu x 0 u s Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
11 J = QX s x Q sup X u x, X s x 0 u s = QX s x E P e νw s ν2 2 s 1 {sup0 u s Wu x,ws x} = QX s x E P e ν W s ν2 2 s 1 {sup0 u s Wu x, W s x} = QX s x E P e ν2x W s ν2 2 s 1 {W s x} = QX s x e 2νx E P e νw s ν2 2 s 1 {W s x} = QX s x e 2νx Q W s x = QW s + νs x e 2νx QW s + νs x x νs = N e 2νx x νs σ 2 N s s Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
12 ... i kończymy dowód To kończy dowód dla σ = 1 Dla dowolnego σ > 0 mamy Q sup σw u + νu x 0 u s Stad mamy pierwszy wzór. = Q sup 0 u s W u + ν σ u x σ Drugi wzór natomiast wynika z tego że W jest także procesem Wienera a więc dla x < 0 mamy Q inf σw u + νu x = Q sup σ W u νu x 0 u s 0 u s Teraz drugi wzór wyprowadzamy z pierwszego co kończy dowód lematu 1. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
13 Rozkład momentu przejścia przez 0 Niech τ := inf {t > 0 : Y t 0}. Zauważmy, że Qτ > s = Q inf Y u > 0 0 u s i korzystajac z lematu mamy Proposition Dla każdego s > 0 mamy = Q inf 0 u s X u y 0 Qτ s = Qτ < s = Nh 1 s + e 2νσ 2 y 0 Nh 2 s gdzie h 1 s = y 0 νs σ, h 2 s = y 0 + νs s σ s Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
14 Rozkład warunkowy przejścia przez 0 Corollary Dla każdego t < s na zdarzeniu {t < τ}, mamy Yt νs t Qτ s F t = N σ + e 2νσ 2 Y Yt t + νs t N s t σ s t Ja udowodnić ten wniosek?. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
15 ZADANIE na ćwiczenia Niech V będzie rozwiazaniem SDE moment τ będzie zadany dv t = V t r κdt + σ V dw t, τ := inf {t > 0 : V t v} dla v < V 0. Pokazać, że na zdarzeniu {t < τ} mamy ln v V Qτ s F t = N t νs t v 2a ln v V + N t + νs t, σ V s t V t σ V s t gdzie ν = r κ 1 2 σ2 V, a = ν σ 2 V = r κ 1 2 σ2 V σ 2 V. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
16 ZADANIE na ćwiczenia Niech V będzie zadane jak w poprzednim zadaniu, moment τ natomiast τ := inf {t > 0 : V t vt} gdzie vt := Ke γt t. Dla stałych K > 0 i γ R +. Pokazać, że na zdarzeniu {t < τ} mamy ln vt V Qτ s F t = N t νs t vt 2ã ln vt V + N t + νs t σ V s t σ V s t gdzie ν = r κ γ 1 2 σ2 V, ã = ν σ 2 V V t = r κ γ 1 2 σ2 V σ 2 V Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
17 Ciag dalszy: Uogólnić poprzednie wyniki tzn. chcemy mieć wzory na QY s y, τ s F t. Wskazówka: Zauważmy, że QY s y, τ s = QY s y, ms Y 0 = QX s y y 0, ms X y 0 = Q X s y 0 y, M X s y 0, gdzie X s := X s = σw s νs = σ W s νs = σ W s νs. X s jest też procesem Wienera z dryfem! Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
18 Znany wynik tego typu to tzw. Zasada odbicia dla procesu Wienera bez dryfu, przypomnijmy ten wynik: Lemma Zasada odbicia dla procesu Wienera Dla każdego s > 0, y 0, i x y mamy: QW s x, M W s y = QW s 2y x = QW s x 2y. Dla zastosowań potrzebujemy analogicznego wyniku dla procesu Wienera z niezerowym dryfem: X t := νt + σw t. lub nawet Y t = y 0 + X t = y 0 + νt + σw t. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
19 Pomocniczy lemat 2 Lemma Dla każdego s 0 łaczny rozkład X s, Ms X jest dany wzorem QX s x, M X s y = e 2νyσ 2 QX s 2y x + 2νs dla każdego x y i y 0. Wystarczy pokazać przypadek σ = 1, gdyż jeżeli σ 1 to definiujac Xt σ = X t σ = W t + ν σ t otrzymujemy QX s x, M X s y = QX σ s xσ 1, M X σ s yσ 1 Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
20 Dowód: Niech σ = 1. Z Twierdzenia Girsanowa wiemy że przy mierze Q o gęstości d Q dq = e νws ν proces W zdef. Wt = X t = W t + νt dla t [[0, s]] jest procesem Wienera. Mamy także 2 2 s dq d Q = eνw s ν2 2 s Stosujac wzór Bayes a otrzymujemy QX s x, Ms X y e =E Q νw s ν2 2 s 1 {Xs x,m s X y} Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
21 Wprowadźmy pomocniczy proces W W t := W t 1 {τy t} + 2y W t 1 {τy <t} W jest procesem Wienera przy mierze Q. kontynuujac otrzymujemy =E Q =E Q e νw s ν2 2 s 1 {W s x,m W s y} =E Q e ν2y W s ν2 2 s 1 {2y W s x,m W s y} ponieważ 2y x y e ν2y W s ν2 2 s 1 {W s 2y x} =E Q = e ν2y P W s 2y x e ν W s ν2 2 s 1 { Ws x,m W s y} =e ν2y E Q e νw s ν2 2 s 1 {W s 2y x} Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
22 gdzie P miara zadana gęstościa d P d Q = e νw s ν2 2 s. Ponieważ przy P proces W t := Wt + νt dla t [0, s] jest procesem Wienera to = e ν2y P Ws 2y x + νs = e ν2y P Ws + νs 2y x + 2νs To kończy dowód. Mamy oczywiście = e ν2y Q W s + νs 2y x + 2νs QX s x, M X s y = QX s < x, M X s > y Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
23 Z powyższego Lematu mamy wniosek Proposition Dla dowolnych x y i y 0 mamy x 2y νs QX s x, Ms X y = e 2νyσ 2 N σ. s Stad wynika QX s x, M X s x νs y = N σ e 2νyσ 2 N s x 2y νs σ s, dla dowolnych x, y R takich że x y i y 0. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
24 Dowód: Pierwsza równość wynika z QX s 2y x + 2νs = Q σw s x 2y νs x 2y νs = N σ, s a druga równość wynika z QX s x, M X s y + QX s x, M X s y = QX s x. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
25 Rozkład łaczny. W bardzo podobny sposób można udowodnić następujace stwierdzenia Proposition Łaczny rozkład X s, ms X dla s > 0 spełnia x + νs 2y x + νs QX s x, ms X y = N σ e 2νσ 2y N s σ, s dla każdego x, y R takiego że y 0 i y x. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
26 Corollary Mamy dla każdego s > 0 i y 0 y + y0 + νs QY s y, τ s = N σ e 2νσ 2 y 0 N s Dowód. Wynika z y y0 + νs σ s QY s y, τ s = QY s y, m Y s 0 = QX s y y 0, m X s y 0, a następnie zastosowania poprzedniego stwierdzenia., Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
27 Ogólniejszy fakt można udowodnić korzystajac z silnej własności Markowa Corollary Dla każdego s > t i y 0 na zbiorze {t τ}, mamy y + Yt + νs t QY s y, τ s F t =N σ s t e 2νσ 2 Y t y Yt + νs t N σ, s t Teraz podamy dwa przykłady zastosowań powyższych wzorów. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
28 MODEL LELAND-TOFT Niech V będzie zadane stochastycznym równaniem różniczkowym postaci dv t = V t r κdt + σ V dw t i niech τ := inf {t > 0 : V t v} gdzie v < V 0. Stosujac lemat do Y t = lnv t / v i y = lnx/ v otrzymujemy dla x v, na zdarzeniu {t τ} wzór: lnvt /x + νs t QV s x, τ s F t =N v V t σ s t 2a ln v 2 lnxv t + νs t N σ s t, gdzie ν = r κ 1 2 σ2 V oraz a = νσ 2 V. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
29 MODEL BLACK-COX Niech V będzie zadane stochastycznym równaniem różniczkowym jak wyżej i niech τ := inf {t > 0 : V t vt} gdzie vt = Ke γt t, dla stałych K > 0 i γ R. Dla Y t = lnv t / vt i y = lnx/ vs otrzymujemy dla t < s T i x vs na zbiorze {t < τ} lnvt /x + νs t QV s x, τ s F t =N σ V s t vt 2ã ln v 2 t lnxv t + νs t N, σ V s t gdzie ν = r κ 1 2 σ2 V, ã = r κ γ 1 2 σ2 V. σv 2 V t Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
30 Wzór Blacka-Cox a Theorem Załóżmy, że ν 2 + 2σ 2 r γ > 0. Wtedy na zbiore {τ > t} t.j. przed momentem default u cena obligacji jest dana wzorem Dt, T =LBt, T Nh 1 V t, T t Rt 2ã Nh 2 V t, T t + β 1 V t e κt t Nh 3 V t, T t Nh 4 V t, T t + β 1 V t e κt t R 2ã+2 t Nh 5 V t, T t Nh 6 V t, T t + β 2 V t R θ+ζ t Nh 7 V t, T t + R θ ζ t Nh 8 V t, T t gdzie ν = r κ 1 ν 2 σ2 V, ν = ν γ, ã = σv 2, R t = vt/v t, θ = ã + 1, ζ = σ 2 ν 2 + 2σ 2 r γ. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
31 h 1 V t, T t = lnv t/l + νt t σ, T t h 2 V t, T t = ln v 2 t lnv t L + νt t σ, T t h 3 V t, T t = lnl/v t ν + σ 2 T t σ, T t h 4 V t, T t = lnk /V t ν + σ 2 T t σ, T t h 5 V t, T t = ln v 2 t lnv t L + ν + σ 2 T t σ, T t h 6 V t, T t = ln v 2 t lnv t K + ν + σ 2 T t σ, T t h 7,8 V t, T t = ln vt/v t ± ζσ 2 T t σ. T t Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
32 Lemma Dla każdego a R i b > 0 mamy wzory prawdziwe dla y > 0, y 0 y 0 lnx + a xdn = e 1 lny + a b 2 b2 a 2 N, b b lnx + a xdn = e 1 lny + a + b 2 b2 +a 2 N. b b Niech a, b, c R spełniaja warunki b < 0 i c 2 > 2a. Wtedy dla każdego y > 0 mamy y 0 e ax dn gdzie d = c 2 2a i gy = e bc d N b cx x = d + c 2d gy + d c 2d hy, b dy b + dy, hy = e bc+d N. y y Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
33 Dowód. Mamy do policzenia D 1 t, T = LBt, T QV T L, τ T F t D 2 t, T = β 1 LBt, T E Q V T 1 {VT <L, τ T } F t D 3 t, T = K β 2 B t e γt E Q e γ r τ 1 {t< τ<t } F t. Wystarczy wtedy ograniczyć się do przypadku t = 0. Wyliczmy najpierw D 1 0, T. Z zadania wiemy że dla L vt = K mamy ln V 0 QV T L, τ T = N L + νt σ R0 2ã T N ln v 2 0 V 0 L + νt σ T co daje nam oczywiście D 1 0, T = LB0, T Nh 1 V 0, T R0 2ã Nh 2V 0, T Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
34 Dowodu cd. Do wyznaczenia D 2 0, T zauważmy że E Q V T 1 {VT <L, τ T } = E Q V T 1 {K VT <L, τ T } = Z przykładu mamy że dla x K zachodzi dqv T < x, τ T = dn ln x V 0 νt σ T L K R 2ã 0 dn xdqv T < x, τ T ln v 2 0 V 0 x + νt σ T Z Lematu otrzymujemy ze I 1 0 pierwsza całka ln L I 1 0 = V 0 e N r κt V 0 νt ln K σ V N 0 νt T σ T gdzie ν = r κ + σ 2 /2. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
35 Dowodu cd. Podobnie dla I 2 0 mamy korzystajac z lematu I 2 0 = V 0 R0 2 er κt N ln v 2 0 LV 0 + νt σ N ln v 2 0 KV 0 + νt T σ T Ponieważ D 2 0, T = β 1 B0, T I Rã0 I 20, to wstawiajac I 1 0 i I 2 0 otrzymujemy D 2 0, T = β 1 V 0 e κt Nh 3 V 0, T Nh 4 V 0, T +β 1 V 0 e κt R 2ã+2 0 Nh 5 V 0, T Nh 6 V 0, T. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
36 Dowód. Pozostaje do wyliczenia D 3 0, T, w tym celu wystarczy skupić się na wyznaczeniu gdzie T v0e Q e γ r τ 1 { τ<t } = v0 e γ rs dq τ s, 0 ln v0/v0 νs v0 2ã Q τ s = N σ ln v0/v0 + νs + N s σ, s oznaczmy T J 1 0 := v0 e γ rs dn 0 J 2 0 := v02ã+1 T V 0 ln v0/v0 νs σ s e γ rs ln v0/v0 + νs dn σ s V0 2ã 0 Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
37 Dowód. z lematu mamy J 1 0 J 1 0 = V 0ã + ζ R θ ζ 2ζ i podobnie dla J 2 0 J 2 0 = V 0ã + ζ R θ+ζ 2ζ 0 Nh 8 V 0, T V 0ã ζ 2ζ 0 Nh 7 V 0, T V 0ã ζ 2ζ R θ+ζ 0 Nh 7 V 0, T R θ ζ 0 Nh 8 V 0, T i w konsekwencji D 3 0, T = β 2 V 0 R θ+ζ 0 Nh 7 V 0, T + R θ ζ 0 Nh 8 V 0, T Sumujac otrzymane wzory na D 1 0, T, D 2 0, T i D 3 0, T otrzymujemy tezę. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
38 Wycena w modelu Black a Cox a poprzez równania czastkowe Ponieważ dynamika procesu wartości firmy jest dana jako proces dyfuzji to można wyprowadzić odpowiednie równanie czastkowe które charakteryzuje proces ceny obligacji. Jeżeli Dt, T = uv t, t to wtedy u spełnia następujace PDE u t v, t + r κvu v v, t σ2 V v 2 u vv v, t ruv, t = 0 w obszarze {v, t R + R + : 0 < t < T, v > Ke γt t } z warunkiem brzegowym i końcowym uke γt t, t = β 2 Ke γt t, uv, T = min {β 1 v, L}. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
39 Wady modelu Black-Cox a: odziedziczone po modelu Mertona Prosta stuktura kapitału, Zupełne rynki finansowe, Stałe stopy procentowe, Może być stosowany dla firm notowanych na giełdzie, Empirycznie nie wiarygodny. Empirycznie nie wiarygodny. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
40 Uogólnienia Modelu Black a-cox a - dyfuzja ze skokami Zhou rozważał przypadek dv t = V t r λνdt + σdw t + dx t gdzie W jest standardowym procesem Wienera, proces X jest złożonym procesem Poissona takim że N t X t = e Y i 1, i=1 gdzie N proces Poissona o intensywności λ, {Y i } ciag zmiennych iid o rozkładzie N a, b 2. Zhou podał aproksymację rozkładu momentu pierwszego dojścia do 0. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
41 Uogólnienia Modelu Black a-cox a - Stochastyczne stopy procentowe Zakładajac dynamiki aktywów firmy postaci dv t = V t r t + κtdt + σtdw t, dbt, T = Bt, T r t dt + bt, T dw t, gdzie W jest d-wymiarowym procesem Wienera, κ,σ,b, T sa ograniczonymi funkcjami można otrzymać wzory na cenę obligacji jak w modelu Black-Cox a: X = L, Z t = β 2 V t, X = β1 V T, τ := {t [0, T ] : V t < v t } gdzie β 1, β 2 [0, 1] sa stałe, natomiast odpowiednia bariera jest dana wzorem v t = { KBt, T e T t κudu, dla t < T, L, dla t = T. Niewęgłowski MiNI PW Modele wartości firmy Warszawa / 41
Modelowanie ryzyka kredytowego Zadania 1.
 1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
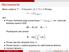 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz. II: CDS y - swapy kredytowe
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
21 maja, Mocna własność Markowa procesu Wienera. Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
28 maja, Problem Dirichleta, proces Wienera. Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Wstęp do analitycznych i numerycznych metod wyceny opcji
 Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
F t+ := s>t. F s = F t.
 M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
System BCD z κ. Adam Slaski na podstawie wykładów, notatek i uwag Pawła Urzyczyna. Semestr letni 2009/10
 System BCD z κ Adam Slaski na podstawie wykładów, notatek i uwag Pawła Urzyczyna Semestr letni 2009/10 Rozważamy system BCD ze stałą typową κ i aksjomatami ω κ κ i κ ω κ. W pierwszej części tej notatki
System BCD z κ Adam Slaski na podstawie wykładów, notatek i uwag Pawła Urzyczyna Semestr letni 2009/10 Rozważamy system BCD ze stałą typową κ i aksjomatami ω κ κ i κ ω κ. W pierwszej części tej notatki
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
n=0 (n + r)a n x n+r 1 (n + r)(n + r 1)a n x n+r 2. Wykorzystując te obliczenia otrzymujemy, że lewa strona równania (1) jest równa
 Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Zadanie 1. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k =
 Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Parametr Λ w populacji ubezpieczonych ma rozkład dany na półosi dodatniej gęstością: 3 f
 Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t)
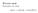 Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Informacja o przestrzeniach Sobolewa
 Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych
 Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych Elżbieta Krajewska Instytut Matematyki Politechnika Łódzka Elżbieta Krajewska Immunizacja ubezpieczycieli życiowych 1/22 Plan prezentacji
Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych Elżbieta Krajewska Instytut Matematyki Politechnika Łódzka Elżbieta Krajewska Immunizacja ubezpieczycieli życiowych 1/22 Plan prezentacji
Ośrodkowość procesów, proces Wienera. Ośrodkowość procesów, proces Wienera Procesy Stochastyczne, wykład, T. Byczkowski,
 Procesy Stochastyczne, wykład, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 27 luty, 2012 Ośrodkowość procesów Dalej zakładamy, że (Ω, Σ, P) jest zupełną przestrzenią miarową. Definicja.
Procesy Stochastyczne, wykład, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 27 luty, 2012 Ośrodkowość procesów Dalej zakładamy, że (Ω, Σ, P) jest zupełną przestrzenią miarową. Definicja.
Modelowanie ryzyka kredytowego: Model Mertona - estymacja
 Modelowanie ryzyka kredytowego: Model Mertona - estymacja Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2010 Niewęgłowski (MiNI PW) Model Mertona Warszawa
Modelowanie ryzyka kredytowego: Model Mertona - estymacja Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2010 Niewęgłowski (MiNI PW) Model Mertona Warszawa
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU
 Modelowanie ryzyka kredyowego MODELOWANIE ZA POMOCA PROCESU HAZARDU Mariusz Niewęgłowski Wydział Maemayki i Nauk Informacyjnych, Poliechniki Warszawskiej Warszawa 2014 hazardu Warszawa 2014 1 / 18 Proces
Modelowanie ryzyka kredyowego MODELOWANIE ZA POMOCA PROCESU HAZARDU Mariusz Niewęgłowski Wydział Maemayki i Nauk Informacyjnych, Poliechniki Warszawskiej Warszawa 2014 hazardu Warszawa 2014 1 / 18 Proces
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz.i
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz.i Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 214 hazardu Warszawa 214 1 /
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz.i Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 214 hazardu Warszawa 214 1 /
2 Równania różniczkowe zwyczajne o rozdzielonych zmiennych
 2. Równania o rozdzielonych zmiennych 2 1 2 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Równaniem różniczkowym zwyczajnym pierwszego rzędu o rozdzielonych zmiennych nazywamy równanie różniczkowe
2. Równania o rozdzielonych zmiennych 2 1 2 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Równaniem różniczkowym zwyczajnym pierwszego rzędu o rozdzielonych zmiennych nazywamy równanie różniczkowe
Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008
 Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych..00 r. Zadanie. Proces szkód w pewnym ubezpieczeniu jest złożonym procesem Poissona z oczekiwaną liczbą szkód w ciągu roku równą λ i rozkładem wartości szkody o dystrybuancie
Matematyka ubezpieczeń majątkowych..00 r. Zadanie. Proces szkód w pewnym ubezpieczeniu jest złożonym procesem Poissona z oczekiwaną liczbą szkód w ciągu roku równą λ i rozkładem wartości szkody o dystrybuancie
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Rachunek prawdopodobieństwa Rozdział 5. Rozkłady łączne
 Rachunek prawdopodobieństwa Rozdział 5. Rozkłady łączne 5.3 Rozkłady warunkowe i warunkowa wartość oczekiwana Katarzyna Rybarczyk-Krzywdzińska semestr zimowy 2015/2016 Prawdopodobieństwo wyraża postawę
Rachunek prawdopodobieństwa Rozdział 5. Rozkłady łączne 5.3 Rozkłady warunkowe i warunkowa wartość oczekiwana Katarzyna Rybarczyk-Krzywdzińska semestr zimowy 2015/2016 Prawdopodobieństwo wyraża postawę
Procesy stochastyczne 2.
 Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Strategie zabezpieczaj ce
 04062008 Plan prezentacji Model binarny Model Black Scholesa Bismut- Elworthy -Li formuła Model binarny i opcja call Niech cena akcji w chwili pocz tkowej wynosi S 0 = 21 Zaªó»my,»e ceny akcji po trzech
04062008 Plan prezentacji Model binarny Model Black Scholesa Bismut- Elworthy -Li formuła Model binarny i opcja call Niech cena akcji w chwili pocz tkowej wynosi S 0 = 21 Zaªó»my,»e ceny akcji po trzech
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
Teoria ze Wstępu do analizy stochastycznej
 eoria ze Wstępu do analizy stochastycznej Marcin Szumski 22 czerwca 21 1 Definicje 1. proces stochastyczny - rodzina zmiennych losowych X = (X t ) t 2. trajektoria - funkcja (losowa) t X t (ω) f : E 3.
eoria ze Wstępu do analizy stochastycznej Marcin Szumski 22 czerwca 21 1 Definicje 1. proces stochastyczny - rodzina zmiennych losowych X = (X t ) t 2. trajektoria - funkcja (losowa) t X t (ω) f : E 3.
Równania różniczkowe. Notatki z wykładu.
 Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Sekantooptyki owali i ich własności
 Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 4.04.0 r. Zadanie. Przy danej wartości λ parametru ryzyka Λ liczby szkód generowane przez ubezpieczającego się w kolejnych latach to niezależne zmienne losowe o rozkładzie
Matematyka ubezpieczeń majątkowych 4.04.0 r. Zadanie. Przy danej wartości λ parametru ryzyka Λ liczby szkód generowane przez ubezpieczającego się w kolejnych latach to niezależne zmienne losowe o rozkładzie
Matematyka ubezpieczeń majątkowych r.
 Zadanie 1. W pewnej populacji podmiotów każdy podmiot narażony jest na ryzyko straty X o rozkładzie normalnym z wartością oczekiwaną równą μ i wariancją równą. Wszystkie podmioty z tej populacji kierują
Zadanie 1. W pewnej populacji podmiotów każdy podmiot narażony jest na ryzyko straty X o rozkładzie normalnym z wartością oczekiwaną równą μ i wariancją równą. Wszystkie podmioty z tej populacji kierują
1. Ubezpieczenia życiowe
 1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
01. dla x 0; 1 2 wynosi:
 Matematyka ubezpieczeń majątkowych 0.0.04 r. Zadanie. Ryzyko X ma rozkład z atomami: Pr X 0 08. Pr X 0. i gęstością: f X x 0. dla x 0; Ryzyko Y ma rozkład z atomami: Pr Y 0 07. Pr Y 0. i gęstością: fy
Matematyka ubezpieczeń majątkowych 0.0.04 r. Zadanie. Ryzyko X ma rozkład z atomami: Pr X 0 08. Pr X 0. i gęstością: f X x 0. dla x 0; Ryzyko Y ma rozkład z atomami: Pr Y 0 07. Pr Y 0. i gęstością: fy
Stochastyczne równania różniczkowe, model Blacka-Scholesa
 Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Detekcja rozkładów o ciężkich ogonach
 Detekcja rozkładów o ciężkich ogonach J. Śmiarowska, P. Jamer Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska 24 kwietnia 2012 J. Śmiarowska, P. Jamer (Politechnika Warszawska) Detekcja
Detekcja rozkładów o ciężkich ogonach J. Śmiarowska, P. Jamer Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska 24 kwietnia 2012 J. Śmiarowska, P. Jamer (Politechnika Warszawska) Detekcja
dla t ściślejsze ograniczenie na prawdopodobieństwo otrzymujemy przyjmując k = 1, zaś dla t > t ściślejsze ograniczenie otrzymujemy przyjmując k = 2.
 Zadanie. Dla dowolnej zmiennej losowej X o wartości oczekiwanej μ, wariancji momencie centralnym μ k rzędu k zachodzą nierówności (typu Czebyszewa): ( X μ k Pr > μ + t σ ) 0. k k t σ *
Zadanie. Dla dowolnej zmiennej losowej X o wartości oczekiwanej μ, wariancji momencie centralnym μ k rzędu k zachodzą nierówności (typu Czebyszewa): ( X μ k Pr > μ + t σ ) 0. k k t σ *
VI. Równania różniczkowe liniowe wyższych rzędów
 VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
13 Równanie struny drgającej. Równanie przewodnictwa ciepła.
 Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
z przedziału 0,1 liczb dodatnich. Rozważmy dwie zmienne losowe:... ma złożony rozkład dwumianowy o parametrach 1,q i, gdzie X, wszystkie składniki X
 Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Zadanie 1. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną:
 Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
O procesie Wienera. O procesie Wienera. Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Proces Wienera. Ruch Browna. Ułamkowe ruchy Browna
 Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Ruch 1 {X t } jest martyngałem dokładnie wtedy, gdy E(X t F s ) = X s, s, t T, s t. Jeżeli EX 2 (t) < +, to E(X t F s ) jest rzutem ortogonalnym zmiennej
Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Ruch 1 {X t } jest martyngałem dokładnie wtedy, gdy E(X t F s ) = X s, s, t T, s t. Jeżeli EX 2 (t) < +, to E(X t F s ) jest rzutem ortogonalnym zmiennej
Prawdopodobieństwo i statystyka
 Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 5.0.00 r. Zadanie. Dla dowolnej zmiennej losowej X o wartości oczekiwanej µ wariancji oraz momencie centralnym µ k rzędu k zachodzą nierówności (typu Czebyszewa): ( X
Matematyka ubezpieczeń majątkowych 5.0.00 r. Zadanie. Dla dowolnej zmiennej losowej X o wartości oczekiwanej µ wariancji oraz momencie centralnym µ k rzędu k zachodzą nierówności (typu Czebyszewa): ( X
Ogólnopolska Konferencja Aktuarialna Zagadnienia aktuarialne teoria i praktyka Warszawa, IE SGH 2009
 Rafał M. Łochowski Szkoła Główna Handlowa w Warszawie O pewnym modelu pojawiania się szkód Ogólnopolska Konferencja Aktuarialna Zagadnienia aktuarialne teoria i praktyka Warszawa, IE SGH 2009 Modele pojawiania
Rafał M. Łochowski Szkoła Główna Handlowa w Warszawie O pewnym modelu pojawiania się szkód Ogólnopolska Konferencja Aktuarialna Zagadnienia aktuarialne teoria i praktyka Warszawa, IE SGH 2009 Modele pojawiania
Rozdziaª 9: Wycena opcji
 Rozdziaª 9: Wycena opcji MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 9) Wycena opcji 1 / 23 Denicja opcji. Opcja nansowa:. Warunkowy kontrakt terminowy na sprzeda» lub kupno instrumentu bazowego,
Rozdziaª 9: Wycena opcji MODELOWANIE POLSKIEJ GOSPODARKI z R MPGzR (rozdz. 9) Wycena opcji 1 / 23 Denicja opcji. Opcja nansowa:. Warunkowy kontrakt terminowy na sprzeda» lub kupno instrumentu bazowego,
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
}, gdzie a = t (n) )(f(t(n) k. ) f(t(n) k 1 ) 1+δ = 0,
 Zadania z Procesów Stochastycznych II - 1 1. Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1
Zadania z Procesów Stochastycznych II - 1 1. Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1
Afiniczne rekursje stochastyczne z macierzami trójkatnymi
 Afiniczne rekursje stochastyczne z macierzami trójkatnymi Ewa Damek (Uniwersytet Wrocławski ) (wyniki wspólne z Witoldem Światkowskim, Jackiem Zienkiewiczem - Uniwersytet Wrocławski, Muneya Matsui - Nanzan
Afiniczne rekursje stochastyczne z macierzami trójkatnymi Ewa Damek (Uniwersytet Wrocławski ) (wyniki wspólne z Witoldem Światkowskim, Jackiem Zienkiewiczem - Uniwersytet Wrocławski, Muneya Matsui - Nanzan
Wykład 2. Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova)
 Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω)
 PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
7 Twierdzenie Fubiniego
 M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
Grzegorz Bobiński. Wykład monograficzny Programowanie Liniowe i Całkowitoliczbowe
 Grzegorz Bobiński Wykład monograficzny Programowanie Liniowe i Całkowitoliczbowe Wydział Matematyki i Informatyki Uniwersytet Mikołaja Kopernika w Toruniu 2012 Spis treści Notacja 1 1 Podstawowe pojęcia
Grzegorz Bobiński Wykład monograficzny Programowanie Liniowe i Całkowitoliczbowe Wydział Matematyki i Informatyki Uniwersytet Mikołaja Kopernika w Toruniu 2012 Spis treści Notacja 1 1 Podstawowe pojęcia
Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. u = 0, (6.1) jest operatorem Laplace a. (x,y)
 Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Rynek, opcje i równania SDE
 Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Stochastyczne równania różniczkowe, studia II stopnia
 Stochastyczne równania różniczkowe, studia II stopnia Niech W t (ewentualnie W, W (t)), t oznacza proces Wienera oraz niech W = Niech W = (W, W 2,, W n ) oznacza n-wymiarowy proces Wienera Pokazać, że
Stochastyczne równania różniczkowe, studia II stopnia Niech W t (ewentualnie W, W (t)), t oznacza proces Wienera oraz niech W = Niech W = (W, W 2,, W n ) oznacza n-wymiarowy proces Wienera Pokazać, że
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
N ma rozkład Poissona z wartością oczekiwaną równą 100 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach:
 Zadanie. O niezależnych zmiennych losowych N, M M, M 2, 3 wiemy, że: N ma rozkład Poissona z wartością oczekiwaną równą 00 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach: 2, 3 Pr( M = )
Zadanie. O niezależnych zmiennych losowych N, M M, M 2, 3 wiemy, że: N ma rozkład Poissona z wartością oczekiwaną równą 00 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach: 2, 3 Pr( M = )
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 6: SKŁADKI OKRESOWE Składki okresowe netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 6: SKŁADKI OKRESOWE Składki okresowe netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową
Wykład 3 Momenty zmiennych losowych.
 Wykład 3 Momenty zmiennych losowych. Wrocław, 19 października 2016r Momenty zmiennych losowych Wartość oczekiwana - przypomnienie Definicja 3.1: 1 Niech X będzie daną zmienną losową. Jeżeli X jest zmienną
Wykład 3 Momenty zmiennych losowych. Wrocław, 19 października 2016r Momenty zmiennych losowych Wartość oczekiwana - przypomnienie Definicja 3.1: 1 Niech X będzie daną zmienną losową. Jeżeli X jest zmienną
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych
 Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Wykład 3 Momenty zmiennych losowych.
 Wykład 3 Momenty zmiennych losowych. Wrocław, 18 października 2017r Momenty zmiennych losowych Wartość oczekiwana - przypomnienie Definicja 3.1: 1 Niech X będzie daną zmienną losową. Jeżeli X jest zmienną
Wykład 3 Momenty zmiennych losowych. Wrocław, 18 października 2017r Momenty zmiennych losowych Wartość oczekiwana - przypomnienie Definicja 3.1: 1 Niech X będzie daną zmienną losową. Jeżeli X jest zmienną
4 Kilka klas procesów
 Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
Geometryczna zbieżność algorytmu Gibbsa
 Geometryczna zbieżność algorytmu Gibbsa Iwona Żerda Wydział Matematyki i Informatyki, Uniwersytet Jagielloński 6 grudnia 2013 6 grudnia 2013 1 / 19 Plan prezentacji 1 Algorytm Gibbsa 2 Tempo zbieżności
Geometryczna zbieżność algorytmu Gibbsa Iwona Żerda Wydział Matematyki i Informatyki, Uniwersytet Jagielloński 6 grudnia 2013 6 grudnia 2013 1 / 19 Plan prezentacji 1 Algorytm Gibbsa 2 Tempo zbieżności
Model Pasywnego Trasera w Lokalnie Ergodycznym Środowisku
 w Lokalnie Ergodycznym Środowisku Tymoteusz Chojecki UMCS, Lublin Tomasz Komorowski IMPAN, Warszawa Kościelisko, 10 września 2016, XLV Konferencja Zastosowań Matematyki T. Komorowski, T. Chojecki w Lokalnie
w Lokalnie Ergodycznym Środowisku Tymoteusz Chojecki UMCS, Lublin Tomasz Komorowski IMPAN, Warszawa Kościelisko, 10 września 2016, XLV Konferencja Zastosowań Matematyki T. Komorowski, T. Chojecki w Lokalnie
Zadanie 1. O rozkładzie pewnego ryzyka X posiadamy następujące informacje: znamy oczekiwaną wartość nadwyżki ponad 20:
 Zadanie 1. O rozkładzie pewnego ryzyka X posiadamy następujące informacje: znamy oczekiwaną wartość nadwyżki ponad 20: E X 20 8 oraz znamy następujące charakterystyki dotyczące przedziału 10, 20 : 3 Pr
Zadanie 1. O rozkładzie pewnego ryzyka X posiadamy następujące informacje: znamy oczekiwaną wartość nadwyżki ponad 20: E X 20 8 oraz znamy następujące charakterystyki dotyczące przedziału 10, 20 : 3 Pr
Składki i rezerwy netto
 ROZDZIAŁ 6 Składki i rezerwy netto 1 Składki netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową Polisa taka zawiera szczegółowe warunki
ROZDZIAŁ 6 Składki i rezerwy netto 1 Składki netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową Polisa taka zawiera szczegółowe warunki
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Matematyka ubezpieczeń majątkowych 1.10.2012 r.
 Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
EGZAMIN MAGISTERSKI, czerwiec 2015 Biomatematyka
 Biomatematyka Rozpatrzmy chorobę, która rozprzestrzenia się za pośrednictwem nosicieli, u których nie występują jej symptomy. Niech C(t) oznacza liczbę nosicieli w chwili t. Zakładamy, że nosiciele są
Biomatematyka Rozpatrzmy chorobę, która rozprzestrzenia się za pośrednictwem nosicieli, u których nie występują jej symptomy. Niech C(t) oznacza liczbę nosicieli w chwili t. Zakładamy, że nosiciele są
Wykład 21 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej
 Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Metody redukcji wariancji
 Metody redukcji wariancji Michał Kołodziejczyk 26 maja 2009 Spis treści 1 Przedstawienie problemu 1 2 Metody redukcji - opis teoretyczny 2 2.1 Metoda Antithetic Variates...............................
Metody redukcji wariancji Michał Kołodziejczyk 26 maja 2009 Spis treści 1 Przedstawienie problemu 1 2 Metody redukcji - opis teoretyczny 2 2.1 Metoda Antithetic Variates...............................
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
Rachunek różniczkowy i całkowy w przestrzeniach R n
 Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
Wykład 3 Równania rózniczkowe cd
 7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Zadania ze Wstępu do Analizy Stochastycznej 1. = 0 p.n.
 Zadania ze Wstępu do Analizy Stochastycznej 1 1. Znajdź rozkład zmiennej 5W 1 W 3 + W 7. 2. Dla jakich parametrów a i b, zmienne aw 1 W 2 oraz W 3 + bw 5 są niezależne? 3. Znajdź rozkład wektora losowego
Zadania ze Wstępu do Analizy Stochastycznej 1 1. Znajdź rozkład zmiennej 5W 1 W 3 + W 7. 2. Dla jakich parametrów a i b, zmienne aw 1 W 2 oraz W 3 + bw 5 są niezależne? 3. Znajdź rozkład wektora losowego
Matematyka A kolokwium: godz. 18:05 20:00, 24 maja 2017 r. rozwiązania. ) zachodzi równość: x (t) ( 1 + x(t) 2)
 Matematyka A kolokwium: godz. 18:05 0:00, 4 maja 017 r. rozwiązania 1. 7 p. Znaleźć wszystkie takie funkcje t xt, że dla każdego t π, π zachodzi równość: x t 1 + xt 1+4t 0. p. Wśród znalezionych w poprzedniej
Matematyka A kolokwium: godz. 18:05 0:00, 4 maja 017 r. rozwiązania 1. 7 p. Znaleźć wszystkie takie funkcje t xt, że dla każdego t π, π zachodzi równość: x t 1 + xt 1+4t 0. p. Wśród znalezionych w poprzedniej
Proces rezerwy w czasie dyskretnym z losową stopą procentową i losową składką
 z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
Algorytm Metropolisa-Hastingsa
 Seminarium szkoleniowe, 25 kwietnia 2006 Plan prezentacji 1 Problem Metoda MCMC 2 Niezależny algorytm Metropolisa-Hastingsa Bła dzenie losowe Zbieżność procedury Metropolisa-Hastingsa Problem Metoda MCMC
Seminarium szkoleniowe, 25 kwietnia 2006 Plan prezentacji 1 Problem Metoda MCMC 2 Niezależny algorytm Metropolisa-Hastingsa Bła dzenie losowe Zbieżność procedury Metropolisa-Hastingsa Problem Metoda MCMC
Współczynniki Greckie
 Wojciech Antniak 05.0.008r. Wstęp Współczynniki greckie określają ryzyko opcji europejskiej na zmiany rynku. ażdy z nich określa w jaki sposób wpłynie zmiana jakiegoś czynnika na cenę akcji. W dalszej
Wojciech Antniak 05.0.008r. Wstęp Współczynniki greckie określają ryzyko opcji europejskiej na zmiany rynku. ażdy z nich określa w jaki sposób wpłynie zmiana jakiegoś czynnika na cenę akcji. W dalszej
Wstęp do równań różniczkowych
 Wstęp do równań różniczkowych Wykład 1 Lech Sławik Instytut Matematyki PK Literatura 1. Arnold W.I., Równania różniczkowe zwyczajne, PWN, Warszawa, 1975. 2. Matwiejew N.M., Metody całkowania równań różniczkowych
Wstęp do równań różniczkowych Wykład 1 Lech Sławik Instytut Matematyki PK Literatura 1. Arnold W.I., Równania różniczkowe zwyczajne, PWN, Warszawa, 1975. 2. Matwiejew N.M., Metody całkowania równań różniczkowych
Lista zadania nr 7 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie
 Lista zadania nr 7 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
Lista zadania nr 7 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
czastkowych Państwo przyk ladowe zadania z rozwiazaniami: karpinw adres strony www, na której znajda
 Zadania z równań różniczkowych czastkowych Za l aczam adres strony www, na której znajda Państwo przyk ladowe zadania z rozwiazaniami: http://math.uni.lodz.pl/ karpinw Zadanie 1. Znaleźć wszystkie rozwiazania
Zadania z równań różniczkowych czastkowych Za l aczam adres strony www, na której znajda Państwo przyk ladowe zadania z rozwiazaniami: http://math.uni.lodz.pl/ karpinw Zadanie 1. Znaleźć wszystkie rozwiazania
Dwa równania kwadratowe z częścią całkowitą
 Dwa równania kwadratowe z częścią całkowitą Andrzej Nowicki Wydział Matematyki i Informatyki Uniwersytet M. Kopernika w Toruniu anow @ mat.uni.torun.pl 4 sierpnia 00 Jeśli r jest liczbą rzeczywistą, to
Dwa równania kwadratowe z częścią całkowitą Andrzej Nowicki Wydział Matematyki i Informatyki Uniwersytet M. Kopernika w Toruniu anow @ mat.uni.torun.pl 4 sierpnia 00 Jeśli r jest liczbą rzeczywistą, to
Problem wyboru optymalnej dywidendy z paryskim opóźnieniem dla spektralnie ujemnych procesów Lévy ego
 Problem wyboru optymalnej dywidendy z paryskim opóźnieniem dla spektralnie ujemnych procesów Lévy ego Zbigniew Palmowski Wspólna praca z I. Czarna Zagadnienia aktuarialne: teoria i praktyka, Wrocław Ekonomiczny
Problem wyboru optymalnej dywidendy z paryskim opóźnieniem dla spektralnie ujemnych procesów Lévy ego Zbigniew Palmowski Wspólna praca z I. Czarna Zagadnienia aktuarialne: teoria i praktyka, Wrocław Ekonomiczny
Lista 6. Kamil Matuszewski 13 kwietnia D n =
 Lista 6 Kamil Matuszewski 3 kwietnia 6 3 4 5 6 7 8 9 Zadanie Mamy Pokaż, że det(d n ) = n.... D n =.... Dowód. Okej. Dla n =, n = trywialne. Załóżmy, że dla n jest ok, sprawdzę dla n. Aby to zrobić skorzystam
Lista 6 Kamil Matuszewski 3 kwietnia 6 3 4 5 6 7 8 9 Zadanie Mamy Pokaż, że det(d n ) = n.... D n =.... Dowód. Okej. Dla n =, n = trywialne. Załóżmy, że dla n jest ok, sprawdzę dla n. Aby to zrobić skorzystam
Zadania z Procesów Stochastycznych 1
 Zadania z Procesów Stochastycznych 1 Definicja Procesem Poissona z parametrem (intensywnością) λ > 0 nazywamy proces stochastyczny N = (N t ) t 0 taki, że N 0 = 0; (P0) N ma przyrosty niezależne; (P1)
Zadania z Procesów Stochastycznych 1 Definicja Procesem Poissona z parametrem (intensywnością) λ > 0 nazywamy proces stochastyczny N = (N t ) t 0 taki, że N 0 = 0; (P0) N ma przyrosty niezależne; (P1)
1 Wykład 3 Generatory liczb losowych o dowolnych rozkładach.
 Wykład 3 Generatory liczb losowych o dowolnych rozkładach.. Metoda odwracania Niech X oznacza zmienna losowa o dystrybuancie F. Oznaczmy F (t) = inf (x : t F (x)). Uwaga Zauważmy, że t [0, ] : F ( F (t)
Wykład 3 Generatory liczb losowych o dowolnych rozkładach.. Metoda odwracania Niech X oznacza zmienna losowa o dystrybuancie F. Oznaczmy F (t) = inf (x : t F (x)). Uwaga Zauważmy, że t [0, ] : F ( F (t)
Prawdopodobieństwo i statystyka
 Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Indukcja matematyczna
 Indukcja matematyczna 1 Zasada indukcji Rozpatrzmy najpierw następujący przykład. Przykład 1 Oblicz sumę 1 + + 5 +... + (n 1). Dyskusja. Widzimy że dla n = 1 ostatnim składnikiem powyższej sumy jest n
Indukcja matematyczna 1 Zasada indukcji Rozpatrzmy najpierw następujący przykład. Przykład 1 Oblicz sumę 1 + + 5 +... + (n 1). Dyskusja. Widzimy że dla n = 1 ostatnim składnikiem powyższej sumy jest n
Algorytmy MCMC i ich zastosowania statystyczne
 Algorytmy MCMC i ich zastosowania statystyczne Wojciech Niemiro Uniwersytet Mikołaja Kopernika, Toruń i Uniwersytet Warszawski Statystyka Matematyczna Wisła, grudzień 2010 Wykład 3 1 Łańcuchy Markowa Oznaczenia
Algorytmy MCMC i ich zastosowania statystyczne Wojciech Niemiro Uniwersytet Mikołaja Kopernika, Toruń i Uniwersytet Warszawski Statystyka Matematyczna Wisła, grudzień 2010 Wykład 3 1 Łańcuchy Markowa Oznaczenia
