1.5 Równanie ruchu układu napędowego
|
|
|
- Halina Karpińska
- 8 lat temu
- Przeglądów:
Transkrypt
1 1.5 Równani ruchu układu napędwg Równani ruchu mżna sfrmułwać na pdsawi zasady najmnijszg działania Hamilna, lub zasady zachwania nrgii, kóra ma prsą inrprację fizyczną. Całkwia nrgia E dsarczna przz silnik SE d maszyny rbczj R (rys.1.14) składa się z nrgii użycznj E u raz nrgii kinycznj zmagazynwanj w układzi napędwym E k (w masach wirujących): SE E R E u E k (J) Rys.1.14 Przpływ nrgii w układzi napędwym w sani dynamicznym czyli: 0 E = Eu + E k P = P+ J u 2 0 ; (1.10) 2. (1.11) Przyjmując ż dsarczna przz silnik mc wynsi: a mc mchaniczna użyczna: P =, (1.12) P =. (1.13) u raz różniczkując względm czasu wyrażni (1.11) i dziląc j nasępni przz rzymuj się: J d = + 2 dj. (1.14) Uwzględniając, ż = d α, (gdzi a - ką bru wału), mamy: J d d dj J d 2 α dj = + = + = 2 dα 2 dα d, (1.15) 12
2 gdzi d js nazywany mmnm dynamicznym napędu. W równaniu (1.15) mmn dynamiczny zawira dwi składw zminnj nrgii kinycznj: - pirwsza - wynikająca z zmiany prędkści d przy sałym mmnci bzwładnści --- J - druga - uwzględniająca zminnść mmnu bzwładnści dj 2 dα W równaniu (1.15) ni wysępują w spsób jasny sray (arci, luzy ) warzysząc prznszniu nrgii d silnika d mchanizmu. W pirwszym przybliżniu mżna przyjąć, ż są n uwzględnin w warściach lub, jak ich ddakw składniki, np.: ( ϕ ) =,, x, +, (1.16) gdzi wyrażn js wzrm (1.8). Większść układów napędwych ma sały, nizalżny d czasu ani d płżnia, mmn bzwładnści. Dla akich napędów równani ruchu przyjmuj psać: J d = = d. (1.17) 1.6 Sany pracy układu napędwg Z punku widznia zmiany prędkści kąwj rzróżnia się dwa sany pracy: - san usalny, w kórym prędkść = cns (lub ϑ p =cns), czyli: d = 0 ϑ lub p = 0, (1.18) - san niusalny (przjściwy, dynamiczny), w kórym prędkść cns (lub ϑ p cns), czyli: d 0 lub ϑ p 0. (1.19) San usalny - równwaga sayczna San usalny, zwany równiż sanm równwagi saycznj napędu wysępuj wówczas, gdy, zgdni z (1.18), mmn dynamiczny d =0, czyli mmn bciążnia js równważny przz mmn silnika. San n js charakryzwany na wykrsi - charakrysyk mchanicznych silnika i maszyny rbczj, punkm przcięcia charakrysyki =f( ) i =f( ). 13
3 Punk js sabilnym punkm równwagi, czyli układ napędwy w sani usalnym js sabilny (saczny) wówczas, gdy zakłócni sanu równwagi wywłuj pwsani mmnu dążącg d sprwadznia układu pnwni d płżnia równwagi w punkci (rys.1.15a). Jżli ni nasąpi, układ js nisabilny (nisaczny b). a) b) Rys.1.15 Ilusracj sabilnści saycznj układu napędwg: a - układ sabilny, b - układ nisabilny. Przy załżniu małych, dsaczni wln przbigających, dchylń d punku pracy usalnj, równania rzczywisych charakrysyk silnika i maszyny rbczj mżna zasąpić równaniami sycznych, pprwadznych przz punk dpwiadający sanwi równwagi (rys.1.15), czyli: gdzi: = a b, raz =, (1.20) a d = d d ; b =. (1.21) d = = Równani ruchu (w przypadku J= cns), napisan dla przyrsów mmnów i prędkści, przyjmuj psać: a b J d =, czyli p przkszałcniu: d a b = 0. (1.22) J 14
4 Rzwiązani równania różniczkwg (1.23) wyznacza przbig prędkści kąwj przy małym zaburzniu w punkci pracy : a b J = C. (1.23) Rzważany punk pracy będzi saczny ylk wówczas, gdy dchyłka prędkści będzi dążyła d zra: lim = 0. (1.24) Warunk (1.24) zsani spłniny, jśli wykładnik pęgi w równaniu (1.23) będzi ujmny, czyli przy uwzględniniu ż J>0, gdy będzi spłniny warunk: a b < 0 lub a < b. Warści a i b krślają nachylnia funkcji w punkci przcięcia charakrysyk mchanicznych. więc punk pracy będzi saczny, jśli będzi spłniny warunk sabilnści saycznj układu napędwg: d d < d d = = Z zalżnści (1.25) wynika, ż:. (1.25) przy pracy sacznj napędu - z wzrsm prędkści kąwj mmn prwy pwinin rsnąć szybcij niż mmn brwy silnika napędwg. Wówczas, przy wzrści prędkści, > i nasępuj hamwani, namias przy jj zmnijszaniu się, < i mamy przyspiszni napędu. W bydwu przypadkach układ napędwy wraca d pprzdnig punku pracy. nalgiczni, na pdsawi analizy równania (1.23) mżna równiż pdać warunk nisabilnści saycznj układu napędwg, a mianwici: d d. (1.26) d d = = W ym przypadku działani zakłócnia pwduj zawsz ddalani się punku pracy układu d pprzdnig punku. Z przdsawinj analizy wynika, ż równwadz saycznj układu napędwg dcyduj charakr przbigów saycznych charakrysyk mchanicznych silnika i maszyny rbczj. Na rys.1.16 przdsawin przykład, z kórg wynika, ż n sam punk pracy usalnj mż być jdnczśni, w zalżnści d przbigu charakrysyki maszyny rbczj: 15
5 - sabilnym (dla krzywj 1), - nisabilnym (dla krzywj 2) punkm pracy. 1( 1 ) B 2( 2 ) 0 B Rys.1.16 Ilusracja sabilnści saycznj układu napędwg: - punk pracy sabilnj dla krzywj 1 ( 1 =C ω 2 ) i nisabilnj dla krzywj 2 ( 2 =cns), B- punk pracy sabilnj dla krzywj 2. Przy szybkich zmianach mmnu i prędkści kąwj układu napędwg, mchaniczn charakrysyki sayczn ni mają charakru dcydującg, nalży więc badać zachwani się układu w sanach dynamicznych (niusalnych) i analizwać j między innymi z punku widznia sabilnści dynamicznj (kryrium Hurwiza, Nyqisa, D-rzbicia płaszczyzny i inn) Sany niusaln San niusalny (przjściwy, dynamiczny) wiąż się z zmianą punku pracy napędu w skuk działania rzch rdzajów zaburzń: zakłócń (np. wahania napięcia lub częsliwści w sici zasilającj), awarii (np. zwarci w układzi zasilania, chwilwy zanik napięcia sici, zablkwani wirnika) clwych działań układu srującg (lub człwika) wymusznych przz spcyfikę prcsu chnlgiczng. Wśród ych sanich mżna wyróżnić nasępując sany dynamiczn: - rzruch - przjści z sanu spczynkwg d krślng sanu pracy usalnj (np. praca przy bciążniu i prędkści znaminwj, praca na bigu jałwym, praca przy bniżnj prędkści kąwj ip.), - zarzymani (wybig) - prcs dwrny d pwyższg, przy czym zmnijszani prędkści d zra nasępuj w spsób nauralny, j. w wyniku sił arcia w układzi, - hamwani - prcs, pdczas kórg układ napędwy js zarzymywany przz dsarczni ddakwg mmnu większg niż mmn arcia; przy czym 16
6 mmn hamujący (spwalniający) mż być uzyskiwany na wil spsbów (mchaniczny, hydrauliczny lub lkrmchaniczny), - nawró (rwrs - czyli zmiana kirunku brów) - prcs w kórym nasępuj przjści z sanu pracy usalnj przy jdnym kirunku wirwania d pracy usalnj w przciwnym kirunku wirwania. Rwrs prędkści związany js z zarzymanim lub hamwanim silnika i nasępni z naychmiaswym rzruchm w przciwnym kirunku wirwania, - rgulacja prędkści kąwj - plga na zmiani charakrysyk =f( ) silnika przy urzymywaniu nizmininj charakrysyki maszyny rbczj. Nasępuj wówczas przjści d jdnj prędkści usalnj (w punkci pracy )d innj (punk ) przy sałj charakrysyc (rys.1,17a), kljn punky pracy lżą na charakrysyc maszyny rbczj, - rgulacja mmnu bciążnia - plga na zmiani charakrysyk =f( ) maszyny rbczj przy nizmininj charakrysyc silnika. Pwduj przjści d inng punku pracy na charakrysyc silnika (rys,1.17b); kljn punky pracy lżą na charakrysyc mchanicznj silnika. W szczgólnych przypadkach rgulacja mż wymagać zmian bu charakrysyk mchanicznych: silnika i maszyny rbczj (np. w układach napędwych lkmyw lkrycznych). W akim przypadku kljn punky pracy pkrywają cały bszar wyznaczny granicznymi charakrysykami uzyskanymi w prcsi rgulacji (rys.1.17c). a) b) c) ' ''' '' ' '' ''' ' '' ''' Ilusracj rgulacji prędkści i mmnu bciążnia Rys
Wykład 6 Pochodna, całka i równania różniczkowe w praktycznych zastosowaniach w elektrotechnice.
 Wykład 6 Pochodna, całka i równania różniczkow w prakycznych zasosowaniach w lkrochnic. Przypomnini: Dfinicja pochodnj: Granica ilorazu różnicowgo-przyros warości funkcji do przyrosu argumnów-przy przyrości
Wykład 6 Pochodna, całka i równania różniczkow w prakycznych zasosowaniach w lkrochnic. Przypomnini: Dfinicja pochodnj: Granica ilorazu różnicowgo-przyros warości funkcji do przyrosu argumnów-przy przyrości
36.2. Przetwornik wartości średniej. Z tej klasy przetworników na wyróżnienie zasługuje przetwornik pokazany na rys [2,
 36.. Przwrni warści śrdnij 4, 6]. Z j lasy przwrniów na wyróżnini zasługuj przwrni pazany na rys. 36.4 [, C R R i R R - W + 0.5R u D D 0.5R i - W +, R R 0. 5R Rys. 36.4. Przwrni warści śrdnij Przwrni n
36.. Przwrni warści śrdnij 4, 6]. Z j lasy przwrniów na wyróżnini zasługuj przwrni pazany na rys. 36.4 [, C R R i R R - W + 0.5R u D D 0.5R i - W +, R R 0. 5R Rys. 36.4. Przwrni warści śrdnij Przwrni n
Wykład 2 Wahadło rezonans parametryczny. l+δ
 Wykład Wahadło rzonans paramryczny θ θ l l+δ C B B Wykład Wahadło - rzonans paramryczny E E E B mg l cos θ θ E kinb m d d l l+δ B B l C I m l E B B kinb' I m B' B' d d d d B l ml d d B ' mgl cos ' B gcos
Wykład Wahadło rzonans paramryczny θ θ l l+δ C B B Wykład Wahadło - rzonans paramryczny E E E B mg l cos θ θ E kinb m d d l l+δ B B l C I m l E B B kinb' I m B' B' d d d d B l ml d d B ' mgl cos ' B gcos
Kształtowanie charakterystyk silnika obcowzbudnego prądu stałego w różnych stanach pracy
 Ćiczni 1 Kszałoani charakrysyk silnika obcozbudngo prądu sałgo różnych sanach pracy 1.1. Program ćicznia 1. Wyznaczni charakrysyk lkromchanicznych i mchanicznych silnika obcozbudngo sanach pracy silnikoj.
Ćiczni 1 Kszałoani charakrysyk silnika obcozbudngo prądu sałgo różnych sanach pracy 1.1. Program ćicznia 1. Wyznaczni charakrysyk lkromchanicznych i mchanicznych silnika obcozbudngo sanach pracy silnikoj.
własność: suma dowolnych rozwiązań jest również rozwiązaniem równania zasada superpozycji
 Składani drgań harnicznch () równani ruchu harniczng js: - liniw -jdnrdn d d własnść: sua dwlnch rzwiązań js równiż rzwiązani równania zasada suprpzcji knskwncj:. snza - (składani) drgań. analiza rzkładani
Składani drgań harnicznch () równani ruchu harniczng js: - liniw -jdnrdn d d własnść: sua dwlnch rzwiązań js równiż rzwiązani równania zasada suprpzcji knskwncj:. snza - (składani) drgań. analiza rzkładani
Układ napędowy z silnikiem szeregowym prądu stałego w różnych stanach pracy
 Ćiczni 2 Układ napędoy z silnikim szrgoym prądu sałgo różnych sanach pracy 2.1. Program ćicznia dla przypadkó: a) U = U N, d = 0 (charakrysyka nauralna), b) U = par, d = 0, c) U = U N, d = par (par paramr),
Ćiczni 2 Układ napędoy z silnikim szrgoym prądu sałgo różnych sanach pracy 2.1. Program ćicznia dla przypadkó: a) U = U N, d = 0 (charakrysyka nauralna), b) U = par, d = 0, c) U = U N, d = par (par paramr),
INFORMACJE DLA OCENIAJĄCYCH 1. Rozwiązania poszczególnych zadań i poleceń oceniamy są na podstawie punktowych kryteriów oceny. 2.
 INFORMACJE DLA OCENIAJĄCYCH 1. Rzwiązania pszczgólnych zadań i plcń cniamy są na pdstawi punktwych krytriów cny.. Przd przystąpinim d cniania prac zdających zachęcamy d samdzilng rzwiązania zstawu zadań,
INFORMACJE DLA OCENIAJĄCYCH 1. Rzwiązania pszczgólnych zadań i plcń cniamy są na pdstawi punktwych krytriów cny.. Przd przystąpinim d cniania prac zdających zachęcamy d samdzilng rzwiązania zstawu zadań,
( t) UKŁADY TRÓJFAZOWE
 KŁDY TRÓJFW kładm wilofazowym nazywamy zbiór obwodów lktrycznych (fazowych) w których działają napięcia żródłow sinusoidaln o jdnakowj częstotliwości przsunięt względm sibi w fazi i wytwarzan przważni
KŁDY TRÓJFW kładm wilofazowym nazywamy zbiór obwodów lktrycznych (fazowych) w których działają napięcia żródłow sinusoidaln o jdnakowj częstotliwości przsunięt względm sibi w fazi i wytwarzan przważni
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
I. KINEMATYKA I DYNAMIKA
 piagoras.d.pl I. KINEMATYKA I DYNAMIKA KINEMATYKA: Położenie ciała w przesrzeni można określić jedynie względem jakiegoś innego ciała lub układu ciał zwanego układem odniesienia. Ruch i spoczynek są względne
piagoras.d.pl I. KINEMATYKA I DYNAMIKA KINEMATYKA: Położenie ciała w przesrzeni można określić jedynie względem jakiegoś innego ciała lub układu ciał zwanego układem odniesienia. Ruch i spoczynek są względne
MAKROEKONOMIA 2. Wykład 3. Dynamiczny model DAD/DAS, część 2. Dagmara Mycielska Joanna Siwińska - Gorzelak
 MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) i E E E i r r = = = = = θ θ ρ ν φ ε ρ α * 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa
MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) i E E E i r r = = = = = θ θ ρ ν φ ε ρ α * 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa
Wał mechaniczny z silnikami prądu stałego
 Ćiczni 3 Wał mchaniczny z silnikami prądu sałgo 3.. Program ćicznia. Poznani przyczyn nirónomirngo obciążania się silnikó pracujących al mchanicznym.. Zapoznani się z srukurą sanoiska badaczgo. 3. Wyznaczni
Ćiczni 3 Wał mchaniczny z silnikami prądu sałgo 3.. Program ćicznia. Poznani przyczyn nirónomirngo obciążania się silnikó pracujących al mchanicznym.. Zapoznani się z srukurą sanoiska badaczgo. 3. Wyznaczni
MASZYNY PRĄDU STAŁEGO
 Zagadninia: Tma: MASZYNY PRĄDU STAŁEGO budowa i zasada działania maszyn prądu sałgo, napięci indukowan i momn obroowy, prądnica obcowzbudna i bocznikowa, silniki charakrysyki mchaniczn, rozruch i rgulacja
Zagadninia: Tma: MASZYNY PRĄDU STAŁEGO budowa i zasada działania maszyn prądu sałgo, napięci indukowan i momn obroowy, prądnica obcowzbudna i bocznikowa, silniki charakrysyki mchaniczn, rozruch i rgulacja
CHARAKTERYSTYKA OBCIĄŻENIOWA
 Opracowani: dr inż. Ewa Fudalj-Kostrzwa CHARAKTERYSTYKA OBCIĄŻENIOWA Charaktrystyki obciążniow są wyznaczan w ramach klasycznych statycznych badań silników zarówno dla silników o zapłoni iskrowym jak i
Opracowani: dr inż. Ewa Fudalj-Kostrzwa CHARAKTERYSTYKA OBCIĄŻENIOWA Charaktrystyki obciążniow są wyznaczan w ramach klasycznych statycznych badań silników zarówno dla silników o zapłoni iskrowym jak i
Termodynamika. Część 10. Elementy fizyki statystycznej klasyczny gaz doskonały. Janusz Brzychczyk, Instytut Fizyki UJ
 Trodynaika Część 1 Elnty fizyki statystycznj klasyczny gaz doskonały Janusz Brzychczyk, Instytut Fizyki UJ Użytczn całki ax2 dx = 1 2 a x ax2 dx = 1 2a ax2 dx = a a x 2 ax2 dx = 1 4a a x 3 ax2 dx = 1 2a
Trodynaika Część 1 Elnty fizyki statystycznj klasyczny gaz doskonały Janusz Brzychczyk, Instytut Fizyki UJ Użytczn całki ax2 dx = 1 2 a x ax2 dx = 1 2a ax2 dx = a a x 2 ax2 dx = 1 4a a x 3 ax2 dx = 1 2a
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Laboratorium Półprzewodniki Dielektryki Magnetyki Ćwiczenie nr 11 Badanie materiałów ferromagnetycznych
 Laboratorium Półprzwodniki Dilktryki Magntyki Ćwiczni nr Badani matriałów frromagntycznych I. Zagadninia do przygotowania:. Podstawow wilkości charaktryzując matriały magntyczn. Związki pomiędzy B, H i
Laboratorium Półprzwodniki Dilktryki Magntyki Ćwiczni nr Badani matriałów frromagntycznych I. Zagadninia do przygotowania:. Podstawow wilkości charaktryzując matriały magntyczn. Związki pomiędzy B, H i
gdzie E jest energią całkowitą cząstki. Postać równania Schrödingera dla stanu stacjonarnego Wprowadźmy do lewej i prawej strony równania Schrödingera
 San sacjonarny cząsk San sacjonarny - San, w kórym ( r, ) ( r ), gęsość prawdopodobńswa znalzna cząsk cząsk w danym obszarz przsrzn n zalży od czasu. San sacjonarny js charakrysyczny dla sacjonarngo pola
San sacjonarny cząsk San sacjonarny - San, w kórym ( r, ) ( r ), gęsość prawdopodobńswa znalzna cząsk cząsk w danym obszarz przsrzn n zalży od czasu. San sacjonarny js charakrysyczny dla sacjonarngo pola
Przykład 1 modelowania jednowymiarowego przepływu ciepła
 Przykład 1 modlowania jdnowymiarowgo przpływu cipła 1. Modl przpływu przz ścianę wilowarstwową Ściana składa się trzch warstw o różnych grubościach wykonana z różnych matriałów. Na jdnj z ścian zwnętrznych
Przykład 1 modlowania jdnowymiarowgo przpływu cipła 1. Modl przpływu przz ścianę wilowarstwową Ściana składa się trzch warstw o różnych grubościach wykonana z różnych matriałów. Na jdnj z ścian zwnętrznych
Uogólnione wektory własne
 Uogólnion wktory własn m Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
Uogólnion wktory własn m Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
Sieci neuronowe - uczenie
 Sici nuronow - uczni http://zajcia.jakubw.pl/nai/ Prcptron - przypomnini x x x n w w w n wi xi θ y w p. p. y Uczni prcptronu Przykład: rozpoznawani znaków 36 wjść Wyjści:, jśli na wjściu pojawia się litra
Sici nuronow - uczni http://zajcia.jakubw.pl/nai/ Prcptron - przypomnini x x x n w w w n wi xi θ y w p. p. y Uczni prcptronu Przykład: rozpoznawani znaków 36 wjść Wyjści:, jśli na wjściu pojawia się litra
ZJAWISKO TERMOEMISJI ELEKTRONÓW
 ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
Definicja: Wektor nazywamy uogólnionym wektorem własnym rzędu m macierzy A
 Uogólnion wktory własnw Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A m do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
Uogólnion wktory własnw Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A m do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
1. Wstęp. 2. Czwórnik symetryczny Ćwiczenie nr 3 Pomiar parametrów czwórników
 TEORI OBWODÓW SPRWODNIE LBORTORIM Pitr Dymaz Pitr Batg Pitr Błażjwski Nr grupy: 4 Trmin: Pnidziałk/ 5-8 Data wyknania ćw.:.4.8 Ćwizni nr Pmiar paramtrów zwórników Ona:. Wstęp Clm ćwiznia był wyznazni pdstawwyh
TEORI OBWODÓW SPRWODNIE LBORTORIM Pitr Dymaz Pitr Batg Pitr Błażjwski Nr grupy: 4 Trmin: Pnidziałk/ 5-8 Data wyknania ćw.:.4.8 Ćwizni nr Pmiar paramtrów zwórników Ona:. Wstęp Clm ćwiznia był wyznazni pdstawwyh
Wydział Elektryczny. Katedra Telekomunikacji i Aparatury Elektronicznej. Instrukcja do pracowni specjalistycznej
 Politchnika Białotocka Wydział Elktryczny Katdra Tlkomunikacji i Aparatury Elktronicznj Intrukcja do pracowni pcjalitycznj Tmat ćwicznia: Dokładność ciągłych i dykrtnych układów rgulacji Numr ćwicznia:
Politchnika Białotocka Wydział Elktryczny Katdra Tlkomunikacji i Aparatury Elktronicznj Intrukcja do pracowni pcjalitycznj Tmat ćwicznia: Dokładność ciągłych i dykrtnych układów rgulacji Numr ćwicznia:
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych LABORATORIUM
 POLITECHNIKA GDAŃSKA Wydział Elktrotchniki i Automatyki Katdra Enrgolktroniki i Maszyn Elktrycznych LABORATORIUM SYSTEMY ELEKTROMECHANICZNE TEMATYKA ĆWICZENIA MASZYNA SYNCHRONICZNA BADANIE PRACY W SYSTEMIE
POLITECHNIKA GDAŃSKA Wydział Elktrotchniki i Automatyki Katdra Enrgolktroniki i Maszyn Elktrycznych LABORATORIUM SYSTEMY ELEKTROMECHANICZNE TEMATYKA ĆWICZENIA MASZYNA SYNCHRONICZNA BADANIE PRACY W SYSTEMIE
Podstawowym prawem opisującym przepływ prądu przez materiał jest prawo Ohma, o makroskopowej postaci: V R (1.1)
 11. Właściwości lktryczn Nizwykl istotnym aspktm funkcjonalnym matriałów, są ich właściwości lktryczn. Mogą być on nizwykl różnorodn, prdysponując matriały do nizwykl szrokij gamy zastosowań. Najbardzij
11. Właściwości lktryczn Nizwykl istotnym aspktm funkcjonalnym matriałów, są ich właściwości lktryczn. Mogą być on nizwykl różnorodn, prdysponując matriały do nizwykl szrokij gamy zastosowań. Najbardzij
ZESPÓŁ B-D ELEKTROTECHNIKI
 ZESÓŁ B-D ELEKTOTECHNIKI Laboratorium Elktrotchniki i Elktroniki Samochodowj Tmat ćwicznia: Badani rozrusznika Opracowani: dr hab. inż. S. DUE 1. Instrukcja Laboratoryjna 2 omiary wykonan: a) omiar napięcia
ZESÓŁ B-D ELEKTOTECHNIKI Laboratorium Elktrotchniki i Elktroniki Samochodowj Tmat ćwicznia: Badani rozrusznika Opracowani: dr hab. inż. S. DUE 1. Instrukcja Laboratoryjna 2 omiary wykonan: a) omiar napięcia
( r) n. = n 10 10 10 YTM + Obligacje zerokuponowe Ŝadne odsetki nie przysługują ich posiadaczowi przed okresem
 Obligacje zerkupnwe Ŝadne dseki nie przysługują ich psiadaczwi przed kresem wykupu. P upływie eg erminu psiadacz bligacji rzymuje kwę równą warści nminalnej bligacji. Oprcenwanie ych bligacji wynika ze
Obligacje zerkupnwe Ŝadne dseki nie przysługują ich psiadaczwi przed kresem wykupu. P upływie eg erminu psiadacz bligacji rzymuje kwę równą warści nminalnej bligacji. Oprcenwanie ych bligacji wynika ze
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Fizyka promieniowania jonizującego. Zygmunt Szefliński
 Fizyka prominiowania jonizującgo ygmunt Szfliński 1 Wykład 10 Rozpady Rozpady - warunki nrgtyczn Ściżka stabilności Nad ściżką znajdują się jądra prominiotwórcz, ulgając rozpadowi -, zaś pod nią - jądra
Fizyka prominiowania jonizującgo ygmunt Szfliński 1 Wykład 10 Rozpady Rozpady - warunki nrgtyczn Ściżka stabilności Nad ściżką znajdują się jądra prominiotwórcz, ulgając rozpadowi -, zaś pod nią - jądra
MAKROEKONOMIA 2. Wykład 3. Dynamiczny model DAD/DAS, część 2. Dagmara Mycielska Joanna Siwińska - Gorzelak
 MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) E i E E i r r ν φ θ θ ρ ε ρ α 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa Oczekiwania
MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) E i E E i r r ν φ θ θ ρ ε ρ α 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa Oczekiwania
LABORATORIUM ESBwT. Optymalizacja niezawodnościowa struktury elektronicznego systemu bezpieczeństwa
 ZESPÓŁ LAORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LAORATORIUM ESwT INSTRUKCJA DO ĆWICZENIA nr Opymalizacja nizawodnościowa srukury
ZESPÓŁ LAORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LAORATORIUM ESwT INSTRUKCJA DO ĆWICZENIA nr Opymalizacja nizawodnościowa srukury
wentylatory promieniowe HPB-F
 Zastswanie Układy transprtu pneumatyczneg, nadmuch w układach suszenia (np. maszyny graficzne i bróbka twrzyw sztucznych), systemy nadmuchu pwietrza w układach spalania/bróbki termicznej (np. piece tpialne),
Zastswanie Układy transprtu pneumatyczneg, nadmuch w układach suszenia (np. maszyny graficzne i bróbka twrzyw sztucznych), systemy nadmuchu pwietrza w układach spalania/bróbki termicznej (np. piece tpialne),
Analiza wybranych własności rozkładu reszt
 Analiza wybranych własności rozkładu rsz Poprawni skonsruowany i oszacowany modl, kóry nasępni ma być wykorzysany do clów analizy i prdykcji, poza wysokim sopnim odzwircidlania zmian warości mpirycznych
Analiza wybranych własności rozkładu rsz Poprawni skonsruowany i oszacowany modl, kóry nasępni ma być wykorzysany do clów analizy i prdykcji, poza wysokim sopnim odzwircidlania zmian warości mpirycznych
Ekonomiczno-techniczne aspekty wykorzystania gazu w energetyce
 Ekonomiczno-chniczn aspky wykorzysania gazu w nrgyc anusz oowicz Wydział Inżynirii i Ochrony Środowiska Polichnika Częsochowska zacowani nakładów inwsycyjnych na projky wykorzysania gazu w nrgyc anusz
Ekonomiczno-chniczn aspky wykorzysania gazu w nrgyc anusz oowicz Wydział Inżynirii i Ochrony Środowiska Polichnika Częsochowska zacowani nakładów inwsycyjnych na projky wykorzysania gazu w nrgyc anusz
Farmakokinetyka furaginy jako przykład procesu pierwszego rzędu w modelu jednokompartmentowym zawierającym sztuczną nerkę jako układ eliminujący lek
 1 Matriał tortyczny do ćwicznia dostępny jst w oddzilnym dokumnci, jak równiż w książc: Hrmann T., Farmakokintyka. Toria i praktyka. Wydawnictwa Lkarski PZWL, Warszawa 2002, s. 13-74 Ćwiczni 6: Farmakokintyka
1 Matriał tortyczny do ćwicznia dostępny jst w oddzilnym dokumnci, jak równiż w książc: Hrmann T., Farmakokintyka. Toria i praktyka. Wydawnictwa Lkarski PZWL, Warszawa 2002, s. 13-74 Ćwiczni 6: Farmakokintyka
Rozkład Maxwell a prędkości cząsteczek gazu Prędkości poszczególnych cząsteczek mogą być w danej chwili dowolne
 Rozkład Maxwll a rędkośi ząstzk gazu 9-9. Rozkład Maxwll a rędkośi ząstzk gazu Prędkośi oszzgólnyh ząstzk ogą być w danj hwili dowoln 3 a tylko rędkość śrdnia kwadratowa wynosi sk. Można się jdnak sodziwać,
Rozkład Maxwll a rędkośi ząstzk gazu 9-9. Rozkład Maxwll a rędkośi ząstzk gazu Prędkośi oszzgólnyh ząstzk ogą być w danj hwili dowoln 3 a tylko rędkość śrdnia kwadratowa wynosi sk. Można się jdnak sodziwać,
CWICZ Nr 1 UKŁAD NAPĘDOWY Z SILNIKIEM WYKONAWCZYM PRĄDU STAŁEGO STEROWANYM IMPULSOWO Z PRZEKSZTAŁTNIKA TRANZYSTOROWEGO
 WIZ Nr 1 UKŁD NPĘDOWY Z SILNIKIE WYKONWZY PRĄDU STŁEGO STEROWNY IPULSOWO Z PRZEKSZTŁTNIK TRNZYSTOROWEGO 1.1. Program ćwicznia Wykonani ćwiczni objmuj następujący zakrs: - zapoznani się z silnikim wykonawczym
WIZ Nr 1 UKŁD NPĘDOWY Z SILNIKIE WYKONWZY PRĄDU STŁEGO STEROWNY IPULSOWO Z PRZEKSZTŁTNIK TRNZYSTOROWEGO 1.1. Program ćwicznia Wykonani ćwiczni objmuj następujący zakrs: - zapoznani się z silnikim wykonawczym
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systemy ciągłe budwa nieliniwych mdeli fenmenlgicznych z praw zachwania.
Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systemy ciągłe budwa nieliniwych mdeli fenmenlgicznych z praw zachwania.
Układy zasilania tranzystorów. Punkt pracy tranzystora Tranzystor bipolarny. Punkt pracy tranzystora Tranzystor unipolarny
 kłady zasilania ranzysorów Wrocław 28 Punk pracy ranzysora Punk pracy ranzysora Tranzysor unipolarny SS GS p GS S S opuszczalny oszar pracy (safe operaing condiions SOA) P max Zniekszałcenia nieliniowe
kłady zasilania ranzysorów Wrocław 28 Punk pracy ranzysora Punk pracy ranzysora Tranzysor unipolarny SS GS p GS S S opuszczalny oszar pracy (safe operaing condiions SOA) P max Zniekszałcenia nieliniowe
Ćwiczenie nr 4. Badanie filtrów składowych symetrycznych prądu i napięcia
 Ćwiczenie nr 4 Badanie filtrów składowych symetrycznych prądu i napięcia 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą składowych symetrycznych, pomiarem składowych w układach praktycznych
Ćwiczenie nr 4 Badanie filtrów składowych symetrycznych prądu i napięcia 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą składowych symetrycznych, pomiarem składowych w układach praktycznych
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów Wykłady 5,6, str. 1
 Poliechnika Poznańska, Kaedra Serowania i Inżynierii Sysemów Wykłady 5,6, sr. 1 18. Klasyfikacja UR ze wzgl. na posać sygn. wejściowego a) regulacja sałowarościowa y () = cons b) regulacja programowa c)
Poliechnika Poznańska, Kaedra Serowania i Inżynierii Sysemów Wykłady 5,6, sr. 1 18. Klasyfikacja UR ze wzgl. na posać sygn. wejściowego a) regulacja sałowarościowa y () = cons b) regulacja programowa c)
Kinematyka W Y K Ł A D I. Ruch jednowymiarowy. 2-1 Przemieszczenie, prędkość. x = x 2 - x x t
 Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Szeregowy obwód RC - model matematyczny układu
 Akadmia Morska w Gdyni Katdra Automatyki Okrętowj Toria strowania Mirosław Tomra Na przykładzi szrgowgo obwodu lktryczngo składającgo się z dwóch lmntów pasywnych: rzystora R i kondnsatora C przdstawiony
Akadmia Morska w Gdyni Katdra Automatyki Okrętowj Toria strowania Mirosław Tomra Na przykładzi szrgowgo obwodu lktryczngo składającgo się z dwóch lmntów pasywnych: rzystora R i kondnsatora C przdstawiony
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
Politechnika Częstochowska Wydział Inżynierii Mechanicznej i Informatyki. Sprawozdanie #2 z przedmiotu: Prognozowanie w systemach multimedialnych
 Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Układ wielofazowy i układ trójfazowy
 7. Rzwiązywani bwdów prądu sinusidalng 43 Wyład XV. PODTWOWE TRKTR OWODÓW TRÓJFOWH ład wilfazwy i uład trójfazwy Trminm uład wilfazwy rśla się zbiór w liczbi dwa lub więszj taich, związanych z sbą struturalni
7. Rzwiązywani bwdów prądu sinusidalng 43 Wyład XV. PODTWOWE TRKTR OWODÓW TRÓJFOWH ład wilfazwy i uład trójfazwy Trminm uład wilfazwy rśla się zbiór w liczbi dwa lub więszj taich, związanych z sbą struturalni
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYCZNYCH
 POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
1. Wprowadzenie do techniki regulacji 1
 1. Wprwadzni d tchnii rglacji 1 Różnic wyniając z strwania w ładzi twartym i zamniętym rzpatrzmy na przyładzi strwania silnia bcwzbdng prąd stałg. Analizę tg ład przprwadzn przy załżni, ż dynamię silnia
1. Wprwadzni d tchnii rglacji 1 Różnic wyniając z strwania w ładzi twartym i zamniętym rzpatrzmy na przyładzi strwania silnia bcwzbdng prąd stałg. Analizę tg ład przprwadzn przy załżni, ż dynamię silnia
2. Tablica routingu dla pewnej sieci złożonej z czterech węzłów wygląda następująco:
 Colloquium 4, Grupa A. Jaką oszczędność w zarządzaniu działm Biura Obsługi Klina (polgającą na rdukcji liczby sanowisk obsługi) mogą odnoować dwa połączon przdsiębiorswa, jżli: a. każda z firm przd połącznim
Colloquium 4, Grupa A. Jaką oszczędność w zarządzaniu działm Biura Obsługi Klina (polgającą na rdukcji liczby sanowisk obsługi) mogą odnoować dwa połączon przdsiębiorswa, jżli: a. każda z firm przd połącznim
PLAN WYKŁADU. Równanie Clausiusa-Clapeyrona 1 /21
 PAN WYKŁADU Równani Clausiusa-Clapyrona 1 /1 Podręczniki Salby, Chaptr 4 C&W, Chaptr 4 R&Y, Chaptr /1 p (mb) 1 C Fusion iquid Solid 113 6.11 Vapor 1 374 (ºC) Kropl chmurow powstają wtdy kidy zostani osiągnięty
PAN WYKŁADU Równani Clausiusa-Clapyrona 1 /1 Podręczniki Salby, Chaptr 4 C&W, Chaptr 4 R&Y, Chaptr /1 p (mb) 1 C Fusion iquid Solid 113 6.11 Vapor 1 374 (ºC) Kropl chmurow powstają wtdy kidy zostani osiągnięty
ĆWICZENIE 11 OPTYMALIZACJA NIEZAWODNOŚCIOWA STRUKTURY ELEKTRONICZNEGO SYSTEMU BEZPIECZEŃSTWA
 ĆWICZENIE OPTYMALIZACJA NIEZAWODNOŚCIOWA STUKTUY ELEKTONICZNEGO SYSTEMU EZPIECZEŃSTWA Cl ćwicznia: zapoznani z analizą nizawodnościowo-ksploaacyjną lkronicznych sysmów bzpiczńswa; wyznaczni wybranych wskaźników
ĆWICZENIE OPTYMALIZACJA NIEZAWODNOŚCIOWA STUKTUY ELEKTONICZNEGO SYSTEMU EZPIECZEŃSTWA Cl ćwicznia: zapoznani z analizą nizawodnościowo-ksploaacyjną lkronicznych sysmów bzpiczńswa; wyznaczni wybranych wskaźników
Obliczenia polowe silnika przełączalnego reluktancyjnego (SRM) w celu jego optymalizacji
 Akademia Górniczo Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Studenckie Koło Naukowe Maszyn Elektrycznych Magnesik Obliczenia polowe silnika
Akademia Górniczo Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Studenckie Koło Naukowe Maszyn Elektrycznych Magnesik Obliczenia polowe silnika
Przykłady ruchu drgającego
 RUCH DRGJĄCY Przyłady ruchu drgająceg ruch huśawi drgania srun w insruenach uzycznych ruch wahadła zegara echaniczneg Uład wejściwy aneny radiwej M drgania szyb iennych przy hałaśliwej ulicy drgania napięcia
RUCH DRGJĄCY Przyłady ruchu drgająceg ruch huśawi drgania srun w insruenach uzycznych ruch wahadła zegara echaniczneg Uład wejściwy aneny radiwej M drgania szyb iennych przy hałaśliwej ulicy drgania napięcia
1. W zależności od sposobu połączenia uzwojenia wzbudzającego rozróżniamy silniki:
 Temat: Silniki prądu stałego i ich właściwości ruchowe. 1. W zależności od sposobu połączenia uzwojenia wzbudzającego rozróżniamy silniki: a) samowzbudne bocznikowe; szeregowe; szeregowo-bocznikowe b)
Temat: Silniki prądu stałego i ich właściwości ruchowe. 1. W zależności od sposobu połączenia uzwojenia wzbudzającego rozróżniamy silniki: a) samowzbudne bocznikowe; szeregowe; szeregowo-bocznikowe b)
Laboratorium Nowoczesna Diagnostyka Materiałowa Pomiar materiałów magnetycznie miękkich
 Laboratorium Nowoczsna Diagnostyka Matriałowa Pomiar matriałów magntyczni miękkich I. Zagadninia do przygotowania:. Podstawow wilkości opisując pol i matriały magntyczn: natężni pola magntyczngo, indukcja
Laboratorium Nowoczsna Diagnostyka Matriałowa Pomiar matriałów magntyczni miękkich I. Zagadninia do przygotowania:. Podstawow wilkości opisując pol i matriały magntyczn: natężni pola magntyczngo, indukcja
II. Statyczny i dynamiczny opis układów
 4. Charakerysyki sayczne Dynamika układów pdsawy analizy i symulacji II. Sayczny i dynamiczny pis układów 4.. Wprwadzenie paramery pisu sayczneg Sayczny mdel układu pwsaje przez uprszczenie mdelu dynamiki
4. Charakerysyki sayczne Dynamika układów pdsawy analizy i symulacji II. Sayczny i dynamiczny pis układów 4.. Wprwadzenie paramery pisu sayczneg Sayczny mdel układu pwsaje przez uprszczenie mdelu dynamiki
Badanie funktorów logicznych TTL - ćwiczenie 1
 adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
Zagadnienie statyki kratownicy płaskiej
 Zagadnini statyki kratownicy płaskij METODY OBLICZENIOWE Budownictwo, studia I stopnia, smstr 6 Instytut L-5, Wydział Inżynirii Lądowj, Politchnika Krakowska Ewa Pabisk () Równania MES dla ustrojów prętowych
Zagadnini statyki kratownicy płaskij METODY OBLICZENIOWE Budownictwo, studia I stopnia, smstr 6 Instytut L-5, Wydział Inżynirii Lądowj, Politchnika Krakowska Ewa Pabisk () Równania MES dla ustrojów prętowych
sin b) Wyznaczyć taką funkcję pierwotną do funkcji sin ( =, która przechodzi przez punkt (0,0)
 Kolokwium z mmki 7.. Tm A godz.. Imię i nzwisko Nr indksu Zdni Wznczć cłkę d cos sin Wznczć ką unkcję pirwoną do unkcji cos sin kór przchodzi przz punk Odp. c cos cos F Zdni Nrsowć wrswic unkcji ln odpowidjąc
Kolokwium z mmki 7.. Tm A godz.. Imię i nzwisko Nr indksu Zdni Wznczć cłkę d cos sin Wznczć ką unkcję pirwoną do unkcji cos sin kór przchodzi przz punk Odp. c cos cos F Zdni Nrsowć wrswic unkcji ln odpowidjąc
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Ćwiczenie 4. Realizacja programowa dwupołożeniowej regulacji temperatury pieca elektrycznego
 Ćwiczni 4 Ralizacja programowa dwupołożniowj rgulacji tmpratury pica lktryczngo. Cl ćwicznia Clm ćwicznia jst zaznajomini z podstawami rgulacji obiktów ciągłych na przykładzi strowania dwupołożniowgo komputrowgo
Ćwiczni 4 Ralizacja programowa dwupołożniowj rgulacji tmpratury pica lktryczngo. Cl ćwicznia Clm ćwicznia jst zaznajomini z podstawami rgulacji obiktów ciągłych na przykładzi strowania dwupołożniowgo komputrowgo
MAKROEKONOMIA 2. Wykład 3. Dynamiczny model DAD/DAS, część 2. Dagmara Mycielska Joanna Siwińska - Gorzelak
 MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak 2 Plan wykładu Zakłócenia w modelu DAD/DAS: Wzros produkcji poencjalnej; Zakłócenie podażowe o sile
MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak 2 Plan wykładu Zakłócenia w modelu DAD/DAS: Wzros produkcji poencjalnej; Zakłócenie podażowe o sile
Układy sekwencyjne asynchroniczne Zadania projektowe
 Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
A. Kanicki: Systemy elektroenergetyczne KRYTERIA NAPIĘCIOWE WYZNACZANIA STABILNOŚCI LOKALNEJ
 . Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
. Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
Rachunek Prawdopodobieństwa MAP1151, 2011/12 Wydział Elektroniki Wykładowca: dr hab. Agnieszka Jurlewicz
 1 Rachunk Prawdopodobiństwa MAP1151, 011/1 Wydział Elktroniki Wykładowca: dr hab. Agniszka Jurlwicz Listy zadań nr 5-6 Opracowani: dr hab. Agniszka Jurlwicz Lista 5. Zminn losow dwuwymiarow. Rozkłady łączn,
1 Rachunk Prawdopodobiństwa MAP1151, 011/1 Wydział Elktroniki Wykładowca: dr hab. Agniszka Jurlwicz Listy zadań nr 5-6 Opracowani: dr hab. Agniszka Jurlwicz Lista 5. Zminn losow dwuwymiarow. Rozkłady łączn,
Zjawisko Zeemana (1896)
 iczby kwantow Zjawisko Zana (1896) Badani inii widowych w siny pou agntyczny, prowadzi do rozszczpini pozioów nrgtycznych. W odu Bohra, kwantowani orbitango ontu pędu n - główna iczba kwantowa n = 1,,
iczby kwantow Zjawisko Zana (1896) Badani inii widowych w siny pou agntyczny, prowadzi do rozszczpini pozioów nrgtycznych. W odu Bohra, kwantowani orbitango ontu pędu n - główna iczba kwantowa n = 1,,
Arkusz 1 - karta pracy Całka oznaczona i jej zastosowania. Całka niewłaściwa
 Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Wszystkie elementy Twojego licznika MySpeedy są do siebie w pełni
 PL Dsign l d Tak różnrdn jak Ty. Krzystając z najbardzij dsignrskig licznika rwrwg, pkazujsz, kim naprawdę jstś. Wybirz swój ulubiny mdl i bądź nipwtarzalny na rwrz. Wszystki lmnty Twjg licznika yspdy
PL Dsign l d Tak różnrdn jak Ty. Krzystając z najbardzij dsignrskig licznika rwrwg, pkazujsz, kim naprawdę jstś. Wybirz swój ulubiny mdl i bądź nipwtarzalny na rwrz. Wszystki lmnty Twjg licznika yspdy
Funkcja nieciągła. Typy nieciągłości funkcji. Autorzy: Anna Barbaszewska-Wiśniowska
 Funkcja niciągła. Typy niciągłości funkcji Autorzy: Anna Barbaszwska-Wiśniowska 2018 Funkcja niciągła. Typy niciągłości funkcji Autor: Anna Barbaszwska-Wiśniowska DEFINICJA Dfinicja 1: Funkcja niciągła
Funkcja niciągła. Typy niciągłości funkcji Autorzy: Anna Barbaszwska-Wiśniowska 2018 Funkcja niciągła. Typy niciągłości funkcji Autor: Anna Barbaszwska-Wiśniowska DEFINICJA Dfinicja 1: Funkcja niciągła
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Pomiar skręcenia płaszczyzny polaryzacji wywołanej przez roztwór sacharozy oraz wyznaczenie skręcalności właściwej
 Pmiar skręcenia płaszczyzny plaryzacji wywłanej przez rzwór sacharzy raz wyznaczenie skręcalnści właściwej I. Cel ćwiczenia: zapznanie ze zjawiskiem plaryzacji, pmiar kąa skręcenia płaszczyzny plaryzacji
Pmiar skręcenia płaszczyzny plaryzacji wywłanej przez rzwór sacharzy raz wyznaczenie skręcalnści właściwej I. Cel ćwiczenia: zapznanie ze zjawiskiem plaryzacji, pmiar kąa skręcenia płaszczyzny plaryzacji
Podstawowe definicje
 W-8 (Jarswc na ba J. Rukwsk) 5 slajów Ruch rgający Psaww fncj Swbn rgana harmncn Drgana łumn Drgana wymusn Skłaan rgań 3/8 L.R. Jarswc Psaww fncj rgana prcsy, w kórych ana wlkść fycna na prman rśn malj
W-8 (Jarswc na ba J. Rukwsk) 5 slajów Ruch rgający Psaww fncj Swbn rgana harmncn Drgana łumn Drgana wymusn Skłaan rgań 3/8 L.R. Jarswc Psaww fncj rgana prcsy, w kórych ana wlkść fycna na prman rśn malj
W-24 (Jaroszewicz) 22 slajdy Na podstawie prezentacji prof. J. Rutkowskiego. Cząstka w studni potencjału. przykłady efektu tunelowego
 Kyongju, Kora, April 999 W-4 (Jaroszwicz) slajdy Na podstawi przntacji prof. J. Rutowsigo Fizya wantowa 3 Cząsta w studni potncjału sończona studnia potncjału barira potncjału barira potncjału o sończonj
Kyongju, Kora, April 999 W-4 (Jaroszwicz) slajdy Na podstawi przntacji prof. J. Rutowsigo Fizya wantowa 3 Cząsta w studni potncjału sończona studnia potncjału barira potncjału barira potncjału o sończonj
Przemieszczeniem ciała nazywamy zmianę jego położenia
 1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
gdzie: E ilość energii wydzielona z zamiany masy na energię m ubytek masy c szybkość światła w próŝni (= m/s).
 1 Co to jst dfkt masy? Ŝli wskutk rakcji chmicznj masa produktów jst mnijsza od masy substratów to zjawisko taki nazywamy dfktm masy Ubytkowi masy towarzyszy wydzilani się nrgii ówimy Ŝ masa jst równowaŝna
1 Co to jst dfkt masy? Ŝli wskutk rakcji chmicznj masa produktów jst mnijsza od masy substratów to zjawisko taki nazywamy dfktm masy Ubytkowi masy towarzyszy wydzilani się nrgii ówimy Ŝ masa jst równowaŝna
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 320 3201
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 320 3201
Opracował: mgr inż. Marcin Wieczorek
 Opracował: mgr inż. Marcin Wieczorek Jeżeli moment napędowy M (elektromagnetyczny) silnika będzie większy od momentu obciążenia M obc o moment strat jałowych M 0 czyli: wirnik będzie wirował z prędkością
Opracował: mgr inż. Marcin Wieczorek Jeżeli moment napędowy M (elektromagnetyczny) silnika będzie większy od momentu obciążenia M obc o moment strat jałowych M 0 czyli: wirnik będzie wirował z prędkością
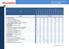
Tabela doboru przekaźników czasowych MTR17
 M17-A07-240-... M17-B07-240-... M17-Q-240-... M17--240-... M17--240-... M17--240-... M17--240-... M17-VW-240-... M17-XY-240-... M17-Z-240-... M17-AB-240-116 M17-CD-240-116 M17-BA-240-116 M17-P-240-...
M17-A07-240-... M17-B07-240-... M17-Q-240-... M17--240-... M17--240-... M17--240-... M17--240-... M17-VW-240-... M17-XY-240-... M17-Z-240-... M17-AB-240-116 M17-CD-240-116 M17-BA-240-116 M17-P-240-...
Silniki prądu stałego. Wiadomości ogólne
 Silniki prądu stałego. Wiadomości ogólne Silniki prądu stałego charakteryzują się dobrymi właściwościami ruchowymi przy czym szczególnie korzystne są: duży zakres regulacji prędkości obrotowej i duży moment
Silniki prądu stałego. Wiadomości ogólne Silniki prądu stałego charakteryzują się dobrymi właściwościami ruchowymi przy czym szczególnie korzystne są: duży zakres regulacji prędkości obrotowej i duży moment
Komitet Główny Olimpiady Fizycznej, Waldemar Gorzkowski: Olimpiady fizyczne XXIII i XXIV. WSiP, Warszawa 1977.
 XXV OLMPADA FZYCZNA (1974/1975). Stopiń, zadani doświadczaln D Źródło: Nazwa zadania: Działy: Słowa kluczow: Komitt Główny Olimpiady Fizycznj, Waldmar Gorzkowski: Olimpiady fizyczn XX i XXV. WSiP, Warszawa
XXV OLMPADA FZYCZNA (1974/1975). Stopiń, zadani doświadczaln D Źródło: Nazwa zadania: Działy: Słowa kluczow: Komitt Główny Olimpiady Fizycznj, Waldmar Gorzkowski: Olimpiady fizyczn XX i XXV. WSiP, Warszawa
Dynamika mechanizmów
 Dynamika mechanizmów napędy zadanie odwrotne dynamiki zadanie proste dynamiki ogniwa maszyny 1 Modelowanie dynamiki mechanizmów wymuszenie siłowe od napędów struktura mechanizmu, wymiary ogniw siły przyłożone
Dynamika mechanizmów napędy zadanie odwrotne dynamiki zadanie proste dynamiki ogniwa maszyny 1 Modelowanie dynamiki mechanizmów wymuszenie siłowe od napędów struktura mechanizmu, wymiary ogniw siły przyłożone
ELEKTRONICZNE PULSACYJNE ZAWORY ROZPRĘŻNE
 wr. 221010 PRZEDSIĘBIORSTWO WIELOBRANŻOWE "AVICOLD" Sp.J. 43 400 CIESZYN, ul. BIELSKA 61c tl. / fax: 0338567444, 0338567445, http://www.avicld.cm.pl 0338567446 mail: avicld@avicld.cm.pl ELEKTRONICZNE PULSACYJNE
wr. 221010 PRZEDSIĘBIORSTWO WIELOBRANŻOWE "AVICOLD" Sp.J. 43 400 CIESZYN, ul. BIELSKA 61c tl. / fax: 0338567444, 0338567445, http://www.avicld.cm.pl 0338567446 mail: avicld@avicld.cm.pl ELEKTRONICZNE PULSACYJNE
Obrabiane części określone są przez wymiary gabarytowe, masę, ciepło właściwe.
 . OBLICZANI CILN ICÓW RZYSTANCYJNYCH iece rezysancyjne sswane są najczęściej d bróbki cieplnej wsadów. rjekwanie akich pieców plega na bliczeniu wyprawy gnirwałej i ermizlacyjnej pieca, mcy sra, mcy elemenów
. OBLICZANI CILN ICÓW RZYSTANCYJNYCH iece rezysancyjne sswane są najczęściej d bróbki cieplnej wsadów. rjekwanie akich pieców plega na bliczeniu wyprawy gnirwałej i ermizlacyjnej pieca, mcy sra, mcy elemenów
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Wstęp... 1. Rozdział 2 Wpływ inflacji na koszt użycia kapitału... 17 2.1 Inflacja i koszt użycia kapitału...17 2.2 Finansowanie pożyczkami...
 Spis rści Wsęp... Rozdział Podakowa rozja kapiału a warość przdsiębiorswa... 3.. Isoa rozji kapiału...3... Gospodarka bz podaków... 3..2. Gospodarka z podakai... 4..3. Ilusracja podakowj rozji kapiału...
Spis rści Wsęp... Rozdział Podakowa rozja kapiału a warość przdsiębiorswa... 3.. Isoa rozji kapiału...3... Gospodarka bz podaków... 3..2. Gospodarka z podakai... 4..3. Ilusracja podakowj rozji kapiału...
ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO OKREŚLENIA PRAWDOPODOBIEŃSTWA SPRZEDAŻY ZASOBU MIESZKANIOWEGO
 ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO OKREŚLENIA PRAWDOPODOBIEŃSTWA SPRZEDAŻY ZASOBU MIESZKANIOWEGO Łukasz MACH Strszczni: W artykul przdstawiono procs budowy modlu rgrsji logistycznj, którgo clm jst wspomagani
ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO OKREŚLENIA PRAWDOPODOBIEŃSTWA SPRZEDAŻY ZASOBU MIESZKANIOWEGO Łukasz MACH Strszczni: W artykul przdstawiono procs budowy modlu rgrsji logistycznj, którgo clm jst wspomagani
15. STANY NIEUSTALONE W OBWODACH SLS
 OBWODY I SYGNAŁY Wykład 5 : Sany niualon w obwodach SS 5. STANY NIUSTAON W OBWODAH SS 5.. WPOWADZNI ozparzmy układ SS, na kóry działamy zdrminowanym wymuznim x okrślonym dla -,. Jśli inruj na funkcja okrślonj
OBWODY I SYGNAŁY Wykład 5 : Sany niualon w obwodach SS 5. STANY NIUSTAON W OBWODAH SS 5.. WPOWADZNI ozparzmy układ SS, na kóry działamy zdrminowanym wymuznim x okrślonym dla -,. Jśli inruj na funkcja okrślonj
Swobodny spadek ciał w ośrodku stawiającym opór
 Ryszard Chybici Swobodny spad ciał w ośrodu stawiający opór (Posłuiwani się przz osoby trzci ty artyuł lub jo istotnyi frantai bz widzy autora jst wzbronion) Milc, 005 Swobodny spad ciała ośrodu stawiający
Ryszard Chybici Swobodny spad ciał w ośrodu stawiający opór (Posłuiwani się przz osoby trzci ty artyuł lub jo istotnyi frantai bz widzy autora jst wzbronion) Milc, 005 Swobodny spad ciała ośrodu stawiający
SPRĘŻ WENTYLATORA stosunek ciśnienia statycznego bezwzględnego w płaszczyźnie
 DEFINICJE OGÓLNE I WIELKOŚCI CHARAKTERYSTYCZNE WENTYLATORA WENTYLATOR maszyna wirnikowa, która otrzymuje energię mechaniczną za pomocą jednego wirnika lub kilku wirników zaopatrzonych w łopatki, użytkuje
DEFINICJE OGÓLNE I WIELKOŚCI CHARAKTERYSTYCZNE WENTYLATORA WENTYLATOR maszyna wirnikowa, która otrzymuje energię mechaniczną za pomocą jednego wirnika lub kilku wirników zaopatrzonych w łopatki, użytkuje
LABORATORIUM PODSTAW SILNIKÓW I NAPĘDÓW SPALINOWYCH. Ćwiczenie 2 POMIARY PODSTAWOWYCH PARAMETRÓW PRACY SILNIKÓW SPALINOWYCH
 Dr inŝ. Sławomir Makowski WYDZIAŁ MECHANICZNY POLITECHNIKI GDAŃSKIEJ KATEDRA SILNIKÓW SPALINOWYCH I SPRĘśAREK Kirownik katdry: prof. dr hab. inŝ. Andrzj Balcrski, prof. zw. PG LABORATORIUM PODSTAW SILNIKÓW
Dr inŝ. Sławomir Makowski WYDZIAŁ MECHANICZNY POLITECHNIKI GDAŃSKIEJ KATEDRA SILNIKÓW SPALINOWYCH I SPRĘśAREK Kirownik katdry: prof. dr hab. inŝ. Andrzj Balcrski, prof. zw. PG LABORATORIUM PODSTAW SILNIKÓW
MECHANIKA 2 Wykład 7 Dynamiczne równania ruchu
 MECHANIKA 2 Wykład 7 Dynamiczne równania ruchu Prowadzący: dr Krzysztof Polko Dynamiczne równania ruchu Druga zasada dynamiki zapisana w postaci: Jest dynamicznym wektorowym równaniem ruchu. Dynamiczne
MECHANIKA 2 Wykład 7 Dynamiczne równania ruchu Prowadzący: dr Krzysztof Polko Dynamiczne równania ruchu Druga zasada dynamiki zapisana w postaci: Jest dynamicznym wektorowym równaniem ruchu. Dynamiczne
 Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż
Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż
 Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż
Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż


