gdzie E jest energią całkowitą cząstki. Postać równania Schrödingera dla stanu stacjonarnego Wprowadźmy do lewej i prawej strony równania Schrödingera
|
|
|
- Kamila Wieczorek
- 8 lat temu
- Przeglądów:
Transkrypt
1 San sacjonarny cząsk San sacjonarny - San, w kórym ( r, ) ( r ), gęsość prawdopodobńswa znalzna cząsk cząsk w danym obszarz przsrzn n zalży od czasu. San sacjonarny js charakrysyczny dla sacjonarngo pola sł U ( r, ) U ( r ). Dla sanu sacjonarngo funkcja falowa moż być zapsana jako loczyn funkcj zalżnj ylko od współrzędnych funkcj zalżnj ylko od czasu. ( r, ) ( r) ( r, ) ( r ) gdz js nrgą całkową cząsk. Posać równana Schrödngra dla sanu sacjonarngo Wprowadźmy do lwj prawj srony równana Schrödngra U m funkcję ( r, ) ( r) charakrysyczną dla sanu sacjonarngo. Podsawy mchank kwanowj 0
2 Posać równana Schrödngra dla sanu sacjonarngo, cd. U m ( r, ) ( r) : ( r ) ( r ) P: U ( r) U ( r) m m Przyrównując praw srony ych wyrażń orzymujmy zw. sacjonarn równan Schrödngra (równan Schrödngra bz czasu). U m Częso wygodna js posać sacjonarngo równana Schrödngra po uporządkowanu m( U ) 0 Podsawy mchank kwanowj
3 Równan Schrödngra w zaps opraorowym Hˆ U m Opraor nrg całkowj, opraor Hamlona, hamlonan. Posać równana Schrödngra z użycm opraora Ĥ U Z czasm m Hˆ U m Ĥ Bz czasu Rozwązan równana Schrödngra dla przypadku nogranczongo ruchu cząsk wzdłuż os x W ym przypadku U( x) cons. Przyjmjmy U( x) 0. Hˆ d U m m dx Ĥ d m dx d dx m 0 Podsawy mchank kwanowj
4 Rozwązan równana Schrödngra dla przypadku nogranczongo ruchu cząsk wzdłuż os x, cd. d m 0 Podsawmy dx d dx k 0 m k m rx Powyższ równan różnczkow rozwążmy przz podsawn dochodząc do zw. równana charakrysyczngo k r k 0 r k r k, r k Rozwązanm ogólnym js kombnacja lnowa dwóch rozwązań szczgólnych ( x) A A kx kx A, A - sał. Płna (zalżna od położna czasu) funkcja falowa ma posać ( x, ) ( x) A A, gdz ( kx) ( kx). A A ( kx) - fala poruszająca sę w dodanm krunku os x, ( kx) - fala poruszająca sę w ujmnym krunku os x. Podsawy mchank kwanowj 3
5 Rozwązan równana Schrödngra dla przypadku nogranczongo ruchu cząsk wzdłuż os x, cd. Orzymalśmy: ( x, ) ( x) A A ( kx) ( kx) a) przypadk cząsk poruszającj sę w dodanm krunku os x A ) ( kx) ( x, ) A (przyjmujmy 0 ( x, ) A A cons * * b) przypadk cząsk poruszającj sę w ujmnym krunku os x A ) ( kx) ( x, ) A (przyjmujmy 0 ( x, ) A A cons * * Funkcj falow w przypadku a) b) przdsawają monochromayczn ( cons, k cons ) fal płask. Kwadra modułu monochromaycznj fal płaskj n js jdnak całkowalny, co oznacza, ż powyższ rozwązana n opsują właścw cząsk swobodnj. Ponważ ( x, ) n zalży od x, położn cząsk n js u okrślon. Właścwą funkcją falową opsującą cząskę swobodną js kombnacja lnowa fal monochromaycznych, czyl paczka falowa. Podsawy mchank kwanowj 4
6 Ogranczony ruch cząsk wzdłuż os x. Nskończn głęboka jdnowymarowa sudna poncjału x 0 U ( x) 0 0 x x Z względu na nskończoną warość nrg poncjalnj, cząska n moż znajdować sę w obszarach I lub I. Sąd ( x) 0, ( x) 0 W obszarz san cząsk okrślony js przz równan Schrödngra d dx k 0 kx ( x) A A Sał A A okrślmy korzysając z warunków brzgowych dla funkcj ( x). Warunk brzgowy dla x 0 (cągłość dla x 0) I kx (0) I (0) 0 AA 0 A A, kx kx czyl ( x) A C sn( kx) C - sała. sn I Podsawy mchank kwanowj 5
7 Ogranczony ruch cząsk wzdłuż os x. Nskończn głęboka jdnowymarowa sudna poncjału, cd. Orzymalśmy: ( x) C sn( kx) Warunk brzgowy dla x (cągłość dla x ) ( ) C sn( k) 0 ( C 0) ( k n, n 0,,,...) Przypadk C 0 n 0 odrzucamy, bo wdy ( x) 0 dla wszyskch x, czyl cząsk n ma w sudn. Ujmn warośc n akż pomjamy, gdyż on jdyn zmnają znak. Z warunku k n orzymujmy k n /, czyl n ( x) C sn x Uprzdno przyjęlśmy m k. Sąd na podsaw k n dochodzmy do wnosku, ż nrga cząsk w sudn poncjału js skwanowana h n n n, n,,... lczba kwanowa. m 8m Podsawy mchank kwanowj 6
8 Nskończn głęboka jdnowymarowa sudna poncjału, cd. nrga cząsk w jam n moż przyjmować warośc zro. Ma o zwązk z zasadą nokrślonośc Hsnbrga. Z względu na ogranczoną szrokość sudn nokrśloność położna cząsk js ogranczona z góry. Sąd nokrśloność jj pędu js zawsz różna od zra, a o wąż sę z ym, ż cząska zawsz mus posadać pwną lość ng n mnjszą nż p m mn ( ) / ( ) Funkcja falowa cząsk w nskończn głębokj jdnowymarowj jam poncjału n n n( x, ) C sn x Warość sałj C można okrślć korzysając z warunku unormowana funkcj falowj n n * dv V CC * 0 n sn xdx Podsawy mchank kwanowj 7
9 Funkcja falowa cząsk w nskończn głębokj jdnowymarowj jam poncjału. cd. * * * n n CC sn x dx CC cos x dx CC 0 0 CC * C Czynnk można pomnąć, gdyż sanow on nsony z punku wdzna ( x) * czynnk fazowy. ( ) sn n n x x n n( x, ) sn x n Podsawy mchank kwanowj 8
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Proces stochastyczny jako funkcja dwóch zmiennych. i niepusty podzbiór zbioru liczb rzeczywistych T. Proces stochastyczny jest to funkcja
 POJĘCI PROCSU STOCHSTYCZNGO Przykład mpluda napęca gnrowango przz prądncę prądu zmnngo zalży od czynnków losowych moż być zapsana jako funkcja X sn c c - sała okrślająca częsolwość - zmnna losowa o rozkładz
POJĘCI PROCSU STOCHSTYCZNGO Przykład mpluda napęca gnrowango przz prądncę prądu zmnngo zalży od czynnków losowych moż być zapsana jako funkcja X sn c c - sała okrślająca częsolwość - zmnna losowa o rozkładz
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
E2. BADANIE OBWODÓW PRĄDU PRZEMIENNEGO
 E. BADANE OBWODÓW PĄDU PZEMENNEGO ks opracowały: Jadwga Szydłowska Bożna Janowska-Dmoch Badać będzmy charakrysyk obwodów zawrających różn układy lmnów akch jak: opornk, cwka kondnsaor, połączonych z sobą
E. BADANE OBWODÓW PĄDU PZEMENNEGO ks opracowały: Jadwga Szydłowska Bożna Janowska-Dmoch Badać będzmy charakrysyk obwodów zawrających różn układy lmnów akch jak: opornk, cwka kondnsaor, połączonych z sobą
Wykład 6 Pochodna, całka i równania różniczkowe w praktycznych zastosowaniach w elektrotechnice.
 Wykład 6 Pochodna, całka i równania różniczkow w prakycznych zasosowaniach w lkrochnic. Przypomnini: Dfinicja pochodnj: Granica ilorazu różnicowgo-przyros warości funkcji do przyrosu argumnów-przy przyrości
Wykład 6 Pochodna, całka i równania różniczkow w prakycznych zasosowaniach w lkrochnic. Przypomnini: Dfinicja pochodnj: Granica ilorazu różnicowgo-przyros warości funkcji do przyrosu argumnów-przy przyrości
BADANIE WYBRANYCH STRUKTUR NIEZAWODNOŚCIOWYCH
 ZAKŁAD EKSPLOATACJI SYSTEMÓW ELEKTOICZYCH ISTYTUT SYSTEMÓW ELEKTOICZYCH WYDZIAŁ ELEKTOIKI WOJSKOWA AKADEMIA TECHICZA ---------------------------------------------------------------------------------------------------------------
ZAKŁAD EKSPLOATACJI SYSTEMÓW ELEKTOICZYCH ISTYTUT SYSTEMÓW ELEKTOICZYCH WYDZIAŁ ELEKTOIKI WOJSKOWA AKADEMIA TECHICZA ---------------------------------------------------------------------------------------------------------------
I. Elementy analizy matematycznej
 WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
9. WYBRANE ZAGADNIENIA DYNAMIKI KONSTRUKCJI
 9. WYBRANE ZAGADNIENIA DYNAMIKI KONSRUKCJI 9. WYBRANE ZAGADNIENIA DYNAMIKI KONSRUKCJI W rozdzal 5 wyprowadzlśmy równan równowag saycznj dla cała analzowango modą lmnów skończonych. Równan o można równż
9. WYBRANE ZAGADNIENIA DYNAMIKI KONSRUKCJI 9. WYBRANE ZAGADNIENIA DYNAMIKI KONSRUKCJI W rozdzal 5 wyprowadzlśmy równan równowag saycznj dla cała analzowango modą lmnów skończonych. Równan o można równż
Wykład 2 Wahadło rezonans parametryczny. l+δ
 Wykład Wahadło rzonans paramryczny θ θ l l+δ C B B Wykład Wahadło - rzonans paramryczny E E E B mg l cos θ θ E kinb m d d l l+δ B B l C I m l E B B kinb' I m B' B' d d d d B l ml d d B ' mgl cos ' B gcos
Wykład Wahadło rzonans paramryczny θ θ l l+δ C B B Wykład Wahadło - rzonans paramryczny E E E B mg l cos θ θ E kinb m d d l l+δ B B l C I m l E B B kinb' I m B' B' d d d d B l ml d d B ' mgl cos ' B gcos
CHEMIA KWANTOWA Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoretycznej Zespół Chemii Kwantowej Grupa Teorii Reaktywności Chemicznej
 CHEMI KWTOW CHEMI KWTOW Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
CHEMI KWTOW CHEMI KWTOW Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
PROBLEM ODWROTNY DLA RÓWNANIA PARABOLICZNEGO W PRZESTRZENI NIESKOŃCZENIE WYMIAROWEJ THE INVERSE PARABOLIC PROBLEM IN THE INFINITE DIMENSIONAL SPACE
 JAN KOOŃSKI POBLEM ODWOTNY DLA ÓWNANIA PAABOLICZNEGO W PZESTZENI NIESKOŃCZENIE WYMIAOWEJ THE INVESE PAABOLIC POBLEM IN THE INFINITE DIMENSIONAL SPACE S r e s z c z e n e A b s r a c W arykule skonsruowano
JAN KOOŃSKI POBLEM ODWOTNY DLA ÓWNANIA PAABOLICZNEGO W PZESTZENI NIESKOŃCZENIE WYMIAOWEJ THE INVESE PAABOLIC POBLEM IN THE INFINITE DIMENSIONAL SPACE S r e s z c z e n e A b s r a c W arykule skonsruowano
Część I. MECHANIKA. Wykład KINEMATYKA PUNKTU MATERIALNEGO. Ruch jednowymiarowy Ruch na płaszczyźnie i w przestrzeni.
 Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Metoda Klasyczna część I
 Tora Obwodów 2 Wykład 2 Moda Klasyczna część I Prowadzący: dr nż. Toasz Skorsk Insyu Podsaw lkrochnk lkrochnolog Wydzał lkryczny Polchnka Wrocławska D-1, 205/8 l: (071) 320 21 60 fax: (071) 320 20 06 al:
Tora Obwodów 2 Wykład 2 Moda Klasyczna część I Prowadzący: dr nż. Toasz Skorsk Insyu Podsaw lkrochnk lkrochnolog Wydzał lkryczny Polchnka Wrocławska D-1, 205/8 l: (071) 320 21 60 fax: (071) 320 20 06 al:
BADANIE WYBRANYCH STRUKTUR NIEZAWODNOŚCIOWYCH
 ZAKŁAD EKSPLOATACJI SYSTEMÓW ELEKTOICZYCH ISTYTUT SYSTEMÓW ELEKTOICZYCH WYDZIAŁ ELEKTOIKI WOJSKOWA AKADEMIA TECHICZA ---------------------------------------------------------------------------------------------------------------
ZAKŁAD EKSPLOATACJI SYSTEMÓW ELEKTOICZYCH ISTYTUT SYSTEMÓW ELEKTOICZYCH WYDZIAŁ ELEKTOIKI WOJSKOWA AKADEMIA TECHICZA ---------------------------------------------------------------------------------------------------------------
Praca domowa nr 1. Metodologia Fizyki. Grupa 1. Szacowanie wartości wielkości fizycznych Zad Stoisz na brzegu oceanu, pogoda jest idealna,
 Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
PODSTAWY CHEMII KWANTOWEJ. Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoretycznej Zespół Chemii Kwantowej Grupa Teorii Reaktywności Chemicznej
 PODSTWY CHEMII KWTOWEJ Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
PODSTWY CHEMII KWTOWEJ Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
PODSTAWY MECHANIKI KWANTOWEJ
 PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
I zasada termodynamiki dla układu zamkniętego (ujęcie masy kontrolnej)
 Wykład 8 I zasada rmodynamk dla układów zamknęyh (uję masy konrolnj) Prwsza zasada rmodynamk jako równan knyzn dla układu zamknęgo (uję masy konrolnj; zmana sanu masy konrolnj) Układy owar; uję masy konrolnj
Wykład 8 I zasada rmodynamk dla układów zamknęyh (uję masy konrolnj) Prwsza zasada rmodynamk jako równan knyzn dla układu zamknęgo (uję masy konrolnj; zmana sanu masy konrolnj) Układy owar; uję masy konrolnj
Algorytmy numeryczne w Delphi. Ksiêga eksperta
 IDZ DO PRZYK ADOWY ROZDZIA SPIS TREŒCI KALOG KSI EK KALOG ONLINE ZAMÓW DRUKOWANY KALOG Algorymy numryczn w Dlph Ksêga kspra Auorzy: Brnard Baron, Arur Pasrbk, Marcn Mac¹ k ISBN: 83-736-95-8 Forma: B5,
IDZ DO PRZYK ADOWY ROZDZIA SPIS TREŒCI KALOG KSI EK KALOG ONLINE ZAMÓW DRUKOWANY KALOG Algorymy numryczn w Dlph Ksêga kspra Auorzy: Brnard Baron, Arur Pasrbk, Marcn Mac¹ k ISBN: 83-736-95-8 Forma: B5,
 Ś Ą Ś Ą Ś Ą Ą Ś Ą Ą ŚĆ Ą Ą Ś Ś ć ź ź Ń Ś Ą ć Ź Ą Ą Ś ć Ą Ą Ą Ś Ą ć Ą Ą ć Ą ć ć Ć Ź ć Ś Ź Ź ć Ź Ź ć Ź ź Ź Ś ź Ź ć ć Ń ź ć ć Ń Ć ź ć ć Ś ć ć ć Ź Ń ć Ź ć ć ź Ą Ś Ć Ź ź ź Ź ć ć Ś ź Ń ć ć ć ź Ą Ś Ń Ś ć ć Ź
Ś Ą Ś Ą Ś Ą Ą Ś Ą Ą ŚĆ Ą Ą Ś Ś ć ź ź Ń Ś Ą ć Ź Ą Ą Ś ć Ą Ą Ą Ś Ą ć Ą Ą ć Ą ć ć Ć Ź ć Ś Ź Ź ć Ź Ź ć Ź ź Ź Ś ź Ź ć ć Ń ź ć ć Ń Ć ź ć ć Ś ć ć ć Ź Ń ć Ź ć ć ź Ą Ś Ć Ź ź ź Ź ć ć Ś ź Ń ć ć ć ź Ą Ś Ń Ś ć ć Ź
Służą opisowi oraz przewidywaniu przyszłego kształtowania się zależności gospodarczych.
 MODEL EOOMERYCZY MODEL EOOMERYCZY DEFIICJA Modl konomtrczn jst równanm matmatcznm (lub układm równao), któr przdstawa zasadncz powązana loścow pomędz rozpatrwanm zjawskam konomcznm., uwzględnającm tlko
MODEL EOOMERYCZY MODEL EOOMERYCZY DEFIICJA Modl konomtrczn jst równanm matmatcznm (lub układm równao), któr przdstawa zasadncz powązana loścow pomędz rozpatrwanm zjawskam konomcznm., uwzględnającm tlko
k m b m Drgania tłumionet β ω0 k m Drgania mechaniczne tłumione i wymuszone Przypadki szczególne
 Wyład II Drgana chanczn łuon wyuzon równana ruchu w obcnośc łuna wyuzna oraz ch rozwązana logaryczny drn łuna rzonan chanczny jgo przyłady wzro apludy drgań wyuzonych wahadła przężon aarofy Drgana łuon
Wyład II Drgana chanczn łuon wyuzon równana ruchu w obcnośc łuna wyuzna oraz ch rozwązana logaryczny drn łuna rzonan chanczny jgo przyłady wzro apludy drgań wyuzonych wahadła przężon aarofy Drgana łuon
Macierze hamiltonianu kp
 Macere halonanu p acer H a, dla wranego, war 44 lu 88 jeśl were jao u n r uncje s>; X>, Y>, Z>, cl uncje ransorujące sę według repreenacj grp weora alowego Γ j. worące aę aej repreenacj - o ora najardej
Macere halonanu p acer H a, dla wranego, war 44 lu 88 jeśl were jao u n r uncje s>; X>, Y>, Z>, cl uncje ransorujące sę według repreenacj grp weora alowego Γ j. worące aę aej repreenacj - o ora najardej
Głównie występuje w ośrodkach gazowych i ciekłych.
 W/g ermodynamiki - ciepło jes jednym ze sposobów ransporu energii do/z bila, zysy przepływ ciepła może wysąpić jedynie w ciałach sałych pozosających w spoczynku. Proces wymiany ciepla: przejmowanie ciepła
W/g ermodynamiki - ciepło jes jednym ze sposobów ransporu energii do/z bila, zysy przepływ ciepła może wysąpić jedynie w ciałach sałych pozosających w spoczynku. Proces wymiany ciepla: przejmowanie ciepła
Wykład FIZYKA I. 2. Kinematyka punktu materialnego. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Obwody elektryczne. Stan ustalony i stan przejściowy. Stan ustalony i stan przejściowy. Stan ustalony i stan przejściowy.
 San salony san prjścoy Obody lkrycn San salony W obod prąd sałgo Warośc prądó napęć n lgają an W obod prąd nngo Warośc śrdn skcn prądó napęć n lgają an Prądy napęca są fnkcja okrsoy o akj saj cęsolośc,
San salony san prjścoy Obody lkrycn San salony W obod prąd sałgo Warośc prądó napęć n lgają an W obod prąd nngo Warośc śrdn skcn prądó napęć n lgają an Prądy napęca są fnkcja okrsoy o akj saj cęsolośc,
Schrödingera. Dr inż. Zbigniew Szklarski. Katedra Elektroniki, paw. C-1, pok
 Wykła 0: Rówae Schrögera Dr ż. Zbgew Szklarsk Kaera lekrok paw. C- pok.3 szkla@agh.eu.pl hp://layer.uc.agh.eu.pl/z.szklarsk/ 0.06.07 Wyzał Iforayk lekrok Telekoukacj - Teleforayka Rówae Schrögera jeo z
Wykła 0: Rówae Schrögera Dr ż. Zbgew Szklarsk Kaera lekrok paw. C- pok.3 szkla@agh.eu.pl hp://layer.uc.agh.eu.pl/z.szklarsk/ 0.06.07 Wyzał Iforayk lekrok Telekoukacj - Teleforayka Rówae Schrögera jeo z
Kier. MTR Programowanie w MATLABie Laboratorium
 Ker. MTR Programowane w MATLABe Laboraorum Ćw. Zasosowane bbloecznych funkcj MATLABa do numerycznego rozwązywana równań różnczkowych. Wprowadzene Układy równań różnczkowych zwyczajnych perwszego rzędu
Ker. MTR Programowane w MATLABe Laboraorum Ćw. Zasosowane bbloecznych funkcj MATLABa do numerycznego rozwązywana równań różnczkowych. Wprowadzene Układy równań różnczkowych zwyczajnych perwszego rzędu
Pobieranie próby. Rozkład χ 2
 Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
Szeregi trygonometryczne Fouriera. sin(
 Szrg rygoomryz Fourr / Szrg rygoomryz Fourr D js ukj: s os Pożj pod są włsoś ukj kór wykorzysmy w późjszym zs Ozzmy przz zę zspooą pos: Wówzs s os orz os s Fukję zpsujmy w pos: s s os os os u os W szzgóoś
Szrg rygoomryz Fourr / Szrg rygoomryz Fourr D js ukj: s os Pożj pod są włsoś ukj kór wykorzysmy w późjszym zs Ozzmy przz zę zspooą pos: Wówzs s os orz os s Fukję zpsujmy w pos: s s os os os u os W szzgóoś
Prąd sinusoidalny. najogólniejszy prąd sinusoidalny ma postać. gdzie: wartości i(t) zmieniają się w czasie sinusoidalnie
 Opracował: mgr nż. Marcn Weczorek www.marwe.ne.pl Prąd snsodalny najogólnejszy prąd snsodalny ma posać ( ) m sn(2π α) gdze: warość chwlowa, m warość maksymalna (amplda), T okres, α ką fazowy. T m α m T
Opracował: mgr nż. Marcn Weczorek www.marwe.ne.pl Prąd snsodalny najogólnejszy prąd snsodalny ma posać ( ) m sn(2π α) gdze: warość chwlowa, m warość maksymalna (amplda), T okres, α ką fazowy. T m α m T
ĆWICZENIE 11 OPTYMALIZACJA NIEZAWODNOŚCIOWA STRUKTURY ELEKTRONICZNEGO SYSTEMU BEZPIECZEŃSTWA
 ĆWICZENIE OPTYMALIZACJA NIEZAWODNOŚCIOWA STUKTUY ELEKTONICZNEGO SYSTEMU EZPIECZEŃSTWA Cl ćwicznia: zapoznani z analizą nizawodnościowo-ksploaacyjną lkronicznych sysmów bzpiczńswa; wyznaczni wybranych wskaźników
ĆWICZENIE OPTYMALIZACJA NIEZAWODNOŚCIOWA STUKTUY ELEKTONICZNEGO SYSTEMU EZPIECZEŃSTWA Cl ćwicznia: zapoznani z analizą nizawodnościowo-ksploaacyjną lkronicznych sysmów bzpiczńswa; wyznaczni wybranych wskaźników
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
Ekscytony Wanniera Motta
 ozpatrzmy oddziaływani lktronu o wktorz falowym bliskim minimum pasma przwodnictwa oraz dziury z obszaru blisko wirzcołka pasma walncyjngo. Zakładamy, ż oba pasma są sfryczni symtryczn, a ic kstrma znajdują
ozpatrzmy oddziaływani lktronu o wktorz falowym bliskim minimum pasma przwodnictwa oraz dziury z obszaru blisko wirzcołka pasma walncyjngo. Zakładamy, ż oba pasma są sfryczni symtryczn, a ic kstrma znajdują
Kinematyka W Y K Ł A D I. Ruch jednowymiarowy. 2-1 Przemieszczenie, prędkość. x = x 2 - x x t
 Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
ć ć ć ć Ń Ę Ś Ę Ę ć Ę ć Ń
 Ź Ź Ó Ń Ó ź ć Ź ć ć ć ć Ń Ę Ś Ę Ę ć Ę ć Ń Ź ć Ź Ę Ę ć ć ź Ę Ę Ź ć Ó Ó Ś Ó Ń ŚĆ Ę Ś Ó ćć Ó Ś Ę Ś Ę Ę Ś Ś ć Ę Ó Ę Ó Ę Ń Ć Ś Ś Ś Ś Ó ŚĆ Ó ć Ń Ń Ó Ę Ó Ó Ó Ś Ę Ć Ó ć ć Ó ź Ę ć ć Ź ć ć ć ć ć ź ć Ź ć Ć ć ć Ś
Ź Ź Ó Ń Ó ź ć Ź ć ć ć ć Ń Ę Ś Ę Ę ć Ę ć Ń Ź ć Ź Ę Ę ć ć ź Ę Ę Ź ć Ó Ó Ś Ó Ń ŚĆ Ę Ś Ó ćć Ó Ś Ę Ś Ę Ę Ś Ś ć Ę Ó Ę Ó Ę Ń Ć Ś Ś Ś Ś Ó ŚĆ Ó ć Ń Ń Ó Ę Ó Ó Ó Ś Ę Ć Ó ć ć Ó ź Ę ć ć Ź ć ć ć ć ć ź ć Ź ć Ć ć ć Ś
Pokazać, że wyżej zdefiniowana struktura algebraiczna jest przestrzenią wektorową nad ciałem
 Zestaw zadań : Przestrzene wektorowe. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar : C C C, (z, v) z v := z v jest przestrzeną lnową nad całem lczb zespolonych
Zestaw zadań : Przestrzene wektorowe. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar : C C C, (z, v) z v := z v jest przestrzeną lnową nad całem lczb zespolonych
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
1.7 Zagadnienia szczegółowe związane z równaniem ruchu Moment bezwładności i moment zamachowy
 .7 Zagadnna zczgółow zwązan z równan ruchu.7. ont bzwładnośc ont zaachowy Równan równowag ł dzałających na lnt ay d poazany na ry..8 będz ało potać: df a tąd lntarny ont dynaczny: d d ϑ d r * d d ϑ r d
.7 Zagadnna zczgółow zwązan z równan ruchu.7. ont bzwładnośc ont zaachowy Równan równowag ł dzałających na lnt ay d poazany na ry..8 będz ało potać: df a tąd lntarny ont dynaczny: d d ϑ d r * d d ϑ r d
MATEMATYKA POZIOM ROZSZERZONY Kryteria oceniania odpowiedzi. Arkusz A II. Strona 1 z 5
 MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
 Ś ź ć ź ć Ź ć ź ć Ą ć ć ć Ą ć ź ć ź ć Ś ć ć ć ć Ą Ą ć ć ć ć ć ć Ś ć Ź ć ć Ą ć ó ń ć ć ó ć ó ń ć ć ć ó ó ń ć ó Śń ó ó ć ó ó ó ó ć ó ń ó ó ó ó Ą ć ź ó ó ó ń ó ó ń ó ó ó ź ó ó ó ó Ść ć Ą ź ć ć ć ć Ś Ą ć ć
Ś ź ć ź ć Ź ć ź ć Ą ć ć ć Ą ć ź ć ź ć Ś ć ć ć ć Ą Ą ć ć ć ć ć ć Ś ć Ź ć ć Ą ć ó ń ć ć ó ć ó ń ć ć ć ó ó ń ć ó Śń ó ó ć ó ó ó ó ć ó ń ó ó ó ó Ą ć ź ó ó ó ń ó ó ń ó ó ó ź ó ó ó ó Ść ć Ą ź ć ć ć ć Ś Ą ć ć
dy dx stąd w przybliżeniu: y
 Przykłady do funkcj nelnowych funkcj Törnqusta Proszę sprawdzć uzasadnć, które z podanych zdań są prawdzwe, a które fałszywe: Przykład 1. Mesęczne wydatk na warzywa (y, w jednostkach penężnych, jp) w zależnośc
Przykłady do funkcj nelnowych funkcj Törnqusta Proszę sprawdzć uzasadnć, które z podanych zdań są prawdzwe, a które fałszywe: Przykład 1. Mesęczne wydatk na warzywa (y, w jednostkach penężnych, jp) w zależnośc
Energia w ruchu harmonicznym
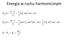 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Zasady dynamiki Newtona. Ilość ruchu, stan ruchu danego ciała opisuje pęd
 Zasady dynamiki Newtona Ilość ruchu, stan ruchu danego ciała opisuje pęd Siły - wektory Ilość ruchu, stan ruchu danego ciała opisuje pęd Zasady dynamiki Newtona I Każde ciało trwa w stanie spoczynku lub
Zasady dynamiki Newtona Ilość ruchu, stan ruchu danego ciała opisuje pęd Siły - wektory Ilość ruchu, stan ruchu danego ciała opisuje pęd Zasady dynamiki Newtona I Każde ciało trwa w stanie spoczynku lub
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
METODA ELEMENTU SKOŃCZONEGO. Termokinetyka
 METODA ELEMENTU SKOŃCZONEGO Termoknetyka Matematyczny ops ruchu cepła (1) Zasada zachowana energ W a Cepło akumulowane, [J] P we Moc wejścowa, [W] P wy Moc wyjścowa, [W] t przedzał czasu, [s] V q S(V)
METODA ELEMENTU SKOŃCZONEGO Termoknetyka Matematyczny ops ruchu cepła (1) Zasada zachowana energ W a Cepło akumulowane, [J] P we Moc wejścowa, [W] P wy Moc wyjścowa, [W] t przedzał czasu, [s] V q S(V)
I. Metoda Klasyczna. Podstawy Elektrotechniki - Stany nieustalone. Zadanie k.1 Wyznaczyć prąd i w na wyłączniku. R RI E
 Podsawy lkohnk - Sany nsalon. Moda Klasyzna Zadan k. Wyznazyć pąd w na wyłąznk. w? kładay ównana na podsaw sha. ównan haakysyzn: w d d w w d d d d d d p p p w Zadan k. Znalźć aką hwlę zas x aby spłnony
Podsawy lkohnk - Sany nsalon. Moda Klasyzna Zadan k. Wyznazyć pąd w na wyłąznk. w? kładay ównana na podsaw sha. ównan haakysyzn: w d d w w d d d d d d p p p w Zadan k. Znalźć aką hwlę zas x aby spłnony
Przyjmijmy, że moment obciążenia jest równy zeru, otrzymamy:
 aszyy prąy sałgo yaka Dla aszyy prą sałgo, ykorzysyaj jako l aoayk, yzaczy ybra rasacj. Sygał jścoy oż być p. apęc orka (la aszyy obcozbj) a sygał yjścoy prękość obrooa. óa Krchhoffa la obo orka oży apsać
aszyy prąy sałgo yaka Dla aszyy prą sałgo, ykorzysyaj jako l aoayk, yzaczy ybra rasacj. Sygał jścoy oż być p. apęc orka (la aszyy obcozbj) a sygał yjścoy prękość obrooa. óa Krchhoffa la obo orka oży apsać
Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE
 Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
ĆWICZENIE 7 WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA. Wprowadzenie
 ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
Całka nieoznaczona Andrzej Musielak Str 1. Całka nieoznaczona
 Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Dyskretny proces Markowa
 Procesy sochasyczne WYKŁAD 4 Dyskreny roces Markowa Rozarujemy roces sochasyczny X, w kórym aramer jes ciągły zwykle. Będziemy zakładać, że zbiór sanów jes co najwyżej rzeliczalny. Proces X, jes rocesem
Procesy sochasyczne WYKŁAD 4 Dyskreny roces Markowa Rozarujemy roces sochasyczny X, w kórym aramer jes ciągły zwykle. Będziemy zakładać, że zbiór sanów jes co najwyżej rzeliczalny. Proces X, jes rocesem
1 n 0,1, exp n
 8. Właścwośc trmczn cał stałych W trakc zajęć będzmy omawać podstawow własnośc trmczn cał stałych, a szczgóln skupmy sę na cpl właścwym. Klasyczna dfncja cpła właścwgo wygląda następująco: C w Q (8.) m
8. Właścwośc trmczn cał stałych W trakc zajęć będzmy omawać podstawow własnośc trmczn cał stałych, a szczgóln skupmy sę na cpl właścwym. Klasyczna dfncja cpła właścwgo wygląda następująco: C w Q (8.) m
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
VI. MATEMATYCZNE PODSTAWY MES
 Kurs na Studac Dotorancc Poltcn Wrocławsj (wrsja: luty 007) 40 I. MATEMATYCZE PODSTAWY MES. Problm abstracyjny Rozwązujmy problm lptyczny np. przstrznn zagadnn tor sprężystośc. Poszuujmy rozwązana u( nmatyczn
Kurs na Studac Dotorancc Poltcn Wrocławsj (wrsja: luty 007) 40 I. MATEMATYCZE PODSTAWY MES. Problm abstracyjny Rozwązujmy problm lptyczny np. przstrznn zagadnn tor sprężystośc. Poszuujmy rozwązana u( nmatyczn
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap szkolny 5 listopada 2013 Czas 90 minut
 Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
Kwantowa natura promieniowania elektromagnetycznego
 Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
IV. WPROWADZENIE DO MES
 Kondra P. Moda mnów Sończonych ora zasosowana 7 IV. WPROWADZNI DO MS Poszuwan rozwązań rzybżonych bazuących na modach rsduanych waracynych naoya na rudnośc w doborz func bazowych orśonych na całym obszarz.
Kondra P. Moda mnów Sończonych ora zasosowana 7 IV. WPROWADZNI DO MS Poszuwan rozwązań rzybżonych bazuących na modach rsduanych waracynych naoya na rudnośc w doborz func bazowych orśonych na całym obszarz.
Metody symulacji w nanostrukturach (III - IS)
 Metody symulacj w nanostrukturach (III - IS) W. Jaskólsk - modelowane nanostruktur węglowych Cz.I wprowadzene do mechank kwantowej Nektóre przyczyny konecznośc pojawena sę kwantowej teor fzycznej (fzyka
Metody symulacj w nanostrukturach (III - IS) W. Jaskólsk - modelowane nanostruktur węglowych Cz.I wprowadzene do mechank kwantowej Nektóre przyczyny konecznośc pojawena sę kwantowej teor fzycznej (fzyka
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ MECHANICZNY TECHNOLOGICZNY Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ MECHANICZNY TECHNOLOGICZNY Katdra Wytrzymałośc Matrałów Mtod Komutrowych Mchank Rozrawa doktorska Tytuł: Analza wrażlwośc otymalzacja wolucyjna układów mchancznych
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ MECHANICZNY TECHNOLOGICZNY Katdra Wytrzymałośc Matrałów Mtod Komutrowych Mchank Rozrawa doktorska Tytuł: Analza wrażlwośc otymalzacja wolucyjna układów mchancznych
 Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż
Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż
 Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż
Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż
 Ł Ł Ś ź ń ź ź ź Ś Ł Ę Ę Ś ż Ś ń Ą Ś Ą Ł ż ż ń ż ć ż ż ż ź ż ć ź Ę Ę ń ć ż Ł ń ż ż ż Ś ż Ś ż ż ż ż ż ż ż ń ń ż ż ż ć ż ń ż ń ź ż ć ż ż ć ń ż Ę Ę ć ń Ę ż ż ń ń ź Ę ź ż ń ż ń ź ż ż ż ń ż ż ż ż ż ż ż ż ń ń
Ł Ł Ś ź ń ź ź ź Ś Ł Ę Ę Ś ż Ś ń Ą Ś Ą Ł ż ż ń ż ć ż ż ż ź ż ć ź Ę Ę ń ć ż Ł ń ż ż ż Ś ż Ś ż ż ż ż ż ż ż ń ń ż ż ż ć ż ń ż ń ź ż ć ż ż ć ń ż Ę Ę ć ń Ę ż ż ń ń ź Ę ź ż ń ż ń ź ż ż ż ń ż ż ż ż ż ż ż ż ń ń
 Ł Ł Ś Ę ź ń ź ź Ś Ę Ę Ś Ą Ś Ę Ż Ł ń Ę Ś ć ć ń ć ń ń ń ź ń Ę ź ń ń ń ź ź Ś ź ź ć ń ń ń ń Ś ć Ś ń ń Ś ź ń Ę ń Ś ź ź ź ź ź Ę Ę Ę Ś ń Ś ć ń ń ń ń ń ń Ę ń ń ń ń ć ń ń ń ń ć ń Ś ć Ł ń ń ń ć ń ć ź ń ź ć ń ń ć
Ł Ł Ś Ę ź ń ź ź Ś Ę Ę Ś Ą Ś Ę Ż Ł ń Ę Ś ć ć ń ć ń ń ń ź ń Ę ź ń ń ń ź ź Ś ź ź ć ń ń ń ń Ś ć Ś ń ń Ś ź ń Ę ń Ś ź ź ź ź ź Ę Ę Ę Ś ń Ś ć ń ń ń ń ń ń Ę ń ń ń ń ć ń ń ń ń ć ń Ś ć Ł ń ń ń ć ń ć ź ń ź ć ń ń ć
Ń Ą Ń Ń Ń
 ŁĄ Ń Ł ć ć ć Ę Ę Ą Ą Ę Ń Ą Ń Ń Ń Ń ć Ą Ź ć Ź ć Ź ć ź ź Ł Ą Ę ć ć Ę Ć Ć Ą ć Ć Ć Ł Ć Ź Ć Ą Ą Ą Ą ĄĄ Ć Ą Ą Ą ć Ć Ł Ć Ę Ć Ć Ę Ę Ć Ć Ę Ą Ć Ć Ń Ń Ć Ę Ć Ł Ć Ł Ą Ę Ź Ć Ł Ę Ł Ł Ł Ę Ę Ł Ę Ł Ć Ć Ą Ę Ł Ą Ć Ą Ź Ą Ę
ŁĄ Ń Ł ć ć ć Ę Ę Ą Ą Ę Ń Ą Ń Ń Ń Ń ć Ą Ź ć Ź ć Ź ć ź ź Ł Ą Ę ć ć Ę Ć Ć Ą ć Ć Ć Ł Ć Ź Ć Ą Ą Ą Ą ĄĄ Ć Ą Ą Ą ć Ć Ł Ć Ę Ć Ć Ę Ę Ć Ć Ę Ą Ć Ć Ń Ń Ć Ę Ć Ł Ć Ł Ą Ę Ź Ć Ł Ę Ł Ł Ł Ę Ę Ł Ę Ł Ć Ć Ą Ę Ł Ą Ć Ą Ź Ą Ę
Podstawowe definicje
 W-8 (Jarswc na ba J. Rukwsk) 5 slajów Ruch rgający Psaww fncj Swbn rgana harmncn Drgana łumn Drgana wymusn Skłaan rgań 3/8 L.R. Jarswc Psaww fncj rgana prcsy, w kórych ana wlkść fycna na prman rśn malj
W-8 (Jarswc na ba J. Rukwsk) 5 slajów Ruch rgający Psaww fncj Swbn rgana harmncn Drgana łumn Drgana wymusn Skłaan rgań 3/8 L.R. Jarswc Psaww fncj rgana prcsy, w kórych ana wlkść fycna na prman rśn malj
Hipotezy o istotności oszacowao parametrów zmiennych objaśniających ˆ ) ˆ
 WERYFIKACJA HIPOTEZY O ISTOTNOŚCI OCEN PARAMETRÓW STRUKTURALNYCH MODELU Hpoezy o sonośc oszacowao paramerów zmennych objaśnających Tesowane sonośc paramerów zmennych objaśnających sprowadza sę do nasępującego
WERYFIKACJA HIPOTEZY O ISTOTNOŚCI OCEN PARAMETRÓW STRUKTURALNYCH MODELU Hpoezy o sonośc oszacowao paramerów zmennych objaśnających Tesowane sonośc paramerów zmennych objaśnających sprowadza sę do nasępującego
Zestaw zadań 4: Przestrzenie wektorowe i podprzestrzenie. Liniowa niezależność. Sumy i sumy proste podprzestrzeni.
 Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
Zasady dynamiki Newtona. Ilość ruchu, stan ruchu danego ciała opisuje pęd
 Zasady dynamiki Newtona Ilość ruchu, stan ruchu danego ciała opisuje pęd Zasady dynamiki Newtona I Każde ciało trwa w stanie spoczynku lub porusza się ruchem prostoliniowym i jednostajnym, jeśli siły przyłożone
Zasady dynamiki Newtona Ilość ruchu, stan ruchu danego ciała opisuje pęd Zasady dynamiki Newtona I Każde ciało trwa w stanie spoczynku lub porusza się ruchem prostoliniowym i jednostajnym, jeśli siły przyłożone
Fizyka promieniowania jonizującego. Zygmunt Szefliński
 Fizyka prominiowania jonizującgo ygmunt Szfliński 1 Wykład 10 Rozpady Rozpady - warunki nrgtyczn Ściżka stabilności Nad ściżką znajdują się jądra prominiotwórcz, ulgając rozpadowi -, zaś pod nią - jądra
Fizyka prominiowania jonizującgo ygmunt Szfliński 1 Wykład 10 Rozpady Rozpady - warunki nrgtyczn Ściżka stabilności Nad ściżką znajdują się jądra prominiotwórcz, ulgając rozpadowi -, zaś pod nią - jądra
Cechy szeregów czasowych
 energecznch Cech szeregów czasowch Rozdział Modelowanie szeregów czasowch 7 proces deerminisczn proces kórego warość może bć preczjnie określona w dowolnm czasie =T+τ = a +b T T+τ czas = sin(ω) T T+τ czas
energecznch Cech szeregów czasowch Rozdział Modelowanie szeregów czasowch 7 proces deerminisczn proces kórego warość może bć preczjnie określona w dowolnm czasie =T+τ = a +b T T+τ czas = sin(ω) T T+τ czas
W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące
 Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
gdzie M to mówimy, że na tym obszarze jest określone pole skalarne u( M) u( r)
 Wykłady z Maemayki sosowanej w inżynierii środowiska, II sem. Wykład. CAŁKA KRZYWOINIOWA ZORIENTOWANA.. Definicje i własności całek krzywoliniowych zorienowanych... Nekóre zasosowania całek krzywoliniowych
Wykłady z Maemayki sosowanej w inżynierii środowiska, II sem. Wykład. CAŁKA KRZYWOINIOWA ZORIENTOWANA.. Definicje i własności całek krzywoliniowych zorienowanych... Nekóre zasosowania całek krzywoliniowych
Wykład 4 Metoda Klasyczna część III
 Teoria Obwodów Wykład 4 Meoda Klasyczna część III Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska D-, 5/8 el: (7) 3 6 fax: (7)
Teoria Obwodów Wykład 4 Meoda Klasyczna część III Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska D-, 5/8 el: (7) 3 6 fax: (7)
Równanie Schrödingera
 Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
 ń ń ź ź ć ń ń Ą Ź ń Ą ĄĄ Ą ń ź Ł Ł ń ć Ó Ą Ą ń ń ć ń ć ź ć ć Ó ć Ó ć Ś ć Ó ń ć ć ć ź ć Ą Ó Ź Ź Ź Ą ź Ó Ą ń ń Ź Ó Ź Ń ć Ń ć ź ń ń ń ń ń ń Ń ń Ź ń Ź Ź Ź ń ń ń Ą Ź Ó ĄĄ ń Ą ń ń Ó Ń Ó Ó ń Ą Ó ź ń ź Ą Ó Ą ź
ń ń ź ź ć ń ń Ą Ź ń Ą ĄĄ Ą ń ź Ł Ł ń ć Ó Ą Ą ń ń ć ń ć ź ć ć Ó ć Ó ć Ś ć Ó ń ć ć ć ź ć Ą Ó Ź Ź Ź Ą ź Ó Ą ń ń Ź Ó Ź Ń ć Ń ć ź ń ń ń ń ń ń Ń ń Ź ń Ź Ź Ź ń ń ń Ą Ź Ó ĄĄ ń Ą ń ń Ó Ń Ó Ó ń Ą Ó ź ń ź Ą Ó Ą ź
 Ę Ę Ę Ó Ę Ę Ó Ź ć Ł Ś Ó Ó Ł Ł Ż ć ć Ż Ą Ż ć Ę Ę ź ć ź Ą Ę Ż ć Ł Ę ć Ż Ę Ę ć ć Ż Ż Ę Ż Ż ć Ó Ę Ę ć Ę ć Ę Ę Ż Ż Ż Ż ź Ż Ę Ę ź Ę ź Ę Ż ć ć Ą Ę Ę ć Ę ć ć Ź Ą Ę ć Ę Ą Ę Ę Ę ć ć ć ć Ć Ą Ą ć Ę ć Ż ć Ę ć ć ć Ą
Ę Ę Ę Ó Ę Ę Ó Ź ć Ł Ś Ó Ó Ł Ł Ż ć ć Ż Ą Ż ć Ę Ę ź ć ź Ą Ę Ż ć Ł Ę ć Ż Ę Ę ć ć Ż Ż Ę Ż Ż ć Ó Ę Ę ć Ę ć Ę Ę Ż Ż Ż Ż ź Ż Ę Ę ź Ę ź Ę Ż ć ć Ą Ę Ę ć Ę ć ć Ź Ą Ę ć Ę Ą Ę Ę Ę ć ć ć ć Ć Ą Ą ć Ę ć Ż ć Ę ć ć ć Ą
 ż ż ć ż Ż ż ż ć Ł ń ń ź ć ń Ś ż Ł ć ż Ź ż ń ż Ż Ś ć ź ż ć Ś ń ń ź ż ź ń Ś ń Ś ż ń ń ż ć ż ż Ą ć ń ń ń ć ż ć Ś ż Ć ć ż Ś Ś ć Ż ż Ś ć Ż Ż Ż Ą ń ń ć ń Ż ć ń ż Ż ń ż Ś ń Ś Ś ć Ż Ż Ć Ó Ż Ść ż Ż ż ż ń Ż Ż ć
ż ż ć ż Ż ż ż ć Ł ń ń ź ć ń Ś ż Ł ć ż Ź ż ń ż Ż Ś ć ź ż ć Ś ń ń ź ż ź ń Ś ń Ś ż ń ń ż ć ż ż Ą ć ń ń ń ć ż ć Ś ż Ć ć ż Ś Ś ć Ż ż Ś ć Ż Ż Ż Ą ń ń ć ń Ż ć ń ż Ż ń ż Ś ń Ś Ś ć Ż Ż Ć Ó Ż Ść ż Ż ż ż ń Ż Ż ć
 Ą Ą Ś Ż Ą ć Ź ć Ó Ś Ż Ź Ó ć Ś Ż ć Ś Ź Ó ć Ż Ż Ź Ż Ó Ź Ó Ż Ż Ż Ż Ż Ś Ź Ś ć ć ć Ź ć ć Ó Ó Ó Ś Ą ć ć Ź Ż Ż Ż Ż ź Ż ź Ó Ś Ą Ź Ż Ż ć Ź Ó Ż Ó Ś Ą Ś Ś Ź Ż Ś Ż Ż Ź Ó ć Ś Ś Ść Ś Ż Ź Ó Ś Ó Ź Ó Ż Ź Ó Ś Ś Ż Ź Ż Ś
Ą Ą Ś Ż Ą ć Ź ć Ó Ś Ż Ź Ó ć Ś Ż ć Ś Ź Ó ć Ż Ż Ź Ż Ó Ź Ó Ż Ż Ż Ż Ż Ś Ź Ś ć ć ć Ź ć ć Ó Ó Ó Ś Ą ć ć Ź Ż Ż Ż Ż ź Ż ź Ó Ś Ą Ź Ż Ż ć Ź Ó Ż Ó Ś Ą Ś Ś Ź Ż Ś Ż Ż Ź Ó ć Ś Ś Ść Ś Ż Ź Ó Ś Ó Ź Ó Ż Ź Ó Ś Ś Ż Ź Ż Ś














