{ } Podstawy opisu rozpraszania 11/27/ /27/2009. I total = I 1 + I I n

Transmisja i odbicie fali na granicy dwóch ośrodków dielektrycznych

Tasmsja odbce fal a gac dwóch ośodków delekcch Now poblem oważaa eegece w óżch ośodkach Dochcas sosowae pojęce eswośc bło wsacające do poówwaa śedego pepłwu moc pomeowaa w m samm ośodku Objawoe fak Moża

Polaryzacja i ośrodki dwójłomne. Częśd I

Polaracja ośrodk dwójłom Cęśd Wkorow ops fal lkromagcj r, H r, D r, B r, -wkor aęża pola lkrcgo -wkor aęża pola magcgo -wkor dukcj dlkrcj -wkor dukcj magcj Wkor, kórch współręd alżą od położa casu, powąa

Transmisja i odbicie fali na granicy dwóch ośrodków dielektrycznych

Tasmisja i odbicie fali a gaic dwóch ośodków dielekczch Now poblem ozważaia eegecze w óżch ośodkach Dochczas sosowae pojęcie ieswości bło wsaczające do poówwaia śediego pzepłwu moc pomieiowaia w m samm

= r. Będziemy szukać takiego rozkładu, który jest najbardziej prawdopodobny, tzn. P=P max. Możemy napisać:

Rokład Boltmaa Roważm odosobo układ cąstek (cost Ucost Załóżm że cąstk układu mogą meć tlko ścśle okeśloe eege (eega cąstek est skwatowaa ech ( oaca lcbę cąstek maącch eegę Możem wted apsać: (* U cost

Falą nazywamy każde rozprzestrzeniające się zaburzenie (odkształcenie) w przestrzeni.

Ruch falow Falą nawam każde opesenające sę abuene (odksałcene) w pesen. Fale mechancne mogą opesenać sę w ośodkach cągłch jak woda powee meal dewno lub eż ośodkach dskench jak układ spężonch osclaoów (np.

DYNAMIKA. Dynamika jest działem mechaniki zajmującym się badaniem ruchu ciał z uwzględnieniem sił działających na ciało i wywołujących ten ruch.

DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża

Novosibirsk, Russia, September 2002

Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego

24-01-0124-01-01 G:\AA_Wyklad 2000\FIN\DOC\Geom20.doc. Drgania i fale III rok Fizyki BC

4-0-04-0-0 G:\AA_Wyklad 000\FIN\DOC\Geom0.doc Dgaa ale III ok Fzyk BC OPTYKA GEOMETRYCZNA. W ośodku jedoodym śwatło ozcodz sę ostolowo.. Pzecające sę omee śwetle e zabuzają sę awzajem. 3. Pawo odbca śwatła.

Optyka falowa. polaryzacja. dwójłomność optyczna. czym jest zjawisko polaryzacji stan a stopień polaryzacji sposoby polaryzacji

W-21 (Jaoszewicz) 16 slajdów Na podsawie pezenacji pof. J. Rukowskiego Opyka falowa polayzacja czym jes zjawisko polayzacji san a sopień polayzacji sposoby polayzacji dwójłomność opyczna pzyczyny mikoskopowe

elektrostatyka ver

elektostatka ve-8.6.7 ładunek ładunek elementan asada achowana ładunku sła (centalna, achowawca) e.6 9 C stała absolutna pawo Coulomba: F ~ dwa ładunk punktowe w póżn: F 4πε ε 8.8585 e F m ε stała ł elektcna

podsumowanie (E) E l Eds 0 V jds

e-8.6.7 fale podsumowanie () Γ dl 1 ds ρ d S ε V D ds ρ d S ( ϕ ) 1 ρ ε D ρ D ρ V D ( D εε ) εε S jds V ρ d t j ρ t j σ podsumowanie (H) Bdl Γ μ S jds B μ j S Bds B ( B A) Hdl Γ S jds H j ( B μμ H ) ε

A B - zawieranie słabe

NAZEWNICTWO: : rówoważość defcj : rówość defcj dla każdego steje! ZBIORY steje dokłade jede {,,,...} - całkowte * - całkowte be era - wmere - ujeme plus ero - recwste - espoloe A B - awerae słabe A :

Całka krzywoliniowa nieskierowana (całka krzywoliniowa funkcji skalarnej)

WYŁAD : CAŁI RZYWOLINIOWE Nech - krwa w R : gde [ α β ] ora C [ α β]. Zaem dowol puk krwej moża predsawć w posac j k krwa adaa jes pre wekor parameracj r : r j k. Decja Jeśl krwa e ma puków welokroch.

Dynamika bryły sztywnej

W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o. oet bewładośc Dyaka cała tywego uch łożoy cała tywego 3/4 L.. Jaoewc j j j j j

14. Zasady zachowania dla punktu i układu punktów materialnych: pędu, krętu, energii, zasada d Alemberta.

4. Zasad achowaa da puktu układu puktów ateach: pędu, kętu, eeg, asada d ebeta. υ p = pęd (ość uchu puktu ateaego υ F d ( υ = F pochoda wgęde casu pędu ówa jest se dałającej a da pukt v v t2 ( υ2 υ = t

G:\WYKLAD IIIBC 2001\FIN2001\Ruch falowy2001.doc. Drgania i fale II rok Fizyki BC

3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Ruh falow: Fala rohodąe się w presreni aburenie lub odsałenie (pole). - impuls lub drgania. Jeśli rohodi się prędośią o po asie : ( r)

falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi

Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich

Opis ruchu we współrzędnych prostokątnych (kartezjańskich)

Opis ruchu we współrędch prosokąch (karejańskich) Opis ruchu we współrędch prosokąch jes podob do opisu a pomocą wekora wodącego, kórego pocąek leż w pocąku układu odiesieia. Położeie. Położeie puku A

cz. 2. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321

Wkład 7: Bła stwna c.. D nż. Zbgnew Sklask Kateda Elektonk, paw. C-1, pok.1 skla@agh.edu.pl http://lae.uc.agh.edu.pl/z.sklask/..17 Wdał nfoatk, Elektonk Telekounkacj - Telenfoatka 1 6..17 Wdał nfoatk,

ψ przedstawia zależność

Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi

[ ] D r ( ) ( ) ( ) POLE ELEKTRYCZNE

LKTYCZNOŚĆ Pole elektcne Lne sł pola elektcnego Pawo Gaussa Dpol elektcn Pole elektcne w delektkach Pawo Gaussa w delektkach Polaacja elektcna Potencjał pola elektcnego Bewowość pola elektcnego óŝnckowa

Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 5, Radosław Chrapkiewicz, Filip Ozimek

Podstaw Fizki IV Optka z elementami fizki współczesnej wkład 5, 27.02.2012 wkład: pokaz: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wkład 4 - przpomnienie dielektrki

Fale elektromagnetyczne. Obrazy.

Fale elektroagnetyczne. Obrazy. Wykład 7 1 Wrocław University of Technology 28-4-212 Tęcza Maxwella 2 1 Tęcza Maxwella 3 ( kx t) ( kx t) E = E sin ω = sin ω Prędkość rozchodzenia się fali: 1 8 c = = 3.

r r r m dt d r r r r 2 dt r m dt dt

Twedee o wale: Roważm cąstę P o mase m a tóą dała sła : W ecalm ułade odesea: dv m / dv m ( Moża auważć że: d d dv dv m ( v m v m mv m dv d m m ( v mv gde v est modułem pędośc Podstawaąc to do ówaa ( mam:

SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA

Z a m a w i a j» c y G D Y S K I O R O D E K S P O R T U I R E K R E A C J I J E D N O S T K A B U D E T O W A 8 1 5 3 8 G d y n i a, u l O l i m p i j s k a 5k 9 Z n a k s p r a w y G O S I R D Z P I

Wyznaczanie reakcji dynamicznych oraz wyważanie ciała w ruchu obrotowym wokół stałej osi 8

Wnacanie reakcji dnaicnch ora wważanie ciała w ruchu oroow wokół sałej osi 8 Wprowadenie Jeśli dowolne ciało swne o asie jes w ruchu oroow wokół osi, o na podporach powsają reakcje A i B. Składowe ch reakcji

Fale biegnące. y t=0 vt. y = f(x), t = 0 y = f(x - vt), t ogólne równanie fali biegnącej w prawo

ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne

latarnia morska wę d elbląg malbork an o el a z o i s olsztyn zamek krzyżacki w malborku Wisła płock żelazowa wola ęży z a me k ól.

T ę Ł ó 499 ż Y ę ą T T ą ść ż B ę ó ąż ę ąż żą ó ę ż ę ś Ś SZ ź ź S żó ż śó ś ść E ó E ń ó ó ó E ó ś ż ó Ł Gó ę ó SZ ś ż ę ę T 6 5 ó ż 6 5 : 685 75 ą ę 8 Ó ńó ę: : U 5 ó ż ó 5 Śą Gó 4 ść ę U żę ż ć Z

Fale elektromagnetyczne spektrum

Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego

FUNKCJE DWÓCH ZMIENNYCH

FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam

Ruch falowy, ośrodek sprężysty

W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę

Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów

Z n a k s p r a w y G C S D Z P I 2 7 1 07 2 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U s ł u g i s p r z» t a n i a o b i e k t Gó w d y s k i e g o C e n

W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące

Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i

Grupa obrotów. - grupa symetrii kuli, R - wszystkie możliwe obroty o dowolne kąty wokół osi przechodzących przez środek kuli

Grupa obrotów - grupa smetr kul R - wsstke możlwe obrot o dowolne kąt wokół os prechodącch pre środek kul nacej O 3 grupa obrotów właścwch - grupa cągła - każd obrót określa sę pre podane os l kąta obrotu

Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku.

Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,

Fotonika. Plan: Wykład 9: Interferencja w układach warstwowych

Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie

Zjawisko interferencji fal

Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich

ρ - gęstość ładunku j - gęstość prądu FALE ELEKTROMAGNETYCZNE W PRÓŻNI: Równania Maxwella: -przenikalność elektryczna próżni=8,8542x10-12 F/m

-- G:\AA_Wklad \FIN\DOC\em.do Drgania i fale III rok Fiki C FAL LKTROMAGNTYCZN W PRÓŻNI: Równania Mawella: di ρ ε ρ di j ρ - gęsość ładunku j - gęsość prądu ro di ro j ε ε -prenikalność elekrna próżni8854

Spójne przestrzenie metryczne

lz Włd 5 d d Ćel cel@gedpl Spóe pzeszee ecze De Pzeszeń eczą ρ zw spóą eżel e d sę e pzedswć w psc s dwóc zów epsc wc złączc ρ - pzeszeń spó ~ we Icze es ze spó eżel dl dwlc pów czl see cągł c γ : : γ

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 5 32 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f W y k o n a n i e p r z e g l» d ó w k o n s e r w a c y j n o -

Ą Ś Ś ż Ż ć Ś Ż Ś Ń Ó Ż ć Ź ć ć Ż Ź Ś Ą Ą Ż Ś Ą ĘĄ Ś Ę ŚĘ Ę Ó Ś Ą ć Ś ź Ś ż Ż Ź ć ć ć Ą ć ć Ź ć ć ć ć Ś ć Ż ć ć Ą ć Ż ć Ż ć Ż Ż Ż ć Ż ć Ż ć Ż ż ź Ą ż ć Ż Ź Ż Ś Ż Ś Ą ż Ą Ż ź Ż ż ć Ż Ż Ą Ś Ź ć Ś ż Ź ż Ł

Ruch drgający i fale

Ruch dgający i fale Dgania Dgania są uchem w kóym układ wykonuje dgania wokół pewnego położenia (odpowiadającego najczęściej położeniu ównowagi) Ruch dgający jes uchem okesowym. Układ znajduje się w ym

q (s, z) = ( ) (λ T) ρc = q

M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X W Y Z N A C Z A N I E O D K S Z T A C E T O W A R Z Y S Z Ą C Y C H H A R T O W A N I U P O W I E R Z C H N I O W Y M W I E

Spójne przestrzenie metryczne

Spóe pzeszee ecze De. Pzeszeń eczą zw spóą eżel e d sę e pzedswć w posc s dwóc zoów epsc owc ozłączc. - pzeszeń spó ~ owe Icze es zoe spó eżel dl dowolc pów czl see cągł c : : = = see dog łącząc Tw. ągł

Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017

Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne

Ł Ł ÓŁ Ń óń Ł Ę Ę ó ą ść ó ń ś ą ą Ę Ęą ó ś ś ś ąś ą ą ą Ł Ł ą ą Ę ą ó ą ść ó ś Ę ą óź ś ń Ś Ę ą ą ść ó ń ś ą ó ś ą Ł Ęś Ń Ę ó ą ść ó Ń ś ą ź ś ść Ś ą Ą ń Ł ĘŚ ĘĄ ą ś ó ś ą ą ą ó ś ść ś ó ą ą Ą ź ó ą ść

Analiza Matematyczna Ćwiczenia. J. de Lucas

Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y

W siła działająca na bryłę zredukowana do środka masy ( = 0

Popęd i popęd bryły Bryła w ruchu posępowym. Zasada pędu i popędu ma posać: p p S gdie: p m v pęd bryły w ruchu posępowym S c W d popęd siły diałającej na bryłę w ruchu posępowym aś: v c prędkość środka

METODY KOMPUTEROWE 1

MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc

Uwaga z alkoholem. Picie na świeżym powietrzu jest zabronione, poza licencjonowanymi ogródkami, a mandat można dostać nawet za niewinne piwko.

B : U U F F U 01 Ę ś ę 3 ż łć ę ę ź ł, Ż 64 ó ł ł óżó, j, j U 02 Ą ś U ł 1925, 1973 łś ą ż ęą fć j j ą j ł 9 ( ) ó 15 F 03 j ąó j j, ę j ż 15 ł, ó f Bść ł łj ł, 1223 j 15 B Ą ć ę j- j ść, j ż ą, ż, ją

Energia w ruchu harmonicznym

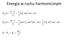Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:

WOJEWÓDZKI IN S P EKT OR A T OC H R ON Y ŚR ODOWIS KA W KR A KOWIE M 2 0 0 2 U RAPORT O STANIE ŚRODOWISK A W WOJ EWÓ DZ TWIE AŁ OPOL SK IM W ROK BIBLIOTEKA MON ITOR IN G U ŚR OD OW IS KA K r a k ó w 2003

23. CAŁKA POWIERZCHNIOWA NIEZORIENTOWANA

. CAŁKA POWIERZCHNIOWA NIEZORIENTOWANA Płat powiechniow o ównaniach paametcnch: ( ) ( ) ( ) () gdie oba jet obaem eglanm nawam płatem gładkim (płatem eglanm) gd w każdm pnkcie tego płata itnieje płacna

Ś ś Ł ń ń ś ś Ś ś Ę ę ś ę ś ĘŚ ś Ęś ę ĘŚĆ ĘŚ Ęś ĘŚ ĘŚ ę ĘŚĆ ĘŚĆ ĘŚĆ ĘŚĆ Ęś ĘŚĆ ĘŚ ĘŚĆ ń ĘŚĆ ĘŚ ĘŚĆ ę ĘŚ ś Ęś ń ś ś ś ę ź ę ś ę ś Ź ń ę ń ś ń ń ę ń ń ń ń Ę ś ń ęś ń ń ń ę ń Ż ś ń ń ę ń ś ń ń ń ę ś ń ś Ż

ć

n n Weźmy f: 3 (x 1, x 2, x 3 ) (y 1, y 2, y 3 ) 3 Jeżeli zdefiniujemy funkcje pomocnicze f j : 3 (x 1, x 2, x 3 ) y j, dla j = 1,2,3, to

"Maemac ą jak Facuzi: cokolwiek im ię powie od azu pzekładają o a wój wła jęzk i wówcza aje ię o czmś zupełie im." Joha Wola Goehe Weźm : Jeżeli zdeiiujem ukcje pomocicze j : j dla j = o = dzie = Czli

Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 18, Radosław Chrapkiewicz, Filip Ozimek

Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie

Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów

Z n a k s p r a w y G C S D Z P I 2 7 1 0 33 2 0 1 7 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U s ł u g i s p r z» t a n i a o b i e k t ó w G d y s k i e g o C e

PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH

PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa

Ś Ą ć ć ć ń ę ę ń ę ę ń ę Ęć Ź Ó ń ę ń ę ę ę ę ę ć Ź ń ć ń Ń ńć ń ń Ś ć Ń Ść ń Ść ę Ść Ź ń Ś ć ń ć ń Ó ć Ź ń ę Ó ć ę ę ń ę ć ę ę Ó ń Ż ę ć ę ę ę Ś ć ę ę Ś Ę ę ń ń ń ę Ó Ć Ę Ć ć ę ć ć ę Ó ć ę Ó Ń ć ę Ś

Elektrodynamika. Część 8. Fale elektromagnetyczne. Ryszard Tanaś. Zakład Optyki Nieliniowej, UAM

Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................

Zjawisko interferencji fal

Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natężenia fal) w którym zachodzi stabilne w czasie ich

Ę ż Ł ś ą ł ść ó ą ż ę ł Ł ś ą ś Ż ż ż ń ż ł ś ń ż żę Ł ż ó ń ę ż ł ńó ó ł ń ą ż ę ż ą ą ż Ń ż ż ż óź ź ź ż Ę ż ś ż ł ó ń ż ć óź ż ę ż ż ńś ś ó ń ó ś

Ę Ł ś ą ł ść ą ę ł Ł ś ą ś Ż ł ś ę Ł ę ł ł ą ę ą ą Ń ź ź ź Ę ś ł ć Ź ę ś ś ś Ę ł ś ć Ę ś ł ś ą ź ą ą ą ą ą ą ą ą ś ą ęń ś ł ą ś Ł ś ś ź Ą ł ć ą ą Ę ą ś ź Ł ź ć ś ę ę ź ą Ż ć ć Ą ć ć ł ł ś ł ś ę ą łą ć

Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 18, Mateusz Winkowski, Łukasz Zinkiewicz

Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie

Równania Maxwella. roth t

, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D

Miary statystyczne. Katowice 2014

Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących

Funkcja generująca rozkład (p-two)

Fucja geerująca rozład (p-wo Defiicja: Fucją geerującą rozład (prawdopodobieńswo (FGP dla zmieej losowej przyjmującej warości całowie ieujeme, azywamy: [ ] g E P Twierdzeie: (o jedozaczości Jeśli i są

w7 58 Prąd zmienny Generator Napięcie skuteczne Moc prądu Dodawanie prądów zmiennych Opór bierny

58 Prąd zienny Generator Napięcie skuteczne Moc prądu Dodawanie prądów ziennych Opór bierny Prąd zienny Prąd zienny 3 Prąd zienny 4 Prąd zienny 5 Prąd zienny Przy stałej prędkości kątowej ω const pola

Elektrodynamika. Część 9. Potencjały i pola źródeł zmiennych w czasie. Ryszard Tanaś

Elektrodynamika Część 9 Potencjały i pola źródeł zmiennych w czasie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 10 Potencjały i pola źródeł zmiennych w

Ruch pod wpływem sił zachowawczych

Ruch pod wpływem sił zachowawczych Fizyka I (B+C) Wykład XV: Energia potencjalna Siły centralne Ruch w polu grawitacyjnym Pole odpychajace Energia potencjalna Równania ruchu Znajomość energii potencjalnej

Ośrodki dielektryczne optycznie nieliniowe

Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola

TEORIA SPRĘŻYSTOŚCI 10

W YKŁ ADY Z T EOII S ĘŻYSTOŚCI ZADANIE BOUSSINESQA I FLAMANTA olitechnika onańska Kopac, Kawck, Łodgowski, łotkowiak, Świtek, Tmpe Olga Kopac, Kstof Kawck, Adam Łodgowski, Michał łotkowiak, Agnieska Świtek,

MECHANIKA. Materiały pomocnicze do wykładu Przedmiot podstawowy w ramach kierunku Mechatronika studia stacjonarne inżynierskie. Semestr II.

ublkacja opacowaa podcas ealacj pojektu la Rowoju oltechk ęstochowskej współfasowaego pe Uę Euopejską w amach Euopejskego Fudusu Społecego. Jacek blsk MEHNIK Mateał pomocce do wkładu edmot podstawow w

Sprzedaż finalna - sprzedaż dóbr i usług konsumentowi lub firmie, którzy ostatecznie je zużytkują, nie poddając dalszemu przetworzeniu.

W 1 Rachu maroeoomcze 1. Produ rajowy bruo Sprzedaż fala - sprzedaż dóbr usług osumeow lub frme, órzy osaecze je zużyują, e poddając dalszemu przeworzeu. Sprzedaż pośreda - sprzedaż dóbr usług zaupoych

Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 12, Mateusz Winkowski, Łukasz Zinkiewicz

Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład, 0..07 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład - przypomnienie superpozycja

PRAWA ZACHOWANIA Prawa zachowania najbardziej fundamentalne prawa:

PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci

W przypadku przepływu potencjalnego y u z. nieściśliwego równanie zachowania masy przekształca się w równanie Laplace a: = + + t

J. Szantr Wkład nr 3 Przepłw potencjalne 1 Jeżeli przepłw płn jest bezwirow, czli wszędzie lb prawie wszędzie w pol przepłw jest rot 0 to oznacza, że istnieje fnkcja skalarna ϕ,, z, t), taka że gradϕ.

Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów

Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe

0 ( 1 ) Q = Q T W + Q W + Q P C + Q P R + Q K T + Q G K + Q D M =

M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X O P T Y M A L I Z A C J A K O N S T R U K C J I F O R M Y W T R Y S K O W E J P O D K Ą T E M E F E K T Y W N O C I C H O D

Rachunek różniczkowy funkcji wielu zmiennych

EAIB-Iormaa-Wład 9- dr Adam Ćmel cmel@.ag.edu.pl Racue różczow ucj welu zmec Z uwag a prosoę zapsu ławe erpreacje gracze ograczm sę jede do ucj lub zmec. Naurale uogólea wprowadzac pojęć a ucje zmec zosawam

Podpis prowadzącego SPRAWOZDANIE

Imię i nazwisko.. Grupa. Data. Podpis prowadzącego. SPRAWOZDANIE LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1 Zadanie nr 1 (plik strip.pro,nazwa ośrodka wypełniającego prowadnicę - "airlossy") Rozważamy przypadek

Fale elektromagnetyczne

Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................

Budowa ścieżki spacerowo-dydaktycznej wokół jezior w Januszkowicach

Biuro Projektowe ECO-UNIT mgr inż. Marek Klyk ul. Cygana 4/213, 45-131 Opole tel. 77 442-81-18 fax. 77 442-81-19 kom. 606 101 958 NIP 754-242-14-40 REGON 532303190 http: www.eco-unit.pl e-mail: m.klyk@eco-unit.pl

Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM

Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................

Wykład 17: Optyka falowa cz.1.

Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza

Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 3, Mateusz Winkowski, Łukasz Zinkiewicz

Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 3, 12.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 2 - przypomnienie

LASERY I ICH ZASTOSOWANIE

LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz

ź -- ć ł ź ł -ł ł --

------ --------- --ł ----ć -------- --------------- ---ę- --- ----------- ------- ------ó- ------------ ----- --- -- ----- - ------------ --ó- --ś -- -- ------- --------- ------ ---- --------- -------ą

1 0 2 / c S t a n d a r d w y m a g a ń e g z a m i n c z e l a d n i c z y dla zawodu R A D I E S T E T A Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji

XLI OLIMPIADA FIZYCZNA ETAP I Zadanie doświadczalne

XLI OLIPIADA FIZYCZNA EAP I Zadanie doświadczalne ZADANIE D Pod działaniem sil zewnęznych ciała sale ulęgają odkszałceniom. Wyznacz zależność pomienia obszau syczniści szklanej soczewki z płyka szklana

Rys Ruch harmoniczny jako rzut ruchu po okręgu

3. DRGANIA I FALE 3.1. Ruch harmoniczny W szkole poznajemy ruch harmoniczny w trakcie analizy ruchu jednostajnego po okręgu jako rzut na prostą (rys. 3.1). Tak jest w istocie, poniewaŝ ruch po okręgu to

1 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu B L A C H A R Z Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji zawodów

Zestaw zadań 12: Przekształcenia liniowe. Macierze przekształceń liniowych. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t

Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n

2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l

Guanajuato, Mexico, August 2015

Guanajuao Meico Augus 15 W-3 Jaosewic 1 slajdów Dnamika punku maeialnego Dnamika Układ inecjaln Zasad dnamiki: piewsa asada dnamiki duga asada dnamiki pęd ciała popęd sił ecia asada dnamiki pawo akcji

Praca domowa nr 1. Metodologia Fizyki. Grupa 1. Szacowanie wartości wielkości fizycznych Zad Stoisz na brzegu oceanu, pogoda jest idealna,

Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje