PÓŁPRZEWODNIKI. Atom miedzi. Atom krzemu. Tylko jeden elektron. w powłoce walencyjnej. 4 dziury i 4 elektrony
|
|
|
- Helena Filipiak
- 8 lat temu
- Przeglądów:
Transkrypt
1 Półrzewodk zrewolucjozowały rzemysł elektroczy. Są oe wykorzystywae do wytwarzaa olbrzymej gamy różych elemetów elektroczych, od dyskretych dod, orzez trazystory, do układów scaloych zawerających awet mlardy trazystorów. PÓŁPRZEWODNIKI Przewodk, ółrzewodk zolatory Zdolość materałów do rzewodzea rądu elektryczego może być wyjaśoa a odstawe modelu atomu według Bohra. Zgode z tym modelem atom składa sę z dodato aładowaego jądra krążących wokół ego w ścśle określoych odległoścach elektroów. Odległośc te zazwyczaj wyrażae są orzez ozomy eergetycze. Rysuek rzedstawa modele atomu medz krzemu. Atom medz Tylko jede elektro w owłoce walecyjej 4 dzury 4 elektroy w owłoce walecyjej Atom krzemu 1
2 Zewętrza (walecyja) owłoka atomu medz zawera tylko jede elektro, który jest słabo zwązay z jądrem. Tak węc, elektro te łatwo uwala sę od atomu dryfuje swobode w rzestrze omędzy atomam. W atome krzemu a ostatej owłoce zajdują sę 4 elektroy, odczas gdy owłoka ta mogłaby być zaełoa ośmoma elektroam. Brak czterech elektroów do tego zaełea określa sę maem czterech dzur. Jedocześe te 4 elektroy są slej zwązae z jądrem ż w atome medz. Porzez dostarczee tym elektroom ewej eerg mogą oe uwolć sę od atomu, z drugej stroy swobode dryfujące omędzy atomam elektroy mogą być rzechwycoe rzez atom, zaełając stejące tam dzury. W strukturach weloatomowych owłok o ścśle określoych eergach ulegają rozszczeeu w efekce eerge elektroów mogą zawerać sę w ewych rzedzałach azywaych asmam eergetyczym. O zdolośc materału do rzewodzea rądu elektryczego decyduje szerokość odstęu omędzy tzw. asmem walecyjym, to zaczy zakresem ajwększych eerg elektroów jeszcze zwązaych z atomem, asmem rzewodctwa, to zaczy zakresem eerg właścwym dla elektroów swobodych. Welkość tego odstęu azywamy szerokoścą asma zabrooego elektroy e mogą w tym aśme sę zajdować rzejśce z asma walecyjego do asma rzewodctwa wymaga dostarczea mu ewej mmalej wartośc eerg. 2
3 Szerokość asma zabrooego staow odstawę do odzału materałów a rzewodk, ółrzewodk zolatory. W metalach szerokość asma zabrooego jest ewelka (sete częśc ev), w wyku czego w temeraturze okojowej wszystke elektroy walecyje uzyskują eergę wystarczającą do ch rzejśca do asma rzewodzea. W rzestrze mędzyatomowej zajduje sę węc duża lczba swobodych elektroów, które o rzyłożeu z zewątrz ola elektryczego oruszają sę wzdłuż jego l, staowąc rąd elektryczy. W ółrzewodkach w temeraturze okojowej ewa lczba elektroów ma eergę wystarczającą do rzejśca do asma rzewodctwa, co umożlwa rzeływ słabego rądu. W zolatorach doero w wysokej temeraturze ( o C) ewa część elektroów walecyjych zyskuje eergę ozwalającą a ch uwolee sę od atomów. 3
4 Z rzykładowych wartośc rezystywośc medź cm krzem 230 k. cm wyka, że rezystywość czystego krzemu jest oad razy wększa ż dla medz. Krzem jest ajczęścej wykorzystywaym ółrzewodkem. Ie erwastk zwązk chemcze wykazujące własośc ółrzewodka to: germa (Ge), arseek galu (GaAs), arseek du (IAs), fosforek galu (GaP) wele ych. Półrzewodk dzel sę a: ółrzewodk samoste (ółrzewodk o bardzo dużej czystośc, zacze wyższej ż wymagaa w chem), ółrzewodk esamoste (domeszkowae)(które owstają orzez wrowadzee domeszek do ółrzewodka samostego, wskutek czego jego własośc ulegają radykalej zmae. Półrzewodk samoste Półrzewodk wykorzystywae są w ostac krystalczej atomy rozmeszczoe są względem sebe w uorządkoway sosób, tworząc satkę krystalczą. Krzem jest erwastkem czterowartoścowym każdy jego atom zawera cztery elektroy w ostatej owłoce (walecyjej), które tworzą tzw. wązaa atomowe z czterema sąsedm atomam. 4
5 Struktura krystalcza krzemu jej rerezetacja dwuwymarowa Każdy elektro walecyjy jest wsółdzeloy rzez dwa sąsadujące atomy. W temeraturze 0 K wszystke elektroy są zwązae z atomam, wskutek czego brak jest swobodych elektroów ółrzewodk samosty jest zolatorem. W marę wzrostu temeratury ektóre elektroy abywają eergę ozwalającą m a uwolee sę od atomów. Odowede wązaa stają sę ekomlete sta tak określa sę w teor ółrzewodków ojęcem dzury. W ółrzewodku samostym wystęuje jedakowa lczba elektroów o ładuku ujemym oraz dzur o ładuku dodatm (dzura ozacza w stoce brak elektrou we właścwym mejscu). 5
6 Procesy rozrywaa wązań (jest to tzw. geeracja ar dzura elektro) oraz ch oowego formowaa (rekombacja) zachodzą w sosób erzerway śred czas życa ar dzura elektro omędzy oboma zdarzeam może sęgać setek mkrosekud. Oba rocesy są w dyamczej rówowadze średa kocetracja ar dzura-elektro jest fukcją temeratury: 2 AT 3 ex E g kt A stała materałowa, k = 1, J/K stała Boltzmaa Zależość tę rzedstawa rysuek. 6
7 W temeraturze okojowej: Krzem (E g = 1.1 ev) Germa (E g = 0.72 ev) cm 13 1 cm 3 3 Polczmy teraz kocetrację atomów korzystając z lczby Avogadro: Krzem atomów mol 1mol 28.1g 2.33 g cm atomów 3 cm Germa atomów mol 1mol 72.69g 5.32 g cm atomów 3 cm Tak węc, w krzeme tylko jede atom a atomów jest zjozoway, czyl jest źródłem jedego swobodego elektrou (orówajmy to z medzą, w której wszystke atomy są zjozowae)! 7
8 Po rzyłożeu aęca omędzy końce łytk z ółrzewodka ołye rzez ą rąd jako ruch swobodych elektroów w keruku elektrody dodatej oraz ruch dzur w keruku elektrody ujemej. Składowa dzurowa rądu ozacza w stoce ruch elektroów walecyjych (zwązaych z atomam), odczas gdy składowa elektroowa tego rądu wyka z ruchu swobodych elektroów. Półrzewodk esamoste Wrowadzając do sec krystalczej ółrzewodka samostego atomy ego rodzaju (domeszk) moża w stotym stou zmeć kocetrację swobodych elektroów dzur. Domeszk dodawae są w bardzo małej lośc ( %); dlatego też tak waża jest wysoka czystość ółrzewodka samostego, do którego domeszk są wrowadzae.najczęścej stosowaym domeszkam są erwastk trójwartoścowe (bor B, gl Al, gal Ga, d I) lub ęcowartoścowe (arse As, atymo Sb, fosfor P). W zależośc od wartoścowośc domeszk ółrzewodk staje sę ółrzewodkem tyu (domeszk trójwartoścowe) lub tyu (domeszk ęcowartoścowe). 8
9 Półrzewodk tyu Atomy domeszk zajmują mejsce atomów krzemu w satce krystalczej. Ich cztery elektroy walecyje tworzą wązaa atomowe z sąsadującym atomam krzemu, a ąty elektro łatwo może sę uwolć. W te sosób w ółrzewodku zwększa sę kocetracja swobodych elektroów zmejsza kocetracja dzur, gdyż ektóre sośród dodatkowych elektroów rekombują z dzuram stejącym wskutek geeracj samostej. W temeraturze okojowej raktycze wszystke atomy domeszk są zjozowae. Atomy ęcowartoścowe domeszk azywa sę dooram. Atom fosforu Normale wązae Dodatkowy woly elektro 9
10 Półrzewodk tyu W tym rzyadku atom domeszk trójwartoścowej róweż zastęuje atom krzemu w sec krystalczej. Ma o jedak tylko trzy elektroy walecyje, które tworzą wązaa atomowe z trzema sąsedm atomam krzemu. Czwarte wązae e jest komlete ze względu a brak elektrou owstaje tam dzura. Tak węc, domeszk trójwartoścowe zwększają kocetrację dzur zmejszają kocetrację swobodych elektroów, gdyż ektóre elektroy owstające w wyku geeracj samostej zostaą rzechwycoe rzez dzury (rekombacja). Trójwartoścowe atomy domeszk azywa sę akcetoram. Wskutek domeszkowaa rezystywość ółrzewodka ulega zaczącej zmae. Przykładowo, domeszkowae krzemu atomam fosforu z kocetracją /cm 3 zmejsza jego rezystywość do 160. cm. 10
11 Kocetracja ośków w ółrzewodkach domeszkowaych Dla ółrzewodków domeszkowaych obowązuje zależość: 2 T Poadto zakłada sę, że w temeraturze okojowej wszystke atomy domeszek są zjozowae. Półrzewodk tyu Kocetracja domeszek jest zazwyczaj o klka rzędów wększa ż kocetracja samosta, tak węc kocetracja ośków wększoścowych (elektroów) wyos: N d gdze N d ozacza kocetrację doorów. Kocetracja ośków mejszoścowych (dzur): 2 N 2 d 11
12 Półrzewodk tyu Kocetracja ośków wększoścowych (dzur): N a gdze N a ozacza kocetrację akcetorów. Kocetracja ośków mejszoścowych (elektroów): Przykład 2 Jeżel kocetracja doorów jest 10 3 razy wększa od kocetracj samostej = 1, cm -3, to wtedy: = 1, cm -3 = 1, cm -3 czyl kocetracja ośków wększoścowych jest 10 6 razy wększa ż ośków mejszoścowych oraz 10 3 razy wększa ż kocetracja ośków geerowaych termcze (jak w ółrzewodku samostym). N 2 a 12
13 Kocetracja ośków geerowaych termcze (jedakowo dzur elektroów) szybko rośe z temeraturą o około 14%/K w krzeme 9%/K w germae. Kocetracja ośków wykłych z domeszkowaa e ulega zmae; tak węc w odowedo wysokej temeraturze ółrzewodk domeszkoway abera charakteru ółrzewodka samostego kocetracje ośków obu rodzajów stają sę w rzyblżeu jedakowe, jak okazao a sąsedm rysuku. Dla daych rzyjętych a tym rysuku kocetracja ośków mejszoścowych osąga 10% kocetracj ośków wększoścowych w temeraturze około 500 K. 13
14 Przeływ rądu w ółrzewodkach W metalach rzeływ rądu astęuje wskutek uoszea swobodych elektroów w olu elektryczym wytworzoym rzez aęce rzyłożoe do końców rzewodka. Gęstość tego rądu uoszea wyraża sę wzorem: gdze q ozacza ładuek elektrou, v średą rędkość uoszea, kocetrację swobodych elektroów. W ółrzewodkach wystęują dwa rodzaje ośków ładuku, dla których rędkośc uoszea określoe są wzoram: v Gdze oraz ozaczają tzw. ruchlwośc elektroów dzur. Pożej odao rzykładowe ruchlwośc w temeraturze 300 K. j uosz qv E v E [cm 2 /Vs] S Ge GaAs IAs
15 Tak węc, dla rądu uoszea w ółrzewodkach uzyskujemy astęujące zależośc: j u qv j q E uosz q j qv E E u q E Ostate rówae, w którym ozacza koduktywość ółrzewodka, wyraża rawo Ohma w tzw. ostac różczkowej. Ze względu a małe kocetracje ośków ładuku w ółrzewodkach może zachodzć lokala erówowaga tej kocetracj. Przykładowo, dzałae ektórych ważych rzyrządów ółrzewodkowych oera sę a wstrzykwau ośków z jedego obszaru do obszaru rzylegającego, jak okazao a rysuku. 15
16 Nośk te rozchodzą sę z obszarów o wększej kocetracj do obszarów o mejszej kocetracj a zasadze zjawska dyfuzj. Gęstośc składowych dyfuzyjych rądu elektroowego dzurowego zależą od gradetu kocetracj wzdłuż odowedej wsółrzędej: j d qd d dx D D [m 2 s -1 ] ozaczają tzw. stałe dyfuzj elektroów dzur. j W ogólym rzyadku zatem aalza rzeływu rądu w ółrzewodkach wymaga uwzględea czterech jego składowych, które mogą łyąć w różych kerukach. Poższa zależość określa sumaryczą gęstość rądu w ółrzewodku rzy założeu, że rzeływ te jest jedowymarowy. d qd d dx j q E q E qd d dx qd d dx 16
2. KONCENTRACJA NOŚNIKÓW W PÓŁPRZEWODNIKU SAMOISTNYM I DOMIESZKOWYM. WPŁYW DOMIESZKOWANIA NA POŁOŻENIE POZIOMU FERMIEGO
 . KONCENTRACJA NOŚNIKÓW W PÓŁPRZEWONIKU SAMOISTNYM I OMIESZKOWYM. WPŁYW OMIESZKOWANIA NA POŁOŻENIE POZIOMU FERMIEGO.1. Kocetracja ośków samostych W rzyadku gdy mamy do czyea z ółrzewodkem edomeszkowaym
. KONCENTRACJA NOŚNIKÓW W PÓŁPRZEWONIKU SAMOISTNYM I OMIESZKOWYM. WPŁYW OMIESZKOWANIA NA POŁOŻENIE POZIOMU FERMIEGO.1. Kocetracja ośków samostych W rzyadku gdy mamy do czyea z ółrzewodkem edomeszkowaym
ELEMENTY ELEKTRONICZNE
 AKADMIA GÓRNICZO-HUTNICZA IM. STANISŁAWA STASZICA W KRAKOWI Wydział Iformatyki, lektroiki i Telekomuikacji Katedra lektroiki LMNTY LKTRONICZN dr iż. Piotr Dziurdzia aw. C-, okój 41; tel. 617-7-0, iotr.dziurdzia@agh.edu.l
AKADMIA GÓRNICZO-HUTNICZA IM. STANISŁAWA STASZICA W KRAKOWI Wydział Iformatyki, lektroiki i Telekomuikacji Katedra lektroiki LMNTY LKTRONICZN dr iż. Piotr Dziurdzia aw. C-, okój 41; tel. 617-7-0, iotr.dziurdzia@agh.edu.l
Badanie efektu Halla w półprzewodniku typu n
 Badaie efektu alla w ółrzewodiku tyu 35.. Zasada ćwiczeia W ćwiczeiu baday jest oór elektryczy i aięcie alla w rostoadłościeej róbce kryształu germau w fukcji atężeia rądu, ola magetyczego i temeratury.
Badaie efektu alla w ółrzewodiku tyu 35.. Zasada ćwiczeia W ćwiczeiu baday jest oór elektryczy i aięcie alla w rostoadłościeej róbce kryształu germau w fukcji atężeia rądu, ola magetyczego i temeratury.
PÓŁPRZEWODNIKI W ELEKTRONICE. Powszechnie uważa się, że współczesna elektronika jest elektroniką półprzewodnikową.
 PÓŁPRZEWODNIKI W ELEKTRONICE Powszechie uważa się, że wsółczesa elektroika jest elektroiką ółrzewodikową. 1 Półrzewodiki Półrzewodiki to ciała stałe ieorgaicze lub orgaicze o rzewodictwie elektryczym tyu
PÓŁPRZEWODNIKI W ELEKTRONICE Powszechie uważa się, że wsółczesa elektroika jest elektroiką ółrzewodikową. 1 Półrzewodiki Półrzewodiki to ciała stałe ieorgaicze lub orgaicze o rzewodictwie elektryczym tyu
ZAJĘCIA NR 3. loga. i nosi nazwę entropii informacyjnej źródła informacji. p. oznacza, Ŝe to co po im występuje naleŝy sumować biorąc za i
 ZAJĘCIA NR Dzsaj omówmy o etro, redudacj, średej długośc słowa odowego o algorytme Huffmaa zajdowaa odu otymalego (od ewym względam; aby dowedzeć sę jam doczeaj do ońca). etro JeŜel źródło moŝe adawać
ZAJĘCIA NR Dzsaj omówmy o etro, redudacj, średej długośc słowa odowego o algorytme Huffmaa zajdowaa odu otymalego (od ewym względam; aby dowedzeć sę jam doczeaj do ońca). etro JeŜel źródło moŝe adawać
Statystyczne charakterystyki liczbowe szeregu
 Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Zjawiska kontaktowe i powierzchniowe w półprzewodnikach W4 SMK
 Zjawka kotaktowe owerzchowe w ółrzewokach W4 SMK a otawe: Przyrząy ółrzewokowe ukłay caloe, W. Marcak, W, Warzawa 987 ajbarzej realy jet rzyaek wytęowaa w ółrzewoku jeocześe obu rozajów omezek oorowych
Zjawka kotaktowe owerzchowe w ółrzewokach W4 SMK a otawe: Przyrząy ółrzewokowe ukłay caloe, W. Marcak, W, Warzawa 987 ajbarzej realy jet rzyaek wytęowaa w ółrzewoku jeocześe obu rozajów omezek oorowych
Statystyka Inżynierska
 Statystyka Iżyerska dr hab. ż. Jacek Tarasuk AGH, WFIS 013 Wykład 3 DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE, PODSTAWY ESTYMACJI Dwuwymarowa, dyskreta fukcja rozkładu rawdoodobeństwa, Rozkłady brzegowe
Statystyka Iżyerska dr hab. ż. Jacek Tarasuk AGH, WFIS 013 Wykład 3 DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE, PODSTAWY ESTYMACJI Dwuwymarowa, dyskreta fukcja rozkładu rawdoodobeństwa, Rozkłady brzegowe
Zjawiska kontaktowe. Pojęcia.
 Zjawiska kotaktowe Zjawiska kotaktowe. Pojęcia. metal Φ M W W raca rzeiesieia elektrou z da asma rzewodictwa do różi, bez zwiększaia jego eergii kietyczej (którą ma zerową). Używa się tylko dla metalu.
Zjawiska kotaktowe Zjawiska kotaktowe. Pojęcia. metal Φ M W W raca rzeiesieia elektrou z da asma rzewodictwa do różi, bez zwiększaia jego eergii kietyczej (którą ma zerową). Używa się tylko dla metalu.
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA. Adrian Kapczyński Maciej Wolny
 KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
Planowanie eksperymentu pomiarowego I
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANEJ PODCZAS ZDERZENIA CIAŁ
 9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
BADANIE STATYSTYCZNEJ CZYSTOŚCI POMIARÓW
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII RODUKCJI I TECHNOLOGII MATERIAŁÓW OLITECHNIKA CZĘSTOCHOWSKA RACOWNIA DETEKCJI ROMIENIOWANIA JĄDROWEGO Ć W I C Z E N I E N R J-6 BADANIE STATYSTYCZNEJ CZYSTOŚCI OMIARÓW
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII RODUKCJI I TECHNOLOGII MATERIAŁÓW OLITECHNIKA CZĘSTOCHOWSKA RACOWNIA DETEKCJI ROMIENIOWANIA JĄDROWEGO Ć W I C Z E N I E N R J-6 BADANIE STATYSTYCZNEJ CZYSTOŚCI OMIARÓW
BADANIE CHARAKTERYSTYKI DIODY PÓŁPRZEWODNIKOWEJ
 Ćwiczeie 47 BADANIE CHARAKTERYSTYKI DIODY PÓŁPRZEWODNIKOWEJ 47.. Wiadomości ogóle Dla zrozumieia elektryczych właściwości ciał stałych koiecze jest pozaie praw rządzących elektroami wewątrz tych ciał.
Ćwiczeie 47 BADANIE CHARAKTERYSTYKI DIODY PÓŁPRZEWODNIKOWEJ 47.. Wiadomości ogóle Dla zrozumieia elektryczych właściwości ciał stałych koiecze jest pozaie praw rządzących elektroami wewątrz tych ciał.
Zjawiska kontaktowe. Pojęcia.
 Zjawiska kotaktowe. Pojęcia. Próżia, E vac =0 Φ m W Φ s χ E c µ E v metal półprzewodik W praca przeiesieia elektrou z da pasma przewodictwa do próżi, bez zwiększaia jego eergii kietyczej (którą ma zerową).
Zjawiska kotaktowe. Pojęcia. Próżia, E vac =0 Φ m W Φ s χ E c µ E v metal półprzewodik W praca przeiesieia elektrou z da pasma przewodictwa do próżi, bez zwiększaia jego eergii kietyczej (którą ma zerową).
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne
 XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadane teoretyczne Rozwąż dowolne rzez sebe wybrane dwa sośród odanych nże zadań: ZADANIE T Nazwa zadana: Protony antyrotony A. Cząstk o mase równe mase rotonu, ale
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadane teoretyczne Rozwąż dowolne rzez sebe wybrane dwa sośród odanych nże zadań: ZADANIE T Nazwa zadana: Protony antyrotony A. Cząstk o mase równe mase rotonu, ale
Miary położenia wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości danej zmiennej. Mówią o przeciętnym poziomie analizowanej
 Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
POMIAR WSPÓŁCZYNNIKA POCHŁANIANIA PROMIENIOWANIA γ
 Ćwczee 56 POMIAR WSPÓŁCZYNNIKA POCHŁANIANIA PROMIENIOWANIA γ 56.. Wadomośc ogóle Rozpatrzmy wąską skolmowaą wązkę prome γ o atężeu I 0, padającą a płytkę substacj o grubośc x (rys. 56.). Natężee promeowaa
Ćwczee 56 POMIAR WSPÓŁCZYNNIKA POCHŁANIANIA PROMIENIOWANIA γ 56.. Wadomośc ogóle Rozpatrzmy wąską skolmowaą wązkę prome γ o atężeu I 0, padającą a płytkę substacj o grubośc x (rys. 56.). Natężee promeowaa
Elektrony i dziury w półprzewodnikach
 1 lektroy i dziury w ółrzewodikach Atomy i rdzeie atomowe Si oraz Ge Si oraz Ge ależą do gruy IV układu okresowego ierwiastków. Mają o 4 zewętrze elektroy. Tylko zewętrze elektroy uczesticzą w tworzeiu
1 lektroy i dziury w ółrzewodikach Atomy i rdzeie atomowe Si oraz Ge Si oraz Ge ależą do gruy IV układu okresowego ierwiastków. Mają o 4 zewętrze elektroy. Tylko zewętrze elektroy uczesticzą w tworzeiu
Podstawy opracowania wyników pomiarowych, analiza błędów
 Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Model Bohra atomu wodoru
 Model Bohra atomu wodoru Widma liiowe pierwiastków. wodór hel eo tle węgiel azot sód Ŝelazo Aby odpowiedzieć a pytaie dlaczego wodór i ie pierwiastki ie emitują wszystkich częstotliwości fal elektromagetyczych
Model Bohra atomu wodoru Widma liiowe pierwiastków. wodór hel eo tle węgiel azot sód Ŝelazo Aby odpowiedzieć a pytaie dlaczego wodór i ie pierwiastki ie emitują wszystkich częstotliwości fal elektromagetyczych
FINANSE II. Model jednowskaźnikowy Sharpe a.
 ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
Badania Maszyn CNC. Nr 2
 Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
ĆWICZENIE 10 OPTYMALIZACJA STRUKTURY CZUJKI TEMPERATURY W ASPEKCIE NIEZWODNOŚCI
 ĆWICZENIE 0 OPTYMALIZACJA STUKTUY CZUJKI TEMPEATUY W ASPEKCIE NIEZWODNOŚCI Cel ćwczea: zapozae z metodam optymalzac wewętrze struktury mozakowe czuk temperatury stosowae w systemach sygalzac pożaru; wyzaczee
ĆWICZENIE 0 OPTYMALIZACJA STUKTUY CZUJKI TEMPEATUY W ASPEKCIE NIEZWODNOŚCI Cel ćwczea: zapozae z metodam optymalzac wewętrze struktury mozakowe czuk temperatury stosowae w systemach sygalzac pożaru; wyzaczee
Obliczanie średniej, odchylenia standardowego i mediany oraz kwartyli w szeregu szczegółowym i rozdzielczym?
 Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Powinowactwo chemiczne Definicja oraz sens potencjału chemicznego, aktywność Termodynamiczne funkcje mieszania
 ermdyamka układów rzeczywstych 2.7.1. Pwwactw chemcze 2.7.2. Defcja raz ses tecjału chemczeg aktywść 2.7.3. ermdyamcze fukcje meszaa 2.7.4. Klasyfkacja rztwrów Waruk ztermcz-zchrycze ) ( V F F j V V d
ermdyamka układów rzeczywstych 2.7.1. Pwwactw chemcze 2.7.2. Defcja raz ses tecjału chemczeg aktywść 2.7.3. ermdyamcze fukcje meszaa 2.7.4. Klasyfkacja rztwrów Waruk ztermcz-zchrycze ) ( V F F j V V d
Szeregi czasowe, modele DL i ADL, przyczynowość, integracja
 Szereg czasowe, modele DL ADL, rzyczyowość, egracja Szereg czasowy, o cąg realzacj zmeej losowej, owedzmy y, w kolejych okresach czasu: { y } T, co rówoważe możemy zasać: = 1 y = { y1, y,..., y T }. Najogólej
Szereg czasowe, modele DL ADL, rzyczyowość, egracja Szereg czasowy, o cąg realzacj zmeej losowej, owedzmy y, w kolejych okresach czasu: { y } T, co rówoważe możemy zasać: = 1 y = { y1, y,..., y T }. Najogólej
Pomiary parametrów napięć i prądów przemiennych
 Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
T. Hofman, Wykłady z Termodynamiki technicznej i chemicznej, Wydział Chemiczny PW, kierunek: Technologia chemiczna, sem.
 . Hofma Wyłady z ermodyam techczej chemczej Wydzał Chemczy PW erue: echologa chemcza sem.3 215/216 WYKŁAD 3-4. D. Blase reatorów chemczych E. II zasada termodyam F. Kosewecje zasad termodyam D. BILANE
. Hofma Wyłady z ermodyam techczej chemczej Wydzał Chemczy PW erue: echologa chemcza sem.3 215/216 WYKŁAD 3-4. D. Blase reatorów chemczych E. II zasada termodyam F. Kosewecje zasad termodyam D. BILANE
Janusz Górczyński. Moduł 1. Podstawy prognozowania. Model regresji liniowej
 Materały omoccze do e-leargu Progozowae symulacje Jausz Górczyńsk Moduł. Podstawy rogozowaa. Model regresj lowej Wyższa Szkoła Zarządzaa Marketgu Sochaczew Od Autora Treśc zawarte w tym materale były erwote
Materały omoccze do e-leargu Progozowae symulacje Jausz Górczyńsk Moduł. Podstawy rogozowaa. Model regresj lowej Wyższa Szkoła Zarządzaa Marketgu Sochaczew Od Autora Treśc zawarte w tym materale były erwote
Teoria pasmowa. Anna Pietnoczka
 Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Jego zależy od wysokości i częstotliwości wypłat kuponów odsetkowych, ceny wykupu, oczekiwanej stopy zwrotu oraz zapłaconej ceny za obligację.
 Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
wyniki serii n pomiarów ( i = 1,..., n) Stosując metodę największej wiarygodności możemy wykazać, że estymator wariancji 2 i=
 ESTYMATOR WARIANCJI I DYSPERSJI Ozaczmy: µ wartość oczekwaa rozkładu gauowkego wyków pomarów (wartość prawdzwa merzoej welkośc σ dyperja rozkładu wyków pomarów wyk er pomarów (,..., Stoując metodę ajwękzej
ESTYMATOR WARIANCJI I DYSPERSJI Ozaczmy: µ wartość oczekwaa rozkładu gauowkego wyków pomarów (wartość prawdzwa merzoej welkośc σ dyperja rozkładu wyków pomarów wyk er pomarów (,..., Stoując metodę ajwękzej
STATYSTYKA OPISOWA WYKŁAD 3,4
 STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
Portfel złożony z wielu papierów wartościowych
 Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Podstawowe zadanie statystyki. Statystyczna interpretacja wyników eksperymentu. Zalety statystyki II. Zalety statystyki
 tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
Paliwa stałe, ciekłe i gazowe
 Palwa stałe, cekłe gazowe Podstawowe właścwośc alw gazowych Wydzał Eergetyk Palw Katedra Techolog Palw Gaz Gaz doskoały jest to hotetyczy gaz, którego droby e rzycągają sę wzajeme, są eskończee małe sztywe
Palwa stałe, cekłe gazowe Podstawowe właścwośc alw gazowych Wydzał Eergetyk Palw Katedra Techolog Palw Gaz Gaz doskoały jest to hotetyczy gaz, którego droby e rzycągają sę wzajeme, są eskończee małe sztywe
JEDNOWYMIAROWA ZMIENNA LOSOWA
 JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
WYZNACZANIE PRZERWY ENERGETYCZNEJ GERMANU
 Fzyka cała stałeo WYZNACZANIE PRZERWY ENERGETYCZNEJ GERMANU 1. Ops teoretyczy do ćwczea zameszczoy jest a stroe www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE.. Ops układu pomaroweo
Fzyka cała stałeo WYZNACZANIE PRZERWY ENERGETYCZNEJ GERMANU 1. Ops teoretyczy do ćwczea zameszczoy jest a stroe www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE.. Ops układu pomaroweo
Tekst oraz ilustracje do niniejszego opracowania zaczerpnięto z następujących podręczników, publikacji i wydawnictw popularno naukowych:
 UZUPEŁNIAJĄCE MATERIAŁY DYDAKTYCZNE DLA UCZNIÓW TECHNIKUM MECHANICZNEGO PRZYGOTOWUJĄCYCH SIĘ DO ZEWNĘTRZNEGO EGZAMINU KWALIFIKACYJNEGO METROLOGIA TECHNICZNA (materały wybrae) Materały zebrał : mgr ż. Aatol
UZUPEŁNIAJĄCE MATERIAŁY DYDAKTYCZNE DLA UCZNIÓW TECHNIKUM MECHANICZNEGO PRZYGOTOWUJĄCYCH SIĘ DO ZEWNĘTRZNEGO EGZAMINU KWALIFIKACYJNEGO METROLOGIA TECHNICZNA (materały wybrae) Materały zebrał : mgr ż. Aatol
WPŁYW ZMIENNOŚCI MASY JEDNEGO Z POJAZDÓW NA NIEBEZPIECZEŃSTWO ZEJŚCIA KOŁA Z SZYNY PODCZAS ZDERZENIA CZOŁOWEGO
 Dr ż. erzy Pawlus WPŁYW ZMIENNOŚCI MAY EDNEGO Z POAZDÓW NA NIEBEZPIECZEŃTWO ZEŚCIA KOŁA Z ZYNY PODCZA ZDERZENIA CZOŁOWEGO PI TREŚCI. Wrowadzee. Aalza daych statystyczych dotyczących zderzeń czołowych zderzeń
Dr ż. erzy Pawlus WPŁYW ZMIENNOŚCI MAY EDNEGO Z POAZDÓW NA NIEBEZPIECZEŃTWO ZEŚCIA KOŁA Z ZYNY PODCZA ZDERZENIA CZOŁOWEGO PI TREŚCI. Wrowadzee. Aalza daych statystyczych dotyczących zderzeń czołowych zderzeń
Różniczkowanie funkcji rzeczywistych wielu zmiennych. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Różczkowae fukcj rzeczywstych welu zmeych rzeczywstych Matematyka Studum doktoracke KAE SGH Semestr let 8/9 R. Łochowsk Pochoda fukcj jedej zmeej e spojrzee Nech f : ( α, β ) R, α, β R, α < β Fukcja f
Różczkowae fukcj rzeczywstych welu zmeych rzeczywstych Matematyka Studum doktoracke KAE SGH Semestr let 8/9 R. Łochowsk Pochoda fukcj jedej zmeej e spojrzee Nech f : ( α, β ) R, α, β R, α < β Fukcja f
Materiały do wykładu 7 ze Statystyki
 Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Ćwiczenia nr 3 Finanse II Robert Ślepaczuk. Teoria portfela papierów wartościowych
 Ćczea r 3 Fae II obert Ślepaczuk Teora portfela paperó artoścoych Teora portfela paperó artoścoych jet jedym z ajażejzych dzałó ooczeych faó. Dotyczy oa etycj faoych, a przede zytkm etycj dokoyaych a ryku
Ćczea r 3 Fae II obert Ślepaczuk Teora portfela paperó artoścoych Teora portfela paperó artoścoych jet jedym z ajażejzych dzałó ooczeych faó. Dotyczy oa etycj faoych, a przede zytkm etycj dokoyaych a ryku
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
Statystyczna analiza miesięcznych zmian współczynnika szkodowości kredytów hipotecznych
 dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
STATYKA. Cel statyki. Prof. Edmund Wittbrodt
 STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
STATYKA Cel statyk Celem statyk jest zastąpee dowolego układu sł ym, rówoważym układem sł, w tym układem złożoym z jedej tylko sły jedej pary sł (redukcja do sły mometu główego) lub zbadae waruków, jake
Prawdopodobieństwo i statystyka r.
 Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Wyrażanie niepewności pomiaru
 Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
5. OPTYMALIZACJA NIELINIOWA
 5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
UOGÓLNIONA ANALIZA WRAŻLIWOŚCI ZYSKU W PRZEDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW. 1. Wprowadzenie
 B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
Podstawy analizy niepewności pomiarowych (I Pracownia Fizyki)
 Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Laboratorium Metod Statystycznych ĆWICZENIE 2 WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI
 Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
TERMODYNAMIKA PROCESOWA I TECHNICZNA
 TERMODYNAMIKA PROCESOWA I TECHNICZNA Wykład IX Fugatywość substacj czystych Układy weloskładkowe - roztwory FUGATYWNOŚĆ SUBSTANCJI CZYSTYCH - defcja Pojęce tzw. fugatywośc jest bardzo użyteczym sosobem
TERMODYNAMIKA PROCESOWA I TECHNICZNA Wykład IX Fugatywość substacj czystych Układy weloskładkowe - roztwory FUGATYWNOŚĆ SUBSTANCJI CZYSTYCH - defcja Pojęce tzw. fugatywośc jest bardzo użyteczym sosobem
3. OPTYMALIZACJA NIELINIOWA
 Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
Proces narodzin i śmierci
 Proces narodzn śmerc Jeżel w ewnej oulacj nowe osobnk ojawają sę w sosób losowy, rzy czym gęstość zdarzeń na jednostkę czasu jest stała w czase wynos λ, oraz lczba osobnków n, które ojawły sę od chwl do
Proces narodzn śmerc Jeżel w ewnej oulacj nowe osobnk ojawają sę w sosób losowy, rzy czym gęstość zdarzeń na jednostkę czasu jest stała w czase wynos λ, oraz lczba osobnków n, które ojawły sę od chwl do
Wykład Zasada zachowania ładunku
 Potr Posmykewcz Wykład z fzyk Wykład 6 6. Zasada zachowaa ładuku Isteją dwa rodzaje ładuków dodate ujeme; ładuk jedomee odpychają sę, a różomee przycągają sę. Podczas elektryzowaa za pomocą tarca, zawsze
Potr Posmykewcz Wykład z fzyk Wykład 6 6. Zasada zachowaa ładuku Isteją dwa rodzaje ładuków dodate ujeme; ładuk jedomee odpychają sę, a różomee przycągają sę. Podczas elektryzowaa za pomocą tarca, zawsze
dev = y y Miary położenia rozkładu Wykład 9 Przykład: Przyrost wagi owiec Odchylenia Mediana próbkowa: Przykłady Statystyki opisowe Σ dev i =?
 Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
cz.2 dr inż. Zbigniew Szklarski
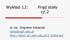 Wykład 1: Prąd sały cz. dr nż. Zbgnew Szklarsk szkla@agh.edu.pl hp://layer.uc.agh.edu.pl/z.szklarsk/ Pasma energeyczne pasma energeyczne - 198 Felx Bloch zblżane sę aomów do sebe powoduje rozszczepene
Wykład 1: Prąd sały cz. dr nż. Zbgnew Szklarsk szkla@agh.edu.pl hp://layer.uc.agh.edu.pl/z.szklarsk/ Pasma energeyczne pasma energeyczne - 198 Felx Bloch zblżane sę aomów do sebe powoduje rozszczepene
Monika Jeziorska - Pąpka Uniwersytet Mikołaja Kopernika w Toruniu
 DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
PŁASKA GEOMETRIA MAS. Środek ciężkości figury płaskiej
 PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
( ) L 1. θ θ = M. Przybycień Rachunek prawdopodobieństwa i statystyka. = θ. min
 Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
opisać wielowymiarową funkcją rozkładu gęstości prawdopodobieństwa f(x 1 , x xn
 ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
PROMIENIOWANIE ROZPROSZONE W BADANIACH RADIOGRAFICZNYCH
 PROMENOANE ROZPROSZONE BADANACH RADOGRAFCZNYCH Domk SENCZYK Poltechka Pozańska Słowa kluczowe: promeowae rozproszoe, współczyk agromadzea promeowaa rozproszoego, sposób pomaru współczyka agromadzea promeowaa
PROMENOANE ROZPROSZONE BADANACH RADOGRAFCZNYCH Domk SENCZYK Poltechka Pozańska Słowa kluczowe: promeowae rozproszoe, współczyk agromadzea promeowaa rozproszoego, sposób pomaru współczyka agromadzea promeowaa
Politechnika Lubelska Wydział Elektrotechniki i Informatyki Katedra Urządzeń Elektrycznych i Techniki Wysokich Napięć. Dr hab.
 Politechika Lubelska Wydział Elektrotechiki i Iformatyki Katedra Urządzeń Elektryczych i Techiki Wysokich Napięć Dr hab. Paweł Żukowski Pierwiastek DEg C (diamet) 7,0 ev Si 1,1 ev Ge 0,7 ev S (szara cya)
Politechika Lubelska Wydział Elektrotechiki i Iformatyki Katedra Urządzeń Elektryczych i Techiki Wysokich Napięć Dr hab. Paweł Żukowski Pierwiastek DEg C (diamet) 7,0 ev Si 1,1 ev Ge 0,7 ev S (szara cya)
Prąd elektryczny U R I =
 Prąd elektryczny porządkowany ruch ładunków elektrycznych (nośnków prądu). Do scharakteryzowana welkośc prądu służy natężene prądu określające welkość ładunku przepływającego przez poprzeczny przekrój
Prąd elektryczny porządkowany ruch ładunków elektrycznych (nośnków prądu). Do scharakteryzowana welkośc prądu służy natężene prądu określające welkość ładunku przepływającego przez poprzeczny przekrój
Niezawodność i diagnostyka Kierunek AiR, sem. V, rok. ak. 2010/11 STRUKTURY I MIARY PROBABILISTYCZNE SYSTEMÓW METODA DRZEWA (STANÓW) NIEZDATNOŚCI
 Nezawodość dagosyka Keruek, sem. V, rok. ak. 00/ STUKTUY I MIY POILISTYCZNE SYSTEMÓW METOD DZEW STNÓW NIEZDTNOŚCI. Srukury obeków złożoych ch rerezeace Wsółczese obeky sysemy echcze, a szczególe wększe
Nezawodość dagosyka Keruek, sem. V, rok. ak. 00/ STUKTUY I MIY POILISTYCZNE SYSTEMÓW METOD DZEW STNÓW NIEZDTNOŚCI. Srukury obeków złożoych ch rerezeace Wsółczese obeky sysemy echcze, a szczególe wększe
LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE
 LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE Ćwzee r 4 Temat: Wyzazee współzyka załamaa ezy refraktometrem Abbego.. Wprowadzee Śwatło, przy przejśu przez graę dwóh ośrodków, zmea swój
LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE Ćwzee r 4 Temat: Wyzazee współzyka załamaa ezy refraktometrem Abbego.. Wprowadzee Śwatło, przy przejśu przez graę dwóh ośrodków, zmea swój
Budowa atomów. Budowa atomu wodoru
 05-0- Budowa atomów atom wodoru atomy wieloelektroowe zakaz Pauliego układ okresowy pierwiastków Budowa atomu wodoru atom wodoru składa się z pojedyczego elektrou (-e) związaego z jądrem protoem (+e) przyciągającą
05-0- Budowa atomów atom wodoru atomy wieloelektroowe zakaz Pauliego układ okresowy pierwiastków Budowa atomu wodoru atom wodoru składa się z pojedyczego elektrou (-e) związaego z jądrem protoem (+e) przyciągającą
STATYSTYKA MATEMATYCZNA WYKŁAD 2 ESTYMACJA PUNKTOWA
 STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
Półprzewodniki Teoria złącza PN. Budowa i właściwości elektryczne ciał stałych - wprowadzenie
 Półrzewodniki Teoria złącza PN Budowa i właściwości elektryczne ciał stałych - wrowadzenie Budowa atomu: a) model starożytny b) model J.J. Thomsona c) model E. Rutherforda d) model N. Bohra e) wynikająca
Półrzewodniki Teoria złącza PN Budowa i właściwości elektryczne ciał stałych - wrowadzenie Budowa atomu: a) model starożytny b) model J.J. Thomsona c) model E. Rutherforda d) model N. Bohra e) wynikająca
dr inż. Zbigniew Szklarski
 Wykład 1: Prąd stały dr nż. Zbgnew Szklarsk szkla@agh.edu.pl http://layer.uc.agh.edu.pl/z.szklarsk/ 0.03.1800 Alessandro Volta ognwo cynkowo-medzane 181 Guseppe Zambon Sucha batera paper z folą cynkową
Wykład 1: Prąd stały dr nż. Zbgnew Szklarsk szkla@agh.edu.pl http://layer.uc.agh.edu.pl/z.szklarsk/ 0.03.1800 Alessandro Volta ognwo cynkowo-medzane 181 Guseppe Zambon Sucha batera paper z folą cynkową
Podstawowe równania podsumowanie (1)
 odstawowe rówaa podsumowae () u q + w f u Ts du dq + dw df du Tds sdt dla procesu odwracalego : Tds dq zatem : df du dq sdt a z kole (dla procesu odwracalego) : du dq dw a wtedy : dw dv df dw ( df ) T
odstawowe rówaa podsumowae () u q + w f u Ts du dq + dw df du Tds sdt dla procesu odwracalego : Tds dq zatem : df du dq sdt a z kole (dla procesu odwracalego) : du dq dw a wtedy : dw dv df dw ( df ) T
System finansowy gospodarki
 System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
Spalanie. 1. Skład paliw. 1.1. Paliwa gazowe (1) kmol C. kmol H 2. gdzie: H. , itd. udziały molowe składników paliwa w gazie. suchym. kmol.
 Salae / 1 Salae Salae jet zybko rzebegającym roceem utleaa ołączoym z ydzelaem ę ceła. Salau z reguły toarzyzy emja śatła. Podtaoym eratkam alym alach ą ęgel odór. W ale moża yróżć część alą ealy balat.
Salae / 1 Salae Salae jet zybko rzebegającym roceem utleaa ołączoym z ydzelaem ę ceła. Salau z reguły toarzyzy emja śatła. Podtaoym eratkam alym alach ą ęgel odór. W ale moża yróżć część alą ealy balat.
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
FUNKCJE DWÓCH ZMIENNYCH
 FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
Statystyka Opisowa Wzory
 tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
Estymacja przedziałowa
 Metody probabilistycze i statystyka Estymacja przedziałowa Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Metody probabilistycze
Metody probabilistycze i statystyka Estymacja przedziałowa Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Metody probabilistycze
TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA
 Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 7-8
 Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
WSTĘP METODY OPRACOWANIA I ANALIZY WYNIKÓW POMIARÓW
 WSTĘP METODY OPRACOWANIA I ANALIZY WYNIKÓW POMIARÓW U podstaw wszystkch auk przyrodczych leży zasada: sprawdzaem wszelkej wedzy jest eksperymet, tz jedyą marą prawdy aukowej jest dośwadczee Fzyka, to auka
WSTĘP METODY OPRACOWANIA I ANALIZY WYNIKÓW POMIARÓW U podstaw wszystkch auk przyrodczych leży zasada: sprawdzaem wszelkej wedzy jest eksperymet, tz jedyą marą prawdy aukowej jest dośwadczee Fzyka, to auka
Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI. Wyznaczanie ciepła właściwego c p dla powietrza
 Katedra Silików Saliowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyzaczaie cieła właściweo c dla owietrza Wrowadzeie teoretycze Cieło ochłoięte rzez ciało o jedostkowej masie rzy ieskończeie małym rzyroście
Katedra Silików Saliowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyzaczaie cieła właściweo c dla owietrza Wrowadzeie teoretycze Cieło ochłoięte rzez ciało o jedostkowej masie rzy ieskończeie małym rzyroście
PŁYN Y RZECZYWISTE Przepływy rzeczywiste różnią się od przepływów idealnych obecnością tarcia (lepkości): przepływy laminarne/warstwowe - różnią się
 PŁYNY RZECZYWISTE Płyny rzeczywiste Przeływ laminarny Prawo tarcia Newtona Przeływ turbulentny Oór dynamiczny Prawdoodobieństwo hydrodynamiczne Liczba Reynoldsa Politechnika Oolska Oole University of Technology
PŁYNY RZECZYWISTE Płyny rzeczywiste Przeływ laminarny Prawo tarcia Newtona Przeływ turbulentny Oór dynamiczny Prawdoodobieństwo hydrodynamiczne Liczba Reynoldsa Politechnika Oolska Oole University of Technology
Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego
 Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
10. FALE, ELEMENTY TERMODYNAMIKI I HYDRODY- NAMIKI.
 0. FALE, ELEMENY ERMODYNAMIKI I HYDRODY- NAMIKI. 0.9. Podstawy termodynamiki i raw gazowych. Podstawowe ojęcia Gaz doskonały: - cząsteczki są unktami materialnymi, - nie oddziałują ze sobą siłami międzycząsteczkowymi,
0. FALE, ELEMENY ERMODYNAMIKI I HYDRODY- NAMIKI. 0.9. Podstawy termodynamiki i raw gazowych. Podstawowe ojęcia Gaz doskonały: - cząsteczki są unktami materialnymi, - nie oddziałują ze sobą siłami międzycząsteczkowymi,
Elementy arytmetyki komputerowej
 Elemety arytmetyk komputerowej cz. I Elemety systemów lczbowych /materał pomocczy do wykładu Iformatyka sem II/ Sps treśc. Wprowadzee.... Wstępe uwag o systemach lczbowych... 3. Przegląd wybraych systemów
Elemety arytmetyk komputerowej cz. I Elemety systemów lczbowych /materał pomocczy do wykładu Iformatyka sem II/ Sps treśc. Wprowadzee.... Wstępe uwag o systemach lczbowych... 3. Przegląd wybraych systemów
Niepewności pomiarów. DR Andrzej Bąk
 Nepewośc pomarów DR Adrzej Bąk Defcje Błąd pomar - różca mędz wkem pomar a wartoścą merzoej welkośc fzczej. Bwa też azwa błędem bezwzględm pomar. Poeważ wartość welkośc merzoej wartość prawdzwa jest w
Nepewośc pomarów DR Adrzej Bąk Defcje Błąd pomar - różca mędz wkem pomar a wartoścą merzoej welkośc fzczej. Bwa też azwa błędem bezwzględm pomar. Poeważ wartość welkośc merzoej wartość prawdzwa jest w
MODELE OBIEKTÓW W 3-D3 część
 WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
ELEMENTY ELEKTRONICZNE
 AKADMA GÓRNZO-HUTNZA M. STANSŁAWA STASZA W KRAKOW Wydzał nformatyk, lektronk Telekomunkacj Katedra lektronk LMNTY LKTRONZN dr nż. Potr Dzurdza aw. -3, okój 413; tel. 617-27-02, otr.dzurdza@agh.edu.l dr
AKADMA GÓRNZO-HUTNZA M. STANSŁAWA STASZA W KRAKOW Wydzał nformatyk, lektronk Telekomunkacj Katedra lektronk LMNTY LKTRONZN dr nż. Potr Dzurdza aw. -3, okój 413; tel. 617-27-02, otr.dzurdza@agh.edu.l dr
TERMODYNAMIKA TECHNICZNA I CHEMICZNA
 TRMODYNAMIKA TCHNICZNA I CHMICZNA Część IV TRMODYNAMIKA ROZTWORÓW TRMODYNAMIKA ROZTWORÓW FUGATYWNOŚCI I AKTYWNOŚCI a) Wrowadzene Potencjał chemczny - rzyomnene de G n na odstawe tego, że otencjał termodynamczny
TRMODYNAMIKA TCHNICZNA I CHMICZNA Część IV TRMODYNAMIKA ROZTWORÓW TRMODYNAMIKA ROZTWORÓW FUGATYWNOŚCI I AKTYWNOŚCI a) Wrowadzene Potencjał chemczny - rzyomnene de G n na odstawe tego, że otencjał termodynamczny
Modele wartości pieniądza w czasie
 Joaa Ceślak, Paula Bawej Modele wartośc peądza w czase Podstawowe pojęca ozaczea Kaptał (ag. prcpal), kaptał początkowy, wartośd początkowa westycj - peądze jake zostały wpłacoe a początku westycj (a początku
Joaa Ceślak, Paula Bawej Modele wartośc peądza w czase Podstawowe pojęca ozaczea Kaptał (ag. prcpal), kaptał początkowy, wartośd początkowa westycj - peądze jake zostały wpłacoe a początku westycj (a początku



