Metody Obliczeniowe Mikrooptyki i Fotoniki
|
|
|
- Czesław Olejniczak
- 6 lat temu
- Przeglądów:
Transkrypt
1 Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy programu Meep (interfejs pythonowy i scheme) Metoda FDTD c.d. - nieciągłości przenikalności elektrycznej, dyspersja M. N. Sadiku, Numerical Techniques in Electromagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Computational Electrodynamics The Finite-Difference Time Domain Method, Artech House, 2005
2 Metody Obliczeniowe Mikrooptyki i Fotoniki Program MEEP (>ver. 1.4) (interfejs w pythonie; elementy języka Scheme) Complete scriptability via Python, Scheme, or C++ APIs.
3 Program MEEP Meep (or MEEP) is a free finite-difference time-domain (FDTD) simulation software package developed at MIT to model electromagnetic systems, along with our MPB eigenmode package. Its features include: Free software under the GNU GPL. Simulation in 1d, 2d, 3d, and cylindrical coordinates. Distributed memory parallelism on any system supporting the MPI standard. Portable to any Unix-like system Arbitrary anisotropic electric permittivity ε and magnetic permeability μ, along with dispersive ε(ω) and μ(ω) (including loss/gain) and nonlinear (Kerr & Pockels) dielectric and magnetic materials, and electric/magnetic conductivities σ. PML absorbing boundaries and/or perfect conductor and/or Bloch-periodic boundary conditions. Exploitation of symmetries to reduce the computation size even/odd mirror symmetries and 90 /180 rotations. Complete scriptability either via a Scheme scripting front-end (as in libctl and MPB), or callable as a C++ library; a Python interface is also available. Field output in the HDF5 standard scientific data format, supported by many visualization tools. Arbitrary material and source distributions including a guided-mode launcher. Frequency-domain solver for finding the response to a continuous-wave source. Field analyses including flux spectra, near to far field transformations, modal depcomposition, frequency extraction, local density of states, modal volume, Maxwell stress tensor, arbitrary functions; completely programmable. Meep officially stands for MIT Electromagnetic Equation Propagation
4 Logowanie na klaster: Uruchomienie spydera (interfejs pythonowy): ssh -X -p10024 spyder Kopiowanie plików: scp -r -P10024 scp -r -P10024./katalog Wywołanie bezpośrednie (interfejs scheme): plik wejściowy (Scheme) -bash-3.00$ Wyniki meep foo.ctl >& foo.out Przy dłuższych symulacjach warto użyć poleceń screen i nice / renice W wersji interaktywnej: -bash-3.00$ meep meep> interpreter poleceń scheme meep> (exit) zakończenie pracy
5 Jednostki w meepie Równania Maxwella w jednostkach znormalizowanych μ 0=1, ϵ 0=1, c =1 Można przyjąć dowolną jednostkę długości (np. a=1 nm). Jeśli jednak używamy predefiniowanych materiałów, to ze względu na dyspersję trzeba określić jednostkę długości i domyślnie jest nią a=1um. Inne jednostki: Jednostki długości (np. długość fali): x [a], Jednostki czasu (podaje się w jednostkach długości): t[a/c] Jednostki częstości: f [c/a] (czyli liczbowo f=1/λ), ω [2πc/a]
6 Interfejs meepa w pythonie (Fragmenty tutoriala) Import modułu pythona: import meep as mp Określamy rozmiar obszaru symulacji (w jednostkach umownych): cell = mp.vector3(16, 8, 0) Tworzymy listę obiektów w obszarze symulacji: geometry = [mp.block(mp.vector3(1e20, 1, 1e20), center=mp.vector3(0, 0), material=mp.medium(epsilon=12))] Tworzymy listę prądowych źródeł pola: sources = [mp.source(mp.continuoussource(frequency=0.15), component=mp.ez, center=mp.vector3(-7,0))]
7 Przedstawienie graficzne wyników symulacji Import modułów numy i matplotlib pythona: import numpy as np import matplotlib.pyplot as plt Zobrazowanie zdefiniowanego rozkładu przenikalności elektrycznej: eps_data = sim.get_array(mp.vector3(), cell, mp.dielectric) plt.figure(dpi=100) plt.imshow(eps_data.transpose(), interpolation='spline36', cmap='binary') plt.axis('off') plt.show() Zobrazowanie końcowego rozkładu pola elektrycznego: ez_data = sim.get_array(mp.vector3(), cell, mp.ez) plt.figure(dpi=100) plt.imshow(eps_data.transpose(), interpolation='spline36', cmap='binary') plt.imshow(ez_data.transpose(), interpolation='spline36', cmap='rdbu', alpha=0.9) plt.axis('off') plt.show()
8 Interfejs meepa w pythonie Określamy grubość warstwy PML: pml_layers = [mp.pml(1.0)] Określamy rozdzielczość siatki (liczba punktów na jednostkę długości) resolution = 10 Tworzymy obiekt opisujący symulację: sim = mp.simulation(cell_size=cell, boundary_layers=pml_layers, geometry=geometry, sources=sources, resolution=resolution) Uruchamiamy symulację sim.run(until=200)
9
10 Zapisywanie pola w trakcie symulacji Zapisywanie przenikalności elektrycznej i pośrednich rozkładów pola do plików sim.run(mp.at_beginning(mp.output_epsilon), mp.to_appended("ez",mp.at_every(0.6,mp.output_efield_z)), until=200) Zapisywanie i przetwarzanie fragmentu pola w pamięci w trakcie symulacji Vals = [] def get_slice(sim): center = mp.vector3(0, -3.5) size = mp.vector3(16, 0) vals.append(sim.get_array(center=center, size=size, component=mp.ez)) sim.run( mp.at_beginning(mp.output_epsilon), mp.at_every(0.6, get_slice), until=200 ) plt.figure(dpi=100) plt.imshow(vals, interpolation='spline36', cmap='rdbu') plt.axis('off') plt.show()
11 Materiały dyspersyjne Przykład: susceptibilities = [mp.lorentziansusceptibility(frequency=1.1, gamma=1e-5, sigma=0.5), mp.lorentziansusceptibility(frequency=0.5, gamma=0.1, sigma=2e-5)] default_material = mp.medium(epsilon=2.25,e_susceptibilities=susceptibilities)
12 Metale Biblioteka materiałowa z metalami A.D. Rakic et al., Applied Optics, Vol. 37, No. 22, pp (1998) import sys sys.path.insert(0, '/path/to/materials_library.py') from materials_library import * Predefiniowane materiały: Ag, Au, Cu, Al, Be, Cr, Ni, Pd, Pt, Ti, W
13 Wektor Poyntinga i gęstość energii Synchronizacja pól (run-until 200 (synchronized-magnetic output-poynting output-tot-pwr)) Dodatkowa opcjonalna i przy częstym obliczaniu kosztowna numerycznie synchronizacja czasowa pola elektrycznego i magnetycznego pozwala zminimalizować wpływ próbkowania tych pól w różnych chwilach czasu.
14 Wygładzanie stałych materiałowych TE TE Pole E ciągłe C=C 1 C 2 TM m f 1 1 f 2 2 TM Pole D ciągłe C =C 1 C m f 1 1 f 2 2 f- procent objętości każdego z dielektryków f f =1 1 2 D. E. Aspnes, Local field effects and effective medium theory: a microscopic perspective Am J. Phys 50, 704 (1982)
15 Wygładzanie stałych materiałowych TE TE m f 1 1 f 2 2 TM TM m f 1 1 f 2 2 R.Meade, A. Rappe, K. Brommer, J. Joannopoulos Accurate theoretical analysis of photonic band-gap materials, Phys. Rev B, 48 (1993)
16 Wygładzanie stałych materiałowych TE TE m f 1 1 f 2 2 Anizotropowy efektywny tensor przenikalności dielektrycznej: Składowe wektora normalnego TE TM Tensor Levi-Civita TM [ m ]i, j m n i n j m e kjl enli n k n n mamy: Dla n= x TM [ TE m 0 0 m = 0 m TM TM m m f 1 1 f 2 2 ] R.Meade, A. Rappe, K. Brommer, J. Joannopoulos Accurate theoretical analysis of photonic band-gap materials, Phys. Rev B, 48 (1993)
17 FDTD materiały dyspersyjne, metoda równania pomocniczego (ADE) (ADE- auxiliary differential equation) Prawo Ampera dla ośrodka dyspersyjnego: D E H= J = E 0 p J p t t J p t P p t t Zapis zespolony J p =i P p =i 0 p E
18 FDTD materiały dyspersyjne, metoda równania pomocniczego (ADE) (ADE- auxiliary differential equation) Prawo Ampera dla ośrodka dyspersyjnego: E H= E 0 p J p t J p t P p t t Zapis zespolony J p =i P p =i 0 p E Model Lorentza: 2 p= 0, p 2 0, p 2 i p = p p 2 J p = i 0, p 0 2 0, p 2 i p E
19 FDTD materiały dyspersyjne, metoda równania pomocniczego (ADE) , p i p J p =i 0, p 0 E IFT Równanie pomocnicze (ADE): 2 E t 20, p 2 p J p t = 20, p 0 t t t
20 FDTD materiały dyspersyjne, metoda równania pomocniczego (ADE) Prawo Ampera: Równanie pomocnicze (ADE): E H= E 0 p J p t 2 E t 2 2 p J p t = 0, p 0 t t t 2 0, p Dyskretyzacja E i J w tych samych punktach n 1 2 n 0, p J p n n 1 J p 2J p J p t 2 n 1 p n 1 J p Jp t 2 = 0, p 0 E n 1 E 2 t n [ H n 1/ 2 Otrzymujemy schemat: E n 1,E, Jp, Jp,H E n 1, E, J p, J p J p E n 1 n n 1 n n 1/ 2 n n 1 n n 1 H n 3/ 2 E n 1 ]i = p n 1 n J p J p 2
21 Język SCHEME
22 Język SCHEME Definicja zmiennej: (define var1 value) Definicja zmiennej lokalnej: (let ((var1 value))... ; scope of var1...) Zmiana wartości zmiennej: (set! var1 value) Działania arytmetyczne: (+ var1 value) (- var1 value) (* var1 value) (/ var1 value) Komentarz
23 Język SCHEME
24 Język SCHEME Funkcje Definicja funkcji: (define (fun arg1 arg2...)...) Wywołanie funkcji: (fun value1 value2) albo (apply fun (list value1 value2))
25 Język SCHEME Definicja listy: (list value1 value2 value3...) Listy można zagnieżdżać: (list value1 (list value2 value3) value4) Pierwszy element listy: (car list1) Reszta listy: (cdr list1) Sklejanie list: (const list1 list2)
26 Język SCHEME
27 Język SCHEME
28 Język SCHEME
29 Funkcje i rekurencja
30 Pętle i rekurencja ogonkowa
31 Język SCHEME
32 Proste konstrukcje w Scheme i C Scheme ( ) C ( ) (< low x high) ((low < x) && (x < high)) (+ (* 2 3) (* 4 5)) ((2 * 3) + (4 * 5)) (f x y) f(x, y) (define (sq x) (* x x)) int sq(int x) {return ( x * x ) }
33 Biblioteka libctl Obiekty (struktury) Obiekt zawiera zbiór własności, którym można przypisać wartości: (make type (property1 value1) (property2 value2)...) Wektorowy typ danych: Vector3 jest trójelementową tablicą: (vector3 x [y [z]]) Odwołanie do elementu wektora: (vector3-x v) (vector3-y v) (vector3-z v Operacje na wektorach: (vector3* a b) (vector3- a b) (vector3+ a b) (vector3-cross v1 v2) (vector3-norm v)
34 Propagacja fali w falowodzie PML
35 Propagacja fali w falowodzie h5topng -S3 eps h5 h5topng -S3 -Zc dkbluered -a yarg -A eps h5 ez h5
36 A 90 bend
37 Wizualizacja pliku hdf5 h5dump test-ez.h5 more HDF5 "test-ez.h5" { GROUP "/" { DATASET "ez" { DATATYPE H5T_IEEE_F64LE DATASPACE SIMPLE { ( 160, 160, 333 ) / ( 160, 160, H5S_UNLIMITED ) } DATA { (0,0,0): 0, 0, 0, 0, e-17, e-11, e-09, (0,0,7): e-10, e-10, e-10, e-10,...
38 Wczytywanie plików wyjściowych w Matlabie
39 Meep + C++
40
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
Metody Obliczeniowe Mikrooptyki i Fotoniki. Podstawy metody różnic skończonych Podstawy metody FDTD
 Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody różnic skończonych Podstawy etody FDTD M. N. Sadiku, Nuerical Techniques in Electroagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Coputational
Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody różnic skończonych Podstawy etody FDTD M. N. Sadiku, Nuerical Techniques in Electroagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Coputational
Metody Obliczeniowe Mikrooptyki i Fotoniki. Program mpb i wyznaczanie struktury pasmowej kryształów fotonicznych
 Metody Obliczeniowe Mikrooptyki i Fotoniki Program mpb i wyznaczanie struktury pasmowej kryształów fotonicznych Kryształy fotoniczne metoda fal płaskich Periodyczność i brak własności magnetycznych i strat:
Metody Obliczeniowe Mikrooptyki i Fotoniki Program mpb i wyznaczanie struktury pasmowej kryształów fotonicznych Kryształy fotoniczne metoda fal płaskich Periodyczność i brak własności magnetycznych i strat:
Metody Obliczeniowe Mikrooptyki i Fotoniki. Metoda propagacji wiązki BPM Modelowanie propagacji
 Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Analiza wpływu średnicy zbrojenia, rozstawu pomiędzy prętami oraz parametrów elektrycznych betonu na wartości natężenia pola elektrycznego
 Agnieszka CHOROSZUCHO Politechnika Białostocka, Wydział Elektryczny Analiza wpływu średnicy zbrojenia, rozstawu pomiędzy prętami oraz parametrów elektrycznych betonu na wartości natężenia pola elektrycznego
Agnieszka CHOROSZUCHO Politechnika Białostocka, Wydział Elektryczny Analiza wpływu średnicy zbrojenia, rozstawu pomiędzy prętami oraz parametrów elektrycznych betonu na wartości natężenia pola elektrycznego
OPTYMALIZACJA SPRZĘGACZY SIATKOWYCH W UKŁADACH OPTYKI ZINTEGROWANEJ
 ELEKTRYKA 9 Zeszyt 4 () Rok LV Przemysław STRUK, Tadeusz PUSTELNY Katedra Optoelektroniki, Politechnika Śląska w Gliwicach OPTYMALIZACJA SPRZĘGACZY SIATKOWYCH W UKŁADACH OPTYKI ZINTEGROWANEJ Streszczenie.
ELEKTRYKA 9 Zeszyt 4 () Rok LV Przemysław STRUK, Tadeusz PUSTELNY Katedra Optoelektroniki, Politechnika Śląska w Gliwicach OPTYMALIZACJA SPRZĘGACZY SIATKOWYCH W UKŁADACH OPTYKI ZINTEGROWANEJ Streszczenie.
Tablice, funkcje - wprowadzenie
 Tablice, funkcje - wprowadzenie Przemysław Gawroński D-10, p. 234 Wykład 5 25 marca 2019 (Wykład 5) Tablice, funkcje - wprowadzenie 25 marca 2019 1 / 12 Outline 1 Tablice jednowymiarowe 2 Funkcje (Wykład
Tablice, funkcje - wprowadzenie Przemysław Gawroński D-10, p. 234 Wykład 5 25 marca 2019 (Wykład 5) Tablice, funkcje - wprowadzenie 25 marca 2019 1 / 12 Outline 1 Tablice jednowymiarowe 2 Funkcje (Wykład
Wprowadzenie do Python
 Wprowadzenie do Python Marcin Orchel 1 Środowisko Python Zalecane korzystanie z dystrybucji Anaconda. W systemie linux może być już dostępny Python. Sprawdzenie wersji Pythona, python -V. Uruchomienie
Wprowadzenie do Python Marcin Orchel 1 Środowisko Python Zalecane korzystanie z dystrybucji Anaconda. W systemie linux może być już dostępny Python. Sprawdzenie wersji Pythona, python -V. Uruchomienie
Instrukcja do wykonania symulacji numerycznych CFD w programie PolyFlow 14.0 przepływu płynów nienewtonowskich o właściwościach lepkosprężystych
 Instrukcja do wykonania symulacji numerycznych CFD w programie PolyFlow 14.0 przepływu płynów nienewtonowskich o właściwościach lepkosprężystych 1. Uruchamianie programu PolyFlow W ramach projektu symulacje
Instrukcja do wykonania symulacji numerycznych CFD w programie PolyFlow 14.0 przepływu płynów nienewtonowskich o właściwościach lepkosprężystych 1. Uruchamianie programu PolyFlow W ramach projektu symulacje
Skład i wilgotność betonu komórkowego jako czynniki wpływające na skuteczność systemów komunikacji bezprzewodowej w budynkach
 Skład i wilgotność betonu komórkowego jako czynniki wpływające na skuteczność systemów komunikacji bezprzewodowej w budynkach Agnieszka Choroszucho, Adam Steckiewicz Wprowadzenie Obecna polityka energetyczna
Skład i wilgotność betonu komórkowego jako czynniki wpływające na skuteczność systemów komunikacji bezprzewodowej w budynkach Agnieszka Choroszucho, Adam Steckiewicz Wprowadzenie Obecna polityka energetyczna
Fotonika. Plan: Wykład 11: Kryształy fotoniczne
 Fotonika Wykład 11: Kryształy fotoniczne Plan: Kryształy fotoniczne Homogenizacja długofalowa Prawo załamania dla kryształów fotonicznych, superkolimacja Tw. Blocha, kryształy, kryształy fotoniczne, kryształy
Fotonika Wykład 11: Kryształy fotoniczne Plan: Kryształy fotoniczne Homogenizacja długofalowa Prawo załamania dla kryształów fotonicznych, superkolimacja Tw. Blocha, kryształy, kryształy fotoniczne, kryształy
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM cd wyznaczanie modów metodą urojonej długości i korelacyjną operowanie efektywnym współczynnikiem załamania metoda FT-BPM metoda
Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM cd wyznaczanie modów metodą urojonej długości i korelacyjną operowanie efektywnym współczynnikiem załamania metoda FT-BPM metoda
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Efektywne symulacje mikromagnetyczne układów magnonicznych przy wykorzystaniu GPGPU.
 Efektywne symulacje mikromagnetyczne układów magnonicznych przy wykorzystaniu GPGPU. Mateusz Zelent, Paweł Gruszecki, Michał Mruczkiewicz, Maciej Krawczyk Wydział Fizyki, Zakład Fizyki Nanomateriałów Fale
Efektywne symulacje mikromagnetyczne układów magnonicznych przy wykorzystaniu GPGPU. Mateusz Zelent, Paweł Gruszecki, Michał Mruczkiewicz, Maciej Krawczyk Wydział Fizyki, Zakład Fizyki Nanomateriałów Fale
Wpływ struktury cegieł klinkierowych oraz ich konduktywności na wartości pola elektrycznego
 Wpływ struktury cegieł klinkierowych oraz ich konduktywności na wartości pola elektrycznego Agnieszka Choroszucho, Bogusław Butryło Wprowadzenie Współczesna technologia budowlana jest oparta głównie na
Wpływ struktury cegieł klinkierowych oraz ich konduktywności na wartości pola elektrycznego Agnieszka Choroszucho, Bogusław Butryło Wprowadzenie Współczesna technologia budowlana jest oparta głównie na
Podstawy elektromagnetyzmu. Wykład 2. Równania Maxwella
 Podstawy elektromagnetyzmu Wykład 2 Równania Maxwella Prawa Maxwella opisują pola Pole elektryczne... to zjawisko występujące w otoczeniu naładowanych elektrycznie obiektów lub jest skutkiem zmiennego
Podstawy elektromagnetyzmu Wykład 2 Równania Maxwella Prawa Maxwella opisują pola Pole elektryczne... to zjawisko występujące w otoczeniu naładowanych elektrycznie obiektów lub jest skutkiem zmiennego
Fotonika. Plan: Wykład 14: podsumowanie, uzupełnienie
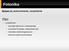 Fotonika Wykład 14: podsumowanie, uzupełnienie Plan: Uzupełnienie: kryształy fotoniczne i metamateriały soczewka Pendrego, nadrozdzielczość Absorbery elektromagnetyczne elementy optyki fourierowskiej Optyka
Fotonika Wykład 14: podsumowanie, uzupełnienie Plan: Uzupełnienie: kryształy fotoniczne i metamateriały soczewka Pendrego, nadrozdzielczość Absorbery elektromagnetyczne elementy optyki fourierowskiej Optyka
Prawdopodobieństwo i statystyka
 Wykład XV: Zagadnienia redukcji wymiaru danych 2 lutego 2015 r. Standaryzacja danych Standaryzacja danych Własności macierzy korelacji Definicja Niech X będzie zmienną losową o skończonym drugim momencie.
Wykład XV: Zagadnienia redukcji wymiaru danych 2 lutego 2015 r. Standaryzacja danych Standaryzacja danych Własności macierzy korelacji Definicja Niech X będzie zmienną losową o skończonym drugim momencie.
Mody sprzężone plazmon-fonon w silnych polach magnetycznych
 Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
Lp Temat Opis Opiekun
 Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 6, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Plan. krótkie opisy modułów. 1 Uwagi na temat wydajności CPython a. 2 Podstawowe techniki poprawiające wydajność obliczeniową
 Plan 1 Uwagi na temat wydajności CPython a 2 Podstawowe techniki poprawiające wydajność obliczeniową 3 Podstawowe techniki poprawiające zużycie pamięci krótkie opisy modułów 1 array - jak oszczędzić na
Plan 1 Uwagi na temat wydajności CPython a 2 Podstawowe techniki poprawiające wydajność obliczeniową 3 Podstawowe techniki poprawiające zużycie pamięci krótkie opisy modułów 1 array - jak oszczędzić na
DIAGRAMY SYNTAKTYCZNE JĘZYKA TURBO PASCAL 6.0
 Uwaga: DIAGRAMY SYNTAKTYCZNE JĘZYKA TURBO PASCAL 6.0 1. Zostały pominięte diagramy: CYFRA, CYFRA SZESNASTKOWA, ZNAK i LITERA. Nie została uwzględniona możliwość posługiwania się komentarzami. 2. Brakuje
Uwaga: DIAGRAMY SYNTAKTYCZNE JĘZYKA TURBO PASCAL 6.0 1. Zostały pominięte diagramy: CYFRA, CYFRA SZESNASTKOWA, ZNAK i LITERA. Nie została uwzględniona możliwość posługiwania się komentarzami. 2. Brakuje
KATEDRA TELEKOMUNIKACJI I FOTONIKI
 ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
SYMULACJA TŁOCZENIA ZAKRYWEK KORONKOWYCH SIMULATION OF CROWN CLOSURES FORMING
 MARIUSZ DOMAGAŁA, STANISŁAW OKOŃSKI ** SYMULACJA TŁOCZENIA ZAKRYWEK KORONKOWYCH SIMULATION OF CROWN CLOSURES FORMING S t r e s z c z e n i e A b s t r a c t W artykule podjęto próbę modelowania procesu
MARIUSZ DOMAGAŁA, STANISŁAW OKOŃSKI ** SYMULACJA TŁOCZENIA ZAKRYWEK KORONKOWYCH SIMULATION OF CROWN CLOSURES FORMING S t r e s z c z e n i e A b s t r a c t W artykule podjęto próbę modelowania procesu
Wykład Ćwiczenia Laboratorium Projekt Seminarium 45
 Zał. nr 4 do ZW /202 WYDZIAŁ PPT / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Studenckie laboratorium obliczeniowe Nazwa w języku angielskim Student computational laboratory Kierunek studiów (jeśli
Zał. nr 4 do ZW /202 WYDZIAŁ PPT / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Studenckie laboratorium obliczeniowe Nazwa w języku angielskim Student computational laboratory Kierunek studiów (jeśli
Wstęp do programowania
 Wstęp do programowania Podstawowe konstrukcje programistyczne Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) WP w. II Jesień 2014 1 / 38 Przypomnienie Programowanie imperatywne Program
Wstęp do programowania Podstawowe konstrukcje programistyczne Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) WP w. II Jesień 2014 1 / 38 Przypomnienie Programowanie imperatywne Program
Pakiety matematyczne. Matematyka Stosowana. dr inż. Krzysztof Burnecki
 Pakiety matematyczne Matematyka Stosowana dr inż. Krzysztof Burnecki 17.04.2013 Wykład 9 Operacje symboliczne w Matlabie Graficzny interfejs użytkownika (GUI) Slajdy powstały na podstawie prezentacji Informatyka
Pakiety matematyczne Matematyka Stosowana dr inż. Krzysztof Burnecki 17.04.2013 Wykład 9 Operacje symboliczne w Matlabie Graficzny interfejs użytkownika (GUI) Slajdy powstały na podstawie prezentacji Informatyka
Lp Temat Opis Opiekun
 Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Statystyka i eksploracja danych
 Wykład XII: Zagadnienia redukcji wymiaru danych 12 maja 2014 Definicja Niech X będzie zmienną losową o skończonym drugim momencie. Standaryzacją zmiennej X nazywamy zmienną losową Z = X EX Var (X ). Definicja
Wykład XII: Zagadnienia redukcji wymiaru danych 12 maja 2014 Definicja Niech X będzie zmienną losową o skończonym drugim momencie. Standaryzacją zmiennej X nazywamy zmienną losową Z = X EX Var (X ). Definicja
Metodyki projektowania i modelowania systemów Cyganek & Kasperek & Rajda 2013 Katedra Elektroniki AGH
 Kierunek Elektronika i Telekomunikacja, Studia II stopnia Specjalność: Systemy wbudowane Metodyki projektowania i modelowania systemów Cyganek & Kasperek & Rajda 2013 Katedra Elektroniki AGH Zagadnienia
Kierunek Elektronika i Telekomunikacja, Studia II stopnia Specjalność: Systemy wbudowane Metodyki projektowania i modelowania systemów Cyganek & Kasperek & Rajda 2013 Katedra Elektroniki AGH Zagadnienia
Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość
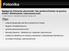 Fotonika Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość S. Maier Plasmonics fundamentals and applications (Springer, 007). Plan: związek dyspersyjny
Fotonika Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość S. Maier Plasmonics fundamentals and applications (Springer, 007). Plan: związek dyspersyjny
Język Python (2) Język Python (2) 1/36
 Język Python (2) Język Python (2) 1/36 Język Python (2) 2/36 Podstawy funkcji Pojęcia podstawowe Instrukcja def tworzy obiekt funkcji i przypisuje go do nazwy Instrukcja return przekazuje obiekt wynikowy
Język Python (2) Język Python (2) 1/36 Język Python (2) 2/36 Podstawy funkcji Pojęcia podstawowe Instrukcja def tworzy obiekt funkcji i przypisuje go do nazwy Instrukcja return przekazuje obiekt wynikowy
Fotonika. Plan: Wykład 15: Elementy plazmoniki: struktury cienkowarstwowe, elementy teorii ośrodków efektywnych
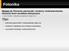 Fotonika Wykład 15: Elementy plazmoniki: struktury cienkowarstwowe, elementy teorii ośrodków efektywnych S. Maier Plasmonics fundamentals and applications (Springer, 2007). Plan: Elementy plazmoniki i
Fotonika Wykład 15: Elementy plazmoniki: struktury cienkowarstwowe, elementy teorii ośrodków efektywnych S. Maier Plasmonics fundamentals and applications (Springer, 2007). Plan: Elementy plazmoniki i
Spis treści. I. Skuteczne. Od autora... Obliczenia inżynierskie i naukowe... Ostrzeżenia...XVII
 Spis treści Od autora..................................................... Obliczenia inżynierskie i naukowe.................................. X XII Ostrzeżenia...................................................XVII
Spis treści Od autora..................................................... Obliczenia inżynierskie i naukowe.................................. X XII Ostrzeżenia...................................................XVII
Od żłobka do przedszkola - mini szkolenie z użytkowania pakietu OpenFOAM. Karol Wędołowski 06.04.2011
 Od żłobka do przedszkola - mini szkolenie z użytkowania pakietu OpenFOAM Karol Wędołowski 06.04.2011 Część 2. Struktura case'u na przykładzie przepływu w zagłębieniu 1. Potrzebne katalog i pliki W tej
Od żłobka do przedszkola - mini szkolenie z użytkowania pakietu OpenFOAM Karol Wędołowski 06.04.2011 Część 2. Struktura case'u na przykładzie przepływu w zagłębieniu 1. Potrzebne katalog i pliki W tej
ZASTOSOWANIE PAKIETU FLUX2D DO ANALIZY POLA ELEKTROMAGNETYCZNEGO I TEMPERATURY W NAGRZEWNICY INDUKCYJNEJ DO WSADÓW PŁASKICH
 Tomasz SZCZEGIELNIAK Zygmunt PIĄTEK ZASTOSOWANIE PAKIETU FLUX2D DO ANALIZY POLA ELEKTROMAGNETYCZNEGO I TEMPERATURY W NAGRZEWNICY INDUKCYJNEJ DO WSADÓW PŁASKICH STRESZCZENIE Praca zawiera wyniki symulacji
Tomasz SZCZEGIELNIAK Zygmunt PIĄTEK ZASTOSOWANIE PAKIETU FLUX2D DO ANALIZY POLA ELEKTROMAGNETYCZNEGO I TEMPERATURY W NAGRZEWNICY INDUKCYJNEJ DO WSADÓW PŁASKICH STRESZCZENIE Praca zawiera wyniki symulacji
Elementy języka Scheme
 Elementy języka Scheme Historia języka Lisp Wyrażenia i ewaluacja wyrażeń Identyfikatory i wyrażenie let Wyrażenia lambda Definicje globalne Wyrażenia warunkowe Przypisanie Kontynuacje Historia języka
Elementy języka Scheme Historia języka Lisp Wyrażenia i ewaluacja wyrażeń Identyfikatory i wyrażenie let Wyrażenia lambda Definicje globalne Wyrażenia warunkowe Przypisanie Kontynuacje Historia języka
Efekt naskórkowy (skin effect)
 Efekt naskórkowy (skin effect) Rozważmy cylindryczny przewód o promieniu a i o nieskończonej długości. Przez przewód płynie prąd I = I 0 cos ωt. Dla niezbyt dużych częstości ω możemy zaniedbać prąd przesunięcia,
Efekt naskórkowy (skin effect) Rozważmy cylindryczny przewód o promieniu a i o nieskończonej długości. Przez przewód płynie prąd I = I 0 cos ωt. Dla niezbyt dużych częstości ω możemy zaniedbać prąd przesunięcia,
Elementy języka Scheme
 Elementy języka Scheme Historia języka Lisp Historia języka Lisp Wyrażenia i ewaluacja wyrażeń Identyfikatory i wyrażenie let Wyrażenia lambda Definicje globalne Wyrażenia warunkowe Przypisanie Kontynuacje
Elementy języka Scheme Historia języka Lisp Historia języka Lisp Wyrażenia i ewaluacja wyrażeń Identyfikatory i wyrażenie let Wyrażenia lambda Definicje globalne Wyrażenia warunkowe Przypisanie Kontynuacje
Lab 9 Podstawy Programowania
 Lab 9 Podstawy Programowania (Kaja.Gutowska@cs.put.poznan.pl) Wszystkie kody/fragmenty kodów dostępne w osobnym pliku.txt. Materiały pomocnicze: Wskaźnik to specjalny rodzaj zmiennej, w której zapisany
Lab 9 Podstawy Programowania (Kaja.Gutowska@cs.put.poznan.pl) Wszystkie kody/fragmenty kodów dostępne w osobnym pliku.txt. Materiały pomocnicze: Wskaźnik to specjalny rodzaj zmiennej, w której zapisany
Fotonika. Plan: Wykład 3: Polaryzacja światła
 Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 18, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 18, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Podstawy elektrodynamiki / David J. Griffiths. - wyd. 2, dodr. 3. Warszawa, 2011 Spis treści. Przedmowa 11
 Podstawy elektrodynamiki / David J. Griffiths. - wyd. 2, dodr. 3. Warszawa, 2011 Spis treści Przedmowa 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce? 13 1. Analiza wektorowa 19
Podstawy elektrodynamiki / David J. Griffiths. - wyd. 2, dodr. 3. Warszawa, 2011 Spis treści Przedmowa 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce? 13 1. Analiza wektorowa 19
Myśl w języku Python! : nauka programowania / Allen B. Downey. Gliwice, cop Spis treści
 Myśl w języku Python! : nauka programowania / Allen B. Downey. Gliwice, cop. 2017 Spis treści Przedmowa 11 1. Jak w programie 21 Czym jest program? 21 Uruchamianie interpretera języka Python 22 Pierwszy
Myśl w języku Python! : nauka programowania / Allen B. Downey. Gliwice, cop. 2017 Spis treści Przedmowa 11 1. Jak w programie 21 Czym jest program? 21 Uruchamianie interpretera języka Python 22 Pierwszy
Fala EM w izotropowym ośrodku absorbującym
 Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Fale elektromagnetyczne
 Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Projektowanie systemów EM. Metoda elementów skończonych
 Projektowanie systemów EM Metoda elementów skończonych Wstęp Podstawy obliczeń MES Etapy definicji modelu numerycznego Rodzaje problemów moduły obliczeniowe Wybrane wyniki obliczeń 2 dr inż. Michał Michna
Projektowanie systemów EM Metoda elementów skończonych Wstęp Podstawy obliczeń MES Etapy definicji modelu numerycznego Rodzaje problemów moduły obliczeniowe Wybrane wyniki obliczeń 2 dr inż. Michał Michna
Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką
 Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Instytut Podstawowych Problemów Techniki PAN Zakład Teorii Ośrodków
Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Instytut Podstawowych Problemów Techniki PAN Zakład Teorii Ośrodków
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Tablice, funkcje, wskaźniki - wprowadzenie
 Tablice, funkcje, wskaźniki - wprowadzenie Przemysław Gawroński D-10, p. 234 Wykład 4 19 listopada 2018 (Wykład 4) Tablice, funkcje, wskaźniki - wprowadzenie 19 listopada 2018 1 / 37 Outline 1 Tablice
Tablice, funkcje, wskaźniki - wprowadzenie Przemysław Gawroński D-10, p. 234 Wykład 4 19 listopada 2018 (Wykład 4) Tablice, funkcje, wskaźniki - wprowadzenie 19 listopada 2018 1 / 37 Outline 1 Tablice
Podpis prowadzącego SPRAWOZDANIE
 Imię i nazwisko.. Grupa. Data. Podpis prowadzącego. SPRAWOZDANIE LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1 Zadanie nr 1 (plik strip.pro,nazwa ośrodka wypełniającego prowadnicę - "airlossy") Rozważamy przypadek
Imię i nazwisko.. Grupa. Data. Podpis prowadzącego. SPRAWOZDANIE LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1 Zadanie nr 1 (plik strip.pro,nazwa ośrodka wypełniającego prowadnicę - "airlossy") Rozważamy przypadek
Automatyczne generowanie testów z modeli. Bogdan Bereza Automatyczne generowanie testów z modeli
 Automatyczne generowanie testów z modeli Numer: 1 (33) Rozkmina: Projektowanie testów na podstawie modeli (potem można je wykonywać ręcznie, lub automatycznie zwykle chce się automatycznie) A ja mówię
Automatyczne generowanie testów z modeli Numer: 1 (33) Rozkmina: Projektowanie testów na podstawie modeli (potem można je wykonywać ręcznie, lub automatycznie zwykle chce się automatycznie) A ja mówię
Metody eksploracji danych Laboratorium 1. Weka + Python + regresja
 Metody eksploracji danych Laboratorium 1 Weka + Python + regresja Zasoby Cel Metody eksploracji danych Weka (gdzieś na dysku) Środowisko dla języka Python (Spyder, Jupyter, gdzieś na dysku) Zbiory danych
Metody eksploracji danych Laboratorium 1 Weka + Python + regresja Zasoby Cel Metody eksploracji danych Weka (gdzieś na dysku) Środowisko dla języka Python (Spyder, Jupyter, gdzieś na dysku) Zbiory danych
Kurs rozszerzony języka Python
 Wykład 2. 13 października 2017 Plan wykładu Klasy i obiekty 1 Klasy i obiekty 2 3 4 Plan wykładu Klasy i obiekty 1 Klasy i obiekty 2 3 4 Deklaracja klasy Klasy i obiekty Przykłady class Figura: Pierwsza
Wykład 2. 13 października 2017 Plan wykładu Klasy i obiekty 1 Klasy i obiekty 2 3 4 Plan wykładu Klasy i obiekty 1 Klasy i obiekty 2 3 4 Deklaracja klasy Klasy i obiekty Przykłady class Figura: Pierwsza
PROGRAMOWANIE SYSTEMÓW CZASU RZECZYWISTEGO
 PROGRAMOWANIE SYSTEMÓW CZASU RZECZYWISTEGO LABORATORIUM Temat: QNX Neutrino Interrupts Mariusz Rudnicki 2016 Wstęp W QNX Neutrino wszystkie przerwania sprzętowe przechwytywane są przez jądro systemu. Obsługę
PROGRAMOWANIE SYSTEMÓW CZASU RZECZYWISTEGO LABORATORIUM Temat: QNX Neutrino Interrupts Mariusz Rudnicki 2016 Wstęp W QNX Neutrino wszystkie przerwania sprzętowe przechwytywane są przez jądro systemu. Obsługę
Języki i metody programowania Java. Wykład 2 (część 2)
 Języki i metody programowania Java INF302W Wykład 2 (część 2) Autor Dr inż. Zofia Kruczkiewicz 1 Struktura wykładu 1. Identyfikacja danych reprezentowanych przez klasy podczas opracowania koncepcji prostego
Języki i metody programowania Java INF302W Wykład 2 (część 2) Autor Dr inż. Zofia Kruczkiewicz 1 Struktura wykładu 1. Identyfikacja danych reprezentowanych przez klasy podczas opracowania koncepcji prostego
RÓWNANIA MAXWELLA. Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego?
 RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki
 Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki Spis treści Przedmowa... 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce?... 13 1. Analiza wektorowa... 19 1.1. Algebra
Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki Spis treści Przedmowa... 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce?... 13 1. Analiza wektorowa... 19 1.1. Algebra
Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji
 Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Motywacja Podstawy. Historia Teoria 2D PhC Podsumowanie. Szymon Lis Photonics Group szymon.lis@pwr.wroc.pl C-2 p.305. Motywacja.
 Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
Badanie uporządkowania magnetycznego w ultracienkich warstwach kobaltu w pobliżu reorientacji spinowej.
 Tel.: +48-85 7457229, Fax: +48-85 7457223 Zakład Fizyki Magnetyków Uniwersytet w Białymstoku Ul.Lipowa 41, 15-424 Białystok E-mail: vstef@uwb.edu.pl http://physics.uwb.edu.pl/zfm Praca magisterska Badanie
Tel.: +48-85 7457229, Fax: +48-85 7457223 Zakład Fizyki Magnetyków Uniwersytet w Białymstoku Ul.Lipowa 41, 15-424 Białystok E-mail: vstef@uwb.edu.pl http://physics.uwb.edu.pl/zfm Praca magisterska Badanie
Wstęp do programowania
 Wstęp do programowania wykład 2 Piotr Cybula Wydział Matematyki i Informatyki UŁ 2012/2013 http://www.math.uni.lodz.pl/~cybula Język programowania Każdy język ma swoją składnię: słowa kluczowe instrukcje
Wstęp do programowania wykład 2 Piotr Cybula Wydział Matematyki i Informatyki UŁ 2012/2013 http://www.math.uni.lodz.pl/~cybula Język programowania Każdy język ma swoją składnię: słowa kluczowe instrukcje
RÓŻNORODNOŚĆ SKŁADU BETONU I JEGO WPŁYW NA NATĘŻENIE POLA ELEKTRYCZNEGO
 POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0016 Agnieszka CHOROSZUCHO * RÓŻNORODNOŚĆ SKŁADU BETONU I JEGO WPŁYW NA NATĘŻENIE POLA
POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0016 Agnieszka CHOROSZUCHO * RÓŻNORODNOŚĆ SKŁADU BETONU I JEGO WPŁYW NA NATĘŻENIE POLA
Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional
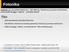 Fotonika Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional Plan: Jednowymiarowe kryształy fotoniczne Fale Blocha, fotoniczna struktura
Fotonika Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional Plan: Jednowymiarowe kryształy fotoniczne Fale Blocha, fotoniczna struktura
Modelowanie numeryczne w fizyce atmosfery Ćwiczenia 3
 Modelowanie numeryczne w fizyce atmosfery Sylwester Arabas (ćwiczenia do wykładu dr. hab. inż. Lecha Łobockiego) Instytut Geofizyki, Wydział Fizyki Uniwersytetu Warszawskiego 3. listopada 2011 r. Schemat
Modelowanie numeryczne w fizyce atmosfery Sylwester Arabas (ćwiczenia do wykładu dr. hab. inż. Lecha Łobockiego) Instytut Geofizyki, Wydział Fizyki Uniwersytetu Warszawskiego 3. listopada 2011 r. Schemat
Logika rozmyta typu 2
 Logika rozmyta typu 2 Zbiory rozmyte Funkcja przynależności Interwałowe zbiory rozmyte Funkcje przynależności przedziałów Zastosowanie.9.5 Francuz Polak Niemiec Arytmetyka przedziałów Operacje zbiorowe
Logika rozmyta typu 2 Zbiory rozmyte Funkcja przynależności Interwałowe zbiory rozmyte Funkcje przynależności przedziałów Zastosowanie.9.5 Francuz Polak Niemiec Arytmetyka przedziałów Operacje zbiorowe
Programowanie obiektowe
 Programowanie obiektowe Wykład 2: Wstęp do języka Java 3/4/2013 S.Deniziak: Programowanie obiektowe - Java 1 Cechy języka Java Wszystko jest obiektem Nie ma zmiennych globalnych Nie ma funkcji globalnych
Programowanie obiektowe Wykład 2: Wstęp do języka Java 3/4/2013 S.Deniziak: Programowanie obiektowe - Java 1 Cechy języka Java Wszystko jest obiektem Nie ma zmiennych globalnych Nie ma funkcji globalnych
Podstawy biblioteki Matplotlib
 Podstawy biblioteki Matplotlib Krzysztof Gdawiec Instytut Informatyki Uniwersytet Śląski Matplotlib jest biblioteką Pythona służącą do tworzenia różnego rodzaju wykresów. Biblioteka ta od samego początku
Podstawy biblioteki Matplotlib Krzysztof Gdawiec Instytut Informatyki Uniwersytet Śląski Matplotlib jest biblioteką Pythona służącą do tworzenia różnego rodzaju wykresów. Biblioteka ta od samego początku
BASH - LINIA POLECEŃ. Bioinformatyka 2018/2019
 BASH - LINIA POLECEŃ Bioinformatyka 2018/2019 PODSTAWOWE DEFINICJE Linux system operacyjny, które oferuje kompletne środowisko programistyczne Powłoka interfejs wiersza poleceń zapewniający komunikację
BASH - LINIA POLECEŃ Bioinformatyka 2018/2019 PODSTAWOWE DEFINICJE Linux system operacyjny, które oferuje kompletne środowisko programistyczne Powłoka interfejs wiersza poleceń zapewniający komunikację
Informatyka i komputerowe wspomaganie prac inżynierskich
 Informatyka i komputerowe wspomaganie prac inżynierskich Dr Zbigniew Kozioł - wykład Dr Grzegorz Górski - laboratorium Wykład III Numeryczne rozwiązywanie równań różniczkowych. MES, Metoda Elementów Skończonych
Informatyka i komputerowe wspomaganie prac inżynierskich Dr Zbigniew Kozioł - wykład Dr Grzegorz Górski - laboratorium Wykład III Numeryczne rozwiązywanie równań różniczkowych. MES, Metoda Elementów Skończonych
Równania Maxwella i równanie falowe
 Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
Język C++ wykład VIII
 Programowanie uzupełnienie notatek: dr Jerzy Białkowski 1 2 3 4 Obiektowość języka C++ ˆ Klasa (rozszerzenie struktury), obiekt instancją klasy, konstruktory i destruktory ˆ Enkapsulacja - kapsułkowanie,
Programowanie uzupełnienie notatek: dr Jerzy Białkowski 1 2 3 4 Obiektowość języka C++ ˆ Klasa (rozszerzenie struktury), obiekt instancją klasy, konstruktory i destruktory ˆ Enkapsulacja - kapsułkowanie,
PRACOWNIA INFORMATYCZNA BASH - PODSTAWOWE INFORMACJE
 PRACOWNIA INFORMATYCZNA BASH - PODSTAWOWE INFORMACJE Magda Mielczarek Pracownia Informatyczna 2015/2016 1 Podstawowe definicje Linux system operacyjny, które oferuje kompletne środowisko programistyczne
PRACOWNIA INFORMATYCZNA BASH - PODSTAWOWE INFORMACJE Magda Mielczarek Pracownia Informatyczna 2015/2016 1 Podstawowe definicje Linux system operacyjny, które oferuje kompletne środowisko programistyczne
How to share data from SQL database table to the OPC Server? Jak udostępnić dane z tabeli bazy SQL do serwera OPC? samouczek ANT.
 Jak udostępnić dane z tabeli bazy SQL do serwera OPC? samouczek ANT How to share data from SQL database table to the OPC Server? ANT tutorial Krok 1: Uruchom ANT Studio i dodaj do drzewka konfiguracyjnego
Jak udostępnić dane z tabeli bazy SQL do serwera OPC? samouczek ANT How to share data from SQL database table to the OPC Server? ANT tutorial Krok 1: Uruchom ANT Studio i dodaj do drzewka konfiguracyjnego
Wykresy i interfejsy użytkownika
 Wrocław, 07.11.2017 Wstęp do informatyki i programowania: Wykresy i interfejsy użytkownika Wydział Matematyki Politechniki Wrocławskiej Andrzej Giniewicz Dzisiaj na zajęciach... Instrukcje sterujące Biblioteka
Wrocław, 07.11.2017 Wstęp do informatyki i programowania: Wykresy i interfejsy użytkownika Wydział Matematyki Politechniki Wrocławskiej Andrzej Giniewicz Dzisiaj na zajęciach... Instrukcje sterujące Biblioteka
Promieniowanie dipolowe
 Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
MentorGraphics ModelSim
 MentorGraphics ModelSim 1. Konfiguracja programu Wszelkie zmiany parametrów systemu symulacji dokonywane są w menu Tools -> Edit Preferences... Wyniki ustawień należy zapisać w skrypcie startowym systemu
MentorGraphics ModelSim 1. Konfiguracja programu Wszelkie zmiany parametrów systemu symulacji dokonywane są w menu Tools -> Edit Preferences... Wyniki ustawień należy zapisać w skrypcie startowym systemu
WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA CIEPŁA
 39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
Bazy Danych i Usługi Sieciowe
 Bazy Danych i Usługi Sieciowe Ćwiczenia I Paweł Daniluk Wydział Fizyki Jesień 2011 P. Daniluk (Wydział Fizyki) BDiUS ćw. I Jesień 2011 1 / 15 Strona wykładu http://bioexploratorium.pl/wiki/ Bazy_Danych_i_Usługi_Sieciowe_-_2011z
Bazy Danych i Usługi Sieciowe Ćwiczenia I Paweł Daniluk Wydział Fizyki Jesień 2011 P. Daniluk (Wydział Fizyki) BDiUS ćw. I Jesień 2011 1 / 15 Strona wykładu http://bioexploratorium.pl/wiki/ Bazy_Danych_i_Usługi_Sieciowe_-_2011z
Zad. 3: Układ równań liniowych
 1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
Wstęp do programowania
 Wstęp do programowania Podstawowe konstrukcje programistyczne Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk (Wydział Fizyki) WP w. II Jesień 2013 1 / 34 Przypomnienie Programowanie imperatywne Program
Wstęp do programowania Podstawowe konstrukcje programistyczne Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk (Wydział Fizyki) WP w. II Jesień 2013 1 / 34 Przypomnienie Programowanie imperatywne Program
Wykład 15. Literatura. Kompilatory. Elementarne różnice. Preprocesor. Słowa kluczowe
 Wykład 15 Wprowadzenie do języka na bazie a Literatura Podobieństwa i różnice Literatura B.W.Kernighan, D.M.Ritchie Język ANSI Kompilatory Elementarne różnice Turbo Delphi FP Kylix GNU (gcc) GNU ++ (g++)
Wykład 15 Wprowadzenie do języka na bazie a Literatura Podobieństwa i różnice Literatura B.W.Kernighan, D.M.Ritchie Język ANSI Kompilatory Elementarne różnice Turbo Delphi FP Kylix GNU (gcc) GNU ++ (g++)
Ćwiczenie 5: Analiza pól elektromagnetycznych w programie FEMM cz. 1
 Komputerowe wspomaganie projektowania ED6, IPEE PL, rok. akad. 2009/2010 Strona 1 Ćwiczenie 5: Analiza pól elektromagnetycznych w programie FEMM cz. 1 1. Wstęp Finite Element Method Magnetics (FEMM) jest
Komputerowe wspomaganie projektowania ED6, IPEE PL, rok. akad. 2009/2010 Strona 1 Ćwiczenie 5: Analiza pól elektromagnetycznych w programie FEMM cz. 1 1. Wstęp Finite Element Method Magnetics (FEMM) jest
ROZWIAZANIE PROBLEMU USTALONEGO PRZEPLYWU CIEPLA W SYSTEMIE ADINA 900 Nodes Version 8.2
 1 Wstęp ROZWIAZANIE PROBLEMU USTALONEGO PRZEPLYWU CIEPLA W SYSTEMIE ADINA 900 Nodes Version 8.2 Struktura systemu ADINA (Automatic Dynamic Incremental Nonlinear Analysis) jest to system programów opartych
1 Wstęp ROZWIAZANIE PROBLEMU USTALONEGO PRZEPLYWU CIEPLA W SYSTEMIE ADINA 900 Nodes Version 8.2 Struktura systemu ADINA (Automatic Dynamic Incremental Nonlinear Analysis) jest to system programów opartych
Podstawowe elementy proceduralne w C++ Program i wyjście. Zmienne i arytmetyka. Wskaźniki i tablice. Testy i pętle. Funkcje.
 Podstawowe elementy proceduralne w C++ Program i wyjście Zmienne i arytmetyka Wskaźniki i tablice Testy i pętle Funkcje Pierwszy program // Niezbędne zaklęcia przygotowawcze ;-) #include using
Podstawowe elementy proceduralne w C++ Program i wyjście Zmienne i arytmetyka Wskaźniki i tablice Testy i pętle Funkcje Pierwszy program // Niezbędne zaklęcia przygotowawcze ;-) #include using
Język programowania PASCAL
 Język programowania PASCAL (wersja podstawowa - standard) Literatura: dowolny podręcznik do języka PASCAL (na laboratoriach Borland) Iglewski, Madey, Matwin PASCAL STANDARD, PASCAL 360 Marciniak TURBO
Język programowania PASCAL (wersja podstawowa - standard) Literatura: dowolny podręcznik do języka PASCAL (na laboratoriach Borland) Iglewski, Madey, Matwin PASCAL STANDARD, PASCAL 360 Marciniak TURBO
Ćwiczenie 3. Python 3: Python 3: Funkcje, moduły i operacje na plikach
 Wizualizacja danych Ćwiczenie 3 Python 3: Python 3: Funkcje, moduły i operacje na plikach Python Comprehension Jest to mechanizm służący do generowania kolekcji (lista, słownik, zbiór) na podstawie jednowierszowej
Wizualizacja danych Ćwiczenie 3 Python 3: Python 3: Funkcje, moduły i operacje na plikach Python Comprehension Jest to mechanizm służący do generowania kolekcji (lista, słownik, zbiór) na podstawie jednowierszowej
Tworzenie języków specyfikacji dla zagadnień numerycznych
 Tworzenie języków specyfikacji dla zagadnień numerycznych prof. dr hab. inż. Norbert Sczygiol dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska 11 września
Tworzenie języków specyfikacji dla zagadnień numerycznych prof. dr hab. inż. Norbert Sczygiol dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska 11 września
PROGRAMOWANIE W PYTHONIE OD PIERWSZYCH KROKÓW
 PROGRAMOWANIE W PYTHONIE OD PIERWSZYCH KROKÓW http://metodycy.torun.pl/ m.informatyka@metodycy.torun.pl 1. Wprowadzenie do Pythona podstawowe informacje Python to język programowania wysokiego poziomu,
PROGRAMOWANIE W PYTHONIE OD PIERWSZYCH KROKÓW http://metodycy.torun.pl/ m.informatyka@metodycy.torun.pl 1. Wprowadzenie do Pythona podstawowe informacje Python to język programowania wysokiego poziomu,
 Własności magnetyczne Magnetic properties Podstawowe własności magnetyczne rdzeni pokazuje tablica 3. The basic core magnetic properties are presented in the following table. Tablica 3. Własności magnetyczne
Własności magnetyczne Magnetic properties Podstawowe własności magnetyczne rdzeni pokazuje tablica 3. The basic core magnetic properties are presented in the following table. Tablica 3. Własności magnetyczne
Równania Maxwella. roth t
 , H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
Podstawy programowania w języku C++
 Podstawy programowania w języku C++ Część dziesiąta Rekordy w C/C++ struktury Autor Roman Simiński Kontakt roman.siminski@us.edu.pl www.programowanie.siminskionline.pl Niniejsze opracowanie zawiera skrót
Podstawy programowania w języku C++ Część dziesiąta Rekordy w C/C++ struktury Autor Roman Simiński Kontakt roman.siminski@us.edu.pl www.programowanie.siminskionline.pl Niniejsze opracowanie zawiera skrót
Fale elektromagnetyczne. Gradient pola. Gradient pola... Gradient pola... Notatki. Notatki. Notatki. Notatki. dr inż. Ireneusz Owczarek 2013/14
 dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
NS-2. Krzysztof Rusek. 26 kwietnia 2010
 NS-2 Krzysztof Rusek 26 kwietnia 2010 1 Opis ćwiczenia Symulator ns-2 jest potężnym narzędziem, szeroko stosowanym w telekomunikacji. Ćwiczenie ma na cele przedstawić podstawy symulatora oraz symulacji
NS-2 Krzysztof Rusek 26 kwietnia 2010 1 Opis ćwiczenia Symulator ns-2 jest potężnym narzędziem, szeroko stosowanym w telekomunikacji. Ćwiczenie ma na cele przedstawić podstawy symulatora oraz symulacji
1. Uruchamianie programu Modeller
 1. Uruchamianie programu Modeller W menu Start systemu MS Windows, w katalogu Programy naleŝy odnaleźć katalog Vector Fields Opera, a w nim program Opera 12.0 i uruchomić go: Start Programy Vector Fields
1. Uruchamianie programu Modeller W menu Start systemu MS Windows, w katalogu Programy naleŝy odnaleźć katalog Vector Fields Opera, a w nim program Opera 12.0 i uruchomić go: Start Programy Vector Fields
