Kondensaty Bosego-Einsteina
|
|
|
- Władysława Skrzypczak
- 6 lat temu
- Przeglądów:
Transkrypt
1 Ostrów Wielkopolski, 14 X 2009 r. Kondensaty Bosego-Einsteina / przegla d współczesnych realizacji / Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej
2 Ostrów Wielkopolski, 14 X 2009 r. Kondensaty Bosego-Einsteina / przegla d współczesnych realizacji / Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej w Lublinie
3 Plan wykładu :
4 Plan wykładu : Wste p
5 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa /
6 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów
7 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego...
8 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego /
9 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego /
10 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony,...
11 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony, kwarki,...
12 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony, kwarki, ekscytony /
13 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony, kwarki, ekscytony /
14 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony, kwarki, ekscytony / Nadprzewodniki wysokotemperaturowe
15 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony, kwarki, ekscytony / Nadprzewodniki wysokotemperaturowe / problem niekoherenetnych par /
16 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony, kwarki, ekscytony / Nadprzewodniki wysokotemperaturowe / problem niekoherenetnych par /
17 Plan wykładu : Wste p / kondensacja BE i relacja z nadciekłościa / Ultrazimne kondensaty BE atomów / typu bozonowego oraz fermionowego / Kilka egzotycznych przykładów BEC / magnony, kwarki, ekscytony / Nadprzewodniki wysokotemperaturowe / problem niekoherenetnych par / Podsumowanie
18 1. Wste p
19 Kondensacja Bosego-Einsteina (BEC) jak również nadciekłość to zjawiska kwantowe, które sa moga realizować poniżej temperatury krytycznej sie T c w gazach, cieczach, ciałach stałych oraz ja drach atomowych a nawet w gwiazdach neutronowych.
20 Kondensacja Bosego-Einsteina (BEC) jak również nadciekłość to zjawiska kwantowe, które sa moga realizować poniżej temperatury krytycznej sie T c w gazach, cieczach, ciałach stałych oraz ja drach atomowych a nawet w gwiazdach neutronowych. W swoim referacie przedstawie kilka konkretnych przykładów.
21 Idea kondensacji BE
22 Idea kondensacji BE Kondensat BE powstaje wtedy, gdy makroskopowa ilość obiektów obsadza identyczny stan kwantowy o najniższej energii dopuszczalnej w układzie.
23 Idea kondensacji BE Kondensat BE powstaje wtedy, gdy makroskopowa ilość obiektów obsadza identyczny stan kwantowy o najniższej energii dopuszczalnej w układzie. Obiekty sa opisane wspólna funkcja falowa Φ(r, t).
24 Idea kondensacji BE Kondensat BE powstaje wtedy, gdy makroskopowa ilość obiektów obsadza identyczny stan kwantowy o najniższej energii dopuszczalnej w układzie. Obiekty sa opisane wspólna funkcja falowa Φ(r, t). Ta makroskopowa fala de Broglie a pełni również role parametru porza dku opisuja cego nowy stan materii.
25 Idea kondensacji BE Kondensat BE powstaje wtedy, gdy makroskopowa ilość obiektów obsadza identyczny stan kwantowy o najniższej energii dopuszczalnej w układzie. Obiekty sa opisane wspólna funkcja falowa Φ(r, t). Ta makroskopowa fala de Broglie a pełni również role parametru porza dku opisuja cego nowy stan materii. Przy użyciu zewne trznych pól kondensaty BE moga być wprawione w bezlepki ruch, zmieniać kształt, oscylować, tworzyć obrazy interferencyjne itp.
26 Idea kondensacji BE Kondensat BE powstaje wtedy, gdy makroskopowa ilość obiektów obsadza identyczny stan kwantowy o najniższej energii dopuszczalnej w układzie. Obiekty sa opisane wspólna funkcja falowa Φ(r, t). Ta makroskopowa fala de Broglie a pełni również role parametru porza dku opisuja cego nowy stan materii. Przy użyciu zewne trznych pól kondensaty BE moga być wprawione w bezlepki ruch, zmieniać kształt, oscylować, tworzyć obrazy interferencyjne itp. Efekty kwantowe można obserwować gołym okiem.
27 Podejście półklasyczne schemat pogla dowy
28 Podejście półklasyczne schemat pogla dowy W swej pracy doktorskiej ksia że Louis Victor de Broglie przedstawił hipoteze, że obiekty materialne można traktować jak fale m v = h λ. Dla cza stek swobodnych: λ 1 m T.
29 Podejście półklasyczne schemat pogla dowy W swej pracy doktorskiej ksia że Louis Victor de Broglie przedstawił hipoteze, że obiekty materialne można traktować jak fale m v = h λ. Dla cza stek swobodnych: λ 1 m T. Inspiracja hipotezy de Broglie a były prace Einsteina nt. korpuskularnej natury światła. / N. Nobla, 1929 r. /
30 Podejście półklasyczne schemat pogla dowy W swej pracy doktorskiej ksia że Louis Victor de Broglie przedstawił hipoteze, że obiekty materialne można traktować jak fale m v = h λ. Dla cza stek swobodnych: λ 1 m T. Inspiracja hipotezy de Broglie a były prace Einsteina nt. korpuskularnej natury światła. Davisson & Thomson doświadczalnie potwiedzili słuszność hipotezy de Broglie a, za co również przyznano Nagrode Nobla w 1937 r. / N. Nobla, 1929 r. /
31 Schemat pogla dowy BEC Wysoka temperatura (cza steczki sa jak kule bilardowe)
32 Schemat pogla dowy BEC Wysoka temperatura (cza steczki sa jak kule bilardowe) Niska temperatura (wzrasta rozmiar długości falowej)
33 Schemat pogla dowy BEC Wysoka temperatura (cza steczki sa jak kule bilardowe) Niska temperatura (wzrasta rozmiar długości falowej) Temperatura krytyczna (fale de Broglie a przekrywaja sie )
34 Schemat pogla dowy BEC Wysoka temperatura (cza steczki sa jak kule bilardowe) Niska temperatura (wzrasta rozmiar długości falowej) Temperatura krytyczna (fale de Broglie a przekrywaja sie ) Zerowa temperatura (makroskopowa funkcja falowa)
35 Schemat pogla dowy BEC W. Ketterle przedstawił królowi taka ilustracje Szwecji przy wre czaniu Nagrody Nobla w 2001 r. Wysoka temperatura (cza steczki sa jak kule bilardowe) Niska temperatura (wzrasta rozmiar długości falowej) Temperatura krytyczna (fale de Broglie a przekrywaja sie ) Zerowa temperatura (makroskopowa funkcja falowa)
36 Rola oddziaływań relacja z nadciekłościa
37 Rola oddziaływań relacja z nadciekłościa Uwzgle dnienie kondensatu BE w uje ciu mechaniki kwantowej: ˆΨ( r, t) = Φ( r, t) + δ ˆΨ( r, t)
38 Rola oddziaływań relacja z nadciekłościa Uwzgle dnienie kondensatu BE w uje ciu mechaniki kwantowej: ˆΨ( r, t) = Φ( r, t) + δ ˆΨ( r, t) Zakładaja c potencjał oddziaływania V ( r 1 r 2 ) = g δ( r 1 r 2 ) funkcja kondensatu spełnia r-nie Grossa-Pitajewskiego Φ( r, t) i h t = ( h2 2 2m +V ext(r)+gn c ) Φ( r, t)
39 Rola oddziaływań relacja z nadciekłościa Uwzgle dnienie kondensatu BE w uje ciu mechaniki kwantowej: ˆΨ( r, t) = Φ( r, t) + δ ˆΨ( r, t) Zakładaja c potencjał oddziaływania V ( r 1 r 2 ) = g δ( r 1 r 2 ) funkcja kondensatu spełnia r-nie Grossa-Pitajewskiego Φ( r, t) i h t = ( h2 2 2m +V ext(r)+gn c ) Φ( r, t) gdzie n c Φ( r, t) 2
40 Sformułowanie hydrodynamiczne
41 Sformułowanie hydrodynamiczne Zespolona funkcje kondensatu Φ( r, t) można opisać poprzez amplitude Φ( r, t) oraz faze θ( r, t) za pomoca wyrażenia
42 Sformułowanie hydrodynamiczne Zespolona funkcje kondensatu Φ( r, t) można opisać poprzez amplitude Φ( r, t) oraz faze θ( r, t) za pomoca wyrażenia Φ( r, t) = n c ( r, t) e iθ( r,t) gdzie n c Φ 2
43 Sformułowanie hydrodynamiczne Zespolona funkcje kondensatu Φ( r, t) można opisać poprzez amplitude Φ( r, t) oraz faze θ( r, t) za pomoca wyrażenia Φ( r, t) = n c ( r, t) e iθ( r,t) gdzie n c Φ 2 GP rozseparowuje sie wówczas na:
44 Sformułowanie hydrodynamiczne Zespolona funkcje kondensatu Φ( r, t) można opisać poprzez amplitude Φ( r, t) oraz faze θ( r, t) za pomoca wyrażenia Φ( r, t) = n c ( r, t) e iθ( r,t) gdzie n c Φ 2 GP rozseparowuje sie wówczas na: a) równanie cia głości n c ( r, t) t + j c ( r, t) = 0
45 Sformułowanie hydrodynamiczne Zespolona funkcje kondensatu Φ( r, t) można opisać poprzez amplitude Φ( r, t) oraz faze θ( r, t) za pomoca wyrażenia Φ( r, t) = n c ( r, t) e iθ( r,t) gdzie n c Φ 2 GP rozseparowuje sie wówczas na: a) równanie cia głości n c ( r, t) t + j c ( r, t) = 0 gdzie ge stość pra du j c h 2i (Φ Φ Φ Φ ) = v c = h m θ( r, t)
46 Sformułowanie hydrodynamiczne Zespolona funkcje kondensatu Φ( r, t) można opisać poprzez amplitude Φ( r, t) oraz faze θ( r, t) za pomoca wyrażenia Φ( r, t) = n c ( r, t) e iθ( r,t) gdzie n c Φ 2 GP rozseparowuje sie wówczas na: a) równanie cia głości b) równanie Josephsona m v c t + [ V eff + gn c mv2 c ] = 0
47 Sformułowanie hydrodynamiczne Zespolona funkcje kondensatu Φ( r, t) można opisać poprzez amplitude Φ( r, t) oraz faze θ( r, t) za pomoca wyrażenia Φ( r, t) = n c ( r, t) e iθ( r,t) gdzie n c Φ 2 GP rozseparowuje sie wówczas na: a) równanie cia głości b) równanie Josephsona (struktura r-nia Naviera-Stokesa) m v c t + [ V eff + gn c mv2 c ] = 0 gdzie V eff = V ext h2 2m n c 2 n c
48 Sformułowanie hydrodynamiczne c.d.
49 Sformułowanie hydrodynamiczne c.d. Równania cia głości i Josephsona przypominaja klasyczna hydrodynamike dla idealnej cieczy.
50 Sformułowanie hydrodynamiczne c.d. Równania cia głości i Josephsona przypominaja klasyczna hydrodynamike dla idealnej cieczy. Patrz np. rozdział II w ksia żce Hydrodynamika, L.D. Landau, E.M. Lifszyc, PWN (1994).
51 Sformułowanie hydrodynamiczne c.d. Równania cia głości i Josephsona przypominaja klasyczna hydrodynamike dla idealnej cieczy. Charakterystyczne właściwości:
52 Sformułowanie hydrodynamiczne c.d. Równania cia głości i Josephsona przypominaja klasyczna hydrodynamike dla idealnej cieczy. Charakterystyczne właściwości: a) wsp. lepkości = 0 nadciekłość
53 Sformułowanie hydrodynamiczne c.d. Równania cia głości i Josephsona przypominaja klasyczna hydrodynamike dla idealnej cieczy. Charakterystyczne właściwości: a) wsp. lepkości = 0 nadciekłość b) v c ( r, t) = 0 bezwirowość
54 Sformułowanie hydrodynamiczne c.d. Równania cia głości i Josephsona przypominaja klasyczna hydrodynamike dla idealnej cieczy. Charakterystyczne właściwości: a) wsp. lepkości = 0 nadciekłość b) v c ( r, t) = 0 bezwirowość Uwaga: Wiry moga ewentualnie pojawić sie w kwantowych defektach topologicznych, gdzie faza θ( r, t) wykazuje osobliwości.
55 Nadciekły 4 He pierwszy przykład BEC
56 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat jedynym znanym kondensatem BE był
57 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat jedynym znanym kondensatem BE był 4 He
58 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat jedynym znanym kondensatem BE był 4 He mimo, iż Landau nigdy takiego opinii nie podzielał.
59 Nadciekły 4 He pierwszy przykład BEC
60 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat używano tzw. opisu dwucieczowego Tiszy
61 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat używano tzw. opisu dwucieczowego Tiszy
62 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat używano tzw. opisu dwucieczowego Tiszy / Laszlo Tisza zmarł w kwietniu 2009 r. w wieku 102 lat /
63 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat używano tzw. opisu dwucieczowego Tiszy / Laszlo Tisza zmarł w kwietniu 2009 r. w wieku 102 lat / Model Tiszy przewidywał m.in. istnienie drugiego dźwie ku.
64 Nadciekły 4 He pierwszy przykład BEC Przez wiele lat używano tzw. opisu dwucieczowego Tiszy / Laszlo Tisza zmarł w kwietniu 2009 r. w wieku 102 lat / Drugi dźwie k faktycznie stwierdzono później doświadczalnie.
65 2. Ultrazimne kondensaty
66 Kilka sloganów zamiast motywacji
67 Kilka sloganów zamiast motywacji hot prospects for cold molecules B. Goss-Levi, Physics Today 53, 46 (2000).
68 Kilka sloganów zamiast motywacji hot prospects for cold molecules B. Goss-Levi, Physics Today 53, 46 (2000). dreams of controlling interactions... come true K. Burnett et al, Nature 416, 255 (2002).
69 Kilka sloganów zamiast motywacji hot prospects for cold molecules B. Goss-Levi, Physics Today 53, 46 (2000). dreams of controlling interactions... come true K. Burnett et al, Nature 416, 255 (2002). molecules are really cool P.S. Julienne, Nature 424, 24 (2003).
70 2.1 Kondensaty BE atomów typu bozonowego
71 Warunki konieczne do uzyskania BEC atomów
72 Warunki konieczne do uzyskania BEC atomów Aby uzyskać BEC spułapkowanych atomów potrzebne sa ultraniskie temperatury (λ d).
73 Warunki konieczne do uzyskania BEC atomów Aby uzyskać BEC spułapkowanych atomów potrzebne sa ultraniskie temperatury (λ d). T BE 0,1 µk
74 Warunki konieczne do uzyskania BEC atomów Aby uzyskać BEC spułapkowanych atomów potrzebne sa ultraniskie temperatury (λ d). Bardzo niska koncentracja sprawia, że atomy oddziałuja jedynie poprzez tzw. kanał -s teorii rozpraszania.
75 Warunki konieczne do uzyskania BEC atomów Aby uzyskać BEC spułapkowanych atomów potrzebne sa ultraniskie temperatury (λ d). Bardzo niska koncentracja sprawia, że atomy oddziałuja jedynie poprzez tzw. kanał -s teorii rozpraszania. Tak rzadkie koncentracje gwarantuja, że przez kilka sekund atomy nie solidyfikuja (tzn. sa metastabilne).
76 Warunki konieczne do uzyskania BEC atomów Aby uzyskać BEC spułapkowanych atomów potrzebne sa ultraniskie temperatury (λ d). Bardzo niska koncentracja sprawia, że atomy oddziałuja jedynie poprzez tzw. kanał -s teorii rozpraszania. Tak rzadkie koncentracje gwarantuja, że przez kilka sekund atomy nie solidyfikuja (tzn. sa metastabilne). Kilka sekund wystarcza na zrealizowanie BEC!
77 Warunki konieczne do uzyskania BEC atomów Aby uzyskać BEC spułapkowanych atomów potrzebne sa ultraniskie temperatury (λ d). Bardzo niska koncentracja sprawia, że atomy oddziałuja jedynie poprzez tzw. kanał -s teorii rozpraszania. Tak rzadkie koncentracje gwarantuja, że przez kilka sekund atomy nie solidyfikuja (tzn. sa metastabilne). Kilka sekund wystarcza na zrealizowanie BEC! Pierwsze kondensaty BE atomów uzyskali w 1995 r. E. Cornell, C. Wieman oraz W. Ketterle. Nagroda Nobla, 2001 r.
78 Kondensacja Bosego-Einsteina 87 Rb JILA 1995 (E. Cornell i wsp.) 23 Na MIT 1995 (W. Ketterle i wsp.) Pierwsze kondensaty BE atomów typu bozonowego.
79 Jak rozpoznać BEC? na przykładzie 40 Ca
80 Jak rozpoznać BEC? na przykładzie 40 Ca W przypadku atomów w pułapkach kondensat BE gromadzi sie na najniżym poziomie oscylatora harmonicznego d) Optical density c) b) a) 230 µm S. Kraft et al, Phys. Rev. Lett. 103, (2009).
81 Jak rozpoznać BEC? na przykładzie 40 Ca W przypadku atomów w pułapkach kondensat BE gromadzi sie na najniżym poziomie oscylatora harmonicznego d) Optical density c) b) a) 230 µm S. Kraft et al, Phys. Rev. Lett. 103, (2009). Symptomem BEC jest bimodalny rozkład atomów.
82 Jak rozpoznać BEC? na przykładzie 40 Ca W przypadku atomów w pułapkach kondensat BE gromadzi sie na najniżym poziomie oscylatora harmonicznego d) Dla T T BE : n(x) exp ( mω x x 2 h ) Optical density c) b) T BE 170 nk a) 230 µm Dla T T BE : n(x) exp ( mω 2 xx 2 2k B T ) S. Kraft et al, Phys. Rev. Lett. 103, (2009). Symptomem BEC jest bimodalny rozkład atomów.
83 Fakty liczbowe oraz komentarze
84 Fakty liczbowe oraz komentarze Obcecnie udaje sie skondesować nawet do 90 % atomów zgromadzonych w pułapce.
85 Fakty liczbowe oraz komentarze Obcecnie udaje sie skondesować nawet do 90 % atomów zgromadzonych w pułapce. W nadciekłym 4 He kondensuje tylko 8 % atomów!
86 Fakty liczbowe oraz komentarze Obcecnie udaje sie skondesować nawet do 90 % atomów zgromadzonych w pułapce. W nadciekłym 4 He kondensuje tylko 8 % atomów! Koncentracje skond. atomów wynosza około cm 3 (tzn. w centrum pułapki).
87 Fakty liczbowe oraz komentarze Obcecnie udaje sie skondesować nawet do 90 % atomów zgromadzonych w pułapce. W nadciekłym 4 He kondensuje tylko 8 % atomów! Koncentracje skond. atomów wynosza około cm 3 (tzn. w centrum pułapki). Jest to mniej niż ge stość powietrza!
88 Fakty liczbowe oraz komentarze Obcecnie udaje sie skondesować nawet do 90 % atomów zgromadzonych w pułapce. W nadciekłym 4 He kondensuje tylko 8 % atomów! Koncentracje skond. atomów wynosza około cm 3 (tzn. w centrum pułapki). Jest to mniej niż ge stość powietrza! Łatwo zaobserwować kondensacje BE atomów, nadciekłość jest natomiast trudna do identyfikacji.
89 Fakty liczbowe oraz komentarze Obcecnie udaje sie skondesować nawet do 90 % atomów zgromadzonych w pułapce. W nadciekłym 4 He kondensuje tylko 8 % atomów! Koncentracje skond. atomów wynosza około cm 3 (tzn. w centrum pułapki). Jest to mniej niż ge stość powietrza! Łatwo zaobserwować kondensacje BE atomów, nadciekłość jest natomiast trudna do identyfikacji. Odwrotnie niż w przypadku 4 He-II!
90
91 Nadciekłość - sposoby identyfikacji
92 Nadciekłość - sposoby identyfikacji 1) zanik lepkości
93 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe
94 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności
95 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe
96 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp)
97 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne
98 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne 4) sieć Abrikosova wirów kwantowych
99 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne 4) sieć Abrikosova wirów kwantowych ok
100 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne 4) sieć Abrikosova wirów kwantowych ok 5) pre dkość krytyczna
101 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne 4) sieć Abrikosova wirów kwantowych ok 5) pre dkość krytyczna OK
102 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne 4) sieć Abrikosova wirów kwantowych ok 5) pre dkość krytyczna OK 6) zjawisko Josephsona
103 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne 4) sieć Abrikosova wirów kwantowych ok 5) pre dkość krytyczna OK 6) zjawisko Josephsona OK
104 Nadciekłość - sposoby identyfikacji 1) zanik lepkości raczej niemożliwe 2) redukcja m. bezwładności raczej niemożliwe 3) cechy kolektywne (drugi dźwie k itp).. specyficzne 4) sieć Abrikosova wirów kwantowych ok 5) pre dkość krytyczna OK 6) zjawisko Josephsona OK...
105 Sieć wirów kwantowych W. Ketterle i wsp. (MIT)
106 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych
107 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych
108 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych J.R. Abo-Shaer et al, Science 292, 476 (2001).
109 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych Atomy 23 Na J.R. Abo-Shaer et al, Science 292, 476 (2001).
110 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych Atomy 23 Na N J.R. Abo-Shaer et al, Science 292, 476 (2001).
111 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych Atomy 23 Na N Uzyskano aż 130 wirów J.R. Abo-Shaer et al, Science 292, 476 (2001).
112 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych Atomy 23 Na N Uzyskano aż 130 wirów τ 40 sek J.R. Abo-Shaer et al, Science 292, 476 (2001).
113 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych Atomy 23 Na N Uzyskano aż 130 wirów τ 40 sek J.R. Abo-Shaer et al, Science 292, 476 (2001). Sieć była regularna mimo niejednorodności BEC!
114 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych J.R. Abo-Shaer et al, Science 292, 476 (2001). Uzyskany obraz sieci 16, 32, 80 oraz 130 wirów.
115 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych J.R. Abo-Shaer et al, Science 292, 476 (2001). Uzyskany obraz sieci 16, 32, 80 oraz 130 wirów. Sieć jest regularna aż do brzegów kondensatu!
116 Sieć wirów kwantowych W. Ketterle i wsp. (MIT) Atomowe kondensaty BE wprawione w rotacje przez lasery wykazały regularna sieć (Abrikosova) wirów kwantowych J.R. Abo-Shaer et al, Science 292, 476 (2001). Uzyskany obraz sieci 16, 32, 80 oraz 130 wirów. Sieć jest regularna aż do brzegów kondensatu! W nadciekłym 4 He udawało sie uzyskać jedynie do 11 wirów!
117 Efekt Josephsona atomowych kondensatów BE
118 Efekt Josephsona atomowych kondensatów BE Idea zjawiska Josephsona dla atomowych kondensatów BE
119 Efekt Josephsona atomowych kondensatów BE Idea zjawiska Josephsona dla atomowych kondensatów BE F. Dalfovo, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999).
120 Efekt Josephsona atomowych kondensatów BE Idea zjawiska Josephsona dla atomowych kondensatów BE F. Dalfovo, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999). Potencjały chemiczne µ 1 µ 2 (czyli N 1 N 2 )
121 Efekt Josephsona atomowych kondensatów BE Idea zjawiska Josephsona dla atomowych kondensatów BE F. Dalfovo, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999). Potencjały chemiczne µ 1 µ 2 (czyli N 1 N 2 ) prowadza do różnicy faz kondensatów θ 1 θ 2
122 Efekt Josephsona atomowych kondensatów BE Idea zjawiska Josephsona dla atomowych kondensatów BE F. Dalfovo, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999). Potencjały chemiczne µ 1 µ 2 (czyli N 1 N 2 ) prowadza do różnicy faz kondensatów θ 1 θ 2 indukuja c przepływ atomów mie dzy kondensatami.
123 Efekt Josephsona atomowych kondensatów BE Idea zjawiska Josephsona dla atomowych kondensatów BE F. Dalfovo, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999). Potencjały chemiczne µ 1 µ 2 (czyli N 1 N 2 ) prowadza do różnicy faz kondensatów θ 1 θ 2 indukuja c przepływ atomów mie dzy kondensatami.
124 Efekt Josephsona atomowych kondensatów BE Idea zjawiska Josephsona dla atomowych kondensatów BE I = I 0 sin [ ] (µ 1 µ 2 )t h F. Dalfovo, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999). Potencjały chemiczne µ 1 µ 2 (czyli N 1 N 2 ) prowadza do różnicy faz kondensatów θ 1 θ 2 indukuja c przepływ atomów mie dzy kondensatami.
125 Efekt Josephsona realizacja zjawiska d.c.
126 Efekt Josephsona realizacja zjawiska d.c. Pierwsza doświadczalna realizacja przez grupe z Heidelberga
127 Efekt Josephsona realizacja zjawiska d.c. Pierwsza doświadczalna realizacja przez grupe z Heidelberga
128 Efekt Josephsona realizacja zjawiska d.c. Pierwsza doświadczalna realizacja przez grupe z Heidelberga M. Albiez et al, Phys. Rev. Lett. 95, (2005).
129 Efekt Josephsona realizacja zjawiska d.c. Pierwsza doświadczalna realizacja przez grupe z Heidelberga Rodzaj atomów: 87 Rb M. Albiez et al, Phys. Rev. Lett. 95, (2005).
130 Efekt Josephsona realizacja zjawiska d.c. Pierwsza doświadczalna realizacja przez grupe z Heidelberga Rodzaj atomów: 87 Rb Ilość atomów: M. Albiez et al, Phys. Rev. Lett. 95, (2005).
131 Efekt Josephsona realizacja zjawiska d.c. Pierwsza doświadczalna realizacja przez grupe z Heidelberga Rodzaj atomów: 87 Rb Ilość atomów: Oscylacje: ω 40 ms M. Albiez et al, Phys. Rev. Lett. 95, (2005).
132 Efekt Josephsona wersja zjawiska a.c.
133 Efekt Josephsona wersja zjawiska a.c. Pierwsza doświadczalna realizacja przez grupe z TECHNION-u
134 Efekt Josephsona wersja zjawiska a.c. Pierwsza doświadczalna realizacja przez grupe z TECHNION-u
135 Efekt Josephsona wersja zjawiska a.c. Pierwsza doświadczalna realizacja przez grupe z TECHNION-u S. Levy et al, Nature 449, 579 (2007).
136 Efekt Josephsona wersja zjawiska a.c. Pierwsza doświadczalna realizacja przez grupe z TECHNION-u Atomy 87 Rb S. Levy et al, Nature 449, 579 (2007).
137 Efekt Josephsona wersja zjawiska a.c. Pierwsza doświadczalna realizacja przez grupe z TECHNION-u Atomy 87 Rb N S. Levy et al, Nature 449, 579 (2007).
138 Efekt Josephsona wersja zjawiska a.c. Pierwsza doświadczalna realizacja przez grupe z TECHNION-u Atomy 87 Rb N S. Levy et al, Nature 449, 579 (2007). Oscylacje fazy odbywaja sie wg r-nia: θ = t µ h
139 2.2 Kondensaty BE atomów typu fermionowego
140 Kondensacja par fermionowych
141 Kondensacja par fermionowych Na przełomie lat 2003 / 2004 uzyskano kondensaty BE par atomów typu fermionowego.
142 Kondensacja par fermionowych Na przełomie lat 2003 / 2004 uzyskano kondensaty BE par atomów typu fermionowego. T c 100 nk
143 Kondensacja par fermionowych Na przełomie lat 2003 / 2004 uzyskano kondensaty BE par atomów typu fermionowego. T c 100 nk [1] M.W. Zwierlein et al, Phys. Rev. Lett. 92, (2004). [2] C.A. Regal et al, Phys. Rev. Lett. 92, (2004). [3] J. Kinast et al, Phys. Rev. Lett. 92, (2004). [4] C. Chin et al, Science 305, 1128 (2004).
144 Kwantowa degeneracja ewidencja dośw.
145 Kwantowa degeneracja ewidencja dośw. Zjawiska kwantowe moga być obserwowalne poniżej T F.
146 Kwantowa degeneracja ewidencja dośw. Zjawiska kwantowe moga być obserwowalne poniżej T F. B. De Marco et al, Phys. Rev. Lett. bf 86, 5409 (2001).
147 Rodzaje stosowanych atomów 6 Li mieszanina stanów nadsubtelnych 1 2, 1 2 oraz 1 2, 1 2 współistnieja cych z bi-molekułami ( 6 Li) 2 40 K mieszanina stanów nadsubtelnych 9 2, 9 2 oraz and 9 2, 7 2 współistnieja cych z bi-molekułami ( 40 K) 2.
148 Uczestnicza ce grupy
149 Uczestnicza ce grupy 6 Li - W. Ketterle (MIT), 40 K - D. Jin (Boulder). R. Grimm (Innsbruck), R. Hulet (Rice), Ch. Salomon (ENS).
150 Rezonans Feshbacha istota mechanizmu
151 Rezonans Feshbacha istota mechanizmu Schemat warunków rozpraszania rezonansowego
152 Rezonans Feshbacha istota mechanizmu Schemat warunków rozpraszania rezonansowego
153 Rezonans Feshbacha istota mechanizmu Schemat warunków rozpraszania rezonansowego a = a bg [ 1 + ] w B B 0 Efektywna amplituda rozpraszania a zależy od pola magnetycznego B.
154 Rezonans Feshbacha istota mechanizmu Schemat warunków rozpraszania rezonansowego I. Bloch, J. Dalibard, W. Zwerger, Rev. Mod. Phys. bf 80, 885 (2008).
155 Rezonans Feshbacha istota mechanizmu Schemat warunków rozpraszania rezonansowego I. Bloch, J. Dalibard, W. Zwerger, Rev. Mod. Phys. bf 80, 885 (2008). Rezonansów Feshbacha może realizować sie kilka.
156 Rezonans Feshbacha realizacja praktyczna
157 Rezonans Feshbacha realizacja praktyczna Rezonans Feshbacha uzyskany doświadczalnie dla atomów 40 K w stanach zeemanowskich 9 2, 9 2 oraz 9 2, 7 2. C.A. Regal and D.S. Jin, Phys. Rev. Lett. 90, (2003).
158 Rezonans Feshbacha realizacja praktyczna B 0 = 543 G Rezonans Feshbacha uzyskany doświadczalnie dla atomów 6 Li w stanach zeemanowskich 1 2, 1 2 oraz 1 2, 1 2. T. Bourdel et al, Phys. Rev. Lett. 91, (2003).
159 Przejście z BEC do BCS
160 Przejście z BEC do BCS
161 Przejście z BEC do BCS B.Goss Levi, Physics Today, July, p. 25 (2005).
162 Przejście z BEC do BCS B.Goss Levi, Physics Today, July, p. 25 (2005).
163 Przejście z BEC do BCS Problem cia głego przejścia od stanu BCS do BEC należy do fundamentalnych zagadnień fizyki teoretycznej: 1969: David Eagles /BEC par fermionowych w niskich koncentracjach/ 1980: Tony Legett / sformułowanie problemu dla T = 0 / 1985: Phillip Nozières & Stefan Smitt-Rink /uogólnienie formalizmu dla niezerowych temperatur/ 1989: Roman Micnas et al /koncepcja niekoherentnych par/ 1993: Mohit Randeria et al /sformułowanie w jezyku całek po trajektoriach/...
164 Przejście z BEC do BCS uniwersalność
165 Przejście z BEC do BCS uniwersalność Uniwersalne zachowanie temperatury krytycznej R. Micnas, J. Ranninger, S. Robaszkiewicz, Rev. Mod. Phys. 62, 113 (1990).
166 Przejście z BEC do BCS uniwersalność θ = T/T F θ C (upper) θ C (lower) θ c,be ( n B 1/3 add ) 1/3 (B) θ c,be ( n add B ) BCS BCS + GM-B ν = 1/k F a Uniwersalne zachowanie temperatury krytycznej R. Haussmann et al, Phys. Rev. A 75, (2007).
167 Obserwacja BEC pierwsze doniesienie Kondensat BE par atomów typu fermionowego w funkcji odległości pola magnetycznego od rezonansu Feshbacha B = B B 0. C.A. Regal et al, Phys. Rev. Lett. 92, (2004).
168 Przejście z BEC do BCS ewolucja spektrum
169 Przejście z BEC do BCS ewolucja spektrum Przewidywana ewolucja widma wzbudzeń jednocza stkowych R. Haussmann et al, cond-mat/ (2009).
170 Nadciekłość pomiar (pseudo)szczeliny
171 Nadciekłość pomiar (pseudo)szczeliny Pomiar widma energetycznego wykonany przez spektroskopie RF dla atomów 6 Li wykazał istnienie przerwy energetycznej! C. Chin et al, Science 305, 1128 (2004).
172 Nadciekłość pomiar ciepła właściwego
173 Nadciekłość pomiar ciepła właściwego Ciepło właściwe wykazuje wykazuje osobliwość typowa dla przejścia do fazy nadciekłej T c 0.27T F. J. Kinast et al, Science 307, 1296 (2005).
174 Nadciekłość obserwacja sieci wirów
175 Nadciekłość obserwacja sieci wirów Sieć wirów Abrikosova dla par atomów typu fermionowego. M.W. Zwierlein et al, Nature 435, 1047 (2005).
176 Nadciekłość w przypadku N N Obserwacja wirów Abrikosova w układzie o nierównej liczebności atomów 6 Li w stanach 1 2, 1 2 oraz 1 2, 1 2. M.W. Zwierlein, A. Schirotzek, C.H. Schnuck & W. Ketterle, Science 311, 492 (2006).
177 3. Egzotyczne przykłady BEC
178 1. BEC magnonów nadciekłość spinowa
179 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu).
180 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu). Odpowiednio długi czas życia tych kwazicza stek umożliwia koherentna kondensacje BE magnonów
181 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu). Odpowiednio długi czas życia tych kwazicza stek umożliwia koherentna kondensacje BE magnonów Zjawisko przejawia sie poprzez:
182 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu). Odpowiednio długi czas życia tych kwazicza stek umożliwia koherentna kondensacje BE magnonów Zjawisko przejawia sie poprzez: a) spinowy superpra d transport magnetyzacji
183 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu). Odpowiednio długi czas życia tych kwazicza stek umożliwia koherentna kondensacje BE magnonów Zjawisko przejawia sie poprzez: a) spinowy superpra d transport magnetyzacji b) efekt Josephsona interferencja kondensatów
184 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu). Odpowiednio długi czas życia tych kwazicza stek umożliwia koherentna kondensacje BE magnonów Zjawisko przejawia sie poprzez: a) spinowy superpra d transport magnetyzacji b) efekt Josephsona interferencja kondensatów c) pra d krytyczny
185 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu). Odpowiednio długi czas życia tych kwazicza stek umożliwia koherentna kondensacje BE magnonów Zjawisko przejawia sie poprzez: a) spinowy superpra d transport magnetyzacji b) efekt Josephsona interferencja kondensatów c) pra d krytyczny d) wiry kwantowe / wykorzystywane do modelowania strun kosmicznych de Wittena /
186 1. BEC magnonów nadciekłość spinowa Wzbudzenia elementarne w magnetykach (tzw. magnony) podlegaja stystyce bozonowej (z powodu całkowitego spinu). Odpowiednio długi czas życia tych kwazicza stek umożliwia koherentna kondensacje BE magnonów Zjawisko przejawia sie poprzez: a) spinowy superpra d transport magnetyzacji b) efekt Josephsona interferencja kondensatów c) pra d krytyczny d) wiry kwantowe / wykorzystywane do modelowania strun kosmicznych de Wittena / e) mody Goldstona
187 1. BEC magnonów realizacja doświadczalna
188 1. BEC magnonów realizacja doświadczalna Oprócz stałego pola magnetycznego H z, które generuje duże namagnesowanie M z wła czono zmienne pole poprzeczne.
189 1. BEC magnonów realizacja doświadczalna Oprócz stałego pola magnetycznego H z, które generuje duże namagnesowanie M z wła czono zmienne pole poprzeczne. Po pewnym czasie spiny przechodza w stan koherentnej precesji indukuja c makroskopowa magnetyzacje M x + im y = M e iωt+iα
190 1. BEC magnonów realizacja doświadczalna Oprócz stałego pola magnetycznego H z, które generuje duże namagnesowanie M z wła czono zmienne pole poprzeczne. Po pewnym czasie spiny przechodza w stan koherentnej precesji indukuja c makroskopowa magnetyzacje M x + im y = M e iωt+iα
191 1. BEC magnonów realizacja doświadczalna Oprócz stałego pola magnetycznego H z, które generuje duże namagnesowanie M z wła czono zmienne pole poprzeczne. Po pewnym czasie spiny przechodza w stan koherentnej precesji indukuja c makroskopowa magnetyzacje M x + im y = M e iωt+iα Realizacja kondensacji BE magnonów w 3 He Y.M. Bunkov, G.E. Volovik, cond-mat/
192 1. Nadciekłość spinowa
193 1. Nadciekłość spinowa Efektywne oddziaływania pomie dzy magnonami pochodza ce ze sprze żenia spin-orbita prowadza do nadciekłości magnonów.
194 1. Nadciekłość spinowa Efektywne oddziaływania pomie dzy magnonami pochodza ce ze sprze żenia spin-orbita prowadza do nadciekłości magnonów.
195 1. Nadciekłość spinowa Efektywne oddziaływania pomie dzy magnonami pochodza ce ze sprze żenia spin-orbita prowadza do nadciekłości magnonów. Efekt Josephsona kondensatów magnonowych w 3 He / spontaniczny przepływ magnetyzacji pomie dzy próbkami / A.S. Borovik-Romanov et al, Phys. Rev. Lett. 62, 323 (1989).
196 2. Idea nadciekłości kwarków w QCD
197 2. Idea nadciekłości kwarków w QCD Oddziaływania w ge stej materii kwarkowej maja charakter przycia gaja cy.
198 2. Idea nadciekłości kwarków w QCD Oddziaływania w ge stej materii kwarkowej maja charakter przycia gaja cy. p F Pe dy Fermiego kwarków r g b różnia sie M s 2 4µ M s 2 4µ d u s red green blue red green blue M.G. Alford et al, Rev. Mod. Phys. 80, 1455 (2008).
199 2. Idea nadciekłości kwarków w QCD Oddziaływania w ge stej materii kwarkowej maja charakter przycia gaja cy. p F Faza SC - dwukolorowe parowanie d u s red greenblue blue M.G. Alford et al, Rev. Mod. Phys. 80, 1455 (2008).
200 2. Idea nadciekłości kwarków w QCD Oddziaływania w ge stej materii kwarkowej maja charakter przycia gaja cy. p F Faza CFL - color flavor locked d u s red greenblue blue M.G. Alford et al, Rev. Mod. Phys. 80, 1455 (2008).
201 2. Faza Wilczka
202 2. Faza Wilczka breached superfluidity
203 2. Faza Wilczka breached superfluidity W materii kwarkowej również wyste puja oddziaływania paruja ce.
204 2. Faza Wilczka breached superfluidity W materii kwarkowej również wyste puja oddziaływania paruja ce. Różnica mas kwarków (np. s oraz u) ε(p) 0 light fermion pairing Fermi surfaces heavy fermion p Pairing occurs along p=p F A Light Fermion p F A p F A < pf B p F B p F A p F B Heavy Fermion
205 2. Faza Wilczka breached superfluidity W materii kwarkowej również wyste puja oddziaływania paruja ce. Różnica mas kwarków (np. s oraz u) ε(p) 0 light fermion pairing Fermi surfaces heavy fermion p Pairing occurs along p=p F A Light Fermion p F A p F A < pf B p F B p F A p F B Heavy Fermion powoduje, że parowanie zachodzić może wśród stanów położonych głe boko po powierzchnia Fermiego (tzw. interior superfluidity).
206 2. Faza Wilczka breached superfluidity W materii kwarkowej również wyste puja oddziaływania paruja ce. Różnica mas kwarków (np. s oraz u) ε(p) 0 light fermion pairing Fermi surfaces heavy fermion p Pairing occurs along p=p F A Light Fermion p F A p F A < pf B p F B p F A p F B Heavy Fermion powoduje, że parowanie zachodzić może wśród stanów położonych głe boko po powierzchnia Fermiego (tzw. interior superfluidity). W.V. Liu and F. Wilczek, Phys. Rev. Lett. 90, (2003).
207 3. Kondensaty ekscytonowe
208 3. Kondensaty ekscytonowe
209 3. Kondensaty ekscytonowe Ekscyton = stan zwia zany elektronu (e) i dziury (h)
210 3. Kondensaty ekscytonowe Ekscyton = stan zwia zany elektronu (e) i dziury (h) Kondensat BE ekscytonów uzyskano w studniach kwantowych GaAs / AgAlAs PLintensity PLpeakintensity PLpeakintensity a c P ex (µw) T(K) e T=2.4 K r(µm) PLintensity r(µm) x4 530 I h e 770 T=14 K D Energy(eV) b d f Energy(eV) Energy(eV)
211 3. Kondensaty ekscytonowe Ekscyton = stan zwia zany elektronu (e) i dziury (h) Kondensat BE ekscytonów uzyskano w studniach kwantowych GaAs / AgAlAs L.V. Butov et al, Nature 418, 751 (2002). PLintensity PLpeakintensity PLpeakintensity a c P ex (µw) T(K) e T=2.4 K 390 r(µm) PLintensity r(µm) x4 530 I h e 770 T=14 K D Energy(eV) b d f Energy(eV) Energy(eV)
212 4 Nadprzewodniki wysokotemp.
213 Intensity (a) E F Energy T c < T stan normalny k F Wave vector ε k Intensity (b) v k 2 u k 2 E F Energy T <T c stan nadprzew. k F Wave vector -E k 2 E k W nadprzewodnikach konwencjonalnych widmo wzbudzeń składa z dwóch gałe zi Bogoliubova oddzielonych sie przerwa 2 sc wokół E F efekty fluktuacyjne sa pominie te.
214 Fakty doświadczalne dla T < T c H. Matsui, T. Sato, and T. Takahashi et al, Phys. Rev. Lett. 90, (2003).
215 Niekoherentne pary powyżej T c przesłanka # 1
216 Niekoherentne pary powyżej T c przesłanka # 1 Resztkowy efekt Meissnera zaobserwowany przy zastosowaniu ultraszybkich pól magnetycznych. J. Corson et al, Nature 398, 221 (1999).
217 Niekoherentne pary powyżej T c przesłanka # 2
218 Niekoherentne pary powyżej T c przesłanka # La 2-x Sr x CuO 4 T (K) T onset 20 T c Sr content x Duży efekt Nernsta obserwowany powyżej fazy sc. Y. Wang et al, Science 299, 86 (2003).
219 Niekoherentne pary powyżej T c przesłanka # 3
220 Niekoherentne pary powyżej T c przesłanka # 3 a) STM tip thin normal metal 20 b) 90 nm LSCO x=0.10 SrTiO 3 R (Ω) 10 Au/0.08 Au/0.10 Au/ T (K) c) 600 nm O. Yuli et al, cond-mat/ (preprint). Pseudoszczeline indukowano w cienkiej warstwie metalicznej na nadprzewodniku La 2 x Sr x CuO 4.
221 Niekoherentne pary powyżej T c przesłanka # 3 Pomiar LDOS a) 8 K x = K 0.0 Indukowana pseudoszczeline obserwowano w zakresie temperatur di/dv b) 4 K K x = 0.10 aż do T = T. 1.0 c) 8 K x = O. Yuli et al, cond-mat/ K Sample Bias (mv)
222 Wpływ preegzystuja cych par - scenariusz BF Przypadek: T < T c T=0 A F (k,ω) ω T. Domański and J. Ranninger, Phys. Rev. Lett. 91, (2003).
223 Wpływ preegzystuja cych par - scenariusz BF Przypadek: T c < T < T T=0.004 A F (k,ω) T. Domański and J. Ranninger, Phys. Rev. Lett. 91, (2003).
224 Wpływ preegzystuja cych par - scenariusz BF Przypadek: T c < T < T T=0.007 A F (k,ω) T. Domański and J. Ranninger, Phys. Rev. Lett. 91, (2003).
225 Wpływ preegzystuja cych par - scenariusz BF Przypadek: T > T T=0.02 A F (k,ω) T. Domański and J. Ranninger, Phys. Rev. Lett. 91, (2003).
226 Dos wiadczalne fakty dla T > Tc
227 Doświadczalne fakty dla T > T c Grupa J. Campuzano (Chicago, USA) Wyniki dla: Bi 2 Sr 2 CaCu 2 O 8 A. Kanigel et al, Phys. Rev. Lett. 101, (2008).
228 Doświadczalne fakty dla T > T c Grupa J. Campuzano (Chicago, USA) Wyniki: Bi 2 Sr 2 CaCu 2 O 8 A. Kanigel et al, Phys. Rev. Lett. 101, (2008).
229 Doświadczalne fakty dla T > T c Grupa PSI (Villigen, Szwajcaria) Max Energy [ev] Cut 1 Cut 1 Intensity [arb. units] Energy [mev] Cut 2 Cut 2 Min Energy [ev] Energy [ev] k - k F [ /a] Wyniki dla: La Sr CuO 4 M. Shi et al, cond-mat/ (preprint).
230 Zależność ka towa ( k) - przypadek T < T c J.E. Hoffman et al, Science 297, 1148 (2002).
231 Zależność ka towa ( k) - przypadek T < T c J.E. Hoffman et al, Science 297, 1148 (2002). Wiele doświadczeń wskazuje, że poniżej T c przerwa energetyczna posiada symetrie typu fali d.
232 Zalez nos c (~ k) powyz ej Tc
233 Zależność ( k) powyżej T c Powyżej T c przerwa energetyczna nadal istnieje. Ze wzrostem temperatury zaczynia zanikać pocza wszy od obszaru nodalnego, gdzie wyłaniaja sie łuki Fermiego.
234 Zależność ( k) powyżej T c Powyżej T c przerwa energetyczna nadal istnieje. Ze wzrostem temperatury zaczynia zanikać pocza wszy od obszaru nodalnego, gdzie wyłaniaja sie łuki Fermiego. A. Kanigel et al, Phys. Rev. Lett. 99, (2007).
235 Zależność ( k) powyżej T c Powyżej T c przerwa energetyczna nadal istnieje. Ze wzrostem temperatury zaczynia zanikać pocza wszy od obszaru nodalnego, gdzie wyłaniaja sie łuki Fermiego. Nadprzewodnik (Bi,Pb) 2 Sr 2 CuO 6 z T c =21K. K. Nakayama et al, Phys. Rev. Lett. 102, (2009).
236 Zależność ( k) powyżej T c Powyżej T c przerwa energetyczna nadal istnieje. Ze wzrostem temperatury zaczynia zanikać pocza wszy od obszaru nodalnego, gdzie wyłaniaja sie łuki Fermiego. Łuki Fermiego w zakresie temperatur T c < T < T. K. McElroy, Nature Physics 2, 441 (2006).
237 Analiza ka towej zależności pg ( k)
238 Analiza ka towej zależności pg ( k) Zbadaliśmy wpływ anizotropowej postaci sprze żenia B-F g k = g [cos(k x) cos(k y )] dla realistycznej dyspersji ε k = 2t [cos(k x)+cos(k y )] 4t cos(k x ) cos(k y ).
239 Analiza ka towej zależności pg ( k) Zbadaliśmy wpływ anizotropowej postaci sprze żenia B-F g k = g [cos(k x) cos(k y )] dla realistycznej dyspersji ε k = 2t [cos(k x)+cos(k y )] 4t cos(k x ) cos(k y ). k y π π/2 t /t= p=0.00 -π/2 -π -π -π/2 0 π/2 π k x
240 Analiza ka towej zależności pg ( k) Zbadaliśmy wpływ anizotropowej postaci sprze żenia B-F g k = g [cos(k x) cos(k y )] dla realistycznej dyspersji ε k = 2t [cos(k x)+cos(k y )] 4t cos(k x ) cos(k y ). k y π π/2 p = 1 - n F t /t= π/2 p=0.00 p=0.12 -π -π -π/2 0 π/2 π k x Topologia k F dla domieszkowania dziurami p = 0.12
241 Analiza ka towej zależności pg ( k) Zbadaliśmy wpływ anizotropowej postaci sprze żenia B-F g k = g [cos(k x) cos(k y )] dla realistycznej dyspersji ε k = 2t [cos(k x)+cos(k y )] 4t cos(k x ) cos(k y ). π π/2 p = 1 - n F φ Ka t planarny t /t= π/2 p=0.00 p=0.12 -π -π -π/2 0 π/2 π k x Topologia k F dla domieszkowania dziurami p = 0.12
242 Relacja pseudoszczeliny z łukami Fermiego
243 Relacja pseudoszczeliny z łukami Fermiego sc (k) T < T c (π,0) (π,π) 0 o 15 o 30 o 45 o 60 o 75 o 90 o k x (0,0) k y (0,π)
244 Relacja pseudoszczeliny z łukami Fermiego pg (k) T < T c T= (π,0) (π,π) 0 o 15 o 30 o 45 o 60 o 75 o 90 o k x Przy wzroście temperatury: (0,0) k y (0,π) w obszarze antynodalnym pg ( k) prawie sie nie zmienia,
245 Relacja pseudoszczeliny z łukami Fermiego pg (k) (π,0) k x T < T c T=0.007 T=0.009 (π,π) 0 o 15 o 30 o 45 o 60 o 75 o 90 o Przy wzroście temperatury: (0,0) k y (0,π) w obszarze antynodalnym pg ( k) prawie sie nie zmienia, pow. Fermiego odbudowuje sie w obszarze nodalnym,
246 Relacja pseudoszczeliny z łukami Fermiego pg (k) (π,0) k x T < T c T=0.007 T=0.009 T=0.011 (π,π) 0 o 15 o 30 o 45 o 60 o 75 o 90 o Przy wzroście temperatury: (0,0) k y (0,π) w obszarze antynodalnym pg ( k) prawie sie nie zmienia, pow. Fermiego odbudowuje sie w obszarze nodalnym, długość łuków Fermi skaluje sie liniowo wzgle dem T.
247 Relacja pseudoszczeliny z łukami Fermiego pg (k) (π,0) k x T < T c T=0.007 T=0.009 T=0.011 (π,π) 0 o 15 o 30 o 45 o 60 o 75 o 90 o Przy wzroście temperatury: (0,0) k y (0,π) w obszarze antynodalnym pg ( k) prawie sie nie zmienia, pow. Fermiego odbudowuje sie w obszarze nodalnym, długość łuków Fermi skaluje sie liniowo wzgle dem T. J. Ranninger and T. Domański, cond-mat/
248 Kwestia ilości biegunów
249 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym:
250 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym: A(k,ω) φ = 0 o k - k F ω
251 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym: A(k,ω) φ = 0 o k - k F ω
252 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym: A(k,ω) φ = 0 o k - k F ω
253 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym: A(k,ω) φ = 0 o k - k F ω
254 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym: A(k,ω) φ = 0 o k - k F ω
255 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym: A(k,ω) φ = 0 o k - k F ω
256 Kwestia ilości biegunów Struktura funkcji spectralnej w stanie pseudoszczelinowym: A(k,ω) φ = 0 o k - k F ω Blisko k F wyste puja 3 bieguny: 2 bieguny pochodza od modów Bogoliubova, trzeci biegun reprezentuje stan wewna trzszczelinowy.
257 Kwestia ilości biegunów
258 Kwestia ilości biegunów Podobny jakościowo wynik podkrślono ostatnio w pracy:
259 Kwestia ilości biegunów Podobny jakościowo wynik podkrślono ostatnio w pracy: T. Senthil and Patrick A. Lee, Phys. Rev. B 79, 245 (2009).
260 Kwestia ilości biegunów Podobny jakościowo wynik podkrślono ostatnio w pracy: T. Senthil and Patrick A. Lee, Phys. Rev. B 79, 245 (2009). A K,Ω Ω Krótko-zasie gowe korelacje par implikuja : wyste powanie 2 pików Bogoliubova oraz stanu in-gap, którego waga wynosi 1/[1 + 1 π ( k/γ) 2 ]
261 Dychotomia: we drowność lokalizacja par
262 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008).
263 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008). Przy zbliżaniu sie do fazy izolatora Motta:
264 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008). Przy zbliżaniu sie do fazy izolatora Motta: wielkość przerwy energetycznej wzrasta, coraz bardziej uwydatniaja sie różnice mie dzy dwoma typami par.
265 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008). Przy zbliżaniu sie do fazy izolatora Motta: wielkość przerwy energetycznej wzrasta, coraz bardziej uwydatniaja sie różnice mie dzy dwoma typami par.
266 Dychotomia: we drowność lokalizacja par
267 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008).
268 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008). Zależnie od obszarów strefy Brillouina widoczne sa :
269 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008). Zależnie od obszarów strefy Brillouina widoczne sa : we drowne pary Cooper a / the low energy itinerant sc features / pary zlokalizowane na wia zaniu Cu-O-Cu / dispersionless features in r-space /
270 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008). Zależnie od obszarów strefy Brillouina widoczne sa : we drowne pary Cooper a / the low energy itinerant sc features / pary zlokalizowane na wia zaniu Cu-O-Cu / dispersionless features in r-space /
271 Dychotomia: we drowność lokalizacja par Y. Kohsaka et al, Nature 454, 1072 (2008). Zale żnie od obszarów strefy Brillouina widoczne sa : we drowne pary Cooper a / the low energy itinerant sc features / pary zlokalizowane na wia zaniu Cu-O-Cu / dispersionless features in r-space /
272 Dychotomia: we drowność lokalizacja par
273 Dychotomia: we drowność lokalizacja par W obszarze antynodalnym pary moga zostać zlokalizowane
Najzimniejsze atomy. Tadeusz Domański. Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie.
 Odolanów, 10 lipca 2008 r. Najzimniejsze atomy Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman Referat be dzie dotyczyć : kondensacji i nadciekłości
Odolanów, 10 lipca 2008 r. Najzimniejsze atomy Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman Referat be dzie dotyczyć : kondensacji i nadciekłości
Kwazicza stki Bogoliubova w nadprzewodnikach
 Lublin, 20 stycznia 2009 r. Kwazicza stki Bogoliubova w nadprzewodnikach TADEUSZ DOMAŃSKI http://kft.umcs.lublin.pl/doman/lectures Plan referatu: Plan referatu: Wprowadzenie / istota stanu nadprzewodza
Lublin, 20 stycznia 2009 r. Kwazicza stki Bogoliubova w nadprzewodnikach TADEUSZ DOMAŃSKI http://kft.umcs.lublin.pl/doman/lectures Plan referatu: Plan referatu: Wprowadzenie / istota stanu nadprzewodza
Kondensat Bosego-Einsteina okiem teoretyka
 Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
Nadprzewodnictwo i nadciekłość w układach oddziałuja. cych mieszanin bozonowo-fermionowych. Tadeusz Domański
 Toruń, 22 września 2006 r. Nadprzewodnictwo i nadciekłość w układach oddziałuja cych mieszanin bozonowo-fermionowych Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures
Toruń, 22 września 2006 r. Nadprzewodnictwo i nadciekłość w układach oddziałuja cych mieszanin bozonowo-fermionowych Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures
Nadpłynność i nadprzewodnictwo
 Nadpłynność i nadprzewodnictwo Krzysztof Byczuk Instytut Fizyki Teoretycznej, Wydział Fizyki, Uniwersytet Warszawski 13 marzec 2019 www.fuw.edu.pl/ byczuk Tarcie, opór, dysypacja... pomaga... przeszkadza...
Nadpłynność i nadprzewodnictwo Krzysztof Byczuk Instytut Fizyki Teoretycznej, Wydział Fizyki, Uniwersytet Warszawski 13 marzec 2019 www.fuw.edu.pl/ byczuk Tarcie, opór, dysypacja... pomaga... przeszkadza...
Lublin, 7 VI ultrazimnych atomów. T. Domański. Instytut Fizyki UMCS.
 Lublin, 7 VI 2006 Nadciekłość w układach ultrazimnych atomów T. Domański Instytut Fizyki UMCS http://kft.umcs.lublin.pl/doman/lectures Tematem tego Sympozjum sa różne zjawiska fizyczne, które maja miejsce
Lublin, 7 VI 2006 Nadciekłość w układach ultrazimnych atomów T. Domański Instytut Fizyki UMCS http://kft.umcs.lublin.pl/doman/lectures Tematem tego Sympozjum sa różne zjawiska fizyczne, które maja miejsce
Odolanów, 4 VII ultrazimnych atomów. T. Domański. Instytut Fizyki UMCS.
 Odolanów, 4 VII 2006 Nadciekłość w układach ultrazimnych atomów T. Domański Instytut Fizyki UMCS http://kft.umcs.lublin.pl/doman/lectures Plan wykładu: Plan wykładu: Kondensacja Bosego-Einsteina Plan wykładu:
Odolanów, 4 VII 2006 Nadciekłość w układach ultrazimnych atomów T. Domański Instytut Fizyki UMCS http://kft.umcs.lublin.pl/doman/lectures Plan wykładu: Plan wykładu: Kondensacja Bosego-Einsteina Plan wykładu:
Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych
 LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach
LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach
Streszczenie W13. pułapki jonowe: siły Kulomba. łodzenie i pułapkowanie neutralnych atomów. 9 pułapki Penninga, Paula
 Streszczenie W13 pułapki jonowe: siły Kulomba 9 pułapki Penninga, Paula G pojedyncze jony mogą być pułapkowane i oglądane 9 kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
Streszczenie W13 pułapki jonowe: siły Kulomba 9 pułapki Penninga, Paula G pojedyncze jony mogą być pułapkowane i oglądane 9 kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych
 Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych B. Piętka, M. Król, R. Mirek, K. Lekenta, J. Szczytko J.-G. Rousset, M. Nawrocki,
Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych B. Piętka, M. Król, R. Mirek, K. Lekenta, J. Szczytko J.-G. Rousset, M. Nawrocki,
Rzadkie gazy bozonów
 Rzadkie gazy bozonów Tomasz Sowiński Proseminarium Fizyki Teoretycznej 15 listopada 2004 Rzadkie gazy bozonów p.1/25 Bardzo medialne zdjęcie Rok 1995. Pierwsza kondensacja. Zaobserwowana w przestrzeni
Rzadkie gazy bozonów Tomasz Sowiński Proseminarium Fizyki Teoretycznej 15 listopada 2004 Rzadkie gazy bozonów p.1/25 Bardzo medialne zdjęcie Rok 1995. Pierwsza kondensacja. Zaobserwowana w przestrzeni
Streszczenie W13. chłodzenie i pułapkowanie neutralnych atomów. pułapki jonowe: siły Coulomba
 Streszczenie W13 pułapki jonowe: siły Coulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów zastosowanie w komputerach kwantowych? przeskoki
Streszczenie W13 pułapki jonowe: siły Coulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów zastosowanie w komputerach kwantowych? przeskoki
pułapki jonowe: siły Kulomba łodzenie i pułapkowanie neutralnych atomów pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane
 Streszczenie W13 pułapki jonowe: siły Kulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
Streszczenie W13 pułapki jonowe: siły Kulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
(obserw. na Ŝywo emisji/abs. pojed. fotonów w pojed. atomach) a) spontaniczne ciśnienie światła (rozpraszają en. chłodzą)
 Streszczenie W11 pułapki jonowe: siły Kulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
Streszczenie W11 pułapki jonowe: siły Kulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
zastosowanie w komputerach kwantowych? przeskoki kwantowe (obserw. na żywo emisji/abs. pojed. fotonów w pojed. atomach)
 Streszczenie W13 pułapki jonowe: siły Coulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
Streszczenie W13 pułapki jonowe: siły Coulomba pułapki Penninga, Paula pojedyncze jony mogą być pułapkowane i oglądane kontrolowanie pojedynczych atomów I zastosowanie w komputerach kwantowych? przeskoki
Nadprzewodniki nowe fakty i teorie
 Warszawa, 13 września 2005 r. Nadprzewodniki nowe fakty i teorie T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Schemat referatu: Schemat referatu: Wste
Warszawa, 13 września 2005 r. Nadprzewodniki nowe fakty i teorie T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Schemat referatu: Schemat referatu: Wste
N a d p r z e w o d n i c t w o - przegla d faktów i koncepcji
 Katowice, 12 listopada 2008 r. N a d p r z e w o d n i c t w o - przegla d faktów i koncepcji T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Plan referatu:
Katowice, 12 listopada 2008 r. N a d p r z e w o d n i c t w o - przegla d faktów i koncepcji T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Plan referatu:
WYKŁAD 15. Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego
 WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Mody sprzężone plazmon-fonon w silnych polach magnetycznych
 Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Statystyka nieoddziaływujących gazów Bosego i Fermiego
 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Światło ma podwójną naturę:
 Światło ma podwójną naturę: przejawia własności fal i cząstek W. C. Roentgen ( Nobel 1901) Istnieje ciągłe przejście pomiędzy tymi własnościami wzdłuż spektrum fal elektromagnetycznych Dla niskich częstości
Światło ma podwójną naturę: przejawia własności fal i cząstek W. C. Roentgen ( Nobel 1901) Istnieje ciągłe przejście pomiędzy tymi własnościami wzdłuż spektrum fal elektromagnetycznych Dla niskich częstości
Nadpłynny gaz, ciecz i ciało stałe
 Nadpłynny gaz, ciecz i ciało stałe Nadpłynność Nadpłynność powstaje wskutek kondensacji Bosego - Einsteina bozonów: hel 4 (1938), gazy atomowe (np. Rb, Na, 1995), kryształ helu 4? S. N. Bose A. Einstein
Nadpłynny gaz, ciecz i ciało stałe Nadpłynność Nadpłynność powstaje wskutek kondensacji Bosego - Einsteina bozonów: hel 4 (1938), gazy atomowe (np. Rb, Na, 1995), kryształ helu 4? S. N. Bose A. Einstein
Statystyka nieoddziaływujących gazów Bosego: kondensacja Bosego- Einsteina
 Statystyka nieoddziaływujących gazów Bosego: kondensacja Bosego- Einsteina Silnie zwyrodniały gaz bozonów o niezerowej masie spoczynkowej Gdy liczba cząstek nie jest zachowywana, termodynamika nieoddziaływujących
Statystyka nieoddziaływujących gazów Bosego: kondensacja Bosego- Einsteina Silnie zwyrodniały gaz bozonów o niezerowej masie spoczynkowej Gdy liczba cząstek nie jest zachowywana, termodynamika nieoddziaływujących
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
w rozrzedzonych gazach atomowych
 w rozrzedzonych gazach atomowych Anna Okopińska Instytut Fizyki S P IS T RE Ś C I I WSTĘP II. TEORIA ZDEGENEROWANYCH GAZÓW DOSKONAŁYCH III. WŁASNOŚCI MATERII W NISKICH TEMPERATURACH IV. METODY CHŁODZENIA
w rozrzedzonych gazach atomowych Anna Okopińska Instytut Fizyki S P IS T RE Ś C I I WSTĘP II. TEORIA ZDEGENEROWANYCH GAZÓW DOSKONAŁYCH III. WŁASNOŚCI MATERII W NISKICH TEMPERATURACH IV. METODY CHŁODZENIA
Fizyka kwantowa. promieniowanie termiczne zjawisko fotoelektryczne. efekt Comptona dualizm korpuskularno-falowy. kwantyzacja światła
 W- (Jaroszewicz) 19 slajdów Na podstawie prezentacji prof. J. Rutkowskiego Fizyka kwantowa promieniowanie termiczne zjawisko fotoelektryczne kwantyzacja światła efekt Comptona dualizm korpuskularno-falowy
W- (Jaroszewicz) 19 slajdów Na podstawie prezentacji prof. J. Rutkowskiego Fizyka kwantowa promieniowanie termiczne zjawisko fotoelektryczne kwantyzacja światła efekt Comptona dualizm korpuskularno-falowy
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Kondensacja Bosego-Einsteina
 Kondensacja Bosego-Einsteina W opisie kwantowo-mechanicznym stan konkretnego uk ladu fizycznego jest określony poprzez funkcje falowa ψ r, r 2,...), gdzie r i oznaczaja po lożenia poszczególnych cza stek.
Kondensacja Bosego-Einsteina W opisie kwantowo-mechanicznym stan konkretnego uk ladu fizycznego jest określony poprzez funkcje falowa ψ r, r 2,...), gdzie r i oznaczaja po lożenia poszczególnych cza stek.
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH
 Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Nadprzewodniki. W takich materiałach kiedy nastąpi przepływ prądu może on płynąć nawet bez przyłożonego napięcia przez długi czas! )Ba 2. Tl 0.2.
 Nadprzewodniki Pewna klasa materiałów wykazuje prawie zerową oporność (R=0) poniżej pewnej temperatury zwanej temperaturą krytyczną T c Większość przewodników wykazuje nadprzewodnictwo dopiero w temperaturze
Nadprzewodniki Pewna klasa materiałów wykazuje prawie zerową oporność (R=0) poniżej pewnej temperatury zwanej temperaturą krytyczną T c Większość przewodników wykazuje nadprzewodnictwo dopiero w temperaturze
Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu rubidowego
 Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
Atom wodoru w mechanice kwantowej. Równanie Schrödingera
 Fizyka atomowa Atom wodoru w mechanice kwantowej Moment pędu Funkcje falowe atomu wodoru Spin Liczby kwantowe Poprawki do równania Schrödingera: struktura subtelna i nadsubtelna; przesunięcie Lamba Zakaz
Fizyka atomowa Atom wodoru w mechanice kwantowej Moment pędu Funkcje falowe atomu wodoru Spin Liczby kwantowe Poprawki do równania Schrödingera: struktura subtelna i nadsubtelna; przesunięcie Lamba Zakaz
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Stara i nowa teoria kwantowa
 Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach
 Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka, Michał Karpiński Wydział
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka, Michał Karpiński Wydział
Ekscyton w morzu dziur
 Ekscyton w morzu dziur P. Kossacki, P. Płochocka, W. Maślana, A. Golnik, C. Radzewicz and J.A. Gaj Institute of Experimental Physics, Warsaw University S. Tatarenko, J. Cibert Laboratoire de Spectrométrie
Ekscyton w morzu dziur P. Kossacki, P. Płochocka, W. Maślana, A. Golnik, C. Radzewicz and J.A. Gaj Institute of Experimental Physics, Warsaw University S. Tatarenko, J. Cibert Laboratoire de Spectrométrie
Podstawy informatyki kwantowej
 Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
 2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
Szczegółowy wgląd w proces chłodzenia jedno-wymiarowego gazu bozonów
 Szczegółowy wgląd w proces chłodzenia jedno-wymiarowego gazu bozonów Piotr Deuar (IF PAN) Emilia Witkowska, Mariusz Gajda (IF PAN) Kazimierz Rzążewski (CFT PAN) Cover of Phys. Rev. Lett., 1 Apr 2011 E.
Szczegółowy wgląd w proces chłodzenia jedno-wymiarowego gazu bozonów Piotr Deuar (IF PAN) Emilia Witkowska, Mariusz Gajda (IF PAN) Kazimierz Rzążewski (CFT PAN) Cover of Phys. Rev. Lett., 1 Apr 2011 E.
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force
 SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
Henryk Szymczak Instytut Fizyki PAN
 NNnnNowe kwazicząstki w magnetykach Henryk Szymczak Instytut Fizyki PAN Zjazd Fizyków 2015 1 Enrico Fermi: nigdy nie należy lekceważyć przyjemności, jaką każdy z nas odczuwa, słysząc coś, o czym już wie
NNnnNowe kwazicząstki w magnetykach Henryk Szymczak Instytut Fizyki PAN Zjazd Fizyków 2015 1 Enrico Fermi: nigdy nie należy lekceważyć przyjemności, jaką każdy z nas odczuwa, słysząc coś, o czym już wie
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Chłodzenie jedno-wymiarowego gazu bozonów
 Chłodzenie jedno-wymiarowego gazu bozonów Piotr Deuar (IF PAN) Emilia Witkowska, Mariusz Gajda (IF PAN) Kazimierz Rzążewski (CFT PAN) Cover of Phys. Rev. Lett., 1 Apr 2011 E. Witkowska, PD, M. Gajda, K.
Chłodzenie jedno-wymiarowego gazu bozonów Piotr Deuar (IF PAN) Emilia Witkowska, Mariusz Gajda (IF PAN) Kazimierz Rzążewski (CFT PAN) Cover of Phys. Rev. Lett., 1 Apr 2011 E. Witkowska, PD, M. Gajda, K.
Menu. Badające rozproszenie światła,
 Menu Badające rozproszenie światła, Instrumenty badające pole magnetyczne Ziemi Pole magnetyczne Ziemi mierzy się za pomocą magnetometrów. Instrumenty badające pole magnetyczne Ziemi Rodzaje magnetometrów:»
Menu Badające rozproszenie światła, Instrumenty badające pole magnetyczne Ziemi Pole magnetyczne Ziemi mierzy się za pomocą magnetometrów. Instrumenty badające pole magnetyczne Ziemi Rodzaje magnetometrów:»
Wykłady z Fizyki. Kwanty
 Wykłady z Fizyki 10 Kwanty Zbigniew Osiak OZ ACZE IA B notka biograficzna C ciekawostka D propozycja wykonania doświadczenia H informacja dotycząca historii fizyki I adres strony internetowej K komentarz
Wykłady z Fizyki 10 Kwanty Zbigniew Osiak OZ ACZE IA B notka biograficzna C ciekawostka D propozycja wykonania doświadczenia H informacja dotycząca historii fizyki I adres strony internetowej K komentarz
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale.
 VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
Przejścia kwantowe w półprzewodnikach (kryształach)
 Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
1.6. Falowa natura cząstek biologicznych i fluorofullerenów Wstęp Porfiryny i fluorofullereny C 60 F
 SPIS TREŚCI Przedmowa 11 Wprowadzenie... 13 Część I. Doświadczenia dyfrakcyjno-interferencyjne z pojedynczymi obiektami mikroświata.. 17 Literatura... 23 1.1. Doświadczenia dyfrakcyjno-interferencyjne
SPIS TREŚCI Przedmowa 11 Wprowadzenie... 13 Część I. Doświadczenia dyfrakcyjno-interferencyjne z pojedynczymi obiektami mikroświata.. 17 Literatura... 23 1.1. Doświadczenia dyfrakcyjno-interferencyjne
Teoria Orbitali Molekularnych. tworzenie wiązań chemicznych
 Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru
 Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Spis treści. Przedmowa Obraz makroskopowy Ciepło i entropia Zastosowania termodynamiki... 29
 Przedmowa... XI 1. Obraz makroskopowy... 1 1.1. Termodynamika... 1 1.2. Parametry termodynamiczne... 2 1.3. Granica termodynamiczna... 3 1.4. Procesy termodynamiczne... 4 1.5. Klasycznygazdoskonały...
Przedmowa... XI 1. Obraz makroskopowy... 1 1.1. Termodynamika... 1 1.2. Parametry termodynamiczne... 2 1.3. Granica termodynamiczna... 3 1.4. Procesy termodynamiczne... 4 1.5. Klasycznygazdoskonały...
Reakcje jądrowe. X 1 + X 2 Y 1 + Y b 1 + b 2
 Reakcje jądrowe X 1 + X 2 Y 1 + Y 2 +...+ b 1 + b 2 kanał wejściowy kanał wyjściowy Reakcje wywołane przez nukleony - mechanizm reakcji Wielkości mierzone Reakcje wywołane przez ciężkie jony a) niskie
Reakcje jądrowe X 1 + X 2 Y 1 + Y 2 +...+ b 1 + b 2 kanał wejściowy kanał wyjściowy Reakcje wywołane przez nukleony - mechanizm reakcji Wielkości mierzone Reakcje wywołane przez ciężkie jony a) niskie
Optyka. Optyka geometryczna Optyka falowa (fizyczna) Interferencja i dyfrakcja Koherencja światła Optyka nieliniowa
 Optyka Optyka geometryczna Optyka falowa (fizyczna) Interferencja i dyfrakcja Koherencja światła Optyka nieliniowa 1 Optyka falowa Opis i zastosowania fal elektromagnetycznych w zakresie widzialnym i bliskim
Optyka Optyka geometryczna Optyka falowa (fizyczna) Interferencja i dyfrakcja Koherencja światła Optyka nieliniowa 1 Optyka falowa Opis i zastosowania fal elektromagnetycznych w zakresie widzialnym i bliskim
Solitony i zjawiska nieliniowe we włóknach optycznych
 Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
FALE MATERII. De Broglie, na podstawie analogii optycznych, w roku 1924 wysunął hipotezę, że
 FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
NMR (MAGNETYCZNY REZONANS JĄDROWY) dr Marcin Lipowczan
 NMR (MAGNETYCZNY REZONANS JĄDROWY) dr Marcin Lipowczan Spis zagadnień Fizyczne podstawy zjawiska NMR Parametry widma NMR Procesy relaksacji jądrowej Metody obrazowania Fizyczne podstawy NMR Proton, neutron,
NMR (MAGNETYCZNY REZONANS JĄDROWY) dr Marcin Lipowczan Spis zagadnień Fizyczne podstawy zjawiska NMR Parametry widma NMR Procesy relaksacji jądrowej Metody obrazowania Fizyczne podstawy NMR Proton, neutron,
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym
 II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe
 Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 3 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 3 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
Fizyka 3.3 WYKŁAD II
 Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków).
 Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
Optyka kwantowa wprowadzenie. Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej
 Optyka kwantowa wprowadzenie Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej Krótka (pre-)historia fotonu (1900-1923) Własności światła i jego oddziaływania
Optyka kwantowa wprowadzenie Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej Krótka (pre-)historia fotonu (1900-1923) Własności światła i jego oddziaływania
ZASADY ZALICZENIA PRZEDMIOTU MBS
 ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka, Michał Karpiński Wydział
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka, Michał Karpiński Wydział
kondensat Bosego-Einsteina
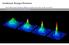 kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
Reakcje jądrowe. kanał wyjściowy
 Reakcje jądrowe X 1 + X 2 Y 1 + Y 2 +...+ b 1 + b 2 kanał wejściowy kanał wyjściowy Reakcje wywołane przez nukleony - mechanizm reakcji Wielkości mierzone Reakcje wywołane przez ciężkie jony a) niskie
Reakcje jądrowe X 1 + X 2 Y 1 + Y 2 +...+ b 1 + b 2 kanał wejściowy kanał wyjściowy Reakcje wywołane przez nukleony - mechanizm reakcji Wielkości mierzone Reakcje wywołane przez ciężkie jony a) niskie
Równanie falowe Schrödingera ( ) ( ) Prostokątna studnia potencjału o skończonej głębokości. i 2 =-1 jednostka urojona. Ψ t. V x.
 Równanie falowe Schrödingera h Ψ( x, t) + V( x, t) Ψ( x, t) W jednym wymiarze ( ) ( ) gdy V x, t = V x x Ψ = ih t Gdy V(x,t)=V =const cząstka swobodna, na którą nie działa siła Fala biegnąca Ψ s ( x, t)
Równanie falowe Schrödingera h Ψ( x, t) + V( x, t) Ψ( x, t) W jednym wymiarze ( ) ( ) gdy V x, t = V x x Ψ = ih t Gdy V(x,t)=V =const cząstka swobodna, na którą nie działa siła Fala biegnąca Ψ s ( x, t)
Widmo fal elektromagnetycznych
 Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Mechanika kwantowa. Erwin Schrödinger ( ) Werner Heisenberg
 Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Zespolona funkcja dielektryczna metalu
 Zespolona funkcja dielektryczna metalu Przenikalność elektryczna ośrodków absorbujących promieniowanie elektromagnetyczne jest zespolona, a także zależna od częstości promieniowania, które przenika przez
Zespolona funkcja dielektryczna metalu Przenikalność elektryczna ośrodków absorbujących promieniowanie elektromagnetyczne jest zespolona, a także zależna od częstości promieniowania, które przenika przez
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY
 WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład Atom o wielu elektronach Laser Rezonans magnetyczny
 Wykład 21. 12.2016 Atom o wielu elektronach Laser Rezonans magnetyczny Jeszcze o atomach Przypomnienie: liczby kwantowe elektronu w atomie wodoru, zakaz Pauliego, powłoki, podpowłoki, orbitale, Atomy wieloelektronowe
Wykład 21. 12.2016 Atom o wielu elektronach Laser Rezonans magnetyczny Jeszcze o atomach Przypomnienie: liczby kwantowe elektronu w atomie wodoru, zakaz Pauliego, powłoki, podpowłoki, orbitale, Atomy wieloelektronowe
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Promieniowanie X. Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X
 Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Mateusz Winkowski, Jan Szczepanek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Nadprzewodniki: właściwości i zastosowania
 Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania Tadeusz Domański Instytut Fizyki Uniwersytet M. Curie-Skłodowskiej Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania
Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania Tadeusz Domański Instytut Fizyki Uniwersytet M. Curie-Skłodowskiej Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania
Podstawy fizyki kwantowej i budowy materii
 Podstawy fizyki kwantowej i budowy materii prof. dr hab. Aleksander Filip Żarnecki Zakład Cząstek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wykład 5 7 listopada 2016 A.F.Żarnecki Podstawy
Podstawy fizyki kwantowej i budowy materii prof. dr hab. Aleksander Filip Żarnecki Zakład Cząstek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wykład 5 7 listopada 2016 A.F.Żarnecki Podstawy
Wstęp do optyki i fizyki materii skondensowanej. O: Wojciech Wasilewski FMS: Mateusz Goryca
 Wstęp do optyki i fizyki materii skondensowanej O: Wojciech Wasilewski FMS: Mateusz Goryca 1 Zasady części O Wykład przeglądowy Ćwiczenia rozszerzające lub ilustrujące Sprawdzane prace domowe psi.fuw.edu.pl/main/wdoifms
Wstęp do optyki i fizyki materii skondensowanej O: Wojciech Wasilewski FMS: Mateusz Goryca 1 Zasady części O Wykład przeglądowy Ćwiczenia rozszerzające lub ilustrujące Sprawdzane prace domowe psi.fuw.edu.pl/main/wdoifms
Fizyka. dr Bohdan Bieg p. 36A. wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe
 Fizyka dr Bohdan Bieg p. 36A wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe Literatura Raymond A. Serway, John W. Jewett, Jr. Physics for Scientists and Engineers, Cengage Learning D. Halliday, D.
Fizyka dr Bohdan Bieg p. 36A wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe Literatura Raymond A. Serway, John W. Jewett, Jr. Physics for Scientists and Engineers, Cengage Learning D. Halliday, D.
Podstawy fizyki sezon 2 7. Układy elektryczne RLC
 Podstawy fizyki sezon 2 7. Układy elektryczne RLC Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Układ RC
Podstawy fizyki sezon 2 7. Układy elektryczne RLC Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Układ RC
Optyczna spektroskopia oscylacyjna. w badaniach powierzchni
 Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Światło fala, czy strumień cząstek?
 1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
Nadprzewodniki: nowe fakty i teorie
 FIZYKA FAZY SKONDENSOWANEJ Nadprzewodniki: nowe fakty i teorie Tadeusz Domański Instytut Fizyki, Uniwersytet Marii Curie-Skłodowskiej, Lublin Superconductors: new facts and theories Abstract: We summarize
FIZYKA FAZY SKONDENSOWANEJ Nadprzewodniki: nowe fakty i teorie Tadeusz Domański Instytut Fizyki, Uniwersytet Marii Curie-Skłodowskiej, Lublin Superconductors: new facts and theories Abstract: We summarize
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
Oddziaływanie promieniowania X z materią. Podstawowe mechanizmy
 Oddziaływanie promieniowania X z materią Podstawowe mechanizmy Promieniowanie od oscylującego elektronu Rozpraszanie Thomsona Dyspersja podejście klasyczne Fala padająca Wymuszony, tłumiony oscylator harmoniczny
Oddziaływanie promieniowania X z materią Podstawowe mechanizmy Promieniowanie od oscylującego elektronu Rozpraszanie Thomsona Dyspersja podejście klasyczne Fala padająca Wymuszony, tłumiony oscylator harmoniczny
