Systemy resztowe. Kongruencje. Liczby kongruentne (przystaj ce) modulo w (w moduł przystawania) (N,M ): N M(modw) k : N M=kw M N=kw
|
|
|
- Weronika Dobrowolska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Kogruecje Lczby ogruete (przytaj ce) modulo w (w moduł przytawaa) (N,M ): N M(modw) : NMw MNw Kogruecja relacja rówowa o c: zwrota (reflexve): N N(modw), ymetrycza (ymmetrc): N M(modw) M N(modw), przechoda (tratve): N M(modw)&M P(modw) N P(modw). LEMAT: Kogruecja jet zachowawcza (oboj ta, dfferet) wobec a dego z dzała : dodawaa, odejmowaa, mo ea ( ) N M(modw) Q P(modw) N Q M P(modw). DOWÓD: Je l NM+aw oraz QP+bw, to N±Q(M±P)+(a±b)w oraz NQMP+(Μb+Pa+abw)w Iloraz całowty Xdvw (w X : XXmodww Xdvw Jauz Berat, AK-5-9-.doc, wrze a 9 RNS
2 Klay ogruecj Klay ogruecj (rówowa o c wzgl dem relacj przytawaa) w:r{z :Z r(modw); w/ r< w/ }, w: w: w:r r rezta z dzelea (redue) lczby całowtej (aturalej) przez moduł w ajmej odległa od zera (ajmejza bezwzgl de) W zborze lczb aturalych jet r mamy: w:r w:r w:r w:r w 7:5{5,,9,6, } 7: {, 9,,5,,9,6, } 7:{,8,5,, } 7:{,, 6,,8,5,, } DEFINICJE Podzel p lczby Q p Q Qmodp, p Odwroto (multyplatywa) x modw lczby x modulo w ax modw ax modw! (je l x w maj wpóly podzel p, to z xmodw e ma rozw zaa) Jauz Berat, AK-5-9-.doc, wrze a 9 RNS
3 Algorytm Euldea Najw zy wpóly (po)dzel NWD (greatet commo dvor, GCD) NWD(X,Y)a (a X a Y) b : (b>a) (b X b Y) TWIERDZENIE: Dla dowolych lczb aturalych m, je l m< oraz pnwd(m,), to:. lczba p jet te ajw zym wpólym dzelem m oraz modm.. tej tae lczby całowte u oraz v, e pu+vm (ajw zy wpóly dzel mo a przedtaw jao ombacj low lczb m oraz ). DOWÓD:. Je l pnwd(m,), to m m p oraz p, to m( m )p, w c m< pnwd(m,)nwd(m,modm). Je l pnwd(,m), to m m p, p oraz NWD(, m ). Mamy zatem vmv m p, uu p v m +u. Poewa NWD(, m ), w c a da lczba u dla u,,, m ale y do ej lay ogruecj modulo m. Iteje w c tae u, e u m +. Rówo jet pełoa gdy v. Jauz Berat, AK-5-9-.doc, wrze a 9 RNS
4 Wła cwo c rezt Lczby wzgl de perwze (relatvely prme): NWD(X,Y). LEMAT: Je el rezty z dzelea lczby przez moduły wzgl de perwze obe rówe, to oe rówe rezce z dzelea przez loczy tych modułów ( w, w ) & X mod w X mod w q X mod( ww ) q. DOWÓD: Je l Xmodw q Xmodw q, to (X q)modw (X q)modw. Zatem X q w X q w, w c X q w w oraz Xmodw w q LEMAT: Kogruecje mo a dzel obutroe przez wpóly czy: (ax)mod(aw)a(xmodw) DOWÓD: (ax)mod(aw)axaw ax/aw a(xw X/w )a(xmodw) Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 4
5 Sto Eratoteea Je l z c gu olejych lczb aturalych uuemy podzele przez (parzyte), at pe podzele przez (co trzec ), at pe podzele przez 5 (co p t po ród wzytch) etc., to w c gu pozota tylo lczby perwze. Je l a N oraz a>n/a, to w c gu N olejych lczb aturalych e ma ju lczb podzelych przez a (zotały wcze ej wyre loe) Wzyte lczby perwze (oprócz ) eparzyte Algorytm:. Utwórz c g olejych lczb eparzytych <N. Zajd w c gu perwz lczb A ró od (jet a pozycj A (A+)/). W mejce a dej lczby c gu umezczoej a pozycj A +A wpz 4. Je el A <N, powró do, w przecwym raze zao cz Najmejza wpóla weloroto NWW(leat commo multply, LCM) NWW(X, X,, X m )W : X W Z : (Z<W) : X Z Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 5
6 Podzelo lczb () ale x mod w ( x mod w)( mod w) mod w, w c, poewa x, mamy mod( ± ) m mod( ± ) ( m), x mod ( ) x mod ( ) x mod ( + ) ( ) x mod ( + ) reguły podzelo c przez 9 w yteme dze tym 785 mod 9 (7+8+5) mod 9, 785 mod (7 8+5) mod 4 Je l a ±, to mod a ± oraz mod a ( ± ) reguły podzelo c przez a w yteme o baze a ± 785 mod (7+8+5) mod mod Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 6
7 Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 7 Podzelo lczb () X x x + / / ) )( (, gdze l x X + warto cam cyfr po owerj ( ). Ale jet j j ) ( ) mod( ) mod( m m ± ±, zatem: ) mod ( ) mod ( / X x ) mod ( ) ( ) mod ( / + + X x 45 mod 45 mod ( +) (45) mod ( +) 5 6 mod FF mod ( ) 6 (+5) 6 mod ( ) mod mod ( ) 8 (+56) 8 mod ( ) 8 8
8 Oreowo rezt a w a mod w ( ) mod ± ± ore ogruecj P(,w) mod w & < : mod w półore ogruecj HP(,w) mod w & < : mod w rezty pot g baz wzgl dem modułów ± powtarzaj oreowo mod( ± ) j m mod( ± ) ( m) j j + j mod( ± ) ( m ) mod( ± ) rezty pot g baz wzgl dem modułów ( ± + mod( ± + ) ) powtarzaj oreowo: mod( ± + ) m mod( ± + ) [ ( m )]mod( ± + ) ± Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 8
9 Małe twerdzee Fermata TWIERDZENIE Nech p b dze lczb perwz. Je l p e jet podzelem lczby a, to wtedy a p (modp) za dla dowolego a zachodz a p a(modp). DOWÓD. Soro p e dzel a, to j p : a j amodp, w c a da lczba c gu a, a, a,,(p ) a ale y do ej lay reztowej p:r, r,,...,p. A zatem [( a)( a)( a) ((p ) a)]modp(p )! modp, czyl a p (p )! (p )!(modp) Poewa NWD(p,a), w c NWD(p,(a p ) (p )!)p, (bowem (p )! e dzel przez p). St d wya, e a p (modp) poewa p e dzel a, w c a a p a(modp), a zatem a p a(modp) Je l NWD(p,a)p, to otata zale o jet trywala (amodp) Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 9
10 Fucja Eulera ϕ(n) co druga aturala jet podzela przez, co trzeca z pozotałych dzel przez, co p ta z epodzelych przez lub dzel przez 5, etc. TWIERDZENIE e e m Je l podzelam lczby N p, p,, p m, czyl N p p... p e m, p, to lczb aturalych mejzych od N wzgl de perwzych z lczb N jet DOWÓD: m ϕ ( N) ( p ) p, p Je l p jet podzelem N, to w zborze {,,,N} jet N N(p ) lczb epodzelych przez p. [N N(p ) ] [N N(p ) ] (p j ) N ( (p ) )( (p j ) ) po ród ch e jet podzelych przez p j. (co p j -ta po ród N po ród p ) Je l w c p,,...,m lczbam perwzym, to w zborze {,,,N} jet e e em e e em p p... p ( )( )...( )... ( )( )...( m p p pm p p pm p p pm ) lczb epodzelych przez ad z ch. Jauz Berat, AK-5-9-.doc, wrze a 9 RNS e WNIOSEK: Je l NWD(N,M), to ϕ(mn)ϕ(m)ϕ(n).
11 Twerdzee Eulera TWIERDZENIE Je l ϕ(n) jet lczb lczb mejzych od N wzgl de perwzych z N, to DOWÓD. ( ) a ϕ N mod N Je l Np twerdzee jet prawdzwe (ϕ(p)p ) (małe tw. Fermata). Załó my, e twerdzee jet prawdzwe dla Np m p p, czyl a m ( ) mod p St d wya, e p ( p) a m mod p p p m a m ( ) + p m+ oraz p p m p a m ( ) ( + p ) + Kpp. Twerdzee jet w c prawdzwe dla Np α, czyl m m., zatem a ϕ ( p m ) mod p m Je l w c a a ϕ ( p ϕ ( p a a b h q... t b h ) q... w ) N... mod q a b h a b h ϕ ( p q... t ) a ϕ ( p ) ϕ ( q... t ) a p q t, to a mod p ( a ) mod p b mod ( p ( a a q b ϕ ( q... w b h ) ) ϕ ( p a... t h ) mod q ( ) ), czyl a ϕ N mod N ϕ ( ) WNIOSEK: a N a (mod N) b Jauz Berat, AK-5-9-.doc, wrze a 9 RNS a b h oraz td.. St d wya teza twerdzea:
12 Ch e twerdzee o reztach ytem RNS Nech W{w,w,...,w m : j: NWD(w,w j )} za W m w Reprezetacja X x,x,,x m : x Xmodw, w W a dej lczby X<W jet uatowa. DOWÓD. Załó my, e X,Y<W, Y X: m:y Xmodw. Zatem m:w (YX), a poewa WNWW(w,w,,w m ), to W (YX). Soro jeda Y X, to Y X W, co przeczy zało eu, w c YX Sytem reztowy RNS(w,w,,w m ) (Redue Number Sytem) Reprezetacja X x modw,x modw,,x m modw m : w W w baze W x {,,...,w } dla ogruecj w zborze, x { w /,,,,,..., w / } dla ogruecj w zborze WNIOSEK: W yteme RNS(w,w,,w m ),, m: x,x,,x m x ± w,x ± w,,x m ± m w m modw Jauz Berat, AK-5-9-.doc, wrze a 9 RNS
13 Ch e twerdzee o reztach owerja odwrota CHI SKIE TWIERDZENIE O RESZTACH (CRT) (SUN-TZU, III W., QIN JIUSHAO, 47) Nech W{w,w,...,w : j: NWD(w,w j )}, W ww... w. Reprezetacja x,x,,x : x Xmodw, w W a dej lczby X<W jet uatowa oraz gdze X X w ˆ Ww, za mod w ( mod w ) x modw odwroto ŵ wzgl dem modułu DOWÓD (eformaly zc dowodu owerj odwrotej). Ze wzgl du a zachowawczo ogruecj wobec dodawaa mamy Jauz Berat, AK-5-9-.doc, wrze a 9 RNS w. x,x,,x x,,,, +x,,,, + +x,,,,. W yteme RNS(w,w,,w m ) lczba p o reprezetacj,,,,,, jet podzela przez a de w oprócz w, jet w c p (lczby p tej, bo ró ych reprezetacj jet dołade W). Poewa jej rezta wzgl dem w jet rówa, w c mod w jet odwroto c ŵ oraz p ( mod w ). x,x,,x jet w c reprezetacj lczby (x p +x p + +x p ) modw.
14 Wybór ytemu reztowego Dobór modułów argumety zare reprezetowaych lczb loczy wzytch modułów łatwo zybo wyoaa dzała modulo łatwo owerj owerj odwrotej moduły,, + dobrze pełaj wymagaa (, ), (, +) oraz (, +) (gdy parzyte) w yteme dwójowym je l (,m), to (, m ) (lczby Meree a) przy pezee dodawaa ~ proporcjoale do log z lczby modułów m w cej modułów tym trudejza owerja odwrota opcje W{ +,, } W{ +,,, } W{,,,,, <...<<, (,,,)} Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 4
15 Kowerja z ytemu tałobazowego a ytem RNS( +,, ) A X x { RNS j : ( a j j mod w )( mod w )} mod w reguły podzelo c reguły owerj z ytemu aturalego a RNS, dla modułów o potac, +. a + l l A a ( a ) A, l l gdze A warto cam cyfr lczby A w yteme o baze. Poewa A, zatem A mod A mod oraz + l l A mod( ) { A }mod( ) { A }mod( ) A mod( + ) { A }mod( + ) { ( ) A }mod( + ) Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 5
16 Kowerja z ytemu reztowego a ytem tałobazowy (CRT) p,,,, jedy reztowe (wag), p mod p mod w w j Warto c lczby X<WΠw o reprezetacj x, x,..., x jet zatem (CRT) X x p + x p +... x p ) modw, ( + W celu wyzaczea -tej jedy p wytarczy wyoa w oblcze. Mamy,...,,..., w w W, mod w w, Oblczae jedye reztowych p ( mod w ) : ( w ˆ( mod w ))mod w mod w ))mod w [( mod w )( rozw zae rówaa, czyl ( ( mod w )] mod w (... je l axmodw, to a xmodwx modw) odwrócoy algorytm Euldea zapujemy jao um weloroto c x ( x mod ) x ( x mod ) [ x dv x + mod x]... ϕ ( ) twerdzee Eulera: a N a (mod N) Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 6
17 Kowerja z ytemu reztowego a ytem tałobazowy Sytem reztowy RNS(a+,a,a ) (ap mu by parzyte) Mamy W(a+) a (a ). Oblczymy lczby ˆ w ww ( a + ) a, w mod w w ˆ ww ( a + )( a ), w ˆ mod w ( ) w w w a( a ), w mod w ( ) ( ) ˆ ŵ j ˆ ˆ oraz ch odwroto c multyplatywe ( mod w ) w ˆ mod w mod( a ) mod( a ) a /, w ˆ mod w mod a mod a w ˆ mod w mod( a + ) mod( a + ) a / + St d z ( a + ) a ( / ), z ( a + ) ( a ), z a ( a ) ( a / ), a zatem warto c lczby X o reprezetacj r,r,r jet X (r z + r z + r z ) mod (a+) a (a ). + Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 7
18 Kowerja z ytemu reztowego a ytem tałobazowy przyłady () Sytem reztowy ( +,, ). Mamy W( +) ( ). Oblczymy lczby ˆ ww ( + ), w ˆ mod w ˆ ww ( + )( ) w ˆ mod w ( ) ˆ ww ( ) w ˆ mod w ( ) ( ) w w, w, oraz ch odwroto c multyplatywe mod w mod( ) mod( w ˆ mod w mod mod w ˆ mod w mod( + ) mod( St d z ) + ) + ŵ j, a ( + ) a, z ( + ) ( ), z ( ) ( ), zatem warto c lczby X o reprezetacj r,r,r jet X (r z + r z + r z ) mod ( ). + Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 8
19 Kowerja z ytemu reztowego a ytem tałobazowy przyłady () W yteme reztowym (7,,) mamy X (7,,),,. Wyzaczmy X. Mamy W 74. Oblczymy lczby ˆ ˆ w W / w 6, w mod w 6mod7 w ˆ W / w 4, w ˆ mod w mod w W / w, w mod w ˆ ŵ j ˆ oraz ch odwroto c multyplatywe w ˆ mod w mod w mod w, w ˆ mod w mod w mod w w mod w ± mod w mod w ˆ ± St d z 6 6mod4, z 4 8mod4, z mod4, zatem X (( ) 6 +( ) 4 + ) mod 4 5 mod 4 7. Rzeczyw ce X (7,,) 7 mod 7, 7 mod, 7 mod,,. Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 9
20 Oblczae odwroto c multyplatywych () Odwrócoy algorytm Euldea x ( x... mod ) p ( A x x ( x mod B ) + ( C x mod D ) mod ) [ x dv x + mod x]... p + Jedy w yteme RNS(7,,) mamy W 74. Oblczymy lczby ˆ ˆ w W / w 6, w mod w 6mod7 w ˆ W / w 4, w ˆ mod w mod w W / w, w mod w oraz ch odwroto c multyplatywe ( ˆ ˆ mod w ) t w 6 7t 6 ( 6 + ) t 6 ( t) t, w ˆ t oraz t, czyl t w 4 t ( 5 ) t (5 t) ˆ, w ˆ oraz t t w t ( + ) t ( t) + ˆ w ˆ oraz t zatem w zatem 5 w zatem Jauz Berat, AK-5-9-.doc, wrze a 9 RNS ŵ j,
21 Oblczae odwroto c multyplatywych () Jedy w yteme RNS(7,,) twerdzee Eulera ( ) w mod w ( Mamy W 74. Oblczymy lczby ˆ ˆ mod w ) ( ) w W / w 6, w mod w 6mod7 w ˆ W / w 4, w ˆ mod w mod w W / w, w mod w ˆ Jauz Berat, AK-5-9-.doc, wrze a 9 RNS ŵ j ˆ oraz ch odwroto c multyplatywe ( 7 w mod w ) ( w ˆ ) mod7 (6 mod7)(6 mod7) 6 mod7, zatem w ˆ 6 mod7 7 mod w ( w ˆ ) mod (4 mod)(4 mod) 4 mod, zatem w ˆ 4 mod ( w ˆ ) mod ( mod )( mod ) mod, zatem w ˆ mod St d z 6 6mod4, z 4 8mod4, z mod4,
22 Wyzaczae reprezetacj reztowych. Z twerdzea Fermata lub Eulera rezty pot g reducja pot g modϕ(p) Poadto a X a x modn(a ϕ (p) ) [ x dv ϕ (p) ] a x mod ϕ (p) modna x mod ϕ (p) modn x x x x mod p a mod p [( a mod p) ( a mod p) ( a mod p)...]mod p. Poewa dla lczby aturalej a> a moda±(±) a moda±[(±)] w c dla a dej lczby aturalej daej w reprezetacj pozycyjej o podtawe rezty mod ± mo a oblczy jao umy lub ró ce lczb -cyfrowych, utworzoych przez cyfry a pozycjach j,j+,,j+ (j,,, ) x mod( ± ) / ( x j j+ / ( x j )( ± ) ) mod( mod( ± ) ± ) Jauz Berat, AK-5-9-.doc, wrze a 9 RNS j j+ j
23 Sytem wadratowo-reztowy QRNS* * arytmetya lczb zepoloych (oblczae traformaty Fourera). reprezetacja reztowa jedot urojoej. q mod w, q mod w. problem: zalezee zboru modułów, dla tórych jet rozw zae rówaa q mod w. DEFINICJA Lczb r, perwz wzgl dem w N ta e rówae x mod w r ma rozw zae, azywa rezt wadratow (quadratc redue) wzgl dem w. Je el atomat rówae x mod w r e ma rozw zaa, to r azywa e-rezt wadratow (quadratc oredue) wzgl dem w. Jauz Berat, AK-5-9-.doc, wrze a 9 RNS *
24 Rezty wadratowe* * Poewa jet dołade (w) rezt ezerowych modulo w, a a de rówae x mod w r ma albo dwa rozw zaa eprzytaj ce x oraz x (lub wx, bo x mod w ( w x) mod w), albo e ma rozw zaa, w c przy eparzytym w teje dołade (w)/ rezt oraz (w)/ e-rezt wadratowych. Rezty wadratowe wzgl dem w wyzaczymy rozw zuj c rówae x mod r metod olejych prób dla x,,..., 6 (.x (w x) mod w) Zajdujemy odpowedo: mod, 4 mod, 4 mod, 4 mod, 5 mod, 6 mod. Zatem reztam wadratowym wzgl dem (w arytmetyce uzupełeowej): 4,,,,, 4. Jauz Berat, AK-5-9-.doc, wrze a 9 RNS *
25 Ch e twerdzee o reztach owerja odwrota* * Nech W{w,w,...,w : j: (w,w j )}, W ww... w oraz w ˆ Ww. Je l X <W, to reprezetacja X x,x,,x : x X modw,w W jet uatowa, przy tym ˆ X X ( mod w ) x modw gdze w mod w odwroto multyplatywa ŵ wzgl dem modułu w. D O W Ó D (formaly). Nech p mod w. Poewa x X mod w oraz W w, zatem ( ( mod w ) x ) modw ( p ( X mod w )) modw ( p ( X w X / w )) modw ( X p ) modw, a podtawe zachowawczo c ogruecj () X p modw Jauz Berat, AK-5-9-.doc, wrze a 9 RNS * ( X modw ) p modw X p modw.
26 Aby dowe prawdzwo c tezy wytarczy w c wyaza, e ( p ) modw. * Poewa z udowodoego wcze ej lematu wya, e NWD(x,y) amodyd amodxd amodxyd, za W w w... w w jet loczyem lczb wzgl de perwzych, w c wytarczy wyaza prawdzwo poprzeda mplacj Ale. () w : ( p )mod w ( p )modw w w : w /, zatem () ( w ˆ p )mod w ( p )mod w ( ( mod w ))mod w. St d wya prawdzwo at pa mplacj (), co dowodz tezy. Jauz Berat, AK-5-9-.doc, wrze a 9 RNS 4*
w zbiorze liczb naturalnych N (N,M N): N Mmodw k N: N M=kw M N=kw w zbiorze liczb całkowitych Z (N,M Z): N Mmodw k Z: N M=kw
 Kogruece Lczby ogruete (przyta ą ce) modulo w N (w moduł przytawaa) w zborze lczb aturalych N (NM N): N Mmodw N: N Mw M Nw w zborze lczb całowtych Z (NM Z): N Mmodw Z: N Mw Kogrueca relaca rówowaŝ oś c:
Kogruece Lczby ogruete (przyta ą ce) modulo w N (w moduł przytawaa) w zborze lczb aturalych N (NM N): N Mmodw N: N Mw M Nw w zborze lczb całowtych Z (NM Z): N Mmodw Z: N Mw Kogrueca relaca rówowaŝ oś c:
Systemy resztowe. Kongruencje. Liczby kongruentne (przystaj ce) modulo w (w moduł przystawania) (N,M ): N M(modw) k : N M=kw M N=kw
 Kongruencje Lczby ongruentne (przytaj ce) modulo w (w moduł przytawana) (N,M ): N M(modw) : N Mw M Nw Kongruencja relacja równowa no c: zwrotna (reflexve): N N(modw), ymetryczna (ymmetrc): N M(modw) M
Kongruencje Lczby ongruentne (przytaj ce) modulo w (w moduł przytawana) (N,M ): N M(modw) : N Mw M Nw Kongruencja relacja równowa no c: zwrotna (reflexve): N N(modw), ymetryczna (ymmetrc): N M(modw) M
Relacje, grupy, ciała
 Relace Relace, grupy, cała Relaca w zborze X podzbór produtu artezańego ρ X X ρ y Relaca rówowaŝośc (equvalece) zwrota ρ ymetrycza ρ y y ρ przechoda ρ y & y ρ z ρ z Zaada abtrac Relaca rówowaŝośc dzel
Relace Relace, grupy, cała Relaca w zborze X podzbór produtu artezańego ρ X X ρ y Relaca rówowaŝośc (equvalece) zwrota ρ ymetrycza ρ y y ρ przechoda ρ y & y ρ z ρ z Zaada abtrac Relaca rówowaŝośc dzel
Indukcja matematyczna
 Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
X R>0 dzielenie znakowane (signed division) znak reszty = znak dzielnej R>0 dzielenie modularne (modulus division) znak reszty dodatni X D D R
 } m ekwecyje dzelee całkowte Iloraz uotet rezta remader z dzelea dzelej dvded rzez dzelk dvor to lczby oraz take e rozw zaa oraz take e rzy tym oraz > dzelee zakowae ged dvo zak rezty zak dzelej > dzelee
} m ekwecyje dzelee całkowte Iloraz uotet rezta remader z dzelea dzelej dvded rzez dzelk dvor to lczby oraz take e rozw zaa oraz take e rzy tym oraz > dzelee zakowae ged dvo zak rezty zak dzelej > dzelee
Analiza Matematyczna I.1
 Aalza Matematycza I. Sera, Potr Nayar Zadae. Nech a k >, k =,..., b d lczbam rzeczywstym o tym samym zaku. Udowodj,»e prawdzwa jest erówo± + a + a... + a + a + a +... + a. Czy zaªo»ee,»e lczby a k maj
Aalza Matematycza I. Sera, Potr Nayar Zadae. Nech a k >, k =,..., b d lczbam rzeczywstym o tym samym zaku. Udowodj,»e prawdzwa jest erówo± + a + a... + a + a + a +... + a. Czy zaªo»ee,»e lczby a k maj
Dzielenie. Dzielenie pozycyjne
 zelene ozycyjne zelene dzelene całkowte: dzelna (dvdend), dzelnk 0 (dvor) Iloraz (uotent) rezta R (remander) z dzelena to lczby take, e R, R rozw zana (,R ) oraz (,R ) take, e R, rzy tym R R, R, R oraz
zelene ozycyjne zelene dzelene całkowte: dzelna (dvdend), dzelnk 0 (dvor) Iloraz (uotent) rezta R (remander) z dzelena to lczby take, e R, R rozw zana (,R ) oraz (,R ) take, e R, rzy tym R R, R, R oraz
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
X i T (X) = i=1. i + 1, X i+1 i + 1. Cov H0. ( X i. k 31 ) 1 Φ(1, 1818) 0, 12.
 Zadae p (X p (X ( ( π 6 6 e 6 X m ( π 6 6 e 6 ( X C e m 6 X, gdze staªa C e zale»y od statystyk X (X,, X 6, a m jest w ksze od zera Zatem p (X/p (X jest emalej c fukcj statystyk T (X 6 X ªatwo pokaza,»e
Zadae p (X p (X ( ( π 6 6 e 6 X m ( π 6 6 e 6 ( X C e m 6 X, gdze staªa C e zale»y od statystyk X (X,, X 6, a m jest w ksze od zera Zatem p (X/p (X jest emalej c fukcj statystyk T (X 6 X ªatwo pokaza,»e
Matematyka dyskretna. 10. Funkcja Möbiusa
 Matematyka dyskreta 10. Fukcja Möbusa Defcja 10.1 Nech (P, ) będze zborem uporządkowaym. Mówmy, że zbór uporządkoway P jest lokale skończoy, jeśl każdy podzał [a, b] P jest skończoy, a, b P Uwaga 10.1
Matematyka dyskreta 10. Fukcja Möbusa Defcja 10.1 Nech (P, ) będze zborem uporządkowaym. Mówmy, że zbór uporządkoway P jest lokale skończoy, jeśl każdy podzał [a, b] P jest skończoy, a, b P Uwaga 10.1
MADE IN CHINA czyli SYSTEM RESZTOWY
 MADE IN CHINA czyli SYSTEM RESZTOWY System ten oznaczmy skrótem RNS (residue number system czyli po prostu resztowy system liczbowy). Wartość liczby w tym systemie reprezentuje wektor (zbiór) reszt z dzielenia
MADE IN CHINA czyli SYSTEM RESZTOWY System ten oznaczmy skrótem RNS (residue number system czyli po prostu resztowy system liczbowy). Wartość liczby w tym systemie reprezentuje wektor (zbiór) reszt z dzielenia
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej. Literatura. W. Rudin: Podstawy analizy matematycznej, PWN, Warszawa, 1982.
 Wyłady z Aalzy rzeczywstej zespoloej w Matematyce stosowaej Lteratura W Rud: Podstawy aalzy matematyczej, PWN, Warszawa, 1982 W Rud: Aalza rzeczywsta zespoloa, PZWS, Warszawa, 1986 W Szabat: Wstęp do aalzy
Wyłady z Aalzy rzeczywstej zespoloej w Matematyce stosowaej Lteratura W Rud: Podstawy aalzy matematyczej, PWN, Warszawa, 1982 W Rud: Aalza rzeczywsta zespoloa, PZWS, Warszawa, 1986 W Szabat: Wstęp do aalzy
Miary statystyczne. Katowice 2014
 Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
JEDNOWYMIAROWA ZMIENNA LOSOWA
 JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
Obliczanie średniej, odchylenia standardowego i mediany oraz kwartyli w szeregu szczegółowym i rozdzielczym?
 Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Repetytorium z Matematyki Elementarnej Wersja Olimpijska
 Repetytorium z Matematyi Elemetarej Wersja Olimpijsa Podae tutaj zadaia rozwiązywae były w jedej z grup ćwiczeiowych Są w więszości ieco trudiejsze od pozostałych zadań przygotowaych w ramach przedmiotu
Repetytorium z Matematyi Elemetarej Wersja Olimpijsa Podae tutaj zadaia rozwiązywae były w jedej z grup ćwiczeiowych Są w więszości ieco trudiejsze od pozostałych zadań przygotowaych w ramach przedmiotu
Analiza Matematyczna Ćwiczenia. J. de Lucas
 Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Twierdzenie Eulera. Kongruencje wykład 6. Twierdzenie Eulera
 Kongruencje wykład 6 ... Euler, 1760, Sankt Petersburg Dla każdego a m zachodzi kongruencja a φ(m) 1 (mod m). Przypomnijmy: φ(m) to liczba reszt modulo m względnie pierwszych z m; φ(m) = m(1 1/p 1 )...
Kongruencje wykład 6 ... Euler, 1760, Sankt Petersburg Dla każdego a m zachodzi kongruencja a φ(m) 1 (mod m). Przypomnijmy: φ(m) to liczba reszt modulo m względnie pierwszych z m; φ(m) = m(1 1/p 1 )...
6. *21!" 4 % rezerwy matematycznej. oraz (ii) $ :;!" "+!"!4 oraz "" % & "!4! " )$!"!4 1 1!4 )$$$ " ' ""
 Memy fow 09..000 r. 6. *!" ( orz ( 4 % rezerwy memycze $ :;!" "+!"!4 orz "" % & "!4! " $!"!4!4 $$$ " ' "" V w dowole chwl d e wzorem V 0 0. &! "! "" 4 < ; ;!" 4 $%: ; $% ; = > %4( $;% 7 4'8 A..85 B..90
Memy fow 09..000 r. 6. *!" ( orz ( 4 % rezerwy memycze $ :;!" "+!"!4 orz "" % & "!4! " $!"!4!4 $$$ " ' "" V w dowole chwl d e wzorem V 0 0. &! "! "" 4 < ; ;!" 4 $%: ; $% ; = > %4( $;% 7 4'8 A..85 B..90
Wybrane zagadnienia teorii liczb
 Wybrane zagadnienia teorii liczb Podzielność liczb NWW, NWD, Algorytm Euklidesa Arytmetyka modularna Potęgowanie modularne Małe twierdzenie Fermata Liczby pierwsze Kryptosystem RSA Podzielność liczb Relacja
Wybrane zagadnienia teorii liczb Podzielność liczb NWW, NWD, Algorytm Euklidesa Arytmetyka modularna Potęgowanie modularne Małe twierdzenie Fermata Liczby pierwsze Kryptosystem RSA Podzielność liczb Relacja
EKSTREMA FUNKCJI EKSTREMA FUNKCJI JEDNEJ ZMIENNEJ. Tw. Weierstrassa Każda funkcja ciągła na przedziale domkniętym ma wartość najmniejszą i największą.
 Joaa Ceślak, aula Bawej ESTREA FUNCJI ESTREA FUNCJI JEDNEJ ZIENNEJ Otoczeem puktu R jest każdy przedzał postac,+, gdze >. Sąsedztwem puktu jest każdy zbór postac,,+, gdze >. Nech R, : R oraz ech. De. ówmy,
Joaa Ceślak, aula Bawej ESTREA FUNCJI ESTREA FUNCJI JEDNEJ ZIENNEJ Otoczeem puktu R jest każdy przedzał postac,+, gdze >. Sąsedztwem puktu jest każdy zbór postac,,+, gdze >. Nech R, : R oraz ech. De. ówmy,
Permutacje. } r ( ) ( ) ( ) 1 2 n. f = M. Przybycień Matematyczne Metody Fizyki I Wykład 2-2
 Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
STATYSTYKA MATEMATYCZNA WYKŁAD 2 ESTYMACJA PUNKTOWA
 STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
Jednoznaczność dzielenia. Jednoznaczność dzielenia
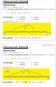 Jednoznaczność dzielenia MNiechmincałkowite,n 0 Wtedy istnieje dokładnie jedna para liczb całkowitych k i l taka że m=n k+l oraz 0 l< n Terminologia: m dzielna n dzielnik Sytuacjadlam 0in>0: k k iloraz
Jednoznaczność dzielenia MNiechmincałkowite,n 0 Wtedy istnieje dokładnie jedna para liczb całkowitych k i l taka że m=n k+l oraz 0 l< n Terminologia: m dzielna n dzielnik Sytuacjadlam 0in>0: k k iloraz
i = 0, 1, 2 i = 0, 1 33,115 1,698 0,087 0,005!0,002 34,813 1,785 0,092 0,003 36,598 1,877 0,095 38,475 1,972 40,447 i = 0, 1, 2, 3
 35 Iterpoaca Herte a 3 f ( x f ( x,,, 3, 4 f ( x,,, 3 f ( x,, 3 f ( x, 4 f ( x 33,5,698,87,5!, 34,83,785,9,3 36,598,877,95 38,475,97 4,447 Na podstawe wzoru (38 ay zate 87,, 5, L4 ( t 335, +, 698t+ t(
35 Iterpoaca Herte a 3 f ( x f ( x,,, 3, 4 f ( x,,, 3 f ( x,, 3 f ( x, 4 f ( x 33,5,698,87,5!, 34,83,785,9,3 36,598,877,95 38,475,97 4,447 Na podstawe wzoru (38 ay zate 87,, 5, L4 ( t 335, +, 698t+ t(
BQR FMECA/FMEA. czujnik DI CPU DO zawór. Rys. 1. Schemat rozpatrywanego systemu zabezpieczeniowego PE
 BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc
 PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
Zmiana bazy i macierz przejścia
 Auomaya Roboya Algebra -Wyład - dr Adam Ćmel cmel@agh.edu.pl Zmaa bazy macerz prześca Nech V będze wymarową przesrzeą lową ad całem K. Nech Be e będze bazą przesrze V. Rozważmy ową bazę B e... e. Oczywśce
Auomaya Roboya Algebra -Wyład - dr Adam Ćmel cmel@agh.edu.pl Zmaa bazy macerz prześca Nech V będze wymarową przesrzeą lową ad całem K. Nech Be e będze bazą przesrze V. Rozważmy ową bazę B e... e. Oczywśce
Teoria liczb. Magdalena Lemańska. Magdalena Lemańska,
 Teoria liczb Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Wstęp Teoria liczb jest dziedziną matematyki,
Teoria liczb Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Wstęp Teoria liczb jest dziedziną matematyki,
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
SOWA - ENERGOOSZCZĘDNE OŚWIETLENIE ULICZNE METODYKA
 Załączk r do Regulamu I kokursu GIS PROGRAM PRIORYTETOWY: SOWA - ENERGOOSZCZĘDNE OŚWIETLENIE ULICZNE METODYKA. Cel opracowaa Celem opracowaa jest spója metodyka oblczaa efektu ograczaa emsj gazów ceplaraych,
Załączk r do Regulamu I kokursu GIS PROGRAM PRIORYTETOWY: SOWA - ENERGOOSZCZĘDNE OŚWIETLENIE ULICZNE METODYKA. Cel opracowaa Celem opracowaa jest spója metodyka oblczaa efektu ograczaa emsj gazów ceplaraych,
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
W. Guzicki: Liczby pierwsze 1 LICZBY PIERWSZE. Warszawa, 11 kwietnia 2013 r.
 W. Guzicki: Liczby pierwsze 1 LICZBY PIERWSZE W. Guzicki: Liczby pierwsze 2 Zagadnienie odróżniania liczb pierwszych od złożonych i rozkładanie tych ostatnich na ich czynniki pierwsze uchodzi za najważniejszeiodużympraktycznymznaczeniuwarytmetyce...samapowaga
W. Guzicki: Liczby pierwsze 1 LICZBY PIERWSZE W. Guzicki: Liczby pierwsze 2 Zagadnienie odróżniania liczb pierwszych od złożonych i rozkładanie tych ostatnich na ich czynniki pierwsze uchodzi za najważniejszeiodużympraktycznymznaczeniuwarytmetyce...samapowaga
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
Podprzestrzenie macierzowe
 Podprzestrzee macerzowe werdzee: Dla dwóch macerzy A B o tych samych wymarach zachodz: ( ) ( ) wersz a) R A R B A ~ B Dowód: wersz a) A ~ B stee P taka że PA B 3 0 A 4 3 0 0 E A B 0 0 0 E B 3 6 4 0 0 0
Podprzestrzee macerzowe werdzee: Dla dwóch macerzy A B o tych samych wymarach zachodz: ( ) ( ) wersz a) R A R B A ~ B Dowód: wersz a) A ~ B stee P taka że PA B 3 0 A 4 3 0 0 E A B 0 0 0 E B 3 6 4 0 0 0
k k M. Przybycień Rachunek Prawdopodobieństwa i Statystyka Wykład 13-2
 Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
ARYTMETYKA KOMPUTERÓW
 Jau Berat, profeor adw. Poltecha Wrocława Wydał Eletro Itytut Iformaty, Automaty Roboty Załad Archtetury Komputerów ARYTMETYKA KOMPUTERÓW Wrocław p. bud. C3 7 3 396 7 3 745 - Jau.Berat@pwr.wroc.pl http://www.a.ct.pwr.wroc.pl/materaly/arytmetya
Jau Berat, profeor adw. Poltecha Wrocława Wydał Eletro Itytut Iformaty, Automaty Roboty Załad Archtetury Komputerów ARYTMETYKA KOMPUTERÓW Wrocław p. bud. C3 7 3 396 7 3 745 - Jau.Berat@pwr.wroc.pl http://www.a.ct.pwr.wroc.pl/materaly/arytmetya
Pierwiastki pierwotne, logarytmy dyskretne
 Kongruencje wykład 7 Definicja Jeżeli rząd elementu a modulo n (dla n będącego liczba naturalną i całkowitego a, a n) wynosi φ(n) to a nazywamy pierwiastkiem pierwotnym modulo n. Przykład Czy 7 jest pierwiastkiem
Kongruencje wykład 7 Definicja Jeżeli rząd elementu a modulo n (dla n będącego liczba naturalną i całkowitego a, a n) wynosi φ(n) to a nazywamy pierwiastkiem pierwotnym modulo n. Przykład Czy 7 jest pierwiastkiem
Rozdział 1. Nazwa i adres Zamawiającego Rozdział 2. Informacja o trybie i stosowaniu przepisów Rozdział 3. Przedmiot zamówienia
 Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 0 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f S p r z» t a n i e i u t r z y m a n i e c z y s t o c i g d y
Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 0 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f S p r z» t a n i e i u t r z y m a n i e c z y s t o c i g d y
Równania rekurencyjne
 Rówaa reurecyje Ja stosować do przelczaa obetów obatoryczych? zaleźć zwąze reurecyjy, oblczyć la początowych wartośc, odgadąć ogóly wzór, tóry astępe udowaday stosując ducję ateatyczą. W etórych przypadach,
Rówaa reurecyje Ja stosować do przelczaa obetów obatoryczych? zaleźć zwąze reurecyjy, oblczyć la początowych wartośc, odgadąć ogóly wzór, tóry astępe udowaday stosując ducję ateatyczą. W etórych przypadach,
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA
 Z a m a w i a j» c y G D Y S K I O R O D E K S P O R T U I R E K R E A C J I J E D N O S T K A B U D E T O W A 8 1 5 3 8 G d y n i a, u l O l i m p i j s k a 5k 9 Z n a k s p r a w y G O S I R D Z P I
Z a m a w i a j» c y G D Y S K I O R O D E K S P O R T U I R E K R E A C J I J E D N O S T K A B U D E T O W A 8 1 5 3 8 G d y n i a, u l O l i m p i j s k a 5k 9 Z n a k s p r a w y G O S I R D Z P I
Kongruencje oraz przykłady ich zastosowań
 Strona 1 z 25 Kongruencje oraz przykłady ich zastosowań Andrzej Sładek, Instytut Matematyki UŚl sladek@ux2.math.us.edu.pl Spotkanie w LO im. Powstańców Śl w Bieruniu Starym 27 października 2005 Strona
Strona 1 z 25 Kongruencje oraz przykłady ich zastosowań Andrzej Sładek, Instytut Matematyki UŚl sladek@ux2.math.us.edu.pl Spotkanie w LO im. Powstańców Śl w Bieruniu Starym 27 października 2005 Strona
Lista 6. Kamil Matuszewski 26 listopada 2015
 Lsta 6 Kaml Matuszews 6 lstopada 5 4 5 6 7 8 9 4 5 X X X X X X X X X X X D X X N Gdze X-spsae, D-Delarowae, N-edelarowae. Zadae Zadae jest westą odpowedego pomalowaa. Weźmy sobe szachowcę x, poumerujmy
Lsta 6 Kaml Matuszews 6 lstopada 5 4 5 6 7 8 9 4 5 X X X X X X X X X X X D X X N Gdze X-spsae, D-Delarowae, N-edelarowae. Zadae Zadae jest westą odpowedego pomalowaa. Weźmy sobe szachowcę x, poumerujmy
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
Projektowanie bazy danych
 Projektowanie bazy danych Pierwszą fazą tworzenia projektu bazy danych jest postawienie definicji celu, założeo wstępnych i określenie podstawowych funkcji aplikacji. Każda baza danych jest projektowana
Projektowanie bazy danych Pierwszą fazą tworzenia projektu bazy danych jest postawienie definicji celu, założeo wstępnych i określenie podstawowych funkcji aplikacji. Każda baza danych jest projektowana
Dla dzielnej X (dividend) i dzielnika D 0 (divisor) liczby Q oraz R takie, Ŝe
 zelene ekwencyjne zelene la dzelnej X (dvdend) dzelnka (dvor) lczby Q oraz R take, Ŝe X=Q R, R < nazywa ę lorazem Q (uotent) reztą R (remander) z dzelena X rzez. Równane dzelena moŝe meć rozwązana ełnające
zelene ekwencyjne zelene la dzelnej X (dvdend) dzelnka (dvor) lczby Q oraz R take, Ŝe X=Q R, R < nazywa ę lorazem Q (uotent) reztą R (remander) z dzelena X rzez. Równane dzelena moŝe meć rozwązana ełnające
Rozdział 6. Pakowanie plecaka. 6.1 Postawienie problemu
 Rozdział 6 Pakowanie plecaka 6.1 Postawienie problemu Jak zauważyliśmy, szyfry oparte na rachunku macierzowym nie są przerażająco trudne do złamania. Zdecydowanie trudniejszy jest kryptosystem oparty na
Rozdział 6 Pakowanie plecaka 6.1 Postawienie problemu Jak zauważyliśmy, szyfry oparte na rachunku macierzowym nie są przerażająco trudne do złamania. Zdecydowanie trudniejszy jest kryptosystem oparty na
Twierdzenie Bezouta i liczby zespolone Javier de Lucas. Rozwi azanie 2. Z twierdzenia dzielenia wielomianów, mamy, że
 Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
Wyższe momenty zmiennej losowej
 Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h( dla dysretej zm. losowej oraz ucji h( dla ciągłej zm. losowej: m E P m E ( d Deiicja: Mometem cetralym µ rzędu dla
Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h( dla dysretej zm. losowej oraz ucji h( dla ciągłej zm. losowej: m E P m E ( d Deiicja: Mometem cetralym µ rzędu dla
n k n k ( ) k ) P r s r s m n m n r s r s x y x y M. Przybycień Rachunek prawdopodobieństwa i statystyka
 Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h() dla dysretej zm. losowej oraz ucji h() dla ciągłej zm. losowej: m E P m E ( ) d Deiicja: Mometem cetralym µ rzędu
Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h() dla dysretej zm. losowej oraz ucji h() dla ciągłej zm. losowej: m E P m E ( ) d Deiicja: Mometem cetralym µ rzędu
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
KOINCYDENTNOŚĆ MODELU EKONOMETRYCZNEGO A JEGO JAKOŚĆ MIERZONA WARTOŚCIĄ WSPÓŁCZYNNIKA R 2 (K)
 STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Mchał Kolupa Poltechnka Radomska w Radomu Joanna Plebanak Szkoła Główna Handlowa w Warszawe KOINCYDENTNOŚĆ MODELU EKONOMETRYCZNEGO A JEGO
STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Mchał Kolupa Poltechnka Radomska w Radomu Joanna Plebanak Szkoła Główna Handlowa w Warszawe KOINCYDENTNOŚĆ MODELU EKONOMETRYCZNEGO A JEGO
Dr inż. Robert Wójcik, p. 313, C-3, tel Katedra Informatyki Technicznej (K-9) Wydział Elektroniki (W-4) Politechnika Wrocławska
 Dr inż. Robert Wójcik, p. 313, C-3, tel. 320-27-40 Katedra Informatyki Technicznej (K-9) Wydział Elektroniki (W-4) Politechnika Wrocławska E-mail: Strona internetowa: robert.wojcik@pwr.edu.pl google: Wójcik
Dr inż. Robert Wójcik, p. 313, C-3, tel. 320-27-40 Katedra Informatyki Technicznej (K-9) Wydział Elektroniki (W-4) Politechnika Wrocławska E-mail: Strona internetowa: robert.wojcik@pwr.edu.pl google: Wójcik
2.Prawo zachowania masy
 2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
I. Podzielność liczb całkowitych
 I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
7 Liczby zespolone. 7.1 Działania na liczbach zespolonych. Liczby zespolone to liczby postaci. z = a + bi,
 7 Liczby zespoloe Liczby zespoloe to liczby postaci z a + bi, gdzie a, b R. Liczbę i azywamy jedostką urojoą, spełia oa waruek i 2 1. Zbiór liczb zespoloych ozaczamy przez C: C {a + bi; a, b R}. Liczba
7 Liczby zespoloe Liczby zespoloe to liczby postaci z a + bi, gdzie a, b R. Liczbę i azywamy jedostką urojoą, spełia oa waruek i 2 1. Zbiór liczb zespoloych ozaczamy przez C: C {a + bi; a, b R}. Liczba
ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ
 ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ Podstawowe pojęca rachuu prawdopodobeństwa: zdarzee losowe, zdarzee elemetare, prawdopodobeństwo, zbór zdarzeń elemetarych. Def. Nech E będze zborem
ZMIENNA LOSOWA JEDNOWYMIAROWA POJĘCIE ZMIENNEJ LOSOWEJ Podstawowe pojęca rachuu prawdopodobeństwa: zdarzee losowe, zdarzee elemetare, prawdopodobeństwo, zbór zdarzeń elemetarych. Def. Nech E będze zborem
Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów
 Z n a k s p r a w y G C S D Z P I 2 7 1 0 4 52 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A W y k o n a n i e p o m i a r ó w i n s t a l a c j i e l e k t r y c
Z n a k s p r a w y G C S D Z P I 2 7 1 0 4 52 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A W y k o n a n i e p o m i a r ó w i n s t a l a c j i e l e k t r y c
Matematyka II. x 3 jest funkcja
 Maemayka II WYKLD. Całka eozaczoa. Rachuek całkowy. Twerdzea o całkach eozaczoych. Całkowae wybraych klas fukcj. Całkowae fukcj wymerych. Całkowae fukcj rygoomeryczych.. Defcja fukcj perwoej. Fukcję F
Maemayka II WYKLD. Całka eozaczoa. Rachuek całkowy. Twerdzea o całkach eozaczoych. Całkowae wybraych klas fukcj. Całkowae fukcj wymerych. Całkowae fukcj rygoomeryczych.. Defcja fukcj perwoej. Fukcję F
7. M i s a K o ł o
 S U P 4 1 2 v. 2 0 16 G R I L L K O C I O Ł E K 5 R E D N I C A 4 2 c m, R U C H O M Y S U P 4 1 2 I N S T R U K C J A M O N T A 7 U I B E Z P I E C Z N E G O U 7 Y T K O W A N I A S z a n o w n i P a
S U P 4 1 2 v. 2 0 16 G R I L L K O C I O Ł E K 5 R E D N I C A 4 2 c m, R U C H O M Y S U P 4 1 2 I N S T R U K C J A M O N T A 7 U I B E Z P I E C Z N E G O U 7 Y T K O W A N I A S z a n o w n i P a
Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa
 W Z Ó R U M O W Y z a w a r t a w G d y n i w d n i u 2 0 1 4 r po m i d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j i j e d n o s t k a b u d e t o w a ( 8 1-5 3 8 G d y n i a ), l
W Z Ó R U M O W Y z a w a r t a w G d y n i w d n i u 2 0 1 4 r po m i d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j i j e d n o s t k a b u d e t o w a ( 8 1-5 3 8 G d y n i a ), l
 ź Ł Ą Ę Ź Ę Ę Ą Ę Ę Ę Ę Ę Ź Ą Ę Ą Ź Ę Ź Ó ć Ź Ó Ę Ź Ź ć ć Ę ć Ó Ó Ę Ę Ę Ę Ó Ę Ę ć Ć Ł Ó Ź ć ć ć Ę ć Ę Ł Ź Ź Ł ć ź ź Ę ć Ś Ą ć ć Ą ć Ś Ę Ź Ę Ź Ę ć Ó Ń Ę Ś Ę ź Ź Ę Ę Ć Ę Ń Ę Ę ć Ą Ę ć Ę ć Ę Ź Ę Ć Ę ź ć
ź Ł Ą Ę Ź Ę Ę Ą Ę Ę Ę Ę Ę Ź Ą Ę Ą Ź Ę Ź Ó ć Ź Ó Ę Ź Ź ć ć Ę ć Ó Ó Ę Ę Ę Ę Ó Ę Ę ć Ć Ł Ó Ź ć ć ć Ę ć Ę Ł Ź Ź Ł ć ź ź Ę ć Ś Ą ć ć Ą ć Ś Ę Ź Ę Ź Ę ć Ó Ń Ę Ś Ę ź Ź Ę Ę Ć Ę Ń Ę Ę ć Ą Ę ć Ę ć Ę Ź Ę Ć Ę ź ć
PŁASKA GEOMETRIA MAS. Środek ciężkości figury płaskiej
 PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
PŁAKA GEOMETRIA MA Środek cężkośc fgury płaskej Mometam statyczym M x M y fgury płaskej względem os x lub y (rys. 7.1) azywamy gracę algebraczej sumy loczyów elemetarych pól d przez ch odległośc od os,
F u l l H D, I P S D, I P F u l l H D, I P 5 M P,
 Z a ł» c z n i k n r 6 d o S p e c y f i k a c j i I s t o t n y c h W a r u n k ó w Z a m ó w i e n i a Z n a k s p r a w yg O S I R D Z P I 2 7 1 02 4 2 0 1 5 W Z Ó R U M O W Y z a w a r t a w G d y
Z a ł» c z n i k n r 6 d o S p e c y f i k a c j i I s t o t n y c h W a r u n k ó w Z a m ó w i e n i a Z n a k s p r a w yg O S I R D Z P I 2 7 1 02 4 2 0 1 5 W Z Ó R U M O W Y z a w a r t a w G d y
PERMUTACJE Permutacją zbioru n-elementowego X nazywamy dowolną wzajemnie jednoznaczną funkcję f : X X X
 PERMUTACJE Permutacą zboru -elemetowego X azywamy dowolą wzaeme edozaczą fucę f : X X f : X X Przyład permutac X = { a, b, c, d } f (a) = d, f (b) = a, f (c) = c, f (d) = b a b c d Zaps permutac w postac
PERMUTACJE Permutacą zboru -elemetowego X azywamy dowolą wzaeme edozaczą fucę f : X X f : X X Przyład permutac X = { a, b, c, d } f (a) = d, f (b) = a, f (c) = c, f (d) = b a b c d Zaps permutac w postac
wi c warunek konieczny zbie»no±ci szeregu jest speªniony. 12 = 9 12 = 3 4 k(k+1) k=1 ( k+1 k(k+1) n+1 = 1 1 n+1 = 1 0 = 1 36 = =
 32 (+) Jest to szereg o wyrazach dodatich Poadto wyraz ogóly tego szeregu jest zbie»y do 0, wi c waruek koieczy zbie»o±ci szeregu jest speªioy s (+) 2 s 2 s + 2 (2+) 2 + 2 3 2 + 6 3 6 + 6 4 6 2 3 s 3 s
32 (+) Jest to szereg o wyrazach dodatich Poadto wyraz ogóly tego szeregu jest zbie»y do 0, wi c waruek koieczy zbie»o±ci szeregu jest speªioy s (+) 2 s 2 s + 2 (2+) 2 + 2 3 2 + 6 3 6 + 6 4 6 2 3 s 3 s
Niezbyt formalny i niezbyt intuicyjny wst p do algebry abstrakcyjnej
 Niezbyt formalny i niezbyt intuicyjny wst p do algebry abstracyjnej 1. Nawiasami [[]] oznacza b d omentarze. 2. Denicja 0.1 Grup z [[jaim± abstracyjnym]] dziaªaniem nazywamy zbiór G speªniaj cy waruni
Niezbyt formalny i niezbyt intuicyjny wst p do algebry abstracyjnej 1. Nawiasami [[]] oznacza b d omentarze. 2. Denicja 0.1 Grup z [[jaim± abstracyjnym]] dziaªaniem nazywamy zbiór G speªniaj cy waruni
Matematyka dyskretna
 Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 2 marca 2017 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod m)),
Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 2 marca 2017 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod m)),
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej
 Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.
 Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 2 32 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f O b s ł u g a o p e r a t o r s k a u r a w i s a m o j e z d n
Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 2 32 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f O b s ł u g a o p e r a t o r s k a u r a w i s a m o j e z d n
 ć ć ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ę Ź ź ń ć ź ń ć ź ń ź ć ń ć ć ć ć Ł Ł ń Ę ć ć ć ń ć ć ć ć Ź ć Ł ć ć Ę ć Ą Ą ć Ę Ą ć ń ź ź ń ć Ę ć ć ć Ś ć ć Ż ć ć Ą ć ć ć ć Ś ć ź Ę ć ć ń ć ć ć ć ć ć Ś ć ć ć ć ń ć ń ź
ć ć ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ę Ź ź ń ć ź ń ć ź ń ź ć ń ć ć ć ć Ł Ł ń Ę ć ć ć ń ć ć ć ć Ź ć Ł ć ć Ę ć Ą Ą ć Ę Ą ć ń ź ź ń ć Ę ć ć ć Ś ć ć Ż ć ć Ą ć ć ć ć Ś ć ź Ę ć ć ń ć ć ć ć ć ć Ś ć ć ć ć ń ć ń ź
Technologie kodowania i oznaczania opakowań leków w gotowych. Koło o ISPE AMG 2007
 Technologie kodowania i oznaczania opakowań leków w gotowych Michał Burdyński Koło o ISPE AMG 2007 Na początek trochę faktów Roczny wzrost przemysłu u opakowań farmaceutycznych szacuje się na poziomie
Technologie kodowania i oznaczania opakowań leków w gotowych Michał Burdyński Koło o ISPE AMG 2007 Na początek trochę faktów Roczny wzrost przemysłu u opakowań farmaceutycznych szacuje się na poziomie
Kongruencje Wykład 4. Kongruencje kwadratowe symbole Legendre a i Jac
 Kogruecje kwadratowe symbole Legedre a i Jacobiego Kogruecje Wykład 4 Defiicja 1 Kogruecję w ostaci x a (mod m), gdzie a m, azywamy kogruecją kwadratową; jej bardziej ogóla ostać ax + bx + c może zostać
Kogruecje kwadratowe symbole Legedre a i Jacobiego Kogruecje Wykład 4 Defiicja 1 Kogruecję w ostaci x a (mod m), gdzie a m, azywamy kogruecją kwadratową; jej bardziej ogóla ostać ax + bx + c może zostać
Tw. 1. Je»eli ci g {a n } ma granic a i ci g {b n } ma granic b, to ci g {a n b n } ma granic a b. Tw. 2. b n. Tw. 3. Tw. 4.
 Tw.. Je»eli ci g {a } ma graic a i ci g {b } ma graic b, to ci g {a + b } ma graic a+b. Tw.. Je»eli ci g {a } ma graic a i ci g {b } ma graic b, to ci g {a b } ma graic a-b. Tw.. Je»eli ci g {a } ma graic
Tw.. Je»eli ci g {a } ma graic a i ci g {b } ma graic b, to ci g {a + b } ma graic a+b. Tw.. Je»eli ci g {a } ma graic a i ci g {b } ma graic b, to ci g {a b } ma graic a-b. Tw.. Je»eli ci g {a } ma graic
Ogólnopolska konferencja Świadectwa charakterystyki energetycznej dla budynków komunalnych. Oświetlenie publiczne. Kraków, 27 września 2010 r.
 w sprawie charakterystyki energetycznej budynków oraz postanowienia przekształconej dyrektywy w sprawie charakterystyki energetycznej budynków Ogólnopolska konferencja Świadectwa charakterystyki energetycznej
w sprawie charakterystyki energetycznej budynków oraz postanowienia przekształconej dyrektywy w sprawie charakterystyki energetycznej budynków Ogólnopolska konferencja Świadectwa charakterystyki energetycznej
I n f o r m a c j e n a t e m a t p o d m i o t u k t ó r e m u z a m a w i a j» c y p o w i e r z y łk p o w i e r z y l i p r o w a d z e p o s t p
 A d r e s s t r o n y i n t e r n e t o w e j, n a k t ó r e j z a m i e s z c z o n a b d z i e s p e c y f i k a c j a i s t o t n y c h w a r u n k ó w z a m ó w i e n i a ( j e e ld io t y c z y )
A d r e s s t r o n y i n t e r n e t o w e j, n a k t ó r e j z a m i e s z c z o n a b d z i e s p e c y f i k a c j a i s t o t n y c h w a r u n k ó w z a m ó w i e n i a ( j e e ld io t y c z y )
W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:
 Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 80 minut Instrukcja dla zdaj¹cego. SprawdŸ, czy arkusz egzaminacyjny zawiera stron (zadania 0). Ewentualny brak zg³oœ przewodnicz¹cemu
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 80 minut Instrukcja dla zdaj¹cego. SprawdŸ, czy arkusz egzaminacyjny zawiera stron (zadania 0). Ewentualny brak zg³oœ przewodnicz¹cemu
Wstęp do prawdopodobieństwa. Dr Krzysztof Piontek. Literatura:
 Studum podyplomowe altyk Fasowy Wstęp do prawdopodobeństwa Lteratura: Ostasewcz S., Rusak Z., Sedlecka U.: Statystyka elemety teor zadaa, kadema Ekoomcza we Wrocławu 998. mr czel: Statystyka w zarządzau,
Studum podyplomowe altyk Fasowy Wstęp do prawdopodobeństwa Lteratura: Ostasewcz S., Rusak Z., Sedlecka U.: Statystyka elemety teor zadaa, kadema Ekoomcza we Wrocławu 998. mr czel: Statystyka w zarządzau,
Rozliczanie kosztów Proces rozliczania kosztów
 Rozlczane kosztów Proces rozlczana kosztów Koszty dzałalnośc jednostek gospodarczych są złoŝoną kategorą ekonomczną, ujmowaną weloprzekrojowo. W systeme rachunku kosztów odbywa sę transformacja jednych
Rozlczane kosztów Proces rozlczana kosztów Koszty dzałalnośc jednostek gospodarczych są złoŝoną kategorą ekonomczną, ujmowaną weloprzekrojowo. W systeme rachunku kosztów odbywa sę transformacja jednych
Indukcja. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Mh n. 2 ε. h h/ n n. Ekstrapolacja Richardsona (szacowanie błędu) błąd. ekstrapolowana wartość całki I. kwadratury z adaptowanym krokiem
 Ekstrapolacja Rchardsoa (szacowae błędu) dla daej, ustaloej metody błąd Mh zakładając, że M jest w przyblżeu ezależe od h I I + Mh h h/ / I I + Mh ekstrapolowaa wartość całk I I e I h / + Ih / ( I h )
Ekstrapolacja Rchardsoa (szacowae błędu) dla daej, ustaloej metody błąd Mh zakładając, że M jest w przyblżeu ezależe od h I I + Mh h h/ / I I + Mh ekstrapolowaa wartość całk I I e I h / + Ih / ( I h )
Podstawowe pojcia. Metody probabilistyczne i statystyka Wykład 7: Statystyka opisowa. Rozkłady prawdopodobiestwa wystpujce w statystyce.
 Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Matematyka dyskretna
 Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
NARZÊDZIA PNEUMATYCZNE
 K l uc z uda ro w y 6 1 0 N m 1 /2 3 68 2, 6 k od: MA 2 4 6 0 Z est a w - k l uc z uda ro w y 36 0 N m 1 /2 260 16 4, 3 K l uc z uda ro w y 1 2 8 0 N m 1 /2 k o mpo zyt K l uc z uda ro w y 1 350 N m 1/2
K l uc z uda ro w y 6 1 0 N m 1 /2 3 68 2, 6 k od: MA 2 4 6 0 Z est a w - k l uc z uda ro w y 36 0 N m 1 /2 260 16 4, 3 K l uc z uda ro w y 1 2 8 0 N m 1 /2 k o mpo zyt K l uc z uda ro w y 1 350 N m 1/2
 Ń Ą Ę Ł Ł Ł Ł ź Ł Ł Ł Ł Ł Ł ź Ł Ł Ł Ł Ś Ś źć Ą ź ź ć ź ć Ś ć Ą ć Ż ć ć Ę ć Ą Ł Ł Ł ź Ś Ą ź Ą Ą Ł Ś Ą Ż Ą Ł Ł ć Ż Ś ź Ó ź Ó ć Ć ź Ś ć Ł ć ć ć ć ć ć Ą Ą Ą Ł Ą ć ć ć ć Ą Ł ź ć ćź ć ć ź Ś ć ć Ą Ą Ą ć Ą ć Ż
Ń Ą Ę Ł Ł Ł Ł ź Ł Ł Ł Ł Ł Ł ź Ł Ł Ł Ł Ś Ś źć Ą ź ź ć ź ć Ś ć Ą ć Ż ć ć Ę ć Ą Ł Ł Ł ź Ś Ą ź Ą Ą Ł Ś Ą Ż Ą Ł Ł ć Ż Ś ź Ó ź Ó ć Ć ź Ś ć Ł ć ć ć ć ć ć Ą Ą Ą Ł Ą ć ć ć ć Ą Ł ź ć ćź ć ć ź Ś ć ć Ą Ą Ą ć Ą ć Ż
 ć ć ć ć ć ć ć źć ć ć ć ć ć ć ź Ś ź ć ć ć Ż ć Ę ć ć ć ć ć ć Ę Ę ć ć ć Ż ź ź ź ć ć ć ć ć Ś ć ć ć ć ć Ż ćż ć ć ć ć ć ć Ż ć ć ć ć ź ć ź Ę ć ć ź ć ć Ś Ż ć ć ć Ą Ż ć ć ć Ę ć ć Ż ć ć ć Ś ć ć ć ć ć ć ć ć ć ć ć
ć ć ć ć ć ć ć źć ć ć ć ć ć ć ź Ś ź ć ć ć Ż ć Ę ć ć ć ć ć ć Ę Ę ć ć ć Ż ź ź ź ć ć ć ć ć Ś ć ć ć ć ć Ż ćż ć ć ć ć ć ć Ż ć ć ć ć ź ć ź Ę ć ć ź ć ć Ś Ż ć ć ć Ą Ż ć ć ć Ę ć ć Ż ć ć ć Ś ć ć ć ć ć ć ć ć ć ć ć
Część matematyczna sprawdzian 2013 r.
 Część matematyczna sprawdzian 2013 r. 1. Szyfr zabezpieczający zamek jest liczbą czterocyfrową podzielną przez 9. Trzy cyfry szyfru są już ustawione. Brakującą cyfrą jest A. 5 B. 2 C. 0 D. 9 4 2? 7 2.
Część matematyczna sprawdzian 2013 r. 1. Szyfr zabezpieczający zamek jest liczbą czterocyfrową podzielną przez 9. Trzy cyfry szyfru są już ustawione. Brakującą cyfrą jest A. 5 B. 2 C. 0 D. 9 4 2? 7 2.
Zestaw 2. Definicje i oznaczenia. inne grupy V 4 grupa czwórkowa Kleina D n grupa dihedralna S n grupa symetryczna A n grupa alternująca.
 Zestaw 2 Definicja grupy Definicje i oznaczenia grupa zbiór z działaniem łącznym, posiadającym element neutralny, w którym każdy element posiada element odwrotny grupa abelowa (przemienna) grupa, w której
Zestaw 2 Definicja grupy Definicje i oznaczenia grupa zbiór z działaniem łącznym, posiadającym element neutralny, w którym każdy element posiada element odwrotny grupa abelowa (przemienna) grupa, w której
WOJEWÓDZKI URZĄD PRACY W SZCZECINIE
 WOJEWÓDZKI URZĄD PRACY W SZCZECINIE Powierzenie pracy cudzoziemcom na podstawie oświadczenia pracodawcy bez konieczności uzyskania zezwolenia na pracę w województwie zachodniopomorskim w 2013 roku Opracowanie:
WOJEWÓDZKI URZĄD PRACY W SZCZECINIE Powierzenie pracy cudzoziemcom na podstawie oświadczenia pracodawcy bez konieczności uzyskania zezwolenia na pracę w województwie zachodniopomorskim w 2013 roku Opracowanie:
Metoda najszybszego spadku
 Metody Gradietowe W tym rozdziale bdziemy rozwaa metody poszuiwaia dla fucji z przestrzei R o wartociach rzeczywistych Metody te wyorzystuj radiet fucji ja rówie wartoci fucji Przypomijmy, czym jest zbiór
Metody Gradietowe W tym rozdziale bdziemy rozwaa metody poszuiwaia dla fucji z przestrzei R o wartociach rzeczywistych Metody te wyorzystuj radiet fucji ja rówie wartoci fucji Przypomijmy, czym jest zbiór
δ δ δ 1 ε δ δ δ 1 ε ε δ δ δ ε ε = T T a b c 1 = T = T = T
 M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 8 9 6-7 7 X M O D E L O W A N I E P A S Z C Z Y Z N B A Z O W Y C H K O R P U S W N A P O D S T A W I E P O M W S P R Z D N O C I O W Y C H
M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 8 9 6-7 7 X M O D E L O W A N I E P A S Z C Z Y Z N B A Z O W Y C H K O R P U S W N A P O D S T A W I E P O M W S P R Z D N O C I O W Y C H
ROZKŁADY ZMIENNYCH LOSOWYCH
 ROZKŁADY ZMIENNYCH LOSOWYCH ZMIENNA LOSOWA Defcja. Zmeą losową jest fukcja: X: E -> R która każdemu zdarzeu elemetaremu E przypsuje lczbę rzeczywstą e X ( e) R DYSTRYBUANTA Dystrybuatą zmeej losowej X
ROZKŁADY ZMIENNYCH LOSOWYCH ZMIENNA LOSOWA Defcja. Zmeą losową jest fukcja: X: E -> R która każdemu zdarzeu elemetaremu E przypsuje lczbę rzeczywstą e X ( e) R DYSTRYBUANTA Dystrybuatą zmeej losowej X
IZBA PRZEMYSŁOWO- HANDLOWA W RZESZOWIE. Księga znaku Izby Przemysłowo-Handlowej w Rzeszowie
 IZBA PRZEMYSŁOWO- HANDLOWA W RZESZOWIE Księga znaku Izby Przemysłowo-Handlowej w Rzeszowie Spis treści Forma podstawowa Odmiany formy podstawowej Formy pionowe Odmiany form pionowych Siatka modułowa Pole
IZBA PRZEMYSŁOWO- HANDLOWA W RZESZOWIE Księga znaku Izby Przemysłowo-Handlowej w Rzeszowie Spis treści Forma podstawowa Odmiany formy podstawowej Formy pionowe Odmiany form pionowych Siatka modułowa Pole
Praca za granicą. Emerytura polska czy zagraniczna?
 Dolnośląski Wojewódzki Urząd pracy radzi: Praca za granicą. Emerytura polska czy zagraniczna? Często pojawia się pytanie, jaki wpływ na emeryturę ma praca za granicą. Wiele osób, które pracowały w różnych
Dolnośląski Wojewódzki Urząd pracy radzi: Praca za granicą. Emerytura polska czy zagraniczna? Często pojawia się pytanie, jaki wpływ na emeryturę ma praca za granicą. Wiele osób, które pracowały w różnych
Metrologia cieplna i przepływowa
 Metrologia cieplna i przepływowa Systemy, Maszyny i Urządzenia Energetyczne, I rok mgr Pomiar małych ciśnień Instrukcja do ćwiczenia Katedra Systemów Energetycznych i Urządzeń Ochrony Środowiska AGH Kraków
Metrologia cieplna i przepływowa Systemy, Maszyny i Urządzenia Energetyczne, I rok mgr Pomiar małych ciśnień Instrukcja do ćwiczenia Katedra Systemów Energetycznych i Urządzeń Ochrony Środowiska AGH Kraków
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania 1-100
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
