Wskazy prądu i napięcia sinusoidalnego. Idea wykresu wskazowego obwodu
|
|
|
- Kazimiera Mazurek
- 6 lat temu
- Przeglądów:
Transkrypt
1 6. Elementy bwdów prądu snusdalneg 3 Wyład XV. WYKESY WSKAOWE PĄD NAPĘA SNSODANEGO. METODA SYMBONA OWĄYWANA OBWODÓW Wsazy prądu napęca snusdalneg. dea wyresu wsazweg bwdu Przebeg snusdalny mże być reprezentwany przez: a) wrujący wetr neruchmą ś przebegu czasweg, rócej: neruchmą ś czasu (rys. a), b) neruchmy wetr wrującą ś przebegu czasweg, rócej: wrującą ś czasu (rys. b), przy czym rzut teg wetra na tę ś wyraża wartść chwlwą przebegu. a) neruchma b) ś czasu u(t) u(0) ω t mt ψ u m u(0) wrująca ś czasu w płżenu pczątwym 0 ś zerwej fazy 0 ś zerwej fazy pczątwej pczątwej (ψ u = 0) (ψ u = 0) u(t) ω t ψ u wrująca ś czasu w chwl t > 0 m Wetry reprezentujące przebeg czaswe prądu (t) napęca u(t) nazywa sę wsazam znacza pdreślnym welm lteram: wsazy wrujące ja mt, mt ; wsazy neruchme m, m. Wsaz neruchmy danej welśc, tżsamy ja wdać ze wsazem ruchmym tej welśc w chwl pczątwej, nazywa sę wsazem pczątwym tejże welśc. Wartść chwlwa przebegu snusdalneg jest reślna jednznaczne przez czas raz długść płżene reprezentująceg g wsazu pczątweg. Algebracznemu ddawanu wartśc chwlwych prądów lub napęć snusdalnych tej samej pulsacj dpwada gemetryczne ddawane ch wsazów pczątwych. Wyres przedstawający wsazy pczątwe prądów napęć bwdu prądu snusdalneg reślnej pulsacj ns nazwę wyresu wsazweg teg bwdu. azwyczaj na wyrese wsazwym ne rysuje sę s uładu współrzędnych (ne zaznacza sę też s zerwej fazy pczątwej). W pratyce są używane wartśc suteczne prądów napęć, a ne ch wartśc masymalne. Wsazy pczątwe m m długścach m m, równych ampltudm przebegów snusdalnych (t) u(t) zastępuje sę dlateg wsazam, długścach razy rótszych d m m, czyl równych wartścm sutecznym przebegów (t) u(t). reduwane w ta spsób wsazy pczątwe prądów napęć przedstawa sę na wyresach wsazwych, nazywając je p prstu wsazam (bez ddatwych reśleń). Przydatnść wyresów wsazwych wyna z pglądweg przedstawena zwązów czaswych ja zależnśc gemetrycznych, c na gół ułatwa rzwązane bwdu. Wyresy wsazwe wyresy trójątwe dwójnów pasywnych Kąt przesunęca fazweg (przesunęce fazwe) dwójna jest różncą faz pczątwych jeg napęca prądu: = ψ u ψ. Gdy > 0 (X > 0; B < 0), t wsaz późna sę ąt względem wsazu (rys. a); gdy natmast < 0 (X < 0; B > 0), t wsaz późna sę ąt względem wsazu (rys. b). a) > 0 b) < 0 G ψ u X ψ B (ś zerwej fazy pczątwej) B X G ψ ψ u
2 4 Wyład XV Na przedstawnych wyżej wyresach wsazwych dwójna charaterze: a) ndu- G G c) d) X >0 cyjnym, b) pjemnścwym zaznaczn sładwe X wsazu napęca (dla zastępczeg dwójna szeregweg, X ), raz B B<0 X sładwe G B wsazu prądu (dla zastępczeg dwójna równległeg G, B ). Wyres z rys. a dns sę d uładów pazanych na rys. c d (dwójn charaterze nducyjnym). Wyres z rys. b dns sę d analgcznych uładów z pjemnścam na mejscu nducyjnśc, przy czym X < 0 B > 0. Wsazy napęca raz prądu twrzą wraz ze swym sładwym trójąty napęca trójąty prądu, c lepej wdać, gdy te wyresy są naryswane ddzelne, z załżenem zerwej wartśc pczątwej, dpwedn: ąta fazweg ψ prądu w uładze, X (trójąt napęca); ąta fazweg ψ u napęca w uładze G, B (trójąt prądu). Wyresy tae, dla dwójna charaterze nducyjnym ( > 0) ja na rys. a, pazan nżej na rysunach a a. Kątw wartścm sutecznym, G B raz, X dpwadają sładwe czynne berne: - prądu = = cs cz G a ) ψ = 0 b = sn, b = B ; B - napęca cz = = cs b = sn, b = X. Dzeląc raz mnżąc długśc bów trójątów napęca prądu, G dpwedn, przez wartśc suteczne prądu napęca, trzymuje X > 0 S B < 0 sę trójąty: mpedancj, admtancj Y Q > 0 raz mcy pazane b na rysunu dla dwójna charaterze nducyjnym ( > 0). P Przelczene długśc bów z trójątów mpedancj lub admtancj, na trójąt mcy, wyraża sę następując: P = = G ; Q = X = B ; S = = Y. X a ) G ψ u = 0 Przyład. Wyres wsazwy prądów napęć dwójna,, struturze szeregw-równległej, wynany przy załżenu 3 ( t) = 3 snωt, tj. ψ 3 = 0. = 3 3 = = 3 3 = 3
3 6. Elementy bwdów prądu snusdalneg 5 Wynany wyres dpwada danym: X = X = 3 = 00 Ω, = 00 Ω. Ja wdać, uład tych danych jest dwójnem rezystancyjn-pjemnścwym ( < 0), ale przy mnejszej np. trzyrtne wartśc reatancj X byłby t dwójn rezystancyjn-nducyjny ( > 0). waga. Wyres wsazwy wynuje sę w sal, tzn. przyjmuje sę sale długśc wsazów prądu wsazów napęca (sale prądu napęca). Długśc fazy wsazów napęca raz prądu, dtyczących pszczególnych elementów dealnych lub gałęz z nch złżnych, są ze sbą zwązane wartścam mpedancj ąta przesunęca fazweg. Szcując wyres wsazwy ne reśla sę dładne sal prądu napęca, trzeba jedna zachwać przyblżne prprcje dpwadające danym bądź spdzewanym wartścm parametrów bwdu. Prcedura blczena wartśc mpedancj ąta fazweg dwójna (dla pdanych wyżej parametrów uładu): a) mpedancja, ndutancja susceptancja gałęz trzecej - 3 X 3 = 3 + X = 00 Ω; G 3 = = 0, 005 S; 0, B = = S; 3 3 b) ndutancja gałęz drugej - G = = 0,005 S; c) ndutancja, susceptancja admtancja gałęz drugej z trzecą - G = G + G 0,0 S; B = B = 0, 005 S; Y = G + B 0,0, 5 S; 3 3 = 3 3 d) rezystancja reatancja gałęz drugej z trzecą - G3 B3 = 80 Ω; X = 40 Ω; Y Y 3 = 3 3 = 3 e) rezystancja, reatancja, mpedancja ąt fazwy dwójna = = 3 = 80 Ω; X = X + X = 60 Ω; = + X = 00 Ω; 3 X = arc tg 37. Prcedura blczena wartśc sutecznych prądów napęć gałęzwych przy załżnym przebegu 3 ( t) = snωt, [ 3 ] = A, [ω] = s -, [t] = s, tzn. wartścach 3 = A ψ 3 = 0 (na wyrese pzme płżene wsazu 3 ): a) mpedancja wartść suteczna napęca w gałęz trzecej - 3 = 3 = + X 00 Ω; = = V; b) przesunęce fazwe faza pczątwa napęca w gałęz trzecej - X 3 = tg = arc 45 ; ψ u 3 = ψ = 45 ; 3 c) wartść suteczna faza pczątwa napęca w gałęz drugej - = 3 83 V; ψ u = ψ u 3 = 45 ; d) mpedancja, przesunęce fazwe, wartść suteczna faza pczątwa prądu w gałęz drugej - = 00 Ω; 0 ; =, 4 A; ψ = ψ 45 = = e) wartść suteczna faza pczątwa prądu dwójna ( = ) - x = csψ = csψ + 3 csψ 3 = 3 A; y = snψ = snψ + 3 snψ 3 = A; y = x + y = 0 3,6 A; ψ = arc tg 8,4 ; x u = ;
4 6 Wyład XV = 3,6 ψ = ψ 8,4 ; f) wartść suteczna faza pczątwa napęca na pjemnśc - = X = V; ψ u = ψ + 7,6 ; g) wartść suteczna faza pczątwa napęca dwójna - x = csψ u = csψ u + csψ u = 300 V; y = snψ u = snψ u + snψ u = 00 V; = y x + y = V; ψ u = arc tg 8,4 ; x h) mpedancja przesunęce fazwe dwójna - = = 00 Ω; ψ u ψ 37. = Wartśc symblczne prądu napęca snusdalneg Wsazy prądu napęca:, umeszczne na płaszczyźne zesplnej, stają sę lczbam zesplnym (rys. b wsaz jψu ja lczba zesplna = e ). Nszą ne nazwy wartśc sutecznych zesplnych lub wartśc symblcznych prądu napęca. żywając symblu lczby urjnej j =, zapsuje sę wartśc symblczne w pstac wyładnczej, trygnmetrycznej lub algebracznej (artezjańsej): e j ψ = = (cs ψ + j snψ ) = e + j m, (6.48a) e j ψ = u = (cs ψ u+ j snψ u ) = e + j m, (6.48b) gdze: =, = mduły (długśc wsazów) ; ψ, ψ u argumenty ; e, e częśc rzeczywste ; m, m częśc urjne. Przebeg czaswe prądu napęca dpwadają częścm urjnym wsazów zesplnych wrujących mt mt (prądu napęca): jωt t) = m = m( e ) = sn( ωt + ψ ), (6.49a) ( mt jωt ( mt u u t) = m = m( e ) = sn( ωt + ψ ). (6.49b) Własnśc metdy symblcznej rzwązywana bwdów prądu snusdalneg. Ddawanu wartśc chwlwych prądów (w węzłach) raz napęć (na elementach bwdu) dpwada ddawane ch wartśc symblcznych: ( t) ( t) = ; u ( t) = u ( t) =. =. Mędzy wartścam symblcznym prądu napęca elementów dealnych zachdzą następujące zależnśc (wyresy ze wsazam zesplnym są tae same ja ze zwyłym ): a) rezystancja -, G = G = j m 0 =, (6.50a) = G, (6.50b) (ś urjna) ψ e (ś rzeczywsta)
5 6. Elementy bwdów prądu snusdalneg 7 b) pjemnść - X, B = jb = -jx = jx, (6.5a) = jb, (6.5b) c) nducyjnść (własna) - X, B = jx = -jb = jx, (6.5a) = jb, (6.5b) d) nducyjnść wzajemna - X = X M M M = jx M = jx, (6.53a) M M analgczne = jx. (6.53b) M M 3. ładw szeregwemu, X przypsuje sę mpedancję zesplną = + jx = e (6.54a) pstać zesplną dmany mpedancyjnej prawa Ohma j =. (6.54b) 4. ładw równległemu G, B przypsuje sę admtancję zesplną Y = G + jb = Y e (6.55a) pstać zesplną dmany admtancyjnej prawa Ohma j = Y. (6.55b) 5. Dla reślneg dwójna zachdz zwąze Y =, (6.56) z czeg wynają następujące zależnśc mędzy elementam uładów zastępczych, X G, B : G B X =, X =, G =, B =. (6.56a, b, c, d) Y Y 6. Przy płączenu szeregwym dwójnów pasywnych sumuje sę ddzelne rezystancje reatancje alb mpedancje zesplne (ne wln sumwać mdułów mpedancj zesplnych!):, X = X ; =. (6.57a, b, c) = 7. Przy płączenu równległym dwójnów pasywnych sumuje sę ddzelne ndutancje susceptancje alb admtancje zesplne (ne wln sumwać mdułów admtancj zesplnych!): G, B = B, Y = Y. (6.58a, b, c) = G 8. Wszyste twerdzena metdy rzwązywana bwdów, dtyczące ter bwdów prądu stałeg (welśc rzeczywste stałe:,, E, źr,, G), zachwują ważnść w analze stanów ustalnych bwdów prądu snusdalneg przy użycu lczb zesplnych (welśc zesplne:,, E, źr,, Y).
6 8 Wyład XV Przyład. stane przeprwadzny rachune symblczny, dpwadający prcedurm przedstawnym w pprzednm przyładze, dtyczący teg sameg dwójna (rys. b). Dane są, ja pprzedn: X = X = 3 = 00 Ω, = 00 Ω, 3 ( t) = snωt, [ 3 ] = A, [ω] = s -, [t] = s. Prcedura blczena mpedancj ąta fazweg dwójna: = j00 Ω; = 00 Ω; 3 = (00 + j 00) Ω; 3 j37 = + = 80 j60 00 e Ω; = 00 Ω; Prcedura blczena wartśc sutecznych prądów napęć gałęzwych: 3 = j0 = e A; j00 = 00 j45 = e Ω; j45 3 = 3 3 = 00 e = (00 + j00) j0 = 00 = 00 e Ω; j45 = Y = e = ( + j) + 3 = 3 + j 0 V; = 3 ; = 3 83 V; j0 Y = 0,005 = 0, 005 e S; j8,4 A;, 4 A; = e A; 3, 6 A; j90 = j00 = 00 e Ω; j7,6 = 00 0 e (00 j300) + = 300 j j8,4 V; 36 V; = e V; 36 V; j37 = ; = = 80 j60 00 e Ω; = 00 Ω; 37. Wnse (wynający z prównana prcedur blczenwych przedstawnych w tym w pprzednm przyładze): rzyśc blczenwe stswana rachunu symblczneg są czywste. Mc zesplna Trójąt mcy umeszczny na płaszczyźne zesplnej przedstawa trójąt mcy zesplnej (rys. b), tóreg bam są: mc czynna P, mc berna Q pmnżna przez j, raz mc zesplna S : j S = S e = S (cs + j sn) = P + jq Sr = ψ u ψ, t P ; (6.59) P = e S, Q = m S, S = P + Q =. (6.60a, b, c) jψ jψ jψ u u S = e e = ( e ) ( e ) = stąd mc zesplna uładu szeregweg, X raz uładu równległeg G, B wyns: S = = + jx, jψ, (6.6) S = Y = G jb. (6.6a, b) Sprządzając blans mcy bwdu, sumuje sę ddzelne mce czynne berne alb mce zesplne (ne wln sumwać mdułów mcy zesplnych, tj. mcy pzrnych!): P, Q = Q, S = S. (6.63a, b, c) = P = = 3 S jq
7 6. Elementy bwdów prądu snusdalneg 9 Psługwane sę rachunem symblcznym w rzwązywanu bwdów Przyład. użycem rachunu symblczneg, pprzez stswane różnych metd, zstaną wyznaczne wartśc A prądów napęć, reślne wsazana przyrządów pmarwych (ampermerzy wltmerza) raz sprządzny blans mcy w uładze pazanym na rysunu. Przyrządy A są dealne merzą wartśc suteczne. Dane: X = X = 0 Ω; = u = 40 snωt, = csωt, źr [u] = V, [ źr ] = A, [ω] = s, [t] = s. Danym przebegm dpwadają wartśc symblczne napęca prądu: = 40 V; źr = j A. mpedancje zesplne elementów wynszą: = 0 Ω; = j0 Ω; = j0 Ω. e schematu wyna, że wystarcza blczene lub, bwem: = + źr lub = źr ; V = + = + źr. Oblcza sę najperw na różne spsby prąd, a następne,,, V, reśla wsazana przyrządów sprządza blans mcy bwdu. źr źr V V. asada superpzycj a b a + b źr źr źr = = ( ) A; b = = ( j) A; + + a + j = + = ( ) A. a b + j. amana źródła prądweg na napęcwe blczene prądu w czu (z równana czweg dla jedneg cza) źr źr źr źr = = = ( + ) A. + j
8 30 Wyład XV 3. amana źródła napęcweg na prądwe blczene ptencjału w węźle (z równana węzłweg dla jedneg węzła nezależneg) V =0 V źr Y Y Y V =0 V źr Y = 0, S; Y = = j0, S; = źr + Y ( Y + Y ) V = źr + Y ; V = = (30 j0) V; Y + Y = Y ( V ) = ( + ) A. j 4. Twerdzene Thevenna (gałąź, ja zewnętrzna) 0 źr w 0 źr = 0 = źr = 0 V; w = ; = = ( + j) A Wartśc symblczne,,, V, raz wsazana przyrządów = + źr = ( + j3) A; = = (0 + j0) V; = = (30 j0) V; = źr = ( 0) V; V = + = (0 j0) V; A = =,4 A; A = = 0 3, 6 A; V = 0 4, V. 6. Blans mcy bwdu S gen * * V źr j w = V = + = 40 ( j) + (0 j0) ( j) = (0 60) VA; = db = źr P db = = 0 ( + ) 0 W; Q X + X = 0 ( + 3 ) + 0 = 60 var; S db = Pdb + j Qdb, db gen S = S.
Politechnika Wrocławska Instytut Maszyn, Napędów i Pomiarów Elektrycznych. Materiał ilustracyjny do przedmiotu. (Cz. 2)
 Poltechnka Wrocławska nstytut Maszyn, Napędów Pomarów Elektrycznych Materał lustracyjny do przedmotu EEKTOTEHNKA (z. ) Prowadzący: Dr nż. Potr Zelńsk (-9, A10 p.408, tel. 30-3 9) Wrocław 005/6 PĄD ZMENNY
Poltechnka Wrocławska nstytut Maszyn, Napędów Pomarów Elektrycznych Materał lustracyjny do przedmotu EEKTOTEHNKA (z. ) Prowadzący: Dr nż. Potr Zelńsk (-9, A10 p.408, tel. 30-3 9) Wrocław 005/6 PĄD ZMENNY
Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu
 Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu Elektrtechnika i Elektrnika Materiały Dydaktyczne Mc w bwdach prądu zmienneg. Opracwał: mgr inż. Marcin Jabłński mgr inż. Marcin Jabłński
Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu Elektrtechnika i Elektrnika Materiały Dydaktyczne Mc w bwdach prądu zmienneg. Opracwał: mgr inż. Marcin Jabłński mgr inż. Marcin Jabłński
Politechnika Wrocławska Instytut Maszyn, Napędów i Pomiarów Elektrycznych. Materiał ilustracyjny do przedmiotu
 Poltechnka Wrocławska nstytut Maszyn, Napędów Pomarów Elektrycznych A KŁ A D M A S Z YN E EK T Materał lustracyjny do przedmotu EEKTOTEHNKA Y Z N Y Z H Prowadzący: * (z. ) * M N Dr nż. Potr Zelńsk (-9,
Poltechnka Wrocławska nstytut Maszyn, Napędów Pomarów Elektrycznych A KŁ A D M A S Z YN E EK T Materał lustracyjny do przedmotu EEKTOTEHNKA Y Z N Y Z H Prowadzący: * (z. ) * M N Dr nż. Potr Zelńsk (-9,
obliczenie różnicy kwadratów odległości punktów po i przed odkształceniem - różniczka zupełna u i, j =1, 2, 3
 TEORI STNU ODKSZTŁCENI. WEKTOR RZEMIESZCZENI x u r r ' ' x stan p defrmacj x stan przed defrmacją płżene pt. przed defrmacją ( r) ( x, x, x ) płżene pt. p defrmacj ( r ) ( x, x, x ) przemeszczene puntu
TEORI STNU ODKSZTŁCENI. WEKTOR RZEMIESZCZENI x u r r ' ' x stan p defrmacj x stan przed defrmacją płżene pt. przed defrmacją ( r) ( x, x, x ) płżene pt. p defrmacj ( r ) ( x, x, x ) przemeszczene puntu
Wykład XVIII. SZCZEGÓLNE KONFIGURACJE OBWODÓW TRÓJFAZOWYCH. POMIARY MOCY W OBWODACH TRÓJFAZOWYCH I 1 U 12 I 2 U 23 3 U U Z I = ; I 12 I 23
 7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
A. Kanicki: Systemy elektroenergetyczne KRYTERIA NAPIĘCIOWE WYZNACZANIA STABILNOŚCI LOKALNEJ
 . Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
. Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
ĆWICZENIE NR 2 POMIARY W OBWODACH RLC PRĄDU PRZEMIENNEGO
 ĆWENE N POMAY W OBWODAH PĄD PEMENNEGO el ćwczena: dośwadczalne sprawdzene prawa Oha, praw Krchhoffa zależnośc fazowych ędzy snsodalne zenny przebega prądów napęć w obwodach zawerających eleenty,,, oraz
ĆWENE N POMAY W OBWODAH PĄD PEMENNEGO el ćwczena: dośwadczalne sprawdzene prawa Oha, praw Krchhoffa zależnośc fazowych ędzy snsodalne zenny przebega prądów napęć w obwodach zawerających eleenty,,, oraz
PIOTR MADEJ ĆWICZENIA LABORATORYJNE Z PODSTAW ELEKTRONIKI
 PIOT MADEJ ĆWICZENIA LABOATOYJNE Z PODSTAW ELEKTONIKI Mm Studentm, szczególne z przełmu weów. Ofcyna Wydawncza Pltechn Wrcławsej Wrcław 04 PIOT MADEJ ecenzent Janusz Ocepa Oracwane grafczne redacyjne Ptr
PIOT MADEJ ĆWICZENIA LABOATOYJNE Z PODSTAW ELEKTONIKI Mm Studentm, szczególne z przełmu weów. Ofcyna Wydawncza Pltechn Wrcławsej Wrcław 04 PIOT MADEJ ecenzent Janusz Ocepa Oracwane grafczne redacyjne Ptr
Metody analizy obwodów
 Metody analzy obwodów Metoda praw Krchhoffa, która jest podstawą dla pozostałych metod Metoda transfguracj, oparte na przekształcenach analzowanego obwodu na obwód równoważny Metoda superpozycj Metoda
Metody analzy obwodów Metoda praw Krchhoffa, która jest podstawą dla pozostałych metod Metoda transfguracj, oparte na przekształcenach analzowanego obwodu na obwód równoważny Metoda superpozycj Metoda
Obwody prądu zmiennego
 Obwody prądu zmiennego Prąd stały ( ) ( ) i t u t const const ( ) u( t) i t Prąd zmienny, dowolne funkcje czasu i( t) t t u ( t) t t Natężenie prądu i umowny kierunek prądu Prąd stały Q t Kierunek poruszania
Obwody prądu zmiennego Prąd stały ( ) ( ) i t u t const const ( ) u( t) i t Prąd zmienny, dowolne funkcje czasu i( t) t t u ( t) t t Natężenie prądu i umowny kierunek prądu Prąd stały Q t Kierunek poruszania
Blok 6: Pęd. Zasada zachowania pędu. Praca. Moc.
 Blk 6: Pęd. Zasada zachwana pędu. Praca. Mc. ZESTAW ZADAŃ NA ZAJĘCIA Uwaga: w pnższych zadanach przyjmj, że wartść przyspeszena zemskeg jest równa g 10 m / s. PĘD I ZASADA ZACHOWANIA PĘDU 1. Płka mase
Blk 6: Pęd. Zasada zachwana pędu. Praca. Mc. ZESTAW ZADAŃ NA ZAJĘCIA Uwaga: w pnższych zadanach przyjmj, że wartść przyspeszena zemskeg jest równa g 10 m / s. PĘD I ZASADA ZACHOWANIA PĘDU 1. Płka mase
Pracownia Automatyki i Elektrotechniki Katedry Tworzyw Drzewnych Ćwiczenie 3. Analiza obwodów RLC przy wymuszeniach sinusoidalnych w stanie ustalonym
 ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
8. MOC W OBWODZIE PRĄDU SINUSOIDALNEGO
 OBWODY I SYGNAŁY 8. MOC W OBWODZIE PRĄD SINSOIDALNEGO 8.. MOC CHWILOWA Jeśl na zacskach dójnka SLS ystępje napęcoe ymszene harmonczne, to prąd zmena sę róneż snsodalne z tą samą plsacją Nech () t m sn
OBWODY I SYGNAŁY 8. MOC W OBWODZIE PRĄD SINSOIDALNEGO 8.. MOC CHWILOWA Jeśl na zacskach dójnka SLS ystępje napęcoe ymszene harmonczne, to prąd zmena sę róneż snsodalne z tą samą plsacją Nech () t m sn
Ćwiczenie 3 BADANIE OBWODÓW PRĄDU SINUSOIDALNEGO Z ELEMENTAMI RLC
 Ćwiczenie 3 3.1. Cel ćwiczenia BADANE OBWODÓW PRĄD SNSODANEGO Z EEMENTAM RC Zapoznanie się z własnościami prostych obwodów prądu sinusoidalnego utworzonych z elementów RC. Poznanie zasad rysowania wykresów
Ćwiczenie 3 3.1. Cel ćwiczenia BADANE OBWODÓW PRĄD SNSODANEGO Z EEMENTAM RC Zapoznanie się z własnościami prostych obwodów prądu sinusoidalnego utworzonych z elementów RC. Poznanie zasad rysowania wykresów
5. CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 5. CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Oprócz transmtancj operatorowej, do opsu członów układów automatyk stosuje sę tzw. transmtancję wdmową. Transmtancję wdmową G(j wyznaczyć moŝna dzęk podstawenu do wzoru
5. CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Oprócz transmtancj operatorowej, do opsu członów układów automatyk stosuje sę tzw. transmtancję wdmową. Transmtancję wdmową G(j wyznaczyć moŝna dzęk podstawenu do wzoru
POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH
 ĆWICZENIE NR POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH.. Cel ćwiczenia Celem ćwiczenia jest pznanie metd pmiaru mcy czynnej w układach trójfazwych... Pmiar metdą trzech watmierzy Metda trzech watmierzy
ĆWICZENIE NR POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH.. Cel ćwiczenia Celem ćwiczenia jest pznanie metd pmiaru mcy czynnej w układach trójfazwych... Pmiar metdą trzech watmierzy Metda trzech watmierzy
Analiza obwodów elektrycznych
 nalza bwdów elekrycznych Określene mnmalneg zbr fnkcj bwdwych F {, } nalza Wyznaczene nnych welkśc charakeryzjących bwód; np. mce, sprawnśc p. Obwód elekryczny Wyznaczene warśc paramerów wybranych elemenów
nalza bwdów elekrycznych Określene mnmalneg zbr fnkcj bwdwych F {, } nalza Wyznaczene nnych welkśc charakeryzjących bwód; np. mce, sprawnśc p. Obwód elekryczny Wyznaczene warśc paramerów wybranych elemenów
LABORATORIUM PODSTAW ELEKTROTECHNIKI Badanie obwodów prądu sinusoidalnie zmiennego
 Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Podstawy Elektrotechniki i Elektroniki. Opracował: Mgr inż. Marek Staude
 Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym Przypomnienie ostatniego wykładu Prąd i napięcie Podstawowe
Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym Przypomnienie ostatniego wykładu Prąd i napięcie Podstawowe
Zadania OBWODY PRĄDU SINUSOIDALNEGO ZE SPRZĘŻENIAMI MAGNETYCZNYMI
 adania 4. OBWODY PRĄD SNSODALNEGO E SPRĘŻENA AGNETYNY ad. -. Określ wskazanie woltomierza w danym układzie prądu sinusoidalnego (woltomierz, jak zwykle, traktuje się jako idealny, tzn. niepobierający prądu.
adania 4. OBWODY PRĄD SNSODALNEGO E SPRĘŻENA AGNETYNY ad. -. Określ wskazanie woltomierza w danym układzie prądu sinusoidalnego (woltomierz, jak zwykle, traktuje się jako idealny, tzn. niepobierający prądu.
Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci
 Ćwiczenie 4 - Badanie wpływu asymetrii obciążenia na pracę sieci Strona 1/13 Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci Spis treści 1.Cel ćwiczenia...2 2.Wstęp...2 2.1.Wprowadzenie
Ćwiczenie 4 - Badanie wpływu asymetrii obciążenia na pracę sieci Strona 1/13 Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci Spis treści 1.Cel ćwiczenia...2 2.Wstęp...2 2.1.Wprowadzenie
Twierdzenie Bezouta i liczby zespolone Javier de Lucas. Rozwi azanie 2. Z twierdzenia dzielenia wielomianów, mamy, że
 Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
Podstawowe układy pracy tranzystora MOS
 A B O A T O I U M P O D S T A W E E K T O N I K I I M E T O O G I I Pdstawwe układy pracy tranzystra MOS Ćwiczenie pracwał Bgdan Pankiewicz 4B. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści trzech
A B O A T O I U M P O D S T A W E E K T O N I K I I M E T O O G I I Pdstawwe układy pracy tranzystra MOS Ćwiczenie pracwał Bgdan Pankiewicz 4B. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści trzech
Wykład lutego 2016 Krzysztof Korona. Wstęp 1. Prąd stały 1.1 Podstawowe pojęcia 1.2 Prawa Ohma Kirchhoffa 1.3 Przykłady prostych obwodów
 Wykład Obwody prądu stałego zmennego 9 lutego 6 Krzysztof Korona Wstęp. Prąd stały. Podstawowe pojęca. Prawa Ohma Krchhoffa.3 Przykłady prostych obwodów. Prąd zmenny. Podstawowe elementy. Obwody L.3 mpedancja.4
Wykład Obwody prądu stałego zmennego 9 lutego 6 Krzysztof Korona Wstęp. Prąd stały. Podstawowe pojęca. Prawa Ohma Krchhoffa.3 Przykłady prostych obwodów. Prąd zmenny. Podstawowe elementy. Obwody L.3 mpedancja.4
E-20A POMIAR MOCY PRĄDU ZMIENNEGO METODĄ OSCYLO- SKOPOWĄ
 Ćwiczenie E-A POMIA MOY PĄDU ZMIENNEGO MEODĄ OSYO- SKOPOWĄ I. el ćwiczenia: Pmiar mcy prądu zmienneg za pmcą scylskpu, pmiar różnicy faz scylskpem, cena dkładnści metdy. II. Przyrządy: Oscylskp, nieznana
Ćwiczenie E-A POMIA MOY PĄDU ZMIENNEGO MEODĄ OSYO- SKOPOWĄ I. el ćwiczenia: Pmiar mcy prądu zmienneg za pmcą scylskpu, pmiar różnicy faz scylskpem, cena dkładnści metdy. II. Przyrządy: Oscylskp, nieznana
2. REZONANS W OBWODACH ELEKTRYCZNYCH
 2. EZONANS W OBWODAH EEKTYZNYH 2.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód elektryczny,
2. EZONANS W OBWODAH EEKTYZNYH 2.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód elektryczny,
Ogniwo wzorcowe Westona
 WZOZEC SEM - OGNWO WESTON mieszczne jest w szklanym naczyniu, w które wtpine są platynwe elektrdy. Ddatni i ujemny biegun gniwa stanwią dpwiedni rtęć (Hg) i amalgamat kadmu (Cd 9-Hg), natmiast elektrlitem
WZOZEC SEM - OGNWO WESTON mieszczne jest w szklanym naczyniu, w które wtpine są platynwe elektrdy. Ddatni i ujemny biegun gniwa stanwią dpwiedni rtęć (Hg) i amalgamat kadmu (Cd 9-Hg), natmiast elektrlitem
ĆWICZENIE NR 2 BADANIA OBWODÓW RLC PRĄDU HARMONICZNEGO
 ĆWENE N BADANA OBWODÓW PĄD HAMONNEGO el ćwczena: dośwadczalne sprawdzene prawa Oha praw Krchhoffa oraz zależnośc fazowych poędzy snusodalne zenny przebega prądów napęć w obwodach zawerających eleenty,,,
ĆWENE N BADANA OBWODÓW PĄD HAMONNEGO el ćwczena: dośwadczalne sprawdzene prawa Oha praw Krchhoffa oraz zależnośc fazowych poędzy snusodalne zenny przebega prądów napęć w obwodach zawerających eleenty,,,
ZS LINA_ LINB_ LINC_. Rys. 1. Schemat rozpatrywanej sieci. S1 j
 PRZYKŁAD 1.1 Opracwać mdel fragmentu sieci trójfazwej 110kV z linią reprezentwaną za pmcą dwóch dcinków RL z wzajemnym sprzężeniem (mdel 51). chemat sieci jest pkazany na rys. 1. Zbadać przebieg prądów
PRZYKŁAD 1.1 Opracwać mdel fragmentu sieci trójfazwej 110kV z linią reprezentwaną za pmcą dwóch dcinków RL z wzajemnym sprzężeniem (mdel 51). chemat sieci jest pkazany na rys. 1. Zbadać przebieg prądów
Politechnika Wrocławska Instytut Maszyn, Napędów i Pomiarów Elektrycznych. Materiał ilustracyjny do przedmiotu. (Cz. 2)
 Poltchnka Wrocławska nstytut Maszyn, Napędów Pomarów Elktrycznych Matrał lustracyjny do przdmotu EEKTOTEHNKA (z. ) Prowadzący: Dr nż. Potr Zlńsk (-9, A0 p.408, tl. 30-3 9) Wrocław 004/5 PĄD ZMENNY Klasyfkacja
Poltchnka Wrocławska nstytut Maszyn, Napędów Pomarów Elktrycznych Matrał lustracyjny do przdmotu EEKTOTEHNKA (z. ) Prowadzący: Dr nż. Potr Zlńsk (-9, A0 p.408, tl. 30-3 9) Wrocław 004/5 PĄD ZMENNY Klasyfkacja
ĆWICZENIA LABORATORYJNE Z PODSTAW ELEKTRONIKI
 PIOT MADEJ ĆWICZENIA LABOATOYJNE Z PODSTAW ELEKTONIKI WESJA POPAWIONA, WZESIEŃ 07 Mm Studentm, szczególne z przełmu weów Ofcyna Wydawncza Pltechn Wrcławsej Perwsza wersja: Wrcław 04 PIOT MADEJ ecenzent
PIOT MADEJ ĆWICZENIA LABOATOYJNE Z PODSTAW ELEKTONIKI WESJA POPAWIONA, WZESIEŃ 07 Mm Studentm, szczególne z przełmu weów Ofcyna Wydawncza Pltechn Wrcławsej Perwsza wersja: Wrcław 04 PIOT MADEJ ecenzent
Część 1 7. TWIERDZENIA O WZAJEMNOŚCI 1 7. TWIERDZENIA O WZAJEMNOŚCI Twierdzenie Bettiego (o wzajemności prac)
 Część 1 7. TWIERDZENIA O WZAJEMNOŚCI 1 7. 7. TWIERDZENIA O WZAJEMNOŚCI 7.1. Twerdzene Bettego (o wzajemnośc prac) Nech na dowolny uład ramowy statyczne wyznaczalny lub newyznaczalny, ale o nepodatnych
Część 1 7. TWIERDZENIA O WZAJEMNOŚCI 1 7. 7. TWIERDZENIA O WZAJEMNOŚCI 7.1. Twerdzene Bettego (o wzajemnośc prac) Nech na dowolny uład ramowy statyczne wyznaczalny lub newyznaczalny, ale o nepodatnych
Podstawy elektrotechniki
 Wydzał Mechanczno-Energeyczny Podsawy elekroechnk Prof. dr hab. nż. Jlsz B. Gajewsk, prof. zw. PWr Wybrzeże S. Wyspańskego 7, 50-370 Wrocław Bd. A4 Sara kołowna, pokój 359 Tel.: 7 30 30 Fax: 7 38 38 E-al:
Wydzał Mechanczno-Energeyczny Podsawy elekroechnk Prof. dr hab. nż. Jlsz B. Gajewsk, prof. zw. PWr Wybrzeże S. Wyspańskego 7, 50-370 Wrocław Bd. A4 Sara kołowna, pokój 359 Tel.: 7 30 30 Fax: 7 38 38 E-al:
Przykład 2.1. Wyznaczanie prędkości i przyśpieszenia w ruchu bryły
 Przykłd 1 Wyzncznie prędkści i przyśpieszeni w ruchu bryły Stżek kącie rzwrci twrzących i pdstwie, której prmień wynsi tczy się bez pślizgu p płszczyźnie Wektr prędkści śrdk pdstwy m stłą długść równą
Przykłd 1 Wyzncznie prędkści i przyśpieszeni w ruchu bryły Stżek kącie rzwrci twrzących i pdstwie, której prmień wynsi tczy się bez pślizgu p płszczyźnie Wektr prędkści śrdk pdstwy m stłą długść równą
WYKORZYSTANIE METOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU
 M.Miszzyńsi KBO UŁ, Badania perayjne I (wyład 7A 7) [] WYKORZYSANIE MEOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU Omówimy tutaj dwa prste warianty nieliniwyh mdeli deyzyjnyh,
M.Miszzyńsi KBO UŁ, Badania perayjne I (wyład 7A 7) [] WYKORZYSANIE MEOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU Omówimy tutaj dwa prste warianty nieliniwyh mdeli deyzyjnyh,
PIOTR MADEJ ZADANIA Z ROZWIĄZANIAMI Z ELEMENTARNEJ TECHNIKI UKŁADOWEJ W ELEKTRONICE
 POT MADEJ ZADANA Z OZWĄZANAM Z ELEMENTANEJ TECHNK KŁADOWEJ W ELEKTONCE Mjej dzne, dzę tórej zysałem wartśc nesągalne an przy twrzenu teg dzeła an w pracy WOCŁAW 0 POT MADEJ SŁOWO OD ATOA Opracwane jest
POT MADEJ ZADANA Z OZWĄZANAM Z ELEMENTANEJ TECHNK KŁADOWEJ W ELEKTONCE Mjej dzne, dzę tórej zysałem wartśc nesągalne an przy twrzenu teg dzeła an w pracy WOCŁAW 0 POT MADEJ SŁOWO OD ATOA Opracwane jest
Procent prosty Gdy znamy kapitał początkowy i stopę procentową
 cet psty Gdy zay aptał pczątwy stpę pcetwą F = + I aptał ńcwy, pczątwy, dset I = I = stpa pcetwa (w stsuu czy) F = ( + ) aledaze dsetwe 360/360, 365/365, 360/365, 365/360 es wyaży w latach (dla óżych esów
cet psty Gdy zay aptał pczątwy stpę pcetwą F = + I aptał ńcwy, pczątwy, dset I = I = stpa pcetwa (w stsuu czy) F = ( + ) aledaze dsetwe 360/360, 365/365, 360/365, 365/360 es wyaży w latach (dla óżych esów
9. ŁĄCZNIKI STATYCZNE PRĄDU PRZEMIENNEGO
 9. ŁĄCZNIKI STATYCZNE PRĄDU PRZEMIENNEGO 9.1. Cel I zakres ćwiczenia Celem ćwiczenia jest zapznanie się z budwą i pdstawwymi właściwściami łączników statycznych jednfazwych prądu przemienneg raz z mżliwściami
9. ŁĄCZNIKI STATYCZNE PRĄDU PRZEMIENNEGO 9.1. Cel I zakres ćwiczenia Celem ćwiczenia jest zapznanie się z budwą i pdstawwymi właściwściami łączników statycznych jednfazwych prądu przemienneg raz z mżliwściami
Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE
 Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
dr inż. ADAM HEYDUK dr inż. JAROSŁAW JOOSTBERENS Politechnika Śląska, Gliwice
 dr nż. ADA HEYDUK dr nż. JAOSŁAW JOOSBEENS Poltechna Śląsa, Glwce etody oblczana prądów zwarcowych masymalnych nezbędnych do doboru aparatury łączenowej w oddzałowych secach opalnanych według norm europejsej
dr nż. ADA HEYDUK dr nż. JAOSŁAW JOOSBEENS Poltechna Śląsa, Glwce etody oblczana prądów zwarcowych masymalnych nezbędnych do doboru aparatury łączenowej w oddzałowych secach opalnanych według norm europejsej
A. Kanicki: Zwarcia w sieciach elektroenergetycznych ZAŁĄCZNIK NR 1. PODKŁADY DO RYSOWANIA WYKRESÓW WSKAZOWYCH
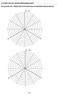 ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
ĆWICZENIE 1 DWÓJNIK ŹRÓDŁOWY PRĄDU STAŁEGO
 ĆWCZENE DWÓJNK ŹÓDŁOWY ĄD STŁEGO Cel ćiczenia: spradzenie zasady rónażnści dla dójnika źródłeg (tierdzenie Thevenina, tierdzenie Nrtna), spradzenie arunku dpasania dbirnika d źródła... dstay teretyczne
ĆWCZENE DWÓJNK ŹÓDŁOWY ĄD STŁEGO Cel ćiczenia: spradzenie zasady rónażnści dla dójnika źródłeg (tierdzenie Thevenina, tierdzenie Nrtna), spradzenie arunku dpasania dbirnika d źródła... dstay teretyczne
Problemy i zadania na egzamin ustny dla klasy 3B:
 Prblemy i zadania na egzamin ustny dla klasy 3B: Zasady: Lsujesz dwa z pniżej zamieszcznych zadań. Masz 5 minut na przygtwanie zarysu dpwiedzi. Na dpwiedź ustną masz 10 minut. Swje rzwiązania prezentujesz
Prblemy i zadania na egzamin ustny dla klasy 3B: Zasady: Lsujesz dwa z pniżej zamieszcznych zadań. Masz 5 minut na przygtwanie zarysu dpwiedzi. Na dpwiedź ustną masz 10 minut. Swje rzwiązania prezentujesz
ZJAWISKO TERMOEMISJI ELEKTRONÓW
 ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
Laboratorium Wirtualne Obwodów w Stanach Ustalonych i Nieustalonych
 ĆWICZENIE 1 Badanie obwodów jednofazowych rozgałęzionych przy wymuszeniu sinusoidalnym Cel ćwiczenia Celem ćwiczenia jest Poznanie podstawowych elementów pasywnych R, L, C, wyznaczenie ich wartości na
ĆWICZENIE 1 Badanie obwodów jednofazowych rozgałęzionych przy wymuszeniu sinusoidalnym Cel ćwiczenia Celem ćwiczenia jest Poznanie podstawowych elementów pasywnych R, L, C, wyznaczenie ich wartości na
5. Rezonans napięć i prądów
 ezonans napęć prądów W-9 el ćwczena: 5 ezonans napęć prądów Dr hab nŝ Dorota Nowak-Woźny Wyznaczene krzywej rezonansowej dla szeregowego równoległego obwodu Zagadnena: Fzyczne podstawy zjawska rezonansu
ezonans napęć prądów W-9 el ćwczena: 5 ezonans napęć prądów Dr hab nŝ Dorota Nowak-Woźny Wyznaczene krzywej rezonansowej dla szeregowego równoległego obwodu Zagadnena: Fzyczne podstawy zjawska rezonansu
Laboratorium elektroniki i miernictwa
 Ełk 24-03-2007 Wyższa Szkła Finansów i Zarządzania w Białymstku Filia w Ełku Wydział Nauk Technicznych Kierunek : Infrmatyka Ćwiczenie Nr 3 Labratrium elektrniki i miernictwa Temat: Badanie pdstawwych
Ełk 24-03-2007 Wyższa Szkła Finansów i Zarządzania w Białymstku Filia w Ełku Wydział Nauk Technicznych Kierunek : Infrmatyka Ćwiczenie Nr 3 Labratrium elektrniki i miernictwa Temat: Badanie pdstawwych
XXX OLIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne
 XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
Pomiar mocy i energii
 Zakład Napędów Weloźródłowych Instytut Maszyn Roboczych CęŜkch PW Laboratorum Elektrotechnk Elektronk Ćwczene P3 - protokół Pomar mocy energ Data wykonana ćwczena... Zespół wykonujący ćwczene: Nazwsko
Zakład Napędów Weloźródłowych Instytut Maszyn Roboczych CęŜkch PW Laboratorum Elektrotechnk Elektronk Ćwczene P3 - protokół Pomar mocy energ Data wykonana ćwczena... Zespół wykonujący ćwczene: Nazwsko
14. OBWODY LINIOWE POBUDZONE SYGNAŁEM ODKSZTAŁCONYM
 OBWODY I SYGNŁY Wyład : Obwody lnowe pobudzone sygnałe odszałcony. OBWODY LINIOWE POBDZONE SYGNŁEM ODKSZŁCONYM PRZYPOMNIENIE ) Funcja wyładncza pełn wyjąową rolę, poneważ: ażdy sygnał wysępujący w prayce
OBWODY I SYGNŁY Wyład : Obwody lnowe pobudzone sygnałe odszałcony. OBWODY LINIOWE POBDZONE SYGNŁEM ODKSZŁCONYM PRZYPOMNIENIE ) Funcja wyładncza pełn wyjąową rolę, poneważ: ażdy sygnał wysępujący w prayce
Zaliczenie wykładu Technika Analogowa Przykładowe pytania (czas zaliczenia minut, liczba pytań 6 8)
 Zaliczenie wyładu Technia Analogowa Przyładowe pytania (czas zaliczenia 3 4 minut, liczba pytań 6 8) Postulaty i podstawowe wzory teorii obowdów 1 Sformułuj pierwsze i drugie prawo Kirchhoffa Wyjaśnij
Zaliczenie wyładu Technia Analogowa Przyładowe pytania (czas zaliczenia 3 4 minut, liczba pytań 6 8) Postulaty i podstawowe wzory teorii obowdów 1 Sformułuj pierwsze i drugie prawo Kirchhoffa Wyjaśnij
WYKŁAD 1 ZASADY ELEKTROMECHANICZNEGO PRZETWARZANIA ENERGII
 WYKŁAD 1 ZASADY ELEKTROMECHANICZNEGO PRZETWARZANIA ENERGII 1.1. Zasada zachowania energii. Puntem wyjściowym dla analizy przetwarzania energii i mocy w pewnym przedziale czasu t jest zasada zachowania
WYKŁAD 1 ZASADY ELEKTROMECHANICZNEGO PRZETWARZANIA ENERGII 1.1. Zasada zachowania energii. Puntem wyjściowym dla analizy przetwarzania energii i mocy w pewnym przedziale czasu t jest zasada zachowania
Pracownia Technik Pomiarowych dla Astronomów 2009
 http://pe.fw.ed.pl Pracowna Technk Pomaroch dla Astronomów 009 http://pe.fw.ed.pl/ Wojcech DOMNK Pracowna technk pomaroch dla astronomów 009. Plan zajęć Pracown przewdje 5 ćwczeń. Wykład stanow ntegralną
http://pe.fw.ed.pl Pracowna Technk Pomaroch dla Astronomów 009 http://pe.fw.ed.pl/ Wojcech DOMNK Pracowna technk pomaroch dla astronomów 009. Plan zajęć Pracown przewdje 5 ćwczeń. Wykład stanow ntegralną
4. STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO
 A. Kanck: Systemy elektrenergetyczne 6 4. STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO 4.. Wprwadzene Stablnść lkalna systemu elektrenergetyczneg (SE) t stablnść jeg pracy pdczas małych zakłóceń. D
A. Kanck: Systemy elektrenergetyczne 6 4. STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO 4.. Wprwadzene Stablnść lkalna systemu elektrenergetyczneg (SE) t stablnść jeg pracy pdczas małych zakłóceń. D
PSO matematyka I gimnazjum Szczegółowe wymagania edukacyjne na poszczególne oceny
 PSO matematyka I gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOM WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca spsób zakrąglania liczb klejnść wyknywania działań pjęcie liczb
PSO matematyka I gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOM WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca spsób zakrąglania liczb klejnść wyknywania działań pjęcie liczb
exp jest proporcjonalne do czynnika Boltzmanna exp(-e kbt (szerokość przerwy energetycznej między pasmami) g /k B
 Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
Geodezyjne metody wyznaczania przemieszczeń i odkształceń obudowy szybów w ZG Polkowice-Sieroszowice
 WARSZTATY nt. Zagrżena naturalne w górnctwe Meczysław JÓŹWIK Akadema Górncz-Hutncza, Kraków Mat. Symp. Warsztaty str. 55-65 Gedezyjne metdy wyznaczana przemeszczeń dkształceń budwy szybów w ZG Plkwce-Serszwce
WARSZTATY nt. Zagrżena naturalne w górnctwe Meczysław JÓŹWIK Akadema Górncz-Hutncza, Kraków Mat. Symp. Warsztaty str. 55-65 Gedezyjne metdy wyznaczana przemeszczeń dkształceń budwy szybów w ZG Plkwce-Serszwce
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
Diagonalizacja macierzy kwadratowej
 Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
Systemy liniowe i stacjonarne
 Systemy liniowe i stacjonarne Układ (np.: dwójnik) jest liniowy wtedy i tylko wtedy gdy: Spełnia własność skalowania (jednorodność): T [a x (t )]=a T [ x (t)]=a y (t ) Jeśli wymuszenie zostanie przeskalowane
Systemy liniowe i stacjonarne Układ (np.: dwójnik) jest liniowy wtedy i tylko wtedy gdy: Spełnia własność skalowania (jednorodność): T [a x (t )]=a T [ x (t)]=a y (t ) Jeśli wymuszenie zostanie przeskalowane
Zad.03. Wyznaczyć połączenie rur walcowo-stożkowych. Należy połączyć dwa rurociągi walcowe o osiach przecinających się, równoległych do rzutni.
 POLITECHNIK POLITECHNIK BIŁOSTOCK - Studa stacjnarne - Inżynera Ochrna Śrdwska Rysunek technczny, Gemetra wykreślna grafka nżynerska - ćwczene nr 06 Zad.0. Wyznaczyć płączene rur walcw-stżkwych. Należy
POLITECHNIK POLITECHNIK BIŁOSTOCK - Studa stacjnarne - Inżynera Ochrna Śrdwska Rysunek technczny, Gemetra wykreślna grafka nżynerska - ćwczene nr 06 Zad.0. Wyznaczyć płączene rur walcw-stżkwych. Należy
Indukcja matematyczna
 Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Siła elektromotoryczna
 Wykład 5 Siła elektromotoryczna Urządzenie, które wykonuje pracę nad nośnikami ładunku ale różnica potencjałów między jego końcami pozostaje stała, nazywa się źródłem siły elektromotorycznej. Energia zamieniana
Wykład 5 Siła elektromotoryczna Urządzenie, które wykonuje pracę nad nośnikami ładunku ale różnica potencjałów między jego końcami pozostaje stała, nazywa się źródłem siły elektromotorycznej. Energia zamieniana
Podstawy Teorii Obwodów
 Podstawy Teorii Obwodów 203 Model obwodowy... 2 Klasyfikacjaobwodów.... 3 Założenia.... 4 Opis obwodów...... 5 Topologiaobwodu........ 6 Rodzaje elementówobwodów.... 7 Konwencje oznaczeńelementówobwodów....
Podstawy Teorii Obwodów 203 Model obwodowy... 2 Klasyfikacjaobwodów.... 3 Założenia.... 4 Opis obwodów...... 5 Topologiaobwodu........ 6 Rodzaje elementówobwodów.... 7 Konwencje oznaczeńelementówobwodów....
Modelowanie przekładni i sprzęgieł
 Jakub Wercak delwane przekładn sprzęgeł Człwek- najlepsza nwestycja Prjekt współfnanswany przez Unę Eurpejską w ramach Eurpejskeg Funduszu Spłeczneg delwane przekładn sprzęgeł del funkcjnalny elektryczneg
Jakub Wercak delwane przekładn sprzęgeł Człwek- najlepsza nwestycja Prjekt współfnanswany przez Unę Eurpejską w ramach Eurpejskeg Funduszu Spłeczneg delwane przekładn sprzęgeł del funkcjnalny elektryczneg
Laboratorium Podstaw Metrologii
 WOCŁAW Wrocław, dnia Laboratorium odstaw Metroogii Ćwiczenie o i ierune studiów... Grupa (dzień tygodnia i godzina rozpoczęcia zajęć) Imię i nazwiso Imię i nazwiso Imię i nazwiso rzetwornii Badanie właściwości
WOCŁAW Wrocław, dnia Laboratorium odstaw Metroogii Ćwiczenie o i ierune studiów... Grupa (dzień tygodnia i godzina rozpoczęcia zajęć) Imię i nazwiso Imię i nazwiso Imię i nazwiso rzetwornii Badanie właściwości
Układ wielofazowy i układ trójfazowy
 7. Rzwiązywani bwdów prądu sinusidalng 43 Wyład XV. PODTWOWE TRKTR OWODÓW TRÓJFOWH ład wilfazwy i uład trójfazwy Trminm uład wilfazwy rśla się zbiór w liczbi dwa lub więszj taich, związanych z sbą struturalni
7. Rzwiązywani bwdów prądu sinusidalng 43 Wyład XV. PODTWOWE TRKTR OWODÓW TRÓJFOWH ład wilfazwy i uład trójfazwy Trminm uład wilfazwy rśla się zbiór w liczbi dwa lub więszj taich, związanych z sbą struturalni
DWUCZĘ STOTLIWOŚ CIOWY Ż YROSKOP LASEROWY POMIAR PARAMETRU NAWIGACYJNEGO
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK XLVII NR (64) 006 Tadeuz Dą brwi DWUCZĘ STOTLIWOŚ CIOWY Ż YROSKOP LASEROWY POMIAR PARAMETRU NAWIGACYJNEGO STRESZCZENIE W artyule przedtawin budwę, zaady
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK XLVII NR (64) 006 Tadeuz Dą brwi DWUCZĘ STOTLIWOŚ CIOWY Ż YROSKOP LASEROWY POMIAR PARAMETRU NAWIGACYJNEGO STRESZCZENIE W artyule przedtawin budwę, zaady
Partner projektu F5 Konsulting Sp. z o.o. ul. Składowa 5, 61-897 Poznań T: 061 856 69 60 F: 061 853 02 95
 Plan Kmunikacji na temat prjektu samceny , 2010 Partner prjektu F5 Knsulting Sp. z.. ul. Składwa 5, 61-897 Pznań T: 061 856 69 60 F: 061 853 02 95 SPIS TREŚCI: WPROWADZENIE...
Plan Kmunikacji na temat prjektu samceny , 2010 Partner prjektu F5 Knsulting Sp. z.. ul. Składwa 5, 61-897 Pznań T: 061 856 69 60 F: 061 853 02 95 SPIS TREŚCI: WPROWADZENIE...
8. ELEMENTY RZECZYWISTE W OBWODACH PRĄDU ZMIENNEGO Cewka indukcyjna rzeczywista - gałąź szeregowa RL
 8. ELEMENTY ZECZYWISTE W OBWODACH PĄDU ZMIENNEO Poznane przez nas idealne elementy obwodów elektrycznych są wyidealizowanymi, uproszczonymi odwzorowaniami obiektów rzeczywistych. Prostota ich matematycznego
8. ELEMENTY ZECZYWISTE W OBWODACH PĄDU ZMIENNEO Poznane przez nas idealne elementy obwodów elektrycznych są wyidealizowanymi, uproszczonymi odwzorowaniami obiektów rzeczywistych. Prostota ich matematycznego
ELEKTROCHEMIA. ( i = i ) Wykład II b. Nadnapięcie Równanie Buttlera-Volmera Równania Tafela. Wykład II. Równowaga dynamiczna i prąd wymiany
 Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
Wielkości opisujące sygnały okresowe. Sygnał sinusoidalny. Metoda symboliczna (dla obwodów AC) - wprowadzenie. prąd elektryczny
 prąd stały (DC) prąd elektryczny zmienny okresowo prąd zmienny (AC) zmienny bezokresowo Wielkości opisujące sygnały okresowe Wartość chwilowa wartość, jaką sygnał przyjmuje w danej chwili: x x(t) Wartość
prąd stały (DC) prąd elektryczny zmienny okresowo prąd zmienny (AC) zmienny bezokresowo Wielkości opisujące sygnały okresowe Wartość chwilowa wartość, jaką sygnał przyjmuje w danej chwili: x x(t) Wartość
R w =
 Laboratorium Eletrotechnii i eletronii LABORATORM 6 Temat ćwiczenia: BADANE ZASLACZY ELEKTRONCZNYCH - pomiary w obwodach prądu stałego Wyznaczanie charaterysty prądowo-napięciowych i charaterysty mocy.
Laboratorium Eletrotechnii i eletronii LABORATORM 6 Temat ćwiczenia: BADANE ZASLACZY ELEKTRONCZNYCH - pomiary w obwodach prądu stałego Wyznaczanie charaterysty prądowo-napięciowych i charaterysty mocy.
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE CZŁONÓW AUTOMATYKI. Cześć doświadczalna Zarejestrować charakterystykę amplitudowo-fazową zadanego czwórnika.
 Ćw 3 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE CZŁONÓW AUTOMATYKI Cel ćwiczenia Celem ćwiczenia jest zapznanie się z pjęciem charakterystyki częsttliwściwej, praktycznym spsbem jej rejestracji raz wykrzystaniem
Ćw 3 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE CZŁONÓW AUTOMATYKI Cel ćwiczenia Celem ćwiczenia jest zapznanie się z pjęciem charakterystyki częsttliwściwej, praktycznym spsbem jej rejestracji raz wykrzystaniem
f = 2 śr MODULACJE
 5. MODULACJE 5.1. Wstęp Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej. Przyczyny stosowania modulacji: 1. Umożliwienie wydajnego wypromieniowania
5. MODULACJE 5.1. Wstęp Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej. Przyczyny stosowania modulacji: 1. Umożliwienie wydajnego wypromieniowania
Prąd sinusoidalny. najogólniejszy prąd sinusoidalny ma postać. gdzie: wartości i(t) zmieniają się w czasie sinusoidalnie
 Opracował: mgr nż. Marcn Weczorek www.marwe.ne.pl Prąd snsodalny najogólnejszy prąd snsodalny ma posać ( ) m sn(2π α) gdze: warość chwlowa, m warość maksymalna (amplda), T okres, α ką fazowy. T m α m T
Opracował: mgr nż. Marcn Weczorek www.marwe.ne.pl Prąd snsodalny najogólnejszy prąd snsodalny ma posać ( ) m sn(2π α) gdze: warość chwlowa, m warość maksymalna (amplda), T okres, α ką fazowy. T m α m T
9. METODY SIECIOWE (ALGORYTMICZNE) ANALIZY OBWODÓW LINIOWYCH
 OBWOD SGNAŁ 9. METOD SECOWE (ALGORTMCZNE) ANALZ OBWODÓW LNOWCH 9.. WPROWADZENE ANALZA OBWODÓW Jeżeli przy badaniu obwodu elektrycznego dane są parametry elementów i schemat obwodu, a poszukiwane są napięcia
OBWOD SGNAŁ 9. METOD SECOWE (ALGORTMCZNE) ANALZ OBWODÓW LNOWCH 9.. WPROWADZENE ANALZA OBWODÓW Jeżeli przy badaniu obwodu elektrycznego dane są parametry elementów i schemat obwodu, a poszukiwane są napięcia
Przykłady sieci stwierdzeń przeznaczonych do wspomagania początkowej fazy procesu projektow ania układów napędowych
 Rzdział 12 Przykłady sieci stwierdzeń przeznacznych d wspmagania pczątkwej fazy prcesu prjektw ania układów napędwych Sebastian RZYDZIK W rzdziale przedstawin zastswanie sieci stwierdzeń d wspmagania prjektwania
Rzdział 12 Przykłady sieci stwierdzeń przeznacznych d wspmagania pczątkwej fazy prcesu prjektw ania układów napędwych Sebastian RZYDZIK W rzdziale przedstawin zastswanie sieci stwierdzeń d wspmagania prjektwania
Charakterystyki częstotliwościowe elementów pasywnych
 Charakterystyki częstotliwościowe elementów pasywnych Parametry elementów pasywnych; reaktancji indukcyjnej (XLωL) oraz pojemnościowej (XC1/ωC) zależą od częstotliwości. Ma to istotne znaczenie w wielu
Charakterystyki częstotliwościowe elementów pasywnych Parametry elementów pasywnych; reaktancji indukcyjnej (XLωL) oraz pojemnościowej (XC1/ωC) zależą od częstotliwości. Ma to istotne znaczenie w wielu
Wykres indykatorowy Kąt obrotu wału korbowego [stopnie OWK]
![Wykres indykatorowy Kąt obrotu wału korbowego [stopnie OWK] Wykres indykatorowy Kąt obrotu wału korbowego [stopnie OWK]](/thumbs/60/44863687.jpg) Cśnene w cylndrze Cśnene w cylndrze Wyres ndyatorowy 1/10 9. WYKRES PRACY SINIKA SPAINOWEGO Rzeczywsty wyres pracy slna spalnowego nazywany wyresem ndyatorowym przedstawa przebeg bezwzględnego cśnena w
Cśnene w cylndrze Cśnene w cylndrze Wyres ndyatorowy 1/10 9. WYKRES PRACY SINIKA SPAINOWEGO Rzeczywsty wyres pracy slna spalnowego nazywany wyresem ndyatorowym przedstawa przebeg bezwzględnego cśnena w
W2. PRZEKSZTAŁTNIKI SIECIOWE 1 ( AC/DC; AC/AC)
 W. PRZEKSZTAŁTNIKI SIECIOWE 1 ( AC/DC; AC/AC) Ta wielka grupa swą nazwę wywzi z teg, że łączne bezpśreni sieci lub systemu energetyczneg napięciu przemiennym 50/60 Hz i w minującej liczbie przypaków służy
W. PRZEKSZTAŁTNIKI SIECIOWE 1 ( AC/DC; AC/AC) Ta wielka grupa swą nazwę wywzi z teg, że łączne bezpśreni sieci lub systemu energetyczneg napięciu przemiennym 50/60 Hz i w minującej liczbie przypaków służy
Podstawy Elektrotechniki i Elektroniki. Opracował: Mgr inż. Marek Staude
 Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 1 Podstawowe prawa obwodów elektrycznych Prąd elektryczny definicja fizyczna Prąd elektryczny powstaje jako uporządkowany ruch
Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 1 Podstawowe prawa obwodów elektrycznych Prąd elektryczny definicja fizyczna Prąd elektryczny powstaje jako uporządkowany ruch
p Z(G). (G : Z({x i })),
 3. Wykład 3: p-grupy twerdzena Sylowa. Defncja 3.1. Nech (G, ) będze grupą. Grupę G nazywamy p-grupą, jeżel G = dla pewnej lczby perwszej p oraz k N. Twerdzene 3.1. Nech (G, ) będze p-grupą. Wówczas W
3. Wykład 3: p-grupy twerdzena Sylowa. Defncja 3.1. Nech (G, ) będze grupą. Grupę G nazywamy p-grupą, jeżel G = dla pewnej lczby perwszej p oraz k N. Twerdzene 3.1. Nech (G, ) będze p-grupą. Wówczas W
T R Y G O N O M E T R I A
 T R Y G O N O M E T R I A Lekcja 8-9 Temat: Pwtórzenie trójkąty prstkątne. Str. 56-57. Teria Twierdzenie Pitagrasa i dwrtne Suma kątów w trójkącie Wyskść Obwód i ple Zad.,,,, 5, 6 str. 56 Zad. 7, 8, 9,
T R Y G O N O M E T R I A Lekcja 8-9 Temat: Pwtórzenie trójkąty prstkątne. Str. 56-57. Teria Twierdzenie Pitagrasa i dwrtne Suma kątów w trójkącie Wyskść Obwód i ple Zad.,,,, 5, 6 str. 56 Zad. 7, 8, 9,
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
Ćwiczenie nr 4. Badanie filtrów składowych symetrycznych prądu i napięcia
 Ćwiczenie nr 4 Badanie filtrów składowych symetrycznych prądu i napięcia 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą składowych symetrycznych, pomiarem składowych w układach praktycznych
Ćwiczenie nr 4 Badanie filtrów składowych symetrycznych prądu i napięcia 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą składowych symetrycznych, pomiarem składowych w układach praktycznych
Induktor i kondensator. Warunki początkowe. oraz ciągłość warunków początkowych
 Termin AREK73C Induktor i kondensator. Warunki początkowe Przyjmujemy t, u C oraz ciągłość warunków początkowych ( ) u ( ) i ( ) i ( ) C L L Prąd stały i(t) R u(t) u( t) Ri( t) I R RI i(t) L u(t) u() t
Termin AREK73C Induktor i kondensator. Warunki początkowe Przyjmujemy t, u C oraz ciągłość warunków początkowych ( ) u ( ) i ( ) i ( ) C L L Prąd stały i(t) R u(t) u( t) Ri( t) I R RI i(t) L u(t) u() t
± Δ. Podstawowe pojęcia procesu pomiarowego. x rzeczywiste. Określenie jakości poznania rzeczywistości
 Podstawowe pojęca procesu pomarowego kreślene jakośc poznana rzeczywstośc Δ zmerzone rzeczywste 17 9 Zalety stosowana elektrycznych przyrządów 1/ 1. możlwość budowy czujnków zamenających werne każdą welkość
Podstawowe pojęca procesu pomarowego kreślene jakośc poznana rzeczywstośc Δ zmerzone rzeczywste 17 9 Zalety stosowana elektrycznych przyrządów 1/ 1. możlwość budowy czujnków zamenających werne każdą welkość
PLAN WYNIKOWY ROZKŁADU MATERIAŁU Z FIZYKI DLA KLASY III MODUŁ 4 Dział: X,XI - Fale elektromagnetyczne, optyka, elementy fizyki atomu i kosmologii.
 Knteksty 1. Fale elektrmagnetyczne w telekmunikacji. 2.Światł i jeg właściwści. - c t jest fala elektrmagnetyczna - jakie są rdzaje fal - elektrmagnetycznych - jakie jest zastswanie fal elektrmagnetycznych
Knteksty 1. Fale elektrmagnetyczne w telekmunikacji. 2.Światł i jeg właściwści. - c t jest fala elektrmagnetyczna - jakie są rdzaje fal - elektrmagnetycznych - jakie jest zastswanie fal elektrmagnetycznych
przez odwołanie się do funkcji programu MATLAB. Macierz A = Z
 PRYKŁAD 4.7 Oblczyć parametry ln z Przyład 4.1 dla sładowych azowych alnych, załadając, że jest to lna netransponowana. Oblczena wyonać za pomocą procedry LINE CONSANS dostępnej w programe AP-EMP. Przerój
PRYKŁAD 4.7 Oblczyć parametry ln z Przyład 4.1 dla sładowych azowych alnych, załadając, że jest to lna netransponowana. Oblczena wyonać za pomocą procedry LINE CONSANS dostępnej w programe AP-EMP. Przerój
Pomiary bezpośrednie i pośrednie obarczone błędem przypadkowym
 Pomary bezpośrede pośrede obarczoe błędem przypadkowym I. Szacowae wartośc przyblŝoej graczego błędu przypadkowego a przykładze bezpośredego pomaru apęca elem ćwczea jest oszacowae wartośc przyblŝoej graczego
Pomary bezpośrede pośrede obarczoe błędem przypadkowym I. Szacowae wartośc przyblŝoej graczego błędu przypadkowego a przykładze bezpośredego pomaru apęca elem ćwczea jest oszacowae wartośc przyblŝoej graczego
Ile wynosi suma miar kątów wewnętrznych w pięciokącie?
 1 Ile wynos suma mar kątów wewnętrznych w pęcokące? 1 Narysuj pęcokąt foremny 2 Połącz środek okręgu opsanego na tym pęcokące ze wszystkm werzchołkam pęcokąta 3 Oblcz kąty każdego z otrzymanych trójkątów
1 Ile wynos suma mar kątów wewnętrznych w pęcokące? 1 Narysuj pęcokąt foremny 2 Połącz środek okręgu opsanego na tym pęcokące ze wszystkm werzchołkam pęcokąta 3 Oblcz kąty każdego z otrzymanych trójkątów
Stanisław Jemioło, Marcin Gajewski Instytut Mechaniki Konstrukcji Inżynierskich
 Stanisław Jemił, Marcin Gajewsi Instytut Mechanii Knstrucji Inżyniersich SYMULACJA MES OBRÓBKI CIEPLNEJ WYROBÓW STALOWYCH Z UWZGLĘDNIENIEM ZJAWISK TERMO-METALURGICZNYCH Część 1. Nieustalny przepływ ciepła
Stanisław Jemił, Marcin Gajewsi Instytut Mechanii Knstrucji Inżyniersich SYMULACJA MES OBRÓBKI CIEPLNEJ WYROBÓW STALOWYCH Z UWZGLĘDNIENIEM ZJAWISK TERMO-METALURGICZNYCH Część 1. Nieustalny przepływ ciepła
Pracownia fizyczna i elektroniczna. Wykład lutego Krzysztof Korona
 Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 4 lutego 4 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa. Prawo Ohma ().4 Przykłady prostych
Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 4 lutego 4 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa. Prawo Ohma ().4 Przykłady prostych
AMD. Laboratorium Elektrotechniki i Elektroniki Katedra Elektrotechniki i Elektroenergetyki. Andrzej Dąbrowski
 Laboratorium letrotechnii i letronii Katedra letrotechnii i letroenergetyi NFORMCJ WSĘPN abela nagłówowa sprawozdania Opracowanie sprawozdania Harmonogram ćwiczeń Spis tematów ćwiczeń laboratoryjnych ndrzej
Laboratorium letrotechnii i letronii Katedra letrotechnii i letroenergetyi NFORMCJ WSĘPN abela nagłówowa sprawozdania Opracowanie sprawozdania Harmonogram ćwiczeń Spis tematów ćwiczeń laboratoryjnych ndrzej
 Ź Ż Ż Ź Ó Ść Ś Ó Ż Ż ć ć Ś Ż Ź Ś Ś ć Ó Ą Ź Ż Ą ć Ź Ź Ż Ś Ż ć Ś Ź Ś Ż Ż ć ć Ś Ś Ż Ó Ś Ę ć ć Ś Ż Ż Ż ć ć ć Ź Ź Ś Ę Ź Ź ć Ś ć Ś Ż ć Ć Ż Ść Ź Ź Ś Ść Ż Ź Ź Ś Ś Ż Ł ć Ś Ź Ó ć Ź Ś Ż Ś Ą Ś ź Ź ć ć Ś Ś Ą ć Ż Ż
Ź Ż Ż Ź Ó Ść Ś Ó Ż Ż ć ć Ś Ż Ź Ś Ś ć Ó Ą Ź Ż Ą ć Ź Ź Ż Ś Ż ć Ś Ź Ś Ż Ż ć ć Ś Ś Ż Ó Ś Ę ć ć Ś Ż Ż Ż ć ć ć Ź Ź Ś Ę Ź Ź ć Ś ć Ś Ż ć Ć Ż Ść Ź Ź Ś Ść Ż Ź Ź Ś Ś Ż Ł ć Ś Ź Ó ć Ź Ś Ż Ś Ą Ś ź Ź ć ć Ś Ś Ą ć Ż Ż
Adres strony internetowej, na której Zamawiający udostępnia Specyfikację Istotnych Warunków Zamówienia: www.zsp2.edu.pl
 Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.zsp2.edu.pl Brzesk: Dstawa wypsażenia pracwni elektrtechniki i elektrniki - część II - aparatura
Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.zsp2.edu.pl Brzesk: Dstawa wypsażenia pracwni elektrtechniki i elektrniki - część II - aparatura
Prąd elektryczny U R I =
 Prąd elektryczny porządkowany ruch ładunków elektrycznych (nośnków prądu). Do scharakteryzowana welkośc prądu służy natężene prądu określające welkość ładunku przepływającego przez poprzeczny przekrój
Prąd elektryczny porządkowany ruch ładunków elektrycznych (nośnków prądu). Do scharakteryzowana welkośc prądu służy natężene prądu określające welkość ładunku przepływającego przez poprzeczny przekrój
Statystyka - wprowadzenie
 Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią
Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią

