E-20A POMIAR MOCY PRĄDU ZMIENNEGO METODĄ OSCYLO- SKOPOWĄ
|
|
|
- Jakub Maksymilian Podgórski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Ćwiczenie E-A POMIA MOY PĄDU ZMIENNEGO MEODĄ OSYO- SKOPOWĄ I. el ćwiczenia: Pmiar mcy prądu zmienneg za pmcą scylskpu, pmiar różnicy faz scylskpem, cena dkładnści metdy. II. Przyrządy: Oscylskp, nieznana pjemnść i indukcyjnść, prnik dekadwy, kndensatr dekadwy, prnik, generatr mcy lub auttransfrmatr, transfrmatr, wltmierz. III. iteratura: [] W. ydzewski Oscylskp elektrniczny [].P. Feynman Feynmana wykłady z fizyki tm I część rzdz., tm II część rzdz.. [3] E.M. Purcell Elektrycznść i magnetyzm rzdz. 8. IV. Wstęp Źródł zmiennej w czasie SEM jest płączne pprzez zaciski i z dbirnikiem energii impedancji (prnści zesplnej) Z (rys.) (kreska pzima pd symblem impedancji czyli pd literą Z znacza liczbę zesplną). ŹÓDŁO SEM E, Z w I(t) U(t) P(t) ODBIONIK ENEGII Z ys. Elementarną pracę źródła SEM równą energii dstarcznej dbirnikwi przedstawić mżemy w pstaci: dw = E I dt jeśli impedancja wewnętrzna źródła jest d zaniedbania tj., gdy ciągu jedneg kresu równa się sumie prac elementarnych czyli W = EIdt a średnia mc P= EIdt Z w «Z. Praca wyknana w zważmy przypadek SEM sinusidalnie zmiennej w czasie i prądu późnineg w stsunku d SEM kąt przesunięcia fazweg φ wówczas: E = E cs ωt I = I cs(ωt φ)
2 Ćwiczenie E-A daje Pnieważ t EI E I P= csωt cs( ωt -ϕ)dt= [csω t+ cs(ωt -ϕ)]dt cs(ωt - ϕ)dt= EI P= cs φ () lub wprwadzając pjęcie wartści skutecznej I s, zdefiniwanej dla natężenia prądu jak trzymujemy gdzie I s = I s = I [I(t)] dt=, I P= E I s s cs φ () E s = E W przypadku, kiedy jest spełniny warunek Z w «Z wzry () i () zastępujemy wzrami : UI P= cs φ (3) lub P= U I s s cs φ (4) gdzie U jest amplitudą, a U s wartścią skuteczną napięcia mierzneg na zaciskach, dbirnika energii (rys.). Średnia mc P bywa nazywana mcą czynną w przeciwieństwie d tzw. mcy biernej P b = U I sin φ = Us I s sin φ raz mdułu mcy zesplnej zwanej mcą pzrną P p = U s I s V. Wyznaczanie mcy średniej z charakterystyki prądw napięciwej układu: źródł SEM dbirnik energii. harakterystyką prądw napięciwą daneg układu nazywamy funkcję I = f(u), pisującą zależnść natężenia prądu płynąceg przez ten układ d przyłżneg napięcia. harakterystykę taką w najprstszym przypadku wyznaczyć mżemy za pmcą ampermierza i wltmierza dużej prnści wewnętrznej łącząc przyrządy według schematu przedstawineg na rys..
3 Ćwiczenie E-A ŹÓDŁO SEM A V ODBIONIK ENEGII ys. Układ taki służyć mże d pmiaru mcy pzrnej P p = U s I s. Jeżeli w układzie tym zastąpimy ba mierniki scylskpem, t zamiast uśredninej p czasie charakterystyki prądwnapięciwej uzyskamy pełną infrmację łącznie z wartścią kąta przesunięcia fazweg (rys.3). I(t) = I cs(ωt + φ), U(t) = U cs ωt ŹÓDŁO SEM I(t) x «Z U(t) ODBIONIK ENEGII Z WeY = WeX = ys. 3 Zdejmwanie charakterystyki prądw - napięciwej układu źródł - dbirnik za pmcą scylskpu XY. Napięcie na zaciskach dbirnika jest wówczas mierzne bezpśredni, natmiast natężenie prądu płynąceg przez dbirnik znajdujemy znając wartści prnści x i spadek ptencjału U x = x I. Pnieważ wiązka elektrnów w lampie scylskpwej jest sterwana prstpadłymi d siebie plami elektrycznymi takiej samej częstści ale różnych kątach fazwych, t na ekranie pwinniśmy w gólnym przypadku uzyskać braz elipsy, z której parametrów mżemy bliczyć wartść kąta fazweg (rys.4 raz przypis). 3
4 Ćwiczenie E-A Y Y β a Y b X X α X a) b) sin φ = b a lub αβ sin φ = XY ys.4 Obliczanie kąta przesunięcia fazweg z parametrów brazu elipsy. Mc średnią bliczamy ze wzru: X sxy sy X sxy s P= csϕ = 8 8 x x y a b gdzie X, Y, szerkść i wyskść brazu elipsy [cm], s x, s y współczynnik dchylania pzimeg i pinweg scylskpu [V/cm], x prnść prnika szeregweg [Ω]. VI. Pmiary VI. Ocena dkładnści metdy wyznaczania kąta przesunięcia fazweg. Płączyć przyrządy według schematu przedstawineg na rys.5a (wariant A) lub na rys.5b (wariant B).. Wybrać wstępnie wartści = Ω i = µf raz ustalić napięcie zasilania bwdu na 3 V przy częstści (dla wersji z generatrem) Hz. Kąt przesunięcia fazweg φ prądu względem napięcia w bwdzie przedstawinym na rys.5 jest funkcją ilczynu wartści i tj. τ = (dla 75 Ω) i częstści kłwej (pulsacji) ω = πf: tg φ = ω = = (6) ωτ πfτ gdzie f jest częstścią, a τ nsi nazwę stałej czaswej. (5) 4
5 Ćwiczenie E-A scylskp ~ PO- 75Ω»75Ω A WeY = WeX = a) Auttransfrmatr»75Ω WeY = scylskp ~ V 75Ω WeX = V/4V lub /6V b) ys.5 Pmiar przesunięcia fazweg. Generatr nie mże mieć budwy uzieminej ani wyzerwanej (tj. nie mże być zasilany z gniazdka sieciweg z blcem zerującym). Obwód mże być zasilany tylk takim napięciem, dla któreg natężenie prądu płynąceg w bwdzie nie przekracza wartści dpuszczalnej, pdanej na budwie prnika dekadweg.. Wyknać kilka kilkanaście pmiarów kąta φ dla różnych wartści stałej czasu τ tak, aby wartść φ zmieniła się w przedziale d zera (braz linii prstej nachylnej d si X na ekranie scylskpu) d π/ (w gólnym przypadku braz elipsy, której siami symetrii są sie pzima X i pinwa Y). Dla układu z rys.5 granice teg przedziału są niedmknięte z bu strn.. Wyniki przedstawić na jednym rysunku w pstaci wykresu zależnści φ = f(τ), blicznej ze wzru (6) i wykresu zależnści dświadczalnej z uwzględnieniem błędów. Gdy bwód zasilany jest transfrmatrem, t istnieje prawdpdbieństw, że braz elipsy bserwwany na ekranie scylskpu będzie zniekształcny. Zniekształcenia takie mgą być pwdwane nasyceniem się rdzenia transfrmatra przy zbyt niskim napięciu w stsunku d napięcia zasilania. Zniekształcenie takie mżna wyeliminwać zmieniając tak napięcie wyjściwe auttransfrmatra, aby nie dchdził d nasycenia rdzenia. UWAGA! Najdgdniej jest zasilać zarówn generatr, jak i scylskp z gniazdek sieciwych pzbawinych blca zerująceg. Obudów bu przyrządów nie uziemiać, a punkt A (zaznaczny na rys.5a) płączyć z budwą (masą) scylskpu. 5
6 Ćwiczenie E-A VI. Pmiar mcy średniej Wariant A Odbirnik energii zasilany z generatra mcy. Płączyć przyrządy według schematu przedstawineg na rys.3, gdzie źródłem SEM jest generatr mcy nieuzieminej i niezerwanej budwie, a dbirnikiem energii jeden z pniżej przedstawinych układów (w przypadku uziemienia budwy generatra dlne z gniazd wyjściwych generatra znajduje się na ptencjale ziemi): a) b) c) d) ys.6. Wyznaczyć średnią mc przekazywaną dbirnikwi w pstaci szeregw płącznej z pjemnścią indukcyjnści (rys.6a) przy napięciu wyjściwym generatra 7 V (zakres 7,75 V, 6 Ω) i częstści 4, 43, 46, 5,, 5 i Hz.. Pwtórzyć pmiary dla pzstałych dbirników przy częstściach 5,, 5 i Hz. 3. Wyniki przedstawić w pstaci wykresu zależnści mcy średniej, przesunięcia fazweg i mdułu mcy zesplnej d częstści. 4. Oszacwać błąd i przeprwadzić dyskusję wyników. Wariant B Odbirnik energii zasilany z transfrmatra. Dla kilku wartści napięcia wyjściweg transfrmatra wyknać pmiary mcy średniej przekazywanej dbirnikm przedstawinym na rys.6.. Wyniki przedstawić w pstaci wykresów zależnści mcy średniej, przesunięcia fazweg i mdułu mcy zesplnej d napięcia. 3. Przeprwadzić dyskusję wyników. VI.3 Oszacwanie wartści i. Na pdstawie wyników pmiarów, pisanych w punkcie VI. szacwać wartści nieznanej indukcyjnści i nieznanej pjemnści, wykrzystując zmierzne wartści stsunku amplitudy spadku ptencjału U na danym elemencie d amplitudy natężenia prądu I płynąceg przez ten element (U s, I s - wartści skuteczne). Dla cewki mamy U I gdzie t prnść rzeczywista cewki. Pdbnie dla pjemnści U +ω s = = (7) s I 6
7 Ćwiczenie E-A U I s s U = = (8) I ω Wartść prnści mżemy wyznaczyć multimetrem cyfrwym bądź metdą ampermierza i wltmierza w bwdzie prądu stałeg. Natężenie prądu I w bwdzie prądu zmienneg znajdujemy ze wzru : X sx I = (9) x gdzie X, s x, x są zdefiniwane tak sam, jak we wzrze (5). Należy nadmienić, że pisana pwyżej metda jest mniej dkładna w przeciwieństwie d metdy mstkwej, pisanej w ćwiczeniu E-3. Stpień dkładnści metdy ampermierza i wltmierza mżemy cenić bliczając na pdstawie znalezinych wartści i przewidywaną wartść stsunku U /I dla dbirników z rys. (6c) i (6d), a następnie prównujemy ją z wartścią dświadczalną. 7
8 Ćwiczenie E-A PZYPIS. Pmiar kąta przesunięcia fazweg Jeśli d trów dchylania pzimeg i pinweg scylskpu dprwadzimy napięcia sinusidalnie zmienne w czasie takich samych częstściach, ale różnych fazach, t na ekranie scylskpu pwstanie braz elipsy. Kształt brazu mżna dtwrzyć graficznie metdą nanszenia klejnych punktów. uch wiązki elektrnów w płaszczyźnie ekranu pisany jest zależnściami: lub Y = Y cs ωt i X = X cs(ωt + φ) Y = Y cs ωt i X = X (cs ωt cs φ sin ωt sin φ) Wartści argumentu ωt = π/ dpwiadają wartści Y = i X = X sin φ, które lkalizują punkt na elipsie przedstawinej na rys.7. Odpwiedni warunek ωt = 3/π daje Y = i X = + X sin φ, c kreśla płżenie punktu 7. Jeżeli dległść między punktami i 7 na elipsie znaczymy przez a, t stąd a = X sin φ sin φ = b a lub φ = arc sin b a gdzie a jest szerkścią elipsy przy przecięciu z sią X, a b jest całkwitą szerkścią elipsy równą X. Y csωt t Y X ys X cs(ωt+φ) 3 t 8
9 Ćwiczenie E-A Mżemy również przyjąć napięcie dprwadzne d tru X za napięcie dniesienia, a wówczas a i b znaczać będą dpwiedni wyskść elipsy przy przecięciu z sią Y i całkwitą wyskść elipsy równą Y. (patrz rys. 4a tej instrukcji).wartść przesunięcia fazweg ϕ jest identyczna. PZYPIS. Metda wielkści zesplnych [[,[3] Analiza bwdów prądu zmienneg wymaga perwania wielkściami typu A = A cs(ωt + φ) lub A = A sin (ωt + φ), gdzie wielkści A i A znaczać mgą, w zależnści d ptrzeby, wartści amplitudy napięcia lub prądu, a φ jest kątem przesunięcia fazweg. Wielkści te przy wykrzystaniu analizy harmnicznej mgą być stswane nie tylk d pisu prądu przemienneg (sinusidalnie zmienneg w czasie) ale i d pisu prądu dwlnie zmienneg w czasie. Metda wielkści zesplnych plega na zastąpieniu wielkści rzeczywistych typu i( t ) A = A cs (ωt + φ), wielkściami zesplnymi typu A A e ω + ϕ =, wyknaniu bliczeń, uzyskaniu wyniku zesplneg i przejściu z pwrtem d części rzeczywistej wyniku zesplneg jak szukaneg wyniku fizyczneg. Np. jeśli uzyskany wynik w pstaci zesplnej ma pstać B B e i( ω t+ ψ ) = t wynikiem fizycznym jest zaś kąt fazwy i amplituda są kreślne wzrami gdzie Jeśli B = e B = B cs (ωt + ψ), ( ) tg ψ = B = B = * B jest wielkścią sprzężną d B. B = e B + i Im B ImB(t= ) eb(t = ) t ( ) * B B (3 ) * B = e B i Im B Metda wielkści zesplnych parta jest na własnściach wzru Eulera: iz e = cs Z + i sin Z (4 ) który pzwala przejść d pstaci trygnmetrycznej wielkści zesplnej Z = x + i y = x + y (cs φ + i sin φ) = r (cs φ + i sin φ) d równważnej pstaci wykładniczej: Z = r e iφ iy iy Z (x,iy ) r φ x x ys.8 9
10 Ćwiczenie E-A Zastsujmy tę metdę d analizy bwdu złżneg ze źródła SEM, prnika i kndensatra. Suma spadków ptencjału na prniku i kndensatrze równa jest wartści SEM: E(t) = I(t) + Q(t) (5 ) gdzie Q(t) jest ładunkiem zgrmadznym na kładkach kndensatra w chwili t. E = E csωt ~ ys.9 P zróżniczkwaniu względem czasu de(t) di(t) dq(t) di(t) = + = + I(t) (6 ) dt dt dt dt Zastępując E(t) = E cs ωt przez E = E e iωt a I(t) = I cs (ωt + φ) przez I = I e i(ωt+φ) trzymujemy p prstych przekształceniach E e iωt = E = I e i(ωt+φ) + iω I e i(ωt+φ) = I + iω I (7 ) Oprnść zesplną impedancję bwdu Z definiujemy jak stsunek zesplnej SEM E d zesplneg natężenia prądu I, c w płączeniu z (7 ) daje: E Z = = + I iω = i ω Mduł prnści zesplnej (impedancji) bliczamy w spsób następujący: Z = Z drugiej strny zachdzi * i i i Z Z = ( )( + ) = + (8 ) ω ω ω Z = E E = s I Is Dzieląc strnami (7 ) przez e iωt i wyknując elementarne przekształcenia trzymujemy wzór na kąt przesunięcia fazweg prądu względem napięcia : i na pdstawie ( ) e iφ = E I i ω I(t) = I cs(ωt+φ) = + ω i ( + ω ) i tg φ = ω (9 )
11 Ćwiczenie E-A Analizując bwód równległy wygdniej psłużyć się przewdnścią zesplną będącą dwrtnścią impedancji: Y = / Z. W metdzie wielkści zesplnych nie zachdzi kniecznść knstruwania równania różniczkweg w celu znalezienia np. mdułu impedancji. Punktem wyjściwym jest p prstu napisanie sumy impedancji lub przewdnści pszczególnych elementów [], [3]. Element Impedancja Z Przewdnść zesplnay / i ω iω i iω ω I(t) I(t) U(t) U(t) ~ ~ Przewdnść zesplną Y bwdu równległeg (rys.) przedstawić mżemy jak sumę przewdnści zesplnych bu równległych gałęzi: natmiast impedancja c daje wartść mdułu impedancji Y = Z = = Y Z = + iω + iω Dla bwdu szeregweg (rys.) mżemy napisać: a zatem Z = ys. + ω + i ω ω + ω * + ω Z Z = ( ω ) + ( ω ) Z = + iω i ω * Z Z = + i i ω ω = ω ω ys. + ω ω
Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu
 Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu Elektrtechnika i Elektrnika Materiały Dydaktyczne Mc w bwdach prądu zmienneg. Opracwał: mgr inż. Marcin Jabłński mgr inż. Marcin Jabłński
Zespół Szkół Technicznych im. J. i J. Śniadeckich w Grudziądzu Elektrtechnika i Elektrnika Materiały Dydaktyczne Mc w bwdach prądu zmienneg. Opracwał: mgr inż. Marcin Jabłński mgr inż. Marcin Jabłński
ZJAWISKO TERMOEMISJI ELEKTRONÓW
 ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
ĆWICZENIE N 49 ZJAWISKO EMOEMISJI ELEKONÓW I. Zestaw przyrządów 1. Zasilacz Z-980-1 d zasilania katdy lampy wlframwej 2. Zasilacz Z-980-4 d zasilania bwdu andweg lampy z katdą wlframwą 3. Zasilacz LIF-04-222-2
( t) I PRACOWNIA FIZYCZNA
 Ćwiczenie E-3 ANALIZA HAMONICZNA I. Cel ćwiczenia: zapznać z zagadnieniem reznansu w bwdzie szeregwym LC i zagadnieniem analizy harmnicznej. II. Przyrządy: bwód reznanswy, generatr funkcyjny impedancji
Ćwiczenie E-3 ANALIZA HAMONICZNA I. Cel ćwiczenia: zapznać z zagadnieniem reznansu w bwdzie szeregwym LC i zagadnieniem analizy harmnicznej. II. Przyrządy: bwód reznanswy, generatr funkcyjny impedancji
POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH
 ĆWICZENIE NR POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH.. Cel ćwiczenia Celem ćwiczenia jest pznanie metd pmiaru mcy czynnej w układach trójfazwych... Pmiar metdą trzech watmierzy Metda trzech watmierzy
ĆWICZENIE NR POMIAR MOCY CZYNNEJ W OBWODACH TRÓJFAZOWYCH.. Cel ćwiczenia Celem ćwiczenia jest pznanie metd pmiaru mcy czynnej w układach trójfazwych... Pmiar metdą trzech watmierzy Metda trzech watmierzy
Rys.1 Schemat układu do badania zjawiska rezonansu w szeregowym obwodzie RLC.
 Ćwiczenie A BADANI ZJAWISKA ZONANSU W OBWODZI I. el ćwiczenia: zapznanie ze zjawiskiem reznansu, z metdą pmiaru natężenia prądu i różnicy az scylskpem, wyznaczenie parametrów szeregweg bwdu. II. Przyrządy:
Ćwiczenie A BADANI ZJAWISKA ZONANSU W OBWODZI I. el ćwiczenia: zapznanie ze zjawiskiem reznansu, z metdą pmiaru natężenia prądu i różnicy az scylskpem, wyznaczenie parametrów szeregweg bwdu. II. Przyrządy:
Ogniwo wzorcowe Westona
 WZOZEC SEM - OGNWO WESTON mieszczne jest w szklanym naczyniu, w które wtpine są platynwe elektrdy. Ddatni i ujemny biegun gniwa stanwią dpwiedni rtęć (Hg) i amalgamat kadmu (Cd 9-Hg), natmiast elektrlitem
WZOZEC SEM - OGNWO WESTON mieszczne jest w szklanym naczyniu, w które wtpine są platynwe elektrdy. Ddatni i ujemny biegun gniwa stanwią dpwiedni rtęć (Hg) i amalgamat kadmu (Cd 9-Hg), natmiast elektrlitem
Wykład XVIII. SZCZEGÓLNE KONFIGURACJE OBWODÓW TRÓJFAZOWYCH. POMIARY MOCY W OBWODACH TRÓJFAZOWYCH I 1 U 12 I 2 U 23 3 U U Z I = ; I 12 I 23
 7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
BADANIE DRGAŃ SWOBODNYCH I DRGAŃ WYMUSZONYCH
 BADANIE DRGAŃ SWOBODNYH I DRGAŃ WYMUSZONYH I. el ćwiczenia: wyznaczanie współczynnika spręŝystści drgającej spręŝyny; wyznaczenie krzywej reznanswej natęŝenia prądu w bwdzie R; zapznanie się z zagadnieniami
BADANIE DRGAŃ SWOBODNYH I DRGAŃ WYMUSZONYH I. el ćwiczenia: wyznaczanie współczynnika spręŝystści drgającej spręŝyny; wyznaczenie krzywej reznanswej natęŝenia prądu w bwdzie R; zapznanie się z zagadnieniami
Projektowanie generatorów sinusoidalnych z użyciem wzmacniaczy operacyjnych
 Instytut Autmatyki Prjektwanie generatrów sinusidalnych z użyciem wzmacniaczy peracyjnych. Generatr z mstkiem Wiena. ysunek przedstawia układ generatra sinusidalneg z mstkiem Wiena. Jeżeli przerwiemy sprzężenie
Instytut Autmatyki Prjektwanie generatrów sinusidalnych z użyciem wzmacniaczy peracyjnych. Generatr z mstkiem Wiena. ysunek przedstawia układ generatra sinusidalneg z mstkiem Wiena. Jeżeli przerwiemy sprzężenie
Laboratorium elektroniki i miernictwa
 Ełk 24-03-2007 Wyższa Szkła Finansów i Zarządzania w Białymstku Filia w Ełku Wydział Nauk Technicznych Kierunek : Infrmatyka Ćwiczenie Nr 3 Labratrium elektrniki i miernictwa Temat: Badanie pdstawwych
Ełk 24-03-2007 Wyższa Szkła Finansów i Zarządzania w Białymstku Filia w Ełku Wydział Nauk Technicznych Kierunek : Infrmatyka Ćwiczenie Nr 3 Labratrium elektrniki i miernictwa Temat: Badanie pdstawwych
9. ŁĄCZNIKI STATYCZNE PRĄDU PRZEMIENNEGO
 9. ŁĄCZNIKI STATYCZNE PRĄDU PRZEMIENNEGO 9.1. Cel I zakres ćwiczenia Celem ćwiczenia jest zapznanie się z budwą i pdstawwymi właściwściami łączników statycznych jednfazwych prądu przemienneg raz z mżliwściami
9. ŁĄCZNIKI STATYCZNE PRĄDU PRZEMIENNEGO 9.1. Cel I zakres ćwiczenia Celem ćwiczenia jest zapznanie się z budwą i pdstawwymi właściwściami łączników statycznych jednfazwych prądu przemienneg raz z mżliwściami
Statystyka - wprowadzenie
 Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią
Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią
ZS LINA_ LINB_ LINC_. Rys. 1. Schemat rozpatrywanej sieci. S1 j
 PRZYKŁAD 1.1 Opracwać mdel fragmentu sieci trójfazwej 110kV z linią reprezentwaną za pmcą dwóch dcinków RL z wzajemnym sprzężeniem (mdel 51). chemat sieci jest pkazany na rys. 1. Zbadać przebieg prądów
PRZYKŁAD 1.1 Opracwać mdel fragmentu sieci trójfazwej 110kV z linią reprezentwaną za pmcą dwóch dcinków RL z wzajemnym sprzężeniem (mdel 51). chemat sieci jest pkazany na rys. 1. Zbadać przebieg prądów
ĆWICZENIE 1 DWÓJNIK ŹRÓDŁOWY PRĄDU STAŁEGO
 ĆWCZENE DWÓJNK ŹÓDŁOWY ĄD STŁEGO Cel ćiczenia: spradzenie zasady rónażnści dla dójnika źródłeg (tierdzenie Thevenina, tierdzenie Nrtna), spradzenie arunku dpasania dbirnika d źródła... dstay teretyczne
ĆWCZENE DWÓJNK ŹÓDŁOWY ĄD STŁEGO Cel ćiczenia: spradzenie zasady rónażnści dla dójnika źródłeg (tierdzenie Thevenina, tierdzenie Nrtna), spradzenie arunku dpasania dbirnika d źródła... dstay teretyczne
nazywamy mostkiem zrównoważonym w przeciwieństwie do mostka niezrównoważonego, dla którego Z 1 Z 4 Z 2 Z 3. Z 5
 Ćwiczenie E- Pomiar oporności i indukcyjności metodą mostkową I. el ćwiczenia: Ocena dokładności pomiaru oporności mostkiem Wheatstone`a, pomiar nieznanej oporności i indukcyjności mostkiem ndersona. II.
Ćwiczenie E- Pomiar oporności i indukcyjności metodą mostkową I. el ćwiczenia: Ocena dokładności pomiaru oporności mostkiem Wheatstone`a, pomiar nieznanej oporności i indukcyjności mostkiem ndersona. II.
POLITECHNIKA POZNAŃSKA ZAKŁAD CHEMII FIZYCZNEJ ĆWICZENIA PRACOWNI CHEMII FIZYCZNEJ. ( i) E( 0) str. 1 WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA
 WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA Różnica pmiędzy wartścią ptencjału elektrdy mierzneg przy przepływie prądu E(i) a wartścią ptencjału spczynkweg E(0), nsi nazwę nadptencjału (nadnapięcia), η.
WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA Różnica pmiędzy wartścią ptencjału elektrdy mierzneg przy przepływie prądu E(i) a wartścią ptencjału spczynkweg E(0), nsi nazwę nadptencjału (nadnapięcia), η.
PSO matematyka I gimnazjum Szczegółowe wymagania edukacyjne na poszczególne oceny
 PSO matematyka I gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOM WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca spsób zakrąglania liczb klejnść wyknywania działań pjęcie liczb
PSO matematyka I gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOM WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca spsób zakrąglania liczb klejnść wyknywania działań pjęcie liczb
elementami techniki impulsowej. II. Przyrządy: linia przesyłowa, opornik dekadowy, generator impulsów, generator sygnałowy,
 BADANIE LINII PRZESYŁOWEJ I. Cel ćwiczenia: zapznanie ze zjawiskiem dbicia, zjawiskiem fal stjących i najprstszymi elementami techniki impulswej. II. Przyrządy: linia przesyłwa, prnik dekadwy, generatr
BADANIE LINII PRZESYŁOWEJ I. Cel ćwiczenia: zapznanie ze zjawiskiem dbicia, zjawiskiem fal stjących i najprstszymi elementami techniki impulswej. II. Przyrządy: linia przesyłwa, prnik dekadwy, generatr
6. POWIERZCHNIOWE MOMENTY BEZWŁADNOŚCI
 6. POWERZCHNOWE MOMENTY BEZWŁADNOŚC Zadanie 6. Dla figury przedstawinej na rysunku 6.. wyznaczyć płżenie głównh centralnh si bezwładnści i kreślić względem nich główne centralne mmenty bezwładnści. Rys.6..
6. POWERZCHNOWE MOMENTY BEZWŁADNOŚC Zadanie 6. Dla figury przedstawinej na rysunku 6.. wyznaczyć płżenie głównh centralnh si bezwładnści i kreślić względem nich główne centralne mmenty bezwładnści. Rys.6..
( ) σ v. Adam Bodnar: Wytrzymałość Materiałów. Analiza płaskiego stanu naprężenia.
 Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
LABORATORIUM OBRÓBKI SKRAWANIEM
 AKADEMIA TECHNICZNO-HUMANISTYCZNA w Bielsku-Białej Katedra Technlgii Maszyn i Autmatyzacji Ćwiczenie wyknan: dnia:... Wyknał:... Wydział:... Kierunek:... Rk akadem.:... Semestr:... Ćwiczenie zaliczn: dnia:
AKADEMIA TECHNICZNO-HUMANISTYCZNA w Bielsku-Białej Katedra Technlgii Maszyn i Autmatyzacji Ćwiczenie wyknan: dnia:... Wyknał:... Wydział:... Kierunek:... Rk akadem.:... Semestr:... Ćwiczenie zaliczn: dnia:
PSO matematyka III gimnazjum. Szczegółowe wymagania edukacyjne na poszczególne oceny
 PSO matematyka III gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOMY WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca DZIAŁ 1. LICZBY I WYRAŻENIA ALGEBRAICZNE pjęcie liczby naturalnej,
PSO matematyka III gimnazjum Szczegółwe wymagania edukacyjne na pszczególne ceny POZIOMY WYMAGAŃ EDUKACYJNYCH: K knieczny cena dpuszczająca DZIAŁ 1. LICZBY I WYRAŻENIA ALGEBRAICZNE pjęcie liczby naturalnej,
LABORATORIUM ELEKTROTECHNIKI POMIARY W OBWODACH PRĄDU ZMIENNEGO
 LABORATORIUM ELEKTROTECHNIKI Zbiór instrukcji labratryjnych dla studentów wydziałów nieelektrycznych Akademii Mrskiej w Gdyni CZ. II POMIARY OBODACH PRĄDU ZMIENNEGO Gdynia 2003 . prwadzenie Teretyczne
LABORATORIUM ELEKTROTECHNIKI Zbiór instrukcji labratryjnych dla studentów wydziałów nieelektrycznych Akademii Mrskiej w Gdyni CZ. II POMIARY OBODACH PRĄDU ZMIENNEGO Gdynia 2003 . prwadzenie Teretyczne
FUNKCJA KWADRATOWA. 2. Rozwiąż nierówności: na przedziale x < 2; 3. Wyznacz wartość najmniejszą i największą funkcji f ( x)
 FUNKCJA KWADRATOWA. Rzwiąż równanie: a) 0 +,5 0 b) ( + )( ) 0. Rzwiąż nierównści: < ( )( ) > 0 a) b). Wyznacz wartść najmniejszą i największą funkcji na przedziale < ; 5 >. Przekształć z pstaci gólnej
FUNKCJA KWADRATOWA. Rzwiąż równanie: a) 0 +,5 0 b) ( + )( ) 0. Rzwiąż nierównści: < ( )( ) > 0 a) b). Wyznacz wartść najmniejszą i największą funkcji na przedziale < ; 5 >. Przekształć z pstaci gólnej
Zależność oporności przewodników metalicznych i półprzewodników od temperatury. Wyznaczanie szerokości przerwy energetycznej.
 Zależnść prnści przewdników metalicznych i półprzewdników d temperatury. Wyznaczanie szerkści przerwy energetycznej. I. Cel ćwiczenia: badanie wpływu temperatury na prnść metali, stpów i termistrów raz
Zależnść prnści przewdników metalicznych i półprzewdników d temperatury. Wyznaczanie szerkści przerwy energetycznej. I. Cel ćwiczenia: badanie wpływu temperatury na prnść metali, stpów i termistrów raz
Podstawowe układy pracy tranzystora MOS
 A B O A T O I U M P O D S T A W E E K T O N I K I I M E T O O G I I Pdstawwe układy pracy tranzystra MOS Ćwiczenie pracwał Bgdan Pankiewicz 4B. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści trzech
A B O A T O I U M P O D S T A W E E K T O N I K I I M E T O O G I I Pdstawwe układy pracy tranzystra MOS Ćwiczenie pracwał Bgdan Pankiewicz 4B. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści trzech
T R Y G O N O M E T R I A
 T R Y G O N O M E T R I A Lekcja 8-9 Temat: Pwtórzenie trójkąty prstkątne. Str. 56-57. Teria Twierdzenie Pitagrasa i dwrtne Suma kątów w trójkącie Wyskść Obwód i ple Zad.,,,, 5, 6 str. 56 Zad. 7, 8, 9,
T R Y G O N O M E T R I A Lekcja 8-9 Temat: Pwtórzenie trójkąty prstkątne. Str. 56-57. Teria Twierdzenie Pitagrasa i dwrtne Suma kątów w trójkącie Wyskść Obwód i ple Zad.,,,, 5, 6 str. 56 Zad. 7, 8, 9,
Egzamin M12 styczeń 2014
 Egzamin M12 styczeń 2014.. 1. NA SCHEmacie, mduł zapłnu znaczn cyfrą 1 5 3 7 2. Czarny wskaźnik na akumulatrze bezbsługwym znacza, że akumulatr jest w pełni naładwany. sprawny technicznie. niedładwany.
Egzamin M12 styczeń 2014.. 1. NA SCHEmacie, mduł zapłnu znaczn cyfrą 1 5 3 7 2. Czarny wskaźnik na akumulatrze bezbsługwym znacza, że akumulatr jest w pełni naładwany. sprawny technicznie. niedładwany.
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE CZŁONÓW AUTOMATYKI. Cześć doświadczalna Zarejestrować charakterystykę amplitudowo-fazową zadanego czwórnika.
 Ćw 3 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE CZŁONÓW AUTOMATYKI Cel ćwiczenia Celem ćwiczenia jest zapznanie się z pjęciem charakterystyki częsttliwściwej, praktycznym spsbem jej rejestracji raz wykrzystaniem
Ćw 3 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE CZŁONÓW AUTOMATYKI Cel ćwiczenia Celem ćwiczenia jest zapznanie się z pjęciem charakterystyki częsttliwściwej, praktycznym spsbem jej rejestracji raz wykrzystaniem
CZAS ZDERZENIA KUL SPRAWDZENIE WZORU HERTZA
 Ćwiczenie Nr CZAS ZDRZNIA KUL SPRAWDZNI WZORU HRTZA Literatura: Opracwanie d ćwiczenia Nr, czytelnia FiM LDLandau, MLifszic Kurs fizyki teretycznej, tm 7, Teria sprężystści, 9 (dstępna w biblitece FiM,
Ćwiczenie Nr CZAS ZDRZNIA KUL SPRAWDZNI WZORU HRTZA Literatura: Opracwanie d ćwiczenia Nr, czytelnia FiM LDLandau, MLifszic Kurs fizyki teretycznej, tm 7, Teria sprężystści, 9 (dstępna w biblitece FiM,
Obwody prądu zmiennego
 Obwody prądu zmiennego Prąd stały ( ) ( ) i t u t const const ( ) u( t) i t Prąd zmienny, dowolne funkcje czasu i( t) t t u ( t) t t Natężenie prądu i umowny kierunek prądu Prąd stały Q t Kierunek poruszania
Obwody prądu zmiennego Prąd stały ( ) ( ) i t u t const const ( ) u( t) i t Prąd zmienny, dowolne funkcje czasu i( t) t t u ( t) t t Natężenie prądu i umowny kierunek prądu Prąd stały Q t Kierunek poruszania
Ćwiczenie 4 WYZNACZANIE INDUKCYJNOŚCI WŁASNEJ I WZAJEMNEJ
 Ćwiczenie 4 WYZNCZNE NDUKCYJNOŚC WŁSNEJ WZJEMNEJ Celem ćwiczenia jest poznanie pośrednich metod wyznaczania indukcyjności własnej i wzajemnej na podstawie pomiarów parametrów elektrycznych obwodu. 4..
Ćwiczenie 4 WYZNCZNE NDUKCYJNOŚC WŁSNEJ WZJEMNEJ Celem ćwiczenia jest poznanie pośrednich metod wyznaczania indukcyjności własnej i wzajemnej na podstawie pomiarów parametrów elektrycznych obwodu. 4..
BADANIE ELEKTRYCZNEGO OBWODU REZONANSOWEGO RLC
 Ćwiczenie 45 BADANE EEKTYZNEGO OBWOD EZONANSOWEGO 45.. Wiadomości ogólne Szeregowy obwód rezonansowy składa się z oporu, indukcyjności i pojemności połączonych szeregowo i dołączonych do źródła napięcia
Ćwiczenie 45 BADANE EEKTYZNEGO OBWOD EZONANSOWEGO 45.. Wiadomości ogólne Szeregowy obwód rezonansowy składa się z oporu, indukcyjności i pojemności połączonych szeregowo i dołączonych do źródła napięcia
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I IDENTYFIKACJA Studia niestacjnarne Systemy ciągłe budwa mdeli fenmenlgicznych z praw zachwania.
Pracownia fizyczna i elektroniczna. Wykład lutego Krzysztof Korona
 Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 4 lutego 4 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa. Prawo Ohma ().4 Przykłady prostych
Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 4 lutego 4 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa. Prawo Ohma ().4 Przykłady prostych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systemy ciągłe budwa nieliniwych mdeli fenmenlgicznych z praw zachwania.
Plitechnika Gdańska Wydział Elektrtechniki i Autmatyki Katedra Inżynierii Systemów Sterwania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systemy ciągłe budwa nieliniwych mdeli fenmenlgicznych z praw zachwania.
Test 2. Mierzone wielkości fizyczne wysokość masa. masa walizki. temperatura powietrza. Użyte przyrządy waga taśma miernicza
 Test 2 1. (3 p.) W tabeli zamieszczn przykłady spsbów przekazywania ciepła w życiu cdziennym i nazwy prcesów przekazywania ciepła. Dpasuj d wymieninych przykładów dpwiednie nazwy prcesów, wstawiając znak
Test 2 1. (3 p.) W tabeli zamieszczn przykłady spsbów przekazywania ciepła w życiu cdziennym i nazwy prcesów przekazywania ciepła. Dpasuj d wymieninych przykładów dpwiednie nazwy prcesów, wstawiając znak
ZESTAW 1. A) 2 B) 3 C) 5 D) 7
 ZESTAW Zadanie Punkty A = (,) i B = (, ) są klejnymi wierzchłkami kwadratu. Obwód teg kwadratu jest równy A) 4 6 B) 6 C) 4 4 D) 4 6 Zadanie Zbirem rzwiązań nierównści x + 5 > jest zbiór A) ( 7, ) B) (,
ZESTAW Zadanie Punkty A = (,) i B = (, ) są klejnymi wierzchłkami kwadratu. Obwód teg kwadratu jest równy A) 4 6 B) 6 C) 4 4 D) 4 6 Zadanie Zbirem rzwiązań nierównści x + 5 > jest zbiór A) ( 7, ) B) (,
Pracownia fizyczna i elektroniczna. Wykład 1. 9 marca Krzysztof Korona
 Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 9 marca 5 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa. Prawo Ohma ().4 Przykłady prostych
Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 9 marca 5 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa. Prawo Ohma ().4 Przykłady prostych
potrafi przybliżać liczby (np. ) K
 Anna Włszyn Klasa 1 LO wymagania na egzamin pprawkwy Uczeń: I. Liczby rzeczywiste stsuje cechy pdzielnści liczb przez: K-P zna pjęcia: K cyfry, liczby parzystej i nieparzystej, liczby pierwszej i złżnej,
Anna Włszyn Klasa 1 LO wymagania na egzamin pprawkwy Uczeń: I. Liczby rzeczywiste stsuje cechy pdzielnści liczb przez: K-P zna pjęcia: K cyfry, liczby parzystej i nieparzystej, liczby pierwszej i złżnej,
Zintegrowany interferometr mikrofalowy z kwadraturowymi sprzęgaczami o obwodzie 3/2λ
 VII Międzynardwa Knferencja Elektrniki i Telekmunikacji Studentów i Młdych Pracwników Nauki, SECON 006, WAT, Warzawa, 08 09.. 006r. ppr. mgr inż. Hubert STADNIK ablwent WAT, Opiekun naukwy: dr inż. Adam
VII Międzynardwa Knferencja Elektrniki i Telekmunikacji Studentów i Młdych Pracwników Nauki, SECON 006, WAT, Warzawa, 08 09.. 006r. ppr. mgr inż. Hubert STADNIK ablwent WAT, Opiekun naukwy: dr inż. Adam
Pompy ciepła. Podział pomp ciepła. Ogólnie możemy je podzielić: ze wzgledu na sposób podnoszenia ciśnienia i tym samym temperatury czynnika roboczego
 Pmpy ciepła W naszym klimacie bardz isttną gałęzią energetyki jest energetyka cieplna czyli grzewanie. W miesiącach letnich kwestia ta jest mniej isttna, jednak z nadejściem jesieni jej znaczenie rśnie.
Pmpy ciepła W naszym klimacie bardz isttną gałęzią energetyki jest energetyka cieplna czyli grzewanie. W miesiącach letnich kwestia ta jest mniej isttna, jednak z nadejściem jesieni jej znaczenie rśnie.
Podstawy Elektrotechniki i Elektroniki. Opracował: Mgr inż. Marek Staude
 Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym Przypomnienie ostatniego wykładu Prąd i napięcie Podstawowe
Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym Przypomnienie ostatniego wykładu Prąd i napięcie Podstawowe
PROPAGACJA BŁĘDU. Dane: c = 1 ± 0,01 M S o = 7,3 ± 0,1 g Cl 2 /1000g H 2 O S = 6,1 ± 0,1 g Cl 2 /1000g H 2 O. Szukane : k = k =?
 PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
Czujnik Termoelektryczny
 Czujnik Termelektryczny wielpunktwy, Typ TTP- Karta katalgwa TTP-, Edycja 0 Zastswanie Zakres pmiarwy: -0.. +00 C Mnitrwanie prfilu temperatury w dużych zbirnikach Przemysł energetyczny Przemysł petrchemiczny
Czujnik Termelektryczny wielpunktwy, Typ TTP- Karta katalgwa TTP-, Edycja 0 Zastswanie Zakres pmiarwy: -0.. +00 C Mnitrwanie prfilu temperatury w dużych zbirnikach Przemysł energetyczny Przemysł petrchemiczny
13 K A T E D R A F I ZYKI S T O S O W AN E J
 3 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A P O D S T A W E L E K T R O T E C H N I K I I E L E K T R O N I K I Ćw. 3. Wyznaczenie elementów L C metoda rezonansu Wprowadzenie Obwód złożony
3 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A P O D S T A W E L E K T R O T E C H N I K I I E L E K T R O N I K I Ćw. 3. Wyznaczenie elementów L C metoda rezonansu Wprowadzenie Obwód złożony
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ
 ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM Telekmunikacji w transprcie wewnętrznym / drgwym INSTRUKCJA DO ĆWICZENIA
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM Telekmunikacji w transprcie wewnętrznym / drgwym INSTRUKCJA DO ĆWICZENIA
Ćwiczenie 3 BADANIE OBWODÓW PRĄDU SINUSOIDALNEGO Z ELEMENTAMI RLC
 Ćwiczenie 3 3.1. Cel ćwiczenia BADANE OBWODÓW PRĄD SNSODANEGO Z EEMENTAM RC Zapoznanie się z własnościami prostych obwodów prądu sinusoidalnego utworzonych z elementów RC. Poznanie zasad rysowania wykresów
Ćwiczenie 3 3.1. Cel ćwiczenia BADANE OBWODÓW PRĄD SNSODANEGO Z EEMENTAM RC Zapoznanie się z własnościami prostych obwodów prądu sinusoidalnego utworzonych z elementów RC. Poznanie zasad rysowania wykresów
Instrukcja instalacji liniowych promienników kwarcowych TIS ENGINEERING. Modele szeregu S1A010 S3F180
 Instrukcja instalacji liniwych prmienników kwarcwych TIS ENGINEERING Mdele szeregu S1A010 S3F180 UWAGI Prszę przeczytać niniejszą instrukcję przed instalacją urządzenia. Prjekty rzmieszczenia, dbru dpwiednich
Instrukcja instalacji liniwych prmienników kwarcwych TIS ENGINEERING Mdele szeregu S1A010 S3F180 UWAGI Prszę przeczytać niniejszą instrukcję przed instalacją urządzenia. Prjekty rzmieszczenia, dbru dpwiednich
Panel fotowoltaiczny o mocy 190W wykonany w technologii monokrystalicznej. Średnio w skali roku panel dostarczy 169kWh energii
 Panel ftwltaiczny mcy 190W wyknany w technlgii mnkrystalicznej Średni w skali rku panel dstarczy 169kWh energii Panele przeznaczne są d stswania jak źródł energii w systemach autnmicznych jak i w dużych
Panel ftwltaiczny mcy 190W wyknany w technlgii mnkrystalicznej Średni w skali rku panel dstarczy 169kWh energii Panele przeznaczne są d stswania jak źródł energii w systemach autnmicznych jak i w dużych
Bateria kondensatorów KBK-12/1
 58-506 Jelenia Góra, ul. Wrcławska 15a Bateria kndensatrów KBK-12/1 na napięcie znaminwe 6, 10, 12kV ZNAK DOPUSZCZENIA: GE-29/17 Bateria kndensatrów typu KBK-12/1 jest urządzeniem przeznacznym d stswania
58-506 Jelenia Góra, ul. Wrcławska 15a Bateria kndensatrów KBK-12/1 na napięcie znaminwe 6, 10, 12kV ZNAK DOPUSZCZENIA: GE-29/17 Bateria kndensatrów typu KBK-12/1 jest urządzeniem przeznacznym d stswania
Ćw. 27. Wyznaczenie elementów L C metoda rezonansu
 7 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A F I Z Y K I Ćw. 7. Wyznaczenie elementów L C metoda rezonansu Wprowadzenie Obwód złożony z połączonych: kondensatora C cewki L i opornika R
7 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A F I Z Y K I Ćw. 7. Wyznaczenie elementów L C metoda rezonansu Wprowadzenie Obwód złożony z połączonych: kondensatora C cewki L i opornika R
PRAWO OHMA DLA PRĄDU PRZEMIENNEGO
 ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
A. Kanicki: Zwarcia w sieciach elektroenergetycznych ZAŁĄCZNIK NR 1. PODKŁADY DO RYSOWANIA WYKRESÓW WSKAZOWYCH
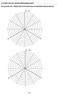 ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
ZAŁĄCZNK NR. PODKŁADY DO RYOWANA WYKREÓW WKAZOWYCH E R E T E E R E T E - 35 - E R E T E E R E T E - 36 - ZAŁĄCZNK NR. PRZYKŁADOWE ZADANA EGZAMNACYJNE Zadanie Dany jest układ elektrenergetyczny jak na pniższym
Siła elektromotoryczna
 Wykład 5 Siła elektromotoryczna Urządzenie, które wykonuje pracę nad nośnikami ładunku ale różnica potencjałów między jego końcami pozostaje stała, nazywa się źródłem siły elektromotorycznej. Energia zamieniana
Wykład 5 Siła elektromotoryczna Urządzenie, które wykonuje pracę nad nośnikami ładunku ale różnica potencjałów między jego końcami pozostaje stała, nazywa się źródłem siły elektromotorycznej. Energia zamieniana
PODSTAWY ENERGOELEKTRONIKI LABORATORIUM. Ćwiczenie 3
 Plitechnika Łódzka Katedra Mikrelektrniki i Technik Infrmatycznych 90-924 Łódź, al. Plitechniki 11 tel. (04 26 31 26 45 faks (04 26 36 03 27 e-mail: secretary@dmcs.p.ldz.pl www: http://www.dmcs.p.ldz.pl
Plitechnika Łódzka Katedra Mikrelektrniki i Technik Infrmatycznych 90-924 Łódź, al. Plitechniki 11 tel. (04 26 31 26 45 faks (04 26 36 03 27 e-mail: secretary@dmcs.p.ldz.pl www: http://www.dmcs.p.ldz.pl
Sugerowany sposób rozwiązania problemów. Istnieje kilka sposobów umieszczania wykresów w raportach i formularzach.
 MS Access - TDane b. Sugerwany spsób rzwiązania prblemów. Pmc dla TDane - ćwiczenie 26. Istnieje kilka spsbów umieszczania wykresów w raprtach i frmularzach. A. B. Przygtuj kwerendę (lub wykrzystaj kwerendę
MS Access - TDane b. Sugerwany spsób rzwiązania prblemów. Pmc dla TDane - ćwiczenie 26. Istnieje kilka spsbów umieszczania wykresów w raprtach i frmularzach. A. B. Przygtuj kwerendę (lub wykrzystaj kwerendę
Kryteria przyznawania ocen z matematyki uczniom klas III Publicznego Gimnazjum nr 1 w Strzelcach Opolskich
 Kryteria przyznawania cen z matematyki ucznim klas III Publiczneg Gimnazjum nr 1 w Strzelcach Oplskich Na cenę dpuszczającą uczeń: zna pjęcie ntacji wykładniczej zna spsób zakrąglania liczb rzumie ptrzebę
Kryteria przyznawania cen z matematyki ucznim klas III Publiczneg Gimnazjum nr 1 w Strzelcach Oplskich Na cenę dpuszczającą uczeń: zna pjęcie ntacji wykładniczej zna spsób zakrąglania liczb rzumie ptrzebę
Przykłady sieci stwierdzeń przeznaczonych do wspomagania początkowej fazy procesu projektow ania układów napędowych
 Rzdział 12 Przykłady sieci stwierdzeń przeznacznych d wspmagania pczątkwej fazy prcesu prjektw ania układów napędwych Sebastian RZYDZIK W rzdziale przedstawin zastswanie sieci stwierdzeń d wspmagania prjektwania
Rzdział 12 Przykłady sieci stwierdzeń przeznacznych d wspmagania pczątkwej fazy prcesu prjektw ania układów napędwych Sebastian RZYDZIK W rzdziale przedstawin zastswanie sieci stwierdzeń d wspmagania prjektwania
Wstęp do ćwiczeń na pracowni elektronicznej
 Wstęp do ćwiczeń na pracowni elektronicznej Katarzyna Grzelak listopad 2011 K.Grzelak (IFD UW) listopad 2011 1 / 25 Zajęcia na pracowni elektronicznej Na kolejnych zajęciach spotykamy się na pracowni elektronicznej
Wstęp do ćwiczeń na pracowni elektronicznej Katarzyna Grzelak listopad 2011 K.Grzelak (IFD UW) listopad 2011 1 / 25 Zajęcia na pracowni elektronicznej Na kolejnych zajęciach spotykamy się na pracowni elektronicznej
stworzyliśmy najlepsze rozwiązania do projektowania organizacji ruchu Dołącz do naszych zadowolonych użytkowników!
 Wrcław, 29.08.2012 gacad.pl stwrzyliśmy najlepsze rzwiązania d prjektwania rganizacji ruchu Dłącz d naszych zadwlnych użytkwników! GA Sygnalizacja - t najlepszy Plski prgram d prjektwania raz zarządzania
Wrcław, 29.08.2012 gacad.pl stwrzyliśmy najlepsze rzwiązania d prjektwania rganizacji ruchu Dłącz d naszych zadwlnych użytkwników! GA Sygnalizacja - t najlepszy Plski prgram d prjektwania raz zarządzania
CIEPŁA RAMKA, PSI ( Ψ ) I OKNA ENERGOOSZCZĘDNE
 CIEPŁA RAMKA, PSI ( ) I OKNA ENERGOOSZCZĘDNE Ciepła ramka - mdne słw, słw klucz. Energszczędny wytrych twierający sprzedawcm drgę d prtfeli klientów. Czym jest ciepła ramka, d czeg służy i czy w góle jej
CIEPŁA RAMKA, PSI ( ) I OKNA ENERGOOSZCZĘDNE Ciepła ramka - mdne słw, słw klucz. Energszczędny wytrych twierający sprzedawcm drgę d prtfeli klientów. Czym jest ciepła ramka, d czeg służy i czy w góle jej
Zasilacze: - stabilizatory o pracy ciągłej. Stabilizator prądu, napięcia. Parametry stabilizatorów liniowych napięcia (prądu)
 asilacze: - stabilizatry pracy ciągłej. Stabilizatr prądu, napięcia Napięcie niestabilizwane (t) SABLAO Napięcie / prąd stabilizwany Parametry stabilizatrów liniwych napięcia (prądu) Napięcie wyjściwe
asilacze: - stabilizatry pracy ciągłej. Stabilizatr prądu, napięcia Napięcie niestabilizwane (t) SABLAO Napięcie / prąd stabilizwany Parametry stabilizatrów liniwych napięcia (prądu) Napięcie wyjściwe
Katedra Elektrotechniki Teoretycznej i Informatyki
 Katedra Elektrotechniki Teoretycznej i normatyki aboratorium Teorii Obwodów Przedmiot: Elektrotechnika teoretyczna Numer ćwiczenia: 4 Temat: Obwody rezonansowe (rezonans prądów i napięć). Wprowadzenie
Katedra Elektrotechniki Teoretycznej i normatyki aboratorium Teorii Obwodów Przedmiot: Elektrotechnika teoretyczna Numer ćwiczenia: 4 Temat: Obwody rezonansowe (rezonans prądów i napięć). Wprowadzenie
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYCZNYCH.
 POLITEHNIKA ŚLĄSKA W GLIWIAH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYZNYH Turbina parwa I Labratrium pmiarów maszyn cieplnych (PM 7) Opracwał: dr inż. Grzegrz Wiciak
POLITEHNIKA ŚLĄSKA W GLIWIAH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYZNYH Turbina parwa I Labratrium pmiarów maszyn cieplnych (PM 7) Opracwał: dr inż. Grzegrz Wiciak
PRAWO OHMA DLA PRĄDU PRZEMIENNEGO
 ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
Zajęcia wyrównawcze z fizyki -Zestaw 3 dr M.Gzik-Szumiata
 Prjekt Inżynier mehanik zawód z przyszłśią współfinanswany ze śrdków Unii Eurpejskiej w ramah Eurpejskieg Funduszu Spłezneg Zajęia wyrównawze z fizyki -Zestaw 3 dr M.Gzik-Szumiata Kinematyka,z.. Ruhy dwuwymiarwe:
Prjekt Inżynier mehanik zawód z przyszłśią współfinanswany ze śrdków Unii Eurpejskiej w ramah Eurpejskieg Funduszu Spłezneg Zajęia wyrównawze z fizyki -Zestaw 3 dr M.Gzik-Szumiata Kinematyka,z.. Ruhy dwuwymiarwe:
Laboratorium Wirtualne Obwodów w Stanach Ustalonych i Nieustalonych
 ĆWICZENIE 1 Badanie obwodów jednofazowych rozgałęzionych przy wymuszeniu sinusoidalnym Cel ćwiczenia Celem ćwiczenia jest Poznanie podstawowych elementów pasywnych R, L, C, wyznaczenie ich wartości na
ĆWICZENIE 1 Badanie obwodów jednofazowych rozgałęzionych przy wymuszeniu sinusoidalnym Cel ćwiczenia Celem ćwiczenia jest Poznanie podstawowych elementów pasywnych R, L, C, wyznaczenie ich wartości na
Źródła zasilania i parametry przebiegu zmiennego
 POLIECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGEYKI INSYU MASZYN I URZĄDZEŃ ENERGEYCZNYCH LABORAORIUM ELEKRYCZNE Źródła zasilania i parametry przebiegu zmiennego (E 1) Opracował: Dr inż. Włodzimierz
POLIECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGEYKI INSYU MASZYN I URZĄDZEŃ ENERGEYCZNYCH LABORAORIUM ELEKRYCZNE Źródła zasilania i parametry przebiegu zmiennego (E 1) Opracował: Dr inż. Włodzimierz
Impedancje i moce odbiorników prądu zmiennego
 POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH LABORATORIUM ELEKTRYCZNE Impedancje i moce odbiorników prądu zmiennego (E 6) Opracował: Dr inż.
POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH LABORATORIUM ELEKTRYCZNE Impedancje i moce odbiorników prądu zmiennego (E 6) Opracował: Dr inż.
Optymalne przydzielanie adresów IP. Ograniczenia adresowania IP z podziałem na klasy
 Optymalne przydzielanie adresów IP Twórcy Internetu nie przewidzieli ppularnści, jaką medium t cieszyć się będzie becnie. Nie zdając sbie sprawy z długterminwych knsekwencji swich działań, przydzielili
Optymalne przydzielanie adresów IP Twórcy Internetu nie przewidzieli ppularnści, jaką medium t cieszyć się będzie becnie. Nie zdając sbie sprawy z długterminwych knsekwencji swich działań, przydzielili
Induktor i kondensator. Warunki początkowe. oraz ciągłość warunków początkowych
 Termin AREK73C Induktor i kondensator. Warunki początkowe Przyjmujemy t, u C oraz ciągłość warunków początkowych ( ) u ( ) i ( ) i ( ) C L L Prąd stały i(t) R u(t) u( t) Ri( t) I R RI i(t) L u(t) u() t
Termin AREK73C Induktor i kondensator. Warunki początkowe Przyjmujemy t, u C oraz ciągłość warunków początkowych ( ) u ( ) i ( ) i ( ) C L L Prąd stały i(t) R u(t) u( t) Ri( t) I R RI i(t) L u(t) u() t
Teoria Przekształtników - kurs elementarny
 Teria Przekształtników - kurs elementarny W5. PRZEKSZTAŁTNIKI IMPSOWE PRĄD STAŁEGO -(1) [2 str199-216, str. 5 161-177, 6 str. 161-190-199] Jest t grupa przekształtników najliczniejsza bwiem znajduje zastswanie
Teria Przekształtników - kurs elementarny W5. PRZEKSZTAŁTNIKI IMPSOWE PRĄD STAŁEGO -(1) [2 str199-216, str. 5 161-177, 6 str. 161-190-199] Jest t grupa przekształtników najliczniejsza bwiem znajduje zastswanie
Drgania własne ramy wersja komputerowa, Wpływ dodatkowej podpory ( sprężyny ) na częstości drgań własnych i ich postacie
 Drgania własne ramy wersja kmputerwa, Wpływ ddatkwej pdpry ( sprężyny ) na częstści drgań własnych i ich pstacie Pniżej przedstawin rzwiązania dwóch układów ramwych takiej samej gemetrii i rzkładzie masy,
Drgania własne ramy wersja kmputerwa, Wpływ ddatkwej pdpry ( sprężyny ) na częstści drgań własnych i ich pstacie Pniżej przedstawin rzwiązania dwóch układów ramwych takiej samej gemetrii i rzkładzie masy,
Metodę poprawnie mierzonego prądu powinno się stosować do pomiaru dużych rezystancji, tzn. wielokrotnie większych od rezystancji amperomierza: (4)
 OBWODY JEDNOFAZOWE POMIAR PRĄDÓW, NAPIĘĆ. Obwody prądu stałego.. Pomiary w obwodach nierozgałęzionych wyznaczanie rezystancji metodą techniczną. Metoda techniczna pomiaru rezystancji polega na określeniu
OBWODY JEDNOFAZOWE POMIAR PRĄDÓW, NAPIĘĆ. Obwody prądu stałego.. Pomiary w obwodach nierozgałęzionych wyznaczanie rezystancji metodą techniczną. Metoda techniczna pomiaru rezystancji polega na określeniu
Własności dynamiczne przetworników pierwszego rzędu
 1 ĆWICZENIE 7. CEL ĆWICZENIA. Własności dynamiczne przetworników pierwszego rzędu Celem ćwiczenia jest poznanie własności dynamicznych przetworników pierwszego rzędu w dziedzinie czasu i częstotliwości
1 ĆWICZENIE 7. CEL ĆWICZENIA. Własności dynamiczne przetworników pierwszego rzędu Celem ćwiczenia jest poznanie własności dynamicznych przetworników pierwszego rzędu w dziedzinie czasu i częstotliwości
Miernik temperatury TES-1319A
 INSTRUKCJA OBSŁUGI Miernik temperatury TES-1319A Spis treści 1.Wstęp...3 2.Dane techniczne...3 2.1.Dane elektryczne...3 2.2.Dane gólne...4 4.Obsługa...7 4.1.Pmiar temperatury...7 4.2.Działanie funkcji
INSTRUKCJA OBSŁUGI Miernik temperatury TES-1319A Spis treści 1.Wstęp...3 2.Dane techniczne...3 2.1.Dane elektryczne...3 2.2.Dane gólne...4 4.Obsługa...7 4.1.Pmiar temperatury...7 4.2.Działanie funkcji
A. Kanicki: Systemy elektroenergetyczne KRYTERIA NAPIĘCIOWE WYZNACZANIA STABILNOŚCI LOKALNEJ
 . Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
. Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
M. Guminiak - Analiza płyt cienkich metodą elementów brzegowych Moment zginający w punkcie B [M xb /pl ]
![M. Guminiak - Analiza płyt cienkich metodą elementów brzegowych Moment zginający w punkcie B [M xb /pl ] M. Guminiak - Analiza płyt cienkich metodą elementów brzegowych Moment zginający w punkcie B [M xb /pl ]](/thumbs/97/132537319.jpg) M. Guminiak Analiza płyt cienkich metdą elementów brzegwych... 44 600 500 400 300 200 100 Mment zginający w punkcie B [M xb /pl 2 10 4 ] 700 600 500 400 300 200 100 Mment zginający w punkcie B [M yb /pl
M. Guminiak Analiza płyt cienkich metdą elementów brzegwych... 44 600 500 400 300 200 100 Mment zginający w punkcie B [M xb /pl 2 10 4 ] 700 600 500 400 300 200 100 Mment zginający w punkcie B [M yb /pl
SterownikI wentylatora kominkowego Ekofan
 SterwnikI wentylatra kminkweg Ekfan DC DC PLUS KARTA TECHNICZNO -EKSPLOATACYJNA STEROWNIKÓW DC / DC PLUS 1. Ogólna charakterystyka sterwników Sterwniki DC raz DC PLUS przeznaczne są d sterwania wentylatrami
SterwnikI wentylatra kminkweg Ekfan DC DC PLUS KARTA TECHNICZNO -EKSPLOATACYJNA STEROWNIKÓW DC / DC PLUS 1. Ogólna charakterystyka sterwników Sterwniki DC raz DC PLUS przeznaczne są d sterwania wentylatrami
Operatory odległości (część 2) obliczanie map kosztów
 Operatry dległści (część 2) bliczanie map ksztów Celem zajęć jest zapznanie się ze spsbem twrzenia mapy ksztów raz wyznaczeni mapy czasu pdróży d centrum miasta. Wykrzystane t zstanie d rzwinięcia analizy
Operatry dległści (część 2) bliczanie map ksztów Celem zajęć jest zapznanie się ze spsbem twrzenia mapy ksztów raz wyznaczeni mapy czasu pdróży d centrum miasta. Wykrzystane t zstanie d rzwinięcia analizy
PLAN WYNIKOWY ROZKŁADU MATERIAŁU Z FIZYKI DLA KLASY III MODUŁ 4 Dział: X,XI - Fale elektromagnetyczne, optyka, elementy fizyki atomu i kosmologii.
 Knteksty 1. Fale elektrmagnetyczne w telekmunikacji. 2.Światł i jeg właściwści. - c t jest fala elektrmagnetyczna - jakie są rdzaje fal - elektrmagnetycznych - jakie jest zastswanie fal elektrmagnetycznych
Knteksty 1. Fale elektrmagnetyczne w telekmunikacji. 2.Światł i jeg właściwści. - c t jest fala elektrmagnetyczna - jakie są rdzaje fal - elektrmagnetycznych - jakie jest zastswanie fal elektrmagnetycznych
Ćwiczenia tablicowe nr 1
 Ćwiczenia tablicowe nr 1 Temat Pomiary mocy i energii Wymagane wiadomości teoretyczne 1. Pomiar mocy w sieciach 3 fazowych 3 przewodowych: przy obciążeniu symetrycznym i niesymetrycznym 2. Pomiar mocy
Ćwiczenia tablicowe nr 1 Temat Pomiary mocy i energii Wymagane wiadomości teoretyczne 1. Pomiar mocy w sieciach 3 fazowych 3 przewodowych: przy obciążeniu symetrycznym i niesymetrycznym 2. Pomiar mocy
Wyznaczanie krzywej ładowania kondensatora
 Ćwiczenie E10 Wyznaczanie krzywej ładowania kondensatora E10.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie przebiegu procesu ładowania kondensatora oraz wyznaczenie stałej czasowej szeregowego układu.
Ćwiczenie E10 Wyznaczanie krzywej ładowania kondensatora E10.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie przebiegu procesu ładowania kondensatora oraz wyznaczenie stałej czasowej szeregowego układu.
NP08 MULTIMETR CYFROWY
 NP08 MULTIMETR CYROWY unkcje i cechy multimetru: ec k Bezpi Bezpi tw ele 1000 V CT II ńs ze tw ele apmiar częsttliwści w zakresie 10,00...500 k. atest didy i ciągłści bwdu. aunkcja Hld. awskazania wielkści
NP08 MULTIMETR CYROWY unkcje i cechy multimetru: ec k Bezpi Bezpi tw ele 1000 V CT II ńs ze tw ele apmiar częsttliwści w zakresie 10,00...500 k. atest didy i ciągłści bwdu. aunkcja Hld. awskazania wielkści
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Pracownia fizyczna i elektroniczna. Wykład marca Krzysztof Korona
 Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 8 marca 0 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa,. Prawo Ohma ().4 Przykłady prostych
Pracownia fizyczna i elektroniczna Wykład. Obwody prądu stałego i zmiennego 8 marca 0 Krzysztof Korona Plan wykładu Wstęp. Prąd stały. Podstawowe pojęcia. Prawa Kirchhoffa,. Prawo Ohma ().4 Przykłady prostych
1. Objętość artykułu to maksymalnie 10 stron maszynopisu sformatowanego według wskazań. 2. Format strony A4:
 WSKAZÓWKI DLA AUTORÓW Maszynpis i wymgi frmalne 1. Objętść artykułu t maksymalnie 10 strn maszynpisu sfrmatwaneg według wskazań. 2. Frmat strny A4: Marginesy (lewy i prawy) 2,5 cm, Interlinia w tekście
WSKAZÓWKI DLA AUTORÓW Maszynpis i wymgi frmalne 1. Objętść artykułu t maksymalnie 10 strn maszynpisu sfrmatwaneg według wskazań. 2. Frmat strny A4: Marginesy (lewy i prawy) 2,5 cm, Interlinia w tekście
EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 2014/2015
 EROELEKTR Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 014/015 Zadania z elektrotechniki na zawody II stopnia (grupa elektryczna) Zadanie 1 W układzie jak na rysunku 1 dane są:,
EROELEKTR Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 014/015 Zadania z elektrotechniki na zawody II stopnia (grupa elektryczna) Zadanie 1 W układzie jak na rysunku 1 dane są:,
Inżynieria Oprogramowania 2013/14. Testy integracyjne
 Testy integracyjne Testwanie integracyjne (integratin testing) wyknywane jest w celu wykrycia błędów w interfejsach i interakcjach pmiędzy integrwanymi mdułami i systemami (sprzęt kmputerwy, system peracyjny).
Testy integracyjne Testwanie integracyjne (integratin testing) wyknywane jest w celu wykrycia błędów w interfejsach i interakcjach pmiędzy integrwanymi mdułami i systemami (sprzęt kmputerwy, system peracyjny).
Uniwersytet Wrocławski Wydział Matematyki i Informatyki Instytut Matematyczny specjalność: matematyka nauczycielska.
 Uniwersytet Wrcławski Wydział Matematyki i Infrmatyki Instytut Matematyczny specjalnść: matematyka nauczycielska Mateusz Suwara PARKIETAŻE PLATOŃSKIE I SZACHOWNICE ARCHIMEDESOWSKIE W GEOMETRII HIPERBOLICZNEJ
Uniwersytet Wrcławski Wydział Matematyki i Infrmatyki Instytut Matematyczny specjalnść: matematyka nauczycielska Mateusz Suwara PARKIETAŻE PLATOŃSKIE I SZACHOWNICE ARCHIMEDESOWSKIE W GEOMETRII HIPERBOLICZNEJ
Ogólne kryteria oceniania z matematyki KLASA I. Klasa I
 Ogólne kryteria ceniania z matematyki KLASA I Uczeń trzymuje ceny za: Wypwiedź ustną, Pracę klaswą Badanie wyników Kartkówkę, Aktywnść pdczas lekcji, Pracę dmwą, referat, gazetki, mdele brył Długterminwy
Ogólne kryteria ceniania z matematyki KLASA I Uczeń trzymuje ceny za: Wypwiedź ustną, Pracę klaswą Badanie wyników Kartkówkę, Aktywnść pdczas lekcji, Pracę dmwą, referat, gazetki, mdele brył Długterminwy
wentylatory oddymiające THGT
 Zastswanie Odprnść na temperaturę 4 C/2h, C/2h i C/2h. Standardwa wersja t 4 C/2h, pzstałe na życzenie. Obudwa krótka Knstrukcja Wentylatry wyknane są zgdnie ze standardem nrmy EN1211-. Wentylatry siwe
Zastswanie Odprnść na temperaturę 4 C/2h, C/2h i C/2h. Standardwa wersja t 4 C/2h, pzstałe na życzenie. Obudwa krótka Knstrukcja Wentylatry wyknane są zgdnie ze standardem nrmy EN1211-. Wentylatry siwe
INSTRUKCJA MONTAŻU przewodu grzejnego PSB typu 07-5801-XXXX
 Przewód grzejny PSB typ 07-5801-XXXX INSTRUKCJA MONTAŻU przewdu grzejneg PSB typu 07-5801-XXXX Spis treści 1. Zastswanie.. str. 1 2. Dane techniczne.... str. 1 3. Zasady bezpieczeństwa..... str. 2 4. Wytyczne
Przewód grzejny PSB typ 07-5801-XXXX INSTRUKCJA MONTAŻU przewdu grzejneg PSB typu 07-5801-XXXX Spis treści 1. Zastswanie.. str. 1 2. Dane techniczne.... str. 1 3. Zasady bezpieczeństwa..... str. 2 4. Wytyczne
BADANIE SZEREGOWEGO OBWODU REZONANSOWEGO RLC
 BADANIE SZEREGOWEGO OBWOD REZONANSOWEGO RLC Marek Górski Celem pomiarów było zbadanie krzywej rezonansowej oraz wyznaczenie częstotliwości rezonansowej. Parametry odu R=00Ω, L=9,8mH, C = 470 nf R=00Ω,
BADANIE SZEREGOWEGO OBWOD REZONANSOWEGO RLC Marek Górski Celem pomiarów było zbadanie krzywej rezonansowej oraz wyznaczenie częstotliwości rezonansowej. Parametry odu R=00Ω, L=9,8mH, C = 470 nf R=00Ω,
LABORATORIUM OBWODÓW I SYGNAŁÓW
 POLITECHNIKA WARSZAWSKA Instytut Radioelektroniki Zakład Radiokomunikacji WIECZOROWE STUDIA ZAWODOWE LABORATORIUM OBWODÓW I SYGNAŁÓW Ćwiczenie Temat: OBWODY PRĄDU SINUSOIDALNIE ZMIENNEGO Opracował: mgr
POLITECHNIKA WARSZAWSKA Instytut Radioelektroniki Zakład Radiokomunikacji WIECZOROWE STUDIA ZAWODOWE LABORATORIUM OBWODÓW I SYGNAŁÓW Ćwiczenie Temat: OBWODY PRĄDU SINUSOIDALNIE ZMIENNEGO Opracował: mgr
Instrukcja korzystania z serwisu Geomelioportal.pl. - Strona 1/12 -
 Instrukcja krzystania z serwisu Gemeliprtal.pl - Strna 1/12 - Spis treści 1. Wstęp... 3 1.1. Słwnik pdstawwych terminów... 3 2. Wyświetlanie i wyszukiwanie danych... 4 2.1. Okn mapy... 5 2.2. Paski z menu
Instrukcja krzystania z serwisu Gemeliprtal.pl - Strna 1/12 - Spis treści 1. Wstęp... 3 1.1. Słwnik pdstawwych terminów... 3 2. Wyświetlanie i wyszukiwanie danych... 4 2.1. Okn mapy... 5 2.2. Paski z menu
2-2. i i. R O R i Av i. Bv o. R of. R if A f v s R S R L. i 2 v 1 v 2. h 11. h22. v o. v i. v s. v f A S. wzmacniacz napięciowy A [V/V] S A Uz.
![2-2. i i. R O R i Av i. Bv o. R of. R if A f v s R S R L. i 2 v 1 v 2. h 11. h22. v o. v i. v s. v f A S. wzmacniacz napięciowy A [V/V] S A Uz. 2-2. i i. R O R i Av i. Bv o. R of. R if A f v s R S R L. i 2 v 1 v 2. h 11. h22. v o. v i. v s. v f A S. wzmacniacz napięciowy A [V/V] S A Uz.](/thumbs/94/118198096.jpg) O T O I U M U K Ł D Ó W I N I O W Y H Ujemne sprzężenie zwrtne 4 Ćwiczenie pracwał Jacek Jakusz. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści teg sameg wzmacniacza pracująceg w następujących kniguracjach:
O T O I U M U K Ł D Ó W I N I O W Y H Ujemne sprzężenie zwrtne 4 Ćwiczenie pracwał Jacek Jakusz. Wstęp Ćwiczenie umżliwia pmiar i prównanie właściwści teg sameg wzmacniacza pracująceg w następujących kniguracjach:
otrzymamy I PRACOWNIA FIZYCZNA
 WYZNACZANE STĘŻENA ROZTWORÓW BARWNYCH PRZY POMOCY KOLORYMETRU FOTOELEKTRYCZNEGO. Cel ćwiczenia: sprawdzenie prawa Beera dla rztwru siarczanu miedziweg CuSO 4, wyznaczenie nieznaneg stężenia rztwru, zapznanie
WYZNACZANE STĘŻENA ROZTWORÓW BARWNYCH PRZY POMOCY KOLORYMETRU FOTOELEKTRYCZNEGO. Cel ćwiczenia: sprawdzenie prawa Beera dla rztwru siarczanu miedziweg CuSO 4, wyznaczenie nieznaneg stężenia rztwru, zapznanie
ZAKŁAD ELEKTRONIKI PRZEMYSŁOWEJ LABORATORIUM TEORII PRZEKSZTAŁTNIKÓW
 ZAKŁAD ELEKTRONIKI PRZEMYSŁOWEJ INSTYTUT STEROWANIA I ELEKTRONIKI PRZEMYSLOWEJ WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ LABORATORIUM TEORII PRZEKSZTAŁTNIKÓW I_PS. UKŁADY PRZEKSZTAŁTNIKÓW SIECIOWYCH
ZAKŁAD ELEKTRONIKI PRZEMYSŁOWEJ INSTYTUT STEROWANIA I ELEKTRONIKI PRZEMYSLOWEJ WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ LABORATORIUM TEORII PRZEKSZTAŁTNIKÓW I_PS. UKŁADY PRZEKSZTAŁTNIKÓW SIECIOWYCH
