Algorytmy wymiany. Dariusz Wawrzyniak 1. Podstawowe pojęcia (1) Podstawowe pojęcia (2) Podstawowe pojęcia (3)
|
|
|
- Grzegorz Łuczak
- 8 lat temu
- Przeglądów:
Transkrypt
1 Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany sron Podsawowe pojęcia () N = {,,, n} zbiór numerów sron wirualnych danego procesu M = {,,, m} zbiór numerów ramek danego procesu w pamięci fizycznej VA wirualna przesrzeń adresowa, va VA adres wirualny va = x, w = x c + w, gdzie c jes rozmiarem srony (ramki) RA fizyczna przesrzeń adresowa ra RA adres fizyczny Sysemy operacyjne Algorymy wymiany sron Podsawowe pojęcia () Podsawowe pojęcia () f( x) c+ w,gdy f( x) ra = nieokreślony, gdy f ( x) = błąd srony y, gdy srona jes w ramce y w chwili f ( x) =, gdy brak srony w pamięci Dynamiczne własności procesu określone są przez ciąg zgłoszeń (odniesień do sron) ω = r, r,, r,, gdzie jes dyskreną chwilą czasową, a r = x (x N ) oznacza, że odniesienie do srony numer x wysąpiło jako -e. S san pamięci operacyjnej zdefiniowany jako zbiór numerów sron wirualnych, znajdujących się w ramkach pamięci fizycznej w chwili (S N, S m) Algorymem wymiany jes przewarzanie ciągu zgłoszeń ω = r, r,, r, i generowanie kolejnych sanów pamięci S, S,, S,, Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Podsawowe pojęcia () X zbiór numerów sron sprowadzonych do pamięci w chwili (X N \ S ) Y zbiór numerów sron usuwanych z pamięci w chwili (Y S ) Zmiana sanu pamięci w chwili w sosunku do chwili wynika z ze sprowadzenia sron o numerach ze zbioru X i usunięciu sron o numerach ze zbioru Y S = S X \ Y Formalna definicja algorymu wymiany sron Algorym wymiany A jes zdefiniowany poprzez funkcję przejścia g A, aką że g A (S, Q, r ) = (S, Q ), gdzie Q san wymiany w chwili, reprezenujący hisorię wymiany S san pamięci operacyjnej w chwili r numer srony, do kórej nasąpiło odniesienie w chwili (S, Q ) nazywana jes konfiguracją algorymu wymiany Algorym sprowadzania A F w chwili określa zbiór X Algorym usuwania A R w chwili określa zbiór Y Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
2 Sysemy operacyjne Algorymy wymiany sron Sprowadzanie i usuwanie na żądanie () Algorym sprowadzania jes algorymem sprowadzania na żądanie A DF, gdy sprowadzenie srony nasępuję ylko przy wysąpieniu odniesienia do niej i ylko wówczas, gdy nie ma jej w pamięci. Algorym usuwania jes algorymem usuwania na żądanie A DR, gdy usunięcie srony z pamięci nasępuje w przypadku braku wolnych ramek i wynika z konieczności zwolnienia ramki na porzeby innej sprowadzanej srony. m Sprowadzanie i usuwanie na żądanie () Algorym sprowadzania na żądanie A DF : m ( {,} ( r = ) ) X S X Algorym usuwania na żądanie A DR : ( {,} ( ( r < m) = ) ) Y S S Y Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Klasyfikacja algorymów wymiany Algorymy wymiany na żądanie A DFDR zarówno sprowadzanie sron, jak i ich usuwanie odbywa się na żądanie. Algorymy wymiany ze sprowadzaniem na żądanie A DFR ylko sprowadzanie sron odbywa się na żądanie, ich usuwanie wykonywane jes przez dowolny algorym. Algorymy wymiany ze wsępnym sronicowaniem na żądanie A DP w wyniku wysąpienia błędu srony sprowadzany do pamięci jes zbiór sron (w ym srona żądana). Sysemy operacyjne Algorymy wymiany sron 9 Algorym wymiany na żądanie A DFDR Funkcja przejścia g ADFDR spełnia w każdej chwili nasępujące warunki: S S jeśli r S r r m r y r m { } jeśli = S S S < S { } \{ } jeśli S S = y numer srony wirualnej usuwanej z pamięci Sysemy operacyjne Algorymy wymiany sron Algorym wymiany ze sprowadzaniem na żądanie A DFR S Funkcja przejścia g ADFR spełnia w każdej chwili nasępujące warunki: S \ Y jeśli r S r Y r r m r r m { }\ jeśli = S Y S S < S { } \ Y Y jeśli S S = S Algorym wymiany ze wsępnym sronicowaniem na żądanie A DP Funkcja przejścia g ADP spełnia w każdej chwili nasępujące warunki: S jeśli r S jeśli = S X r S r X S X m S X \ Y jeśli S X S X \ Y = r r m Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
3 Sysemy operacyjne Algorymy wymiany sron Kosz wymiany sron () Z punku widzenia efekywności przewarzania kosz wymiany możemy uożsamiać z czasem realizacji wymiany. W celu uproszczenia analizy możemy przyjąć, że kosz usunięcia srony sanowi sałą część koszu jej sprowadzenia. Kosz wynika zaem z czasu sprowadzania, kóry w ogólności zależy od ciągu zgłoszeń, liczby dosępnych ramek i algorymu wymiany C(A, m, ω) Sysemy operacyjne Algorymy wymiany sron Kosz wymiany sron () Niech h(k) oznacza kosz jednorazowego sprowadzenia grupy k sron, przy czym: h() =, h() =. Całkowiy kosz sprowadzenia sron i ym samym posać funkcji C(A, m, ω) w przypadku ogólnym dana jes wzorem: C( A, m, ω ) = h( X ) Sysemy operacyjne Algorymy wymiany sron Kosz wymiany sron () W przypadku zasosowania dysku jako urządzenia wymiany, na czas sprowadzania wypływ mają: T w czas oczekiwania (suma czasu oczekiwania w kolejce do urządzenia oraz czasu przygoowania urządzenia do ransmisji) T r czas ransmisji danych Posać funkcji h(k) jes zaem nasępująca: h(k) = T w + k T r Sysemy operacyjne Algorymy wymiany sron Kosz wymiany sron () Własność funkcji h(k) przy założeniu, że T w > i k > : h(k) < k (T w + T r ) h(k) k h() Wniosek: sprowadzenie kilku sron jako wyniku realizacji jednego żądania jes bardziej koszowne niż sprowadzenie jednej srony, ale mniej koszowne niż sprowadzanie poszczególnych sron osobno. Sysemy operacyjne Algorymy wymiany sron Kosz wymiany sron () Kosz wymiany można aproksymować za pomocą paramerów FN (liczba wygenerowanych błędów srony) i TN (liczba ransmisji sron). Całkowiy czas oczekiwania na urządzenie (isona składowa czasu wymiany) również jes zależny od liczby błędów srony. Wniosek: należy minimalizować liczbę błędów srony i ym samym redukować czas realizacji wymiany, czyli kosz. Klasyfik. alg. wymiany ze wzgl. na sposób zasępowania sron Zasępowanie lokalne (ang. local replacemen) algorym wymiany zasępuje ylko srony w ramkach przydzielonych procesowi, kóry spowodował błąd srony sronicowanie sayczne. Zasępowanie globalne (ang. global replacemen) algorym wymiany zasępuje srony znajdujące się w dosępnej puli ramek w całym sysemie (w szczególności zaem usuwa srony innych procesów) sronicowanie dynamiczne. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
4 Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany na żądanie definicje pomocnicze Dysans w przód: k gdy r+ k= x r+ i x << i k d ( x) = gdy r+ i x < i Dysans w ył: k gdy r k= x r i x << i k b ( x) = gdy ri x i< Chwila osaniego sprowadzenia do pamięci: g ( x) = max{ i: i x X } Sysemy operacyjne Algorymy wymiany sron 9 i Algorymy wymiany na żądanie własności Srona x sprowadzana jes w chwili ylko wówczas, gdy r = x i x S Srona y usuwana jes w chwili ylko wówczas, gdy S = m i r S Zachodzi warunek Y X O specyfice algorymu wymiany na żądanie decyduje algorym usuwania sron. Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany na żądanie funkcja koszu Funkcja koszu sprowadza się do nasępującej posaci C( A, m, ω ) = X Algorymy wymiany na żądanie MIN Wybór srony usuwanej w chwili : y = min{ z S : d ( z) = max{ d ( u)}} u S Twierdzenie: w klasie algorymów wymiany na żądanie algorym MIN minimalizuje kosz C(A, m, ω) dla każdego m i ω. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany na żądanie LRU (Leas Recenly Used) Wybór srony usuwanej w chwili : usuwana jes srona y, dla kórej b( y) = max{ b( u)} u S Algorym daje dobre wyniki w przypadku procesów wykazujących lokalność czasową odwołań do pamięci, gdyż dysans w ył dobrze przybliża dysans w przód. Sysemy operacyjne Algorymy wymiany sron Alg. wymiany na żąd. LFU/MFU (Leas/Mos Frequenly Used) Niech FREQ (x) oznacza liczbę odniesień do srony x w ciągu: r, r,..., r - lub r k, r k+,..., r -, gdzie k = g (x) Wybór srony usuwanej w chwili : usuwana jes srona y, dla kórej LFU: FREQ ( y) min{freq ( u)} = u S MFU: FREQ ( y) = max{freq ( u)} u S Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
5 Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany na żądanie FIFO (ang. Firs In Firs Ou) Wybór srony usuwanej w chwili : usuwana jes srona y, dla kórej g ( y) min{ g ( u)} = u S Algorym daje dobre wyniki w przypadku programów z sekwencyjnym przepływem serowania (mało pęli, wywołań procedur) Algorymy wymiany na żądanie LIFO (ang. Las In Firs Ou) Wybór srony usuwanej w chwili : usuwana jes srona y, dla kórej g ( y) = max{ g ( u)} u S Algorym daje dobre wyniki w przypadku realizacji fragmenu programu zawierającego pęlę, gdyż ponowne wykonanie ej samej insrukcji nasąpi dopiero po wykonaniu całej kolejnej ieracji. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany na żądanie LD (ang. Loop Deecion) Definicja czasu biernego l : niech k = - b (z) l( z) = bk( z) Wybór srony usuwanej w chwili : usuwana jes srona y, dla kórej b ( y) = max{ b ( z)} jeśli b ( z) > l ( z) z S z S l ( y) b ( y) = max{ l ( z) b ( z)} jeśli z S b ( z) l ( z) z S momen osaniego odniesienia do srony w przeszłości Sysemy operacyjne Algorymy wymiany sron Zagadnienia implemenacyjne Implemenacja algorymu FIFO Implemenacja algorymu LRU Algorymy przybliżające meodę LRU algorym drugiej szansy (FINUFO) algorym dodakowych biów odwołań ulepszony algorym drugiej szansy Implemenacja algorymów licznikowych Sysemy operacyjne Algorymy wymiany sron Implemenacja algorymu FIFO Urzymywanie lisy numerów sron w kolejności ich sprowadzania do pamięci Umieszczanie numeru sprowadzanej srony na końcu lisy Usuwanie z pamięci (i z lisy) srony, kórej numer znajduje się na począku lisy Możliwość wysąpienia anomalii Belady ego Sysemy operacyjne Algorymy wymiany sron 9 dla ramek mamy 9 błędów srony, a dla ramek mamy błędów srony Przykład anomalii Belady ego Ciąg odniesień:,,,,,,,,,,, Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
6 Sysemy operacyjne Algorymy wymiany sron Implemenacja algorymu LRU Licznik przed każdym odwołaniem do pamięci zwiększana jes warość pewnego licznika i wpisywana do odpowiedniej pozycji opisującej sronę w ablicy sron (lub w innej specjalnej srukurze sysemu operacyjnego). Z pamięci usuwana jes wówczas srona z najmniejszą warością ego licznika, co wymaga przejrzenia całej ablicy sron. Sos numery sron, do kórych nasępuje odwołanie, odkładane są na szczycie sosu. Przed odłożeniem na szczycie numer srony musi być wydobyy ze środka sosu, czyli z miejsca, gdzie był osanio odłożony. W ej implemenacji pamięci usuwana jes srona z dna sosu. Algorymy przybliżające meodę LRU Niezbędne wspomaganie sprzęowe: bi odniesienia (ang. reference bi) usawiany dla danej srony przez sprzę zawsze, gdy nasępuje zapis lub odczy na ej sronie, bi modyfikacji (ang. modify bi) usawiany dla danej srony przez sprzę zawsze, gdy nasępuje zapis na ej sronie. Algorymy korzysające ze wspomagania sprzęowego: algorym drugiej szansy wykorzysuje bi odniesienia, algorym dodakowych biów odwołań wykorzysuje bi odniesienia, ulepszony algorym drugiej szansy wykorzysuje bi odniesienia i bi modyfikacji. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron ablica sron Algorym drugiej szansy (FINUFO) bi odnies. srona do usunięcia lisa sron Algorym dodakowych biów odwołań ablica sron bi odnies. ablica dodakowych biów odwołań osania srony do usunięcia Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron ablica sron Ulepszony algorym drugiej szansy bi odnies. bi modyf. srona do usunięcia lisa sron Sysemy operacyjne Algorymy wymiany sron Implemenacja algorymów LFU i MFU Urzymywanie liczników odniesień do każdej ze sron i ich inkremenacja przy każdym odwołaniu do odpowiedniej srony Usuwanie srony z najmniejszą (LFU) lub największą (MFU) warością licznika Zerowanie licznika po usunięciu srony z pamięci Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
7 Sysemy operacyjne Algorymy wymiany sron Dobór liczby ramek Minimalna liczba ramek zdefiniowana przez archiekurę kompuera (zależna od maksymalnej liczby komórek adresowanych przez jeden rozkaz). Liczba ramek przydzielona dla procesu podział równomierny (ang. equal allocaion) podział proporcjonalny (ang. proporional allocaion) przydział zależny od prioryeu procesu Przydział ramek Sronicowanie sayczne liczba ramek jes usalona na cały czas cyklu przewarzania procesu, Sronicowanie dynamiczne liczba przydzielonych ramek jes zmienna. liczba ramek przydzielonych procesowi zmienia się w czasie w zależności od porzeb samego procesu oraz działań i porzeb innych procesów w sysemie. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Problem sronicowania saycznego Niech f i, f j i f oznaczają średnią częsość błędów srony odpowiednio procesu P i, P j oraz całego sysemu. Niech m i i m j oznacza liczbę ramek odpowiednio procesu P i, P j. Niech f i oznacza średnią częsość błędów srony procesu P i przy liczbie ramek m i f > f m < m f > f ( ) j i i i i Sysemy operacyjne Algorymy wymiany sron 9 Zjawisko szamoania (migoania) sron (ang. rashing) Szamoanie oznacza isony wzros częsości generowania błędu srony, wynikający z niemożności urzymania w pamięci sron akywnych. Przyczyna szamoania: zby mała liczba dosępnych ramek. Sysemy operacyjne Algorymy wymiany sron Szamoanie w przypadku sronicowania saycznego Szamoanie w przypadku sronicowania dynamicznego Założenie: program wykazuje lokalność przesrzenną odwołań do pamięci. Model srefowy (ang. localiy model) srefa zbiór sron akywnych w czasie wykonywania określonego fragmenu programu, wykonanie programu sprowadza się do przechodzenia z jednej srefy do drugiej, program składa się z wielu sref, najczęściej zachodzących na siebie. Przyczyna szamoania: liczba dosępnych ramek jes mniejsza od rozmiaru srefy. spadek liczby procesów goowych spadek wykorzysania procesora wzros liczby procesów oczekujących zwiększenie liczby zadań w sysemie Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
8 Sysemy operacyjne Algorymy wymiany sron Zapobieganie szamoaniu W sysemie sronicowania dynamicznego szamoanie można ograniczyć przez zasosowanie algorymu zasępowania lokalnego lub prioryeowego (nie likwiduje o jednak problemu!!!). Szamoanie można zlikwidować, dosarczając procesowi ylu wolnych ramek ilu porzebuje do wykonania określonego fragmenu programu (np. procedury, pęli). Jak się dowiedzieć ile wolnych ramek jes porzebnych procesowi? Alg. wymiany ze sprowadzaniem na żądanie własności Srona x sprowadzana jes w chwili ylko wówczas, gdy r = x i x S Możliwe jes usunięcie srony nawe w przypadku odniesienia, kóre nie powoduje błędu srony Możliwy jes warunek: Y > X ( X ) Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Alg. wymiany ze sprowadzaniem na żąd. dodakowe oznaczenia f średnia częsość błędów srony c pf kosz obsługi błędu srony c u kosz przechowywania srony w pamięci przez jednoskę czasu wirualnego Sysemy operacyjne Algorymy wymiany sron Alg. wymiany ze sprow. na żąd. VMIN (ang. Variable-space MIN) Wybór srony usuwanej w chwili : srona usuwana jes naychmias po jej przeworzeniu i ylko wówczas, gdy nie będzie ona wykorzysywana przez czas dłuższy niż c pf /c u jednosek czasu wirualnego cpf Y { r } jeśli d( r ) = > cu Twierdzenie: w klasie algorymów wymiany ze sprowadzaniem na żądanie, przy określonym średnim rozmiarze przydzielonej procesowi pamięci operacyjnej m w, algorym VMIN minimalizuje średnią częsość generowania błędów srony. Sysemy operacyjne Algorymy wymiany sron Zbiór roboczy definicja Zbiór roboczy przykład Zbiór roboczy procesu (ang. working-se) zbiór sron, do kórych nasąpiło odwołanie w ciągu osanich τ odwołań (zw. oknie zbioru roboczego) w czasie działania procesu Okno zbioru roboczego (ang. working-se window) liczba odwołań do pamięci, przez kóre dana srona pozosaje w zbiorze roboczym od osaniego odwołania do niej τ = τ =,,,,,,,,,,,, {,,, } = W(, ) {,,, } = W(, ) {,,,, } = W(, ) {,,, } = W(, ) Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
9 Sysemy operacyjne Algorymy wymiany sron Usalanie liczby porzebnych ramek Zaporzebowanie na ramki w całym sysemie jes sumą rozmiarów zbiorów roboczych, czyli Z = Σ W i, gdzie W i jes mocą (liczbą elemenów) zbioru W i, czyli zaporzebowaniem i-ego procesu na ramki. Jeśli Z > m, gdzie m jes całkowią liczbą ramek w sysemie dosępną dla procesów użykownika, o zaporzebowanie jes zby duże i może powsać szamoanie. Sysem operacyjny musi wówczas wsrzymać wykonywanie jakiegoś procesu i zwolnić zajmowane przez niego ramki Jeśli w sysemie są wolne ramki (Z < m), o można rozpocząć nowy proces. Sysemy operacyjne Algorymy wymiany sron 9 Alg. wymiany ze sprow. na żąd. WS (ang. Working Se) Formalna definicja zbioru roboczego W(, τ) W(, τ ) = z: r i= z = { z: b( z) < τ} < i τ Wybór srony usuwanej w chwili : usuwana jes srona, kóra nie była używana w osanich τ jednoskach czasu wirualnego { τ } Y = y: y S y W(, ) = S \ W(, τ ) Problem: jak dobrać rozmiar okna zbioru roboczego τ? Sysemy operacyjne Algorymy wymiany sron Alg. wymiany ze sprow. na żąd. WS (ang. Working Se) Jak należałoby zinerpreować fak wysąpienia problemu zasępowania (brak wolnej ramki) w przypadku obsługi błędu srony? Alg. wymiany ze sprow. na żąd. DWS (ang. Damped Working Se) Wybór srony usuwanej w chwili : usuwana jes srona, kóra nie była używana w osanich τ jednoskach czasu wirualnego lub w przypadku wysąpienia błędu srony srona, kóre nie była wykorzysywana przez więcej niż ατ jednosek czasu wirualnego (α < ). S \ W(, τ ) jeśli r S Y = { y: b( y) = max{ b( z)} b( y) > ατ} jeśli r S z S Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Koncepcja idenyfikacji zbioru roboczego Dla każdej ramki urzymywany jes wirualny czas osaniego odniesienia do niej. Po każdym odniesieniu do srony zwiększana jes warość licznika odniesień i wpisywana do odpowiedniej ablicy na pozycji odpowiadającej ramce, w kórej znajduję się adresowana srona. Do zbioru roboczego należą e srony, dla kórych różnica pomiędzy bieżącą warością licznika odniesień, a warością wpisaną w ablicy jes mniejsza lub równa rozmiarowi okna zbioru rob. Problemy zasosowania koncepcji zbioru roboczego Kwesia zasadności przesłanki o lokalności czasowej odniesień do pamięci Problem precyzyjnej idenyfikacji zbioru roboczego: moniorowanie odniesień do pamięci urzymywanie odpowiednich srukur danych Problem doboru rozmiaru okna zbioru roboczego Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak 9
10 Sysemy operacyjne Algorymy wymiany sron Problemy idenyfikacji zbioru roboczego Problem moniorowania odniesień do sron zby duży kosz (narzu czasowy) dosępu do pamięci w przypadku rozwiązań programowych zby duży kosz realizacji rozwiązań sprzęowych Problem złożoności obliczeniowej pamięciowej duża złożoność srukur danych czasowej czas porzebny na akualizację srukur danych oraz na zidenyfikowanie sron (ramek), kóre znalazły się poza zbiorem roboczym Sysemy operacyjne Algorymy wymiany sron Przybliżona realizacja koncepcji zbioru roboczego Wspomaganie sprzęowe bi odniesienia. Okresowe (wyznaczone przez czasomierz lub przez wysąpienie błędu srony) inkremenowanie licznika reprezenującego czas wirualny oraz sprawdzanie biu odniesienia dla każdej z ramek. Jeśli bi odniesienia jes usawiony, o skasowanie biu odniesienia i wpisanie bieżącej warości licznika do ablicy na pozycji odpowiadającej ramce. Jeśli bi odniesienia jes skasowany o sprawdzenie różnicy pomiędzy bieżącą warością licznika a warością wpisaną na odpowiedniej pozycji w ablicy i usunięcie srony, gdy różnica jes większa niż rozmiar okna. Sysemy operacyjne Algorymy wymiany sron Algorym WSClock (). Dla każdej ramki urzymywany jes wirualny czas (przybliżony) osaniego odniesienia do niej.. Wszyskie srony w pamięci (niezależnie od przynależności do procesu) powiązane są w cykl zgodnie z kolejnością ich sprowadzenia (podobnie jak w przypadku alg. drugiej szansy). W wyniku wysąpienia błędu srony sprawdzany jes bi odniesienia do srony wskazywanej jako kolejna do usunięcia.. Jeśli bi odniesienia jes usawiony, zosaje on skasowany, nasępuje wskazanie srony nasępnej w cyklu i sprawdzenie biu odniesienia. Sysemy operacyjne Algorymy wymiany sron Algorym WSClock (). Jeśli bi odniesienia jes skasowany, sprawdzana jes różnica pomiędzy wirualnym czasem bieżącym, a czasem osaniego odniesienia do wskazywanej srony. jeśli różnica jes większa od rozmiaru okna zbioru roboczego, srona jes usuwana, a ramka zosaje wykorzysana dla srony sprowadzanej, w przeciwnym razie srona pozosaje i nasępuje wskazanie srony nasępnej w cyklu i ponawiany jes ciąg działań począwszy od punku algorymu.. W przypadku braku wolnych ramek nasępuje wsrzymanie (zawieszenie) jakiegoś procesu ( planisa średnioerminowy). Sysemy operacyjne Algorymy wymiany sron Algorym WSClock przykład ablica sron bi odnies. czas odnies. 9 9 rozmiar okna: czas bieżący: srona do usunięcia lisa sron Algorym WSClock a koncepcja zbioru roboczego. Na czym polega naruszenie idei zbioru roboczego przez algorym WSClock?. Dlaczego w przypadku zbioru roboczego jes sens sosować algorym usuwania inny niż na żądanie? Sysemy operacyjne Algorymy wymiany sron 9 Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
11 Sysemy operacyjne Algorymy wymiany sron Algorym zegarowy dwuwskazówkowy. Wszyskie srony w pamięci (niezależnie od przynależności do procesu) powiązane są w lisę cykliczną zgodnie z kolejnością ich sprowadzenia (podobnie jak w przypadku alg. drugiej szansy). Lisa przeglądana jes okresowo przez wskazówki: przednią i ylną.. Przednia wskazówka zeruje bi odniesienia.. Jeśli bi odniesienia przed nadejściem ylnej wskazówki zosanie ponownie usawiony, srona pozosaje w pamięci, w przeciwnym przypadku jes usuwana.. Algorym serowany jes nasępującymi paramerami: empo przeglądania, rozsunięcie wskazówek. Sysemy operacyjne Algorymy wymiany sron Algorym dwuwskazówkowy przykład ablica sron bi odnies. srona do usunięcia lisa sron Sysemy operacyjne Algorymy wymiany sron Implemenacja przybliżająca algorym DWS () Dla każdej ramki w sysemie urzymywany jes przybliżony czas osaniego odniesienia. W przypadku wysąpienia błędu srony lub w wyniku przerwania od czasomierza sprawdzany jes bi odniesienia dla każdej ramki. jeśli bi odniesienia jes usawiony, jes on kasowany i nasępuje akualizacja czasu odniesienia do ramki, jeśli bi odniesienia jes skasowany sprawdzany jes zarejesrowany wcześniej czas osaniego odniesienia i obliczany jes dysans w ył b. Implemenacja przybliżająca algorym DWS () W zależności od warości dysansu w ył podejmowane są nasępujące akcje: b > τ srona jes usuwana, a ramka dołączana do puli wolnych ramek, ατ < b τ ramka jes dołączana do zbioru poencjalnych ramek-ofiar, ale srona nie jes usuwana, b ατ srona pozosaje w zbiorze roboczym. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Implemenacja przybliżająca algorym DWS () W przypadku wysąpienia błędu srony podejmowane są nasępujące akcje: jeśli isnieją wolne ramki, jedna z nich zosanie wykorzysana do sprowadzenia srony, jeśli nie ma wolnych ramek ale isnieją poencjalne ramki-ofiary, nasępuje zasąpienie srony w wybranej ramce przez sronę sprowadzaną, jeśli wszyskie ramki są zajęe nasępuje zawieszenie jednego z procesów ( planisa średnioerminowy) i wykorzysanie zwolnionych przez niego ramek. Alg. wymiany ze sprow. na żąd. PFF (ang. Page Faul Frequency) Jeśli częsoliwość błędów srony generowanych przez proces przekroczy usalony poziom f H, o dla sron ego procesu sprowadzanych do pamięci przydzielana są nowe ramki. Jeśli częsoliwość błędów srony spadnie poniżej usalonego poziomu f L, o usuwane są wszyskie srony, do kórych nie było odniesienia od chwili wysąpienia osaniego błędu srony w danym procesie. W szczególności f H = f L Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
12 Sysemy operacyjne Algorymy wymiany sron Implemenacja PFF konrola częsości błędów srony Przy każdym błędzie srony generowanym przez proces zwiększany jes licznik błędów srony danego procesu oraz zerowane są biy odniesienia do jego sron. W określonych okresach czasu (generowanych przez czasomierz) sprawdzane są (a nasępnie zerowane) warości liczników poszczególnych procesów. Jeśli warość licznika jes większa od usalonej górnej granicy, o procesowi przydzielana jes dodakowa ramka. Jeśli warość licznika jes mniejsza od usalonej dolnej granicy, o procesowi zabierana jes jedna ramka (lub wszyskie ramki z wykasowanym biem odniesienia). Implemenacja PFF konrola okresu pomiędzy błędami srony Przy każdym błędzie srony sprawdzany jes czas jaki upłynął od poprzedniego błędu srony. Jeśli czas jes mniejszy od usalonej wielkości T min, o na porzeby sprowadzanej srony przydzielana jes dodakowa ramka. Jeśli czas jes większy od usalonej wielkości T max, o wszyskie srony ze skasowanym biem odniesienia są usuwane (ramki są zwalniane), a bi odniesienia dla sron pozosających w pamięci jes kasowany. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Alg. wymiany ze sprowadzaniem na żąd. VSWS (ang. variableinerval sampled working se) Przy każdym błędzie srony zwiększany jes licznik błędów srony danego procesu n. Co pewien okres czasu T, wynikający ze sanu wymiany, nasępuje konrola odniesień do sron. W ramach konroli e srony, do kórych nie było odniesienia są usuwane (ich ramki są zwalniane), a biy odniesienia sron pozosających na nasępny okres (do kórych było odniesienie) są kasowane. Warość licznika n jes zerowana. Sysemy operacyjne Algorymy wymiany sron 9 Wielkość inerwału czasu dla algorymu VSWS Alg. serowany jes nasępującymi paramerami: T max maksymalna wielkość inerwału czasu T min minimalna wielkość inerwału czasu n max maksymalna liczba błędów srony Konrola nasępuje w chwili, po czasie T od momenu poprzedniej konroli, usalanym nasępująco: n < nmax T = Tmax n n T T < T max min max Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany z wsępnym sronicowaniem dodakowe oznaczenia PRED(x) funkcja określająca numer srony, kórą należy ewenualnie wsępnie sprowadzić w przypadku wysąpienia błędu srony w momencie odniesienie do srony nr x. Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany z wsępnym sronicowaniem DPMIN (ang. Demand Prepaging MIN) W chwili wysąpienia błędu srony do pamięci sprowadzane jes m pierwszych sron w przyszłym ciągu odniesień. S jeśli r S S = { x, x,, xl} ( l m) jeśli r S Twierdzenie: w klasie algorymów wymiany z wsępnym sronicowaniem na żądanie algorym DPMIN jes opymalny ze względu na liczbę błędów srony. Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
13 Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany z wsępnym sronicowaniem OBL (ang. One Block Lookahead) Niech PRED(i) = i + W chwili wysąpienia błędu srony nasępuje sprowadzenie srony x = r i wymiana zgodnie z algorymem LRU. Jeśli srona nr x = PRED(x ) S -, o nasępuje sprowadzenie srony x i wymiana zgodnie z algorymem LRU. Algorymy wymiany z wsępnym sronicowaniem SL (ang. Spaial Lookahead) () Niech u oznacza nr srony osanio sprowadzanej do pamięci w wyniku odniesienia do niej. Niech począkowo PRED(i) = i + Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany z wsępnym sronicowaniem SL () W chwili wysąpienia błędu srony nasępuje sprowadzenie srony x = r i wymiana zgodnie z algorymem LRU. Jeśli przy poprzedniej wymianie nie dokonano wsępnego sprowadzenia lub nie było odniesienia do srony wsępnie sprowadzonej do chwili obecnej PRED(u) := r. Jeśli srona nr x = PRED(x ) S -, o nasępuje sprowadzenie srony x i wymiana zgodnie z algorymem LRU. u := r. Algorymy wymiany z wsępnym sronic. FDPA (Fixed-space Demand Prepaging Alg.) () Algorym wykorzysuje dodakową wiedzę wynikającą ze saycznej analizy kodu (przed wykonaniem programu) lub z informacji dosarczonych przez programisę. Uzyskana wiedza reprezenowana jes w ciągu zgłoszeń przez dodakowe insrukcje dla sysemu operacyjnego: FREE(x) srona x nie będzie wykorzysywana w niedalekiej przyszłości, PRE(x) srona x będzie wkróce wykorzysywana. Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany z wsępnym sronicowaniem FDPA () Z każdą sroną x skojarzone są nasępujące biy: bi usunięcia D(x) bi wsępnego sprowadzenia P(x) Z zbiorze sron w pamięci S wyróżnia się nasępujące podzbiory: D = {x : x S D(x) = } P = {x : x S P(x) = } Algorymy wymiany z wsępnym sronicowaniem FDPA () Zasady usuwania sron jeśli S < m y D jeśli D zgodnie z LRU w pozosałych przypadkach Sysemy operacyjne Algorymy wymiany sron Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
14 Sysemy operacyjne Algorymy wymiany sron Algorymy wymiany z wsępnym sronicowaniem FDPA () Obsługa odniesienia do srony r = FREE( x) x S D( x): = r = PRE( x) x S P( x) : = r = x x S S : = S, P( x): = r = x x S dokonaj wymiany Algorymy wymiany z wsępnym sronicowaniem FDPA () Realizacja wymiany: sprowadzenie żądanej srony x, usawienie D(x) :=, i usunięcie, jeśli o konieczne, srony ze zbioru S - \P -. Wsępne sronicowanie: jeśli S - \D - < m i x:p(x) =, dokonaj sprowadzenia srony x z ewenualną wymianą. Sysemy operacyjne Algorymy wymiany sron 9 Sysemy operacyjne Algorymy wymiany sron Dariusz Wawrzyniak
Algorytmy wymiany. Podstawowe pojęcia (1)
 Algorymy wymiany sron Podsawowe pojęcia () N = {,,, n} zbiór numerów sron wirualnych danego procesu M = {,,, m} zbiór numerów ramek danego procesu w pamięci fizycznej VA wirualna przesrzeń adresowa, va
Algorymy wymiany sron Podsawowe pojęcia () N = {,,, n} zbiór numerów sron wirualnych danego procesu M = {,,, m} zbiór numerów ramek danego procesu w pamięci fizycznej VA wirualna przesrzeń adresowa, va
Zarządzanie pamięcią operacyjną i pamięć wirtualna
 Zarządzanie pamięcią operacyjną i pamięć wirtualna Pamięć jako zasób systemu komputerowego. Wsparcie dla zarządzania pamięcią na poziomie architektury komputera. Podział i przydział pamięci. Obraz procesu
Zarządzanie pamięcią operacyjną i pamięć wirtualna Pamięć jako zasób systemu komputerowego. Wsparcie dla zarządzania pamięcią na poziomie architektury komputera. Podział i przydział pamięci. Obraz procesu
SOE Systemy Operacyjne Wykład 8 Pamięć wirtualna dr inż. Andrzej Wielgus
 SOE Systemy Operacyjne Wykład 8 Pamięć wirtualna dr inż. Andrzej Wielgus Instytut Mikroelektroniki i Optoelektroniki WEiTI PW Pamięć wirtualna Stronicowanie na żądanie większość współczesnych systemów
SOE Systemy Operacyjne Wykład 8 Pamięć wirtualna dr inż. Andrzej Wielgus Instytut Mikroelektroniki i Optoelektroniki WEiTI PW Pamięć wirtualna Stronicowanie na żądanie większość współczesnych systemów
Pamięć wirtualna. Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak
 Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak jest organizacją zasobów pamięci, zrealizowaną w oparciu o tzw. przestrzeń wymiany w pamięci drugiego rzędu (na dysku). Pamięć operacyjna (fizyczna)
Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak jest organizacją zasobów pamięci, zrealizowaną w oparciu o tzw. przestrzeń wymiany w pamięci drugiego rzędu (na dysku). Pamięć operacyjna (fizyczna)
Stronicowanie w systemie pamięci wirtualnej
 Pamięć wirtualna Stronicowanie w systemie pamięci wirtualnej Stronicowanie z wymianą stron pomiędzy pamięcią pierwszego i drugiego rzędu. Zalety w porównaniu z prostym stronicowaniem: rozszerzenie przestrzeni
Pamięć wirtualna Stronicowanie w systemie pamięci wirtualnej Stronicowanie z wymianą stron pomiędzy pamięcią pierwszego i drugiego rzędu. Zalety w porównaniu z prostym stronicowaniem: rozszerzenie przestrzeni
Architektura Systemów Komputerowych. Architektura potokowa Klasyfikacja architektur równoległych
 Archiekura Sysemów Kompuerowych Archiekura pookowa Klasyfikacja archiekur równoległych 1 Archiekura pookowa Sekwencyjne wykonanie programu w mikroprocesorze o archiekurze von Neumanna Insr.1 Φ1 Insr.1
Archiekura Sysemów Kompuerowych Archiekura pookowa Klasyfikacja archiekur równoległych 1 Archiekura pookowa Sekwencyjne wykonanie programu w mikroprocesorze o archiekurze von Neumanna Insr.1 Φ1 Insr.1
Pamięć wirtualna jest organizacją zasobów pamięci, zrealizowaną w oparciu o tzw. przestrzeń wymiany w pamięci drugiego rzędu (na dysku).
 jest organizacją zasobów pamięci, zrealizowaną w oparciu o tzw. przestrzeń wymiany w pamięci drugiego rzędu (na dysku). Pamięć operacyjna (fizyczna) jest dla tych zasobów tylko pewnym oknem, przechowującym
jest organizacją zasobów pamięci, zrealizowaną w oparciu o tzw. przestrzeń wymiany w pamięci drugiego rzędu (na dysku). Pamięć operacyjna (fizyczna) jest dla tych zasobów tylko pewnym oknem, przechowującym
Temat: Weryfikacja nienaruszalności bezpieczeństwa SIL struktury sprzętowej realizującej funkcje bezpieczeństwa
 1 Lab3: Bezpieczeńswo funkcjonalne i ochrona informacji Tema: Weryfikacja nienaruszalności bezpieczeńswa SIL srukury sprzęowej realizującej funkcje bezpieczeńswa Kryeria probabilisyczne bezpieczeńswa funkcjonalnego
1 Lab3: Bezpieczeńswo funkcjonalne i ochrona informacji Tema: Weryfikacja nienaruszalności bezpieczeńswa SIL srukury sprzęowej realizującej funkcje bezpieczeńswa Kryeria probabilisyczne bezpieczeńswa funkcjonalnego
Podstawy. Pamięć wirtualna. (demand paging)
 Pamięć wirtualna Podstawy Podstawy Stronicowanie na żądanie Wymiana strony Przydział ramek Szamotanie (thrashing) Pamięć wirtualna (virtual memory) oddzielenie pamięci logicznej użytkownika od fizycznej.
Pamięć wirtualna Podstawy Podstawy Stronicowanie na żądanie Wymiana strony Przydział ramek Szamotanie (thrashing) Pamięć wirtualna (virtual memory) oddzielenie pamięci logicznej użytkownika od fizycznej.
Układy sekwencyjne asynchroniczne Zadania projektowe
 Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
Pobieranie próby. Rozkład χ 2
 Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
REGULAMIN FUNDUSZU ROZLICZENIOWEGO
 REGULAMIN FUNDUSZU ROZLICZENIOEGO przyjęy uchwałą nr 10/60/98 Rady Nadzorczej Krajowego Depozyu Papierów arościowych S.A. z dnia 28 września 1998 r., zawierdzony decyzją Komisji Papierów arościowych i
REGULAMIN FUNDUSZU ROZLICZENIOEGO przyjęy uchwałą nr 10/60/98 Rady Nadzorczej Krajowego Depozyu Papierów arościowych S.A. z dnia 28 września 1998 r., zawierdzony decyzją Komisji Papierów arościowych i
Pamięć wirtualna. Jan Tuziemski Źródło części materiałów: os-book.com
 Pamięć wirtualna Jan Tuziemski Źródło części materiałów: os-book.com Pamięć wirtualna Na poprzednich wykładach omówiono sposoby zarządzania pamięcią Są one potrzebne ponieważ wykonywane rozkazy procesów
Pamięć wirtualna Jan Tuziemski Źródło części materiałów: os-book.com Pamięć wirtualna Na poprzednich wykładach omówiono sposoby zarządzania pamięcią Są one potrzebne ponieważ wykonywane rozkazy procesów
KURS EKONOMETRIA. Lekcja 1 Wprowadzenie do modelowania ekonometrycznego ZADANIE DOMOWE. Strona 1
 KURS EKONOMETRIA Lekcja 1 Wprowadzenie do modelowania ekonomerycznego ZADANIE DOMOWE www.erapez.pl Srona 1 Część 1: TEST Zaznacz poprawną odpowiedź (ylko jedna jes prawdziwa). Pyanie 1 Kóre z poniższych
KURS EKONOMETRIA Lekcja 1 Wprowadzenie do modelowania ekonomerycznego ZADANIE DOMOWE www.erapez.pl Srona 1 Część 1: TEST Zaznacz poprawną odpowiedź (ylko jedna jes prawdziwa). Pyanie 1 Kóre z poniższych
System zielonych inwestycji (GIS Green Investment Scheme)
 PROGRAM PRIORYTETOWY Tyuł programu: Sysem zielonych inwesycji (GIS Green Invesmen Scheme) Część 6) SOWA Energooszczędne oświelenie uliczne. 1. Cel programu Ograniczenie lub uniknięcie emisji dwulenku węgla
PROGRAM PRIORYTETOWY Tyuł programu: Sysem zielonych inwesycji (GIS Green Invesmen Scheme) Część 6) SOWA Energooszczędne oświelenie uliczne. 1. Cel programu Ograniczenie lub uniknięcie emisji dwulenku węgla
Rozdział 4 Instrukcje sekwencyjne
 Rozdział 4 Insrukcje sekwencyjne Lisa insrukcji sekwencyjnych FBs-PLC przedsawionych w niniejszym rozdziale znajduje się w rozdziale 3.. Zasady kodowania przy zasosowaniu ych insrukcji opisane są w rozdziale
Rozdział 4 Insrukcje sekwencyjne Lisa insrukcji sekwencyjnych FBs-PLC przedsawionych w niniejszym rozdziale znajduje się w rozdziale 3.. Zasady kodowania przy zasosowaniu ych insrukcji opisane są w rozdziale
Metody rachunku kosztów Metoda rachunku kosztu działań Podstawowe pojęcia metody ABC Kalkulacja obiektów kosztowych metodą ABC Zasobowy rachunek
 Meody rachunku koszów Meoda rachunku koszu Podsawowe pojęcia meody ABC Kalkulacja obieków koszowych meodą ABC Zasobowy rachunek koszów Kalkulacja koszów meodą ABC podsawową informacja dla rachunkowości
Meody rachunku koszów Meoda rachunku koszu Podsawowe pojęcia meody ABC Kalkulacja obieków koszowych meodą ABC Zasobowy rachunek koszów Kalkulacja koszów meodą ABC podsawową informacja dla rachunkowości
PROGNOZOWANIE I SYMULACJE. mgr Żaneta Pruska. Ćwiczenia 2 Zadanie 1
 PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
Tabela doboru przekaźników czasowych MTR17
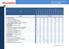 M17-A07-240-... M17-B07-240-... M17-Q-240-... M17--240-... M17--240-... M17--240-... M17--240-... M17-VW-240-... M17-XY-240-... M17-Z-240-... M17-AB-240-116 M17-CD-240-116 M17-BA-240-116 M17-P-240-...
M17-A07-240-... M17-B07-240-... M17-Q-240-... M17--240-... M17--240-... M17--240-... M17--240-... M17-VW-240-... M17-XY-240-... M17-Z-240-... M17-AB-240-116 M17-CD-240-116 M17-BA-240-116 M17-P-240-...
ZASTOSOWANIE TEORII MASOWEJ OBSŁUGI DO MODELOWANIA SYSTEMÓW TRANSPORTOWYCH
 Pior KISIELEWSKI, Łukasz SOBOTA ZASTOSOWANIE TEORII MASOWEJ OBSŁUGI DO MODELOWANIA SYSTEMÓW TRANSPORTOWYCH W arykule przedsawiono zasosowanie eorii masowej obsługi do analizy i modelowania wybranych sysemów
Pior KISIELEWSKI, Łukasz SOBOTA ZASTOSOWANIE TEORII MASOWEJ OBSŁUGI DO MODELOWANIA SYSTEMÓW TRANSPORTOWYCH W arykule przedsawiono zasosowanie eorii masowej obsługi do analizy i modelowania wybranych sysemów
dr inż. Jarosław Forenc
 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równoległy algorytm analizy sygnału na podstawie niewielkiej liczby próbek
 Nauka Zezwala się na korzysanie z arykułu na warunkach licencji Creaive Commons Uznanie auorswa 3.0 Równoległy algorym analizy sygnału na podsawie niewielkiej liczby próbek Pior Kardasz Wydział Elekryczny,
Nauka Zezwala się na korzysanie z arykułu na warunkach licencji Creaive Commons Uznanie auorswa 3.0 Równoległy algorym analizy sygnału na podsawie niewielkiej liczby próbek Pior Kardasz Wydział Elekryczny,
LABORATORIUM PODSTAWY ELEKTRONIKI Badanie Bramki X-OR
 LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
Stronicowanie na ¹danie
 Pamiêæ wirtualna Umo liwia wykonywanie procesów, pomimo e nie s¹ one w ca³oœci przechowywane w pamiêci operacyjnej Logiczna przestrzeñ adresowa mo e byæ du o wiêksza od fizycznej przestrzeni adresowej
Pamiêæ wirtualna Umo liwia wykonywanie procesów, pomimo e nie s¹ one w ca³oœci przechowywane w pamiêci operacyjnej Logiczna przestrzeñ adresowa mo e byæ du o wiêksza od fizycznej przestrzeni adresowej
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
Kontroler ruchu i kierunku obrotów KFD2-SR2-2.W.SM. Charakterystyka. Konstrukcja. Funkcja. Przyłącze
 Konroler ruchu i kierunku obroów Charakerysyka Konsrukcja -kanałowy separaor galwaniczny Zasilanie 4 V DC Wejścia ypu PNP/push-pull, syk lub Programowane częsoliwości graniczne wyjścia syku przekaźnika
Konroler ruchu i kierunku obroów Charakerysyka Konsrukcja -kanałowy separaor galwaniczny Zasilanie 4 V DC Wejścia ypu PNP/push-pull, syk lub Programowane częsoliwości graniczne wyjścia syku przekaźnika
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1
 ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
Jednofazowe przekształtniki DC AC i AC DC z eliminacją składowej podwójnej częstotliwości po stronie DC
 Akademia Górniczo-Hunicza im. Sanisława Saszica w Krakowie Wydział Elekroechniki, Auomayki, Informayki i Inżynierii Biomedycznej Kaedra Energoelekroniki i Auomayki Sysemów Przewarzania Energii Auorefera
Akademia Górniczo-Hunicza im. Sanisława Saszica w Krakowie Wydział Elekroechniki, Auomayki, Informayki i Inżynierii Biomedycznej Kaedra Energoelekroniki i Auomayki Sysemów Przewarzania Energii Auorefera
Podstawy Elektroniki dla Elektrotechniki
 AGH Kaedra Elekroniki Podsawy Elekroniki dla Elekroechniki Klucze Insrukcja do ćwiczeń symulacyjnych (5a) Insrukcja do ćwiczeń sprzęowych (5b) Ćwiczenie 5a, 5b 2015 r. 1 1. Wsęp. Celem ćwiczenia jes ugrunowanie
AGH Kaedra Elekroniki Podsawy Elekroniki dla Elekroechniki Klucze Insrukcja do ćwiczeń symulacyjnych (5a) Insrukcja do ćwiczeń sprzęowych (5b) Ćwiczenie 5a, 5b 2015 r. 1 1. Wsęp. Celem ćwiczenia jes ugrunowanie
Zarządzanie Projektami. Wykład 3 Techniki sieciowe (część 1)
 Zarządzanie Projekami Wykład 3 Techniki sieciowe (część ) Przedsięwzięcie wieloczynnościowe Przedsięwzięcie wieloczynnościowe skończona liczba wzajemnie ze sobą powiązanych czynności (eapów). Powiązania
Zarządzanie Projekami Wykład 3 Techniki sieciowe (część ) Przedsięwzięcie wieloczynnościowe Przedsięwzięcie wieloczynnościowe skończona liczba wzajemnie ze sobą powiązanych czynności (eapów). Powiązania
5. Usługodawca jest administratorem danych swoich klientów. Oznacza to, że jeśli posiadasz Konto na naszej
 .1 Posanowienia Ogólne 1. Adminisraorem danych jes Sunday Morning Doradzwo Personalne Aleksandra Bukowska z siedzibą w Łodzi, ul Bałycka 32b/22, NIP: 7282225534, REGON: 365983994. Ochrona danych odbywa
.1 Posanowienia Ogólne 1. Adminisraorem danych jes Sunday Morning Doradzwo Personalne Aleksandra Bukowska z siedzibą w Łodzi, ul Bałycka 32b/22, NIP: 7282225534, REGON: 365983994. Ochrona danych odbywa
Pamięć wirtualna. A gdyby tak w pamięci przebywała tylko ta część programu, która jest aktualnie wykonywana?
 Pamięć wirtualna Pytanie: Czy proces rezerwuje pamięć i gospodaruje nią w sposób oszczędny? Procesy często zawierają ogromne fragmenty kodu obsługujące sytuacje wyjątkowe Zadeklarowane tablice lub rozmiary
Pamięć wirtualna Pytanie: Czy proces rezerwuje pamięć i gospodaruje nią w sposób oszczędny? Procesy często zawierają ogromne fragmenty kodu obsługujące sytuacje wyjątkowe Zadeklarowane tablice lub rozmiary
EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH. dr inż. Robert Stachniewicz
 EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH dr inż. Rober Sachniewicz METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH Jednymi z licznych celów i zadań przedsiębiorswa są: - wzros warości przedsiębiorswa
EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH dr inż. Rober Sachniewicz METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH Jednymi z licznych celów i zadań przedsiębiorswa są: - wzros warości przedsiębiorswa
WYKORZYSTANIE STATISTICA DATA MINER DO PROGNOZOWANIA W KRAJOWYM DEPOZYCIE PAPIERÓW WARTOŚCIOWYCH
 SaSof Polska, el. 12 428 43 00, 601 41 41 51, info@sasof.pl, www.sasof.pl WYKORZYSTANIE STATISTICA DATA MINER DO PROGNOZOWANIA W KRAJOWYM DEPOZYCIE PAPIERÓW WARTOŚCIOWYCH Joanna Maych, Krajowy Depozy Papierów
SaSof Polska, el. 12 428 43 00, 601 41 41 51, info@sasof.pl, www.sasof.pl WYKORZYSTANIE STATISTICA DATA MINER DO PROGNOZOWANIA W KRAJOWYM DEPOZYCIE PAPIERÓW WARTOŚCIOWYCH Joanna Maych, Krajowy Depozy Papierów
dr inż. MARCIN MAŁACHOWSKI Instytut Technik Innowacyjnych EMAG
 dr inż. MARCIN MAŁACHOWSKI Insyu Technik Innowacyjnych EMAG Wykorzysanie opycznej meody pomiaru sężenia pyłu do wspomagania oceny paramerów wpływających na możliwość zaisnienia wybuchu osiadłego pyłu węglowego
dr inż. MARCIN MAŁACHOWSKI Insyu Technik Innowacyjnych EMAG Wykorzysanie opycznej meody pomiaru sężenia pyłu do wspomagania oceny paramerów wpływających na możliwość zaisnienia wybuchu osiadłego pyłu węglowego
Kontroler ruchu i kierunku obrotów KFD2-SR2-2.W.SM. Charakterystyka. Konstrukcja. Funkcja. Przyłącze
 Konroler ruchu i kierunku obroów Charakerysyka Konsrukcja -kanałowy separaor galwaniczny Zasilanie 4 V DC Wejścia ypu PNP/push-pull, syk lub NAMUR Programowane częsoliwości graniczne wyjścia syku przekaźnika
Konroler ruchu i kierunku obroów Charakerysyka Konsrukcja -kanałowy separaor galwaniczny Zasilanie 4 V DC Wejścia ypu PNP/push-pull, syk lub NAMUR Programowane częsoliwości graniczne wyjścia syku przekaźnika
Parytet stóp procentowych a premia za ryzyko na przykładzie kursu EURUSD
 Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Marcin Gajewski Uniwersye Łódzki 4.12.2008 Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Niezabazpieczony UIP)
Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Marcin Gajewski Uniwersye Łódzki 4.12.2008 Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Niezabazpieczony UIP)
Badanie funktorów logicznych TTL - ćwiczenie 1
 adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
Kombinowanie prognoz. - dlaczego należy kombinować prognozy? - obejmowanie prognoz. - podstawowe metody kombinowania prognoz
 Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
dr inż. Jarosław Forenc
 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010 Wykład nr 8 (29.01.2009) dr inż. Jarosław Forenc Rok akademicki
Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010 Wykład nr 8 (29.01.2009) dr inż. Jarosław Forenc Rok akademicki
dr inŝ. Jarosław Forenc
 Rok akademicki 2009/2010, Wykład nr 8 2/19 Plan wykładu nr 8 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010
Rok akademicki 2009/2010, Wykład nr 8 2/19 Plan wykładu nr 8 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010
Kluczowe wnioski ze Światowego Badania Bezpieczeństwa Informacji 2012. 4 grudnia 2012
 Kluczowe wnioski ze Świaowego Badania Bezpieczeńswa Informacji 2012 4 grudnia 2012 Erns & Young 2012 Świaowe Badanie Bezpieczeńswa Informacji Świaowe Badanie Bezpieczeńswa Informacji Erns & Young 2012
Kluczowe wnioski ze Świaowego Badania Bezpieczeńswa Informacji 2012 4 grudnia 2012 Erns & Young 2012 Świaowe Badanie Bezpieczeńswa Informacji Świaowe Badanie Bezpieczeńswa Informacji Erns & Young 2012
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Bezpieczeństwo - Elastyczność - Efektywność. safetydrive: Bezpieczeństwo funkcjonalne
 Technika napędowa \ Auomayzacja napędów \ Inegracja sysemowa \ Usługi 1 Bezpieczeńswo - Elasyczność - Efekywność safeydrive: Bezpieczeńswo funkcjonalne 2 safeydrive: Bezpieczeńswo funkcjonalne : Bezpieczeńswo
Technika napędowa \ Auomayzacja napędów \ Inegracja sysemowa \ Usługi 1 Bezpieczeńswo - Elasyczność - Efekywność safeydrive: Bezpieczeńswo funkcjonalne 2 safeydrive: Bezpieczeńswo funkcjonalne : Bezpieczeńswo
Ocena płynności wybranymi metodami szacowania osadu 1
 Bogdan Ludwiczak Wprowadzenie Ocena płynności wybranymi meodami szacowania osadu W ubiegłym roku zaszły znaczące zmiany doyczące pomiaru i zarządzania ryzykiem bankowym. Są one konsekwencją nowowprowadzonych
Bogdan Ludwiczak Wprowadzenie Ocena płynności wybranymi meodami szacowania osadu W ubiegłym roku zaszły znaczące zmiany doyczące pomiaru i zarządzania ryzykiem bankowym. Są one konsekwencją nowowprowadzonych
Wykład 8. Pamięć wirtualna. Wojciech Kwedlo, Wykład z Systemów Operacyjnych -1- Wydział Informatyki PB
 Wykład 8 Pamięć wirtualna Wojciech Kwedlo, Wykład z Systemów Operacyjnych -1- Wydział Informatyki PB Wprowadzenie Podstawowa idea: System operacyjny pozwala na wykorzystanie pamięci o pojemności większej,
Wykład 8 Pamięć wirtualna Wojciech Kwedlo, Wykład z Systemów Operacyjnych -1- Wydział Informatyki PB Wprowadzenie Podstawowa idea: System operacyjny pozwala na wykorzystanie pamięci o pojemności większej,
POMIAR PARAMETRÓW SYGNAŁOW NAPIĘCIOWYCH METODĄ PRÓKOWANIA I CYFROWEGO PRZETWARZANIA SYGNAŁU
 Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
Badanie transformatora 3-fazowego
 adanie ransormaora 3-azowego ) Próba sanu jałowego ransormaora przy = N = cons adania przeprowadza się w układzie połączeń pokazanych na Rys.. Rys.. Schema połączeń do próby sanu jałowego ransormaora.
adanie ransormaora 3-azowego ) Próba sanu jałowego ransormaora przy = N = cons adania przeprowadza się w układzie połączeń pokazanych na Rys.. Rys.. Schema połączeń do próby sanu jałowego ransormaora.
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
PODSTAWY PROGRAMOWANIA STEROWNIKÓW PLC
 PODSTAWY PROGRAMOWANIA STEROWNIKÓW PLC SPIS TREŚCI WSTĘP JĘZYK SCHEMATÓW DRABINKOWYCH JĘZYK SCHEMATÓW BLOKÓW FUNKCYJNYCH JĘZYK INSTRUKCJI JĘZYK STRUKTURALNY SEKWENCYJNY SCHEMAT FUNKCYJNY PRZYKŁADY PROGRAMÓW
PODSTAWY PROGRAMOWANIA STEROWNIKÓW PLC SPIS TREŚCI WSTĘP JĘZYK SCHEMATÓW DRABINKOWYCH JĘZYK SCHEMATÓW BLOKÓW FUNKCYJNYCH JĘZYK INSTRUKCJI JĘZYK STRUKTURALNY SEKWENCYJNY SCHEMAT FUNKCYJNY PRZYKŁADY PROGRAMÓW
SPRAWOZDANIE Z PROJEKTU Dioda jako czujnik temperatury
 emperaury 1. Cele Sprawdzenie zależności między emperaurą a naężeniem świała emiowanego przez diodę LED (napięciem baza-emier na ranzysorze) w układzie z Rys.1 (parz srona 1 Budowa układu ). 2. Wykaz przyrządów
emperaury 1. Cele Sprawdzenie zależności między emperaurą a naężeniem świała emiowanego przez diodę LED (napięciem baza-emier na ranzysorze) w układzie z Rys.1 (parz srona 1 Budowa układu ). 2. Wykaz przyrządów
Obszary zainteresowań (ang. area of interest - AOI) jako metoda analizy wyników badania eye tracking
 Inerfejs użykownika - Kansei w prakyce 2009 107 Obszary zaineresowań (ang. area of ineres - AOI) jako meoda analizy wyników badania eye racking Pior Jardanowski, Agencja e-biznes Symeria Ul. Wyspiańskiego
Inerfejs użykownika - Kansei w prakyce 2009 107 Obszary zaineresowań (ang. area of ineres - AOI) jako meoda analizy wyników badania eye racking Pior Jardanowski, Agencja e-biznes Symeria Ul. Wyspiańskiego
Model logistycznego wsparcia systemu eksploatacji środków transportu
 Poliechnika Wrocławska Insyu Konsrukcji i Eksploaacji Maszyn Zakład Logisyki i Sysemów Transporowych Rozprawa dokorska Model logisycznego wsparcia sysemu eksploaacji środków ransporu Rapor serii: PRE nr
Poliechnika Wrocławska Insyu Konsrukcji i Eksploaacji Maszyn Zakład Logisyki i Sysemów Transporowych Rozprawa dokorska Model logisycznego wsparcia sysemu eksploaacji środków ransporu Rapor serii: PRE nr
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Zastosowanie predykcji sygnału odchylenia regulacyjnego do centralnej regulacji mocy czynnej i częstotliwości w systemie elektroenergetycznym
 INSTYTUT AUTOMATYKI SYSTEMÓW ENERGETYCZNYCH Zasosowanie predykcji sygnału odchylenia regulacyjnego do cenralnej regulacji mocy czynnej i częsoliwości w sysemie elekroenergeycznym Prof. dr hab. inż. Tadeusz
INSTYTUT AUTOMATYKI SYSTEMÓW ENERGETYCZNYCH Zasosowanie predykcji sygnału odchylenia regulacyjnego do cenralnej regulacji mocy czynnej i częsoliwości w sysemie elekroenergeycznym Prof. dr hab. inż. Tadeusz
Nakładki. Kod przebiegu 2: 80 kb Tablica symboli: 20 kb wspólne podprogramy: 30 kb Razem: 200 kb
 Pamięć wirtualna Nakładki Nakładki są potrzebne jeśli proces jest większy niż ilość dostępnej pamięci. Przykład - dwuprzebiegowy asembler mamy do dyspozycji 150 kb pamięci, a poszczególne elementy zadania
Pamięć wirtualna Nakładki Nakładki są potrzebne jeśli proces jest większy niż ilość dostępnej pamięci. Przykład - dwuprzebiegowy asembler mamy do dyspozycji 150 kb pamięci, a poszczególne elementy zadania
Podstawy Programowania semestr drugi. Wykład trzeci
 1. Kolejki Wykład rzeci Kolejka jes, podobnie jak sos, absrakcyjn ą srukur ą danyc opar ą na liście liniowej. Elemeny kolejki e ż s ą połączone w lis ę, ale inaczej ni ż w sosie przebiegają operacje dodawania
1. Kolejki Wykład rzeci Kolejka jes, podobnie jak sos, absrakcyjn ą srukur ą danyc opar ą na liście liniowej. Elemeny kolejki e ż s ą połączone w lis ę, ale inaczej ni ż w sosie przebiegają operacje dodawania
Przekaźniki czasowe ATI opóźnienie załączania Czas Napięcie sterowania Styki Numer katalogowy
 W celu realizowania prosych układów opóźniających można wykorzysać przekaźniki czasowe dedykowane do poszczególnych aplikacji. Kompakowa obudowa - moduł 22,5 mm, monaż na szynie DIN, sygnalizacja sanu
W celu realizowania prosych układów opóźniających można wykorzysać przekaźniki czasowe dedykowane do poszczególnych aplikacji. Kompakowa obudowa - moduł 22,5 mm, monaż na szynie DIN, sygnalizacja sanu
Matematyka finansowa 20.03.2006 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r.
 Komisja Egzaminacyjna dla Akuariuszy XXXVIII Egzamin dla Akuariuszy z 20 marca 2006 r. Część I Maemayka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minu 1 1. Ile
Komisja Egzaminacyjna dla Akuariuszy XXXVIII Egzamin dla Akuariuszy z 20 marca 2006 r. Część I Maemayka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minu 1 1. Ile
RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE
 RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE PYTANIA KONTROLNE Czym charakeryzują się wskaźniki saycznej meody oceny projeku inwesycyjnego Dla kórego wskaźnika wyliczamy średnią księgową
RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE PYTANIA KONTROLNE Czym charakeryzują się wskaźniki saycznej meody oceny projeku inwesycyjnego Dla kórego wskaźnika wyliczamy średnią księgową
Systemy Operacyjne Pamięć wirtualna cz. 1
 Systemy Operacyjne Pamięć wirtualna cz. 1 Arkadiusz Chrobot Katedra Informatyki, Politechnika Świętokrzyska w Kielcach Kielce, 4 stycznia 2007 1 1 Zasady lokalności czasowej i przestrzennej 2 Pamięć wirtualna
Systemy Operacyjne Pamięć wirtualna cz. 1 Arkadiusz Chrobot Katedra Informatyki, Politechnika Świętokrzyska w Kielcach Kielce, 4 stycznia 2007 1 1 Zasady lokalności czasowej i przestrzennej 2 Pamięć wirtualna
Różnica bilansowa dla Operatorów Systemów Dystrybucyjnych na lata (którzy dokonali z dniem 1 lipca 2007 r. rozdzielenia działalności)
 Różnica bilansowa dla Operaorów Sysemów Dysrybucyjnych na laa 2016-2020 (kórzy dokonali z dniem 1 lipca 2007 r. rozdzielenia działalności) Deparamen Rynków Energii Elekrycznej i Ciepła Warszawa 201 Spis
Różnica bilansowa dla Operaorów Sysemów Dysrybucyjnych na laa 2016-2020 (kórzy dokonali z dniem 1 lipca 2007 r. rozdzielenia działalności) Deparamen Rynków Energii Elekrycznej i Ciepła Warszawa 201 Spis
METODA DOBORU ŚCIEŻEK TRANSMISYJNYCH DLA POPRAWY JAKOŚCI POŁĄCZEŃ GŁOSOWYCH IP
 Krysian Ryłko Zakład Sieci Kompuerowych Wydział Informayki Poliechnika Szczecińska krysian@ps.pl 2005 Poznańskie Warszay Telekomunikacyjne Poznań 8-9 grudnia 2005 METODA DOBORU ŚCIEŻEK TRANSMISYJNYCH DLA
Krysian Ryłko Zakład Sieci Kompuerowych Wydział Informayki Poliechnika Szczecińska krysian@ps.pl 2005 Poznańskie Warszay Telekomunikacyjne Poznań 8-9 grudnia 2005 METODA DOBORU ŚCIEŻEK TRANSMISYJNYCH DLA
Systemy operacyjne III
 Systemy operacyjne III WYKŁAD Jan Kazimirski Pamięć wirtualna Stronicowanie Pamięć podzielona na niewielki bloki Bloki procesu to strony a bloki fizyczne to ramki System operacyjny przechowuje dla każdego
Systemy operacyjne III WYKŁAD Jan Kazimirski Pamięć wirtualna Stronicowanie Pamięć podzielona na niewielki bloki Bloki procesu to strony a bloki fizyczne to ramki System operacyjny przechowuje dla każdego
Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO. z dnia 2 czerwca 2017 r.
 DZIENNIK URZĘDOWY NARODOWEGO BANKU POLSKIEGO Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO z dnia 2 czerwca 2017 r. zmieniająca uchwałę w sprawie wprowadzenia
DZIENNIK URZĘDOWY NARODOWEGO BANKU POLSKIEGO Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO z dnia 2 czerwca 2017 r. zmieniająca uchwałę w sprawie wprowadzenia
Pamięć wirtualna. Pamięć wirtualna
 Pamięć wirtualna Pamięć wirtualna Podstawy. Stronicowanie na żądanie. Kopiowanie przy zapisie. Zastępowanie stron. Algorytmy zastępowania stron. Przydział ramek. Szamotanie (migotanie). Pliki odwzorowywane
Pamięć wirtualna Pamięć wirtualna Podstawy. Stronicowanie na żądanie. Kopiowanie przy zapisie. Zastępowanie stron. Algorytmy zastępowania stron. Przydział ramek. Szamotanie (migotanie). Pliki odwzorowywane
Instrukcja do ćwiczenia laboratoryjnego. Badanie liczników
 Insrukcja do ćwiczenia laboraoryjnego Badanie liczników Opracował: mgr inż. Andrzej Biedka Wymagania, znajomość zagadnień: 3. 4. Budowa licznika cyfrowego. zielnik częsoliwości, różnice między licznikiem
Insrukcja do ćwiczenia laboraoryjnego Badanie liczników Opracował: mgr inż. Andrzej Biedka Wymagania, znajomość zagadnień: 3. 4. Budowa licznika cyfrowego. zielnik częsoliwości, różnice między licznikiem
WENTYLACJA i KLIMATYZACJA 2. Ćwiczenia nr 1
 Insyu Inżynierii Cieplnej i Ochrony Powierza Poliechniki Krakowskiej Zakład Wenylacji Klimayzacji i Chłodnicwa WENTYLACJA i KLIMATYZACJA 2 Ćwiczenia nr 1 Urządzenia do uzdania powierza w klimayzacji Dr
Insyu Inżynierii Cieplnej i Ochrony Powierza Poliechniki Krakowskiej Zakład Wenylacji Klimayzacji i Chłodnicwa WENTYLACJA i KLIMATYZACJA 2 Ćwiczenia nr 1 Urządzenia do uzdania powierza w klimayzacji Dr
MICROMASTER 420. Lista Parametrów Wydanie 06/04. Dokumentacja Użytkownika 6SE6400-5BA00-0AP0_PL
 MICROMASTER 4 Lisa Paramerów Wydanie 6/4 Dokumenacja Użykownika 6SE64-5BA-AP_PL Dokumenacja do MICROMASTER 4 Insrukcja Skrócona Służy do szybkiego uruchamiania przy pomocy panela SDP i BOP. Insrukcja Obsługi
MICROMASTER 4 Lisa Paramerów Wydanie 6/4 Dokumenacja Użykownika 6SE64-5BA-AP_PL Dokumenacja do MICROMASTER 4 Insrukcja Skrócona Służy do szybkiego uruchamiania przy pomocy panela SDP i BOP. Insrukcja Obsługi
Rozwiązanie uogólnionego problemu optymalnej alokacji zasobów. Cezary S. Zaremba*, Leszek S. Zaremba ** WPROWADZENIE
 Rozwiązanie uogólnionego problemu opymalnej alokacji zasobów Cezary S. Zaremba*, Leszek S. Zaremba ** WPROWADZENIE Niniejszy arykuł rozwiązuje problem owary posawiony w [4], dzięki czemu będzie można znaleźć
Rozwiązanie uogólnionego problemu opymalnej alokacji zasobów Cezary S. Zaremba*, Leszek S. Zaremba ** WPROWADZENIE Niniejszy arykuł rozwiązuje problem owary posawiony w [4], dzięki czemu będzie można znaleźć
Matematyka ubezpieczeń majątkowych r. ma złożony rozkład Poissona. W tabeli poniżej podano rozkład prawdopodobieństwa ( )
 Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
WNIOSKOWANIE STATYSTYCZNE
 Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
Wykład 5 Elementy teorii układów liniowych stacjonarnych odpowiedź na dowolne wymuszenie
 Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
Modelowanie i obliczenia techniczne. Równania różniczkowe Numeryczne rozwiązywanie równań różniczkowych zwyczajnych
 Moelowanie i obliczenia echniczne Równania różniczowe Numeryczne rozwiązywanie równań różniczowych zwyczajnych Przyła ułau ynamicznego E Uła ynamiczny R 0 Zachozi porzeba wyznaczenia: C u C () i() ur ir
Moelowanie i obliczenia echniczne Równania różniczowe Numeryczne rozwiązywanie równań różniczowych zwyczajnych Przyła ułau ynamicznego E Uła ynamiczny R 0 Zachozi porzeba wyznaczenia: C u C () i() ur ir
1.2.1 Ogólny algorytm podejmowania decyzji... 18. 1.2.2 Algorytm postępowania diagnostycznego... 23. 1.2.3 Analiza decyzyjna... 27
 3 Spis reści Spis reści... 3 Użye oznaczenia... 7 Wsęp i założenia pracy... 9 1. Akualny san wiedzy medycznej i echnicznej związanej zagadnieniami analizy decyzyjnej w chorobach górnego odcinka przewodu
3 Spis reści Spis reści... 3 Użye oznaczenia... 7 Wsęp i założenia pracy... 9 1. Akualny san wiedzy medycznej i echnicznej związanej zagadnieniami analizy decyzyjnej w chorobach górnego odcinka przewodu
Struktura sektorowa finansowania wydatków na B+R w krajach strefy euro
 Rozdział i. Srukura sekorowa finansowania wydaków na B+R w krajach srefy euro Rober W. Włodarczyk 1 Sreszczenie W arykule podjęo próbę oceny srukury sekorowej (sekor przedsiębiorsw, sekor rządowy, sekor
Rozdział i. Srukura sekorowa finansowania wydaków na B+R w krajach srefy euro Rober W. Włodarczyk 1 Sreszczenie W arykule podjęo próbę oceny srukury sekorowej (sekor przedsiębiorsw, sekor rządowy, sekor
( ) ( ) ( τ) ( t) = 0
 Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
PROGNOZOWANIE I SYMULACJE EXCEL 2 AUTOR: MARTYNA MALAK PROGNOZOWANIE I SYMULACJE EXCEL 2 AUTOR: MARTYNA MALAK
 1 PROGNOZOWANIE I SYMULACJE 2 hp://www.oucome-seo.pl/excel2.xls DODATEK SOLVER WERSJE EXCELA 5.0, 95, 97, 2000, 2002/XP i 2003. 3 Dodaek Solver jes dosępny w menu Narzędzia. Jeżeli Solver nie jes dosępny
1 PROGNOZOWANIE I SYMULACJE 2 hp://www.oucome-seo.pl/excel2.xls DODATEK SOLVER WERSJE EXCELA 5.0, 95, 97, 2000, 2002/XP i 2003. 3 Dodaek Solver jes dosępny w menu Narzędzia. Jeżeli Solver nie jes dosępny
Spis treści ZASTOSOWANIE PAKIETU MATLAB W OBLICZENIACH ZAGADNIEŃ ELEKTRYCZNYCH I41
 Ćwiczenie I4 Poliechnika Białosocka Wydział Elekryczny Kaedra Elekroechniki Teoreycznej i Merologii Spis reści Insrukcja do pracowni specjalisycznej INFORMTYK Kod zajęć ESC 9 Tyuł ćwiczenia ZSTOSOWNIE
Ćwiczenie I4 Poliechnika Białosocka Wydział Elekryczny Kaedra Elekroechniki Teoreycznej i Merologii Spis reści Insrukcja do pracowni specjalisycznej INFORMTYK Kod zajęć ESC 9 Tyuł ćwiczenia ZSTOSOWNIE
Widok z przodu kω. II 10 kω kω Ω R 2 kω. Power Rail
 Konroler ruchu i kierunku obroów Charakerysyka Konsrukcja -kanałowa bariera rozdzielająca zasilanie 4 V DC (szyna zasilająca) wejścia sykowe lub ypu NAMUR Programowane częsoliwości graniczne wyjścia syku
Konroler ruchu i kierunku obroów Charakerysyka Konsrukcja -kanałowa bariera rozdzielająca zasilanie 4 V DC (szyna zasilająca) wejścia sykowe lub ypu NAMUR Programowane częsoliwości graniczne wyjścia syku
Zarządzanie ryzykiem. Lista 3
 Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
Uniwersytet Mikołaja Kopernika Wydział Fizyki, Astronomii i Informatyki Stosowanej. Adam Sosnowski
 Uniwersye Mikołaja Kopernika Wydział Fizyki, Asronomii i Informayki Sosowanej Adam Sosnowski Implemenacja i porównanie meod numerycznych sosowanych do realisycznych symulacji dynamiki zbioru punków maerialnych.
Uniwersye Mikołaja Kopernika Wydział Fizyki, Asronomii i Informayki Sosowanej Adam Sosnowski Implemenacja i porównanie meod numerycznych sosowanych do realisycznych symulacji dynamiki zbioru punków maerialnych.
Analiza metod oceny efektywności inwestycji rzeczowych**
 Ekonomia Menedżerska 2009, nr 6, s. 119 128 Marek Łukasz Michalski* Analiza meod oceny efekywności inwesycji rzeczowych** 1. Wsęp Podsawowymi celami przedsiębiorswa w długim okresie jes rozwój i osiąganie
Ekonomia Menedżerska 2009, nr 6, s. 119 128 Marek Łukasz Michalski* Analiza meod oceny efekywności inwesycji rzeczowych** 1. Wsęp Podsawowymi celami przedsiębiorswa w długim okresie jes rozwój i osiąganie
SYSTEMY OPERACYJNE LABORATORIUM 2014/2015
 1 SYSTEMY OPERACYJNE LABORATORIUM 2014/2015 ZASADY OCENIANIA ZADAŃ PROGRAMISTYCZNYCH: Zadania laboratoryjne polegają na symulacji i badaniu własności algorytmów/mechanizmów stosowanych w systemach operacyjnych.
1 SYSTEMY OPERACYJNE LABORATORIUM 2014/2015 ZASADY OCENIANIA ZADAŃ PROGRAMISTYCZNYCH: Zadania laboratoryjne polegają na symulacji i badaniu własności algorytmów/mechanizmów stosowanych w systemach operacyjnych.
Architektura komputerów
 Architektura komputerów Wykład 7 Jan Kazimirski 1 Pamięć podręczna 2 Pamięć komputera - charakterystyka Położenie Procesor rejestry, pamięć podręczna Pamięć wewnętrzna pamięć podręczna, główna Pamięć zewnętrzna
Architektura komputerów Wykład 7 Jan Kazimirski 1 Pamięć podręczna 2 Pamięć komputera - charakterystyka Położenie Procesor rejestry, pamięć podręczna Pamięć wewnętrzna pamięć podręczna, główna Pamięć zewnętrzna
Ocena efektywności procedury Congruent Specyfication dla małych prób
 243 Zeszyy Naukowe Wyższej Szkoły Bankowej we Wrocławiu Nr 20/2011 Wyższa Szkoła Bankowa w Toruniu Ocena efekywności procedury Congruen Specyficaion dla małych prób Sreszczenie. Procedura specyfikacji
243 Zeszyy Naukowe Wyższej Szkoły Bankowej we Wrocławiu Nr 20/2011 Wyższa Szkoła Bankowa w Toruniu Ocena efekywności procedury Congruen Specyficaion dla małych prób Sreszczenie. Procedura specyfikacji
Zespół zaparzacza z przekładnią zębatą
 Zespół zaparzacza z przekładnią zębaą MS MS Z mikroprzełącznikami Przekładnia jes zasilana za pomocą silnika prądu sałego, kóry eż wprawia w ruch mniejsze koło zębae sprzęgnięe z dużym kołem zębaym. Do
Zespół zaparzacza z przekładnią zębaą MS MS Z mikroprzełącznikami Przekładnia jes zasilana za pomocą silnika prądu sałego, kóry eż wprawia w ruch mniejsze koło zębae sprzęgnięe z dużym kołem zębaym. Do
XXXIV Olimpiada Wiedzy Elektrycznej i Elektronicznej Kraków 31 marca 2011. Test dla grupy elektronicznej
 XXXIV Olimpiada Wiedzy lekrycznej i lekronicznej Kraków marca Tes dla grupy elekronicznej.ezysancja zasępcza widziana z zacisków B wynosi:,,4,6,8 B. W poniższym układzie do wyznaczenia prądu w rezysancji
XXXIV Olimpiada Wiedzy lekrycznej i lekronicznej Kraków marca Tes dla grupy elekronicznej.ezysancja zasępcza widziana z zacisków B wynosi:,,4,6,8 B. W poniższym układzie do wyznaczenia prądu w rezysancji
MODELE AUTOREGRESYJNE JAKO INSTRUMENT ZARZĄDZANIA ZAPASAMI NA PRZYKŁADZIE ELEKTROWNI CIEPLNEJ
 Agaa MESJASZ-LECH * MODELE AUTOREGRESYJNE JAKO INSTRUMENT ZARZĄDZANIA ZAPASAMI NA PRZYKŁADZIE ELEKTROWNI CIEPLNEJ Sreszczenie W arykule przedsawiono wyniki analizy ekonomerycznej miesięcznych warości w
Agaa MESJASZ-LECH * MODELE AUTOREGRESYJNE JAKO INSTRUMENT ZARZĄDZANIA ZAPASAMI NA PRZYKŁADZIE ELEKTROWNI CIEPLNEJ Sreszczenie W arykule przedsawiono wyniki analizy ekonomerycznej miesięcznych warości w
Stanisław Cichocki Natalia Nehrebecka. Wykład 3
 Sanisław Cichocki Naalia Nehrebecka Wykład 3 1 1. Zmienne sacjonarne 2. Zmienne zinegrowane 3. Regresja pozorna 4. Funkcje ACF i PACF 5. Badanie sacjonarności Tes Dickey-Fullera (DF) 2 1. Zmienne sacjonarne
Sanisław Cichocki Naalia Nehrebecka Wykład 3 1 1. Zmienne sacjonarne 2. Zmienne zinegrowane 3. Regresja pozorna 4. Funkcje ACF i PACF 5. Badanie sacjonarności Tes Dickey-Fullera (DF) 2 1. Zmienne sacjonarne
Postęp techniczny. Model lidera-naśladowcy. Dr hab. Joanna Siwińska-Gorzelak
 Posęp echniczny. Model lidera-naśladowcy Dr hab. Joanna Siwińska-Gorzelak Założenia Rozparujemy dwa kraje; kraj 1 jes bardziej zaawansowany echnologicznie (lider); kraj 2 jes mniej zaawansowany i nie worzy
Posęp echniczny. Model lidera-naśladowcy Dr hab. Joanna Siwińska-Gorzelak Założenia Rozparujemy dwa kraje; kraj 1 jes bardziej zaawansowany echnologicznie (lider); kraj 2 jes mniej zaawansowany i nie worzy
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
PROGNOZOWANIE I SYMULACJE EXCEL 2 PROGNOZOWANIE I SYMULACJE EXCEL AUTOR: ŻANETA PRUSKA
 1 PROGNOZOWANIE I SYMULACJE EXCEL 2 AUTOR: mgr inż. ŻANETA PRUSKA DODATEK SOLVER 2 Sprawdzić czy w zakładce Dane znajduję się Solver 1. Kliknij przycisk Microsof Office, a nasępnie kliknij przycisk Opcje
1 PROGNOZOWANIE I SYMULACJE EXCEL 2 AUTOR: mgr inż. ŻANETA PRUSKA DODATEK SOLVER 2 Sprawdzić czy w zakładce Dane znajduję się Solver 1. Kliknij przycisk Microsof Office, a nasępnie kliknij przycisk Opcje
Założenia metodyczne optymalizacji ekonomicznego wieku rębności drzewostanów Prof. dr hab. Stanisław Zając Dr inż. Emilia Wysocka-Fijorek
 Założenia meodyczne opymalizacji ekonomicznego wieku rębności drzewosanów Prof. dr hab. Sanisław Zając Dr inż. Emilia Wysocka-Fijorek Plan 1. Wsęp 2. Podsawy eoreyczne opymalizacji ekonomicznego wieku
Założenia meodyczne opymalizacji ekonomicznego wieku rębności drzewosanów Prof. dr hab. Sanisław Zając Dr inż. Emilia Wysocka-Fijorek Plan 1. Wsęp 2. Podsawy eoreyczne opymalizacji ekonomicznego wieku
Politechnika Częstochowska Wydział Inżynierii Mechanicznej i Informatyki. Sprawozdanie #2 z przedmiotu: Prognozowanie w systemach multimedialnych
 Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Cyfrowe przetwarzanie sygnału przetwornika obrotowo-impulsowego
 Cyfrowe przewarzanie sygnału przewornika obroowo-impulsowego Eligiusz PAWŁOWSKI Poliechnika Lubelska, Kaedra Auomayki i Merologii ul. Nadbysrzycka 38 A, 20-68 Lublin, email: elekp@elekron.pol.lublin.pl
Cyfrowe przewarzanie sygnału przewornika obroowo-impulsowego Eligiusz PAWŁOWSKI Poliechnika Lubelska, Kaedra Auomayki i Merologii ul. Nadbysrzycka 38 A, 20-68 Lublin, email: elekp@elekron.pol.lublin.pl
Eksploracja danych. KLASYFIKACJA I REGRESJA cz. 1. Wojciech Waloszek. Teresa Zawadzka.
 Eksploracja danych KLASYFIKACJA I REGRESJA cz. 1 Wojciech Waloszek wowal@ei.pg.gda.pl Teresa Zawadzka egra@ei.pg.gda.pl Kaedra Inżyrii Oprogramowania Wydział Elekroniki, Telekomunikacji i Informayki Poliechnika
Eksploracja danych KLASYFIKACJA I REGRESJA cz. 1 Wojciech Waloszek wowal@ei.pg.gda.pl Teresa Zawadzka egra@ei.pg.gda.pl Kaedra Inżyrii Oprogramowania Wydział Elekroniki, Telekomunikacji i Informayki Poliechnika
