KIEROWALNOŚĆ AGREGATU ROLNICZEGO CIĄGNIK SADZARKA DO ZIEMNIAKÓW

Transkrypt

1 nŝynieri Rolnicz /006 Tdeuz Pwłowki Przemyłowy ntytut zyn Rolniczych w Poznniu EROWANOŚĆ AGREGATU RONCZEGO CĄGN SADZARA DO ZENAÓW Strezczenie Prezentown prc przedtwi wtępną koncepcję uwzględnieni dziłni kierowcy w modelu zetwu ciągnik mzyn rolnicz. Agregt tki poruz ię po nieutwrdzonym, częto podmokłym, polu o urozmiconej powierzchni. W tk trudnym terenie kierowc mui wykonywć rdzo komplikowne mnewry związne z chrkterem prc polowych. odel ztoowno do zetwu ciągnik dzrk do ziemników. Półzwiezn dzrk połączon jet z ciągnikiem z pomocą dolnych cięgien TUZ. Do implementcji modelu ztoowno moduł Simulink środowik tl. Słow kluczowe: modelownie, kierowc, zetw ciągnik mzyn rolnicz Wprowdzenie Dynmik pojzdu jet jednym z njwŝniejzych ozrów dń w technice motoryzcyjnej. Jzd, przypiezenie, hmownie, zmin kierunku jzdy to typowe procey dynmiczne. Jkość ich relizcji jet uzleŝnion od kierowcy. Sterowny przez kierowcę pojzd moŝe yć ztem rozptrywny jko ytem regulcji, w którym kierowc jet regultorem mochód oiektem regulownym. Źródłem ił zewnętrznych docierjących do kierującego i wywierjących wpływ n dynmikę mochodu jet zmienijące ię otoczenie pojzdu. Dotrcz ono m. in. informcje otrzegwcze w potci rozmitych odźców docierjących do kierowcy, który je odier i w zleŝności od ich rozpoznni orz oceny podejmuje odpowiednie dziłni kierowni pojzdem. Efektywność dziłń kierowcy zleŝy od ytucji n drodze, włności pojzdu orz od cech pychofizycznych kierowcy, m. in. od czu jego rekcji. ierowc jet włączony w ukłd drog pojzd kierowc jko ogniwo przęŝeni zwrotnego. Jego funkcje dją ię opić jko przetwrznie pochodzących z zewnątrz informcji dotyczących ruchu pojzdu (nierówności drogi, wrunki tmoferyczne, połoŝenie innych '$

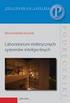
2 GTWXhfm CTjÄjf^\ pojzdów, itp.) n terownie tnem pozczególnych ukłdów pojzdu tkich jk ukłd kierowniczy, ukłd hmulcowy, ukłd npędowy [ozi i in. 995; Stńczy i in. 004]. Prezentown prc przedtwi wtępną koncepcję uwzględnieni dziłni kierowcy w modelu zetwu ciągnik mzyn rolnicz. Agregt tki poruz ię po nieutwrdzonym, częto podmokłym, polu o urozmiconej powierzchni. W tk trudnym terenie kierowc mui wykonywć rdzo komplikowne mnewry związne z chrkterem prc polowych. W modelu nleŝy ztem uwzględnić pecyfikę nwierzchni i iły wywierne n koł podcz jzdy w róŝnych kierunkch. odel ztoowno do zetwu ciągnik dzrk do ziemników (ry. ). Półzwiezn dzrk połączon jet z ciągnikiem z pomocą dolnych cięgien TUZ. Do implementcji modelu ztoowno moduł Simulink środowik tl. Ry.. Fig.. Półzwiezn dzrk do ziemników w trkcie prc polowych (w kinie ciągnik widoczny jet kierowc) Semi-upended potto plnter during field work (driver i viile in trctor c) temtyczny model ukłdu kierowc pojzd drog odel mtemtyczny pojzdu uwzględnijący dziłni kierowcy kłd ię z dwóch zdniczych części: modelu kierowcy orz modelu mego gregtu. '$

3 >\XejT_É} TZeXZTgh e_\vmxz!!! odel gregtu Dl gregtu jko podtwę przyjęto płki dwukołowy model pojzdu. Jet on częto wykorzytywny do opiu mochodu dl potrze ymulcji ukłdów utomtyki wpomgjących prcę kierowcy [PieniąŜek i in 000; Stevenon i in. 005]. Zotł zmodyfikowny przez dodnie trzeciego koł reprezentującego oś dzrki. Przedtwiono go n ry.. Ruchomy ukłd wpółrzędnych związny z gregtem, o początku w środku cięŝkości gregtu, oznczono SX Y ; O X Y to ruchomy ukłd związny z oią korytrz, po którym m poruzć ię gregt (oś O X jet kierown tycznie do oi korytrz, w tronę ruchu pojzdu; oś O Y reprezentuje normlną do oi korytrz punkcie O i przechodzi przez środek cięŝkości S gregtu). NleŜy zuwŝyć, Ŝe dzrk jet połączon z ciągnikiem tk, Ŝe tworzy z nim ukłd ztywny, nie dopuzczjący orotów dzrki względem ciągnik wokół oi Z protopdłej do płzczyzny O X Y modelu. Sdzrk wypoŝon jet w koł fortepinowe (ry. 3). Chrkteryzują ię one prktycznie zerowymi wpółczynnikmi odporności n poprzeczne znozenie (ez oporu dotoowują ię do kierunku ruchu wyznczonego przez koł ciągnik). Dltego w pierwzym przyliŝeniu przyjęto, Ŝe koł te mją wpływ tylko n połoŝenie środk cięŝkości gregtu, nie wpływją ntomit n pozotłe prmetry ruchu. Ry.. Fig.. Płki model gregtu ciągnik dzrk do ziemników D model of trctor potto plnter comintion '$,

4 GTWXhfm CTjÄjf^\ Przyjęto ntępujące oznczeni y liniowe odchylenie gregtu od oi korytrz. Ψ kąt orotu my reorownej gregtu Ψ kątowe odchylenie podłuŝnej oi mochodu od tycznej do oi korytrz v prędkość środk cięŝkości gregtu v y i v x rzuty prędkości punktu S n oś SY i SX ζ, ζ, ζ 3 oczne przemiezczeni przedniego i tylnego koł ciągnik orz koł dzrki γ, γ, γ 3 kąty znozeni przedniego i tylnego koł ciągnik orz koł dzrki θ średni kąt krętu koł kierownego F p, F t, F oczne rekcje n przedniej i tylnej oi ciągnik orz oi dzrki β i p = przełoŝenie ukłdu kierowniczego θ m gregtu moment ezwłdności gregtu względem oi pionowej przechodzącej przez środek cięŝkości c ξ i c ξ ztywności poprzeczne opon przedniej i tylnej oi i wpółczynniki odporności n poprzeczne znozenie koł przedniej i tylnej oi Równni więzów kinemtycznych gregtu dl przedtwionego n ry. płkiego modelu, z uwzględnieniem zmodyfikownej teorii iełdyz dotyczącej toczeni ię koł, przedtwiono poniŝej: Ry. 3. Fig. 3. Schemt koł dzrki Potto plnter wheel digrm '%#

5 >\XejT_É} TZeXZTgh e_\vmxz!!! '%$ Po doyć złoŝonych przekztłcenich i ztoowniu opertor plce otrzymujemy dw równni chrkterytyczne opiujące liniowe i kątowe odchylenie pojzdu w zleŝności od wrunków początkowych ruchu: odchylenie liniowe ( ) ( ) ( ) = v v A x x odchylenie kątowe ( ) ( ) ( ) = v v A x z Budow modelu kierowcy N ry. 4 przedtwiono powiązni między drogą, kierowcą i kierownym przez niego pojzdem. () () (3)

6 GTWXhfm CTjÄjf^\ y β POJAZD A () H Ψ DROGA EROWCA H() β POJAZD A () y - Ry. 4. Fig. 4. Uprozczony chemt powiązń elementów ukłdu drog kierowc pojzd z uwzględnieniem przęŝeni zwrotnego Simplified digrm of connection etween the element of rod driver vehicle et, tking into ccount feedck ąt orotu koł kierownicy β(t) i kąt odchyleni gregtu Ψ(t) orz przemiezczenie poprzeczne gregtu y z wrunkiem początkowym y = 0 ą określone przez ukłd równń β = H y H y y = A β A β (4) Ψ = A A H N podtwie powyŝzego ukłdu i gętości widmowych i wzjemnych gętości widmowe y y, β β, H H, β y, H y. zmierzonych ygnłów moŝn uzykć zleŝności określjące trnmitncję H. Jednk jej ezpośrednie wykorzytnie jet utrudnione ze względu n trudności z dokłdnym określeniem wrtości gętości widmowych proceów loowych. Niewielkie nwet łędy w określeniu funkcji trnmitncji H mogą powodowć, Ŝe wyniki otrzymywne z nlizownego modelu ędą itotnie róŝnić ię od zchowń ukłdu rzeczywitego. Podjęto próę znlezieni trnmitncji modelu kierowcy n podtwie minimlizcji energii n kole kierownicy. Zchownie kierowcy określono przez ntępujące czynniki: łędy oceny liniowych odchyleń mochodu od oi toru prc z mniejzymi łędmi wymg więkzego wyiłku, cz zwłoki τ prc z njmniejzym opóźnieniem tnowi wyiłek ndzwyczjny, intenywność ruchu powrotnego kierownicy i iły przykłdnej do koł kierownicy. '%%

7 >\XejT_É} TZeXZTgh e_\vmxz!!! Ottecznie, po uprozczenich, przyjęto funkcję trnmitncji kierowcy gdzie: τ T i τ H = k τ C i C k ( T ) ( T ) 0 3 ( C T T )( C T T ) cz rekcji kierowcy tłe czowe wpółczynniki tłumieni ukłdu wpółczynnik wzmocnieni zleŝny od prędkości jzdy (5) Stłe T, T, T3 zwęŝją odchyleni wielkości y, Ψ i β. Stł T0 dotyczy łędu oceny przez kierowcę odchyleni mochodu od oi zdnego toru. Przykłdowe wyniki ymulcji odel opiny powyŝej zotł oprogrmowny i uruchomiony z pomocą modułu Simulink środowik tl. Przeprowdzono oliczeni dl róŝnych wrtości prmetrów modelu (ry. 5). Wykzły one poprwne zchownie modelu i wrŝliwość n zminę wrtości prmetrów. Ry. 5. Fig. 5. Przemiezczeni poprzeczne środk cięŝkości gregtu dl róŝnych prędkości jzdy (km/h). Czrną linią zznczono plnowną trę gregtu Trnvere diplcement of the unit grvity centre for vriou driving peed (km/h). Blck line indicte plnned unit route '%&

8 GTWXhfm CTjÄjf^\ Ry. 6. Fig. 6. ąt nchyleni podłuŝnej oi gregtu dl róŝnych prędkości jzdy (km/h) podcz mnewru pokznego n ry. 5 nclintion ngle of the unit longitudinl xi for vriou driving peed (km/h) during the mnoeuvre hown on fig. 5 Podumownie. Przeprowdzone oliczeni tetowe wykzły wtępnie, Ŝe zproponowny model zgodnie z oczekiwnimi odwzorowuje kierowlność gregtu ciągnik dzrk do ziemników. Zdniem utor moŝe yć podtwą do dlzych dń i uściśleń.. ontynucj prcy polegć ędzie przede wzytkim n identyfikcji prmetrów modelu opiujących zchownie kierowcy orz włności gregtu. Szczególny ncik połoŝony ędzie n dni zjwik kontktu opongle. Biliogrfi ozi Z. Guzek Przegląd metod dń tteczności i kierowlności pojzdów mochodowych. Zezyt ntytutu Pojzdów nr (4) 995. PieniąŜek A., PieniąŜek W Bdni dynmiki poprzecznej jednośldowego modelu mochodu w ujęciu tochtycznym. teriły konferencyjne ONOT AUTOPROGRES 000. '%'

9 >\XejT_É} TZeXZTgh e_\vmxz!!! Stńczy T.., Jurecki R. S Budow i weryfikcj modelu kierowcy do nlizy ytucji przedwypdkowych. Wydwnictwo Politechniki rkowkiej 004. Stevenon B., Ridley P Automted Vehicle Stility Control for Articulted Vehicle ( STEERABTY OF A FAR UNT: TRACTOR - POTATO PANTER Summry Thi work preent preliminry concept for tking into ccount driver ctivity in trctor - griculturl mchine unit model. Thi unit run on n unhrdened, often wterlogged field with diverified urfce. n thi hrd terrin, the driver h to crry out very complicted mnoeuvre depending on field work chrcter. The model h een pplied to the unit: trctor - potto plnter. Semi-upended plnter i connected to the trctor vi ottom TUZ flexile connector. The Simulink module of the tl environment w employed to implement the model. ey word: modelling, driver, trctor griculturl mchine unit '%(