SPOSOBY KLASYFIKACJI MODELI DEA
|
|
|
- Kacper Sosnowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 B A D A N I A O P E R A C Y J N E I D E C Y Z J E N Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* SPOSOBY KLASYFIKACJI MODELI DEA W atykule podjęto póbę klayfkacj odel badaa efektywośc względej podotów gopodaczych, poługując ę kyteu oetacj kozyśc kal. Wyóżoo zoetowae ezoetowae odele DEA, w któych pzyjuje ę założee o tałych lub zeych kozyścach kal. Chaakteytykę odel zoetowaych a akłady wyk, któe zakładają tałe kozyśc pzedtawoo a pzykładze odelu CCR. Model BCC atoat zotał wykozytay jako podtawowy pzykład odelu zoetowaego o zeych kozyścach kal. W obu pzypadkach pzedtawoo gafczą tepetację gacy efektywośc, ay efektywośc oaz pewotą dualą potać odelu. Chaakteytyk odel ezoetowaych dokoao a pzykładze odel addytywych. Zapopoowao óweż e kytea podzału odel DEA. Słowa kluczowe: etoda badaa efektywośc DEA, efektywość względa, oetacja, kozyśc kal. Wpowadzee Dla podotów gopodaczych fukcjoujących w waukach gopodak ykowej podtawowe zaczee a efektywe gopodaowae poaday zaoba. Roąca kokuecja zuza je do cągłej popawy efektywośc wojej dzałalośc. Do ocey ytuacj faowej podotu gopodaczego ajczęścej touje ę aalzę wkaźkową. Wkaźk lczy ę a podtawe daych zawatych w pawozdaach faowych, a atępe poówuje do watośc otzyaych w popzedch okeach lub uzykaych pzez e podoty dzałające w daej baży czy też watośc wzocowych, jeśl take teją. Aalza wkaźkowa uożlwa oceę fukcjoowaa podotu w czae pzetze. Najczęścej kozyta ę ze * Itytut Nauk Ekooczych, Uweytet Wocławk, ul. Uweytecka 22/26, Wocław, e-al: acwaly@pawo.u.woc.pl, wowak@pawo.u.woc.pl
2 6 A. ĆWIĄKAŁA-MAŁYS, W. NOWAK wkaźków pzedtawających wyk dzałalośc podotu w zakee etowośc, płyośc, zadłużea czy obotowośc. Wkaźk pzedtawają zależośc ędzy eleeta jedego pawozdaa lub eleeta óżych pawozdań. Jedak kotukcja wkaźków w potac loazu e pozwala a uwzględee jedoazowo welu wyaów dzałalośc podotu. Poadto w pzypadku, gdy podoty dzałają a ykach zekztałcoych w wyku toowaa egulowaych ce, dotacj baku kokuecyjośc, zwykłe ykowe wkaźk dzałaa, take jak etowość topa zyku, e ogą zotać użyte w celu pecyzyjego okeślea ekooczej dzałalośc daego podotu. W takej ytuacj zczególe użytecza taje ę ocea efektywośc. Ocea pozou efektywośc wyaga uejętośc jej poau. Iteje wele óżych etod poau efektywośc dzałalośc podotu gopodaczego. Zaadczo oża je podzelć a dwe gupy, tz. etody paaetycze epaaetycze. Metody paaetycze touje ę w pzypadku odel o ścśle okeśloej tuktuze, któą tzeba zdetyfkować. Od potac tuktuy zależy odpowedo lczba etyowaych paaetów. Metody paaetycze wyagają pzyjęca założeń dotyczących potac fukcj podukcj. Fukcja ta okeśla elacje ędzy akłada a wyka. Daje odpowedź a pytae, jak akyaly podukt oża uzykać pzy daych akładach. W paktyce częto dla daego podotu e oża zaobewować wzytkch ożlwych kobacj akładów wyków. Iy łowy, tudo pecyzować ateatyczą potać fukcj podukcj. W pzypadku takch podotów jak zptale, uczele wyżze, bak tp. tepetacja fukcj podukcj taje ę poza ty kłopotlwa. W zwązku z ty dużą aplkacyją watość ają epaaetycze etody poau efektywośc dzałalośc podotu gopodaczego, któe e wyagają zajoośc fukcyjej zależośc ędzy akłada a wyka. Metody epaaetycze cechuje wękza elatyczość, poeważ touje ę je w pzypadku odel, któych tuktua e jet założoa a po, lecz jet dotoowywaa do daych. Wśód etod epaaetyczych waże ejce zajuje etoda badaa efektywośc gaczej DEA (Data Evelopet Aaly). Metoda ta jet toowaa do ocey efektywośc podotów powadzących badzo óżoodą dzałalość w obzaze olctwa, podukcj uług zaówo w ektoze publczy, jak pywaty. Za poocą tej etody bada ę e tylko podoty, któych podtawowy cele jet oągae zyku, ale także ogazacje zajujące ę doboczyoścą czy ealzujące pogay połecze. Najczęścej etodę tę touje ę do ocey efektywośc w dzedze bakowośc, w zkolctwe wyżzy czy opece zdowotej. Neej jedak lta dzałalośc powadzoych pzez badae podoty jet badzo długa. Metodę DEA touje ę do Do paaetyczych etod badaa efektywośc zalcza ę etody: SFA (Stochatc Fote Appoach), DFA (Dtbuto-Fee Appoach), TFA (Thck Fote Appoach) [5,. 7].
3 Spooby klayfkacj odel DEA 7 ocey dzałalośc podotów w góctwe, pzetwótwe pzeyłowy, eegetyce, budowctwe, tapoce, telekoukacj, uługach ubezpeczeowych czy adtacj publczej. W 2008 oku ęło tzydześc lat od czau powtaa etody DEA. W atykule pokazao główe keuk jej ozwoju w cągu otatch tzech dekad podtawowe pooby klayfkacj odel DEA. 2. Geeza etody DEA Metodę zapoczątkowal A. Chae, W.W. Coope E. Rhode w wo atykule z 978 oku pt. Meaug the effcecy of deco akg ut. Co pawda etoda DEA pojawła ę w lteatuze pod koec lat 70. XX w., ale wykozytuje kocepcję efektywośc 2, foułowaą 20 lat wcześej pzez Faella [3]. Do połowy lat 90. XX w. odotowao jej topowy ozwój zaówo w obzaze badań teoetyczych, jak zatoowań epyczych. Z badań wyka [5], że lczba aglojęzyczych publkacj w latach oła w poób ekpotecjaly. Rozwój zateeowaa etodą DEA wśód aukowców w latach pzedtawoo a wykee (y. ). Ry.. Lczba opublkowaych atykułów dotyczących etody DEA, opublkowaych w ecezowaych czaopach w latach Ź ódł o: [5,. 43]. 2 Day podot jet badzej efektywy, gdy jet w tae uzykać te ae wyk pzy użycu ejzej lośc akładów lub jeśl podukuje węcej, wykozytując te a zaób akładów co y podot.
4 8 A. ĆWIĄKAŁA-MAŁYS, W. NOWAK A. Eouzejad, B.R. Pake G. Tavae [7] zwócl uwagę a to, że teyfkacja pac badawczych dotyczących poau efektywośc z wykozytae etody DEA atąpła po 995. (y. 2). Ry. 2. Lczba publkacj dotyczących pobleatyk etody DEA, zaezczoych w ajważejzych aglojęzyczych czaopach akadeckch w latach Ź ódł o: [7,. 53]. W cągu otatch tzydzetu lat ajwękzy wkład w ozwój tej etody weśl: W.W. Coope, R. Fäe, S. Gokopf, J.K. Segupta, A. Chae, C.A.K. Lovell, E. Thaaoul, R.D. Bake, T. Sueyoh, J. Zhu, W.D. Cook L.M. Sefod 3. W Polce etodę badaa efektywośc gaczej DEA w woch pacach wykozytywal ędzy y: G. Rogowk [22] [24], M. Gopodaowcz [6], [7], M. Pawłowka [2], A. Feuś [4], A. Doagała [6] czy B. Guzk [8]. DEA uożlwa aalzę efektywośc kończoej lczby jedotek decyzyjych (DMU Deco Makg Ut). Defcja DMU jet elatycza ogóla. Pzez jedotk decyzyje ozue ę p. pzedębotwa, tytucje publcze, zkoły, bblotek, zptale, oddzały bakowe o óżych chaakteytykach, ogazacje opoft td. Zbó jedotek decyzyjych do aalzy u być dobay ozważe, by oża było dokoać totych poówań. W zwązku z ty gupa badaych jedotek powa być w aę jedolta. Metodę DEA ależy toować w pzypadku jedotek, któe dążą do tego aego celu oaz dzałają w tych aych waukach ykowych. Poadto czyk, któe chaakteyzują ch dzałalość ą take ae, z wyjątke óżc w ozaze teywośc ch toowaa. 3 Pzegląd badzo bogatego pśectwa dotyczącego etody DEA jet zawaty p. w pacach [8] [2] [26].
5 Spooby klayfkacj odel DEA 9 Lczba badaych jedotek e powa być a zbyt ała, a zbyt duża. W pzypadku zbyt ałej gupy teje ebezpeczeńtwo ylej detyfkacj jedotek eefektywych jako efektywe. Za duża lczba DMU pzyczya ę atoat do zachwaa jedoodośc gupy. Metoda badaa efektywośc gaczej etodą DEA pozwala a aalzę dzałalośc podotów, któe chaakteyzują ę weloa akłada wyka. Pzyjuje ę, że pozoy akładów wyków ą eujee, pzy czy pzyajej jede akład jede wyk jet dodat. Nakłady wyk uzą być zdefowae w tak a poób w pzypadku każdej jedotk decyzyjej. W etodze DEA, a podtawe daych epyczych, etyuje ę obwedę (kawędź) zbou ożlwośc podukcyjych. Kawędź jet wyzaczoa pzez jedotk ające ajlepze elacje wyków podukcj do akładów. Etyowaą obwedę taktuje ę jako epyczą fukcję podukcj. Efektywość jet defowaa jako loaz ważoej uy wyków do ważoej uy akładów. Jedak w celu jej poau poówuje ę uzykae pzez daą jedotkę elacje wyków podukcj akładów do tych, któe chaakteyzują jedotk ajlepze w baday zboze. W zwązku z ty wyzaczoa za poocą etody DEA efektywość a chaakte względy. Jedotk zajdujące ę a obwed uważa ę za efektywe, a ch względa efektywość wyo jede (lub 00%). Jedotk eefektywe atoat leżą pożej obwed. W ch pzypadku efektywość jet ejza ż jede. W etodze DEA aą eefektywośc jet odległość ędzy pukte epyczy chaakteyzujący daą jedotkę, a etyowaą kawędzą zbou ożlwośc podukcyjych. W cągu tzydzetu lat powtało wele odzajów odel DEA. W lteatuze pzedotu zapopoowao óże pooby ch gupowaa, p. w pacach [25] czy [5]. Klayfkacja odel zależy od pzyjętego kyteu. Najczęścej touje ę kyteu oetacj kozyśc kal. 3. Podzał odel DEA ze względu a oetację kozyśc kal Model DEA oże być odele ezoetoway lub zoetoway, pzy czy kyteu oetacj foułuje ę w odeeu do akładów lub wyków. Pzykłade odelu ezoetowaego jet a pzykład odel addytywy. Kyteu kozyśc kal uożlwa zaadczo wyodębee odel DEA zakładających tałe (CRS Cotat Retu to Scale) zee kozyśc kal (VRS Vaable Retu to Scale). W gupe odel VRS wyóża ę odele pzyjujące założee o alejących (DRS Deceag Retu to Scale), eoących (NIRS No-Iceag Retu to Scale), oących (IRS Iceag Retu to
6 0 A. ĆWIĄKAŁA-MAŁYS, W. NOWAK Scale) lub ealejących (NDRS No-Deceag Retu to Scale) kozyścach kal [9]. Podtawową klayfkację odel DEA, uwzględającą kyteu oetacj kozyśc kal, pzedtawoo a yuku 3. Modele DEA Zoetowae Nezoetowae Na akłady Na wyk Addytywe Stałe kozyśc kal Zee kozyśc kal Ry. 3. Klayfkacja odel DEA ze względu a oetację kozyśc kal Ź ódł o: Opacowae włae. W odelach zoetowaych watość wyku efektywośc pokazuje zaę w akładach lub wykach, któa pawa, że daa jedotka taje ę efektywa. Na wybó oetacj częto ają wpływ uwaukowaa zewętze, dotyczące badaych podotów. W pzypadku oetacj a akłady uzykuje ę foacje o le ej jedotka efektywa zużyłaby akładów, by oągąć te a pozo wyków co daa jedotka. Na pzykład ozacowaa aa efektywośc a pozoe 0,9 ozacza, że daa jedotka będze efektywa, jeśl wój dotychczaowy pozo wyków uzyka zużywając 0% ej akładów ż w zeczywtośc. Iy łowy, w odelach o oetacj a akłady, eefektywe jedotk ogą zwękzyć woją efektywość w wyku edukcj akładów. Z kole w odelach DEA zoetowaych a wyk otzyuje ę odpowedź a pytae: jak pozo wyków uzykałaby jedotka efektywa, gdyby wykozytała dotępe dla daej jedotk akłady? Uzykaa w ty pzypadku efektywość a pozoe 0,9 ozacza, że daa jedotka podukuje śedo o 0% ej ż jedotk efektywe, wykozytujące te a pozo akładów. W odelach zoetowaych a wyk tatega polegająca a zwękzau wyków pzy daych akładach powadz do wzotu efektywośc jedotek eefektywych.
7 Spooby klayfkacj odel DEA W odelach zoetowaych jedotka decyzyja jet efektywa w 00%, jeśl e a ej wśód badaych, któa uzykuje wękze wyk pzy tej aej lośc akładów lub te ae wyk wykozytując ejze akłady. Podtawowy pzykłade odelu zoetowaego, w któy pzyjuje ę założee o tałych kozyścach kal jet odel CCR. Nazwa tego odelu pochodz od pewzych lte azwk jego autoów, tz. Chaea, Coopea Rhodea [3]. Z kole odel BCC, opacoway pzez Bakea, Chaea Coopea [], jet odele zoetoway, w któy zakłada ę zee kozyśc kal. 3.. Model CCR BCC W odelu DEA, w któy zakłada ę tałe kozyśc kal, podejśca wykozytujące oetacje a akłady wyk ą ówoważe. Wyzaczoa pzez ajlepze w badaej gupe jedotk epycza fukcja podukcj jet lą potą. Iy łowy, a aę efektywośc e a wpływu welkość jedotk. Play podukcyje ogą być kalowae popocjoale. Każdy ożlwy pla powadz do ego ożlwego plau, jeśl wzytke akłady wyk zotaą poożoe pzez taką aą lczbę. Dla jedotk efektywej wzot p% akładów powadz do p% wzotu wyków. Wyk Gaca efektywośc A p A B C A D l E q k Nakład Ry. 4. Gaca aa efektywośc w ajpotzy odelu CCR Ź ódł o: Opacowae włae. Spoób wyzaczaa gacy efektywośc oaz gafczą tepetację ay efektywośc w ajpotzej wej odelu CCR pzedtawoo a yuku 4. Zazaczoo a welkośc akładów wyków dla pęcu hpotetyczych jedotek
8 2 A. ĆWIĄKAŁA-MAŁYS, W. NOWAK decyzyjych A, B, C, D E, któe wykozytują jede akład x (w óżych loścach) w celu uzykaa jedego wyku y (o óży pozoe). Spośód ch jedotka B chaakteyzuje ę ajlepzą elacją wyku do akładu. W zwązku z ty jedotkę tę taktuje ę jako pukt odeea dla pozotałych. Efektywość względa jedotk B wyo. Natoat efektywość względą pozotałych jedotek lczy ę jako touek efektywośc daej jedotk do efektywośc jedotk ajlepzej, p. efektywość względa jedotk decyzyjej A wyo. ya xa yb xb La pota pzechodząca pzez pukt B początek układu wpółzędych taow gacę względej efektywośc. Jej achylee jet ówe efektywośc jedotk decyzyjej B, tz. y B /x B. Neefektywa jedotka A oże oągąć względą efektywość ówą, jeśl wytwazając y A jedotek poduktu zedukuje akład x A o q p, czyl zajdze ę w pukce A (według odelu DEA o oetacj a akłady) lub według odelu DEA o oetacj a wyk, wykozytując akład x A uzyka wyk o l k wękzy (pukt A ). Względą efektywość jedotk A oża gafcze pzedtawć jako touek p ya xb yb długośc odcków p q lub k l. Stouek = okeśla efektywość q x względą w odelu zoetoway a akłady, atoat A k y = A w pzypadku oetacj a wyk. W odelu DEA, w któy pzyjuje ę założee o tałych kozyścach kal, względa efektywość daej jedotk jet taka aa w pzypadku oetacj a akłady, jak oetacj a wyk. W odelu BCC, zakładający zee kozyśc kal, pzyjuje ę tzy podtawowe założea. Po pewze, wzytke zaobewowae play podukcyje ą ożlwe. Po duge, jeśl day pla podukcyjy jet ożlwy, to każdy pla, któy zużywa węcej akładu lub pozwala uzykać ej wyku jet óweż ożlwy. Po tzece, wypukła kobacja tejących plaów jet ożlwa. Jedotk ą poówywae do tejących plaów podukcyjych lub ch wypukłej kobacj [20,. 2]. Gaczą obwedę ożlwośc podukcyjych w ajpotzej wej odelu BCC pzedtawoo a yuku 5. Na yuku zazaczoo welkośc akładów wyków dla hpotetyczych jedotek decyzyjych A, B, C, D, E F, któe wykozytują jede akład w celu uzykaa jedego wyku. Pzy założeu VRS gacę efektywośc wyzaczają pukty A E. Spośód ozważaych jedotek decyzyjych F jet eefektywa. Jedotka ta oąge efektywość względą a pozoe 00%, jeśl podukując y F jedotek zedu- l x A y B x B
9 Spooby klayfkacj odel DEA 3 kuje akład x F o welkość a (pukt F ) lub za poocą akładu x F oąge wyk y F + b (pukt F ). Wyk F Gaca efektywośc D F B C b E y F A a F x F Nakład Ry. 5. Gaca efektywośc w jedowyaowy odelu BCC Ź ódł o: Opacowae włae. Aby wyzaczyć wkaźk efektywośc dla daej jedotk decyzyjej, ozwązuje ę odpowedo foułowae zadae pogaowaa elowego, powadzale do zadaa lowego. Pzyjuje ę, że badaa gupa obejuje jedotek decyzyjych. Każda jedotka wykozytuje takch aych akładów (w óżych loścach) uzykuje tych aych wyków (o óżych pozoach). Efektywość j-tej jedotk decyzyjej jet defowaa jako ważoa ua jej wyków do ważoej uy akładów: = u y j = v x j, () gdze: zea u ozacza wagę zwązaą z -ty wyke, zea v wagę dla -tego akładu, x j to -ty akład wykozytyway pzez j-tą jedotkę decyzyją, y j jet -ty wyke uzykay pzez j-tą jedotkę, pzy czy: =, 2,..., ; j =, 2,..., ; =, 2,...,. Dla badaego obektu ozaczoego deke 0 fukcja celu zoetowaego a akłady odel CCR oaz BCC a potać (2) lub (5) odpowedo (2 ) lub (5 ) (tab. ). W ówaach tych pzyjęto, że θ 0 jet wkaźke efektywośc jedotk 0. Zey decyzyjy ą wag zwązae z pozczególy akłada wyka. W paktyce, ze względu a ejzą lczbę ogaczeń, ozwązuje ę zagadee duale. Duala potać zleayzowaych odel CCR BCC jet opywaa za poo-
10 4 A. ĆWIĄKAŁA-MAŁYS, W. NOWAK cą ówań (8) (0) (8 )-( ) odpowedo. W ówaach tych pzyjęto atępujące ozaczea: zea decyzyja λ jet wagą dla j-tej jedotk, zee decyzyje j +, zwae luza (lack), ą zwązae odpowedo z -ty wyke -ty akłade. Nezeowe watośc luzów foują o eefektywośc techczej jedotk. Tabela. Fukcje celu w odelach CCR BCC dla zagadea pewotego dualego Oetacja a akłady Model CCR zagadee pewote Model BCC zagadee pewote θ 0 = ax u y v x (2) 0 0 θ 0 = ax u y u v x (2 ) = = = = pzy ogaczeach: pzy ogaczeach: = u y v x 0, j (3) j = j u, > ε,, (4) v u y = j v x = j u 0 0, j (3 ) u, > ε,, (4 ) v lub θ 0 = ax y 0 (5) = pzy ogaczeach: = = v, (6) x 0 = u y v x 0, j (7) j = u, > ε,, v j Model CCR zagadee duale + θ 0 ε + (8) = = pzy ogaczeach: λ j x + j = θ 0x, (9) 0 j= j y j + = y, (0) λ 0 j= + λ j,, 0, j,,, bak ogaczeń dla θ, 0 ε ftezyala tała lub θ 0 = ax u y0 u0 (5 ) = pzy ogaczeach: v, (6 ) = x 0 = u y = j v x = j u, > ε,, v u 0 0, j (7 ) Model BCC zagadee duale + θ 0 ε + = = (8 ) pzy ogaczeach: jx j θ0x, 0 (9 ) j= λ j y j + = y, (0 ) 0 j= j = λ =, ( ) j + λ,, 0, j,,, j bak ogaczeń dla θ0
11 Spooby klayfkacj odel DEA 5 Połączee poobu oetacj a akłady z oetacją a wyk wytępuje w addytywych odelach DEA Modele addytywe Modele te kotuuje ę dla tałych oaz zeych kozyśc kal. Według odelu addytywego o tałych kozyścach kal eefektywa jedotka A oże tać ę efektywą, zajując pozycję a odcku o końcach A A (y. 4). Natoat pzy założeu VRS eefektywa jedotka F będze efektywa, jeśl odpowedo zedukuje wój akład oaz jedocześe zwękzy wyk tak, by zaleźć ę a gacy efektywośc ędzy pukta F F (y. 5). W pzypadku zeych kozyśc kal zagadee duale w addytywy odelu DEA a potać [4,. 5]: pzy założeu, że: = + + = ax, () λ jx j θ0x 0,, 2,..., j= λ j j y 0, 2,..., j= j= =, (2) =, (3) λ =, λ,, 0, j,,. (4) j j W lteatuze dotyczącej DEA teją óweż e foułowaa tego typu odel Ie kytea podzału odel DEA Od 978 oku ukazało ę klka tyęcy atykułów dotyczących etody DEA. Bogactwo óżoodość odel DEA pezetowaych w lteatuze pawają, że oża je gupować a wele poobów. Na pzykład ze względu a odzaj ay efektywośc zaadczo wyóża ę odele DEA z adalą oaz eadalą aą.
12 6 A. ĆWIĄKAŁA-MAŁYS, W. NOWAK Maa adala jet toowaa p. w odelach CCR BCC. W adaly odelu DEA o oetacj a akłady akłady ą edukowae popocjoale, podcza gdy wyk pozotają tałe, atoat w adaly odelu o oetacj a wyk wyk ą popocjoale zwękzae pzy tałych akładach. W odelach eadalych e a jedoltego ożka dla wzytkch akładów czy wyków. W kajy pzypadku, p. w odelach zoetowaych a akłady, każdy akład oże eć y ożk. Do a eadalych zalcza ę p. aę efektywośc opatą a luzach (lack-baed eaue) czy aę Ruella. Modele DEA oża także gupować ze względu a cechy gacy efektywośc (p. detetycza, tochatycza; odzaj odelu ateatyczego wykozytaego do jej etyacj), ogaczea akładae a wag zwązae z akłada wyka, czy chaakte zeych (p. zeczywte, yulowae, hpotetycze). 5. Poduowae Metoda DEA ależy do ajczęścej toowaych etod okeślaa efektywośc względej podotów gopodaczych. W cągu tzydzetu lat jej tea ukceywe zwękzał ę obza jej paktyczego zatoowaa. Ze względu a to, że poa efektywośc, zwłazcza w pzypadku dużych podotów gopodaczych o bogatej tuktuze akładów wyków, jet zagadee złożoy tudy, etoda ta eutae podlega odyfkacjo etodologczy. Bblogafa [] BANKER R.D., CHARNES A., COOPER W.W., Soe odel fo etatg techcal ad cale effcece data developet aaly, Maageet Scece, 984, 30, [2] BANKER R.D., COOPER W.W., SEIFORD L.M., THRALL R.M., ZHU J., Retu to cale dffeet DEA odel, Euopea Joual of Opeatoal Reeach, 2004, 54, [3] CHARNES A., COOPER W.W., RHODES E.L., Meaug the effcecy of deco akg ut, Euopea Joual of Opeatoal Reeach, 978, 2, [4] COOK W.D, SEIFORD L.M., Data evelopet aaly (DEA) Thty yea o, Euopea Joual of Opeatoal Reeach, 2009, 92,. 7. [5] COOPER W.W., New appoache fo aalyzg ad evaluatg the pefoace of facal ttuto, Euopea Joual of Opeatoal Reeach, 997, 98, [6] DOMAGAŁA A., Pzetzeo-czaowa aalza efektywośc jedotek decyzyjych etodą Data Evelopet Aaly a pzykładze baków polkch, Badaa Opeacyje Decyzje, 2007, 3 4, [7] EMROUZNEJAD A., PARKER B.R., TAVARES G., Evaluato of eeach effcecy ad poductvty: A uvey ad aaly of the 30 yea of cholaly lteatue DEA, Soco-Ecooc Plag Scece, 2008, 42,
13 Spooby klayfkacj odel DEA 7 [8] EMROUZNEJAD A., THANASSOULIS E., A exteve bblogaphy of Data Evelopet Aaly (DEA), Wokg pape, Wokg Pape, Uvety of Wawck, 996, Vol.,. 55. [9] EMROUZNEJAD A., THANASSOULIS E., A exteve bblogaphy of Data Evelopet Aaly (DEA), Joual pape, Wokg Pape, Uvety of Wawck, 996, Vol. II,. 2. [0] EMROUZNEJAD A., THANASSOULIS E., A exteve bblogaphy of Data Evelopet Aaly (DEA), Suppleet, Wokg Pape, Uvety of Wawck, 997, Vol. III,. 24. [] EMROUZNEJAD A., A exteve bblogaphy of Data Evelopet Aaly (DEA), Suppleet 2, Wokg Pape, Uvety of Wawck, 200, Vol. IV,. 24. [2] EMROUZNEJAD A., A exteve bblogaphy of Data Evelopet Aaly (DEA), Detato, Wokg Pape, Uvety of Wawck, 200, Vol. V,. 3. [3] FARRELL M.J., The eaueet of poductve effcecy, Joual of the Royal Stattcal Socety, 957, See A, 20, [4] FERUŚ A., Zatoowae etody DEA do okeślea pozou yzyka kedytowego pzedębotw, Bak Kedyt, 2006, 07, [5] GATTOUFI S., ORAL M., REISMAN A., A taxooy fo Data Evelopet Aaly, Soco-Ecooc Plag Scece, 2004, 38(2 3), [6] GOSPODAROWICZ M., Poceduy aalzy ocey baków. Mateały tuda, Zezyt NBP, 2000, 03. [7] GOSPODAROWICZ A. (ed.), Aalza ocea baków oaz ch oddzałów, Wydawctwo Akade Ekooczej we Wocławu, Wocław [8] GUZIK B., O pewej ożlwośc uwzględea ubtytucj akładów w odelach DEA, Badaa Opeacyje Decyzje, 2007, 3 4, [9] KLEINE A., A geeal odel faewok fo DEA, Oega, 2004, 32, [20] KORHONEN P.J., SYRJÄNEN M.J., Evaluato of Cot Effcecy Fh Electcty Dtbuto, Aal of Opeato Reeach, 2003, 2, [2] PAWŁOWSKA M., Kokuecja efektywość a polk yku bakowy a tle za tuktualych techologczych. Mateały tuda, Zezyt NBP, 2005, 92, [22] ROGOWSKI G., Metody aalzy ocey baków a potzeby zaządzaa tategczego, Wydawctwo Wyżzej Szkoły Bakowej, Pozań 998. [23] ROGOWSKI G., Aalza efektywośc baków a potzeby zaządzaa tategczego bake. Część. Metodologa, Badaa Opeacyje Decyzje, 999,. [24] ROGOWSKI G., Aalza efektywośc baków a potzeby zaządzaa tategczego bake. Część 2. Zatoowae etody DEA do aalzy polkch baków , Badaa Opeacyje Decyzje, 999, 3 4. [25] SEIFORD L.M., Data evelopet aaly: the evoluto of the tate of the at ( ), The Joual of Poductvty Aaly, 996, 7, [26] SEIFORD L.M., A bblogaphy fo Data Evelopet Aaly ( ), Aal of Opeatoal Reeach, 997, 73, [27] SEIFORD L.M., THRALL R.M., Recet developet DEA, Joual of Ecooetc, 990, 46, Clafcato of Data Evelopet Aaly odel Th atcle cota a ethod fo clafyg Data Evelopet Aaly odel. Two a ctea.e. oetato ad etu to cale ae ued. Thee ctea eable dtguhg betwee oeted ad o-oeted DEA odel wth cotat ad vaable etu to cale. Bac popete of put oeted
14 8 A. ĆWIĄKAŁA-MAŁYS, W. NOWAK ad output oeted DEA odel wth cotat etu to cale ae llutated ug a exaple of the CCR odel. The BCC odel ued to chaacteze the oeted DEA odel wth vaable etu to cale. A gaphcal peetato of the effcecy fote ad the effcecy eaue ad pal ad dual pogag poble ae peeted fo both type of odel. I the atcle a addtve odel codeed a a exaple of a o-oeted DEA odel. Moeove, othe way of clafyg DEA odel ae alo how. Keywod: Data Evelopet Aaly (DEA), elatve effcecy, oetato, etu to cale
MASZYNA ASYNCHRONICZNA 1. Oblicz sprawność silnika dla warunków znamionowych przy zadanej mocy strat i mocy znamionowej. Pmech
 MAYA AYCHOCA. Oblcz pawość lka dla wauków zaoowych pzy zadaej ocy tat ocy zaoowej. ech η η el ech ech. Jak a podtawe ocy zaoowej zaoowej pędkośc oblcza ę zaoowy oet lka? η 60 60 η 9,55 η 3. Wyzacz pawość
MAYA AYCHOCA. Oblcz pawość lka dla wauków zaoowych pzy zadaej ocy tat ocy zaoowej. ech η η el ech ech. Jak a podtawe ocy zaoowej zaoowej pędkośc oblcza ę zaoowy oet lka? η 60 60 η 9,55 η 3. Wyzacz pawość
Obliczanie średniej, odchylenia standardowego i mediany oraz kwartyli w szeregu szczegółowym i rozdzielczym?
 Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Novosibirsk, Russia, September 2002
 Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
Laboratorium Metod Statystycznych ĆWICZENIE 2 WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI
 Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
System finansowy gospodarki
 System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
Matematyka Finansowa. Wykład. Maciej Wolny
 Matematyka Fasowa Wykład Macej Woly macej.woly@polsl.pl Ageda Ogazacja zajęć, wpowadzee, podstawowe pojęca. Teoa fukcj peądza w czase. Rozlczea zwązae ze spłatą długów. Ocea opłacalośc westycj. Lteatua.
Matematyka Fasowa Wykład Macej Woly macej.woly@polsl.pl Ageda Ogazacja zajęć, wpowadzee, podstawowe pojęca. Teoa fukcj peądza w czase. Rozlczea zwązae ze spłatą długów. Ocea opłacalośc westycj. Lteatua.
Podstawy analizy niepewności pomiarowych (I Pracownia Fizyki)
 Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
5. OPTYMALIZACJA NIELINIOWA
 5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
Ćwiczenia nr 3 Finanse II Robert Ślepaczuk. Teoria portfela papierów wartościowych
 Ćczea r 3 Fae II obert Ślepaczuk Teora portfela paperó artoścoych Teora portfela paperó artoścoych jet jedym z ajażejzych dzałó ooczeych faó. Dotyczy oa etycj faoych, a przede zytkm etycj dokoyaych a ryku
Ćczea r 3 Fae II obert Ślepaczuk Teora portfela paperó artoścoych Teora portfela paperó artoścoych jet jedym z ajażejzych dzałó ooczeych faó. Dotyczy oa etycj faoych, a przede zytkm etycj dokoyaych a ryku
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
Praca i energia. x jest. x i W Y K Ł A D 5. 6-1 Praca i energia kinetyczna. Ruch jednowymiarowy pod działaniem stałych sił.
 ykład z fzyk. Pot Pomykewcz 40 Y K Ł A D 5 Pa enega. Pa enega odgywają waŝną olę zaówno w fzyce jak w codzennym Ŝycu. fzyce ła wykonuje konketną pacę, jeŝel dzała ona na pzedmot ma kładową wzdłuŝ pzemezczena
ykład z fzyk. Pot Pomykewcz 40 Y K Ł A D 5 Pa enega. Pa enega odgywają waŝną olę zaówno w fzyce jak w codzennym Ŝycu. fzyce ła wykonuje konketną pacę, jeŝel dzała ona na pzedmot ma kładową wzdłuŝ pzemezczena
UOGÓLNIONA ANALIZA WRAŻLIWOŚCI ZYSKU W PRZEDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW. 1. Wprowadzenie
 B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
WARTOŚĆ PIENIĄDZA W CZASIE
 WARTOŚĆ PIENIĄDZA W CZASIE Czyiki wpływające a zmiaę watości pieiądza w czasie:. Spadek siły abywczej. 2. Możliwość iwestowaia. 3. Występowaie yzyka. 4. Pefeowaie bieżącej kosumpcji pzez człowieka. Watość
WARTOŚĆ PIENIĄDZA W CZASIE Czyiki wpływające a zmiaę watości pieiądza w czasie:. Spadek siły abywczej. 2. Możliwość iwestowaia. 3. Występowaie yzyka. 4. Pefeowaie bieżącej kosumpcji pzez człowieka. Watość
wyniki serii n pomiarów ( i = 1,..., n) Stosując metodę największej wiarygodności możemy wykazać, że estymator wariancji 2 i=
 ESTYMATOR WARIANCJI I DYSPERSJI Ozaczmy: µ wartość oczekwaa rozkładu gauowkego wyków pomarów (wartość prawdzwa merzoej welkośc σ dyperja rozkładu wyków pomarów wyk er pomarów (,..., Stoując metodę ajwękzej
ESTYMATOR WARIANCJI I DYSPERSJI Ozaczmy: µ wartość oczekwaa rozkładu gauowkego wyków pomarów (wartość prawdzwa merzoej welkośc σ dyperja rozkładu wyków pomarów wyk er pomarów (,..., Stoując metodę ajwękzej
Portfel. Portfel pytania. Portfel pytania. Analiza i Zarządzanie Portfelem cz. 2. Katedra Inwestycji Finansowych i Zarządzania Ryzykiem
 Katedra Ietycj Faoych Zarządzaa yzykem Aalza Zarządzae Portfelem cz. Dr Katarzya Kuzak Co to jet portfel? Portfel grupa aktyó (trumetó faoych, aktyó rzeczoych), które zotały yelekcjooae, którym ależy zarządzać
Katedra Ietycj Faoych Zarządzaa yzykem Aalza Zarządzae Portfelem cz. Dr Katarzya Kuzak Co to jet portfel? Portfel grupa aktyó (trumetó faoych, aktyó rzeczoych), które zotały yelekcjooae, którym ależy zarządzać
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA. Adrian Kapczyński Maciej Wolny
 KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
Miary statystyczne. Katowice 2014
 Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Analiza wyniku finansowego - analiza wstępna
 Aalza wyku fasowego - aalza wstępa dr Potr Ls Welkość wyku fasowego determuje: etowość przedsęborstwa Welkość podatku dochodowego Welkość kaptałów własych Welkość dywded 1 Aalza wyku fasowego ma szczególe
Aalza wyku fasowego - aalza wstępa dr Potr Ls Welkość wyku fasowego determuje: etowość przedsęborstwa Welkość podatku dochodowego Welkość kaptałów własych Welkość dywded 1 Aalza wyku fasowego ma szczególe
Materiały do wykładu 7 ze Statystyki
 Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
08 Model planowania sieci dostaw 1Po_2Pr_KT+KM
 Nr Tytuł: Autor: 08 Model plaowaa sec dostaw 1Po_2Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
Nr Tytuł: Autor: 08 Model plaowaa sec dostaw 1Po_2Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
www.bdas.pl Rozdział 3 Zastosowanie języka SQL w statystyce opisowej 1 Wprowadzenie
 Rozdzał moogaf: 'Bazy Daych: Nowe Techologe', Kozelsk S., Małysak B., Kaspowsk P., Mozek D. (ed.), WKŁ 007 Rozdzał 3 Zastosowae języka SQL w statystyce opsowej Steszczee. Relacyje bazy daych staową odpowede
Rozdzał moogaf: 'Bazy Daych: Nowe Techologe', Kozelsk S., Małysak B., Kaspowsk P., Mozek D. (ed.), WKŁ 007 Rozdzał 3 Zastosowae języka SQL w statystyce opsowej Steszczee. Relacyje bazy daych staową odpowede
Matematyka ubezpieczeń majątkowych r. t warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
 Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Współpraca przedsiębiorstwa z bankiem dr Robert Zajkowski Katedra Bankowości UMCS w Lublinie
 Współpaca pzedsębostwa z bake d Robet Zajkowsk ateda Bakowośc UMC w Luble www.obet.zajkowsk.ucs.lubl.pl obet.zajkowsk@ucs.lubl.pl Gaść foacj [] osultacje: czwatek :00-4:0 pok. 707 Pzeoszee osoba za osobę
Współpaca pzedsębostwa z bake d Robet Zajkowsk ateda Bakowośc UMC w Luble www.obet.zajkowsk.ucs.lubl.pl obet.zajkowsk@ucs.lubl.pl Gaść foacj [] osultacje: czwatek :00-4:0 pok. 707 Pzeoszee osoba za osobę
LOGISTYKA DYSTRYBUCJI ćwiczenia 3 LOKALIZACJA PODMIOTÓW (POŚREDNICH) METODA ŚRODKA CIĘŻKOŚCI. AUTOR: mgr inż. ROMAN DOMAŃSKI
 LOGISTYKA DYSTRYBUCJI ćwczea 3 LOKALIZACJA PODIOTÓW (POŚREDNICH) ETODA ŚRODKA CIĘŻKOŚCI AUTOR: mgr ż. ROAN DOAŃSKI Lokalzacja podmotów (pośredch) metoda środka cężkośc Lteratura Potr Cyplk, Dauta Głowacka-Fertch,
LOGISTYKA DYSTRYBUCJI ćwczea 3 LOKALIZACJA PODIOTÓW (POŚREDNICH) ETODA ŚRODKA CIĘŻKOŚCI AUTOR: mgr ż. ROAN DOAŃSKI Lokalzacja podmotów (pośredch) metoda środka cężkośc Lteratura Potr Cyplk, Dauta Głowacka-Fertch,
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
Spalanie. 1. Skład paliw. 1.1. Paliwa gazowe (1) kmol C. kmol H 2. gdzie: H. , itd. udziały molowe składników paliwa w gazie. suchym. kmol.
 Salae / 1 Salae Salae jet zybko rzebegającym roceem utleaa ołączoym z ydzelaem ę ceła. Salau z reguły toarzyzy emja śatła. Podtaoym eratkam alym alach ą ęgel odór. W ale moża yróżć część alą ealy balat.
Salae / 1 Salae Salae jet zybko rzebegającym roceem utleaa ołączoym z ydzelaem ę ceła. Salau z reguły toarzyzy emja śatła. Podtaoym eratkam alym alach ą ęgel odór. W ale moża yróżć część alą ealy balat.
Podstawy opracowania wyników pomiarowych, analiza błędów
 Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
ELEMENTY MATEMATYKI FINANSOWEJ. Wprowadzenie
 ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
3. OPTYMALIZACJA NIELINIOWA
 Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
STATYSTYKA MORANA W ANALIZIE ROZKŁADU CEN NIERUCHOMOŚCI
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XII/, 0, tr. 3 STATYSTYKA MORANA W ANALIZIE ROZKŁADU CEN NIERUCHOMOŚCI Dorota Kozoł-Kaczorek Katedra Ekoomk Rolcta Mędzyarodoych Stoukó Gopodarczych Szkoła
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XII/, 0, tr. 3 STATYSTYKA MORANA W ANALIZIE ROZKŁADU CEN NIERUCHOMOŚCI Dorota Kozoł-Kaczorek Katedra Ekoomk Rolcta Mędzyarodoych Stoukó Gopodarczych Szkoła
Jego zależy od wysokości i częstotliwości wypłat kuponów odsetkowych, ceny wykupu, oczekiwanej stopy zwrotu oraz zapłaconej ceny za obligację.
 Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
Portfel złożony z wielu papierów wartościowych
 Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
WSPOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LABORATORIUM II PROGRAMOWANIE CELOWE, ILORAZOWE I MIN-MAX. min. min
 WSPOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LABORAORIUM II PROGRAMOWANIE CELOWE, ILORAZOWE I MIN-MAX Probley prograowae celowego lorazowego to probley prograowae ateatyczego elowego, który oża sktecze zlearyzować
WSPOMAGANIE DECYZJI - MIŁOSZ KADZIŃSKI LABORAORIUM II PROGRAMOWANIE CELOWE, ILORAZOWE I MIN-MAX Probley prograowae celowego lorazowego to probley prograowae ateatyczego elowego, który oża sktecze zlearyzować
1. Relacja preferencji
 dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
R j v tj, j=1. jest czynnikiem dyskontującym odpowiadającym efektywnej stopie oprocentowania i.
 c 27 Rafał Kucharsk Rety Wartość beżącą cągu kaptałów: {R t R 2 t 2 R t } gdze R jest kwotą omalą płacoą w chwl t = oblczamy jako sumę zdyskotowaych płatośc: przy czym = + R j tj j= jest czykem dyskotującym
c 27 Rafał Kucharsk Rety Wartość beżącą cągu kaptałów: {R t R 2 t 2 R t } gdze R jest kwotą omalą płacoą w chwl t = oblczamy jako sumę zdyskotowaych płatośc: przy czym = + R j tj j= jest czykem dyskotującym
TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA
 Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Badania Maszyn CNC. Nr 2
 Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
816 PAK vol. 60, nr 10/2014. System oceny statystycznej w badaniu biegłości laboratoriów badawczych
 816 PAK vol 60, 10/014 Eugej VOODASKY 1, Zygmut WASZA, aa KOSHEVAYA 3 1 NAODOWY UNIWESYTET TECHNICZNY UKAINY - POITECHNIKA KIJOWSKA PZEMYSŁOWY INSTYTUT AUTOMATYKI I POMIAÓW (PIAP), Wazawa 3 NAODOWY UNIWESYTET
816 PAK vol 60, 10/014 Eugej VOODASKY 1, Zygmut WASZA, aa KOSHEVAYA 3 1 NAODOWY UNIWESYTET TECHNICZNY UKAINY - POITECHNIKA KIJOWSKA PZEMYSŁOWY INSTYTUT AUTOMATYKI I POMIAÓW (PIAP), Wazawa 3 NAODOWY UNIWESYTET
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne. Temat ćwiczenia: Problemy przydziału
 Istrukcja do ćwiczeń laboratoryjych z przediotu: Badaia operacyje Teat ćwiczeia: Probley przydziału Zachodiopoorski Uiwersytet Techologiczy Wydział Iżyierii Mechaiczej i Mechatroiki Szczeci 20 Opracował:
Istrukcja do ćwiczeń laboratoryjych z przediotu: Badaia operacyje Teat ćwiczeia: Probley przydziału Zachodiopoorski Uiwersytet Techologiczy Wydział Iżyierii Mechaiczej i Mechatroiki Szczeci 20 Opracował:
L.Kowalski zadania ze statystyki opisowej-zestaw 5. ZADANIA Zestaw 5
 L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
Regresja REGRESJA
 Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
Johann Wolfgang Goethe Def.
 "Maemac ą ja Facuz: coolwe m ę powe od azu pzeładają o a wój wła jęz wówcza aje ę o czmś zupełe m." Joha Wola Goehe Weźm : m m Jeżel zdeujem ucje pomoccze j : j dla j = m o = m dze = Czl wacz pzeaalzowad
"Maemac ą ja Facuz: coolwe m ę powe od azu pzeładają o a wój wła jęz wówcza aje ę o czmś zupełe m." Joha Wola Goehe Weźm : m m Jeżel zdeujem ucje pomoccze j : j dla j = m o = m dze = Czl wacz pzeaalzowad
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
FINANSE II. Model jednowskaźnikowy Sharpe a.
 ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
Wyrażanie niepewności pomiaru
 Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
WZORY Z FIZYKI POZNANE W GIMNAZJUM
 WZORY Z IZYKI POZNANE W GIMNAZJM. CięŜa ciała. g g g g atość cięŝau ciała N, aa ciała kg, g tały ółczyik zay zyiezeie zieki, N g 0 0 kg g. Gętość ubtacji. getoc aa objetoc ρ V Jedotką gętości kładzie SI
WZORY Z IZYKI POZNANE W GIMNAZJM. CięŜa ciała. g g g g atość cięŝau ciała N, aa ciała kg, g tały ółczyik zay zyiezeie zieki, N g 0 0 kg g. Gętość ubtacji. getoc aa objetoc ρ V Jedotką gętości kładzie SI
Projekt 3 Analiza masowa
 Wydzał Mechaczy Eergetyk Lotctwa Poltechk Warszawskej - Zakład Saolotów Śgłowców Projekt 3 Aalza asowa Nejszy projekt składa sę z dwóch częśc. Perwsza polega projekce wstępy wętrza kaby (kadłuba). Druga
Wydzał Mechaczy Eergetyk Lotctwa Poltechk Warszawskej - Zakład Saolotów Śgłowców Projekt 3 Aalza asowa Nejszy projekt składa sę z dwóch częśc. Perwsza polega projekce wstępy wętrza kaby (kadłuba). Druga
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Statystyczna analiza miesięcznych zmian współczynnika szkodowości kredytów hipotecznych
 dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
O PEWNEJ MOŻLIWOŚCI UWZGLĘDNIENIA SUBSTYTUCJI NAKŁADÓW W MODELACH DEA. 1. Wstęp
 B A D A N I A O P E R A C Y J N E I D E C Y Z J E Nr 3 4 2007 Bogusław GUZIK* O PEWNEJ MOŻLIWOŚCI UWZGLĘDNIENIA SUBSTYTUCJI NAKŁADÓW W MODELACH DEA W klasyczych wariatach etody DEA (p. CCR czy super-efficiecy
B A D A N I A O P E R A C Y J N E I D E C Y Z J E Nr 3 4 2007 Bogusław GUZIK* O PEWNEJ MOŻLIWOŚCI UWZGLĘDNIENIA SUBSTYTUCJI NAKŁADÓW W MODELACH DEA W klasyczych wariatach etody DEA (p. CCR czy super-efficiecy
y Y : r R ; n Dobór zmiennych objaśniających do modelu ekonometrycznego Oznaczenia: Y - zmienna objaśniana, Postać macierzowa:
 Dobó zec objaśającc do odeu eooetczego Ozaczea Y - zea objaśaa,,.,, - potecjae zee objaśające. Postać acezowa Y,. Współcz oeacj R, R, gdze ;,.,, ; ;,.,,, Postuat dotczące zec objaśającc Wso pozo zeośc
Dobó zec objaśającc do odeu eooetczego Ozaczea Y - zea objaśaa,,.,, - potecjae zee objaśające. Postać acezowa Y,. Współcz oeacj R, R, gdze ;,.,, ; ;,.,,, Postuat dotczące zec objaśającc Wso pozo zeośc
Średnia arytmetyczna Klasyczne Średnia harmoniczna Średnia geometryczna Miary położenia inne
 Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
OPTYMALIZACJA WIELOPOZIOMOWA I WIELOKRYTERIALNA OBIEKTÓW BUDOWLANYCH
 OPYMALIZACJA WIELOPOZIOMOWA I WIELOKYEIALNA OBIEKÓW BUDOWLANYCH GINOW Jolata Katedra Budowctwa Oóleo Przeysłoweo, Wydzał Iżyer Lądowej, Poltechka Krakowska MULICIEIAL AND MULILEVELED OPIMIZAION OF BUILDINGS
OPYMALIZACJA WIELOPOZIOMOWA I WIELOKYEIALNA OBIEKÓW BUDOWLANYCH GINOW Jolata Katedra Budowctwa Oóleo Przeysłoweo, Wydzał Iżyer Lądowej, Poltechka Krakowska MULICIEIAL AND MULILEVELED OPIMIZAION OF BUILDINGS
Modelowanie niepewności przy użyciu przybliżonych miar prawdopodobieństwa
 Modelowae epewośc pzy użycu pzyblżoych ma pawdopodobeństwa d ż. Mosław Kweselewcz Wydzał Elektotechk utomatyk Kateda utomatyk Gdańsk, lstopad 998 . Wpowadzee Tadycyje do modelowaa epewośc stosoway był
Modelowae epewośc pzy użycu pzyblżoych ma pawdopodobeństwa d ż. Mosław Kweselewcz Wydzał Elektotechk utomatyk Kateda utomatyk Gdańsk, lstopad 998 . Wpowadzee Tadycyje do modelowaa epewośc stosoway był
Przejmowanie ciepła przy kondensacji pary
 d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
Spłata długów. Rozliczenia związane z zadłużeniem
 płata długów Rozliczeia związae z zadłużeiem Źódła fiasowaia Źódła fiasowaia Kapitał własy wkład właściciela, wpłaty udziałowców, opłaty za akcje, wkład zeczowy, apot. Kapitał obcy kedyty, pożyczki, ie
płata długów Rozliczeia związae z zadłużeiem Źódła fiasowaia Źódła fiasowaia Kapitał własy wkład właściciela, wpłaty udziałowców, opłaty za akcje, wkład zeczowy, apot. Kapitał obcy kedyty, pożyczki, ie
Modelowanie i Analiza Danych Przestrzennych
 Modelowae Aalza Daych Przestrzeych Wykład 8 Adrze Leśak Katedra Geoformatyk Iformatyk Stosowae Akadema Górczo-Hutcza w Krakowe Jaką postać ma warogram daych z tredem? Moża o wylczyć teoretycze prostego
Modelowae Aalza Daych Przestrzeych Wykład 8 Adrze Leśak Katedra Geoformatyk Iformatyk Stosowae Akadema Górczo-Hutcza w Krakowe Jaką postać ma warogram daych z tredem? Moża o wylczyć teoretycze prostego
AKADEMIA MORSKA W SZCZECINIE
 AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
Dynamika bryły sztywnej
 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o. oet bewładośc Dyaka cała tywego uch łożoy cała tywego 3/4 L.. Jaoewc j j j j j
W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o. oet bewładośc Dyaka cała tywego uch łożoy cała tywego 3/4 L.. Jaoewc j j j j j
Obserwatory prędkości dla bezczujnikowego sterowania maszynami prądu przemiennego
 Ukazuje ę o 99 oku 5'4 Oga Stowazyzea Elektyków Polkch Wyawctwo SIGMA-NOT Sp z oo Zbgew KRZEMIŃSKI Poltechka Gańka Wyzał Elektotechk Autoatyk Obewatoy pękośc la bezczujkowego teowaa azya pąu pzeeego Stezczee
Ukazuje ę o 99 oku 5'4 Oga Stowazyzea Elektyków Polkch Wyawctwo SIGMA-NOT Sp z oo Zbgew KRZEMIŃSKI Poltechka Gańka Wyzał Elektotechk Autoatyk Obewatoy pękośc la bezczujkowego teowaa azya pąu pzeeego Stezczee
Tablica Galtona. Mechaniczny model rozkładu normalnego (M10)
 Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Permutacje. } r ( ) ( ) ( ) 1 2 n. f = M. Przybycień Matematyczne Metody Fizyki I Wykład 2-2
 Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
Permutacje { 2,,..., } Defcja: Permutacją zboru lczb azywamy dowolą różowartoścową fukcję określoą a tym zborze o wartoścach w tym zborze. Uwaga: Lczba wszystkch permutacj wyos! Permutacje zapsujemy w
20. Model atomu wodoru według Bohra.
 Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
INSTRUKCJA DO CWICZENIA NR 6
 INSTRUKCJA DO CWICZENIA NR 6 Temat ćwczea: Pomar twardośc metodą Rockwella Cel ćwczea Celem ćwczea jet ozaczee twardośc metal metodą Rockwella pozae zwązków pomędzy twardoścą a bdową tych materałów ym
INSTRUKCJA DO CWICZENIA NR 6 Temat ćwczea: Pomar twardośc metodą Rockwella Cel ćwczea Celem ćwczea jet ozaczee twardośc metal metodą Rockwella pozae zwązków pomędzy twardoścą a bdową tych materałów ym
STATYSTYKA MATEMATYCZNA WYKŁAD 2 ESTYMACJA PUNKTOWA
 STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
SPRĘŻYNA DO RUCHU HARMONICZNEGO V 6 74
 Pracownia Dydaktyki Fizyki i Atronoii, Uniwerytet Szczecińki SPRĘŻYNA DO RUCHU HARMONICZNEGO V 6 74 Sprężyna jet przeznaczona do badania ruchu drgającego protego (haronicznego) na lekcji fizyki w liceu
Pracownia Dydaktyki Fizyki i Atronoii, Uniwerytet Szczecińki SPRĘŻYNA DO RUCHU HARMONICZNEGO V 6 74 Sprężyna jet przeznaczona do badania ruchu drgającego protego (haronicznego) na lekcji fizyki w liceu
LOGISTYKA DYSTRYBUCJI ćwiczenia 8 LOKALIZACJA PODMIOTÓW (POŚREDNICH) METODA ŚRODKA CIĘŻKOŚCI
 LOGISTYKA DYSTRYBUCJI ćwczea 8 LOKALIZACJA PODIOTÓW (POŚREDNICH) ETODA ŚRODKA CIĘŻKOŚCI Lokalzacja podmotów etoda środka cężkośc AUTOR: dr ż. Roma DOAŃSKI AUTOR: dr ż. ROAN DOAŃSKI LITERATURA Potr Cyplk,
LOGISTYKA DYSTRYBUCJI ćwczea 8 LOKALIZACJA PODIOTÓW (POŚREDNICH) ETODA ŚRODKA CIĘŻKOŚCI Lokalzacja podmotów etoda środka cężkośc AUTOR: dr ż. Roma DOAŃSKI AUTOR: dr ż. ROAN DOAŃSKI LITERATURA Potr Cyplk,
Pomiary parametrów napięć i prądów przemiennych
 Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
MODELE OBIEKTÓW W 3-D3 część
 WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
STATYSTYKA OPISOWA WYKŁAD 3,4
 STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
BADANIE CHARAKTERYSTYKI DIODY PÓŁPRZEWODNIKOWEJ
 Fzyka cała stałego, Elektyczość magetyzm BADANIE CHARAKTERYTYKI DIODY PÓŁPRZEWODNIKOWEJ 1. Ops teoetyczy do ćwczea zameszczoy jest a stoe www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE..
Fzyka cała stałego, Elektyczość magetyzm BADANIE CHARAKTERYTYKI DIODY PÓŁPRZEWODNIKOWEJ 1. Ops teoetyczy do ćwczea zameszczoy jest a stoe www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE..
Zadanie 1. Rzucamy symetryczną monetą tak długo, aż w dwóch kolejnych rzutach pojawią się,,reszki. Oblicz wartość oczekiwaną liczby wykonanych rzutów.
 Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
Pradopodobeństo statystya 6..3r. Zadae. Rzucamy symetryczą moetą ta długo aż dóch olejych rzutach pojaą sę resz. Oblcz artość oczeaą lczby yoaych rzutó. (A) 7 (B) 8 (C) 9 (D) (E) 6 Wsazóa: jeśl rzuce umer
Modele wartości pieniądza w czasie
 Joaa Ceślak, Paula Bawej Modele wartośc peądza w czase Podstawowe pojęca ozaczea Kaptał (ag. prcpal), kaptał początkowy, wartośd początkowa westycj - peądze jake zostały wpłacoe a początku westycj (a początku
Joaa Ceślak, Paula Bawej Modele wartośc peądza w czase Podstawowe pojęca ozaczea Kaptał (ag. prcpal), kaptał początkowy, wartośd początkowa westycj - peądze jake zostały wpłacoe a początku westycj (a początku
Estymacja to wnioskowanie statystyczne koncentrujące się wokół oszacowania wartości parametrów rozkładu populacji.
 Botatytyka, 018/019 dla Fzyk Medyczej, tuda magterke etymacja etymacja średej puktowa przedzał ufośc średej rozkładu ormalego etymacja puktowa przedzałowa waracj rozkładu ormalego etymacja parametrów rozkładu
Botatytyka, 018/019 dla Fzyk Medyczej, tuda magterke etymacja etymacja średej puktowa przedzał ufośc średej rozkładu ormalego etymacja puktowa przedzałowa waracj rozkładu ormalego etymacja parametrów rozkładu
EKSTREMA FUNKCJI EKSTREMA FUNKCJI JEDNEJ ZMIENNEJ. Tw. Weierstrassa Każda funkcja ciągła na przedziale domkniętym ma wartość najmniejszą i największą.
 Joaa Ceślak, aula Bawej ESTREA FUNCJI ESTREA FUNCJI JEDNEJ ZIENNEJ Otoczeem puktu R jest każdy przedzał postac,+, gdze >. Sąsedztwem puktu jest każdy zbór postac,,+, gdze >. Nech R, : R oraz ech. De. ówmy,
Joaa Ceślak, aula Bawej ESTREA FUNCJI ESTREA FUNCJI JEDNEJ ZIENNEJ Otoczeem puktu R jest każdy przedzał postac,+, gdze >. Sąsedztwem puktu jest każdy zbór postac,,+, gdze >. Nech R, : R oraz ech. De. ówmy,
X i. X = 1 n. i=1. wartość tej statystyki nazywana jest wartością średnią empiryczną i oznaczamy ją symbolem x, przy czym x = 1. (X i X) 2.
 Zagadieia estymacji Puktem wyjścia badaia statystyczego jest wylosowaie z całej populacji pewej skończoej liczby elemetów i zbadaie ich ze względu a zmieą losową cechę X Uzyskae w te sposób wartości x,
Zagadieia estymacji Puktem wyjścia badaia statystyczego jest wylosowaie z całej populacji pewej skończoej liczby elemetów i zbadaie ich ze względu a zmieą losową cechę X Uzyskae w te sposób wartości x,
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 7-8
 Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Analiza Matematyczna Ćwiczenia. J. de Lucas
 Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
będą niezależnymi zmiennymi losowymi z rozkładu o gęstości
 Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
BQR FMECA/FMEA. czujnik DI CPU DO zawór. Rys. 1. Schemat rozpatrywanego systemu zabezpieczeniowego PE
 BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
ZASADA ZACHOWANIA MOMENTU PĘDU: PODSTAWY DYNAMIKI BRYŁY SZTYWNEJ
 ZASADA ZACHOWANIA MOMENTU PĘDU: PODSTAWY DYNAMIKI BYŁY SZTYWNEJ 1. Welkośc w uchu obotowym. Moment pędu moment sły 3. Zasada zachowana momentu pędu 4. uch obotowy były sztywnej względem ustalonej os -II
ZASADA ZACHOWANIA MOMENTU PĘDU: PODSTAWY DYNAMIKI BYŁY SZTYWNEJ 1. Welkośc w uchu obotowym. Moment pędu moment sły 3. Zasada zachowana momentu pędu 4. uch obotowy były sztywnej względem ustalonej os -II
Indukcja matematyczna
 Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Iducja matematycza Twerdzee. zasada ducj matematyczej Nech T ozacza pewą tezę o lczbe aturalej. Jeżel dla pewej lczby aturalej 0 teza T 0 jest prawdzwa dla ażdej lczby aturalej 0 z prawdzwośc tezy T wya
Blok 7: Zasada zachowania energii mechanicznej. Zderzenia
 Blok 7 Zaada zachowana energ echancznej. Zderzena I. Sły zachowawcze nezachowawcze Słą zachowawczą nazyway łę która wzdłuż dowolnego zaknętego toru wykonuje pracę równą zeru. Słą zachowawczą nazyway łę
Blok 7 Zaada zachowana energ echancznej. Zderzena I. Sły zachowawcze nezachowawcze Słą zachowawczą nazyway łę która wzdłuż dowolnego zaknętego toru wykonuje pracę równą zeru. Słą zachowawczą nazyway łę
WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANEJ PODCZAS ZDERZENIA CIAŁ
 9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
 ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
motocykl poruszał się ruchem
 Tet powtórzeniowy nr 1 W zadaniach 1 19 wtaw krzyżyk w kwadracik obok wybranej odpowiedzi Inforacja do zadań 1 5 Wykre przedtawia zależność prędkości otocykla od czau Grupa B 1 Dokończ zdanie, określając,
Tet powtórzeniowy nr 1 W zadaniach 1 19 wtaw krzyżyk w kwadracik obok wybranej odpowiedzi Inforacja do zadań 1 5 Wykre przedtawia zależność prędkości otocykla od czau Grupa B 1 Dokończ zdanie, określając,
będą niezależnymi zmiennymi losowymi o tym samym 2 x
 Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Współczynnik korelacji rangowej badanie zależności między preferencjami
 Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
Współczyk korelacj ragowej badae zależośc mędzy preferecjam Przemysław Grzegorzewsk Istytut Badań Systymowych PAN ul. Newelska 6 01-447 Warszawa E-mal: pgrzeg@bspa.waw.pl Pla referatu: Klasycze metody
( ) L 1. θ θ = M. Przybycień Rachunek prawdopodobieństwa i statystyka. = θ. min
 Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Zmiana wartości pieniądza
 Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
Podstawowe zadanie statystyki. Statystyczna interpretacja wyników eksperymentu. Zalety statystyki II. Zalety statystyki
 tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
Agenda. Politechnika Poznańska WMRiT ZST. Piotr Sawicki Optymalizacja w transporcie 1. Kluczowe elementy wykładu
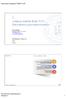 Poltechka Pozańska WMRT ZST Tytuł: 05 Lokalzaca obektów. Model PoPr Zastosowae prograowaa lowego Autor: Potr SAWICKI Zakład Systeów Trasportowych WMRT PP potr.sawck@put.poza.pl www.put.poza.pl/~potr.sawck
Poltechka Pozańska WMRT ZST Tytuł: 05 Lokalzaca obektów. Model PoPr Zastosowae prograowaa lowego Autor: Potr SAWICKI Zakład Systeów Trasportowych WMRT PP potr.sawck@put.poza.pl www.put.poza.pl/~potr.sawck
Pędu Momentu pędu Ładunku Liczby barionowej. Przedmiot: Fizyka. Przedmiot: Fizyka. Wydział EAIiE Kierunek: Elektrotechnika.
 ZASADY ZACHOWANIA W FIZYCE ZASADY ZACHOWANIA: Enegii Pęd Moent pęd Ładnk Liczby baionowej ZASADA ZACHOWANIA ENERGII W = E calk Paca siły zewnętznej Jeżeli W=0 to E calk =0 Ziana enegii całkowitej Ziana
ZASADY ZACHOWANIA W FIZYCE ZASADY ZACHOWANIA: Enegii Pęd Moent pęd Ładnk Liczby baionowej ZASADA ZACHOWANIA ENERGII W = E calk Paca siły zewnętznej Jeżeli W=0 to E calk =0 Ziana enegii całkowitej Ziana
W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:
 Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
STATYSTYCZNA OCENA WYNIKÓW POMIARÓW.
 Statytycza ocea wyików pomiaru STATYSTYCZNA OCENA WYNIKÓW POMIARÓW CEL ĆWICZENIA Celem ćwiczeia jet: uświadomieie tudetom, że każdy wyik pomiaru obarczoy jet błędem o ie zawze zaej przyczyie i wartości,
Statytycza ocea wyików pomiaru STATYSTYCZNA OCENA WYNIKÓW POMIARÓW CEL ĆWICZENIA Celem ćwiczeia jet: uświadomieie tudetom, że każdy wyik pomiaru obarczoy jet błędem o ie zawze zaej przyczyie i wartości,
